Revision as of 11:08, 5 July 2017

Subm: 25/04/2017

Accep.: 27/06/2017

Resumo

Apresenta-se a simulação numérica bidimensional do escoamento de água em um canal retangular com chicanas submersas distribuídas alternadamente nas suas margens. As equações governantes do escoamento são as equações de águas rasas, que serão resolvidas por meio do método do reticulado de Boltzmann (LBM) com múltiplos tempos de relaxamento (MRT). Utilizou-se condições de contorno adequadas para escoamento em canal, vazão e altura da água constante na entrada e saída, respectivamente. Devido às características do problema que pretende-se simular, incorporou-se ao código computacional uma técnica de simulação em grandes escalas (LES - Large Eddy Simulation) a qual permite obter resultados mais próximos do comportamento real do escoamento. Além disso, avalia-se a estabilidade da simulação em todos os pontos da malha para cada passo de tempo e, juntamente com a propriedade da consistência do LBM, obtém-se a convergência da solução. A simulação fornece a profundidade, velocidades nas direções ${\textstyle x}$ e ${\textstyle y}$, e a magnitude da vorticidade da água.

Palavras-chave: Método do reticulado de Boltzmann; equações de águas rasas; escoamento em canal; obstáculos submersos.

Summary

A two-dimensional numerical simulation of the water flow in a rectangular channel with submerged obstacles distributed alternately along its banks is presented. The governing equations of flow are the shallow water equations, which will be solved by the Boltzmann lattice method (LBM) with multiple relaxation times (MRT). The non-slip bounce-back scheme was used on walls and obstacles, constant discharge at the inlet and fixed depth at the outlet of the channel. Due to the characteristics of the problem to be simulated, a large eddy simulation (LES) technique was incorporated into the computational code, which allows to obtain results that are closer to the actual behavior of the flow. In addition, the stability of the simulation at all points of the mesh is evaluated for each step of time and, together with the property of the consistency of the LBM, the convergence of the solution is obtained. The simulation provides the depth, velocities in the x and y directions, and the magnitude of water vorticity.

1. Introdução

O Método do reticulado do Boltzmann é eficiente e mostra-se competitivo nas aplicações de mecânica dos fluidos computacional, sendo especialmente útil em aplicações com geometrias complexas [1]. Uma de suas principais características é a abordagem diferenciada quando comparado aos métodos numéricos tradicionais (volumes finitos [2], diferenças finitas [3], método das características [4], elementos finitos [5]), pois não utiliza discretizações nas equações macroscópicas governantes do escoamento [6]. O LBM considera o comportamento de um conjunto de partículas caracterizando-o como um método em mesoescala, possui equação governante caracterizada pelas etapas de transmissão e colisão, e pode ser visto como uma forma discretizada da equação cinética de Boltzmann em que somente são mantidos os detalhes moleculares essenciais para recuperar o comportamento macroscópico do escoamento.

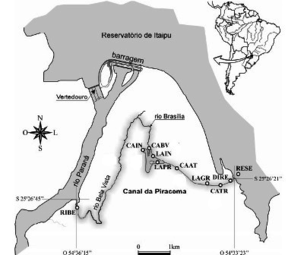
Derivadas do sistema de Navier-Stokes [7], as equações de águas rasas modelam escoamentos muito comuns na natureza e importantes, como por exemplo, canais, rios e estuários. Canais de navegação, de irrigação, de drenagem e canal da piracema, são exemplos de canais artificiais que ajudam no desenvolvimentos das cidades e da agricultura. Objeto de estudo deste trabalho, o canal da piracema, construído no parque da usina hidrelétrica de Itaipu, possui grande importância para a região. Pode-se perceber os benefícios que esta obra trouxe, permitindo que diversas espécies de peixes existentes na Costa Oeste do Estado, possam transpor a barragem da usina e, assim, voltam a utilizar sua antiga rota migratória para a desova [8].

Devido a natureza do problema de estudo deste trabalho e também ao fato que o operador BGK ser menos estável [9], optou-se por utilizar o método do reticulado de Boltzmann com múltiplos tempos de relaxamento (LBM-MRT). A capacidade do LBM-MRT foi testada em simulações de escoamento em canais abertos governados pelas equações de águas rasas e apresentaram resultados satisfatórios [10,6,1,11]. Além disso, incorporou-se o fenômeno da turbulência, por meio da abordagem LES e do modelo de Smagorinsky. De acordo com Zhou [7], a incorporação da turbulência fornece soluções mais próximas da situação real. Utilizou-se o reticulado quadrado ${\textstyle D2Q9}$, considerado uma boa opção para simulação em canais [12]. As condições de contorno Bounce-back para as paredes do canal, vazão e altura constantes na entrada e saída do canal, respectivamente, também são consideradas levando em conta as características do canal [13].

O estudo de caso abordado neste trabalho e simulado por meio do LBM, se ratifica por dois principais motivos. O primeiro deles está no fato de que o LBM-MRT é uma alternativa potencial para simular escoamento de água em canal, com fundo descontínuo, governado pelas equações de águas rasas. Com código de simples implementação e a possibilidade de utilizar computação paralela, o LBM mostra-se um método promissor na dinâmica de fluidos computacional, respeitando as suas restrições. O outro motivo está relacionado com a importância do canal da piracema, permitindo que diversas espécies de peixes possam retomar a rota migratória que utilizavam antes da construção da usina hidrelétrica. Além disso, a contribuição principal deste trabalho está no fato de que não exite na literatura simulação numérica bidimensional do problema proposto.

O trabalho está organizado conforme segue. Na seção 3 têm-se as equações governantes do escoamento. Em seguida, na seção 4 apresenta-se o método numérico que será usado na simulação do estudo de caso que é apresentado na seção 5. As simulações numéricas e discussões foram detalhadas na seção 7, e, em seguida, na seção 8, apresentam-se as conclusões.

2. Equações de águas rasas

Neste trabalho, têm-se um canal em que a água está em contato com a atmosfera e a profundidade da água é bem menor do que a largura do canal. Este escoamento é governado pelas equações de águas rasas (1) e são apresentadas aqui com a notação tensorial [7],

onde ${\textstyle t}$ é o tempo, ${\textstyle h}$ é a profundidade da água, ${\textstyle x_{j}}$ são as coordenadas espaciais ${\textstyle x}$ e ${\textstyle y}$, ${\textstyle u_{i}}$ são as componentes do vetor velocidade nas direções ${\textstyle x}$ e ${\textstyle y}$, isto é, ${\textstyle u}$ e ${\textstyle v}$, ${\textstyle g}$ é a aceleração da gravidade, ${\textstyle \nu }$ é a viscosidade cinemática e ${\textstyle {F_{i}}}$ é o termo de força dado por,

em que ${\textstyle {\partial {z_{b}}}/{\partial {x_{i}}}}$ é a declividade do fundo, ${\textstyle \rho }$ é a densidade e ${\textstyle \tau _{bi}}$ é a tensão de cisalhamento com o fundo do canal, definida por,

onde ${\textstyle C_{b}}$ é o coeficiente de atrito do leito do canal, que pode ser um valor constante ou estimado por ${\textstyle {C_{b}}=g/C_{z}^{2}}$, em que ${\textstyle C_{z}}$ é o coeficiente de Chezy.

3. Método do reticulado de Boltzmann

A equação do reticulado de Boltzmann (LBE) (4), com o operador de colisão BGK é,

onde ${\textstyle e={{\Delta x}{\mathord {\left/{{\Delta x}{\Delta t}}\right.}}{\Delta t}}}$ é a velocidade no reticulado, ${\textstyle \Delta x=\Delta y}$ é o espaçamento da malha, ${\textstyle \Delta t}$ é o incremento no tempo, ${\textstyle \displaystyle e_{\alpha }}$ são as direções de movimento das partículas, ${\textstyle f_{\alpha }}$ é a função distribuição de partículas, ${\textstyle F_{i}}$ é a componente da força na direção ${\textstyle i}$, ${\textstyle N_{\alpha }={\frac {1}{e^{2}}}\sum \limits {{e_{\alpha i}}{e_{\alpha i}}}}$ é uma constante estabelecida de acordo com o reticulado, ${\textstyle \tau }$ é o parâmetro de relaxamento e ${\textstyle f_{\alpha }^{eq}}$ é a função distribuição de equilíbrio.

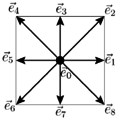
Utilizar-se-a o reticulado ${\textstyle D2Q9}$, conforme figura 1, cujas direções do movimento são [12,7],

Figure 1: Reticulado ${\displaystyle D2Q9}$

A função distribuição de equilíbrio (6) é determinada de forma que se recuperem as equações de águas rasas. Este processo é feito por meio da análise de Chapman-Enskog que conecta a LBE com as equações macroscópicas governantes [7,13],

As quantidades físicas de interesse, a profundidade (7) e a velocidade da água (8), são determinadas de forma a recuperar as equações de águas rasas,

e

Como o operador BGK é menos estável [9], optou-se por utilizar o MRT. Proposto por d'Humieres [14], O MRT captura as informações físicas do escoamento de forma mais completa e alcança estabilidade numérica de maneira mais eficiente do que o LBM-BGK. Foram Lallemand e Luo [15] que fizeram uma análise sobre a estabilidade do LBM-MRT, mostrando como melhorar o modelo de forma satisfatória. A principal mudança entre o LBM-BGK e o LBM-MRT está no operador de colisão. Migra-se do espaço de velocidades, utilizado do LBM-BGK, para o espaço dos momentos, no LBM-MRT [15]. A equação do reticulado de Boltzmann com múltiplos tempos de relaxamento é [1],

em que ${\textstyle M}$ é a matriz que transforma um vetor do espaço ${\textstyle {V}={R}^{i}}$ , gerado pelas velocidades discretas, em um vetor do espaço dos momentos ${\textstyle M=R}{^{i}}$, ${\textstyle M^{-1}}$ é a matriz inversa de ${\textstyle M}$, ${\textstyle {m_{i}{\alpha }}}$ são as funções de distribuição no espaço dos momentos, onde ${\textstyle \left|m\right\rangle =M\left|f\right\rangle }$ e ${\textstyle \left|.\right\rangle }$ é uma notação para vetor coluna, ${\textstyle m_{\alpha }^{eq}}$ são as funções de distribuição de equilíbrio no espaço dos momentos, onde ${\textstyle \left|{m^{eq}}\right\rangle =M\left|{f^{eq}}\right\rangle }$ e ${\textstyle {\widehat {S}}}$ é uma matriz diagonal ${\textstyle {\widehat {S}}=diag\left({{s_{0}},\,{s_{1}},\,...,\,{s_{{\alpha }-1}}}\right)}$, onde os seus valores são definidos de acordo com o problema estudado.

Pode-se separar a equação (9) nas etapas de colisão,

com ${\textstyle \alpha =1,...,\,M}$, e a propagação,

O termo de força em (10), ${\textstyle {\frac {\Delta t}{N_{\alpha }e^{2}}}e_{\alpha i}{F_{i}}\left({\bf {x}},t\right)}$ está sendo somado ao operador de colisão, ou seja, ele não faz parte do operador de colisão. Deste modo, o termo de força pode ser posicionado tanto somando juntamente com o operador de colisão, como na etapa de transmissão.

Considerando-se o reticulado ${\textstyle D2Q9}$, são escolhidos momentos para cada uma das 9 velocidades [15]. Estes momentos formam a matriz ${\textstyle M_{9\times {9}}}$ em (12), que é a matriz transformação do espaço das velocidades para o espaço dos momentos,

Assim, como ${\textstyle \left|m\right\rangle =M\left|f\right\rangle }$, pode-se caracterizar as funções distribuição de equilíbrio do espaço dos momentos (${\textstyle m_{\alpha }^{eq}}$) da seguinte forma,

Com relação a estabilidade linear do LBM, não é possível fazer sua caracterização completa [16], porém Zhou [7] estabelece indica algumas condições necessárias para se obter estabilidade na simulação. A respeito das condições para promover a estabilidade do LBM, um primeiro olhar deve ser dirigido para a viscosidade cinemática ${\textstyle \nu }$. Ela deve ser sempre positiva em problemas de escoamento envolvendo fenômenos de difusão. É uma propriedade do fluido e relaciona-se com o parâmetro de relaxamento, ${\textstyle \tau }$, presente no termo de colisão da LBE,

com ${\textstyle \tau >1/2}$ [16].

Deve-se garantir que a magnitude da velocidade física resultante do fluido é menor do que a velocidade no reticulado, conforme (15) [7]. O lado esquerdo de (15) é o denominado número de Courant [16],

e também registra-se a condição (16) para a celeridade,

onde ${\textstyle {\bf {u}}}$ é o vetor de velocidade física do fluido, ${\textstyle g}$ é a aceleração da gravidade e ${\textstyle h}$ é a altura da água.

Além das condições necessárias citadas acima, o LBM está limitado a fluxos de baixa velocidade e isto sugere que o LBM é adequado para escoamentos subcríticos de águas pouco profundas [7]. Desta forma impõe-se que,

As condições (15), (16) e (17) serão incorporadas ao código computacional e o teste será feito em todos os pontos da malha para cada passo de tempo, garantindo-se, deste forma, que a simulação seja estável.

Atualmente, a limitação (17) está em estudo, como pode ser visto nos trabalhos de Chopard, Pham e Lefèvre [17] e [18], onde o escoamento é supercrítico, e no trabalho de Rocca et al. [19], onde o escoamento é transcrítico. As pesquisas indicam o uso de um reticulado assimétrico para tornar possível a abordagem de problemas envolvendo escoamento supercrítico, pois são apropriados para descrever fluxos com grandes velocidades em uma direção, além disso, são necessários mais estudos para a aplicação em simulações bidimensionais [17].

Utiliza-se, com frequência, no LBM uma viscosidade mais elevada do que a viscosidade cinemática do fluido e os resultados estão em concordância com as simulações disponíveis na literatura [7,20,21,22,23]. A justificativa para esta abordagem, de acordo com Rocca, Adduce e Sciortino [21], é que o LBM é um modelo intrinsecamente viscoso e a viscosidade numérica pode ser adequadamente ajustada em concordância com os parâmetros da discretização, possibilitando evitar instabilidades numéricas. Em particular, Janben, Grilli e Krafczyk [22], simularam escoamento de água com viscosidade no LBM várias vezes mais elevada do que a viscosidade cinemática. Simulações foram feitas no mesmo problema, com o objetivo de manter a estabilidade e aproximar a viscosidade do LBM com a viscosidade cinemática. Observou-se que uma redução ainda maior na viscosidade no LBM não altera significativamente os resultados.

A incorporação do fenômeno da turbulência é realizada na equação governante do LBM-MRT (9), em que o parâmetro de relaxamento ${\textstyle \tau }$ é substituído pelo parâmetro de relaxamento total ${\textstyle \tau _{t}=\tau +\tau _{e}}$ (18), onde ${\textstyle \tau _{e}}$ é o parâmetro de relaxamento turbulento. Utilizou-se a simulação de grandes escalas (LES), por meio do modelo de Smagorinsky. É uma técnica que oferece resultados refinados e utiliza menos recursos computacionais. A incorporação da turbulência apresentou resultados satisfatórios em diversos trabalhos [7,13],

onde ${\textstyle C_{s}}$ é a constante de Smagorinsky escolhida de forma coerente com o problema e ${\textstyle {\Pi _{ij}}}$ faz parte do tensor taxa de deformação nas simulações em grandes escalas,

4. Estudo de caso

O problema que pretende-se simular é baseado no primeiro trecho do canal de alimentação em trincheira, conforme figura 2, com comprimento de ${\textstyle 30\,m}$ e largura de ${\textstyle 8\,m}$, o qual faz parte do sistema de transposição de peixes (canal da piracema) construído na usina hidrelétrica de Itaipu em 2002. Itaipu está localizada no rio Paraná, em um trecho de fronteira entre o Brasil e o Paraguai [24]. O canal de alimentação em trincheira está localizado entre o dique de regulagem e o lago das Grevilhas. O dique de regulagem atua junto com a estrutura de tomada da água e controlam a vazão que escoa pelo canal. O lago das Grevilhas é uma lagoa artificial construída como local de descanso para os peixes [8].

Figure 2: Canal da Piracema incluindo o rio Paraná, rio Bela Vista(RIBE), riacho Brasília, Canal de Deságüe do rio Bela Vista (CABV), Canal de Iniciação (CAIN), Lago Inferior (LAIN), Lago Principal (LAPR), Canal de Alimentação em Aterro (CAAT), Lago das Grevilhas (LAGR), Canal de Alimentação em Trincheiras (CATR), Dique de Regulagem (DIRE) e Reservatório (RESE).

As dimensões e parâmetros reais do trecho escolhido, podem ser vistos no relatório técnico elaborado por Muller e Gibertoni [25] e encontram-se listadas na tabela 1. As chicanas possuem as mesmas características do problema simulado, porém a altura real é igual a ${\textstyle 0,6\,m}$.

Devido a problemas de instabilidade numérica, ocasionada principalmente pelo número de Froude maior do que 1, escolheu-se a caracterização para o trecho de acordo com a Tabela 2.

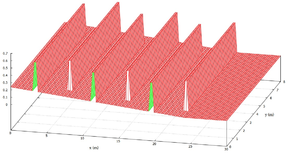
Cada chicana possui ${\textstyle 7\,m}$ de comprimento, largura da base igual a ${\textstyle 1\,m}$, largura do topo igual a ${\textstyle 0,5\,m}$ e altura igual a ${\textstyle 0,4\,m}$. Na figura 3 ilustra-se ver o trecho do canal da piracema que será simulado e na figura 4, tem-se a representação computacional para o fundo do canal.

Figure 3: Trecho do canal da piracema que será simulado.

Figure 4: Representação computacional para o fundo do trecho escolhido.

A ocorrência da piracema está condicionada às seguintes restrições: velocidades médias não superiores a ${\textstyle 3\,m/s}$ nas seções transversais ao longo do complexo do parque de barragem, profundidade da água superior a ${\textstyle 0,8\,m}$ e áreas molhadas nas seções transversais superiores a ${\textstyle 6\,m^{2}}$ (pode ser de ${\textstyle 4\,m^{2}}$ em trechos curtos). O não atendimento aos requisitos citados somente serão permitidos em trechos bastante curtos e em condições especiais, como por exemplo, sobre os obstáculos (chicanas) construídas ao longo do canal e nas aberturas das chicanas [25]. Simulações computacionais do escoamento unidimensional realizadas por Muller e Gibertoni [25], concluíram que nas proximidades das chicanas ocorre a diminuição da profundidade da água acompanhada de um aumento de velocidade e no trecho onde o canal não apresenta obstáculo, o fluxo tende a voltar a condição anterior acontecendo um aumento de profundidade e consequentemente diminuição de velocidade. Além disso, a vazão ideal no canal é de ${\textstyle Q=11,5\,m^{3}/s}$.

5. Algoritmo para o LBM-MRT

O algoritmo para o programa desenvolvido com base no LBM-MRT possui todas as etapas do algoritmo para o LBM-BGK. Porém, são necessárias mais etapas no LBM-MRT, pois o operador de colisão MRT necessita de mais cálculos. Portanto, a principal diferença entre os dois algoritmos está na abordagem do operador de colisão.

Na equação governante do LBM-BGK (4), tanto no lado esquerdo como no direito, têm-se a mesma função distribuição de partículas ${\textstyle f_{\alpha }}$, isto porque todo o processo de simulação do LBM-BGK ocorre no espaço das velocidades. Observando-se agora a equação governante do LBM-MRT (9), percebe-se que as funções (${\textstyle {m_{\alpha }}}$ e ${\textstyle m_{\alpha }^{eq}}$) que compõem o termo de colisão não são as mesmas que estão do lado esquerdo. Isto ocorre pelo fato de que ${\textstyle {m_{\alpha }}}$ e ${\textstyle m_{\alpha }^{eq}}$ são funções distribuição que estão no espaço dos momentos.

A transformação do espaço de velocidades para o espaço dos momentos é feita por meio da matriz ${\textstyle M}$ apresentada em (12). Além disso, pode-se proceder com a obtenção de funções que estão no espaço de velocidades a partir das funções que estão no espaço dos momentos e isto pode feito conforme apresentado na seção 4 e que será descrito a seguir com mais detalhes,

• Escrever a função distribuição de partículas, que está no espaço de velocidades, no espaço dos momentos: ${\textstyle \left|m\right\rangle =M\left|f\right\rangle }$;

• Escrever a função distribuição de equilíbrio, que está no espaço de velocidades, no espaço dos momentos: ${\textstyle \left|{m^{eq}}\right\rangle =M\left|{f^{eq}}\right\rangle }$;

• Escrever a função distribuição de partículas, que está no espaço dos momentos, no espaço gerado pelas velocidades: ${\textstyle \left|f\right\rangle ={M^{-1}}\left|m\right\rangle }$;

• Escrever a função distribuição de equilíbrio, que está no espaço dos momentos, no espaço gerado pelas velocidades: ${\textstyle \left|f^{eq}\right\rangle ={M^{-1}}\left|{m^{eq}}\right\rangle }$
  

Portanto, somente o operador de colisão do LBM-MRT opera no espaço dos momentos. Neste sentido, observa-se que na etapa do operador de colisão, o código recebe ${\textstyle f_{\alpha }}$ e ${\textstyle f_{\alpha }^{eq}}$, mas precisa transformá-las em ${\textstyle {m_{\alpha }}}$ e ${\textstyle m_{\alpha }^{eq}}$. Procedimento análogo acorre na saída do operador de colisão, têm-se ${\textstyle {m_{\alpha }}}$ e ${\textstyle m_{\alpha }^{eq}}$ e é necessário obter ${\textstyle f_{\alpha }}$ e ${\textstyle f_{\alpha }^{eq}}$.

O algoritmo para o programa desenvolvido utilizando o LBM-MRT é fornecido a seguir:

1. Escolha o reticulado. Identifique o tamanho da malha, o passo de temporal e o espacial. Estabeleça o valor para a constante de Smagorinsky, valor inicial para o parâmetro de relaxamento, valores da matriz diagonal ${\textstyle {\widehat {S}}}$ e caracterize a geometria do canal.
2. Inicialização (${\textstyle t=0}$):
• Inicializa-se o valor da velocidade macroscópica nas direções ${\textstyle x}$ e ${\textstyle y}$, ${\textstyle u\left({x,y,0}\right)}$ e ${\textstyle v\left({x,y,0}\right)}$, respectivamente;
• Inicializa-se o valor da profundidade da água ${\textstyle h\left({x,y,0}\right)}$;
• Calcular ${\textstyle f_{\alpha }^{eq}}$, utilizando ${\textstyle h\left({x,y,0}\right)}$, ${\textstyle u\left({x,y,0}\right)}$ e ${\textstyle v\left({x,y,0}\right)}$, por meio de (6);
• Inicializar ${\textstyle {f_{\alpha }}\left({\displaystyle x,0}\right)}$ utilizando ${\textstyle f_{\alpha }^{eq}\left({h,u,v}\right)}$, ou seja ${\textstyle {f_{\alpha }}\left({\displaystyle x,0}\right)=f_{\alpha }^{eq}\left({h,u,v}\right)}$.
3. Loop principal (${\textstyle t=1}$ até ${\textstyle t_{max}}$):
• Informar quais condições de contorno serão utilizadas e incorporar no código;
• Atualizar as variáveis macroscópicas, profundidade e velocidades nas direções ${\textstyle x}$ e ${\textstyle y}$, utilizando (7) e (8), respectivamente. Além disso, atualiza-se o parâmetro de relaxamento total por meio de (18);
• Calcular ${\textstyle m_{\alpha }^{eq}}$ utilizando (13);
• Cálculo do termo de força utilizando (2);
• Cálculo da colisão usando a expressão (10). Neste momento ocorrem todas as etapas de transformação descritas nesta seção;
• Cálculo da propagação usando (11);
• Verificar as condições de estabilidade descritas em (15), (16) e (17);
• calcular o erro relativo entre a simulação no tempo atual e no tempo anterior.
• Escrever os resultados.
4. Plotar os resultados.

6. Resultados e Discussões

6.1 Etapa I: Validação do modelo

Antes de avaliar o problema proposto, procede-se com a validação do modelo desenvolvido por meio da simulação numérica do escoamento de água ao redor de um cilindro, localizado perpendicularmente ao fundo e no centro do canal. Este problema clássico da Engenharia Hidráulica é bastante utilizado na validação de simulações numéricas. Em Yulistiyanto [26] encontra-se a comparação entre a solução numérica, por meio de diferenças finitas, e os dados experimentais. Em 2004, Zhou [7] refez esta simulação utilizando o LBM com um tempo de relaxamento. Os parâmetros utilizados são encontrados em Yulistiyanto [26], possibilitando a comparação com os dados experimentais. O comprimento do canal é ${\textstyle L_{x}=4\,m}$, a largura é ${\textstyle L_{y}=2\,m}$, a vazão na entrada é ${\textstyle Q=0,248\,m^{3}/s}$, a altura da água na saída é ${\textstyle h=0,185\,m}$, a inclinação do fundo do canal é ${\textstyle {{\partial {z_{b}}}{\mathord {\left/{{\partial {z_{b}}}{\partial x}}\right.}}{\partial x}}=-6,25\times {10^{-4}}}$ na direção do escoamento. O coeficiente de Manning é ${\textstyle n_{b}=0,012\,m/s^{1/3}}$. A constante de Smagorinsky escolhida é ${\textstyle C_{s}=0,3}$ [7], ${\textstyle {s_{0}}=...={s_{6}}=1,0}$ e ${\textstyle {s_{7}}={s_{8}}={1{\mathord {\left/{1\tau }\right.}}\tau _{t}}}$ [1]. A simulação foi realizada utilizando-se passo espacial ${\textstyle \Delta x=\Delta y=0,035\,m}$ , o temporal ${\textstyle \Delta t=0,007\,m}$ e o parâmetro de relaxamento, ${\textstyle \tau =0,60}$. Com relação as condições de contorno, nas paredes do cilindro, é conveniente utilizar a condição de contorno bounce-back para representar velocidade nula e nas paredes do canal utilizou-se condição de escorregamento. Na entrada do canal utilizou-se vazão constante. Na saída do canal têm-se altura fixa [7,13]. O número de iterações realizadas foi de 40000, o que corresponde a um tempo de 280 segundos de medição. Utilizou-se o compilador GNU Fortran 5.3.0 em um computador com processador intel i7, CPU 2,2 GHz, 16 GB de memória RAM e sistema operacional 64-bit Windows 10. O tempo de processamento gasto foi de 298 segundos.

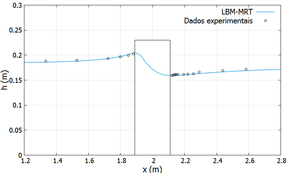
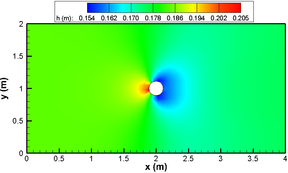
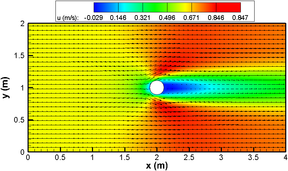
Na figura 5, tem-se o perfil da profundidade da água no meio do canal e na direção do escoamento com o parâmetro de relaxamento ${\textstyle \tau =0,60}$, e os dados experimentais. O erro relativo na simulação é menor do que ${\textstyle 1\%}$ no decorrer de todo o canal. Na figura 6, é possível observar que a profundidade da água aumenta ao se aproximar do cilindro, diminui nas laterais e atinge seu valor mínimo logo depois do cilindro. Tem-se na figura 7 a velocidade da água na direção do escoamento, nota-se que ela aumenta nas laterias do cilidro e atinge o valor mínimo logo depois do cilindro.

Figure 5: Perfil da profundidade da água no centro do canal e na direção do escoamento.

Figure 6: Solução numérica para a profundidade da água.

Figure 7: Solução numérica para a velocidade da água na direção ${\displaystyle u}$.

Observa-se a ótima concordância entre a simulação e os dados experimentais, demonstrando a capacidade, eficiência e precisão do modelo desenvolvido. Procede-se então, na simulação do problema principal, descrito na seção 5, onde será usado o mesmo modelo desenvolvido. Devido às instabilidades numéricas ocasionadas principalmente pelo número de Froude ser maior do que um, não foi possível utilizar todos os dados reais na simulação e deste modo, os parâmetros foram escolhidos de forma mais próxima possível ao modelo real, de modo a obter estabilidade numérica. Conforme apresentado anteriormente, mais estudos são necessários para simular escoamentos bidimensionais supercríticos no LBM.

6.2 Etapa II: Simulação do estudo de caso proposto

Os parâmetros reais do problema proposto na seção 5 são, o comprimento do canal é ${\textstyle L_{x}=30\,m}$, a largura do canal é ${\textstyle L_{y}=8\,m}$, a altura inicial da água é ${\textstyle h_{0}=1,17\,m}$, a velocidade inicial na direção ${\textstyle x}$ é ${\textstyle u_{0}=1,2\,m/s}$ e a velocidade inicial na direção ${\textstyle y}$ é ${\textstyle v_{0}=0,0\,m/s}$.

Nesta simulação, os parâmetros utilizados são, o comprimento do canal é ${\textstyle L_{x}=30\,m}$, a largura do canal é ${\textstyle L_{y}=8\,m}$, a altura inicial da água é ${\textstyle h_{0}=1,40\,m}$, a velocidade inicial na direção ${\textstyle x}$ é ${\textstyle u_{0}=1,0\,m/s}$, a velocidade inicial na direção ${\textstyle y}$ é ${\textstyle v_{0}=0,0\,m/s}$ e o parâmetro de relaxamento é ${\textstyle \tau =1.1}$. Os parâmetros foram escolhidos de forma mais próxima possível ao modelo real. O parâmetros de relaxamento foi escolhido o mais próximo possível do valor mínimo limite, que é ${\textstyle \tau >0,5}$, de forma que a simulação retorne resultado estáveis. A constante de Smagorinsky escolhida é ${\textstyle C_{s}=0,3}$ [27], ${\textstyle {s_{0}}=...={s_{6}}=1,0}$ e ${\textstyle {s_{7}}={s_{8}}={1{\mathord {\left/{1\tau }\right.}}\tau }}$ [1].

Com relação as condições de contorno, nas paredes do canal e nas chicanas, é conveniente utilizar a condição de contorno bounce-back para representar velocidade nula [7,13]. Na entrada do canal utilizou-se vazão constante. Na saída do canal tem-se altura constante. Além disso, é necessário um tratamento para cada um dos quatro pontos localizados nos cantos da malha. Estas configurações podem ser vistas em Liu [13].

Foram feitas simulações conforme apresentadas na tabela 3, porém os resultados apresentados nas próximas figuras são para o caso em que a velocidade no reticulado é de ${\textstyle e=5,7\,m/s}$, o espaçamento na malha é ${\textstyle \Delta x=\Delta y=0,04\,m}$ e o passo de tempo ${\textstyle \Delta t=0,007\,s}$. O número de iterações realizadas foi de ${\textstyle 50000}$, o que corresponde a um tempo de ${\textstyle 350}$ segundos de medição. Utilizou-se o compilador GNU Fortran 5.3.0 em um computador com processador intel i7, CPU 2,2 GHz, 16 GB de memória RAM e sistema operacional 64-bit Windows 10. O tempo de processamento gasto no processamento foi de ${\textstyle 8988}$ segundos.

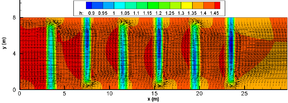
A figura 8 apresenta a profundidade da água ao longo do canal. Nota-se que a restrição de altura mínima ${\textstyle 0,80\,m}$ foi satisfeita. Verifica-se também que, ao se aproximar da chicana, a profundidade da água aumenta. Ligeiramente depois da chicana, a profundidade diminui. Em cima da chicana a lamina de água é menor do que no restante do canal. Além disso, observa-se que na abertura da chicana, a profundidade diminui e torna a subir quando se aproxima da próxima chicana.

Figure 8: Profundidade da água no canal com chicanas.

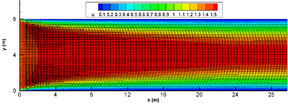
Nota-se que na figura 9, somente nos pontos em cima e na abertura das chicanas, a velocidade na direção ${\textstyle x}$ atinge seu ponto máximo. Esta previsão é feita no trabalho de Muller e Gibertoni [25]. Na maioria dos pontos do canal a velocidade é menor do que ${\textstyle 1,2\,m/s}$. Este resultado mostra que, de fato, as chicanas exercem seu papel de conter a velocidade da água. Verifica-se também que, a velocidade máxima é menor do que ${\textstyle 3\,m/s}$, que é a velocidade máxima permitida para a ocorrência da piracema. Esta velocidade só pode ser excedida, na abertura ou em cima da chicana [25]. A figura 10 mostra que, utilizando os mesmos parâmetros de simulação, porém sem as chicanas, a velocidade na direção ${\textstyle x}$, é máxima em uma grande região do canal. A comparação entre as figura 9 e 10, ratifica a importância das chicanas.

Figure 9: Velocidade da água na direção ${\displaystyle x}$ no canal com chicana.

Figure 10: Velocidade da água na direção ${\displaystyle x}$ no canal sem chicana.

Tem-se também, a velocidade da água na direção ${\textstyle y}$, conforme figura 11. Observa-se a simetria da simulação e percebe-se que nas aberturas das chicanas, a velocidade é mais representativa. Na figura 12, os vórtices acorrem com maior intensidade nas paredes do canal próximo da abertura das chicanas.

Figure 11: Velocidade da água na direção ${\displaystyle y}$ no canal com chicana.

Figure 12: Magnitude dos vórtices no canal com chicana.

7. Conclusão

Considerando que o estudo de caso apresentado neste trabalho é um escoamento complexo, os resultados apresentados mostram a capacidade e a precisão do LBM na simulação de escoamento em canais com obstáculos submersos, governados pelas equações de águas rasas. Observa-se que a simulação cumpriu as condições para a ocorrência da piracema descritas na seção 5, ou seja, as velocidades não ultrapassaram ${\textstyle 3\,m/s}$ nas seções transversais ao longo do trecho analisado, a profundidade da água é superior a ${\textstyle 0,8\,m}$ e áreas molhadas nas seções transversais superiores a ${\textstyle 6\,m^{2}}$. Além disso, conforme mencionado na seção 5, ao se aproximar da chicana, a profundidade da água aumenta. Em cima da chicana e na abertura da chicana, a profundidade diminui e a velocidade aumenta. Nota-se também que a profundidade da água logo depois da chicana é menor que antes da chicana. Este processo se repete ao longo do trecho analisado. Outro ponto interessante é que o LBM-MRT foi capaz de confirmar que as chicanas exercem o papel de reduzir a velocidade da água.

O modelo de Smagorinsky e o MRT permitiram a diminuição do parâmetro de relaxamento e consequentemente, os resultados descrevem a situação física de forma mais realista. Sem esta implementação, utilizando o LBM-BGK, o valor mínimo alcançado para o parâmetro de relaxamento foi ${\textstyle 1,5}$, enquanto que no LBM-MRT ${\textstyle \tau =1,1}$. Além disso, a presença no código da rotina de estabilidade trouxe, juntamente com a consistência do método, a garantia da convergência da solução numérica. Observou-se que o erro relativo é maior apenas nos dois cantos da entrada do canal. Mesmo com o tratamento aplicado nestes pontos, o erro relativo nesta região é ${\textstyle 10}$ vezes maior do que o erro ao longo do canal. Pretende-se desenvolver mais estudos e melhor abordar a condição de contorno na entrada do canal.

Neste estudo, o escoamento é permanente. Como trabalhos futuros, pretende-se repetir as simulações para o caso de vazão variável na entrada do canal, onde tem-se um escoamento não-permanente. Além disso, a presença das chicanas com abertura lateral no canal da piracema, faz com a que água descreva um caminho que se assemelha a meadros. Pretende-se então incorporar a pressão não-hidrostática na simulação e como isto, representar de maneira mais real o escoamento. Outros pontos de interesse são paralelizar o código LBM-MRT e compará-lo com o LBM-BGK e, adaptá-lo para que seja possível simular escoamento supercrítico bidimensional.

Bibliography