Revision as of 13:40, 1 June 2017 (view source) Scipediacontent (talk | contribs) (Created page with " ==Abstract== In recent years, research about the application and optimization of PV panels has grown rapidly. Especially for stand-alone solar systems there have been some...")	Latest revision as of 14:09, 1 June 2017 (view source) Scipediacontent (talk | contribs) m (Scipediacontent moved page Draft Content 330476121 to Fadaeenejad et al 2014a)
(No difference)

---

Latest revision as of 14:09, 1 June 2017

Abstract

In recent years, research about the application and optimization of PV panels has grown rapidly. Especially for stand-alone solar systems there have been some problems related to first stages of design and application. Finding the optimum slope of PV panels in order to maximize the absorbed solar radiation is considered as one of the major obstacles. Although in Malaysia there have been some research works about finding of optimal tilt angle, however, this research work aims to start investigation about slope of PV panels for three villages without electricity and prior research. The Liu and Jordan model is applied to find the monthly optimal tilt angle and fixed tilt angle for the application of solar energy in these rural locations. The results demonstrate that the optimal tilt angle in these locations is less than 5°.

Introduction

Nowadays, the role of solar energy as an appropriate source of renewable energy is growing rapidly. The availability of solar energy, CO₂ emission reduction, and its low cost are some of the essential factors that make the application of solar energy necessary for rural areas [1]. Although improvement in environmental quality is the main factor for the application of renewable energies; however, there are a few barriers against the utilization of renewable energy projects in remote locations. Some of these obstacles are cost, reliability, and performance. Thus, various types of optimization have been developed to mitigate these problems in rural locations [2].

Optimization of the tilt angle for a solar system is one of the most essential processes which is related to the annual output energy of the whole system [3]. In a system without a sun tracker, the maximum solar power can be received by utilizing the optimum PV tilt angle in a stand-alone solar unit. The optimized slope of a PV panel could maximize the absorbed solar radiation and minimize the shading for a solar system in rural buildings. Moreover, common calculation for tilt angle of solar panels according to the latitude of location is not accurate [4]. Therefore, the best optimal tilt angle has been adopted from monthly and daily calculations.

In Malaysia, although much research has been conducted into the optimum PV tilt angle [5-9], however, finding and comparing this angle in various locations in Malaysia has not been discussed. Furthermore, there are some villages without any study in design and application of solar systems. Hence, an investigation into the optimal PV angle in three different villages within Malaysia is presented in this research article by applying the Liu and Jordan model, iHOGA, and Microsoft Office tools for the three case studies.

Methodology

This study uses the Liu and Jordan model for simulation and optimization in a hybrid renewable energy system. iHOGA is used for this purpose as an accurate tool for many types of optimization of hybrid renewable energy systems, including solar panels [10].

Although there are many methods available for the distribution of direct, diffuse, and total solar radiation, amongst the most common models, the calculation model by Liu and Jordan [11] is applied in this research.

Modeling of tilt angle

Firstly, solar radiation data on a horizontal surface must be converted to a monthly average clearness index using the Rietveld model [12]. The simplest form of Angstrom type formula is given by:

${\displaystyle H/H_{0}=a+b\left(n/N\right),}$

(1)

where H/H₀ is the monthly average amount of the total solar radiation incident on a horizontal surface divided by the monthly average incoming top-of-atmosphere radiation, n is the number of measured hours of sunshine, N is the determined day length, a is the percentage of H₀ (solar radiation on a horizontal surface) reaching the earth surface on a completely cloud-covered day, and b is the percentage of H₀ that is absorbed by the clouds on a completely cloud-covered day.

Many values of a and b were examined by Rietveld [12] and the following equations were obtained:

${\displaystyle a=0.1+0.24(n/N),}$

(2)

${\displaystyle b=0.37+0.08(n/N).}$

(3)

Modeling of solar radiation on a tilted surface

The second step of modeling is related to the calculation of the global hourly irradiation (kWh/m²) for the tilted surface of PV modules.

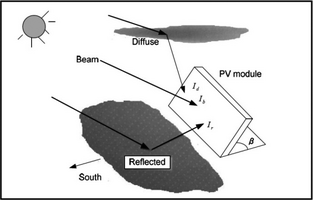
As shown in Figure 1 [8], the hourly total solar irradiance on a tilted surface (I_tt) consists of diffuse radiation (I_d), beam (direct) radiation (I_b), and reflected solar radiation (I_r).

Figure 1. Total solar irradiance on a tilted surface.

These components can be expressed by the following equation:

${\displaystyle I_{tt}=I_{b}R_{b}+I_{d}R_{d}+I_{r}R_{r},}$

(4)

where, R_b, R_d, and R_r are defined as follows: R_b is the ratio of the direct radiation on the tilted surface to the horizontal direct radiation, R_d is ratio of diffuse radiation on the tilted surface to the horizontal diffuse radiation, and R_r is the ratio of the reflected radiation on the tilted surface to the horizontal reflected radiation.

Equation (4) can be rewritten by considering I_b = I − I_d and I_r = Iρ as follows:

${\displaystyle I_{tt}=\left(I-I_{d}\right)R_{b}+I_{d}R_{d}+I\rho R_{r},}$

(5)

where I is the global horizontal irradiation, I_d is the monthly average daily global radiation, and ρ is the ground reflectance which is typically assumed to be 0.2.

The calculation of R_b is based on the formula below:

${\displaystyle R_{b}={\frac {cos\left(\varphi -\beta \right)cos\delta sinw_{s}+w_{s}sin\left(\varphi -\beta \right)sin\delta }{cos\varphi cos\delta sinw_{s}+w_{s}sin\varphi sin\delta }}.}$

(6)

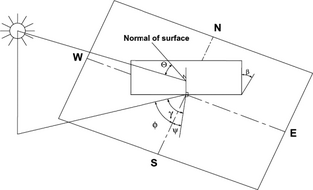
In equation (6), there are some major angles related to the solar panels as shown in Figure 2 [13]. β is the tilt angle of the PV module (the angle between the tilted surface and the horizontal), φ is the latitude of the location, γ is the azimuth angle for which a solar system without a sun tracker is considered to be 0° in the Northern Hemisphere and orientated to the south.

Figure 2. Major angles for PV panel.

The hour angle, w_s, is the solar hour angle corresponding to the sun set time. Each 15° of the solar hour angle is equivalent to 1 h. The w_s is calculated by:

${\displaystyle w_{s}={cos}^{-1}\left(-tan\varphi tan\delta \right),}$

(7)

where δ is the solar declination angle (angular displacement of the sun to the center of the earth). It is further formulated as below:

${\displaystyle \delta =23.45sin\left[{\frac {360(284+d)}{365}}\right],}$

(8)

where, d is the day of the year. If d = 1, for example, it means the first day in January.

Finally, the R_d and R_r coefficients are expressed by:

${\displaystyle R_{d}=R_{r}={\frac {1-cos\beta }{2}}}$

(9)

Meteorological and climate data

The collected data in this research for solar radiation on the horizontal surface is conducted based on NASAs Atmospheric Science Data Centre for 22 years (NASA SSE) [14]. Vignola et al. [15] compared meteorological data from various sources and concluded that long-term data like 22 years NASA SSE are better for systems with long life-time (the life time of this hybrid system is 25 years). The meteorological data are collected from NASA due to availability of long-term and free of charge data. The other climate data such as daily hours of sunshine, temperature, and amount of rainfall are collected from the annual and monthly report of the MMD [16].

Results and Discussion

Study cases

Sabah, Sarawak, and Peninsular Malaysia are three federal territories of Malaysia separated by the South China Sea [17]. According to data from the Malaysian Meteorological Department (MMD) [16], the amount of solar radiation reported in these three territories differs.

Therefore, for precise calculation of the tilt angle, three study cases from three federal territories of Malaysia are considered (red points in Fig. 3 [18]). These three study cases are situated in three villages that are in urgent need of electricity. Thus, data preparation and finding optimal tilt angle of solar system in these villages is one of the main novelties of this research.

Figure 3. Three study cases are defined by red points.

As shown in the figure above, the red points are Kampung Opar in Sarawak, Kampung Labi near Beaufort in Sabah, and Kampung Orang Asli Kemandol in Peninsular Malaysia (the West part of Malaysia). All study cases are rural areas without electricity or with only grid-off diesel generators [19, 20]. The detailed information of the above study cases are provided in Table 1.

Table 1. Three study cases

Village Name	Location	Latitude	Longitude	Elevation
Kampung Opar	Sarawak	1.44	110.074	81
Kampung Labi, Beaufort	Sabah	5.316603	115.599947	237
Kampung Orang Asli kemandol	Selangor	2.94663	101.53896	67

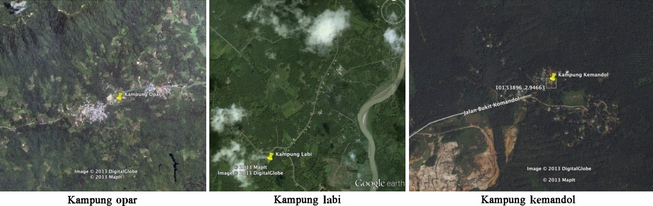
These villages are without electricity since it is impossible to extend the transmission power line from the grid to these dispersed populated villages because of their locations in rugged places. In Figure 4, the three villages are shown by Google earth 2014.

Figure 4. Locations of study cases (Google earth 2014).

Solar irradiation

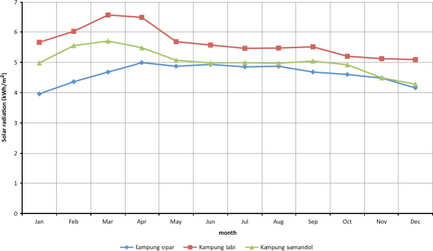
The meteorological data in this study is obtained from the NASA Atmospheric Science Data Center [21]. The monthly average radiation incident on a horizontal surface (kWh/m² per day) for the three above-mentioned locations is demonstrated in the graph below:

As shown in Figure 5, Kampong Labi in Sabah territory has the maximum solar radiation among the three various locations. Moreover, Kampong Opar in Sarawak has the lowest potential to absorb the solar radiation which might be due to the abundant rainfall in this area [16].

Figure 5. Monthly solar radiation for three study cases.

Optimal slope of PV panels in Malaysia

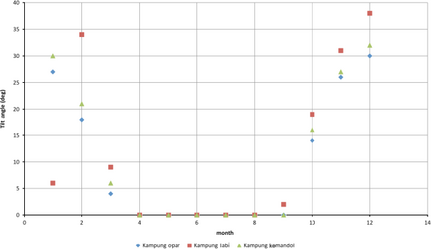
In this study, finding a fixed angle for a stand-alone solar system is investigated by monthly optimized tilt angles. Therefore, the monthly slope of a PV panel is calculated and the results for the three off-grid villages based on the calculation are provided in Figure 6.

Figure 6. Monthly optimum tilt angle in three study cases.

As plotted in the above graph, the optimum slope of PV panels from March to October is 0° for these three villages. Tamer Khatib in his research [3] proves that though optimal monthly tilt angle of PV panels in summer is less than the tilt angle in winter, however, the monthly optimal angle is not negative for Kuala Terengganu in Malaysia. Furthermore, Chang [22] discussed that monthly sunshine duration in the southern sky is more than in the northern sky and consequently there will be a positive angle for solar radiation. He mentioned that there are exceptions for the Suns movement from April to September in lower latitudes.

The month with the lowest irradiation on a horizontal surface in Kampung Opar, Sarawak is in January (Fig. 4). Hence, to maximize the solar irradiation on a tilted surface in this month, the optimal slope of a PV panel is suggested to be set as 27° (Fig. 6). Similarly, the months with the lowest irradiation in Kampong Labi and Kampung Kemandol are November and December. Therefore, the optimum tilt angles for these months in these villages are 31° and 32°, respectively.

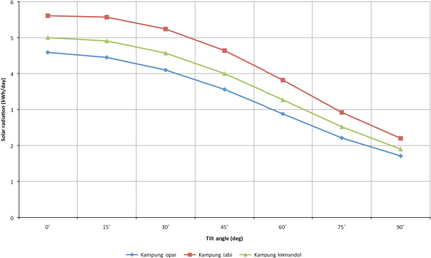
A complementary graph to show the ratio of solar radiation on a tilted surface to various tilt angles is illustrated in Figure 7. In this graph, the irradiation for slopes of 0°, 15°, 30°, 45°, 60°, 75°, and 90° for the whole year is provided.

Figure 7. Amount of solar radiation for different tilt angles in three study cases.

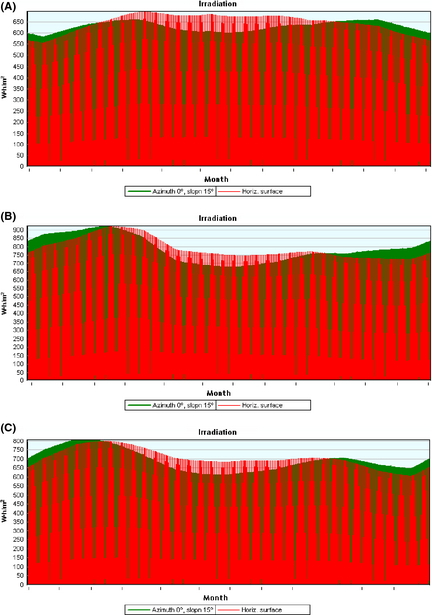
In other words, in the above figure, the amount of solar radiation collected by a tilted surface with various angles from 0° to 90° is shown. Obviously, the range of 0° to 15° is suitable to receive the maximum solar radiation in any location in Malaysia. Thus, further detailed discussion for an angle range of 0° and 15° is considered in Figure 8A–C.

Figure 8. (A) Annual solar radiation on PV panel with slope of 0° and 15° in Kampung Opar, Sarawak. (B) Annual solar radiation on PV panel with slope of 0° and 15° in Kampung Labi, Sabah. (C) Annual solar radiation on PV panel with slope of 0° and 15° in Kampung Kemandol, Selangor, Peninsular Malaysia.

As illustrated in Figure 8A–C, although the amount of solar radiation for a slope of 15° is higher than for 0° in the first and last months of the year, however, the total amount of received radiation on a tilted surface with slope of 0° is more than 15° as detailed in Table 2.

Table 2. Annual amount of solar radiation (kWh/m²) for optimum tilt angles in three study cases

Village name	0°	5°	10°	15°
Kampung Opar, Sarawak	1673.98	1667.26	1650.97	1625.24
Kampung Labi, Beaufort, Sabah	2046.4	2054.79	2050.6	2033.84
Kampung Orang Asli Kemandol, Selangor	1824	1823.79	1812.81	1791.14

Table 2 shows the annual amount of solar radiation on a tilted surface of a PV panel for four angles to detect the best optimum angle in the range of 0° to 15°.

From the data given in Table 2, it can be seen that for Kampung Opar in Sarawak, 0° can be considered as the optimal-fixed tilt angle. In Sabah, for the village of Kampong Labi, the fixed slope for a PV panel for maximum solar radiation is around 5° and for Kampung Kemandol in Peninsular Malaysia it is 0°.

In the present study, the essential factors for tilt angle are included. The major issue addressed in this work is a comparison of tilt angle in three study cases from three federal territories in Malaysia. The monthly optimum angle for the three villages is investigated and the fixed slope of a PV panel is explained. Furthermore, an azimuth angle of zero with a direction toward the South is applied for the optimization process.

Comparison analysis

Muhida et al. [5] analyzed the optimum values for tilt angle and direction of PV panels in Kuala Lumpur for a building integrated photovoltaic (BIPV) system. The authors concluded that the optimal module tilt angle in Malaysia is between 0° and 15°. They used Solar Pro software for their calculation. Sunderan [6] applied a relation between tilt angle, latitude of location, and declination angle to find the monthly optimum slope of a PV panel in Ipoh over one year. His suggestion is convenient for a PV panel with a sun tracking system.

By using PVSYS-50, Excel, and Matlab tools, other authors in [9], discussed the optimum tilt angle in Kuala Lumpur. The result indicated that a PV slope of 15° facing the south is the best choice. This work was undertaken by the Solar Energy Research Institute (SERI), National University of Malaysia. Moreover, solar irradiance for a tilt angle range between −17.16° and 29.74° was discussed in [8]. The optimum slope for a fixed type of PV module was not proposed in this article.

Khatib et al. [3] calculated the suitable slope of a PV panel for their research work based on the Liu and Jordan Model. In this study, the monthly optimal tilt angle for a hybrid system in Kuala Terengganu was less than 23°. Finally, in other research, the optimum tilt angle in Kuala Lumpur was defined as 10° [7]. The mathematical method of this research has been based on Coopers equation and Visual Basic Applications (VBA) in Microsoft Excel.

Table 3 explains previous research works on this issue by classification of case study, monthly optimum angle, optimum-fixed tilt angle, applied tools, method, and orientation of the PV. In most of the recent works concerning optimization, the fixed tilt angle is proposed due to the importance of using a fixed slope for PV panels in remote locations. Sunderan [6], Khatib et al. [23] and Daut et al. [8] in their articles discussed fixed and monthly optimum slopes.

Table 3. Previous works about optimum tilt angle in Malaysia

Papers	Case study	Monthly optimum angle	Optimum-fixed tilt angle	Applied tool	Method	Orientation of PV
Muhida et al. [5]	Kuala Lumpur	–	1° to 15°	Solar Pro		No difference
Sunderan [6]	Ipoh, Perak	Provided	0° or tilt angle = latitude of location	–	Collares- Pereira and Rabl	Facing south when tilt angle is positive and facing north when tilt angle is negative
Elhassan et al. [9]	Kuala Lumpur	–	15° to 30°	PVSYS-50, Excel, Matlab	–	East, North
Daut et al. [8]	Perlis	Provided	–	–	–	–
Khatib et al. [3]	Kuala Terengganu	Provided	0° to 23°	Matlab	Liu and Jordan	–
Omidreza Saadatian et al. [7]	Kuala lumpur	–	10°	Excel	Coopers equation	–

According to Table 3, the calculated optimum tilt angle in this research work is assumed to be correct. As shown in Table 3, previous research works concluded that optimum tilt angle according to the monthly calculation in Malaysia has been positive and facing south. Therefore, in this research finding, the optimal tilt angle for three villages in Malaysia has been according to the monthly positive slope of the PV panel.

Conclusion

Finding the optimum slope of a PV panel to maximize solar radiation on a tilted surface in Malaysia has become an important challenge in recent years. Therefore, the variable and fixed optimal tilt angle for each month over a complete year using the Liu and Jordan method is presented. Moreover, the following results and findings are concluded:

• The azimuth angle, orientation, and tilt angle are some of the most important aspects for the optimization of PV panels. The effect of various azimuth angles and orientations on solar energy is very low when the panel slope is fixed.
• A suitable range for a fixed tilt angle for solar systems in rural buildings in Malaysia is between 0° and 15°.
• Solar output power can be increased by a horizontal solar tracker to follow a monthly tilt angle and by a vertical tracker for the azimuth angle.
• The optimum-fixed tilt angle for Kampung Opar in Sarawak, Kampong Labi in Sabah, and Kampung Kemandol in Peninsular Malaysia is 0°, 5°, and 0°, respectively.
• The annual amount of solar radiation for an optimized tilted surface of PV panels in Kampong Opar, Kampung Labi, and Kampung Kemandol is 1673.98, 2054.79 and 1824 kWh/m², respectively.

Conflict of Interest

None declared.

References

1. Cucchiella, F., I. D'Adamo, M. Gastaldi, and S. C. L. Koh. 2012. Renewable energy options for buildings: performance evaluations of integrated photovoltaic systems. Energy Build.55:208–217.
2. Fadaee, M., and M. A. M. Radzi. 2012. Multi-objective optimization of a stand-alone hybrid renewable energy system by using evolutionary algorithms: a review. Renew. Sustain. Energy Rev.16:3364–3369.
3. Khatib, T., A. Mohamed, and K. Sopian. 2012. Optimization of a PV/wind micro-grid for rural housing electrification using a hybrid iterative/genetic algorithm: case study of Kuala Terengganu, Malaysia. Energy Build.47:321–331.
4. Yakup, M. A. B. H. M., A. Q. Malik. 2001. Optimum tilt angle and orientation for solar collector in Brunei Darussalam. Renew. Energy24:223–234.
5. Riza Muhida, M. A., P. S. Jahn Kassim, M. A. Eusuf, A. G. Sutjipto, and A. Afzeri. 2009. A simulation method to find the optimal design of photovoltaic home system in Malaysia, case study: a building integrated photovoltaic in Putra Jaya, World Acad. Sci. Eng. Technol.29:694–698.
6. Sunderan P.2011. Optimum tilt angle and orientation of stand-alone photovoltaic electricity generation system for rural electrification. J. Appl. Sci. 11:1219–1224.
7. Omidreza Saadatian, K. S., B. Elhab, M. H. Ruslan, and N. Asim. 2012. Optimal solar panels’ tilt angles and orientations in Kuala Lumpur, Malaysia. In: Proceedings of the 1st WSEAS International Conference on Energy and Environment Technologies and Equipment (EEETE' 12). Adv. Environ. Biotechnol. Biomed. P.100.
8. Daut, M. I. I., Y. M. Irwan, N. Gomesh, and N. S. Rosnazri. 2011. Ahmad. Clear Sky Global Solar Irradiance on Tilt Angles of Photovoltaic Module in Perlis, Northern Malaysia, International Conference on Electrical, Control and Computer Engineering, IEEE, Pahang, Malaysia.
9. Elhassan, Z. A. M., M. F. M. Zain, K. Sopian, and A. Awadalla. 2011. Output energy of photovoltaic module directed at optimum slope angle in Kuala Lumpur, Malaysia. Res. J. Appl. Sci.6:104–1109.
10. Dufo-López, R.2012. iUser Manual HOGA, U. O. Zaragoza, ed. Available at: http://www.unizar.es/rdufo/User%20Manual.pdf (accessed September 2012).
11. Liu, B. Y., and R. C. Jordan. 1960. The interrelationship and charactristic distribution of direct diffuse and total solar radiation. Sol. Energy4:1–19.
12. Rietveld, M. R.1978. A new method for estimating the regression coefficients in the formula relating solar radiation to sunshine. Agric. Meteorol.19:243–252.
13. Skeiker, K.2009. Optimum tilt angle and orientation for solar collectors in Syria. Energy Convers. Manage.50:2439–2448.
14. NASA. Surface meteorology and solar energy-location. Atmospheric Science Data center. Twenty two years average data of NASA SSE model (1983–2005). Available at: http://www.eosweb.laec.nasa.gov (accessed 16 December 2014).
15. Vignola, F., C. Grover, N. Lemon, and A. McMahan. 2012. Building a bankable solar radiation dataset. Sol. Energy86:2218–2229.
16. Malaysian Meteorological Department (MMD). Malaysian Meteorological Department - MMD Annual Report. Available at: http://www.met.gov.my (accessed 5 May 2012).
17. Federal Territories and State Governments. 2013. The Malaysian Governments Official Portal. Available at: http://www.malaysia.gov.my/EN/Main/MsianGov/StateGovAndFederalTerritories/Pages/StateGovAndFederalTerritories.aspx (accessed 11 October 2013).
18. Department of Foreign Affairs and Trade, Australian Government. 2013. Malaysia. Available at: http://www.smartraveller.gov.au/zw-cgi/view/Advice/Malaysia (accessed 10 October 2013).
19. Borneo Post. 2012. Ensure better power supply to rural areas is SESBs priority. Available at: http://www.theborneopost.com/2012/12/12/ensure-better-power-supply-to-rural-areas-is-sesbs-priority (accessed 12 December 2012).
20. Tawie J.2011. Give us electricity or else…, in: Free Malaysia Today. Available at: http://www.freemalaysiatoday.com/category/nation/2011/11/09/%E2%80%98give-us-electricity-or-else-%E2%80%99/ (accessed 9 December 2011).
21. NASA. 2013. Atmospheric Science Data Center. Available at http://eosweb.larc.nasa.gov (accessed 5 September 2013).
22. Chang, T. P.2009. The Suns apparent position and the optimal tilt angle of a solar collector in the northern hemisphere. Sol. Energy83:1274–1284.
23. Khatib, T., A. Mohamed, K. Sopian, and M. Mahmoud. 2011. Optimal sizing of building integrated hybrid PV/diesel generator system for zero load rejection for Malaysia. Energy Build.43:3430–3435.