| (2 intermediate revisions by the same user not shown) | |||
| Line 378: | Line 378: | ||
[[#bfn0005|1]]. La matriz <math display="inline">A\in \mathbb{C}^{n\times n}</math> es no normal si ''AA''<sup>*</sup> ≠ ''A''<sup>*</sup>''A'' , donde ''A''<sup>*</sup> es la matriz conjugada traspuesta de ''A'' . | [[#bfn0005|1]]. La matriz <math display="inline">A\in \mathbb{C}^{n\times n}</math> es no normal si ''AA''<sup>*</sup> ≠ ''A''<sup>*</sup>''A'' , donde ''A''<sup>*</sup> es la matriz conjugada traspuesta de ''A'' . | ||
| − | [[#bfn0010|2]]. <math display="inline">\begin{array}{l}\displaystyle \Lambda (A)=\lbrace z\in \mathbb{C}:rank(zI-A)<n\rbrace =\lbrace z\in \mathbb{C}:(zI-\\\displaystyle -A)es singular\rbrace \end{array}</math> . | + | [[#bfn0010|2]]. <math display="inline">\begin{array}{l}\displaystyle \Lambda (A)=\lbrace z\in \mathbb{C}:rank(zI-A)<n\rbrace =\lbrace z\in \mathbb{C}:(zI-\\\displaystyle -A) \text { es singular}\rbrace \end{array}</math> . |
| − | [[#bfn0015|3]]. Λ<sub>''ϵ''</sub> (''A | + | [[#bfn0015|3]]. Λ<sub>''ϵ''</sub> (''A'') es el conjunto de números <math display="inline">z\in \mathbb{C}</math> tales que: ∥(''zI'' − ''A'' )<sup>−1</sup> ∥ > ''ϵ''<sup>−1</sup> , ''ϵ'' > 0. |
Latest revision as of 10:29, 18 April 2017
Resumen
El pseudoespectro es una gran herramienta para el estudio de sistemas dinámicos asociados a matrices no normales. En las últimas décadas su estudio y aplicación se ha intensificado, por lo que realizar su cálculo de forma eficiente resulta de especial interés para la comunidad científica. Para matrices de grandes dimensiones se han empleado diferentes métodos, entre los cuales destacan los métodos de proyección en espacios de Krylov. En este trabajo se utiliza la idea propuesta por Wright y Trefethen para aproximar el pseudoespectro de la matriz usando una proyección Hm de menor tamaño. Adicionalmente, se propone una descomposición del dominio en subregiones asignando a cada procesador una subregión. Cada procesador calcula el menor valor singular de la matriz (zI − Hm ) para todos los valores z = x + yi que representan los puntos de la subregión asignada. Se realizaron diferentes experimentos numéricos cuyos resultados fueron contrastados con los obtenidos en la bibliografía. En todos los casos estudiados el método implementado muestra una reducción del tiempo de ejecución respecto a la versión secuencial del programa desde 41x hasta 101x .
Abstract
The pseudospectra is a powerful tool to study the behavior of dynamic systems associated to non-normal matrices. Studies and applications have increased in the last decades, thus, its efficient computation has become of interest for the scientific community. In the large scale setting, different approaches have been proposed, some of them based on projection on Krylov subspaces. In this work we use the idea proposed by Wright and Trefethen to approximate the pseudospectra of a matrix A using a projection Hm of smaller size. Additionally, we propose a domain decomposition of the interest region into subregions which are assigned to a set of processors. Each processor calculates the minimal singular values of matrices (zI − Hm ) where z = x + yi represents a point of the corresponding subregion. We conduct a numerical experimentation comparing the results with those on the literature of the topic. In all cases the proposed scheme shows a reduction in CPU time with respect to the sequential version, achieving from 41x to 101x .
Palabras clave
Pseudoespectro ; Métodos de Krylov ; Proyección ; Paralelización de datos
Keywords
Pseudospectra ; Krylov methods ; Projection ; Data parallelism
1. Introducción
El cálculo de los autovalores y los autovectores de las matrices es un paso importante en muchas aplicaciones derivadas de diferentes ramas de la ciencia y la ingeniería; sin embargo, cuando la matriz es altamente no normal1 la información que nos ofrece el espectro2 de la matriz resulta insuficiente para analizar ciertos fenómenos importantes, como por ejemplo el comportamiento de las soluciones de sistemas dinámicos o el estudio de los operadores y de sus perturbaciones [1] .
Cuando la matriz A es de grandes dimensiones el interés se centra en calcular solo una parte del pseudoespectro 3 , y es suficiente utilizar alguna técnica de proyección para aproximarlo. En la práctica, las proyecciones en espacios de Krylov han resultado ser efectivas en el cálculo del pseudoespectro [2] and [3] , ya que brindan información importante sobre los autovalores y tienen bajo costo computacional en comparación con métodos clásicos que obtienen una descomposición en valores singulares de la matriz en cada punto de la malla, incrementando el costo computacional de O (n3 ) [3] . Como sabemos, cada autovalor de una matriz A de orden n es un número complejo λ = a + bi que puede ser representado en el plano mediante las coordenadas (a , b ). El pseudoespectro de A puede ser caracterizado por una serie de contornos o curvas de nivel que encierran el conjunto de autovalores de esta matriz, lo cual significa que calcular el pseudoespectro es equivalente a hallar estas curvas; por esta razón, en la práctica el resultado de este cálculo es una gráfica de contornos.
En este trabajo se calcula el pseudoespectro de matrices grandes y dispersas usando el método de reinicio implícito de Sorensen [4] para hallar una proyección Hm de A en un subespacio de Krylov. Adicionalmente, se propone la implementación de un paralelismo de datos y se realiza un análisis de rendimiento de la propuesta comparada con los resultados obtenidos al ejecutar la versión secuencial. La idea principal detrás del paralelismo de datos está intrínseca en la metodología del cálculo del pseudoespectro, una vez que se trata de hallar una serie de contornos o curvas de nivel alrededor de los puntos (a , b ) que representan los autovalores λi (i = 1, …, n ) de la matriz A de orden n . El proceso natural para hallar estos contornos comienza con la definición de una malla de puntos en el plano. La ubicación de la malla de puntos generalmente se hace en una región de interés (por ejemplo, en aquella donde se encuentran los autovalores de mayor magnitud), mientras que el tamaño de la malla obedece a la relación posición/costo computacional y ambas decisiones quedan a juicio del usuario. Posteriormente, y tomando en cuenta que el cálculo del pseudoespectro requiere conocer el mínimo valor singular de (zI − A ) para todos los puntos z = x + yi , donde (x , y ) es un punto de la grilla, y que este cálculo puede realizarse en paralelo, basta con dividir la grilla de acuerdo al número de procesadores disponibles de manera balanceada.
Para describir el trabajo realizado hemos dividido el documento en 6 secciones: la sección 2 comenta los trabajos relacionados con los métodos utilizados para el cálculo del pseudoespectro y sus implementaciones paralelas; la sección 3 describe el método de proyección con estrategia de reinicio implícito; la sección 4 muestra la propuesta paralela realizada y define las matrices utilizadas en la experimentación numérica; la sección 5 realiza el análisis de los resultados obtenidos para las matrices estudiadas utilizando como métricas de rendimiento el speedup y la eficiencia. Finalmente, la sección 6 muestra las conclusiones del trabajo y señala futuras líneas de investigación.
2. Trabajos relacionados
En esta sección mostramos los aportes que anteriormente han realizado otros autores y que están relacionados con los métodos para el cálculo del pseudoespectro y sus implementaciones paralelas.
2.1. Métodos para el cálculo del pseudoespectro
Nuestro interés se centra en calcular ∥(zI − A )−1 ∥ utilizando ∥ ★ ∥ 2 , para lo cual se necesita calcular el mínimo valor singular de A en cada punto z de la malla (smin (zI − A )). Este valor puede obtenerse aplicando la iteración inversa a B = (zI − A )* (zI − A ), con (zI − A )* la matriz conjugada traspuesta de (zI − A ), en lugar de hallar la descomposición en valores singulares de A .
Un esquema más eficiente para calcular smin (zI − A ) usa el método de Lanczos inverso aplicado a la matriz B = (zI − A )* (zI − A ). En cada iteración de este método es necesario resolver sistemas de ecuaciones lineales con (zI − A )* y (zI − A ), de manera que resulta aconsejable obtener inicialmente la factorización de Schur de la matriz A para reducir el costo computacional por iteración. Este procedimiento es el núcleo de eigs , el principal paquete computacional de MATLAB para el cálculo del pseudoespectro desarrollado por T.G. Wright y mantenido por M. Embree [5] . No obstante, aunque este método es de uso común, su aplicación a matrices de gran dimensión no es posible debido a limitaciones de memoria o a su alto costo computacional. Adicionalmente, cuando la matriz es dispersa, manejar esta limitación puede llevar a destruir o a no poder sacar partido del patrón de dispersión de la matriz. En este caso, es preferible utilizar un método de proyección que permita trabajar con una matriz Hm de menor dimensión (m << n ). En [6] K. Toh y L. Trefethen proponen usar la iteración de Arnoldi para obtener la siguiente factorización:
|
|
( 1) |
o
|
|
( 2) |
donde Vm es una matriz de n × m cuyas columnas son ortonormales y es la matriz de Hessenberg superior de (m + 1) × m . De esta forma, el pseudoespectro de la matriz A puede ser aproximado por el pseudoespectro de la matriz rectangular de menor dimensión [7] . Sin embargo, y a pesar de que la iteración de Arnoldi puede ser usada para obtener la factorización en (2) , es posible que el pseudoespectro de sea una aproximación deficiente del pseudoespectro de A , razón por la cual se utilizan estrategias de reiniciación.
Una de las implementaciones más robustas del método de Arnoldi con estrategia de reinicio es IRAM (Implicitly Restarted Arnoldi Method) . Esta implementación fue propuesta por Sorensen en [4] and [8] e implementada en MATLAB (eigs) y Fortran (ARPACK [9] ). Wright y Trefethen [2] usaron IRAM en el cálculo del pseudoespectro de matrices dispersas de gran tamaño. Actualmente, IRAM y otros métodos basados en funciones de transferencia son ampliamente usados para calcular el pseudoespectro a gran escala (véanse, por ejemplo, los trabajos de [3] , [7] and [10] ). En particular, en este trabajo usaremos ARPACK [9] debido a su comprobada eficiencia computacional en el cálculo de autovalores de matrices de grandes dimensiones.
2.2. Paralelización del cálculo del pseudoespectro
Hasta ahora hemos comentado los métodos más comúnmente utilizados para realizar el cálculo del pseudoespectro en una arquitectura convencional. Sin embargo, en la literatura también existen otras investigaciones relacionadas con el cálculo en paralelo del pseudoespectro [11] , [12] and [13] . Todos estos trabajos han evaluado diferentes métodos utilizando una red de computadores formada por unos pocos procesadores y usando MATLAB como lenguaje de programación junto con alguna interfaz de comunicación para realizar el paso de mensajes entre los procesadores tales como MPITB, PVMTB y MultiMATLAB, entre otras [11] and [12] . Sin embargo, es bien conocido por todos que la funcionalidad de MATLAB es permitir implementar de forma rápida prototipos de nuevos métodos numéricos para evaluar su comportamiento y resolver problemas, para luego implementarlos en otros entornos de programación que mejoren el rendimiento computacional del método [14] y permitan resolver problemas a gran escala.
En este trabajo proponemos la paralelización de datos para el cálculo del pseudoespectro utilizando como método de proyección IRAM. La implementación propuesta utiliza Fortran como lenguaje de programación y MPI para realizar el paso de mensajes entre los procesadores.
3. Método de proyección con estrategia de reinicio: IRAM
Tal y como se establece en [15] , la idea detrás de IRAM puede resumirse en 3 pasos:
- Paso 1: extender una factorización de Arnoldi de orden k a una factorización de Arnoldi de orden m , con k < m .
|
|
( 3) |
- Paso 2: reordenar la factorización de Arnoldi de orden m de tal manera que los autovalores aparezcan en la submatriz principal de Hm .
|
|
( 4) |
- Paso 3: deflactar la factorización reordenada para obtener una nueva factorización de orden k .
|
|
( 5) |
El paso 2 de este proceso requiere p = m − k aplicaciones de la iteración QR con desplazamiento sobre la matriz Hm , usando como parámetros de desplazamiento los p = m − k autovalores no deseados (exact shifts) . Esto produce una matriz similar a Hm , que contiene los autovalores ordenados de manera que la información deseada se encuentra en la submatriz principal de . Más aún, por cada aplicación del método QR con desplazamiento, usando μ (un autovalor no deseado), la matriz resultante es también una matriz de Hessenberg. De esta manera, la deflación en el paso 3 se logra seleccionando apropiadamente cada componente de la factorización de orden m del paso 2 hasta obtener una factorización de orden k , con la misma estructura que la original pero enriquecida con la información de los autovalores deseados.
En este trabajo usaremos IRAM para obtener la matriz rectangular y aproximar el pseudoespectro de A calculando el pseudoespectro de . Siguiendo la recomentación de Wright en [2] para reducir el tiempo computacional realizamos una factorización QR de por cada punto z de la región de interés, y aplicamos Lanczos inverso a R*R , donde R* es la matriz conjugada traspuesta de R . El siguiente algoritmo describe este proceso:
Algoritmo 1.
Cálculo del pseudoespectro usando IRAM
| 1. | Seleccionar los parámetros de reinicio k , m |
| 2. | Ejecutar ARPACK para obtener la matriz |
| 3. | Definir y discretizar la región de interés en el plano complejo |
| Para cada punto de la región discretizada | |
| 4. | Calcular la descomposición QR de |
| 5. | Obtener λmax (z ) usando Lanczos inverso sobre R*R |
| 6. | Obtener |
4. Paralelización del cálculo del pseudoespectro
La idea general de la paralelización de datos para el cálculo del pseudoespectro consiste en aplicar el algoritmo anterior simultáneamente en varios puntos de la región. Para realizar esto dividimos la región discretizada en p subregiones, donde p es el número de procesadores utilizados para determinar el pseudoespectro. De esta forma, cada procesador calcula smin (zI − A ) para sus correspondientes puntos z .
La cantidad de puntos en cada subregión puede variar, ya que es posible que la cantidad de puntos en la malla no sea múltiplo del número de procesadores. Si consideramos una malla formada por mx × my puntos y si el cociente (c ) de no es un valor entero, entonces asignamos a cada procesador tantos puntos como corresponda a la parte entera del cociente c y el resto de puntos los distribuimos entre los primeros ((mx × my ) mod p ) procesadores. La distribución de puntos en los procesadores no es objeto de este trabajo y se puede usar cualquier esquema de repartición. Anteriormente, se describió el esquema que usaremos al realizar las pruebas numéricas. Al finalizar el cálculo, cada procesador envía al procesador master la tripleta de vectores . El procesador master guarda todos estos datos en un fichero para posteriormente visualizar el contorno del pseudoespectro hallado.
Todos los experimentos numéricos se realizaron en un cluster formado por 113 nodos, de los cuales 73 son Xeon Dual-Core 5148 y el resto son Xeon L 5630 Dual. Para obtener la proyección de la matriz A utilizamos ARPACK [9] . La aplicación fue implementada usando el lenguaje de programación gfortran 4.5.3 para desarrollar la versión secuencial y MPI-f90 para la versión paralela. Finalmente, usamos la función contour de MATLAB 7.8.0 (R2009a) para visualizar las curvas de nivel que muestran el pseudoespectro de las matrices estudiadas. La tabla 1 muestra las características de estas matrices.
| Nombre | Dimensión | Intervalo de la región | Aplicación |
|---|---|---|---|
| Rbd [16] | 800 × 800 | [− 1,1 ; 1,1] × [−0,2 ; 2,5] | Ingeniería química |
| Bwm4 | 2.000 × 2.000 | [− 25 ; 5] × [−7 ; 7] | Reacciones químicas |
| Crystal5 | 10.000 × 10.000 | [3 ; 7] × [−1,5 ; 1,5] | Crecimiento del cristal |
| Airfoil6 | 23.560 × 23.560 | [− 1,5 ; 0] × [−1,5 ; 1,5] | Interacción fluido estructura |
4http://math.nist.gov/MatrixMarket/data/NEP/mvmbwm/mvmbwm.html
5http://math.nist.gov/MatrixMarket/data/NEP/crystal/crystal.html
6http://math.nist.gov/MatrixMarket/data/NEP/airfoil/airfoil.html
5. Análisis de los resultados
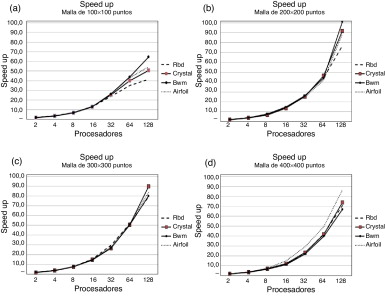
El rendimiento de nuestra mejor versión secuencial fue contrastado en tiempo y precisión con el esquema paralelo implementado usando 2, 4, 8, 16, 32, 64 y 128 procesadores. Con respecto al tiempo obtenido por la aplicación, la figura 1 muestra el speedup alcanzado en cada caso considerando mallas formadas por 100 × 100, 200 × 200, 300 × 300 y 400 × 400 puntos.
|
|
|
Figura 1. Speedup obtenido al aumentar la cantidad de puntos en las mallas: a) 100 × 100; b) 200 × 200; c) 300 × 300; d) 400 × 400. |
Los resultados mostrados representan el promedio del rendimiento obtenido después de realizar 30 ejecuciones de cada experimento numérico. Se puede observar que al incrementar la cantidad de procesadores utilizados en las ejecuciones sin variar la cantidad de puntos en las mallas, se incrementa el rendimiento de la aplicación para todas las matrices. Por otra parte, la figura 1 también muestra cómo al aumentar la cantidad de puntos en las mallas varía el speedup alcanzado, siendo máximo para mallas de 200 × 200 puntos (101x ).
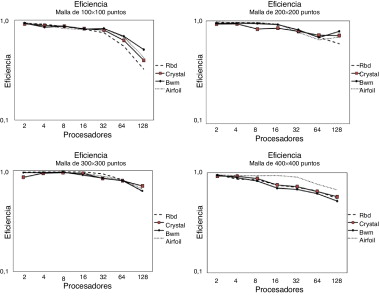
Para mallas de 100 × 100 la escalabilidad de la aplicación está cerca de alcanzar su valor óptimo (número de procesadores de la ejecución) cuando utilizamos 2, 4, 8 y 16 procesadores. Para estos casos puede observarse que la eficiencia obtenida es de casi 1 (fig. 2 a). Sin embargo, a partir de 32 procesadores el tiempo de cálculo de cada procesador no compensa el tiempo de comunicación requerido. La cantidad de cálculo para cada procesador en este experimento resulta insuficiente cuando utilizamos más de 32 procesadores. Adicionalmente, para las mallas de 200 × 200 y 300 × 300 los valores de la eficiencia aumentan y el rango de la eficiencia para todas las ejecuciones se encuentra entre 0,6 y 0,98 (figs. 2 b y 2 c).
|
|
|
Figura 2. Eficiencia de la implementación (mostrada en escala logarítmica) aumentando la cantidad de puntos en las mallas: a) 100×100; b) 200×200; c) 300×300; d) 400×400. |
Para mallas de 400×400, el incremento en la cantidad de procesadores mejora el speedup obtenido, aunque los resultados de rendimiento no mejoran los alcanzados en las mallas de 200×200 y 300×300 ya que, en este caso, el tiempo de comunicación y la cantidad de puntos de la malla (tamaño de los mensajes) comienzan a degradar el paralelismo. Los mejores resultados para todas las matrices estudiadas y ejecuciones realizadas se obtuvieron para las mallas de 200×200, donde el speedup obtenido con 128 procesadores aumenta entre 35x y 41x respecto al rendimiento conseguido por la aplicación para las mallas de 100×100 ( tabla 2 ). La eficiencia promedio obtenida en este caso es de 0.79 (fig. 2 b).
| Matriz/Mallas | 100×100 | 200×200 | 300×300 | 400×400 |
|---|---|---|---|---|
| Rdb | 41x | 77x | 79x | 71x |
| Bwm | 65x | 101x | 80x | 67x |
| Crystal | 51x | 92x | 90x | 74x |
| Airfoil | 54x | 89x | 84x | 87x |
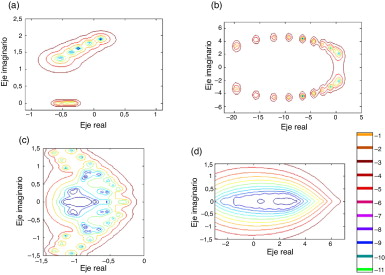
Hasta ahora hemos analizado la reducción obtenida en los tiempos de ejecución de la implementación propuesta. A continuación comentaremos los resultados obtenidos en función de la precisión obtenida al calcular el pseudoespectro de las matrices. La figura 3 muestra las curvas de contornos del pseudoespectro obtenidas para las matrices estudiadas. Estas curvas ofrecen información sobre el comportamiento de los autovalores de las matrices en condiciones de perturbación en los niveles ϵ = 10−1 , 10−2 , …, 10−11 . Es importante señalar que hasta ahora no existe una forma robusta y precisa de medir la precisión del cálculo del pseudoespectro, una vez que el resultado se presenta a través de gráficas de contornos alrededor de los autovalores, donde cada contorno representa un nivel del pseudoespectro. Sin embargo, en cada uno de los experimentos contrastamos estas imágenes con las ya obtenidas por otros autores de la bibliografía, específicamente con las presentadas por K. Toh y L. Trefethen en [6] y las que pueden ser observadas en la página web mantenida por M. Embree [5] .
|
|
|
Figura 3. Pseudoespectro de las matrices: a) Rdb; b) Bwm; c) Airfoil; d) Crystal para ϵ = 10−1 , 10−2 , …, 10−11 . |
Por otra parte, existen métodos para medir el grado de similitud de 2 imágenes gráficas, y pueden ser aplicados a estos resultados. En particular, en [17] (apéndice B) R. Astudillo muestra una comparación de este tipo en términos de diferencia entre píxeles y como ejemplos utiliza las matrices que se presentan en este documento. Sin embargo, este interesante tema está fuera del alcance de este artículo y se remite al lector a los trabajos señalados.
Para cada caso comprobamos que las imágenes obtenidas del pseudoespectro de cada matriz coinciden con las presentadas en la bibliografía, específicamente con las presentadas por Toh y Trefethen en [6] y que pueden observarse en la figura 3 . Estos resultados son los esperados en todos los casos.
6. Conclusiones
En este trabajo se desarrolla y evalúa un esquema paralelo para el cálculo del pseudoespectro de matrices utilizando el método de reinicio implícito. Específicamente se propone una paralelización de datos realizando una división del dominio de la región donde deseamos conocer el comportamiento de los autovalores. De esta manera, los procesadores pueden trabajar en paralelo para determinar el pseudoespectro. Esta propuesta disminuye significativamente el tiempo de cómputo. Para evaluar el rendimiento de la implementación propuesta se utilizaron diferentes matrices procedentes de la bibliografía, incluyendo en este documento una muestra representativa de las mismas. En general, los mejores resultados obtenidos se registraron para mallas de 200×200, obteniendo una eficiencia promedio de hasta 0,79 y un speedup de 101x al ejecutar la aplicación paralela en 128 procesadores.
Un análisis comparativo indica que el esquema paralelo supera computacionalmente y con buen rendimiento la versión secuencial. El documento incorpora un análisis de escalabilidad del esquema paralelo propuesto, el cual sugiere la conveniencia de usar este esquema siempre que se disponga de una arquitectura con capacidad de cálculo en paralelo. Las matrices se proyectaron inicialmente para trabajar con matrices de menor dimensión; las pruebas muestran lo efectivo de esta estrategia.
En general, los resultados son alentadores y apoyan la propuesta de aproximar el pseudoespectro de grandes matrices usando una proyección o una aproximación de la matriz a otra matriz de menor dimensión, para luego dividir la región de interés y paralelizar el cálculo del pseudoespectro. Por esta razón, continuamos trabajando en esta dirección implementando este esquema paralelo, pero ahora en una plataforma con GPUs (Graphics Processing Unit) .
Agradecimientos
Este trabajo ha sido posible gracias al apoyo del Consejo de Desarrollo Científico y Humanístico de la Universidad Central de Venezuela (CDCH) y del Ministerio de Ciencia y Tecnología de España (TIN2012-34557).
References
- [1] L.N. Trefethen, M. Embree; Spectra and pseudospectra: The behavior of nonnormal matrices and operators; Princeton University Press (2005)
- [2] T.G. Wright, L.N. Trefethen; Large-scale computation of pseudospectra using ARPACK and eigs; SIAM J. Sci. Comput., 23 (2) (2002), pp. 591–605
- [3] R. Astudillo, Z. Castillo; Computing peudospectra using Block Implicitly Arnoldi Iteration; Math. Comput. Modell., 57 (2013), pp. 2149–2157
- [4] D. Sorensen, Implicitly Restarted Arnoldi/Lanczos methods for large scale eigenvalue calculations, Tech. Rep. TR-96-40 (1996).
- [5] M. Embree, L.N. Trefethen, Pseudospectra gateway [consultado 26 Mar 2014]. Disponible en: http://www.cs.ox.ac.uk/pseudospectra/ .
- [6] K. Toh, L.N. Trefethen; Calculation of pseudospectra by the Arnoldi Iteration; SIAM J. Sci. Comput., 17 (1) (1996), pp. 1–15
- [7] T.G. Wright, L.N. Trefethen; Pseudospectra of rectangular matrices; IMAJNA, 22 (4) (2002), pp. 501–519
- [8] D. Sorensen; Implicit application of polynomial filters in a k -step Arnoldi method ; SIAM J. Matrix Anal. Appl., 13 (1) (1992), pp. 357–385
- [9] R. Lehoucq, D. Sorensen, C. Yang; ARPACK users guide: Solution of large scale eigenvalue problems by Implicitly Restarted Arnoldi methods; SIAM (1998)
- [10] V. Simoncini, E. Gallopoulos; Transfer functions and resolvent norm approximation of large matrices; Electron. Trans. Numer. Anal., 7 (1998), pp. 190–201
- [11] C. Bekas, E. Kokiopoulou, E. Gallopoulos, V. Simoncini; Parallel computation of pseudospectra using transfer functions on a MATLAB-MPI cluster platform; Recent Advances in Parallel Virtual Machine and Message Passing Interface, Lecture Notes in Computer Science, 2474 (2002), pp. 199–207
- [12] C. Bekas, E. Kokiopoulou, E. Gallopoulos; The design of a distributed MATLAB-based environment for computing pseudospectra; Future Gener. Comp. Sy., 21 (6) (2005), pp. 930–941
- [13] C. Bekas, E. Gallopoulos; Cobra: Parallel path following for computing the matrix pseudospectrum; Parallel Comput., 27 (14) (2001), pp. 1879–1896
- [14] J. Dongarra, V. Eijkhout; Numerical linear algebra algorithms and software; J. Comput. Appl. Math., 123 (2000), pp. 489–514
- [15] Z. Castillo, A new algorithm for continuation and bifurcation analysis of large scale free surface flows, Ph.D. thesis, Rice University (2004).
- [16] B. Hassard, N. Kazarinoff, Y. Wan; Theory and Applications of Hopf Bifurcation; Cambridge University Press (1981)
- [17] R. Astudillo, Análisis e implementación de nuevos esquemas para el cálculo del pseudoespectro, Masters thesis, Escuela de Computación, Facultad de Ciencias, Universidad Central de Venezuela (2011).
Notes
1. La matriz es no normal si AA* ≠ A*A , donde A* es la matriz conjugada traspuesta de A .
2. .
3. Λϵ (A) es el conjunto de números tales que: ∥(zI − A )−1 ∥ > ϵ−1 , ϵ > 0.
Document information
Published on 01/03/15
Accepted on 31/10/13
Submitted on 10/07/13
Volume 31, Issue 1, 2015
DOI: 10.1016/j.rimni.2013.10.004
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?