Revision as of 15:20, 10 April 2017 (view source) Scipediacontent (talk | contribs) (Created page with "==Abstract== Performance and emission characteristics of HCCI engines depend on achieving a good in-cylinder homogeneous mixture. The formation of in-cylinder mixture depends...")	Latest revision as of 15:25, 10 April 2017 (view source) Scipediacontent (talk | contribs) m (Scipediacontent moved page Draft Content 996662326 to Ramesh Mallikarjuna 2016a)
(No difference)

---

Latest revision as of 15:25, 10 April 2017

Abstract

Performance and emission characteristics of HCCI engines depend on achieving a good in-cylinder homogeneous mixture. The formation of in-cylinder mixture depends on many engine parameters, which need optimization. In addition, as of now, there is no direct way to clearly describe and estimate in-cylinder mixture homogeneity. In the CFD analysis, it is evaluated indirectly using contour plots of equivalence ratio, variation of in-cylinder pressure with crank angles, heat release curves or by the comparison of emissions. In this study, an attempt has been made to develop methods to evaluate the in-cylinder mixture homogeneity by the CFD analysis using AVL-FIRE. Here, global and local in-cylinder fuel distribution and in-cylinder fuel distribution index are used to evaluate the mixture homogeneity. In order to evaluate these methods, mixture homogeneities in two cases of fuel injections with 7- and 10-hole injector are compared. Finally, we found that the global fuel distribution (GFD) plot helps direct quantitative assessment of mixture distribution in various ER range. However, the GFD method cannot explain the spatial variation of fuel distribution and does not provide mixture homogeneity on a simple scale. In the method of plotting fuel distribution index, the overall homogeneity will be evaluated on a scale of 0 to 1 by a simple way. In the method of plotting local fuel distribution (LFD), the spatial variation of mixture homogeneity is well defined in local zones both in radial and axial directions. Further, these proposed methods help us to reduce the computation time significantly.

Keywords

Equivalence ratio (ER) ; Global fuel distribution (GFD) ; Homogeneous charge compression ignition (HCCI) ; In-cylinder mixture homogeneity ; Local fuel distribution (LFD)

Nomenclature

NOx- Nitrogen oxide

PM- Particulate matter

HC- Hydrocarbon emission

CO- Carbon monoxide

UI- Uniformity index

CFD- Computational fluid dynamics

ECFM-3Z- Extended coherent flame model

SOI- Start of injection

SOC- Start of combustion

EOC- End of combustion

UDF- User defined function

FDI- Fuel distribution index

1. Introduction

Diesel engines constitute a major portion of transportation sector worldwide. But a main problem associated with the diesel engines is of high emissions of smoke, nitric oxides (NOx) and particulate matters (PM). There are many ways to overcome this problem in diesel engines. One of the solutions is homogeneous charge compression ignition (HCCI) concept, which is becoming very popular today.

The HCCI concept mainly involves a low temperature combustion of a homogeneous air–fuel mixture, which leads to simultaneous reduction of smoke, NOx and PM emissions. But the main challenge to the concept of HCCI is that it requires preparation of the homogeneous air–fuel mixture in short time duration. In addition, the homogeneity of air–fuel mixture is also influenced by many engine parameters viz., combustion chamber geometry, fuel injection parameters and engine operating conditions, etc. Therefore, understanding how the mixture homogeneity is affected under different operating conditions in a HCCI engine is very much essential.

Late injection HCCI concept [1] , [2] , [3] , [4] , [5]  and [6] is a promising solution that is being explored by many researchers around the world for emission reduction in diesel engines because of the ease of control of the start of combustion and the rate of pressure rise. In order to achieve a good in-cylinder mixture homogeneity, engine parameters viz., compression ratio, piston bowl shape, number of injector holes, swirl ratio, fuel spray cone angle, fuel injector flow rate etc., need to be optimized. At present, even though a good amount of research work is being carried out to optimize the engine parameters to get good in-cylinder mixture homogeneity, there are no direct ways – either experimental or theoretical to evaluate the mixture homogeneity. Generally, the optimization of engine parameters is done by using CFD analysis [7] , [8] , [9] , [10]  and [11] . Some of the current methods used are as follows.

1.1. Contour plots of equivalence ratio (ER)

The contour plots of ER show the variation of ER inside a combustion chamber. It is a widely used method for an assessment of in-cylinder mixture homogeneity [7] , [8] , [9] , [10] , [12] , [20] , [21]  and [22] . In this method, the in-cylinder the mixture homogeneity is better and the range of ER in contour plots is better. Rich and lean mixture zones can be assessed by studying ER contour plots at different sections of combustion geometry. However, this method has certain limitations like: (i) it gives only a qualitative assessment and change in mixture homogeneity cannot be quantified, (ii) time consuming and interpretation of results can vary from person to person, and (iii) marginal changes in mixture homogeneity cannot be identified during a parametric study.

1.2. Plots of rate of heat release and in-cylinder pressure

Plots of the variation of rates of heat release and in-cylinder pressure with crank angle are used to indirectly assess the mixture homogeneity [7] , [9] , [10] , [13] , [14]  and [15] . In this method, the mixture homogeneity is better, the rate of pressure rise and heat release is higher, and the combustion duration is shorter. However, using this method, one cannot explain the reasons for the change in mixture homogeneity and spatial variation of ER.

1.3. Plots of exhaust emissions

NOx, PM, hydrocarbon (HC) and carbon monoxide (CO) emission levels in the exhaust gas are analyzed to indirectly assess the mixture homogeneity [7] , [9] , [10] , [13] , [14] , [15] , [16]  and [17] . In this method, the mixture homogeneity is better and the engine out PM and NOx emissions are lower. This method also lacks in explaining the reasons for the change in mixture homogeneity and the spatial variation of ER.

1.4. Plots of temperature versus ER (T-ϕ)

T-ϕ plot is made at different crank angle during combustion, which helps understand variations of local gas temperature and equivalence ratio. In this method, the mixture homogeneity is better, combustion temperature and ER in each zone will be in the target ER range. Researchers used temperature versus ER plots to understand the combustion process and the mechanism of emissions formation [9]  and [18]. However, with this method, it is difficult to quantify the spatial variation of ER and changes in mixture homogeneity.

1.5. Uniformity index (UI)

In this method, a non-dimensional parameter called uniformity index is used [19] . It is defined as,

${\displaystyle {\mbox{UI}}=1-{\frac {1}{2n}}{\sum }_{i=1}^{n}{\frac {\sqrt {{\left(w_{i}-w\right)}^{2}}}{w_{i}}}}$

( 1)

where, n is the total number of cells; w and ${\textstyle w_{i}}$ are the average and local fuel mass fraction in the domain respectively. UI equal to 1 indicates that the fuel distribution is homogeneous, whereas UI equal to zero indicates that the fuel is completely unmixed with the air. It is a simple way of defining the in-cylinder mixture homogeneity.

From the above discussion, we understand that, at present, there are no direct methods available to assess the in-cylinder mixture homogeneity. However, it is important to establish a direct method to evaluate the in-cylinder mixture homogeneity especially for HCCI engines. Therefore, in this study, we have developed direct methods to evaluate the mixture homogeneity.

2. The CFD analysis

2.1. The geometric modelling and meshing

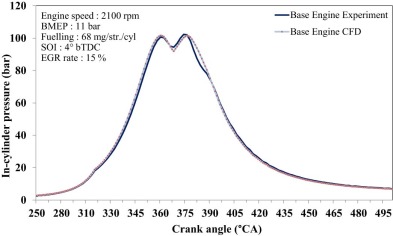
In this study, three-cylinder, water-cooled, direct injection (DI) diesel engine is considered for the CFD analysis. The detailed specifications of the engine considered are given in Table A1 of the Appendix. The AVL-FIRE, a commercial CFD code, is used for this purpose. An engine cycle simulation including combustion has been performed between intake-valve-closure (IVC) to exhaust-valve-opening (EVO) period, i.e., the closed part of the cycle. A diesel engine simulation environment (ESE) tool is used to model and mesh the combustion geometry as shown in Fig. 1 . Mesh size and number are selected based on the work carried out by Juttu [10] . The base engine results from the CFD are validated with experimental results as shown in Fig. 2 .

Fig. 1. Computational grid of the combustion chamber used for the CFD study.

Fig. 2. Comparison of in-cylinder pressures of the base engine.

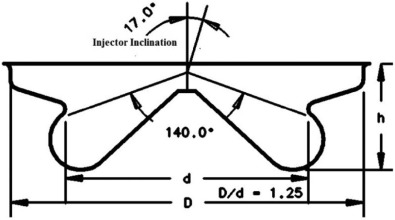
Fig. 3 shows the dimensions of the combustion chamber shape and injector inclinations of the base engine used for CFD study. Re-entrant type piston bowl with two different injector configuration is used for the study.

Fig. 3. Combustion chamber dimensions with injector inclination.

2.2. The governing equations

The CFD code, FIRE, solves the general conservation equations of mass, momentum and enthalpy along with transport equations for turbulence, conservation of chemical species and additional scalar quantities viz., mixture fraction, reaction progress variable, flame surface density, etc. The solution method is based on a fully conservative finite-volume approach. All dependent variables of momentum, pressure, density, turbulent kinetic energy, dissipation rate and scalar quantities are evaluated at the centre of computational cells. A second-order midpoint rule is used for integral approximation and a second order linear approximation for any value on the cell-face.

For discretization of the convection term, a second order accurate scheme is adopted. The rate of change is discretized by using the Euler implicit scheme. The overall solution procedure is iterative and is based on the Semi-Implicit Method for Pressure-Linked Equations algorithm (SIMPLE) applicable to turbulent flow at all speeds including super-sonic flow. For solving large sets of linear equations evolving from the discretization of the governing equations, an efficient pre-conditioned conjugate gradient method is adopted. For execution on multi-processor hardware, a domain decomposition parallelization approach is employed.

The general conversation equation in integral form being used in AVL-FIRE for any scalar ϕ shown in below equation,

${\displaystyle {\frac {d}{\mbox{dt}}}{\int }_{V}\rho \phi {\mbox{dV}}+{\sum }_{j=1}^{n_{f}}{\int }_{A_{j}}\rho \phi \left(U_{k}-U_{\mbox{bk}}\right){\mbox{dA}}_{k}}$ ${\displaystyle {\mbox{ }}={\sum }_{j=1}^{n_{f}}{\int }_{A_{j}}{\Gamma }_{\phi }^{\mbox{kk}}{\frac {\partial \phi }{\partial x_{k}}}{\mbox{dA}}_{k}+}$${\displaystyle {\int }_{V}S_{\phi }^{V}{\mbox{dV}}}$

( 2)

where, ϕ is a mean flow variable like velocity, pressure, density, temperature, etc. (i.e., conservation property per unit mass), which can represent either a scalar or a vector or a tensor, ?? is the fluid density, ${\textstyle U_{k}}$ is the velocity vector, ${\textstyle U_{\mbox{bk}}}$ is the velocity vector of moving boundary surface, and ${\textstyle S_{\phi }}$ is the source/sink term. In Eq. (2) , the first term represents the conservation property per unit volume, the second term represents the convection of ϕ, the third term represents the diffusion of ϕ, and the last term represents the source/sink of ϕ in a given computational domain.

2.3. Models for fuel spray, combustion and emissions

In the present study, liquid fuel spray is modelled according to the Lagrangian discrete droplet method. The continuous gaseous phase is described by the standard Eulerian conservation equation. The transport of the dispersed phase is calculated by tracking the trajectories of a certain number of representative parcels. A parcel consists of a number of droplets and it is assumed that all the droplets within one parcel have the same physical properties and behave equally when they move, break up, hit a wall or evaporate. The coupling between the liquid and the gaseous phase is achieved by the exchange of source term of mass, momentum, energy and turbulence. Various sub-models are used to account the effects of turbulent dispersion, coalescence, evaporation, wall interaction and droplet primary and secondary break up. In the present study, the blob-injection method in combination with the WAVE break-up model is used to model liquid fuel break-up downstream of the injector. Half of spray angle required for the spray modelling is calculated as [23] :

${\displaystyle tan\left({\frac {\theta }{2}}\right)={\frac {1}{A}}4\pi {\left({\frac {{\rho }_{g}}{{\rho }_{f}}}\right)}^{2}{\frac {\sqrt {3}}{6}}}$

( 3)

and the duration of injection (Δθ) is calculated as [23] :

${\displaystyle m_{f}=C_{D}A_{n}{\sqrt {2{\rho }_{f}\Delta p}}{\frac {\Delta \theta }{360N}}}$

( 4)

where, ${\textstyle {\rho }_{g}{\mbox{​}},{\mbox{ }}{\rho }_{f}{\mbox{​}},{\mbox{ }}C_{D}{\mbox{​}},{\mbox{ }}A_{n}{\mbox{ }}and{\mbox{ }}m_{f}}$ are the in-cylinder gas density, liquid fuel density, flow discharge coefficient and total mass of fuel injected respectively.

An extended coherent flame model (ECFM-3Z) is used for the simulation of the diesel HCCI combustion. This model is developed for simulating the combustion in perfectly or partially mixed conditions and also it accounts for unmixed portion. In this model, it is assumed that the chemical time delay in the reaction zone is much smaller than the time needed for the diffusion process. Therefore the rate of reaction during diffusion combustion is determined entirely by the intermixing of fuel and oxidizer. The amount of mixing is computed based upon a characteristic time-scale obtained from the solution of the k-ε turbulence model. The NOx formation is modelled by extended Zeldovichs mechanism that considers the effect of oxygen, nitrogen and hydrogen radicals on NO formation. The kinetic soot model based on detailed chemical reaction scheme is used for the calculation of soot formation and oxidation. It combines the mechanisms of formation of polyaromatic hydrocarbons, polyynes, two mechanisms of soot precursor formation due to condensation of polyaromatic and polyyne molecules, soot particle growth by the reactions of HACA mechanism and polyyne molecule addition, the mechanism of acetylene pyrolysis and pure carbon cluster formation, as well as the reactions of hydrocarbon (n-heptane) oxidation.

2.4. The boundary and initial conditions

For boundary conditions, the cylinder head surface is specified as a fixed wall and the piston top surface as a moving wall. The temperatures of the surfaces of the combustion chamber are set based on the available experimental data [23] . The surface temperature of the cylinder liner, piston and cylinder head are set at 375, 525 and 575 K respectively. The CFD simulation of the closed part of the engine cycle is performed at an engine speed of 2100 rev/min. Fuel injection pressure, timing and quantities have kept the same in both 7- and 10-hole injector cases (which are referred to as case-1 and case-2 hereafter). The operating conditions of the two cases are shown in Table 1 .

Table 1. The operating conditions.

Parameter	Case-1	Case-2
Engine speed (rpm)	2100
Intake swirl ratio	1.2
Compression ratio	15.3
Charge temperature @ IVC (K)	335
In-cylinder pressure @ IVC (bar)	1.4
No. of injector holes	7	10
EGR mass fraction	0.4

2.5. A user defined function

The cell information is extracted during the CFD simulation at required crank angles by the user defined function (UDF). The data extracted are: coordinates, velocity magnitude, gas temperature, turbulent kinetic energy, mass fractions of emissions, mass fraction of fuel, and mass fraction of EGR. The mass of fuel and ER in each cell is calculated from the mass fraction of the fuel. Since writing cell information at every crank angle consumes lot of computer memory, a UDF is activated only from the start of injection (SOI) to the end of combustion (EOC). Also, data are recorded at a frequency of five per crank angle.

3. Evaluation of mixture homogeneity

In this study, in order to assess the in-cylinder mixture homogeneity in a diesel engine, the following methods are proposed: (i) plot of the global fuel distribution (GFD), (ii) plot of the fuel distribution index (FDI), and (iii) plot of the local fuel distribution (LFD). In the following discussion, the term “global” refers to the entire combustion chamber and “local” refers to a specific radial or axial zone inside the combustion chamber.

3.1. The plot of global fuel distribution

The plot of GFD helps understand how well the injected fuel is dispersed inside the combustion chamber in a quantitative way. It shows the percentage of mass of evaporated fuel lying in various ER range. The plot of the GFD will be prepared by grouping cells based on their average ER in a step size of 0.3. The mass of fuel in each group is summed up and the percentage of fuel injected lying in each group is plotted. If the air and fuel are thoroughly mixed, then the mixture will be at the level of the mean ER. The percentage of fuel injected, which satisfies the desired ER range, will be then used to assess the mixture homogeneity. Advantages of this method are: (i) fuel distribution inside the combustion chamber can be quantified precisely, and (ii) from a single plot, dispersion of mass of fuel can be understood, whereas contour plot method requires many sections across the combustion chamber. However, limitations of this method are: mixture homogeneity is not defined by a simple scale from 0 to 1, and the spatial variation of the fuel mass inside combustion chamber cannot be understood.

3.2. Plot of fuel distribution index

The fuel distribution index is defined as the ratio of mass of evaporated fuel in cell groups for a given ER range to the total mass of evaporated fuel inside the combustion chamber. It is calculated for lean, target and rich conditions of the mixture. In this study, practical target ER range inside the combustion chamber is selected as 0.3 to 1.2 [3]. The fuel distribution index is calculated as,

${\displaystyle M_{F}=\Sigma \left(M_{\mbox{FL}}+M_{\mbox{FT}}+M_{\mbox{FR}}\right)}$

( 5)

${\displaystyle {\mbox{LFDI}}=M_{\mbox{FL}}/M_{F}{\mbox{​}},{\mbox{ }}{\mbox{TFDI}}=}$${\displaystyle M_{\mbox{FT}}/M_{F}{\mbox{​}},{\mbox{ }}{\mbox{RFDI}}=}$${\displaystyle M_{\mbox{FR}}/M_{F}}$

( 6)

${\displaystyle {\mbox{LFDI}}+{\mbox{TFDI}}+{\mbox{RFDI}}=1}$

( 7)

where

• M_F – Total injected fuel mass inside combustion chamber
• M_{FL –} Total fuel mass lying in cells having ER less than 0.3
• M_{FT –} Total fuel mass lying in cells having ER of 0.3 to 0.1.2
• M_{FR –} Total fuel mass lying in cells having ER greater than 1.2
• LFDI – Lean fuel distribution index
• TFDI – Target fuel distribution index
• RFDI – Rich fuel distribution index

The mixture homogeneity will be in the desired ER range if the TFDI is one. Advantage of this method is that the fuel distribution is evaluated in the scale from 0 to 1 making interpretation very simple and can be quantified precisely. However, a limitation of this method is that the spatial variation of the fuel mass inside the combustion chamber cannot be understood.

3.3. Plot of local fuel distribution (LFD)

The plots of the GFD and the FDI are not capable of explaining the spatial variation of the injected fuel mass inside a combustion chamber. Hence, we need to develop a new method to understand the mixture distribution in local zones of the combustion chamber. In the proposed method of the plot of LFD, the combustion chamber is divided into local zones both in radial and axial directions as shown in Fig. 4 . Cells are grouped based on the coordinate position and the sum of the mass of fuel in each local zone is computed. In each zone, cells are grouped based on their average ER with the step of 0.5 and the LFD in various zones is plotted as the percentage of total injected mass of fuel lying in various ER range. Since piston bowl volume is divided at a fixed interval of distance, volume of each zone is different. Hence, the ratio of the mass of fuel to volume of each zone is used to compare fuel concentration in various zones. The mixture homogeneity will be better, if the fuel density in each radial/axial zone is closer to the GFD and all the injected mass of fuel will get distributed in the target ER range. Then the LFD is analyzed by three types of plots: (i) type 1: plot of local axial or radial zone versus percentage of total injected mass of fuel, (ii) type 2: plot of local ER range versus percentage of total mass of injected fuel, and (iii) type 3: plot of local axial or radial zone versus local fuel density.

Fig. 4. Zones in radial and axial directions inside the piston bowl.

Advantages of the plot of LFD are: (i) spatial variation of mixture homogeneity can be directly assessed and quantified, (ii) by comparing results of LFD and ER contour plots, the physical phenomenon driving the mixing process can be understood. These methods can be integrated with CFD analysis and can be used for easy post-processing of results.

4. Results and discussion

The results of case-1 and case-2 are used to demonstrate the existing and proposed mixture homogeneity evaluation methods. The advantages and the limitations of all methods will be assessed.

4.1. Existing in-cylinder mixture homogeneity evaluation methods

4.1.1. Contour plots of ER

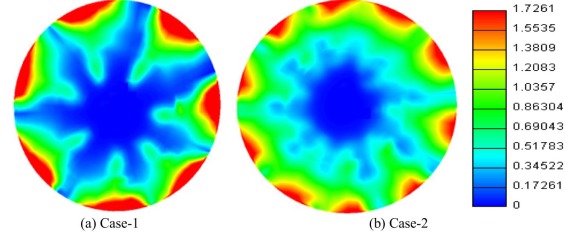
Fig. 5 shows contour plots of ER on a horizontal plane located at 12 mm below the piston top surface for case-1 and case-2. A visual observation shows an improvement in fuel distribution with case-2 compared to case-1 and the degree of mixture homogeneity is increased. Both very lean and rich mixture zones are reduced in case-2. In order to understand the mixture distribution throughout the combustion chamber, we need to look at many contour plots of ER at various planes. Hence, this method is time consuming, mixture homogeneity cannot be quantified and interpretation of results can vary from person to person.

Fig. 5. Contour plots of ER on horizontal planes-12 mm from piston top.

4.1.2. Plot of heat release rate

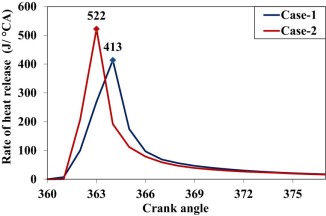
Fig. 6 shows the comparison of variation of heat release rates for case-1 and case-2. In both the cases, the start of combustion occurs almost at the same crank angle. The maximum heat release rate is about 521 J/CA in case-2, whereas it is 413 J/CA in case-1. An increase in the level of heat release rate and reduction in combustion duration in case-2 indirectly indicates the improvement in the mixture homogeneity. Additionally, this method can be used for the analysis of both CFD and experimental results.

Fig. 6. Comparison of variation of heat release rate for case-1 and case-2.

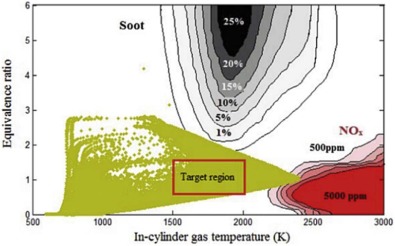
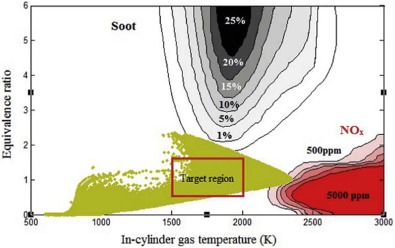
4.1.3. Plot of in-cylinder temperature versus equivalence ratio

Fig. 7  and Fig. 8 show plots of mixture temperatures versus equivalence ratios (T-ϕ) at 50% heat release conditions for case-1 and case-2. In both case-1 and case-2, in most of the local zones, the ER and in-cylinder temperature conditions are such that they do not favour the formation of NOx and PM. In case-1, the number of cells having ER greater than 1.5 is about 26 500, whereas in case-2, it is about 18 000. This reduction is because of the improvement in mixture homogeneity in case-2.

Fig. 7. Plot of temperature–equivalence ratio for case-1 at 50% heat release.

Fig. 8. Plot of temperature–equivalence ratio in case-2 at 50% heat release.

4.2. Proposed methods for the evaluation of in-cylinder mixture homogeneity

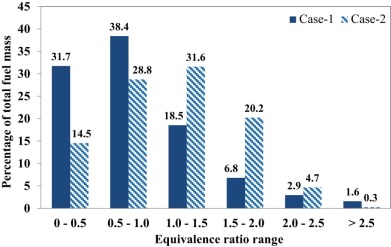
4.2.1. Plot of global fuel distribution (GFD)

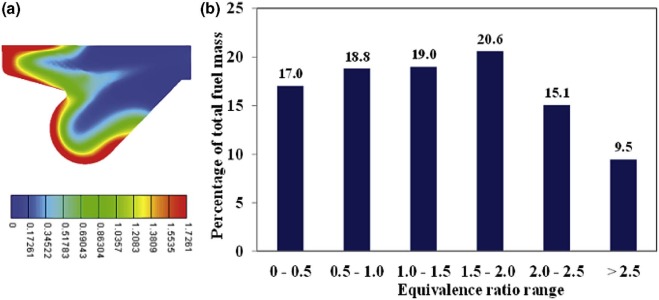
Fig. 9 (a) and (b) shows the plot of ER contour and the GFD at the SOC for case-1 respectively. From Fig. 9 (a), it is evident that the rich region observed along the periphery of the piston bowl in an omega shape and very lean region around the centre of the piston bowl. From Fig. 9 (b), we can observe that about 37.8% of the fuel lies in the desired ER level at the SOC. Also about 17 and 45.1% of the fuel lies in very lean and rich mixture levels.

Fig. 9. (a) ER contour plot at SOC for case-1. (b) Plot of global fuel distribution at SOC for case-1.

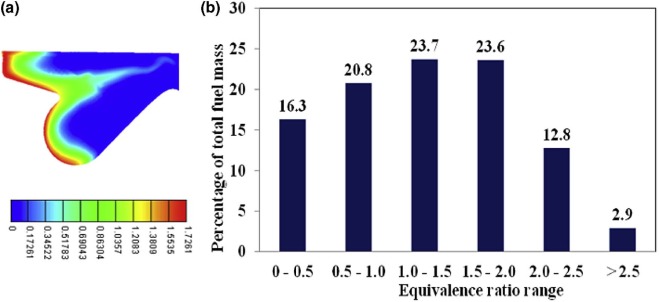
Fig. 10 (a) and (b) shows the plot of ER contour and GFD at SOC for case-2 respectively. From Fig. 10 (a), it is evident that the rich region along the periphery of the piston bowl has reduced significantly and very lean region has increased.

Fig. 10. (a) ER contour plot at SOC for case-2. (b) Plot of global fuel distribution at SOC for case-2.

From Fig. 10 (b), we can observe that in case-2, the fuel lying in the rich mixture region has reduced to 39.3% and fuel lying in the desired ER level has increased to 44.4%. Therefore, case-2 has better mixture homogeneity and the fuel lying in the required ER level has increased by about 17% compared to that of case-1. Hence, when contour plot is analyzed along with GFD plot, we can understand the fuel distribution both qualitatively and quantitatively.

4.2.2. Plot of fuel distribution index

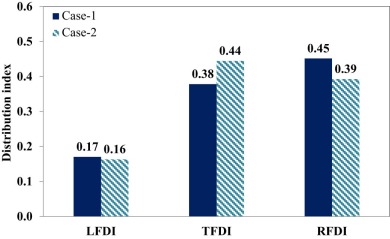
Fig. 11 shows the plot of fuel distribution index for case-1 and case-2. The target fuel distribution index (TFDI) is 0.38 in case-1, whereas it is 0.44 in case-2, which means 44% of the total injected fuel is in the desired ER range. Rich fuel distribution index (RFDI) has reduced to 0.39 from 0.45 in case-2. An increase in the TFDI and a decrease in the RFDI are the indications of the improvement of mixture homogeneity in case-2.

Fig. 11. Plot of fuel distribution index for case-1 and case-2.

4.2.3. Plot of local fuel distribution (LFD)

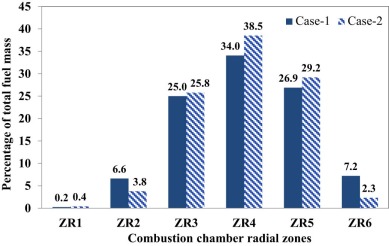
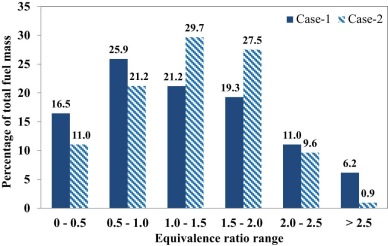
Fig. 12 shows the plot of the local fuel distribution in radial zones of the combustion chamber for case-1 and-2. From Fig. 12 , we can see that for case-1, about 34, 26.9 and 25% of the total mass of the evaporated fuel are in ZR4, ZR5 and ZR3 zones, respectively, whereas in case 2, they are about 38.5, 29.2 and 25.8% respectively. From Fig. 12 , we found that the fuel mass percentages in zone ZR2 and ZR6 have reduced to 3.8 and 2.3% in case-2 compared to those of case-1, which is due to increase in number of injector hole. The zone ZZ4 has the highest percentage of the total mass of injected fuel. Fig. 13 shows the LFD at the zone ZR4 for case-1 and case-2. The mass of fuel lying in the very rich zone (ER > 2) has reduced to 10.5%, whereas that in the lean zone (ER < 0.5) is reduced to 11% in case-2 compared to those of case-1. The mass of fuel lying in the ER range of 1 and 2 has increased by about 21% in case-2.

Fig. 12. Plot of local fuel distribution for case-1 and case-2 along radial zones.

Fig. 13. Plot of local fuel distribution in the radial zone ZR4 for case-1 and case-2.

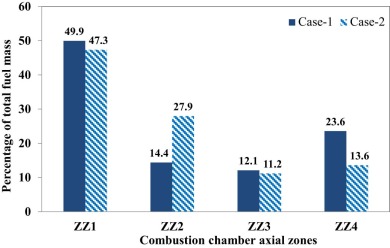
Hence, it is evident that the mixture distribution got improved in the zone ZR4 for case-2. Fig. 14 shows the plot of LFD in the axial zones of the combustion chamber for case-1 and case-2. From Fig. 14 , we see that the percentages mass of the total fuel in the zone ZZ1 in both the cases are comparable. In case-2, the fuel in the zone ZZ2 has increased to 28% from 14.4%, whereas in the zone ZZ4, it has reduced to about 13.6% from 23.6% compared to those of case-1.

Fig. 14. Plot of local fuel distribution for case-1 and case-2 along axial zones.

Fig. 15 shows the LFD in the zone ZZ2 for case-1 and case-2. From Fig. 15 , we see that the mass of fuel lying in the very lean zone (ER < 0.5) has reduced by about 54.2% in case-2 compared to that of case-1. The mass of fuel lying in the ER range of 1 and 2 has increased by about 105% in case-2. Hence, it is evident that the mixture distribution has improved in case-2. From Fig. 9  and Fig. 10 , we observe an omega shaped fuel distribution along the periphery of the combustion chamber. From Fig. 9 , Fig. 10 , Fig. 12  and Fig. 14 , we can make an accurate qualitative and quantitative assessment of the mixture homogeneity with a better understanding of the spatial distribution of fuel in a combustion chamber.

Fig. 15. Plot of local fuel distribution in the axial zone ZZ2 for case-1 and case-2.

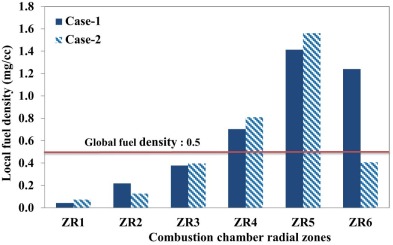
Fig. 16 shows the plot of local fuel density in radial zones of the combustion chamber for case-1 and case-2. From Fig. 16 , it is clearly evident that the local fuel density in zones ZR1, ZR2 and ZR3 are less than the global fuel density, whereas in zone ZR4, ZR5 and ZR6, the local fuel densities are more than the global fuel density. Hence the mass of the injected fuel is concentrated nearer the periphery of the piston bowl. The local fuel density in the zone ZR6 has reduced to 0.67 from 1.2 in case-2 compared to that of case-1. This indicates that there is an improvement in the fuel distribution along the periphery of the combustion chamber.

Fig. 16. Variation of local fuel density in radial zones of the combustion chamber.

5. Conclusions

In this study, a CFD analysis has been carried out on a DI diesel engine in a premixed combustion mode with two fuel injector configurations. The results obtained in this study are used to compare the existing and the proposed methods for the evaluation of mixture homogeneity. From the analysis, the following conclusions are drawn.

• Currently, researchers are using plots of the contour of ER and heat release rate, emissions and plot of temperature versus ER for the evaluation of air–fuel mixture homogeneity in engines. However, these methods can assess the change in fuel distribution only qualitatively and they fail to quantify.
• The proposed methods to assess the mixture homogeneity can effectively quantify the change in fuel distribution pattern in all the conditions of the engine. Using the plot of the global fuel distribution, one can clearly understand how the injected fuel is distributed in a various ER range inside the combustion chamber.
• The fuel distribution index is a simple and quick assessment tool for the study of mixture homogeneity inside a combustion chamber of an engine. However, with GFD and fuel distribution index methods, spatial variation of ER cannot be understood.
• Using the plot of the local fuel distribution (LFD), one can assess the mixture distribution both qualitatively and quantitatively with a better understanding of the spatial variation of fuel inside the combustion chamber in an engine.

Acknowledgements

The authors would like to convey their sincere thanks to the management of M/s Mahindra and Mahindra Ltd., Chennai, India, for supporting the research work and granting the permission to publish this paper.

Appendix

Table A1. The engine specifications.

Engine type	Three cylinders, inline DI diesel engine
Bore × stroke (mm)	96 × 122
Displacement (cm3 )	2647 (882 cm3 /cylinder)
Aspiration	Turbocharger intercooled (TCI)
Engine cooling	Water cooled
Compression ratio	15.3:1
Combustion chamber type	Re-entrant bowl
Swirl ratio	1.2
Fuel injection pump	Bosch CRDI pump
CRDI injector	7-hole × 0.135 mm diameter
EGR	Electronic control valve
Intake charge control	Intercooler
Valve timings	IVC = 35° aBDC EVO = 35° bBDC

References

1. [1] S. Kimura, O. Aoki, Y. Kitahara, E. Aiyoshizawa; Ultra clean combustion technology combining a low temperature and premixed combustion concept for meeting future emission standards; SAE paper no 2001-01-0200  (2001)
2. [2] K. Nakagome, N. Shimazaki, S. Kobayashi; Combustion and emissions characteristics of premixed lean diesel combustion engine; SAE paper no 970898  (1997)
3. [3] K. Akihama, Y. Takatori, K. Inagaki; Mechanism of the smokeless rich diesel combustion by reducing temperature; SAE paper no 2001-01-0655  (2001)
4. [4] T.J. Jacobs, D.N. Assanis; The attainment of premixed compression ignition low temperature combustion in a compression ignition direct injection engine; Proceed. Combust. Inst, 31 (2007), pp. 2913–2920
5. [5] C.L. Genzale, R.D. Reitz, M.P.B. Musculus; Effects of spray targeting on mixture development and emissions formation in late-injection low-temperature heavy-duty diesel combustion; Proceed. Combust. Inst, 32 (2009), pp. 2767–2774
6. [6] J.E. Dec; Advanced compression-ignition engines – understanding the in-cylinder processes; Proceed. Combust. Inst, 32 (2009), pp. 2727–2742
7. [7] D. Choi, P.C. Miles, H. Yun, R.D. Reitz; A parametric study of low temperature late injection HCCI combustion concept; JSME, Series B, 48 (4) (2005)
8. [8] K. Kawamoto, T. Araki, S. Kimura; Combination of combustion concept and fuel property for ultra-clean DI diesel; SAE paper no 2004-01-1868  (2004)
9. [9] L. Cao, A. Bhave, S. Mosbach, M. Kraft; Influence of injection timing and piston bowl geometry on PCCI combustion and emissions; SAE paper no 2009-01-1102  (2009)
10. [10] S. Juttu; Computational and experimental investigations in to the development strategies for reducing emissions in diesel HCCI engines; Ph.D., Thesis; Indian Institute of Technology Delhi  (2010)
11. [11] R. Davarnejad, M. Jamshidzadeh; CFD modeling of heat transfer performance of MgO–water nanofluid under turbulent flow; Eng. Sci. Technol, 18 (4) (2015), pp. 536–542
12. [12] S. Choi, W. Park, S. Lee, K. Min, H. Choi; Methods for in-cylinder EGR stratification and its effects on combustion and emission characteristics in a diesel engine; Energy, 36 (2011), p. 6948e6959
13. [13] R.D. Reitz, G. Duraisamy; Review of high efficiency and clean reactivity controlled compression ignition (RCCI) combustion in internal combustion engines; Prog. Energy Combust. Sci, 46 (2015), p. 12e71
14. [14] S. Saxena, I.D. Bedoya; Fundamental phenomena affecting low temperature combustion and HCCI engines, high load limits and strategies for extending these limits; Prog. Energy Combust. Sci, 39 (2013), pp. 457–488
15. [15] H. Bendu, S. Murugan; Homogeneous charge compression ignition (HCCI) combustion: mixture preparation and control strategies in diesel engine; Renew. Sustain. Energy Rev, 38 (2014), pp. 732–746
16. [16] M.H. Salmani, S. Rehman, K. Zaidi, A.K. Hasan; Study of ignition characteristics of micro emulsion of coconut oil under off diesel engine conditions; Eng. Sci. Technol, 18 (3) (2015), pp. 318–324
17. [17] A. Elfasakhany; Investigations on the effects of ethanol–methanol–gasoline blends in a spark-ignition engine: performance and emissions analysis; Eng. Sci. Technol, 18 (4) (2015), pp. 713–719
18. [18] B. Miriam, G. Valeri; Application of on transient temperature versus equivalence ratio emission maps on engine simulation; SAE paper no 2007-01-1086  (2007)
19. [19] ESE; Engine simulation environment (ESE) tutorial; AVL FIRE manual  (2011)
20. [20] Y. Mingfa, Z. Zheng, H. Liu; Progress and recent trends in homogeneous charge compression ignition (HCCI) engines; Prog. Energy Combust. Sci, 35 (2009), pp. 398–437
21. [21] S. Khalilarya, S. Jafarmadar, H. Khatamnezhad, G. Javadirad, M. Pourfallah; Simultaneous reduction of NOx and soot emissions in a DI heavy duty diesel engine operating at high cooled EGR rates; Int. J. Aerosp. Mech. Eng, 6 (2012), p. 1
22. [22] R. Tatschl, P. Priesching; 3D-CFD simulation of DI-diesel engine combustion and pollutant formation; Sci. Bull (2010) University of Pitesti
23. [23] J.B. Heywood; Internal Combustion Engine Fundamentals; McGraw-Hill (1988)