Revision as of 14:05, 28 February 2017 (view source) Scipediacontent (talk | contribs) (Created page with "==Resumen== La etapa de precongelación es un importante paso en el proceso de manufactura de helados y sorbetes dado que las condiciones de operación tienen una fuerte infl...")	Latest revision as of 14:10, 28 February 2017 (view source) Scipediacontent (talk | contribs) m (Scipediacontent moved page Draft Content 980186070 to Gonzalez-Ramirez et al 2012a)
(No difference)

---

Latest revision as of 14:10, 28 February 2017

Resumen

La etapa de precongelación es un importante paso en el proceso de manufactura de helados y sorbetes dado que las condiciones de operación tienen una fuerte influencia sobre la microestructura y por consecuencia sobre los atributos sensoriales del producto final. Esta etapa de precongelación es llevada a cabo en un intercambiador de calor de superficie raspada donde la calidad del producto es fuertemente influenciada por las condiciones de operación tales como la temperatura de evaporación de un refrigerante, el gasto másico de la alimentación, la velocidad del raspador y una presión provocada por la introducción de aire. Con la finalidad de estudiar la pertinencia de un sistema de control basado en la influencia de las variables del proceso sobre la calidad del producto, este trabajo presenta un modelo para una cristalización continua de un sorbete utilizando la metodología de momentos, el cual es validado con datos experimentales. El modelo realizado por esta metodología de momentos es capaz de representar la influencia de las condiciones de operación durante la cristalización de sorbete sobre las características finales del producto tales como el tamaño de cristal y la temperatura de salida del intercambiador de superficie raspada (ICSR) en ausencia de aire. El modelo basado en momentos se estudia, entonces, como la reducción del modelo de la ecuación de balance de población e incluye los fenómenos de nucleación heterogénea y crecimiento. De este modo, el modelo desarrollado representa requerimientos computacionales mínimos y está altamente adaptado para tareas de optimización y/o control del proceso.

Abstract

Freezing is an important step in the manufacturing process of ice-cream and sorbet, since the operating conditions have a strong influence on the micro-structure, and consequently on the sensorial attributes of the final product. This steep of freezing is carried out by a scraped surface heat exchanger (SSHE) where the product quality is conditioned by process conditions as the evaporation temperature of a refrigerant fluid, the mix flow rate, the dasher speed and the cylinder pressure due to the air introduction. In order to study the relevance of a control system based on the influence of process variables on product quality, this paper presents a model for a continuous crystallization of a sorbet using the method of moments, which is validated by experimental data.The model created by this methodology has been able to represent the influence of the process conditions during the crystallization of the sorbet on the final product characteristics such as crystal size and the draw temperature in the outlet of the SSHE in absence of air. The model based in moments is studied as a reduced model of the population balance equation and includes the phenomena of heterogeneous nucleation and growth. This model developed represents minimal computational requirements and is highly adapted for optimization and/or process control tasks.

Palabras clave

Modelo de cristalización ; Sorbete ; Helado ; Reducción de modelo ; Método de momentos

Keywords

Crystallization model ; Sorbet ; Ice cream ; Model reduction ; Method of moments

Nomenclatura

Letras latinas

Cp- Capacidad calorífica [J kg⁻¹ K⁻¹ ]

D- Diámetro [m]

G- Velocidad de crecimiento [m s⁻¹ ]

L- Medida de cristal [m]

L_c- Medida critica de cristales [m]

L_ech- Longitud del intercambiador [m]

M_j- Momento j de cristalización

N- Velocidad de nucleación [m⁻³ s⁻¹ ]

PS- Superficie ponderada por el volumen [m⁻¹ ]

Q- Flujo de calor [W]

r_e- Radio externo [m]

r_i- Radio interno [m]

S- Superficie de intercambio de calor [m² ]

t- Tiempo [s]

T- Temperatura del producto [C o K]

T_e- Temperatura de evaporación [C o K]

T_sat- Temperatura de saturación [C o K]

U- Coeficiente global de transferencia de calor [W m⁻² K⁻¹ ]

u- Energía interna[W m-3]

V- Volumen [m³ ]

${\textstyle {\overset {\mbox{ˆ}}{V}}}$- Volumen específico [m³ Kg⁻¹ ]

VR- Velocidad de rotación [rps]

x_g ∘ - Volumen másico [m³  kg⁻¹ ]

Letras griegas

α- Coeficiente de nucleación homogénea [m⁻³ s⁻¹ ]

α′- Coeficiente de nucleación homogénea [m⁻² s⁻¹ ]

β- Coeficiente de crecimiento [ms⁻¹ ]

χ- Factor de corrección de la velocidad de cizallamiento [-]

γ- Potencia para la ecuación de nucleación homogénea [-]

γ′- Potencia para la ecuación de nucleación heterogénea [-]

${\textstyle {\dot {\gamma }}}$- Velocidad de cizallamiento [s⁻¹ ]

Γ- Factor de corrección de viscosidad [-]

φ_g- Fracción volumétrica de hielo

λ- Conductividad térmica [W m⁻¹  K⁻¹ ]

μ- Viscosidad del producto [Pa-s]

μ_s- Viscosidad de la solución [Pa-s]

ρ- Masa volumétrica [kg m⁻³ ]

σ- Potencia para la ecuación de crecimiento

ω₀- Fracción inicial de sólidos [-]

ψ- Termino de población de cristales [np m⁻³ ]

Abreviaciones

ICSR- Intercambiador de calor de superficie raspada

DTC- Distribución del tamaño de cristal

PBE- Ecuación de balance de población

Subíndices

frigo- Frigorífica

crist- De cristalización

visc- De disipación viscosa

1. Introducción

El proceso actual para la producción del helado y/o sorbete se basa en la utilización de intercambiadores de calor de superficie raspada (ICSR) que permite el óptimo intercambio de calor entre una mezcla líquida y la superficie del intercambiador. Este ICSR tiene como principal objetivo funcionar como un cristalizador y está compuesto conceptualmente por 2 tubos concéntricos. Por el tubo exterior se vaporiza un fluido refrigerante que es desplazado por una máquina de refrigeración. De manera similar, por el tubo interior se encuentra un eje giratorio provisto de cuchillas raspadoras. El objetivo de estas cuchillas es raspar la pared mientras una mezcla liquida pasa a través de este tubo interior y se cristaliza utilizando la energía donada por la vaporización del refrigerante al otro lado del intercambiador [1] . El objetivo general de este proceso es la obtención de una textura ligera, una buena «cremosidad», una alta «cucharabilidad» y sensación de frio. Esto conlleva, por consecuencia, al objetivo en común de diversos trabajos, que el producto contenga los cristales más pequeños posibles [2]  and [3] .

Un gran número de trabajos en la literatura han desarrollado estudios sobre el rol del tamaño de cristal sobre la microestructura y las propiedades sensoriales de helados y sorbetes. Por ejemplo se ha mostrado que el tamaño de cristal afecta la dureza; así un helado con cristales grandes es más duro que otro con cristales pequeños [3] . Por otro lado, se ha reportado una clara correlación entre la «detectabilidad» del tamaño medio de los cristales [4] . La «cremosidad» del producto como atributo es también relacionada con la microestructura de un helado, donde una alta densidad de partículas resulta en un producto naturalmente cremoso [5] .

Todos estos trabajos mencionados hacen enfocar a los investigadores en el área para trabajar sobre la optimización de los procesos de producción de helados. Por ejemplo, Inoue et al. [6] establecen un modelo empírico del proceso de helado usando la metodología de superficie de respuesta. Ellos realizaron un análisis estadístico de la influencia de 5 variables dirigidas hacia el proceso y el producto mismo. Dichas variables fueron el gasto másico de mezcla, la cantidad de aire inyectado a la microestructura del producto, la presión del cilindro de cristalización, la velocidad del raspador y la temperatura de salida del producto. Ligan cada una de estas variables con las mediciones de tamaño de partícula y la desestabilización de la grasa. Por otro lado, Drewett y Hartel [7] realizaron también un modelo empírico basado en el análisis estadístico (ANOVA) para la predicción del tamaño medio de partícula controlando el tipo de endulzante, la velocidad del raspador y el tiempo de residencia de la mezcla en el cristalizador. A pesar de este tipo de aproximaciones, los modelos realizados no pueden ser utilizados para predecir el comportamiento de alguna otra fórmula u otro proceso de producción de helado. Estos modelos son apropiados para el conocimiento de las propiedades del producto bajo ciertas condiciones en régimen estacionario, pero para la predicción del comportamiento del producto acoplado al proceso se necesita el buen conocimiento de la cinética de cristalización, así como de la transferencia de calor en el ICSR.

Son muy pocos los trabajos enfocados al modelado físico para la cristalización del helado. En estos trabajos el fenómeno de cristalización es comúnmente descrito por una ecuación de balance de población (BPE por sus siglas en inglés). Este modelo de cristalización ha sido propuesto para la obtención de una distribución de talla de los cristales (DTC), teniendo el inconveniente de ser complejo a resolver [8]  and [9] .

${\displaystyle {\underset {Acumulaci{\mbox{ó}}n}{\underbrace {\frac {\partial n}{\partial t}} }}+}$${\displaystyle {\underset {Convenci{\mbox{ó}}n}{\underbrace {{\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}n} }}+}$${\displaystyle {\underset {Crecimiento}{\underbrace {{\frac {\partial }{\partial L}}(Gn)} }}=}$${\displaystyle {\underset {Nacimiento}{\underbrace {N} }}-{\underset {Desaparici{\acute {o}}n}{\underbrace {F} }}}$

( 1)

La integración de esta ecuación se basa en derivadas parciales que necesitan dividirse en talla de las partículas así como en tiempo. La resolución numérica de este tipo de división se puede mostrar suficientemente costosa en tiempo de cálculo, y entonces poco adaptada para el control de un proceso.

Así, en el marco de la investigación de un modelo robusto con vistas del control de mando de un proceso de cristalización, el método nombrado «método de momentos» se vuelve atractivo, el cual puede ser utilizado como una vía para reducir el modelo de BP. El principio de la metodología consiste en calcular los diferentes momentos de la ecuación definidos por:

${\displaystyle M_{j}={\int }_{0}^{\infty }L^{j}n(L,t)dL}$

( 2)

En este caso, solo los 4 primeros momentos (j = 0 a 3) son los más interesantes para una utilidad en optimización-control. Así, el momento cero (M₀) representa el numero de partículas, M₁ proporciona la talla media de los cristales, M₂ la superficie total de los cristales y M₃ la suma de los volúmenes de cristales por unidad de volumen de producto [10] , [11]  and [12] .

El modelado de la cristalización por el método de momentos ha sido largamente estudiado, siempre tomando como base la ecuación de balance de población. Algunos consideran que la reducción del BP hacia los momentos proporciona una aproximación favorable a un modelo completo. Por ejemplo, Chiu y Christofides [13] utilizan el método de momentos reduciendo la ecuación de BP para implementarlo en un lazo de control para un cristalizador continuo. En otro trabajo, D. Shi et al. [14] reducen, de igual manera, el modelo de balance de población por el método de momentos. Ellos investigan la reducción de grados de libertad por el control de la distribución de talla de cristales sobre un cristalizador continuo y/o por lotes. Por otro lado, Chang y Hartel [15] se han propuesto la reducción de la ecuación de BP por el método de momentos como una nueva estrategia de procesos de cristalización evaporatoria en batch o semibatch.

Se constata, entonces, que el método de momentos es una opción real a ser implantada sobre el modelado de cristalizadores en superficie raspada, objetivo principal de este trabajo. De esta manera, la presente investigación proporcionará una descripción minuciosa sobre la reducción del modelo BPE mediante el método de momentos con la finalidad de crear un modelo capaz de simular un proceso de cristalización de un sorbete en un ICSR continuo. Este modelo integrará los efectos de cada una de las variables del proceso, así como de la cinética de nucleación y crecimiento de cristales. Una de las principales ventajas de este modelo es su eficiencia numérica, por lo cual puede ser usado para la optimización y control de procesos de producción de helados y sorbetes.

2. Formulación del modelo

2.1. Modelo de cristalización y método de momentos

El modelo de cristalización por medio del balance de población ha sido aplicado a numerosos procesos industriales dando como resultado una aproximación apropiada para el modelado dinámico de procesos de cristalización de hielo. La ecuación de balance de población (PBE por sus siglas en inglés) permite describir el estado del sistema por medio de una función de densidad, tomando en cuenta los diferentes fenómenos que controlan dicha función de densidad, tal como lo son la fragmentación, la coalescencia, el crecimiento y la conservación de movimiento de las partículas. La ecuación resultante de este modelo es una ecuación derivativa parcial altamente no lineal, la cual requiere de un método numérico para resolverla (ec. 3).

${\displaystyle {\frac {\partial \psi }{\partial t}}+{\overset {\rightarrow }{v}}\cdot {\overset {\rightarrow }{\nabla }}\cdot \psi {\underset {Crecimiento}{\underbrace {{\frac {\partial }{\partial L}}(G\psi )} }}=}$${\displaystyle {\underset {Creaci{\mbox{ó}}n}{\underbrace {B} }}-{\underset {Desaparici{\mbox{ó}}n}{\underbrace {D} }}}$

( 3)

donde t es el tiempo, ψ(L,x,y,z,t) es la función de densidad (función de distribución de cristales), L es la dimensión característica, v es el vector de velocidad convectiva, G es la tasa de cambio de la dimensión característica, B y D son los términos de formación de nuevos cristales y la remoción de cristales ya existentes respectivamente.

Una manera tradicional para resolver esta ecuación no lineal es utilizando el método de clases, el cual implica la creación de más de un centenar de ecuaciones diferenciales para la determinación de una distribución de tamaños de partícula, lo cual conlleva a altos requerimientos computacionales y por tanto un modelo no apto para el control del proceso donde se requiere tener respuestas rápidas para la solución de problemas ocasionados por perturbaciones en el proceso. Para resolver este problema, una alternativa viable es el uso de la metodología de momentos, la cual es una aproximación discreta y directa para la resolución de la PBE. Este método transforma la PBE en un grupo de ecuaciones diferenciales ordinarias [16] , el cual tiene requerimientos computacionales pequeños permitiendo su uso eficientemente en el diseño de sistemas de control. El modelo físico final en este caso es un modelo «reducido» mas no uno simplificado empleando cierto número de hipótesis sobre las propiedades termodinámicas que permiten hacer una aproximación a la PBE. La única restricción para este modelo es la cantidad limitada de información que es capaz de arrojar.

Los momentos de esta metodología son definidos por la expresión:

${\displaystyle M_{j}={\int }_{0}^{\infty }L^{j}\psi (L,t)dL}$

( 4)

De esta forma los 4 primeros momentos (j = 0 a 3) pueden ser interpretados físicamente: si se supone por ejemplo que las partículas son esféricas, que L es el diámetro de la partícula y que ψ es la densidad de partículas por unidad de volumen, el momento de orden cero (M₀) representa entonces, por unidad de volumen, el número total de partículas, M₁ la suma de diámetros, M₂ un número proporcional a la suma de sus superficies y M₃ a la suma de sus volúmenes [10] , [11]  and [12] .

A fin de transformar la PBE en momentos se reordena la ecuación (1) tomando en cuenta solamente la nucleación de partículas, con las siguientes consideraciones:

• Se realiza la suposición de un tamaño inicial L_c para los cristales una vez que se han creado. Este tamaño es, sin embargo, difícil de caracterizar experimentalmente, por lo que se puede crear con un valor arbitrario.
• El fenómeno de atrición y/o erosión de partículas son despreciados.
• El fenómeno de aglomeración es igualmente discriminado [14] .

Dadas las consideraciones expuestas surge como primera aproximación la ecuación (5):

${\displaystyle {\frac {\partial \psi (L,t)}{\partial t}}+{\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}\psi +}$${\displaystyle {\frac {\partial }{\partial L}}\left(G\psi \right)=N\delta \left(L-\right.}$${\displaystyle \left.L_{c}\right)}$

( 5)

donde δ es la función de Dirac y L_c el diámetro inicial de la partícula una vez que su creación. Esta primera aproximación considera un diámetro crítico de cristal (L_c) estimado en 5 × 10⁻⁶ m para ser considerado como tal. Para este caso la velocidad de nucleación se considera constante al igual que su homóloga para el crecimiento de cristales. Tal como se verá en la deducción de los momentos de cristalización, la función de Dirac será despreciada al tener como objetivo la obtención de un tamaño medio de partícula, por lo que la función de nucleación es función solamente de la velocidad de la misma y del diámetro crítico de cristales de hielo.

Aplicando entonces la metodología de momentos se obtiene:

${\displaystyle {\int }_{0}^{\infty }L^{j}\left({\frac {\partial \psi (L,t)}{\partial t}}+\right.}$${\displaystyle \left.{\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}\psi +\right.}$${\displaystyle \left.{\frac {\partial }{\partial L}}\left(G\psi \right)\right)dL=}$${\displaystyle \int _{0}^{\infty }L^{j}\left(N\delta \left(L-L_{c}\right)\right)dL}$

( 6)

Para facilitar el estudio de la transformación de la PBE se estudia detalladamente cada uno de los términos de la ecuación (6).

• Término de acumulación: si se refiere a la definición del momento de orden j, el término se convierte en la ecuación (7):

${\displaystyle {\int }_{0}^{\infty }L^{j}{\frac {\partial \psi \left(L,t\right)}{\partial t}}dL=}$${\displaystyle {\frac {dM_{j}}{dt}}}$

( 7)

• Término de convección de partículas: para el término de convección se considera que todas las partículas tienen la misma velocidad, por lo que se convierte en la ecuación (8).

${\displaystyle {\int }_{0}^{\infty }L^{j}{\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}\psi dL=}$${\displaystyle {\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}M_{j}}$

( 8)

• Término de crecimiento: la integración del término de crecimiento de las partículas, considerando que G es independiente del tamaño característico, conlleva a la ecuación (9) y por consecuencia a la ecuación (10):

${\displaystyle {\int }_{0}^{\infty }L^{j}{\frac {\partial }{\partial L}}\left(G\psi \left(L,t\right)\right)dL=}$${\displaystyle G{\left[L^{j}\psi \right]}_{0}^{\infty }-jG{\int }_{0}^{\infty }L^{j-1}\psi dL}$

( 9)

Como ${\textstyle L^{j}\psi (L){\overset {L\rightarrow \infty }{\longrightarrow }}0}$ y que ${\textstyle L^{j}\psi (L){\overset {L\rightarrow 0}{\longrightarrow }}0}$ , se obtiene:

${\displaystyle {\int }_{0}^{\infty }L^{j}{\frac {\partial }{\partial L}}\left(G\psi \left(L,t\right)\right)dL=}$${\displaystyle -jG\cdot M_{j-1}}$

( 10)

• Término de nucleación: teniendo en cuenta una velocidad de nucleación constante, la integración de nucleación nos lleva a la ecuación (11):

${\displaystyle {\int }_{0}^{\infty }L^{j}N\delta \left(L-L_{c}\right)dL=}$${\displaystyle L_{c}^{j}N}$

( 11)

Así, el sistema de ecuaciones final que se obtiene, si solo consideramos los primeros 4 momentos, se representa por el sistema de ecuaciones diferenciales representado por la ecuación (12):

${\displaystyle {\frac {dM_{0}}{dt}}+{\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}M_{0}-N=0}$ ${\displaystyle {\frac {dM_{1}}{dt}}+{\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}M_{1}-GM_{0}-L_{c}N=0}$ ${\displaystyle {\frac {dM_{2}}{dt}}+{\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}M_{2}-2GM_{1}-L_{c}^{2}N=0}$ ${\displaystyle {\frac {dM_{3}}{dt}}+{\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}M_{3}-3GM_{2}-L_{c}^{3}B=0}$

( 12)

A fin de modelar en estado estacionario el proceso de cristalización de un sorbete, se plantean diversas hipótesis que se presentan a continuación:

• Se supone que solo cristaliza agua y que las partículas formadas son esféricas.
• Se discrimina la difusión radial en el intercambiador.
• La temperatura de evaporación o de pared del cristalizador se supone constante sobre toda el largo del intercambiador.
• Se considera un flujo de tipo pistón, por consecuencia, el término de convección no se utiliza en las ecuaciones del modelo.

Para determinar finalmente el modelo es necesaria la definición de la cinética de cristalización, así como el fenómeno de transferencia de calor dentro del intercambiador. En el caso de la cinética de cristalización se deben tomar en cuenta las cinéticas de nucleación y de crecimiento de cristales, que son descritas a continuación:

• Velocidad de nucleación y de crecimiento de cristales

La velocidad de nucleación propuesta es expresada a partir de la ecuación 13 [17] :

${\displaystyle N={\underset {\begin{array}{cc}Nucleaci{\mbox{ó}}n&homog{\mbox{é}}nea\end{array}}{\underbrace {\alpha {\left(T_{sat}-T\right)}^{\delta }} }}+}$${\displaystyle {\underset {\begin{array}{cc}Nucleaci{\mbox{ó}}n&heterog{\mbox{é}}nea\end{array}}{\underbrace {{\alpha }^{'}{\left(T-T_{e}\right)}^{{\delta }^{'}}} }}}$

( 13)

donde α y α’ son los coeficientes de velocidad de nucleación homogénea y heterogénea respectivamente, δ y δ’ es el orden de cristalización, T_sat la temperatura en el equilibrio termodinámico o la temperatura de saturación y T_e es la temperatura de la pared del intercambiador.

Se distinguen aquí 2 categorías de nucleación: la nucleación homogénea y la nucleación heterogénea. La primera se produce espontáneamente sobre cualquier punto sobre el fluido cristalizado caracterizada por ser calculada con el principio de un desequilibrio termodinámico y la segunda solo se produce sobre la pared del cristalizador controlada principalmente por la temperatura de pared.

De la parte del crecimiento de partículas, este fenómeno puede ser modelado a partir de expresiones empíricas reportadas en la bibliografía, las cuales se basan en un desequilibrio termodinámico. Las ecuaciones se observan en la ecuación (14) [17] .

${\displaystyle G=K_{G}{\left(C-C\ast \right)}^{m}{\mbox{ }}o{\mbox{ }}G=}$${\displaystyle \beta {\left(T_{sat}-T\right)}^{\sigma }}$

( 14)

donde K_G o β son los coeficientes de velocidad de crecimiento de los cristales, m o σ son potencias, C es la concentración de partículas. Para este estudio, la velocidad de crecimiento se expresa en función del subenfriamiento de la solución mediante la diferencia de temperatura del fluido con respecto a la temperatura de saturación.

• Aspectos térmicos

El aspecto térmico del modelo se realiza basándose en el balance de energía por unidad de volumen de un cristalizador, donde se toma en cuenta la energía interna «u» . Así, la expresión 15 determina las diferentes transferencias de calor que intervienen en el equipo.

${\displaystyle {\frac {du}{dt}}={\overset {\rightarrow }{v}}{\overset {\rightarrow }{\nabla }}u+}$${\displaystyle q_{crist}+q_{visc}}$

( 15)

En este caso u es la energía interna por unidad de volumen. En el equilibrio, esta variable es una función de la temperatura T y de la fracción volumétrica de hielo φ_g . Considerando las capacidades térmicas constantes con respecto a la temperatura para cada uno de sus constituyentes, discriminando el calor de mezcla y tomando como referencia T_R  = 0 °C, la ecuación de estado se escribe como se muestra en la fórmula 16.

${\displaystyle u={\underset {\frac {kg{\mbox{ }}hielo}{m^{3}{\mbox{ }}sorbete}}{\underbrace {\frac {{\varphi }_{g}}{{\overset {\mbox{ˆ}}{V}}_{e}}} }}\left(-\right.}$${\displaystyle \left.\Delta H_{f}+Cp_{g}T\right)+{\underset {\frac {kg{\mbox{ }}soluci{\mbox{ó}}n}{m^{3}{\mbox{ }}sorbete}}{\underbrace {\frac {{\varpi }_{0}}{\overset {\mbox{ˆ}}{V}}} }}Cp_{s}T+}$${\displaystyle {\underset {\frac {kg{\mbox{   }}agua{\mbox{ }}(l{\mbox{í}}quida)}{m^{3}{\mbox{ }}sorbete}}{\underbrace {\left({\frac {1-{\varpi }_{0}}{\overset {\mbox{ˆ}}{V}}}-{\frac {{\varphi }_{g}}{{\overset {\mbox{ˆ}}{V}}_{e}}}\right)} }}Cp_{e}T}$

( 16)

dondeΔH_f es el calor latente de fusión a 0 °C por unidad de masa de agua, Cp_g , Cp_s y Cp_e son las capacidades caloríficas másicas del hielo, del soluto y del agua respectivamente, ϖ₀ la fracción de sólidos inicial y ${\textstyle {\overset {\mbox{ˆ}}{V}}}$ y ${\textstyle {\overset {\mbox{ˆ}}{V}}_{e}}$ son los volúmenes específicos de la solución y del hielo respectivamente.

Despreciando la diferencia en las capacidades caloríficas del agua y del hielo (que se convierte en la consideración que el calor de fusión es independiente de la temperatura), se plantea la ecuación (17).

${\displaystyle u={\frac {{\varphi }_{g}}{{\overset {\mbox{ˆ}}{V}}_{e}}}\left(-\right.}$${\displaystyle \left.\Delta H_{f}\right)+\left({\frac {{\varpi }_{0}Cp_{s}+(1-{\varpi }_{0})Cp_{e}}{\overset {\mbox{ˆ}}{V}}}\right)T}$

( 17)

Se puede así obtener una ecuación explícita de la temperatura en función de u y φ g dada por la ecuación (18).

${\displaystyle T=a\cdot u+b\cdot \nabla {\varphi }_{g}}$

( 18)

donde

${\displaystyle a={\frac {1}{\rho \left({\varpi }_{0}\cdot Cp_{s}+(1-{\varpi }_{0})\cdot Cp_{e}\right)}}}$

( 19)

y

${\displaystyle b={\frac {\Delta H_{f}\cdot {\rho }_{e}}{{\rho }_{s}\left({\varpi }_{0}\cdot Cp_{s}+(1-{\varpi }_{0})\cdot Cp_{e}\right)}}}$

( 20)

Descomponiendo la ecuación (15), el término q_crist que representa el flujo de calor sobre la pared del cristalizador define la expresión (21).

${\displaystyle q_{crist}=PS\cdot U\left(T_{e}-T\right)}$

( 21)

donde U es el coeficiente global de transferencia de calor, T_e la temperatura de pared considerada igual a la temperatura de evaporación (despreciando los efectos de resistencia de conducción en la pared) y PS la superficie de intercambio de calor por unidad de volumen, esta última definida por la ecuación (22).

${\displaystyle PS={\frac {Superficie_{cambio}}{Volumen_{cristalizador}}}=}$${\displaystyle {\frac {2\pi r_{e}L_{ech}}{\pi \left(r_{e}^{2}-r_{i}^{2}\right)L_{ech}}}=}$${\displaystyle {\frac {2r_{e}}{\left(r_{e}^{2}-r_{i}^{2}\right)}}}$

( 22)

donde r_e es el radio del cristalizador, r_i el radio equivalente del raspador y L_ech la longitud del cristalizador.

Por otro lado, q_visc de la ecuación (15) representa la producción de calor provocada por la disipación viscosa. Para su cálculo, utilizamos entonces la ecuación (23), la cual es ampliamente utilizada en la literatura ara los equipos que utilizan velocidades de agitación o cizallamiento [9] , [18]  and [19] .

${\displaystyle q_{visc}=\mu {\dot {\gamma }}^{2}{\begin{array}{ccc}{\mbox{ }}&con&{\dot {\gamma }}=\chi \cdot 2\pi VR\end{array}}}$

( 23)

donde μ   es la viscosidad del fluido, ${\textstyle {\dot {\gamma }}}$ la velocidad de cizallamiento, χ un coeficiente de ajuste y VR la velocidad de rotación del raspador. Para este caso, la viscosidad del fluido ha sido evaluada a partir de la relación de Thomas (1965) utilizada también por Qin et al. [20] . Esta relación utiliza la viscosidad de la solución no congelada (${\textstyle {\mu }_{s}=}$${\displaystyle f\left(T,C_{s},{\dot {\gamma }}\right)}$ , la fracción volumétrica de hielo φ_g y un factor de corrección Γ , que se observa en la ecuación (24):

${\displaystyle \mu ={\mu }_{s}\left(1+2,5{\varphi }_{g}+10,5{\varphi }_{g}^{2}+\right.}$${\displaystyle \left.\Gamma \cdot 0,00273exp\left(16,6{\varphi }_{g}\right)\right)}$

( 24)

Con todo lo anterior, ha sido posible la construcción de un grupo de ecuaciones diferenciales ordinarias para el modelo del cristalizador, visto por el sistema (25), el cual está compuesto por 5 ecuaciones diferenciales y una ecuación algebraica:

${\displaystyle T=a\cdot u+b\cdot {\frac {\pi }{6}}M_{3}}$ ${\displaystyle {\frac {du}{dt}}=U\cdot PS\left(T_{e}-T\right)+\mu {\dot {\gamma }}^{2}}$ ${\displaystyle {\frac {dM_{0}}{dt}}-N=0}$ ${\displaystyle {\frac {dM_{1}}{dt}}-GM_{0}-L_{c}N=0}$ ${\displaystyle {\frac {dM_{2}}{dt}}-2GM_{1}-L_{c}^{2}N=0}$ ${\displaystyle {\frac {dM_{3}}{dt}}-3GM_{2}-L_{c}^{3}N=0}$

( 25)

La tabla 1 recapitula uno por uno las diferentes variables que intervienen en este sistema de ecuaciones, dividiendo por ecuaciones de estado del modelo, los parámetros fijados de acuerdo con la literatura y aquellos que se tienen que identificar por medio experimental.

Tabla 1. Lista de parámetros y variables del modelo de cristalización. Parámetros fijados por medio de literatura [9]  and [17] o por medio experimental

Descripción	Variables o parámetros
Variables de estado	M0, M1,M2, M3 y u
Parámetros a identificar	χ , Γ y U
Parámetros fijados de acuerdo con la literatura o por experiencias anteriores	α  = 0, α ′ = 5x 108
	δ  = 1, δ ′ = 2
	β  = 5x 10−7 , σ  = 1
	Lc  = 5 × 10−6

Las ecuaciones diferenciales se integran utilizando un método de Runge Kutta por pasos de variables mediante la herramienta de resolución de sistema de ecuaciones diferenciales ordinarias del programa Matlab^® (ODE45). Esta integración se efectúa sobre un periodo de tiempo que corresponde al tiempo de residencia medio de la mezcla a cristalizar sobre ICSR. Este modelo, aunque se entiende que se define a partir de sistemas de ecuaciones diferenciales, es un modelo que determina las propiedades del proceso en el régimen estacionario.

3. Materiales y métodos

3.1. Mezcla de sorbete

Para la elaboración del sorbete se utiliza una mezcla industrial prefabricada de aroma limón. Dicha mezcla tiene como principales constituyentes agua, jugo de limón concentrado, azúcar, fructosa, goma de xantano y de guar. El contenido de solidos se evalúa en 25,2 °C Brix, con una densidad a 293,15 K de 1.110 kg/cm³ y un punto de congelación inicial de 270,55 K.

3.2. Equipo de cristalización

Para llevar a cabo la cristalización y formación del sorbete se utiliza un piloto WCB Technohoy^® modelo MF-50 de escala semiindustrial (fig. 1 ). La máquina cuenta con una bomba de alimentación de materia prima capaz de enviar un caudal entre 25 y 75 kg/h, un rotor para el ICSR capaz de girar entre 4 a 16,7 revoluciones por segundo (rps), una alimentación de aire y una máquina de refrigeración que utiliza como gas refrigerante el R22. El diámetro interno del tubo de intercambio de calor del equipo es de 0,40 cm con un volumen total del cilindro de 0,785 cm³ . Al interior del cilindro se encuentra una barra sólida que está provista de 2 cuchillas montadas de manera flotante, formando así el rotor mencionado, el cual funciona como raspador de la superficie con un volumen total de 0,351 cm³ .

Figura 1. Diagrama del piloto experimental MF-50. Tanque de almacenamiento de mezcla para sorbete con sistema para mantener temperatura constante de 278 K. Bomba de alimentación de la mezcla ICSR Salida del producto Sensor de temperatura Sensor para la DTC

3.3. Sensores en línea

Medición de la distribución del tamaño de cristal (DTC) . La medida de la distribución de tamaño de cristal fue realizada inmediatamente a la salida del cristalizador mediante la utilización del sensor Mettler-Toledo Lasentec^® Focused Beam Reflectance Method probe (FBRM Model S400A-8). El sensor FBRM provee la información mediante una medida de la dispersión de cristales haciendo un barrido mediante un láser que gira a gran velocidad. Para esto, se inserta la FBRM directamente al tubo de salida del equipo, con un ángulo de 45° y con una alimentación interna de nitrógeno de 8,33 × 10⁻⁵ m³ •s⁻¹ para evitar la condensación sobre la ventana de zafiro, que es la interface entre el material medido y el láser que proporciona la medición. Los datos son calculados por medio de la ponderación del tiempo de reflectancia medido y la velocidad tangencial del láser, dando así un diámetro de cuerda de las partículas. Este método ya ha sido empleado en otras aplicaciones de cristalización, principalmente en procesos farmacéuticos y químicos con lo cual se ha comprobado su funcionalidad como sensor en línea [17] . De una manera similar, se empleó como nuevo sistema para el seguimiento de la evolución de la distribución del tamaño de cristales de agua en cristalizadores alimenticios donde se emplea la congelación mostrando de igual manera su amplia gama de aplicaciones [21]  and [22] .

Temperatura de salida del sorbete y cálculo de la fracción de hielo . La temperatura de salida del sorbete fue medida mediante el uso de un sensor de precisión de tipo PT100 marca Baumer^® (± 0,1k) con una funcionalidad en el rango de −50 a +205 °C. Este sensor ha sido calibrado con una sonda de calibración en nuestro laboratorio de ajuste de sensores. Este sensor con un diámetro de 5,8 y longitud de 50 mm fue posicionado sobre la canalización de salida del sorbete a solo 50 mm de distancia de la sonda de medida de la DTC.

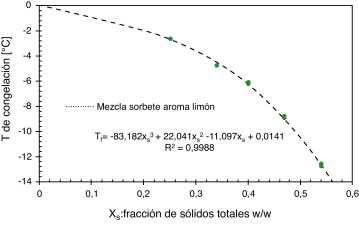
Para el cálculo de la cantidad de hielo producido, se supone el equilibrio termodinámico a la salida del ICSR. Para esto se utiliza la expresión (26) para el cálculo de la fracción de sólidos residuales en combinación con la ecuación (27). Es necesario aclarar que la expresión (26) ha sido obtenida mediante la curva de saturación de la mezcla de sorbete observada en la figura 2 , donde además de tener un medio para calcular la fracción de hielo la regresión hecha permite calcular la temperatura de saturación de la mezcla a partir de los puntos iniciales de congelación. Esta figura fue obtenida a partir de soluciones de la misma mezcla de sorbete a diferentes concentraciones de sólidos. Dichas soluciones fueron sometidas a un análisis de microcalorimetría DSC mediante el uso de un equipo Mettler-Toledo^® DSC (modelo DSC 822e/200W). Para la realización de cada una de las pruebas se pesaron entre 8 y 15 mg de muestra en una microbalanza (Mettler-Toledo^® modelo DT5 con una resolución de 0,001 mg) sobre una celda estándar de aluminio de 40 μl y se posiciona en el equipo. La muestra es entonces expuesta a una rampa de calentamiento que va de −40 a 20 °C a una velocidad de 2 °C min⁻¹ .

${\displaystyle x_{sr}=-5,29\times {10}^{-5}\cdot T^{4}-1,6737\times {10}^{-3}\cdot T^{3}-}$${\displaystyle 2,0195\times {10}^{-2}\cdot T^{2}-0,13738\cdot T}$

( 26)

${\displaystyle x_{si}=(1-x_{mg})x_{sr}\Leftrightarrow x_{mg}=1-{\frac {x_{si}}{x_{sr}}}}$

( 27)

Figura 2. Curva de saturación para la mezcla de sorbete aroma limón.

3.4. Diseño experimental

El diseño experimental se plantea mediante un arreglo factorial usando la teoría del compuesto central con 3 niveles de control. En este caso, los 3 niveles de control son las variable del proceso (temperatura de evaporación T_evap , velocidad del raspador VR y el gasto másico de alimentación al cristalizador MFR). Este diseño se aprecia en las Tabla 2  and Tabla 3 .

Tabla 2. Plan de experiencias codificado

	Valores codificados
Parámetros del proceso	−α	−1	0	+1	+α
MFR [kg/s]	0,0069	0,0097	0,0139	0,0181	0,0208
TEvap [K]	262,55	260,65	257,9	255,15	253,25
VR [rps]	9,1	10	12,5	15	16,7

Tabla 3. Plan de experiencias completo

	Valores codificados			Valores decodificados
No	MFR	TEvap.	VR	MFR [kg/s]	TEvap. [K]	VR [rpm]
1	0	0	0	0,0139	257,9	12,5
2	+1	+1	+1	0,0181	255,15	15,0
3	−1	+1	+1	0,0097	255,15	15,0
4	−1	−1	+1	0,0097	260,65	15,0
5	−1	−1	−1	0,0097	260,65	10,0
6	+1	−1	−1	0,0181	260,65	10.0
7	+1	+1	−1	0,0181	255,15	10,0
8	+1	−1	+1	0,0181	260,65	15,0
9	−1	+1	−1	0,0097	255,15	10,0
10	+α	0	0	0,0208	257,9	12,5
11	−α	0	0	0,0069	257,9	12,5
12	0	+α	0	0,0139	253,25	12,5
13	0	−α	0	0,0139	262,55	12,5
14	0	0	+α	0,0139	257,9	16,7
15	0	0	−α	0,0139	257,9	9,1
Experimentos suplementarios
16	---	---	---	0,0097	257,9	12,5
17	---	---	---	0,0097	253,25	12,5
18	---	---	---	0,0097	262,55	12,5
19	---	---	---	0,0097	260,65	12,5
20	---	---	---	0,0097	255,15	12,5

Este plan de experimentos cuenta con 4 repeticiones del punto central para el cálculo del error experimental, aunque se realizan todos los puntos del diseño por duplicado. Se realizan, así mismo, pruebas fuera del plan de experimentos con la finalidad de estudiar la funcionalidad del modelo para cada una de las variables del proceso, las cuales de igual manera se realizan por duplicado y se observan en los últimos 3 puntos de la tabla 3 . Todas las pruebas son realizadas sin alimentación de aire al proceso.

4. Resultados y discusión

Los resultados se basan en la validación del modelo de cristalización, la cual se realiza en 2 etapas. La primera etapa consistió en el ajuste del modelo con los datos experimentales obtenidos con respecto a la temperatura y el tamaño de cuerda medio en el sorbete a la salida del equipo por medio de un algoritmo de optimización basado en la diferencia de mínimos cuadrados. En la segunda etapa se realiza el análisis comparativo entre los valores experimentales y los resultados del modelo verificando las diferentes tendencias de acuerdo a las variables de control de la máquina (MFR, T_evap y VR). Todas las comparaciones hechas han sido en el régimen estacionario del proceso, debe ser considerada que ninguna de las variables y respuestas varían con respecto al tiempo. Con este propósito la máquina debe ser estabilizada para después realizar mediciones de 10 min de cada una de las respuestas con un paso de tiempo de 5 s.

4.1. Ajuste de los parámetros del modelo

La tabla 4 muestra los resultados experimentales obtenidos a partir del diseño de experimentos planteado en la parte de materiales y métodos. Los resultados mostrados en esta tabla representan los datos de tamaño medio de cuerda y temperatura de salida del producto cristalizado a partir una adquisición de valores durante 600 s después de alcanzar el régimen estable, donde se considera que las propiedades no exceden un grado de tolerancia máximo de ± 1% con respecto a la lectura.

Tabla 4. Resultados experimentales para el diseño de experimentos

	Variables de respuesta
No	T [K]	TC [m. 106 ]
1	269,11 ± 0,05	6,59 ± 0,06
2	268,6 ± 0,04	6,6 ± 0,05
3	267,65 ± 0,08	6,66 ± 0,07
4	269,32 ± 0,01	6,58 ± 0,06
5	269,21 ± 0,05	6,21 ± 0,02
6	269,93 ± 0,02	6,57 ± 0,06
7	268,62 ± 0,02	7,01 ± 0,05
8	269,92 ± 0,03	6,45 ± 0,05
9	266,92 ± 0,04	6,77 ± 0,01
10	269,76 ± 0,08	6,65 ± 0,03
11	267,99 ± 0,04	6,62 ± 0,05
12	267,19 ± 0,05	6,67 ± 0,07
13	270,04 ± 0,04	6,29 ± 0,02
14	269,37 ± 0,16	6,53 ± 0,05
15	269,06 ± 0,05	7,44 ± 0,01
Experimentos suplementarios
16	268,32 ± 0,03	7,01 ± 0,05
17	266,99 ± 0,01	6,48 ± 0,01
18	269,71 ± 0,07	6,97 ± 0,03
19	269.19 ± 0,03	6,45 ± 0,04
20	267,3 ± 0,04	6,63 ± 0,05

T: temperatura del producto; TC: tamaño medio de cuerda de los cristales.

Para la realización del ajuste de los parámetros del modelo de cristalización se escribió una rutina de optimización donde se analiza el error absoluto de cada uno de los resultados experimentales con los del modelo. Los valores iniciales para los parámetros de la cinética de cristalización se obtuvieron por la literatura [9] . Para el coeficiente global de transferencia de calor (U) se propone como valor inicial la media aritmética de los valores medidos. Este coeficiente se estima a partir de la hipótesis de la nula existencia del fenómeno de subfusión, es decir que la mezcla desciende bruscamente a la temperatura inicial de congelación seguido la disminución progresiva de la temperatura mientras se aumenta la cantidad de hielo formado (fig. 3 ). El cálculo de este coeficiente, entonces, se lleva a cabo mediante el siguiente sistema de ecuaciones:

${\displaystyle Q_{frigo}={\overset {0}{m_{R22}}}(\Delta H_{evap})}$

( 28)

Figura 3. Perfil de temperatura del producto vista de acuerdo a la superficie de transferencia de calor disponible. Si: superficie de transferencia de calor utilizada para enfriar o congelar la mezcla; S1: superficie de transferencia de calor utilizada para enfriar la mezcla;S2: superficie de transferencia de calor utilizada para congelar la mezcla; S: superficie de transferencia de calor total.

donde Q_frigo es la potencia frigorífica, ${\textstyle {\dot {m}}_{R22}}$ es el flujo másico del refrigerante R22 y ΔH_evap es el calor latente de en el evaporado.

${\displaystyle S=pi\cdot De\cdot L_{ech}}$ ${\displaystyle Q_{1}=U\cdot S_{1}\ast ((T_{i}+T_{cong})/2-T_{evap})}$ ${\displaystyle Q_{2}=U\cdot S_{2}\ast ((T_{cong}+T_{prod})/2-T_{evap})}$ ${\displaystyle S=S_{1}+S_{2}}$ ${\displaystyle {\frac {S_{1}}{S_{2}}}={\frac {MFRCp_{mix}(T_{i}-T_{cong})}{MFR\Delta H_{cong}x_{mg}}}}$ ${\displaystyle Q_{frigo}=Q_{1}+Q_{2}}$

( 29)

donde S es la superficie de intercambio de calor en el ICSR, D_e es el diámetro del ICSR (0,05 m), T_i es la temperatura de entrada de la mezcla, T_cong corresponde a la temperatura de inicial de congelación de la mezcla del sorbete, Q₁ es la potencia requerida para el enfriamiento de la mezcla de su temperatura de entrada a la temperatura de congelación y Q₂ la potencia utilizada para llevar al producto de su temperatura de congelación a la temperatura de salida (S₁ y S₂ son las superficies de transferencia de calor utilizadas para cada potencia respectivamente).

La rutina escrita se lanza con el grupo completo de pruebas experimentales, el cual analiza cada una de las respuestas del modelo con los datos experimentales. Con el objetivo de minimizar el error global absoluto de todo el grupo de experimentos se obtienen finalmente los parámetros ajustados del modelo que se observan en la tabla 5 .

Tabla 5. Parámetros del modelo ajustados con resultados experimentales

Parámetro	Valor ajustado
U [W/m2 -C]	2.400
α [s−1m−3K−1]	0
α’ [s−1m−3K−1]	7,6 × 108
β [m s−1K−1]	5 × 10−7
δ [–]	1
δ’ [–]	2
Γ [–]	1
Lc[m]	5 × 10−6

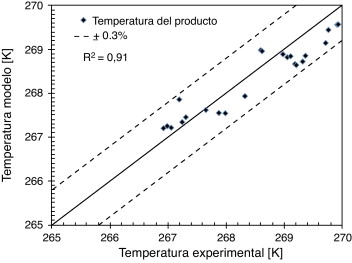
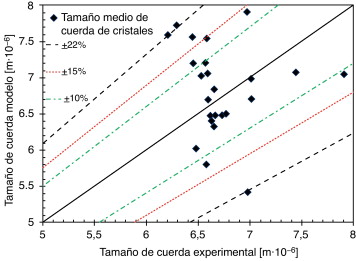
El modelo con los parámetros ajustados es resuelto por la herramienta ODE 45 del programa Matlab en un tiempo de 0,05 s con un ordenador que cuenta con un procesador Core Duo 2 GHz Intel. La funcionalidad del modelo es mostrada con las figuras 4 y 5 donde se observa el ajuste del modelo con los datos experimentales. En el caso de la temperatura del producto (fig. 4 ) el error máximo entre los valores obtenidos con el modelo y los datos experimentales fue de ± 0,3 %. En el caso del tamaño medio de cuerda para los cristales (fig. 5 ) el error máximo se localiza en 22 % haciendo la comparación modelo-experimentación, donde el 80 % de los puntos comparados exhiben un error absoluto inferior al 15 % y la mayor aglomeración de puntos se encuentra en un campo inferior al 10 % del mismo tipo de error.

Figura 4. Comparación de todos los datos experimentales y modelados de temperatura del sorbete a la salida del equipo en régimen estacionario.

Figura 5. Comparación de todos los datos experimentales y modelados del tamaño medio de cuerda en el sorbete a la salida del equipo en régimen estacionario.

4.2. Validación de la influencia de las variables del proceso

4.2.1. Gasto másico de la mezcla del sorbete

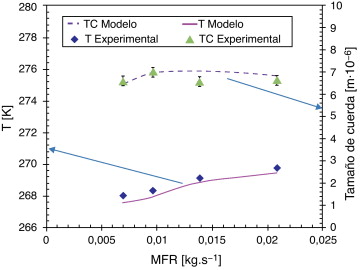
El gasto másico de la mezcla tiene efecto directo sobre el tiempo de residencia del producto dentro del ICSR. Consecuentemente, la temperatura de salida del sorbete aumenta con el incremento del gasto másico a la misma temperatura de pared o de evaporación [1] , [2]  and [4] . Esto ha sido confirmado experimentalmente, lo cual fue reproducido por el modelo (fig. 6 ). En la figura 6 se aprecia también la evolución del tamaño de cristal con el aumento del flujo másico, lo cual es atribuido a la modificación del tiempo de residencia del producto en el ICSR, el cual conlleva los fenómenos de nucleación y de recristalización de las partículas formadas [7] .

Figura 6. Comparación de la temperatura y el tamaño medio de cuerda predichos y experimentales en función del gasto másico de la mezcla de sorbete (temperatura de evaporación 257,9 K, velocidad del raspador 12,5 rps).

4.2.2. Influencia de la temperatura de evaporación

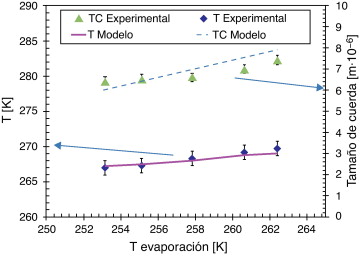
Es bien conocido que la temperatura de evaporación tiene un efecto directo sobre el tamaño de cristal de hielo y la temperatura de salida del producto [4] . Una reducción de la temperatura de evaporación incrementa directamente la velocidad de enfriamiento que intensifica la velocidad de nucleación e inhibe la tasa de crecimiento. Usualmente el efecto sobre la nucleación es más significativo que el efecto de crecimiento. Consecuentemente, el diámetro medio de partículas tiende a disminuir debido al gran número de pequeños cristales presentes en la microestructura del producto. El efecto sobre la temperatura de salida del producto es más intuitivo; una reducción de la temperatura de evaporación intensifica la transferencia de calor, el contenido de hielo aumenta y por tanto la temperatura del producto decrece significativamente. Los 2 efectos descritos se observan en la fig. 7 .

Figura 7. Comparación de la temperatura y el tamaño medio de cuerda predichos y experimentales en función la temperatura de evaporación (gasto másico 0,0097 kg•s−1 , velocidad del raspador 12,5 rps).

Los 2 efectos descritos anteriormente debidos a la temperatura de evaporación son reproducidos por el modelo. Las medidas experimentales muestran una importante reducción el tamaño de cuerda en función de la reducción en la temperatura de evaporación.

4.2.3. Efecto de la velocidad del raspador

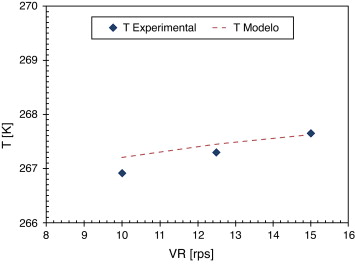
La velocidad del raspador tiene su principal influencia sobre la temperatura del producto debido a la energía transmitida por el fenómeno de fricción al sorbete. Esta influencia es tomada en cuenta en el modelo mediante la variación de la viscosidad y la energía de disipación viscosa. La temperatura de salida que se predice con el modelo y los datos experimentales muestran un incremento de 1 °C cuando la velocidad varía de 600 a 900 rpm, que es plasmado en la figura 8 . Este efecto ya ha sido anteriormente analizado o estudiado [1]  and [6] .

Figura 8. Comparación de la temperatura predichos y experimentales en función la de la velocidad de rotación del raspador (gasto másico 0,0097 kg•h−1 , temperatura de evaporación 257,9K).

Se observa una diferencia máxima de 9% entre los resultados experimentales y simulados para la temperatura de salida del sorbete. Estas diferencias son menores cuando el gasto másico incrementa. A lo concerniente a los resultados para el tamaño de cuerda, los datos no muestran un cambio significativo experimentalmente para el rango en las condiciones de operación utilizadas.

5. Conclusión

Se ha realizado con éxito la reducción del modelo de cristalización basado en la PBE. Esta reducción se llevó a cabo aplicando la metodología de momentos la cual permite reducir considerablemente los requerimientos computacionales para la simulación del proceso en estado estacionario. El diseño experimental empleado ha permitido la obtención de datos de tamaño medio de cuerda y de temperatura de salida del sorbete cristalizado, los cuales han sido utilizados para la validación del modelo desarrollado. A partir de un algoritmo de optimización y de datos obtenidos de investigaciones previas se ha podido ajustar los parámetros del modelo. De este modo, se ha constatado que el modelo es capaz de reproducir la influencia de las variables del proceso sobre la calidad del producto con errores inferiores al 10% con respecto a la escala utilizada. El modelo presentado en este trabajo es altamente recomendado para su implementación en sistemas de control de cristalización de helados y sorbetes.

Agradecimientos

Este artículo científico incluye resultados del proyecto CAFE que es soportado por el programa de Alimentación, Agricultura y Pesca, y Biotecnología de la comunidad europea (Número de contrato KBBE-212754). La responsabilidad científica queda a cargo de los autores.

This paper includes results of the CAFE project that is supported by the Food, Agriculture and Fisheries, and Biotechnology program of the European Community (Contract number KBBE-212754). The scientific responsibility rests with its authors.

Bibliografía

1. [1] R.W. Hartel; Ice crystallization during the manufacture of ice cream; Trends Food Sci Technol, 7 (1996), pp. 315–321
2. [2] K.L.K. Cook, R.W. Hartel; Mechanisms of ice crystallization in ice cream production; Compr Rev Food Sci, 9 (2010), pp. 213–222
3. [3] M.R. Muse, R.W. Hartel; Ice cream structural elements that affect melting rate and hardness; J Dairy Sci, 87 (2004), pp. 1–10
4. [4] A.B. Russell, P.E. Cheney, S.D. Wantling; Influence of freezing conditions on ice crystallisation in ice cream; J Food Eng, 39 (1999), pp. 179–191
5. [5] N. Richardson, D. Booth, N. Stanley; Effect of homogenization and fat content on oral perception of low and high viscosity model creams; J Sens Stud, 8 (1993), pp. 133–143
6. [6] K. Inoue, H. Ochi, M. Taketsuka, H. Saito, K. Sakurai, N. Ichihashi, et al.; Modeling of the effect of freezer conditions on the principal constituent parameters of ice cream by using response surface methodology; J Dairy Sci, 91 (2008), pp. 1722–1732
7. [7] E.M. Drewett, R.W. Hartel; Ice crystallization in a scraped surface freezer; J Food Eng, 78 (2007), pp. 1060–1066
8. [8] A. Mersmann, B. Braun, M. Löffelmann; Prediction of crystallization coefficients of the population balance; Chem Eng Sci, 57 (2002), pp. 4267–4275
9. [9] G. Lian, S. Moore, L. Heeney; Population balance and computational fluid dynamics modelling of ice crystallisation in a scraped surface freezer; Chem Eng Sci, 61 (2006), pp. 7819–7826
10. [10] C.B.B. Costa, M.R.W. Maciel, R. Maciel; Considerations on the crystallization modeling: Population balance solution; Comp Chem Eng, 31 (2007), pp. 206–218
11. [11] R.B. Diemer, J.H. Olson; A moment methodology for coagulation and breakage problems: Part 2--moment models and distribution reconstruction; Chem Eng Sci, 57 (2002), pp. 2211–2228
12. [12] R.B. Diemer, J.H. Olson; A moment methodology for coagulation and breakage problems: Part 1 - Analytical solution of the steady-state population balance; Chem Eng Sci, 57 (2002), pp. 2193–2209
13. [13] T. Chiu, P.D. Christofides; Robust nonlinear control of a continuous crystallizer; Comp Chem Eng. (Supplement 1), 23 (1999), pp. S257–S260
14. [14] D. Shi, N.H. El-Farra, M. Li, P. Mhaskar, P.D. Christofides; Predictive control of particle size distribution in particulate processes; Chem Eng Sci, 61 (2006), pp. 268–281
15. [15] Y. Chang, R.W. Hartel; Development of air cells in a batch ice cream freezer; J Food Eng, 55 (2002), pp. 71–78
16. [16] A.D. Randolph, M.A. Larson; Theory of particulate processes; (2^nd edition)Academic Pres, New York (1998)
17. [17] A. Haddad. Thèse: Couplage entre écoulements, transferts thermiques et transformation lors du changement de phase d’un produit alimentaire liquide complexe – application a la maitrise de la texture. Thèse. AgroParisTech (2009).
18. [18] J.F. Steffe; Rheological methods in food process engineering; (second edition)Freeman press (1996)
19. [19] S. Choulak, F. Couenne, Y. Le Gorrec, C. Jallut, P. Cassagnau, A. Michel; Generic dynamic model for simulation and control of reactive extrusion; Ind Eng Chem Res, 43 (2004), pp. 7373–7382
20. [20] F. Qin, X.D. Chen, S. Ramachandra, K. Free; Heat transfer and power consumption in a scraped-surface heat exchanger while freezing aqueous solutions; Sep Pur Technol, 48 (2006), pp. 150–158
21. [21] A. Haddad Amamou, H. Benkhelifa, G. Alvarez, D. Flick; Study of crystal size evolution by focused-beam reflectance measurement during the freezing of sucrose/water solutions in a scraped-surface heat exchanger; Process Biochem, 45 (2010), pp. 1821–1825
22. [22] M. Arellano, J.E. Gonzalez, D. Leducq, H. Benkhelifa, D. Flick, G. Alvarez; Effect of sorbet freezing process on draw temperature and ice crystal size using focused beam reflectance method (FBRM) online measurements”. The 23rd IIR International Congress of Refrigeration, Refrigeration for Sustainable Development; Prague, Czech Republic August, 21–26 (2011)