Revision as of 03:58, 22 November 2024 (view source) Justino (talk | contribs) ← Older edit	Latest revision as of 04:25, 25 November 2024 (view source) Gstinoco (talk | contribs) m (Gstinoco moved page Review 818876912398 to Gonzalez et al 2024b)
(No difference)

---

Latest revision as of 04:25, 25 November 2024

1 Introduction

Reaction-diffusion systems are mathematical models that allow us to describe how the concentration of one or more substances distributed in a medium changes under the influence of two physical processes: a chemical reaction, which transform the substances into each other, and diffusion, which causes the substances to spread in the medium. Applications for these systems have been found in a wide range of scientific and technological areas, from biology to physics, as well as chemistry, and even in the social sciences.

A fascinating aspect of a great variety of reaction-diffusion systems is their ability to generate spatio-temporal patterns from the solution of their governing equations. These patterns, such as those studied by Turing in 1952 (see [1]), not only reveal ordered structures in biological systems, such as the models of morphogenesis that explain how complex patterns can form on an animal skin, like spots on a leopard or stripes on a zebra, but can also be found in more abstract contexts, such as in the distribution of resources in complex networks as well as in the organization of neural patterns in the brain.

The adaptability and versatility of reaction-diffusion systems have allowed these models to be applied to more complex problems that require an analysis similar to that used in the study of Turing patterns. For example, they have been used to model tumour growth, cell organization in tissues, and ecosystem dynamics. The ability of these systems to capture both the complexity of local dynamics and the global interaction within a system makes them valuable tools in scientific research.

In this work we explore the numerical generation of Turing patterns on three dimensional surfaces using as a guideline the well known conditions that arise form the analysis of reaction-diffusion systems on planar regions. Several numerical schemes have been applied to solve numerically the reaction–diffusion system on surfaces. For instance, the finite element method is employed in [2], while a lifted local Galerkin method on implicit surfaces is proposed in [3], a finite difference method has been introduced in [4], and mesh-free kernel method like the ration basis function (RBF) is proposed in [5]. In this work we aim to introduce with some detail a simple but effective scheme based on a linear finite element method for space dicretization combined with a semi-implicit (some time named IMPEX) Euler time dicretization. It is applied directly on the discrete surface in Cartesian coordinates and yield accurate results in an efficient way, as shown with some numerical examples.

2 Mechanism for Turing pattern formation on planar regions

The model proposed by Alan Turing to describe patterns in nature was a model based on reaction-diffusion systems. Turing's main idea lies in the following sentence:

"A system in a stable state can be guided to an unstable state through diffusion, and in that state, the patterns will appear.".

The general form of reaction-diffusion systems that allow generating spatial patterns through their temporal solutions is the following:

${\displaystyle {\frac {\partial {u}}{\partial {t}}}=D_{u}\nabla ^{2}u+\gamma \,f(u,v),}$ (1) ${\displaystyle {\frac {\partial {v}}{\partial {t}}}=D_{v}\nabla ^{2}v+\gamma \,g(u,v),}$ (2) ${\displaystyle ({\hat {\mathbf {n} }}\cdot \nabla )u=({\hat {\mathbf {n} }}\cdot \nabla )v=0,\quad \forall \,\mathbf {x} \in \partial {\Omega },}$ (3) ${\displaystyle u(\mathbf {x} ,0)=u_{0}(\mathbf {x} ),\,\,u(\mathbf {x} ,0)=v_{0}(\mathbf {x} ),\quad \forall \,\mathbf {x} \in \Omega ,}$ (4)

where ${\textstyle \nabla ^{2}}$ is the Laplace operator and ${\textstyle \gamma {>0}}$ is known as scale factor that determines the size and the complexity of the patterns generated by the Turing conditions, as it will be shown later. Functions ${\textstyle u(\mathbf {x} ,t)}$, ${\textstyle v(\mathbf {x} ,t)}$ represent the concentrations of two substances mixing in a medium ${\textstyle \Omega \subset \mathbb {R} ^{2}}$ at time ${\textstyle t}$ whose initial concentrations are given by (4), respectively. The diffusion coefficients ${\textstyle D_{u},D_{v}>0}$ are assumed constant, and ${\textstyle {\hat {\mathbf {n} }}}$ denotes the outer unit normal vector to the boundary ${\textstyle \partial \Omega }$ of ${\textstyle \Omega }$. Zero flow conditions (3) are introduced for open surfaces (${\textstyle \partial \Omega \neq \emptyset }$) to ensure pattern formation due to self-organization only, avoiding the influence of external forces.

2.1 Turing conditions for pattern formation

Turing conditions are those that ensure the generation of spatial patterns from the temporal solutions of the reaction-diffusion systems (1-4), and they can be derived from Turing's idea already expressed before. First, under the absence of diffusion, ${\textstyle D_{u}=D_{v}=0}$, we assume the existence of an equilibrium point ${\textstyle \mathbf {w} ^{\ast }=(u^{\ast },v^{\ast })^{T}}$ and linearize the system (1-2) around ${\textstyle \mathbf {w} =(u,v)^{T}}$:

${\displaystyle {\dot {\mathbf {w} }}\approx \gamma \,\mathbb {J} \,(\mathbf {w} -\mathbf {w} ^{\ast })}$

(5)

with

${\displaystyle \mathbb {J} ={\begin{pmatrix}f_{u}(\mathbf {w} ^{\ast })&f_{v}(\mathbf {w} ^{\ast })\\g_{u}(\mathbf {w} ^{\ast })&g_{v}(\mathbf {w} ^{\ast })\end{pmatrix}}.}$

By setting ${\textstyle \mathbf {z} =\mathbf {w} -\mathbf {w} ^{\ast }}$ and assuming equality in (5) we have ${\textstyle {\dot {\mathbf {z} }}=\gamma \,\mathbb {J} \,\mathbf {z} }$, and then proposing a non trivial solution of (1-4), say ${\textstyle \mathbf {z} =\mathbf {K} e^{\lambda t}}$, with ${\textstyle \mathbf {K} }$ eigenvector of the Jacobian matrix ${\textstyle \mathbb {J} }$ and ${\textstyle \lambda }$ it's associated eigenvalue, we get

${\displaystyle \lambda =\displaystyle {\frac {\gamma }{2}}\left[{\hbox{Tr}}(\mathbb {J} )\,\pm \,{\sqrt {\left[{\hbox{Tr}}(\mathbb {J} )\right]^{2}-4\,{\hbox{det}}(\mathbb {J} )}}\,\right].}$

(6)

Since we look for a stable point, then from the Hartman-Grobman theorem ([6], p. 120), ([7], p. 155) we must assume that ${\textstyle \mathbf {w} ^{\ast }}$ is a hyperbolic equilibrium point, that is ${\textstyle Re(\lambda )\not =0}$, and to ensure such stability it is necessary that

${\displaystyle {\hbox{Tr}}(\mathbb {J} )<0,}$ (7) ${\displaystyle {\hbox{ det}}(\mathbb {J} )>0.}$ (8)

Thus, obtaining the first conditions. Next, as a second step, diffusion is reintroduced in (1-2), that is ${\textstyle D_{u},D_{v}>0}$, and assuming that ${\textstyle \mathbf {w} ^{\ast }=(u^{\ast },v^{\ast })^{T}}$ is still an equilibrium point, then it must satisfy ${\textstyle f(\mathbf {w} ^{\ast })=g(\mathbf {w} ^{\ast })=0}$ and ${\textstyle \nabla ^{2}u^{\ast }=\nabla ^{2}v^{\ast }=0}$. But now, we want that ${\textstyle \mathbf {w} ^{\ast }}$ be an unstable equilibrium point (diffusion destabilize the system). To derive the mathematical condition for this new situation, the following linear system with diffusion is analysed.

${\displaystyle {\dot {\mathbf {z} }}=\mathbb {D} \nabla ^{2}\mathbf {z} +\gamma \,\mathbb {J} \,\mathbf {z} ,}$

(9)

with ${\textstyle \nabla ^{2}\mathbf {z} =\nabla ^{2}(\mathbf {w} -\mathbf {w} ^{\ast })}$ and ${\textstyle \mathbb {D} ={\begin{pmatrix}D_{u}&0\\0&D_{v}\end{pmatrix}}}$. This time we consider a separated solution

${\displaystyle z(\mathbf {x} ,t)=\mathbf {Z} (\mathbf {x} )\,T(t),}$

(10)

where ${\textstyle \mathbf {Z} (\mathbf {x} )=\left(Z_{1}(\mathbf {x} ),Z_{2}(\mathbf {x} )\right)^{T}}$ is a vectorial function in ${\textstyle \mathbb {R} ^{2}}$ and ${\textstyle T(t)}$ is a scalar function. From (9) we obtain

${\displaystyle T(t)=Ce^{\lambda {t}},\quad C\in \mathbb {R} ,}$

(11)

${\displaystyle {\nabla }^{2}\mathbf {Z} +{\mathbb {D} }^{-1}(\gamma \,\mathbb {J} -\lambda \,{\mathbb {I} }_{2})\mathbf {Z} =\mathbf {0} .}$

(12)

It is worth mentioning that the constant ${\textstyle \lambda }$ in (11) is not the same as the one in (6), but it plays an equivalent role, as will be see below. We denote by ${\textstyle k^{2}}$ the eigenvalues¹ of matrix ${\textstyle \mathbf {A} =\mathbb {D} ^{-1}(\gamma \,\mathbb {J} -\lambda \,\mathbb {I} _{2})}$. If ${\textstyle Z_{k}(\mathbf {x} )}$ is the associated eigenfunction, then from (12) it must solve the following Helmholtz equation with zero-flux at the boundary

${\displaystyle {\nabla }^{2}\mathbf {Z} _{k}+k^{2}\mathbf {Z} _{k}=\mathbf {0} ,}$ (13) ${\displaystyle ({\hat {\mathbf {n} }}\cdot \nabla )\mathbf {Z} _{k}=\mathbf {0} .}$ (14)

Solutions ${\textstyle \mathbf {Z} _{k}}$ are commonly oscillatory and depend exclusively on system's geometry. For bounded domains, values ${\textstyle k}$ are discrete and can be enumerated, they represent the oscillatory mode of the solution and are called the wave numbers. Therefore, ${\textstyle \mathbf {z} _{k}(\mathbf {x} ,t)=e^{\lambda _{k}t}\mathbf {Z} _{k}(\mathbf {x} )}$ is a solution of (9) with zero flux on the boundary, and

${\displaystyle \lambda _{k}=\displaystyle {\frac {\left[\gamma {\hbox{Tr}}(\mathbb {J} )-k^{2}{\hbox{Tr}}(\mathbb {D} )\right]\,\pm \,{\sqrt {\left[k^{2}{\hbox{Tr}}(\mathbb {D} )-\gamma {\hbox{Tr}}(\mathbb {J} )\right]^{2}-4h(k^{2})}}}{2}},}$

(15)

with

${\displaystyle h(k^{2})={\hbox{det}}(\mathbb {D} )k^{4}-\gamma (D_{v}f_{u}+D_{u}g_{v})k^{2}+\gamma ^{2}{\hbox{det}}(\mathbb {J} ).}$

(16)

The roots of the function ${\textstyle h(k^{2})}$ determine an interval ${\textstyle (k_{1}^{2},k_{2}^{2})}$, and any wave number ${\textstyle k^{2}}$ inside this interval will allow the generation of spatial patterns in the medium ${\textstyle \Omega }$. Those roots are positive and are given by

${\displaystyle k_{1}^{2},k_{2}^{2}=\displaystyle {\frac {\gamma }{2\,D_{v}}}\left[(d\,f_{u}+g_{v})\,\mp \,{\sqrt {(d\,f_{u}+g_{v})^{2}-4\,d\,\det(\mathbb {J} )}}\,\right].}$

(17)

where ${\textstyle d=D_{v}/D_{u}>0}$ is the diffusivity ratio. This means that only the modes with wave number ${\textstyle k}$ between these two values are able to produce spatial patterns, all other modes, out this range, have an exponential decay in time and eventually vanish. Thus, the equilibrium point ${\textstyle \mathbf {w} ^{\ast }}$ is unstable if ${\textstyle Re[\lambda _{k}]>0}$ for some ${\textstyle k^{2}\in (k_{1}^{2},k_{2}^{2})}$. This occurs when ${\textstyle h(k^{2})<0}$, and from (16) and (17) the following inequalities must be satisfied

${\displaystyle d\,f_{u}+g_{v}>0,}$ (18) ${\displaystyle (d\,f_{u}+g_{v})^{2}-4d\,\det(\mathbb {J} )>0,}$ (19) ${\displaystyle k_{1}^{2}<k^{2}<k_{2}^{2}.}$ (20)

Combining these conditions with (7-8), we obtain the so called Turing conditions for pattern generation:

${\displaystyle f_{u}+g_{v}<0,}$ (21) ${\displaystyle f_{u}\,g_{v}-f_{v}\,g_{u}>0,}$ (22) ${\displaystyle d\,f_{u}+g_{v}>0,}$ (23) ${\displaystyle (d\,f_{u}+g_{v})^{2}-4d\,\det(\mathbb {J} )>0,}$ (24) ${\displaystyle k_{1}^{2}<k^{2}<k_{2}^{2}.}$ (25)

Furthermore, from these conditions and some simple algebraic calculations, it can be shown that the following must hold: ${\textstyle d>1}$, ${\textstyle f_{u}>0}$, ${\textstyle g_{v}<0}$ and ${\textstyle f_{v}g_{u}<0}$.

(¹) The squared exponent is for algebraic convenience when performing calculations.

3 Finite element approximation of the Laplace-Beltrami operator

In this part, we will focus on the numerical approximation of the following elliptic equation

${\displaystyle \alpha \,\phi -D_{\Sigma }\,\nabla _{\Sigma }^{2}\,\phi =f,}$

(26)

with homogeneous Neumann boundary conditions when the bounded surface ${\textstyle \Sigma }$ is open. Of course if the surface is closed (like an sphere), there are no boundary conditions. In this equation ${\textstyle \alpha }$ and ${\textstyle D_{\Sigma }}$ are positive constants, ${\textstyle \nabla _{\Sigma }^{2}}$ denotes the so called Laplace-Beltrami operator, defined on ${\textstyle \Sigma }$, and ${\textstyle f}$ is a source term. This numerical approximation will be performed by a linear finite element method. This methodology will be the basis, with some minimal adjustments, to numerically solve the reaction-diffusion systems for the generation of Turing patterns on those surfaces, as shown in next sections.

3.1 The Laplace-Beltrami operator (LBO)

The Laplace-Beltrami operator is a generalization of the usual Laplace operator. This operator acts on functions defined on surfaces in the Euclidean space and, more generally, on Riemannian surfaces and manifolds. We will use it for functions defined on three-dimensional surfaces in the Euclidean space ${\textstyle \mathbb {R} ^{3}}$.

Definición 1: Let ${\textstyle \Sigma \subset \mathbb {R} ^{3}}$ be a smooth oriented surface, and let ${\textstyle {\hat {\mathbf {n} }}={\hat {\mathbf {n} }}(\mathbf {x} )}$ be a unit normal vector at ${\textstyle \mathbf {x} }$, exterior to ${\textstyle \Sigma }$, and ${\textstyle \phi \,:\,\Sigma \subset R^{3}\longmapsto \,\mathbb {R} }$ a function defined on ${\textstyle \Sigma }$ of class ${\textstyle {\mathcal {C}}^{1}}$. The tangential gradient of ${\textstyle \phi }$ at ${\textstyle \mathbf {x} \in \Sigma }$ is defined by

${\displaystyle \nabla _{\Sigma }\phi (\mathbf {x} )=\nabla {\phi (\mathbf {x} )}-\langle {\nabla {\phi (\mathbf {x} )},{\hat {\mathbf {n} }}}\rangle \,{\hat {\mathbf {n} }}}$

(27)

where ${\textstyle \langle {\cdot ,\cdot }\rangle }$ denotes the inner product in ${\textstyle \mathbb {R} ^{3}}$.

Geometrically, the tangential gradient is the orthogonal projection of the gradient vector ${\textstyle \nabla {\phi (\mathbf {x} )}}$ onto the tangent plane at ${\textstyle \mathbf {x} }$ with normal vector ${\textstyle {\hat {\mathbf {n} }}(\mathbf {x} )}$ as shown in figure 1. The projection matrix to the normal vector is ${\textstyle \mathbb {P} ={\hat {\mathbf {n} }}\,{\hat {\mathbf {n} }}^{T}}$, and ${\textstyle \nabla _{\Sigma }\phi (\mathbf {x} )}$ can also be expressed as:

${\displaystyle \nabla _{\Sigma }\phi (\mathbf {x} )=(\mathbb {I} -\mathbb {P} )\nabla {\phi (\mathbf {x} )},}$

(28)

where ${\textstyle \mathbb {I} }$ represents the identity matrix of size ${\textstyle 3\times {3}}$ and ${\textstyle \mathbb {I} -\mathbb {P} }$ is the complementary orthogonal projection to ${\displaystyle \mathbb {P} }$.

Figure 1: Tangential gradient ${\displaystyle \nabla _{\Sigma }\phi (\mathbf {x} )}$.

Definición 2: Let ${\textstyle \phi \,:\,\Sigma \subset {\mathbb {R} }^{3}\longmapsto \,\mathbb {R} }$ be of class ${\textstyle {\mathcal {C}}^{2}}$. We define the Laplace-Beltrami operator of ${\textstyle \phi }$ denoted by ${\textstyle \nabla _{\Sigma }^{2}\phi }$, by

${\displaystyle \nabla _{\Sigma }^{2}\phi ={\hbox{div}}(\nabla _{\Sigma }\phi ),}$

(29)

or equivalently, ${\textstyle \nabla _{\Sigma }^{2}\phi =\nabla _{\Sigma }\cdot \nabla _{\Sigma }\phi }$. In many texts, this operator is denoted by ${\textstyle \Delta _{\Sigma }\phi }$.

3.2 Weak form of equation (26)

In order to numerically solve the elliptic equation (26) using a finite element method, we must find its weak or variational formulation. It is obtained by multiplying that equation by a test function ${\textstyle v}$ and integrating over the surface ${\textstyle \Sigma }$. After applying integration by parts we obtain the following problem:

Find ${\textstyle \phi \in {\mathcal {L}}^{2}(\Sigma )}$ such that, for all ${\textstyle v\in {\mathcal {H}}^{1}(\Sigma )}$, it satisfies

${\displaystyle \alpha \displaystyle \int _{\Sigma }\phi \,v\,d\Sigma +D_{\Sigma }\displaystyle \int _{\Sigma }{\nabla }_{\Sigma }\phi \cdot {\nabla }_{\Sigma }v\,d\Sigma =\displaystyle \int _{\Sigma }f\,v\,d\Sigma ,}$

(30)

where

${\displaystyle {\mathcal {H}}^{1}(\Sigma )=\left\{v\in {\mathcal {L}}^{2}(\Sigma )\,:\,\displaystyle \int _{\Sigma }|{\nabla }_{\Sigma }v|^{2}\,d\Sigma {<\infty }\right\}}$

and where ${\textstyle d\Sigma }$ represents the surface differential.

Note. The integral equation (30) does not include boundary integral terms, because either the surface is closed (${\textstyle \partial \Sigma =\emptyset }$) or it is open with zero-flux boundary conditions. So, the above variational formulation is the same for both cases.

3.2.1 Approximation of the variational problem

To obtain a finite element approximation to the variational problem (30) we use a Ritz-Galerkin approach, where the Hilbert space ${\textstyle {\mathcal {H}}^{1}(\Sigma )}$ is approximated by a finite-dimensional subspace. One possible way is approximating each function in ${\textstyle {\mathcal {H}}^{1}(\Sigma )}$ by a continuous piecewise polynomial. One of the most simple approximations is obtained with continuous piecewise polynomials of degree one. So, if we denote by ${\textstyle \mathbb {P} _{1}}$ the set of polynomials in two variables of degree 1, and we approximate the surface ${\textstyle \Sigma }$ by a triangular mesh ${\textstyle {\mathcal {T}}_{h}}$, then ${\textstyle {\mathcal {H}}^{1}(\Sigma )}$ is approximated by the following finite-dimensional space of piecewise linear functions:

${\displaystyle H_{h}=\left\{v\in {\mathcal {C}}^{0}({\widehat {\Sigma }})\,:\,v\,|_{_{T}}\in \mathbb {P} _{1},\,\,\forall \,T\in {\mathcal {T}}_{h}\right\},}$

(31)

We denote by ${\textstyle {\mathcal {V}}_{h}}$ the set of vertices of ${\textstyle {\mathcal {T}}_{h}}$ and for each vertex (node point) ${\textstyle P\in {\mathcal {V}}_{h}}$ there is a `hat function', denoted by ${\textstyle \varphi _{P}\in H_{h}}$, that satisfies the following basic property for each vertex ${\textstyle Q\in {\mathcal {V}}_{h}}$ (see Figure 2):

Figure 2: Pyramidal or 'hat' function.

${\displaystyle \varphi _{P}(Q)={\begin{cases}1\quad {\hbox{if}}\quad Q=P,\\0\quad {\hbox{if}}\quad Q\neq P.\end{cases}}}$

The set of hat (pyramidal) functions ${\textstyle \beta _{h}=\left\{\varphi _{P}\,|\,P\in {\mathcal {V}}_{h}\right\}}$ form a basis of the finite element space ${\textstyle H_{h}}$. Furthermore, the dimension ${\textstyle N_{I}}$ of ${\textstyle H_{h}}$ is number of vertex nodes in the triangulation ${\textstyle {\mathcal {T}}_{h}}$.

We can now discretize the variational problem (30) as follows: Find ${\textstyle \phi _{h}\in H_{h}}$ such that

${\displaystyle \alpha \displaystyle \int _{\widehat {\Sigma }}\phi _{h}\,v_{h}\,d\Sigma +D_{\Sigma }\displaystyle \int _{\widehat {\Sigma }}{\nabla }_{\Sigma }\phi _{h}\cdot {\nabla }_{\Sigma }v_{h}\,d\Sigma =\displaystyle \int _{\widehat {\Sigma }}f\,v_{h}\,d\Sigma ,\quad \quad \forall \,v_{h}\in H_{h}.}$

(32)

It is enough that (32) be satisfied for each basis function ${\textstyle \varphi _{P}}$. Furthermore, by expressing ${\textstyle \phi _{h}\in {H_{h}}}$ as linear combination of the basis functions ${\textstyle \phi _{h}(\mathbf {x} )=\displaystyle \sum _{P\in {\mathcal {V}}_{h}}\phi _{h}(P)\,\varphi _{P}(\mathbf {x} )}$, we get the following reformulation of (32):

${\displaystyle \sum _{P\in {\mathcal {V}}_{h}}\left(\alpha \displaystyle \int _{\widehat {\Sigma }}\varphi _{P}\,\varphi _{Q}\,d\Sigma +D_{\Sigma }\int _{\widehat {\Sigma }}\nabla _{\Sigma }\varphi _{P}\cdot \nabla _{\Sigma }\varphi _{Q}\,d\Sigma \right)\,\phi _{h}(P)=\int _{\widehat {\Sigma }}f\,\varphi _{Q}\,d\Sigma ,\quad \forall \,Q\in {\mathcal {V}}_{h},}$

(33)

which can be expressed in the following form (after enumerating the vertices in the mesh):

Find the values ${\textstyle \phi _{i}=\phi _{h}(P_{i})}$, ${\textstyle i=1,2,\ldots ,N_{I}}$ such that

${\displaystyle {\begin{aligned}\displaystyle \sum _{i=1}^{N_{I}}\left(\alpha \displaystyle \int _{\widehat {\Sigma }}\varphi _{i}\,\varphi _{j}\,d\Sigma +D_{\Sigma }\displaystyle \int _{\widehat {\Sigma }}{\nabla }_{\Sigma }\varphi _{i}\cdot {\nabla }_{\Sigma }\varphi _{j}\,d\Sigma \right)\,\phi _{i}=\displaystyle \int _{\widehat {\Sigma }}f\,\varphi _{j}\,d\Sigma ,\quad \forall \,j=1,2,\ldots ,N_{I}.\end{aligned}}}$

(34)

Written in matrix form, we obtain

${\displaystyle (\alpha \,\mathbb {M} +D_{\Sigma }\mathbb {K} )\,{\boldsymbol {\phi }}=\mathbf {F} ,}$

(35)

where ${\textstyle {\boldsymbol {\phi }}}$ is the vector of unknowns ${\textstyle \{\phi _{i}\}}$, ${\textstyle {\mathbb {M} }=(M_{ij})}$, ${\textstyle \mathbb {K} =(K_{ij})}$ and ${\textstyle \mathbf {F} =(F_{1},\ldots ,F_{N_{I}})^{T}}$, with

${\displaystyle M_{ij}=\displaystyle \int _{\widehat {\Sigma }}\varphi _{i}\,\varphi _{j}\,d\Sigma ,}$ (36) ${\displaystyle K_{ij}=\displaystyle \int _{\widehat {\Sigma }}{\nabla }_{\Sigma }\varphi _{i}\cdot {\nabla }_{\Sigma }\varphi _{j}\,d\Sigma ,}$ (37) ${\displaystyle F_{j}=\displaystyle \int _{\widehat {\Sigma }}f\,\varphi _{j}\,d\Sigma {.}}$ (38)

${\textstyle \mathbb {M} }$ and ${\textstyle \mathbb {K} }$ are called the mass matrix and stiffness matrix, respectively, and ${\textstyle \mathbf {F} }$ is known as the load vector. Since ${\textstyle \displaystyle {\widehat {\Sigma }}=\bigcup _{T\in {\mathcal {T}}_{h}}T}$, we obtain

${\displaystyle M_{ij}=\displaystyle \sum _{T\in {\mathcal {T}}_{h}^{ij}}\int _{T}\varphi _{i}\,\varphi _{j}\,dT,}$ (39) ${\displaystyle K_{ij}=\displaystyle \sum _{T\in {\mathcal {T}}_{h}^{ij}}\int _{T}{\nabla }_{_{T}}\varphi _{i}\cdot {\nabla }_{_{T}}\varphi _{j}\,dT}$ (40)

where ${\textstyle {\mathcal {T}}_{h}^{ij}}$ represents the triangular elements containing the adjacent vertices ${\textstyle P_{i}}$, ${\textstyle P_{j}}$ and ${\textstyle {\nabla }_{T}}$ is the tangential gradient over the triangle ${\textstyle T}$.

3.2.2 Building local basis functions on each element

Let ${\textstyle ne}$ be the number of triangular elements in the mesh. For each ${\textstyle e=1,2,\ldots ,ne}$, the triangular element ${\textstyle T_{e}\in {\mathcal {T}}_{h}}$ has vertices ${\textstyle P_{1}^{e}}$, ${\textstyle P_{2}^{e}}$, ${\textstyle P_{3}^{e}}$, with coordinates ${\textstyle (x_{1}^{e},y_{1}^{e},z_{1}^{e})}$, ${\textstyle (x_{2}^{e},y_{2}^{e},z_{2}^{e})}$,${\textstyle (x_{3}^{e},y_{3}^{e},z_{3}^{e})}$, respectively. The connectivity matrix ${\textstyle \{g(e,\lambda )\}}$, ${\textstyle 1\leq {e}\leq {ne}}$, ${\textstyle 1\leq {\lambda }\leq {3}}$, relates local node numbering to the global one. More precisely, the local vertices ${\textstyle \lambda =1,2,3}$ of an element ${\textstyle T_{e}}$ have global numbering ${\textstyle i=g(e,1)}$, ${\textstyle j=g(e,2)}$, ${\textstyle k=g(e,3)}$, respectively. So, a basis function ${\textstyle \varphi _{i}}$ restricted to the element ${\textstyle T_{e}}$ can be denoted by

${\displaystyle {\varphi }_{\lambda }^{e}(\mathbf {x} )={\varphi }_{i}(\mathbf {x} )|_{T_{e}},\quad {\hbox{with}}\quad i=g(e,\lambda {).}}$

These local basis function thus have the following properties

1. ${\textstyle \varphi _{\lambda }^{e}(x,y,z)}$ is a polynomial of degree ${\textstyle \leq 1}$ on ${\textstyle T_{e}}$.
2. ${\textstyle {\varphi }_{\lambda }^{e}(x_{\mu }^{e},y_{\mu }^{e},z_{\mu }^{e})=\delta _{\lambda {\mu }}}$, ${\textstyle 1\leq {\lambda ,\mu }\leq {3}}$.
3. ${\textstyle \varphi _{1}^{e}(\mathbf {x} )\!+\!{\varphi }_{2}^{e}(\mathbf {x} )\!+\!{\varphi }_{3}^{e}(\mathbf {x} )\!=\!1}$, ${\textstyle \forall \mathbf {x} \!=\!(x,y,z)\in T_{e}}$.

and ${\textstyle \mathbf {x} }$ can be expressed as a weighted average of the vertices of the triangle with weights determined by the local basis functions. That is,

${\displaystyle \mathbf {x} =\varphi _{1}^{e}(\mathbf {x} )\,P_{1}^{\,e}+\varphi _{2}^{e}(\mathbf {x} )\,P_{2}^{\,e}+\varphi _{3}^{e}(\mathbf {x} )\,P_{3}^{\,e}}$

(41)

where ${\textstyle P_{1}^{\,e}=(x_{1}^{e},y_{1}^{e},z_{1}^{e})}$, ${\textstyle P_{2}^{\,e}=(x_{2}^{e},y_{2}^{e},z_{2}^{e})}$ y ${\textstyle P_{3}^{\,e}=(x_{3}^{e},y_{3}^{e},z_{3}^{e})}$ are the coordinates of the vertices of triangle ${\textstyle T_{e}}$.

3.2.3 Reference element and affine transformation

We consider a reference unit triangle ${\textstyle {\widehat {T}}}$ in the coordinates ${\textstyle \xi }$-${\textstyle \eta }$ and a triangular element ${\textstyle T_{e}\in {\mathcal {T}}_{h}}$ in the Cartesian system ${\textstyle x}$-${\textstyle y}$-${\textstyle z}$ as in Figure 3.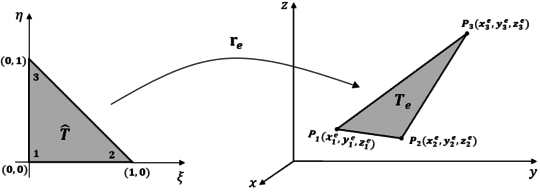

Figure 3: Affine transformation from the reference element ${\displaystyle {\widehat {T}}}$ to the physical element ${\displaystyle T_{e}}$.

Assuming a counter-clockwise node numbering, the affine transformation ${\textstyle \mathbf {r} _{e}\,:\,{\widehat {T}}\longmapsto \,T_{e}}$ is given by

${\displaystyle \mathbf {r} _{e}(\xi ,\eta )={\hat {\varphi }}_{1}(\xi ,\eta )(x_{1}^{e},y_{1}^{e},z_{1}^{e})^{T}+{\hat {\varphi }}_{2}(\xi ,\eta )(x_{2}^{e},y_{2}^{e},z_{2}^{e})^{T}+{\hat {\varphi }}_{3}(\xi ,\eta )(x_{3}^{e},y_{3}^{e},z_{3}^{e})^{T},}$

(42)

where

${\displaystyle {\hat {\varphi }}_{1}(\xi ,\eta )=1-\xi {-\eta },}$ ${\displaystyle {\hat {\varphi }}_{2}(\xi ,\eta )=\xi ,}$ ${\displaystyle {\hat {\varphi }}_{3}(\xi ,\eta )=\eta {.}}$

The Jacobian matrix ${\textstyle \mathbb {J} _{e}}$ of the affine transformation (42) is

${\displaystyle \mathbb {J} _{e}=\left[{\begin{array}{cc}x_{2}^{e}-x_{1}^{e}&x_{3}^{e}-x_{1}^{e}\\y_{2}^{e}-y_{1}^{e}&y_{3}^{e}-y_{1}^{e}\\z_{2}^{e}-z_{1}^{e}&z_{3}^{e}-z_{1}^{e}\end{array}}\right].}$

(43)

The column vectors of this matrix are the fundamental vectors ${\textstyle \mathbf {r} _{\xi }^{e}}$, ${\textstyle \mathbf {r} _{\eta }^{e}}$. This vectors, along the normal vector to the triangular element ${\textstyle T_{e}}$ are:

${\displaystyle \mathbf {r} _{\xi }^{e}={\begin{pmatrix}x_{2}^{e}-x_{1}^{e}\\y_{2}^{e}-y_{1}^{e}\\z_{2}^{e}-z_{1}^{e}\end{pmatrix}},\qquad \mathbf {r} _{\eta }^{e}={\begin{pmatrix}x_{3}^{e}-x_{1}^{e}\\y_{3}^{e}-y_{1}^{e}\\z_{3}^{e}-z_{1}^{e}\end{pmatrix}},\qquad {\hat {\mathbf {n} }}^{e}=\mathbf {r} _{\xi }^{e}\times \mathbf {r} _{\eta }^{e}}$

(44)

3.2.4 Assembly of mass and stiffness matrices using the reference element

Assembly of the mass matrix ${\displaystyle \mathbb {M} }$. From equation (39), and the connectivity matrix relating local to global nodes, we get

${\displaystyle M_{ij}=\sum _{T_{e}\in {\mathcal {T}}_{h}^{ij}}\int _{T_{e}}\varphi _{\lambda }^{e}\,\varphi _{\mu }^{e}\,dT_{e},}$

with ${\textstyle i=g(e,\lambda )}$ and ${\textstyle j=g(e,\mu )}$ adjacent nodes. These integrals are computed in the reference element employing the affine transformation (42), so

${\displaystyle M_{ij}=\displaystyle \sum _{T_{e}\in {\mathcal {T}}_{h}^{ij}}\iint _{\widehat {T}}{\hat {\varphi }}_{\lambda }\,{\hat {\varphi }}_{\mu }\,||\mathbf {r} _{\xi }^{e}\times \mathbf {r} _{\eta }^{e}||\,d\xi \,d\eta =\displaystyle \sum _{T_{e}\in {\mathcal {T}}_{h}^{ij}}||\mathbf {r} _{\xi }^{e}\times \mathbf {r} _{\eta }^{e}||\,{\widehat {M}}_{\lambda \mu },}$

(45)

where, for ${\textstyle 1\leq \lambda ,\mu \leq 3}$

${\displaystyle {\widehat {M}}_{\lambda \mu }=\displaystyle \iint _{\widehat {T}}{\hat {\varphi }}_{\lambda }(\xi ,\eta ){\hat {\varphi }}_{\mu }(\xi ,\eta )\,d\xi \,d\eta ,}$

(46)

are the coefficients of the ${\textstyle 3\times 3}$ local mass matrix ${\textstyle {\widehat {M}}}$. Double integral notation has been used to emphasize that they are surface integrals. Coefficients ${\textstyle {\widehat {M}}_{\lambda \mu }}$ may be computed exactly or approximated by Simpson's rule or a Gaussian quadrature only once and stored in memory.

Assembly of the stiffness matrix ${\displaystyle \mathbb {K} }$. From (40), we get

${\displaystyle K_{ij}=\sum _{T_{e}\in {\mathcal {T}}_{h}^{ij}}\int _{T_{e}}\nabla _{T_{e}}\varphi _{\lambda }^{e}\cdot \nabla _{T_{e}}\varphi _{\mu }^{e}\,dT_{e},}$

with ${\textstyle i=g(e,\lambda )}$ and ${\textstyle j=g(e,\mu )}$ as before. Here ${\textstyle \nabla _{T_{e}}\varphi _{\lambda }^{e}=(\mathbb {I} -\mathbb {P} _{e})\nabla \varphi _{\lambda }^{e}}$, where ${\textstyle \mathbb {P} _{e}={\widehat {\mathbf {n} }}^{e}({\widehat {\mathbf {n} }}^{e})^{T}}$ is the projection matrix over the normal vector ${\textstyle {\widehat {\mathbf {n} }}^{e}}$ to the triangular element ${\textstyle T_{e}}$. Then, we can write

${\displaystyle K_{ij}=\!\!\!\sum _{T_{e}\in {\mathcal {T}}_{h}^{ij}}\!\int _{T_{e}}\!\!(\mathbb {I} -\mathbb {P} _{e})\nabla \varphi _{\lambda }^{e}\cdot (\mathbb {I} -\mathbb {P} _{e})\nabla \varphi _{\mu }^{e}\,dT_{e}.}$

(47)

Again, these integrals are calculated in the reference element using the affine transformation. Observing that ${\textstyle \nabla {\hat {\varphi }}_{\lambda }=\mathbb {J} _{e}^{T}\,\nabla \varphi _{\lambda }^{e}}$, and that ${\textstyle \nabla \varphi _{\lambda }^{e}}$ is a linear combination of the local fundamental vectors ${\textstyle \mathbf {r} _{\xi }^{e}}$, ${\textstyle \mathbf {r} _{\eta }^{e}}$, ${\textstyle {\hat {\mathbf {n} }}^{e}}$, we obtain

${\displaystyle (\mathbb {I} -\mathbb {P} _{e})\nabla \varphi _{\lambda }^{e}=\mathbb {J} _{e}\,(\mathbb {J} _{e}^{T}\mathbb {J} _{e})^{-1}\nabla {\hat {\varphi }}_{\lambda },\lambda =1,2,3.}$

(48)

Therefore,

${\displaystyle K_{ij}=\sum _{T_{e}\in {\mathcal {T}}_{h}^{ij}}\iint _{\hat {T}}(\nabla {\hat {\varphi }}_{\lambda })^{T}(\mathbb {J} _{e}^{T}\mathbb {J} _{e})^{-1}\nabla {\hat {\varphi }}_{\mu }\,||\mathbf {r} _{\xi }^{e}\times \mathbf {r} _{\mu }^{e}||\,d\xi d\eta =\sum _{T_{e}\in {\mathcal {T}}_{h}^{ij}}||\mathbf {r} _{\xi }^{e}\times \mathbf {r} _{\mu }^{e}||\,{\widehat {K}}_{\lambda \mu }^{e},}$

(49)

where, for ${\textstyle 1\leq \lambda ,\mu \leq 3}$,

${\displaystyle {\widehat {K}}_{\lambda \mu }^{e}=\displaystyle {\frac {1}{2}}(\nabla {\hat {\varphi }}_{\lambda })^{T}(\mathbb {J} _{e}^{T}\mathbb {J} _{e})^{-1}\nabla {\hat {\varphi }}_{\mu },}$

(50)

and the gradients are the constant column vectors ${\textstyle \nabla {\hat {\varphi }}_{1}(\xi ,\eta )=(-1,-1)^{T}}$, ${\textstyle \nabla {\hat {\varphi }}_{2}(\xi ,\eta )=(1,0)^{T}}$ and ${\textstyle \nabla {\hat {\varphi }}_{3}(\xi ,\eta )=(0,1)^{T}}$.

In summary, the coefficients of the matrix

${\displaystyle \mathbb {A} =\alpha \,\mathbb {M} +D_{\Sigma }\,\mathbb {K} ,}$

associated to the finite element approximation of the elliptic equation (26) are computed by means of the formula:

${\displaystyle a_{ij}=\sum _{T_{e}\in {\mathcal {T}}_{h}^{ij}}||\mathbf {r} _{\xi }^{e}\times \mathbf {r} _{\eta }^{e}||\,\left(\alpha \,{\widehat {M}}_{\lambda \mu }+D_{\Sigma }\,{\widehat {K}}_{\lambda \mu }^{e}\right),}$

(51)

with ${\textstyle i=g(e,\lambda )}$ y ${\textstyle j=g(e,\mu )}$.

3.2.5 Calculation of the coefficients F_j of the load vector F

Using again the relationship between the global index and the local index we can approximate the load vector (38). First, the source term ${\textstyle f(x,y,z)}$ is approximated on each triangular element as

${\displaystyle f(x,y,z)\approx \displaystyle \sum _{\lambda =1}^{3}f\left(x_{\lambda }^{e},y_{\lambda }^{e},z_{\lambda }^{e}\right)\varphi _{\lambda }^{e}(x,y,z),}$

then, we have

${\displaystyle F_{j}=\displaystyle \sum _{T_{e}\in {\mathcal {T}}_{h}^{ij}}||\mathbf {r} _{\xi }^{e}\times \mathbf {r} _{\eta }^{e}||\displaystyle \sum _{\lambda =1}^{3}f\left(x_{\lambda }^{e},y_{\lambda }^{e},z_{\lambda }^{e}\right){\widehat {M}}_{\lambda \mu },}$

(52)

assuming that ${\textstyle j=g(e,\mu )}$ in ${\textstyle T_{e}}$, so ${\textstyle i=g(e,\lambda )}$ run over the adjacent nodes.

4 Full discretization of the reaction diffusion model for 3–D surfaces

Coming back to the generation of Turing patterns on three-dimensional surfaces, we must solve the following reaction-diffusion system on a given surface ${\textstyle \Sigma }$.

${\displaystyle \displaystyle {\frac {\partial {u}}{\partial {t}}}=D_{u}\nabla _{\Sigma }^{2}u+\gamma \,f(u,v){\hbox{ in}}\quad \Sigma ,}$ (53) ${\displaystyle \displaystyle {\frac {\partial {v}}{\partial {t}}}=D_{v}\nabla _{\Sigma }^{2}v+\gamma \,g(u,v){\hbox{ in}}\quad \Sigma ,}$ (54) ${\displaystyle ({\hat {\mathbf {n} }}\cdot \nabla )u=({\hat {\mathbf {n} }}\cdot \nabla )v=0,{\hbox{ on}}\quad \partial {\Sigma },}$ (55) ${\displaystyle u(\mathbf {x} ,0)=u_{0}(\mathbf {x} ),\,\,v(\mathbf {x} ,0)=v_{0}(\mathbf {x} ),\quad \forall \,\mathbf {x} \in \Sigma {.}}$ (56)

A similar analysis to the one done in Section (3.1) may be performed for this system. However, the analysis is not as simple as before, because surface geometry and topology (curvature, for instance) play an important role in pattern formation and in pattern dynamics. Nowadays there is a limited understanding about this phenomena [8]. In fact, a static pattern on a flat plane can become a propagating pattern on a curved surface [9]. Also, it is well-known that geometric aspects influence the transport properties of particles that diffuse on curved surfaces, as shown in [10] and some reference therein. For these reasons, we will take advantage of what has been done for planar regions and use it as a guideline to generate Turing patterns on curved surfaces. Therefore, we will consider the Turing conditions (21-25) for planar regions and, with some slight variation of the parameter values, depending of the particular surface, we will generate some Turing patterns by solving numerically the above reaction-diffusion equations and show some results with the numerical methodology developed in the previous sections.

4.1 Semi-implicit scheme for discretizing the parabolic form of the Laplace-Beltrami equation

A full discretization of the reaction-diffusion system (53)-(56) is may be obtained by a combination of finite difference dicretization with respect to time and finite element discretization with respect to space variables. One of the simplest, but still very effective, schemes is obtained by means of Euler time discretization. The time-interval ${\textstyle [0,T]}$ with ${\textstyle T>0}$ is divided into ${\textstyle N}$ subintervals of small length ${\textstyle \Delta t=T/N}$, say ${\textstyle [(n-1)\Delta t,n\Delta t]}$, ${\textstyle n=1,\ldots ,N}$. From the initial conditions we obtain the starting values ${\textstyle (u^{0}(\mathbf {x} ),v^{0}(\mathbf {x} ))=(u_{0}(\mathbf {x} ),v_{0}(\mathbf {x} ))}$, and assuming that approximations ${\textstyle (u^{1}(\mathbf {x} ),v^{1}(\mathbf {x} ))\approx (u(\mathbf {x} ,\Delta {t}),v(\mathbf {x} ,\Delta {t}))}$,${\textstyle \ldots }$, ${\textstyle (u^{n}(\mathbf {x} ),v^{n}(\mathbf {x} ))\approx (u(\mathbf {x} ,n\,\Delta {t}),v(\mathbf {x} ,n\,\Delta {t}))}$, are already known, we can compute the next approximation ${\textstyle (u^{n+1}(\mathbf {x} ),v^{n+1}(\mathbf {x} ))}$ by solving the system

${\displaystyle \displaystyle {\frac {u^{n+1}-u^{n}}{\Delta {t}}}-D_{u}\,\nabla _{\Sigma }^{2}\,u^{n+1}=\gamma \,f(u^{n},v^{n}),\quad }$ (57) ${\displaystyle \displaystyle {\frac {v^{n+1}-v^{n}}{\Delta {t}}}-D_{v}\,\nabla _{\Sigma }^{2}\,v^{n+1}=\gamma \,g(u^{n+1},v^{n}),}$ (58)

where the boundary conditions ${\textstyle ({\hat {\mathbf {n} }}\cdot \nabla )u^{n+1}=0}$ and ${\textstyle ({\hat {\mathbf {n} }}\cdot \nabla )v^{n+1}=0}$ must be satisfied if ${\textstyle \partial \Sigma \neq \emptyset }$. It is easy to see that these equations are of elliptic type (26). For instance for the first equation we can set ${\textstyle u=u^{n+1}}$, ${\textstyle \alpha =1/\Delta {t}}$ and ${\textstyle f=\gamma \,f(u^{n},v^{n})+\alpha \,u^{n}}$, obtaining a system of the form (26). So, the numerical solution of both equations at each time step is obtained by the finite element method developed in Section 4. The full discretization scheme is called semi-implicit (see [11]) because the diffusion terms are evaluated implicitly while the reaction terms are evaluated explicitly, at each time step.

4.2 Validation of the proposed methodology

According to the full discretization scheme, we must solve the elliptic equation (26) at every time step. So, it it very important to have an effective and accurate numerical solution to this equation. Let ${\textstyle \Sigma }$ be the unit sphere, ${\textstyle \alpha =0}$, ${\textstyle D_{\Sigma }=1}$ and ${\textstyle f(x,y,z)=12xyz}$, then the exact solution of (26) is ${\textstyle \phi (x,y,z)=xyz}$. We can compare the numerical solution ${\textstyle \phi _{h}}$ with this exact solution and find the accuracy of the numerical method. We generate triangular meshes on the unit sphere by the subdivision of an inscribed icosahedron, and we denote by ${\textstyle N_{s}}$ the number of the subdivisions. We show the generated meshes for ${\textstyle N_{s}=0,3,4,5}$ in Figure 4.

Figure 4: Triangular meshes

The rate of convergence ${\textstyle r}$ of the linear finite element method is obtained from the error estimate

${\displaystyle \Vert \phi -\phi _{h}\Vert _{L^{2}(\Sigma )}\leq C\Vert \phi \Vert _{L^{2}(\Sigma )}h^{r},}$

(59)

where ${\textstyle \phi _{h}}$ is the numerical solution on a triangular mesh with mesh-size ${\textstyle h}$ (the average diameter of the triangular elements), ${\textstyle C}$ is a constant independent of ${\textstyle h}$. It we show that ${\textstyle r}$ is close to 2, then our numerical method achieves the optimal convergence rate. This parameter is estimated from the relation

${\displaystyle {\frac {\Vert \phi -\phi _{h}\Vert _{L^{2}(\Sigma )}}{\Vert \phi -\phi _{h/2}\Vert _{L^{2}(\Sigma )}}}\approx 2^{r},}$

(60)

for two meshes, one with mesh-size ${\textstyle h}$ and a refinement with mesh-size ${\textstyle h/2}$, for ${\textstyle h}$ small enough. We obtained ${\textstyle r=2.0155}$ with mesh-sizes ${\textstyle h}$ and ${\textstyle h/2}$, corresponding ${\textstyle N_{s}=4}$ and 5, respectively.

On the other hand, for parabolic PDE the methodology has been tested in the context of optimal control on a toroidal surface and on a sphere, as shown in references [12,13].

5 Numerical results

Example 1. We consider the Schnakenberg model, which is a classical and simple model to generate spot patterns, among other structures. Its reaction terms give rise to one of the simplest oscillating reactions between two chemical species, and was introduced by Schnakenberg in 1979 [14]. These reaction terms, in dimensionless form, are

${\displaystyle f(u,v)=\gamma \,(a-u+u^{2}v),}$ (61) ${\displaystyle g(u,v)=\gamma \,(b-u^{2}v),}$ (62)

with ${\textstyle a,b,\gamma }$ positive constants. We assume homogeneous Neumann-type boundary conditions for the case of open and bounded surfaces, and initial conditions as in (55–56). The stable equilibrium of the chemical reaction is

${\displaystyle u^{\ast }=a+b,\quad v^{\ast }=\displaystyle {\frac {b}{(a+b)^{2}}}.}$

(63)

The Jacobian matrix at the equilibrium point (63) is

${\displaystyle \mathbb {J} ={\begin{pmatrix}\displaystyle {\frac {b-a}{a+b}}&(a+b)^{2}\\-\displaystyle {\frac {2b}{a+b}}&-(a+b)^{2}\end{pmatrix}}}$

(64)

Considering ${\textstyle a<b}$ the conditions (21-24) translate into

1. ${\textstyle 0<b-a<(a+b)^{3}}$,
2. ${\textstyle D_{\Sigma }(b-a)>(a+b)^{3}}$,
3. ${\textstyle \left[D_{\Sigma }(b-a)-(a+b)^{3}\right]^{2}>4D_{\Sigma }(a+b)^{4}}$.

For more details we recommend references [15,16,17].

We present numerical results for four different 3-D surfaces for which we show coarse meshes in Figure 5: The first two are closed surfaces and the other two are open. Actual meshes to compute numerical solutions are refinement of these meshes (the number of nodes and triangular elements are included along with each numerical result below. These meshes were generated using their parametric equations:

• `Blood cell'¹: ${\textstyle -\pi /2\leq \theta \leq \pi /2}$, ${\textstyle 0\leq \phi \leq 2\pi }$,

${\displaystyle x=r_{0}\,{\hbox{ cos}}\,\phi \,{\hbox{ cos}}\,\theta }$ ${\displaystyle y=r_{0}\,{\hbox{ sin}}\,\phi \,{\hbox{ cos}}\,\theta }$ ${\displaystyle z=\displaystyle {\frac {1}{2}}{\hbox{ sin}}\,\theta \,(c_{0}+c_{2}{\hbox{ cos}}^{2}\theta +c_{4}{\hbox{ cos}}^{4}\theta )}$

where ${\textstyle r_{0}=3.91/3.39}$, ${\textstyle c_{0}=0.81/3.39}$, ${\textstyle c_{2}=7.83/3.39}$ and ${\textstyle c_{4}=-4.39/3.39}$.

• `Strawberry': ${\textstyle \mathbf {x^{2}+y^{2}+(z-{\sqrt {x^{2}+y^{2}}})^{2}=1} }$.
• `Coiled toroid': ${\textstyle 0\leq \theta \leq 2\pi }$, ${\textstyle 0\leq \phi \leq 4\pi }$,

${\displaystyle x=(3+{\hbox{ cos}}\,\theta )\,{\hbox{ cos}}\,\phi }$ ${\displaystyle y=(3+{\hbox{ cos}}\,\theta )\,{\hbox{ sin}}\,\phi }$ ${\displaystyle z={\hbox{ sin}}\,\theta -0.325\,\phi }$

• `Helical shell' ²: ${\textstyle 0\leq \theta \leq 2\pi }$ and ${\textstyle t\in [-40,-1]}$,

${\displaystyle x=e^{0.05\,t}(1.5+{\hbox{ cos}}\,\theta )\,{\hbox{ cos}}\,t}$ ${\displaystyle y=-e^{0.05\,t}(1.5+{\hbox{ cos}}\,\theta )\,{\hbox{ sin}}\,t}$ ${\displaystyle z=e^{0.05\,t}(-8.5+1.2\,{\hbox{ sin}}\,\theta )}$

Figure 5: Surfaces used for the Schnakenberg model to generate spot patterns.

For all these cases we fix the parameter values ${\textstyle D_{\Sigma }=20}$, ${\textstyle a=0.126779}$ and ${\textstyle b=0.792366}$, for which it is known that generate spot like patterns in a planar region for different values ${\textstyle \gamma }$. The initial conditions ${\textstyle (u_{0},v_{0})}$ were generated by a 10% perturbation of the equilibrium ${\textstyle (u^{\ast },v^{\ast })}$.

• `Blood cell'. Discretization parameters: ${\textstyle \Delta t=10^{-4}}$, mesh with 40962 nodes and 81920 triangular elements. Scale factor ${\textstyle \gamma =1000}$.

Figure 6: Concentrations at ${\displaystyle t=0}$ and ${\displaystyle t=4}$.

• `Strawberry surface' Discretization parameters: ${\textstyle \Delta t=10^{-4}}$, mesh with 40962 nodes and 81920 triangular elements. Scale factor ${\textstyle \gamma =500}$.

Figure 7: Concentrations at ${\displaystyle t=0}$ and ${\displaystyle t=1.}$.

• 'Coiled toroid'. Discretization parameters: ${\textstyle \Delta t=10^{-4}}$, mesh with 48690 nodes and 97200 elements. Scale factor ${\textstyle \gamma =100}$.

Figure 8: Concentrations at ${\displaystyle t=0}$ and ${\displaystyle t=4.}$.

• `Helical shell'. Discretization parameters: ${\textstyle \Delta t=10^{-4}}$, mesh with 90150 nodes and 180000 elements. Scale factor ${\textstyle \gamma =500}$.

Figure 9: Concentrations at ${\displaystyle t=0}$ and ${\displaystyle t=2}$.

Example 2. Now, we consider the BVAM model³ taken from [20], which expressed in its Laplace-Beltrami form for surface domains is given by:

${\displaystyle {\frac {\partial {u}}{\partial {t}}}=D_{\Sigma }\delta \nabla _{\Sigma }^{2}u+\gamma \left[\alpha u(1-r_{1}v^{2})+v(1-r_{2}u)\right],}$ ${\displaystyle {\frac {\partial {v}}{\partial {t}}}=\delta {\nabla }_{\Sigma }^{2}v+\gamma \left[\beta v\left(1+\displaystyle {\frac {\alpha r_{1}}{\beta }}uv\right)+u(\epsilon +r_{2}v)\right],}$

where ${\textstyle \alpha ,\beta ,\delta ,\epsilon ,D}$ are constants. The scale factor ${\textstyle \gamma >0}$ has been added to allow for more convenient manipulation of pattern sizes. The stable equilibria of the chemical reaction, ${\textstyle \mathbf {w} ^{\ast }=(u^{\ast },v^{\ast })^{T}}$, must satisfy

${\displaystyle v^{\ast }=-\displaystyle {\frac {(\alpha +\epsilon )}{1+\beta }}u^{\ast },\quad \beta \not =1.}$

(65)

For ${\textstyle \epsilon =-\alpha }$, ${\textstyle v^{\ast }=0}$. For simplicity, we consider ${\textstyle \mathbf {w} ^{\ast }=(0,0)^{T}}$ as the equilibrium point. In this case the Jacobian matrix at the equilibrium point ${\textstyle \mathbf {w} ^{\ast }=(0,0)^{T}}$ is given by

${\displaystyle \mathbb {J} ={\begin{pmatrix}\alpha &1\\\epsilon &\beta \end{pmatrix}}.}$

(66)

Thus, the conditions (21-24) for this case are:

1. ${\textstyle \alpha +\beta <0}$,
2. ${\textstyle \alpha \beta -\epsilon >0}$,
3. ${\textstyle D\alpha +\beta >0}$,
4. ${\textstyle \left(D\alpha +\beta \right)^{2}>4D(\alpha \beta -\epsilon )}$,

with ${\textstyle \alpha ,\delta >0}$, ${\textstyle \beta ,\epsilon <0}$ and ${\textstyle 0<D<1}$.

Again, we present numerical results for four different 3-D surfaces shown in Figure 10, three of them are closed surfaces and the other one is open. These meshes were generated using their parametric equations:

• Unit sphere: standard parametrization with radius ${\textstyle R=1}$
• Toroid: usual parametrization with major radius ${\textstyle R=2.5}$ and minor radius ${\textstyle r=1}$.
• Dupin's cyclide⁴: ${\textstyle 0\leq \phi ,\theta \leq 2\pi }$,

${\displaystyle x=\displaystyle {\frac {d(c-a\,{\hbox{cos}}\,\phi \,{\hbox{cos}}\,\theta )+b^{2}{\hbox{cos}}\,\phi }{a-c\,{\hbox{cos}}\,\phi \,{\hbox{cos}}\,\theta }}}$ ${\displaystyle y=\displaystyle {\frac {b\,{\hbox{sin}}\,\phi \,(a-d\,{\hbox{cos}}\,\theta )}{a-c\,{\hbox{cos}}\,\phi \,{\hbox{cos}}\,\theta }}}$ ${\displaystyle z=\displaystyle {\frac {b\,{\hbox{sin}}\,\theta \,(c\,{\hbox{cos}}\,\phi -d)}{a-c\,{\hbox{cos}}\,\phi \,{\hbox{cos}}\,\theta }}}$

with ${\textstyle a=2}$, ${\textstyle b=1.95}$, ${\textstyle c^{2}=a^{2}-b^{2}}$, ${\textstyle d=c+0.2}$.

• Wavy cylinder without covers: ${\textstyle 0\leq \theta \leq 2\pi }$, ${\textstyle 0\leq z\leq 2}$

${\displaystyle x=R(z)\,{\hbox{ cos}}\theta }$ ${\displaystyle y=R(z)\,{\hbox{ sin}}\theta }$ ${\displaystyle z=z}$

with ${\textstyle R(z)=0.5\,{\hbox{cos}}^{2}(3z)+1}$.

Figure 10: Surfaces used for the BVAM model to generate Turing patterns.

The following numerical results were obtained with parameter values ${\textstyle \alpha }$, ${\textstyle \beta }$, ${\textstyle \delta }$, ${\textstyle \epsilon }$, ${\textstyle r_{1}}$, ${\textstyle r_{2}}$, ${\textstyle D_{\Sigma }}$ within the range proposed in [18]. In particular, the following parameters are common for the four cases: ${\textstyle \alpha =0.899}$, ${\textstyle \beta =-0.91}$, ${\textstyle \delta =0.516}$, ${\textstyle \epsilon =-0.899}$.

• Sphere. Discretization parameters: ${\textstyle \Delta t=10^{-2}}$, mesh with 40962 nodes and 81920 triangular elements. Scale factor ${\textstyle \gamma =10}$. Parameters: ${\textstyle r_{1}=3.5}$, ${\textstyle r_{2}=0}$, ${\textstyle D_{\Sigma }=2.1\times {10^{-3}}}$.

Figure 11: Concentrations at ${\displaystyle t=0}$ and ${\displaystyle t=600}$.

• Toroid. Discretization parameters: ${\textstyle \Delta t=10^{-2}}$, mesh with 20000 nodes and 40000 triangular elements. Scale factor ${\textstyle \gamma =0.5}$. Parameters: ${\textstyle r_{1}=0.02}$, ${\textstyle r_{2}=0.2}$, ${\textstyle D_{\Sigma }=4.5\times {10^{-3}}}$.

Figure 12: Concentrations at ${\displaystyle t=0}$ and ${\displaystyle t=800}$.

• Dupin's cyclide. Discretization parameters: ${\textstyle \Delta {t}=10^{-2}}$, mesh with 22500 nodes and 45000 elements. Scale factor ${\textstyle \gamma =10}$. Parameters: ${\textstyle r_{1}=3.5}$, ${\textstyle r_{2}=0}$, ${\textstyle D_{\Sigma }=2.1\times {10^{-3}}}$.

Figure 13: Concentrations at ${\displaystyle t=0}$ and ${\displaystyle t=1350}$.

• Wavy cylinder without covers. Discretization parameters: ${\textstyle \Delta t=10^{-2}}$, mesh with 29040 nodes and 57600 elements. Scale factor value ${\textstyle \gamma =2}$. Parameters: ${\textstyle r_{1}=0.02}$, ${\textstyle r_{2}=0.2}$, ${\textstyle D_{\Sigma }=4.5\times {10^{-3}}}$.

Figure 14: Concentrations at ${\displaystyle t=0}$ and ${\displaystyle t=500}$.

(¹) Equations obtained from [18]

(²) Equations obtained from [19]

(³) Named after the initials of its authors: Barrio, Varea, Aragón and Maini.

(⁴) Equations obtained from [21].

6 Conclusions

• When transferring the mathematical conditions for pattern generation from planar regions to surfaces, the Laplace-Beltrami operator was used and computational simulations were performed. In these simulations, spatial patterns similar to those already known in planar regions were observed. In some cases, it was necessary to adjust the value of the scale factor ${\textstyle \gamma }$, which is closely related to the wave modes in the analytical solution; this adjustment was crucial to obtain patterns on surfaces.

• The numerical methodology for the solution of the Laplace-Beltrami equation, using the finite element method, allowed the development of a simple way for calculating the mass matrices ${\textstyle \mathbb {M} }$, the stiffness matrix ${\textstyle \mathbb {K} }$ and the load vector ${\textstyle \mathbf {F} }$. This resulted in an optimized code to perform the computational simulations. A great advantage of this implementation is that the calculations to determine the mass matrices ${\textstyle \mathbb {M} }$, stiffness ${\textstyle \mathbb {K} }$ and the load vector ${\textstyle \mathbf {F} }$ depend only on the coordinates of the nodes of the triangular mesh associated with the surface and on the gradients of the functions ${\textstyle {\hat {\varphi }}_{1}}$, ${\textstyle {\hat {\varphi }}_{2}}$ and ${\textstyle {\hat {\varphi }}_{3}}$, which, as previously seen, are constant.

• Although the strategy for solving the system ${\textstyle (\alpha \mathbb {M} +D_{\Sigma }\mathbb {K} ){\boldsymbol {\phi }}=\mathbf {F} }$ obtained in (35) was not presented, the Cholesky-type factorization was used in the matrix ${\textstyle \mathbb {A} =\alpha \mathbb {M} +D_{\Sigma }\mathbb {K} }$ because it is a positive definite symmetric matrix. Additionally, since matrix ${\textstyle \mathbb {A} }$ is sparse, different methods are available to further speed up the calculations (see [22], [23]). In our case, the Minimum Degree Permutation Method was used, which significantly optimized the computation time.

• It is important to mention that, for the most part, the triangular meshes are generated from known parametrizations of the surfaces. It is crucial that these meshes are of good quality to obtain optimal numerical results, as poor-quality meshes can lead to significant numerical errors. Reference [24] can be consulted for an introduction to the study of triangular mesh quality. It is worth mention that parametrizations are not used for the numerical solution of the reaction diffusion-models, instead they are solved directly in Euclidean coordinates, as indicated in Section 3.

BIBLIOGRAPHY

[1] Turing, Alan Mathison. (1990) "The chemical basis of morphogenesis", Volume 52. Springer. Bulletin of mathematical biology 153–197

[2] Lacitignola, Deborah and Bozzini, Benedetto and Frittelli, Massimo and Sgura, Ivonne. (2017) "Turing pattern formation on the sphere for a morphochemical reaction-diffusion model for electrodeposition", Volume 48. Elsevier. Communications in Nonlinear Science and Numerical Simulation 484–508

[3] Xiao, Xufeng and Wang, Kun and Feng, Xinlong. (2018) "A lifted local Galerkin method for solving the reaction–diffusion equations on implicit surfaces", Volume 231. Elsevier. Computer Physics Communications 107–113

[4] Kim, Hyundong and Yun, Ana and Yoon, Sungha and Lee, Chaeyoung and Park, Jintae and Kim, Junseok. (2020) "Pattern formation in reaction–diffusion systems on evolving surfaces", Volume 80. Elsevier. Computers & Mathematics with Applications 9 2019–2028

[5] Song, Xin and Li, Yibao. (2022) "An efficient numerical method for reaction–diffusion equation on the general curved surfaces", Volume 133. Elsevier. Applied Mathematics Letters 108268

[6] Perko, Lawrence. (2013) "Differential equations and dynamical systems", Volume 7. Springer Science & Business Media

[7] Strogatz, Steven H. (2018) "Nonlinear dynamics and chaos: with applications to physics, biology, chemistry, and engineering". CRC press

[8] Nishide, Ryosuke and Ishihara, Shuji. (2024) "Weakly nonlinear analysis of Turing pattern dynamics on curved surfaces". arXiv preprint arXiv:2403.12444

[9] Nishide, Ryosuke and Ishihara, Shuji. (2022) "Pattern propagation driven by surface curvature", Volume 128. APS. Physical Review Letters 22 224101

[10] Ledesma Durán, A. and Juárez Valencia, L.H. (2023) "Diffusion coefficients and MSD measurements on curved membranes and porous media", Volume 46. Springer. The European Physical Journal E 8 70

[11] Juárez Valencia, L.H. (2023) "Notas Método del Elemento Finito". UAM-I

[12] León Velasco, D.A. and Glowinski, Roland and Juárez Valencia, L. H. (2015) "On the controllability of diffusion processes on the surface of a torus: a computational approach", Volume 11. Pac J Optim 763–790

[13] León Velasco, D.A. and Glowinski, Roland and Juárez Valencia, L.H. (2016) "On the controllability of diffusion processes on a sphere: a numerical study", Volume 22. ESAIM: Control, Optimisation and Calculus of Variations 4 1054–1077

[14] Schnakenberg, J. (1979) "Simple chemical reaction systems with limit cycle behaviour", Volume 81. Elsevier. Journal of theoretical biology 3 389–400

[15] Madzvamuse, Anotida. (2006) "Time-stepping schemes for moving grid finite elements applied to reaction–diffusion systems on fixed and growing domains", Volume 214. Elsevier. Journal of computational physics 1 239–263

[16] Dufiet, V. and Boissonade, J. (1992) "Numerical studies of Turing patterns selection in a two-dimensional system", Volume 188. Elsevier. Physica A: Statistical Mechanics and its Applications 1-3 158–171

[17] Ledesma Durán, A. (2012) "Patrones de turing en sistemas biológicos". Universidad Autónoma Metropolitana, CDMX

[18] Fuselier, Edward J. and Wright, Grady B. (2013) "A high-order kernel method for diffusion and reaction-diffusion equations on surfaces", Volume 56. Springer. Journal of Scientific Computing 3 535–565

[19] American Mathematical Society "Mathematical Features on Shells" https://www.ams.org/publicoutreach/feature-column/fcarc-shell5

[20] Barrio, R.A. and Varea, C. and Aragón, J.L. and Maini, P.K. (1999) "A two-dimensional numerical study of spatial pattern formation in interacting Turing systems", Volume 61. Elsevier. Bulletin of mathematical biology 3 483–505

[21] Wikipedia "Dupin cyclide" https://en.wikipedia.org/wiki/Dupin_cyclide

[22] Davis, Timothy A. (2006) "Direct methods for sparse linear systems". SIAM

[23] Duff, Iain S. and Erisman, Albert Maurice and Reid, John Ker. (2017) "Direct methods for sparse matrices". Oxford University Press

[24] Sarrate, J. and Palau, J. and Huerta, Antonio. (2003) "Numerical representation of the quality measures of triangles and triangular meshes", Volume 19. Wiley Online Library. Communications in numerical methods in engineering 7 551–561

[25] León Velasco, D. A. and Chacón Acosta, G. (2021). "Full Finite Element Scheme for Reaction‐Diffusion Systems on Embedded Curved Surfaces in ${\textstyle \mathbb {R} ^{3}}$". Advances in Mathematical Physics 1 8898484.