Bayesian Estimation of the Basic Reproductive Number in a Chikungunya Outbreak in Acapulco, Guerrero

Latest revision as of 17:51, 19 November 2024

1 Introducción

La fiebre chikungunya es una enfermedad viral transmitida a los humanos por mosquitos del género Aedes [1]. El virus, que da nombre a la enfermedad, se describió en humanos por primera vez en 1952 en Tanzania, África, donde entre el 60% y el 80% de la población presentó síntomas de artralgia, fiebre y erupciones cutáneas. Muchas personas, tras el periodo agudo de la enfermedad, continuaron experimentando dolores articulares durante meses [2].

Entre 1960 y 1990, hubo brotes de fiebre chikungunya en varios países africanos, como República Democrática del Congo, Uganda, Angola, Sudáfrica y Nigeria [3]. En América, el primer caso se reportó en la isla de San Martín ubicada en el Caribe} en 2013, y para diciembre de 2014, la enfermedad se había extendido a 17 países sudamericanos. Actualmente, se ha identificado en 45 países en el Caribe, América del Norte, América del Sur y América Central [3].

En México, el primer caso importado de fiebre chikungunya se presentó en mayo de 2014 [4]. A finales de ese año, se reportaron 155 casos en los estados de Chiapas, Guerrero, Oaxaca, Sonora y Sinaloa. Para la semana epidemiológica 40, en 2015 se habían contabilizado 8,668 casos confirmados, siendo Guerrero el estado con la mayor cantidad de infectados, con el 18.38% [5]. Al final de ese año, se confirmaron un total de 12,588 casos de chikungunya en México [6].

Cuando una persona es picada por un mosquito infectado, los síntomas suelen comenzar entre 3 y 7 días después del período de incubación. Durante este tiempo, el virus se multiplica en el organismo del infectado, pero la persona no presenta síntomas ni es contagiosa para otros. Los síntomas incluyen dolor intenso en las articulaciones, fiebre superior a 39°C, dolor muscular y, ocasionalmente, náuseas, vómitos y erupciones cutáneas. El dolor articular puede ser tan intenso que resulta debilitante o incapacitante [2]. Tras una semana, la mayoría de los pacientes experimenta una notable mejora: la fiebre, el cansancio y la artralgia disminuyen significativamente en 1 o 2 semanas, aunque frecuentemente se produce una recaída [7]. Actualmente, no existe un tratamiento específico para la infección por chikungunya; el manejo se limita a aliviar los síntomas con medicación analgésica y antiinflamatoria [2].

Se ha reportado el fenómeno de recaída en las infecciones por chikungunya [8,9,10]. La recaída se define como la reaparición de artralgia debido a la persistencia del virus en las células del tejido musculoesquelético después de un período sin síntomas de al menos una semana [8] o después de un mes [10]. En un estudio de cohortes realizado en Francia, basado en datos de un sistema de vigilancia de laboratorio, se confirmó la infección inicial mediante una prueba de anticuerpos o PCR (reacción en cadena de la polimerasa). En ese estudio, se reportaron recaídas de artralgia en el 72% de los pacientes; el número promedio de recaídas fue de 4 y el tiempo promedio entre dos recaídas fue de 8 semanas [8]. Por otro lado, un estudio transversal realizado en Acapulco, Guerrero, en diciembre de 2015, encontró que el 66% de la población (3,531 de 5,870 personas) autoreportó haber estado infectada. De los cuales, el 31.1% (1,098 de 3,531) experimentó al menos una recaída un mes después de recuperarse. Entre ellos, el 13% informó una recaída, el 12% tuvo dos, el 4% tres y solo el 2% reportó más de cuatro recaídas [10].

La edad como factor de riesgo es común en las enfermedades infecciosas transmitidas por vectores. En el caso del chikungunya, un estudio de seropositividad reportó la frecuencia de positivos al virus en los siguientes grupos etarios: 33% en el grupo de 0 a 19 años, 62% en el de 20 a 39 años, 67.4% en el de 40 a 49 años, 75% en el de 50 a 59 años, 59% en el de 60 a 69 años, 25% en el de 70 a 79 años y 33% en el de 80 años y más [11], lo que muestra una variabilidad en la susceptibilidad al virus.

La variabilidad en el período de recaídas y en la susceptibilidad al virus del chikungunya motivó a Vázquez-Peña, Vargas-De-León y Velázquez-Castro [12] a desarrollar un modelo hospedero-vector que considera tanto la edad cronológica como la edad de la infección asintomática. Este modelo se presentará en la Sección 2.

A partir de este modelo hospedero-vector con dos estructuras de edad, obtendremos un modelo en ecuaciones diferenciales ordinarias para el virus del chikungunya, tal como fue propuesto por Vázquez-Peña et al. [13], el cual se discutirá en la Sección 3.

En este trabajo, se propone estimar los parámetros y el número reproductivo básico utilizando un enfoque Bayesiano con los datos del brote de chikungunya en Acapulco, Guerrero [10]. Para ello, emplearemos el modelo hospedero-vector presentado en la Sección 3. La metodología del enfoque Bayesiano se describirá en la Sección 4, mientras que la estimación Bayesiana de los parámetros y del número reproductivo básico (12) se presentará en la Sección 5. Finalmente, en la Sección 6, se realizarán algunas comentarios finales.

2 Modelo hospedero-vector con dos estructura de edades

Denotamos por ${\textstyle N_{h}}$ y ${\textstyle N_{v}}$ el número total de hospederos y vectores, respectivamente. Las poblaciones de hospederos y vectores se dividen en clases disjuntas según su estado epidemiológico. Para los hospederos, consideramos cuatro grupos: susceptibles ( ${\textstyle S_{h}(t,\tau )}$ ), infectados ( ${\textstyle I_{h}(t,\tau )}$ ), asintomáticos ( ${\textstyle A_{h}(t,\omega )}$ ) y recuperados ( ${\textstyle R_{h}(t,\tau )}$ ). En contraste, los vectores se dividen únicamente en susceptibles ( ${\textstyle S_{v}(t)}$ ) e infectados ( ${\textstyle I_{v}(t)}$ ).

La edad cronológica se denota por ${\textstyle \tau }$ , de manera que ${\textstyle s_{h}(t,\tau )}$ representa la cantidad de hospederos susceptibles con edad cronológica ${\textstyle \tau }$ en el tiempo ${\textstyle t}$ . Entonces, el total de hospederos susceptibles está dado por

(1)

Suponemos que la probabilidad de transmisión del vector al hospedero depende de la edad del hospedero, lo cual se denota por ${\textstyle \beta _{h}(\tau )}$ .

La tasa de transmisión del vector infectado al hospedero susceptible está definida por ${\textstyle {\frac {b}{N_{h}}}\beta _{h}(\tau )s_{h}(t,\tau )I_{v}(t)}$ , donde ${\textstyle b}$ es el promedio de picaduras por unidad de tiempo y ${\textstyle {\frac {b}{N_{h}}}}$ representa el número promedio de picaduras por unidad de tiempo por cada hospedero. Esto significa que se está distribuyendo el número total de picaduras entre el total de hospederos. Al mismo tiempo, la clase de hospederos susceptibles disminuye debido a la muerte natural a una tasa ${\textstyle \mu _{h}}$ y a alguna estrategia de prevención, como la vacunación, enfocada únicamente a ciertos grupos de edad, la cual será modelada por el parámetro ${\textstyle \rho (\tau )}$ . Por lo tanto, definimos ${\textstyle \varepsilon (\tau )=\mu _{h}+\rho (\tau )}$ .

Bajo estas hipótesis, se formula la primera ecuación del modelo:

Suponemos que todos los individuos nacen susceptibles a una tasa ${\textstyle \mu _{h}N_{h}}$ , de manera que obtenemos la condición de frontera:

Una vez que un hospedero se ha infectado, permanece en dicha clase hasta que los síntomas desaparecen a una tasa ${\textstyle \gamma }$ o por muerte por causas naturales a una tasa ${\textstyle \mu _{h}}$ . Consideramos que una fracción ${\textstyle p}$ no se recuperará y pasará a la fase asintomática durante un tiempo ${\textstyle \omega }$ , que representa la edad de la infección asintomática. La clase de hospederos asintomáticos se representa por ${\textstyle a_{h}(t,\omega )}$ , donde

(2)

es el total de hospederos asintomáticos. Además, la tasa en que los síntomas de la enfermedad vuelven a manifestarse depende de la edad de la infección asintomática; por ende, los hospederos asintomáticos retornan a la clase de hospederos infectados en un tiempo ${\textstyle 1/\delta _{h}(\omega )}$ . Con esto, se propone la segunda ecuación del modelo.

La clase de hospederos asintomáticos se reduce cuando los síntomas vuelven a manifestarse o por muerte por causas naturales, lo que da lugar a la siguiente ecuación del modelo:

Los hospederos infectados entran en la clase asintomática a una tasa ${\textstyle p\gamma }$ , comenzando el conteo de la edad de la infección asintomática, lo que se traduce en la condición de frontera

Los hospederos infectados se recuperan de manera permanente a una tasa ${\textstyle (1-p)\gamma }$ y permanecen en esa clase hasta la muerte por causas naturales a una tasa ${\textstyle \mu _{h}}$ , lo que se representa en la cuarta ecuación diferencial del modelo

En cuanto a los vectores, suponemos que nacen y mueren a la misma tasa ${\textstyle \mu _{v}}$ . Un vector nace susceptible y se infecta al picar a una persona con el virus, ya sea un hospedador infectado o un hospedador asintomático. De manera análoga al caso de los hospedadores, la tasa de transmisión ${\textstyle {\frac {\beta _{v}b}{N_{h}}}S_{v}(t)I_{h}(t)}$ depende de la probabilidad de que el contacto entre un hospedador infectado y un vector susceptible sea efectivo. Esta probabilidad se modela con el producto de la probabilidad de transmisión del virus ${\textstyle \beta _{v}}$ y el número promedio de picaduras por unidad de tiempo por cada hospedero ${\textstyle {\frac {b}{N_{h}}}}$ . Adicionalmente, se introduce el parámetro ${\textstyle \kappa }$ para tener en cuenta que la probabilidad de transmisión de un hospedero infectado a un vector es mayor que la tasa de transmisión de un hospedero asintomático a un vector. Por lo tanto, se considera que ${\textstyle 0\leq \kappa \leq 1}$ . Bajo estas suposiciones, obtenemos la quinta ecuación del modelo:

Después de que el vector se infecta de la forma descrita, permanece en esa clase hasta morir, lo que se modela en la última ecuación del modelo:

Por lo que se obtiene el siguiente sistema integro-diferencial recientemente propuesto por Vázquez-Peña, Vargas-De-León y Velázquez-Castro para el virus de chikungunya [12].

{\begin{aligned}{\frac {\partial s_{h}(t,\tau )}{\partial t}}+{\frac {\partial s_{h}(t,\tau )}{\partial \tau }}&=-{\frac {b}{N_{h}}}\beta _{h}(\tau )s_{h}(t,\tau )I_{v}(t)-\varepsilon _{h}(\tau )s_{h}(t,\tau ),\\s_{h}(t,0)&=\mu _{h}N_{h},\\{\frac {dI_{h}(t)}{dt}}&={\frac {b}{N_{h}}}\int _{0}^{\infty }\beta _{h}(\tau )s_{h}(t,\tau )I_{v}(t)d\tau -(\mu _{h}+\gamma )I_{h}(t)+\int _{0}^{\infty }\delta _{h}(\omega )a_{h}(t,\omega )d\omega ,\\{\frac {\partial a_{h}(t,\omega )}{\partial t}}+{\frac {\partial a_{h}(t,\omega )}{\partial \omega }}&=-(\mu _{h}+\delta _{h}(\omega ))a_{h}(t,\omega ),\\a_{h}(t,0)&=p\gamma I_{h}(t),\\{\frac {dR_{h}(t)}{dt}}&=(1-p)\gamma I_{h}(t)-\mu _{h}R_{h}(t),\\{\frac {dS_{v}(t)}{dt}}&=\mu _{v}N_{v}-{\frac {\beta _{v}b}{N_{h}}}S_{v}(t)I_{h}(t)-{\frac {\kappa \beta _{v}b}{N_{h}}}S_{v}(t)\int _{0}^{\infty }a_{h}(t,\omega )d\omega -\mu _{v}S_{v}(t),\\{\frac {dI_{v}(t)}{dt}}&={\frac {\beta _{v}b}{N_{h}}}S_{v}(t)I_{h}(t)+{\frac {\kappa \beta _{v}b}{N_{h}}}S_{v}(t)\int _{0}^{\infty }a_{h}(t,\omega )d\omega -\mu _{v}I_{v}(t).\end{aligned}}

(3)

Si consideramos que el tamaño de la población de vectores se mantiene constante en el tiempo, ${\textstyle N_{v}=S_{v}(t)+I_{v}(t)}$ , y observamos que la variable ${\textstyle R(t)}$ no esta acoplada en las demás ecuaciones, el modelo se reduce a

{\begin{aligned}{\frac {\partial s_{h}(t,\tau )}{\partial t}}+{\frac {\partial s_{h}(t,\tau )}{\partial \tau }}&=-{\frac {b}{N_{h}}}\beta _{h}(\tau )s_{h}(t,\tau )I_{v}(t)-\varepsilon _{h}(\tau )s_{h}(t,\tau ),\\s_{h}(t,0)&=\mu _{h}N_{h},\\{\frac {dI_{h}(t)}{dt}}&={\frac {b}{N_{h}}}\int _{0}^{\infty }\beta _{h}(\tau )s_{h}(t,\tau )I_{v}(t)d\tau -(\mu _{h}+\gamma )I_{h}(t)+\int _{0}^{\infty }\delta _{h}(\omega )a_{h}(t,\omega )d\omega ,\\{\frac {\partial a_{h}(t,\omega )}{\partial t}}+{\frac {\partial a_{h}(t,\omega )}{\partial \omega }}&=-\alpha (\omega )a_{h}(t,\omega ),{\hbox{ con }}\alpha (\omega )=\mu _{h}+\delta _{h}(\omega ),\\a_{h}(t,0)&=p\gamma I_{h}(t),\\{\frac {dI_{v}(t)}{dt}}&={\frac {\beta _{v}b}{N_{h}}}(N_{v}-I_{v}(t))\left(I_{h}(t)+\kappa \int _{0}^{\infty }a_{h}(t,\omega )d\omega \right)-\mu _{v}I_{v}(t).\end{aligned}}

(4)

Las condiciones iniciales están dadas por

Donde ${\textstyle s_{h0}(\tau )}$ y ${\textstyle a_{h0}(\omega )}$ representan la distribución inicial de los huéspedes susceptibles y de los hospederos asintomáticos con edad cronológica y edad de infección asintomática, respectivamente. ${\textstyle I_{h0}}$ e ${\textstyle I_{v0}}$ son el número inicial de hospederos y de vectores infectados, respectivamente.

2.1 Propiedades del sistema

El número reproductivo básico para el modelo (4) fue obtenido en [12]

(5)

donde ${\textstyle D}$ está dada por

(6)

y ${\textstyle \eta }$ por

(7)

El punto de equilibrio libre de la enfermedad ${\textstyle E^{0}}$ del sistema integro-diferencial (4) se obtiene al considerar ${\textstyle I_{h}(t)}$ , ${\textstyle a_{h}(t,\omega )}$ e ${\textstyle I_{v}(t)}$ iguales a cero simultáneamente, lo que resulta en ${\textstyle E^{0}=(s_{h}^{0}(\tau ),0,0,0)}$ , donde

(8)

En [12], se utiliza una estrategia geométrica para demostrar la existencia del punto de equilibrio endémico ${\textstyle E^{*}=(s_{h}^{*}(\tau ),I_{h}^{*},a_{h}^{*}(\omega ),I_{m}^{*})}$ cuando ${\textstyle R_{0}(\tau ,\omega )>1}$ .

Las propiedades de las soluciones a tiempos largos se resumen en el siguiente teorema:

Teorema 1: (Ver [12])

i) Si ${\textstyle R_{0}(\tau ,\omega )\leq {1}}$ , el punto de equilibrio libre de la enfermedad ${\textstyle E^{0}}$ del sistema integro-diferencial (4) es global asintóticamente estable.

ii) Si ${\textstyle R_{0}(\tau ,\omega )>1}$ , existe un único punto de equilibrio endémico ${\textstyle E^{*}}$ del sistema (4) y es global asintóticamente estable.

El ítem i) del Teorema 1 se demostró utilizando el segundo método de Lyapunov. Se construyó el siguiente funcional de Lyapunov ${\textstyle W(t)}$ , que es una combinación de una funcional tipo Volterra ${\textstyle f(x)=x-1-\ln {x}}$ y funcionales lineales

donde ${\textstyle g_{0}(w)}$ es la siguiente función auxiliar:

(9)

para todo ${\textstyle w\geq {0}}$ .

El ítem ii) del Teorema 1 se demostró usando una funcional de Lyapunov ${\textstyle L(t)}$ , que es una combinación de funcionales tipo Volterra ${\textstyle f(x)=x-1-\ln {x}}$ , definida por

L(t)={\frac {\mu _{v}N_{h}}{I_{v}^{*}b}}\int _{0}^{\infty }s_{h}^{*}(\tau )f\left({\frac {s_{h}(t,\tau )}{s_{h}^{*}(\tau )}}\right)d\tau +{\frac {I_{h}^{*}\mu _{v}N_{h}}{I_{v}^{*}b}}f\left({\frac {I_{h}(t)}{I_{h}^{*}}}\right)

+{\frac {\mu _{v}N_{h}}{I_{v}^{*}b}}\int _{0}^{\infty }a_{h}^{*}(\omega )g_{e}(\omega )f\left({\frac {a_{h}(t,\omega )}{a_{h}^{*}(\omega )}}\right)d\omega +f\left({\frac {I_{v}(t)}{I_{v}^{*}}}\right)\int _{0}^{\infty }\beta _{h}(\tau )s_{h}^{*}(\tau )d\tau ,

donde ${\textstyle g_{e}(w)}$ es la siguiente función auxiliar:

para todo ${\textstyle w\geq {0}}$ .

La estrategia de construcción de funcionales de Lyapunov tipo Volterra ha sido ampliamente utilizada en epidemiología matemática [14,15,16,17,18,19,20].

3 Modelo hospedero-vector independientemente de las edades

Usando las siguientes tranformaciones (1) y (2) donde ${\textstyle S_{h}(t)}$ es el total de hospederos susceptibles de cualquier edad cronológica y ${\textstyle A_{h}(t)}$ es el total de hospederos asintomáticos con cualquier edad de la infección asintomática. Además, para simplificar la complejidad del modelo, proponemos que las funciones dependientes de la edad se definan como constantes: ${\textstyle \delta _{h}(\omega )=\delta _{h}}$ , ${\textstyle \beta _{h}(\tau )=\beta _{h}}$ , y ${\textstyle \varepsilon _{h}(\tau )=\mu _{h}}$ . Al integrar la primera ecuación del sistema (3) con respecto de ${\textstyle \tau }$ y la cuarta ecuación de (3) con respecto de ${\textstyle \omega }$ utilizando las respectivas condiciones de frontera, el sistema integro-diferencial (3) se reduce a un modelo en ecuaciones diferenciales ordinarias para el virus de chikungunya que ha sido estudiado por Vázquez-Peña et al. [13].

{\begin{aligned}{\frac {dS_{h}}{dt}}&=\mu _{h}N_{h}-{\frac {\beta _{h}b}{N_{h}}}S_{h}I_{v}-\mu _{h}S_{h},\\{\frac {dI_{h}}{dt}}&={\frac {\beta _{h}b}{N_{h}}}S_{h}I_{v}-(\mu _{h}+\gamma )I_{h}+\delta _{h}A_{h},\\{\frac {dA_{h}}{dt}}&=p\gamma I_{h}-(\mu _{h}+\delta _{h})A_{h},\\{\frac {dR_{h}}{dt}}&=(1-p)\gamma I_{h}-\mu _{h}R_{h},\\{\frac {dS_{v}}{dt}}&=\mu _{v}N_{v}-{\frac {\beta _{v}b}{N_{h}}}S_{v}I_{h}-{\frac {\kappa \beta _{v}b}{N_{h}}}S_{v}A_{h}-\mu _{v}S_{v},\\{\frac {dI_{v}}{dt}}&={\frac {\beta _{v}b}{N_{h}}}S_{v}I_{h}+{\frac {\kappa \beta _{v}b}{N_{h}}}S_{v}A_{h}-\mu _{v}I_{v}.\end{aligned}}

(10)

Considerando ambas poblaciones constantes ${\textstyle N_{h}=S_{h}+I_{h}+A_{h}+R_{h}}$ y ${\textstyle N_{v}=S_{v}+I_{v}}$ el sistema se reduce a

{\begin{aligned}{\frac {dS_{h}}{dt}}&=\mu _{h}N_{h}-{\frac {\beta _{h}b}{N_{h}}}S_{h}I_{v}-\mu _{h}S_{h},\\{\frac {dI_{h}}{dt}}&={\frac {\beta _{h}b}{N_{h}}}S_{h}I_{v}-(\mu _{h}+\gamma )I_{h}+\delta _{h}A_{h},\\{\frac {dA_{h}}{dt}}&=p\gamma I_{h}-(\mu _{h}+\delta _{h})A_{h},\\{\frac {dI_{v}}{dt}}&={\frac {\beta _{v}b}{N_{h}}}(N_{v}-I_{v})(I_{h}+\kappa A_{h})-\mu _{v}I_{v}.\end{aligned}}

(11)

Las condiciones iniciales del sistema (11) están dadas por

Donde ${\textstyle I_{h0}}$ e ${\textstyle I_{v0}}$ no son cero simultáneamente.

La región factible de las soluciones del modelo (11) es

3.1 Número reproductivo básico

Para calcular el número reproductivo básico, Vázquez-Peña et al. [13] utilizaron el método de la matriz de la siguiente generación [21]. Separaron las ecuaciones en ${\textstyle {\boldsymbol {\mathcal {F}}}}$ , que contiene los términos asociados a nuevas infecciones, y ${\textstyle {\boldsymbol {\mathcal {V}}}}$ , que incluye los términos de transiciones individuales en cada clase, es decir,

y

Tras calcular las matrices Jacobianas de ${\textstyle {\boldsymbol {\mathcal {F}}}}$ y ${\textstyle {\boldsymbol {\mathcal {V}}}}$ y evaluarlas en el punto de equilibrio libre de la enfermedad ${\textstyle E^{0}=(N_{h},0,0,0)}$ se obtienen, respectivamente, una matriz no negativa ${\textstyle {\boldsymbol {\mathcal {F}}}}$ y una ${\textstyle M}$ -matriz ${\textstyle {\boldsymbol {\mathcal {V}}}}$ .

{\boldsymbol {F}}=\left({\begin{array}{ccc}0&0&\beta _{h}b\\0&0&0\\{\frac {\beta _{v}bN_{v}}{N_{h}}}&{\frac {\kappa \beta _{v}bN_{v}}{N_{h}}}&0\\\end{array}}\right)\quad {\text{ y }}\quad {\boldsymbol {\mathcal {V}}}=\left({\begin{array}{ccc}\mu _{h}+\gamma &-\delta _{h}&0\\-p\gamma &\mu _{h}+\delta _{h}&0\\0&0&\mu _{v}\\\end{array}}\right).

Entonces, el número reproductivo básico está dado por el radio espectral de la matriz ${\textstyle {\boldsymbol {\mathcal {F}}}{\boldsymbol {\mathcal {V}}}^{-1}}$ , es decir

(12)

donde

(13)

${\textstyle R_{0}}$ denota el número promedio de casos secundarios que produce un individuo infectado al introducirlo a una población totalmente susceptible. Esto se puede entender de la siguiente manera: un mosquito infectado distribuye picaduras en la población humana durante el resto de su vida, y una proporción ${\textstyle {\frac {\beta _{h}bN_{v}}{\mu _{v}N_{h}}}}$ de estas picaduras se convierte en nuevas infecciones. Por otro lado, el número de nuevas infecciones en los mosquitos por parte de hospederos infectados y asintomáticos durante el periodo infeccioso está dado por ${\textstyle \beta _{v}b{\frac {\kappa p\gamma +\mu _{h}+\delta _{h}}{(\mu _{h}+\gamma )(\mu _{h}+\delta _{h})-\delta _{h}p\gamma }}}$ , respectivamente. La media geométrica de estas dos cantidades, que es igual a ${\textstyle R_{0}}$ , proporciona el número promedio de infecciones secundarias. En el contexto de enfermedades transmitidas por vectores, como el chikungunya, un ${\textstyle R_{0}>1}$ sugiere que la enfermedad se propagará en la población, mientras que un ${\textstyle R_{0}<1}$ indica que la enfermedad eventualmente se extinguirá.

3.2 Puntos de equilibrio y su estabilidad global

Además del punto de equilibrio libre de la enfermedad ${\textstyle E^{0}}$ , el modelo (11) tiene un punto de equilibrio endémico ${\textstyle E^{*}=(S_{h}^{*},I_{h}^{*},A_{h}^{*},I_{v}^{*})}$ , con

{\begin{aligned}&S_{h}^{*}={\frac {N_{h}(N_{h}N_{v}^{-1}\mu _{h}{\hat {R}}_{0}+\beta _{h}b)}{{\hat {R}}_{0}(N_{h}N_{v}^{-1}\mu _{h}+\beta _{h}b)}},\\&I_{h}^{*}=\left({\frac {\mu _{h}N_{h}(\mu _{h}+\delta _{h})\beta _{h}b}{(\mu _{h}+\gamma )(\mu _{h}+\delta _{h})-\delta _{h}p\gamma }}\right)\left({\frac {{\hat {R}}_{0}-1}{{\hat {R}}_{0}(N_{h}N_{v}^{-1}\mu _{h}+\beta _{h}b)}}\right),\\&A_{h}^{*}=\left({\frac {\mu _{h}N_{h}\beta _{h}bp\gamma }{(\mu _{h}+\gamma )(\mu _{h}+\delta _{h})-\delta _{h}p\gamma }}\right)\left({\frac {{\hat {R}}_{0}-1}{{\hat {R}}_{0}(N_{h}N_{v}^{-1}\mu _{h}+\beta _{h}b)}}\right),\\&I_{v}^{*}={\frac {\mu _{h}N_{h}({\hat {R}}_{0}-1)}{N_{h}N_{v}^{-1}\mu _{h}{\hat {R}}_{0}+\beta _{h}b}}.\end{aligned}}

(14)

Dado que el sistema (11) es un caso particular del sistema integro-diferencial (4), obtenemos el siguiente corolario derivado del Teorema 1.

Corolario 1: i) Cuando ${\textstyle R_{0}\leq 1}$ entonces el punto de equilibrio libre de la enfermedad ${\textstyle E_{0}}$ del sistema (11) es global asintóticamente estable. ii) Cuando ${\textstyle R_{0}>1}$ entonces el punto de equilibrio endémico ${\textstyle E^{*}}$ del sistema (11) es global asintóticamente estable.

4 Estimación Bayesiana

4.1 Brote de chikungunya en Acapulco

En 2015, Acapulco, Guerrero, experimentó un brote de chikungunya. En [10] se realizó un estudio transversal para caracterizar dicho brote epidémico, que incluyó encuestas en 1,305 viviendas distribuidas en ocho conglomerados urbanos considerados representativos de Acapulco. En total, se administraron 5,870 cuestionarios, identificando 3,531 casos de chikungunya entre enero y diciembre de 2015. Para asegurar la representatividad en el estudio [10], se realizó un muestreo intencional que buscaba reflejar las condiciones urbanas promedio de Acapulco, lo cual es clave en contextos donde no se puede utilizar un muestreo probabilístico.

Para reducir el impacto de las fluctuaciones aleatorias o ruido en los datos reportados de los casos de chikungunya [10], se aplica el método de suavizamiento exponencial:

donde ${\textstyle F_{t+1}}$ es el pronóstico de casos de chikungunya para el tiempo ${\textstyle t+1}$ de la serie de tiempo, donde ${\textstyle Y_{t}}$ representa el valor observado de casos de chikungunya en el tiempo ${\textstyle t}$ , ${\textstyle F_{t}}$ es el pronóstico de casos de chikungunya para el tiempo ${\textstyle t}$ , y ${\textstyle \alpha }$ es la constante de suavizamiento ( ${\textstyle 0<\alpha <1}$ ). Se supone que el pronóstico inicial ${\textstyle F_{0}}$ de casos de chikungunya es igual al primer valor observado ${\textstyle Y_{0}}$ . Con el suavizado, logramos obtener valores con menor variabilidad, lo que permite observar mejor la evolución de la serie temporal. La estimación Bayesiana se realizará con ${\textstyle F_{t+1}}$ .

Utilizando los datos recabados por [10] sobre los casos mensuales autoinformados de chikungunya y el método de suavizamiento exponencial con un valor de ${\textstyle \alpha =0.7}$ , se ajustará la curva de los humanos infectados ${\textstyle I_{h}}$ para estimar de manera puntual y por intervalo los parámetros y el número reproductivo básico ${\textstyle R_{0}}$ (12) del modelo (11).

4.2 Modelo estadístico

Para ${\textstyle {\boldsymbol {y}}=(y(t_{1})}$ , ${\textstyle y(t_{2}),\dots ,y(t_{n}))}$ el vector de ${\textstyle n}$ observaciones del número de humanos infectados ( ${\textstyle I_{h}(t)}$ ) en el tiempo ${\textstyle t}$ , considere el siguiente modelo estadístico:

(15)

donde:

${\textstyle y(t_{i})}$ es el número de humanos infectados ( ${\textstyle I_{h}(t)}$ ) en el tiempo ${\textstyle t_{i}}$ .
${\textstyle {\boldsymbol {\theta }}}$ es vector de parámetros en la estimación Bayesiana.
${\textstyle G({\mathcal {M}}(t_{i},{\boldsymbol {\theta }}))}$ es la solución numérica del modelo ${\textstyle {\mathcal {M}}}$ (11) con el método ${\textstyle G}$ . En este caso se usó el método numérico de Runge-Kutta de orden 4.
${\textstyle \varepsilon (t_{i})}$ es el error aleatorio en el tiempo ${\textstyle t_{i}}$ , los errores son independientes para cada tiempo, normalmente distribuidos con media cero y varianza ${\textstyle \sigma ^{2}}$ .

4.3 Función de verosimilitud

Considerando el supuesto de normalidad para el error aleatorio ${\textstyle \varepsilon (t_{i})\sim N(0,\sigma ^{2})}$ , entonces se tiene que ${\textstyle y(t_{i})\sim N\left(G({\mathcal {M}}(t_{i},{\boldsymbol {\theta }})),\sigma ^{2}\right)}$ . Por tal razón, la función de verosimilitud está dada por la ecuación (16):

(16)

4.4 Distribución a priori y a posteriori

La estadística Bayesiana permite al investigador incorporar conocimiento de los parámetros al proceso de inferencia. Esta información se especifica por medio de una distribución a priori ( ${\textstyle P({\boldsymbol {\theta }})}$ ) y puede restringir la inferencia a un rango de interés y asignar mayor probabilidad a un subconjunto de valores. Esto permite enfocarse en los rangos plausibles según el conocimiento de la literatura o la definición del parámetro en el modelo matemático. Por ejemplo, la probabilidad de transmisión de vector a humano está definida en el intervalo ${\textstyle [0,1]}$ . Dado que se trata de una probabilidad, es conveniente utilizar o definir distribuciones a priori con soporte en este mismo intervalo, como la distribución uniforme ${\textstyle U(0,1)}$ o la distribución Beta ${\textstyle Beta(\alpha ,\beta )}$ , entre otras. Para proponer la distribución a priori de ${\textstyle {\boldsymbol {\theta }}}$ se consultaron en la literatura los valores que se han reportado y se muestran en la Tabla 1.

Tabla. 1 Distribuciones a priori seleccionadas con base en los valores reportados en la literatura.
Parámetro	Descripción	Referencia	Valor medio o rango de valores	Distribución a priori
$\beta _{h}$	Probabilidad de transmisión de vector a humano	[22]	$0.99[0.6,1]$	$Beta(5,2)$
		[23]	$0.37$
		[24]	$[0.5,0.8]$
		[25]	$0.67[0.26,1]$
$\beta _{v}$	Probabilidad de transmisión de humano a vector	[22]	$0.6[0.6,1]$	$Beta(5,2)$
		[23]	$0.375$
		[24]	$0.37$
$b$	Número de picaduras	[22]	$2.46[1,3]$	$U(0,4)$
		[23]	$1$
		[24]	$0.5$ or $1$
$\mu _{v}$	Tasa de muerte y nacimiento de vectores $[{\hbox{mes}}^{-1}]$	[23]	$2.72$	$U(2,4.5)$
		[24]	$4.28$
		[26]	$2.14$
$\gamma$	Tasa de recuperación $[{\hbox{mes}}^{-1}]$	[22]	$[3.7,4.5]$	$U(2.5,7.5)$

		[26]	$[2,6]$
${\textstyle p}$	Fracción de infectados que se vuelven asintomáticos	Supuesto		$U(0,1)$
$\delta _{h}$	Tasa de recaída $[{\hbox{mes}}^{-1}]$	[8]	$0.5$	$U(0,1)$
$\delta _{h}$	Tasa de recaída $[{\hbox{mes}}^{-1}]$	[10]	$0.66$	$U(0,1)$
${\textstyle \kappa }$	Fracción de transmisión de humano asintomático a vector	Supuesto		$Beta(2,5)$
${\textstyle N_{v}}$	Número total de vectores	Supuesto	$2$ a $4.5$ veces el número total de humanos	$U(11740,26415)$
${\textstyle \mu _{h}}$	Tasa de muerte y nacimiento de humanos ${\textstyle [{\hbox{mes}}^{-1}]}$	[27]	${\frac {1}{75\times {12}}}\approx {0.0011}$	Valor fijo
${\textstyle N_{h}}$	Número total de humanos	[10]	$5870$	Valor fijo

Nota: En las distribuciones Beta

,

y

son parámetros de forma, mientras que en las distribuciones uniformes

,

y

son los valores mínimo y máximo.

La inferencia Bayesiana se basa en la distribución a posteriori, por el teorema de Bayes la distribución a posteriori esta definida por (17):

(17)

donde

${\textstyle P({\boldsymbol {\theta }}\mid {\boldsymbol {y}})}$ es la distribución a posteriori de ${\textstyle {\boldsymbol {\theta }}}$ dada un conjunto de observaciones ${\textstyle Y}$ .
${\textstyle P({\boldsymbol {y}}\mid {\boldsymbol {\theta }})}$ es la distribución de las observaciones ${\textstyle {\boldsymbol {Y}}}$ para un valor específico del vector ${\textstyle {\boldsymbol {\theta }}}$ .
${\textstyle P({\boldsymbol {\theta }})}$ distribución a priori.
${\textstyle P({\boldsymbol {y}})}$ es una constante de normalización ${\textstyle \int _{p}P({\boldsymbol {y}}\mid {\boldsymbol {\theta }})P({\boldsymbol {\theta }})d{\boldsymbol {\theta }}}$ .

Note que la expresión (17) está bien definida si ${\textstyle P(\mathbf {y} )\neq 0}$ . ${\textstyle P(\mathbf {y} )}$ es constante, por tanto podemos reescribir (17) como (18):

(18)

En la inferencia Bayesiana es necesario obtener integrales que involucran la distribución a posteriori. Un ejemplo es la media de la distribución a posteriori.

(19)

Sin embargo, en la gran mayoría de los casos, la integral de la marginalización (19) no puede resolverse de forma analítica debido a la complejidad de ${\textstyle P\left({\boldsymbol {\theta }}\mid {\boldsymbol {y}}\right)}$ y alta dimensionalidad de ${\textstyle {\boldsymbol {\theta }}}$ . En la práctica, se usan cadenas de Markov Chain Monte Carlo (MCMC por sus siglas en inglés) para aproximar la distribución a posteriori [28].

Las cadenas de Markov se conforman de valores muestrales de la distribución a posteriori y se obtienen a partir del uso de algoritmos de muestreo, los más empleados son el muestreador de Gibbs, el algoritmo de muestreo Metropolis-Hastings y Hamiltoniano Monte Carlo (HMC). El proceso de muestrear la distribución a posteriori, es un proceso iterativo que continua hasta que la cadena de Markov converja. Es común que durante un período inicial los valores muestreados estén alejados del valor verdadero, por lo que se recomienda descartar este período inicial. A este período se le conoce como periodo de quemado.

4.5 Estimador de Bayes

Una vez obtenida la muestra de los parámetros de interés, para realizar inferencias se utiliza el estimador de Bayes ${\textstyle T^{B}}$ , definido como la solución de (20).

(20)

${\textstyle L(T,{\boldsymbol {\theta }})=(T-{\boldsymbol {\theta }})^{2}}$ la función de pérdida cuadrática, se obtiene el mínimo en ${\textstyle T=E\left[{\boldsymbol {\theta }}\right]}$ , es decir el estimador obtenido es el valor medio ${\textstyle T^{B}=E({\boldsymbol {\theta }})}$ .

4.6 Intervalos creibles de alta densidad

Para la estimación por intervalo se utilizó el método de intervalos de alta densidad a posteriori (HPD, por sus siglas en inglés Highest Posterior Density). Un HPD conserva los valores más probables de la distribución a posteriori a un porcentaje deseado. Los HPD al ${\textstyle 95\%}$ contienen los valores de ${\textstyle {\boldsymbol {\theta }}}$ tales que ${\textstyle p({\boldsymbol {\theta }}\mid \mathbf {y} )>W}$ , donde ${\textstyle W}$ satisface ${\textstyle \int _{p({\boldsymbol {\theta }}\mid \mathbf {y} )>W}\mathrm {~d} {\boldsymbol {\theta }}p({\boldsymbol {\theta }}\mid \mathbf {y} )=0,95}$ [29]. Se prefieren los intervalos HPD sobre el método de percentiles debido a que los HPD son los intervalos de menor longitud entre todos los posibles intervalos de probabilidad para un nivel de credibilidad deseado.

4.7 Método Hamiltoniano de Monte Carlo

El método de Hamiltoniano Monte Carlo (HMC) ha demostrado ser un muestreador más eficiente que el muestreador de Gibbs, y el algoritmo de muestreo Metropolis-Hastings. Su tasa de aceptación es aproximadamente el doble de la tasa de aceptación del algoritmo de Metropolis-Hastings [30]. Esta técnica de muestreo se basa en la mecánica Hamiltoniana para explorar distribuciones de alta dimensionalidad. El estudio detallado de esta técnica avanzada está fuera del alcance de este trabajo; para una comprensión más profunda de HMC, se recomienda consultar el trabajo de Betancourt [31].

4.8 Convergencia de Cadenas

Método de inspección visual: Este método se basa en la observación empírica de las cadenas de Markov para verificar que sus trazas estén adecuadamente mezcladas. Es común que esta mezcla produzca visualmente una figura similar a una oruga.

Diagnóstico de Gelman-Rubin: Este diagnóstico es uno de los más populares para determinar la convergencia de las cadenas de Markov. Se basa en comparar la varianza dentro de las cadenas con la varianza entre cadenas utilizando el cociente ${\textstyle {\hat {R}}}$ , tambien conocido como Rhat debido al acento circunflejo de R. En la práctica, se considera que las cadenas convergen si ${\textstyle {\hat {R}}\leq 1.1}$ , mientras que si ${\textstyle {\hat {R}}>1.1}$ , al menos una de las cadenas aún no ha convergido [32].

4.9 Número reproductivo básico

El número reproductivo básico ${\textstyle R_{0}}$ (12) del modelo (11) se estimará utilizando las distribuciones a posteriori de los parámetros, para lo cual se operan de forma ordenada los estados de las cadenas de Markov de los parámetros usando la ecuación (12), así como su propiedad de invarianza. Además, se evaluará la convergencia de la cadena ${\textstyle R_{0}}$ .

4.10 Software estadístico

En este trabajo se utilizó el lenguaje de programación Julia [33] con el paquete de análisis Bayesiano Turing.jl [34] para estimar los parámetros. Se ejecutaron tres cadenas de Markov, cada una inicializada de manera aleatoria y con 20,000 iteraciones. Las primeras 1,000 iteraciones de cada cadena se descartaron como periodo de quemado, resultando en una muestra final de 19,000 valores por cadena. El diagnóstico de convergencia de Gelman-Rubin se realizó por defecto utilizando el paquete Turing.

Se utilizó la paquetería MCMChains.jl [35] para estimar los intervalos de HPD al 95%.

5 Resultados

De la muestra posterior de cada parámetro se obtienen los valores de media y mediana muestral, intervalos de HPD del 95% y ${\textstyle Rhat}$ . La estimación Bayesiana se resume en la Tabla 2.

Tabla. 2 Resultados de la estimación Bayesiana.
Parámetro	Media	Mediana	Intervalos de HPD del 95%	Rhat
${\textstyle \beta _{h}}$	0.72	0.74	(0.46, 0.97)	1.00
$\beta _{v}$	0.75	0.76	(0.49, 0.98)	1.00
$b$	3.13	3.15	(2.29, 4.00)	1.00
$\mu _{v}$ ${\textstyle [{\hbox{mes}}^{-1}]}$	3.42	3.49	(2.08, 4.44)	1.00
$\gamma$ ${\textstyle [{\hbox{mes}}^{-1}]}$	4.44	4.32	(2.50, 6.63)	1.00
$p$	0.65	0.66	(0.41, 0.84)	1.00
$\delta _{h}$ ${\textstyle [{\hbox{mes}}^{-1}]}$	0.75	0.79	(0.38, 1.00)	1.00
$\kappa$	0.24	0.21	(0.01, 0.52)	1.00
$N_{v}$	19183	19179	(12589, 26358)	1.00
$R_{0}$	2.61	2.46	(1.66, 3.80)	1.00

Las trazas de las cadenas de Markov de los parámetros del modelo (11) y del ${\textstyle R_{0}}$ (12) se muestran en la Tabla 3 , las cuales se observan mezcladas y no presenta patrones extraños. Más aún, en la Tabla 2 los valores de ${\textstyle {\hat {R}}}$ son menores a 1.1, por lo tanto las cadenas presentadas convergen.

Las probabilidades de transmisión de vector a humano ${\textstyle \beta _{h}}$ y de humano a vector ${\textstyle \beta _{v}}$ tienen medias de 0.72 y 0.75 (medianas de 0.74 y 0.76), respectivamente, con intervalos de credibilidad del 95% de (0.46, 0.97) y (0.49, 0.98). Esto representa probabilidades altas de transmisión. Nuestras estimaciones son consistentes con lo publicado en [22,24,25] que se muestran en la Tabla 1.

La media y mediana del número de picaduras ${\textstyle b}$ de los vectores son de 3.13 y 3.15, respectivamente, con un intervalo de credibilidad del 95% de (2.29, 4.00). La estimación de ${\textstyle b}$ es consistente con lo publicado en [22], que se muestra en la Tabla 1.

La media y la mediana de la tasa de muerte y nacimiento de vectores ${\textstyle \mu _{v}}$ son de 3.42 y 3.49 ${\textstyle {\text{mes}}^{-1}}$ , respectivamente, con un intervalo de credibilidad del 95% de (2.08, 4.44), lo que equivale a un periodo de vida de los vectores de 6.7 a 14.4 ${\textstyle {\text{días}}}$ . Esta estimación es consistente con el hecho de que el periodo de vida de un mosquito adulto puede ser de aproximadamente 8 a 28 días [36,37]. Se estima una media del número total de vectores ${\textstyle N_{v}}$ de 19183, con un intervalo de credibilidad del 95% de (12589, 26358).

La tasa de recuperación ${\textstyle \gamma }$ tiene una media y mediana de 4.44 y 4.32, respectivamente, con un intervalo de credibilidad del 95% de (2.50, 6.63), lo que corresponde a un periodo de recuperación de 4.5 a 12 ${\textstyle {\text{días}}}$ . Esta estimación es consistente con lo publicado en [22], que se muestra en la Tabla 1. La tasa de recaídas ${\textstyle \delta _{h}}$ muestra una media y mediana de 0.75 y 0.79 ${\textstyle {\text{mes}}^{-1}}$ , respectivamente, con un intervalo de credibilidad del 95% de (0.38, 1.00), lo que equivale a un periodo de recaída de 30 a 77.7 ${\textstyle {\text{días}}}$ . Nuestras estimaciones son consistentes con lo reportado en [10], que señala que las recaídas se presentan después de un mes de la primera infección.

La media y la mediana de la fracción de infectados que se vuelven asintomáticos ${\textstyle p}$ son 0.65 y 0.66, respectivamente, con un intervalo de credibilidad del 95% que varía entre una fracción baja de 0.41 y una alta de 0.84. La media y la mediana de la fracción de transmisión de humano asintomático a vector ${\textstyle \kappa }$ son de 0.24 y 0.21, con un intervalo de credibilidad del 95% de (0.01, 0.52), que va de una fracción casi nula a moderada. Esto podría sugerir que la fracción de transmisión de humanos asintomáticos a vectores no desempeña un papel relevante en la propagación de la enfermedad.

En la Figura 1 se muestra el ajuste del modelo a la curva de humanos infectados con chikungunya, así como la simulación de las cuatro clases: hospederos susceptibles ${\textstyle S_{h}}$ , hospederos infectados ${\textstyle I_{h}}$ , hospederos asintomáticos ${\textstyle A_{h}}$ y vectores infectados ${\textstyle I_{v}}$ . Los puntos sólidos representan los datos obtenidos por [10] que se han suavizado por el modelo de suavizamiento exponencial con ${\textstyle \alpha =0.7}$ .


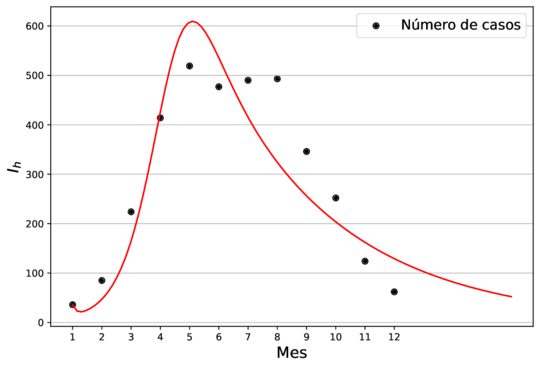
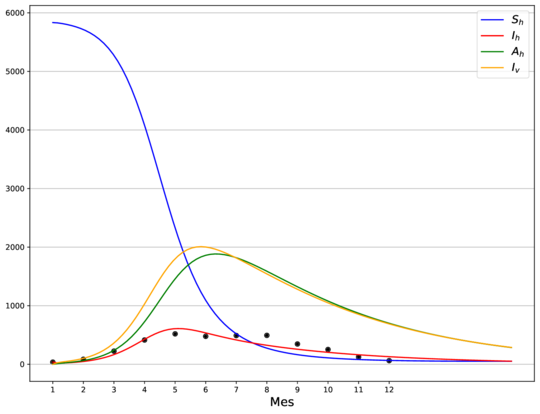
(1) Modelo ajustado usando la media como estimador puntual.

Finalmente, el número reproductivo básico ${\textstyle R_{0}}$ presentó una media de 2.61 y una mediana de 2.46, con un intervalo de credibilidad del 95% de (1.66, 3.80). En [38], se estima que el ${\textstyle R_{0}}$ es de 4.1, con un intervalo de confianza del 95% que va de 1.50 a 6.60 para los vectores Aedes aegypti. Esto sugiere que el brote de chikungunya en Acapulco se propagó rápidamente. Nuestras estimaciones son consistentes con lo publicado en [38].

Tabla. 3 Trazas y distribuciones a posteriori de los parámetros y el número reproductivo básico del modelo de chikungunya.
Parámetro	Trazas	Distribución a posteriori
$\beta _{h}$
$\beta _{v}$
$b$
$\mu _{v}$
$\gamma$
$p$
$\delta _{h}$
$\kappa$
$N_{v}$
$R_{0}$
$\sigma ^{2}$

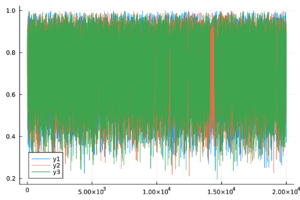
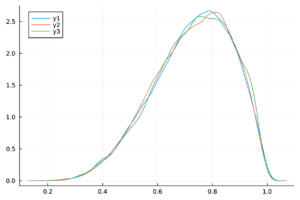
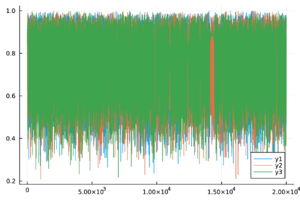
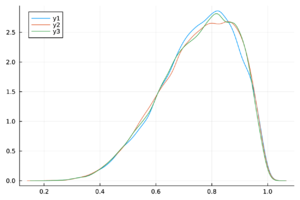
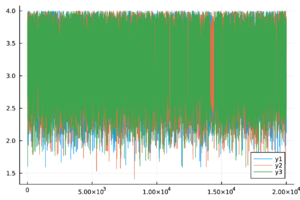
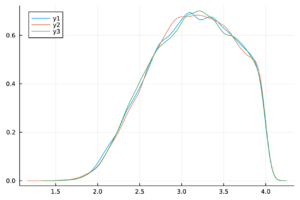
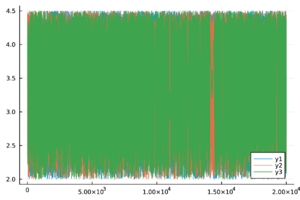
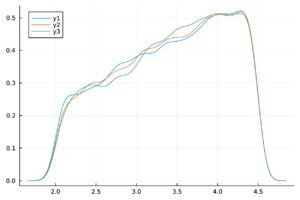
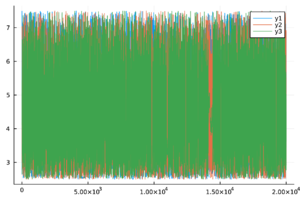
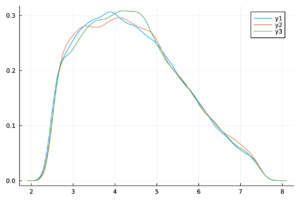
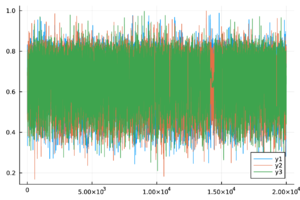
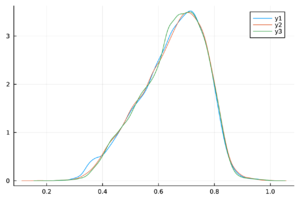
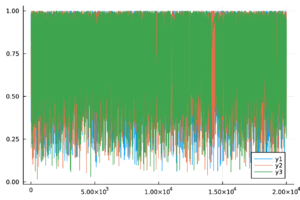
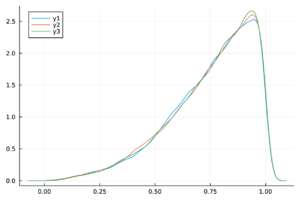
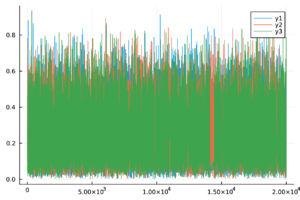
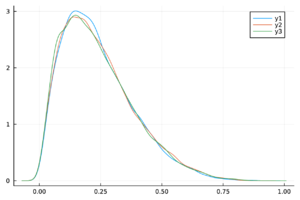
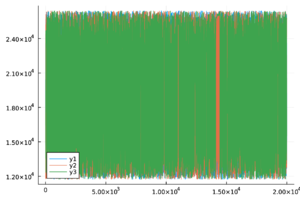
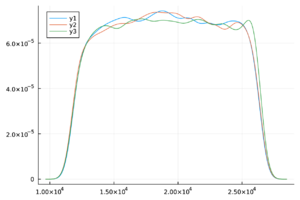
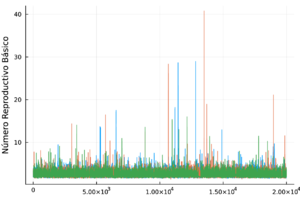
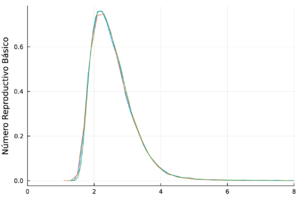
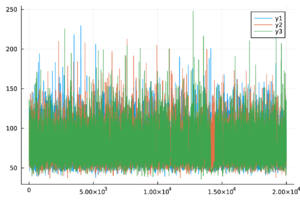
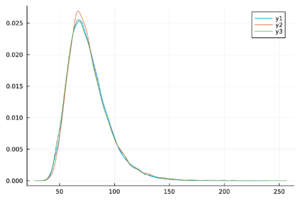
6 Conclusiones

En este trabajo, presentamos una revisión de modelos recientemente desarrollados para el virus del chikungunya. Uno de estos modelos incorpora dos estructuras de edad, mientras que el otro es un caso particular, independiente de la edad. Para este último modelo, se estimó el número reproductivo básico ${\textstyle R_{0}}$ del brote de chikungunya en Acapulco, con el que alcanzamos el objetivo planteado en este trabajo.

El valor estimado de ${\textstyle R_{0}}$ mostró la capacidad del virus para expandirse rápidamente, lo cual fue consistente con estudios previos que indicaron una rápida expansión del chikungunya. La fracción de transmisión de humanos asintomáticos a vectores varió de baja a moderada, lo que podría haber sugerido que esta fracción no desempeñó un papel relevante en la propagación de la enfermedad. La estimación de los parámetros del brote en Acapulco sugirió que la transmisión del virus fue alta tanto de vectores a humanos como de humanos a vectores, lo que indicó un alto riesgo de propagación. El elevado número de picaduras contribuyó a la propagación continua del virus.

Estos resultados subrayan la importancia de implementar medidas de control y prevención contra las picaduras de mosquitos. Para ello, se recomienda eliminar las aguas estancadas, realizar fumigaciones y utilizar mosquiteros en zonas residenciales. De este modo, se puede evitar la reproducción de estos mosquitos, el contagio de la enfermedad y la propagación del virus.

El enfoque Bayesiano ofrece ventajas en el trabajo: permite incorporar información previa mediante distribuciones a priori, lo que mejora la precisión de las estimaciones. Además, facilita la obtención de intervalos de credibilidad, proporcionando no solo valores puntuales, sino también un rango de valores en el cual se encuentra un parámetro con una cierta probabilidad.

BIBLIOGRAFÍA

[1] Agusto, Folashade B and Easley, Shamise and Freeman, Kenneth and Thomas, Madison. (2016) "Mathematical model of three age-structured transmission dynamics of chikungunya virus", Volume 2016. Wiley Online Library. Computational and mathematical methods in medicine 1 4320514

[2] Vu, David M and Jungkind, Donald and LaBeaud, Angelle Desiree. (2017) "Chikungunya virus", Volume 37. Elsevier. Clinics in laboratory medicine 2 371–382

[3] Wahid, Braira and Ali, Amjad and Rafique, Shazia and Idrees, Muhammad. (2017) "Global expansion of chikungunya virus: mapping the 64-year history", Volume 58. Elsevier. International Journal of Infectious Diseases 69–76

[4] Rivera-Ávila, Roberto Carlos. (2014) "Fiebre chikungunya en México: caso confirmado y apuntes para la respuesta epidemiológica", Volume 56. SciELO Public Health. Salud pública de México 4 402–404

[5] Garay-Morán, Carolina and Román-Pedroza, Juan Francisco and López-Martínez, Irma and Rodríguez-Martínez, José Cruz and Ruiz-Matus, Cuitláhuac and Kuri-Morales, Pablo and Díaz-Quiñonez, José Alberto. (2017) "Caracterización clínica y epidemiológica de fiebre Chikungunya en México", Volume 41. SciELO Public Health. Revista Panamericana de Salud Pública e58

[6] Méndez, Nina and Baeza-Herrera, Luis and Ojeda-Baranda, Rafael and Huchim-Lara, Oswaldo and Gómez-Carro, Salvador. (2018) "Perfil clinicoepidemiológico de la infección por Chikungunya en casos hospitalarios atendidos en 2015 en Mérida, México", Volume 41. SciELO Public Health. Revista Panamericana de Salud Pública e91

[7] Simon, Fabrice and Javelle, Emilie and Oliver, Manuela and Leparc-Goffart, Isabelle and Marimoutou, Catherine. (2011) "Chikungunya virus infection", Volume 13. Springer. Current infectious disease reports 218–228

[8] Couturier, Elisabeth and Guillemin, Francis and Mura, Marie and Léon, Lucie and Virion, Jean-Marc and Letort, Marie-José and De Valk, Henriette and Simon, Fabrice and Vaillant, Véronique. (2012) "Impaired quality of life after Chikungunya virus infection: a 2-year follow-up study", Volume 51. Oxford University Press. Rheumatology 7 1315–1322

[9] Staikowsky, Frederik and Le Roux, Karin and Schuffenecker, Isabelle and Laurent, Philippe and Grivard, Philippe and Develay, A and Michault, Alain. (2008) "Retrospective survey of Chikungunya disease in Reunion Island hospital staff", Volume 136. Cambridge University Press. Epidemiology & Infection 2 196–206

[10] de La Cruz-Castro, Ixtac Xochitl and Nava-Aguilera, Elizabeth and Morales-Pérez, Arcadio and Betanzos-Reyes, Ángel Francisco and Flores-Moreno, Miguel and Morales-Nava, Liliana and Balanzar-Martínez, Alejandro and Serrano-de Los Santos, Felipe René and Andersson, Neil. (2020) "Factors associated with chikungunya relapse in Acapulco, Mexico: a cross-sectional study", Volume 20. Mary Ann Liebert, Inc., publishers 140 Huguenot Street, 3rd Floor New …. Vector-Borne and Zoonotic Diseases 10 782–787

[11] Mac, P. A. and Airiohuodion, P. E. and Velayudhan, R. and others. (2023) "Antibody seropositivity and endemicity of chikungunya and Zika viruses in Nigeria", Volume 3. Animal Diseases 7

[12] Vázquez-Peña, María Guadalupe and Vargas-De-León, Cruz and Velázquez-Castro, Jorge. (2024) "Global stability for a mosquito-borne disease model with continuous-time age structure in the susceptible and relapsed host classes", Volume 21. Mathematical Biosciences and Engineering 11 7582–7600

[13] Vázquez-Peña, María Guadalupe and Vargas-De-León, Cruz and Camacho-Pérez, Jorge Fernando and Velázquez-Castro, Jorge. (2023) "Analysis and Bayesian estimation of a model for Chikungunya dynamics with relapse: An outbreak in Acapulco, Mexico", Volume 20. Mathematical Biosciences and Engineering 10 18123–18145

[14] Korobeinikov, Andrei. (2004) "Lyapunov functions and global properties for SEIR and SEIS epidemic models", Volume 21. Mathematical Medicine and Biology 2 75–83

[15] Korobeinikov, Andrei. (2004) "Global properties of basic virus dynamics models", Volume 66. Bulletin of Mathematical Biology 4 879–883

[16] Vargas-De-León, Cruz. and Castro-Hernández, J. A. (2008) "Local and global stability of host-vector disease models", Volume 25. Foro-Red-Mat: Revista Electrónica de Contenido Matemático 1–9

[17] Vargas-De-León, Cruz. (2012) "Global analysis of a delayed vector-bias model for malaria transmission with incubation period in mosquitoes", Volume 9. Mathematical Biosciences and Engineering 1 165–174

[18] Vargas-De-León, Cruz. (2014) "On the global stability of infectious diseases models with relapse", Volume 9. Abstraction and Application Magazine

[19] Vargas-De-León, Cruz and Esteva, Lourdes and Korobeinikov, Andrei. (2014) "Age-dependency in host-vector models: The global analysis", Volume 243. Elsevier. Applied Mathematics and Computation 969–981

[20] Vargas-De-León, Cruz. (2016) "Global stability properties of age-dependent epidemic models with varying rates of recurrence", Volume 39. Wiley Online Library. Mathematical Methods in the Applied Sciences 8 2057–2064

[21] Van den Driessche, Pauline and Watmough, James. (2002) "Reproduction numbers and sub-threshold endemic equilibria for compartmental models of disease transmission", Volume 180. Elsevier. Mathematical biosciences 1-2 29–48

[22] Abboubakar, Hamadjam and Guidzavaï, Albert Kouchéré and Yangla, Joseph and Damakoa, Irépran and Mouangue, Ruben. (2021) "Mathematical modeling and projections of a vector-borne disease with optimal control strategies: A case study of the Chikungunya in Chad", Volume 150. Elsevier. Chaos, Solitons & Fractals 111197

[23] Dumont, Yves and Chiroleu, Frederic. (2010) "Vector control for the Chikungunya disease", Volume 7. Mathematical Biosciences & Engineering. Mathematical Biosciences & Engineering 2 313–345

[24] Dumont, Yves and Chiroleu, Frédéric and Domerg, Caroline. (2008) "On a temporal model for the Chikungunya disease: modeling, theory and numerics", Volume 213. Elsevier. Mathematical biosciences 1 80–91

[25] Ruiz-Moreno, Diego and Vargas, Irma Sanchez and Olson, Ken E and Harrington, Laura C. (2012) "Modeling dynamic introduction of Chikungunya virus in the United States", Volume 6. Public Library of Science San Francisco, USA. PLoS Neglected Tropical Diseases 11 e1918

[26] González-Parra, Gilberto C and Aranda, Diego F and Chen-Charpentier, Benito and Díaz-Rodríguez, Miguel and Castellanos, Jaime E. (2019) "Mathematical modeling and characterization of the spread of chikungunya in Colombia", Volume 24. MDPI. Mathematical and Computational Applications 1 6

[27] Consejo Nacional de Población. (2022) "Indicadores demográficos de México de 1950 a 2050 (Spanish) [National Population Council, Demographic Indicators of Mexico from 1950 to 2050]"

[28] Gelman, Andrew and Carlin, John B. and Stern, Hal S. and Rubin, Donald B. (1995) "Bayesian Data Analysis". Chapman and Hall/CRC

[29] Kruschke, John K. (2015) "Doing Bayesian Data Analysis: A Tutorial with R, JAGS, and Stan". Academic Press.

[30] Rodríguez-Parra, M. A. and Vargas-De-León, C. and Godinez-Jaimes, F. and Martinez-Lázaro, C. (2023) "Bayesian estimation of parameters in viral dynamics models with antiviral effect of interferons in a cell culture", Volume 20. Mathematical Biosciences and Engineering 11033–11062

[31] Betancourt, Michael. (2017) "A Conceptual Introduction to Hamiltonian Monte Carlo", arXiv

[32] Vehtari, Aki and Gelman, Andrew and Simpson, Daniel and Carpenter, Bob and Bürkner, Paul-Christian. (2021) "Rank-Normalization, Folding, and Localization: An Improved Rˆ for Assessing Convergence of MCMC (with Discussion)", Volume 16. Bayesian Analysis 1–70

[33] Bezanson, Jeff and Edelman, Alan and Karpinski, Stefan and Shah, Viral B. (2017) "Julia: A Fresh Approach to Numerical Computing", Volume 59. SIAM Review 65–98

[34] Ge, He and Xu, Kun and Ghahramani, Zoubin. (2018) "Turing: a language for flexible probabilistic inference". International Conference on Artificial Intelligence and Statistics. PMLR 1682–1690

[35] Cameron Pfiffer and David Widmann and Martin Trapp and Rob J Goedman and Michael Krabbe Borregaard and Rik Huijzer and Seth Axen and Hong Ge and Kai Xu and dfish and Tor Erlend Fjelde and Andreas Noack and PaulinaMartin96 and Chris Elrod and Jeremiah and Julia TagBot and Matt Karikomi and Hessam Mehr and Xianda Sun and Will Tebbutt. (2024) "TuringLang/MCMCChains.jl: v6.0.6", Volume v6.0.6. Zenodo

[36] Alvarado-Castro, Víctor Manuel and Vargas-De-León, Cruz and Paredes-Solis, Sergio and Li-Martin, Alian and Nava-Aguilera, Elizabeth and Morales-Pérez, Arcadio and Legorreta-Soberanis, José and Sánchez-Gervacio, Belén Madeline and Cockcroft, Anne and Andersson, Neil. (2024) "The influence of gender and temephos exposure on community participation in dengue prevention: a compartmental mathematical model", BMC Infectious Diseases, 24(1)–463.

[37] Gill, Graham V. and Beeching, Nick (2014) "Tropical Medicine: Lecture Notes". Wiley, Oxford, 7th edition

[38] Haider, N. and Vairo, F. and Ippolito, G. and Zumla, A. and Kock, R. A. (2020) "Basic reproduction number of Chikungunya virus transmitted by Aedes mosquitoes", Volume 26. Emerging Infectious Diseases 10 2429–2431