(Created page with "==Un modelo matemático de la formación de la orina== ''' Fernanda Isabel Domínguez Pérez Fernandaisabeldp@gmail.com Jorge López López ''' ==Resumen== En este traba...") |
m (Gstinoco moved page Review 593654234986 to Dominguez Perez LOPEZ 2024a) |
||
| (11 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | ==1 Introducción== |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
Junto al cerebro y el corazón, el riñón es un órgano fundamental en el sistema cardiovascular, ya que recibe aproximadamente el 20% de la sangre que el corazón expulsa hacia el organismo, en cada latido. Entre sus principales funciones se encuentran: regular la presión arterial, eliminar los desechos tóxicos a través de la orina y producir la hormona que estimula la formación de los glóbulos rojos <span id='citeF-5'></span>[[#cite-5|[5]]]. | Junto al cerebro y el corazón, el riñón es un órgano fundamental en el sistema cardiovascular, ya que recibe aproximadamente el 20% de la sangre que el corazón expulsa hacia el organismo, en cada latido. Entre sus principales funciones se encuentran: regular la presión arterial, eliminar los desechos tóxicos a través de la orina y producir la hormona que estimula la formación de los glóbulos rojos <span id='citeF-5'></span>[[#cite-5|[5]]]. | ||
| − | Cuando no hay un | + | Cuando no hay un funcionamiento adecuado del riñón, pueden presentarse enfermedades renales de diversas formas, desde infecciones y cálculos renales hasta enfermedades crónicas como la nefropatía diabética y la enfermedad renal crónica (ERC). Estas generan un problema de salud cada vez más importante a nivel global, afectando no solo la vida de los pacientes, sino también generando una carga significativa para los sistemas de salud debido a su alta prevalencia y costos asociados. |
| − | + | Por otra parte, los modelos hemodinámicos renales proporcionan una comprensión profunda sobre los patrones y comportamientos del flujo sanguíneo renal, lo que puede permitir detectar anomalías y disfunciones que de otra manera podrían pasar desapercibidas. Asimismo contribuyen a tener una perspectiva global e integral del problema, lo que coadyuva a avanzar en el diagnóstico, tratamiento y prevención de las afecciones renales. | |
| − | + | Ahora bien, el torrente sanguíneo arrastra una gran cantidad de sustancias, muchas de la cuales entran al riñón y alguna proporción de estas pasa a formar parte de la orina. Sin embargo, la mayoría de los modelos nefrológicos consideran solo la concentración de una sustancia <span id='citeF-7'></span>[[#cite-7|[7]]]. Estos modelos se han utilizado con fines terapéuticos o tratamiento de enfermedades vía control (cantidad de medicamentos) <span id='citeF-1'></span>[[#cite-1|[1]]], y también con fines de diseño de riñones artificiales. En general el modelado del proceso de hemodiálisis se basa en ecuaciones cinético-hemodinámicas <span id='citeF-3'></span>[[#cite-3|[3]]] o ecuaciones cinético-matemáticas <span id='citeF-2'></span>[[#cite-2|[2]]]. | |
<div id='img-1'></div> | <div id='img-1'></div> | ||
| Line 34: | Line 16: | ||
| colspan="1" | '''Figura 1:''' '' Esquema de las etapas de la formación de la orina en la nefrona <span id='citeF-7'></span>[[#cite-7|[7]]]. '' | | colspan="1" | '''Figura 1:''' '' Esquema de las etapas de la formación de la orina en la nefrona <span id='citeF-7'></span>[[#cite-7|[7]]]. '' | ||
|} | |} | ||
| − | En este contexto, el propósito de este trabajo es analizar la hemodinámica renal modelando matemáticamente los procesos básicos de la producción de la orina, siguiendo las ideas expuestas en <span id='citeF-7'></span>[[#cite-7|[7]]]. Para esto se asumen varias cosas: que el tejido renal es homogéneo, que ciertos parámetros fisiológicos son constantes y que la anatomía del riñón es simple. Además, se supone que el flujo sanguíneo es uniforme, se simplifican las interacciones químicas y se asume la ausencia de patologías. Con estos supuestos, el modelo resultante se puede resolver al menos numéricamente. | + | En este contexto, el propósito de este trabajo es analizar la hemodinámica renal modelando matemáticamente los procesos básicos de la producción de la orina, siguiendo las ideas expuestas en <span id='citeF-7'></span>[[#cite-7|[7]]]. Para esto se asumen varias cosas: que el tejido renal es homogéneo, que ciertos parámetros fisiológicos son constantes y que la anatomía del riñón es simple. Además, se supone que el flujo sanguíneo es uniforme, se simplifican las interacciones químicas y se asume la ausencia de patologías. Con estos supuestos, el modelo resultante se puede resolver al menos numéricamente. En su mayoría este trabajo es expositivo, aunque se complementa con el desarrollo de los detalles que justifican las afirmaciones, y con los resultados de las simulaciones propias respectivas que no están en el artículo. El modelo que se considera está formado por: i) una EDO de primer orden con dos condiciones de frontera (el valor de una de ellas es también desconocido y debe determinarse como parte del modelo), ii) una EDP con una condición de frontera y su respectiva condición inicial, y iii) 8 EDOs adicionales con sus respectivas condiciones iniciales. |
| − | == | + | ==2 Formulación del modelo == |
La principal unidad operativa del riñón se llama nefrona, de la que hay aproximadamente un millón en cada riñón y cada nefrona es capaz de formar orina por sí misma. Es en esta donde se llevan acabo las 3 etapas para la producción de la orina (ver figura [[#img-1|1]]). En la primer etapa, la etapa de filtración glomerular, el glomérulo filtra el agua y otras sustancias del torrente sanguíneo. | La principal unidad operativa del riñón se llama nefrona, de la que hay aproximadamente un millón en cada riñón y cada nefrona es capaz de formar orina por sí misma. Es en esta donde se llevan acabo las 3 etapas para la producción de la orina (ver figura [[#img-1|1]]). En la primer etapa, la etapa de filtración glomerular, el glomérulo filtra el agua y otras sustancias del torrente sanguíneo. | ||
| Line 42: | Line 24: | ||
Cada nefrona tiene un glomérulo cuya función es un filtrado inicial de la sangre. El glomérulo consta de una red de capilares envuelto por la cápsula de Bowman (una estructura en forma de copa). La presión arterial de la sangre en los capilares empuja el agua y los solutos pequeños hacia la cápsula de Bowman, a través de una membrana de filtrado. Con esto inicia el proceso de formación de la orina <span id='citeF-7'></span>[[#cite-7|[7]]]. Aproximadamente el 20% de la sangre que entra a la nefrona, se filtra hacia la cápsula de Bowman. Tanto las plaquetas como las proteínas plasmáticas y células sanguíneas son demasiado grandes para pasar por el filtro, por lo que éstas continúan por la arteriola eferente, formando el 80% del líquido que no se filtró <span id='citeF-5'></span>[[#cite-5|[5]]]. | Cada nefrona tiene un glomérulo cuya función es un filtrado inicial de la sangre. El glomérulo consta de una red de capilares envuelto por la cápsula de Bowman (una estructura en forma de copa). La presión arterial de la sangre en los capilares empuja el agua y los solutos pequeños hacia la cápsula de Bowman, a través de una membrana de filtrado. Con esto inicia el proceso de formación de la orina <span id='citeF-7'></span>[[#cite-7|[7]]]. Aproximadamente el 20% de la sangre que entra a la nefrona, se filtra hacia la cápsula de Bowman. Tanto las plaquetas como las proteínas plasmáticas y células sanguíneas son demasiado grandes para pasar por el filtro, por lo que éstas continúan por la arteriola eferente, formando el 80% del líquido que no se filtró <span id='citeF-5'></span>[[#cite-5|[5]]]. | ||
| − | === | + | ===2.1 Modelo para la filtración glomerular.=== |
| − | Para modelar matemáticamente la dinámica del filtrado glomerular <span id='citeF-7'></span>[[#cite-7|[7]]], suponemos que los capilares glomerulares se distribuyen en una región en forma de un tubo unidimensional con flujo <math display="inline">q_1</math> y que la cápsula de Bowman que lo rodea también tienen la misma forma y flujo <math display="inline">q_2</math> (ver figura [[#img-2|2]]). Suponemos que el filtrado glomerular se da a través de una pared capilar de logitud <math display="inline">L</math> (linea punteada de la figura [[#img-2|2]]). Dado que el flujo a través de los capilares glomerulares es proporcional a la diferencia de presión a través de la pared capilar, el modelo para la filtración glomerular es | + | Para modelar matemáticamente la dinámica del filtrado glomerular <span id='citeF-7'></span>[[#cite-7|[7]]], suponemos que los capilares glomerulares se distribuyen en una región en forma de un tubo unidimensional con flujo <math display="inline">q_1</math> y que la cápsula de Bowman que lo rodea también tienen la misma forma y flujo <math display="inline">q_2</math> (ver figura [[#img-2|2]]). Suponemos que el filtrado glomerular se da a través de una pared capilar de logitud <math display="inline">L</math> (linea punteada de la figura [[#img-2|2]]). Dado que el flujo a través de los capilares glomerulares es proporcional a la diferencia de presión a través de la pared capilar, el modelo para la filtración glomerular es |
| − | + | [[Image:Draft_Dominguez Perez_785959114-diagramanuevo.png|480px|Modelo tubular del glomérulo <span id='citeF-7'></span>[[#cite-7|[7]]].]] | |
| − | + | '''Figura 2:''' Modelo tubular del glomérulo <span id='citeF-7'></span>[[#cite-7|[7]]]. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
<span id="eq-1"></span> | <span id="eq-1"></span> | ||
| Line 100: | Line 78: | ||
donde | donde | ||
| − | * <math display="inline">P_1</math> y <math display="inline">P_2</math> son las presiones hidrostáticas del fluido en los tubos 1 y 2 respectivamente (como se muestra en la figura [[#img-2|2]]) y satisfacen las relaciones ([[#eq-2|2]]),([[#eq-3|3]]), ([[#eq-4|4]]), donde <math display="inline">P_{i}</math> representa las presiones, <math display="inline">R_{i}</math> las resistencias y <math display="inline">Q_{i}</math> los flujos. Aquí, <math display="inline">i=a,e,d </math> y <math display="inline">a</math> hace referencia a la arteriola aferente, <math display="inline">e</math> hace referencia a la arteriola eferente y <math display="inline">d</math> hace referencia al túbulo descendente. <math display="inline">Q_i</math> denota el flujo de entrada, es decir el flujo en <math display="inline">x=0</math>. <math display="inline">Q_i</math> y <math display="inline">Q_e</math> son ambas desconocidas y deben determinarse. Esto hace que este problema esté bien definido y sea no trivial. | + | * <math display="inline">P_1</math> y <math display="inline">P_2</math> son las presiones hidrostáticas del fluido en los tubos 1 y 2 respectivamente (como se muestra en la figura [[#img-2|2]], donde el tubo 1 esta en rojo y el tubo 2 en verde) y satisfacen las relaciones ([[#eq-2|2]]),([[#eq-3|3]]), ([[#eq-4|4]]), donde <math display="inline">P_{i}</math> representa las presiones, <math display="inline">R_{i}</math> las resistencias y <math display="inline">Q_{i}</math> los flujos. Aquí, <math display="inline">i=a,e,d </math> y <math display="inline">a</math> hace referencia a la arteriola aferente, <math display="inline">e</math> hace referencia a la arteriola eferente y <math display="inline">d</math> hace referencia al túbulo descendente. <math display="inline">Q_i</math> denota el flujo de entrada, es decir el flujo en <math display="inline">x=0</math>. <math display="inline">Q_i</math> y <math display="inline">Q_e</math> son ambas desconocidas y deben determinarse. Esto hace que este problema esté bien definido y sea no trivial. |
* <math display="inline">K_f</math> es la tasa de filtración capilar. | * <math display="inline">K_f</math> es la tasa de filtración capilar. | ||
* <math display="inline">\pi _i</math> es la presión osmótica tanto de las proteínas suspendidas como de otras sustancias de alto peso molecular y depende de <math display="inline">q_1</math>. | * <math display="inline">\pi _i</math> es la presión osmótica tanto de las proteínas suspendidas como de otras sustancias de alto peso molecular y depende de <math display="inline">q_1</math>. | ||
| − | ==== | + | ====2.1.1 Solución del modelo para la filtración glomerular.==== |
| − | ==== | + | ====2.1.1.1 Solución analítica implícita==== |
Con unas simplificaciones algebraicas, la EDO en ([[#eq-1|1]]) se puede resolver por el método de separación de variables. La solución está definida implícitamente por | Con unas simplificaciones algebraicas, la EDO en ([[#eq-1|1]]) se puede resolver por el método de separación de variables. La solución está definida implícitamente por | ||
| Line 121: | Line 99: | ||
|} | |} | ||
| − | Usando la condición inicial <math display="inline">q_1(0)= Q_i</math> y final <math display="inline"> q_1(L)= Q_e,</math> determinamos la constante de integración <math display="inline">C.</math> Usando propiedades de logaritmo y haciendo algunas manipulaciones algebraicas (ver <span id='citeF-6'></span>[[#cite-6|[6]]]), se llega a la siguiente expresión | + | Usando la condición inicial <math display="inline">q_1(0)= Q_i</math> y la condición final <math display="inline"> q_1(L)= Q_e,</math> determinamos la constante de integración <math display="inline">C.</math> Usando propiedades de logaritmo y haciendo algunas manipulaciones algebraicas (ver <span id='citeF-6'></span>[[#cite-6|[6]]]), se llega a la siguiente expresión |
<span id="eq-6"></span> | <span id="eq-6"></span> | ||
| Line 140: | Line 118: | ||
Aún con esto no podemos obtener una formula explícita para <math display="inline">q_1</math> pero sí podemos resolver numéricamente, como lo explicaremos en la siguiente sección. | Aún con esto no podemos obtener una formula explícita para <math display="inline">q_1</math> pero sí podemos resolver numéricamente, como lo explicaremos en la siguiente sección. | ||
| − | ==== | + | ====2.1.1.2 Solución numérica==== |
| − | Los valores típicos de los parámetros son <math display="inline">P_1 = 60, P_2 = 18, P_a = 100, P_e = 18, P_d = 14 - 18, \pi _i = 25 mm Hg</math>, con <math display="inline">Q_i = 650, Q_d = Q_i - Q_e = 125 ml/min.</math> Estos valores corresponden a una dinámica estacionaria del riñón, donde los parámetros permanecen constantes. La solución del modelo con estos parámetros se ilustra en la figura [[#img-3|3]] (izquierda) para <math display="inline">q_1</math> obtenida cuando <math display="inline">Q_d=125,</math> que se obtuvo dandole valor a <math display="inline">Q_d</math>, a las resistencias <math display="inline">R_a,R_e</math> y a las presiones <math display="inline">P_e, | + | Los valores típicos de los parámetros son <math display="inline">P_1 = 60, P_2 = 18, P_a = 100, P_e = 18, P_d = 14 - 18, \pi _i = 25 mm Hg</math>, con <math display="inline">Q_i = 650, Q_d = Q_i - Q_e = 125 ml/min.</math> Estos valores corresponden a una dinámica estacionaria del riñón, donde los parámetros permanecen constantes. La solución del modelo con estos parámetros se ilustra en la figura [[#img-3|3]] (izquierda) para <math display="inline">q_1</math> obtenida cuando <math display="inline">Q_d=125,</math> que se obtuvo dandole valor a <math display="inline">Q_d</math>, a las resistencias <math display="inline">R_a,R_e</math> y a las presiones <math display="inline">P_e, P_d</math> y <math display="inline">\pi _i</math> especificadas y fijadas en niveles típicos. Con esto, resolvemos ([[#eq-6|6]]) para <math display="inline">Q_i</math> (utilizando un simple algoritmo de bisección) y <math display="inline"> Q_e,</math> a partir de ello, las presiones correspondientes <math display="inline"> P_1, P_2, P_a</math> se determinan con ayuda de ([[#eq-2|2]])-([[#eq-4|4]]). Con los valores de <math display="inline">Q_e</math> y <math display="inline">Q_i</math> podemos darle solución la ecuación ([[#eq-5|5]]) por medio de bisección para encontrar a <math display="inline">q_1</math> o bien aplicar un método como Runge Kutta para problemas de valor inicial. |
Si quisiéramos estudiar el funcionamiento del riñón en estado no estacionario, por ejemplo, en una situación donde variara la presión de la arteria aferente <math display="inline">P_a</math> entonces esto haría variar todos los demás parámetros. Los flujos y las presiones varían en función de la presión arterial. Para entender algo de esta variación, se dan valores para <math display="inline">Q_d</math> y para cada una de ellas se hace el procedimiento explicado anteriormente, obteniendo a <math display="inline">Q_i,Q_e, P_1, P_2, P_a</math> correspondientes a cada <math display="inline">Q_d</math> y se grafican (como se muestran en la figura [[#img-3|3]] derecha) la tasa de flujo sanguíneo renal <math display="inline">Q_i</math> y la tasa de flujo de filtración glomerular <math display="inline">Q_e</math> como funciones de la presión arterial <math display="inline">P_a</math>. Observamos que tanto <math display="inline">Q_i</math> como <math display="inline">Q_d</math> crecen linealmente con respecto a <math display="inline">P_a</math>. Sin embargo, en la realidad (según los datos mostrados en la figura [[#img-4|4]]), la tasa de filtración glomerular permanece relativamente constante incluso cuando la presión arterial varía entre 75 y 160 mmHg, lo que sugiere que existe cierta autorregulación en la tasa de filtración y por tanto en las tasas de flujo <math display="inline">Q_i.</math> Este fenómeno lo estudiaremos en la siguiente sección. | Si quisiéramos estudiar el funcionamiento del riñón en estado no estacionario, por ejemplo, en una situación donde variara la presión de la arteria aferente <math display="inline">P_a</math> entonces esto haría variar todos los demás parámetros. Los flujos y las presiones varían en función de la presión arterial. Para entender algo de esta variación, se dan valores para <math display="inline">Q_d</math> y para cada una de ellas se hace el procedimiento explicado anteriormente, obteniendo a <math display="inline">Q_i,Q_e, P_1, P_2, P_a</math> correspondientes a cada <math display="inline">Q_d</math> y se grafican (como se muestran en la figura [[#img-3|3]] derecha) la tasa de flujo sanguíneo renal <math display="inline">Q_i</math> y la tasa de flujo de filtración glomerular <math display="inline">Q_e</math> como funciones de la presión arterial <math display="inline">P_a</math>. Observamos que tanto <math display="inline">Q_i</math> como <math display="inline">Q_d</math> crecen linealmente con respecto a <math display="inline">P_a</math>. Sin embargo, en la realidad (según los datos mostrados en la figura [[#img-4|4]]), la tasa de filtración glomerular permanece relativamente constante incluso cuando la presión arterial varía entre 75 y 160 mmHg, lo que sugiere que existe cierta autorregulación en la tasa de filtración y por tanto en las tasas de flujo <math display="inline">Q_i.</math> Este fenómeno lo estudiaremos en la siguiente sección. | ||
| Line 162: | Line 140: | ||
|} | |} | ||
| − | === | + | ===2.2 Autorregulación=== |
En la segunda etapa, que es la reabsorción, algunos nutrientes y agua del líquido filtrado que fluye por el túbulo renal se reincorporan al torrente sanguíneo (capilares peritubulares). Lo que retorna son grandes cantidades de: aminoácidos, vitaminas, agua, glucosa, parte de la urea, los iones <math display="inline">K^+</math>, <math display="inline">Na^+</math>, <math display="inline">NaHCO_3</math> (bicarbonato), <math display="inline">Cl^-</math>, <math display="inline">HPO_4</math> (fosfato). | En la segunda etapa, que es la reabsorción, algunos nutrientes y agua del líquido filtrado que fluye por el túbulo renal se reincorporan al torrente sanguíneo (capilares peritubulares). Lo que retorna son grandes cantidades de: aminoácidos, vitaminas, agua, glucosa, parte de la urea, los iones <math display="inline">K^+</math>, <math display="inline">Na^+</math>, <math display="inline">NaHCO_3</math> (bicarbonato), <math display="inline">Cl^-</math>, <math display="inline">HPO_4</math> (fosfato). | ||
| − | Por lo que se concluyó en la sección anterior, es claro que el riñón necesita regular la tasa de filtración glomerular. La función principal del túbulo ascendente grueso es bombear iones de sodio <math display="inline">Na^+</math> fuera de éste hacia el espacio intersticial, siendo casi totalmente impermeable al agua. Si la velocidad de flujo es lenta a través del túbulo, habrá una mayor reabsorción y una concentración de <math display="inline">Cl^-</math> baja al final del túbulo que esta conectado con la mácula densa y el glomérulo. Por otro lado, cuando la velocidad de flujo es alta, hay una baja reabsorción y se produce una mayor concentración de <math display="inline">Na^+</math> y <math display="inline">Cl^-</math> en la mácula densa. Esto se resume en | + | Por lo que se concluyó en la sección anterior, es claro que el riñón necesita regular la tasa de filtración glomerular. La función principal del túbulo ascendente grueso es bombear iones de sodio <math display="inline">Na^+</math> fuera de éste hacia el espacio intersticial, siendo casi totalmente impermeable al agua. Si la velocidad de flujo es lenta a través del túbulo, habrá una mayor reabsorción y una concentración de <math display="inline">Cl^-</math> baja al final del túbulo que esta conectado con la mácula densa y el glomérulo. Por otro lado, cuando la velocidad de flujo es alta, hay una baja reabsorción y se produce una mayor concentración de <math display="inline">Na^+</math> y <math display="inline">Cl^-</math> en la mácula densa. Esto se resume en la tabla [[#table-1|1]]. |
| Line 210: | Line 188: | ||
|} | |} | ||
| − | Para normalizar el flujo del túbulo ascendente ya sea porque este sea lento o rápido, las células de la mácula densa responden a la disminución de la concentración de NaCl (a través de un mecanismo no completamente conocido) liberando un vasodilatador que aumenta o disminuye la resistencia de las arteriolas aferentes. En el caso 1, es decir cuando el flujo es lento, las células yuxtaglomerulares liberan renina, una enzima que promueve la formación de angiotensina II, la cual constriñe las arteriolas eferentes. Esto resulta en un aumento simultáneo del flujo de filtrado a través del glomérulo. En cambio, en el caso 2, cuando el flujo es rápido, la concentración de NaCl en la mácula densa aumenta, se disminuye la resistencia de la arteriola aferente y aumenta la resistencia de la arteriola eferente, lo que disminuye la tasa de filtración y el flujo a lo largo del túbulo. Esto se resume en | + | Para normalizar el flujo del túbulo ascendente ya sea porque este sea lento o rápido, las células de la mácula densa responden a la disminución de la concentración de NaCl (a través de un mecanismo no completamente conocido) liberando un vasodilatador que aumenta o disminuye la resistencia de las arteriolas aferentes. En el caso 1, es decir cuando el flujo es lento, las células yuxtaglomerulares liberan renina, una enzima que promueve la formación de angiotensina II, la cual constriñe las arteriolas eferentes. Esto resulta en un aumento simultáneo del flujo de filtrado a través del glomérulo. En cambio, en el caso 2, cuando el flujo es rápido, la concentración de NaCl en la mácula densa aumenta, se disminuye la resistencia de la arteriola aferente y aumenta la resistencia de la arteriola eferente, lo que disminuye la tasa de filtración y el flujo a lo largo del túbulo. Esto se resume en la tabla [[#table-2|2]]. |
| − | ==== | + | ====2.2.1 <span id='lb-3.2.1'></span>Modelado de la concentración de <math display="inline">Cl^-</math> para la autorregulación==== |
Un modelo sencillo de las oscilaciones tubuloglomerulares <span id='citeF-7'></span>[[#cite-7|[7]]], se centra en el papel de la concentración de cloruro en la rama ascendente gruesa. Para modelar matemáticamente esta dinámica, suponemos que la rama ascendente gruesa tiene forma de un tubo unidimensional de longitud <math display="inline">L</math> y radio constante, a través del cual el <math display="inline">Cl^-</math> es transportado y al mismo tiempo bombeado a través de las paredes del túbulo (es el <math display="inline">Na^+</math> el que se elimina activamente, pero como el <math display="inline">Cl^-</math> sigue pasivamente, el efecto es el mismo). | Un modelo sencillo de las oscilaciones tubuloglomerulares <span id='citeF-7'></span>[[#cite-7|[7]]], se centra en el papel de la concentración de cloruro en la rama ascendente gruesa. Para modelar matemáticamente esta dinámica, suponemos que la rama ascendente gruesa tiene forma de un tubo unidimensional de longitud <math display="inline">L</math> y radio constante, a través del cual el <math display="inline">Cl^-</math> es transportado y al mismo tiempo bombeado a través de las paredes del túbulo (es el <math display="inline">Na^+</math> el que se elimina activamente, pero como el <math display="inline">Cl^-</math> sigue pasivamente, el efecto es el mismo). | ||
| Line 242: | Line 220: | ||
con <math display="inline">\alpha </math> constante, <math display="inline">F_{\delta }</math> una diferencia de presiones, <math display="inline"> F_o</math> el flujo de referencia de una persona normal y <math display="inline">\overline{C}</math> la concentración de <math display="inline">Cl^-</math> para la cual <math display="inline">\phi </math> tiene un punto de inflexión, constante. A esta ecuación de transporte le asociamos la condición inicial <math display="inline">C(0,\tau )=C_0\equiv cte</math>. | con <math display="inline">\alpha </math> constante, <math display="inline">F_{\delta }</math> una diferencia de presiones, <math display="inline"> F_o</math> el flujo de referencia de una persona normal y <math display="inline">\overline{C}</math> la concentración de <math display="inline">Cl^-</math> para la cual <math display="inline">\phi </math> tiene un punto de inflexión, constante. A esta ecuación de transporte le asociamos la condición inicial <math display="inline">C(0,\tau )=C_0\equiv cte</math>. | ||
| − | ==== | + | ====2.2.2 Análisis cualitativo de la solución del modelo para la autorregulación==== |
Introducimos el cambio de variable <math display="inline"> y =Lx, \tau = \frac{L}{F_{o}} t, C(y,\tau )=C_0 c(x,t)</math> y definimos <math display="inline"> \overline{\tau }=\frac{L}{F_o}\overline{t}, K_1=\frac{F_{\delta }}{F_o}, K_2= C_0, \Omega = (0,1) \times (0,T)</math> donde <math display="inline"> \overline{t}</math> es el periodo de retardo adimensional. | Introducimos el cambio de variable <math display="inline"> y =Lx, \tau = \frac{L}{F_{o}} t, C(y,\tau )=C_0 c(x,t)</math> y definimos <math display="inline"> \overline{\tau }=\frac{L}{F_o}\overline{t}, K_1=\frac{F_{\delta }}{F_o}, K_2= C_0, \Omega = (0,1) \times (0,T)</math> donde <math display="inline"> \overline{t}</math> es el periodo de retardo adimensional. | ||
| Line 302: | Line 280: | ||
Al analizar la estabilidad de <math display="inline">s(x)</math> se presentan oscilaciones en la concentración de <math display="inline">Cl^-</math> de la mácula densa, y por tanto en las demás variables como la tasa de flujo y la presión glomerular, estas podrían ser explicadas por un mecanismo similar al de una bifurcación de Hopf. En este mecanismo, existen algunos parámetros que dentro de un rango producen soluciones oscilatorias que convergen al estado estacionario, mientras que para otro rango de valores de los parámetros resultan soluciones que oscilan sin acercarse, alrededor del estado estacionario. Podemos encontrar más sobre esto en <span id='citeF-6'></span>[[#cite-6|[6]]]. | Al analizar la estabilidad de <math display="inline">s(x)</math> se presentan oscilaciones en la concentración de <math display="inline">Cl^-</math> de la mácula densa, y por tanto en las demás variables como la tasa de flujo y la presión glomerular, estas podrían ser explicadas por un mecanismo similar al de una bifurcación de Hopf. En este mecanismo, existen algunos parámetros que dentro de un rango producen soluciones oscilatorias que convergen al estado estacionario, mientras que para otro rango de valores de los parámetros resultan soluciones que oscilan sin acercarse, alrededor del estado estacionario. Podemos encontrar más sobre esto en <span id='citeF-6'></span>[[#cite-6|[6]]]. | ||
| − | ==== | + | ====2.2.3 <span id='lb-3.2.3'></span>Solución numérica de la concentración de <math display="inline">Cl^-</math> a través del tiempo==== |
Se realizó un programa para aproximar numéricamente la solución del problema ([[#eq-8|8]]). Para ello realizamos los siguientes pasos: | Se realizó un programa para aproximar numéricamente la solución del problema ([[#eq-8|8]]). Para ello realizamos los siguientes pasos: | ||
| Line 352: | Line 330: | ||
para <math display="inline">i=1,2,...,N</math> y <math display="inline">j=1,2,...,M</math> con <math display="inline">\rho =(1/Nx)/(T/Nt)</math> y <math display="inline">s=F(c(1,t_i-\overline{t}))=F(c_{(i-itg)M}),</math> donde <math display="inline">itg</math> es la parte entera de <math display="inline">\frac{\overline{t}}{Nt}</math>. | para <math display="inline">i=1,2,...,N</math> y <math display="inline">j=1,2,...,M</math> con <math display="inline">\rho =(1/Nx)/(T/Nt)</math> y <math display="inline">s=F(c(1,t_i-\overline{t}))=F(c_{(i-itg)M}),</math> donde <math display="inline">itg</math> es la parte entera de <math display="inline">\frac{\overline{t}}{Nt}</math>. | ||
| − | <li> Finalmente construimos una función <math display="inline">\overline{c}</math> continua por pedazos, a partir de los valores de aproximación obtenidos en lo anterior. Esta función será la aproximación numérica de la solución para la ecuación ([[#eq-8|8]]) y graficándola obtenemos gráficas dadas en las figuras [[#img-6|6]] y | + | <li> Finalmente construimos una función <math display="inline">\overline{c}</math> continua por pedazos, a partir de los valores de aproximación obtenidos en lo anterior. Esta función será la aproximación numérica de la solución para la ecuación ([[#eq-8|8]]) y graficándola obtenemos gráficas dadas en las figuras [[#img-6|6]] y [[#img-7|7]] . </li> |
</ol> | </ol> | ||
| − | Dado el dominio <math display="inline">\Omega = (0, 1) \times (0, T),</math> con <math display="inline">F(z) =1+ k_1 tanh(k_2(\overline{c}-z))</math> y los valores típicos de los parámetros <math display="inline">K_1=1, K_2=10, \overline{c}=e^{(-0.91)}, \mu=0.5,</math> con las ideas anteriores, hicimos un programa para encontrar las soluciones numéricas de la concentración de <math display="inline"> Cl^-</math> a través del tiempo y con los datos siguientes para el caso estable <math display="inline">\gamma=0.1223,\overline{t}=0.2,\frac{k}{\mu }=1,</math> (ver figura [[#img-6|6]]) y para el caso inestable <math display="inline">\gamma=3.1787, \overline{t}=0.2,\frac{k}{\mu }=1</math> (ver figura | + | Dado el dominio <math display="inline">\Omega = (0, 1) \times (0, T),</math> con <math display="inline">F(z) =1+ k_1 tanh(k_2(\overline{c}-z))</math> y los valores típicos de los parámetros <math display="inline">K_1=1, K_2=10, \overline{c}=e^{(-0.91)}, \mu=0.5,</math> con las ideas anteriores, hicimos un programa para encontrar las soluciones numéricas de la concentración de <math display="inline"> Cl^-</math> a través del tiempo y con los datos siguientes para el caso estable <math display="inline">\gamma=0.1223,\overline{t}=0.2,\frac{k}{\mu }=1,</math> (ver figura [[#img-6|6]]) y para el caso inestable <math display="inline">\gamma=3.1787, \overline{t}=0.2,\frac{k}{\mu }=1</math> (ver figura [[#img-7|7]]). La concentración de <math display="inline">Cl^-</math> se representa en unidades adimensionales y la concentración al inicio de la rama ascendente gruesa es 1. La variable <math display="inline">t</math> también es adimensional; para obtener segundos se debe multiplicar por 15.5 . |
| − | Una vez obtenida la concentración de <math display="inline">Cl^-</math> como función global es decir la superficie obtenida para cada <math display="inline">x</math> y <math display="inline">t,</math> para nuestros propósitos la grafíca de la concentración de <math display="inline">Cl^-</math> que nos interesa es cuando estamos al final del asa ascendente de Henle, es decir en este caso para <math display="inline">x=1,</math> gráficas a la derecha en las figuras [[#img-6|6]] y | + | Una vez obtenida la concentración de <math display="inline">Cl^-</math> como función global es decir la superficie obtenida para cada <math display="inline">x</math> y <math display="inline">t,</math> para nuestros propósitos la grafíca de la concentración de <math display="inline">Cl^-</math> que nos interesa es cuando estamos al final del asa ascendente de Henle, es decir en este caso para <math display="inline">x=1,</math> gráficas a la derecha en las figuras [[#img-6|6]] y [[#img-7|7]]. Esta será la concentración (en <math display="inline">x=1</math>) que vamos a monitorear para saber cuál debe ser la cantidad de flujo en la filtración glomerular <math display="inline">Q_d</math> (la variable <math display="inline">Q_d</math> es adimensional, para hacerla dimensional se debe multiplicar por <math display="inline">F_o=10</math>). Si se da que en cierto tiempo <math display="inline">c(1,t)>>s(1),</math> se tendría que acelerar el flujo, al contrario, si en cierto tiempo se da que <math display="inline">c(1,t)<<s(1)</math> se tendría que disminuir el flujo. Esto se hace modificando las resistencias de las arteriolas aferente y eferente, lo cual tienen como efecto la modificación respectiva de la presión, del flujo y de la concentración. A este efecto le llamamos autorregulación. |
Con las acciones que se hacen para los dos casos anteriores, se puede regular el flujo para que a medida que la presión aumente, el flujo <math display="inline">Q_d</math> se vuelva casi constante, como se muestra en la figura [[#img-8|8]], que se obtuvo fijando la resistencia <math display="inline">R_a</math> y variando la resistencia <math display="inline">R_e</math>. Con esto observamos que aunque la presión aumente, <math display="inline">Q_d</math> se puede mantener acotada variando adecuadamente las resistencias. <div id='img-6'></div> | Con las acciones que se hacen para los dos casos anteriores, se puede regular el flujo para que a medida que la presión aumente, el flujo <math display="inline">Q_d</math> se vuelva casi constante, como se muestra en la figura [[#img-8|8]], que se obtuvo fijando la resistencia <math display="inline">R_a</math> y variando la resistencia <math display="inline">R_e</math>. Con esto observamos que aunque la presión aumente, <math display="inline">Q_d</math> se puede mantener acotada variando adecuadamente las resistencias. <div id='img-6'></div> | ||
| Line 384: | Line 362: | ||
|} | |} | ||
| − | === | + | ===2.3 Modelado de la reabsorción y la secreción=== |
En esta etapa de secreción, se eliminan sustancias no deseadas hacia los túbulos renales, funcionando como un proceso inverso a la secreción. En la nefrona, el fluido dentro del asa de Henle fluye en direcciones opuestas en los segmentos ascendente y descendente, lo que permite la creación de un gradiente osmótico en la médula renal. Este gradiente facilita la reabsorción de agua. Además, debido a la conexión en el extremo inferior del asa de Henle, el flujo y la concentración de solutos que salen del tubo descendente deben coincidir con los que entran en el tubo ascendente. | En esta etapa de secreción, se eliminan sustancias no deseadas hacia los túbulos renales, funcionando como un proceso inverso a la secreción. En la nefrona, el fluido dentro del asa de Henle fluye en direcciones opuestas en los segmentos ascendente y descendente, lo que permite la creación de un gradiente osmótico en la médula renal. Este gradiente facilita la reabsorción de agua. Además, debido a la conexión en el extremo inferior del asa de Henle, el flujo y la concentración de solutos que salen del tubo descendente deben coincidir con los que entran en el tubo ascendente. | ||
| Line 413: | Line 391: | ||
|} | |} | ||
| − | ==== | + | ====2.3.1 Solución del modelo para la reabsorción y secreción==== |
Con fines de simplificar la descripción de la solución del modelo, haremos una adimensionalización al sistema de ecuaciones ([[#eq-13|13]]), normalizando los flujos y las concentraciones de solutos, con | Con fines de simplificar la descripción de la solución del modelo, haremos una adimensionalización al sistema de ecuaciones ([[#eq-13|13]]), normalizando los flujos y las concentraciones de solutos, con | ||
| Line 608: | Line 586: | ||
|} | |} | ||
| − | La solución implícita del modelo de 8 ecuaciones ([[#eq-14|14]])- ([[#eq-21|21]]) dice que si conocemos <math display="inline">Q_d(y),</math> entonces <math display="inline">C_d</math> está determinada, <math display="inline"> | + | La solución implícita del modelo de 8 ecuaciones ([[#eq-14|14]])- ([[#eq-21|21]]) dice que si conocemos <math display="inline">Q_d(y),</math> entonces <math display="inline">C_d</math> está determinada, <math display="inline">Q_a(y)</math> está determinada si conocemos <math display="inline">Q_a</math> y <math display="inline">C_a(y),</math> si conocemos <math display="inline">Q_a,</math> <math display="inline">Q_c(y),</math> entonces <math display="inline">C_c</math> está determinada y finalmente si conocemos <math display="inline">Q_d,Q_a,Q_c,</math> entonces <math display="inline">Q_s</math> y <math display="inline">C_s</math> están determinadas. En resumen si <math display="inline">Q_d</math> y <math display="inline">Q_c</math> están determinadas, las seis ecuaciones diferenciales restantes ([[#eq-15|15]]), ([[#eq-16|16]]),([[#eq-17|17]]),([[#eq-19|19]]),([[#eq-20|20]]) y ([[#eq-21|21]]) tienen solución y por lo tanto el sistema original de ocho ecuaciones estaría resuelto. Así que lo que hace falta es resolver el siguiente sistema de dos ecuaciones de primer orden en dos incógnitas. |
<span id="eq-30"></span> | <span id="eq-30"></span> | ||
| Line 636: | Line 614: | ||
En las siguientes secciones estudiaremos un poco del comportamiento de la solución de esta ecuación, considerando un caso particular o un caso límite que es cuando se considera ausencia de ADH en la formación de orina. | En las siguientes secciones estudiaremos un poco del comportamiento de la solución de esta ecuación, considerando un caso particular o un caso límite que es cuando se considera ausencia de ADH en la formación de orina. | ||
| − | ==== | + | ====2.3.2 Solución del modelo en ausencia de ADH y de aldosterona==== |
La hormona antidiurética (ADH) regula la permeabilidad al agua en los riñones, mientras que la aldosterona controla la permeabilidad al sodio. La falta de ADH, como en la diabetes insípida central, provoca la producción de grandes cantidades de orina diluida. La aldosterona, producida en la corteza suprarrenal, modula la cantidad de canales de sodio y la actividad de la ATPasa <math display="inline">Na+/K+</math>, afectando la eliminación de sodio y potasio. Desórdenes como la enfermedad de Addison o el síndrome de Conn ilustran desequilibrios causados por niveles anormales de aldosterona. Vamos a considerar un caso en particular, suponemos que no hay ADH presente, entonces <math display="inline">\rho _c =\infty </math> y que no hay aldosterona presente, <math display="inline">H_c = 0</math>. En este caso se deduce que | La hormona antidiurética (ADH) regula la permeabilidad al agua en los riñones, mientras que la aldosterona controla la permeabilidad al sodio. La falta de ADH, como en la diabetes insípida central, provoca la producción de grandes cantidades de orina diluida. La aldosterona, producida en la corteza suprarrenal, modula la cantidad de canales de sodio y la actividad de la ATPasa <math display="inline">Na+/K+</math>, afectando la eliminación de sodio y potasio. Desórdenes como la enfermedad de Addison o el síndrome de Conn ilustran desequilibrios causados por niveles anormales de aldosterona. Vamos a considerar un caso en particular, suponemos que no hay ADH presente, entonces <math display="inline">\rho _c =\infty </math> y que no hay aldosterona presente, <math display="inline">H_c = 0</math>. En este caso se deduce que | ||
| Line 746: | Line 724: | ||
| colspan="1" | '''Figura 11:''' '' Curva de la concentración en el túbulo descendente <math>C_d</math> con los valores de los parámetros: <math>P=0.09,\Delta P_d=0.15, H_d=0.1, \rho _d=0.12,</math> <math>H_c=0.</math>'' | | colspan="1" | '''Figura 11:''' '' Curva de la concentración en el túbulo descendente <math>C_d</math> con los valores de los parámetros: <math>P=0.09,\Delta P_d=0.15, H_d=0.1, \rho _d=0.12,</math> <math>H_c=0.</math>'' | ||
|} | |} | ||
| − | A partir de las gráficas anteriores observamos que la función <math display="inline">Q_d</math> es decreciente ya que hay ausencia de ADH y de aldosteorona en el tubo descendente, es decir no hay regulación en el fujo de agua, produciendo una gran cantidad de orina diluída y un flujo rápido. En el caso de la función <math display="inline">C_d</math> es creciente ya que no hay una adecuada | + | A partir de las gráficas anteriores observamos que la función <math display="inline">Q_d</math> es decreciente ya que hay ausencia de ADH y de aldosteorona en el tubo descendente, es decir no hay regulación en el fujo de agua, produciendo una gran cantidad de orina diluída y un flujo rápido. En el caso de la función <math display="inline">C_d</math> es creciente ya que no hay una adecuada reabsorción, quedando gran cantidad de sodio en el túbulo descendente. |
| − | == | + | ==3 Conclusión == |
En este trabajo, se presenta un modelo para la hemodinámica renal, centrado en la producción de orina. El modelo se descompone en tres submodelos: | En este trabajo, se presenta un modelo para la hemodinámica renal, centrado en la producción de orina. El modelo se descompone en tres submodelos: | ||
Latest revision as of 17:45, 19 November 2024
1 Introducción
Junto al cerebro y el corazón, el riñón es un órgano fundamental en el sistema cardiovascular, ya que recibe aproximadamente el 20% de la sangre que el corazón expulsa hacia el organismo, en cada latido. Entre sus principales funciones se encuentran: regular la presión arterial, eliminar los desechos tóxicos a través de la orina y producir la hormona que estimula la formación de los glóbulos rojos [5].
Cuando no hay un funcionamiento adecuado del riñón, pueden presentarse enfermedades renales de diversas formas, desde infecciones y cálculos renales hasta enfermedades crónicas como la nefropatía diabética y la enfermedad renal crónica (ERC). Estas generan un problema de salud cada vez más importante a nivel global, afectando no solo la vida de los pacientes, sino también generando una carga significativa para los sistemas de salud debido a su alta prevalencia y costos asociados.
Por otra parte, los modelos hemodinámicos renales proporcionan una comprensión profunda sobre los patrones y comportamientos del flujo sanguíneo renal, lo que puede permitir detectar anomalías y disfunciones que de otra manera podrían pasar desapercibidas. Asimismo contribuyen a tener una perspectiva global e integral del problema, lo que coadyuva a avanzar en el diagnóstico, tratamiento y prevención de las afecciones renales.
Ahora bien, el torrente sanguíneo arrastra una gran cantidad de sustancias, muchas de la cuales entran al riñón y alguna proporción de estas pasa a formar parte de la orina. Sin embargo, la mayoría de los modelos nefrológicos consideran solo la concentración de una sustancia [7]. Estos modelos se han utilizado con fines terapéuticos o tratamiento de enfermedades vía control (cantidad de medicamentos) [1], y también con fines de diseño de riñones artificiales. En general el modelado del proceso de hemodiálisis se basa en ecuaciones cinético-hemodinámicas [3] o ecuaciones cinético-matemáticas [2].
![Esquema de las etapas de la formación de la orina en la nefrona [7].](/wd/images/thumb/8/86/Draft_Dominguez_Perez_785959114-imagenref.png/480px-Draft_Dominguez_Perez_785959114-imagenref.png)
|
| Figura 1: Esquema de las etapas de la formación de la orina en la nefrona [7]. |
En este contexto, el propósito de este trabajo es analizar la hemodinámica renal modelando matemáticamente los procesos básicos de la producción de la orina, siguiendo las ideas expuestas en [7]. Para esto se asumen varias cosas: que el tejido renal es homogéneo, que ciertos parámetros fisiológicos son constantes y que la anatomía del riñón es simple. Además, se supone que el flujo sanguíneo es uniforme, se simplifican las interacciones químicas y se asume la ausencia de patologías. Con estos supuestos, el modelo resultante se puede resolver al menos numéricamente. En su mayoría este trabajo es expositivo, aunque se complementa con el desarrollo de los detalles que justifican las afirmaciones, y con los resultados de las simulaciones propias respectivas que no están en el artículo. El modelo que se considera está formado por: i) una EDO de primer orden con dos condiciones de frontera (el valor de una de ellas es también desconocido y debe determinarse como parte del modelo), ii) una EDP con una condición de frontera y su respectiva condición inicial, y iii) 8 EDOs adicionales con sus respectivas condiciones iniciales.
2 Formulación del modelo
La principal unidad operativa del riñón se llama nefrona, de la que hay aproximadamente un millón en cada riñón y cada nefrona es capaz de formar orina por sí misma. Es en esta donde se llevan acabo las 3 etapas para la producción de la orina (ver figura 1). En la primer etapa, la etapa de filtración glomerular, el glomérulo filtra el agua y otras sustancias del torrente sanguíneo.
Cada nefrona tiene un glomérulo cuya función es un filtrado inicial de la sangre. El glomérulo consta de una red de capilares envuelto por la cápsula de Bowman (una estructura en forma de copa). La presión arterial de la sangre en los capilares empuja el agua y los solutos pequeños hacia la cápsula de Bowman, a través de una membrana de filtrado. Con esto inicia el proceso de formación de la orina [7]. Aproximadamente el 20% de la sangre que entra a la nefrona, se filtra hacia la cápsula de Bowman. Tanto las plaquetas como las proteínas plasmáticas y células sanguíneas son demasiado grandes para pasar por el filtro, por lo que éstas continúan por la arteriola eferente, formando el 80% del líquido que no se filtró [5].
2.1 Modelo para la filtración glomerular.
Para modelar matemáticamente la dinámica del filtrado glomerular [7], suponemos que los capilares glomerulares se distribuyen en una región en forma de un tubo unidimensional con flujo y que la cápsula de Bowman que lo rodea también tienen la misma forma y flujo (ver figura 2). Suponemos que el filtrado glomerular se da a través de una pared capilar de logitud (linea punteada de la figura 2). Dado que el flujo a través de los capilares glomerulares es proporcional a la diferencia de presión a través de la pared capilar, el modelo para la filtración glomerular es
![Modelo tubular del glomérulo [7].](/wd/images/thumb/1/1f/Draft_Dominguez_Perez_785959114-diagramanuevo.png/480px-Draft_Dominguez_Perez_785959114-diagramanuevo.png)
Figura 2: Modelo tubular del glomérulo [7].
|
|
(1) |
junto con las relaciones
|
|
(2) |
|
|
(3) |
|
|
(4) |
donde
- y son las presiones hidrostáticas del fluido en los tubos 1 y 2 respectivamente (como se muestra en la figura 2, donde el tubo 1 esta en rojo y el tubo 2 en verde) y satisfacen las relaciones (2),(3), (4), donde representa las presiones, las resistencias y los flujos. Aquí, y hace referencia a la arteriola aferente, hace referencia a la arteriola eferente y hace referencia al túbulo descendente. denota el flujo de entrada, es decir el flujo en . y son ambas desconocidas y deben determinarse. Esto hace que este problema esté bien definido y sea no trivial.
- es la tasa de filtración capilar.
- es la presión osmótica tanto de las proteínas suspendidas como de otras sustancias de alto peso molecular y depende de .
2.1.1 Solución del modelo para la filtración glomerular.
2.1.1.1 Solución analítica implícita
Con unas simplificaciones algebraicas, la EDO en (1) se puede resolver por el método de separación de variables. La solución está definida implícitamente por
|
|
(5) |
Usando la condición inicial y la condición final determinamos la constante de integración Usando propiedades de logaritmo y haciendo algunas manipulaciones algebraicas (ver [6]), se llega a la siguiente expresión
|
|
(6) |
donde
En resumen, hasta ahora tenemos la solución implícita para dada por (5) y la de dada por (6) y además tenemos la relación . Así que si damos un valor para podemos resolver (6) para y obtener o de igual forma resolver (6) para y obtener . También obtenemos , vía la relación (2).
Aún con esto no podemos obtener una formula explícita para pero sí podemos resolver numéricamente, como lo explicaremos en la siguiente sección.
2.1.1.2 Solución numérica
Los valores típicos de los parámetros son , con Estos valores corresponden a una dinámica estacionaria del riñón, donde los parámetros permanecen constantes. La solución del modelo con estos parámetros se ilustra en la figura 3 (izquierda) para obtenida cuando que se obtuvo dandole valor a , a las resistencias y a las presiones y especificadas y fijadas en niveles típicos. Con esto, resolvemos (6) para (utilizando un simple algoritmo de bisección) y a partir de ello, las presiones correspondientes se determinan con ayuda de (2)-(4). Con los valores de y podemos darle solución la ecuación (5) por medio de bisección para encontrar a o bien aplicar un método como Runge Kutta para problemas de valor inicial.
Si quisiéramos estudiar el funcionamiento del riñón en estado no estacionario, por ejemplo, en una situación donde variara la presión de la arteria aferente entonces esto haría variar todos los demás parámetros. Los flujos y las presiones varían en función de la presión arterial. Para entender algo de esta variación, se dan valores para y para cada una de ellas se hace el procedimiento explicado anteriormente, obteniendo a correspondientes a cada y se grafican (como se muestran en la figura 3 derecha) la tasa de flujo sanguíneo renal y la tasa de flujo de filtración glomerular como funciones de la presión arterial . Observamos que tanto como crecen linealmente con respecto a . Sin embargo, en la realidad (según los datos mostrados en la figura 4), la tasa de filtración glomerular permanece relativamente constante incluso cuando la presión arterial varía entre 75 y 160 mmHg, lo que sugiere que existe cierta autorregulación en la tasa de filtración y por tanto en las tasas de flujo Este fenómeno lo estudiaremos en la siguiente sección.
![Gráfica de la Curva q₁(x) correspondiente a Qd=125. Para este caso, Qi=652.1 y Qₑ=527.1, x ퟄ[0,L] (izquierda). Gráficas de \fracQi5 y Qd contra Pₐ (derecha).](/wd/images/thumb/e/ed/Draft_Dominguez_Perez_785959114-q1dex.png/330px-Draft_Dominguez_Perez_785959114-q1dex.png)
|
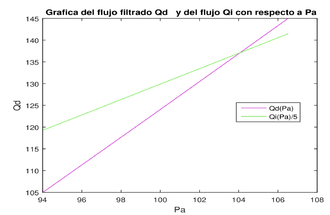
|
| (3) Gráfica de la Curva correspondiente a . Para este caso, y , (izquierda). Gráficas de y contra (derecha). |
![Gráficas reales del flujo sanguíneo renal con autorregulación y de la tasa de filtración glomerular [7].](/wd/images/thumb/5/56/Draft_Dominguez_Perez_785959114-realqa.png/480px-Draft_Dominguez_Perez_785959114-realqa.png)
|
| Figura 4: Gráficas reales del flujo sanguíneo renal con autorregulación y de la tasa de filtración glomerular [7]. |
2.2 Autorregulación
En la segunda etapa, que es la reabsorción, algunos nutrientes y agua del líquido filtrado que fluye por el túbulo renal se reincorporan al torrente sanguíneo (capilares peritubulares). Lo que retorna son grandes cantidades de: aminoácidos, vitaminas, agua, glucosa, parte de la urea, los iones , , (bicarbonato), , (fosfato).
Por lo que se concluyó en la sección anterior, es claro que el riñón necesita regular la tasa de filtración glomerular. La función principal del túbulo ascendente grueso es bombear iones de sodio fuera de éste hacia el espacio intersticial, siendo casi totalmente impermeable al agua. Si la velocidad de flujo es lenta a través del túbulo, habrá una mayor reabsorción y una concentración de baja al final del túbulo que esta conectado con la mácula densa y el glomérulo. Por otro lado, cuando la velocidad de flujo es alta, hay una baja reabsorción y se produce una mayor concentración de y en la mácula densa. Esto se resume en la tabla 1.
| Flujo del túbulo ascendente | Reabsorción | |
| Caso 1: lento | Alta | Baja |
| Caso 2: rápido | Baja | Alta |
| Flujo | Filtración | |||
| Caso 1: Aumentar | Aumentar | Aumentar | Disminuir | Disminuir |
| Caso 2: Disminuir | Disminuir | Disminuir | Disminuir | Aumentar |
Para normalizar el flujo del túbulo ascendente ya sea porque este sea lento o rápido, las células de la mácula densa responden a la disminución de la concentración de NaCl (a través de un mecanismo no completamente conocido) liberando un vasodilatador que aumenta o disminuye la resistencia de las arteriolas aferentes. En el caso 1, es decir cuando el flujo es lento, las células yuxtaglomerulares liberan renina, una enzima que promueve la formación de angiotensina II, la cual constriñe las arteriolas eferentes. Esto resulta en un aumento simultáneo del flujo de filtrado a través del glomérulo. En cambio, en el caso 2, cuando el flujo es rápido, la concentración de NaCl en la mácula densa aumenta, se disminuye la resistencia de la arteriola aferente y aumenta la resistencia de la arteriola eferente, lo que disminuye la tasa de filtración y el flujo a lo largo del túbulo. Esto se resume en la tabla 2.
2.2.1 Modelado de la concentración de para la autorregulación2.2.1 Modelado de la concentración de
C
l
−
{\textstyle Cl^{-}}
para la autorregulación
Un modelo sencillo de las oscilaciones tubuloglomerulares [7], se centra en el papel de la concentración de cloruro en la rama ascendente gruesa. Para modelar matemáticamente esta dinámica, suponemos que la rama ascendente gruesa tiene forma de un tubo unidimensional de longitud y radio constante, a través del cual el es transportado y al mismo tiempo bombeado a través de las paredes del túbulo (es el el que se elimina activamente, pero como el sigue pasivamente, el efecto es el mismo).
Supondremos que la concentración de cloruro es uniforme en cada sección transversal. Si usamos una coordenada para describir cada sección transversal del túbulo y dado los supuestos que hemos mencionado, denotamos por la concentración de en la sección transversal asociada con en el momento y modelamos esa concentración con la siguiente ecuación diferencial parcial de transporte
|
|
(7) |
donde representa la tasa de eliminación de del tubo mediante el bombeo de y la tasa de cloro que pasa a través de cada sección transversal. Consideramos las expresiones siguientes
|
|
con constante, una diferencia de presiones, el flujo de referencia de una persona normal y la concentración de para la cual tiene un punto de inflexión, constante. A esta ecuación de transporte le asociamos la condición inicial .
2.2.2 Análisis cualitativo de la solución del modelo para la autorregulación
Introducimos el cambio de variable y definimos donde es el periodo de retardo adimensional.
De donde obtenemos la ecuación diferencial parcial retardada
|
|
(8) |
con y . Para iniciar el estudio de la ecuación (8), vamos a obtener las soluciones en estado estacionario. Es decir le daremos solución a la ecuación
|
|
(9) |
con . Claramente la solución de esta ecuación es
|
|
(10) |
con . El valor de debe ser determinado y tomando en cuenta que el valor de debe satisfacer
|
|
(11) |
Dado que es una función decreciente de ya que así existe un único valor de para el cual se cumple (11) y por tanto, una solución única en estado estacionario.
Al analizar la estabilidad de se presentan oscilaciones en la concentración de de la mácula densa, y por tanto en las demás variables como la tasa de flujo y la presión glomerular, estas podrían ser explicadas por un mecanismo similar al de una bifurcación de Hopf. En este mecanismo, existen algunos parámetros que dentro de un rango producen soluciones oscilatorias que convergen al estado estacionario, mientras que para otro rango de valores de los parámetros resultan soluciones que oscilan sin acercarse, alrededor del estado estacionario. Podemos encontrar más sobre esto en [6].
2.2.3 Solución numérica de la concentración de a través del tiempo2.2.3 Solución numérica de la concentración de
C
l
−
{\textstyle Cl^{-}}
a través del tiempo
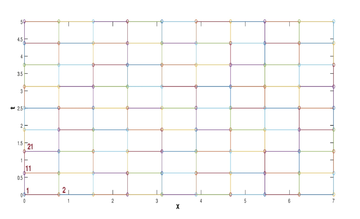
Se realizó un programa para aproximar numéricamente la solución del problema (8). Para ello realizamos los siguientes pasos:
- Discretizamos en nodos (() rectángulos) a . Para esto, consideramos una partición en , donde
- Construimos una aproximación para , es decir, para la solución en cada nodo . De acuedo a las condiciones de frontera para toda conocemos el valor de la función en entonces simplemente le asignamos a los nodos con esta característica el valor 1. Para todos los demás nodos se aproxima la solución mediante el método de Euler explícito, que se resume en el siguiente esquema
(12) - Finalmente construimos una función continua por pedazos, a partir de los valores de aproximación obtenidos en lo anterior. Esta función será la aproximación numérica de la solución para la ecuación (8) y graficándola obtenemos gráficas dadas en las figuras 6 y 7 .
|
|
y una partición en , donde
|
|
|
| Figura 5: Resultado del paso 1: Malla computacional. |
para y con y donde es la parte entera de .
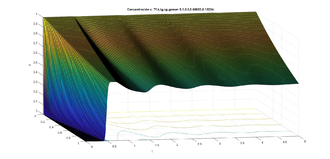
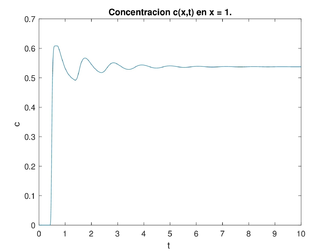
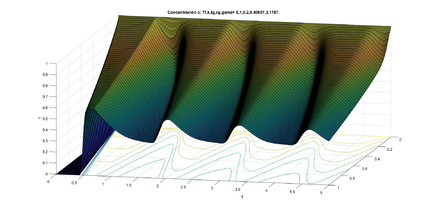
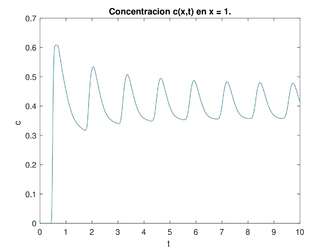
Dado el dominio con y los valores típicos de los parámetros con las ideas anteriores, hicimos un programa para encontrar las soluciones numéricas de la concentración de a través del tiempo y con los datos siguientes para el caso estable (ver figura 6) y para el caso inestable (ver figura 7). La concentración de se representa en unidades adimensionales y la concentración al inicio de la rama ascendente gruesa es 1. La variable también es adimensional; para obtener segundos se debe multiplicar por 15.5 .
Una vez obtenida la concentración de como función global es decir la superficie obtenida para cada y para nuestros propósitos la grafíca de la concentración de que nos interesa es cuando estamos al final del asa ascendente de Henle, es decir en este caso para gráficas a la derecha en las figuras 6 y 7. Esta será la concentración (en ) que vamos a monitorear para saber cuál debe ser la cantidad de flujo en la filtración glomerular (la variable es adimensional, para hacerla dimensional se debe multiplicar por ). Si se da que en cierto tiempo se tendría que acelerar el flujo, al contrario, si en cierto tiempo se da que se tendría que disminuir el flujo. Esto se hace modificando las resistencias de las arteriolas aferente y eferente, lo cual tienen como efecto la modificación respectiva de la presión, del flujo y de la concentración. A este efecto le llamamos autorregulación.
Con las acciones que se hacen para los dos casos anteriores, se puede regular el flujo para que a medida que la presión aumente, el flujo se vuelva casi constante, como se muestra en la figura 8, que se obtuvo fijando la resistencia y variando la resistencia . Con esto observamos que aunque la presión aumente, se puede mantener acotada variando adecuadamente las resistencias.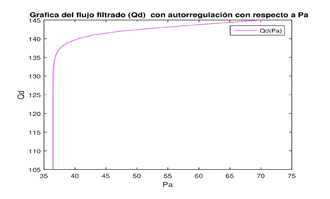
|
| Figura 8: Grafica del flujo con el proceso de autorregulación. |
2.3 Modelado de la reabsorción y la secreción
En esta etapa de secreción, se eliminan sustancias no deseadas hacia los túbulos renales, funcionando como un proceso inverso a la secreción. En la nefrona, el fluido dentro del asa de Henle fluye en direcciones opuestas en los segmentos ascendente y descendente, lo que permite la creación de un gradiente osmótico en la médula renal. Este gradiente facilita la reabsorción de agua. Además, debido a la conexión en el extremo inferior del asa de Henle, el flujo y la concentración de solutos que salen del tubo descendente deben coincidir con los que entran en el tubo ascendente.
Siguiendo a [7], consideramos que el asa de Henle consta de cuatro compartimentos: tres túbulos (rama descendente, rama ascendente y conducto colector (túbulo amarillo en la figura 1)) y un compartimento único para el intersticio y los capilares peritubulares (túbulo rojo en la figura 1). El lecho intersticial/capilar se trata como un tubo unidimensional que recibe líquido de los otros tres túbulos y lo entrega a las vénulas. En cada uno de estos compartimentos, seguimos el flujo de agua y la concentración de solutos.
Suponemos que el flujo en cada uno de los tubos sigue un patrón simple (positivo en la dirección positiva), con tasas de flujo para los túbulos descendentes, ascendentes, colectores y los túbulos intersticiales, respectivamente. De igual manera, la concentración de soluto en cada uno de estos se representa como . Se considera que los túbulos son unidimensionales, con el flujo del filtrado glomerular ingresando a la rama descendente en , pasando de la rama descendente a la ascendente en , dirigiéndose desde la rama ascendente al conducto colector en , y finalmente saliendo del conducto colector en . Se asume que el intersticio/compartimento capilar se vacía en , y que no hay flujo en . Para una mejor comprensión de lo anterior, ver figura 9.
![Diagrama del modelo de cuatro compartimentos del asa de Henle [7].](/wd/images/thumb/6/6c/Draft_Dominguez_Perez_785959114-asadehenle.png/360px-Draft_Dominguez_Perez_785959114-asadehenle.png)
|
| Figura 9: Diagrama del modelo de cuatro compartimentos del asa de Henle [7]. |
El sistema de ecuaciones que resultan en nuestra modelación de la actividad en el asa de Henle es:
|
|
(13) |
2.3.1 Solución del modelo para la reabsorción y secreción
Con fines de simplificar la descripción de la solución del modelo, haremos una adimensionalización al sistema de ecuaciones (13), normalizando los flujos y las concentraciones de solutos, con
|
|
y los parámetros adimensionales
La versión adimensional de (13) es
|
|
(14) |
|
|
(15) |
|
|
(16) |
|
|
(17) |
|
|
(18) |
|
|
(19) |
|
|
(20) |
|
|
(21) |
La ecuaciones (14)- (21) tienen las siguientes soluciones implícitas, respectivamente
|
|
(22) |
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
|
|
(27) |
|
|
(28) |
|
|
(29) |
La solución implícita del modelo de 8 ecuaciones (14)- (21) dice que si conocemos entonces está determinada, está determinada si conocemos y si conocemos entonces está determinada y finalmente si conocemos entonces y están determinadas. En resumen si y están determinadas, las seis ecuaciones diferenciales restantes (15), (16),(17),(19),(20) y (21) tienen solución y por lo tanto el sistema original de ocho ecuaciones estaría resuelto. Así que lo que hace falta es resolver el siguiente sistema de dos ecuaciones de primer orden en dos incógnitas.
|
|
(30) |
|
|
(31) |
donde y son funciones de y . Aunque hay tres condiciones iniciales para dos ecuaciones de primer orden, el número también es desconocido, por lo que este problema está bien planteado. Con esto observamos que la solución del modelo completo de 8 ecuaciones se reduce a resolver el modelo de que en general es difícil de resolver tanto analítica como numéricamente.
En las siguientes secciones estudiaremos un poco del comportamiento de la solución de esta ecuación, considerando un caso particular o un caso límite que es cuando se considera ausencia de ADH en la formación de orina.
2.3.2 Solución del modelo en ausencia de ADH y de aldosterona
La hormona antidiurética (ADH) regula la permeabilidad al agua en los riñones, mientras que la aldosterona controla la permeabilidad al sodio. La falta de ADH, como en la diabetes insípida central, provoca la producción de grandes cantidades de orina diluida. La aldosterona, producida en la corteza suprarrenal, modula la cantidad de canales de sodio y la actividad de la ATPasa , afectando la eliminación de sodio y potasio. Desórdenes como la enfermedad de Addison o el síndrome de Conn ilustran desequilibrios causados por niveles anormales de aldosterona. Vamos a considerar un caso en particular, suponemos que no hay ADH presente, entonces y que no hay aldosterona presente, . En este caso se deduce que
|
|
En otras palabras, no hay pérdida de agua o de en el conducto colector por lo que la ecuación para (31) ha sido reducida a una ecuación algebraica. Por lo que ahora, queda por determinar lo que ocurre en los túbulos descendente y ascendente. El flujo se rige por las siguientes ecuaciones
|
|
(32) |
con De las ecuaciones (22) y (27) se deduce que
|
|
Con constante ya que el miembro ascendente es impermeable al agua y una función linealmente decreciente de .
Observamos que el problema (32), tiene asociadas dos condiciones de frontera, pero una de ellas está en términos de un parámetro desconocido que se debe determinar como parte del problema.
En el caso que nos ocupa (ausencia de ADH), adicionalmente consideraremos que el túbulo descendente sea bastante permeable al agua. Lo cual implicaría que debemos tomar pequeño en el problema (32). Pero entonces, la ecuación diferencial (32) es difícil de resolver tanto analítica como numéricamente ya que resulta ser singular. Dado que es diferenciable e invertible, por el teorema de la función inversa, podemos resolver este problema buscando una solución en la forma que satisface la ecuación diferencial
|
|
(33) |
Para resolver este problema buscamos en función de como serie de potencias de
|
|
(34) |
sustituyendo en (33), igualando y expandiendo en potencias de se tiene que
|
|
(35) |
Ahora determinamos haciendo en (35), y despejando para determinarla, obteniendo
|
|
(36) |
Ahora podemos graficar en función de y girar los ejes para ver en función de . Esto se representa en las figuras 10. Una vez que se determina en función de , podemos graficar la concentración en función de , dada en la figura 11.

|

|
| Figura 10: Curva del flujo (izquierda) y la curva de la función (derecha) con los valores de los parámetros con los valores de los parámetros: | |

|
| Figura 11: Curva de la concentración en el túbulo descendente con los valores de los parámetros: |
A partir de las gráficas anteriores observamos que la función es decreciente ya que hay ausencia de ADH y de aldosteorona en el tubo descendente, es decir no hay regulación en el fujo de agua, produciendo una gran cantidad de orina diluída y un flujo rápido. En el caso de la función es creciente ya que no hay una adecuada reabsorción, quedando gran cantidad de sodio en el túbulo descendente.
3 Conclusión
En este trabajo, se presenta un modelo para la hemodinámica renal, centrado en la producción de orina. El modelo se descompone en tres submodelos:
1. Filtración glomerular: Se modela mediante una ecuación diferencial de primer orden con dos condiciones de frontera desconocidas, mostrando que el flujo resultante es lineal con respecto a la presión arterial, lo cual no es del todo preciso en la realidad debido a un proceso de autorregulación renal que mantiene constante el filtrado a pesar de variaciones en la presión.
2. Autorregulación: Se utiliza una ecuación diferencial parcial de transporte con retardo para modelar la concentración de cloro en el túbulo ascendente del asa de Henle. Se descubrió que, dependiendo de algunos rangos de parámetros, las oscilaciones en la concentración de pueden llevar a soluciones que convergen rápidamente al estado estacionario o a soluciones casi periódicas, lo que sugiere la posibilidad de una bifurcación en el sistema.
3. Reabsorción y secreción: Se aborda mediante un sistema de ecuaciones diferenciales ordinarias que modela el flujo de agua y sodio en el asa de Henle. Se demuestra que, en ausencia de ADH y aldosterona, se produce un flujo decreciente de agua, lo que resulta en una gran cantidad de orina diluida y un aumento en la concentración de cloro.
En conjunto, aunque el modelo presenta limitaciones, logra simular satisfactoriamente la dinámica de la eliminación de desechos metabólicos a través de la orina en situaciones específicas.
BIBLIOGRAFÍA
[1] Bazaev, N.A, Grinvald, V. M. Selischev, S. V. (2010). A Mathematical Model for a Biotechnological Hemodialysis system. Biomedical Engineering, Vol. 44(No.3), 79-84. [2] Baigent, S. Unwin, R. Yeng, C. (2001). Mathematical Modelling of Profiled Hemodialysis: A Simplified Approach. Journal of Theoretical Medicine, Vol 3(2), 143-160. https://doi.org/10.1080/10273660108833070.[3] Cavalcanti, S. Ciandrini, A. Avanzolini, G. (2006). Mathematical modeling of arterial pressure response to hemodialysis-induced hypovolemia. Computers in Biology and Medicine, Vol 36(2), 128- 144. https://doi.org/10.1016/j.compbiomed.2004.08.00.
[4] Cooper, J. (2000). Introduction to partial Differential Equations with MATLAB, (3ed). New York. Birkhauser.
[5] Escuela Universitaria de Enfermería. Universidad de Barcelona,. Sistema urinario: anatomía. https://www.infermeravirtual.com/files/media/file/103/Sistema
[6] Domínguez, F. (2024). Un modelo matemático del funcionamiento del riñon [Tesis de Maestría en Ciencias en Matemáticas Aplicadas, Universidad Juárez Autónoma de Tabasco]. [7] James, K. James, S. (2009). Renal Physiology, Mathematical Physiology Systems Physiology , (2ed),(821-850). Midtown Manhattan. Springer.[8] Perko, L. (2008). Differential Equations and Dynamical Systems, (3ed). New York. Springer.
Document information
Published on 19/11/24
Submitted on 12/09/24
Licence: CC BY-NC-SA license