(→2.2 Boundary conditions for permeability analysis of support structures) |
m (WERQERQWERQWER) (Tag: Visual edit) |
||
| (23 intermediate revisions by 2 users not shown) | |||
| Line 33: | Line 33: | ||
<div id='img-1'></div> | <div id='img-1'></div> | ||
| − | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width: | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:85%;" |
|-style="background:white;" | |-style="background:white;" | ||
| − | |style="text-align: center;padding:10px;"| [[Image:Draft_Zhang_149466663-image1-c.png|center| | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Zhang_149466663-image1-c.png|center|700px]] |
|- | |- | ||
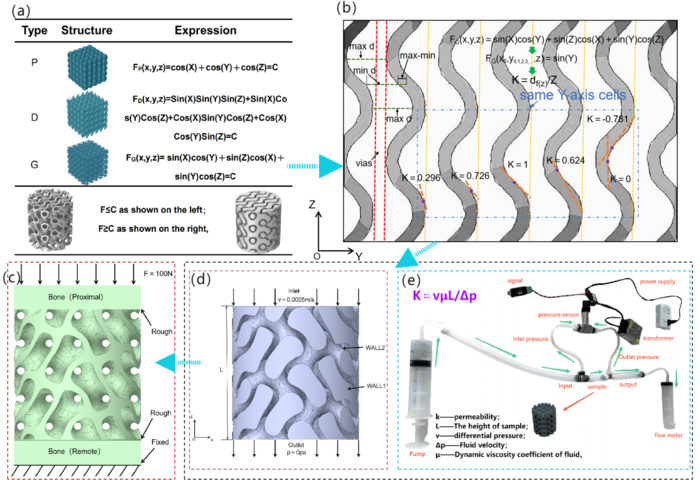
| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 1'''. (a) Schematic representation and mathematical model implicit function expressions of P, D, and G models. (b) Representation and curvature calculation of the YZ interface. (c) Stress conduction boundary conditions. (d) Fluid flow boundary conditions. (e) Schematic diagram of the permeability experimental apparatus | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 1'''. (a) Schematic representation and mathematical model implicit function expressions of P, D, and G models. (b) Representation and curvature calculation of the YZ interface. (c) Stress conduction boundary conditions. (d) Fluid flow boundary conditions. (e) Schematic diagram of the permeability experimental apparatus | ||
| Line 54: | Line 54: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> \left\{ \begin{matrix}\rho \frac{\partial u}{\partial t}-\mu {\nabla }^{2}u+\rho (u\cdot \nabla )u+\nabla P=F\\\nabla \cdot u=0\end{matrix}.\right. </math> | + | | style="text-align: center;" | <math> \left\{ \begin{matrix}\rho \displaystyle\frac{\partial u}{\partial t}-\mu {\nabla }^{2}u+\rho (u\cdot \nabla )u+\nabla P=F\\\nabla \cdot u=0\end{matrix}.\right. </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" |(1) | | style="width: 5px;text-align: right;white-space: nowrap;" |(1) | ||
|} | |} | ||
| − | where, <math display="inline">\rho</math> is the fluid density; <math display="inline">u</math> the fluid velocity; <math display="inline">t</math> the time; <math display="inline">\mu</math> the dynamic viscosity of fluid; <math display="inline">\nabla</math> the del operator; <math display="inline">P</math> | + | where, <math display="inline">\rho</math> is the fluid density; <math display="inline">u</math> the fluid velocity; <math display="inline">t</math> the time; <math display="inline">\mu</math> the dynamic viscosity of fluid; <math display="inline">\nabla</math> the del operator; <math display="inline">P</math> the pressure; and <math display="inline">F</math> the gravity or centrifugal force. |
| − | The boundary conditions applied for CFD analysis are shown in [[#img-1|Figure 1]](d), and the region with <math display="inline">F \ge C</math> is considered as the fluid model. The inflow surface (Inlet), outflow surface (Outlet), solid wall 1 (Wall1), and solid wall 2 (Wall2) are shown in the figure. The liquid flowing through the pore area of the scaffold is assumed to be capillary blood, with an inlet flow rate of 0.0005m/s applied on the inlet surface and 0 outlet pressure applied on the outlet surface. Wall1 and Wall2 are defined as non sliding wall surfaces, with a fluid viscosity of 4. | + | The boundary conditions applied for CFD analysis are shown in [[#img-1|Figure 1]](d), and the region with <math display="inline">F \ge C</math> is considered as the fluid model. The inflow surface (Inlet), outflow surface (Outlet), solid wall 1 (Wall1), and solid wall 2 (Wall2) are shown in the figure. The liquid flowing through the pore area of the scaffold is assumed to be capillary blood, with an inlet flow rate of 0.0005m/s applied on the inlet surface and 0 outlet pressure applied on the outlet surface. Wall1 and Wall2 are defined as non sliding wall surfaces, with a fluid viscosity of 4.2mPa·s. The relevant settings are summarized in [[#tab-1|Table 1]]. |
<div class="center" style="font-size: 85%;">'''Table 1'''. Related settings in permeability calculation</div> | <div class="center" style="font-size: 85%;">'''Table 1'''. Related settings in permeability calculation</div> | ||
| Line 91: | Line 91: | ||
Combined with Darcy's law, in order to measure the permeability <math display="inline"> k </math> of the stent, [[#img-1|Figure 1]](e) is a permeability experimental device. The water from the water pump gets the pressure difference between the two sides of the bracket through the pressure difference sensor, and the bracket is wrapped in the sample warehouse made of heat-shrinkable pipe to ensure the close cooperation of the bracket and prevent the liquid from leaking from both sides. The Flowmeter is used to control the flow into the sample and finally the liquid flows out. Repeat the measurement five times for each sample. | Combined with Darcy's law, in order to measure the permeability <math display="inline"> k </math> of the stent, [[#img-1|Figure 1]](e) is a permeability experimental device. The water from the water pump gets the pressure difference between the two sides of the bracket through the pressure difference sensor, and the bracket is wrapped in the sample warehouse made of heat-shrinkable pipe to ensure the close cooperation of the bracket and prevent the liquid from leaking from both sides. The Flowmeter is used to control the flow into the sample and finally the liquid flows out. Repeat the measurement five times for each sample. | ||
| − | =3. Construction of stent for segmental bone defect of tibia and analysis of finite element results= | + | ==3. Construction of stent for segmental bone defect of tibia and analysis of finite element results== |
| − | == | + | ===3.1 Finite element results and discussion of different cell structures=== |
| − | ===3.1.1 Analysis of stress and strain results of different cell structures=== | + | ====3.1.1 Analysis of stress and strain results of different cell structures==== |
| − | As shown in | + | As shown in [[#img-2|Figure 2]], the minimum equivalent stress is G-type stent and the maximum is D-type stent; the minimum displacement on the main section of YZ is G-type stent and the maximum is P-type stent; the minimum equivalent stress is G and the maximum is P-type stent. As shown in [[#tab-2|Table 2]], the stress distribution of G-type support is more uniform and the axial displacement is lower under the same load. The stress of P-type stent is concentrated on the surface, and the stress distribution of P-type stent is more uniform at the same horizontal position, but the axial displacement is the largest. From the mises stress distribution of YZ cross section, it is known that the stress value of G-type single crystal is the lowest at the curvature = 1 and the maximum at the curvature of 0. [[#img-3|Figure 3]] shows the mises stress values of G-type stents with different curvature changes in the single cell. |
| − | [[Image:Draft_Zhang_149466663-picture- 1.svg|center|600px]] | + | <div id='img-2'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Zhang_149466663-picture- 1.svg|center|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. FEA results of scaffolds with different cell structures | ||
| + | |} | ||
| − | |||
| − | |||
| − | Table 2. Maximum Von mises and Disp tables of different cell structures | + | <div class="center" style="font-size: 85%;">'''Table 2'''. Maximum Von mises and Disp tables of different cell structures |
</div> | </div> | ||
| − | {| style=" | + | <div id='tab-2'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! Type !! Mises (N/m<sup>2</sup>) !! Disp (mm) !! YZ-mises (N/m<sup>2</sup>) !! YZ-Disp (mm) | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|'''G''' |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|<math display="inline">5.51\times 10^9</math> |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|<math display="inline">0.0106</math> |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|<math display="inline">2.3\times 10^8</math> |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|<math display="inline">0.0556</math> |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|'''D''' |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|<math display="inline">1.51\times 10^9</math> |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|<math display="inline">0.0552</math> |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|<math display="inline">5.83\times 10^9</math> |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|<math>0.00965</math> |
|- | |- | ||
| − | | style="text-align: center;vertical-align: top;"| | + | | style="text-align: center;vertical-align: top;"|'''P''' |
| − | + | | style="text-align: center;vertical-align: top;"|<math display="inline">7.45\times 10^9</math> | |
| − | + | | style="text-align: center;vertical-align: top;"|<math display="inline">0.0195</math> | |
| − | + | | style="text-align: center;vertical-align: top;"|<math display="inline">6.6\times 10^9</math> | |
| − | + | | style="text-align: center;vertical-align: top;"|<math display="inline">0.01850</math> | |
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|} | |} | ||
| − | <div class=" | + | <div id='img-3'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Zhang_149466663-image26-c.png|center|456px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Mises stress values of different curvature changes in the single cell of G-type stents | ||
| + | |} | ||
| − | |||
| − | |||
| − | ===3.1.2 Analysis of CFD results with different cell structures=== | + | ====3.1.2 Analysis of CFD results with different cell structures==== |
| − | Figure 4 shows the results of CFD flow velocity with different cell structures. The maximum flow velocity of G-type stent is smaller than that of other stents, which is due to the good connectivity of G-type and the formation of axial through-hole is smaller than the other two types. It can be seen that the flow velocity in the center of the channel is significantly higher than that in the surrounding area, which can transport nutrients to deeper pores, which is conducive to cell migration, proliferation and differentiation [17, 18]. Because the flow velocity in the center is higher than that on both sides, the nutrients in the center of the channel are squeezed to the surrounding area, and the curvature of the surrounding area is large. Osteoblasts adhere to the surrounding area for osteogenesis and differentiation, and P-type scaffolds form external flow field and internal flow field. The velocity of the external flow field is obviously lower than that of the internal flow field. in the internal flow field, the velocity in the region with low curvature is obviously higher than that in the region with high curvature, and the smaller the curvature in Z direction is, the higher the velocity is. Because the curvature of P type at the cell junction is close to 0, so the velocity at the junction is abnormally high, so the nutrient flow rate of P type stent will be faster, but the efficiency of osteogenic adhesion on the surface with high curvature in Z direction will be lower. The osteogenic adhesion formed on both sides of the low curvature can not be converted into large pieces of bone between the crystal cells, so in the microstructure design of the porous scaffold, the high curvature in the Z direction should not be used to form the through hole directly, but the cross of the cell structure should be used to form the through hole. The through hole formed by the D-shaped support due to structural reasons is not a Z-direction through hole, but a 45°oblique through hole, and the surface has no curvature change. therefore, after constructing the boundary conditions shown in | + | [[#img-4|Figure 4]] shows the results of CFD flow velocity with different cell structures. The maximum flow velocity of G-type stent is smaller than that of other stents, which is due to the good connectivity of G-type and the formation of axial through-hole is smaller than the other two types. It can be seen that the flow velocity in the center of the channel is significantly higher than that in the surrounding area, which can transport nutrients to deeper pores, which is conducive to cell migration, proliferation and differentiation [17,18]. Because the flow velocity in the center is higher than that on both sides, the nutrients in the center of the channel are squeezed to the surrounding area, and the curvature of the surrounding area is large. Osteoblasts adhere to the surrounding area for osteogenesis and differentiation, and P-type scaffolds form external flow field and internal flow field. The velocity of the external flow field is obviously lower than that of the internal flow field. in the internal flow field, the velocity in the region with low curvature is obviously higher than that in the region with high curvature, and the smaller the curvature in <math display="inline"> Z</math> direction is, the higher the velocity is. Because the curvature of P type at the cell junction is close to 0, so the velocity at the junction is abnormally high, so the nutrient flow rate of P type stent will be faster, but the efficiency of osteogenic adhesion on the surface with high curvature in <math display="inline"> Z</math> direction will be lower. The osteogenic adhesion formed on both sides of the low curvature can not be converted into large pieces of bone between the crystal cells, so in the microstructure design of the porous scaffold, the high curvature in the <math display="inline"> Z</math> direction should not be used to form the through hole directly, but the cross of the cell structure should be used to form the through hole. The through hole formed by the D-shaped support due to structural reasons is not a <math display="inline"> Z</math>-direction through hole, but a 45°oblique through hole, and the surface has no curvature change. therefore, after constructing the boundary conditions shown in [[#img-1|Figure 1]](d), it is found that there is no outflow at the bottom, and the flow velocity is concentrated on both sides of the support. |
| − | [[ | + | <div id='img-4'></div> |
| − | Figure 4. CFD Velocity results with different | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"|[[File:4 upscayl 4x realesrgan-x4plus.png|centre|600x600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. CFD Velocity results with different cell structures | ||
| + | |} | ||
| − | Figure 5 shows the CFD flow pressure results for different crystal cell structures, where the flow pressure results are directly proportional to the flow velocity results. Both G-type and P-type scaffolds exhibit the formation of two flow domains within the scaffold, with significant differences in flow velocity and pressure drop between the two domains, particularly evident in the P-type scaffold. The D-type scaffold forms multiple flow domains. | + | [[#img-5|Figure 5]] shows the CFD flow pressure results for different crystal cell structures, where the flow pressure results are directly proportional to the flow velocity results. Both G-type and P-type scaffolds exhibit the formation of two flow domains within the scaffold, with significant differences in flow velocity and pressure drop between the two domains, particularly evident in the P-type scaffold. The D-type scaffold forms multiple flow domains. |
| − | [[ | + | <div id='img-5'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"|[[File:5 upscayl 4x realesrgan-x4plus.png|centre|600x600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. Results of CFD flow pressure with different cell structures | ||
| + | |} | ||
| − | |||
| − | == | + | ===3.2 Construction and finite element results of tibial segmental bone defect scaffold=== |
A hybrid scaffold structure was designed from a functional perspective. The finite element results mentioned above indicate stress concentration on the "tooth surface" of the D-type scaffold. Utilizing this phenomenon, it can be advantageous for the initial stability of the bone defect scaffold. The stress distribution on the same XY section of the P-type scaffold is uniform. Therefore, we assumed a composite bone scaffold, with the G-type scaffold as the main body. The D-type scaffold is integrated axially proximally to the scaffold, providing initial mechanical fit with its unique "tooth surface". The P-type bone scaffold is integrated axially distally to the scaffold to ensure a larger contact area at the bone/scaffold interface. | A hybrid scaffold structure was designed from a functional perspective. The finite element results mentioned above indicate stress concentration on the "tooth surface" of the D-type scaffold. Utilizing this phenomenon, it can be advantageous for the initial stability of the bone defect scaffold. The stress distribution on the same XY section of the P-type scaffold is uniform. Therefore, we assumed a composite bone scaffold, with the G-type scaffold as the main body. The D-type scaffold is integrated axially proximally to the scaffold, providing initial mechanical fit with its unique "tooth surface". The P-type bone scaffold is integrated axially distally to the scaffold to ensure a larger contact area at the bone/scaffold interface. | ||
| − | When constructing the mixed cell structure, when observing the G, D and P models [19-21], it is found that the function of the D type structure can be changed into the similar structure of the G P type under certain conditions. | + | When constructing the mixed cell structure, when observing the G, D and P models [19-21], it is found that the function of the D type structure can be changed into the similar structure of the G P type under certain conditions. When Z, X and Y are 0, respectively, the D structure becomes: |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \begin{align} F_D (x,y) & =\sin[X] \cos[Y] + \cos[X]\sin[Y]\\ | ||
| + | F_D (y,z) & =\sin[Y] \cos[Z] + \cos[Y]\sin[Z]\\ | ||
| + | F_D (x,z) & =\sin[X] \cos[Z] + \cos[X]\sin[Z]\end{align} | ||
| + | </math> | ||
| + | |} | ||
| + | |} | ||
| − | < | + | In this case, the <math display="inline">D </math> structure is similar to the G function to some extent. According to this phenomenon, we establish the <math display="inline"> D </math> function to rotate its <math display="inline"> x, y, z</math>, that is: |
| − | + | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \begin{align} | ||
| + | x\to & {\rm tran}[1], \,\, y\to {\rm tran}[2],\,\, z\to {\rm tran}[3]\\ | ||
| + | & {\rm tran} ={\rm EulerMatrix} \, \{x,y,z\} | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |} | ||
| + | |} | ||
| − | + | where EulerMatrix represents the rotation matrix Euler rotation angle, on this basis, another rotation under the current coordinate axis, that is, | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> {\displaystyle {\begin{aligned}x\to &{\rm {tran}}[[1]],\,\,y\to {\rm {tran}}[[2]], | ||
| − | + | \,\,z\to {\rm {tran}}[[3]]\\\end{aligned}}} | |
| − | + | ||
| − | |||
| − | + | </math> | |
| + | |} | ||
| + | |} | ||
| − | |||
| − | |||
| − | When the rotation returns the Z axis to its original position, the function becomes: | + | When the rotation returns the <math display="inline">Z </math> axis to its original position, the function becomes: |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \begin{align} F_{GDP} (x,y,z) = &\sin[AX+BY] \sin [BX-AY]\sin [Z]+\sin[BX-AY] | ||
| + | \cos[AX+BY]\cos[Z] + \cos [BX-AY]\\ | ||
| + | &\sin[AX+BY]\cos[Z]+ \cos [BX-AY]\cos[AX+BY]\sin[Z]=C | ||
| + | \end{align} | ||
| + | </math> | ||
| + | |} | ||
| + | |} | ||
| − | </ | + | where <math display="inline"> A </math> and <math display="inline"> B </math> are constants and <math display="inline">A^2 +B^2=1</math>. As shown in [[#img-6|Figure 6]], the orthographic, upper, and lower diagrams of the constructed function are presented, respectively. The upper surface is similar to the G structure, the middle surface is similar to the D structure, and the lower surface is similar to the P structure. Therefore, the model of this mixed microstructure is defined as the GDP scaffold. |
| − | + | <div id='img-6'></div> | |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Zhang_149466663-picture- 4.svg|center|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 6'''. Front view, top view, bottom view of the GDP Scaffold | ||
| + | |} | ||
| − | |||
| − | [[ | + | [[#img-7|Figure 7]] displays the finite element analysis results of the GDP scaffold. The GDP scaffold meets the preliminary design requirements for tibial scaffold. The proximal interface exhibits a tooth-like structure to provide initial mechanical bonding, while the distal interface offers a larger bone contact area, thus confirming the initial assumption. |
| − | + | ||
| − | </div> | + | <div id='img-7'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Zhang_149466663-picture- 5.svg|center|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 7'''. Finite element analysis results of the GDP scaffold | ||
| + | |} | ||
| − | |||
| − | |||
| − | < | + | [[#img-8|Figure 8]] shows the fluid analysis results of the GDP pore scaffold. There is a greater difference in flow velocity between the center of the channels and the surrounding areas. In the <math display="inline"> Z </math>-direction, the fluid exhibits a "gourd" shape, and it is observed that the middle flow velocity of the GDP pore scaffold is faster. This is mainly because the design parameters of the GDP pore scaffold include the P structure, where the sides of the P structure are in a closed state, resulting in larger diameters of the central channels. Additionally, the curvature of the triply periodic minimal surface (TPMS) around the channels in the peripheral area of the flow is lower due to the presence of the P structure, and the connectivity of the P structure is not as strong as that of the G structure. Therefore, owing to the presence of the G structure elements, the scaffold exhibits higher flow velocity regardless of whether it is viewed from the <math display="inline"> Y </math>-axis or <math display="inline"> Z </math>-axis in the <math display="inline"> YZ </math> direction. Since the flow velocity on the outer side of the scaffold is lower, bone ingrowth is more likely to occur on the inner walls of the holes on the outer side. This further confirms that the GDP pore scaffold is more suitable for large segmental defects of the tibial diaphysis. |
| − | + | ||
| − | </div> | + | <div id='img-8'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Zhang_149466663-picture- 6.svg|center|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 8'''. CFD finite element analysis results of the GDP scaffold | ||
| + | |} | ||
| − | |||
| − | + | [[#img-9|Figure 9]] depicts the stress conduction process of the GDP scaffold. The stress variations of the bone and scaffold at the proximal end during the first, second, and third elastic stages are relatively close, indicating a good fit between the proximal interface bone and scaffold. After the third elastic deformation, the stress values within the bone decrease and gradually approach those of the distal scaffold. The Mises stress transfer process in the distal bone of the GDP scaffold exhibits a more stable range of variation. After the third elastic deformation, the Mises stress of the scaffold begins to stabilize, while the proximal bone continues to undergo 8 deformations after the third elastic deformation before reaching stability, due to its integration with the scaffold. Therefore, the stress conduction process of the GDP scaffold demonstrates optimal mechanical performance. The fitting mechanism at the proximal bone interface provides assurance for later mechanical stability, while the stable stress changes in the distal bone provide a platform for further bone ingrowth into the scaffold. | |
| − | [[Image:Draft_Zhang_149466663-picture- | + | <div id='img-9'></div> |
| − | Figure | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Zhang_149466663-picture- 7.svg|center|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 9'''. Stress conduction process of the GDP scaffold | ||
| + | |} | ||
| − | |||
| − | + | As shown in [[#img-10|Figure 10]], the calculated elastic modulus and compressive strength of the support are 7.38Gpa and 326Mpa, and there is no excess deviation of the support during the compression process. | |
| − | Figure | + | |
| − | </div> | + | <div id='img-10'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Zhang_149466663-picture- 8.svg|center|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 10'''. 3D printing of GDP bracket and its mechanical properties | ||
| + | |} | ||
| + | |||
| + | ==4. Conclusion== | ||
| − | + | In this study, the microstructure design of tibial segmental implant scaffolds was the focus of research. Finite element analysis was initially conducted on three scaffold structures. The results showed that the structural performance of the G-type scaffold was more stable, with a uniform distribution of Mises stress. Within the microscale curvature range of 0-1, the Mises stress decreased as the curvature increased. When the curvature was 1, the local Mises stress value was <math display="inline">0.07\times 10^8</math> N/m<math display="inline">^2</math>. The G-type scaffold had the lowest flow velocity compared to the P and D-type scaffolds, but it exhibited better fluidity, making it suitable for inward bone tissue ingrowth. Based on these findings and considering the mechanical and biological requirements of tibial implant scaffolds, a composite scaffold structure, termed GDP, was constructed. Through finite element analysis and discussion, it was concluded that the GDP scaffold meets the design requirements of the tibial diaphysis. | |
| − | + | ||
| − | In this study, the microstructure design of tibial segmental implant scaffolds was the focus of research. Finite element analysis was initially conducted on three scaffold structures. The results showed that the structural performance of the G-type scaffold was more stable, with a uniform distribution of Mises stress. Within the microscale curvature range of 0-1, the Mises stress decreased as the curvature increased. When the curvature was 1, the local Mises stress value was 0. | + | |
| − | =Acknowledgments= | + | ==Acknowledgments== |
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: National Natural Science Foundation of China(No.52165026),Open Subjects of State Key Laboratory of Mechanical Manufacturing Systems Engineering, Xi'an Jiaotong University (No.sklms2021011) for their support to this research. | The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: National Natural Science Foundation of China(No.52165026),Open Subjects of State Key Laboratory of Mechanical Manufacturing Systems Engineering, Xi'an Jiaotong University (No.sklms2021011) for their support to this research. | ||
| − | == | + | ==References== |
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
| − | [1] Li L.,Wang P.,Liang H.X.,Jin J.,Zhang Y.B.,Shi J.P.,Zhang Y.,He S.Y.,Mao H.L.,Xue B.,Lai J.C.,Zhu L.,Jiang Q. Design of a Haversian system-like gradient porous scaffold based on triply periodic minimal surfaces for promoting bone regeneration. Journal of | + | [1] Li L., Wang P., Liang H.X., Jin J., Zhang Y.B., Shi J.P., Zhang Y., He S.Y., Mao H.L., Xue B., Lai J.C., Zhu L., Jiang Q. Design of a Haversian system-like gradient porous scaffold based on triply periodic minimal surfaces for promoting bone regeneration. Journal of Advanced Research, 54:89-104, 2023. |
| − | [2] Jin H., Zhuo Y., Sun Y., Fu H., Han Z. Microstructure design and degradation performance in vitro of three-dimensional printed bioscaffold for bone tissue engineering. Advances in Mechanical Engineering, 11(10) | + | [2] Jin H., Zhuo Y., Sun Y., Fu H., Han Z. Microstructure design and degradation performance in vitro of three-dimensional printed bioscaffold for bone tissue engineering. Advances in Mechanical Engineering, 11(10), 2019. |
| − | [3] Pei H.L.,Fan Q.W.,Ma D., Yang Y. F. Design and | + | [3] Pei H.L., Fan Q.W., Ma D., Yang Y.F. Design and geometric characterization of three-dimensional gradient heterogeneous bone tissue structures based on Voronoi. Science of Advanced Materials, 15(4):561-570, 2023. |
| − | [4] Gryko A.,Prochor P.,Sajewicz E. Finite element analysis of the influence of porosity and pore geometry on mechanical properties of orthopaedic scaffolds. Journal of the Mechanical Behavior of Biomedical Materials, 132, 105275, 2022. | + | [4] Gryko A., Prochor P., Sajewicz E. Finite element analysis of the influence of porosity and pore geometry on mechanical properties of orthopaedic scaffolds. Journal of the Mechanical Behavior of Biomedical Materials, 132, 105275, 2022. |
| − | [5] Peng W.,Liu Y.,Wang C. Definition, measurement, and function of pore structure dimensions of bioengineered porous bone tissue materials based on additive manufacturing: A review. Frontiers in Bioengineering and Biotechnology, 10, 1081548, 2023. | + | [5] Peng W., Liu Y., Wang C. Definition, measurement, and function of pore structure dimensions of bioengineered porous bone tissue materials based on additive manufacturing: A review. Frontiers in Bioengineering and Biotechnology, 10, 1081548, 2023. |
| − | [6] Lv Y.,Liu G.,Wang B., Tang Y.,Lin Z.,Liu J.,Wang L. Pore strategy design of a novel NiTi-Nb biomedical porous scaffold based on a triply periodic minimal surface. Frontiers in Bioengineering and Biotechnology, 10, 910475, 2022. | + | [6] Lv Y., Liu G., Wang B., Tang Y., Lin Z., Liu J., Wang L. Pore strategy design of a novel NiTi-Nb biomedical porous scaffold based on a triply periodic minimal surface. Frontiers in Bioengineering and Biotechnology, 10, 910475, 2022. |
| − | [7] Alkentar R.,Kladovasilakis N.,Tzetzis D.,Mankovits T. Effects of | + | [7] Alkentar R., Kladovasilakis N., Tzetzis D., Mankovits T. Effects of pore size parameters of titanium additively manufactured lattice structures on the osseointegration process in orthopedic applications: A comprehensive review. Crystals, 13(1), 113, 2023. |
| − | [8] Yao Y.T.,Yang Y.,Ye Q.,Cao S.S.,Zhang X.P., Zhao,K.,Jian Y. Effects of pore size and porosity on cytocompatibility and osteogenic differentiation of porous titanium. Journal of Materials Science: Materials in Medicine, 32(6), 72, 2021. | + | [8] Yao Y.T., Yang Y., Ye Q., Cao S.S., Zhang X.P., Zhao, K., Jian Y. Effects of pore size and porosity on cytocompatibility and osteogenic differentiation of porous titanium. Journal of Materials Science: Materials in Medicine, 32(6), 72, 2021. |
| − | [9] Bisht B.,Hope A.,Mukherjee A.,Paul M.K. Advances in the fabrication of scaffold and 3D printing of biomimetic bone graft. Annals of | + | [9] Bisht B., Hope A., Mukherjee A., Paul M.K. Advances in the fabrication of scaffold and 3D printing of biomimetic bone graft. Annals of Biomedical Engineering, 49(4):1128-1150, 2021. |
| − | [10] Al-Barqawi M.O.,Church B.,Thevamaran M.,Thoma D.J.,Rahman A. Design and | + | [10] Al-Barqawi M.O., Church B., Thevamaran M., Thoma D.J., Rahman A. Design and validation of additively manufactured metallic cellular scaffold structures for bone tissue engineering. Materials, 15(9), 3310, 2022. |
| − | [11] Li L.,Li J.,Zou Q.,Zuo Y.,Lin L.,Cai B.,Li Y. Lotus root and osteons‐inspired channel structural scaffold mediate cell biomineralization and vascularized bone tissue regeneration. Journal of Biomedical Materials Research Part B: Applied Biomaterials, 110(5) | + | [11] Li L., Li J., Zou Q., Zuo Y., Lin L., Cai B., Li Y. Lotus root and osteons‐inspired channel structural scaffold mediate cell biomineralization and vascularized bone tissue regeneration. Journal of Biomedical Materials Research Part B: Applied Biomaterials, 110(5):1178-1191, 2022. |
| − | [12] Zhang J.,Chen X.,Sun Y.,Yang J.,Chen R., Xong Y.,Bai L. Design of a biomimetic graded TPMS scaffold with quantitatively adjustable pore size. Materials & Design, 218, 110665, 2022. | + | [12] Zhang J., Chen X., Sun Y., Yang J., Chen R., Xong Y., Bai L. Design of a biomimetic graded TPMS scaffold with quantitatively adjustable pore size. Materials & Design, 218, 110665, 2022. |
| − | [13] Chen X.,Gao C.Y.,Chu X.Y.,Zheng C.Y.,Luan Y.Y.,He X.,Zhang D.L. VEGF-loaded heparinised gelatine-hydroxyapatite-tricalcium phosphate scaffold accelerates bone regeneration via enhancing osteogenesis-angiogenesis coupling. Frontiers in Bioengineering and Biotechnology, 10, 915181, 2022. | + | [13] Chen X., Gao C.Y., Chu X.Y., Zheng C.Y., Luan Y.Y., He X., Zhang D.L. VEGF-loaded heparinised gelatine-hydroxyapatite-tricalcium phosphate scaffold accelerates bone regeneration via enhancing osteogenesis-angiogenesis coupling. Frontiers in Bioengineering and Biotechnology, 10, 915181, 2022. |
| − | [14] Zhang Y.,Wang P., | + | [14] Zhang Y., Wang P., Jin J.Y., Li L., He S.Y., Zhou P., Wen C. In silico and in vivo studies of the effect of surface curvature on the osteoconduction of porous scaffolds. Biotechnology and Bioengineering, 119(2):591-604, 2022. |
| − | [15] Nauman E.A.,Fong K.E.,Keaveny T.M. Dependence of intertrabecular permeability on flow direction and anatomic site. Annals of | + | [15] Nauman E.A., Fong K.E., Keaveny T.M. Dependence of intertrabecular permeability on flow direction and anatomic site. Annals of Biomedical Engineering, 27:517-524, 1999. |
| − | [16] Ali D.,Sen S. Finite element analysis of mechanical behavior, permeability and fluid induced wall shear stress of high porosity scaffolds with gyroid and lattice-based architectures. Journal of the | + | [16] Ali D., Sen S. Finite element analysis of mechanical behavior, permeability and fluid induced wall shear stress of high porosity scaffolds with gyroid and lattice-based architectures. Journal of the Mechanical Behavior of Biomedical Materials, 75:262-270, 2017. |
| − | [17] Ma S.,Tang Q., Han X., Feng Q., Song J., Setchi R., Liu Y., Liu Y., Goulas A., Engstrom D.S., Tse Y.Y., Zhen N. Manufacturability, mechanical properties, mass-transport properties and biocompatibility of TPMS scaffolds fabricated by selective laser melting. Materials & Design, 195, 2020, 109034. | + | [17] Ma S., Tang Q., Han X., Feng Q., Song J., Setchi R., Liu Y., Liu Y., Goulas A., Engstrom D.S., Tse Y.Y., Zhen N. Manufacturability, mechanical properties, mass-transport properties and biocompatibility of TPMS scaffolds fabricated by selective laser melting. Materials & Design, 195, 2020, 109034. |
| − | [18] Pires T.,Santos J.,Ruben R.B.,Gouveia B.P.,Castro A.P.,Fernandes P. R. Numerical-experimental analysis of the permeability-porosity relationship in triply periodic minimal surfaces scaffolds. Journal of Biomechanics, 117, 110263, 2021. | + | [18] Pires T., Santos J., Ruben R.B., Gouveia B.P., Castro A.P., Fernandes P.R. Numerical-experimental analysis of the permeability-porosity relationship in triply periodic minimal surfaces scaffolds. Journal of Biomechanics, 117, 110263, 2021. |
| − | [19] Zhang Z.,Zhang H.,Li Y.,Duan M.,Qin S. A | + | [19] Zhang Z., Zhang H., Li Y., Duan M., Qin S. A modeling method of graded porous scaffold based on triply periodic minimal surfaces. Mathematical Problems in Engineering, 2022:1-18, 7129482, 2022. |
| − | [20] Günther F.,Pilz S.,Hirsch F.,Wagner M.,Kästner M.,Gebert A.,Zimmermann M. Shape optimization of additively manufactured lattices based on triply periodic minimal surfaces. Additive Manufacturing, 73, 103659, 2023. | + | [20] Günther F., Pilz S., Hirsch F., Wagner M., Kästner M., Gebert A., Zimmermann M. Shape optimization of additively manufactured lattices based on triply periodic minimal surfaces. Additive Manufacturing, 73, 103659, 2023. |
| − | [21] Li Y.,Guo S. Triply periodic minimal surface using a modified Allen–Cahn equation. Applied Mathematics and Computation, 295 | + | [21] Li Y.,Guo S. Triply periodic minimal surface using a modified Allen–Cahn equation. Applied Mathematics and Computation, 295:84-94, 2017. |
Latest revision as of 16:18, 13 November 2024
Abstract
Segmental tibial bone defects caused by bone tumors, open fractures, and non-union of large bone segments are one of the challenges in orthopedic diseases. In existing research on load-bearing implants, it has been found that stress mismatch at the bone/implant interface leading to implant loosening and biological instability due to limited depth of bone ingrowth are key obstacles to the development of tibial implants. Therefore, in this study, the mechanical properties and internal fluid properties of three existing bone scaffold microstructures were investigated by finite element analysis. Based on the requirements of tibial segmental bone defect scaffolds, a composite scaffold with a GDP pore structure is prepared. The stress transmission mechanism of its microstructure model and the influence of internal scaffold microstructure on the transport of nutrients are studied. The newly proposed GDP pore structure is suitable for segmental bone defects similar to the tibial diaphysis.
Keywords: Triply periodic minimal surface (TPMS), stress transmission, curvature, bone ingrowth
1. Introduction
In recent years, research in tibial implant tissue engineering has primarily focused on the structural and functional regeneration of target tissues. Three-dimensional scaffolds with appropriate pore structures, geometric shapes, and porosity play a crucial role in achieving this goal [1-3]. The pore structure of the implant is a direct determinant of the scaffold's mechanical performance, with key parameters including pore size [4], pore connectivity, uniform distribution, pore shape, and specific surface area [5,6]. Regions with high connectivity provide sufficient space for the migration, proliferation, and differentiation of bone cells, while regions with low connectivity provide adequate mechanical performance for bone implants [7,8]. From a biomimetic perspective, the purpose of designing porous metals via 3D printing is to fully achieve a structure, mechanical properties, and biological effects identical to the trabecular structure in natural bone [9]. However, this presents significant challenges, primarily due to the requirement that the metal used should approximate bone in mechanical properties, and the basic units, pore size, and porosity of the pores should be similar to natural bone [10]. Additionally, the material design must satisfy mechanical anisotropy. Therefore, biomimetic bone scaffolds are often designed based on functional biomimicry of bone.
Excellent bone defect scaffolds not only need to provide good initial mechanical stability postoperatively, but also require biological stability in the later stages. Vascularization within the porous structure and the speed of bone regeneration are key factors in achieving biological stability [11]. Therefore, scaffolds with good material transport properties are also essential for osteogenesis [12]. After implantation of the scaffold into the bone defect area, blood flow carries nutrients, oxygen, and cell-activating factors into the interior of the scaffold, which are important for early vascular regeneration within the scaffold [13]. Appropriate pore size and pore structure are necessary conditions for osteoblast adhesion within the porous scaffold, and osteogenesis and vascularization often occur in concave areas within the porous scaffold [14]. Thus, larger axial curvature regions are needed to provide more space for osteogenesis and vascularization.
Therefore, in this study, starting from the structural design of tibial segmental bone defect scaffolds, an analysis was conducted on the mechanical properties and material transport characteristics of different crystal cell structures of TPMS. Based on the analysis results, implicit function parameters were redesigned, and scaffolds were constructed. The stress transmission process between bone and scaffold was analyzed, ultimately determining the microstructure of the novel scaffold, providing reference for the design of tibial segmental bone defect scaffolds.
2. Methods
In this study, three types of TPMS structures were initially constructed, namely: SchwartzD (D), Gyroid (G), and SchwartzP (P), to analyze the stress-strain patterns and scaffold material transport properties of different crystal cell structures. Based on the actual bone morphology of the tibial diaphysis, a hybrid crystal cell structure scaffold was constructed. Figure 1(a) illustrates the three TPMS microstructure functions. To express the variation of curvature along the scaffold axis. Figure 1(b) depicts the curvature expression of the G-type scaffold in the YZ section. Figures 1(c) and (d) represent the boundary conditions used in this study, while Figure 1(e) illustrates the experimental apparatus designed for permeability testing in this study.
| Figure 1. (a) Schematic representation and mathematical model implicit function expressions of P, D, and G models. (b) Representation and curvature calculation of the YZ interface. (c) Stress conduction boundary conditions. (d) Fluid flow boundary conditions. (e) Schematic diagram of the permeability experimental apparatus |
2.1 Boundary conditions for bone/implant stress conduction numerical analysis
As shown in Figure 1(c), the boundary conditions for stress conduction are as follows. The material properties of the implant are defined as TC4 titanium alloy. The proximal and distal bones are defined as normal bone tissue. The mesh contact between the implant and the scaffold interface is defined as rough contact. No constraints are applied on both sides of the scaffold/implant. The upper boundary of the proximal end is defined as a compressive load of 100N. The lower boundary of the distal end is defined as a fixed constraint.
2.2 Boundary conditions for permeability analysis of support structures
The permeability needs to be analyzed in the corresponding fluid domain. As far as the bone scaffold is concerned, the pore area is the required fluid domain. According to the literature report [15], the permeability range of human bone is m2 - m2. In the process of CFD analysis, the Navier-Stokes equation of incompressible steady laminar flow is described calculate [16]:
|
|
(1) |
where, is the fluid density; the fluid velocity; the time; the dynamic viscosity of fluid; the del operator; the pressure; and the gravity or centrifugal force.
The boundary conditions applied for CFD analysis are shown in Figure 1(d), and the region with is considered as the fluid model. The inflow surface (Inlet), outflow surface (Outlet), solid wall 1 (Wall1), and solid wall 2 (Wall2) are shown in the figure. The liquid flowing through the pore area of the scaffold is assumed to be capillary blood, with an inlet flow rate of 0.0005m/s applied on the inlet surface and 0 outlet pressure applied on the outlet surface. Wall1 and Wall2 are defined as non sliding wall surfaces, with a fluid viscosity of 4.2mPa·s. The relevant settings are summarized in Table 1.
| Permeability calculation | |
|---|---|
| Analogy procedure | Single-phase flow in direction Z |
| Metallic liquid | Capillary blood (incompressible: viscosity 0.0042kg/ms, density 1050kg/m3) |
| Size of mesh opening | Octahedral unit, size approx:0.0002mm (0.002% of structural size) |
| Boundary conditions | IN:Inlet velocity 0.0005m/s |
| OUT:outlet pressure 0Pa | |
| Output parameter | Inlet volume flow, inlet pressure |
Combined with Darcy's law, in order to measure the permeability of the stent, Figure 1(e) is a permeability experimental device. The water from the water pump gets the pressure difference between the two sides of the bracket through the pressure difference sensor, and the bracket is wrapped in the sample warehouse made of heat-shrinkable pipe to ensure the close cooperation of the bracket and prevent the liquid from leaking from both sides. The Flowmeter is used to control the flow into the sample and finally the liquid flows out. Repeat the measurement five times for each sample.
3. Construction of stent for segmental bone defect of tibia and analysis of finite element results
3.1 Finite element results and discussion of different cell structures
3.1.1 Analysis of stress and strain results of different cell structures
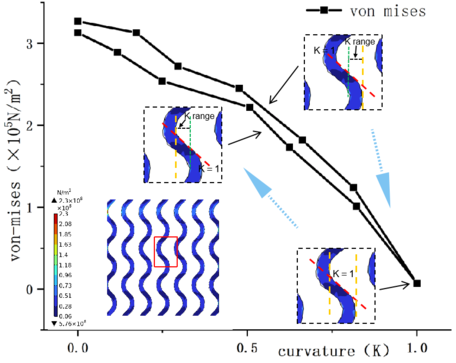
As shown in Figure 2, the minimum equivalent stress is G-type stent and the maximum is D-type stent; the minimum displacement on the main section of YZ is G-type stent and the maximum is P-type stent; the minimum equivalent stress is G and the maximum is P-type stent. As shown in Table 2, the stress distribution of G-type support is more uniform and the axial displacement is lower under the same load. The stress of P-type stent is concentrated on the surface, and the stress distribution of P-type stent is more uniform at the same horizontal position, but the axial displacement is the largest. From the mises stress distribution of YZ cross section, it is known that the stress value of G-type single crystal is the lowest at the curvature = 1 and the maximum at the curvature of 0. Figure 3 shows the mises stress values of G-type stents with different curvature changes in the single cell.
| Figure 2. FEA results of scaffolds with different cell structures |
| Type | Mises (N/m2) | Disp (mm) | YZ-mises (N/m2) | YZ-Disp (mm) |
|---|---|---|---|---|
| G | ||||
| D | ||||
| P |
| Figure 3. Mises stress values of different curvature changes in the single cell of G-type stents |
3.1.2 Analysis of CFD results with different cell structures
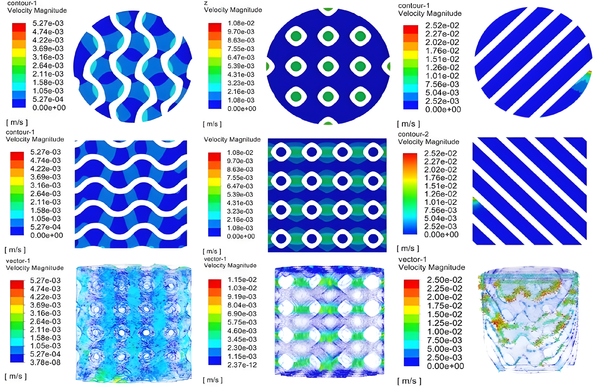
Figure 4 shows the results of CFD flow velocity with different cell structures. The maximum flow velocity of G-type stent is smaller than that of other stents, which is due to the good connectivity of G-type and the formation of axial through-hole is smaller than the other two types. It can be seen that the flow velocity in the center of the channel is significantly higher than that in the surrounding area, which can transport nutrients to deeper pores, which is conducive to cell migration, proliferation and differentiation [17,18]. Because the flow velocity in the center is higher than that on both sides, the nutrients in the center of the channel are squeezed to the surrounding area, and the curvature of the surrounding area is large. Osteoblasts adhere to the surrounding area for osteogenesis and differentiation, and P-type scaffolds form external flow field and internal flow field. The velocity of the external flow field is obviously lower than that of the internal flow field. in the internal flow field, the velocity in the region with low curvature is obviously higher than that in the region with high curvature, and the smaller the curvature in direction is, the higher the velocity is. Because the curvature of P type at the cell junction is close to 0, so the velocity at the junction is abnormally high, so the nutrient flow rate of P type stent will be faster, but the efficiency of osteogenic adhesion on the surface with high curvature in direction will be lower. The osteogenic adhesion formed on both sides of the low curvature can not be converted into large pieces of bone between the crystal cells, so in the microstructure design of the porous scaffold, the high curvature in the direction should not be used to form the through hole directly, but the cross of the cell structure should be used to form the through hole. The through hole formed by the D-shaped support due to structural reasons is not a -direction through hole, but a 45°oblique through hole, and the surface has no curvature change. therefore, after constructing the boundary conditions shown in Figure 1(d), it is found that there is no outflow at the bottom, and the flow velocity is concentrated on both sides of the support.
| Figure 4. CFD Velocity results with different cell structures |
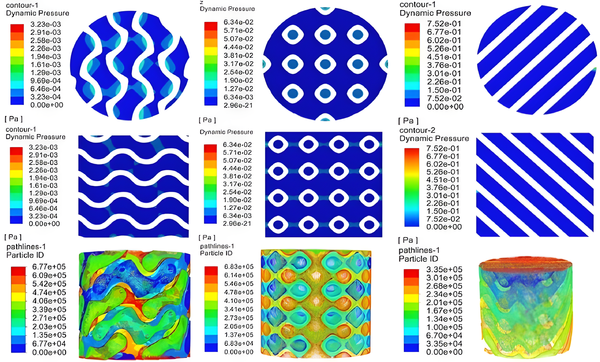
Figure 5 shows the CFD flow pressure results for different crystal cell structures, where the flow pressure results are directly proportional to the flow velocity results. Both G-type and P-type scaffolds exhibit the formation of two flow domains within the scaffold, with significant differences in flow velocity and pressure drop between the two domains, particularly evident in the P-type scaffold. The D-type scaffold forms multiple flow domains.
| Figure 5. Results of CFD flow pressure with different cell structures |
3.2 Construction and finite element results of tibial segmental bone defect scaffold
A hybrid scaffold structure was designed from a functional perspective. The finite element results mentioned above indicate stress concentration on the "tooth surface" of the D-type scaffold. Utilizing this phenomenon, it can be advantageous for the initial stability of the bone defect scaffold. The stress distribution on the same XY section of the P-type scaffold is uniform. Therefore, we assumed a composite bone scaffold, with the G-type scaffold as the main body. The D-type scaffold is integrated axially proximally to the scaffold, providing initial mechanical fit with its unique "tooth surface". The P-type bone scaffold is integrated axially distally to the scaffold to ensure a larger contact area at the bone/scaffold interface.
When constructing the mixed cell structure, when observing the G, D and P models [19-21], it is found that the function of the D type structure can be changed into the similar structure of the G P type under certain conditions. When Z, X and Y are 0, respectively, the D structure becomes:
|
|
In this case, the structure is similar to the G function to some extent. According to this phenomenon, we establish the function to rotate its , that is:
|
|
where EulerMatrix represents the rotation matrix Euler rotation angle, on this basis, another rotation under the current coordinate axis, that is,
|
|
When the rotation returns the axis to its original position, the function becomes:
|
|
where and are constants and . As shown in Figure 6, the orthographic, upper, and lower diagrams of the constructed function are presented, respectively. The upper surface is similar to the G structure, the middle surface is similar to the D structure, and the lower surface is similar to the P structure. Therefore, the model of this mixed microstructure is defined as the GDP scaffold.
| Figure 6. Front view, top view, bottom view of the GDP Scaffold |
Figure 7 displays the finite element analysis results of the GDP scaffold. The GDP scaffold meets the preliminary design requirements for tibial scaffold. The proximal interface exhibits a tooth-like structure to provide initial mechanical bonding, while the distal interface offers a larger bone contact area, thus confirming the initial assumption.
| Figure 7. Finite element analysis results of the GDP scaffold |
Figure 8 shows the fluid analysis results of the GDP pore scaffold. There is a greater difference in flow velocity between the center of the channels and the surrounding areas. In the -direction, the fluid exhibits a "gourd" shape, and it is observed that the middle flow velocity of the GDP pore scaffold is faster. This is mainly because the design parameters of the GDP pore scaffold include the P structure, where the sides of the P structure are in a closed state, resulting in larger diameters of the central channels. Additionally, the curvature of the triply periodic minimal surface (TPMS) around the channels in the peripheral area of the flow is lower due to the presence of the P structure, and the connectivity of the P structure is not as strong as that of the G structure. Therefore, owing to the presence of the G structure elements, the scaffold exhibits higher flow velocity regardless of whether it is viewed from the -axis or -axis in the direction. Since the flow velocity on the outer side of the scaffold is lower, bone ingrowth is more likely to occur on the inner walls of the holes on the outer side. This further confirms that the GDP pore scaffold is more suitable for large segmental defects of the tibial diaphysis.
| Figure 8. CFD finite element analysis results of the GDP scaffold |
Figure 9 depicts the stress conduction process of the GDP scaffold. The stress variations of the bone and scaffold at the proximal end during the first, second, and third elastic stages are relatively close, indicating a good fit between the proximal interface bone and scaffold. After the third elastic deformation, the stress values within the bone decrease and gradually approach those of the distal scaffold. The Mises stress transfer process in the distal bone of the GDP scaffold exhibits a more stable range of variation. After the third elastic deformation, the Mises stress of the scaffold begins to stabilize, while the proximal bone continues to undergo 8 deformations after the third elastic deformation before reaching stability, due to its integration with the scaffold. Therefore, the stress conduction process of the GDP scaffold demonstrates optimal mechanical performance. The fitting mechanism at the proximal bone interface provides assurance for later mechanical stability, while the stable stress changes in the distal bone provide a platform for further bone ingrowth into the scaffold.
| Figure 9. Stress conduction process of the GDP scaffold |
As shown in Figure 10, the calculated elastic modulus and compressive strength of the support are 7.38Gpa and 326Mpa, and there is no excess deviation of the support during the compression process.
| Figure 10. 3D printing of GDP bracket and its mechanical properties |
4. Conclusion
In this study, the microstructure design of tibial segmental implant scaffolds was the focus of research. Finite element analysis was initially conducted on three scaffold structures. The results showed that the structural performance of the G-type scaffold was more stable, with a uniform distribution of Mises stress. Within the microscale curvature range of 0-1, the Mises stress decreased as the curvature increased. When the curvature was 1, the local Mises stress value was N/m. The G-type scaffold had the lowest flow velocity compared to the P and D-type scaffolds, but it exhibited better fluidity, making it suitable for inward bone tissue ingrowth. Based on these findings and considering the mechanical and biological requirements of tibial implant scaffolds, a composite scaffold structure, termed GDP, was constructed. Through finite element analysis and discussion, it was concluded that the GDP scaffold meets the design requirements of the tibial diaphysis.
Acknowledgments
The author(s) disclosed receipt of the following financial support for the research, authorship, and/or publication of this article: National Natural Science Foundation of China(No.52165026),Open Subjects of State Key Laboratory of Mechanical Manufacturing Systems Engineering, Xi'an Jiaotong University (No.sklms2021011) for their support to this research.
References
[1] Li L., Wang P., Liang H.X., Jin J., Zhang Y.B., Shi J.P., Zhang Y., He S.Y., Mao H.L., Xue B., Lai J.C., Zhu L., Jiang Q. Design of a Haversian system-like gradient porous scaffold based on triply periodic minimal surfaces for promoting bone regeneration. Journal of Advanced Research, 54:89-104, 2023.
[2] Jin H., Zhuo Y., Sun Y., Fu H., Han Z. Microstructure design and degradation performance in vitro of three-dimensional printed bioscaffold for bone tissue engineering. Advances in Mechanical Engineering, 11(10), 2019.
[3] Pei H.L., Fan Q.W., Ma D., Yang Y.F. Design and geometric characterization of three-dimensional gradient heterogeneous bone tissue structures based on Voronoi. Science of Advanced Materials, 15(4):561-570, 2023.
[4] Gryko A., Prochor P., Sajewicz E. Finite element analysis of the influence of porosity and pore geometry on mechanical properties of orthopaedic scaffolds. Journal of the Mechanical Behavior of Biomedical Materials, 132, 105275, 2022.
[5] Peng W., Liu Y., Wang C. Definition, measurement, and function of pore structure dimensions of bioengineered porous bone tissue materials based on additive manufacturing: A review. Frontiers in Bioengineering and Biotechnology, 10, 1081548, 2023.
[6] Lv Y., Liu G., Wang B., Tang Y., Lin Z., Liu J., Wang L. Pore strategy design of a novel NiTi-Nb biomedical porous scaffold based on a triply periodic minimal surface. Frontiers in Bioengineering and Biotechnology, 10, 910475, 2022.
[7] Alkentar R., Kladovasilakis N., Tzetzis D., Mankovits T. Effects of pore size parameters of titanium additively manufactured lattice structures on the osseointegration process in orthopedic applications: A comprehensive review. Crystals, 13(1), 113, 2023.
[8] Yao Y.T., Yang Y., Ye Q., Cao S.S., Zhang X.P., Zhao, K., Jian Y. Effects of pore size and porosity on cytocompatibility and osteogenic differentiation of porous titanium. Journal of Materials Science: Materials in Medicine, 32(6), 72, 2021.
[9] Bisht B., Hope A., Mukherjee A., Paul M.K. Advances in the fabrication of scaffold and 3D printing of biomimetic bone graft. Annals of Biomedical Engineering, 49(4):1128-1150, 2021.
[10] Al-Barqawi M.O., Church B., Thevamaran M., Thoma D.J., Rahman A. Design and validation of additively manufactured metallic cellular scaffold structures for bone tissue engineering. Materials, 15(9), 3310, 2022.
[11] Li L., Li J., Zou Q., Zuo Y., Lin L., Cai B., Li Y. Lotus root and osteons‐inspired channel structural scaffold mediate cell biomineralization and vascularized bone tissue regeneration. Journal of Biomedical Materials Research Part B: Applied Biomaterials, 110(5):1178-1191, 2022.
[12] Zhang J., Chen X., Sun Y., Yang J., Chen R., Xong Y., Bai L. Design of a biomimetic graded TPMS scaffold with quantitatively adjustable pore size. Materials & Design, 218, 110665, 2022.
[13] Chen X., Gao C.Y., Chu X.Y., Zheng C.Y., Luan Y.Y., He X., Zhang D.L. VEGF-loaded heparinised gelatine-hydroxyapatite-tricalcium phosphate scaffold accelerates bone regeneration via enhancing osteogenesis-angiogenesis coupling. Frontiers in Bioengineering and Biotechnology, 10, 915181, 2022.
[14] Zhang Y., Wang P., Jin J.Y., Li L., He S.Y., Zhou P., Wen C. In silico and in vivo studies of the effect of surface curvature on the osteoconduction of porous scaffolds. Biotechnology and Bioengineering, 119(2):591-604, 2022.
[15] Nauman E.A., Fong K.E., Keaveny T.M. Dependence of intertrabecular permeability on flow direction and anatomic site. Annals of Biomedical Engineering, 27:517-524, 1999.
[16] Ali D., Sen S. Finite element analysis of mechanical behavior, permeability and fluid induced wall shear stress of high porosity scaffolds with gyroid and lattice-based architectures. Journal of the Mechanical Behavior of Biomedical Materials, 75:262-270, 2017.
[17] Ma S., Tang Q., Han X., Feng Q., Song J., Setchi R., Liu Y., Liu Y., Goulas A., Engstrom D.S., Tse Y.Y., Zhen N. Manufacturability, mechanical properties, mass-transport properties and biocompatibility of TPMS scaffolds fabricated by selective laser melting. Materials & Design, 195, 2020, 109034.
[18] Pires T., Santos J., Ruben R.B., Gouveia B.P., Castro A.P., Fernandes P.R. Numerical-experimental analysis of the permeability-porosity relationship in triply periodic minimal surfaces scaffolds. Journal of Biomechanics, 117, 110263, 2021.
[19] Zhang Z., Zhang H., Li Y., Duan M., Qin S. A modeling method of graded porous scaffold based on triply periodic minimal surfaces. Mathematical Problems in Engineering, 2022:1-18, 7129482, 2022.
[20] Günther F., Pilz S., Hirsch F., Wagner M., Kästner M., Gebert A., Zimmermann M. Shape optimization of additively manufactured lattices based on triply periodic minimal surfaces. Additive Manufacturing, 73, 103659, 2023.
[21] Li Y.,Guo S. Triply periodic minimal surface using a modified Allen–Cahn equation. Applied Mathematics and Computation, 295:84-94, 2017.Document information
Published on 14/06/24
Accepted on 24/05/24
Submitted on 16/05/24
Volume 40, Issue 2, 2024
DOI: 10.23967/j.rimni.2024.05.014
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?