| (25 intermediate revisions by the same user not shown) | |||
| Line 28: | Line 28: | ||
In a similar vein, Ma et al. [8] ventured into the realm of topology identification for fractional-order complex networks, employing a strategy of variable substitution control. By devising a response network predicated on this control mechanism and a concurrent parameter update law, they derived a set of criteria for achieving both topology identification and network synchronization, with numerical simulations serving as a testament to the method’s validity. Collectively, these scholarly endeavors within the domains of switching topology and fractional-order complex networks not only enrich theoretical discourse but also chart a definitive course for empirical inquiry. | In a similar vein, Ma et al. [8] ventured into the realm of topology identification for fractional-order complex networks, employing a strategy of variable substitution control. By devising a response network predicated on this control mechanism and a concurrent parameter update law, they derived a set of criteria for achieving both topology identification and network synchronization, with numerical simulations serving as a testament to the method’s validity. Collectively, these scholarly endeavors within the domains of switching topology and fractional-order complex networks not only enrich theoretical discourse but also chart a definitive course for empirical inquiry. | ||
| − | In the realm of global research on switching topology and fractional-order complex networks, Ding et al. [9] have probed the intricacies of complex modified projective synchronization (CMPS) and the parameter estimation within time-varying coupled fractional-order complex-valued dynamic networks (FOCDN). Their theoretical discourse posits that FOCDN, when faced with time-varying delays, can attain CMPS via adaptive controllers—a premise substantiated by two numerical exemplars within the complex-valued domain, thereby affirming the potency of the refined projection strategy for fractional-order complex networks. Concurrently, | + | In the realm of global research on switching topology and fractional-order complex networks, Ding et al. [9] have probed the intricacies of complex modified projective synchronization (CMPS) and the parameter estimation within time-varying coupled fractional-order complex-valued dynamic networks (FOCDN). Their theoretical discourse posits that FOCDN, when faced with time-varying delays, can attain CMPS via adaptive controllers—a premise substantiated by two numerical exemplars within the complex-valued domain, thereby affirming the potency of the refined projection strategy for fractional-order complex networks. Concurrently, Du et al. [10] have delved into the delay-dependent finite-time synchronization (FTS) criterion pertinent to a subset of fractional-order delay complex networks (FODCNs). By leveraging the Young inequality and the rules governing fractional-order derivatives of composite functions, they unveiled a novel delay-dependent fractional-order finite-time convergence principle (FOFTCP), wherein the stability duration is contingent upon the temporal delay. This newly minted FOFTCP, in concert with a meticulously crafted feedback controller, has yielded a fresh FTS criterion for FODCNs, the efficacy of which has been corroborated through two numerical demonstrations. In a parallel vein, Behinfaraz and Ghaemi [11] have embarked on an exploration of the identification and synchronization within fractional-order complex networks, characterized by switching topology and time-variant delays, through the lens of fuzzy methodologies. The dynamics of the network nodes, deemed chaotic, were instantiated via a circuit realization tailored to these time-delay fractional-order dynamics. Employing T-S fuzzy modeling, they introduced an innovative representational paradigm for fractional-order chaotic systems, with simulations and empirical outcomes underscoring the proposed method's performance. Selvaraj et al. [12] scrutinized the cluster synchronization and the mitigation of disturbances within fractional-order complex networks, beset by coupling delays, unknown uncertainties, and disturbances (UDs). A modified repetitive control (MRC) block was seamlessly integrated into a closed-loop feedback control circuit to tackle these challenges. Furthermore, they formulated a comprehensive suite of sufficient linear matrix inequality constraints to guarantee the system's cluster synchronization. The merits, practicability, and resilience of the MRC framework, predicated on UDE, were validated through two illustrative cases. This overview elucidates that international research endeavors in switching topology and fractional-order complex networks are markedly more focused than their domestic counterparts, thereby serving as a repository of valuable insights and benchmarks for domestic scholarly pursuits in these spheres. |
==2. Research content== | ==2. Research content== | ||
| Line 46: | Line 46: | ||
===2.3 Design of models and controllers=== | ===2.3 Design of models and controllers=== | ||
| − | + | First, in terms of model design, consider a Caputo fractional-order complex network with switching topology composed of multiple nodes. All communication topology can be designed as a finite set of undirected graphs, denoted as <math>\left\{G^1\left(V,\varepsilon^1,\xi^1\right),...,G^n\left(V,\varepsilon^n,\xi^n\right)\right\}</math>, where the first item in the set <math display="inline">(V)</math> is a collection of all network nodes, expressed as <math display="inline">V=v_1, v_2,v_3,\ldots ,v_n</math>, <math>\varepsilon^n</math> represents the set of undirected edges for the <math display="inline">n </math><sup>th</sup> topology, <math display="inline">\zeta^n</math> is the adjacency matrix for the <math display="inline"> n</math><sup>th</sup> topology graph, <math display="inline">n</math> being a natural number. For clarity, <math display="inline">G^n</math> be represented as <math display="inline">G^n (V, \varepsilon^n, \zeta^n)</math>. Also, represent the nodes <math display="inline">(v_i,v_j)</math> as the edges between nodes, and define the elements in the matrix <math display="inline">\zeta^n</math>. The equation is as follows: | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> a_{ij}^n \begin{cases}c_{ij},\quad i\neq j\,\text{just}\, \left(\nu_i,\nu_j\right)\in\varepsilon^n\\ 0,\quad \text{Other situations}\end{cases} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(1) | ||
| + | |} | ||
| − | + | where <math display="inline">c_{ij}</math> are positive numbers satisfying the relation <math display="inline">c_{ij} =c_{ij}, i,j=1,2, ..., n</math>. This gives the Laplace matrix of the topology graph. Then, <math display="inline">G^n (V, \varepsilon^n, \zeta^n)</math> is represented as the union graph of the topology, with the matrix <math display="inline">\zeta^n</math> serving as the adjacency matrix of the topology graph. The matrix elements <math display="inline">a^*_{ij}</math> satisfy the relation. The equation is as follows: | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> a_{ij}^*=\max_{n\in(1,2,3,...,n)}a_{ij}^n,\quad i,j=1,2,3,...,n </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(2) | ||
| + | |} | ||
| − | |||
| − | < | + | From Eq. (2), the Laplace matrix of the topology graph is given, and a function is used to represent the corresponding switching signal. It is assumed that the network's communication topology will switch at time <math display="inline">t_s </math>, and when <math display="inline">t\in [t_s, t_{s+1}]</math>, the function will be equal to a certain number in the set. The mathematical model of the considered switching network is then given. The equation is as follows: |
| − | + | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> _{t_0}^C D_t^\alpha x_i(t)=f\left(x_i(t)\right)+\sum_{j=1,j\neq i}^na_{ij}^{\sigma(t)}\left[x_j(t)-x_i(t)\right]+u_i(t) </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(3) | ||
| + | |} | ||
| − | + | where <math>\sigma(t)</math> is a function; t0is the initial moment; <math>\alpha</math> is in the interval <math>0 -1</math>, and <math>\not = 0,1</math>, <math>x_i(t)</math> is the state vector of the node; <math>f</math> is a continuously differentiable nonlinear vector function; <math>u_i(t)</math> is the node control output. To satisfy the design of this model, the following assumptions are made: | |
| − | + | ''Assumption 1'': It is assumed that for the function <math>f(x)</math>, there exists a non-negative constant such that for any sets <math display="inline"> u </math> and <math display="inline"> v </math>, an inequality exists, represented as: | |
| − | + | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \left\|f\left(u\right)-f\left(\nu\right)\right\|\leq\eta\left\|u-\nu\right\| </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(4) | ||
| + | |} | ||
| − | |||
| − | + | ''Assumption 2'': Since at the switching moments, each individual time interval corresponding to a single switching moment shows a non-degenerate state, at the same time, <math>\lim_{n\to\infty}t_n=\infty </math>. | |
| − | < | + | ''Assumption 3'': There exists a positive number such that for any given moment, the network communication topology is jointly connected in that time range. That is, if the moment <math>t</math> is greater than the initial moment <math>t0+</math> a positive number, then within that time interval, the union graph of all communication topology will appear, and the union graph of this union with the∪ function <math>\sigma(t)</math> is in a connected state. |
| − | + | ||
| − | In the | + | In the architectural conception of controllers, the potentiality for topology switching warrants meticulous consideration. Such switching may precipitate the severance of connections or the forfeiture of linkages with proximate nodes. Under these circumstances, the impacted nodes are precluded from accessing a spectrum of state information from their adjacent counterparts, engendering impediments to the attainment of efficacious synchronicity control. To augment the orchestration of the control apparatus within complex networks and to attenuate the adverse ramifications of disconnections, a controller has been devised. This apparatus empowers network nodes to archive state information procured from neighboring nodes amid communication exchanges. Should a node find itself estranged from its neighbors and incapable of contemporaneous state recording, the repository of antecedent state data is rendered accessible. This historical data is then assimilated into the control schema, serving as a dynamic compensatory mechanism, thus enabling the regulation of nodal behavior. Ergo, a controller, endowed with an information storage mechanism strategy, has been engineered for the network model, encapsulated by the ensuing equation: |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> u_i(t)=\sum_{j=1,j\neq i}^n g_{ij}(t)[x_j(\tau_{ij}(t))-x_i(\tau_{ij}(t))] </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(5) | ||
| + | |} | ||
| − | + | where <math display="inline">i </math> is a natural number <math display="inline">i=1,2,3,...,n</math>; <math display="inline">\tau_{ij}</math> (<math display="inline">t</math> is the communication time closest to the current moment from the initial moment between two nodes); if <math display="inline">t \not = \tau_{ij}(t)</math>, it indicates that the edge between two nodes is disconnected at the current moment <math display="inline">t</math>, and the relationship between the initial moment <math display="inline">t_0</math>, the current moment <math display="inline">t</math>, and the nearest communication time <math display="inline">\tau_{ij}(t)</math>. The equation is represented as: | |
| − | = | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>t_0\leq\tau_{ij}(t)\leq t </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(6) | ||
| + | |} | ||
| − | |||
| − | + | Furthermore, according to the definition of <math display="inline">g_{ij}(t) </math> in Eq. (5), it is known that when disconnection occurs between two nodes, the controller will transmit the saved historical state information between the nodes to the network node. However, according to the definition of <math display="inline">g_{ij}(t) </math>, the controller only transmits the most recently saved state information between nodes, rather than transmitting all saved historical state information. Therefore, past saved node history state information can be considered as not having reference or application value. | |
| − | + | ==3. Results and discussion== | |
| − | + | ||
| − | + | ===3.1 Theoretical results=== | |
| − | + | First, regarding boundedness control of complex networks based on topology switching: Initially, all nodes in the network are set to a mean state, and a corresponding dynamical equation is given. The equation is as follows: | |
| − | + | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \overline{x}\big(t\big)=\frac1n\sum_{i=1}^nx_i\big(t\big) </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(7) | ||
| + | |} | ||
| − | |||
| − | |||
| − | Assuming the three assumptions mentioned earlier are valid, the synchronization error will exhibit a bounded final state and will approach the interior of the set asymptotically over time. This proves the related inequality to be true. A Lyapunov function is then established, and its fractional derivative is taken, ensuring the inequality | + | Then, the synchronization error between the network node <math display="inline"> v_i </math> and the node state <math display="inline"> x_i (t)</math> is defined as: |
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> e_i(t)=x_i(t)-\bar{x}(t) </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(8) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Based on Eqs. (3) and (7), the specific form of the error system is given as: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> _{t_{0}}^{c}D_{t}^{\alpha}x_{i}\big(t\big)=f\big(x_{i}\big(t\big)\big)-\frac{1}{n}\sum_{j=1}^{n}f\big(x_{j}\big(t\big)\big)+</math><math>\sum_{j=1,j\neq i}^{n}a_{ij}^{\sigma(t)}\big[e_{j}\big(t\big)-e_{i}\big(t\big)\big]+</math><math>\sum_{j=1,j\neq i}^{n}g_{ij}\big(t\big)\big[e_{j}\big(\tau_{ij}\big(t\big)\big)-e_{i}\big(\tau_{ij}\big(t\big)\big] </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(9) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Assuming the three assumptions mentioned earlier are valid, the synchronization error will exhibit a bounded final state and will approach the interior of the set asymptotically over time. This proves the related inequality to be true. A Lyapunov function is then established, and its fractional derivative is taken, ensuring the inequality <math> t\ge t_0</math> holds. Through the derivation process, two inequalities are initially set, and their correctness is proved using mathematical induction: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \begin{cases}\varepsilon\big(t\big)\leq\mu,\quad t\geq t_0\\\\ | ||
| + | V\big(t\big)\leq V\big(t_0\big)+\dfrac{2\big(1-\xi\big)\widetilde{\lambda}\varsigma\bigg[V\big(t_0\big)+\dfrac{\mu}{2\eta}\bigg]+\mu}{2\big(\big(1-\xi\big)\big)\widetilde{\lambda}-\eta},\quad t\geq t_0\end{cases} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(10) | ||
| + | |} | ||
| − | |||
| − | |||
The proof process is as follows: | The proof process is as follows: | ||
| − | If the condition | + | If the condition <math display="inline">t \in [t_0, t_1)</math> holds, then according to Eq. (5), when <math display="inline">t\in [t_0, t_1)</math>, <math display="inline">g_{ij}(t)=0</math>, <math display="inline">i, j\in \{1,2,3,...,n\}</math>. According to the definition of function <math display="inline">\varepsilon (t)</math>, we get:: |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \varepsilon (t)=0\leq\mu,t \in [t_0,t_1) </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(11) | ||
| + | |} | ||
| − | Then, based on the assumption t | + | Then, based on the assumption <math display="inline">t \in [t_0, t_1)</math>, two possible scenarios are discussed: |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \begin{cases}t_1\le t_0+\varpi\\t_1\ge t_0+\varpi\end{cases} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(12) | ||
| + | |} | ||
| − | |||
| − | < | + | Assuming the inequalities hold for <math display="inline">t \in [t_0, t_p)</math> (where <math display="inline"> p </math> is a positive integer), the case for <math display="inline">t \in [t_0, t_{p+1})</math> needs to be considered. This case also presents two scenarios, each discussed separately: |
| − | + | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \begin{cases}t_{p+1}\leq t_0+\varpi\\t_{p+1}>t_0+\varpi\end{cases} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(13) | ||
| + | |} | ||
| − | |||
| − | + | By discussing the two scenarios of inequalities (12) and (13), the validity of Eq. (10) is proven, showing that the synchronization error is bounded for <math>t\ge t_0</math>. Ultimately, it is understood that as the variable time <math display="inline"> t </math> approaches infinity, the synchronization error gradually approaches the set. | |
| − | + | ||
| − | + | Next, regarding synchronization control of complex networks based on topology switching: In the discussion of synchronization control for complex networks based on topology switching, the special case of <math display="inline">\alpha =1</math> in Eq. (3) is considered, i.e., the control of integer-order topology-switching complex networks. Equation (3) is then adapted to the special case of <math display="inline">\alpha =1</math>, transforming it as follows: | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \dot{x}_i\begin{pmatrix}t\end{pmatrix}=f\begin{pmatrix}x_i\begin{pmatrix}t\end{pmatrix}\end{pmatrix}+\sum_{j=1,j\neq i}^na_{ij}^{\sigma(t)}\begin{bmatrix}x_j\begin{pmatrix}t\end{pmatrix}-x_i\begin{pmatrix}t\end{pmatrix}\end{bmatrix}+u_i\begin{pmatrix}t\end{pmatrix} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(14) | ||
| + | |} | ||
| − | |||
| − | + | Equation (9) is similarly transformed: | |
| − | <math>V(t)=\frac12\sum_{i=1}^ne_i^T(t)e_i(t)</math> | + | |
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \dot{e}_i(t)=f(x_i(t))-\frac{1}{n}\sum_{j=1}^nf(x_j(t))+</math><math>\sum_{j=1,j\neq i}^na_{ij}^{\sigma(t)}\Big[e_j(t)-e_i(t)\Big]+</math><math>\sum_{j=1,j\neq i}^ng_{ij}(t)\Big[e_j\big(\tau_{ij}(t)\big)-e_i\big(\tau_{ij}(t)\big)\Big] </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(15) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Assuming the three assumptions for the model design are valid, then under the action of Eq. (5), Eq. (14) will achieve a synchronized state, i.e., <math>\lim_{\mathfrak{t}\to\infty}\lVert e(t)\rVert=0</math>. A Lyapunov function is established as: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> V(t)=\frac12\sum_{i=1}^ne_i^T(t)e_i(t) </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(16) | ||
| + | |} | ||
| + | |||
Similar derivations of related inequalities are performed, leading to a series of differential inequalities. Using mathematical induction, the correctness of the two set inequalities is proven: | Similar derivations of related inequalities are performed, leading to a series of differential inequalities. Using mathematical induction, the correctness of the two set inequalities is proven: | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \varepsilon(t)\leq\gamma e^T(t)e(t),t\geq t_0 </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(17) | ||
| + | |} | ||
| − | |||
| − | < | + | Following the definition of function <math display="inline">g_{ij}(t)</math>, assume for <math display="inline">t \in [t_0, t_1)</math>, according to Eq. (17), we get: <math>\varepsilon(t)=0\leq\gamma e^T(t)e(t),t\geq t_0</math>. Next, assuming the inequalities hold for <math display="inline">t \in [t_0, t_p)</math> (where <math display="inline"> p </math> is a positive integer), the case for <math display="inline">t \in [t_0, t_{p+1})</math> is considered. This case also presents two scenarios, each discussed separately: |
| − | + | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> \begin{cases}t_{p+1}\leq t_0+\varpi\\t_{p+1}>t_0+\varpi\end{cases} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(18) | ||
| + | |} | ||
| − | 3.2 Numerical | + | |
| + | Finally, based on the inequality derivations from Eqs. (17) and (18), as well as mathematical induction, <math>\varepsilon(t)\leq\gamma e^T(t)e(t),t\in\begin{bmatrix}t_0,&t_p\end{bmatrix}</math>, the validity of Eq. (17) is proven. Furthermore, using the established Lyapunov function stability theorem, the validity of the formula <math>\lim_{\mathfrak{t}\to\infty}\lVert e(t)\rVert=0</math> can be demonstrated. | ||
| + | |||
| + | ===3.2 Numerical simulation=== | ||
To validate the correctness and effectiveness of the theoretical results proposed in this study, numerical simulations are conducted using two numerical examples. The details are as follows: | To validate the correctness and effectiveness of the theoretical results proposed in this study, numerical simulations are conducted using two numerical examples. The details are as follows: | ||
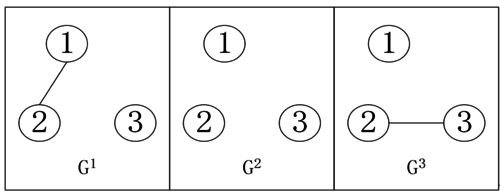
| − | From the theoretical results, it is known that a one-dimensional fractional-order switching complex network formed by three nodes is considered. Assuming the initial moment | + | From the theoretical results, it is known that a one-dimensional fractional-order switching complex network formed by three nodes is considered. Assuming the initial moment <math display="inline"> t_0 </math> is set to 0, <math display="inline"> \alpha</math> is set to 0.8, and the function <math display="inline"> f </math> is set to 0.3. It is also assumed that the network has three communication topologies, which are labeled and presented graphically as shown in [[#img-1|Figure 1]]. |
| − | <div class=" | + | <div id='img-1'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:1111.png|500px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 1'''. Schematic of the three communication topologies | ||
| + | |} | ||
| − | |||
| − | |||
The adjacency matrices for the three communication topologies are given, with their elements defined as: | The adjacency matrices for the three communication topologies are given, with their elements defined as: | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> a_{ij}^n=\begin{cases}1, \quad i\neq j\, \text{just}\,\Big(\nu_i,\nu_j\Big)\in\varepsilon^n\\0,\quad \text{Other situations}\end{cases} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(19) | ||
| + | |} | ||
| + | |||
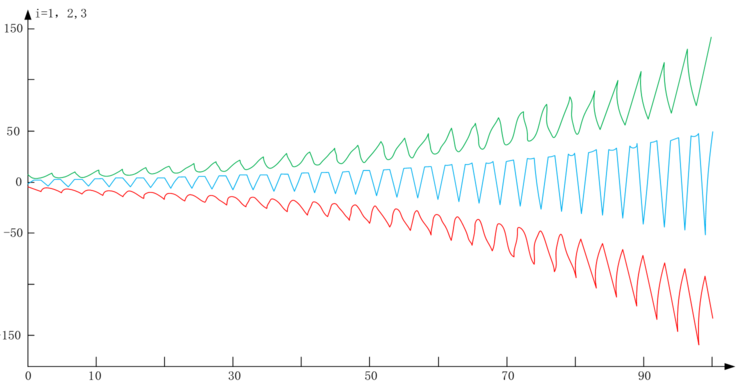
| − | Here, n is a natural number equal to 1, 2, 3. Assuming the switching moments are | + | Here, <math display="inline"> n </math> is a natural number equal to <math display="inline">1,\, 2,\, 3</math>. Assuming the switching moments are <math display="inline">t_k=k</math>, the sequence of switching among the three communication topology is represented as <math display="inline">1\to 2\to 3\to 1\to...</math>. Thus, it can be seen that in this section's assumption, the joint connectivity adjustment between nodes is feasible. Selecting the initial conditions from the model design, numerical verification can be performed as shown in [[#img-2|Figures 2]] and [[#img-3|3]]. |
| − | [[File:2222.png|744x744px]] | + | <div id='img-2'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:2222.png|744x744px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. Time course change of synchronization error under an uncontrolled state | ||
| + | |} | ||
| − | |||
| − | As seen in Figure 2, without the addition of a controller in the network design model, the change in synchronization error tends to diverge as time extends. | + | As seen in [[#img-2|Figure 2]], without the addition of a controller in the network design model, the change in synchronization error tends to diverge as time extends. |
| − | <div class=" | + | <div id='img-3'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:3333.png|744x744px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Time course change of synchronization error under the influence of a controller | ||
| + | |} | ||
| − | |||
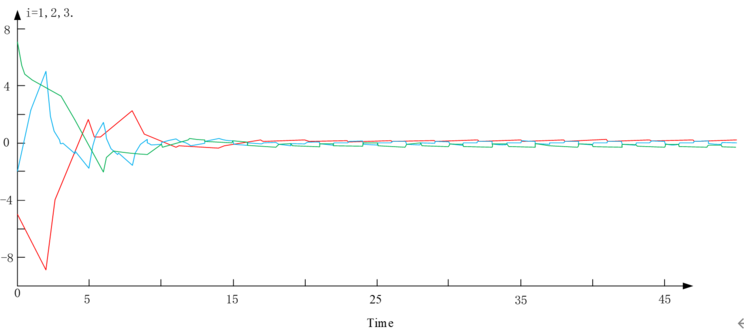
| − | As depicted in Figure 3, the integration of a controller into the network design paradigm ensures that the trajectory of synchronization error remains confined and converges within a predetermined bounded domain. This empirical evidence, derived from numerical simulations, corroborates the efficacy of the dual strategies employed: the boundedness control and the synchronization control within complex networks, predicated on the dynamics of topology switching. | + | As depicted in [[#img-3|Figure 3]], the integration of a controller into the network design paradigm ensures that the trajectory of synchronization error remains confined and converges within a predetermined bounded domain. This empirical evidence, derived from numerical simulations, corroborates the efficacy of the dual strategies employed: the boundedness control and the synchronization control within complex networks, predicated on the dynamics of topology switching. |
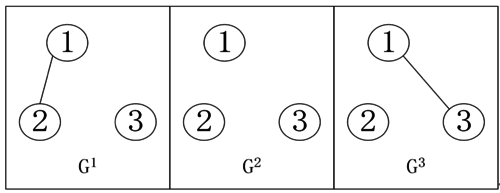
| − | Additionally, based on the theoretical results, a one-dimensional switching complex network formed by three nodes is considered. Assuming the initial moment | + | Additionally, based on the theoretical results, a one-dimensional switching complex network formed by three nodes is considered. Assuming the initial moment <math display="inline"> t_0 </math> is set to 0 and <math display="inline"> f</math> is set to 0.92sin, it is also assumed that the network has three communication topologies. These are labeled and graphically represented as shown in [[#img-4|Figure 4]]. |
| − | <div class=" | + | <div id='img-4'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:4444.png|500px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. Schematic of the three communication topologies | ||
| + | |} | ||
| − | |||
The adjacency matrices for the three communication topologies are defined as follows: | The adjacency matrices for the three communication topologies are defined as follows: | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> a_{ij}^\mathrm{k}=\begin{cases}1, \quad i\neq j \, \text{just}\Big(\nu_i,\nu_j\Big)\in\varepsilon^\mathrm{k}\\ | ||
| + | 0,\quad \text{Other situations}\end{cases} </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(20) | ||
| + | |} | ||
| − | + | where <math display="inline">k </math> is a natural number equal to <math display="inline">1,\, 2,\, 3</math>. Assuming the switching moments are <math display="inline">t_k=1.5</math>k, the sequence of switching among the three communication topologies is represented as <math display="inline">1\to 2\to 3\to 2 \to 1\to...</math>. This shows that the joint connectivity adjustment between nodes is feasible within the assumptions of this section. Numerical verification is then conducted based on the initial conditions set in Eq. (14), as illustrated in [[#img-5|Figures 5]] and [[#img-6|6]]. | |
| − | [[File:5555.png| | + | <div id='img-5'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:5555.png|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. Time course change of synchronization error in an uncontrolled state | ||
| + | |} | ||
| − | |||
| − | As seen in Figure 5, without control in | + | As seen in [[#img-5|Figure 5]], without control in Eq. (14), the network is unable to achieve synchronization. |
| − | [[File:6666.png| | + | <div id='img-6'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:6666.png|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 6'''. Time course change of synchronization error under the influence of a controller | ||
| + | |} | ||
| − | |||
| − | According to Figure 6, the network in | + | According to [[#img-6|Figure 6]], the network in Eq. (14), under the influence of the controller, can achieve synchronization. This numerical verification thus proves the validity of the three assumptions made in the model design. |
| − | =4. | + | ==4. Conclusions== |
This scholarly endeavor commences with a meticulous literature review, canvassing both domestic and international sources to scaffold the theoretical underpinnings and discern the contemporary landscape of research in fractional-order complex networks. The exposition progresses to delineate the employed research methodologies, models, and controller architectures, thereby accentuating the pivotal themes under investigation. Culminating in a synthesis and discourse of the findings, the study arrives at several salient conclusions: | This scholarly endeavor commences with a meticulous literature review, canvassing both domestic and international sources to scaffold the theoretical underpinnings and discern the contemporary landscape of research in fractional-order complex networks. The exposition progresses to delineate the employed research methodologies, models, and controller architectures, thereby accentuating the pivotal themes under investigation. Culminating in a synthesis and discourse of the findings, the study arrives at several salient conclusions: | ||
| Line 226: | Line 409: | ||
(5) Notwithstanding, the study acknowledges its constraints, notably the simplicity of the numerical simulations and the absence of an exhaustive dialogue. Future research trajectories will encompass a spectrum of simulation scenarios, varying parameters to dissect the outcomes under diverse conditions, thus rendering the conclusions more holistic and robust. | (5) Notwithstanding, the study acknowledges its constraints, notably the simplicity of the numerical simulations and the absence of an exhaustive dialogue. Future research trajectories will encompass a spectrum of simulation scenarios, varying parameters to dissect the outcomes under diverse conditions, thus rendering the conclusions more holistic and robust. | ||
| − | ==References | + | ==References== |
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
| − | [1] Wei | + | [1] Wei Z., Weng Z., Hua Y., et al. Formation-encirclement tracking control of heterogeneous unmanned clusters under switching topology. Journal of Aeronautics, 44(2):252-267, 2023. |
| − | [2] Chen | + | [2] Chen Y., Ning X., Wei Y., et al. Consistency iterative learning control of measurement restricted multi-agent systems under switching topology. Control Theory and Applications, 40(8):1384-1394, 2023. |
| − | [3] Huang | + | [3] Huang R., Jiang N., Liu X., et al. Bipartite synchronization of coupled complex-valued neural networks under switching topology. Journal of Jiangsu Normal University (Natural Science Edition), 41(2):51-58, 2023. |
| − | [4] Wang | + | [4] Wang Q., Wang X. Adaptive neural network consistency of nonlinear multi-agent systems under switching topology. Control Theory and Applications, 40(4):633-640, 2023. |
| − | [5] Meng | + | [5] Meng X., Mao B. Two methods of sliding mode synchronization for fractional-order uncertain complex network systems. Journal of Anhui University (Natural Science Edition), 45(6):13-18, 2021. |
| − | [6] Meng | + | [6] Meng X. Adaptive proportional-integral sliding mode synchronization of fractional-order uncertain complex network systems. Journal of Zhengzhou Institute of Aeronautical Industry Management, 40(6):102-104, 2022. |
| − | [7] Yang | + | [7] Yang X., Zhang G., Li X., et al. Delayed projection synchronization and parameter identification of two fractional-order complex networks with coupling delays. Control and Decision, 37(6):1479-1488, 2022. |
| − | [8] Ma | + | [8] Ma W., Li Z., Dai C. Topology identification of fractional-order complex networks based on variable substitution control. Journal of Shandong University (Science Edition), 58(11):53-60, 2023. |
| − | [9]Ding D,Jiang Q,Hu Y,et al.Complex modified projective synchronization of fractional-order complex-valued dynamic network with time-varying coupling and parameters estimation.International Journal of Modern Physics C | + | [9] Ding D., Jiang Q., Hu Y., et al. Complex modified projective synchronization of fractional-order complex-valued dynamic network with time-varying coupling and parameters estimation. International Journal of Modern Physics C, 34(07), 2350084, 2023. |
| − | [10] | + | [10] Du F., Lu J.G., Zhang Q.H.. Delay-dependent finite-time synchronization criterion of fractional-order delayed complex networks. Communications in Nonlinear Science and Numerical Simulation, 119, 107072, 2023. |
| − | [11] | + | [11] Behinfaraz R., Ghaemi S. Identification and synchronization of switching fractional-order complex networks with time-varying delays based on a fuzzy method. International Journal of Fuzzy Systems, 24(5):2203-2214, 2022. |
| − | [12]P. | + | [12] Selvaraj P., Kwon O.M., Lee S.H., Sakthivel R. Cluster synchronization of fractional-order complex networks via uncertainty and disturbance estimator-based modified repetitive control. Journal of the Franklin Institute, 358(18):9951-9974, 2021. |
Latest revision as of 12:47, 21 June 2024
Abstract
In the contemporary epoch, bolstered by information technology, the quintessence of networks is ubiquitously manifested, with a plethora of network types—ranging from the Internet, vehicular traffic frameworks, electrical distribution systems, cellular communication matrices, to social interconnection webs—being intricately woven into the fabric of societal functionality and quotidian existence. The domain of complex networks has burgeoned into a fervently pursued research vector, magnetizing an eclectic cohort of investigators from disciplines as variegated as mathematics, biosciences, and engineering. Notably, the fractional calculus has eclipsed its integer-order counterpart by offering enhanced precision in the depiction of real-world systems and phenomena. Consequently, the infusion of fractional calculus into the modeling of complex networks, to dissect their dynamic attributes and attendant control paradigms, has crystallized as a research nexus of burgeoning interest, eliciting scholarly discourse at both national and international echelons. [Purpose] This inquiry into the synchronization control of fractional-order complex networks, predicated on switching topology, endeavors to harness said topology as a scaffold for probing the synchronicity inherent within fractional-order complex networks. The objective is to augment the operational efficacy of these networks, broaden their sphere of applicability, and fortify the synchronal linkage amongst fractional-order complex networks and their counterparts. [Method] Predominantly, this exploration is underpinned by a synthesis of bibliographic scrutiny and analytical modeling, employing an extensive compendium of model equations to elucidate the subject matter. The spotlight is cast upon the Caputo fractional-order differential equation, with a focus on assaying the stability traits of its equilibrium junctures and formulating more expansive and pragmatic conditions for stability. In addition, to facilitate the precise estimation of elusive topologies within complex networks, a supplementary network—comprising isolated nodes and a regulatory protocol—is conceptualized. [Results] The findings suggest that the investigation into synchronization control based on switching topology propels the advancement of fractional-order complex networks and has substantial reference value. It serves to substantiate, to a certain degree, the postulations of antecedent theorists and chart a trajectory for ensuing scholarly endeavors in cognate domains, thereby perpetually amplifying the pragmatic utility of fractional-order complex networks.
Keywords: Switching topology, fractional-order complex networks, synchronization control, information storage mechanism
1. Introduction
In the vanguard of the information epoch, the incursion of information technology into myriad sectors is irrefutable. Networks of diverse ilk—encompassing transportation, the Internet, and mobile communications—have burgeoned under its aegis. The enhancement of these networks’ utilitarian value stands as a scholarly conundrum, engaging academia and industry alike. Notably, the flexibility of distributed networks, enabled by switching topology, is commendable; nodes within these structures exhibit temporal dynamics. Moreover, fractional calculus, with its fidelity in characterizing entities bearing memory and hereditary attributes, offers a veracious lens for dynamic analysis. Ergo, the integration of fractional calculus into complex network studies is not merely advantageous but pivotal, encapsulating the mnemonic and genetic dynamics of nodal interactions. The investigation into the orchestration of fractional-order complex networks, through the prism of switching topology, is thus seminal. It lays the groundwork for comprehending network coordination, aspiring to amplify network adaptability and inter-network consonance.
Within the Chinese academic milieu, the exploration of switching topology and fractional-order complex networks has been undertaken from multifarious vantage points. Research by Wei et al [1] delved into the orchestration and encirclement tracking control of disparate unmanned entities within a cluster, leveraging switching topology. The common Lyapunov stability theorem was employed to substantiate the requisite conditions for the attainment of output formation and encirclement tracking within these heterogeneous assemblages. The proposed methodology's efficacy was corroborated via simulation, specifically within heterogeneous clusters comprising unmanned aerial and ground vehicles. In parallel, Chen et al. [2] probed the iterative learning control for consistency within a measurement-constrained multi-agent system, also under the purview of switching topology. A distributed protocol predicated on the followers' local data was formulated, furnishing two adequate conditions to surmount the challenges of output consistency. One stipulation facilitated the real-time acquisition of iterative learning gains by the followers, thereby obviating the dependency on global information for learning gain formulation and affirming the algorithm's distributed execution. The algorithm's convergence was validated through the λ-norm theory and disc theorem, with simulations substantiating its effectiveness. Concurrently, Huang et al. [3] embarked on an inquiry into the bipartite synchronization within coupled complex-valued neural networks, again within the context of switching topology. Their focus was twofold: scenarios bereft of a directed spanning tree (FDST) and those where each sub-network possesses one (PDST). Utilizing an array of Lyapunov functions and the average dwelling time approach, they scrutinized the error system's convergence, with numerical simulations affirming the study's validity. Lastly, Wang and Wang [4] examined the adaptive neural network consistency in nonlinear multi-agent systems subject to switching topology. They addressed the systems' inherent uncertainties via neural network function approximation techniques and introduced an adaptive smoothing term to mitigate bounded perturbations and approximation errors. Subsequently, they authenticated the consistency of nonlinear multi-agent systems with indeterminate control coefficients within the framework of switching topology, ensuring the closed-loop system's boundedness. In the ambit of fractional-order complex network systems, Meng and Mao [5] have delineated two novel sliding mode synchronization methodologies. Predicated on the tenets of fractional-order stability theory, a duo of fractional-order controllers alongside corresponding sliding surfaces were conceptualized, culminating in the establishment of two robust conditions conducive to the system’s sliding mode synchronization. This research substantiates that, given optimally calibrated sliding surfaces and controllers, synchronization within fractional-order uncertain complex network systems is attainable.
Subsequently, Meng [6] extended this paradigm by probing the adaptive proportional-integral sliding mode synchronization within analogous systems. Harnessing the synergies of fractional-order stability theory and matrix theory, an adaptive synchronization schema was realized, with numerical simulations affirming the soundness of this approach. Concurrently, Yang et al. [7] embarked on an exploration of delay projection synchronization and parameter identification in two fractional-order complex networks, particularly those encumbered with coupling delays. Through meticulous analysis and numerical exemplification, they elucidated the efficacy of their proposed methodologies, addressing three distinct synchronization scenarios and dissecting the influence of coupling strength, temporal delays, and projection ratios.
In a similar vein, Ma et al. [8] ventured into the realm of topology identification for fractional-order complex networks, employing a strategy of variable substitution control. By devising a response network predicated on this control mechanism and a concurrent parameter update law, they derived a set of criteria for achieving both topology identification and network synchronization, with numerical simulations serving as a testament to the method’s validity. Collectively, these scholarly endeavors within the domains of switching topology and fractional-order complex networks not only enrich theoretical discourse but also chart a definitive course for empirical inquiry.
In the realm of global research on switching topology and fractional-order complex networks, Ding et al. [9] have probed the intricacies of complex modified projective synchronization (CMPS) and the parameter estimation within time-varying coupled fractional-order complex-valued dynamic networks (FOCDN). Their theoretical discourse posits that FOCDN, when faced with time-varying delays, can attain CMPS via adaptive controllers—a premise substantiated by two numerical exemplars within the complex-valued domain, thereby affirming the potency of the refined projection strategy for fractional-order complex networks. Concurrently, Du et al. [10] have delved into the delay-dependent finite-time synchronization (FTS) criterion pertinent to a subset of fractional-order delay complex networks (FODCNs). By leveraging the Young inequality and the rules governing fractional-order derivatives of composite functions, they unveiled a novel delay-dependent fractional-order finite-time convergence principle (FOFTCP), wherein the stability duration is contingent upon the temporal delay. This newly minted FOFTCP, in concert with a meticulously crafted feedback controller, has yielded a fresh FTS criterion for FODCNs, the efficacy of which has been corroborated through two numerical demonstrations. In a parallel vein, Behinfaraz and Ghaemi [11] have embarked on an exploration of the identification and synchronization within fractional-order complex networks, characterized by switching topology and time-variant delays, through the lens of fuzzy methodologies. The dynamics of the network nodes, deemed chaotic, were instantiated via a circuit realization tailored to these time-delay fractional-order dynamics. Employing T-S fuzzy modeling, they introduced an innovative representational paradigm for fractional-order chaotic systems, with simulations and empirical outcomes underscoring the proposed method's performance. Selvaraj et al. [12] scrutinized the cluster synchronization and the mitigation of disturbances within fractional-order complex networks, beset by coupling delays, unknown uncertainties, and disturbances (UDs). A modified repetitive control (MRC) block was seamlessly integrated into a closed-loop feedback control circuit to tackle these challenges. Furthermore, they formulated a comprehensive suite of sufficient linear matrix inequality constraints to guarantee the system's cluster synchronization. The merits, practicability, and resilience of the MRC framework, predicated on UDE, were validated through two illustrative cases. This overview elucidates that international research endeavors in switching topology and fractional-order complex networks are markedly more focused than their domestic counterparts, thereby serving as a repository of valuable insights and benchmarks for domestic scholarly pursuits in these spheres.
2. Research content
2.1 Basic theory
In the discourse of distributed architectures, switching topology is characterized by its dynamic inter-nodal relationships, which, unlike their fixed counterparts, are subject to temporal fluctuations, thereby imbuing the system with enhanced flexibility, randomness, and variability.
Complex networks, when viewed through the prism of practical application, are construed as intricate tapestries woven by nonlinear dynamic interactions, with nodes interlinked in a multitude of configurations. These networks, often vast and convoluted in their nodal interconnections, serve as pragmatic mathematical models that mirror the intricacies of real-world networks and systems. Their study is of paramount theoretical and practical significance, offering insights that refine our comprehension of the world and inform societal progression.
The realm of synchronization control within fractional-order complex networks is primarily concerned with the harmonization of network behavior. Research in this field typically embodies a holistic and idealized ethos, with a pronounced emphasis on the multifaceted environmental variables that pervade the real world, acknowledged as pivotal influences on network dynamics and their modeling. This approach ensures that the networks and models under scrutiny possess profound emblematic and representational value. Contemporary investigations into network synchrony control span a spectrum from the macroscopic to the microscopic and from the theoretical to the applied. Consequently, the taxonomy of synchrony control strategies encompasses a diverse array, including structural traction control, a gamut of design-centric control tactics (encompassing impulse, sampled, and model predictive control), robust control predicated on performance metrics, and cost-effective control methodologies, among others.
2.2 Research methodology
This investigation predominantly harnesses literature review and model analysis as methodological pillars. The former entails a systematic trawl through esteemed repositories such as CNKI, Wanfang, and CQVIP, to amass both domestic and international scholarly works germane to the focal theme. The collated corpus is meticulously curated to distill pivotal insights, thereby erecting the principal theoretical scaffold for this inquiry. Concurrently, the model analysis technique encompasses the formulation of a fractional-order complex network model, predicated on switching topology, to anchor the research into synchrony control. Furthermore, it posits an information storage mechanism control strategy as a conjectural approach, the viability of which is rigorously assessed, thus underpinning the study's scientific rigor and holistic integrity.
2.3 Design of models and controllers
First, in terms of model design, consider a Caputo fractional-order complex network with switching topology composed of multiple nodes. All communication topology can be designed as a finite set of undirected graphs, denoted as , where the first item in the set is a collection of all network nodes, expressed as , represents the set of undirected edges for the th topology, is the adjacency matrix for the th topology graph, being a natural number. For clarity, be represented as . Also, represent the nodes as the edges between nodes, and define the elements in the matrix . The equation is as follows:
|
|
(1) |
where are positive numbers satisfying the relation . This gives the Laplace matrix of the topology graph. Then, is represented as the union graph of the topology, with the matrix serving as the adjacency matrix of the topology graph. The matrix elements satisfy the relation. The equation is as follows:
|
|
(2) |
From Eq. (2), the Laplace matrix of the topology graph is given, and a function is used to represent the corresponding switching signal. It is assumed that the network's communication topology will switch at time , and when , the function will be equal to a certain number in the set. The mathematical model of the considered switching network is then given. The equation is as follows:
|
|
(3) |
where is a function; t0is the initial moment; is in the interval , and , is the state vector of the node; is a continuously differentiable nonlinear vector function; is the node control output. To satisfy the design of this model, the following assumptions are made:
Assumption 1: It is assumed that for the function , there exists a non-negative constant such that for any sets and , an inequality exists, represented as:
|
|
(4) |
Assumption 2: Since at the switching moments, each individual time interval corresponding to a single switching moment shows a non-degenerate state, at the same time, .
Assumption 3: There exists a positive number such that for any given moment, the network communication topology is jointly connected in that time range. That is, if the moment is greater than the initial moment a positive number, then within that time interval, the union graph of all communication topology will appear, and the union graph of this union with the∪ function is in a connected state.
In the architectural conception of controllers, the potentiality for topology switching warrants meticulous consideration. Such switching may precipitate the severance of connections or the forfeiture of linkages with proximate nodes. Under these circumstances, the impacted nodes are precluded from accessing a spectrum of state information from their adjacent counterparts, engendering impediments to the attainment of efficacious synchronicity control. To augment the orchestration of the control apparatus within complex networks and to attenuate the adverse ramifications of disconnections, a controller has been devised. This apparatus empowers network nodes to archive state information procured from neighboring nodes amid communication exchanges. Should a node find itself estranged from its neighbors and incapable of contemporaneous state recording, the repository of antecedent state data is rendered accessible. This historical data is then assimilated into the control schema, serving as a dynamic compensatory mechanism, thus enabling the regulation of nodal behavior. Ergo, a controller, endowed with an information storage mechanism strategy, has been engineered for the network model, encapsulated by the ensuing equation:
|
|
(5) |
where is a natural number ; ( is the communication time closest to the current moment from the initial moment between two nodes); if , it indicates that the edge between two nodes is disconnected at the current moment , and the relationship between the initial moment , the current moment , and the nearest communication time . The equation is represented as:
|
|
(6) |
Furthermore, according to the definition of in Eq. (5), it is known that when disconnection occurs between two nodes, the controller will transmit the saved historical state information between the nodes to the network node. However, according to the definition of , the controller only transmits the most recently saved state information between nodes, rather than transmitting all saved historical state information. Therefore, past saved node history state information can be considered as not having reference or application value.
3. Results and discussion
3.1 Theoretical results
First, regarding boundedness control of complex networks based on topology switching: Initially, all nodes in the network are set to a mean state, and a corresponding dynamical equation is given. The equation is as follows:
|
|
(7) |
Then, the synchronization error between the network node and the node state is defined as:
|
|
(8) |
Based on Eqs. (3) and (7), the specific form of the error system is given as:
|
|
(9) |
Assuming the three assumptions mentioned earlier are valid, the synchronization error will exhibit a bounded final state and will approach the interior of the set asymptotically over time. This proves the related inequality to be true. A Lyapunov function is then established, and its fractional derivative is taken, ensuring the inequality holds. Through the derivation process, two inequalities are initially set, and their correctness is proved using mathematical induction:
|
|
(10) |
The proof process is as follows:
If the condition holds, then according to Eq. (5), when , , . According to the definition of function , we get::
|
|
(11) |
Then, based on the assumption , two possible scenarios are discussed:
|
|
(12) |
Assuming the inequalities hold for (where is a positive integer), the case for needs to be considered. This case also presents two scenarios, each discussed separately:
|
|
(13) |
By discussing the two scenarios of inequalities (12) and (13), the validity of Eq. (10) is proven, showing that the synchronization error is bounded for . Ultimately, it is understood that as the variable time approaches infinity, the synchronization error gradually approaches the set.
Next, regarding synchronization control of complex networks based on topology switching: In the discussion of synchronization control for complex networks based on topology switching, the special case of in Eq. (3) is considered, i.e., the control of integer-order topology-switching complex networks. Equation (3) is then adapted to the special case of , transforming it as follows:
|
|
(14) |
Equation (9) is similarly transformed:
|
|
(15) |
Assuming the three assumptions for the model design are valid, then under the action of Eq. (5), Eq. (14) will achieve a synchronized state, i.e., . A Lyapunov function is established as:
|
|
(16) |
Similar derivations of related inequalities are performed, leading to a series of differential inequalities. Using mathematical induction, the correctness of the two set inequalities is proven:
|
|
(17) |
Following the definition of function , assume for , according to Eq. (17), we get: . Next, assuming the inequalities hold for (where is a positive integer), the case for is considered. This case also presents two scenarios, each discussed separately:
|
|
(18) |
Finally, based on the inequality derivations from Eqs. (17) and (18), as well as mathematical induction, , the validity of Eq. (17) is proven. Furthermore, using the established Lyapunov function stability theorem, the validity of the formula can be demonstrated.
3.2 Numerical simulation
To validate the correctness and effectiveness of the theoretical results proposed in this study, numerical simulations are conducted using two numerical examples. The details are as follows:
From the theoretical results, it is known that a one-dimensional fractional-order switching complex network formed by three nodes is considered. Assuming the initial moment is set to 0, is set to 0.8, and the function is set to 0.3. It is also assumed that the network has three communication topologies, which are labeled and presented graphically as shown in Figure 1.
|
| Figure 1. Schematic of the three communication topologies |
The adjacency matrices for the three communication topologies are given, with their elements defined as:
|
|
(19) |
Here, is a natural number equal to . Assuming the switching moments are , the sequence of switching among the three communication topology is represented as . Thus, it can be seen that in this section's assumption, the joint connectivity adjustment between nodes is feasible. Selecting the initial conditions from the model design, numerical verification can be performed as shown in Figures 2 and 3.
|
| Figure 2. Time course change of synchronization error under an uncontrolled state |
As seen in Figure 2, without the addition of a controller in the network design model, the change in synchronization error tends to diverge as time extends.
|
| Figure 3. Time course change of synchronization error under the influence of a controller |
As depicted in Figure 3, the integration of a controller into the network design paradigm ensures that the trajectory of synchronization error remains confined and converges within a predetermined bounded domain. This empirical evidence, derived from numerical simulations, corroborates the efficacy of the dual strategies employed: the boundedness control and the synchronization control within complex networks, predicated on the dynamics of topology switching.
Additionally, based on the theoretical results, a one-dimensional switching complex network formed by three nodes is considered. Assuming the initial moment is set to 0 and is set to 0.92sin, it is also assumed that the network has three communication topologies. These are labeled and graphically represented as shown in Figure 4.
|
| Figure 4. Schematic of the three communication topologies |
The adjacency matrices for the three communication topologies are defined as follows:
|
|
(20) |
where is a natural number equal to . Assuming the switching moments are k, the sequence of switching among the three communication topologies is represented as . This shows that the joint connectivity adjustment between nodes is feasible within the assumptions of this section. Numerical verification is then conducted based on the initial conditions set in Eq. (14), as illustrated in Figures 5 and 6.
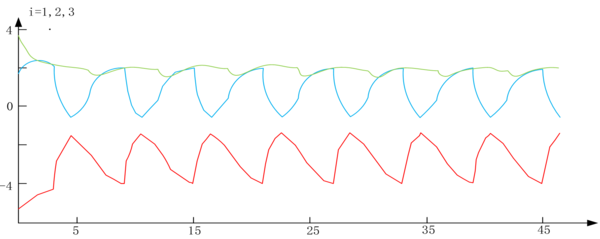
|
| Figure 5. Time course change of synchronization error in an uncontrolled state |
As seen in Figure 5, without control in Eq. (14), the network is unable to achieve synchronization.
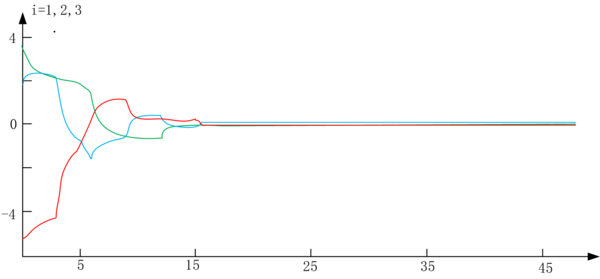
|
| Figure 6. Time course change of synchronization error under the influence of a controller |
According to Figure 6, the network in Eq. (14), under the influence of the controller, can achieve synchronization. This numerical verification thus proves the validity of the three assumptions made in the model design.
4. Conclusions
This scholarly endeavor commences with a meticulous literature review, canvassing both domestic and international sources to scaffold the theoretical underpinnings and discern the contemporary landscape of research in fractional-order complex networks. The exposition progresses to delineate the employed research methodologies, models, and controller architectures, thereby accentuating the pivotal themes under investigation. Culminating in a synthesis and discourse of the findings, the study arrives at several salient conclusions:
(1) Given the profound research implications and expansive application vistas of fractional-order and complex network theories, this inquiry is anchored in the study of fractional-order complex networks, with a focus on elucidating topology identification and synchronization control mechanisms within such networks.
(2) The design ethos of network models and topology switchers, coupled with the integration of state information preservation strategies, is aimed at mitigating potential adversities during synchronization control processes. In instances of node disconnection resultant from topology shifts, the repository of historical state data is leveraged for dynamic behavioral compensation, facilitating seamless transitions.
(3) The investigation predominantly revolves around the stability of fractional-order differential equations, bifurcated into two distinct segments. The initial segment engages with Caputo fractional-order differential equations, applying Lyapunov’s direct method to probe the stability characteristics of equilibrium points, thereby forging more encompassing and applicable stability conditions.
(4) The research hypothesis is substantiated through the deployment of two numerical exemplars, affirming the research’s foundational premises.
(5) Notwithstanding, the study acknowledges its constraints, notably the simplicity of the numerical simulations and the absence of an exhaustive dialogue. Future research trajectories will encompass a spectrum of simulation scenarios, varying parameters to dissect the outcomes under diverse conditions, thus rendering the conclusions more holistic and robust.
References
[1] Wei Z., Weng Z., Hua Y., et al. Formation-encirclement tracking control of heterogeneous unmanned clusters under switching topology. Journal of Aeronautics, 44(2):252-267, 2023.
[2] Chen Y., Ning X., Wei Y., et al. Consistency iterative learning control of measurement restricted multi-agent systems under switching topology. Control Theory and Applications, 40(8):1384-1394, 2023.
[3] Huang R., Jiang N., Liu X., et al. Bipartite synchronization of coupled complex-valued neural networks under switching topology. Journal of Jiangsu Normal University (Natural Science Edition), 41(2):51-58, 2023.
[4] Wang Q., Wang X. Adaptive neural network consistency of nonlinear multi-agent systems under switching topology. Control Theory and Applications, 40(4):633-640, 2023.
[5] Meng X., Mao B. Two methods of sliding mode synchronization for fractional-order uncertain complex network systems. Journal of Anhui University (Natural Science Edition), 45(6):13-18, 2021.
[6] Meng X. Adaptive proportional-integral sliding mode synchronization of fractional-order uncertain complex network systems. Journal of Zhengzhou Institute of Aeronautical Industry Management, 40(6):102-104, 2022.
[7] Yang X., Zhang G., Li X., et al. Delayed projection synchronization and parameter identification of two fractional-order complex networks with coupling delays. Control and Decision, 37(6):1479-1488, 2022.
[8] Ma W., Li Z., Dai C. Topology identification of fractional-order complex networks based on variable substitution control. Journal of Shandong University (Science Edition), 58(11):53-60, 2023.
[9] Ding D., Jiang Q., Hu Y., et al. Complex modified projective synchronization of fractional-order complex-valued dynamic network with time-varying coupling and parameters estimation. International Journal of Modern Physics C, 34(07), 2350084, 2023.
[10] Du F., Lu J.G., Zhang Q.H.. Delay-dependent finite-time synchronization criterion of fractional-order delayed complex networks. Communications in Nonlinear Science and Numerical Simulation, 119, 107072, 2023.
[11] Behinfaraz R., Ghaemi S. Identification and synchronization of switching fractional-order complex networks with time-varying delays based on a fuzzy method. International Journal of Fuzzy Systems, 24(5):2203-2214, 2022.
[12] Selvaraj P., Kwon O.M., Lee S.H., Sakthivel R. Cluster synchronization of fractional-order complex networks via uncertainty and disturbance estimator-based modified repetitive control. Journal of the Franklin Institute, 358(18):9951-9974, 2021.Document information
Published on 21/06/24
Accepted on 11/06/24
Submitted on 18/04/24
Volume 40, Issue 2, 2024
DOI: 10.23967/j.rimni.2024.06.003
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?