(→2.2 Distributed scheduling model) |
|||
| (22 intermediate revisions by the same user not shown) | |||
| Line 28: | Line 28: | ||
In light of these challenges, the necessity for a distributed scheduling framework becomes critical, one that allocates scheduling responsibilities to regional dispatching centers. This paradigm shift paves the way for globally optimal power scheduling based on a distributed architecture that minimizes the need for extensive inter-regional information sharing. Consequently, Distributed Dynamic Scheduling (DDS) has attracted increasing academic attention, emerging from research on Distributed Optimal Power Flow (DOPF) optimization approaches. | In light of these challenges, the necessity for a distributed scheduling framework becomes critical, one that allocates scheduling responsibilities to regional dispatching centers. This paradigm shift paves the way for globally optimal power scheduling based on a distributed architecture that minimizes the need for extensive inter-regional information sharing. Consequently, Distributed Dynamic Scheduling (DDS) has attracted increasing academic attention, emerging from research on Distributed Optimal Power Flow (DOPF) optimization approaches. | ||
| − | In the scholarly discourse on power systems, the concept of virtual nodes has been introduced as a means to balance power flow post-decoupling within subregions, thus enabling the formulation of a multi-regional decomposition algorithm. Significantly, | + | In the scholarly discourse on power systems, the concept of virtual nodes has been introduced as a means to balance power flow post-decoupling within subregions, thus enabling the formulation of a multi-regional decomposition algorithm. Significantly, Kim and Baldick [12] endorse a parallel Distributed Optimal Power Flow (DOPF) model, designed for extensive regional interconnection systems, validated through simulations on systems of moderate size. Further, Kim and Baldick [13] mathematically implement the proposed distributed framework by amalgamating two distinct decomposition methods: the Predictor-Corrector Proximal Multiplier (PCPM) and the Alternating Direction Method (ADM). Additionally, Cheng et al. [14] addresse the distributed processing of the multi-objective reactive power optimization issue within large-scale power systems, effectively resolving the centralized reactive power optimization challenge. |
| − | Furthermore, | + | Furthermore, Conejo and Aguado [15] incorporate network loss into the foundational DOPF model using cosine approximation. The Auxiliary Problem Principle (APP) is employed in literature [16-18] to manage regional coupling constraints, leading to the development of the DOPF algorithm. The Alternating Direction Multiplier Method (ADMM), thoroughly examined in literature [19-23], has been extensively refined for deployment within the Distributed Dynamic Scheduling (DDS) sphere. Notably, Dall'Anese et al. [19] convert the optimal power flow problem within microgrids into a convex issue via semi-definite programming relaxation techniques, thereafter seeking a distributed solution through the ADMM. Sulc et al. [20] utilize the ADMM, predicated on consistency, for the distributed optimal control of reactive power in power systems, demonstrating its superiority to the dual-ascent method. |
This research articulates a fully distributed algorithm to address the centralized dynamic scheduling issue within power systems featuring a multi-regional interconnection structure. Based on the inherent characteristics of power systems and employing the ADMM for the decoupling of inter-regional connections, this approach decomposes the central issue into individual sub-optimization tasks for each region. Simultaneously, the traditional role of the data center, responsible for multiplier updates, becomes redundant, resulting in a completely distributed scheduling framework. The achievement of an optimal system-wide solution is accomplished through the iterative resolution of economic scheduling sub-problems specific to each region. An illustrative analysis, utilizing a multi-regional interconnected system modeled on the IEEE standard test system, affirms the effectiveness and precision of the proposed model in managing the intricacies of multi-regional distributed dynamic scheduling in power systems. | This research articulates a fully distributed algorithm to address the centralized dynamic scheduling issue within power systems featuring a multi-regional interconnection structure. Based on the inherent characteristics of power systems and employing the ADMM for the decoupling of inter-regional connections, this approach decomposes the central issue into individual sub-optimization tasks for each region. Simultaneously, the traditional role of the data center, responsible for multiplier updates, becomes redundant, resulting in a completely distributed scheduling framework. The achievement of an optimal system-wide solution is accomplished through the iterative resolution of economic scheduling sub-problems specific to each region. An illustrative analysis, utilizing a multi-regional interconnected system modeled on the IEEE standard test system, affirms the effectiveness and precision of the proposed model in managing the intricacies of multi-regional distributed dynamic scheduling in power systems. | ||
| Line 76: | Line 76: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math>\sum_{n=1}^NP_{n,t}=\sum_{n_\mbox{B}=1}^{N_\mbox{B}}D_{n_\mbox{B},t}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (2) | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
| Line 90: | Line 90: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>P_n^{min}\leqslant P_{n,t}\leqslant P_n^{max}</math> | + | | <math>P_n^{\min}\leqslant P_{n,t}\leqslant P_n^{\max}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (3) | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
|} | |} | ||
| − | where <math display="inline">P_n^{min}</math> and <math display="inline">P_n^{max}</math> are, respectively, the lower limit and upper limit of output of generator set <math display="inline">n</math> in any period. | + | where <math display="inline">P_n^{\min}</math> and <math display="inline">P_n^{\max}</math> are, respectively, the lower limit and upper limit of output of generator set <math display="inline">n</math> in any period. |
c) The upper and lower limits of the generator set climbing: | c) The upper and lower limits of the generator set climbing: | ||
| Line 104: | Line 104: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\ | + | | <math>\Delta P_n^{\min}\leqslant P_{n,t}-P_{n,t-1}\leqslant \Delta P_n^{\max}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (4) | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
|} | |} | ||
| − | where <math display="inline">\ | + | where <math display="inline">\Delta P_n^{\min}</math> and <math display="inline">\Delta P_n^{\max}</math> indicate the minimum climb rate (i.e. maximum downward climb rate) and maximum climb rate (i.e. maximum upward climb rate) of generator set <math display="inline">n</math>, respectively. |
d) The power constraint of the generator set contract, that is, the total power generation of the generator set within a given period of time must comply with the agreed contract: | d) The power constraint of the generator set contract, that is, the total power generation of the generator set within a given period of time must comply with the agreed contract: | ||
| Line 132: | Line 132: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>E_n^{\mbox{day},\ | + | | <math>E_n^{\mbox{day},\min}\leqslant E_{n,d}^{\mbox{day}}\leqslant E_n^{\mbox{day},\max}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (6) | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
|} | |} | ||
| − | where <math display="inline">d</math> is the number of the dispatch date; <math display="inline">E_{n,d}^{\mbox{day}}</math> is the generation capacity of generator set <math display="inline">n</math> in date <math display="inline">d</math>; <math display="inline">E_n^{\mbox{day},\ | + | where <math display="inline">d</math> is the number of the dispatch date; <math display="inline">E_{n,d}^{\mbox{day}}</math> is the generation capacity of generator set <math display="inline">n</math> in date <math display="inline">d</math>; <math display="inline">E_n^{\mbox{day},\min}</math> and <math display="inline">E_n^{\mbox{day},\max}</math> are the planned allowable minimum and maximum of the energy decomposition value of the generator set <math display="inline">n</math>, respectively. |
f) Transmission line maximum capacity constraints: | f) Transmission line maximum capacity constraints: | ||
| Line 146: | Line 146: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>-P_l^{max}\leqslant P_{l,t}\leqslant P_l^{max}</math> | + | | <math>-P_l^{\max}\leqslant P_{l,t}\leqslant P_l^{\max}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (7) | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
|} | |} | ||
| − | where <math display="inline">P_{l,t}</math> is the transmission power of line <math display="inline">l</math> in the time period <math display="inline">t</math>; <math display="inline">P_l^{max}</math> is the maximum transmission power of line <math display="inline">l</math>. The maximum capacity of the two-way transmission of the line is equal. | + | where <math display="inline">P_{l,t}</math> is the transmission power of line <math display="inline">l</math> in the time period <math display="inline">t</math>; <math display="inline">P_l^{\max}</math> is the maximum transmission power of line <math display="inline">l</math>. The maximum capacity of the two-way transmission of the line is equal. |
g) Maximum capacity constraint of regional liaison line: | g) Maximum capacity constraint of regional liaison line: | ||
| Line 160: | Line 160: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>-T_{ij}^{max}\leqslant T_{ij,t}\leqslant T_{ij}^{max}</math> | + | | <math>-T_{ij}^{\max}\leqslant T_{ij,t}\leqslant T_{ij}^{\max}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (8) | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
| Line 166: | Line 166: | ||
| − | Among them: <math display="inline">T_{ij,t}</math> is a vector variable, representing the transmission power of each contact line between region <math display="inline">i</math> and region <math display="inline">j</math> in the time period <math display="inline">t</math>; <math display="inline">T_{ij}^{max}</math> is a vector constant that represents the maximum transmission power of the contact lines between region <math display="inline">i</math> and region <math display="inline">j</math>. This paper assumes that the maximum two-way transmission capacity of each link line is equal. | + | Among them: <math display="inline">T_{ij,t}</math> is a vector variable, representing the transmission power of each contact line between region <math display="inline">i</math> and region <math display="inline">j</math> in the time period <math display="inline">t</math>; <math display="inline">T_{ij}^{\max}</math> is a vector constant that represents the maximum transmission power of the contact lines between region <math display="inline">i</math> and region <math display="inline">j</math>. This paper assumes that the maximum two-way transmission capacity of each link line is equal. |
h) Constraint on the power of the regional contact line transaction, that is, the power of the contact line transaction within a given period must comply with the agreement between regions: | h) Constraint on the power of the regional contact line transaction, that is, the power of the contact line transaction within a given period must comply with the agreement between regions: | ||
| Line 189: | Line 189: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>T_{ij}^{kh,min}\leqslant \boldsymbol{1}^\mbox{T}T_{ij,t}\leqslant T_{ij}^{kh,max}</math> | + | | <math>T_{ij}^{kh,\min}\leqslant \boldsymbol{1}^\mbox{T}T_{ij,t}\leqslant T_{ij}^{kh,\max}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (10) | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
|} | |} | ||
| − | where <math display="inline">T_{ij}^{kh,min}</math> and <math display="inline">T_{ij}^{kh,max}</math> are the minimum and maximum value allowed by the switching power plan between region <math display="inline">i</math> and region <math display="inline">j</math> during the <math display="inline">t</math> period, respectively. | + | where <math display="inline">T_{ij}^{kh,\min}</math> and <math display="inline">T_{ij}^{kh,\max}</math> are the minimum and maximum value allowed by the switching power plan between region <math display="inline">i</math> and region <math display="inline">j</math> during the <math display="inline">t</math> period, respectively. |
The power transmission distribution factor (PTDF) matrix can be used to obtain the power transmission lines. The PTDF matrix directly links the net injected power of each node to the power transmission of each branch, and its main advantage is that it avoids introducing redundant voltage phase angle variables, and only depends on the grid structure and line parameters, and is independent of the variation of the injected power of each node, that is, for a given network, only one PTDF matrix is needed to be reused. The basic format of its application is: | The power transmission distribution factor (PTDF) matrix can be used to obtain the power transmission lines. The PTDF matrix directly links the net injected power of each node to the power transmission of each branch, and its main advantage is that it avoids introducing redundant voltage phase angle variables, and only depends on the grid structure and line parameters, and is independent of the variation of the injected power of each node, that is, for a given network, only one PTDF matrix is needed to be reused. The basic format of its application is: | ||
| Line 230: | Line 230: | ||
To surmount this impediment, the present study introduces the augmented Lagrangian relaxation method (ALR), which incorporates a quadratic penalty term for the relaxed constraints within the objective function and adheres to a fixed step length for multiplier updates, thereby enhancing convergence. However, this incorporation of a quadratic penalty term compromises the factorability of the optimization problem, representing a significant limitation of the ALR approach. Two prevalent resolutions are the auxiliary problem principle method (APP) [24-27] and the alternating direction multiplier method (ADMM) [28-32]. Each methodology exhibits its own merits and demerits: the APP method facilitates parallel solutions albeit with moderate convergence velocity, whereas the ADMM approach necessitates serial resolution but boasts rapid convergence rates. Given the relatively modest number of regions within the extant power system architecture, the ADMM method is selected for resolving the multi-regional distributed power dispatching conundrum. | To surmount this impediment, the present study introduces the augmented Lagrangian relaxation method (ALR), which incorporates a quadratic penalty term for the relaxed constraints within the objective function and adheres to a fixed step length for multiplier updates, thereby enhancing convergence. However, this incorporation of a quadratic penalty term compromises the factorability of the optimization problem, representing a significant limitation of the ALR approach. Two prevalent resolutions are the auxiliary problem principle method (APP) [24-27] and the alternating direction multiplier method (ADMM) [28-32]. Each methodology exhibits its own merits and demerits: the APP method facilitates parallel solutions albeit with moderate convergence velocity, whereas the ADMM approach necessitates serial resolution but boasts rapid convergence rates. Given the relatively modest number of regions within the extant power system architecture, the ADMM method is selected for resolving the multi-regional distributed power dispatching conundrum. | ||
| − | 1) Traditional ADMM method | + | '''1) Traditional ADMM method''' |
Consider the following optimization problems: | Consider the following optimization problems: | ||
| Line 262: | Line 262: | ||
{| style='margin:auto;width: 100%; text-align:center;' | {| style='margin:auto;width: 100%; text-align:center;' | ||
|- | |- | ||
| − | | <math> | + | | <math>\mbox{min}f(x)+g(z)+{\lambda }^\mbox{T}(Ax+Bz-c)+\frac{\rho }{2}Ax+Bz-c_2^2</math> |
| − | \mbox{min}f(x)+g(z)+{\lambda }^\mbox{T}(Ax+Bz-c)+ | + | |
| − | \frac{\rho }{2}Ax+Bz-c_2^2 | + | |
| − | + | ||
|} | |} | ||
| style='width: 5px;text-align: right;white-space: nowrap;' | (15) | | style='width: 5px;text-align: right;white-space: nowrap;' | (15) | ||
| Line 279: | Line 276: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>x^{k+1}:=arg\underset{x}{min}L_{\rho }(x,z^k,{\lambda }^k)</math> | + | | <math>x^{k+1}:=arg\underset{x}{\min}L_{\rho }(x,z^k,{\lambda }^k)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (16) | | style="width: 5px;text-align: right;white-space: nowrap;" | (16) | ||
| Line 289: | Line 286: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>z^{k+1}:=arg\underset{z}{min}L_{\rho }(x^{k+1},z,{\lambda }^k)</math> | + | | <math>z^{k+1}:=arg\underset{z}{\min}L_{\rho }(x^{k+1},z,{\lambda }^k)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (17) | | style="width: 5px;text-align: right;white-space: nowrap;" | (17) | ||
| Line 307: | Line 304: | ||
This iterates over and over again until the iteration termination condition is met. | This iterates over and over again until the iteration termination condition is met. | ||
| − | 2) Multi-region distributed power scheduling based on traditional ADMM method | + | '''2) Multi-region distributed power scheduling based on traditional ADMM method''' |
A multi-region distributed power dispatching model is derived from the centralized dispatching model by applying the conventional ADMM method. The main process is as follows: The centralized scheduling model reveals that the coupling constraint between regions is manifested in the constraint related to the liaison line, that is, the maximum capacity constraint of the regional liaison line <math display="inline">-T_{ij}^{max}\leqslant T_{ij,t}^{}\leqslant T_{ij}^{max}</math>. However, the <math display="inline">T_{ij,t}^{}</math> variable is correlated with both region <math display="inline"> i </math> and region <math display="inline"> j </math>. If the constraint is directly relaxed, the decoupling in the true sense cannot be achieved. Therefore, the constraint should be first rewritten as follows: | A multi-region distributed power dispatching model is derived from the centralized dispatching model by applying the conventional ADMM method. The main process is as follows: The centralized scheduling model reveals that the coupling constraint between regions is manifested in the constraint related to the liaison line, that is, the maximum capacity constraint of the regional liaison line <math display="inline">-T_{ij}^{max}\leqslant T_{ij,t}^{}\leqslant T_{ij}^{max}</math>. However, the <math display="inline">T_{ij,t}^{}</math> variable is correlated with both region <math display="inline"> i </math> and region <math display="inline"> j </math>. If the constraint is directly relaxed, the decoupling in the true sense cannot be achieved. Therefore, the constraint should be first rewritten as follows: | ||
| Line 326: | Line 323: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>-T_{ij}^{max}\leqslant T_{ij,t}^i\leqslant T_{ij}^{max}</math> | + | | <math>-T_{ij}^{\max}\leqslant T_{ij,t}^i\leqslant T_{ij}^{\max}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (20) | | style="width: 5px;text-align: right;white-space: nowrap;" | (20) | ||
| Line 336: | Line 333: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>-T_{ij}^{max}\leqslant T_{ij,t}^j\leqslant T_{ij}^{max}</math> | + | | <math>-T_{ij}^{\max}\leqslant T_{ij,t}^j\leqslant T_{ij}^{\max}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (21) | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) | ||
| Line 347: | Line 344: | ||
{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
|-style="background:white;" | |-style="background:white;" | ||
| − | |style="text-align: center;padding:10px;"| [[Image:Draft_He_943252806-image67.jpeg| | + | |style="text-align: center;padding:10px;"| [[Image:Draft_He_943252806-image67.jpeg|350px]] |
|- | |- | ||
| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. Schematic diagram of constraint rewriting of the contact line | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. Schematic diagram of constraint rewriting of the contact line | ||
| Line 361: | Line 358: | ||
|- | |- | ||
| <math>\begin{array}{c} | | <math>\begin{array}{c} | ||
| − | F_\mbox{L}=\sum_{t=1}^T\sum_{n=1}^N\left(a_nP_{n,t}^2+b_nP_{n,t}+c_n\right)+\\ | + | F_\mbox{L}=\displaystyle\sum_{t=1}^T\sum_{n=1}^N\left(a_nP_{n,t}^2+b_nP_{n,t}+c_n\right)+\\ |
| − | \sum_{j\in i,j\not =i}{\lambda }_{ij,t}^\mbox{T}(T_{ij,t}^i-T_{ij,t}^j)+\\ | + | \displaystyle\sum_{j\in i,j\not =i}{\lambda }_{ij,t}^\mbox{T}(T_{ij,t}^i-T_{ij,t}^j)+\\ |
| − | \sum_{j\in i,j\not =i}\rho \parallel T_{ij,t}^i-T_{ij,t}^j{\parallel }_2^2 | + | \displaystyle\sum_{j\in i,j\not =i}\rho \parallel T_{ij,t}^i-T_{ij,t}^j{\parallel }_2^2 |
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (22) | | style="width: 5px;text-align: right;white-space: nowrap;" | (22) | ||
|} | |} | ||
| − | |||
where <math display="inline">{\lambda }_{ij,t}^\mbox{T}</math> is the Lagrangian vector multiplier of the relaxed constraint <math display="inline">T_{ij,t}^i=T_{ij,t}^j</math>; <math>\rho</math> is the positive coefficient of the corresponding quadratic penalty term. Notice that the quadratic penalty term <math display="inline">\sum_{j\in i,j\not =i}\rho \parallel T_{ij,t}^i-T_{ij,t}^j{\parallel }_2^2</math> destroyed the decomposability of the problem, so the ADMM method was applied for distributed solution, that is, each region was solved separately, and the variables of other regions were regarded as constants in each solution, and the latest iteration results were used. The ''k-th'' iteration optimization problem for region <math display="inline"> i </math> can be given as follows: | where <math display="inline">{\lambda }_{ij,t}^\mbox{T}</math> is the Lagrangian vector multiplier of the relaxed constraint <math display="inline">T_{ij,t}^i=T_{ij,t}^j</math>; <math>\rho</math> is the positive coefficient of the corresponding quadratic penalty term. Notice that the quadratic penalty term <math display="inline">\sum_{j\in i,j\not =i}\rho \parallel T_{ij,t}^i-T_{ij,t}^j{\parallel }_2^2</math> destroyed the decomposability of the problem, so the ADMM method was applied for distributed solution, that is, each region was solved separately, and the variables of other regions were regarded as constants in each solution, and the latest iteration results were used. The ''k-th'' iteration optimization problem for region <math display="inline"> i </math> can be given as follows: | ||
| Line 378: | Line 374: | ||
|- | |- | ||
| <math>\begin{array}{c} | | <math>\begin{array}{c} | ||
| − | + | \min F_\mbox{L}^{i(k)}=\displaystyle\sum_{t=1}^T\sum_{n\in A^i}\left(a_nP_{n,t}^2+b_nP_{n,t}+c_n\right)+\\ | |
| − | \sum_{j\in i,j\not =i}{\lambda }_{ij,t}^{(k-1)T}T_{ij,t}^i+\\ | + | \displaystyle\sum_{j\in i,j\not =i}{\lambda }_{ij,t}^{(k-1)T}T_{ij,t}^i+\\ |
| − | \sum_{j\in i,j\not =i}\rho \parallel T_{ij,t}^i-T_{ij,t}^{j(\mbox{newest})}{\parallel }_2^2 | + | \displaystyle\sum_{j\in i,j\not =i}\rho \parallel T_{ij,t}^i-T_{ij,t}^{j(\mbox{newest})}{\parallel }_2^2 |
\end{array}</math> | \end{array}</math> | ||
|} | |} | ||
| Line 401: | Line 397: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>P_n^{min}\leqslant P_{n,t}\leqslant P_n^{max},n\in A^i</math> | + | | <math>P_n^{\min}\leqslant P_{n,t}\leqslant P_n^{\max},n\in A^i</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (25) | | style="width: 5px;text-align: right;white-space: nowrap;" | (25) | ||
| Line 411: | Line 407: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\ | + | | <math>\Delta P_n^{\min}\leqslant P_{n,t}-P_{n,t-1}\leqslant \Delta P_n^{\max},n\in A^i</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (26) | | style="width: 5px;text-align: right;white-space: nowrap;" | (26) | ||
| Line 431: | Line 427: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>-P_l^{max}\leqslant P_{l,t}\leqslant P_l^{max},l\in A^i</math> | + | | <math>-P_l^{\max}\leqslant P_{l,t}\leqslant P_l^{\max},l\in A^i</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (28) | | style="width: 5px;text-align: right;white-space: nowrap;" | (28) | ||
| Line 441: | Line 437: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>-T_{ij}^{max}\leqslant T_{ij,t}\leqslant T_{ij}^{max},j\in i,j\not = | + | | <math>-T_{ij}^{\max}\leqslant T_{ij,t}\leqslant T_{ij}^{\max},j\in i,j\not =i</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (29) | | style="width: 5px;text-align: right;white-space: nowrap;" | (29) | ||
| Line 463: | Line 459: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\boldsymbol{T}_{ij,t}^{j(\mbox{newest})}=\left\{ \begin{array}{ll} |
\boldsymbol{T}_{ij,t}^{j(k)}, & j<i\\ | \boldsymbol{T}_{ij,t}^{j(k)}, & j<i\\ | ||
\boldsymbol{T}_{ij,t}^{j(k-1)}, & j>i | \boldsymbol{T}_{ij,t}^{j(k-1)}, & j>i | ||
| − | \end{array}</math> | + | \end{array}\right.</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (31) | | style="width: 5px;text-align: right;white-space: nowrap;" | (31) | ||
| Line 479: | Line 475: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | |<math>{\lambda }_{ij,t}^{\left(k\right)}={\lambda }_{ij,t}^{\left(k-1\right)}+ | + | |<math>{\lambda }_{ij,t}^{\left(k\right)}={\lambda }_{ij,t}^{\left(k-1\right)}+\rho (T_{ij,t}^{i(k)}-T_{ij,t}^{j(k)})</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (32) | | style="width: 5px;text-align: right;white-space: nowrap;" | (32) | ||
| Line 494: | Line 490: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math> | + | | <math>P_{l,t}=H_i\cdot [(CP_{n,t}+C_\mbox{w}W_{n_\mbox{w},t}+ |
| − | P_{l,t}=H_i\cdot [(CP_{n,t}+C_\mbox{w}W_{n_\mbox{w},t}+ | + | C_\mbox{s}S_{n_\mbox{s},t}-D_{n_\mbox{B},t}),T_{ij,t}^i,T_{i-j+1,t}^i]</math> |
| − | C_\mbox{s}S_{n_\mbox{s},t}-D_{n_\mbox{B},t}),T_{ij,t}^i,T_{i-j+1,t}^i] | + | |
| − | + | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (33) | | style="width: 5px;text-align: right;white-space: nowrap;" | (33) | ||
| Line 506: | Line 500: | ||
{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
|-style="background:white;" | |-style="background:white;" | ||
| − | |style="text-align: center;padding:10px;"| [[Image:Draft_He_943252806-image85.jpeg| | + | |style="text-align: center;padding:10px;"| [[Image:Draft_He_943252806-image85.jpeg|500px]] |
|- | |- | ||
| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Schematic diagram of PTDF matrix construction corresponding to region <math display="inline"> i </math> | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Schematic diagram of PTDF matrix construction corresponding to region <math display="inline"> i </math> | ||
| Line 514: | Line 508: | ||
Similarly, the corresponding PTDF matrix can be solved for other regions. The PTDF for all regions still only needs to be solved once and can be used in all iterations with great convenience. | Similarly, the corresponding PTDF matrix can be solved for other regions. The PTDF for all regions still only needs to be solved once and can be used in all iterations with great convenience. | ||
| − | 3) Multi-region distributed power dispatching with fully distributed ADMM method | + | '''3) Multi-region distributed power dispatching with fully distributed ADMM method''' |
A limitation of traditional ADMM is that it still requires an upper level data center to collect data from each contact line, and perform the calculation and distribution of multipliers. Although each region does not need to share its own key power information, such upper-level data centers still have a certain authority in practical applications, which is hard to achieve. As shown in [[#tab-1|Table 1]], the only relaxed constraint in the whole iteration process of the traditional ADMM method is the contact line constraint, and the information on each contact line is only generated and used by the two areas of the contact, and is irrelevant to other areas. | A limitation of traditional ADMM is that it still requires an upper level data center to collect data from each contact line, and perform the calculation and distribution of multipliers. Although each region does not need to share its own key power information, such upper-level data centers still have a certain authority in practical applications, which is hard to achieve. As shown in [[#tab-1|Table 1]], the only relaxed constraint in the whole iteration process of the traditional ADMM method is the contact line constraint, and the information on each contact line is only generated and used by the two areas of the contact, and is irrelevant to other areas. | ||
| Line 525: | Line 519: | ||
{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
|-style="text-align:left" | |-style="text-align:left" | ||
| − | ! Relax constraints !! Global constraints !! Contact line constraints | + | ! style="text-align:left;"| Relax constraints !! style="text-align:left;"| Global constraints !! style="text-align:left;"| Contact line constraints |
|-style="text-align:left" | |-style="text-align:left" | ||
| Multiplier update features | | Multiplier update features | ||
| Line 541: | Line 535: | ||
| − | Figure 4 illustrates the transformation from traditional ADMM method to fully distributed ADMM method. The solid line denotes the power connection line, and the dashed line denotes the information connection line. The traditional ADMM method performs power transmission between regions, and each region transmits information to the upper data center. The fully distributed ADMM method eliminates the upper layer data center, and accomplishes the transmission of power and information directly between regions. The specific process is as follows: in the | + | [[#img-4|Figure 4]] illustrates the transformation from traditional ADMM method to fully distributed ADMM method. The solid line denotes the power connection line, and the dashed line denotes the information connection line. The traditional ADMM method performs power transmission between regions, and each region transmits information to the upper data center. The fully distributed ADMM method eliminates the upper layer data center, and accomplishes the transmission of power and information directly between regions. The specific process is as follows: in the <math display="inline"> k </math>-th iteration, the problem of region <math display="inline"> i </math> is solved sequentially, and the corresponding power result of the tie line is obtained. Region <math display="inline"> i </math> sends this result to region <math display="inline"> i+1 </math> and participates in the problem solving of region <math display="inline"> i+1 </math>, as the latest iteration result. After solving the problem for region <math display="inline"> i+1 </math>, region <math display="inline"> i+1 </math> already has the necessary information to update the line multiplier between region <math display="inline"> i </math> and region <math display="inline"> i+1 </math>, namely <math display="inline">T_{i-j+1,t}^{i(k)}</math> and <math display="inline">T_{i-j+1,t}^{i+1(k)}</math>, so the update of the corresponding multiplier can be done directly in the region <math display="inline"> i+1 </math>. Before the <math display="inline"> k+1 </math> iteration, region <math display="inline"> i+1 </math> passes the updated multiplier back to region <math display="inline"> i </math>, starting the next iteration. Similarly, region <math display="inline"> i+2 </math> can update the multipliers of region <math display="inline"> i </math> with region <math display="inline"> i+2 </math> and region <math display="inline"> i+1 </math> with region <math display="inline"> i+2 </math>. Ultimately, all multiplier updates are done by the regions, without the involvement of the upper data center. In addition, the stop condition of the iteration can also be determined by each region. The region responsible for updating the multiplier can further calculate the corresponding relaxed constrained error and compare it with the given error tolerance. |
| − | [[Image:Draft_He_943252806-image88.jpeg| | + | <div id='img-4'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_He_943252806-image88.jpeg|500px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. Schematic diagram of transformation from traditional ADMM method to fully distributed ADMM method | ||
| + | |} | ||
| − | |||
If the conditions are not met, this signal can be transmitted to each area through the entire information network, and the iteration continues. The solution steps of multi-region distributed power scheduling with fully distributed ADMM method are as follows: | If the conditions are not met, this signal can be transmitted to each area through the entire information network, and the iteration continues. The solution steps of multi-region distributed power scheduling with fully distributed ADMM method are as follows: | ||
| − | |||
| − | Step | + | Step 1: Give the initial values of all variables and parameters (number of iterations <math display="inline">k=0</math>, area number <math display="inline"> i=1 </math>). |
| − | Step | + | Step 2: Solve the subproblem of region <math display="inline"> i </math> based on the ADMM method. |
| − | Step | + | Step 3: Compare the number of area <math display="inline"> i </math> and the interconnection area. If <math display="inline"> i </math> is greater than the number of any interconnect zone, zone <math display="inline"> i </math> is responsible for updating the corresponding multiplier and transmitting the result to the corresponding interconnect zone. |
| − | Step | + | Step 4: <math display="inline"> i=i+1 </math>. If <math display="inline"> i </math> is greater than the maximum area number, go to Step 5. Otherwise, go to Step 2. |
| − | + | Step 5: Compare the maximum error bound by the tie line with the specified allowable error. If the error requirement is met, the iteration ends and the result is output. Otherwise, <math display="inline">k=k+1</math>, <math display="inline"> i=1 </math>, go to Step 2. | |
| − | + | ==3. Simulation result analysis== | |
| − | and a maximal tie line constraint deviation of 0.1 MW, the model underwent resolution via both the centralized approach and the fully distributed ADMM technique, with the outcomes delineated in Table 2. | + | In this investigation, the efficacy of the proposed methodology was substantiated through the development of a tripartite interconnection test case, predicated on the IEEE 30-node, 39-node, and 57-node benchmark test systems. The schematic representation of the interconnected system’s architecture is illustrated in [[#img-5|Figure 5]]. Pertaining to each subsystem, the network’s topology and ancillary parameters were preserved in congruence with the original configuration, with modifications confined solely to the corresponding numerals to fulfill the prerequisites of the interconnected framework. In alignment with the archetypal diurnal load fluctuation pattern, characterized by “two peaks and one trough” [33], a 24-hour load dataset was synthesized. Subsequently, generators situated at nodes 13, 23, 61, 68, 72, and 81 were designated as contractual power entities, with the stipulated power being allocated at a quantum equating to half of the maximal power output. The tie line’s maximal capacity threshold was established at 500 MW, while the transactional power interlinking the 30-node and 39-node systems was ascertained at 2 GWh, and the exchange power schedule was constrained within a bandwidth spanning from −50 MW to 400 MW. Employing a parameterization of <math>\rho =0.1</math> and a maximal tie line constraint deviation of 0.1 MW, the model underwent resolution via both the centralized approach and the fully distributed ADMM technique, with the outcomes delineated in [[#tab-2|Table 2]]. |
| − | [[Image:Draft_He_943252806-image89.jpeg|600px]] | + | <div id='img-5'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_He_943252806-image89.jpeg|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. Schematic diagram of the three-system interconnection example | ||
| + | |} | ||
| − | |||
| − | As delineated in Table 2, the methodology articulated herein is corroborated to engender precise solution outcomes, with the iteration count remaining well within an acceptable ambit. In pragmatic deployment, this approach is adept at navigating the complexities of inter-regional interconnected power dispatching quandaries, particularly in scenarios where centralized coordination proves to be infeasible. | + | As delineated in [[#tab-2|Table 2]], the methodology articulated herein is corroborated to engender precise solution outcomes, with the iteration count remaining well within an acceptable ambit. In pragmatic deployment, this approach is adept at navigating the complexities of inter-regional interconnected power dispatching quandaries, particularly in scenarios where centralized coordination proves to be infeasible. |
| − | Table 2 Comparison of solution results between centralized method and distributed method model | + | <div class="center" style="font-size: 85%;">'''Table 2'''. Comparison of solution results between centralized method and distributed method model</div> |
| − | {| style=" | + | <div id='tab-2'></div> |
| − | |- | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | + | |-style="text-align:center" | |
| − | + | ! style="text-align:left;"|Scheduling method !! <math display="inline">P_{21,1}</math>/MW !! <math display="inline">1^{T} T_{30-39,1}</math>/ MW !! <math display="inline">F/10^6 </math> yuan !! Number of iterations | |
| − | + | |-style="text-align:center" | |
| − | + | | style="text-align:left;"| Centralized | |
| − | + | | 314.8780 | |
| − | |- | + | | −131.0152 |
| − | + | | 1.8167 | |
| − | | style=" | + | | — |
| − | | | + | |-style="text-align:center" |
| − | | | + | | style="text-align:left;"| Distributed |
| − | | | + | | 314.9792 |
| − | |- | + | | −130.8220 |
| − | + | | 1.8167 | |
| − | | | + | | 23 |
| − | | | + | |
| − | | | + | |
| − | | | + | |
|} | |} | ||
| − | The exhibit delineates the fluctuation in the iteration count consequent to the selection of disparate regional iteration sequences within the distributed modality, given the parameter | + | The exhibit delineates the fluctuation in the iteration count consequent to the selection of disparate regional iteration sequences within the distributed modality, given the parameter <math>\rho =0.1</math>. It is discernible that the sequential order of iterations across the various regions exerts a negligible influence on the iteration quantity ([[#tab-3|Table 3]]). This implies that, within the distributed resolution framework, the iteration of each region may proceed in an arbitrary sequence, yet still achieve expeditious convergence. The determination of the parameter <math>\rho</math> is subjected to additional scrutiny in the ensuing discourse. |
| − | Table 3 Influences of regional iteration order on iteration times | + | <div class="center" style="font-size: 85%;">'''Table 3'''. Influences of regional iteration order on iteration times</div> |
| − | {| style=" | + | <div id='tab-3'></div> |
| − | |- | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | + | |-style="text-align:center" | |
| − | | | + | ! style="text-align:left"| Region iteration sequence |
| − | | | + | | 30–39–57 |
| − | | style=" | + | | 30–57–39 |
| − | + | | 39–30–57 | |
| − | + | |-style="text-align:center" | |
| − | + | ! style="text-align:left"|Number of iterations | |
| − | | | + | | 23 |
| − | | style=" | + | | 24 |
| − | + | | 21 | |
| − | + | |-style="text-align:center" | |
| − | | | + | ! style="text-align:left"|Region iteration sequence |
| − | | | + | | 39–57–30 |
| − | | style=" | + | | 57–30–39 |
| − | + | | 57–39–30 | |
| − | + | |-style="text-align:center" | |
| − | | | + | ! style="text-align:left"| Number of iterations |
| − | | | + | | 20 |
| − | | | + | | 23 |
| + | | 24 | ||
|} | |} | ||
| − | Table 4 elucidates the variability of solution outcomes contingent upon the selection of divergent values for the parameter | + | [[#tab-4|Table 4]] elucidates the variability of solution outcomes contingent upon the selection of divergent values for the parameter <math>\rho</math>. It is observed that the objective function’s value, derived from varying <math>\rho</math> parameters, manifests with commendable precision. However, the iteration frequency exhibits discernible disparities: an excessively augmented or diminished ρ value precipitates an escalation in iteration quantity. Additionally, the error trajectory corresponding to <math>\rho =0.01</math> and <math>\rho =2</math> is graphically represented in [[#img-6|Figures 6]] and [[#img-7|7]], respectively. |
| − | + | <div class="center" style="font-size: 85%;">'''Table 4'''. Influence of the selection of parameter <math>\rho</math> on the solution results</div> | |
| − | + | ||
| − | | | + | <div id='tab-4'></div> |
| − | | | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | + | |-style="text-align:center" | |
| − | | | + | ! style="text-align:left;"|<math>\rho</math> |
| − | | style=" | + | | 0.01 |
| − | + | | 0.05 | |
| − | + | | 0.1 | |
| − | + | | 0.5 | |
| − | + | | 2 | |
| − | | | + | |-style="text-align:center" |
| − | | | + | ! style="text-align:left;"|<math display="inline">F/10^6 </math> yuan |
| − | | | + | | 1.8168 |
| − | | style=" | + | | 1.8166 |
| − | + | | 1.8167 | |
| − | + | | 1.8167 | |
| − | | | + | | 1.8172 |
| − | | | + | |-style="text-align:center" |
| − | | | + | ! style="text-align:left;"|Number of iterations |
| − | + | | 79 | |
| − | | | + | | 21 |
| + | | 23 | ||
| + | | 24 | ||
| + | | 34 | ||
|} | |} | ||
| − | [[Image:Draft_He_943252806-image90.jpeg| | + | <div id='img-6'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_He_943252806-image90.jpeg|380px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 6'''. Iterative error curve of parameter <math>\rho =0.01</math> | ||
| + | |} | ||
| − | |||
| − | [[Image:Draft_He_943252806-image91.jpeg| | + | <div id='img-7'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_He_943252806-image91.jpeg|380px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 7'''. Iterative error curve of parameter <math>\rho =2</math> | ||
| + | |} | ||
| − | |||
| − | Figures 6 and 7 elucidate the trajectory of iterative errors, revealing that with | + | [[#img-6|Figures 6]] and [[#img-7|7]] elucidate the trajectory of iterative errors, revealing that with <math>\rho =0.01</math>, the error curve is characterized by a smooth yet gradual decline, necessitating an increased number of iterations. Conversely, when <math>\rho =2</math> is employed, the error curve exhibits a precipitous descent accompanied by notable fluctuations, resulting in a heightened iteration count. Consequently, the parameter <math>\rho</math> serves a dual function: it not only modulates the multiplier correction step within the iterative sequence but also impacts the oscillatory nature of the process. These dual roles exert antithetical effects on the rate of convergence. In practical scenarios, the optimal relative value of <math>\rho</math> can be ascertained through empirical experimentation. |
| − | =4. Conclusion= | + | ==4. Conclusion== |
| − | The current investigation addresses the dynamic economic dispatch (DED) dilemma within a trans-regional power system context, advancing a model that leverages the alternating direction multiplier method (ADMM). This model innovatively obviates the traditional requirement for a superior data center to perform multiplier updates, thus fostering a fully distributed dynamic economic scheduling (DDES) framework. The model’s validation was conducted through simulation tests on a set of interconnected systems, based on the IEEE standard test system. The results from these simulations substantiate the model’s ability to generate highly precise solutions across a prudent range of iterations. The valuation strategy for the | + | The current investigation addresses the dynamic economic dispatch (DED) dilemma within a trans-regional power system context, advancing a model that leverages the alternating direction multiplier method (ADMM). This model innovatively obviates the traditional requirement for a superior data center to perform multiplier updates, thus fostering a fully distributed dynamic economic scheduling (DDES) framework. The model’s validation was conducted through simulation tests on a set of interconnected systems, based on the IEEE standard test system. The results from these simulations substantiate the model’s ability to generate highly precise solutions across a prudent range of iterations. The valuation strategy for the parameter <math display="inline">\rho </math> was scrutinized, revealing its significant impact on the iteration count. It was observed that an overly large or small <math display="inline">\rho </math> value could either amplify fluctuations in the iteration process or slow down the multiplier’s update speed, both of which are counterproductive to rapid iterative convergence. In practical scenarios, optimizing the parameter <math display="inline">\rho </math> can be achieved through iterative experimental adjustments. |
| − | References | + | ==References== |
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
| − | [1] G. | + | [1] Hu G., Bie Z., Wang X. Optimal dispatch in wind integrated system considering operation reliability. Trans. China Electrotech. Soc., 28(5):58-65, 2013. |
| − | [2] D. C. | + | [2] Walters D.C., Sheble G.B. Genetic algorithm solution of economic dispatch with valve point loading. IEEE Trans. Power Syst., 8(3):1325-1332, 1993. |
| − | [3] C. L. | + | [3] Chiang C.L. Improved genetic algorithm for power economic dispatch of units with valve-point effects and multiple fuels. IEEE Trans. Power Syst., 20(4):1690-1699, 2005. |
| − | [4] J. | + | [4] Hetzer J., David C.Y., Bhattarai K. An economic dispatch model incorporating wind power. IEEE Trans. Energy Convers., 23(2):603-611, 2008. |
| − | [5] T. | + | [5] Ding T., Bo R., Gu W., et al. Big-M based MIQP method for economic dispatch with disjoint prohibited zones. IEEE Trans. Power Syst., 29(2):976-977, 2014. |
| − | [6] T. | + | [6] Ding T., Bo R., Li F.X., et al. A bi-level branch and bound method for economic dispatch with disjoint prohibited zones considering network losses. IEEE Trans. Power Syst., 30(6):2841-2855, 2015. |
| − | [7] P. | + | [7] Attaviriyanupap P., Kita H., Tanaka E., et al. A hybrid EP and SQP for dynamic economic dispatch with nonsmooth fuel cost function. IEEE Trans. Power Syst., 17(2):411-416, 2002. |
| − | [8] H. | + | [8] Chen H., Wang Y., Xuan P., et al. Robust economic dispatch method of microgrid containing high proportion of wind power. Control Theory & Appl., 34(8):1104-1111, 2017. |
| − | [9] W. M. | + | [9] Lin W.M., Chen S.J. Bid-based dynamic economic dispatch with an efficient interior point algorithm. Int. J. Electr. Power Energy Syst., 24(1):51-57, 2002. |
| − | [10] C. E. | + | [10] Lin C.E., Viviani G.L. Hierarchical economic dispatch for piecewise quadratic cost functions. IEEE Trans. Power Appar. Syst., 103(6):1170-1175, 1984. |
| − | [11] T. | + | [11] Guo T., Henwood M.I., van Ooijen M. An algorithm for combined heat and power economic dispatch. IEEE Trans. Power Syst., 11(4):1778-1784, 1996. |
| − | [12] B. H. | + | [12] Kim B.H., Baldick R. Coarse-grained distributed optimal power flow. IEEE Trans. Power Syst., 12(2):932-939, 1997. |
| − | [13] B. H. | + | [13] Kim B.H., Baldick R. A comparison of distributed optimal power flow algorithms. IEEE Trans. Power Syst., 15(2):599-604, 2000. |
| − | [14] X. | + | [14] Cheng X., Li J., Cao L., et al. Multi-objective distributed parallel reactive power optimization based on subarea division of the power systems. Proc. CSEE, 23(10): 109-113, 2003. |
| − | [15] A. J. | + | [15] Conejo A.J., Aguado J.A. Multi-area coordinated decentralized DC optimal power flow. IEEE Trans. Power Syst., 13(4):1272-1278, 1998. |
| − | [16] W. | + | [16] Zheng W., Wu W., Zhang B., et al. Fully distributed multi-area economic dispatch method for active distribution networks. IET Gener. Transm. Distrib., 9(12):1341-1351, 2015. |
| − | [17] X. | + | [17] Cheng X., Li J., Cao L., et al. Distributed and parallel optimal power flow solution of electronic power systems. Autom. Electr. Power Syst., 27(24):23-27, 2003. |
| − | [18] F. J. | + | [18] Nogales F.J., Prieto F.J., Conejo A.J. A decomposition methodology applied to the multi-area optimal power flow problem. Ann. Oper. Res., 120(1/4):99-116, 2003. |
| − | [19] | + | [19] Dall'Anese E., Zhu H., Giannakis G.B. Distributed optimal power flow for smart microgrids. IEEE Trans. Smart Grid, 4(3):1464-1475, 2013. |
| − | [20] P. | + | [20] Sulc P., Backhaus S., Chertkov M. Optimal distributed control of reactive power via the alternating direction method of multipliers. IEEE Trans. Energy Convers., 29(4):968-977, 2014. |
| − | [21] T. | + | [21] Erseghe T. Distributed optimal power flow using ADMM. IEEE Trans. Power Syst., 29(5):2370-2380, 2014. |
| − | [22] H. | + | [22] Zhang H., Li Y., Gao W.D., et al. Distributed optimal energy management for energy internet. IEEE Trans. Ind. Inform., 13(6):3081-3097, 2017. |
| − | [23] Y. | + | [23] Wang Y., Wu L., Wang S. A fully-decentralized consensus-based ADMM approach for DC-OPF with demand response. IEEE Trans. Smart Grid, 8(6):2637-2647, 2017. |
| − | [24] G. | + | [24] Cohen G. Auxiliary problem principle and decomposition of optimization problems. J. Optim. Theory Appl., 32(3):277-305, 1980. |
| − | [25] G. | + | [25] Cohen G. Auxiliary problem principle extended to variational inequalities. J. Optim. Theory Appl., 59(2):325-333, 1988. |
| − | [26] D. | + | [26] Hur D., Park J.K., Kim B.H. Evaluation of convergence rate in the auxiliary problem principle for distributed optimal power flow. IEE Proc.-Gener. Transm. Distrib., 149(5):525-532, 2002. |
| − | [27] A. | + | [27] Losi A., Russo M. On the application of the auxiliary problem principle. J. Optim. Theory Appl. 117(2):377-396, 2003. |
| − | [28] C. | + | [28] Chen C., He B., Ye Y., et al. The direct extension of ADMM for multi-block convex minimization problems is not necessarily convergent. Math. Program., 155(1/2):57-79, 2016. |
| − | [29] E. | + | [29] Ghadimi E., Teixeira A., Shames I., et al. Optimal parameter selection for the alternating direction method of multipliers (ADMM): quadratic problems. IEEE Trans. Autom. Control, 60(3):644-658, 2015. |
| − | [30] M. | + | [30] Hong M., Luo Z.Q. On the linear convergence of the alternating direction method of multipliers. Math. Program., 162(1/2):165-199, 2017. |
| − | [31] M. | + | [31] Fukushima M. Application of the alternating direction method of multipliers to separable convex programming problems. Comput. Optim. Appl., 1(1):93-111, 1992. |
| − | [32] E. | + | [32] Wei E., Ozdaglar A. Distributed alternating direction method of multipliers. In: The 51st IEEE Conf. on Decision and Control, Maui, HI, USA: IEEE, pp. 5445-5450, 2012. |
| − | [33] D. | + | [33] Xia D. Power system analysis. 2nd ed., Beijing: China Electric Power Press, 2011. |
Latest revision as of 13:14, 13 May 2024
Abstract
In this study, a novel approach to dynamic economic dispatch for multi-region power systems is introduced, leveraging the alternating direction multiplier method (ADMM) for computational efficiency. The method begins by dividing an interconnected power system into coherent groups, assigning local processors to each area to estimate black-box transfer function models using Lagrange multipliers. These processors then collaborate to form a global transfer function model through a consensus algorithm, leading to the derivation of a transfer function residue for the optimal wide-area control loop. A wide-area damping controller is designed from this residue, and its effectiveness is validated on two area and IEEE-39 bus test systems using RTDS/RSCAD and MATLAB co-simulation platforms. Simultaneously, the study proposes an economic scheduling model that aims to minimize operational costs while meeting various operational constraints. By severing inter-regional connections, the ADMM enables distributed resolution of the optimization problem, breaking it down into regional sub-problems that are iteratively solved to reach the global optimum. This process eliminates the need for a centralized data repository for multiplier updates, supporting a fully distributed scheduling approach. Additionally, a multi-period optimization technique is integrated to address the power system’s temporal dependencies. The approach's validity is demonstrated through empirical analysis of a tri-regional interconnected system based on the IEEE standard test system, confirming the strategy's effectiveness in economic dispatch.
Keywords: Microgrid, distribution side power market, intermediation, supply function equilibrium, distributed optimization
1. Introduction
Within the domain of power systems, Economic Dispatch (ED) is characterized as an optimization dilemma aimed at minimizing network losses or generation costs while conforming to the constraints of power flow and operational parameters [1-8]. The integration of renewable energy sources, notably photovoltaic and wind power, has introduced a heightened degree of intertemporal coupling in power systems. Such advancements have deemed static ED, reliant on single temporal analysis, insufficient for the complex scenarios of modern power systems, thereby necessitating a transition to dynamic ED. The burgeoning power market demands increased interconnectivity and more frequent power exchanges across regions, achievable through centralized dispatching by an authoritative cross-regional center or via coordination among regional centers. Nevertheless, centralized scheduling (CS), which requires a central entity to collect detailed data and centrally determine operational strategies, faces numerous challenges. Scholars globally have explored centralized dispatching, utilizing classical optimization algorithms like the interior point method [9], Lambda iteration method [10], and Lagrange method [11], which are intrinsically centralized. Centralized scheduling algorithms eliminate iterative processes, facilitating direct global optimization. However, this method is impractical for large-scale scheduling due to the exponential increase in variable volume and complexity. Moreover, research intensification on the global energy Internet and the development of transnational regional UHV power grids aim to enhance power complementarity, load peak shifting, and support. China has achieved some power interconnection with neighboring countries, including Russia, Mongolia, Vietnam, Laos, and Myanmar, totaling an interconnection capacity of roughly 2.6 million kilowatts. Nonetheless, the reluctance of nations to share detailed power system information, for strategic confidentiality reasons, limits the viability of higher-level dispatch centers with global authority.
In light of these challenges, the necessity for a distributed scheduling framework becomes critical, one that allocates scheduling responsibilities to regional dispatching centers. This paradigm shift paves the way for globally optimal power scheduling based on a distributed architecture that minimizes the need for extensive inter-regional information sharing. Consequently, Distributed Dynamic Scheduling (DDS) has attracted increasing academic attention, emerging from research on Distributed Optimal Power Flow (DOPF) optimization approaches.
In the scholarly discourse on power systems, the concept of virtual nodes has been introduced as a means to balance power flow post-decoupling within subregions, thus enabling the formulation of a multi-regional decomposition algorithm. Significantly, Kim and Baldick [12] endorse a parallel Distributed Optimal Power Flow (DOPF) model, designed for extensive regional interconnection systems, validated through simulations on systems of moderate size. Further, Kim and Baldick [13] mathematically implement the proposed distributed framework by amalgamating two distinct decomposition methods: the Predictor-Corrector Proximal Multiplier (PCPM) and the Alternating Direction Method (ADM). Additionally, Cheng et al. [14] addresse the distributed processing of the multi-objective reactive power optimization issue within large-scale power systems, effectively resolving the centralized reactive power optimization challenge.
Furthermore, Conejo and Aguado [15] incorporate network loss into the foundational DOPF model using cosine approximation. The Auxiliary Problem Principle (APP) is employed in literature [16-18] to manage regional coupling constraints, leading to the development of the DOPF algorithm. The Alternating Direction Multiplier Method (ADMM), thoroughly examined in literature [19-23], has been extensively refined for deployment within the Distributed Dynamic Scheduling (DDS) sphere. Notably, Dall'Anese et al. [19] convert the optimal power flow problem within microgrids into a convex issue via semi-definite programming relaxation techniques, thereafter seeking a distributed solution through the ADMM. Sulc et al. [20] utilize the ADMM, predicated on consistency, for the distributed optimal control of reactive power in power systems, demonstrating its superiority to the dual-ascent method.
This research articulates a fully distributed algorithm to address the centralized dynamic scheduling issue within power systems featuring a multi-regional interconnection structure. Based on the inherent characteristics of power systems and employing the ADMM for the decoupling of inter-regional connections, this approach decomposes the central issue into individual sub-optimization tasks for each region. Simultaneously, the traditional role of the data center, responsible for multiplier updates, becomes redundant, resulting in a completely distributed scheduling framework. The achievement of an optimal system-wide solution is accomplished through the iterative resolution of economic scheduling sub-problems specific to each region. An illustrative analysis, utilizing a multi-regional interconnected system modeled on the IEEE standard test system, affirms the effectiveness and precision of the proposed model in managing the intricacies of multi-regional distributed dynamic scheduling in power systems.
2. Multi-region dynamic scheduling model
The multi-regional power scheduling model, as depicted in Figure 1, encapsulates the intricate scheduling dynamics extant among various regions within a power system. It is constituted by an array of generator sets and loads, each interlinked via transmission lines. The transfer of power and information is facilitated through contact lines bridging regions, thereby enabling their interconnectivity. Owing to the autonomous dispatching attributes inherent to each region, the real-time sharing of comprehensive power dispatching data presents a formidable challenge. Consequently, the adoption of a distributed scheduling approach is necessitated, one that eschews the traditional dispatching center, and through iterative processes, converges upon the globally optimal power scheduling, all while minimizing the exchange of information between regions.

|
| Figure 1. Multi-region economic dispatch model |
2.1 Traditional centralized scheduling model
The traditional centralized power dispatching model can be established as follows:
1) Objective function
The objective function is to minimize the total operating cost of the system. Among them, the main consideration of the operating cost of the generator set. The expression of the objective function is as follows:
|
|
(1) |
where is the total operating cost of the system; is the number of each scheduling period; represents the total number of scheduling periods; and are the number of the generator set and the system node respectively; and are the total number of generator sets and system nodes respectively; represents the actual output of generator set during the period ; , and are the coefficient of output characteristic of generator set .
2) Constraints
a) System power balance constraint, that is, the total generator output at any time is equal to the load demand:
|
|
(2) |
where is the load demand of node during the period .
b) Constraints on the upper and lower limits of generator set output:
|
|
(3) |
where and are, respectively, the lower limit and upper limit of output of generator set in any period.
c) The upper and lower limits of the generator set climbing:
|
|
(4) |
where and indicate the minimum climb rate (i.e. maximum downward climb rate) and maximum climb rate (i.e. maximum upward climb rate) of generator set , respectively.
d) The power constraint of the generator set contract, that is, the total power generation of the generator set within a given period of time must comply with the agreed contract:
|
|
(5) |
where is the contracted electricity quantity of generator set in a given period of time; is the set of generator sets for which the contracted electricity quantity is agreed.
e) The contract unit can be decomposed value deviation constraint, that is, the contract electricity decomposed to the day needs to be within a certain deviation range:
|
|
(6) |
where is the number of the dispatch date; is the generation capacity of generator set in date ; and are the planned allowable minimum and maximum of the energy decomposition value of the generator set , respectively.
f) Transmission line maximum capacity constraints:
|
|
(7) |
where is the transmission power of line in the time period ; is the maximum transmission power of line . The maximum capacity of the two-way transmission of the line is equal.
g) Maximum capacity constraint of regional liaison line:
|
|
(8) |
Among them: is a vector variable, representing the transmission power of each contact line between region and region in the time period ; is a vector constant that represents the maximum transmission power of the contact lines between region and region . This paper assumes that the maximum two-way transmission capacity of each link line is equal.
h) Constraint on the power of the regional contact line transaction, that is, the power of the contact line transaction within a given period must comply with the agreement between regions:
|
|
(9) |
where ; is the total amount of agreed transaction power between region and region in a given period of time; is the set of region pairs for the agreed transaction of electricity.
i) Regional liaison line switching power plan constraints, that is, the regional liaison line switching power of each period should be within the allowable range of assessment deviation:
|
|
(10) |
where and are the minimum and maximum value allowed by the switching power plan between region and region during the period, respectively.
The power transmission distribution factor (PTDF) matrix can be used to obtain the power transmission lines. The PTDF matrix directly links the net injected power of each node to the power transmission of each branch, and its main advantage is that it avoids introducing redundant voltage phase angle variables, and only depends on the grid structure and line parameters, and is independent of the variation of the injected power of each node, that is, for a given network, only one PTDF matrix is needed to be reused. The basic format of its application is:
|
|
(11) |
where is the vector composed of the power of each branch; is the corresponding PTDF matrix; is the vector composed of the net injected power of each node.
For this centralized scheduling problem:
|
|
(12) |
where is the sorting matrix, the generator sets are rearranged in the order of node numbers.
2.2 Distributed scheduling model
In the discourse of distributed scheduling (DS), the concept is predicated on the decoupling of inter-regional connections, thereby enabling the segmentation of the aggregate power scheduling optimization quandary into distinct regional sub-problems. These sub-problems are iteratively addressed until a pre-defined error threshold is attained. Within the mathematical frameworks employed for DS, Lagrange relaxation (LR) is commonly invoked. This method mitigates the constraints, amalgamates them into the objective function, and iteratively refines the Lagrange multipliers until the cessation criteria of the iteration are fulfilled. Nonetheless, the LR method grapples with the challenge of selecting an appropriate step size for updating the multipliers, which impinges upon convergence rates.
To surmount this impediment, the present study introduces the augmented Lagrangian relaxation method (ALR), which incorporates a quadratic penalty term for the relaxed constraints within the objective function and adheres to a fixed step length for multiplier updates, thereby enhancing convergence. However, this incorporation of a quadratic penalty term compromises the factorability of the optimization problem, representing a significant limitation of the ALR approach. Two prevalent resolutions are the auxiliary problem principle method (APP) [24-27] and the alternating direction multiplier method (ADMM) [28-32]. Each methodology exhibits its own merits and demerits: the APP method facilitates parallel solutions albeit with moderate convergence velocity, whereas the ADMM approach necessitates serial resolution but boasts rapid convergence rates. Given the relatively modest number of regions within the extant power system architecture, the ADMM method is selected for resolving the multi-regional distributed power dispatching conundrum.
1) Traditional ADMM method
Consider the following optimization problems:
|
|
(13) |
|
|
(14) |
Applying augmented Lagrange relaxation to equality constraints, the unconstrained optimization problem is
|
|
(15) |
where is the Lagrange multiplier and is the positive quadratic penalty term coefficient.
The quintessence of the Alternating Direction Method of Multipliers (ADMM) approach resides in the premise that, during the resolution of a variable, concomitant variables are held constant, utilizing the outcomes from the antecedent iteration. This stratagem effectively “decouples” the inter-variable nexus, thereby adroitly circumventing the complexities associated with the quadratic penalty term. The fundamental iterative schema of ADMM unfolds in the ensuing manner:
|
|
(16) |
|
|
(17) |
|
|
(18) |
This iterates over and over again until the iteration termination condition is met.
2) Multi-region distributed power scheduling based on traditional ADMM method
A multi-region distributed power dispatching model is derived from the centralized dispatching model by applying the conventional ADMM method. The main process is as follows: The centralized scheduling model reveals that the coupling constraint between regions is manifested in the constraint related to the liaison line, that is, the maximum capacity constraint of the regional liaison line . However, the variable is correlated with both region and region . If the constraint is directly relaxed, the decoupling in the true sense cannot be achieved. Therefore, the constraint should be first rewritten as follows:
|
|
(19) |
|
|
(20) |
|
|
(21) |
Among them: represents the transmission power of the contact lines between region and region in the time period when solving the sub-problem of region ; represents the transmission power of the contact lines between region and region in the time period when solving the subproblem of region . Figure 2 illustrates this process by treating the contact lines between region and region as two, each belonging to its own region and satisfying the same maximum capacity constraint, and finally ensuring that the power of the two contact lines is equal at all times. After processing, the relationship between the two regions is clearly reflected in the constraint .
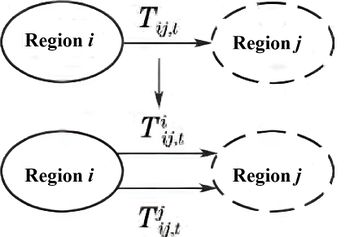
|
| Figure 2. Schematic diagram of constraint rewriting of the contact line |
For constraint , applying augmented Lagrange relaxation, the objective function is:
|
|
(22) |
where is the Lagrangian vector multiplier of the relaxed constraint ; is the positive coefficient of the corresponding quadratic penalty term. Notice that the quadratic penalty term destroyed the decomposability of the problem, so the ADMM method was applied for distributed solution, that is, each region was solved separately, and the variables of other regions were regarded as constants in each solution, and the latest iteration results were used. The k-th iteration optimization problem for region can be given as follows:
|
|
(23) |
|
|
(24) |
|
|
(25) |
|
|
(26) |
|
|
(27) |
|
|
(28) |
|
|
(29) |
|
|
(30) |
where represents the set of all elements in region ; is the value of the latest iteration of :
|
|
(31) |
After each iteration, the update process of the multiplier is:
|
|
(32) |
The PTDF matrix can still be used to calculate the power transmission of the lines in region . However, the whole network PTDF matrix derived from the centralized scheduling requires the information of all nodes, which obviously cannot be directly applied to the problem solving of region . Therefore, the corresponding PTDF matrix needs to be found, which can utilize the information of region and the information of the contact lines between region and other regions to obtain the power transmission of the lines in region .
Figure 3 illustrates the solution method of the target PTDF matrix. First, all regions connected to region (i.e., regions and in the figure) are equivalent to nodes outside region , whose injected power is the corresponding power transmitted by the liaison line. Then, the PTDF matrix is computed for this equivalent network. Using the PTDF matrix, the power transmission of the lines in region can be acquired by using the information of region and the information of the contact lines between region and other regions. Its formula is as follows (all variables belong to region ):
|
|
(33) |
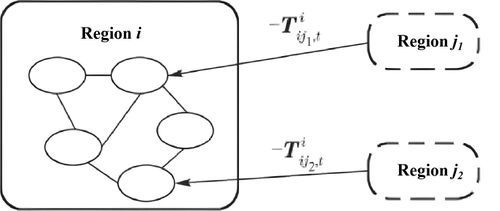
|
| Figure 3. Schematic diagram of PTDF matrix construction corresponding to region |
Similarly, the corresponding PTDF matrix can be solved for other regions. The PTDF for all regions still only needs to be solved once and can be used in all iterations with great convenience.
3) Multi-region distributed power dispatching with fully distributed ADMM method
A limitation of traditional ADMM is that it still requires an upper level data center to collect data from each contact line, and perform the calculation and distribution of multipliers. Although each region does not need to share its own key power information, such upper-level data centers still have a certain authority in practical applications, which is hard to achieve. As shown in Table 1, the only relaxed constraint in the whole iteration process of the traditional ADMM method is the contact line constraint, and the information on each contact line is only generated and used by the two areas of the contact, and is irrelevant to other areas.
Hence, by exploiting the feature that the contact line is not a global constraint, the update process of the corresponding multiplier for each contact line can be completed between the two interconnection areas, without uploading to the data center. Thus, the multiplier calculation and assignment of each contact line can be done by the relevant subareas, and the upper data center can be eliminated, resulting in a fully distributed ADMM method. It should be noted that the mathematical formulas for solving subproblems and updating multipliers for each region are unchanged, so the method has the same mathematical properties as the traditional ADMM method.
| Relax constraints | Global constraints | Contact line constraints |
|---|---|---|
| Multiplier update features | Information for all regions is required | Only contact area information is required |
| Multiplier assignment features | Assignment to all regions is required | Only need to be assigned to the contact area |
| Upper-tier data center | Need | No, the corresponding work can be transferred to the liaison area |
Figure 4 illustrates the transformation from traditional ADMM method to fully distributed ADMM method. The solid line denotes the power connection line, and the dashed line denotes the information connection line. The traditional ADMM method performs power transmission between regions, and each region transmits information to the upper data center. The fully distributed ADMM method eliminates the upper layer data center, and accomplishes the transmission of power and information directly between regions. The specific process is as follows: in the -th iteration, the problem of region is solved sequentially, and the corresponding power result of the tie line is obtained. Region sends this result to region and participates in the problem solving of region , as the latest iteration result. After solving the problem for region , region already has the necessary information to update the line multiplier between region and region , namely and , so the update of the corresponding multiplier can be done directly in the region . Before the iteration, region passes the updated multiplier back to region , starting the next iteration. Similarly, region can update the multipliers of region with region and region with region . Ultimately, all multiplier updates are done by the regions, without the involvement of the upper data center. In addition, the stop condition of the iteration can also be determined by each region. The region responsible for updating the multiplier can further calculate the corresponding relaxed constrained error and compare it with the given error tolerance.
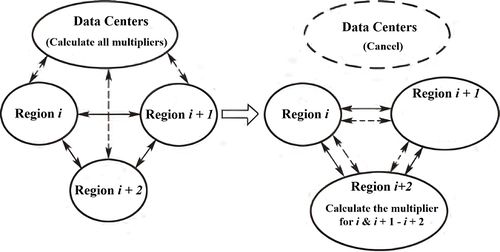
|
| Figure 4. Schematic diagram of transformation from traditional ADMM method to fully distributed ADMM method |
If the conditions are not met, this signal can be transmitted to each area through the entire information network, and the iteration continues. The solution steps of multi-region distributed power scheduling with fully distributed ADMM method are as follows:
Step 1: Give the initial values of all variables and parameters (number of iterations , area number ).
Step 2: Solve the subproblem of region based on the ADMM method.
Step 3: Compare the number of area and the interconnection area. If is greater than the number of any interconnect zone, zone is responsible for updating the corresponding multiplier and transmitting the result to the corresponding interconnect zone.
Step 4: . If is greater than the maximum area number, go to Step 5. Otherwise, go to Step 2.
Step 5: Compare the maximum error bound by the tie line with the specified allowable error. If the error requirement is met, the iteration ends and the result is output. Otherwise, , , go to Step 2.
3. Simulation result analysis
In this investigation, the efficacy of the proposed methodology was substantiated through the development of a tripartite interconnection test case, predicated on the IEEE 30-node, 39-node, and 57-node benchmark test systems. The schematic representation of the interconnected system’s architecture is illustrated in Figure 5. Pertaining to each subsystem, the network’s topology and ancillary parameters were preserved in congruence with the original configuration, with modifications confined solely to the corresponding numerals to fulfill the prerequisites of the interconnected framework. In alignment with the archetypal diurnal load fluctuation pattern, characterized by “two peaks and one trough” [33], a 24-hour load dataset was synthesized. Subsequently, generators situated at nodes 13, 23, 61, 68, 72, and 81 were designated as contractual power entities, with the stipulated power being allocated at a quantum equating to half of the maximal power output. The tie line’s maximal capacity threshold was established at 500 MW, while the transactional power interlinking the 30-node and 39-node systems was ascertained at 2 GWh, and the exchange power schedule was constrained within a bandwidth spanning from −50 MW to 400 MW. Employing a parameterization of and a maximal tie line constraint deviation of 0.1 MW, the model underwent resolution via both the centralized approach and the fully distributed ADMM technique, with the outcomes delineated in Table 2.

|
| Figure 5. Schematic diagram of the three-system interconnection example |
As delineated in Table 2, the methodology articulated herein is corroborated to engender precise solution outcomes, with the iteration count remaining well within an acceptable ambit. In pragmatic deployment, this approach is adept at navigating the complexities of inter-regional interconnected power dispatching quandaries, particularly in scenarios where centralized coordination proves to be infeasible.
| Scheduling method | /MW | / MW | yuan | Number of iterations |
|---|---|---|---|---|
| Centralized | 314.8780 | −131.0152 | 1.8167 | — |
| Distributed | 314.9792 | −130.8220 | 1.8167 | 23 |
The exhibit delineates the fluctuation in the iteration count consequent to the selection of disparate regional iteration sequences within the distributed modality, given the parameter . It is discernible that the sequential order of iterations across the various regions exerts a negligible influence on the iteration quantity (Table 3). This implies that, within the distributed resolution framework, the iteration of each region may proceed in an arbitrary sequence, yet still achieve expeditious convergence. The determination of the parameter is subjected to additional scrutiny in the ensuing discourse.
| Region iteration sequence | 30–39–57 | 30–57–39 | 39–30–57 |
|---|---|---|---|
| Number of iterations | 23 | 24 | 21 |
| Region iteration sequence | 39–57–30 | 57–30–39 | 57–39–30 |
| Number of iterations | 20 | 23 | 24 |
Table 4 elucidates the variability of solution outcomes contingent upon the selection of divergent values for the parameter . It is observed that the objective function’s value, derived from varying parameters, manifests with commendable precision. However, the iteration frequency exhibits discernible disparities: an excessively augmented or diminished ρ value precipitates an escalation in iteration quantity. Additionally, the error trajectory corresponding to and is graphically represented in Figures 6 and 7, respectively.
| 0.01 | 0.05 | 0.1 | 0.5 | 2 | |
| yuan | 1.8168 | 1.8166 | 1.8167 | 1.8167 | 1.8172 |
| Number of iterations | 79 | 21 | 23 | 24 | 34 |
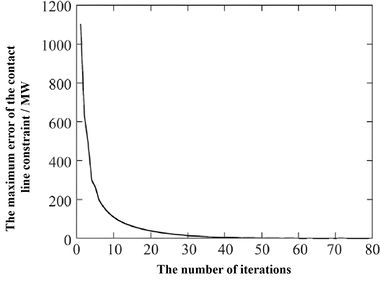
|
| Figure 6. Iterative error curve of parameter |
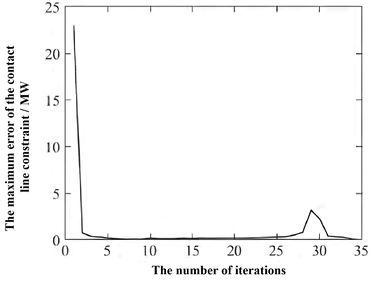
|
| Figure 7. Iterative error curve of parameter |
Figures 6 and 7 elucidate the trajectory of iterative errors, revealing that with , the error curve is characterized by a smooth yet gradual decline, necessitating an increased number of iterations. Conversely, when is employed, the error curve exhibits a precipitous descent accompanied by notable fluctuations, resulting in a heightened iteration count. Consequently, the parameter serves a dual function: it not only modulates the multiplier correction step within the iterative sequence but also impacts the oscillatory nature of the process. These dual roles exert antithetical effects on the rate of convergence. In practical scenarios, the optimal relative value of can be ascertained through empirical experimentation.
4. Conclusion
The current investigation addresses the dynamic economic dispatch (DED) dilemma within a trans-regional power system context, advancing a model that leverages the alternating direction multiplier method (ADMM). This model innovatively obviates the traditional requirement for a superior data center to perform multiplier updates, thus fostering a fully distributed dynamic economic scheduling (DDES) framework. The model’s validation was conducted through simulation tests on a set of interconnected systems, based on the IEEE standard test system. The results from these simulations substantiate the model’s ability to generate highly precise solutions across a prudent range of iterations. The valuation strategy for the parameter was scrutinized, revealing its significant impact on the iteration count. It was observed that an overly large or small value could either amplify fluctuations in the iteration process or slow down the multiplier’s update speed, both of which are counterproductive to rapid iterative convergence. In practical scenarios, optimizing the parameter can be achieved through iterative experimental adjustments.
References
[1] Hu G., Bie Z., Wang X. Optimal dispatch in wind integrated system considering operation reliability. Trans. China Electrotech. Soc., 28(5):58-65, 2013.
[2] Walters D.C., Sheble G.B. Genetic algorithm solution of economic dispatch with valve point loading. IEEE Trans. Power Syst., 8(3):1325-1332, 1993.
[3] Chiang C.L. Improved genetic algorithm for power economic dispatch of units with valve-point effects and multiple fuels. IEEE Trans. Power Syst., 20(4):1690-1699, 2005.
[4] Hetzer J., David C.Y., Bhattarai K. An economic dispatch model incorporating wind power. IEEE Trans. Energy Convers., 23(2):603-611, 2008.
[5] Ding T., Bo R., Gu W., et al. Big-M based MIQP method for economic dispatch with disjoint prohibited zones. IEEE Trans. Power Syst., 29(2):976-977, 2014.
[6] Ding T., Bo R., Li F.X., et al. A bi-level branch and bound method for economic dispatch with disjoint prohibited zones considering network losses. IEEE Trans. Power Syst., 30(6):2841-2855, 2015.
[7] Attaviriyanupap P., Kita H., Tanaka E., et al. A hybrid EP and SQP for dynamic economic dispatch with nonsmooth fuel cost function. IEEE Trans. Power Syst., 17(2):411-416, 2002.
[8] Chen H., Wang Y., Xuan P., et al. Robust economic dispatch method of microgrid containing high proportion of wind power. Control Theory & Appl., 34(8):1104-1111, 2017.
[9] Lin W.M., Chen S.J. Bid-based dynamic economic dispatch with an efficient interior point algorithm. Int. J. Electr. Power Energy Syst., 24(1):51-57, 2002.
[10] Lin C.E., Viviani G.L. Hierarchical economic dispatch for piecewise quadratic cost functions. IEEE Trans. Power Appar. Syst., 103(6):1170-1175, 1984.
[11] Guo T., Henwood M.I., van Ooijen M. An algorithm for combined heat and power economic dispatch. IEEE Trans. Power Syst., 11(4):1778-1784, 1996.
[12] Kim B.H., Baldick R. Coarse-grained distributed optimal power flow. IEEE Trans. Power Syst., 12(2):932-939, 1997.
[13] Kim B.H., Baldick R. A comparison of distributed optimal power flow algorithms. IEEE Trans. Power Syst., 15(2):599-604, 2000.
[14] Cheng X., Li J., Cao L., et al. Multi-objective distributed parallel reactive power optimization based on subarea division of the power systems. Proc. CSEE, 23(10): 109-113, 2003.
[15] Conejo A.J., Aguado J.A. Multi-area coordinated decentralized DC optimal power flow. IEEE Trans. Power Syst., 13(4):1272-1278, 1998.
[16] Zheng W., Wu W., Zhang B., et al. Fully distributed multi-area economic dispatch method for active distribution networks. IET Gener. Transm. Distrib., 9(12):1341-1351, 2015.
[17] Cheng X., Li J., Cao L., et al. Distributed and parallel optimal power flow solution of electronic power systems. Autom. Electr. Power Syst., 27(24):23-27, 2003.
[18] Nogales F.J., Prieto F.J., Conejo A.J. A decomposition methodology applied to the multi-area optimal power flow problem. Ann. Oper. Res., 120(1/4):99-116, 2003.
[19] Dall'Anese E., Zhu H., Giannakis G.B. Distributed optimal power flow for smart microgrids. IEEE Trans. Smart Grid, 4(3):1464-1475, 2013.
[20] Sulc P., Backhaus S., Chertkov M. Optimal distributed control of reactive power via the alternating direction method of multipliers. IEEE Trans. Energy Convers., 29(4):968-977, 2014.
[21] Erseghe T. Distributed optimal power flow using ADMM. IEEE Trans. Power Syst., 29(5):2370-2380, 2014.
[22] Zhang H., Li Y., Gao W.D., et al. Distributed optimal energy management for energy internet. IEEE Trans. Ind. Inform., 13(6):3081-3097, 2017.
[23] Wang Y., Wu L., Wang S. A fully-decentralized consensus-based ADMM approach for DC-OPF with demand response. IEEE Trans. Smart Grid, 8(6):2637-2647, 2017.
[24] Cohen G. Auxiliary problem principle and decomposition of optimization problems. J. Optim. Theory Appl., 32(3):277-305, 1980.
[25] Cohen G. Auxiliary problem principle extended to variational inequalities. J. Optim. Theory Appl., 59(2):325-333, 1988.
[26] Hur D., Park J.K., Kim B.H. Evaluation of convergence rate in the auxiliary problem principle for distributed optimal power flow. IEE Proc.-Gener. Transm. Distrib., 149(5):525-532, 2002.
[27] Losi A., Russo M. On the application of the auxiliary problem principle. J. Optim. Theory Appl. 117(2):377-396, 2003.
[28] Chen C., He B., Ye Y., et al. The direct extension of ADMM for multi-block convex minimization problems is not necessarily convergent. Math. Program., 155(1/2):57-79, 2016.
[29] Ghadimi E., Teixeira A., Shames I., et al. Optimal parameter selection for the alternating direction method of multipliers (ADMM): quadratic problems. IEEE Trans. Autom. Control, 60(3):644-658, 2015.
[30] Hong M., Luo Z.Q. On the linear convergence of the alternating direction method of multipliers. Math. Program., 162(1/2):165-199, 2017.
[31] Fukushima M. Application of the alternating direction method of multipliers to separable convex programming problems. Comput. Optim. Appl., 1(1):93-111, 1992.
[32] Wei E., Ozdaglar A. Distributed alternating direction method of multipliers. In: The 51st IEEE Conf. on Decision and Control, Maui, HI, USA: IEEE, pp. 5445-5450, 2012.
[33] Xia D. Power system analysis. 2nd ed., Beijing: China Electric Power Press, 2011.Document information
Published on 13/05/24
Accepted on 26/04/24
Submitted on 18/03/24
Volume 40, Issue 2, 2024
DOI: 10.23967/j.rimni.2024.05.003
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?