(→References) |
|||
| (47 intermediate revisions by 3 users not shown) | |||
| Line 3: | Line 3: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | + | Research on seismic performance of corrugated web steel structures</div> | |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | + | Hui-min Cao <sup>1,2</sup>,Guo-juan Wang<sup>1</sup>,Hong-bing Liu<sup>2</sup></div> | |
| − | < | + | <span id='_GoBack'></span>1,Xi’an Traffic Engineering Institute, Xi'an, China; 2, Northwestern Polytechnical University,Xi'an,China |
| − | + | ||
| + | Fund Project:1.The Youth Innovation Team of Shaanxi Universities(Key Technology Innovation Team for Urban Rail Transit Track Bed); 2.Young and middle-aged fund project at Xi’an Traffic Engineering Institute(2023KY-39); 3.The Scientific Research Program Funded by Education Department of Shaanxi Provincial Government (Program No.23JK0532). | ||
--> | --> | ||
| + | ==Abstract== | ||
| − | + | Corrugated web H-beam refers to a steel beam with a wavy shape along its length, which is extensively utilized in various parts of building structures such as beams, columns, and walls. It serves the purpose of connection and support, while the corrugated or folded design enhances the shear resistance and out-of-plane stiffness of the web to some extent. However, despite their advantages including high strength, stiffness, and lightweight construction, relevant regulations stipulate that these members can only be used in lower-intensity applications or higher-intensity scenarios if specific conditions are met. One crucial condition is that the ratio between the design value of axial force subjected to seismic action and the product of the member's flange section area and steel's tensile strength should not exceed 0.4. In this study, we aim to further investigate the seismic characteristics and applicable intensity of corrugated steel structures under earthquakes through large-scale finite element ABAQUS simulations. We will observe dynamic characteristics and failure modes of corrugated rigid frame structures using elastic-plastic time-history analysis methods as well as examine plastic deformation features of steel beam members under low cyclic loads via hysteretic analysis methods. The findings demonstrate that when properly designed with reasonable beam spans, corrugated web rigid frame structures can still be employed in high-intensity areas above 7 degrees even when subjected to an axial compression ratio up to 0.5. | |
| − | '''Keywords''': Corrugated web | + | '''Keywords''': Corrugated web, intensity, hysteretic behavior, axial pressure ratio |
| − | =1 Introduction= | + | ==1. Introduction== |
| − | The concept of green building is comprehensively implemented in project construction and building, integrating principles of environmental protection and energy conservation to achieve features of sustainable development. Furthermore, the advancement of assembled steel structures effectively promotes the progress of green building<span id='citeF-1'></span>[[#cite-1|[1]]]. | + | The concept of green building is comprehensively implemented in project construction and building, integrating principles of environmental protection and energy conservation to achieve features of sustainable development. Furthermore, the advancement of assembled steel structures effectively promotes the progress of green building <span id='citeF-1'></span>[[#cite-1|[1]]]. |
| − | Corrugated steel profiles represent a novel form of environmentally friendly construction steel that has emerged in recent decades. The availability of materials, on-site component cutting and assembly capabilities, waste-free production processes, reduced transportation costs, and the ability to select sections based on load requirements have facilitated ongoing research in this field<span id='citeF-1'></span>[[#cite-1|[2]]]. With the recent comprehensive investigations conducted by scientific researchers, static studies on corrugated steel profiles have reached a relatively advanced stage while dynamic research has been progressively expanding. In terms of bridge applications, Jiang | + | Corrugated steel profiles represent a novel form of environmentally friendly construction steel that has emerged in recent decades. The availability of materials, on-site component cutting and assembly capabilities, waste-free production processes, reduced transportation costs, and the ability to select sections based on load requirements have facilitated ongoing research in this field <span id='citeF-1'></span>[[#cite-1|[2]]]. With the recent comprehensive investigations conducted by scientific researchers, static studies on corrugated steel profiles have reached a relatively advanced stage while dynamic research has been progressively expanding. In terms of bridge applications, Jiang et al. <span id='citeF-1'></span>[[#cite-1|[3]]] experimentally demonstrated that corrugated web steel-concrete composite box girders exhibit well-defined load-displacement hysteresis loops under low-cycle repeated loads without any noticeable pinching phenomenon, thereby displaying excellent seismic performance. According to the principle of equal shear capacity in box girder sections, Feng et al. <span id='citeF-1'></span>[[#cite-1|[4]]] developed finite element models for both corrugated steel web continuous rigid frame bridges and corresponding concrete web continuous rigid frame bridges. A comparative analysis was conducted on the dynamic characteristics and seismic performance of these two types. The findings reveal that under earthquake loading, corrugated steel web rigid frame bridges exhibit reduced internal forces at low piers and top shears at high piers compared to concrete web rigid frame bridges; however, they experience increased top bending moment at high piers and bottom internal forces at piers. Through mechanical formula analysis, Li et al. <span id='citeF-1'></span>[[#cite-1|[5]]] have demonstrated that the implementation of hollow piers not only results in reduced weight but also effectively enhances the torsional performance of the upper structure in continuous rigid frame bridges with corrugated steel webs, thereby increasing its transverse compressive stiffness. Consequently, when designing continuous rigid frame box girder bridges with corrugated steel webs, employing hollow piers offers significant advantages. In terms of architecture. The seismic performance of the H-beam cantilever beam and frame with corrugated web was analyzed using the ABAQUS finite element model, as conducted by Wanyu <span id='citeF-1'></span>[[#cite-1|[6]]]. The seismic performance of corrugated web dampers has been enhanced through Peng <span id='citeF-1'></span>[[#cite-1|[7]]] experimental research, thereby expanding the potential applications of corrugated steel materials. Xingyu et al. <span id='citeF-1'></span>[[#cite-1|[8]]] proposed a novel composite shear wall configuration comprising a frame consisting of corrugated concrete-filled steel tubular columns and filled corrugated steel plates, and demonstrated the excellent seismic performance of this composite structure through numerical analysis and experimental investigations. According to the current investigation, despite the numerous advantages of corrugated web profiles, their promotion and utilization in China remain inadequate due to the intricate production process and limited seismic performance <span id='citeF-1'></span>[[#cite-1|[9,10]]]. Therefore, conducting research on corrugated steel within the realm of seismic applications for industrial and civil buildings holds immense significance <span id='citeF-1'></span>[[#cite-1|[11]]]. |
| − | The simulation analysis in this study employed a combination of dynamic and quasi-static approaches. Time-history analysis was conducted on the rigid frame, while hysteresis analysis was performed on the steel beam[12]. These analyses were utilized to further investigate the ratio between the seismic-induced axial force design value and the product of the member's flange section area and its steel tensile strength design value. This research provides a theoretical basis for utilizing such components in high-intensity earthquake zones. | + | The simulation analysis in this study employed a combination of dynamic and quasi-static approaches. Time-history analysis was conducted on the rigid frame, while hysteresis analysis was performed on the steel beam [12]. These analyses were utilized to further investigate the ratio between the seismic-induced axial force design value and the product of the member's flange section area and its steel tensile strength design value. This research provides a theoretical basis for utilizing such components in high-intensity earthquake zones. |
| − | =2 Modeling and analytical hypotheses= | + | ==2. Modeling and analytical hypotheses== |
| − | ==2.1 Analytical model and its corresponding parameters== | + | ===2.1 Analytical model and its corresponding parameters=== |
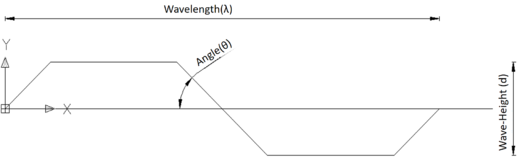
| − | The material parameters are presented in Table 1, as depicted in Figure 1. Additionally, the web fluctuation parameters utilized in this study can be found in Table 2 and Figure 2. | + | The material parameters are presented in [[#tab-1|Table 1]], as depicted in [[#img-1|Figure 1]]. Additionally, the web fluctuation parameters utilized in this study can be found in [[#tab-2|Table 2]] and [[#img-2|Figure 2]]. |
| − | + | <div class="center" style="font-size: 75%;">'''Table 1'''. Material parameters</div> | |
| + | |||
| + | <div id='tab-1'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! Steel !! Ε !! <math display="inline"> \rho </math>!! <math display="inline"> \mu</math> !! <math display="inline"> fy</math> | ||
|- | |- | ||
| − | + | | style="text-align: center;"|Q345 | |
| − | + | | style="text-align: center;"|2.06<math>\times</math>10<sup>11</sup> N/m<sup>2</sup> | |
| − | | style=" | + | | style="text-align: center;"|7850 kg/m<sup>3</sup> |
| − | | style=" | + | | style="text-align: center;"|0.28 |
| − | + | | style="text-align: center;"|310 N/mm<sup>2</sup> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|} | |} | ||
| − | {| style=" | + | <div id='img-1'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image1.png|430px]] | ||
|- | |- | ||
| − | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 1'''. Material constitutive model | |
| − | + | |} | |
| − | | | + | |
| − | | | + | |
| − | |||
| − | |||
| − | < | + | <div class="center" style="font-size: 75%;">'''Table 2'''. Comparison of geometric parameters</div> |
| − | | | + | |
| − | | | + | <div id='tab-2'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! style="vertical-align:top;text-align:center" |'''Angle (°)''' !! '''Wave length''' <br>'''(mm)''' !! '''Wave height'''<br>'''(mm)''' !! '''Flange thickness-to- <br>width ratio !! '''Thick-ness''' <br>'''(mm)''' !! '''Wave height'''<br>'''(mm)''' | ||
| + | |-style="text-align:center" | ||
| + | | 45 | ||
| + | | 240 | ||
| + | | 25 | ||
| + | | 0.05 | ||
| + | | 2 | ||
| + | | 520 | ||
| + | |} | ||
| − | |||
| − | |||
| − | < | + | <div id='img-2'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_737505923211_7586_Review_737505923211-image2.png|520px]] | ||
|- | |- | ||
| − | | | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. Web plate bending parameters |
| − | | | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| + | As depicted in [[#img-3|Figure 3]], Model 1 represents a rigid frame structure with zero ridge slope, featuring corrugated beam members of lengths 6m, 12m, 18m, and 24m, along with uniformly sized column heights of 6m. The node serves as a rigid junction connecting the <math> x </math>-direction (column height), <math> y </math>-direction (perpendicular to the beam axis), and <math> z </math>-direction (span direction) of the rigid frame. On the other hand, Model 2 exemplifies an ordinary rigid frame beam member model used for observing the hysteretic characteristics of corrugated steel beams under low-cycle reciprocating loads. | ||
| − | <div | + | <div id='img-3'></div> |
| − | ' | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" |
| − | + | |-style="background:white;" | |
| − | + | |align="center" | | |
| − | + | {|style="margin: 0em auto 0.1em auto;width:auto;" | |
| − | + | |+ | |
| − | + | |- | |
| − | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image3-c.png|center|310px]] | |
| − | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image4.png|center|340px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Rigid frame structure model |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Steel beam structure model | |
| − | | | + | |} |
| − | + | |- | |
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Model diagram | ||
|} | |} | ||
| − | |||
| − | |||
| − | ==2.2 Analytical assumptions== | + | ===2.2 Analytical assumptions=== |
| − | (1)In the ideal state, it is assumed that the connection between the node of the member and the support in a rigid frame is perfectly rigid. | + | (1) In the ideal state, it is assumed that the connection between the node of the member and the support in a rigid frame is perfectly rigid. |
| − | (2)The beam of a rigid frame structure is assumed to be supported solely by pressure-type steel plate roofs and cold-formed steel purlins. | + | (2) The beam of a rigid frame structure is assumed to be supported solely by pressure-type steel plate roofs and cold-formed steel purlins. |
| − | (3)It is assumed that the structures are subjected to ideal conditions when under stress. | + | (3) It is assumed that the structures are subjected to ideal conditions when under stress. |
| − | =3 The dynamic analysis of a rigid frame structure= | + | ==3. The dynamic analysis of a rigid frame structure== |
| − | ==3.1 Modal analysis== | + | ===3.1 Modal analysis=== |
| − | Taking the rigid frame with a span of 12 meters as an example, the modal analysis of the structure is carried out, and each mode is shown in Figure 4. | + | Taking the rigid frame with a span of 12 meters as an example, the modal analysis of the structure is carried out, and each mode is shown in [[#img-4|Figure 4]] . |
| − | {| style="width: | + | <div id='img-4'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image5.png|center|258px]] |
| − | [[Image:Draft_Hui-min_632690981-image5.png|center|258px]] | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image6.png|center|252px]] |
| − | + | ||
| − | | | + | |
| − | [[Image:Draft_Hui-min_632690981-image6.png|center|252px]] | + | |
| − | + | ||
|- | |- | ||
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) First-order mode |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Second-order mode | |
| − | + | |- | |
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image7.png|288px]] |
| − | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image8.png|288px]] | |
| − | + | |- | |
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(c) Third-order mode | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(d) Fourth-order mode | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. Modal analysis diagram | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | In this model, a subspace iterative method was employed to extract the first four modes, with the first frequency being 1.3058 Hz, corresponding to a period of 0.74 s for the model. The results obtained from both manual calculation and software using the formula <math display="inline">\boldsymbol{\omega} = \sqrt{K/M}</math> showed little discrepancy, indicating that the structural model is accurate and reliable. | |
| − | In the Time-history analysis, a pair of eccentric forces is applied to simulate the beam as a flexural member and control it at the required axial compression ratio. The formula used for calculating the axial compression ratio is given by <math>n=N/(f\ast A_f)</math> , where <math>N</math> represents the axial pressure value, <math>A_f</math> denotes the net cross-sectional area of the flange, and <math>f</math> represents the design value of steel's tensile strength. | + | ===3.2 Time-history analysis=== |
| + | |||
| + | In the Time-history analysis, a pair of eccentric forces is applied to simulate the beam as a flexural member and control it at the required axial compression ratio. The formula used for calculating the axial compression ratio is given by <math>n=N/(f\ast A_f)</math>, where <math>N</math> represents the axial pressure value, <math>A_f</math> denotes the net cross-sectional area of the flange, and <math>f</math> represents the design value of steel's tensile strength. | ||
===3.2.1 The modulation of seismic wave amplitude=== | ===3.2.1 The modulation of seismic wave amplitude=== | ||
| − | Under the column base constraint Ux, UR1, UR2, and UR3 are set to zero,Uy and Uz represent the translational degrees of freedom along the y-axis and z-axis respectively, while Ux representing the translational degree of freedom along the x-axis. Similarly, UR1, UR2 and UR3 represent the rotational degrees of freedom around the x-axis, y-axis, and z-axis respectively. The EL-Centro seismic waves are applied to Uy and Uz . Amplitude modulation is performed using the formula <math>a_0(t_i)=\frac{a_{0, | + | Under the column base constraint <math>Ux, UR1, UR2</math>, and <math>UR3</math> are set to zero, <math>Uy</math> and <math>Uz</math> represent the translational degrees of freedom along the <math>y</math>-axis and <math>z</math>-axis respectively, while <math>Ux</math> representing the translational degree of freedom along the <math>x</math>-axis. Similarly, <math>UR1, UR2</math>, and <math>UR3</math> represent the rotational degrees of freedom around the <math>x</math>-axis, <math>y</math>-axis, and <math>z</math>-axis respectively. The EL-Centro seismic waves are applied to <math>Uy</math> and <math>Uz</math>. Amplitude modulation is performed using the formula <math>a_0(t_i)=\frac{a_{0,max}}{a_m}a(t_i)</math>, where <math>a_{0,max}</math> denotes the designed maximum acceleration; <math>a_m</math> represents the maximum acceleration from the selected seismic record; and <math>t_i</math> signifies an actual seismic acceleration time coordinate point with <math>i=1, 2, 3...</math> These points should be recorded. |
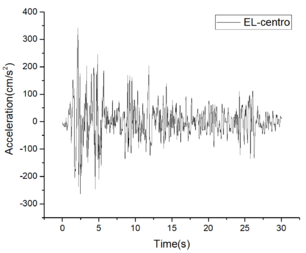
| − | Taking the ''EL-Centro'' wave as an example, it exhibits a peak acceleration of 2.20 m/s<sup>2</sup> [[#cite-1|[13]]] and is depicted in Figure 5. | + | Taking the ''EL-Centro'' wave as an example, it exhibits a peak acceleration of 2.20 m/s<sup>2</sup> [[#cite-1|[13]]] and is depicted in [[#img-5|Figure 5]]. |
| − | {| style="width: | + | <div id='img-5'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image13.png|center|306px]] |
| − | [[Image:Review_737505923211- | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image14.png|center|306px]] |
| − | (a) Before the ''EL-Centro '' | + | |- |
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Before the ''EL-Centro '' amplitude modulation |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) After the ''EL-Centro '' amplitude modulation | |
| − | + | |} | |
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. Comparison of EL-Centro wave before and after amplitude modulation | ||
|} | |} | ||
| − | |||
| − | |||
===3.2.2 The basis for analysis=== | ===3.2.2 The basis for analysis=== | ||
| − | According to the Stipulate of the | + | According to the Stipulate of the ''Technical Specification for Steel Structures of Lightweight Buildings with Portal Frames(GB51022:2015)'' <span id='citeF-1'></span>[[#cite-1|[12]]] 3.3.1: In a single-layer portal frame configuration, excluding crane and light steel wallboard, the maximum displacement of the column's top should not exceed H/60. This implies that the angular displacement between layers must be less than 0.017. |
| − | According to the Stipulate of the | + | According to the Stipulate of the ''Technical Specification for Steel Structures of Lightweight Buildings with Portal Frames(GB51022:2015)'' <span id='citeF-1'></span>[[#cite-1|[12]]] 3.3.2: The deflection limit for members of inclined beams in portal frames, supporting only profiled steel roofs and cold-formed steel purlins, is L/180, where L represents the full-span length. |
===3.2.3 The analysis of the results=== | ===3.2.3 The analysis of the results=== | ||
| − | (1) Comparative analysis under seismic conditions at axial compression ratios of 0.4 and 0.5 | + | '''''(1) Comparative analysis under seismic conditions at axial compression ratios of 0.4 and 0.5''''' |
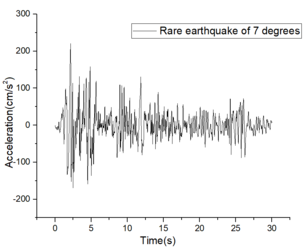
The eccentric load is applied to the beam of the rigid frame structure, subjecting the member to a specified axial compression ratio, and seismic waves are applied during rare earthquakes at the base of the rigid frame column. Firstly, we compare and analyze the structural stress and failure under earthquake conditions with an axial compression ratio of 0.4 and 0.5. | The eccentric load is applied to the beam of the rigid frame structure, subjecting the member to a specified axial compression ratio, and seismic waves are applied during rare earthquakes at the base of the rigid frame column. Firstly, we compare and analyze the structural stress and failure under earthquake conditions with an axial compression ratio of 0.4 and 0.5. | ||
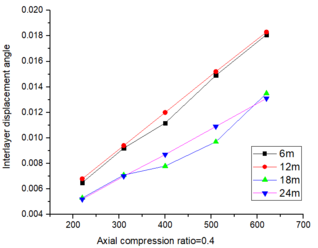
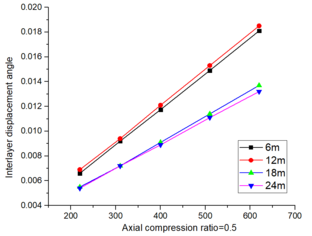
| − | According to the analysis in Section 3.2.2, it is evident that for beam spans of 6m and 12m as shown in Table 3, the inter-story displacement angle fails to meet the design requirements for seismic activity of a magnitude of nine degrees in high-risk areas. However, it does satisfy the intensity criteria under various coaxial pressure ratios at spans of 18m and 24m. The deflection meets the design specifications across different spans. | + | According to the analysis in Section 3.2.2, it is evident that for beam spans of 6m and 12m as shown in [[#tab-3|Table 3]], the inter-story displacement angle fails to meet the design requirements for seismic activity of a magnitude of nine degrees in high-risk areas. However, it does satisfy the intensity criteria under various coaxial pressure ratios at spans of 18m and 24m. The deflection meets the design specifications across different spans. |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 3'''. Variables associated with distinct seismic waves</div> |
| − | + | ||
| − | {| style=" | + | <div id='tab-1'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! '''Beam span'''!! '''n''' !! '''Wave peak value'''!! '''220'''!! '''310'''!! '''400''' !! '''510''' !! '''620''' | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''6m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | | + | | style=" text-align:center;"|(Interlayer displacement) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|39.29 |
| − | | style=" | + | | style="text-align: center;"|54.91 |
| − | | style=" | + | | style="text-align: center;"|70 |
| − | | style=" | + | | style="text-align: center;"|89.60 |
| − | | style=" | + | | style="text-align: center;"|'''108.61''' |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''6m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement angle) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|0.0065 |
| − | | style=" | + | | style="text-align: center;"|0.0092 |
| − | | style=" | + | | style="text-align: center;"|0.0117 |
| − | | style=" | + | | style="text-align: center;"|0.0149 |
| − | | style=" | + | | style="text-align: center;"|'''0.0181''' |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''6m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Mid-span deflection)<sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|5.30 |
| − | | style=" | + | | style="text-align: center;"|5.46 |
| − | | style=" | + | | style="text-align: center;"|5.60 |
| − | | style=" | + | | style="text-align: center;"|5.76 |
| − | | style=" | + | | style="text-align: center;"|5.90 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''6m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|39.63 |
| − | | style=" | + | | style="text-align: center;"|55.20 |
| − | | style=" | + | | style="text-align: center;"|70.45 |
| − | | style=" | + | | style="text-align: center;"|89.34 |
| − | | style=" | + | | style="text-align: center;"|'''108.67''' |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''6m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement angle) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|0.0066 |
| − | | style=" | + | | style="text-align: center;"|0.0092 |
| − | | style=" | + | | style="text-align: center;"|0.01174 |
| − | | style=" | + | | style="text-align: center;"|0.0149 |
| − | | style=" | + | | style="text-align: center;"|'''0.0181''' |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''6m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Mid-span deflection)<sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|6.65 |
| − | | style=" | + | | style="text-align: center;"|6.68 |
| − | | style=" | + | | style="text-align: center;"|6.81 |
| − | | style=" | + | | style="text-align: center;"|7.10 |
| − | | style=" | + | | style="text-align: center;"|7.14 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''12m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|40.79 |
| − | | style=" | + | | style="text-align: center;"|56.36 |
| − | | style=" | + | | style="text-align: center;"|72.03 |
| − | | style=" | + | | style="text-align: center;"|91.21 |
| − | | style=" | + | | style="text-align: center;"|'''109.89''' |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''12m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement angle) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|0.0068 |
| − | | style=" | + | | style="text-align: center;"|0.0094 |
| − | | style=" | + | | style="text-align: center;"|0.0120 |
| − | | style=" | + | | style="text-align: center;"|0.0152 |
| − | | style=" | + | | style="text-align: center;"|'''0.0183''' |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''12m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Mid-span deflection)<sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|13.51 |
| − | | style=" | + | | style="text-align: center;"|13.62 |
| − | | style=" | + | | style="text-align: center;"|13.79 |
| − | | style=" | + | | style="text-align: center;"|13.92 |
| − | | style=" | + | | style="text-align: center;"|14.01 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''12m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|41.30 |
| − | | style=" | + | | style="text-align: center;"|56.51 |
| − | | style=" | + | | style="text-align: center;"|72.66 |
| − | | style=" | + | | style="text-align: center;"|91.86 |
| − | | style=" | + | | style="text-align: center;"|'''111.04''' |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''12m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement angle) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|0.0069 |
| − | | style=" | + | | style="text-align: center;"|0.0094 |
| − | | style=" | + | | style="text-align: center;"|0.0121 |
| − | | style=" | + | | style="text-align: center;"|0.0153 |
| − | | style=" | + | | style="text-align: center;"|'''0.0185''' |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''12m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Mid-span deflection)<sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|16.57 |
| − | | style=" | + | | style="text-align: center;"|16.72 |
| − | | style=" | + | | style="text-align: center;"|16.80 |
| − | | style=" | + | | style="text-align: center;"|16.91 |
| − | | style=" | + | | style="text-align: center;"|17.07 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''18m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|31.65 |
| − | | style=" | + | | style="text-align: center;"|42.57 |
| − | | style=" | + | | style="text-align: center;"|46.57 |
| − | | style=" | + | | style="text-align: center;"|58.31 |
| − | | style=" | + | | style="text-align: center;"|81.41 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|<span id='_GoBack'>'''18m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement angle) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|0.0053 |
| − | | style=" | + | | style="text-align: center;"|0.0071 |
| − | | style=" | + | | style="text-align: center;"|0.0078 |
| − | | style=" | + | | style="text-align: center;"|0.0097 |
| − | | style=" | + | | style="text-align: center;"|0.013665 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''18m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Mid-span deflection)<sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|24.98 |
| − | | style=" | + | | style="text-align: center;"|24.99 |
| − | | style=" | + | | style="text-align: center;"|25.12 |
| − | | style=" | + | | style="text-align: center;"|25.68 |
| − | | style=" | + | | style="text-align: center;"|25.82 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''18m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|32.70 |
| − | | style=" | + | | style="text-align: center;"|43.20 |
| − | | style=" | + | | style="text-align: center;"|54.79 |
| − | | style=" | + | | style="text-align: center;"|68.57 |
| − | | style=" | + | | style="text-align: center;"|82.26 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''18m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement angle) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|0.0055 |
| − | | style=" | + | | style="text-align: center;"|0.0072 |
| − | | style=" | + | | style="text-align: center;"|0.0091 |
| − | | style=" | + | | style="text-align: center;"|0.0114 |
| − | | style=" | + | | style="text-align: center;"|0.0137 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''18m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Mid-span deflection)<sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|30.24 |
| − | | style=" | + | | style="text-align: center;"|30.33 |
| − | | style=" | + | | style="text-align: center;"|30.61 |
| − | | style=" | + | | style="text-align: center;"|30.94 |
| − | | style=" | + | | style="text-align: center;"|31.10 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''24m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|31.20 |
| − | | style=" | + | | style="text-align: center;"|41.82 |
| − | | style=" | + | | style="text-align: center;"|52.35 |
| − | | style=" | + | | style="text-align: center;"|65.33 |
| − | | style=" | + | | style="text-align: center;"|78.57 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''24m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement angle) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|0.0052 |
| − | | style=" | + | | style="text-align: center;"|0.0070 |
| − | | style=" | + | | style="text-align: center;"|0.0087 |
| − | | style=" | + | | style="text-align: center;"|0.0109 |
| − | | style=" | + | | style="text-align: center;"|0.0131 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''24m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.4''' |
| − | | style=" | + | | style="text-align: center;"|(Mid-span deflection)<sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|42.47 |
| − | | style=" | + | | style="text-align: center;"|40.76 |
| − | | style=" | + | | style="text-align: center;"|41.02 |
| − | | style=" | + | | style="text-align: center;"|41.27 |
| − | | style=" | + | | style="text-align: center;"|41.61 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''24m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|32.48 |
| − | | style=" | + | | style="text-align: center;"|43.45 |
| − | | style=" | + | | style="text-align: center;"|53.5 |
| − | | style=" | + | | style="text-align: center;"|66.40 |
| − | | style=" | + | | style="text-align: center;"|79.36 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''24m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Interlayer displacement angle) <sub>max</sub> |
| − | | style=" | + | | style="text-align: center;"|0.0054 |
| − | | style=" | + | | style="text-align: center;"|0.0072 |
| − | | style=" | + | | style="text-align: center;"|0.0089 |
| − | | style=" | + | | style="text-align: center;"|0.0111 |
| − | | style=" | + | | style="text-align: center;"|0.0132 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|'''24m''' |
| − | | style=" | + | | style="text-align: center;"|'''0.5''' |
| − | | style=" | + | | style="text-align: center;"|(Mid-span deflection)<sub>max</sub> |
| − | + | | style="text-align: center;"|50.31 | |
| − | + | | style="text-align: center;"|48.03 | |
| − | + | | style="text-align: center;"|50.61 | |
| − | + | | style="text-align: center;"|50.98 | |
| − | + | | style="text-align: center;"|50.14 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|} | |} | ||
| − | |||
| + | <div style="text-align: center; font-size: 75%;">Note: The peak amplitude of seismic waves is measured in cm/s2, while displacement and deflection are measured in mm.</div> | ||
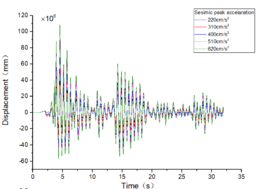
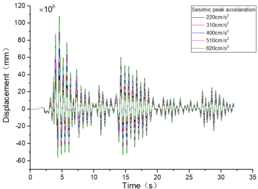
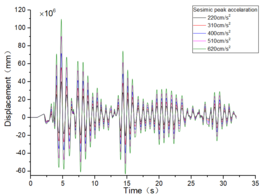
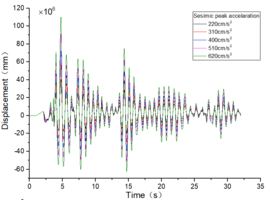
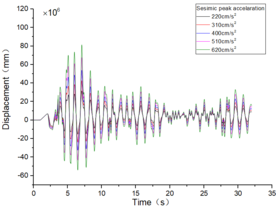
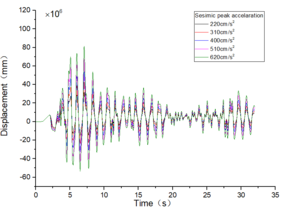
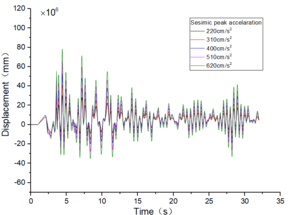
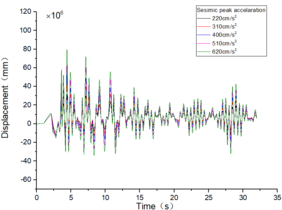
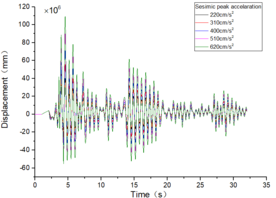
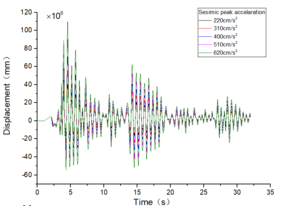
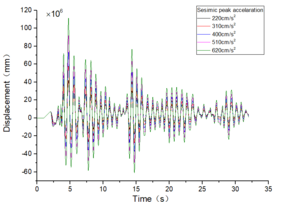
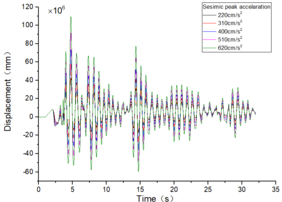
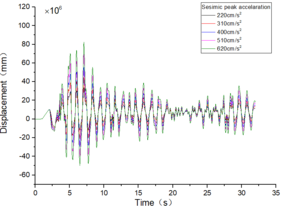
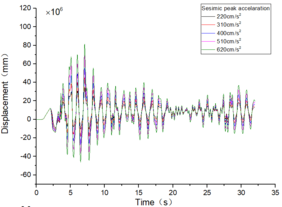
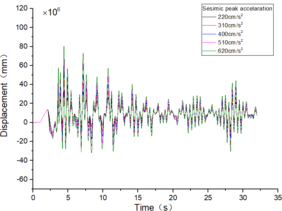
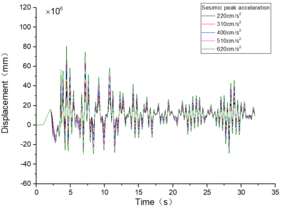
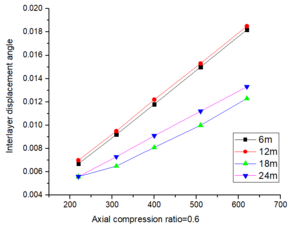
| + | The inter-story displacement and inter-story displacement angle remain unaffected by the axial compression ratio, as evidenced in [[#img-6|Figures 6]] and [[#img-7|7]], while their values exhibit an increasing trend with higher seismic wave intensity. | ||
| − | + | <div id='img-6'></div> | |
| − | {| style=" | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" |
| + | |-style="background:white;" | ||
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image15.png|center|318px]] |
| − | [[Image:Review_737505923211-image15.png|center|318px]] | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image16.png|center|312px]] |
| − | + | |} | |
| − | | | + | |- |
| − | [[Image:Review_737505923211-image16.png|center|312px]] | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 6'''. Maximum angle of inter-story displacement |
| − | + | ||
|} | |} | ||
| − | |||
| − | |||
| − | + | <div id='img-7'></div> | |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | {| style="width: | + | |-style="background:white;" |
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image17.png|center|258px]] |
| − | [[Image:Review_737505923211-image17.png|center|258px]] | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image18-c.png|center|258px]] |
| − | + | ||
| − | | | + | |
| − | [[Image:Review_737505923211-image18-c.png|center|258px]] | + | |
| − | + | ||
|- | |- | ||
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Span-6m-axial compression ratio=0.4 |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Span-6m-axial compression ratio=0.5 | |
| − | + | ||
| − | + | ||
| − | | | + | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image19.png|center|264px]] |
| − | [[Image:Review_737505923211- | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image20.png|center|270px]] |
| − | + | ||
| − | + | ||
| − | | | + | |
| − | [[Image:Review_737505923211- | + | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(c) Span-12m-axial compression ratio=0.4 |
| − | [[Image: | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(d) Span-12m-axial compression ratio=0.5 |
| − | + | |- | |
| − | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_253388665-image31.png|center|276px]] | |
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_253388665-image32.png|center|282px]] |
| − | [[Image: | + | |- |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(e) Span-18m-axial compression ratio=0.4 | |
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(f) Span-18m-Axial compression ratio=0.5 | ||
| + | |- | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_253388665-image33-c.png|center|288px]] | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_253388665-image34.png|center|282px]] | ||
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Span-24m-axial compression ratio=0.4 | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Span-24m-axial compression ratio=0.5 | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 7'''. Time-history curves illustrating the response of different spans and axial compression ratios | ||
|} | |} | ||
| − | |||
| − | |||
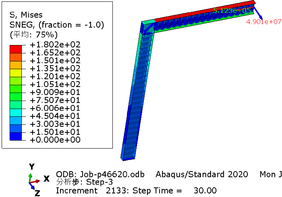
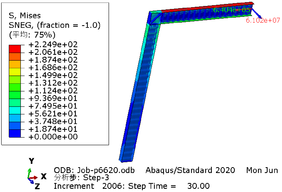
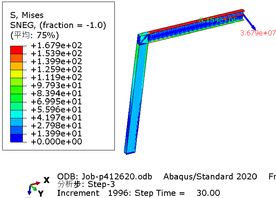
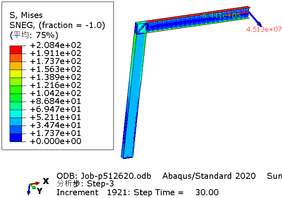
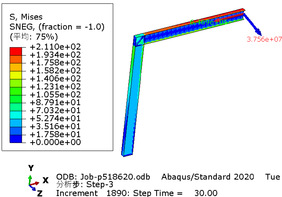
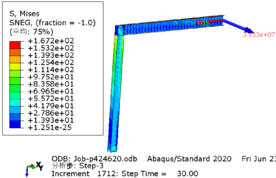
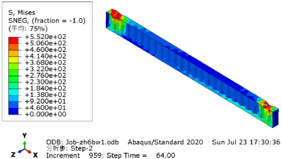
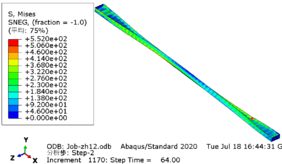
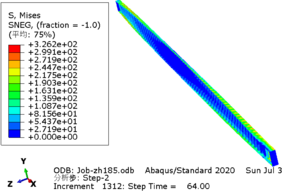
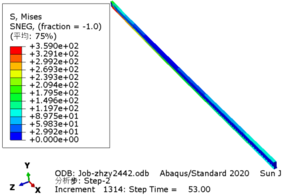
| − | The greater the acceleration of an earthquake, the more severe the structural damage it inflicts. In this case study, we analyze the force cloud diagram of a member subjected to an intensity level of 9 degrees. According to Table 4, when the axial compression ratio ranges from 0.4 to 0.5, the member does not reach its yield strength and stress values decrease as span length increases. The structure experiences a maximum internal force of 647.7kN at an axial compression ratio approximately equal to 0.52 | + | The greater the acceleration of an earthquake, the more severe the structural damage it inflicts. In this case study, we analyze the force cloud diagram of a member subjected to an intensity level of 9 degrees. According to [[#tab-4|Table 4]], when the axial compression ratio ranges from 0.4 to 0.5, the member does not reach its yield strength and stress values decrease as span length increases. The structure experiences a maximum internal force of 647.7kN at an axial compression ratio approximately equal to 0.52. However, even at its highest stress value of 224.9MPa, it remains below its yield point and thus avoids any structural damage. |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 4'''. Cloud picture with varying spans and axial compression ratios</div> |
| − | + | ||
| − | {| style=" | + | <div id='tab-4'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | + | |-style="text-align:center" | |
| − | + | ! '''Span''' !! '''Axial compression ratio is 0.4''' !! Axial compression ratio is 0.5''' | |
| − | + | ||
|- | |- | ||
| tyle="text-align: center;vertical-align: centre;width: 50%""|6m | | tyle="text-align: center;vertical-align: centre;width: 50%""|6m | ||
| Line 482: | Line 482: | ||
| tyle="text-align: center;vertical-align: centre;width: 50%""| [[Image:Review_737505923211-image30.png|center|282px]] | | tyle="text-align: center;vertical-align: centre;width: 50%""| [[Image:Review_737505923211-image30.png|center|282px]] | ||
|- | |- | ||
| − | | style=" | + | | style="vertical-align: center;"|24m |
| − | | style=" | + | | style="vertical-align: center;"| [[Image:Review_737505923211-image31.png|center|276px]] |
| − | | style=" | + | | style="vertical-align: center;"| [[Image:Review_737505923211-image32.png|center|282px]] |
|} | |} | ||
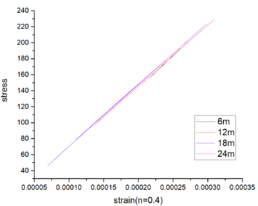
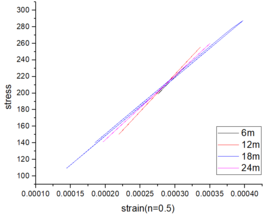
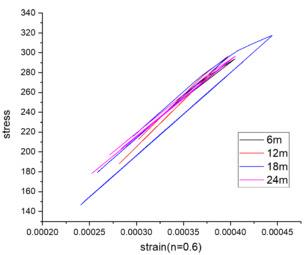
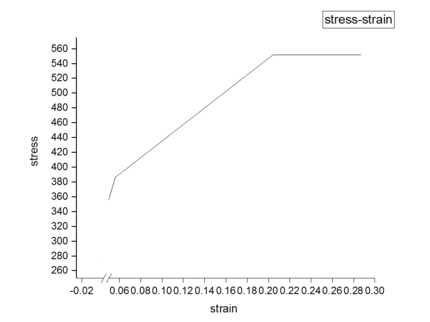
| − | {| style="width: | + | The stress-strain curves depicted in [[#img-8|Figure 8]] for various beam spans and axial compression ratios demonstrate that irrespective of whether the axial compression ratio is 0.4 or 0.5, the observed elastic behavior persists within the range of beam spans from 6 to 24m. This characteristic enhances its ability to withstand external loads and seismic forces. |
| + | |||
| + | <div id='img-8'></div> | ||
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image33.png|center|258px]] |
| − | [[Image:Review_737505923211-image33.png|center|258px]] | + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image34.png|center|276px]] |
| − | + | |} | |
| − | | | + | |- |
| − | [[Image:Review_737505923211-image34.png|center|276px]] | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 8'''. Stress-strain curves for various spans and axial compression ratios |
| − | ''' | + | |
|} | |} | ||
| − | |||
| − | |||
| − | + | '''''(2) When the axial compression ratio is 0.6, 0.7 and 0.8''''' | |
| − | + | ||
| − | (2) When the axial compression ratio is 0.6, 0.7 and 0.8 | + | |
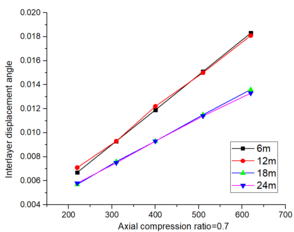
As analyzed in the previous text, it can be seen that when the beam spans are 6m and 12m, the inter-story displacement limit cannot be satisfied under the influence of rare earthquakes at a magnitude of 9 degrees. This is primarily attributed to the susceptibility of small span-to-height ratio connected beams to brittle shear failure during seismic events. However, as the span-to-height ratio increases, their mechanical behavior gradually approaches that of conventional frame beams, resulting in improved seismic performance <span id='citeF-1'></span>[[#cite-1|[14-17]]]. Consequently, it can be inferred that even with larger axial pressure ratios, both 6m and 12m spans still fail to meet the requirements for rare earthquakes at a magnitude of 9 degrees. To further investigate the maximum achievable axial compression ratio for corrugated rigid frames, similar methods will be employed to analyze structural failure under rare earthquake conditions at magnitudes of 9 degrees when subjected to axial compression ratios of 0.6 and 0.7. | As analyzed in the previous text, it can be seen that when the beam spans are 6m and 12m, the inter-story displacement limit cannot be satisfied under the influence of rare earthquakes at a magnitude of 9 degrees. This is primarily attributed to the susceptibility of small span-to-height ratio connected beams to brittle shear failure during seismic events. However, as the span-to-height ratio increases, their mechanical behavior gradually approaches that of conventional frame beams, resulting in improved seismic performance <span id='citeF-1'></span>[[#cite-1|[14-17]]]. Consequently, it can be inferred that even with larger axial pressure ratios, both 6m and 12m spans still fail to meet the requirements for rare earthquakes at a magnitude of 9 degrees. To further investigate the maximum achievable axial compression ratio for corrugated rigid frames, similar methods will be employed to analyze structural failure under rare earthquake conditions at magnitudes of 9 degrees when subjected to axial compression ratios of 0.6 and 0.7. | ||
| − | {| style="width: | + | ''The Technical code for the steel structure of the light-weight building with gabled frames(GB51022:2015)'', and [[#img-9|Figures 9]] and [[#img-10|10]] showed the inter-story displacement fails to meet the code requirements under the influence of a 9-degree rare earthquake for beam spans of 6m and 12m, but it satisfies the requirements for spans of 18m and 24m. [[#img-11|Figure 11]] demonstrates that the deflection complies with the code specifications. This conclusion remains consistent when considering coaxial compression ratios of both 0.4 and 0.5. |
| + | |||
| + | <div id='img-9'></div> | ||
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image45.png|center|276px]] |
| − | [[Image:Draft_Hui-min_632690981-image45.png|center | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image46.png|center|282px]] |
| − | + | ||
| − | | | + | |
| − | [[Image:Draft_Hui-min_632690981-image46.png|center|282px]] | + | |
| − | + | ||
|- | |- | ||
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Span-6m-axial compression ratio=0.6 |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Span-6m-axial compression ratio=0.7 | |
| − | + | ||
| − | | | + | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image47.png|center|282px]] |
| − | [[Image:Draft_Hui-min_632690981- | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image48.png|center|282px]] |
| − | + | ||
| − | | | + | |
| − | [[Image:Draft_Hui-min_632690981- | + | |
| − | + | ||
|- | |- | ||
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(c) Span-12m-axial compression ratio=0.6 |
| − | [[Image:Draft_Hui- | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(d) Span-12m-axial compression ratio=0.7 |
| − | + | |- | |
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_253388665-image49.png|center|282px]] |
| − | [[Image:Draft_Hui- | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_253388665-image50.png|center|282px]] |
| − | + | |- | |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(e) Span-18m-axial compression ratio=0.6 | |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(f) Span-18m-Axial compression ratio=0.7 | |
| + | |- | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_253388665-image51.png|center|282px]] | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_253388665-image52.png|center|282px]] | ||
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Span-24m-axial compression ratio=0.6 | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Span-24m-axial compression ratio=0.7 | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 9'''. Interlayer displacement curves with varying spans and coaxial pressure ratios | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | {| style="width: | + | <div id='img-10'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image53.png|center|294px]] |
| − | [[Image:Draft_Hui-min_632690981-image53.png|center|294px]] | + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image54.png|center|294px]] |
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 10'''. Maximum angle of inter-story displacement | ||
| + | |} | ||
| − | |||
| − | |||
| + | <div id='img-11'></div> | ||
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image55.png|348px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 11'''. Deflection and limit values under different spans and <br> axial compression ratios for 9-degree rare earthquakes | ||
|} | |} | ||
| − | |||
| − | |||
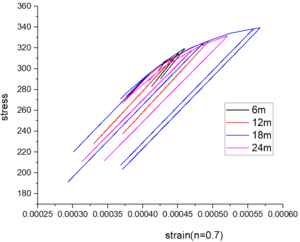
| − | + | The stress-strain curve in [[#img-12|Figure 12]] demonstrates a distinct hysteretic characteristic as the axial compression ratio increases, with a more pronounced effect observed at higher ratios. This indicates that the rigid frame beam undergoes plastic deformation as the axial compression ratio rises, and this deformation becomes more significant with increasing compression. To ensure optimal seismic characteristics of the rigid frame structure, it is advisable to maintain the structure predominantly within the elastic stress stage. Therefore, based on the aforementioned conclusion, it can be inferred that even with an axial compression ratio of 0.5, the rigid frame structure still exhibits favorable seismic characteristics. | |
| − | + | ||
| − | <div id= | + | <div id='img-12'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
| + | |- | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image56.png|306px]] | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Draft_Hui-min_632690981-image57.png|300px]] | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 12'''. Stress-strain curves for various spans and axial compression ratios | ||
| + | |} | ||
| + | ==4. Quasi-static analysis== | ||
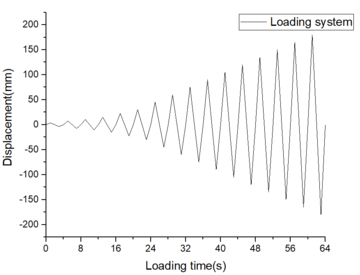
| − | + | In the section of quasi-static hysteretic analysis, one end is fully consolidated, meaning that all six degrees of freedom are constrained to zero, while the other end is subjected to loading. The loading end applies a displacement amplitude in the vertical beam direction when the axial compression ratio is set at 0.4 and 0.5 respectively. The displacement starts from 0 mm and incrementally increases to 180 mm step by step. Simultaneously, the corresponding duration of each amplitude is defined in the analysis step <span id='citeF-1'></span>[[#cite-1|[18,19]]], as depicted in [[#img-13|Figure 13]]. | |
| − | {| style="width: | + | <div id='img-13'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_737505923211-image43.png|center|360px]] | ||
|- | |- | ||
| − | | | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 13'''. Loading system |
| − | + | ||
|} | |} | ||
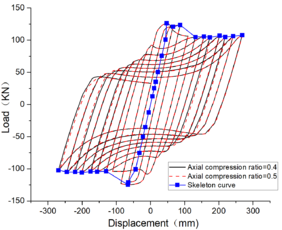
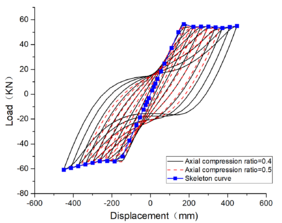
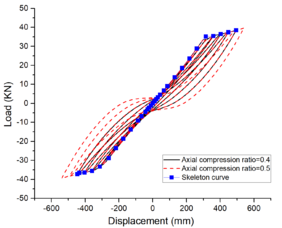
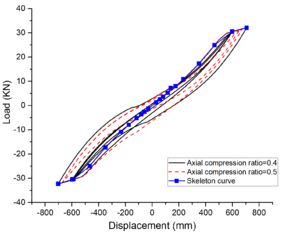
| − | + | The hysteresis curves presented in [[#tab-5|Table 5]] and the Mises cloud graph demonstrate that variations in axial compression ratio have minimal influence on the hysteresis loop. At a span of 6m, the hysteresis curve exhibits maximum completeness with a slight pinch and possesses the highest capacity for energy dissipation. The skeleton curve encompasses all three stages of elasticity, elastic-plasticity, and plasticity<span id='citeF-1'></span>[[#cite-1|[20]]], while localized failure occurs at the beam ends upon reaching their yield limit. | |
| − | <span | + | |
| + | When the beam span is 12m, the hysteretic curve exhibits significant pinching, and the beam undergoes noticeable torsion under displacement loading. At this juncture, failure of the steel beam no longer occurs solely at its end but rather manifests as local buckling at the point of torsion. | ||
| − | + | The area enclosed by the hysteretic loop gradually decreases with an increase in the shear-span ratio, as illustrated in [[#tab-5|Table 5]]. Moreover, the hysteretic curve exhibits significant pinching and slipping, resulting in a reduced external force required for the same displacement and diminished energy dissipation. At an 18m span, the torsional slip of the member is pronounced; however, at a 24m span, the member demonstrates nearly elastic deformation albeit with noticeably decreased energy dissipation <span id='citeF-1'></span>[[#cite-1|[21]]]. | |
| − | + | The conclusion can be inferred that, for a specific axial compression ratio, the hysteresis analysis load capacity of the structure decreases as the span length increases. Moreover, it is observed that the hysteretic performance is minimally affected by the axial compression ratio. However, low cyclic loads still provide valuable insights for seismic analysis. | |
| − | + | <div class="center" style="font-size: 75%;">'''Table 5'''. Time delay loop curve and cloud chart for different axial pressure ratio</div> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | <div class="center" style=" | + | |
| − | ''' | + | |
| − | + | <div id='tab-1'></div> | |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | + | |-style="text-align:center" | |
| − | + | !'''Span''' !! '''Hysteretic curve''' !! '''Mises cloud picture''' | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |- | + | |
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | 6m |
| − | | | + | | style="text-align: center;vertical-align: centre;"|[[Image:Review_737505923211-image44.png|center|282px]] |
| − | | | + | | style="text-align: center;vertical-align:centre;"|[[Image:Review_737505923211-image45.png|center|282px]] |
|- | |- | ||
| − | + | | 12m | |
| − | | | + | | style="text-align: center;vertical-align:centre;"|[[Image:Review_737505923211-image46.png|center|282px]] |
| − | | | + | | style="text-align: center;vertical-align:centre;"|[[Image:Review_737505923211-image47.png|center|282px]] |
|- | |- | ||
| − | | | + | | 18 |
| − | | | + | | style="text-align: center;vertical-align:centre;"| [[Image:Review_737505923211-image48.png|center|282px]] |
| − | | | + | | style="text-align: center;vertical-align:centre;"|[[Image:Review_737505923211-image49.png|center|282px]] |
|- | |- | ||
| − | | | + | | 24m |
| − | | | + | | style="text-align: center;vertical-align:centre;"|[[Image:Review_737505923211-image50.png|center|282px]] |
| − | | | + | | style="text-align: center;vertical-align:centre;"| [[File:Review_737505923211_3847_1700309441883.jpg|center|282px]] |
|} | |} | ||
| − | == | + | ==5. Conclusions== |
| − | + | The rigid frame beam spans ranging from 6 to 24m are designed to withstand earthquakes of up to 8 degrees or lower, while the spans of 18m and 24m can simultaneously resist earthquakes of magnitude 9 and below. Therefore, it is essential to carefully control the beam span to ensure optimal seismic resistance for the structure. | |
| − | + | To ensure that structural failure always occurs within the elastic stage, it is crucial to limit the axial compression ratio and ensure a sound structural design. The utilization of corrugated web rigid frame structures may be appropriate in regions with infrequent seismic activity exceeding 7 degrees, provided that the axial compression ratio does not surpass 0.5. | |
| − | + | The axial compression ratio has little influence on the hysteretic performance of the members. With the increase of the span, the members will slip, the hysteretic curve will shrink, and the energy dissipation will become smaller, which is not conducive to the earthquake resistance of the structure. | |
| − | == | + | ==Acknowledgments== |
| − | The authors would like to thank The | + | The authors would like to thank The Youth Innovation Team of Shaanxi Universities (Key Technology Innovation Team for Urban Rail Transit Track Bed). Young and middle-aged fund project at Xi’an Traffic Engineering Institute (2023KY-39), and The Scientific Research Program Funded by Education Department of Shaanxi Provincial Government (Program No.23JK0532). |
| + | |||
| + | ==References== | ||
| + | |||
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
| − | |||
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[1]]] Chen H. Analysis and discussion on the application of prefabricated design and construction in green buildings (in Chinese). China Residential Facilities, 06(37-39), 2023. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[2]]] Ibragimov A., Zinoveva E., Rosinskiy S. Prefabricated steel structures with a corrugated web (part 1: beam). IOP Conference Series Materials Science and Engineering, 869:072041, 2020. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[3]]] Jiang L., Zhong T., Tan Z., Zhou W., Wu L., Xu T. Study on seismic performance of steel-concrete composite box girder with corrugated web (in Chinese). Journal of Railway Science and Engineering, 18(555-563), 2021. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[4]]] Feng W.Z., Liu B., Mou K., Wang H. Research on seismic performance of continuous rigid-frame bridge with corrugated steel webs (in Chinese). Earthquake Resistant Engineering and Retrofitting, 37(70-74), 2015. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[5]]] Li P., Liu B., Xiaoying-nan. Influence of pier types on dynamic characteristics of continuous rigid frame bridge with corrugated steel webs (in Chinese). Bridge Construction, (2):3, 2011. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[6]]] Wan-yu. Seismic performance analysis of h-shaped steel cantilever beam and frame with corrugated web (in Chinese). Master’s Thesis, Nanchang University, 2022. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[7]]] Peng J. Theoretical and experimental study and analysis of damping effects on corrugated web damper. Master’s Thesis, Huazhong University of Science and Technology, 2020. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[8]]] Mou X., Lv H., Li X. Seismic performance of corrugated steel plate composite shear walls with various configurations. Structures, 57, 105133, 2023. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[9]]] CECS 291:2011 Technical specification for application of corrugated web steel structures (in Chinese). Beijing, China Publishing Press, 2011. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[10]]] Ltd. China Institute of Building Standard Design Research Co. Technical specification for steel structures of ligh-tweight buildings with gabled frames GB51022-2015. Technical Specification for Steel Structures of Ligh-tweight Buildings with gabled frames GB51022-2015, 2003. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[11]]] Cheng J. Analysis of overall stability performance of h-shaped steel axial compression members with corrugated webs. Master’s Thesis, Southwest Petroleum University, 2017. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[12]]] Shahnewaz M., Dickof C., Tannert T. Experimental investigation of the hysteretic behaviour of single-story single-and coupled-panel CLT shear walls with nailed connections. Engineering Structures, 291, 116443, 2023. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[13]]] Hu Y. Earthquake Engineering (in Chinese). Beijing, Seismological Press, 2006. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[14]]] Hu Q. Study on the seismic performance of coupling beam in coupled shearwall (in Chinese). PhD Thesis, Hefei University of Technology, 2013. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[15]]] Han X., Liang Q. Strutural control of coupled shear walls with a stiffening beam (in Chinese). Journal of South China University of Technology (Natural Science Edition), (09):89-94, 1999. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[16]]] Liang O., Han X. Performance of rigid and ordinary connecting beams under low cycle repeated loading (in Chinese). Journal of South China University of Technology (Natural Sciences), 000(001):27–33, 1995. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[17]]] Federal Emergency Management Agency and American Society Of Civil Engineers. Prestandard and commentary for the seismic rehabilitation of buildings. Federal Emergency Management Agency, Washington, DC, USA, Fema 356, 2000. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[18]]] Wang M., Zhang Z., Chen Z., Han Y., Liu Y. Seismic performance analysis of new connection nodes between embedded wall panels and steel frames. Science Technology and Engineering, 23(18):7868–7877, 2023. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[19]]] Xue G., Bao W., Jiang J., Shao Y. Hysteretic behavior of beam-to-column joints with cast steel connectors. Shock and Vibration, 2019:1–20, 2019. | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[20]]] Li Z., Xu Y. Analysis of the influence of different axial compression ratios on the hysteresis performance of carbon fiber reinforced steel reinforced concrete filled steel tube columns. In Proceedings of the 8th Shenyang Scientific Academic Annual Conference, 601–606, 2011. | |
| + | |||
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[21]]] Lv L., Sun G., Yang W. Influence of axial compression ratio on hysteretic behavior of i-shaped steel tube bundle high strength concrete composite shear wall. Journal of Suzhou University of Science and Technology (Engineering and Technology Edition), 36(1):8–14, 2023. | |
Latest revision as of 10:21, 21 March 2024
Abstract
Corrugated web H-beam refers to a steel beam with a wavy shape along its length, which is extensively utilized in various parts of building structures such as beams, columns, and walls. It serves the purpose of connection and support, while the corrugated or folded design enhances the shear resistance and out-of-plane stiffness of the web to some extent. However, despite their advantages including high strength, stiffness, and lightweight construction, relevant regulations stipulate that these members can only be used in lower-intensity applications or higher-intensity scenarios if specific conditions are met. One crucial condition is that the ratio between the design value of axial force subjected to seismic action and the product of the member's flange section area and steel's tensile strength should not exceed 0.4. In this study, we aim to further investigate the seismic characteristics and applicable intensity of corrugated steel structures under earthquakes through large-scale finite element ABAQUS simulations. We will observe dynamic characteristics and failure modes of corrugated rigid frame structures using elastic-plastic time-history analysis methods as well as examine plastic deformation features of steel beam members under low cyclic loads via hysteretic analysis methods. The findings demonstrate that when properly designed with reasonable beam spans, corrugated web rigid frame structures can still be employed in high-intensity areas above 7 degrees even when subjected to an axial compression ratio up to 0.5.
Keywords: Corrugated web, intensity, hysteretic behavior, axial pressure ratio
1. Introduction
The concept of green building is comprehensively implemented in project construction and building, integrating principles of environmental protection and energy conservation to achieve features of sustainable development. Furthermore, the advancement of assembled steel structures effectively promotes the progress of green building [1].
Corrugated steel profiles represent a novel form of environmentally friendly construction steel that has emerged in recent decades. The availability of materials, on-site component cutting and assembly capabilities, waste-free production processes, reduced transportation costs, and the ability to select sections based on load requirements have facilitated ongoing research in this field [2]. With the recent comprehensive investigations conducted by scientific researchers, static studies on corrugated steel profiles have reached a relatively advanced stage while dynamic research has been progressively expanding. In terms of bridge applications, Jiang et al. [3] experimentally demonstrated that corrugated web steel-concrete composite box girders exhibit well-defined load-displacement hysteresis loops under low-cycle repeated loads without any noticeable pinching phenomenon, thereby displaying excellent seismic performance. According to the principle of equal shear capacity in box girder sections, Feng et al. [4] developed finite element models for both corrugated steel web continuous rigid frame bridges and corresponding concrete web continuous rigid frame bridges. A comparative analysis was conducted on the dynamic characteristics and seismic performance of these two types. The findings reveal that under earthquake loading, corrugated steel web rigid frame bridges exhibit reduced internal forces at low piers and top shears at high piers compared to concrete web rigid frame bridges; however, they experience increased top bending moment at high piers and bottom internal forces at piers. Through mechanical formula analysis, Li et al. [5] have demonstrated that the implementation of hollow piers not only results in reduced weight but also effectively enhances the torsional performance of the upper structure in continuous rigid frame bridges with corrugated steel webs, thereby increasing its transverse compressive stiffness. Consequently, when designing continuous rigid frame box girder bridges with corrugated steel webs, employing hollow piers offers significant advantages. In terms of architecture. The seismic performance of the H-beam cantilever beam and frame with corrugated web was analyzed using the ABAQUS finite element model, as conducted by Wanyu [6]. The seismic performance of corrugated web dampers has been enhanced through Peng [7] experimental research, thereby expanding the potential applications of corrugated steel materials. Xingyu et al. [8] proposed a novel composite shear wall configuration comprising a frame consisting of corrugated concrete-filled steel tubular columns and filled corrugated steel plates, and demonstrated the excellent seismic performance of this composite structure through numerical analysis and experimental investigations. According to the current investigation, despite the numerous advantages of corrugated web profiles, their promotion and utilization in China remain inadequate due to the intricate production process and limited seismic performance [9,10]. Therefore, conducting research on corrugated steel within the realm of seismic applications for industrial and civil buildings holds immense significance [11].
The simulation analysis in this study employed a combination of dynamic and quasi-static approaches. Time-history analysis was conducted on the rigid frame, while hysteresis analysis was performed on the steel beam [12]. These analyses were utilized to further investigate the ratio between the seismic-induced axial force design value and the product of the member's flange section area and its steel tensile strength design value. This research provides a theoretical basis for utilizing such components in high-intensity earthquake zones.
2. Modeling and analytical hypotheses
2.1 Analytical model and its corresponding parameters
The material parameters are presented in Table 1, as depicted in Figure 1. Additionally, the web fluctuation parameters utilized in this study can be found in Table 2 and Figure 2.
| Steel | Ε | |||
|---|---|---|---|---|
| Q345 | 2.061011 N/m2 | 7850 kg/m3 | 0.28 | 310 N/mm2 |
|
| Figure 1. Material constitutive model |
| Angle (°) | Wave length (mm) |
Wave height (mm) |
Flange thickness-to- width ratio |
Thick-ness (mm) |
Wave height (mm) |
|---|---|---|---|---|---|
| 45 | 240 | 25 | 0.05 | 2 | 520 |
|
| Figure 2. Web plate bending parameters |
As depicted in Figure 3, Model 1 represents a rigid frame structure with zero ridge slope, featuring corrugated beam members of lengths 6m, 12m, 18m, and 24m, along with uniformly sized column heights of 6m. The node serves as a rigid junction connecting the -direction (column height), -direction (perpendicular to the beam axis), and -direction (span direction) of the rigid frame. On the other hand, Model 2 exemplifies an ordinary rigid frame beam member model used for observing the hysteretic characteristics of corrugated steel beams under low-cycle reciprocating loads.
| ||||
| Figure 3. Model diagram |
2.2 Analytical assumptions
(1) In the ideal state, it is assumed that the connection between the node of the member and the support in a rigid frame is perfectly rigid.
(2) The beam of a rigid frame structure is assumed to be supported solely by pressure-type steel plate roofs and cold-formed steel purlins.
(3) It is assumed that the structures are subjected to ideal conditions when under stress.
3. The dynamic analysis of a rigid frame structure
3.1 Modal analysis
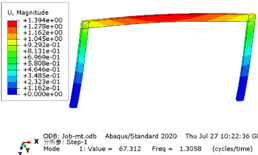
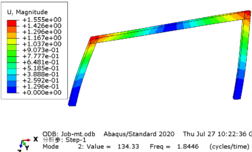
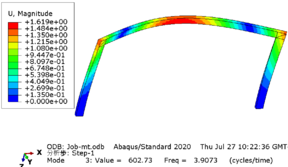
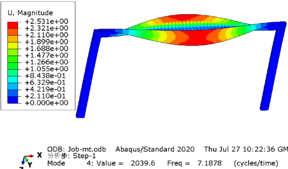
Taking the rigid frame with a span of 12 meters as an example, the modal analysis of the structure is carried out, and each mode is shown in Figure 4 .
| ||||||||
| Figure 4. Modal analysis diagram |
In this model, a subspace iterative method was employed to extract the first four modes, with the first frequency being 1.3058 Hz, corresponding to a period of 0.74 s for the model. The results obtained from both manual calculation and software using the formula showed little discrepancy, indicating that the structural model is accurate and reliable.
3.2 Time-history analysis
In the Time-history analysis, a pair of eccentric forces is applied to simulate the beam as a flexural member and control it at the required axial compression ratio. The formula used for calculating the axial compression ratio is given by , where represents the axial pressure value, denotes the net cross-sectional area of the flange, and represents the design value of steel's tensile strength.
3.2.1 The modulation of seismic wave amplitude
Under the column base constraint , and are set to zero, and represent the translational degrees of freedom along the -axis and -axis respectively, while representing the translational degree of freedom along the -axis. Similarly, , and represent the rotational degrees of freedom around the -axis, -axis, and -axis respectively. The EL-Centro seismic waves are applied to and . Amplitude modulation is performed using the formula , where denotes the designed maximum acceleration; represents the maximum acceleration from the selected seismic record; and signifies an actual seismic acceleration time coordinate point with These points should be recorded.
Taking the EL-Centro wave as an example, it exhibits a peak acceleration of 2.20 m/s2 [13] and is depicted in Figure 5.
| ||||
| Figure 5. Comparison of EL-Centro wave before and after amplitude modulation |
3.2.2 The basis for analysis
According to the Stipulate of the Technical Specification for Steel Structures of Lightweight Buildings with Portal Frames(GB51022:2015) [12] 3.3.1: In a single-layer portal frame configuration, excluding crane and light steel wallboard, the maximum displacement of the column's top should not exceed H/60. This implies that the angular displacement between layers must be less than 0.017.
According to the Stipulate of the Technical Specification for Steel Structures of Lightweight Buildings with Portal Frames(GB51022:2015) [12] 3.3.2: The deflection limit for members of inclined beams in portal frames, supporting only profiled steel roofs and cold-formed steel purlins, is L/180, where L represents the full-span length.
3.2.3 The analysis of the results
(1) Comparative analysis under seismic conditions at axial compression ratios of 0.4 and 0.5
The eccentric load is applied to the beam of the rigid frame structure, subjecting the member to a specified axial compression ratio, and seismic waves are applied during rare earthquakes at the base of the rigid frame column. Firstly, we compare and analyze the structural stress and failure under earthquake conditions with an axial compression ratio of 0.4 and 0.5.
According to the analysis in Section 3.2.2, it is evident that for beam spans of 6m and 12m as shown in Table 3, the inter-story displacement angle fails to meet the design requirements for seismic activity of a magnitude of nine degrees in high-risk areas. However, it does satisfy the intensity criteria under various coaxial pressure ratios at spans of 18m and 24m. The deflection meets the design specifications across different spans.
| Beam span | n | Wave peak value | 220 | 310 | 400 | 510 | 620 |
|---|---|---|---|---|---|---|---|
| 6m | 0.4 | (Interlayer displacement) max | 39.29 | 54.91 | 70 | 89.60 | 108.61 |
| 6m | 0.4 | (Interlayer displacement angle) max | 0.0065 | 0.0092 | 0.0117 | 0.0149 | 0.0181 |
| 6m | 0.4 | (Mid-span deflection)max | 5.30 | 5.46 | 5.60 | 5.76 | 5.90 |
| 6m | 0.5 | (Interlayer displacement) max | 39.63 | 55.20 | 70.45 | 89.34 | 108.67 |
| 6m | 0.5 | (Interlayer displacement angle) max | 0.0066 | 0.0092 | 0.01174 | 0.0149 | 0.0181 |
| 6m | 0.5 | (Mid-span deflection)max | 6.65 | 6.68 | 6.81 | 7.10 | 7.14 |
| 12m | 0.4 | (Interlayer displacement) max | 40.79 | 56.36 | 72.03 | 91.21 | 109.89 |
| 12m | 0.4 | (Interlayer displacement angle) max | 0.0068 | 0.0094 | 0.0120 | 0.0152 | 0.0183 |
| 12m | 0.4 | (Mid-span deflection)max | 13.51 | 13.62 | 13.79 | 13.92 | 14.01 |
| 12m | 0.5 | (Interlayer displacement) max | 41.30 | 56.51 | 72.66 | 91.86 | 111.04 |
| 12m | 0.5 | (Interlayer displacement angle) max | 0.0069 | 0.0094 | 0.0121 | 0.0153 | 0.0185 |
| 12m | 0.5 | (Mid-span deflection)max | 16.57 | 16.72 | 16.80 | 16.91 | 17.07 |
| 18m | 0.4 | (Interlayer displacement) max | 31.65 | 42.57 | 46.57 | 58.31 | 81.41 |
| 18m | 0.4 | (Interlayer displacement angle) max | 0.0053 | 0.0071 | 0.0078 | 0.0097 | 0.013665 |
| 18m | 0.4 | (Mid-span deflection)max | 24.98 | 24.99 | 25.12 | 25.68 | 25.82 |
| 18m | 0.5 | (Interlayer displacement) max | 32.70 | 43.20 | 54.79 | 68.57 | 82.26 |
| 18m | 0.5 | (Interlayer displacement angle) max | 0.0055 | 0.0072 | 0.0091 | 0.0114 | 0.0137 |
| 18m | 0.5 | (Mid-span deflection)max | 30.24 | 30.33 | 30.61 | 30.94 | 31.10 |
| 24m | 0.4 | (Interlayer displacement) max | 31.20 | 41.82 | 52.35 | 65.33 | 78.57 |
| 24m | 0.4 | (Interlayer displacement angle) max | 0.0052 | 0.0070 | 0.0087 | 0.0109 | 0.0131 |
| 24m | 0.4 | (Mid-span deflection)max | 42.47 | 40.76 | 41.02 | 41.27 | 41.61 |
| 24m | 0.5 | (Interlayer displacement) max | 32.48 | 43.45 | 53.5 | 66.40 | 79.36 |
| 24m | 0.5 | (Interlayer displacement angle) max | 0.0054 | 0.0072 | 0.0089 | 0.0111 | 0.0132 |
| 24m | 0.5 | (Mid-span deflection)max | 50.31 | 48.03 | 50.61 | 50.98 | 50.14 |
The inter-story displacement and inter-story displacement angle remain unaffected by the axial compression ratio, as evidenced in Figures 6 and 7, while their values exhibit an increasing trend with higher seismic wave intensity.
|
| ||
| Figure 6. Maximum angle of inter-story displacement |
| ||||||||||||||||
| Figure 7. Time-history curves illustrating the response of different spans and axial compression ratios |
The greater the acceleration of an earthquake, the more severe the structural damage it inflicts. In this case study, we analyze the force cloud diagram of a member subjected to an intensity level of 9 degrees. According to Table 4, when the axial compression ratio ranges from 0.4 to 0.5, the member does not reach its yield strength and stress values decrease as span length increases. The structure experiences a maximum internal force of 647.7kN at an axial compression ratio approximately equal to 0.52. However, even at its highest stress value of 224.9MPa, it remains below its yield point and thus avoids any structural damage.
| Span | Axial compression ratio is 0.4 | Axial compression ratio is 0.5 |
|---|---|---|
| 6m | ||
| 12m | ||
| 18m | ||
| 24m |
The stress-strain curves depicted in Figure 8 for various beam spans and axial compression ratios demonstrate that irrespective of whether the axial compression ratio is 0.4 or 0.5, the observed elastic behavior persists within the range of beam spans from 6 to 24m. This characteristic enhances its ability to withstand external loads and seismic forces.
|
| ||
| Figure 8. Stress-strain curves for various spans and axial compression ratios |
(2) When the axial compression ratio is 0.6, 0.7 and 0.8
As analyzed in the previous text, it can be seen that when the beam spans are 6m and 12m, the inter-story displacement limit cannot be satisfied under the influence of rare earthquakes at a magnitude of 9 degrees. This is primarily attributed to the susceptibility of small span-to-height ratio connected beams to brittle shear failure during seismic events. However, as the span-to-height ratio increases, their mechanical behavior gradually approaches that of conventional frame beams, resulting in improved seismic performance [14-17]. Consequently, it can be inferred that even with larger axial pressure ratios, both 6m and 12m spans still fail to meet the requirements for rare earthquakes at a magnitude of 9 degrees. To further investigate the maximum achievable axial compression ratio for corrugated rigid frames, similar methods will be employed to analyze structural failure under rare earthquake conditions at magnitudes of 9 degrees when subjected to axial compression ratios of 0.6 and 0.7.
The Technical code for the steel structure of the light-weight building with gabled frames(GB51022:2015), and Figures 9 and 10 showed the inter-story displacement fails to meet the code requirements under the influence of a 9-degree rare earthquake for beam spans of 6m and 12m, but it satisfies the requirements for spans of 18m and 24m. Figure 11 demonstrates that the deflection complies with the code specifications. This conclusion remains consistent when considering coaxial compression ratios of both 0.4 and 0.5.
| ||||||||||||||||
| Figure 9. Interlayer displacement curves with varying spans and coaxial pressure ratios |
|
| ||
| Figure 10. Maximum angle of inter-story displacement |
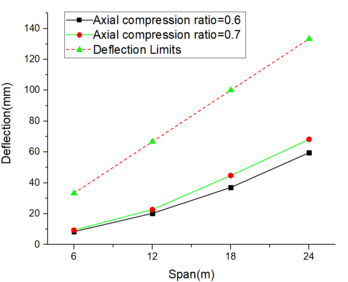
|
| Figure 11. Deflection and limit values under different spans and axial compression ratios for 9-degree rare earthquakes |
The stress-strain curve in Figure 12 demonstrates a distinct hysteretic characteristic as the axial compression ratio increases, with a more pronounced effect observed at higher ratios. This indicates that the rigid frame beam undergoes plastic deformation as the axial compression ratio rises, and this deformation becomes more significant with increasing compression. To ensure optimal seismic characteristics of the rigid frame structure, it is advisable to maintain the structure predominantly within the elastic stress stage. Therefore, based on the aforementioned conclusion, it can be inferred that even with an axial compression ratio of 0.5, the rigid frame structure still exhibits favorable seismic characteristics.
| ||
| Figure 12. Stress-strain curves for various spans and axial compression ratios |
4. Quasi-static analysis
In the section of quasi-static hysteretic analysis, one end is fully consolidated, meaning that all six degrees of freedom are constrained to zero, while the other end is subjected to loading. The loading end applies a displacement amplitude in the vertical beam direction when the axial compression ratio is set at 0.4 and 0.5 respectively. The displacement starts from 0 mm and incrementally increases to 180 mm step by step. Simultaneously, the corresponding duration of each amplitude is defined in the analysis step [18,19], as depicted in Figure 13.
| Figure 13. Loading system |
The hysteresis curves presented in Table 5 and the Mises cloud graph demonstrate that variations in axial compression ratio have minimal influence on the hysteresis loop. At a span of 6m, the hysteresis curve exhibits maximum completeness with a slight pinch and possesses the highest capacity for energy dissipation. The skeleton curve encompasses all three stages of elasticity, elastic-plasticity, and plasticity[20], while localized failure occurs at the beam ends upon reaching their yield limit.
When the beam span is 12m, the hysteretic curve exhibits significant pinching, and the beam undergoes noticeable torsion under displacement loading. At this juncture, failure of the steel beam no longer occurs solely at its end but rather manifests as local buckling at the point of torsion.
The area enclosed by the hysteretic loop gradually decreases with an increase in the shear-span ratio, as illustrated in Table 5. Moreover, the hysteretic curve exhibits significant pinching and slipping, resulting in a reduced external force required for the same displacement and diminished energy dissipation. At an 18m span, the torsional slip of the member is pronounced; however, at a 24m span, the member demonstrates nearly elastic deformation albeit with noticeably decreased energy dissipation [21].
The conclusion can be inferred that, for a specific axial compression ratio, the hysteresis analysis load capacity of the structure decreases as the span length increases. Moreover, it is observed that the hysteretic performance is minimally affected by the axial compression ratio. However, low cyclic loads still provide valuable insights for seismic analysis.
| Span | Hysteretic curve | Mises cloud picture |
|---|---|---|
| 6m | ||
| 12m | ||
| 18 | ||
| 24m |
5. Conclusions
The rigid frame beam spans ranging from 6 to 24m are designed to withstand earthquakes of up to 8 degrees or lower, while the spans of 18m and 24m can simultaneously resist earthquakes of magnitude 9 and below. Therefore, it is essential to carefully control the beam span to ensure optimal seismic resistance for the structure.
To ensure that structural failure always occurs within the elastic stage, it is crucial to limit the axial compression ratio and ensure a sound structural design. The utilization of corrugated web rigid frame structures may be appropriate in regions with infrequent seismic activity exceeding 7 degrees, provided that the axial compression ratio does not surpass 0.5.
The axial compression ratio has little influence on the hysteretic performance of the members. With the increase of the span, the members will slip, the hysteretic curve will shrink, and the energy dissipation will become smaller, which is not conducive to the earthquake resistance of the structure.
Acknowledgments
The authors would like to thank The Youth Innovation Team of Shaanxi Universities (Key Technology Innovation Team for Urban Rail Transit Track Bed). Young and middle-aged fund project at Xi’an Traffic Engineering Institute (2023KY-39), and The Scientific Research Program Funded by Education Department of Shaanxi Provincial Government (Program No.23JK0532).
References
[1] Chen H. Analysis and discussion on the application of prefabricated design and construction in green buildings (in Chinese). China Residential Facilities, 06(37-39), 2023.
[2] Ibragimov A., Zinoveva E., Rosinskiy S. Prefabricated steel structures with a corrugated web (part 1: beam). IOP Conference Series Materials Science and Engineering, 869:072041, 2020.
[3] Jiang L., Zhong T., Tan Z., Zhou W., Wu L., Xu T. Study on seismic performance of steel-concrete composite box girder with corrugated web (in Chinese). Journal of Railway Science and Engineering, 18(555-563), 2021.
[4] Feng W.Z., Liu B., Mou K., Wang H. Research on seismic performance of continuous rigid-frame bridge with corrugated steel webs (in Chinese). Earthquake Resistant Engineering and Retrofitting, 37(70-74), 2015.
[5] Li P., Liu B., Xiaoying-nan. Influence of pier types on dynamic characteristics of continuous rigid frame bridge with corrugated steel webs (in Chinese). Bridge Construction, (2):3, 2011.
[6] Wan-yu. Seismic performance analysis of h-shaped steel cantilever beam and frame with corrugated web (in Chinese). Master’s Thesis, Nanchang University, 2022.
[7] Peng J. Theoretical and experimental study and analysis of damping effects on corrugated web damper. Master’s Thesis, Huazhong University of Science and Technology, 2020.
[8] Mou X., Lv H., Li X. Seismic performance of corrugated steel plate composite shear walls with various configurations. Structures, 57, 105133, 2023.
[9] CECS 291:2011 Technical specification for application of corrugated web steel structures (in Chinese). Beijing, China Publishing Press, 2011.
[10] Ltd. China Institute of Building Standard Design Research Co. Technical specification for steel structures of ligh-tweight buildings with gabled frames GB51022-2015. Technical Specification for Steel Structures of Ligh-tweight Buildings with gabled frames GB51022-2015, 2003.
[11] Cheng J. Analysis of overall stability performance of h-shaped steel axial compression members with corrugated webs. Master’s Thesis, Southwest Petroleum University, 2017.
[12] Shahnewaz M., Dickof C., Tannert T. Experimental investigation of the hysteretic behaviour of single-story single-and coupled-panel CLT shear walls with nailed connections. Engineering Structures, 291, 116443, 2023.
[13] Hu Y. Earthquake Engineering (in Chinese). Beijing, Seismological Press, 2006.
[14] Hu Q. Study on the seismic performance of coupling beam in coupled shearwall (in Chinese). PhD Thesis, Hefei University of Technology, 2013.
[15] Han X., Liang Q. Strutural control of coupled shear walls with a stiffening beam (in Chinese). Journal of South China University of Technology (Natural Science Edition), (09):89-94, 1999.
[16] Liang O., Han X. Performance of rigid and ordinary connecting beams under low cycle repeated loading (in Chinese). Journal of South China University of Technology (Natural Sciences), 000(001):27–33, 1995.
[17] Federal Emergency Management Agency and American Society Of Civil Engineers. Prestandard and commentary for the seismic rehabilitation of buildings. Federal Emergency Management Agency, Washington, DC, USA, Fema 356, 2000.
[18] Wang M., Zhang Z., Chen Z., Han Y., Liu Y. Seismic performance analysis of new connection nodes between embedded wall panels and steel frames. Science Technology and Engineering, 23(18):7868–7877, 2023.
[19] Xue G., Bao W., Jiang J., Shao Y. Hysteretic behavior of beam-to-column joints with cast steel connectors. Shock and Vibration, 2019:1–20, 2019.
[20] Li Z., Xu Y. Analysis of the influence of different axial compression ratios on the hysteresis performance of carbon fiber reinforced steel reinforced concrete filled steel tube columns. In Proceedings of the 8th Shenyang Scientific Academic Annual Conference, 601–606, 2011.
[21] Lv L., Sun G., Yang W. Influence of axial compression ratio on hysteretic behavior of i-shaped steel tube bundle high strength concrete composite shear wall. Journal of Suzhou University of Science and Technology (Engineering and Technology Edition), 36(1):8–14, 2023.
Document information
Published on 21/03/24
Accepted on 29/02/24
Submitted on 23/10/23
Volume 40, Issue 1, 2024
DOI: 10.23967/j.rimni.2024.03.001
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?