| (48 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | <!--== Analytical solution for one-dimensional consolidation of structured soft soils with continuous drainage boundary == | + | <!--== '''Analytical solution for one-dimensional consolidation of structured soft soils with continuous drainage boundary''' == |
{| class="MsoTableGrid" | {| class="MsoTableGrid" | ||
| Line 34: | Line 34: | ||
| | | | ||
| − | <nowiki> </nowiki>longwang@jiangnan.edu. | + | <nowiki> </nowiki>longwang@jiangnan.edu.cn |
|- | |- | ||
| Line 42: | Line 42: | ||
| | | | ||
<nowiki> </nowiki>zhjwgeo@163.com | <nowiki> </nowiki>zhjwgeo@163.com | ||
| + | |||
| + | |- | ||
| + | | | ||
| + | <nowiki> </nowiki>Guoxiong Mei<sup>2, 5</sup> | ||
| + | |||
| + | | | ||
| + | <nowiki> </nowiki>meiguox@163.com | ||
|} | |} | ||
| Line 47: | Line 54: | ||
'''Affiliations:''' | '''Affiliations:''' | ||
| − | <sup>1</sup>Guangxi Communications Investment Group Corporation Ltd., Nanning 530021, China; | + | <sup>1</sup>Guangxi Communications Investment Group Corporation Ltd., Nanning 530021, China; |
<sup>2</sup>Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education, Guangxi University, College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China. | <sup>2</sup>Key Laboratory of Disaster Prevention and Structural Safety of Ministry of Education, Guangxi University, College of Civil Engineering and Architecture, Guangxi University, Nanning 530004, China. | ||
| − | <sup>3</sup> | + | <sup>3</sup>School of Civil Engineering and Architecture, Guizhou Minzu University, Guiyang 550025, China. |
<sup>4</sup>School of Environment and Civil Engineering, Jiangnan University, Wuxi 214122, Jiangsu, China | <sup>4</sup>School of Environment and Civil Engineering, Jiangnan University, Wuxi 214122, Jiangsu, China | ||
| + | |||
| + | <sup>5</sup>Ocean College, Zhejiang University, Zhoushan 316021, China. | ||
--> | --> | ||
| − | + | ==Abstract== | |
A closed form analytical solution is proposed to analyze the one-dimensional consolidation behavior of structured saturated clay soils under continuous drainage boundary. Firstly, the soil structural properties and arbitrary loading conditions are taken into account in the established mathematical model. Using the finite sine Fourier transform and characteristic function methods, analytical calculation is conducted, and the solution effectiveness is evaluated against the degradation of solutions and the results of finite difference analysis. Finally, the influences of interface parameter, properties of soil structure and structural yield stress on consolidation behaviors are discussed. Results show that the larger the interface parameter is, the easier the soil structure enters the failure stage, and the smaller the consolidation degree is. Furthermore, the time for initiating the failure stage does not change, when the interface parameter and structural yield stress keep unchanged; in the meanwhile, the greater the consolidation coefficient is, the greater the consolidation degree of foundation becomes when the soil structure begins to fail, and the earlier the soil enters the complete failure stage. When the interface parameter is determined, the ratio of structural yield stress to load can accelerate the soil consolidation rate, but all consolidation curves coincide for the same ratio. | A closed form analytical solution is proposed to analyze the one-dimensional consolidation behavior of structured saturated clay soils under continuous drainage boundary. Firstly, the soil structural properties and arbitrary loading conditions are taken into account in the established mathematical model. Using the finite sine Fourier transform and characteristic function methods, analytical calculation is conducted, and the solution effectiveness is evaluated against the degradation of solutions and the results of finite difference analysis. Finally, the influences of interface parameter, properties of soil structure and structural yield stress on consolidation behaviors are discussed. Results show that the larger the interface parameter is, the easier the soil structure enters the failure stage, and the smaller the consolidation degree is. Furthermore, the time for initiating the failure stage does not change, when the interface parameter and structural yield stress keep unchanged; in the meanwhile, the greater the consolidation coefficient is, the greater the consolidation degree of foundation becomes when the soil structure begins to fail, and the earlier the soil enters the complete failure stage. When the interface parameter is determined, the ratio of structural yield stress to load can accelerate the soil consolidation rate, but all consolidation curves coincide for the same ratio. | ||
| − | ''' | + | '''Keywords''': Analytical solution, consolidation, structured soil, continuous drainage boundary, structural yield stress |
| − | == | + | ==1. Introduction== |
| − | Natural saturated soft soils not only have the characteristics of high-water content, high compressibility, and low permeability, but also have the structural features owing to the influence of geological environment in the deposition process [1 | + | Natural saturated soft soils not only have the characteristics of high-water content, high compressibility, and low permeability, but also have the structural features owing to the influence of geological environment in the deposition process [1-3]. The structural properties of soft soil have a significant influence on its consolidation behavior, especially affecting the permeability and compressibility of the soil. Therefore, saturated soft soils usually show the features of longer consolidation time, larger compression deformation and lower bearing capacity in the process of foundation treatment [4-7]. |
| − | To characterize the mechanical properties of structural soft soil, linear segmented [ | + | To characterize the mechanical properties of structural soft soil, linear segmented [8,9] and nonlinear models [10] have been proposed for modeling the variations of permeability and compression coefficients with effective stress based on the results from experimental studies. In terms of linear segmented consolidation models, An et al. [11] proposed an approximate solution for one-dimensional consolidation of single-layer soil, whereas one-dimensional semi-analytical consolidation solution of double-layer soils [12] and layered soils [13] have been derived. Furthermore, Hu et al. [14] carried out analyses for nonlinear one-dimensional consolidation of single-layer foundation under variable loads, and their model was further modified to account for one-dimensional nonlinear large deformation consolidation analysis of structural soils [15]. In terms of nonlinear consolidation models, a plenty of works have been conducted by many scholars. For example, Cao et al. [16] derived the one-dimensional nonlinear consolidation equations of structural soils under arbitrary load with nonlinear permeability and compressibility coefficients, and then obtained the numerical solution by using the Crank-Nicolson finite difference method. Considering the influence of self-weight stress and nonlinearity of compressibility and permeability of structural soft soil, Tang and Zhou [10] obtained a semi-analytical solution for one-dimensional consolidation of layered soils. A semi-analytical solution for one-dimensional nonlinear consolidation of double-layer foundation, considering the soil structure characteristics, under variable loads was proposed by Cui et al. [17]. Furthermore, using the finite difference method, the one-dimensional large deformation consolidation behavior of marine soft clay was discussed by Li et al. [18]. Xia et al. [19] derived a theoretical solution for multi-layered marine soft clays considering large-strain rheological and natural structural characteristics. |
| − | It should be noted that all analyses mentioned above were conducted based on the fully permeable boundary conditions. Once the load acting on structural soft soil exceeds the soil structure yield stress, the soil will be damaged from the boundary. However, the drainage boundary of soil in practice should be described as a semi-permeable boundary related to time, which is so-called the Neumann boundary condition. It has the disadvantage that it is not easy to obtain an analytical solution. In view of this, a time dependent continuous drainage boundary, which is essentially a Dirichlet boundary condition, has been proposed by Mei et al. [ | + | It should be noted that all analyses mentioned above were conducted based on the fully permeable boundary conditions. Once the load acting on structural soft soil exceeds the soil structure yield stress, the soil will be damaged from the boundary. However, the drainage boundary of soil in practice should be described as a semi-permeable boundary related to time, which is so-called the Neumann boundary condition. It has the disadvantage that it is not easy to obtain an analytical solution. In view of this, a time dependent continuous drainage boundary, which is essentially a Dirichlet boundary condition, has been proposed by Mei et al. [20]. However, there is no reference about the derivation of consolidation solution for structural soils under continuous drainage boundary condition. |
| − | The consolidation theory of continuous drainage boundary mainly includes linear and nonlinear aspects in the literature. In terms of linear consolidation, using Laplace transformation, finite Fourier sine transform, separation of variables and finite element method, scholars have developed solutions that can account for many factors, such as the self-weight [ | + | The consolidation theory of continuous drainage boundary mainly includes linear and nonlinear aspects in the literature. In terms of linear consolidation, using Laplace transformation, finite Fourier sine transform, separation of variables and finite element method, scholars have developed solutions that can account for many factors, such as the self-weight [21,22], linear loading [23,24], variable loading [25,26], double-layered soils [27,28] , and layered soils [26,29]. On the other hand, research of nonlinear consolidation includes material nonlinear consolidation [30-33] and geometric large deformation nonlinear consolidation [34]. For instance, Zong and Wu [31] proposed analytical solutions for one-dimensional nonlinear consolidation, and Tong and Wang [32] derived viscoelastic analytical solutions on the basis of continuous drainage boundary under variable loading [35]. In addition, using separation of variables and Laplace transform methods, an analytical solution for one-dimensional large-deformation consolidation of soils was calculated by Jiang and Zhan [34]. However, it is worth pointing out that none of above research considered the influence of structural properties of soil on consolidation behaviors. |
The objective of this paper is to establish a mathematical model for one-dimensional consolidation, considering the influence of soil structural properties, under continuous drainage boundary and arbitrary loading conditions. Subsequently, using finite Fourier sine transform and integral transform techniques, an analytical solution is derived, the correctness of which is evaluated by comparing with the results of boundary condition degradation and numerical calculation using the backward finite-difference method. Furthermore, the influences of interface parameters and soil structural properties on the consolidation process are discussed. | The objective of this paper is to establish a mathematical model for one-dimensional consolidation, considering the influence of soil structural properties, under continuous drainage boundary and arbitrary loading conditions. Subsequently, using finite Fourier sine transform and integral transform techniques, an analytical solution is derived, the correctness of which is evaluated by comparing with the results of boundary condition degradation and numerical calculation using the backward finite-difference method. Furthermore, the influences of interface parameters and soil structural properties on the consolidation process are discussed. | ||
| − | + | ==2. Model description== | |
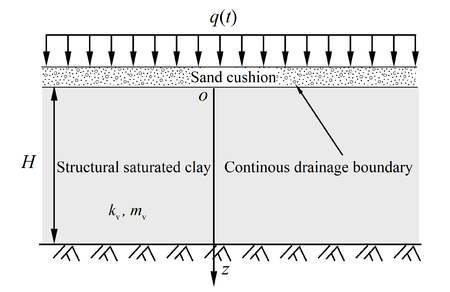
| − | A schematic diagram of one-dimensional consolidation for structural soils is illustrated in | + | A schematic diagram of one-dimensional consolidation for structural soils is illustrated in [[#img-1|Figure 1]], where a uniformly distributed constant load <math display="inline">q</math> is applied on the surface of soil with a total thickness of <math display="inline">H </math>. The upper surface is a continuous drainage boundary, and the bottom surface is an impermeable boundary. In the meanwhile, the coordinate axis <math display="inline">z </math> originates from the top boundary, and the positive direction points downwardly. |
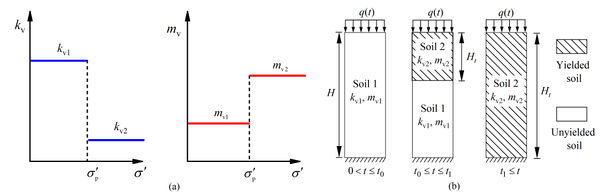
| − | The simplified segmental models [ | + | The simplified segmental models [13] of permeability and compression modulus are shown in [[#img-2|Figure 2]], where <math display="inline">k_{\mbox{v1}}</math> and <math display="inline">m_{\mbox{v1}}</math> are the permeability coefficient and compression modulus of structural in-situ soils, respectively, and <math>k_{\mbox{v2}}</math> and <math display="inline">m_{\mbox{v2}}</math> are the permeability coefficient and compression modulus of remodeled soils, and <math display="inline">q\left(t\right)</math> is the uniformly distributed load applied on the top surface of the structured soil. However, it should be noted that the permeability coefficient of the soil is changing during the consolidation process, and the model described in this study is valid under the classic Terzaghi hypothesis. |
| − | <div class=" | + | <div id='img-1'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | [[File:Review_399419094854_1850_Fig.1.png|centre| | + | |-style="background:white;" |
| − | + | |style="text-align: center;padding:10px;"| [[File:Review_399419094854_1850_Fig.1.png|centre|450px]] | |
| − | + | |- | |
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 1'''. Sketch of one-dimensional consolidation of structured soils | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | + | <div id='img-2'></div> | |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:75%;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_399419094854_5839_Fig.2.jpg|centre|600x600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. Simplified model of structured soil. (a) Segmented pattern of permeability and compression coefficient. (b) Classification diagram (single-drainage situation) | ||
| + | |} | ||
| − | |||
| − | |||
| − | <div class=" | + | According to the process of soil structure failure, the consolidation behavior of structural soil can be divided into three stages ([[#img-3|Figure 3]](a)), including undamaged stage of soil structure, failure stage and complete failure stage [11]. Undamaged stage of soil structure describes the condition that the effective stress at the soil surface is less than the structural yield stress, and the soil parameters (e.g., compression coefficient and permeability coefficient) are equal to the values of undisturbed soils. Hence, the collapse of structure will not occur, and the soil consolidation process belongs to normal consolidation. Failure stage is defined when the soil effective stress on the upper surface exceeds the structural yield stress, and the soil structure begins to damage, forcing a moving boundary of the structural failure surface, as shown in [[#img-3|Figure 3]](b). It must be emphasized that the permeability and compression coefficient of the soil above the moving boundary have been changed, being equivalent to the parameters of remodeled soil, The foundation soil can then be considered as a double-layer foundation at this moment. With the development of consolidation, the stage of complete soil structure failure denotes that the moving boundary of the structure failure surface has reached the bottom of the foundation, and the soil structure has been completely destroyed. The permeability coefficient and compression coefficient of the soil should be simulated with the values of remodeled soil in the stage of complete soil structure failure, and the soil is transformed from a double-layer foundation into a single layer foundation. |
| − | + | ||
| + | <div id='img-3'></div> | ||
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:75%;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_399419094854-image8.png|528px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Sketch of one-dimensional consolidation of structured soils. (a) Division of different soil structure failure stages. (b) Moving boundary due to the development of boundary failure | ||
| + | |} | ||
| − | + | ==3. Solving procedures== | |
| − | + | ===3.1 Solution of excess pore-water pressure=== | |
| − | ===3.1.1 Undamaged stage=== | + | ====3.1.1 Undamaged stage==== |
| − | The effective stress of soil at the upper boundary is less than the yield stress of the structure, when the consolidation time | + | The effective stress of soil at the upper boundary is less than the yield stress of the structure, when the consolidation time <math display="inline"> t </math> belongs to the interval <math display="inline">\left[0,t_0\right]</math>, at which the soil structure has not been damaged. Hence, the mathematical model described in [[#img-1|Figure 1]] is one-dimensional consolidation of single-layer soil with continuous drainage boundary under constant load. The governing equation of the system can be written as |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 117: | Line 134: | ||
|} | |} | ||
| − | + | where <math>u_1</math> is the excess pore-water pressure in the soil at the undamaged stage; <math>c_\mbox{v}</math> is the consolidation coefficient; and parameters <math display="inline"> t </math>, <math display="inline"> H </math> and <math display="inline">z </math> represent the time, the thickness of the soil layer and the vertical coordinate, respectively. | |
| − | + | ||
Initial condition and boundary conditions can be expressed as follows: | Initial condition and boundary conditions can be expressed as follows: | ||
| Line 138: | Line 154: | ||
|- | |- | ||
| <math>\left\{ \begin{array}{c} | | <math>\left\{ \begin{array}{c} | ||
| − | {u_1\ | + | {u_1\Big| }_{z=0}=q\left(t\right)\mbox{e}^{-bt}\\ |
| − | {\frac{\partial u_1}{\partial t}\ | + | {\displaystyle\frac{\partial u_1}{\partial t}\Big| }_{z=H}=0 |
\end{array}\right.</math> | \end{array}\right.</math> | ||
|} | |} | ||
| Line 145: | Line 161: | ||
|} | |} | ||
| − | + | where <math>q\left(t\right)</math> is a uniformly distributed load applied on the surface of structural soil foundation, and parameter <math display="inline"> b </math> is the interface parameter. | |
| − | where <math>q\left(t\right)</math> is a uniformly distributed load applied on the surface of structural soil foundation, and parameter | + | |
By combining the solution conditions and using the finite Fourier sine transform method, the analytical solution can be expressed as follow: | By combining the solution conditions and using the finite Fourier sine transform method, the analytical solution can be expressed as follow: | ||
| Line 155: | Line 170: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>u_1=\sum_{n=1}^{\infty }\frac{2}{N_n}\frac{qb}{{\beta }_n-b}\left(\mbox{e}^{-bt}-\right. </math><math>\left. e^{-{\beta }_nt}\right) | + | | <math>u_1=\sum_{n=1}^{\infty }\frac{2}{N_n}\frac{qb}{{\beta }_n-b}\left(\mbox{e}^{-bt}-\right. </math><math>\left. e^{-{\beta }_nt}\right)\sin N_n\frac{z}{H}+q\mbox{e}^{-bt}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (4) | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
|} | |} | ||
| − | + | where <math>N_n=\frac{2n-1}{2}\mbox{π}</math>, and <math>{\beta }_n=\frac{C_\mbox{v}N_n^2}{H^2}</math> <math>(n=1,2,3\ldots )</math>. | |
| − | where <math>N_n=\frac{2n-1}{2}\mbox{π}</math> , and <math>{\beta }_n=\frac{C_\mbox{v}N_n^2}{H^2}</math> ( | + | |
===3.1.2 Failure stage=== | ===3.1.2 Failure stage=== | ||
| Line 167: | Line 181: | ||
In the failure stage of soil structure, the time ''t'' belongs to the interval <math>\left[\begin{array}{cc} | In the failure stage of soil structure, the time ''t'' belongs to the interval <math>\left[\begin{array}{cc} | ||
t_0 & t_1 | t_0 & t_1 | ||
| − | \end{array}\right]</math> , and the soil structure begins to break down. Hence, the effective stress on the upper boundary of soil is greater than the yield stress of the structure, and the single-layer foundation is transformed into a double-layer foundation (a remolded soil layer overlying an undamaged soil layer). Taking <math>t^ | + | \end{array}\right]</math>, and the soil structure begins to break down. Hence, the effective stress on the upper boundary of soil is greater than the yield stress of the structure, and the single-layer foundation is transformed into a double-layer foundation (a remolded soil layer overlying an undamaged soil layer). Taking <math>t^{'}=t-t_0</math> as the time coordinate, the consolidation behaviors in this stage can be considered as a linear consolidation of double-layered foundation with non-uniform initial pore pressure under continuous drainage boundary conditions, and the initial pore pressure is <math>u_1\left(t_0,z\right)</math> . Therefore, the governing equation and the definite solution conditions can be written as follows: |
| − | Governing equation: | + | ''Governing equation'': |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 180: | Line 194: | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (5) | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
|} | |} | ||
| − | |||
where <math>u_2^1</math> and <math>c_\mbox{v}^1</math> are the excess pore-water pressure and the consolidation coefficient of soil element above the moving boundary, respectively; <math>u_2^2</math> and <math>c_\mbox{v}^2=c_\mbox{v}</math> are the excess pore-water pressure and the consolidation coefficient of soil element under the moving boundary, respectively. | where <math>u_2^1</math> and <math>c_\mbox{v}^1</math> are the excess pore-water pressure and the consolidation coefficient of soil element above the moving boundary, respectively; <math>u_2^2</math> and <math>c_\mbox{v}^2=c_\mbox{v}</math> are the excess pore-water pressure and the consolidation coefficient of soil element under the moving boundary, respectively. | ||
| − | Initial condition: | + | ''Initial condition'': |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 191: | Line 204: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math>{u_2^i(t^{{'}},z)\vert }_{t'=0}={\sigma }_2\left(z\right)=</math><math>u_1\left(t_0,z\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (6) | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
|} | |} | ||
| + | where <math>{\sigma }_2\left(z\right)</math> is the surcharge stress in the soil at any depth <math>z</math> in the failure stage. | ||
| − | + | ''Boundary conditions'': | |
| − | + | ||
| − | Boundary conditions: | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 207: | Line 219: | ||
|- | |- | ||
| <math>\left\{ \begin{array}{c} | | <math>\left\{ \begin{array}{c} | ||
| − | {u_2^1\left(t | + | {u_2^1\left(t',z\right)\Big| }_{z=0}=q\mbox{e}^{-b\left(t'+t_0\right)}\\ |
| − | {\frac{\partial u_2^2\left(t | + | {\frac{\partial u_2^2\left(t',z\right)}{\partial z}\Big| }_{z=H}\mbox{ }=0 |
\end{array}\right.</math> | \end{array}\right.</math> | ||
|} | |} | ||
| Line 223: | Line 235: | ||
|- | |- | ||
| <span id='ZEqnNum370091'></span> <math>\left\{ \begin{array}{c} | | <span id='ZEqnNum370091'></span> <math>\left\{ \begin{array}{c} | ||
| − | {u_2^1\ | + | {u_2^1\Big|}_{z=h_1}={u_2^2\Big|}_{z=h_1}\\ |
| − | {k_{\mbox{v1}}\frac{\partial u_2^1}{\partial z}\ | + | {k_{\mbox{v1}}\displaystyle\frac{\partial u_2^1}{\partial z}\Big| }_{z=h_1}={k_{\mbox{v2}}\displaystyle\frac{\partial u_2^2}{\partial z}\Big| }_{z=h_1} |
\end{array}\right.</math> | \end{array}\right.</math> | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (8) | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
|} | |} | ||
| − | |||
where <math>k_{\mbox{v}1}</math> and <math>h_1</math> are the permeability coefficient and the thickness of remolded soil, respectively; <math>k_{\mbox{v}2}</math> and <math>h_2</math> are the permeability coefficient and the thickness of undamaged soil, respectively. | where <math>k_{\mbox{v}1}</math> and <math>h_1</math> are the permeability coefficient and the thickness of remolded soil, respectively; <math>k_{\mbox{v}2}</math> and <math>h_2</math> are the permeability coefficient and the thickness of undamaged soil, respectively. | ||
| Line 240: | Line 251: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <span id='ZEqnNum794044'></span> <math>u_2^i=v_i+q\mbox{e}^{-b\left(t | + | | <span id='ZEqnNum794044'></span> <math>u_2^i=v_i+q\mbox{e}^{-b\left(t'+t_0\right)}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (9) | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
| Line 253: | Line 264: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <span id='ZEqnNum495202'></span> <math>\frac{\partial v_i}{\partial t | + | | <span id='ZEqnNum495202'></span> <math>\frac{\partial v_i}{\partial t'}=c_{\mbox{v}i}\frac{{\partial }^2v_i}{\partial z^2}+</math><math>R_1(t')</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (10) | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
|} | |} | ||
| + | where <math>R_1\left(t'\right)=bq\mbox{e}^{-b\left(t'+t_0\right)}</math>, | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| − | + | |- | |
| − | <math>\left\{ \begin{array}{c} | + | | |
| − | {v_1\left(t | + | {| style="text-align: center; margin:auto;width: 100%;" |
| − | {\frac{\partial v_2\left(t | + | |- |
| − | \end{array}\right.</math> (11) | + | | style="text-align: center;" |<math>\left\{ \begin{array}{c} |
| + | {v_1\left(t',z\right)\Big|}_{z=0}=0\\ | ||
| + | {\displaystyle\frac{\partial v_2\left(t',z\right)}{\partial z}\Big| }_{z=H}\mbox{ }\mbox{ }=0 | ||
| + | \end{array}\right.</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(11) | ||
| + | |} | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 271: | Line 289: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <span id='ZEqnNum310255'></span> <math>{v_i(t | + | | <span id='ZEqnNum310255'></span> <math>{v_i(t',z)\Big| }_{t'=0}={\sigma }_2\left(z\right)-</math><math>q\mbox{e}^{-b\left(t'+t_0\right)}\mbox{=}{\sigma }'\left(z\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (12) | | style="width: 5px;text-align: right;white-space: nowrap;" | (12) | ||
| Line 281: | Line 299: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{v_1\ | + | | <math>{v_1\Big| }_{z=h_1}={v_2\Big|}_{z=h_1}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (13) | | style="width: 5px;text-align: right;white-space: nowrap;" | (13) | ||
| Line 291: | Line 309: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{k_{\mbox{v1}}\frac{\partial v_1}{\partial z}\ | + | | <math>{k_{\mbox{v1}}\frac{\partial v_1}{\partial z}\Big| }_{z=h_1}={k_{\mbox{v2}}\frac{\partial v_2}{\partial z}\Big| }_{z=h_1}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (14) | | style="width: 5px;text-align: right;white-space: nowrap;" | (14) | ||
| Line 314: | Line 332: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <span id='ZEqnNum258662'></span> <math>v_i=\sum_{m=1}^{\infty }g_{mi}\left(z\right)\mbox{e}^{-{\beta } | + | | <span id='ZEqnNum258662'></span> <math>v_i=\sum_{m=1}^{\infty }g_{mi}\left(z\right)\mbox{e}^{-{\beta }_m t'}\left[B_m+\right. </math><math>\left. C_mT_m\left(t'\right)\right]</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (15) | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) | ||
| Line 320: | Line 338: | ||
| − | where <math>g_{m1}\left(z\right)=sin\left({\lambda }_m\frac{z}{H}\right), | + | where <math>g_{m1}\left(z\right)=\sin\left({\lambda }_m\frac{z}{H}\right),g_{m2}\left(z\right)=</math><math>A_m\cos \left({\lambda }_m\mu \frac{H-z}{H}\right),\mbox{ }\mbox{and}\mbox{ }{\beta }_m=</math><math>{\lambda }_m{}^2c_{\mbox{v1}}/H^2.</math> |
Substituting Eq. <span id='cite-ZEqnNum258662'></span>[[#ZEqnNum258662|(15)]] into the interlayer continuity condition, it leads: | Substituting Eq. <span id='cite-ZEqnNum258662'></span>[[#ZEqnNum258662|(15)]] into the interlayer continuity condition, it leads: | ||
| Line 329: | Line 347: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>A_m=sin\left({\rho }_1{\lambda }_m\right)/cos\left(\mu {\rho }_2{\lambda }_m\right)</math> | + | | <math>A_m=\sin\left({\rho }_1{\lambda }_m\right)/\cos\left(\mu {\rho }_2{\lambda }_m\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (16) | | style="width: 5px;text-align: right;white-space: nowrap;" | (16) | ||
| Line 339: | Line 357: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\sqrt{\kappa \eta }tan\left({\rho }_1{\lambda }_m\right)tan\left(\mu {\rho }_2{\lambda }_m\right)=</math><math>1</math> | + | | <math>\sqrt{\kappa \eta }\tan\left({\rho }_1{\lambda }_m\right)\tan\left(\mu {\rho }_2{\lambda }_m\right)=</math><math>1</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (17) | | style="width: 5px;text-align: right;white-space: nowrap;" | (17) | ||
| Line 352: | Line 370: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <span id='ZEqnNum214015'></span> <math>T_m={\int }_0^{t | + | | <span id='ZEqnNum214015'></span> <math>T_m={\int }_0^{t'}\mbox{e}^{{\beta }_m\tau }R_1\left(\tau \right)\mbox{d}\tau </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (18) | | style="width: 5px;text-align: right;white-space: nowrap;" | (18) | ||
| Line 380: | Line 398: | ||
| <span id='ZEqnNum405293'></span> <math>{\int }_0^{H_t}m_{\mbox{v1}}g_{m1}\left(z\right)\cdot g_{n1}\left(z\right)\mbox{d}z+</math><math>{\int }_{H_t}^Hm_{\mbox{v2}}g_{m2}\left(z\right)g_{n2}\left(z\right)\mbox{d}z=</math><math>\left\{ \begin{array}{c} | | <span id='ZEqnNum405293'></span> <math>{\int }_0^{H_t}m_{\mbox{v1}}g_{m1}\left(z\right)\cdot g_{n1}\left(z\right)\mbox{d}z+</math><math>{\int }_{H_t}^Hm_{\mbox{v2}}g_{m2}\left(z\right)g_{n2}\left(z\right)\mbox{d}z=</math><math>\left\{ \begin{array}{c} | ||
0\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\left(m\not =n\right)\\ | 0\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\left(m\not =n\right)\\ | ||
| − | \frac{1}{2}Hm_{\mbox{v1}}\left({\rho }_1+\eta {\rho }_2A_m{}^2\right)\mbox{ }\left(m=n\right) | + | \displaystyle\frac{1}{2}Hm_{\mbox{v1}}\left({\rho }_1+\eta {\rho }_2A_m{}^2\right)\mbox{ }\left(m=n\right) |
\end{array}\right.</math> | \end{array}\right.</math> | ||
|} | |} | ||
| Line 394: | Line 412: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>C_m=\frac{{\int }_0^{H_t}g_{m1}\left(z\right)\mbox{d}z+\eta {\int }_{H_t}^Hg_{m2}\left(z\right)\mbox{d}z}{{\int }_0^{H_t}g_{m1}{}^2\left(z\right)\mbox{d}z+\eta {\int }_{H_t}^Hg_{m2}{}^2\left(z\right)\mbox{d}z | + | | <math>C_m=\frac{\displaystyle{\int }_0^{H_t}g_{m1}\left(z\right)\mbox{d}z+\eta {\displaystyle\int }_{H_t}^Hg_{m2}\left(z\right)\mbox{d}z}{{\displaystyle\int }_0^{H_t}g_{m1}{}^2\left(z\right)\mbox{d}z+\eta {\displaystyle\int }_{H_t}^Hg_{m2}{}^2\left(z\right)\mbox{d}z}=</math><math>\frac{2}{{\lambda }_m\left({\rho }_1+\eta {\rho }_2A_m{}^2\right)}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (21) | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) | ||
| Line 407: | Line 425: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <span id='ZEqnNum448304'></span> <math>\sum_{m=1}^{\infty }B_mg_{mi}\left(z\right)={\sigma } | + | | <span id='ZEqnNum448304'></span> <math>\sum_{m=1}^{\infty }B_mg_{mi}\left(z\right)={\sigma }'\left(z\right)\mbox{ }\mbox{ }\left(z_i\geq z\geq z_{i-1},\mbox{ }i=\right. </math><math>\left. 1,2\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (22) | | style="width: 5px;text-align: right;white-space: nowrap;" | (22) | ||
| Line 420: | Line 438: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>B_m=\frac{{\int }_0^{H_t}g_{m1}\left(z\right)\mbox{d}z+\eta {\int }_{H_t}^Hg_{m2}\left(z\right)\mbox{d}z}{{\int }_0^{H_t}g_{m1}{}^2\left(z\right)\mbox{d}z+\eta {\int }_{H_t}^Hg_{m2}{}^2\left(z\right)\mbox{d}z | + | | <math>B_m=\frac{{\displaystyle\int }_0^{H_t}g_{m1}\left(z\right)\mbox{d}z+\eta {\displaystyle\int }_{H_t}^Hg_{m2}\left(z\right)\mbox{d}z}{{\displaystyle\int }_0^{H_t}g_{m1}{}^2\left(z\right)\mbox{d}z+\eta {\displaystyle\int }_{H_t}^Hg_{m2}{}^2\left(z\right)\mbox{d}z}=</math><math>\frac{2}{{\lambda }_m\left({\rho }_1+\eta {\rho }_2A_m{}^2\right)}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (23) | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) | ||
| Line 433: | Line 451: | ||
|- | |- | ||
| <math>\left\{ \begin{align} | | <math>\left\{ \begin{align} | ||
| − | & {{v}_{1}}=\sum\limits_{m=1}^{\infty }{\sin \left( {{\lambda }_{m}}\frac{z}{H} \right){{\text{e}}^{-{{\beta }_{m}}{t}'}}{{B}_{m}}}+\sum\limits_{m=1}^{\infty }{\sin \left( {{\lambda }_{m}}\frac{z}{H} \right){{\text{e}}^{-{{\beta }_{m}}{t}'}}{{C}_{m}}\int_{0}^ | + | & {{v}_{1}}=\sum\limits_{m=1}^{\infty }{\sin \left( {{\lambda }_{m}}\frac{z}{H} \right){{\text{e}}^{-{{\beta }_{m}}{t}'}}{{B}_{m}}}+\sum\limits_{m=1}^{\infty }{\sin \left( {{\lambda }_{m}}\frac{z}{H} \right){{\text{e}}^{-{{\beta }_{m}}{t}'}}{{C}_{m}}\int_{0}^{t'}{{{R}_{1}}\left( \tau \right){{\text{e}}^{{{\beta }_{m}}\tau }}\text{d}\tau }} \\ |
| − | & {{v}_{2}}=\sum\limits_{m=1}^{\infty }{{{A}_{m}}\cos \left( \mu {{\lambda }_{m}}\frac{H-z}{H} \right){{\text{e}}^{-{{\beta }_{m}}{t}'}}{{B}_{m}}}+\sum\limits_{m=1}^{\infty }{{{A}_{m}}\cos \left( \mu {{\lambda }_{m}}\frac{H-z}{H} \right){{\text{e}}^{-{{\beta }_{m}}{t}'}}{{C}_{m}}\int_{0}^ | + | & {{v}_{2}}=\sum\limits_{m=1}^{\infty }{{{A}_{m}}\cos \left( \mu {{\lambda }_{m}}\frac{H-z}{H} \right){{\text{e}}^{-{{\beta }_{m}}{t}'}}{{B}_{m}}}+\sum\limits_{m=1}^{\infty }{{{A}_{m}}\cos \left( \mu {{\lambda }_{m}}\frac{H-z}{H} \right){{\text{e}}^{-{{\beta }_{m}}{t}'}}{{C}_{m}}\int_{0}^{t'}{{{R}_{1}}\left( \tau \right){{\text{e}}^{{{\beta }_{m}}\tau }}\text{d}\tau }} \end{align} \right. </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (24) | | style="width: 5px;text-align: right;white-space: nowrap;" | (24) | ||
| Line 448: | Line 466: | ||
|- | |- | ||
| <math>\left\{ \begin{array}{c} | | <math>\left\{ \begin{array}{c} | ||
| − | u_2^1\left(t | + | u_2^1\left(t',z\right)=\displaystyle\sum_{m=1}^{\displaystyle\infty }\sin\left({\lambda }_m\frac{z}{H}\right)\mbox{e}^{-{\beta }_m t'}\left[B_m\mbox{+}C_m{\displaystyle\int }_0^{t'}R_1\left(\tau \right)\mbox{e}^{{\beta }_m\tau }\mbox{d}\tau \right]+q\mbox{e}^{-b\left(t'+t_0\right)}\\ |
| − | u_2^2\left(t | + | u_2^2\left(t',z\right)=\displaystyle\sum_{m=1}^{\infty }A_m \cos\left(\mu {\lambda }_m\frac{H-z}{H}\right)\mbox{e}^{-{\beta }_m t'}\left[B_m +C_m{\displaystyle\int }_0^{t^{{'}}}R_1\left(\tau \right)\mbox{e}^{{\beta }_m\tau }\mbox{d}\tau \right]+q\mbox{e}^{-b\left(t'+t_0\right)} |
\end{array}\right.</math> | \end{array}\right.</math> | ||
|} | |} | ||
| Line 455: | Line 473: | ||
|} | |} | ||
| + | where <math>H_t</math> is an unknown quantity related to <math display="inline">t^{{'}}</math>, and its relationship can be obtained according to the effective stress at depth <math>H_t</math> that is equal to the yield stress of the structure. | ||
| − | + | When <math>z=H_t</math>, the expression <math>{\sigma }^{{'}}=q-u_1\left(z\right)={\sigma }_\mbox{p}{}^{{'}}</math> could be meet, and it yields: | |
| − | + | ||
| − | When <math>z=H_t</math> , the expression <math>{\sigma }^{{'}}=q-u_1\left(z\right)={\sigma }_\mbox{p}{}^{{'}}</math> could be meet, and it yields: | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 465: | Line 482: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <span id='ZEqnNum713445'></span> <math>q\left(1-\mbox{e}^{-b\left(t^ | + | | <span id='ZEqnNum713445'></span> <math>q\left(1-\mbox{e}^{-b\left(t^{'}+t_0\right)}\right)-</math><math>{\sigma }_\mbox{p}{}^{'}-\sum_{m=1}^{\infty }\sin\left({\rho }_1{\lambda }_m\right)\left[\mbox{e}^{-{\beta }_mt^{'}}B_m-\right. </math><math>\left. C_m\frac{b}{{\beta }_m-b}\left(\mbox{e}^{-bt^{'}}-\right. \right. </math><math>\left. \left. \mbox{e}^{-{\beta }_mt^{'}}\right)\right]=</math><math>0</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (26) | | style="width: 5px;text-align: right;white-space: nowrap;" | (26) | ||
| Line 471: | Line 488: | ||
| − | Eq. <span id='cite-ZEqnNum713445'></span>[[#ZEqnNum713445|(26)]] is the corresponding relationship between <math>H_t</math> and <math display="inline">t^{{'}}</math> , from which the depth <math>H_t</math> of the moving boundary can be obtained by an iterative method when the time is <math display="inline">t^{{'}}</math> fixed. | + | Eq. <span id='cite-ZEqnNum713445'></span>[[#ZEqnNum713445|(26)]] is the corresponding relationship between <math>H_t</math> and <math display="inline">t^{{'}}</math>, from which the depth <math>H_t</math> of the moving boundary can be obtained by an iterative method when the time is <math display="inline">t^{{'}}</math> fixed. |
===3.1.3 Complete failure stage=== | ===3.1.3 Complete failure stage=== | ||
| − | The effective stress of soil at the bottom boundary is greater than the structural yield stress when the time <math>t>t_1</math> , and as such the soil structure has been damaged completely. Taking <math>t^{{''}}=t-t_1</math> as the time coordinate, the consolidation model has been transformed from a two-layer foundation under continuous drainage boundary into a one-dimensional consolidation for a single-layer soil with non-homogeneous initial excess pore pressure, where the initial pore pressure is <math>{u_2^1\left(t^{{'}},z\right)\vert }_{t^{{'}}=t_1-t_0}</math> . The governing equation and the definite solution conditions are given below: | + | The effective stress of soil at the bottom boundary is greater than the structural yield stress when the time <math>t>t_1</math>, and as such the soil structure has been damaged completely. Taking <math>t^{{''}}=t-t_1</math> as the time coordinate, the consolidation model has been transformed from a two-layer foundation under continuous drainage boundary into a one-dimensional consolidation for a single-layer soil with non-homogeneous initial excess pore pressure, where the initial pore pressure is <math>{u_2^1\left(t^{{'}},z\right)\vert }_{t^{{'}}=t_1-t_0}</math>. The governing equation and the definite solution conditions are given below: |
| − | Governing equation: | + | ''Governing equation'': |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 492: | Line 509: | ||
where <math>u_3</math> and <math>{c^{{'}}}_\mbox{v}</math> are the excess pore-water pressure and consolidation coefficient of soil element at the complete failure stage, respectively. | where <math>u_3</math> and <math>{c^{{'}}}_\mbox{v}</math> are the excess pore-water pressure and consolidation coefficient of soil element at the complete failure stage, respectively. | ||
| − | Boundary conditions: | + | ''Boundary conditions'': |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 500: | Line 517: | ||
|- | |- | ||
| <math>\left\{ \begin{array}{c} | | <math>\left\{ \begin{array}{c} | ||
| − | {u_3\left(t^{{''}},z\right)\ | + | {u_3\left(t^{{''}},z\right)\Big| }_{z=0}=q\mbox{e}^{-bt_1}\mbox{e}^{-bt^{{''}}}\mbox{ }\\ |
| − | {\frac{\partial u_3\left(t^{{''}},z\right)}{\partial z}\ | + | {\displaystyle\frac{\partial u_3\left(t^{{''}},z\right)}{\partial z}\Big| }_{z=H}\mbox{ }\mbox{ }=0 |
\end{array}\right.</math> | \end{array}\right.</math> | ||
|} | |} | ||
| Line 508: | Line 525: | ||
| − | Initial condition: | + | ''Initial condition'': |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 515: | Line 532: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{u_3(t^{{''}},z)\ | + | | <math>{u_3(t^{{''}},z)\Big| }_{t^{{''}}=0}={u_2^1\left(t^{{'}},z\right)\Big| }_{t^{{'}}=t_1-t_0}\mbox{=}{\sigma }_3\left(z\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (29) | | style="width: 5px;text-align: right;white-space: nowrap;" | (29) | ||
|} | |} | ||
| − | + | where <math>{\sigma }_3\left(z\right)</math> represents the surcharge stress of soil at any depth <math display="inline"> z</math> in the complete failure stage. | |
| − | where <math>{\sigma }_3\left(z\right)</math> represents the surcharge stress of soil at any depth | + | |
In order to achieve the purpose of homogenization for non-homogeneous boundary, the excess pore-water pressure of soil element at the complete failure stage is supposed as: | In order to achieve the purpose of homogenization for non-homogeneous boundary, the excess pore-water pressure of soil element at the complete failure stage is supposed as: | ||
| Line 548: | Line 564: | ||
|} | |} | ||
| − | + | where <math>R_2(t^{{''}})=bq\mbox{e}^{-b\left(t^{{''}}+t_1\right)}</math>. | |
| − | where <math>R_2(t^{{''}})=bq\mbox{e}^{-b\left(t^{{''}}+t_1\right)}</math> . | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 556: | Line 571: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{v_3\left(t^{{''}},z\right)\ | + | | <math>{v_3\left(t^{{''}},z\right)\Big| }_{z=0}=0,\mbox{ }{\frac{\partial v_3\left(t^{{''}},z\right)}{\partial z}\Big| }_{z=H}\mbox{ }\mbox{ }=</math><math>0</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (32) | | style="width: 5px;text-align: right;white-space: nowrap;" | (32) | ||
| Line 566: | Line 581: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{v_3(t^{{''}},z)\ | + | | <math>{v_3(t^{{''}},z)\Big| }_{t^{{''}}=0}={\sigma }^{{''}}\left(z\right)={\sigma }_3\left(z\right)-q\mbox{e}^{-bt_1}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (33) | | style="width: 5px;text-align: right;white-space: nowrap;" | (33) | ||
| Line 595: | Line 610: | ||
|- | |- | ||
| <math>U_p=\left\{ \begin{array}{c} | | <math>U_p=\left\{ \begin{array}{c} | ||
| − | \frac{q\left(t\right)H-{\int }_0^Hu_1\mbox{d}z}{q_\mbox{u}H},\mbox{ }0<t\leq t_0\\ | + | \frac{q\left(t\right)H-{\displaystyle\int }_0^Hu_1\mbox{d}z}{q_\mbox{u}H},\mbox{ }0<t\leq t_0\\ |
| − | \frac{q\left(t\right)H-\left({\int }_0^{H_t}u_2^1\mbox{d}z+{\int }_{H_t}^Hu_2^2\mbox{d}z\right)}{q_\mbox{u}H},\mbox{ }t_0<t\leq t_1\\ | + | \frac{q\left(t\right)H-\left({\displaystyle\int }_0^{H_t}u_2^1\mbox{d}z+{\displaystyle\int }_{H_t}^Hu_2^2\mbox{d}z\right)}{q_\mbox{u}H},\mbox{ }t_0<t\leq t_1\\ |
| − | \frac{q\left(t\right)H-{\int }_0^Hu_3\mbox{d}z}{q_\mbox{u}H},\mbox{ }t_1<t | + | \frac{q\left(t\right)H-{\displaystyle\int }_0^Hu_3\mbox{d}z}{q_\mbox{u}H},\mbox{ }t_1<t |
\end{array}\right.</math> | \end{array}\right.</math> | ||
|} | |} | ||
| Line 610: | Line 625: | ||
===3.2.1 Comparison against degenerated cases=== | ===3.2.1 Comparison against degenerated cases=== | ||
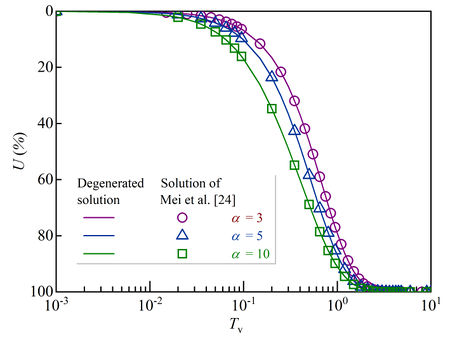
| − | Based on the analytical solution of consolidation process for non-structural soil with continuous drainage boundary derived by Mei et al [ | + | Based on the analytical solution of consolidation process for non-structural soil with continuous drainage boundary derived by Mei et al [24], the structural soil parameters in this study have been transformed into the non-structural soil parameters, i.e., <math>k_\mbox{v}/{k^{{'}}}_\mbox{v}=1</math> and <math>m_\mbox{v}/{m^{{'}}}_\mbox{v}=1</math>. The comparisons between the two approaches for different interface parameters (e.g., <math>\alpha =</math> 3, 5 and 10) are shown in [[#img-4|Figure 4]]. It can be seen that the proposed solution matches with the solution calculated by Mei et al [24] well. Therefore, the correctness of the present solution is preliminarily demonstrated. |
| − | <div class=" | + | <div id='img-4'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | [[File: | + | |-style="background:white;" |
| − | + | |style="text-align: center;padding:10px;"| [[File:Revision.jpg|centre|450px]] | |
| − | + | |- | |
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. Calculation results of degenerated solution | ||
| + | |} | ||
| − | ===3.2.2 Comparison against numerical calculations=== | + | ====3.2.2 Comparison against numerical calculations==== |
| − | To further assess the efficacy of the proposed analytical solution, numerical results calculated by the backward difference method ( | + | To further assess the efficacy of the proposed analytical solution, numerical results calculated by the backward difference method ([[#img-5|Figure 5]]) are adopted for derivation, in which the backward difference and central difference schemes are used for time and space, respectively. In addition, the space and time nodes of the soil layer are expressed as <math display="inline"> i </math> and <math display="inline"> j </math>, respectively, and the space and time step lengths are <math display="inline">\Delta z</math> and <math display="inline">\Delta t</math>. The space nodes of the soil layer are taken from top to bottom in the order of <math display="inline">i=0,1\cdots ,I</math>, where <math>I=H/\Delta z</math>. Finally, it is assumed that the node of failure surface for the moving boundary is <math>i=m</math>. |
| − | <div class=" | + | <div id='img-5'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_399419094854-image102.png|315px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. Finite difference element mesh discretization | ||
| + | |} | ||
| − | |||
| − | |||
When the space nodes of the soil layer <math>i\not =m</math> , the difference formula of the governing equation can be expressed as follows: | When the space nodes of the soil layer <math>i\not =m</math> , the difference formula of the governing equation can be expressed as follows: | ||
| Line 640: | Line 660: | ||
|} | |} | ||
| + | where <math>{\zeta }_1={C^{{'}}}_\mbox{v}\Delta t/\Delta z^2</math>, and <math>{\zeta }_2=C_\mbox{v}\Delta t/\Delta z^2</math>. | ||
| − | + | When the space nodes of the soil layer <math>i=m</math>, the interlayer continuity condition is expressed as follows: | |
| − | + | ||
| − | When the space nodes of the soil layer <math>i=m</math> , the interlayer continuity condition is expressed as follows: | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 656: | Line 675: | ||
| − | Substituting <math display="inline">u_{m-1}^{j-1}</math> and <math display="inline">u_{m-1}^{j-1}</math> in Eq. <span id='cite-ZEqnNum982344'></span>[[#ZEqnNum982344|(37)]] into the left hand of Eq. <span id='cite-ZEqnNum724897'></span>[[#ZEqnNum724897|(36)]], the difference scheme of the governing equation at point | + | Substituting <math display="inline">u_{m-1}^{j-1}</math> and <math display="inline">u_{m-1}^{j-1}</math> in Eq. <span id='cite-ZEqnNum982344'></span>[[#ZEqnNum982344|(37)]] into the left hand of Eq. <span id='cite-ZEqnNum724897'></span>[[#ZEqnNum724897|(36)]], the difference scheme of the governing equation at point <math display="inline"> m </math> can be obtained as follows: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 668: | Line 687: | ||
|} | |} | ||
| − | + | where <math display="inline">\nu =k_{\mbox{v2}}/\left(k_{\mbox{v1}}+k_{\mbox{v2}}\right)</math>. | |
| − | where <math display="inline">\nu =k_{\mbox{v2}}/\left(k_{\mbox{v1}}+k_{\mbox{v2}}\right)</math> . | + | |
Initial condition and boundary condition are written in the following forms: | Initial condition and boundary condition are written in the following forms: | ||
| Line 694: | Line 712: | ||
| − | Determination condition of point | + | Determination condition of point <math display="inline"> m </math>: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 707: | Line 725: | ||
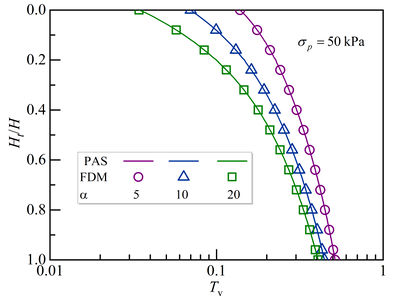
| − | The calculated results from the proposed method and the numerical technique are shown in | + | The calculated results from the proposed method and the numerical technique are shown in [[#img-6|Figure 6]], where the calculation parameters are employed as follows: <math>q_\mbox{u}=100\mbox{ }\mbox{kPa}</math>, <math>{{\sigma }^{{'}}}_\mbox{p}=50\mbox{ }\mbox{kPa}</math>, <math>\kappa =2</math>, <math>\eta =0.5</math>, <math>H=10\mbox{ }\mbox{m}</math>, and three interface parameters <math>\alpha =5</math>, 10 and 20. As can be seen, the proposed analytical solutions (PAS) are in good agreement with the results of finite difference method (FDM), so that the reliability of the proposed solution in is further illustrated. |
| − | <div class=" | + | <div id='img-6'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:55%;" | |
| − | [[File:Review_399419094854_7427_Fig.6.jpg|centre| | + | |-style="background:white;" |
| − | + | |style="text-align: center;padding:10px;"| [[File:Review_399419094854_7427_Fig.6.jpg|centre|400px]] | |
| − | + | |- | |
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 6'''. Comparison of consolidation between the proposed analytical solution (PAS) and finite difference method (FDM) | ||
| + | |} | ||
| − | + | ==4. Results and discussions== | |
| − | In order to study the influence of interface parameter, structural properties and structural yield stress of soil on consolidation behaviors, the calculation parameters are taken as <math>q_\mbox{u}=100\mbox{ }\mbox{kPa}</math> , <math> | + | In order to study the influence of interface parameter, structural properties and structural yield stress of soil on consolidation behaviors, the calculation parameters are taken as <math>q_\mbox{u}=100\mbox{ }\mbox{kPa}</math>, <math>{\sigma}'_\mbox{p}=50</math> kPa, <math>H=10</math> m. The dimensionless consolidation coefficient ratio is defined as <math>C_i=C_\mbox{v}/{C'}_\mbox{v}</math>, and the structural yield stress ratio is written as <math>R={\sigma }'_\mbox{p}/q_\mbox{u}</math>. To be specific, the consolidation model is equipped with a continuous drainage boundary on the soil surface and an impermeable drainage on the bottom boundary. Other detailed computational parameters are shown in [[#tab-1|Table 1]]. |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 1'''. Calculating parameters of structured soil</div> |
| − | Table. | + | |
| − | {| style=" | + | <div id='tab-1'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! rowspan='2' style="text-align: center;vertical-align: top;"|Case !! colspan='2' style="text-align: center;"|Permeability coefficient <br>(<math display="inline">10^{-8}</math> m <math display="inline">\cdot</math> s<sup>-1</sup>) !! colspan='2' style="text-align: center;"|Volume compressibility coefficient <br> (MPa<sup>-1</sup>) | ||
|- | |- | ||
| − | + | ! style="text-align: center;width: 19%;"|<math>k_\mbox{v}</math> !! style="text-align: center;width: 21%;"|<math>{k'}_\mbox{v}</math> !! style="text-align: center;width: 22%;"|<math>m_\mbox{v}</math> !! style="text-align: center;width: 25%;"|<math>{m'}_\mbox{v}</math> | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|1 |
| − | + | | style="text-align: center;"|1.25 | |
| − | + | | style="text-align: center;"|0.75 | |
| − | + | | style="text-align: center;"|0.75 | |
| − | + | | style="text-align: center;"|0.75 | |
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|- | |- | ||
| style="text-align: center;"|2 | | style="text-align: center;"|2 | ||
| Line 757: | Line 772: | ||
| style="text-align: center;"|0.75 | | style="text-align: center;"|0.75 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|5 |
| − | | style=" | + | | style="text-align: center;"|0.3 |
| − | | style=" | + | | style="text-align: center;"|0.75 |
| − | | style=" | + | | style="text-align: center;"|2.7 |
| − | | style=" | + | | style="text-align: center;"|0.75 |
|} | |} | ||
| Line 767: | Line 782: | ||
====4.1 Influence of interface parameter ==== | ====4.1 Influence of interface parameter ==== | ||
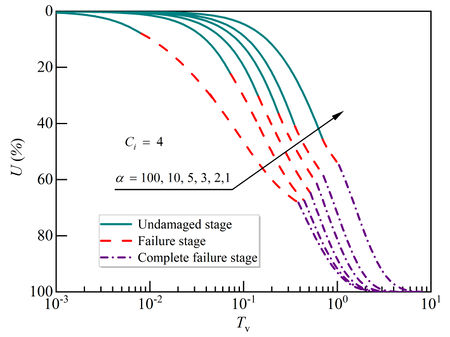
| − | + | [[#img-7|Figure 7]] illustrates the influence of interface parameter on consolidation degree for the case with a constant consolidation coefficient ratio of <math display="inline">C_i = 4</math> (i.e., case 3) and different interface parameters of <math display="inline">= 1, 2, 3, 5, 10</math>, and <math display="inline">100</math>. It can be seen that the larger the interface parameter is, the faster the excess pore-pressure dissipates and the earlier the effective stress reaches the structural yield stress. Hence, the time in the undamaged stage becomes shorter and the consolidation rate becomes faster. Moreover, it can also be seen that the smaller the interface parameter is, the greater the degree of consolidation of structural soil is after entering the failure stage. | |
| − | <div class=" | + | <div id='img-7'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:55%;" | |
| − | [[File:Review_399419094854_5761_Fig.7.jpg|centre| | + | |-style="background:white;" |
| − | + | |style="text-align: center;padding:10px;"| [[File:Review_399419094854_5761_Fig.7.jpg|centre|450px]] | |
| − | + | |- | |
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 7'''. Influence of interface parameter on consolidation degree of structured soil | ||
| + | |} | ||
====4.2 Influence of structural properties of soil==== | ====4.2 Influence of structural properties of soil==== | ||
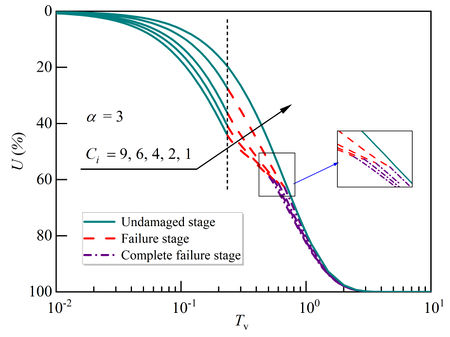
| − | The influence of consolidation coefficient ratio | + | The influence of consolidation coefficient ratio <math display="inline">C_i</math> for structural soils (i.e., cases 1-5), when the interface parameter is fixed at 3, is plotted in [[#img-8|Figure 8]]. As seen from the figure, there is no inflection point in the consolidation curve when the consolidation coefficient ratio is 1, and it represents the condition that structural soil degrades to homogeneous nonstructural soil (i.e., undamaged stage throughout the analysis). It is interesting that structural soil enters the failure stage at the same time, since the interface parameter is identical. However, the greater the consolidation coefficient ratio (<math display="inline">C_i</math>) is, the greater the consolidation degree becomes at a specific time in the failure stage, and the earlier the consolidation process enters the complete failure stage. It other words, neglecting the distinct difference in three failure stages for undamaged and remolded soils, consolidation analysis could lead to underestimation of degree of consolidation or overestimation of consolidation settlement, resulting in conservative design in ground treatment. |
| + | |||
| + | <div id='img-8'></div> | ||
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:55%;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_399419094854_2226_Fig.8.jpg|centre|450px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 8'''. Influence of structural properties of soil on degree of consolidation | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
====4.3 Influence of structural yield stress of soil==== | ====4.3 Influence of structural yield stress of soil==== | ||
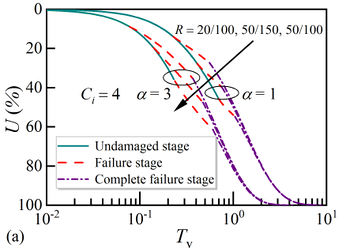
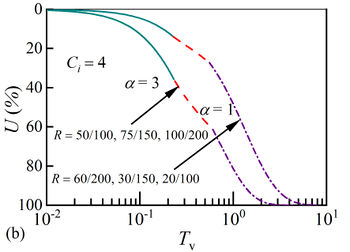
| − | The influence of ratio between soil structural yield stress and load | + | The influence of ratio between soil structural yield stress and load <math display="inline">R</math> on the consolidation behavior is depicted in [[#img-9|Figure 9]](a), where the consolidation coefficient ratio is <math display="inline">C_i = 4</math> and the interface parameters are <math display="inline">\alpha =3</math> and <math display="inline">\alpha =1</math> . It can be seen that the trends of consolidation curves under different interface parameters are the same. The larger the interface parameter is, the faster the consolidation rate is. When the yield stress is the same (e.g., the structural yield stress is 50 kPa), the soil consolidation rate slows down with the increase of load level, but the soil enters the failure stage earlier, which is caused by the smaller consolidation coefficient of remolded soil. In addition, the higher the yield stress is, the later the structure failure occurs and the faster the soil consolidation rate becomes for a fixed load (e.g., the value of load is 100 kPa). In summary, the consolidation rate increases with the increase of interface parameter and parameter <math display="inline">R</math>. |
| − | Moreover, | + | Moreover, [[#img-9|Figure 9]](b) shows the trends of consolidation curves with a fixed parameter <math display="inline">R</math> under two groups of interface parameters. It is clearly seen that the consolidation curves are consistent when <math display="inline">R</math> is taken to be the same value, which indicates that the ratio of structural yield stress to load is positively related with the consolidation rate. |
| − | <div class=" | + | <div id='img-9'></div> |
| − | + | <div id='img-1'></div> | |
| − | [[File:Review_399419094854_9995_Fig.9a.jpg|centre| | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" |
| − | + | |-style="background:white;" | |
| − | [[File: | + | |align="center" | |
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
| + | |- | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_399419094854_9995_Fig.9a.jpg|centre|350px]] | ||
| + | |style="text-align: center;padding:10px;"|[[File:Fig.9b.jpg|centre|350px]] | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 9'''. Effect of yield stress on consolidation degree of structured soil | ||
| + | |} | ||
| − | + | ==5. Conclusions== | |
| − | + | ||
| − | + | ||
To fill the knowledge gap in consolidation solutions for structural soft soil foundation, the one-dimensional consolidation equation of structured soft soil foundation under continuous drainage boundary conditions with the consideration of soil structure is established. An analytical solution is then proposed by using finite Fourier sine transform and integral transform methods. The effectiveness of the present solution is discussed by comparing against degenerated cases and numerical results calculated by the finite difference method. Sensitivity analysis is carried out to study the influence of interface parameter, structural characteristics of soil elements and structural yield stress on consolidation behaviors of foundation soils. The main conclusions in this study are summarized as follows: | To fill the knowledge gap in consolidation solutions for structural soft soil foundation, the one-dimensional consolidation equation of structured soft soil foundation under continuous drainage boundary conditions with the consideration of soil structure is established. An analytical solution is then proposed by using finite Fourier sine transform and integral transform methods. The effectiveness of the present solution is discussed by comparing against degenerated cases and numerical results calculated by the finite difference method. Sensitivity analysis is carried out to study the influence of interface parameter, structural characteristics of soil elements and structural yield stress on consolidation behaviors of foundation soils. The main conclusions in this study are summarized as follows: | ||
| Line 807: | Line 834: | ||
(2) Soil consolidation coefficient and failure time are positively correlated, i.e., the larger the consolidation coefficient is, the earlier the soil enters the failure stage and the greater the consolidation degree becomes. | (2) Soil consolidation coefficient and failure time are positively correlated, i.e., the larger the consolidation coefficient is, the earlier the soil enters the failure stage and the greater the consolidation degree becomes. | ||
| − | (3) The ratio of structure yield stress to load, | + | (3) The ratio of structure yield stress to load, <math display="inline"> R </math>, does not change the degree of consolidation curve. |
(4) For remolded soil, without considering the three failure stages, the degree of consolidation can be underestimated, leading to extremely conservative design in practice of ground improvement. | (4) For remolded soil, without considering the three failure stages, the degree of consolidation can be underestimated, leading to extremely conservative design in practice of ground improvement. | ||
| − | + | ==Declaration of interests== | |
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. | The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper. | ||
| − | + | ==Acknowledgements== | |
This work was supported by the National Natural Science Foundation of China (52008124, 52268054 and 52208345), the China Postdoctoral Science Foundation (2020M683210), and the Natural Science Foundation of Guangxi Province (2021AC18008). | This work was supported by the National Natural Science Foundation of China (52008124, 52268054 and 52208345), the China Postdoctoral Science Foundation (2020M683210), and the Natural Science Foundation of Guangxi Province (2021AC18008). | ||
| − | + | ==References== | |
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
| + | |||
| + | [1] Burland J. On the compressibility and shear strength of natural clays. Géotechnique, 40(3):329-378, 1990. | ||
| + | |||
| + | [2] Poskitt T. The consolidation of saturated clay with variable permeability and compressibility. Géotechnique, 9(2):234-352, 1969. | ||
| + | |||
| + | [3] Yang W, Xu J. One-dimensional consolidation of multilayered aquifer systems with viscoelastic properties induced by time-dependent groundwater drawdown. Quarterly Journal of Engineering Geology and Hydrogeology, 55(2), qjegh2021-073, 2022. | ||
| − | [ | + | [4] Yang W., Ni P., Chen Z., Feng J., Mei G. Consolidation analysis of composite ground improved by granular piles with a high replacement ratio considering overlapping smear zones. Computers and Geotechnics, 162, 105636, 2023. |
| − | [ | + | [5] Zhang C. Geotechnical characteristics of two structural clays. Hydro-Science and Engineering, 4(4):68-74, 1983. |
| − | [ | + | [6] Shen Z. Engineering properties of soft soils and design of soft ground. Chinese Journal of Geotechnical Engineering, 20(1):100-111, 1998. |
| − | [ | + | [7] Leroueil S., Vaughan P.R. The general and congruent effects of structure in natural soils and weak rocks. Géotechnique, 40(3):467-488, 1990. |
| − | [ | + | [8] Wang J., Cheney Y. Analytical solution to 1-D consolidation of uniform structured soft foundation. Journal of Hydraulic Engineering, 3(3):19-24, 2003. |
| − | [ | + | [9] Wang L., Ding L., Chen Y., Li L. Study on compressibility of structured soft soil. China Civil Engineering Journal, 37(4):46-53, 2004. |
| − | [ | + | [10] Tang Y., Zhou M. One dmiensional non-linear semi-analytical solution for structured soft soils. Chinese Journal of Under ground Space and Engineering, 3(4):605-8, 2007. |
| − | [ | + | [11] An R., Xie K, Deng Y., Wang K. Approximate solution for one-dimensional consolidation of structured soils under time-dependent loading. Rock and Soil Mechanics, 33(10):3194-3200, 2012. |
| − | [ | + | [12] Xie K., Xia C., An R., Ying H., Wu H. A study on one-dimensional consolidation of layered structured soils. International Journal for Numerical and Analytical Methods in Geomechanics, 40(7):1081-1098, 2016. |
| − | [ | + | [13] Xie K., Xia C., An R., Hu A., Zhang W. A study on the one-dimensional consolidation of double-layered structured soils. Computers and Geotechnics, 73(1):189-198, 2016. |
| − | [ | + | [14] Hu A., Xia C., Cui J., Li C., Xie K. Nonlinear consolidation analysis of natural structured clays under time-dependent loading. International Journal of Geomechanics, 18(2):04017140, 2018. |
| − | [ | + | [15] Hu A., Zhou Y., Chen Y., Xia C., Xie K. Semi-analytical solutions for one-dimensional nonlinear large strain consolidation of structured soft clay. Rock and Soil Mechanics, 41(8):2583-2591, 2019. |
| − | [ | + | [16] Cao Y., Chen Y., Huang M. One-dimensional nonlinear consolidation analysis of structured natural soft clay subjected to arbitrarily time-dependent construction loading. Chinese Journal of Geotechnical Engineering, 28(5):569-574, 2006. |
| − | [ | + | [17] Cui J., Xie K., Xia C., Hu A., Zhou Y. One-dimensional nonlinear consolidation analysis of double layered structured soils under time-dependent loading. Journal of Central South University (Science and Technology), 49(7):1710-17, 2018. |
| − | [ | + | [18] Li C., Xiao J., Wu W., Mei G., Ni P., Leo C. Analysis of 1D large strain consolidation of structured marine soft clays. Journal of Zhejiang University Science, 21(1):29-43, 2020. |
| − | [ | + | [19] Xia C., Zhu M., Chen W., Peng Y., Xie K. Large-strain rheological consolidation analysis of multi-layered marine soft clays exhibiting natural structural characteristics. Marine Georesources & Geotechnology, 41(10):1142-1155, 2023. |
| − | [ | + | [20] Mei G., Feng J., Xu M., Ni P. Estimation of interface parameter for one-dimensional consolidation with continuous drainage boundary conditions. International Journal of Geomechanics, 22(3):04021292, 2022. |
| − | [ | + | [21] Cai F., He L., Zhang Q., Xu M., Mei G. Finte element analysis of undrained symmetry plane with self-weigh. Jouranl of Zhejiang University (Engineering Science), 47(12):2132-2140, 2013. |
| − | [ | + | [22] Feng J., Ni P., Mei G. One‐dimensional self‐weight consolidation with continuous drainage boundary conditions: Solution and application to clay‐drain reclamation. International Journal for Numerical and Analytical Methods in Geomechanics, 43(8):1634-1652, 2019. |
| − | [ | + | [23] Cai F., He L., Zhou X., Xu M., Mei G. Finite element analysis of one-dimensional consolidation of undrained symmetry plane under continuous drainage boundary. Chinese Journal of Geotechnical Engineering, 34(11):2141-2147, 2012. |
| − | [ | + | [24] Mei G., Xia J., Mei L. Terzaghi’s one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary. Chinese Journal of Geotechnical Engineering, 33(1):28-31, 2011. |
| − | [ | + | [25] Feng J., Chen Z., Li Y., Mei G. Analytical solution for one-dimensional consolidation of soft clayey soil with a continuous drainage boundary under linear loading. Engineering Mechanics, 36(6):219-226, 2019. |
| − | [ | + | [26] Tian Y., Wu W., Jiang G., El Naggar M.H., Mei G., Xu M., et al. One‐dimensional consolidation of soil under multistage load based on continuous drainage boundary. International Journal for Numerical and Analytical Methods in Geomechanics, 44(8):1170-1183, 2020. |
| − | [ | + | [27] Liu J., Lei G. One-dimensional consolidation of layered soils with exponentially time-growing drainage boundaries. Computers and Geotechnics, 54(10):202-209, 2013. |
| − | [ | + | [28] Wu W., Zong M., El Naggar M.H., Mei G., Liang R. Analytical solution for one-dimensional consolidation of double-layered soil with exponentially time-growing drainage boundary. International Journal of Distributed Sensor Networks, 14(10):1550147718806716, 2018. |
| − | [ | + | [29] Chen X., Chen W., Yue Z. One-dimensional consolidation of multilayered soil with continuous drainage boundaries and under time-dependent loading. International Journal of Geomechanics, 22(9):04022142, 2022. |
| − | [ | + | [30] Chen Z., Wang X., Zeng J. 1-D non-linear consolidation solution to unsteady pore pressure boundary of foundation soil. Journal of Nanjing Tech Univesity (Natural Science Edition), 36(5):90-94, 2014. |
| − | [ | + | [31] Zong M., Wu W., Mei G., Liang R., Tian Y. Analytical solution for one-dimensional nonlinear consolidation of soil based on continuous drainage boundary. Chinese Journal of Rock Mechanics and Engineering, 37(1):1-10, 2018. |
| − | [ | + | [32] Tong L., Wang Y., Guo S., Zhu H., Xu C. On one-dimension consolidation characteristics of viscoelastic subgrade with continuous drainage boundary under time- dependent loading. Rock and Soil Mechanics, 40(05):1862-1868, 2019. |
| − | [ | + | [33] Zong M., Wu W., El Naggar M.H., Mei G., Ni P., Xu M. Analytical solution for one-dimensional nonlinear consolidation of double-layered soil with improved continuous drainage boundary. European Journal of Environmental and Civil Engineering, 27(8):2746-2767, 2023. |
| − | [ | + | [34] Jiang W., Zhan L., Yang C. Analytical solution for one-dimensional large strain consolidation of saturated soft soils with continuous drainage boundary. Journal of Central South University (Science and Technology), 1(5):1289-1298, 2020. |
| − | [ | + | [35] Yang X., Zong M., Tian Y., Jiang G., El Naggar M.H., Wu W., et al. One‐dimensional consolidation of layered soils under ramp load based on continuous drainage boundary. International Journal for Numerical and Analytical Methods in Geomechanics, 45(6):738-752, 2021. |
Latest revision as of 14:01, 12 February 2024
Abstract
A closed form analytical solution is proposed to analyze the one-dimensional consolidation behavior of structured saturated clay soils under continuous drainage boundary. Firstly, the soil structural properties and arbitrary loading conditions are taken into account in the established mathematical model. Using the finite sine Fourier transform and characteristic function methods, analytical calculation is conducted, and the solution effectiveness is evaluated against the degradation of solutions and the results of finite difference analysis. Finally, the influences of interface parameter, properties of soil structure and structural yield stress on consolidation behaviors are discussed. Results show that the larger the interface parameter is, the easier the soil structure enters the failure stage, and the smaller the consolidation degree is. Furthermore, the time for initiating the failure stage does not change, when the interface parameter and structural yield stress keep unchanged; in the meanwhile, the greater the consolidation coefficient is, the greater the consolidation degree of foundation becomes when the soil structure begins to fail, and the earlier the soil enters the complete failure stage. When the interface parameter is determined, the ratio of structural yield stress to load can accelerate the soil consolidation rate, but all consolidation curves coincide for the same ratio.
Keywords: Analytical solution, consolidation, structured soil, continuous drainage boundary, structural yield stress
1. Introduction
Natural saturated soft soils not only have the characteristics of high-water content, high compressibility, and low permeability, but also have the structural features owing to the influence of geological environment in the deposition process [1-3]. The structural properties of soft soil have a significant influence on its consolidation behavior, especially affecting the permeability and compressibility of the soil. Therefore, saturated soft soils usually show the features of longer consolidation time, larger compression deformation and lower bearing capacity in the process of foundation treatment [4-7].
To characterize the mechanical properties of structural soft soil, linear segmented [8,9] and nonlinear models [10] have been proposed for modeling the variations of permeability and compression coefficients with effective stress based on the results from experimental studies. In terms of linear segmented consolidation models, An et al. [11] proposed an approximate solution for one-dimensional consolidation of single-layer soil, whereas one-dimensional semi-analytical consolidation solution of double-layer soils [12] and layered soils [13] have been derived. Furthermore, Hu et al. [14] carried out analyses for nonlinear one-dimensional consolidation of single-layer foundation under variable loads, and their model was further modified to account for one-dimensional nonlinear large deformation consolidation analysis of structural soils [15]. In terms of nonlinear consolidation models, a plenty of works have been conducted by many scholars. For example, Cao et al. [16] derived the one-dimensional nonlinear consolidation equations of structural soils under arbitrary load with nonlinear permeability and compressibility coefficients, and then obtained the numerical solution by using the Crank-Nicolson finite difference method. Considering the influence of self-weight stress and nonlinearity of compressibility and permeability of structural soft soil, Tang and Zhou [10] obtained a semi-analytical solution for one-dimensional consolidation of layered soils. A semi-analytical solution for one-dimensional nonlinear consolidation of double-layer foundation, considering the soil structure characteristics, under variable loads was proposed by Cui et al. [17]. Furthermore, using the finite difference method, the one-dimensional large deformation consolidation behavior of marine soft clay was discussed by Li et al. [18]. Xia et al. [19] derived a theoretical solution for multi-layered marine soft clays considering large-strain rheological and natural structural characteristics.
It should be noted that all analyses mentioned above were conducted based on the fully permeable boundary conditions. Once the load acting on structural soft soil exceeds the soil structure yield stress, the soil will be damaged from the boundary. However, the drainage boundary of soil in practice should be described as a semi-permeable boundary related to time, which is so-called the Neumann boundary condition. It has the disadvantage that it is not easy to obtain an analytical solution. In view of this, a time dependent continuous drainage boundary, which is essentially a Dirichlet boundary condition, has been proposed by Mei et al. [20]. However, there is no reference about the derivation of consolidation solution for structural soils under continuous drainage boundary condition.
The consolidation theory of continuous drainage boundary mainly includes linear and nonlinear aspects in the literature. In terms of linear consolidation, using Laplace transformation, finite Fourier sine transform, separation of variables and finite element method, scholars have developed solutions that can account for many factors, such as the self-weight [21,22], linear loading [23,24], variable loading [25,26], double-layered soils [27,28] , and layered soils [26,29]. On the other hand, research of nonlinear consolidation includes material nonlinear consolidation [30-33] and geometric large deformation nonlinear consolidation [34]. For instance, Zong and Wu [31] proposed analytical solutions for one-dimensional nonlinear consolidation, and Tong and Wang [32] derived viscoelastic analytical solutions on the basis of continuous drainage boundary under variable loading [35]. In addition, using separation of variables and Laplace transform methods, an analytical solution for one-dimensional large-deformation consolidation of soils was calculated by Jiang and Zhan [34]. However, it is worth pointing out that none of above research considered the influence of structural properties of soil on consolidation behaviors.
The objective of this paper is to establish a mathematical model for one-dimensional consolidation, considering the influence of soil structural properties, under continuous drainage boundary and arbitrary loading conditions. Subsequently, using finite Fourier sine transform and integral transform techniques, an analytical solution is derived, the correctness of which is evaluated by comparing with the results of boundary condition degradation and numerical calculation using the backward finite-difference method. Furthermore, the influences of interface parameters and soil structural properties on the consolidation process are discussed.
2. Model description
A schematic diagram of one-dimensional consolidation for structural soils is illustrated in Figure 1, where a uniformly distributed constant load is applied on the surface of soil with a total thickness of . The upper surface is a continuous drainage boundary, and the bottom surface is an impermeable boundary. In the meanwhile, the coordinate axis originates from the top boundary, and the positive direction points downwardly.
The simplified segmental models [13] of permeability and compression modulus are shown in Figure 2, where and are the permeability coefficient and compression modulus of structural in-situ soils, respectively, and and are the permeability coefficient and compression modulus of remodeled soils, and is the uniformly distributed load applied on the top surface of the structured soil. However, it should be noted that the permeability coefficient of the soil is changing during the consolidation process, and the model described in this study is valid under the classic Terzaghi hypothesis.
| Figure 1. Sketch of one-dimensional consolidation of structured soils |
| Figure 2. Simplified model of structured soil. (a) Segmented pattern of permeability and compression coefficient. (b) Classification diagram (single-drainage situation) |
According to the process of soil structure failure, the consolidation behavior of structural soil can be divided into three stages (Figure 3(a)), including undamaged stage of soil structure, failure stage and complete failure stage [11]. Undamaged stage of soil structure describes the condition that the effective stress at the soil surface is less than the structural yield stress, and the soil parameters (e.g., compression coefficient and permeability coefficient) are equal to the values of undisturbed soils. Hence, the collapse of structure will not occur, and the soil consolidation process belongs to normal consolidation. Failure stage is defined when the soil effective stress on the upper surface exceeds the structural yield stress, and the soil structure begins to damage, forcing a moving boundary of the structural failure surface, as shown in Figure 3(b). It must be emphasized that the permeability and compression coefficient of the soil above the moving boundary have been changed, being equivalent to the parameters of remodeled soil, The foundation soil can then be considered as a double-layer foundation at this moment. With the development of consolidation, the stage of complete soil structure failure denotes that the moving boundary of the structure failure surface has reached the bottom of the foundation, and the soil structure has been completely destroyed. The permeability coefficient and compression coefficient of the soil should be simulated with the values of remodeled soil in the stage of complete soil structure failure, and the soil is transformed from a double-layer foundation into a single layer foundation.
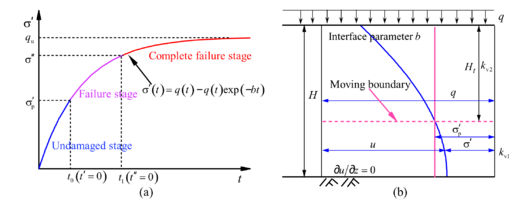
|
| Figure 3. Sketch of one-dimensional consolidation of structured soils. (a) Division of different soil structure failure stages. (b) Moving boundary due to the development of boundary failure |
3. Solving procedures
3.1 Solution of excess pore-water pressure
3.1.1 Undamaged stage
The effective stress of soil at the upper boundary is less than the yield stress of the structure, when the consolidation time belongs to the interval , at which the soil structure has not been damaged. Hence, the mathematical model described in Figure 1 is one-dimensional consolidation of single-layer soil with continuous drainage boundary under constant load. The governing equation of the system can be written as
|
|
(1) |
where is the excess pore-water pressure in the soil at the undamaged stage; is the consolidation coefficient; and parameters , and represent the time, the thickness of the soil layer and the vertical coordinate, respectively.
Initial condition and boundary conditions can be expressed as follows:
|
|
(2) |
|
|
(3) |
where is a uniformly distributed load applied on the surface of structural soil foundation, and parameter is the interface parameter.
By combining the solution conditions and using the finite Fourier sine transform method, the analytical solution can be expressed as follow:
|
|
(4) |
where , and .
3.1.2 Failure stage
In the failure stage of soil structure, the time t belongs to the interval , and the soil structure begins to break down. Hence, the effective stress on the upper boundary of soil is greater than the yield stress of the structure, and the single-layer foundation is transformed into a double-layer foundation (a remolded soil layer overlying an undamaged soil layer). Taking as the time coordinate, the consolidation behaviors in this stage can be considered as a linear consolidation of double-layered foundation with non-uniform initial pore pressure under continuous drainage boundary conditions, and the initial pore pressure is . Therefore, the governing equation and the definite solution conditions can be written as follows:
Governing equation:
|
|
(5) |
where and are the excess pore-water pressure and the consolidation coefficient of soil element above the moving boundary, respectively; and are the excess pore-water pressure and the consolidation coefficient of soil element under the moving boundary, respectively.
Initial condition:
|
|
(6) |
where is the surcharge stress in the soil at any depth in the failure stage.
Boundary conditions:
|
|
(7) |
Continuous condition of interlayer flow can be expressed as follows:
|
|
(8) |
where and are the permeability coefficient and the thickness of remolded soil, respectively; and are the permeability coefficient and the thickness of undamaged soil, respectively.
For the homogenization of non-homogeneous boundary, let
|
|
(9) |
Substituting Eq. (9) into the governing equation and definite solution conditions Eq.(6)~(8), it yields:
|
|
(10) |
where ,
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
For convenience, normalization is generally conducted to simplify the problem by eliminating the influence of measured units. In this paper, dimensionless variables are given as follow:
(1) represents the ratio of permeability coefficient between undamaged and remolded soils;
(2) means the ratio of consolidation coefficient between undamaged and remolded soils;
(3) and are the ratio of thickness of remolded soil and undamaged soil, respectively, to total thickness of foundation;
(4) .
The solution form of is given as follows:
|
|
(15) |
where
Substituting Eq. (15) into the interlayer continuity condition, it leads:
|
|
(16) |
|
|
(17) |
Subsequently, substituting Eq. (15) into Eq. (10), it yields:
|
|
(18) |
In the meanwhile, the undetermined coefficient should meet the constraint as given by:
|
|
(19) |
Using the orthogonal relationship of characteristic function system, it can be written as follows:
|
|
(20) |
By conducting orthogonal integration on both sides of Eq. (19), it yields:
|
|
(21) |
Based on the initial condition, the following formation can be derived:
|
|
(22) |
Combining Eq. (22) and the orthogonality of the characteristic function system, Bm can be given by:
|
|
(23) |
Hence, the solution of can be written as follows:
|
|
(24) |
By substituting Eq. (24) into Eq. (9), the solution of excess pore-water pressure of soil element can be expressed as follows:
|
|
(25) |
where is an unknown quantity related to , and its relationship can be obtained according to the effective stress at depth that is equal to the yield stress of the structure.
When , the expression could be meet, and it yields:
|
|
(26) |
Eq. (26) is the corresponding relationship between and , from which the depth of the moving boundary can be obtained by an iterative method when the time is fixed.
3.1.3 Complete failure stage
The effective stress of soil at the bottom boundary is greater than the structural yield stress when the time , and as such the soil structure has been damaged completely. Taking as the time coordinate, the consolidation model has been transformed from a two-layer foundation under continuous drainage boundary into a one-dimensional consolidation for a single-layer soil with non-homogeneous initial excess pore pressure, where the initial pore pressure is . The governing equation and the definite solution conditions are given below:
Governing equation:
|
|
(27) |
where and are the excess pore-water pressure and consolidation coefficient of soil element at the complete failure stage, respectively.
Boundary conditions:
|
|
(28) |
Initial condition:
|
|
(29) |
where represents the surcharge stress of soil at any depth in the complete failure stage.
In order to achieve the purpose of homogenization for non-homogeneous boundary, the excess pore-water pressure of soil element at the complete failure stage is supposed as:
|
|
(30) |
Substituting Eq. (30) into the governing equation and definite solution conditions, it leads:
|
|
(31) |
where .
|
|
(32) |
|
(33) |
Using the finite Fourier sine transform, the solution of excess pore-water pressure in the complete failure stage can be written as follows:
|
|
(34) |
where .
Therefore, the average consolidation degree defined by excess pore-water pressure can be expressed as follows:
|
|
(35) |
3.2 Evaluation of the proposed solution
To demonstrate the effectiveness of the present solutions, comparisons between the analytical solutions with the results of degradation cases and numerical analyses calculated by the finite difference technique are carried out. Moreover, the dimensionless interface parameter and time factor are introduced for facilitating the analyses.
3.2.1 Comparison against degenerated cases
Based on the analytical solution of consolidation process for non-structural soil with continuous drainage boundary derived by Mei et al [24], the structural soil parameters in this study have been transformed into the non-structural soil parameters, i.e., and . The comparisons between the two approaches for different interface parameters (e.g., 3, 5 and 10) are shown in Figure 4. It can be seen that the proposed solution matches with the solution calculated by Mei et al [24] well. Therefore, the correctness of the present solution is preliminarily demonstrated.
| Figure 4. Calculation results of degenerated solution |
3.2.2 Comparison against numerical calculations
To further assess the efficacy of the proposed analytical solution, numerical results calculated by the backward difference method (Figure 5) are adopted for derivation, in which the backward difference and central difference schemes are used for time and space, respectively. In addition, the space and time nodes of the soil layer are expressed as and , respectively, and the space and time step lengths are and . The space nodes of the soil layer are taken from top to bottom in the order of , where . Finally, it is assumed that the node of failure surface for the moving boundary is .

|
| Figure 5. Finite difference element mesh discretization |
When the space nodes of the soil layer , the difference formula of the governing equation can be expressed as follows:
|
|
(36) |
where , and .
When the space nodes of the soil layer , the interlayer continuity condition is expressed as follows:
|
|
(37) |
Substituting and in Eq. (37) into the left hand of Eq. (36), the difference scheme of the governing equation at point can be obtained as follows:
|
(38) |
where .
Initial condition and boundary condition are written in the following forms:
|
|
(39) |
|
|
(40) |
Determination condition of point :
|
|
(41) |
The calculated results from the proposed method and the numerical technique are shown in Figure 6, where the calculation parameters are employed as follows: , , , , , and three interface parameters , 10 and 20. As can be seen, the proposed analytical solutions (PAS) are in good agreement with the results of finite difference method (FDM), so that the reliability of the proposed solution in is further illustrated.
| Figure 6. Comparison of consolidation between the proposed analytical solution (PAS) and finite difference method (FDM) |
4. Results and discussions
In order to study the influence of interface parameter, structural properties and structural yield stress of soil on consolidation behaviors, the calculation parameters are taken as , kPa, m. The dimensionless consolidation coefficient ratio is defined as , and the structural yield stress ratio is written as . To be specific, the consolidation model is equipped with a continuous drainage boundary on the soil surface and an impermeable drainage on the bottom boundary. Other detailed computational parameters are shown in Table 1.
| Case | Permeability coefficient ( m s-1) |
Volume compressibility coefficient (MPa-1) | ||
|---|---|---|---|---|
| 1 | 1.25 | 0.75 | 0.75 | 0.75 |
| 2 | 0.7 | 0.75 | 1.4 | 0.75 |
| 3 | 0.5 | 0.75 | 2 | 0.75 |
| 4 | 0.4 | 0.75 | 2.4 | 0.75 |
| 5 | 0.3 | 0.75 | 2.7 | 0.75 |
4.1 Influence of interface parameter
Figure 7 illustrates the influence of interface parameter on consolidation degree for the case with a constant consolidation coefficient ratio of (i.e., case 3) and different interface parameters of , and . It can be seen that the larger the interface parameter is, the faster the excess pore-pressure dissipates and the earlier the effective stress reaches the structural yield stress. Hence, the time in the undamaged stage becomes shorter and the consolidation rate becomes faster. Moreover, it can also be seen that the smaller the interface parameter is, the greater the degree of consolidation of structural soil is after entering the failure stage.
| Figure 7. Influence of interface parameter on consolidation degree of structured soil |
4.2 Influence of structural properties of soil
The influence of consolidation coefficient ratio for structural soils (i.e., cases 1-5), when the interface parameter is fixed at 3, is plotted in Figure 8. As seen from the figure, there is no inflection point in the consolidation curve when the consolidation coefficient ratio is 1, and it represents the condition that structural soil degrades to homogeneous nonstructural soil (i.e., undamaged stage throughout the analysis). It is interesting that structural soil enters the failure stage at the same time, since the interface parameter is identical. However, the greater the consolidation coefficient ratio () is, the greater the consolidation degree becomes at a specific time in the failure stage, and the earlier the consolidation process enters the complete failure stage. It other words, neglecting the distinct difference in three failure stages for undamaged and remolded soils, consolidation analysis could lead to underestimation of degree of consolidation or overestimation of consolidation settlement, resulting in conservative design in ground treatment.
| Figure 8. Influence of structural properties of soil on degree of consolidation |
4.3 Influence of structural yield stress of soil
The influence of ratio between soil structural yield stress and load on the consolidation behavior is depicted in Figure 9(a), where the consolidation coefficient ratio is and the interface parameters are and . It can be seen that the trends of consolidation curves under different interface parameters are the same. The larger the interface parameter is, the faster the consolidation rate is. When the yield stress is the same (e.g., the structural yield stress is 50 kPa), the soil consolidation rate slows down with the increase of load level, but the soil enters the failure stage earlier, which is caused by the smaller consolidation coefficient of remolded soil. In addition, the higher the yield stress is, the later the structure failure occurs and the faster the soil consolidation rate becomes for a fixed load (e.g., the value of load is 100 kPa). In summary, the consolidation rate increases with the increase of interface parameter and parameter .
Moreover, Figure 9(b) shows the trends of consolidation curves with a fixed parameter under two groups of interface parameters. It is clearly seen that the consolidation curves are consistent when is taken to be the same value, which indicates that the ratio of structural yield stress to load is positively related with the consolidation rate.
|
| ||
| Figure 9. Effect of yield stress on consolidation degree of structured soil |
5. Conclusions
To fill the knowledge gap in consolidation solutions for structural soft soil foundation, the one-dimensional consolidation equation of structured soft soil foundation under continuous drainage boundary conditions with the consideration of soil structure is established. An analytical solution is then proposed by using finite Fourier sine transform and integral transform methods. The effectiveness of the present solution is discussed by comparing against degenerated cases and numerical results calculated by the finite difference method. Sensitivity analysis is carried out to study the influence of interface parameter, structural characteristics of soil elements and structural yield stress on consolidation behaviors of foundation soils. The main conclusions in this study are summarized as follows:
(1) The interface parameters are positively correlated with the time when soil structure failure initiates, i.e., the larger the interface parameter is, the earlier the soil enters the failure stage, and vice versa.
(2) Soil consolidation coefficient and failure time are positively correlated, i.e., the larger the consolidation coefficient is, the earlier the soil enters the failure stage and the greater the consolidation degree becomes.
(3) The ratio of structure yield stress to load, , does not change the degree of consolidation curve.
(4) For remolded soil, without considering the three failure stages, the degree of consolidation can be underestimated, leading to extremely conservative design in practice of ground improvement.
Declaration of interests
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
Acknowledgements
This work was supported by the National Natural Science Foundation of China (52008124, 52268054 and 52208345), the China Postdoctoral Science Foundation (2020M683210), and the Natural Science Foundation of Guangxi Province (2021AC18008).
References
[1] Burland J. On the compressibility and shear strength of natural clays. Géotechnique, 40(3):329-378, 1990.
[2] Poskitt T. The consolidation of saturated clay with variable permeability and compressibility. Géotechnique, 9(2):234-352, 1969.
[3] Yang W, Xu J. One-dimensional consolidation of multilayered aquifer systems with viscoelastic properties induced by time-dependent groundwater drawdown. Quarterly Journal of Engineering Geology and Hydrogeology, 55(2), qjegh2021-073, 2022.
[4] Yang W., Ni P., Chen Z., Feng J., Mei G. Consolidation analysis of composite ground improved by granular piles with a high replacement ratio considering overlapping smear zones. Computers and Geotechnics, 162, 105636, 2023.
[5] Zhang C. Geotechnical characteristics of two structural clays. Hydro-Science and Engineering, 4(4):68-74, 1983.
[6] Shen Z. Engineering properties of soft soils and design of soft ground. Chinese Journal of Geotechnical Engineering, 20(1):100-111, 1998.
[7] Leroueil S., Vaughan P.R. The general and congruent effects of structure in natural soils and weak rocks. Géotechnique, 40(3):467-488, 1990.
[8] Wang J., Cheney Y. Analytical solution to 1-D consolidation of uniform structured soft foundation. Journal of Hydraulic Engineering, 3(3):19-24, 2003.
[9] Wang L., Ding L., Chen Y., Li L. Study on compressibility of structured soft soil. China Civil Engineering Journal, 37(4):46-53, 2004.
[10] Tang Y., Zhou M. One dmiensional non-linear semi-analytical solution for structured soft soils. Chinese Journal of Under ground Space and Engineering, 3(4):605-8, 2007.
[11] An R., Xie K, Deng Y., Wang K. Approximate solution for one-dimensional consolidation of structured soils under time-dependent loading. Rock and Soil Mechanics, 33(10):3194-3200, 2012.
[12] Xie K., Xia C., An R., Ying H., Wu H. A study on one-dimensional consolidation of layered structured soils. International Journal for Numerical and Analytical Methods in Geomechanics, 40(7):1081-1098, 2016.
[13] Xie K., Xia C., An R., Hu A., Zhang W. A study on the one-dimensional consolidation of double-layered structured soils. Computers and Geotechnics, 73(1):189-198, 2016.
[14] Hu A., Xia C., Cui J., Li C., Xie K. Nonlinear consolidation analysis of natural structured clays under time-dependent loading. International Journal of Geomechanics, 18(2):04017140, 2018.
[15] Hu A., Zhou Y., Chen Y., Xia C., Xie K. Semi-analytical solutions for one-dimensional nonlinear large strain consolidation of structured soft clay. Rock and Soil Mechanics, 41(8):2583-2591, 2019.
[16] Cao Y., Chen Y., Huang M. One-dimensional nonlinear consolidation analysis of structured natural soft clay subjected to arbitrarily time-dependent construction loading. Chinese Journal of Geotechnical Engineering, 28(5):569-574, 2006.
[17] Cui J., Xie K., Xia C., Hu A., Zhou Y. One-dimensional nonlinear consolidation analysis of double layered structured soils under time-dependent loading. Journal of Central South University (Science and Technology), 49(7):1710-17, 2018.
[18] Li C., Xiao J., Wu W., Mei G., Ni P., Leo C. Analysis of 1D large strain consolidation of structured marine soft clays. Journal of Zhejiang University Science, 21(1):29-43, 2020.
[19] Xia C., Zhu M., Chen W., Peng Y., Xie K. Large-strain rheological consolidation analysis of multi-layered marine soft clays exhibiting natural structural characteristics. Marine Georesources & Geotechnology, 41(10):1142-1155, 2023.
[20] Mei G., Feng J., Xu M., Ni P. Estimation of interface parameter for one-dimensional consolidation with continuous drainage boundary conditions. International Journal of Geomechanics, 22(3):04021292, 2022.
[21] Cai F., He L., Zhang Q., Xu M., Mei G. Finte element analysis of undrained symmetry plane with self-weigh. Jouranl of Zhejiang University (Engineering Science), 47(12):2132-2140, 2013.
[22] Feng J., Ni P., Mei G. One‐dimensional self‐weight consolidation with continuous drainage boundary conditions: Solution and application to clay‐drain reclamation. International Journal for Numerical and Analytical Methods in Geomechanics, 43(8):1634-1652, 2019.
[23] Cai F., He L., Zhou X., Xu M., Mei G. Finite element analysis of one-dimensional consolidation of undrained symmetry plane under continuous drainage boundary. Chinese Journal of Geotechnical Engineering, 34(11):2141-2147, 2012.
[24] Mei G., Xia J., Mei L. Terzaghi’s one-dimensional consolidation equation and its solution based on asymmetric continuous drainage boundary. Chinese Journal of Geotechnical Engineering, 33(1):28-31, 2011.
[25] Feng J., Chen Z., Li Y., Mei G. Analytical solution for one-dimensional consolidation of soft clayey soil with a continuous drainage boundary under linear loading. Engineering Mechanics, 36(6):219-226, 2019.
[26] Tian Y., Wu W., Jiang G., El Naggar M.H., Mei G., Xu M., et al. One‐dimensional consolidation of soil under multistage load based on continuous drainage boundary. International Journal for Numerical and Analytical Methods in Geomechanics, 44(8):1170-1183, 2020.
[27] Liu J., Lei G. One-dimensional consolidation of layered soils with exponentially time-growing drainage boundaries. Computers and Geotechnics, 54(10):202-209, 2013.
[28] Wu W., Zong M., El Naggar M.H., Mei G., Liang R. Analytical solution for one-dimensional consolidation of double-layered soil with exponentially time-growing drainage boundary. International Journal of Distributed Sensor Networks, 14(10):1550147718806716, 2018.
[29] Chen X., Chen W., Yue Z. One-dimensional consolidation of multilayered soil with continuous drainage boundaries and under time-dependent loading. International Journal of Geomechanics, 22(9):04022142, 2022.
[30] Chen Z., Wang X., Zeng J. 1-D non-linear consolidation solution to unsteady pore pressure boundary of foundation soil. Journal of Nanjing Tech Univesity (Natural Science Edition), 36(5):90-94, 2014.
[31] Zong M., Wu W., Mei G., Liang R., Tian Y. Analytical solution for one-dimensional nonlinear consolidation of soil based on continuous drainage boundary. Chinese Journal of Rock Mechanics and Engineering, 37(1):1-10, 2018.
[32] Tong L., Wang Y., Guo S., Zhu H., Xu C. On one-dimension consolidation characteristics of viscoelastic subgrade with continuous drainage boundary under time- dependent loading. Rock and Soil Mechanics, 40(05):1862-1868, 2019.
[33] Zong M., Wu W., El Naggar M.H., Mei G., Ni P., Xu M. Analytical solution for one-dimensional nonlinear consolidation of double-layered soil with improved continuous drainage boundary. European Journal of Environmental and Civil Engineering, 27(8):2746-2767, 2023.
[34] Jiang W., Zhan L., Yang C. Analytical solution for one-dimensional large strain consolidation of saturated soft soils with continuous drainage boundary. Journal of Central South University (Science and Technology), 1(5):1289-1298, 2020.
[35] Yang X., Zong M., Tian Y., Jiang G., El Naggar M.H., Wu W., et al. One‐dimensional consolidation of layered soils under ramp load based on continuous drainage boundary. International Journal for Numerical and Analytical Methods in Geomechanics, 45(6):738-752, 2021.Document information
Published on 12/02/24
Accepted on 24/01/24
Submitted on 08/01/24
Volume 40, Issue 1, 2024
DOI: 10.23967/j.rimni.2024.01.007
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?