m (Move page script moved page Et al 2023a to Yu et al 2023e) |
|||
| (5 intermediate revisions by one other user not shown) | |||
| Line 409: | Line 409: | ||
|- | |- | ||
| <math>\left\{\begin{array}{c} | | <math>\left\{\begin{array}{c} | ||
| − | M=K_m{\theta }_r=\frac{{\theta }_rK_nB^2}{12},{\theta }_r\leq {\theta }_r^0\\ | + | M=K_m{\theta }_r=\displaystyle\frac{{\theta }_rK_nB^2}{12}\quad ,\quad {\theta }_r\leq {\theta }_r^0\\ |
| − | M=M_0=\frac{1}{6}\left(F_nB\right),{\theta }_r>{\theta }_r^0 | + | M=M_0=\displaystyle\frac{1}{6}\left(F_nB\right)\quad ,\quad {\theta }_r>{\theta }_r^0 |
\end{array}\right\}</math> | \end{array}\right\}</math> | ||
|} | |} | ||
| Line 424: | Line 424: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\left\{\begin{array}{ | + | | <math>\left\{\begin{array}{cc} |
| − | M=K_m{\theta }_r=\frac{{\theta }_rK_nB^2}{12},{\theta }_r\leq {\theta }_r^0\\ | + | M=K_m{\theta }_r=\displaystyle\frac{{\theta }_rK_nB^2}{12}\quad ,\quad & {\theta }_r\leq {\theta }_r^0\\ |
| − | M=\mbox{0}\ | + | M=\mbox{0} \quad ,\quad & {\theta }_r>{\theta }_r^0 |
\end{array}\right\}</math> | \end{array}\right\}</math> | ||
|} | |} | ||
| Line 586: | Line 586: | ||
|- | |- | ||
| <math>\left\{\begin{array}{c} | | <math>\left\{\begin{array}{c} | ||
| − | M=IK_m{\theta }_r=\frac{{\theta }_rK_nB^2}{12},{\theta }_r\leq {\theta }_r^0\\ | + | M=IK_m{\theta }_r=\displaystyle \frac{{\theta }_rK_nB^2}{12}\quad ,\quad {\theta }_r\leq {\theta }_r^0\\ |
| − | M=M_0=\frac{1}{6}\left(F_nB\right),{\theta }_r>{\theta }_r^0 | + | M=M_0=\displaystyle\frac{1}{6}\left(F_nB\right)\quad ,\quad{\theta }_r>{\theta }_r^0 |
\end{array}\right\}</math> | \end{array}\right\}</math> | ||
|} | |} | ||
| Line 601: | Line 601: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math display="inline">\left\{\begin{array}{ | + | | <math display="inline">\left\{\begin{array}{cc} |
| − | M=IK_m{\theta }_r=\frac{{\theta }_rK_nB^2}{12},{\theta }_r\leq {\theta }_r^0\\ | + | M=IK_m{\theta }_r=\displaystyle\frac{{\theta }_rK_nB^2}{12}\quad ,\quad & {\theta }_r\leq {\theta }_r^0\\ |
| − | M=\mbox{0}\ | + | M=\mbox{0} \quad ,\quad & {\theta }_r>{\theta }_r^0 |
\end{array}\right\}</math> | \end{array}\right\}</math> | ||
|} | |} | ||
Latest revision as of 11:09, 14 December 2023
Abstract
At present, the researches on the mechanical properties of sand aggregate mainly focus on the shaping process of particles, and lack the researches on the crushing mechanism. This paper first defines the shaping process of stone powder wall, and explores the crushing mechanism of sand aggregate by adopting multiple times of small energy crushing. The effect of energy is investigated by simulation and experiment. The machine-made sand crushing mechanism is analyzed by establishing corresponding contact mathematical models. The result shows that the stone powder wall involves two mathematical models under impact: the elastic-plastic model at low impact velocity and the elastic-brittle model at high impact velocity.
Keywords: Machine-made sand, stone powder wall, crushing mechanism, mechanical contact model
1. Introduction
Compared with natural sand, machine-made sand has richer resources. Ore, rock, construction waste etc. can be made into aggregate after crushing and shaping by equipment like crushers. It not only alleviates the problem of resource shortage, but also protects the environment. With the demand of high-performance concrete for infrastructure applications, high quality aggregate has become the most needed basic raw material for high-grade buildings.
Ma et al. [1] proposed a novel and feasible method to pulverize recycled aggregate into recycled machine-made sand. Zheng and Tannant [2] introduced the discrete element simulation results of sand crushing calibrated by laboratory data of one-dimensional compression test. Benyessad et al. [3] proposed an expression to quantify the mathematical model of crushed sand grains. Gongalves et al. [4] compared the performance of artificial sand, produced by impact crushing or cone crushing, and natural sand in cement preparation. Cepuritis et al. [5] introduced micro-proportioning of full-size aggregates achieved through high-speed vertical shaft impact crushing and static air classification. Petit et al. [6] designed a device for sustainable air classification, which improved the production efficiency by overcoming the disadvantage of conventional method, which only produced a single machine-made sand. The study by Wu et al. [7] showed that the application of fine aggregates and fine powders obtained from concrete waste in recycled mortar is conducive to resource recycling. Santhosh et al. [8] proposed the substitute of industrial by-products for river sand to manufacture concrete. Shen et al. [9] recommended digital control manufactured sand to achieve zero discharge of solid waste such as waste stone, dust and slurry. Wei et al. [10] analyzed the effect of different amounts of CaO expansion agent on the physical mechanics and frost resistance of concrete by adding mixed sand in concrete. Hou [11] studied the influence of various performance indexes of machine-made sand on concrete work performance and admixture adaptability. Tan et al. [12] studied effects of polypropylene fibers on the frost resistance of natural sand concrete and machine-made sand concrete. Liu et al. [13] compared the factors affecting the mechanical properties of machine-made sand concrete using grey correlation analysis. All above discussed the effects of machine-made sand and natural sand respectively as an aggregate added to concrete. Chen et al. [14] investigated the effect of machine-made sand gradation and fineness modulus on the workability and rheological properties of mortar. Deng et al. [15] determined the methylene blue (MB) value of machine-made sand by experiment and analyzed the mineral composition of machine-made sand. Chen et al. [16] analyzed the big data about machine-made sand performance. Fei et al. [17] used computed tomography (CT) scanned images of four dry sands and network analysis to predict effective thermal conductivity in sands. He et al. [18] developed a physical packing model together with the related mathematical model of fresh mortar. All these studied and explored the property of machine-made sand itself. Wang et al. [19] investigated the effect of aggregate micro fines in machine-made sand on the volume stability of concrete in plastic stage. Tang et al. [20] analyzed the properties of machine-made mortar with different stone powder contents through experiments. Wang [21] studied the effect of boulder powder on the compressive strength of concrete. Wang et al. [22] studied the effect of basalt powder, as a substitute for cement and machine-made sand, on the properties of dry mixed mortar to determine the best usage of basalt powder. These explored the shaping of the machine-made sand from the perspective of the stone powder and the effect it has as an additive.
The above literature has focused on the shaping process of machine-made sand. Shaping process plays a decisive role in improving the quality of sand, however, what is the mechanism of sand shaping? It is worth exploring. At present, the studies on the particle crushing mechanism are relatively few and not closely related to the technology of crushing equipment. Therefore, the study of sand shaping mechanism and process parameters is particularly important [23]. Sand shaping involves the techniques of removing sharps of irregular aggregates by collision. Common irregular aggregates are shown in Figure 1 and Figure 2.

|
| Figure 1. Strip aggregates |
| Figure 2. Flat-elongated aggregates |
That is, particles accelerated by the impeller collide with and rub against other particles and liners in the crushing chamber [24]. Therefore, the essence of stone powder wall shaping process is multiple times of crushing of particles and aggregates with small energy. This paper will focus on the stone powder wall formation, its shaping mechanism, the establishment and validation of the theoretical contact model, and based on all these, discusses the design of the stone powder wall segments.
2. Stone powder wall formation mechanism
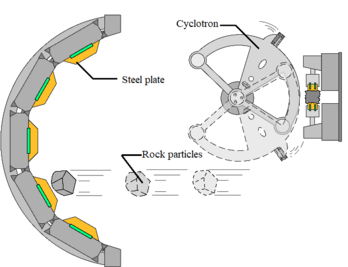
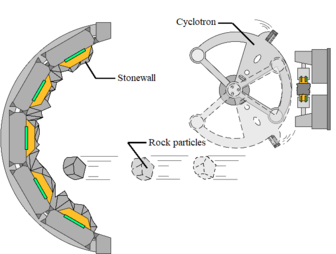
When the crusher is working, the stones enter the machine through the feeder and pass through the divider to the rotor chamber and contact with the high-speed rotating impeller. After being accelerated by the centrifugal force in the impeller, they are ejected from the three flow channels evenly distributed around the rotor chamber at high speed. Part of them are piled up in the crushing chamber by the action of the particle liner to form a physical solid wall. And the particles flying out from the impeller flow passage collide with them again, achieving the shaping effect, hence the stone powder wall (or stone wall) mechanism.
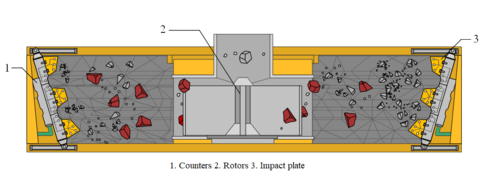
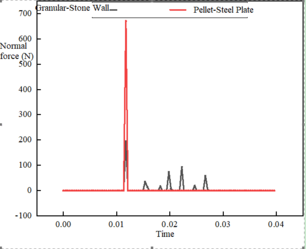
Figure 3 shows two types of contact for sand shaping: rock-metal contact and rock-rock contact. The gray particles and red particles are the first and second group of particles ejected from the rotor, respectively. The gray particles hit the sensor counter inside the impact plate and collide with the red particles again after rebounding from the contact point of the impact plate. The collision of the particles with the impact plate and the chamber forms a rock-metal contact, while the collision between the particles forms a rock-rock contact. A study showed that rock-rock contact is the main way of particle formation [25].
|
| Figure 3. Sand particle crushing test bench |
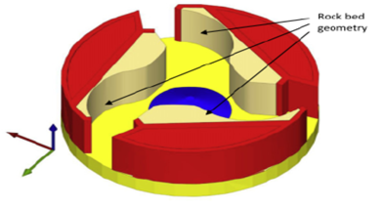
According to da Cunha et al. [25], the inter-particle collision energy is higher in the rock-rock contact mode than in the rock-metal contact mode (Figure 4). In addition, the collision between rock bed and sand not only crushes the particles, but also protects the interior of the crushing chamber from wear and tear, thus extending the service life of the machine.
|
| Figure 4. Rock bed geometry from the references |
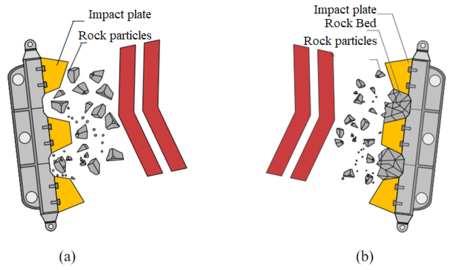
As shown in Figure 5, most current crushers are equipped with a smooth impact plate with pits on the surface after a period of collision with the particles. These pits deposit rock powders, forming a “rock bed”. As shown in Figure 6(a), the rock particles collide with the impact plate and the rock powder accumulates in the pits, forming a rock bed that not only crushes the particles, but also protects the interior of the crushing chamber from wear and tear. As shown in Figure 6(b), the pits deposit rock particles, and although it accelerates the wear of the impact plate, the rock layer will protect it from abrasion, thus still extending the service life of the machine.

|
| Figure 5. The rock bed in a real machine |
|
| Figure 6. The formation of “stone powder wall” |
3. Stone powder wall shaping mechanism
As the impact velocity of particles keeps increasing, the energy gained by particles on the cyclotron accelerator is gradually elevated. The kinetic energy is determined by , where is the mass of particles and is the velocity of particles.
Residence Time: the length of time that a particle exists in the simulation. “Residence Time = Simulation Time - Particle Creation Time”.
Normal force: it is generated when two objects are in direct contact. It is always perpendicular to the object that exerts the force. The force depends on the contact model, which is usually a spring force with a damping component.
3.1 Analysis and comparison of the data of “rock-rock” and “rock-metal” models
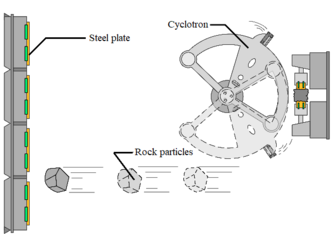
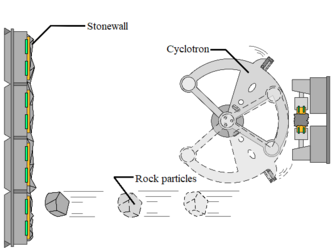
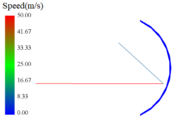
As shown in Figure 7(a), the particles accelerate through the cyclotron accelerator and impact on the flat steel plate, and are ejected from the impact plate to the crushing chamber. With the increase of working time, a layer of stone powders will form on the surface of the flat steel plate, as shown in Figure 7(b).
| ||||
| Figure 7. Experiments of shaping on flat surface |
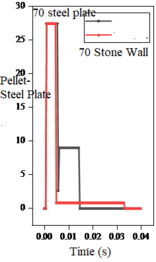
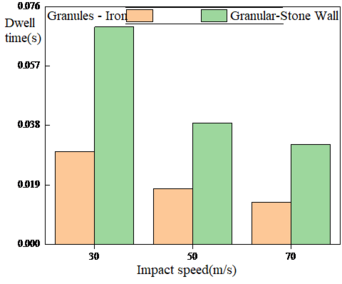
When the simulation is done on a flat impact plate, as shown in Figure 8, the residence time of particle-stone wall is larger than that of particle-metal in the same group, thus the stone powder wall has a damping effect on the particles. Both have decreasing residence time as the impact velocity of particles increases. However, the range of variation of particle-metal residence time is small, proving that the overall velocity change has a less effect on particle-metal residence time than that of the particle-stone wall. By comparing the simulation data, it is found that under the impact load, the energy of “rock-metal” model is 3 to 8 times larger than that of “rock-rock” model. The stone powder wall stores and decomposes impact energy, having an obvious elastic damping effect.
|
| Figure 8. Particle residence time under different impact velocities on flat surface |
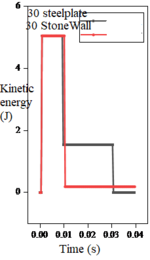
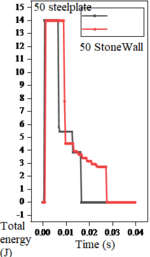
Figure 9 shows the particle energy when simulated on a flat impact plate, which further verified a significant elastic damping effect of the stone powder wall.
| |||
| Figure 9. Energy under different impact velocities on flat surface |
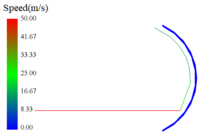
As shown in Figure 10(a), the particles accelerate through the cyclotron accelerator and impact on the arc steel plate, and are ejected from the impact plate once or twice to the crushing chamber. With the increase of working time, a layer of stone powders will form on the surface of the arc steel plate, as shown in Figure 10(b).
| ||||
| Figure 10. Experiments of shaping on arc surface |
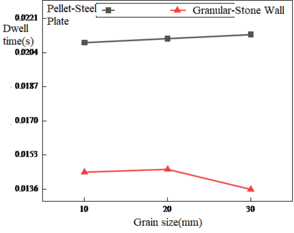
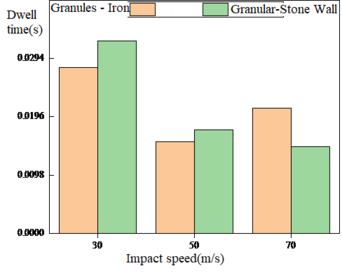
As shown in Figure 11, in the simulation on the arc impact plate, the particle-steel plate residence time is smaller than the particle-stone wall residence time at a low to medium speed of 30-50 m/s; between 50-70 m/s, the particle-steel plate residence time gradually becomes larger than the particle-stone wall residence time. However, the particle-stone wall residence time decreases gradually with the increase of impact velocity, and the variation ranges of particle-stone wall residence time and particle-steel plate residence time are both small, proving that the arc has a positive effect on prolonging the particle residence time.
|
| Figure 11. Particle residence time under different impact velocities on arc surface |
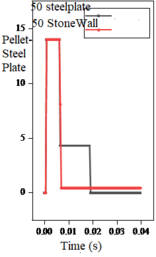
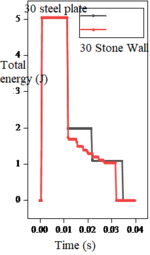
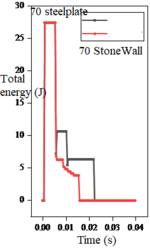
The same impact velocity is applied to the particles so that the initial energy of the particles is the same, and as shown in Figure 12, the maximum value of energy carried by the particles increases with the increase of velocity. The energy of particle- stone wall model decreases more slowly and the frequency of the particle energy exchange is much higher than that of the particle-steel plate model at the same velocity.
| |||
| Figure 12. Energy under different impact velocities on flat surface |
3.2 Particle contact model in shaping process
Figure 13 shows the elastic-plastic contact model formed by the stone particles when they act on the stone wall.
|
| Figure 13. Shaping contact model |
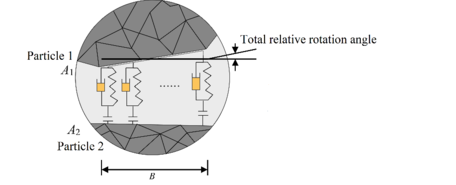
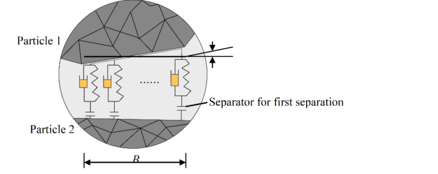
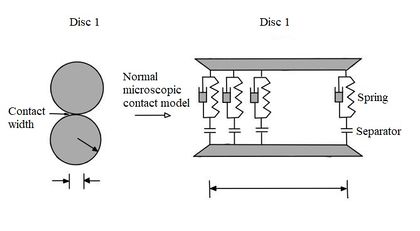
As shown in Figure 14, and are the diameters of particle 1 and particle 2, respectively, and is the width of the contact surface, the expression of which is defined as:
|
|
(1) |
The non-dimensional shape parameter can be determined by comparing the data results of the internal friction angle parameter obtained from numerical simulations and the particle shape test with the target test results. In Figure 14, a normal basic unit is fixed on the contact surface, which consists of a spring and a damper connected in parallel and is then connected in series with the separator. The stiffness of the spring is (N/m2), reflecting the elasticity of particle contact point and the damping coefficient of the damping generator. To achieve energy dissipation, a separator is used to simulate the absence of tension (N/m) when the cement fails. Similarly, a tangential basic unit is defined, which consists of a spring and a damper connected in parallel and is connected in series with the slider. The difference between the tangential basic unit and the normal basic unit is that the spring and damper in the former are on the tangent and the slider replaces the separator in the normal unit. The slider is used to simulate plastic sliding at the contact point under a certain shear strength, which is determined by the normal pressure at a specified point and the Mohr - Coulomb criterion. The result shows that the normal basic unit has a cementing effect at the contact point, which resists inter-particle torsion, while the tangential basic unit does not have this effect.
|
| Figure 14. Normal contact model |
Assume that the thickness of the contact area is constant and normal and tangential basic units are continuously distributed on the contact surface. The overall normal stiffness and tangential stiffness (N/m) of particles, the damping coefficient , and the stiffness of normal basic elements and the stiffness of tangential basic elements satisfy the following requirements:
|
|
(2) |
If a finite relative rotation angle is specified, denote or by B. The cementing between the particles will produce a force couple that will be transferred from particle 1 to particle 2.
Derive the relationship between the force couple and with small rotation angles.
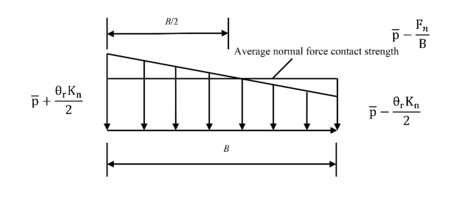
The first step is to consider the absence of sliding, which corresponds to the linear elastic phase. As shown in Figure 15(a), with a constant normal force , particle 1 is rotated counterclockwise by a small angle relative to particle 2. The concentration of the normal contact force is linearly distributed along the contact area, as shown in Figure 15(b), and the load intensity at the left and the load intensity at the right are expressed as
|
|
(3) |
where is the average intensity of normal forces, defined as
|
|
(4) |
| ||||
| Figure 15. Normal force distribution on contact surface without sliding |
The distribution of the normal force on the contact surface causes the bending moment :
|
|
(5) |
where is the rolling stiffness, in N·m
|
|
(6) |
where depends on , and . If is a constant, then increases linearly with it.
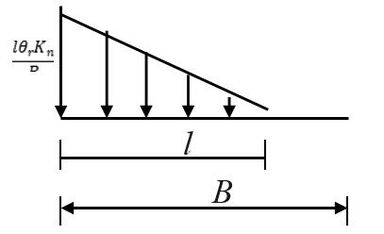
The second step is to consider the partial sliding, which corresponds to the plastic phase. The plastic mechanism is defined by the separation of the separator. According to Figure 16(a), when particle 1 is rotated counterclockwise relative to particle 2 with a constant normal force , its basic contact unit at the right edge and the separator fail and crack. With the increase of the damage of normal elements and the cracking of the separator continue to move inwards from the edge, so that at the corresponding point is 0 and is redistributed linearly, as shown in Figure 16(b). Let be the contact width and indicate the minimum (maximum) normal contact force located at the rightmost (leftmost) end of the contact area (the width is l)
|
|
(7) |
The bending moment and the normal force are:
|
|
(8) |
|
|
(9) |
| ||||||
| Figure 16. Separation model of the separator |
When , the normal contact point is not damaged and the separator does not separate, i.e., there is no plasticity, and the critical values of the relative rotation angle and bending moment are and , respectively:
|
|
(10) |
Put the equation into the following equation, the rolling bending moment with can be obtained:
|
|
(11) |
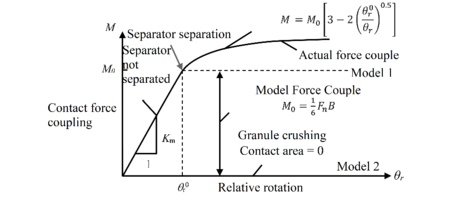
Once the above process is completed, the linear elastic and plastic phases represented by the Eqs. (5) and (11) are combined to establish the rolling contact model. As shown in Figure 16(c), theoretical and numerical analysis for plastic process is more difficult. Two types of simple models for stone powder wall contact are proposed.
Type 1: Elastic-plastic model
|
|
(12) |
Type 2: Elastic-brittle model
|
|
(13) |
when , the contact model is a simplified model in the classical particle discrete element method. The dashed lines in Figure 16(c) indicate type 1 and type 2, respectively, where the former is more like the rolling contact model and represents the elastic-plastic action that approximates the Mohr-Coulomb criterion. Type 2 is used to simulate particle crushing, in which particle crushing is achieved by the disappearance of rolling caused by the sudden disappearance of contact width.
Based on the stone powder wall shaping contact model, the overall shear contact model is made to cover the continuously distributed tangential basic units and control the relevant tangential motion on the shear surface; the overall normal contact model is obtained from the continuously distributed normal basic units, which determines the normal motion of the contact surface on the contact surface.
The mechanical contact model of stone powder wall shaping is now derived, but there is a certain correlation between stone powder wall shaping and the particles’ angle of incidence, so based on the above conclusion, an incidence angle factor is added to improve the contact model of stone powder wall shaping.
3.3 The verification of the contact models
By simulating the incidence angles at different positions of the arc plate (Figure 17), particles can be ejected at a certain position for several times, and hence meeting the demand of the shaping mechanism.
| |||
| Figure 17. Ejection trajectory |
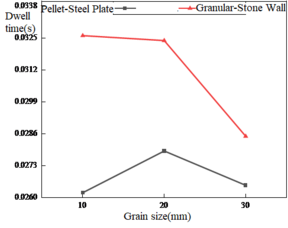
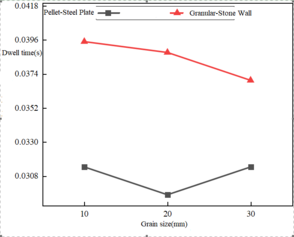
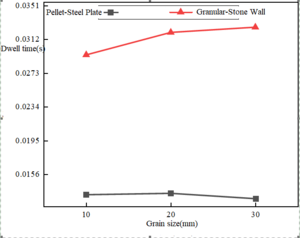
The impact simulation tests were conducted on the arc impact plate at velocities of 30, 50, and 70 m/s, respectively, as shown in Figure 18(a). At the low impact velocity of 30 m/s, the residence time of particles of 20 mm-diameter was the longest, and showed an increasing to decreasing trend. The residence time of particles of 20 mm-diameter in the particle-steel group was the smallest at the impact velocity of 50 m/s, as shown in Figure 18(b). At the impact velocity of 70 m/s, the overall residence time did not fluctuate much, and the residence time of the steel plate group was larger than that of the stone wall group, as shown in Figure 18(c).
| ||||||
| Figure 18. Particle residence time under arc impact with different particle sizes |
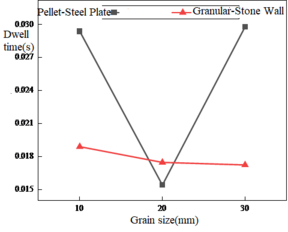
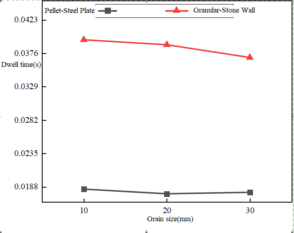
The impact simulation tests were conducted on the flat impact plate at velocities of 30, 50, and 70 m/s, respectively, as shown in Figure 19. The analysis showed that the residence time of the steel plate group was less than that of the stone wall group. As shown in Figure 19(a), at low impact velocities of 30 and 50 m/s, the difference of residence time was not great, and the residence time stayed stable as the particle size increased. As shown in Figure 19(b) and (c), the difference between the residence time of the particles of the steel plate group and the stone wall group is larger at the medium and high impact velocities of 50 and 70 m/s.
| ||||||
| Figure 19. Particle residence time under flat impact with different particle sizes |
Particle shaping is achieved by multiple times of crushing between particles and shaping plates with small energy, as shown in Figure 20. The arc impact plate can effectively increase the time and chance of collision. The mechanical contact model of stone powder wall shaping is now derived, but there is a certain correlation between stone powder wall shaping and the particles’ angle of incidence, so based on the above conclusion, an incidence angle factor is added to improve the contact model of stone powder wall shaping. Under the impact velocity of 30 m/s, the contact model of particles is mainly type 1, that is, the elastic-plastic model, and the incidence angle factor ranges reasonably from 0.9 to 1.1. Under the impact velocity of 50-70 m/s, which is conventional, the contact model of particles is mainly type 2, that is, the elastic-brittle model, and the incidence angle factor ranges from 1.0 to 1.2.
|
| Figure 20. Impact energy |
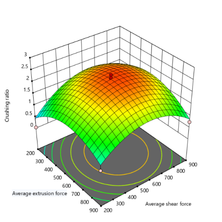
According to Figure 21 shows the effect of average shear force and average extrusion force on the crushing ratio. When only a single force of the two are at its maximum or minimum, the crushing ratio of rock particles will be greatly reduced, while when the two forces act simultaneously and are balanced, the crushing effect is the best.
|
| Figure 21. Multi-factor cloud image |
Based on the cross-sectional scanning electron microscope (SEM) images of the crushed particles, and by comparison, the crushing mechanisms of three typical rocks were analyzed (Figure 22).
| ||||
| Figure 22. Comparison of aggregate forms before and after shaping |
According to the comparison of sand aggregates before and after crushing, shown in Figure 22, and the SEM image in Figure 23, it is found that in the process of crushing, when the acceleration exerted by the main impeller on the rock particles causes the impact stress on the particles more than what they can withstand, the particles are prone to crushing. The crushed samples are mostly limestone, and the crushed surface gets thicker from the outer edge, which is generally of arc shape, to the center. The crushed surface is not neat but presents a step-like shape. With the same external factors and the same initial state, larger particles need greater crushing energy, and the crushing effect is better. With the same mass, the number of elongated shapes crushed out of larger particles is also larger.
| ||||
| Figure 23. Comparison of sand aggregate SEM images before and after crushing |
As shown in Figure 24, the fracture surface has the same fracture along the crystal surface direction, while the overall damage is not very significant, so it can be judged that the particle shaping is mainly achieved by “small energy” of shear force. Based on the above analysis, the essence of the stone powder wall shaping mechanism is “multiple times of small energy crushing”. The contact models involve:
Type 1: Elastic-plastic model
|
|
(14) |
Type 2: Elastic-brittle model
|
|
(15) |
The established mathematical models can reasonably reflect the change of rolling bending moment of sand aggregate under different contact models. The SEM image are in agreement with the theory to a certain extent, indicating that the mathematical models are reasonable.

|
| Figure 24. SEM image of crushed surface |
4. Experiment verification
4.1 lntroduction of experimental prototype
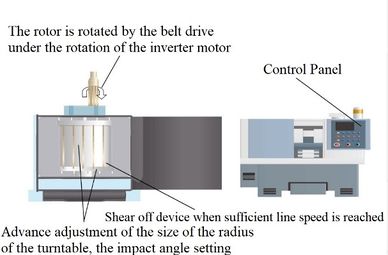
The equipment used in this test is the sand impact mechanism test machine, which has the advantages of being easy to use and use, and can simulate the situation of sand and gravel material being thrown and crushed in the crushing process, which can more intuitively understand the crushing process. The hardware first sets the linear velocity of the material collision, and obtains the corresponding motor velocity, and then adjusts the motor velocity through the control box, in order to adjust the speed of the rotor that is connected to the belt, in order for the material on the turn table's locking mechanism to achieve the corresponding linear velocity, once the turntable reaches the tuned linear speed, the electromagnetic push-pull connecting rod of the cutting mechanism can be set. As the turntable reaches the set linear velocity, the electromagnetic push-pull rod of the shear mechanism extends to cause the cutting knife to cut the string, and the movable baffle pivots rap idly outward to open at the same time. At the same time, the gravel material also spirals out ward at high velocity and collides with the impact plate. Figure 25 shows the specific schematic diagram, and Figure 26 shows the actual image of the experimental machine.
| Figure 25. Schematic diagram of test prototype |
| Figure 26. Actual internal view of experimental machine |
4.2 Analysis of experimental process and results
The prototype is tested on the self-designed impact-crushing simulation test machine. Since area I is a stone -walled structure in the optimization model, since the angle control is not yet designed in this paper, 3D printing technology is used to print the shape in a manner similar to the strength of the rock wall. Figure 27 below shows the shape of the printed cavity, and the strength of the stone wall is achieved by adjusting the fill rate of the 3D components.
| Figure 27. 3D printed stone wall shape |
The surface is then coated with a layer of stone beating raw materials to perform simulation of the surface contact parameters, which can be seen in Figure 28 (limestone, pebble and granite) from the left to the right.
| Figure 28. Optimized stone wall shape |
To simulate the different contact properties of different materials, we coated the 3D printed specimen with a certain particle thickness of stone wall material in order to realize the actual contact parameters of the particles. Since the influence of stone wall material thickness on the test cannot be ascertained, to test the influence of stone wall thickness, we designed an orthogonal test set. Select the appropriate orthogonal array based on the number of factors and levels. In most cases the number of factors less than or equal to the number of columns of the orthogonal array, and the number of factor levels should be consistent with the number of levels in the orthogonal table. Assuming the above conditions are satisfied, the orthogonal array with smaller specifications should be chosen. We adopt the three-factor, three- level test for this mud wall thickness test. Due to its three-tiered nature, is adopted. Table 1 shows the factor-level table, and Table 2 shows the trained test table and the final data.
| Impact velocity (m/s) | Thickness of earth wall (mm) | Impact angle (°) | |
|---|---|---|---|
| 1 | 60 | 1 | 10 |
| 2 | 70 | 3 | 20 |
| 3 | 80 | 5 | 30 |
| Test number | Impact velocity | Thickness of earth wall | Impact angle | Empty column | Crushing ratio |
|---|---|---|---|---|---|
| 1 | 1 | 1 | 1 | 1 | 0.5000 |
| 2 | 1 | 2 | 2 | 2 | 0.7500 |
| 3 | 1 | 3 | 3 | 3 | 0.5526 |
| 4 | 2 | 1 | 2 | 3 | 0.8667 |
| 5 | 2 | 2 | 3 | 1 | 0.6786 |
| 6 | 2 | 3 | 1 | 2 | 0.6552 |
| 7 | 3 | 1 | 3 | 2 | 0.6316 |
| 8 | 3 | 2 | 1 | 3 | 0.3714 |
| 9 | 3 | 3 | 2 | 1 | 0.6923 |
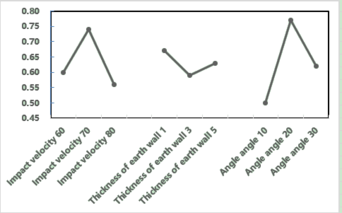
Figure 29 shows that with increasing impact velocity, the particle break ratio initially increases and then decreases at a speed of 70m/s. With a maximum angle of incidence of 20 degrees.
| Figure 29. Visual analysis trend chart |
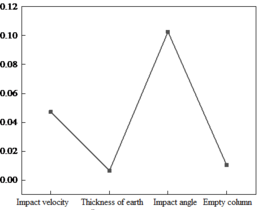
It can be seen from the range analysis Figure 30 that the angle of impact has the largest influence on the crush ratio, followed by the velocity of the impact, and the thickness of the mud wall has little effect.
| Figure 30. Range scatter plot |
The results of the Analysis of Variance Table 3 show that the impact angle and impact velocity have a large influence on the particle break up ratio, but the thickness of the mud wall of the test target has little impact.
| Difference source | SS | df | MS | F | p-value | Significance |
|---|---|---|---|---|---|---|
| Impact angle | 0.1027 | 2 | 0.0513 | 12.05 | 0.020269 | * |
| Impact velocity | 0.0472 | 2 | 0.0236 | 5.54 | 0.070385 | * |
| Thickness of earth wall | 0.0066 | 2 | 0.0033 | |||
| Error | 0.0105 | 2 | 0.0052 | |||
| Error | 0.0170 | 4 | 0.0043 | |||
| Summation | 0.17 | 8.00 |
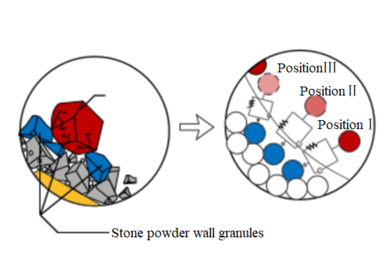
For the purposes of this paper, in order to adjust the use of the test prototype, firstly, to change the shape of the new counter plate, and repeating the test of each contraption plate four times, and calculating the materials broken respectively. Insert this optimized component into a proof machine, the relative position is illustrated in Figure 31, The left side is the optimized cavity shape, the left side is the sand making machine, and the particle impact velocity is adjusted by controlling the rotational speed of the rotor. Figure 32 shows a photograph of the stone wall after impact crushing. The particles can be seen to impact in to the I region of the stone wall, and the stone wall in I area is broken, which is consistent with the definition of the crushing function in I area in the test simulation. A large amount of energy is absorbed into the stone wall and the particles are broken. The material then ejected upwards to Zone II, and the particles from the stone wall on the surface were disrupted by friction, and eventually flew along Zone III of the rock wall with only minor friction.
| Figure 31. Installation of test prototype |
| Figure 32. Change of stone wall after impact crushing |
As can be seen in Table 4, only the advantages and disadvantages of the four shock plate shapes are compared by different methods, focusing on how they differ from the original shock plate shapes. Thus, depending on the grinding ratio, the grinding performance of the three impact plates can be compared.
| Counterattack plate | Crushing ratio | Average | |||
|---|---|---|---|---|---|
| After optimization | 0.525 | 0.5526 | 0.6782 | 0.6552 | 0.60275 |
| Before optimization | 0.423 | 0.5124 | 0.5322 | 0.4978 | 0.49135 |
By means of experimental verification, the structural parameters that can make the best crushing performance of the new counter plate are obtained: when the angle of the I area is 35 degrees, area angle II is 100 degrees, and area angle III is 10 degrees, the shape of the shaped particles is relatively optimum, and the value of the performance index can be improved by about 8%-10% compared to the counter plate commonly used in the industry. These results provide strong support for the machine-made sand shaping mechanism.
5. Conclusions
The following conclusions were obtained:
(1) The numerical analysis of “rock-rock” and “rock-metal” models verifies that the energy of “rock-metal” model under impact is 3 - 8 times greater than that of “rock-rock” model. The stone powder wall plays a damping role in the impact process, which effectively reduces the impact energy.
(2) The residence time of particle-stone wall model is about 0.002s longer than that of particle-metal model at low to medium speed of 30-50 m/s on the arc impact plate, and about 0.01s longer than that of particle-metal model at the speed of 50-70 m/s. The comparison between flat and arc impact plates shows that the arc impact plate has a positive effect on particle residence.
(3) Mathematical models of stone powder wall particles shaping mechanism were established, and the incidence angle factor is considered to analyze particles’ tangential and normal motion. At low impact velocity, it is mainly the elastic-plastic model, while at high impact velocity, it is mainly the elastic-brittle model. It is concluded that the mechanism of stone powder wall shaping is multiple times of low-energy shear crushing in nature.
Data Availability
The data will be provided upon request, and all of them can be used without any conflict of interest.
Acknowledgements
This project is funded by Fujian University of Technology and is a scientific and technological project of Fujian University of Technology. Project number is (GY-Z220201). And the Youth Project of Fujian Natural Science Foundation, with the grant number of 2020J05180.
References
[1] Ma Z., Shen J., Wang C., et al. Characterization of sustainable mortar containing high-quality recycled manufactured sand crushed from recycled coarse aggregate. Cement and Concrete Composites, 132:104629, 2022.
[2] Zheng W., Tannant D.D. Grain breakage criteria for discrete element models of sand crushing under one-dimensional compression. Computers and Geotechnics, 95:231-239, 2018.
[3] Benyessad D., Arkoub H., Seghir A. Modeling and optimization of sand crushing plant using experimental design methodology. World Journal of Engineering, 16(4):487–496, 2019.
[4] Gonçalves J.P., Tavares L.M., Toledo Filho R.D., et al. Comparison of natural and manufactured fine aggregates in cement mortars. Cement and Concrete Research, 37(6):924-932, 2007.
[5] Cepuritis R., Jacobsen S. Onnela T. Sand production with VSI crushing and air classification: Optimising fines grading for concrete production with micro-proportioning. Minerals Engineering, 78:1-14, 2015.
[6] Petit A., Cordoba G., Paulo C.I., et al. Novel air classification process to sustainable production of manufactured sands for aggregate industry. Journal of cleaner production, 198:112-120, 2018.
[7] Wu H., Wang C., Ma Z. Drying shrinkage, mechanical and transport properties of sustainable mortar with both recycled aggregate and powder from concrete waste. Journal of Building Engineering, 49:104048, 2022.
[8] Santhosh K.G., Subhani S.M., Bahurudeen A. Cleaner production of concrete by using industrial by-products as fine aggregate: A sustainable solution to excessive river sand mining. Journal of Building Engineering, 42:102415, 2021.
[9] Shen W., Wu J., Du X., et al. Cleaner production of high-quality manufactured sand and ecological utilization of recycled stone powder in concrete. Journal of Cleaner Production, 375:134146, 2022.
[10] Wei F., Zhang F., Gao L., et al. Mechanical properties and micromorphology of calcium oxide expansion agent on river sand/machine-made sand concrete. Advances in Civil Engineering, 2022:9407640, 2022.
[11] Hou H. Influence of machine-made sand performance on concrete. E3S Web of Conferences, EDP Sciences, 233(1):01040, 2021.
[12] Tan Y., Long J., Xiong W., et al. Effects of polypropylene fibers on the frost resistance of natural sand concrete and machine-made sand concrete. Polymers, 14(19):4054, 2022.
[13] Liu D., Zhang W., Tang Y., et al. Orthogonal experimental study on concrete properties of machine-made tuff sand. Materials, 15(10):3516, 2022.
[14] Chen C., Yang H., Fan Z. Research on the influence of machine-made sand gradation and fineness modulus on the workability and rheological properties of mortar. IOP Conference Series: Earth and Environmental Science, IOP Publishing, 760(1):012031, 2021.
[15] Deng L., Shen J., Lu S., et al. Study on how to determine the methylene blue (MB) value of machine-made sand and its effects on admixture dosage and compressive strength of concrete. IOP Conference Series: Earth and Environmental Science, IOP Publishing, 676(1):012104, 2021.
[16] Chen Z., Yu K., Miao D., et al. Analysis of machine-made sand parameters in Shaanxi. E3S Web of Conferences, EDP Sciences, 233:01099, 2021.
[17] Fei W., Narsilio G.A., Disfani M.M. Predicting effective thermal conductivity in sands using an artificial neural network with multiscale microstructural parameters. International Journal of Heat and Mass Transfer, 170:120997, 2021.
[18] He H., Wang Y., Wang J. Compactness and hardened properties of machine-made sand mortar with aggregate micro fines. Construction and Building Materials, 250:118828, 2020.
[19] Wang Y., He H., Wang J., et al. Effect of aggregate micro fines in machine-made sand on bleeding, autogenous shrinkage and plastic shrinkage cracking of concrete. Materials and Structures, 55(3):1-15, 2022.
[20] Tang Y., Qiu W., Liu D., et al. Experimental study on the properties of mortar and concrete made with tunnel slag machine-made sand. Materials, 15(14):4817, 2022.
[21] Wang P. Influence of boulder machine-made sand powder on compressive strength of concrete. E3S Web of Conferences, EDP Sciences, 293:02023, 2021.
[22] Wang X., Rao Y., Wang L., et al. Study on the effect of basalt rock powder on the properties of dry mixed mortar with machine-made sand. Hans Journal of Civil Engineering, 9(05):496-502, 2020.
[23] Cleary P.W., Sinnott M.D. Simulation of particle flows and breakage in crushers using DEM: Part 1–Compression crushers. Minerals Engineering, 74:178-197, 2015.
[24] Quist J., Evertsson C.M. Cone crusher modelling and simulation using DEM. Minerals Engineering, 85:92-105, 2016.
[25] da Cunha E.R., de Carvalho R.M., Tavares L.M. Simulation of solids flow and energy transfer in a vertical shaft impact crusher using DEM. Minerals Engineering, 43:85-90, 2013.Document information
Published on 18/09/23
Accepted on 06/09/23
Submitted on 25/05/23
Volume 39, Issue 3, 2023
DOI: 10.23967/j.rimni.2023.09.005
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?