Revision as of 02:09, 6 December 2023 (view source) Gstinoco (talk | contribs) ← Older edit	Latest revision as of 01:09, 13 December 2023 (view source) Gstinoco (talk | contribs) m (Gstinoco moved page Review 139704671734 to Torres Aguirre et al 2023a)
(No difference)

---

Latest revision as of 01:09, 13 December 2023

1 Introducción

El big data está inmerso hoy en día en las áreas de investigación de las distintas ramas de las matemáticas aplicadas, es un tema relevante de investigación actual. Sin embargo, abordar o estudiar conjuntos de datos inmensos con técnicas computacionales en forma secuencial e incluso con hardware especializado, ya no es un camino viable. Es por eso que en las distintas áreas de la matemática aplicada surge el problema de cómo obtener información relevante en las distintas bases de datos que se tengan del estudio de algún fenómeno o problema a estudiar. Uno de ellos es el problema de agrupamiento de datos cuya solución resuelve e incentiva a la mejora en la toma de decisiones dando una metodología de clasificación de ellos.

El problema puede ser tratado utilizando computadoras personales con recursos computacionales rápidos y eficientes que obtienen buenos resultados. Sin embargo, este problema demanda alto desempeño al recurso físico (hardware), por medio de lógica computacional escrita en diversos lenguajes de programación de alto nivel, generando así altas demandas de procesamiento y por tanto es necesario disponer de una capacidad de cómputo mayor. Este poder de cómputo lo puede ofrecer un arreglo de PCs interconectadas bajo una red de área local. A este tipo de interconexión de computadoras se le conoce como Cluster de PCs (computadoras personales interconectadas para obtener un comportamiento único). Un tipo de estos clusters de PCs son los llamados cluster beowulf diseñados para cálculo numérico intensivo.

El agrupamiento de estos datos (clustering) es una metodología ampliamente utilizada, que resuelve los problemas antes mencionados. Entre los algoritmos de clustering más simples y fáciles de implementar computacionalmente está el llamado KMeans. Es uno de los algoritmos de Machine Learning no supervisados más utilizados por la Ciencia de Datos y que además es muy fácil de usar como de interpretar. Su objetivo es agrupar observaciones similares para descubrir patrones que a simple vista se desconocen. Para conseguirlo, el algoritmo busca un número fijo (${\textstyle k}$) de clusters en una base de datos. Sin embargo, las aplicaciones del mundo real producen grandes volúmenes de datos, por lo tanto, el cómo tratar con estas grandes cantidades de datos el problema de agrupamiento es un problema significativo y desafiante

Una metodología para trabajar con altas prestaciones de datos, escalabilidad y portabilidad es Apache Spark, ideal para interconectar PCs y que unidas trabajen en un mismo problema. Por lo tanto, con la unión de Apache Spark y el algoritmo KMeans, se puede abordar el problema de agrupamiento de datos, que es el tema inicial en este trabajo que aún se encuentra en desarrollo y una primera etapa en él es comenzar por estudiar el algoritmo KMeans.

2 Preliminares

En esta sección se presenta el algoritmo KMeans. Se describe la idea general del algoritmo por medio de una descripción textual y puntualizando los conceptos de centroide y métrica utilizada. Esto hace evidente la idea geométrica detrás del algoritmo KMeans y que se describe por medio de los diagramas de Voronoi y la envoltura convexa.

2.1 El algoritmo

El algoritmo KMeans es uno de los más simples y conocidos algoritmos de agrupamiento. Utiliza una forma fácil y sencilla para dividir un conjunto de datos en ${\textstyle k}$ grupos (${\textstyle k}$ fijado de antemano)[1]. El método se basa en la idea de que los elementos de un cluster están agrupados alrededor de un centro o centroide geométrico. La tarea entonces es encontrar dichos centroides. Para ello se definen ${\textstyle k}$ centroides iniciales, luego se toma cada punto del conjunto de datos y se sitúa en la clase del centroide más cercano. El paso siguiente consiste en recalcular el centroide de cada grupo y volver a distribuir todos los objetos según el centroide más cercano [2,1]. El proceso se repite una y otra vez hasta que ya no haya cambio en los grupos de un paso al siguiente.

Conviene puntualizar lo que se entiende por un centroide y que el criterio de cercanía está basado en la distancia euclidiana, a menos que se señale otra cosa [1,3]. La idea más importante es que a cada grupo se le puede asignar un centroide, que corresponde al promedio de los datos de cada grupo. A continuación se presenta la definición de centroide.

Definición 1: El centro o centroide de una clase ${\textstyle \pi _{i}}$ se define como:

${\displaystyle c_{i}={\frac {1}{n_{i}}}\sum \limits _{v\in \pi _{i}}a_{v}}$

donde ${\textstyle n_{i}}$ es el número de elementos de la clase ${\textstyle \pi _{i}=\{v|a_{v}\;{\mbox{pertenece al grupo i}}\}}$.

Otro concepto a tomar en cuenta es la métrica, con ella se determina si un punto del conjunto de datos está más próximo a uno de los centroides, en tal caso ese punto pertenecerá al grupo de dicho centroide, la métrica utilizada para este trabajo es la euclidiana que se define de la manera siguiente[2].

Definición 2: En el espacio euclidiano la distancia entre dos puntos ${\textstyle X=(x_{1},x_{2},\ldots ,x_{n})}$ y ${\textstyle Y=(y_{1},y_{2},\ldots ,y_{n})}$ se define así:

${\displaystyle d_{E}(X,Y)={\sqrt {\sum \limits _{i=1}^{n}(y_{i}-x_{i})^{2}}}}$

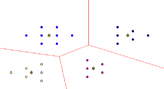
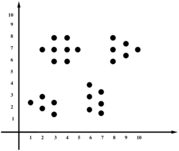
Un ejemplo sencillo de aplicación del algoritmo es el siguiente. Se toma un conjunto de datos en ${\textstyle \mathbb {R} ^{2}}$, en donde a sus coordenadas ${\textstyle (x,y)}$ se les conoce como atributos de los datos (ver Figura 1). Para encontrar los centroides, seguimos los pasos siguientes[1]:

1. Se escoge ${\textstyle k}$ centroides iniciales de manera arbitraria ${\textstyle (k=4)}$
2. Se forman cuatro grupos de la forma siguiente: se toman las distancias de un dato a los ${\textstyle k}$ centroides y ese dato pertenecerá al grupo del centroide más cercano, así se construyen los grupos.
3. Se toma el promedio de cada grupo y estos serán los centroides siguientes.
4. Se repiten los pasos 2 y 3 hasta que los centroides ya no cambian.

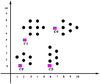
Figura 1: Ejemplo de conjuntos de puntos en el plano y su proceso de agrupamiento con KMeans. Fuente: Elaboración propia.

Con el ejemplo anterior se ha descrito de una manera simple el funcionamiento del algoritmo KMeans. Ahora se está en condiciones de mostrar el algoritmo, que de acuerdo a la literatura consultada [1], está definido de la siguiente manera.

Paso 1. Inicialización: Se define un conjunto de datos a particionar, el número de grupos y un centroide por cada grupo de forma arbitraria o aleatoria.

Paso 2. Clasificación: Para cada dato del conjunto, se calcula su distancia a cada centroide, se determina el centroide más cercano, y el conjunto es incorporado al grupo relacionado con ese centroide.

Paso 3. Cálculo de centroides: Para cada grupo generado en el paso anterior se vuelve a calcular su centroide.

Paso 4. Condición de convergencia: El algoritmo converge cuando no existe un intercambio de objetos entre los grupos, si la condición de convergencia no se satisface, se repiten los pasos 2 y 3 del algoritmo.

2.2 Diagramas de Voronoi

Definición 3: El diagrama de Voronoi de ${\textstyle P=\{p_{1},p_{2},\ldots ,p_{n}\}}$, está formado por todos los puntos ${\textstyle x}$ que equidistan de los dos elementos de ${\textstyle P}$ más cercanos a ${\textstyle x}$.

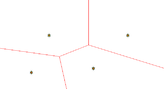
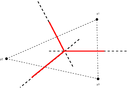
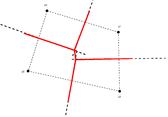
En la Figura 2 se muestran ejemplos de diagramas de Voronoi en el plano: para dos, tres y cuatro puntos, siendo las lineas rojas los diagramas de Voronoi.

Figura 2: Ejemplos de los diagramas de Voronoi en el plano. Fuente: Elaboración propia.

Cada punto ${\textstyle p_{i}\in P}$ determina una región en el plano, a saber los puntos del plano que están más cerca de ${\textstyle p_{i}}$ que del resto de los puntos de ${\textstyle P}$; a esto se le conoce como Celdas de Voronoi y se definen de la manera siguiente.

Definición 4: Sea ${\textstyle p_{i}\in P}$

${\displaystyle V(p_{i})=\{p|\;d(p,p_{i})\leq d(p,p_{j}),\;p_{j}\in P\}}$

2.3 Envoltura Convexa

Definición 5: Se llama envoltura convexa de un conjunto dado ${\textstyle X}$ al menor (por inclusión) conjunto convexo que contiene a ${\textstyle X}$ y se define como:

${\displaystyle conv(X)=\{tx+(1-t)y|x,y\in X,t\in [0,1]}$

si ${\textstyle X\subseteq P}$, y ${\textstyle P}$ es un conjunto convexo, entonces ${\textstyle X\subseteq conv(X)\subseteq P}$.

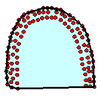
Las Figura 3 representa un ejemplo de envolturas convexas de varios conjuntos de puntos en el plano.

Figura 3: Ejemplos de la cascara convexa de puntos en el plano. Fuente: Elaboración propia.

3 Objetivos

3.1 Objetivo General

• Estudiar el problema de agrupamiento de datos utilizando el algoritmo KMeans

3.2 Objetivos Específicos

• Revisar literatura especializada sobre el algoritmo KMeans.
• Caracterizar el algoritmo KMeans.
• Estudiar la idea geométrica del algoritmo.
• Presentar el marco de trabajo llamado ApacheSpark.

4 Metodología

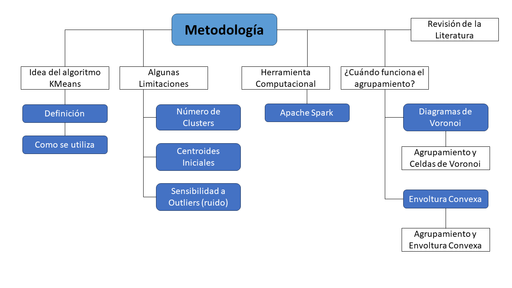
En esta sección se presenta la metodología a utilizar para llevar a cabo este trabajo. Se describe el proceso de la búsqueda de bibliografía y la idea del algoritmo. El algoritmo tiene la característica de ser simple, compacto y fácil de implementar computacionalmente. Sin embargo no está exento de limitaciones, es por eso que se hace la siguiente pregunta ¿Cuando funciona el algoritmo?, y se da una respuesta en base a la idea geométrica del mismo. Así mismo se presenta el marco de trabajo computacional en el cual se basará el trabajo, el llamado Apache Spark.

Figura 4: Metodología de trabajo para el desarrollo de esta investigación. Fuente: Elaboración propia.

4.1 Revisión de la literatura

La revisión de la literatura para esta investigación se realiza utilizando los motores de búsqueda especializados como Google Académico, Journal of citation of reports (JCR) y otros como Latinindex. La busqueda se realiza mediante los criterios siguientes:

• Frases claves en inglés como Unsupervised algorithms, kmeans aplications. paralel kmeans.
• Análisis de la información centrado en las algoritmos no supervisados de tipo particionales, enfocándose en aspectos tales como: (i) geometrías, (ii) centroides iniciales y (iii) posibles aplicaciones.
• Se indagó sobre el problema de agrupamiento poco estudiadas como lo son los algoritmos en paralelo y algoritmos robustos.

4.2 La idea del KMeans

El problema es encontrar grupos en un conjunto de datos. Una pregunta que surge de manera natural es la siguiente: ¿Cómo encontrar grupos en un conjunto de datos óptimos de manera automatizada? Veámoslo por medio de un ejemplo.

Tenemos un conjunto de datos (Tabla 1), cada dato se representa como un punto en el plano cartesiano con coordenadas ${\textstyle (x,y)}$, y lo que se quiere realizar con dicho conjunto de datos, es encontrar grupos de manera automatizada.

Tabla. 1 Representación de los datos en coordenadas ${\displaystyle (x,y)}$.

x	1	2	2	3	3	3	2	3	3	3	4	4	4	5	6	6	6	7	7	8	8	8	9	9	10
y	2.5	2.3	1.5	2.5	3.5	7	6	7	8	6	6	8	7	2	3	4	2.5	3.5	6	7	8	6.5	7.5	7	7

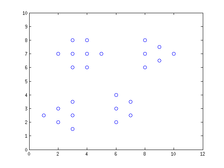
La representación de los puntos de la Tabla 1 en el plano cartesiano es la siguiente:

Figura 5: Representación gráfica del conjunto de datos en el plano de la forma ${\displaystyle (x,y)}$ de la Tabla 1.

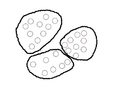
En la Figura 5 es fácil localizar visualmente cuatro grupos. Sin embargo, aún en dos dimensiones no siempre está claro cuántos cluster hay y cómo se agrupan los datos. Por ejemplo, del siguiente conjunto de datos, se requiere encontrar los grupos asociados a ellos.

Figura 6: Conjunto de datos a agrupar.

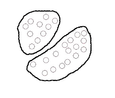
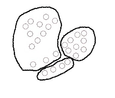
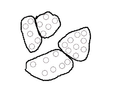
De la Figura 6, se pueden citar aquí cuatro opciones distintas de agrupar los datos que se observan a continuación:

Figura 7: Distintos agrupamientos.

Para problemas de mayor dimensión, encontrar grupos se vuelve mucho más complicado, porque no podemos apoyarnos de la parte visual, como en los casos de dos dimensiones ${\textstyle \mathbb {R} ^{2}}$ y en los de tres dimensiones ${\textstyle \mathbb {R} ^{3}}$.

4.3 Ejemplo

En el artículo [3] se plantea un ejemplo numérico del algoritmo, veamos este ejemplo. Se supone en él que se tienen cuatro tipos de medicamentos con dos atributos cada uno a saber (Peso e Índice PH) como se muestra en la tabla siguiente:

Medicina	Peso	Índice PH
A	1	1
B	2	1
C	4	3
D	5	4

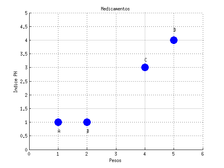
Se quieren encontrar dos grupos basados en los dos atributos de los datos. Cada medicamento puede ser representado como un punto en el plano cartesiano de la manera siguiente:

Figura 8: Representación gráfica de los atributos de los medicamentos en ${\displaystyle \mathbb {R} ^{2}}$. Fuente Elaboración propia.

Iteración 1

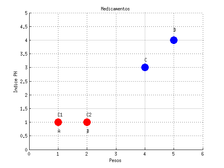
Se elige el número de grupos que se desea encontrar, es decir el valor del número ${\textstyle k}$, en este caso ${\textstyle k=2}$. Se seleccionan dos centroides iniciales, que en este caso serán los primeros dos medicamentos, es decir:

${\displaystyle c_{1}=(1,1)\qquad \qquad c_{2}(2,1)}$

Figura 9: Elección de los centroides iniciales, en este caso son los primeros dos medicamentos que están coloreados de color rojo. Fuente: Elaboración propia.

Para encontrar los grupos se calcula las distancias de los datos a los centroides ${\textstyle c_{1}}$ y ${\textstyle c_{2}}$, tomando la distancia mínima para asignarlos al centroide más cercano.

Tabla. 2

	${\displaystyle c_{1}}$	${\displaystyle c_{2}}$
A	0	1
B	1	0
C	3.61	2.83
D	5	4.24

Los nuevos grupos son ${\textstyle G_{1}=\{A\}}$ y ${\textstyle G_{2}=\{B,\;C,\;D\}}$

Iteración 2

En el grupo 1 solo se tiene a un miembro, el centroide de ese grupo será nuevamente

${\displaystyle c_{1}=(1,1)}$

Mientras en el grupo 2, se tienen tres miembros que son ${\textstyle B(2,1)}$, ${\textstyle C(4,3)}$, ${\textstyle D(5,4)}$

Para calcular ${\textstyle c_{2}}$ lo hacemos de la manera siguiente

${\displaystyle c_{2}=\left({\frac {2+4+5}{3}},{\frac {1+3+4}{3}}\right)=\left({\frac {11}{3}},{\frac {8}{3}}\right)}$

Por lo tanto los nuevos centroides son: ${\textstyle c_{1}=(1,1)}$ y ${\textstyle c_{2}=({\frac {11}{3}},{\frac {8}{3}})}$

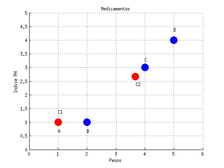
Figura 10: Calcular los nuevos centroides ${\displaystyle c_{1}}$ y ${\displaystyle c_{2}}$ calculando la distancia de ellos a todos los datos y en base a la distancia mínima. Fuente: Elaboración propia.

Se vuelven a encontrar nuevos grupos calculando las distancias de los datos a los centroides ${\textstyle c_{1}}$ y ${\textstyle c_{2}}$

	${\displaystyle c_{1}}$	${\displaystyle c_{2}}$
A	0	3.14
B	1	2.36
C	3.61	0.47
D	5	1.89

Los nuevos grupos son ${\textstyle G_{1}=\{A,\;B\}}$ y ${\textstyle G_{2}=\{C,\;D\}}$

Iteración 3

El grupo 1 tiene como miembros ${\textstyle A=(1,1)}$, ${\textstyle B=(2,1)}$

Para calcular ${\textstyle c_{1}}$ lo hacemos de la manera siguiente

${\displaystyle c_{1}=\left({\frac {1+2}{2}},{\frac {1+1}{2}}\right)=\left({\frac {3}{2}},1\right)}$

El grupo 2 tiene dos miembros que son ${\textstyle C=(4,3)}$, ${\textstyle D=(5,4)}$

Para calcular ${\textstyle c_{2}}$ lo hacemos de la manera siguiente

${\displaystyle c_{2}=\left({\frac {4+5}{2}},{\frac {3+4}{2}}\right)=\left({\frac {9}{2}},{\frac {7}{2}}\right)}$

Por lo tanto, los nuevos centroides son: ${\textstyle c_{1}=\left({\frac {3}{2}},1\right)}$ y ${\textstyle c_{2}=\left({\frac {9}{2}},{\frac {7}{2}}\right)}$

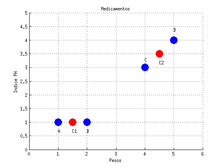
Figura 11: Elección de los nuevos centroides en base al procedimiento basado en la Iteración 2. Fuente: Elaboración propia.

Se vuelve a encontrar nuevos grupos calculando las distancias de los datos a los centroides ${\textstyle c_{1}}$ y ${\textstyle c_{2}}$

	${\displaystyle c_{1}}$	${\displaystyle c_{2}}$
A	0.5	4.30
B	0.5	3.54
C	3.20	0.71
D	4.61	0.71

Nuevos grupos ${\textstyle G_{1}=\{A,\;B\}}$ y ${\textstyle G_{2}=\{C,\;D\}}$

Es fácil ver que en el paso siguiente los centroides no cambian, por lo tanto tampoco los grupos, de tal forma que el proceso termina.

Medicina	Peso	Índice PH	Grupo
A	1	1	1
B	2	1	1
C	4	3	2
D	5	4	2

Los medicamentos ${\textstyle A}$ y ${\textstyle B}$ difieren en una unidad en la propiedad de peso, mientras que en la propiedad del índice PH son iguales, por esa razón son muy parecidos y el algoritmo KMeans los clasifica en un mismo grupo, mientras que los medicamentos ${\textstyle C}$ y ${\textstyle D}$ difieren en una unidad en ambas propiedades, quedando así en el segundo grupo. Como puede observarse los medicamentos con características similares pertenecen al mismo grupo.

Con el ejemplo se ha mostrado el funcionamiento del algoritmo KMeans, en donde cada medicamento se representa como un punto en el plano ${\textstyle \mathbb {R} ^{2}}$. Se pudo graficar cada dato debido a la naturaleza de los mismos. En el caso en donde los datos son de mayor dimensión, esa representación visual no puede auxiliarnos, esto no es un impedimento ya que el algoritmo puede realizar agrupamientos en cualquier dimensión.

4.4 ¿Cuándo funciona?

Se presentó la idea del algoritmo KMeans, su definición y se mostró un ejemplo de como se utiliza, para encontrar grupos de conjuntos de datos. KMeans encuentra buenos agrupamientos y malos agrupamientos también, la cuestión es ¿Cuándo hace buenos agrupamientos?

A continuación se presenta un ejemplo donde el algoritmo hace un buen agrupamiento y otro ejemplo donde hace un mal agrupamiento.

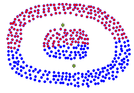
Figura 12: Ejemplos en ${\displaystyle \mathbb {R} ^{2}}$ donde el algoritmo KMeans agrupa bien y otro ejemplo donde agrupa mal. Fuente: elaboración propia.

En el caso del buen agrupamiento ver Figura 12 es posible trazar una línea recta que divide al plano por regiones, cada una de estas regiones contendrá a uno de los grupos. Por lo contrario, no será posible trazar una línea recta con las características mencionadas. Esta es una característica relevante para dar respuesta a esta cuestión.

(a)	(b)
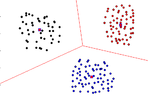
Figura 13: Ejemplos de buenos agrupamientos porque los datos están linealmente separados. Fuente: Elaboración propia

Estos conjuntos se consideran linealmente separables en el plano, dada la existencia de una recta tal que cada grupo incluido en el semiplano diferente, como se observa en la Figura13 a). En el conjunto ${\textstyle \mathbb {R} ^{n}}$ se dice que dos conjuntos son linealmente separables si existe un hiperplano tal que cada grupo cae en uno de los subconjuntos determinados dicho hiperplano.

Una colección de estos grupos es linealmente separable, si cada par de ellos es linealmente separable, ver Figura13 b). Esta idea se puede observar más fácilmente con diagramas de Voronoi.

4.5 Agrupamiento y Celdas de Voronoi

Si se considera el diagrama de Voronoi de los centroides de un agrupamiento, a este diagrama lo llamamos diagrama de Voronoi del agrupamiento. Se considera como ejemplo el grupo de datos siguiente, el agrupamiento de datos, el agrupamiento junto con el diagrama de Voronoi y por ultimo el diagrama de Voronoi de este agrupamiento, con respecto a sus centroides, Figura 14.

(a) Conjunto de datos.	(b) Agrupamiento de los datos	(c) Diagramas de Voronoi y el agrupamiento
(d) Diagrama de Voronoi del agrupamiento
Figura 14: Buenos agrupamientos y su diagrama de Voronoi. Fuente: Elaboración propia.

Cuando el algoritmo KMeans proporciona un mal agrupamiento, es fácil observarlo mediante los diagramas de Voronoi. Se puede observar un ejemplo de mal agrupamiento en la Figura 15 (b), que corresponde al conjunto de datos a agrupar con KMeans de la Figura 14 (a).

(a) Conjunto de datos a agrupar.	(b) Agrupamiento de los datos con KMeans.	(c) Agrupamiento de datos y diagramas de Voronoi.
Figura 15: Malos agrupamientos y su diagrama de Voronoi. Fuente: Elaboración propia.

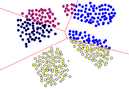
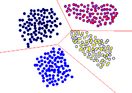
En la Figura 16 (a) se muestra el mismo conjunto de datos, pero con un buen agrupamiento con KMeans. Ver su diagrama de Voronoi en la Figura 16 (b).

(a) Conjunto de datos bien agrupados con KMeans	(b) Buen agrupamiento y su diagrama de Voronoi
Figura 16

Los grupos que produce KMeans siempre están en distintas celdas de Voronoi generadas por los centroides del agrupamiento [4]. Por lo tanto, KMeans agrupa bien cuando los grupos están en diferentes celdas de Voronoi, o bien cuando están linealmente separados dos a dos.

Otra forma de ver la separación lineal es mediante la envoltura convexa (convex hull) de los conjuntos que conforman el agrupamiento.

4.6 Agrupamiento y envoltura convexa

Es evidente observar que dos conjuntos de puntos son linealmente separables si su cascaras convexas no se intersectan. Es decir, dado un agrupamiento, se considera linealmente separable si estas envolturas de sus grupos no se intersectan dos a dos.

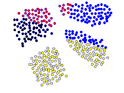
Se considera los siguientes 4 grupos y sus envolturas correspondientes. Estos grupos están linealmente separados y sus envolturas convexas no se intersectan dos a dos. Ver Figura 17

(a) Buen agrupamiento con KMeans	(b) Buen agrupamiento y su envoltura convexa
Figura 17: Ejemplo de conjunto de puntos en el plano que son linealmente separables. Fuente: Elaboración propia.

5 Algunas limitaciones

A pesar de ser utilizado ampliamente en una gama de aplicaciones, el algoritmo KMeans no está exento de limitaciones. Algunos de estos inconvenientes han sido ampliamente descritos en la literatura [5], y son los siguientes:

Número de clusters: El número de clusters tiene que ser conocido por el algoritmo en su inicialización. Por lo tanto, ${\textstyle k}$ tiene que ser un parámetro de entrada del algoritmo. Centroides iniciales: Sensibilidad a la inicialización de los centroides. Sensibilidad a outliers (ruido): La existencia de un conjunto pequeño de datos que distan mucho de las clases afecta el desempeño del algoritmo.

6 El Marco de trabajo llamado Apache Spark

El rápido aumento de usuarios de internet en los últimos años, combinado con la gran cantidad de datos que se generan, ha creado la necesidad de servicios, herramientas para proporcionar y procesar de manera confiable grandes conjuntos de datos. La computación en la nube cumple este propósito como un conjunto compartido de recursos informáticos (redes, servidores, almacenamiento, aplicaciones, servicios, etc.) que se puede alimentar e interactuar inmediatamente utilizando el concepto de computación en la nube, que permite el acceso a internet bajo demanda a la red [6].

Uno de los marcos más utilizados para aplicaciones de análisis de datos basados en la nube es Apache Spark [7,8]. Es una potente plataforma informática Hadoop de código abierto escrita en el lenguaje de programación Scala. Como Apache Spark es una infraestructura de propósito general para clústeres de computadoras, se utiliza principalmente para diversas aplicaciones. Además, el desarrollo de infraestructuras de computación en la nube ha llevado a la creación de nuevas técnicas y algoritmos para el procesamiento y análisis de datos, así como bibliotecas de aprendizaje automático destinadas a explotar su potencial [9].

Desde el punto de vista del aprendizaje automático, Apache Spark proporciona a los usuarios técnicas tradicionales, como clasificación, agrupamiento y regresión, que constituyen la llamada biblioteca MLlib [10]. Este marco de trabajo se caracteriza por altas velocidades de ejecución, paralelización de tareas y utilización de la memoria caché del sistema al implementar diferentes algoritmos.

Por lo descrito anteriormente, es de gran interés en esta investigación implantar y conocer este tipo de herramientas computacionales dada la necesidad constante de obtener información oculta en los datos y tener mayor conocimiento de algún problema en particular haciendo que los mismos datos de problema, muestren indicios o correlaciones importantes para encontrar los grupos de datos de interés.

7 Consideraciones finales

KMeans es un algoritmo heurístico que ha demostrado que tiene relación con otros métodos de agrupamiento como factorizaciones matriciales no negativas y análisis de componentes principales, por ejemplo. Este último será de especial interés en este trabajo en desarrollo.

El análisis de componentes principales (PCA) es una técnica estadística ampliamente utilizada para la reducción de dimensiones no supervisada. La agrupación de KMeans es una agrupación de datos de uso común para tareas de aprendizaje no supervisadas. Uno de los objetivos de este trabajo es mostrar que los componentes principales pueden ser una solución óptima a la inicialización de los centroides para la agrupación de KMeans, tal como lo indican diversos autores [11,12] y que es un punto inicial del cual se partirá para seguir con este trabajo..

En esta investigación se estudiará la conexión entre estos dos métodos ampliamente utilizados. Se estudiará si la reducción de dimensiones no supervisada está estrechamente relacionada con el aprendizaje no supervisado.

Por otro lado, los datos de alta dimensión a menudo se transforman en datos de menor dimensión mediante el análisis de componentes principales (PCA) (o descomposición de valores singulares), donde se pueden detectar patrones coherentes con mayor claridad. Esta reducción de dimensiones no supervisada se utiliza en áreas muy amplias como la meteorología, el procesamiento de imágenes, el análisis genómico y la recuperación de información. También es común que se utilice PCA para proyectar datos a un subespacio de dimensiones inferiores y luego se aplique KMeans en el subespacio, pero esto es un trabajo futuro en este trabajo inicial y sustentado en diversas publicaciones base para su desarrollo [11,13].

Por último se implementará una metodología basada en el cómputo en la nube. Implantando un marco de trabajo llamado Apache Spark para el trabajo con grandes cantidades de datos implantándolo en un cluster de computadoras personales y que será del tipo Beowulf para el alto desempeño de cálculo numérico. Es por eso que en este trabajo se implantará un cluster de computadoras instalando este marco de trabajo para trabajar con alta densidad de datos y poder estudiar el problema de los centróides iniciales usando la técnica de PCA dado que se espera que esta técnica proporcione centroides iniciales óptimos para realizar buenos agrupamientos con KMeans.

BIBLIOGRAFÍA

[1] Gan, Guojun and Ma, Chaoqun and Wu, Jianhong. (2007) "Data clustering: theory, algorithms, and applications", Volume 20. Society for Industrial and Applied Mathematics

[2] Elden, Lars. (2019) "Matrix Methods in Data Mining and Pattern Recognition". SIAM-Society for Industrial and Applied Mathematics, 2nd Edition

[3] Teknomo, Kardi. (2006) "K-Means Clustering Tutorial", Volume 100. Medicine 4 3

[4] Wikipedia "KMeans" http://es.wikipedia.org/wiki/K-means

[5] Pérez, J and Henriques, MF and Pazos, R and Cruz, L and Reyes, G and Salinas, J and Mexicano, A. (2007) "Mejora al algoritmo de agrupamiento K-means mediante un nuevo criterio de convergencia y su aplicación a bases de datos poblacionales de cáncer". II Taller Latino Iberoamericano de Investigación de Operaciones

[6] Rashid, Aaqib and Chaturvedi, Amit. (2019) "Cloud computing characteristics and services: a brief review", Volume 7. International Journal of Computer Sciences and Engineering 2 421–426

[7] Dritsas, Elias and Livieris, Ioannis E and Giotopoulos, Konstantinos and Theodorakopoulos, Leonidas. (2018) "An apache spark implementation for graph-based hashtag sentiment classification on twitter". Proceedings of the 22nd Pan-Hellenic Conference on Informatics 255–260

[8] Ntaliakouras, Nikolaos and Vonitsanos, Gerasimos and Kanavos, Andreas and Dritsas, Elias. (2019) "An apache spark methodology for forecasting tourism demand in greece". IEEE. 2019 10th International Conference on Information, Intelligence, Systems and Applications (IISA) 1–5

[9] Salloum, Salman and Dautov, Ruslan and Chen, Xiaojun and Peng, Patrick Xiaogang and Huang, Joshua Zhexue. (2016) "Big data analytics on Apache Spark", Volume 1. Springer. International Journal of Data Science and Analytics 145–164

[10] Meng, Xiangrui and Bradley, Joseph and Yavuz, Burak and Sparks, Evan and Venkataraman, Shivaram and Liu, Davies and Freeman, Jeremy and Tsai, DB and Amde, Manish and Owen, Sean and others. (2016) "Mllib: Machine learning in apache spark", Volume 17. JMLR. org. The journal of machine learning research 1 1235–1241

[11] Chen, Jingwei and Zhu, Jianyong and Jiang, Hongyun and Yang, Hui and Nie, Feiping. (2022) "Sparsity Fuzzy C-Means Clustering with Principal Component Analysis Embedding". IEEE. IEEE Transactions on Fuzzy Systems

[12] Lu, Shizeng and Yu, Hongliang and Wang, Xiaohong and Zhang, Qiang and Li, Fanjun and Liu, Zhao and Ning, Fangqian. (2018) "Clustering method of raw meal composition based on PCA and Kmeans". IEEE. 2018 37th Chinese control conference (CCC) 9007–9010

[13] Divya, V and Devi, K Nirmala. (2018) "An Efficient Approach to Determine Number of Clusters Using Principal Component Analysis". IEEE. 2018 International Conference on Current Trends towards Converging Technologies (ICCTCT) 1–6