(→References) |
|||
| (20 intermediate revisions by the same user not shown) | |||
| Line 7: | Line 7: | ||
==Abstract== | ==Abstract== | ||
| − | The transverse deformation of the tunnel under various loads is unavoidable with the long-term operation of the subway, and the problem of uneven settlement is gradually highlighted. A three-dimensional of tunnel lining model is established in ABAQUS to simulate the uneven settlement and transverse deformation on the safety performance, in which the deformation, internal force, and damage are further analyzed. Based on the simulation, safe settlement values for the shield tunnel with different level of existing transverse deformations (L) are suggested. Because the internal force and damage are not only related to the settlement value ( | + | The transverse deformation of the tunnel under various loads is unavoidable with the long-term operation of the subway, and the problem of uneven settlement is gradually highlighted. A three-dimensional of tunnel lining model is established in ABAQUS to simulate the uneven settlement and transverse deformation on the safety performance, in which the deformation, internal force, and damage are further analyzed. Based on the simulation, safe settlement values for the shield tunnel with different level of existing transverse deformations (<math display="inline">L</math>) are suggested. Because the internal force and damage are not only related to the settlement value (<math display="inline"> \Delta</math>) but also to the length of the tunnel where the settlement occurs, the ratio of the settlement value (<math display="inline"> \Delta</math>) to the corresponding length (<math display="inline">L</math>) of the shield tunnel <math display="inline"> \Delta /L</math> which is called the uneven settlement coefficient is proposed as an index. The uneven settlement coefficient <math display="inline"> \Delta /L</math> is given for different transverse deformations to extend the applicability of the safe settlement values, which provides theoretical support for on-site monitoring and tunnel maintenance to some extent. |
'''Keywords''': Shield tunnelling, uneven settlement, transverse deformation, recommended value of safe settlement | '''Keywords''': Shield tunnelling, uneven settlement, transverse deformation, recommended value of safe settlement | ||
| Line 25: | Line 25: | ||
According to the study by Liu et al. [8] a three-dimensional model is built in ABAQUS. The parameters of lining are shown in [[#tab-1|Table 1]]. The parameters of concrete utilized to construct the lining are shown in [[#tab-2|Table 2]]. 42 rings are built with staggered -180°assembly. In order to simplify the calculation, the joint weakening model is used, the joint width is taken as 6mm, the transverse effective rigidity ratio is taken as 0.75, so the joint elastic modulus E is 176Mpa [9]. The tunnel model is shown in [[#img-1|Figure 1]]. | According to the study by Liu et al. [8] a three-dimensional model is built in ABAQUS. The parameters of lining are shown in [[#tab-1|Table 1]]. The parameters of concrete utilized to construct the lining are shown in [[#tab-2|Table 2]]. 42 rings are built with staggered -180°assembly. In order to simplify the calculation, the joint weakening model is used, the joint width is taken as 6mm, the transverse effective rigidity ratio is taken as 0.75, so the joint elastic modulus E is 176Mpa [9]. The tunnel model is shown in [[#img-1|Figure 1]]. | ||
| − | <div class="center" style="font-size: 75%;">'''Table 1 | + | <div class="center" style="font-size: 75%;">'''Table 1'''. Parameters of lining </div> |
<div id='tab-1'></div> | <div id='tab-1'></div> | ||
| Line 39: | Line 39: | ||
| − | <div class="center" style="font-size: 75%;">'''Table 2 | + | <div class="center" style="font-size: 75%;">'''Table 2'''. Parameters of concrete</div> |
<div id='tab-2'></div> | <div id='tab-2'></div> | ||
| Line 88: | Line 88: | ||
Multiple working conditions are considered show in [[#tab-3|Table 3]] in order to analyze the internal force and deformation of shield tunnel with different transverse deformations under the influence of uneven settlement. The transverse convergence rate of the lining is the ratio of lateral convergence value to tunnel diameter, which is altered by changing the value of water and soil pressure (not exceeding the control value of the transverse convergence rate of 5‰).The transverse convergence rate of condition 1 is 0‰, which represents the new built tunnel. The transverse convergence rates of condition 2 to condition 5 are 1‰, 2‰, 3‰ and 4‰ respectively, representing the tunnel conditions in different periods. | Multiple working conditions are considered show in [[#tab-3|Table 3]] in order to analyze the internal force and deformation of shield tunnel with different transverse deformations under the influence of uneven settlement. The transverse convergence rate of the lining is the ratio of lateral convergence value to tunnel diameter, which is altered by changing the value of water and soil pressure (not exceeding the control value of the transverse convergence rate of 5‰).The transverse convergence rate of condition 1 is 0‰, which represents the new built tunnel. The transverse convergence rates of condition 2 to condition 5 are 1‰, 2‰, 3‰ and 4‰ respectively, representing the tunnel conditions in different periods. | ||
| − | <div class="center" style="font-size: 75%;">'''Table 3 | + | <div class="center" style="font-size: 75%;">'''Table 3'''. Condition information</div> |
<div id='tab-1'></div> | <div id='tab-1'></div> | ||
| Line 94: | Line 94: | ||
|-style="text-align:center" | |-style="text-align:center" | ||
! Working condition !! Transverse convergence rate | ! Working condition !! Transverse convergence rate | ||
| − | |- | + | |-style="text-align:center" |
| Condition 1 | | Condition 1 | ||
| 0‰ | | 0‰ | ||
| − | |- | + | |-style="text-align:center" |
| Condition 2 | | Condition 2 | ||
| 1‰ | | 1‰ | ||
| − | |- | + | |-style="text-align:center" |
| Condition 3 | | Condition 3 | ||
| 2‰ | | 2‰ | ||
| − | |- | + | |-style="text-align:center" |
| Condition 4 | | Condition 4 | ||
| 3‰ | | 3‰ | ||
| − | |- | + | |-style="text-align:center" |
| Condition 5 | | Condition 5 | ||
| 4‰ | | 4‰ | ||
| Line 115: | Line 115: | ||
===3.1 Transverse deformation characteristics === | ===3.1 Transverse deformation characteristics === | ||
| − | Figure 3 depicts the displacement of the model along the X direction due to uneven settlement. Only the detailed study of the tunnel along the X direction in conditions 1 and 5 are provided,due to the variation of transverse deformation in other conditions similar to 5. | + | [[#img-3|Figure 3]] depicts the displacement of the model along the X direction due to uneven settlement. Only the detailed study of the tunnel along the X direction in conditions 1 and 5 are provided,due to the variation of transverse deformation in other conditions similar to 5. |
| − | In condition 1, no water or soil pressure is supplied before uneven settlement, thus there is no transverse deformation caused before settlement. The deformation of the tunnel in the X direction under condition 1 is shown in Figure 3(a),in which the center ring of the tunnel deforms like an oval. It can be observed that there is a coupling effect between the transverse and longitudinal deformation of the shield tunnel, which means that the longitudinal deformation of the shield tunnel will affect the transverse deformation. In | + | In condition 1, no water or soil pressure is supplied before uneven settlement, thus there is no transverse deformation caused before settlement. The deformation of the tunnel in the X direction under condition 1 is shown in [[#img-3|Figure 3]](a),in which the center ring of the tunnel deforms like an oval. It can be observed that there is a coupling effect between the transverse and longitudinal deformation of the shield tunnel, which means that the longitudinal deformation of the shield tunnel will affect the transverse deformation. In Liao et al. [10] study of the tunnel under uneven settlement, when the tunnel's maximum settlement is 10 mm, the deformation of the lining ring cross-section at the center of settlement shows an elliptical shape, which is similar to the results of this numerical analysis. |
| − | The deformation of the tunnel in the X direction under condition 5 is shown in Figure 3(b). Tunnel lining transverse convergence value under water and soil load in condition 5 is 12.4 mm. After the settlement, the transverse convergence value has increased to 13.95 mm. The result shows that the longitudinal and transverse deformation of the shield tube are coupled again. | + | The deformation of the tunnel in the X direction under condition 5 is shown in [[#img-3|Figure 3]](b). Tunnel lining transverse convergence value under water and soil load in condition 5 is 12.4 mm. After the settlement, the transverse convergence value has increased to 13.95 mm. The result shows that the longitudinal and transverse deformation of the shield tube are coupled again. |
| − | <div | + | <div id='img-3'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | + | |-style="background:white;" | |
| − | + | |align="center" | | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{| | {| | ||
| + | |+ | ||
| + | |- | ||
| + | |style="text-align: center;padding:10px;"|[[Image:Review_847150402842-image5.png|406px]] | ||
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Condition 1 (transverse convergence rate 0‰) | ||
| + | |- | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_847150402842-image6.png|400px]] | ||
|- | |- | ||
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Condition 5 (transverse convergence rate 5‰ ) |
| − | | | + | |} |
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Deformation of tunnel in <math> X</math> direction | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | ===3.2 Internal force analysis === | |
| − | + | ||
| − | + | In [[#img-4|Figure 4]] the internal forces of the tunnel are shown when the settlement of the shield tunnel center reaches 20 mm under various working conditions. The value of internal forces are given in [[#tab-4|Table 4]]. Shear force is maximum in the 28th ring of the tunnel, while axial force and bending moment are maximum in the tunnel's center ring. | |
| − | + | ||
| − | + | It shows that, although there is a slight change in value, the trend of the axial force under conditions 1 and 2–5 is essentially the same in [[#img-4|Figure 4]](a) and [[#tab-4|Table 4]]. Due to the transverse deformation of the lining ring in conditions 2-5, there is a larger difference between the axial force in condition 1 and condition 2-5 which is the increment of the axial force caused by the uneven settlement. | |
| − | + | ||
| + | It shows that the trend of shear force and bending moment is essentially the same under different working conditions, with just a slight numerical change in [[#img-4|Figure 4]](b)-(c) and [[#tab-4|Table 4]]. | ||
| − | <div class=" | + | <div id='img-4'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | + | |-style="background:white;" | |
| − | {| style=" | + | |align="center" | |
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Review_847150402842-image7.png|258px]] |
| − | | | + | |style="text-align: center;padding:10px;"| [[Image:Review_847150402842-image8.png|center|276px]] |
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Axial force | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Shear force | ||
| + | |- | ||
| + | | colspan='2' style="text-align: center;padding:10px;"| [[Image:Review_847150402842-image9.png|288px]] | ||
| + | |- | ||
| + | |colspan='2' style="text-align: center;font-size: 75%;padding-bottom:10px;"|(c) Bending moment | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. Force curve of tunnel | ||
| + | |} | ||
| − | + | <div class="center" style="font-size: 75%;">'''Table 4'''. Tunnel key ring internal force value</div> | |
| − | + | ||
| + | <div id='tab-4'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! rowspan='2' | Working condition !! colspan='2' style="text-align: center;"|Tunnel center ring !! 28th Ring | ||
|- | |- | ||
| − | + | ! style="text-align: center;"|Axial force (kN) !! style="text-align: center;"|Bending moment (kN·m) !! style="text-align: center;"|Shear force (kN) | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|Condition 1 |
| − | | style=" | + | | style="text-align: center;"|4307 |
| − | | style=" | + | | style="text-align: center;"|-31750 |
| − | | style=" | + | | style="text-align: center;"|4101 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|Condition 2 |
| − | | style=" | + | | style="text-align: center;"|5033 |
| − | | style=" | + | | style="text-align: center;"|-32460 |
| − | | style=" | + | | style="text-align: center;"|4356 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|Condition 3 |
| − | | style=" | + | | style="text-align: center;"|5069 |
| − | | style=" | + | | style="text-align: center;"|-31850 |
| − | | style=" | + | | style="text-align: center;"|3907 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|Condition 4 |
| − | | style=" | + | | style="text-align: center;"|5076 |
| − | | style=" | + | | style="text-align: center;"|-31470 |
| − | | style=" | + | | style="text-align: center;"|3824 |
|- | |- | ||
| − | | style=" | + | | style="text-align: center;"|Condition 5 |
| − | | style=" | + | | style="text-align: center;"|4964 |
| − | | style=" | + | | style="text-align: center;"|-31160 |
| − | | style=" | + | | style="text-align: center;"|3819 |
|} | |} | ||
| Line 221: | Line 217: | ||
===4.1 Lining damage analysis === | ===4.1 Lining damage analysis === | ||
| − | The occurrence and development of damage in lining rings caused by uneven settlement under varied working conditions is shown in Table 5. The cross section shown in the table is the central section of the shield tunnellining (20th and 21st lining rings). | + | The occurrence and development of damage in lining rings caused by uneven settlement under varied working conditions is shown in [[#tab-5|Table 5]]. The cross section shown in the table is the central section of the shield tunnellining (20th and 21st lining rings). |
| − | It can be seen that in condition 1 the arch bottom displays tensile damage when the uneven settlement reaches 8. | + | It can be seen that in condition 1 the arch bottom displays tensile damage when the uneven settlement reaches 8.56mm; the damage range significantly expands, and a significant portion of the arch bottom is damaged when settlement is 9.27mm; the damage range expands toward the arch waist, and the damage area fills the lower half of the ring when settlement is 11.15mm. In condition 2, after the uneven settlement is applied, tension damage develops at the base of the lining when the uneven settlement reaches 7.84mm. The uneven settlement when damage occurs is less than condition 1, because the shield tunnel has already experienced transverse deformation and damage to the bottom of the liner ring before uneven settlement is applied. The damage develops towards the right arch waist of the liner ring when the settlement reaches 8.90mm; the damage expands towards the arch waist, gradually increasing at the bottom of the arch when the settlement value continues to increase. The reason for this is the increase in the transverse convergence value of the lining ring due to uneven settlement. |
In conditions 3-5, after the application of uneven settlement, the development pattern of the damage is basically the same as in condition 2. | In conditions 3-5, after the application of uneven settlement, the development pattern of the damage is basically the same as in condition 2. | ||
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 5'''. Damage development diagram of tunnel lining under different working conditions</div> |
| − | + | ||
| − | {| style=" | + | <div id='tab-5'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! !! Any injury !! Primary development !! Stability phase !! Final development | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;"|Damage diagram |
| − | | | + | | colspan='4' style="text-align: center;vertical-align: center;padding-top:10px;padding-bottom:10px;"| Condition 1 (transverse convergence rate 0‰)<br> [[Image:Review_847150402842-image10.png|396px]] |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;"|Corresponding settlement (mm) |
| − | | | + | | style="text-align: center;"|8.56 |
| − | + | | style="text-align: center;"|9.27 | |
| − | + | | style="text-align: center;"|11.15 | |
| + | | style="text-align: center;"|20 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;"|Damage diagram |
| − | | | + | | colspan='4' style="text-align: center;vertical-align: center;padding-top:10px;padding-bottom:10px;"| Condition 2 (transverse convergence rate 1‰) <br> [[Image:Review_847150402842-image11.png|396px]] |
| − | + | ||
| − | + | ||
| − | | | + | |
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;"|Settlement value (mm) |
| − | | | + | | style="text-align: center;"|7.84 |
| − | + | | style="text-align: center;"|8.90 | |
| − | + | | style="text-align: center;"|12.14 | |
| + | | style="text-align: center;"|20 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;padding-top:10px;padding-bottom:10px;"|Damage diagram |
| − | + | | colspan='4' style="text-align: center;vertical-align: center;"| Condition 3 (transverse convergence rate 2‰)<br> [[Image:Review_847150402842-image12.png|396px]] | |
| − | | | + | |
| − | + | ||
| − | | | + | |
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;"|Settlement value (mm) |
| − | | | + | | style="text-align: center;"|7.61 |
| − | + | | style="text-align: center;"|8.95 | |
| − | + | | style="text-align: center;"|12.08 | |
| + | | style="text-align: center;"|20 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;"|Damage diagram |
| − | | style=" | + | | colspan='4' style="text-align: center;vertical-align: center;padding-top:10px;padding-bottom:10px;"|Condition 4 (transverse convergence rate 3‰)<br> [[Image:Review_847150402842-image13.png|396px]] |
| − | + | ||
| − | + | ||
| − | | | + | |
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;"|Settlement value (mm) |
| − | | | + | | style="text-align: center;"|6.39 |
| − | + | | style="text-align: center;"|8.57 | |
| − | + | | style="text-align: center;"|11.89 | |
| + | | style="text-align: center;"|20 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;"|Damage diagram |
| − | | | + | | colspan='4' style="text-align: center;vertical-align: center;padding-top:10px;padding-bottom:10px;"| Condition 5 (transverse convergence rate 4‰) <br> [[Image:Review_847150402842-image14.png|396px]] |
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: left;vertical-align: center;"|Settlement value (mm) |
| − | | | + | | style="text-align: center;"|4.58 |
| − | + | | style="text-align: center;"|8.92 | |
| − | + | | style="text-align: center;"|12.56 | |
| − | + | | style="text-align: center;"|20 | |
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|} | |} | ||
| Line 303: | Line 281: | ||
Based on the above analysis, under the action of uneven settlement displacement load, the greater the transverse convergence rate of the shield tunnel, the smaller the settlement corresponding to the tensile damage of lining, the slower the development of damage, but the more lining rings damaged due to settlement. | Based on the above analysis, under the action of uneven settlement displacement load, the greater the transverse convergence rate of the shield tunnel, the smaller the settlement corresponding to the tensile damage of lining, the slower the development of damage, but the more lining rings damaged due to settlement. | ||
| − | ==4.2 Recommended settlement value == | + | ===4.2 Recommended settlement value=== |
| − | Combined with the analysis of the damage in the shield tunnel under the action of uneven settlement, the settlement corresponding to the damage of the center ring is approximated as the recommended value of the safety settlement of the tunnel. For shield tunnels with different transverse deformations during operation, the recommended safe settlement value of the tunnel when the monitoring distance is 24 m is given, as shown in Table 6. | + | Combined with the analysis of the damage in the shield tunnel under the action of uneven settlement, the settlement corresponding to the damage of the center ring is approximated as the recommended value of the safety settlement of the tunnel. For shield tunnels with different transverse deformations during operation, the recommended safe settlement value of the tunnel when the monitoring distance is 24 m is given, as shown in [[#tab-6|Table 6]]. |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 6'''. Recommended settlement safety values for different transverse deformation</div> |
| − | + | ||
| − | {| style=" | + | <div id='tab-6'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | + | |-style="text-align:center" | |
| − | | | + | ! Transverse convergence rate !! Settlement value (mm) |
| − | + | |-style="text-align:center" | |
| − | | | + | | 0‰ |
| − | | | + | | 8.5 |
| − | |- | + | |-style="text-align:center" |
| − | + | | 1‰ | |
| − | | | + | | 8.0 |
| − | |- | + | |-style="text-align:center" |
| − | + | | 2‰ | |
| − | | | + | | 7.5 |
| − | |- | + | |-style="text-align:center" |
| − | + | | 3‰ | |
| − | | | + | | 6.5 |
| − | |- | + | |-style="text-align:center" |
| − | + | | 4‰ | |
| − | | | + | | 4.5 |
|} | |} | ||
| Line 336: | Line 313: | ||
==5. Effect of uneven settlement of shield tunnel on the mechanical properties == | ==5. Effect of uneven settlement of shield tunnel on the mechanical properties == | ||
| − | The settlement is a key factor affecting the mechanical behavior of the tunnel. The ratio of the maximum settlement value ( | + | The settlement is a key factor affecting the mechanical behavior of the tunnel. The ratio of the maximum settlement value (<math display="inline"> \Delta</math>) to the length of the shield tunnel (<math display="inline">L</math>) where the settlement occurs <math display="inline"> \Delta /L</math> is used to express the non-uniformity of the settlement. The degree of tunnel settlement non-uniformity varies with the value of <math display="inline"> \Delta /L</math>. By changing <math display="inline"> \Delta /L</math>, the influence of uneven settlement on the safety performance of shield tunnel is analyzed, and further, the safety settlement values corresponding to different monitoring distance are given. |
===5.1 Condition information=== | ===5.1 Condition information=== | ||
| − | Taking the transverse convergence rate of 1‰ as an example, the maximum settlement of conditions 1, 2 and 3 is 20 mm when the number of lining rings is 36, 42 and 48 respectively, and the maximum settlement of conditions 4 and 5 is 25 and 15 mm when the number of lining rings is 42. The settlement control range L is the tunnel length corresponding to the settlement difference | + | Taking the transverse convergence rate of 1‰ as an example, the maximum settlement of conditions 1, 2 and 3 is 20 mm when the number of lining rings is 36, 42 and 48 respectively, and the maximum settlement of conditions 4 and 5 is 25 and 15 mm when the number of lining rings is 42. The settlement control range <math display="inline">L</math> is the tunnel length corresponding to the settlement difference <math display="inline"> \Delta</math>. The specific working condition information is shown in [[#tab-7|Table 7]], and other parameters are the same as before. |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 7'''. Condition information</div> |
| − | + | ||
| − | {| style=" | + | <div id='tab-7'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | + | |-style="text-align:center" | |
| − | | | + | ! Working condition !! Transverse convergence rate !! Number of lining rings !! Settlement control range L (m) !! Settlement value <math display="inline"> \Delta</math> (mm) !! Uneven settlement coefficient <math display="inline"> \Delta /L</math> |
| − | + | |-style="text-align:center" | |
| − | + | | Condition 1 | |
| − | + | | 1‰ | |
| − | + | | 36 | |
| − | |- | + | | 20.4 |
| − | + | | 20 | |
| − | | | + | | 0.9804 |
| − | | | + | |-style="text-align:center" |
| − | | | + | | Condition 2 |
| − | | | + | | 1‰ |
| − | | | + | | 42 |
| − | |- | + | | 24 |
| − | + | | 20 | |
| − | | | + | | 0.8333 |
| − | | | + | |-style="text-align:center" |
| − | | | + | | Condition 3 |
| − | | | + | | 1‰ |
| − | | | + | | 48 |
| − | |- | + | | 27.6 |
| − | + | | 20 | |
| − | | | + | | 0.7246 |
| − | | | + | |-style="text-align:center" |
| − | | | + | | Condition 4 |
| − | | | + | | 1‰ |
| − | | | + | | 42 |
| − | |- | + | | 24 |
| − | + | | 25 | |
| − | | | + | | 1.0417 |
| − | | | + | |-style="text-align:center" |
| − | | | + | | Condition 5 |
| − | | | + | | 1‰ |
| − | | | + | | 42 |
| − | |- | + | | 24 |
| − | + | | 15 | |
| − | | | + | | 0.6250 |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
|} | |} | ||
| Line 393: | Line 365: | ||
===5.2 Internal force analysis === | ===5.2 Internal force analysis === | ||
| − | The axial force, shear force and bending moment of the five working conditions are shown in Figure 5. Obviously, the axial forces are very different for the five conditions. The axial forces are smallest in condition 5, whose uneven settlement coefficient | + | The axial force, shear force and bending moment of the five working conditions are shown in [[#img-5|Figure 5]]. Obviously, the axial forces are very different for the five conditions. The axial forces are smallest in condition 5, whose uneven settlement coefficient <math display="inline"> \Delta /L</math> is 0.6250. The largest axial forces are in condition 4, whose uneven settlement coefficient <math display="inline"> \Delta /L</math> is 1.0417. The axial forces increase with the increase of uneven settlement coefficient <math display="inline"> \Delta /L</math>. It can be seen from [[#img-5|Figure 5]](b)-(c) that the varying of shear force and bending moment with <math display="inline"> \Delta /L</math> is similar to that of axial force. |
| − | <div class=" | + | <div id='img-5'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | + | |-style="background:white;" | |
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
| + | |- | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_847150402842-image15.png|308px]] | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_847150402842-image16.png|center|302px]] | ||
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Axial force | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Shear force | ||
| + | |- | ||
| + | | colspan='2' style="text-align: center;padding:10px;"| [[Image:Review_847150402842-image17-c.png|326px]] | ||
| + | |- | ||
| + | |colspan='2' style="text-align: center;font-size: 75%;padding-bottom:10px;"|(c) Bending moment | ||
| + | |} | ||
|- | |- | ||
| − | | | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. Internal force varying along the axis of tunnelling |
| − | + | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | < | + | The magnitude of the internal force of the tunnel under each working condition increases with the increase of <math display="inline"> \Delta /L</math>. In order to further study the relationship between the ∆/L and the internal forces, the bending moment is used as the object. |
| − | < | + | |
| − | < | + | The <math display="inline"> \Delta /L</math> value of uneven settlement and the maximum bending moment value at center lining ring in five different working conditions are compared. In condition 1, the <math display="inline"> \Delta /L</math> is 0.9804, and the maximum bending moment corresponding to the central ring is −36400 kN∙m. In condition 2, the ∆/L is 0.8333, and the maximum bending moment is -30800 kN·m. In condition 3, <math display="inline"> \Delta /L</math> is 0.7246, and the maximum bending moment is − 28000 kN·m. In condition 4, the <math display="inline"> \Delta /L</math> is 1.0417, and the maximum bending moment is -37,000 kN·m. In condition 5, the uneven settlement <math display="inline"> \Delta /L</math> is 0.6250, and the maximum bending moment is -25400kN·m. It is shown in [[#tab-8|Table 8]] and [[#img-6|Figure 6]]. It can be seen that the relationship between uneven settlement <math display="inline"> \Delta /L</math> and maximum bending moment is approximately linear. |
| − | < | + | |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 8'''. Central ring bending moment information</div> |
| − | + | ||
| + | <div id='tab-8'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! Working condition !! Uneven settlement coefficient <math display="inline"> \Delta /L</math> !! Bending moment(kN·m) | ||
| + | |-style="text-align:center" | ||
| + | | Condition 1 | ||
| + | | 0.9804 | ||
| + | | -36400 | ||
| + | |-style="text-align:center" | ||
| + | | Condition 2 | ||
| + | | 0.8333 | ||
| + | | -30800 | ||
| + | |-style="text-align:center" | ||
| + | | Condition 3 | ||
| + | | 0.7246 | ||
| + | | -28000 | ||
| + | |-style="text-align:center" | ||
| + | | Condition 4 | ||
| + | | 1.0417 | ||
| + | | -37000 | ||
| + | |-style="text-align:center" | ||
| + | | Condition 5 | ||
| + | | 0.6250 | ||
| + | | -25400 | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | <div | + | <div id='img-6'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | + | |-style="background:white;" | |
| − | {| style=" | + | |style="text-align: center;padding:10px;"| [[Image:Review_847150402842-image18.png|400px]] |
| − | + | ||
| − | + | ||
| − | | | + | |
| − | | | + | |
|- | |- | ||
| − | | | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 6'''. Relationship between uneven settlement coefficient <math display="inline"> \Delta /L</math> and bending moment |
| − | | | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | < | + | By analyzing and comparing the internal forces of the five working conditions, it is found that the value of the <math display="inline"> \Delta /L</math> directly affects the internal forces of the tunnel. The larger the <math display="inline"> \Delta /L</math> is, the greater the internal forces of the tunnel are. Therefore, the value of <math display="inline"> \Delta /L</math> is taken as the key index. The recommended value of uneven settlement coefficient <math display="inline"> \Delta /L</math> under each transverse convergence rate is further analyzed and summarized in next section, which provides intuitive theoretical support for tunnel health monitoring. |
| − | < | + | |
| − | + | ===5.3 Recommended value of uneven settlement coefficient=== | |
| − | + | ||
| − | + | According to the analysis results of five different working conditions with a transverse convergence rate of 1 ‰ in Section 5.2, it can be seen that the uneven settlement coefficient <math display="inline"> \Delta /L</math> is directly related to the internal forces of the shield tunnel, so the damage is also related to it. Based on the recommended settlement value of 24 m monitoring distance under different transverse convergence rates in Section 4.2, the recommended value of uneven settlement coefficient <math display="inline"> \Delta /L</math> under different transverse convergence rates is given in [[#tab-9|Table 9]], which can provide the safety settlement value applicable to different monitoring distances. | |
| − | == | + | <div class="center" style="font-size: 75%;">'''Table 9'''. Recommended value of uneven settlement coefficient</div> |
| − | + | <div id='tab-9'></div> | |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | <div | + | |-style="text-align:center" |
| − | + | ! Transverse convergence rate !! Settlement value <math display="inline"> \Delta</math> (mm) !! Settlement control range <math display="inline">L</math> (m) !! Uneven settlement coefficient [<math display="inline"> \Delta /L</math>] | |
| − | + | |-style="text-align:center" | |
| − | {| style=" | + | | 0‰D |
| − | + | | 8.5 | |
| − | + | | 24 | |
| − | + | | 0.3542 | |
| − | + | |-style="text-align:center" | |
| − | + | | 1‰D | |
| − | |- | + | | 8.0 |
| − | + | | 24 | |
| − | | | + | | 0.3333 |
| − | | | + | |-style="text-align:center" |
| − | | | + | | 2‰D |
| − | |- | + | | 7.5 |
| − | + | | 24 | |
| − | | | + | | 0.3125 |
| − | | | + | |-style="text-align:center" |
| − | | | + | | 3‰D |
| − | |- | + | | 6.5 |
| − | + | | 24 | |
| − | | | + | | 0.2708 |
| − | | | + | |-style="text-align:center" |
| − | | | + | | 4‰D |
| − | |- | + | | 4.5 |
| − | + | | 24 | |
| − | | | + | | 0.1875 |
| − | | | + | |
| − | | | + | |
| − | |- | + | |
| − | + | ||
| − | | | + | |
| − | | | + | |
| − | | | + | |
|} | |} | ||
| − | The uneven settlement coefficient ∆/L under five different transverse convergence rates of 0‰D, 1‰D, 2‰D, 3‰D and 4‰D are 0.3542,0.3333,0.3125,0.2708 and 0.1875, respectively. According to Table 9, the damage to the tunnel lining can be preliminarily judged or the spacing of monitoring points can be reasonably arranged according to recommended value | + | The uneven settlement coefficient ∆/L under five different transverse convergence rates of 0‰D, 1‰D, 2‰D, 3‰D and 4‰D are 0.3542,0.3333,0.3125,0.2708 and 0.1875, respectively. According to [[#tab-9|Table 9]], the damage to the tunnel lining can be preliminarily judged or the spacing of monitoring points can be reasonably arranged according to recommended value [<math display="inline"> \Delta /L</math>]. |
| − | ==6. | + | ==6. Conclusions == |
| − | A three-dimensional numerical model is established to study the mechanical behavior of tunnel lining when uneven settlement occurs under different transverse deformations of lining. The uneven settlement coefficient ∆/L is proposed as an index to reflect the mechanical properties of the tunnel. Based on the analysis, the following conclusions are drawn : | + | A three-dimensional numerical model is established to study the mechanical behavior of tunnel lining when uneven settlement occurs under different transverse deformations of lining. The uneven settlement coefficient ∆/L is proposed as an index to reflect the mechanical properties of the tunnel. Based on the analysis, the following conclusions are drawn: |
(1) The transverse and longitudinal deformation of the shield tunnel are coupled. The uneven settlement displacement of the tunnel will cause the transverse deformation of the lining ring to a certain extent. The transverse deformation of the lining has little effect on the force characteristics of the tunnel, and the settlement is the main factor affecting the force characteristics of the tunnel. | (1) The transverse and longitudinal deformation of the shield tunnel are coupled. The uneven settlement displacement of the tunnel will cause the transverse deformation of the lining ring to a certain extent. The transverse deformation of the lining has little effect on the force characteristics of the tunnel, and the settlement is the main factor affecting the force characteristics of the tunnel. | ||
| Line 519: | Line 489: | ||
==References== | ==References== | ||
| − | + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | |
| − | [1] Han B.M., Li Y.W., Lu F., Yang Z.X., Yang R.X., Chen Y.X., Sun Y.J., XI Z., Wang L.Y., Dai Y.J. Statistical | + | [1] Han B.M., Li Y.W., Lu F., Yang Z.X., Yang R.X., Chen Y.X., Sun Y.J., XI Z., Wang L.Y., Dai Y.J. Statistical analysis of urban rail transit operations in the world in 2021: A Review (in Chinese). Urban Rapid Rail Transit, 35:5-11, 2022. |
[2] Lin Y.G., Liao S.M., Lin G.B. A discussion of the factors effecting on longitudinal deformation of subway tunnel. Undergr. Space, 20:264-267, 2000. | [2] Lin Y.G., Liao S.M., Lin G.B. A discussion of the factors effecting on longitudinal deformation of subway tunnel. Undergr. Space, 20:264-267, 2000. | ||
| − | [3] Wei K., Gong Q.M., Zhou S.H. Ant | + | [3] Wei K., Gong Q.M., Zhou S.H. Ant colony algorithms of long-term uneven settlement prediction in tunne. Journal of Tongji University(Natural Science), 37:993-998, 2009. |
[4] Tan W.L., Pathegama R.G. Parameters and considerations in soft ground tunneling. Electronic Journal of Geotechnical Engineering, 8:1-17, 2003. | [4] Tan W.L., Pathegama R.G. Parameters and considerations in soft ground tunneling. Electronic Journal of Geotechnical Engineering, 8:1-17, 2003. | ||
| − | [5] Zheng Y.L., Han W.X., Tong Q.H., Yang L.F., Pan J. Study on longitudinal crack of shield tunnel segment joint due to asymmetric settlement in soft soil (in Chinese). Chinese | + | [5] Zheng Y.L., Han W.X., Tong Q.H., Yang L.F., Pan J. Study on longitudinal crack of shield tunnel segment joint due to asymmetric settlement in soft soil (in Chinese). Chinese Journal of Rock Mechanics and Engineering, 24(24):4552-4558, 2005. |
| − | [6]Ye Y.D., Zhu H.H., Wang R.L. Analysis on the current status of metro operating tunnel damage in soft ground and its causes (in Chinese). Chinese | + | [6]Ye Y.D., Zhu H.H., Wang R.L. Analysis on the current status of metro operating tunnel damage in soft ground and its causes (in Chinese). Chinese Journal of Underground Space and Engineering, 3:157-160, 2007. |
| − | [7] Wang R.L. Factors influencing deformation of Shanghai soft soil metro tunnel and deformation analysis (in Chinese). Underground | + | [7] Wang R.L. Factors influencing deformation of Shanghai soft soil metro tunnel and deformation analysis (in Chinese). Underground Engineering and Tunnels, 1:1-6, 2009. |
[8] Liu X., Dong Z.B., Bai Y., Zhu Y.H. Investigation of the structural effect induced by stagger joints in segmental tunnel linings: First results from full-scale ring tests. Tunn. Undergr. Space Tech., 66:1-18, 2017. | [8] Liu X., Dong Z.B., Bai Y., Zhu Y.H. Investigation of the structural effect induced by stagger joints in segmental tunnel linings: First results from full-scale ring tests. Tunn. Undergr. Space Tech., 66:1-18, 2017. | ||
| − | [9] Xiao Z.R., Wang J.C. A | + | [9] Xiao Z.R., Wang J.C. A three-dimensional model of shield tunnel considering tnteraction of soil and lining. Math. Probl. Eng., 2022, 4245384, 2022. |
[10] Liao S.M., Peng F.L., Shen S.L. Analysis of shearing effect on tunnel induced by load transfer along longitudinal direction. Tunn. Undergr. Space Tech., 23:421-430, 2008, | [10] Liao S.M., Peng F.L., Shen S.L. Analysis of shearing effect on tunnel induced by load transfer along longitudinal direction. Tunn. Undergr. Space Tech., 23:421-430, 2008, | ||
Latest revision as of 09:12, 11 October 2023
Abstract
The transverse deformation of the tunnel under various loads is unavoidable with the long-term operation of the subway, and the problem of uneven settlement is gradually highlighted. A three-dimensional of tunnel lining model is established in ABAQUS to simulate the uneven settlement and transverse deformation on the safety performance, in which the deformation, internal force, and damage are further analyzed. Based on the simulation, safe settlement values for the shield tunnel with different level of existing transverse deformations () are suggested. Because the internal force and damage are not only related to the settlement value () but also to the length of the tunnel where the settlement occurs, the ratio of the settlement value () to the corresponding length () of the shield tunnel which is called the uneven settlement coefficient is proposed as an index. The uneven settlement coefficient is given for different transverse deformations to extend the applicability of the safe settlement values, which provides theoretical support for on-site monitoring and tunnel maintenance to some extent.
Keywords: Shield tunnelling, uneven settlement, transverse deformation, recommended value of safe settlement
1. Introduction
Due to its quick, safe, and effective qualities, urban rail transportation has grown to be a significant part of urban traffic. By the end of 2021, the total mileage of urban rail transit operation in the world is about 3685420 km, and the total mileage of urban rail transit operation in China has reached about 9724 km, accounting for 26.4 % of the total mileage in the world, and ranking first in the world [1]. With the operation of the subway, the problem of uneven settlement in the shield tunnel has gradually become prominent.
The issue of the shield tunnel's uneven settlement has been extensively researched. Lin et al. [2] conclude that the disturbance of the soil during the construction period, the settlement of the soil lying under the tunnel, the change of the load around the tunnel, the vibration of the subway during operation, and the earthquake are all causes of the uneven settlement based on the analysis of the factors affecting the settlement of the cross-river highway tunnel in Shanghai. Wei et al. [3] propose a model based on ant colony algorithm to predict the long-term uneven settlement of tunnel according to a large number of measured settlement data during the operation of shield tunnel in Shanghai. In addition to describe the development law of longitudinal and transverse deformation, Tan and Pathegama [4] provide an empirical formula for the longitudinal surface settlement along the axis of tunnel. In the studyof uneven settlement on joint ring seam cracking in a soft soil location, Zheng et al. [5] establish the relationship between the longitudinal deformation curvature of the tunnel and the opening of joint ring seam.
There is no detailed and systematic analysis of the influence of uneven settlement on shield tunnel with the existing transverse deformation, which is not uncommon in practice. For instance, the Shanghai Metro Line 1 has been discovered that the maximum settlement exceeds 80 mm and settlement has no stable trend during 20-times monitoring since 1995. Moreover, it is discovered from the monitoring results of 46 rings that 85% of the rings have transverse convergence greater than the permitted value, which is 5‰ of the diameter [6], indicating that the transverse and longitudinal deformation of shield tunnel usually occur simultaneously. Wang [7] also finds that there is mutual influence between transverse and longitudinal deformation through monitoring results.
Therefore, a three-dimensional model of shield tunnel is established in this paper to conduct a comprehensive analysis of the influence of uneven settlement on the mechanical performance of shield tunnel with existing transverse deformation. Based on the analysis, the safe settlement value of the tunnel is obtained in order to provide certain guidance for tunnel monitoring and maintenance.
2. Shield tunnel model
According to the study by Liu et al. [8] a three-dimensional model is built in ABAQUS. The parameters of lining are shown in Table 1. The parameters of concrete utilized to construct the lining are shown in Table 2. 42 rings are built with staggered -180°assembly. In order to simplify the calculation, the joint weakening model is used, the joint width is taken as 6mm, the transverse effective rigidity ratio is taken as 0.75, so the joint elastic modulus E is 176Mpa [9]. The tunnel model is shown in Figure 1.
| Outer diameter (mm) | Inside diameter (mm) | Ring width (mm) | Thickness (mm) |
|---|---|---|---|
| 6200 | 5500 | 1200 | 350 |
| Concrete grade | Density (kg/m3) | Elastic modulus (MPa) | Poisson’s ratio | Expansion angle | Eccentric ratio |
|---|---|---|---|---|---|
| C50 | 2500 | 34500 | 0.2 | 30° | 0.1 |

|
| Figure 1. Tunnel model diagram |
As illustrated in Figure 2, two phases are built up in the simulation calculation to represent the impact of uneven settling. Firstly, apply soil pressure to the tunnel, which leads elliptical deformation. This step is used to imitate the existing transverse deformation. Then, the uneven displacement is applied along the tunnel's longitudinal direction until the settlement value of the middle ring (the 20th ring lining) achieves 20 mm.
| ||||
| Figure 2. Load flow chart |
Multiple working conditions are considered show in Table 3 in order to analyze the internal force and deformation of shield tunnel with different transverse deformations under the influence of uneven settlement. The transverse convergence rate of the lining is the ratio of lateral convergence value to tunnel diameter, which is altered by changing the value of water and soil pressure (not exceeding the control value of the transverse convergence rate of 5‰).The transverse convergence rate of condition 1 is 0‰, which represents the new built tunnel. The transverse convergence rates of condition 2 to condition 5 are 1‰, 2‰, 3‰ and 4‰ respectively, representing the tunnel conditions in different periods.
| Working condition | Transverse convergence rate |
|---|---|
| Condition 1 | 0‰ |
| Condition 2 | 1‰ |
| Condition 3 | 2‰ |
| Condition 4 | 3‰ |
| Condition 5 | 4‰ |
3. Shield tunnel deformation and internal force analysis
3.1 Transverse deformation characteristics
Figure 3 depicts the displacement of the model along the X direction due to uneven settlement. Only the detailed study of the tunnel along the X direction in conditions 1 and 5 are provided,due to the variation of transverse deformation in other conditions similar to 5.
In condition 1, no water or soil pressure is supplied before uneven settlement, thus there is no transverse deformation caused before settlement. The deformation of the tunnel in the X direction under condition 1 is shown in Figure 3(a),in which the center ring of the tunnel deforms like an oval. It can be observed that there is a coupling effect between the transverse and longitudinal deformation of the shield tunnel, which means that the longitudinal deformation of the shield tunnel will affect the transverse deformation. In Liao et al. [10] study of the tunnel under uneven settlement, when the tunnel's maximum settlement is 10 mm, the deformation of the lining ring cross-section at the center of settlement shows an elliptical shape, which is similar to the results of this numerical analysis.
The deformation of the tunnel in the X direction under condition 5 is shown in Figure 3(b). Tunnel lining transverse convergence value under water and soil load in condition 5 is 12.4 mm. After the settlement, the transverse convergence value has increased to 13.95 mm. The result shows that the longitudinal and transverse deformation of the shield tube are coupled again.
| ||||
| Figure 3. Deformation of tunnel in direction |
3.2 Internal force analysis
In Figure 4 the internal forces of the tunnel are shown when the settlement of the shield tunnel center reaches 20 mm under various working conditions. The value of internal forces are given in Table 4. Shear force is maximum in the 28th ring of the tunnel, while axial force and bending moment are maximum in the tunnel's center ring.
It shows that, although there is a slight change in value, the trend of the axial force under conditions 1 and 2–5 is essentially the same in Figure 4(a) and Table 4. Due to the transverse deformation of the lining ring in conditions 2-5, there is a larger difference between the axial force in condition 1 and condition 2-5 which is the increment of the axial force caused by the uneven settlement.
It shows that the trend of shear force and bending moment is essentially the same under different working conditions, with just a slight numerical change in Figure 4(b)-(c) and Table 4.
| ||||||||
| Figure 4. Force curve of tunnel | ||||||||
| Working condition | Tunnel center ring | 28th Ring | |
|---|---|---|---|
| Axial force (kN) | Bending moment (kN·m) | Shear force (kN) | |
| Condition 1 | 4307 | -31750 | 4101 |
| Condition 2 | 5033 | -32460 | 4356 |
| Condition 3 | 5069 | -31850 | 3907 |
| Condition 4 | 5076 | -31470 | 3824 |
| Condition 5 | 4964 | -31160 | 3819 |
It can be seen that the transverse deformation of the lining has a certain influence on the axial force and very little influence on the shear force and bending moment. The force characteristics of the tunnel are primarily influenced by settlement deformation.
The center ring will be analyzed when examining the safety of the tunnel because it is where the largest bending moment and the maximum settlement are located. On the basis of the damage analysis of the ring, the suggested values for safe settlement are presented in the next section.
4. Analysis of shield tunnel damage and safe settlement values
It is known from 3.1 that the coupling effect between transverse and longitudinal deformation will exacerbate the damage to the shield tunnel lining. Therefore, the recommended value of safe settlement is given according to the damage caused by uneven settlement applied to the lining at different transverse convergence rates. It can provide a theoretical basis for uneven settlement monitoring.
4.1 Lining damage analysis
The occurrence and development of damage in lining rings caused by uneven settlement under varied working conditions is shown in Table 5. The cross section shown in the table is the central section of the shield tunnellining (20th and 21st lining rings).
It can be seen that in condition 1 the arch bottom displays tensile damage when the uneven settlement reaches 8.56mm; the damage range significantly expands, and a significant portion of the arch bottom is damaged when settlement is 9.27mm; the damage range expands toward the arch waist, and the damage area fills the lower half of the ring when settlement is 11.15mm. In condition 2, after the uneven settlement is applied, tension damage develops at the base of the lining when the uneven settlement reaches 7.84mm. The uneven settlement when damage occurs is less than condition 1, because the shield tunnel has already experienced transverse deformation and damage to the bottom of the liner ring before uneven settlement is applied. The damage develops towards the right arch waist of the liner ring when the settlement reaches 8.90mm; the damage expands towards the arch waist, gradually increasing at the bottom of the arch when the settlement value continues to increase. The reason for this is the increase in the transverse convergence value of the lining ring due to uneven settlement.
In conditions 3-5, after the application of uneven settlement, the development pattern of the damage is basically the same as in condition 2.
The settlement of tunnel damage caused by uneven settlement under different working conditions is different. The settlement corresponding to the damage in conditions 1-5 is 8.56 mm, 7.84 mm, 7.61 mm, 6.39 mm and 4.58 mm, respectively. With the increase in the transverse convergence rate, the settlement value corresponding to the damage occurring decreases.
Based on the above analysis, under the action of uneven settlement displacement load, the greater the transverse convergence rate of the shield tunnel, the smaller the settlement corresponding to the tensile damage of lining, the slower the development of damage, but the more lining rings damaged due to settlement.
4.2 Recommended settlement value
Combined with the analysis of the damage in the shield tunnel under the action of uneven settlement, the settlement corresponding to the damage of the center ring is approximated as the recommended value of the safety settlement of the tunnel. For shield tunnels with different transverse deformations during operation, the recommended safe settlement value of the tunnel when the monitoring distance is 24 m is given, as shown in Table 6.
| Transverse convergence rate | Settlement value (mm) |
|---|---|
| 0‰ | 8.5 |
| 1‰ | 8.0 |
| 2‰ | 7.5 |
| 3‰ | 6.5 |
| 4‰ | 4.5 |
For the tunnel with the transverse deformation of the lining ring less than 1‰D (1‰ of the diameter), when the settlement value is within 8mm, the transverse deformation and settlement are within the safety control value, and the tunnel is in normal working condition. When the settlement value exceeds 8.0mm, the maximum settlement of lining ring should be tested for concrete damage to avoid continued expansion of the damage. For the tunnel with the transverse deformation of the lining ring reaching 2‰D, the transverse deformation has reached the control value, which should be reinforced, and it is also necessary to prevent the uneven settlement of the lining ring more than 7.5 mm because the combined action of settlement and transverse deformation will lead to the aggravation of lining concrete damage. For tunnels with transverse convergence values of 3‰D and 4‰D, the development of transverse deformation and the occurrence of uneven settlement should also be controlled in time.
5. Effect of uneven settlement of shield tunnel on the mechanical properties
The settlement is a key factor affecting the mechanical behavior of the tunnel. The ratio of the maximum settlement value () to the length of the shield tunnel () where the settlement occurs is used to express the non-uniformity of the settlement. The degree of tunnel settlement non-uniformity varies with the value of . By changing , the influence of uneven settlement on the safety performance of shield tunnel is analyzed, and further, the safety settlement values corresponding to different monitoring distance are given.
5.1 Condition information
Taking the transverse convergence rate of 1‰ as an example, the maximum settlement of conditions 1, 2 and 3 is 20 mm when the number of lining rings is 36, 42 and 48 respectively, and the maximum settlement of conditions 4 and 5 is 25 and 15 mm when the number of lining rings is 42. The settlement control range is the tunnel length corresponding to the settlement difference . The specific working condition information is shown in Table 7, and other parameters are the same as before.
| Working condition | Transverse convergence rate | Number of lining rings | Settlement control range L (m) | Settlement value (mm) | Uneven settlement coefficient |
|---|---|---|---|---|---|
| Condition 1 | 1‰ | 36 | 20.4 | 20 | 0.9804 |
| Condition 2 | 1‰ | 42 | 24 | 20 | 0.8333 |
| Condition 3 | 1‰ | 48 | 27.6 | 20 | 0.7246 |
| Condition 4 | 1‰ | 42 | 24 | 25 | 1.0417 |
| Condition 5 | 1‰ | 42 | 24 | 15 | 0.6250 |
5.2 Internal force analysis
The axial force, shear force and bending moment of the five working conditions are shown in Figure 5. Obviously, the axial forces are very different for the five conditions. The axial forces are smallest in condition 5, whose uneven settlement coefficient is 0.6250. The largest axial forces are in condition 4, whose uneven settlement coefficient is 1.0417. The axial forces increase with the increase of uneven settlement coefficient . It can be seen from Figure 5(b)-(c) that the varying of shear force and bending moment with is similar to that of axial force.
| ||||||||
| Figure 5. Internal force varying along the axis of tunnelling | ||||||||
The magnitude of the internal force of the tunnel under each working condition increases with the increase of . In order to further study the relationship between the ∆/L and the internal forces, the bending moment is used as the object.
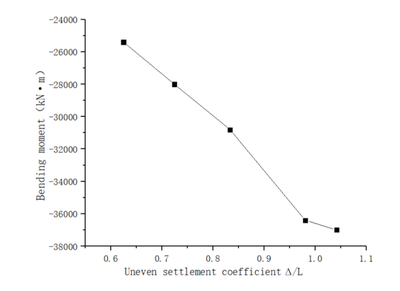
The value of uneven settlement and the maximum bending moment value at center lining ring in five different working conditions are compared. In condition 1, the is 0.9804, and the maximum bending moment corresponding to the central ring is −36400 kN∙m. In condition 2, the ∆/L is 0.8333, and the maximum bending moment is -30800 kN·m. In condition 3, is 0.7246, and the maximum bending moment is − 28000 kN·m. In condition 4, the is 1.0417, and the maximum bending moment is -37,000 kN·m. In condition 5, the uneven settlement is 0.6250, and the maximum bending moment is -25400kN·m. It is shown in Table 8 and Figure 6. It can be seen that the relationship between uneven settlement and maximum bending moment is approximately linear.
| Working condition | Uneven settlement coefficient | Bending moment(kN·m) |
|---|---|---|
| Condition 1 | 0.9804 | -36400 |
| Condition 2 | 0.8333 | -30800 |
| Condition 3 | 0.7246 | -28000 |
| Condition 4 | 1.0417 | -37000 |
| Condition 5 | 0.6250 | -25400 |
|
| Figure 6. Relationship between uneven settlement coefficient and bending moment |
By analyzing and comparing the internal forces of the five working conditions, it is found that the value of the directly affects the internal forces of the tunnel. The larger the is, the greater the internal forces of the tunnel are. Therefore, the value of is taken as the key index. The recommended value of uneven settlement coefficient under each transverse convergence rate is further analyzed and summarized in next section, which provides intuitive theoretical support for tunnel health monitoring.
5.3 Recommended value of uneven settlement coefficient
According to the analysis results of five different working conditions with a transverse convergence rate of 1 ‰ in Section 5.2, it can be seen that the uneven settlement coefficient is directly related to the internal forces of the shield tunnel, so the damage is also related to it. Based on the recommended settlement value of 24 m monitoring distance under different transverse convergence rates in Section 4.2, the recommended value of uneven settlement coefficient under different transverse convergence rates is given in Table 9, which can provide the safety settlement value applicable to different monitoring distances.
| Transverse convergence rate | Settlement value (mm) | Settlement control range (m) | Uneven settlement coefficient [] |
|---|---|---|---|
| 0‰D | 8.5 | 24 | 0.3542 |
| 1‰D | 8.0 | 24 | 0.3333 |
| 2‰D | 7.5 | 24 | 0.3125 |
| 3‰D | 6.5 | 24 | 0.2708 |
| 4‰D | 4.5 | 24 | 0.1875 |
The uneven settlement coefficient ∆/L under five different transverse convergence rates of 0‰D, 1‰D, 2‰D, 3‰D and 4‰D are 0.3542,0.3333,0.3125,0.2708 and 0.1875, respectively. According to Table 9, the damage to the tunnel lining can be preliminarily judged or the spacing of monitoring points can be reasonably arranged according to recommended value [].
6. Conclusions
A three-dimensional numerical model is established to study the mechanical behavior of tunnel lining when uneven settlement occurs under different transverse deformations of lining. The uneven settlement coefficient ∆/L is proposed as an index to reflect the mechanical properties of the tunnel. Based on the analysis, the following conclusions are drawn:
(1) The transverse and longitudinal deformation of the shield tunnel are coupled. The uneven settlement displacement of the tunnel will cause the transverse deformation of the lining ring to a certain extent. The transverse deformation of the lining has little effect on the force characteristics of the tunnel, and the settlement is the main factor affecting the force characteristics of the tunnel.
(2) The damage of the tunnel usually occurs on the outer surface of the arch waist, the inner surface of the arch bottom and the vault. When the uneven settlement occurs, the larger the transverse convergence rate of the shield tunnel is, the smaller the settlement value corresponding to the damage to the lining ring is, and the slower the damage develops.
(3) According to the occurrence and development of lining damage when uneven settlement occurs in shield tunnels under different transverse deformations, the recommended values of safe settlement of shield tunnels with different transverse deformations are proposed. The larger the transverse convergence rate of the tunnel lining is, the smaller the recommended value of longitudinal safety settlement of tunnel is. When the transverse deformation or uneven settlement reaches the control value, the concrete damage detection of the lining ring should be carried out, and the corresponding reinforcement measures should be taken.
(4) The ratio between the maximum settlement value and the length of the shield tunnel with uneven settlement ∆/L is proposed as an index to reflect the degree of uneven settlement. Under transverse convergence rates of 0‰D, 1‰D, 2‰D, 3‰D and 4‰D, the uneven settlement coefficients are 0.3542, 0.3333, 0.3125, 0.2708 and 0.1875, respectively.
Acknowledgment
This research was supported by the National Natural Science Foundation of China (Grant number: 52378419).
References
[1] Han B.M., Li Y.W., Lu F., Yang Z.X., Yang R.X., Chen Y.X., Sun Y.J., XI Z., Wang L.Y., Dai Y.J. Statistical analysis of urban rail transit operations in the world in 2021: A Review (in Chinese). Urban Rapid Rail Transit, 35:5-11, 2022.
[2] Lin Y.G., Liao S.M., Lin G.B. A discussion of the factors effecting on longitudinal deformation of subway tunnel. Undergr. Space, 20:264-267, 2000.
[3] Wei K., Gong Q.M., Zhou S.H. Ant colony algorithms of long-term uneven settlement prediction in tunne. Journal of Tongji University(Natural Science), 37:993-998, 2009.
[4] Tan W.L., Pathegama R.G. Parameters and considerations in soft ground tunneling. Electronic Journal of Geotechnical Engineering, 8:1-17, 2003.
[5] Zheng Y.L., Han W.X., Tong Q.H., Yang L.F., Pan J. Study on longitudinal crack of shield tunnel segment joint due to asymmetric settlement in soft soil (in Chinese). Chinese Journal of Rock Mechanics and Engineering, 24(24):4552-4558, 2005.
[6]Ye Y.D., Zhu H.H., Wang R.L. Analysis on the current status of metro operating tunnel damage in soft ground and its causes (in Chinese). Chinese Journal of Underground Space and Engineering, 3:157-160, 2007.
[7] Wang R.L. Factors influencing deformation of Shanghai soft soil metro tunnel and deformation analysis (in Chinese). Underground Engineering and Tunnels, 1:1-6, 2009.
[8] Liu X., Dong Z.B., Bai Y., Zhu Y.H. Investigation of the structural effect induced by stagger joints in segmental tunnel linings: First results from full-scale ring tests. Tunn. Undergr. Space Tech., 66:1-18, 2017.
[9] Xiao Z.R., Wang J.C. A three-dimensional model of shield tunnel considering tnteraction of soil and lining. Math. Probl. Eng., 2022, 4245384, 2022.
[10] Liao S.M., Peng F.L., Shen S.L. Analysis of shearing effect on tunnel induced by load transfer along longitudinal direction. Tunn. Undergr. Space Tech., 23:421-430, 2008,Document information
Published on 17/10/23
Accepted on 03/10/23
Submitted on 14/07/23
Volume 39, Issue 4, 2023
DOI: 10.23967/j.rimni.2023.10.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?