(Created page with " ==Numerical Simulation on Free Motion Response of a Submarine Induced by Internal Solitary Wave== <div class="center" style="width: auto; margin-left: auto; margin-right: a...") |
|||
| (38 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| + | ==Abstract== | ||
| + | The internal solitary waves (ISWs) in the ocean carry huge energy and pose a serious threat to the safety of underwater vehicle. In order to obtain the dynamic response of the submarine under the action of ISWs, the amplified SUBOFF model was placed in a large numerical water tank with a length of 5000m, a width of 200m and a depth of 500m. The Korteweg-de Vries (KdV) theory was adopted to simulate the generation of ISWs in the two-layer flow, and overset grid technology was used to ensure the grid quality during the submarine movement. The results show that before the ISWs peak reaches the position of the submarine, the submarine will move, which causes the submarine to sink, move laterally and pitch. The longitudinal velocity is obviously greater than the lateral velocity, and the submarine finally hits the water tank bottom. With the increase of the ISWs amplitude, the time needed for submarine to reach the bottom increases, and the pitching angle increases greatly. The ISWs amplitude has no effect on the motion trajectory of the submarine's center of gravity, and has little effect on the lateral and longitudinal velocity. With the decrease of submergence depth of the submarine, the time required for submarine to reach the bottom will also increase, and the motion trajectory will change, but the trend of change is basically the same. The submergence depth has little influence on the variation range of lateral velocity, longitudinal velocity and pitching angle. | ||
| − | + | '''Keywords''': internal solitary waves, submarine, dynamic response, numerical simulation | |
| − | + | ||
| − | + | ||
| − | ''' | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==1. Introduction== | ==1. Introduction== | ||
| − | Internal solitary waves (ISWs) are common phenomenon in the stratified ocean, which has the characteristics of medium-fine scale, large amplitude and strong velocity | + | Internal solitary waves (ISWs) are common phenomenon in the stratified ocean, which has the characteristics of medium-fine scale, large amplitude and strong velocity [1]. The shear currents and turbulence generated by ISWs contribute to global energy transport and dissipation in the ocean, but also affect biological activities, offshore engineering and submarine navigation [2]. Due to the development of ISWs below the sea surface, low propagation frequency and long distance, it is difficult to observe them which seriously threaten the safety of ocean engineering structures and underwater vehicle [3]. |
| − | In view of the influence of ISWs on ocean engineering and underwater vehicles, the current research focuses on the monitoring of ISWs | + | In view of the influence of ISWs on ocean engineering and underwater vehicles, the current research focuses on the monitoring of ISWs [1,4], and the simulation of ISWs [3,5], as well as the influence of ISWs on submerged tunnels [6], semi-submersible platforms [7-8] and submarines [9-11]. Research on the interaction between ISWs and submarines has focused on the standard submarine model proposed by the Defense Advanced Research Projects Agency (DARPA), known as the DARPA SUBOFF model [12]. CHEN studied the submarine load variation induced by ISWs with and without submarine speed [9]. LI used the numerical model of ISWs in a continuously stratified fluid, numerically analyzed the forces and moments of SUBOFF when it encountered ISWs in different submergence depths, discussed the influence of rotation center position on the moment, and proposed the optimal rotation center position [10]. GUAN numerically studied the hydrodynamic properties and load characteristics of submarine when it encountered ISWs in the ocean [11]. |
| − | It is worth noting that in the above studies, the freedom of the submarine is constrained when the submarine encounters the ISWs. The submarine position is fixed and in a static state. As matter | + | It is worth noting that in the above studies, the freedom of the submarine is constrained when the submarine encounters the ISWs. The submarine position is fixed and in a static state. As matter of fact, the submarine will inevitably move or even sink when it encounters the ISWs. So the submarine movement must be taken into account in the research. DU studied the kinematics characteristic and the mass center trace of the slender model in the density stratification fluid with a semi-flexible restriction technique, and obtained the properties such as heave, surge, roll, pitch, but the slender body was bound by the flexible line in the water tank [13]. CUI used experimental methods to study the dynamic response of submerged body under the action of ISWs, and obtained the influence of different wave amplitudes, the thickness ratio of the upper and lower layers of fluid, and the shape of the submarine section, etc. Strong currents in the horizontal and vertical directions caused by ISWs can greatly move submerged body and cause damage to its structure. Limited by the experimental tank, the section of the submerged model is less than 10cm [14]. In general, the submerged body is affected by ISWs, which will lead to lateral, longitudinal and pitching motions. |
In order to simulate the situation of large submarine encountering ISWs in the ocean, a large numerical tank and a large submarine model are constructed by numerical simulation method, and the dynamic response of submarine under the action of ISWs is studied in a numerical tank with continuous density changes. | In order to simulate the situation of large submarine encountering ISWs in the ocean, a large numerical tank and a large submarine model are constructed by numerical simulation method, and the dynamic response of submarine under the action of ISWs is studied in a numerical tank with continuous density changes. | ||
| − | ==2 Simulation configurations== | + | ==2. Simulation configurations== |
===2.1 Submarine model=== | ===2.1 Submarine model=== | ||
| − | The standard submarine model of Defense Advanced Research Projects Agency (DARPA), which called DARPA SUBOFF, has an overall length of 4.356m and a maximum diameter of 0.508m, as shown in Figure 1(a). The SUBOFF model itself is small in scale, so a 1:25.5 scale of DARPA SUBOFF is used to simulate the actual submarine. In order to | + | The standard submarine model of Defense Advanced Research Projects Agency (DARPA), which called DARPA SUBOFF, has an overall length of 4.356m and a maximum diameter of 0.508m, as shown in [[#img-1|Figure 1]](a). The SUBOFF model itself is small in scale, so a 1:25.5 scale of DARPA SUBOFF is used to simulate the actual submarine. In order to ensure the quality of the grids, the grids in the submarine appendage area must be refined and the time step must be reduced to ensure a reasonable Courant number, which consumes more computational resources. However the main purpose of this work is to study the free motion of the submarine and the influence of appendages on free motion is minimal. Here, the model used in this work was simplified and the appendages of SUBOFF model were removed, as shown in [[#img-1|Figure 1]](b). The enlarged bare hull has an overall length of 111m and a maximum diameter of 12.954m. The gravity center of the submarine is placed on the axis of the hull, 51 m away from the bow. |
| − | <div class=" | + | <div id='img-1'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | {| | + | |-style="background:white;" |
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image1-c.png|376px]] |
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image2.png|center|370px]] |
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) DARPA SUBOFF model | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) SUBOFF simplified model | ||
|} | |} | ||
| − | + | |- | |
| − | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 1'''. SUBOFF model | |
| − | + | |} | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | Figure 1 SUBOFF model | + | |
===2.2 Numerical flume=== | ===2.2 Numerical flume=== | ||
| − | The numerical flume is shown in the Figure 2 and has a total length of 5000 m, width of 200 m and depth of 500 m, including the working zone which has a length of 4000 m and the wave damping zone which has a length of 1000 m. The fluid densities of the upper and lower layers are different. The upper layer fluid density | + | The numerical flume is shown in the [[#img-2|Figure 2]] and has a total length of 5000 m, width of 200 m and depth of 500 m, including the working zone which has a length of 4000 m and the wave damping zone which has a length of 1000 m. The fluid densities of the upper and lower layers are different. The density varies continuously along depth in each layer of fluid, as shown in [[#img-3|Figure 3]]. The Dimensionless density means the density/ <math display="inline">1000.00</math> kg/m<math display="inline">^3</math>. The upper layer fluid density <math display="inline">{\rho }_1</math> varies from <math display="inline">997.00</math> kg/m<math display="inline">^3</math> to <math display="inline">997.50</math> kg/m<math display="inline">^3</math> and the lower layer fluid density <math display="inline">{\rho }_2</math> varies from <math display="inline">1034.00</math> kg/m<math display="inline">^3</math> to <math display="inline">1036.00</math> kg/m<math display="inline">^3</math>. The depth of the upper and lower fluid are 100m and 400m, respectively. |
| − | <div class=" | + | <div id='img-2'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image10.png|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. Sketch of numerical flume | ||
| + | |} | ||
| − | |||
| − | |||
| − | <div class=" | + | <div id='img-3'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image11.png|288px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Change of density along the water depth | ||
| + | |} | ||
| − | |||
| − | |||
The distance between submarine location and the two layers interface is defined as the submergence depth H. The inlet and outlet are on the left side of the flume. Speed entrance method is adopted to make the numerical wave and pressure boundary condition is inducted for outlet. The inlet boundary is set by the user-defined function (UDF), which produces the ISWs. The bottom, top and right of the flume are all using the solid wall boundary. | The distance between submarine location and the two layers interface is defined as the submergence depth H. The inlet and outlet are on the left side of the flume. Speed entrance method is adopted to make the numerical wave and pressure boundary condition is inducted for outlet. The inlet boundary is set by the user-defined function (UDF), which produces the ISWs. The bottom, top and right of the flume are all using the solid wall boundary. | ||
| Line 64: | Line 64: | ||
===2.3 ISW theory=== | ===2.3 ISW theory=== | ||
| − | The Korteweg-de Vires (KdV) equation has a wide range of applications for small amplitude and weak nonlinear ISWs | + | The Korteweg-de Vires (KdV) equation has a wide range of applications for small amplitude and weak nonlinear ISWs [3]. For the numerical flume established in this paper, the ratio of wave amplitude to the depth of the flume <math display="inline">{\eta }_0/(h_1+h_2)<0.1</math> (<math display="inline">{\eta }_0</math> is the ISW amplitude), so the KdV theory can be used [15]. The propagation of a wave along the horizontal x direction is expressed as [16-17]: |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math>\frac{\partial \eta }{\partial t}+c_0\frac{\partial \eta }{\partial x}+</math><math>c_1\eta \frac{\partial \eta }{\partial x}+c_2\frac{{\partial }^3\eta }{\partial x^3}=0</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
| + | |} | ||
| − | where <math display="inline">c_0</math> , <math display="inline">c_1</math> and <math display="inline">c_2</math> are the linear phase speed, nonlinear coefficient, measure of dispersion respectively, which can be wright as: | + | where <math display="inline">c_0</math>, <math display="inline">c_1</math> and <math display="inline">c_2</math> are the linear phase speed, nonlinear coefficient, measure of dispersion respectively, which can be wright as: |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math>c_0={\left[\frac{gh_1h_2({\rho }_2-{\rho }_1)}{{\rho }_1h_2+{\rho }_2h_1}\right]}^{1/2}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
| + | |} | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math>c_1=-\frac{3}{2}\frac{c_0}{h_1h_2}\frac{{\rho }_1h_2^2-{\rho }_2h_1^2}{{\rho }_1h_2+{\rho }_2h_1}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
| + | |} | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math>c_2=\frac{c_0h_1h_2({\rho }_1h_1+{\rho }_2h_2)}{6({\rho }_1h_2+{\rho }_2h_1)}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
| + | |} | ||
| − | |||
| − | |||
The KdV expression for the ISW is: | The KdV expression for the ISW is: | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math>\eta (x,t)={\eta }_0{sech}^2(\frac{x-Vt}{\lambda })</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
| + | |} | ||
| + | |||
The soliton velocity and characteristic wavelength based on KdV theory are: | The soliton velocity and characteristic wavelength based on KdV theory are: | ||
| − | + | {| class="formulaSCP" style="width: 100%; text-align: center;" | |
| − | + | |- | |
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math>V=c_0(1+\frac{{\eta }_0c_1}{3c_0})</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
| + | |} | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math>\lambda ={\left(\frac{12c_2}{{\eta }_0c_1}\right)}^{1/2}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
| + | |} | ||
| − | |||
| − | |||
===2.4 Meshing scheme and simulation method=== | ===2.4 Meshing scheme and simulation method=== | ||
| − | (1) Meshing scheme | + | '''(1) Meshing scheme''' |
| − | The submarine will move horizontally and vertically, accompanied by pitching motion which affected by ISWs, as shown in Figure 4. The moving mesh is easy to be generated with negative volume, and the grid update takes a long time, resulting in a very long computation time. So the overset mesh technology is adopted in this paper. A separate component mesh was constructed in the SUBOFF region, the size of which was 160 m×20 m×60 m. The unstructured grids were adopted with total grids of 1.42 million. In addition, structured grid was used in the flume as the background grid with total grids of 5.31 million, as shown in Figure 5. In the overlapping regions, the overset interfaces connect cell zones by interpolating cell data. The overset mesh method can maintain mesh quality well during submarine motion. | + | The submarine will move horizontally and vertically, accompanied by pitching motion which affected by ISWs, as shown in [[#img-4|Figure 4]]. The moving mesh is easy to be generated with negative volume, and the grid update takes a long time, resulting in a very long computation time. So the overset mesh technology is adopted in this paper. A separate component mesh was constructed in the SUBOFF region, the size of which was 160 m×20 m×60 m. The unstructured grids were adopted with total grids of 1.42 million. In addition, structured grid was used in the flume as the background grid with total grids of 5.31 million, as shown in [[#img-5|Figure 5]]. In the overlapping regions, the overset interfaces connect cell zones by interpolating cell data. The overset mesh method can maintain mesh quality well during submarine motion. |
| − | <div class=" | + | <div id='img-4'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image24.png|246px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. Sketch of submarine motion | ||
| + | |} | ||
| − | |||
| − | |||
| − | <div class=" | + | <div id='img-5'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | {| | + | |-style="background:white;" |
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image25-c.jpeg|346px]] |
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image26.jpeg|center|388px]] |
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Unstructered grids around the SUBOFF | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Sketch of overset mesh | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. The computational grid in the domain | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(2) Simulation method''' | |
| − | + | ||
| − | + | The unsteady Reynolds- Averaged Navier-Stokes equations with the <math display="inline">k-\epsilon </math> turbulence model are applied to simulate the flow field. The <math display="inline">k-\epsilon </math> turbulence added two variables to the governing equation which are turbulence kinetic energy <math display="inline">k</math> and dissipation rate of turbulence kinetic energy <math display="inline">\epsilon </math>. <math display="inline">k</math> represents the change of velocity fluctuation and <math display="inline">\epsilon </math> represents dissipation rate of velocity fluctuation. The mass continuity equation and momentum equation are shown as follows: | |
| − | + | ||
| − | The unsteady Reynolds- Averaged | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 129: | Line 187: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\frac{\partial \rho }{\partial t}+\nabla \cdot (\rho \boldsymbol{u})=</math><math>0</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (8) | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
| Line 139: | Line 197: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\frac{\partial \rho \boldsymbol{u}}{\partial t}+\nabla \cdot (\rho \boldsymbol{u}\otimes \boldsymbol{u})-\nabla \cdot ({\mu }_{\mbox{eff}}\nabla \boldsymbol{u})=\nabla \cdot p^'+</math><math>\nabla \cdot {\left({\mu }_{\mbox{eff}}\nabla \boldsymbol{u}\right)}^T+</math><math>S_M</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (9) | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
|} | |} | ||
| − | + | where <math display="inline">{\mu }_{\mbox{eff}}</math> is effective viscosity, <math display="inline">p^'</math> is the modified pressure, and <math display="inline">S_M</math> is the sum of body forces. | |
| − | where <math display="inline">{\mu }_{\mbox{eff}}</math> is effective viscosity | + | |
The <math display="inline">k</math> and <math display="inline">\epsilon </math> can be solved by following equations: | The <math display="inline">k</math> and <math display="inline">\epsilon </math> can be solved by following equations: | ||
| Line 154: | Line 211: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\frac{\partial (\rho k)}{\partial t}+\nabla \cdot (\rho \boldsymbol{u}k)=</math><math>\nabla \cdot \left[\left(\mu +\frac{{\mu }_t}{{\sigma }_k}\right)\nabla k\right]+</math><math>P_k-\rho \epsilon </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (10) | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
| Line 164: | Line 221: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\frac{\partial (\rho \epsilon )}{\partial t}+\nabla \cdot (\rho \boldsymbol{u}\epsilon )=\nabla \cdot \left[\left(\mu +\frac{{\mu }_t}{{\sigma }_{\epsilon }}\right)\nabla \epsilon \right]+</math><math>C_{\epsilon 1}\frac{\epsilon }{k}P_k-C_{\epsilon 2}\rho \frac{{\epsilon }^2}{k}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (11) | | style="width: 5px;text-align: right;white-space: nowrap;" | (11) | ||
|} | |} | ||
| + | where <math display="inline">{\sigma }_k</math> and <math display="inline">{\sigma }_{\epsilon }</math> are Prandtl numbers corresponding to turbulence kinetic energy and dissipation rate, respectively; <math display="inline">P_k</math> is the turbulence production due to viscous forces; <math display="inline">C_{\epsilon 1}</math> and <math display="inline">C_{\epsilon 2}</math> are constants; <math display="inline">\mu </math> is the dynamic viscosity and <math display="inline">{\mu }_\mbox{t}</math> is the turbulent viscosity. | ||
| − | + | The ISW wave surface was tracked by Volume of fluid (VOF) method [18]. The fluid’s volume fraction <math display="inline">{\alpha }_i</math> represents the ratio of the <math display="inline">i^{th}</math> fluid’s volume in a cell to the total volume of the cell. For the <math display="inline">{\alpha }_i</math>, the equation has the following form: | |
| − | + | ||
| − | The ISW wave surface was tracked by Volume of fluid (VOF) method | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 179: | Line 235: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math | + | | <math>\frac{\partial {\alpha }_\mbox{i}}{\partial t}+\frac{\partial (u{\alpha }_\mbox{i})}{\partial x}+</math><math>\frac{\partial (v{\alpha }_\mbox{i})}{\partial y}=</math><math>0</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (12) | | style="width: 5px;text-align: right;white-space: nowrap;" | (12) | ||
| Line 185: | Line 241: | ||
| − | For every control volume, the volume fractions of all phases sum to unit. When <math display="inline">{\alpha }_i | + | For every control volume, the volume fractions of all phases sum to unit. When <math display="inline">{\alpha }_i=1</math>, the cell is full of the <math display="inline">i^{th}</math> fluid; when <math display="inline">{\alpha }_i=0</math>, the cell is empty of the <math display="inline">i^{th}</math> fluid; when <math display="inline">0<{\alpha }_i<1</math>, the cell contains the interface [19]. For the two-layer fluid in this paper, <math display="inline">i=1</math> or 2. |
| − | == | + | ==3. Numerical results and discussions== |
The submarine is located in the numerical flume and the distance between the gravity center and the flume inlet is 1500 m. The submarine is in a state of equilibrium with its own buoyancy. The power of the submarine is not taken into account, so it has no initial speed and its freedom of motion is not constrained. | The submarine is located in the numerical flume and the distance between the gravity center and the flume inlet is 1500 m. The submarine is in a state of equilibrium with its own buoyancy. The power of the submarine is not taken into account, so it has no initial speed and its freedom of motion is not constrained. | ||
| − | In order to study the interactions between different ISWs and submarine, three ISW amplitudes and two submergence depths are used in this part, which include <math display="inline">{\eta }_0 | + | In order to study the interactions between different ISWs and submarine, three ISW amplitudes and two submergence depths are used in this part, which include <math display="inline">{\eta }_0 =10</math>m, <math display="inline">{\eta }_0=20</math>m, <math display="inline">{\eta }_0=30</math>m and <math display="inline">H=45</math>m, <math display="inline">H=15</math>m, as shown in [[#tab-1|Table 1]]. |
| − | <div class="center" style=" | + | <div class="center" style="font-size: 75%;">'''Table 1'''. Calculation cases</div> |
| − | Table 1 Calculation cases</div> | + | |
| − | {| style=" | + | <div id='tab-1'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! H (m)<br> <math display="inline">{\eta }_0</math> (m)!! style="text-align: center;vertical-align: center;"| 45 !! style="text-align: center;vertical-align: center;" |15 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|10 |
| − | + | | style="text-align: center;vertical-align: top;"|C11 | |
| − | + | | style="text-align: center;vertical-align: top;"|C12 | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | | style=" | + | |
| − | | style=" | + | |
|- | |- | ||
| style="text-align: center;vertical-align: top;"|20 | | style="text-align: center;vertical-align: top;"|20 | ||
| Line 212: | Line 264: | ||
| style="text-align: center;vertical-align: top;"|C22 | | style="text-align: center;vertical-align: top;"|C22 | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|30 |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|C31 |
| − | | style=" | + | | style="text-align: center;vertical-align: top;"|C32 |
|} | |} | ||
| − | The case C31 was selected to verify the numerical flume established in this paper, and the formation of ISWs was monitored at x=1500m. As can be seen from Figure 6, the wave generation of the numerical flume was highly consistent with that of KdV theory, which met the requirements of numerical simulation. | + | The case C31 was selected to verify the numerical flume established in this paper, and the formation of ISWs was monitored at x=1500m. As can be seen from [[#img-6|Figure 6]], the wave generation of the numerical flume was highly consistent with that of KdV theory, which met the requirements of numerical simulation. |
| − | <div class=" | + | <div id='img-6'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image55.png|330px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 6'''. Numerical result verification | ||
| + | |} | ||
| − | |||
| − | |||
===3.1 Trajectory of submarine motion=== | ===3.1 Trajectory of submarine motion=== | ||
| − | The initial submergence depth of SUBOFF was 45m or 15m below the interface. When the ISWs flow field was formed by the numerical flume, the motion of the submarine was observed. Figure 7 shows the motion trajectory of SUBOFF's center of gravity under different submergence depths. As can be seen from Figure 7, no matter the depth is 45m or 15m, SUBOFF's center of gravity moved in a similar trajectory, moving to the lower left under the influence of the ISWs. And the longitudinal displacement was significantly greater than the lateral displacement. Restricted by the size of the numerical flume, SUBOFF rebounded after impacting the bottom of the flume, and then continued to move to the upper left. At the same depth, the ISWs amplitude had no effect on the trajectory of submarine motion. Different wave amplitudes had no effect on the position of the impact point of SUBOFF, and the trajectory of the submarine basically coincided after rebound. | + | The initial submergence depth of SUBOFF was 45m or 15m below the interface. When the ISWs flow field was formed by the numerical flume, the motion of the submarine was observed. [[#img-7|Figure 7]] shows the motion trajectory of SUBOFF's center of gravity under different submergence depths. As can be seen from [[#img-7|Figure 7]], no matter the depth is 45m or 15m, SUBOFF's center of gravity moved in a similar trajectory, moving to the lower left under the influence of the ISWs. And the longitudinal displacement was significantly greater than the lateral displacement. Restricted by the size of the numerical flume, SUBOFF rebounded after impacting the bottom of the flume, and then continued to move to the upper left. At the same depth, the ISWs amplitude had no effect on the trajectory of submarine motion. Different wave amplitudes had no effect on the position of the impact point of SUBOFF, and the trajectory of the submarine basically coincided after rebound. |
| − | <div class=" | + | <div id='img-7'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | {| | + | |-style="background:white;" |
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image56.png|288px]] |
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image57.png|center|288px]] |
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) <math display="inline">H=45</math>m | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) <math display="inline">H=15</math>m | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 7'''. Trajectory of submarine motion | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | The change of submarine longitudinal position with time is shown in [[#img-8|Figure 8]]. For the first 100s, SUBOFF kept its position unchanged. Because the flow field of ISWs had not reached the zone where the submarine was located, and the submarine was in a state of equilibrium. Then it began to dive under the influence of the ISWs flow field, and finally hit bottom and rebounded. As can be seen from [[#img-8|Figure 8]], with the increase of ISWs amplitude, the time required for the submarine to reach the bottom was longer, and the time required for C11, C21 and C31 to reach the bottom were 269s, 278s and 282s, respectively. So with the higher ISW amplitude, the submarine longitudinal velocity reduced. According to KdV theory, the ISWs speed decreased with the increase of the ISWs amplitudes, which was the reason for the change of submarine bottoming time. The position of the submarine was 1500m away from the flume inlet, and it took less than 300s for the submarine sink more than 300m. It can be seen that the ISWs can cause serious damage to the submarine. | |
| − | Figure | + | |
| − | + | <div id='img-8'></div> | |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | <div class=" | + | |-style="background:white;" |
| − | + | |align="center" | | |
| − | {| | + | {|style="margin: 0em auto 0.1em auto;width:auto;" |
| + | |+ | ||
| + | |- | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image58.png|288px]] | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image59.png|center|288px]] | ||
|- | |- | ||
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) <math display="inline">H=45</math>m |
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) <math display="inline">H=15</math>m |
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 8'''. Change of submarine longitudinal position with time | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | In order to compare the influence of different submergence depth on the submarine motion trajectory, C31 and C32 with a wave amplitude of 30m were selected, as shown in [[#img-9|Figure 9]]. The distance between the submarine and the flume bottom became greater with the decrease of the submergence depth, which lead to the lateral displacement was greater when the submarine hit the bottom, and the longitudinal displacement was smaller after the rebound which was affected by the ISWs. As can be seen from [[#img-9|Figure 9]](b), as the depth <math display="inline"> H </math> decreased, the time required for the submarine to reach the bottom increased. | |
| − | Figure | + | |
| − | + | <div id='img-9'></div> | |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | <div class=" | + | |-style="background:white;" |
| − | + | |align="center" | | |
| − | {| | + | {|style="margin: 0em auto 0.1em auto;width:auto;" |
| + | |+ | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image60.png|288px]] |
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image61.png|center|288px]] |
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Motion trajectory | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Longitudinal position change with time | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 9'''. Trajectory of submarine motion with different <math display="inline"> H </math> | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
It is well known that the submarine will be dragged into the seabed by ISWs, and the impact on the bottom will produce strong load and lead to serious damage to its structure. The data after the rebound on the bottom has little significance. Therefore, this paper focuses on the analysis before the submarine hits the bottom. | It is well known that the submarine will be dragged into the seabed by ISWs, and the impact on the bottom will produce strong load and lead to serious damage to its structure. The data after the rebound on the bottom has little significance. Therefore, this paper focuses on the analysis before the submarine hits the bottom. | ||
| Line 283: | Line 347: | ||
===3.2 Characteristics of the motion=== | ===3.2 Characteristics of the motion=== | ||
| − | The motion characteristics of the marine in the flume were studied when the wave amplitude was 20m and the submergence depth was 15m (C22). Figure 10 shows the movement of SUBOFF at six moments before it hits the bottom. The color mark the upper and lower layers of fluid with different densities respectively, and the submarine is below the interface. During the first 100s, the position of the submarine remained basically unchanged. After that, the submarine began to sink, and Figure 10(d) showed obvious sinking of the submarine. At t= | + | The motion characteristics of the marine in the flume were studied when the wave amplitude was 20m and the submergence depth was 15m (C22). [[#img-10|Figure 10]] shows the movement of SUBOFF at six moments before it hits the bottom. The color mark the upper and lower layers of fluid with different densities respectively, and the submarine is below the interface. During the first 100s, the position of the submarine remained basically unchanged. After that, the submarine began to sink, and [[#img-10|Figure 10]](d) showed obvious sinking of the submarine. At <math display="inline">t=200</math>s, it can be seen that the submarine was starting to pitch, the submarine's bow was up. At <math>t=250</math>s, the change of pitching and sinking was obvious. At this time, the ISWs peak has not reached the location of the submarine. The flow field formed by ISWs had a strong influence on the submarine before the peak of the ISW reached the position of the submarine, resulting in not only submarine transverse and longitudinal displacement but also the pitching. |
| − | <div class=" | + | <div id='img-10'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | {| | + | |-style="background:white;" |
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image62.jpeg|266px]] |
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image63.jpeg|center|266px]] |
| − | | | + | |- |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) 0s | |
| − | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) 50s | |
| − | + | |- | |
| − | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image64.jpeg|266px]] | |
| − | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image65.jpeg|center|266px]] | |
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(c) 100s |
| − | | [[Image: | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(d) 150s |
| + | |- | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image66.jpeg|266px]] | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image67.jpeg|center|266px]] | ||
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(c) 200s | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(d) 250s | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|- | |- | ||
| − | | | + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 10'''. Submarine motion characteristics at different times |
| − | + | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
===3.3 Motion parameters=== | ===3.3 Motion parameters=== | ||
| − | (1)The effect of different ISWs amplitudes | + | '''(1) The effect of different ISWs amplitudes''' |
| − | The lateral velocity of the submarine under different ISW amplitudes is shown in Figure 11. After t=100 s, the absolute lateral value of velocity increased along the negative x-direction. Under the same submergence depth, lateral acceleration decreased with the increase of wave amplitude. When H=45 m and t=260 s, the lateral velocities of C11, C21 and C31 were -0.51 m/s, -0.41 m/s and -0.39 m/s, respectively. By comparison with | + | The lateral velocity of the submarine under different ISW amplitudes is shown in [[#img-11|Figure 11]]. After <math>t=100</math> s, the absolute lateral value of velocity increased along the negative <math>x</math>-direction. Under the same submergence depth, lateral acceleration decreased with the increase of wave amplitude. When <math>H=45</math>m and <math>t=260</math>s, the lateral velocities of C11, C21 and C31 were -0.51 m/s, -0.41 m/s and -0.39 m/s, respectively. By comparison with [[#img-11|Figure 11]](a) and [[#img-11|Figure 11]](b), it is found that the submergence depth has little influence on the lateral velocity variation trend. |
| − | <div class=" | + | <div id='img-11'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | {| | + | |-style="background:white;" |
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image68.png|300px]] |
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image69.png|center|300px]] |
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) <math display="inline">H=45</math>m | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) <math display="inline">H=15</math>m | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 11'''. Lateral velocity at different ISW amplitudes | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | The longitudinal velocity of the submarine under different depths is shown in Figure 12. Similar to the lateral velocity, the longitudinal velocity increased along the negative y-direction, and the change of longitudinal velocity was one order of magnitude larger than that of the lateral velocity. Before t= | + | The longitudinal velocity of the submarine under different depths is shown in [[#img-12|Figure 12]] . Similar to the lateral velocity, the longitudinal velocity increased along the negative y-direction, and the change of longitudinal velocity was one order of magnitude larger than that of the lateral velocity. Before <math>t=180</math>s, the submarine was accelerating longitudinally. After <math>t=180</math>s, the longitudinal velocity began to keep basically stable at about -2.5m/s. |
| − | <div class=" | + | <div id='img-12'></div> |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | {| | + | |-style="background:white;" |
| + | |align="center" | | ||
| + | {|style="margin: 0em auto 0.1em auto;width:auto;" | ||
| + | |+ | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image70.png|300px]] |
| − | | [[Image: | + | |style="text-align: center;padding:10px;"|[[Image:Review_420808633416-image71.png|center|300px]] |
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) <math display="inline">H=45</math>m | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) <math display="inline">H=15</math>m | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 12'''. Longitudinal velocity at different ISW amplitudes | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | < | + | The pitch angle of the submarine under different ISW amplitudes is shown in [[#img-13|Figure 13]]. When the submergence depth was 45m, as shown in [[#img-13|Figure 13]](a), the submarine basically keeps level without pitching before <math>t=180</math>s; after <math>t=180</math>s, the submarine began to pitch. The pitch angle gradually increased with time, and the pitch angle variation decreased with the increase of ISW amplitudes. When <math>t=260</math>s, the pitch angles of C11, C21 and C31 were -21.10°, -17.16° and -14.50°, respectively. When the submergence depth <math display="inline">H=15</math>m, the changes of pitch angle were similar to <math display="inline">H=45</math>m. |
| − | + | ||
| − | + | <div id='img-13'></div> | |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | <div class=" | + | |-style="background:white;" |
| − | + | |align="center" | | |
| − | {| | + | {|style="margin: 0em auto 0.1em auto;width:auto;" |
| + | |+ | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image72.png|300px]] |
| − | | [[Image: | + | |style="text-align: center;padding:10px;"|[[Image:Review_420808633416-image73.png|center|300px]] |
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) <math display="inline">H=45</math>m | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) <math display="inline">H=15</math>m | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 13'''. Pitch angle at different ISW amplitudes | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | '''(2) The effect of submergence depths''' | |
| − | + | ||
| − | + | [[#img-14|Figure 14]] shows the comparison of the submarine velocity under different submergence depths. When the wave amplitude was constant, the influence of the submergence depth on the change of the lateral velocity and longitudinal velocity can be ignored. | |
| − | + | <div id='img-1'></div> | |
| − | + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| − | <div class=" | + | |-style="background:white;" |
| − | + | |align="center" | | |
| − | {| | + | {|style="margin: 0em auto 0.1em auto;width:auto;" |
| + | |+ | ||
|- | |- | ||
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image74.png|300px]] |
| − | | [[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image75.png|center|300px]] |
| + | |- | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) Comparison of lateral velocity | ||
| + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) Comparison of longitudinal velocity | ||
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 14'''. Comparison of velocity at different depths | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | + | The variations of pitch angle with time at the same wave amplitude but different submergence depths are shown in [[#img-15|Figure 15]]. As shown in the figure, submergence depths had little influence on the variation of pitch angle. | |
| − | + | ||
| − | + | <div id='img-15'></div> | |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_420808633416-image76.png|300px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 15'''. Comparison of pitch angle at different depths | ||
| + | |} | ||
| − | + | ==4. Conclusions== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
The dynamic response of large submarine induced by ISWs was simulated by establishing the ISWs numerical flume. The flume was a stratified fluid of two layers, and the fluid density varied with the depth which was more in line with the actual ocean. The track of gravity center, variations in lateral, longitudinal and pitch motion are studied. The conclusions of this study are listed as follows: | The dynamic response of large submarine induced by ISWs was simulated by establishing the ISWs numerical flume. The flume was a stratified fluid of two layers, and the fluid density varied with the depth which was more in line with the actual ocean. The track of gravity center, variations in lateral, longitudinal and pitch motion are studied. The conclusions of this study are listed as follows: | ||
| Line 412: | Line 480: | ||
(1) When the submarine is located under the two-layer interface, the submarine moves to the lower left, then impacts on bottom and rebounds which is affected by ISWs. The submarine motion trajectory and the impact location are not affected by the initial submergence depth. | (1) When the submarine is located under the two-layer interface, the submarine moves to the lower left, then impacts on bottom and rebounds which is affected by ISWs. The submarine motion trajectory and the impact location are not affected by the initial submergence depth. | ||
| − | (2) | + | (2) The ISW amplitude also affects the time for the submarine impacting the flume bottom, and as the ISW amplitude increases, the longer the time is required. |
| + | |||
| + | (3) The submarine will move which is affected by ISWs. The longitudinal velocity is bigger than lateral velocity. The motion of the submarine is accompanied by pitching. The influence of submergence depth on the submarine lateral velocity and longitudinal velocity is negligible. Before the submarine reaches the bottom, the horizontal velocity is increasing. The higher the ISW amplitude, the smaller the longitudinal velocity is. The longitudinal velocity also accelerates first, and then the value fluctuation is maintained. In the process of the sinking, the pitch angle gradually becomes larger, and the pitch angle decreases as the ISW amplitude increases. The changes in the pitch angle are not affected by the submergence depth. | ||
| + | |||
| + | ==Acknowledgments== | ||
| − | + | This work was supported by Natural Science Foundation of Sichuan Province of China No. 2022NSFSC0478, CAFUC Foundation J2022-035 and Foundation of Key Laboratory of Flight Techniques and Flight Safety,CAAC, FZ2020ZZ05. | |
==Conflict of interest statement== | ==Conflict of interest statement== | ||
| Line 421: | Line 493: | ||
==References== | ==References== | ||
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
| − | <span id='_nebA1B3473E_F351_4D32_B948_3DA0003B2C7B'></span>[1] Huang X, Chen Z, Zhao W, et al. An extreme internal solitary wave event observed in the northern South China Sea. Scientific Reports | + | <span id='_nebA1B3473E_F351_4D32_B948_3DA0003B2C7B'></span>[1] Huang X., Chen Z., Zhao W., et al. An extreme internal solitary wave event observed in the northern South China Sea. Scientific Reports, 6(1):30041, 2016. |
| − | <span id='_nebDA44E60A_2C14_425A_BBE8_EB5D1EB74680'></span> [2] Guo C, Chen X. A review of internal solitary wave dynamics in the northern South China Sea. Progress in | + | <span id='_nebDA44E60A_2C14_425A_BBE8_EB5D1EB74680'></span> [2] Guo C., Chen X. A review of internal solitary wave dynamics in the northern South China Sea. Progress in Oceanography, 121:7-23, 2014. |
| − | <span id='_neb9E7607E2_8CC5_4704_8EDC_65232DC3188C'></span> [3] Cui J, Dong S, Wang Z. Study on applicability of internal solitary wave theories by theoretical and numerical method. Applied Ocean Research | + | <span id='_neb9E7607E2_8CC5_4704_8EDC_65232DC3188C'></span> [3] Cui J., Dong S., Wang Z. Study on applicability of internal solitary wave theories by theoretical and numerical method. Applied Ocean Research, 111:102629, 2021. |
| − | <span id='_nebB0B99C6E_F214_49DB_8071_899C36AE0AD7'></span> [4] Alford | + | <span id='_nebB0B99C6E_F214_49DB_8071_899C36AE0AD7'></span> [4] Alford M.H., Lien R., Simmons H., et al. Speed and evolution of nonlinear internal waves transiting the South China Sea. Journal of Physical Oceanography, 40(6):1338-1355, 2010. |
| − | <span id='_nebEA94831D_DAD0_43BF_ADD5_AE940F12B5B4'></span> [5] Chen | + | <span id='_nebEA94831D_DAD0_43BF_ADD5_AE940F12B5B4'></span> [5] Chen C.Y., Hsu R.C., Chen H.H., et al. Laboratory observations on internal solitary wave evolution on steep and inverse uniform slopes. Ocean Engineering, 34(1):157-170, 2007. |
| − | <span id='_neb70BE7145_9EDC_4C2E_9BA7_36B1DEEAC8FB'></span> [6] Zou | + | <span id='_neb70BE7145_9EDC_4C2E_9BA7_36B1DEEAC8FB'></span> [6] Zou P.X., Bricker J.D., Uijttewaal W.S.J. The impacts of internal solitary waves on a submerged floating tunnel. Ocean Engineering, 238:109762, 2021. |
| − | <span id='_neb6406592C_E197_46DF_A377_D720346DEC31'></span> [7] Wang X, Zhou J, Wang Z, et al. A numerical and experimental study of internal solitary wave loads on semi-submersible platforms. Ocean | + | <span id='_neb6406592C_E197_46DF_A377_D720346DEC31'></span> [7] Wang X., Zhou J., Wang Z., et al. A numerical and experimental study of internal solitary wave loads on semi-submersible platforms. Ocean Engineering, 150:298-308, 2018. |
| − | <span id='_neb7E1675DA_6A67_46D0_BD31_11035A3811E1'></span> [8] Ding W, Ai C, Jin S, et al. 3D Numerical investigation of forces and flow field around the semi-submersible platform in an internal solitary wave. Water | + | <span id='_neb7E1675DA_6A67_46D0_BD31_11035A3811E1'></span> [8] Ding W., Ai C., Jin S., et al. 3D Numerical investigation of forces and flow field around the semi-submersible platform in an internal solitary wave. Water, 12(1):208, 2020. |
| − | <span id='_nebC1AB4008_0311_447F_B3B9_585AFCDB0050'></span>[9] Chen J, You | + | <span id='_nebC1AB4008_0311_447F_B3B9_585AFCDB0050'></span>[9] Chen J., You Y.X., Liu X.D., et al. Numerical simulation of interaction of internal solitary waves with a moving submarine. Chinese Journal of Hydrodynamics, 2010. |
| − | <span id='_nebF9F37563_C5E0_47BA_A3E6_AB43CB4808D0'></span>[10] Li J, Zhang Q, Chen T. Numerical investigation of internal solitary wave forces on submarines in continuously stratified fluids. Journal of | + | <span id='_nebF9F37563_C5E0_47BA_A3E6_AB43CB4808D0'></span>[10] Li J., Zhang Q., Chen T. Numerical investigation of internal solitary wave forces on submarines in continuously stratified fluids. Journal of Marine Science and Engineering, 9(12):1374, 2021. |
| − | [11] Guan H, Wei G, Hui | + | [11] Guan H., Wei G., Hui D.U. Hydrodynamic properties of interactions of three-dimensional internal solitary waves with submarine. Journal of PLA University of Science and Technology (Natural Science Edition), 13(05):577-582, 2012. |
| − | [12] Groves | + | [12] Groves N.C., Huang T.T., Chang M.S. Geometric characteristics of DARPA SUBOFF models (DTRC Model Nos. 5470 and 5471). Technical Report (No.DTRC/SHD-1298-01), 1989. |
| − | [13] Du H , Wei G , Zeng | + | [13] Du H., Wei G., Zeng W.H., et al. Experimental investigation on the kinematics characteristic of submerged slender body under internal solitary wave of depression. Journal of Ship Mechanics, 21(10):1210-1217, 2017. |
| − | <span id='_neb0F8BB81C_4ACB_4A46_A5D8_18B1A98389B0'></span>[14] Cui J, Dong S, Wang Z, et al. Kinematic response of submerged structures under the action of internal solitary waves. Ocean Engineering | + | <span id='_neb0F8BB81C_4ACB_4A46_A5D8_18B1A98389B0'></span>[14] Cui J., Dong S., Wang Z., et al. Kinematic response of submerged structures under the action of internal solitary waves. Ocean Engineering, 196:106814, 2020. |
| − | <span id='_nebEC3BF0DB_6ED8_4811_B654_126EBF70E930'></span>[15] Koop | + | <span id='_nebEC3BF0DB_6ED8_4811_B654_126EBF70E930'></span>[15] Koop C.G., Butler G. An investigation of internal solitary waves in a two-fluid system. Journal of Fluid Mechanics, 112:225-251, 1981. |
| − | <span id='_neb5D2BFFF9_2F16_43A6_AB2F_57B09F6E6048'></span>[16] Korteweg | + | <span id='_neb5D2BFFF9_2F16_43A6_AB2F_57B09F6E6048'></span>[16] Korteweg D.J., de Vries G. XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 39(240):422-443, 1895. |
| − | <span id='_neb7CE8CB30_1770_4BDA_8C4F_A16DCD76F9E1'></span>[17] Ostrovsky | + | <span id='_neb7CE8CB30_1770_4BDA_8C4F_A16DCD76F9E1'></span>[17] Ostrovsky L.A., Stepanyants Y.A. Do internal solitons exist in the ocean?. Reviews of Geophysics, 27(3):293-310, 1989. |
| − | <span id='_neb84F0F059_30BA_4914_B0DA_14413D389C9F'></span>[18] Hirt | + | <span id='_neb84F0F059_30BA_4914_B0DA_14413D389C9F'></span>[18] Hirt C.W., Nichols B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 39(1):201-225, 1981. |
| − | <span id='_nebD785F48B_4786_4E6C_9DEE_7ABA5D7FCD5E'></span>[19] Ma W, Li Y, Ding Y, et al. Numerical investigation of internal wave and free surface wave induced by the DARPA SUBOFF moving in a strongly stratified fluid. Ships and | + | <span id='_nebD785F48B_4786_4E6C_9DEE_7ABA5D7FCD5E'></span>[19] Ma W., Li Y., Ding Y., et al. Numerical investigation of internal wave and free surface wave induced by the DARPA SUBOFF moving in a strongly stratified fluid. Ships and Offshore Structures, 15(6):587-604, 2020. |
Latest revision as of 15:23, 5 October 2023
Abstract
The internal solitary waves (ISWs) in the ocean carry huge energy and pose a serious threat to the safety of underwater vehicle. In order to obtain the dynamic response of the submarine under the action of ISWs, the amplified SUBOFF model was placed in a large numerical water tank with a length of 5000m, a width of 200m and a depth of 500m. The Korteweg-de Vries (KdV) theory was adopted to simulate the generation of ISWs in the two-layer flow, and overset grid technology was used to ensure the grid quality during the submarine movement. The results show that before the ISWs peak reaches the position of the submarine, the submarine will move, which causes the submarine to sink, move laterally and pitch. The longitudinal velocity is obviously greater than the lateral velocity, and the submarine finally hits the water tank bottom. With the increase of the ISWs amplitude, the time needed for submarine to reach the bottom increases, and the pitching angle increases greatly. The ISWs amplitude has no effect on the motion trajectory of the submarine's center of gravity, and has little effect on the lateral and longitudinal velocity. With the decrease of submergence depth of the submarine, the time required for submarine to reach the bottom will also increase, and the motion trajectory will change, but the trend of change is basically the same. The submergence depth has little influence on the variation range of lateral velocity, longitudinal velocity and pitching angle.
Keywords: internal solitary waves, submarine, dynamic response, numerical simulation
1. Introduction
Internal solitary waves (ISWs) are common phenomenon in the stratified ocean, which has the characteristics of medium-fine scale, large amplitude and strong velocity [1]. The shear currents and turbulence generated by ISWs contribute to global energy transport and dissipation in the ocean, but also affect biological activities, offshore engineering and submarine navigation [2]. Due to the development of ISWs below the sea surface, low propagation frequency and long distance, it is difficult to observe them which seriously threaten the safety of ocean engineering structures and underwater vehicle [3].
In view of the influence of ISWs on ocean engineering and underwater vehicles, the current research focuses on the monitoring of ISWs [1,4], and the simulation of ISWs [3,5], as well as the influence of ISWs on submerged tunnels [6], semi-submersible platforms [7-8] and submarines [9-11]. Research on the interaction between ISWs and submarines has focused on the standard submarine model proposed by the Defense Advanced Research Projects Agency (DARPA), known as the DARPA SUBOFF model [12]. CHEN studied the submarine load variation induced by ISWs with and without submarine speed [9]. LI used the numerical model of ISWs in a continuously stratified fluid, numerically analyzed the forces and moments of SUBOFF when it encountered ISWs in different submergence depths, discussed the influence of rotation center position on the moment, and proposed the optimal rotation center position [10]. GUAN numerically studied the hydrodynamic properties and load characteristics of submarine when it encountered ISWs in the ocean [11].
It is worth noting that in the above studies, the freedom of the submarine is constrained when the submarine encounters the ISWs. The submarine position is fixed and in a static state. As matter of fact, the submarine will inevitably move or even sink when it encounters the ISWs. So the submarine movement must be taken into account in the research. DU studied the kinematics characteristic and the mass center trace of the slender model in the density stratification fluid with a semi-flexible restriction technique, and obtained the properties such as heave, surge, roll, pitch, but the slender body was bound by the flexible line in the water tank [13]. CUI used experimental methods to study the dynamic response of submerged body under the action of ISWs, and obtained the influence of different wave amplitudes, the thickness ratio of the upper and lower layers of fluid, and the shape of the submarine section, etc. Strong currents in the horizontal and vertical directions caused by ISWs can greatly move submerged body and cause damage to its structure. Limited by the experimental tank, the section of the submerged model is less than 10cm [14]. In general, the submerged body is affected by ISWs, which will lead to lateral, longitudinal and pitching motions.
In order to simulate the situation of large submarine encountering ISWs in the ocean, a large numerical tank and a large submarine model are constructed by numerical simulation method, and the dynamic response of submarine under the action of ISWs is studied in a numerical tank with continuous density changes.
2. Simulation configurations
2.1 Submarine model
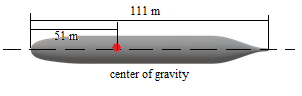
The standard submarine model of Defense Advanced Research Projects Agency (DARPA), which called DARPA SUBOFF, has an overall length of 4.356m and a maximum diameter of 0.508m, as shown in Figure 1(a). The SUBOFF model itself is small in scale, so a 1:25.5 scale of DARPA SUBOFF is used to simulate the actual submarine. In order to ensure the quality of the grids, the grids in the submarine appendage area must be refined and the time step must be reduced to ensure a reasonable Courant number, which consumes more computational resources. However the main purpose of this work is to study the free motion of the submarine and the influence of appendages on free motion is minimal. Here, the model used in this work was simplified and the appendages of SUBOFF model were removed, as shown in Figure 1(b). The enlarged bare hull has an overall length of 111m and a maximum diameter of 12.954m. The gravity center of the submarine is placed on the axis of the hull, 51 m away from the bow.
| ||||
| Figure 1. SUBOFF model |
2.2 Numerical flume
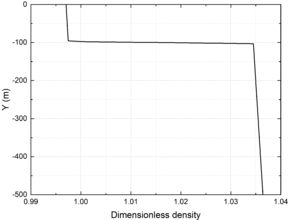
The numerical flume is shown in the Figure 2 and has a total length of 5000 m, width of 200 m and depth of 500 m, including the working zone which has a length of 4000 m and the wave damping zone which has a length of 1000 m. The fluid densities of the upper and lower layers are different. The density varies continuously along depth in each layer of fluid, as shown in Figure 3. The Dimensionless density means the density/ kg/m. The upper layer fluid density varies from kg/m to kg/m and the lower layer fluid density varies from kg/m to kg/m. The depth of the upper and lower fluid are 100m and 400m, respectively.

|
| Figure 2. Sketch of numerical flume |
|
| Figure 3. Change of density along the water depth |
The distance between submarine location and the two layers interface is defined as the submergence depth H. The inlet and outlet are on the left side of the flume. Speed entrance method is adopted to make the numerical wave and pressure boundary condition is inducted for outlet. The inlet boundary is set by the user-defined function (UDF), which produces the ISWs. The bottom, top and right of the flume are all using the solid wall boundary.
2.3 ISW theory
The Korteweg-de Vires (KdV) equation has a wide range of applications for small amplitude and weak nonlinear ISWs [3]. For the numerical flume established in this paper, the ratio of wave amplitude to the depth of the flume ( is the ISW amplitude), so the KdV theory can be used [15]. The propagation of a wave along the horizontal x direction is expressed as [16-17]:
|
|
(1) |
where , and are the linear phase speed, nonlinear coefficient, measure of dispersion respectively, which can be wright as:
|
|
(2) |
|
|
(3) |
|
|
(4) |
The KdV expression for the ISW is:
|
|
(5) |
The soliton velocity and characteristic wavelength based on KdV theory are:
|
|
(6) |
|
|
(7) |
2.4 Meshing scheme and simulation method
(1) Meshing scheme
The submarine will move horizontally and vertically, accompanied by pitching motion which affected by ISWs, as shown in Figure 4. The moving mesh is easy to be generated with negative volume, and the grid update takes a long time, resulting in a very long computation time. So the overset mesh technology is adopted in this paper. A separate component mesh was constructed in the SUBOFF region, the size of which was 160 m×20 m×60 m. The unstructured grids were adopted with total grids of 1.42 million. In addition, structured grid was used in the flume as the background grid with total grids of 5.31 million, as shown in Figure 5. In the overlapping regions, the overset interfaces connect cell zones by interpolating cell data. The overset mesh method can maintain mesh quality well during submarine motion.
|
| Figure 4. Sketch of submarine motion |
| ||||
| Figure 5. The computational grid in the domain |
(2) Simulation method
The unsteady Reynolds- Averaged Navier-Stokes equations with the turbulence model are applied to simulate the flow field. The turbulence added two variables to the governing equation which are turbulence kinetic energy and dissipation rate of turbulence kinetic energy . represents the change of velocity fluctuation and represents dissipation rate of velocity fluctuation. The mass continuity equation and momentum equation are shown as follows:
|
|
(8) |
|
|
(9) |
where is effective viscosity, is the modified pressure, and is the sum of body forces.
The and can be solved by following equations:
|
|
(10) |
|
|
(11) |
where and are Prandtl numbers corresponding to turbulence kinetic energy and dissipation rate, respectively; is the turbulence production due to viscous forces; and are constants; is the dynamic viscosity and is the turbulent viscosity.
The ISW wave surface was tracked by Volume of fluid (VOF) method [18]. The fluid’s volume fraction represents the ratio of the fluid’s volume in a cell to the total volume of the cell. For the , the equation has the following form:
|
|
(12) |
For every control volume, the volume fractions of all phases sum to unit. When , the cell is full of the fluid; when , the cell is empty of the fluid; when , the cell contains the interface [19]. For the two-layer fluid in this paper, or 2.
3. Numerical results and discussions
The submarine is located in the numerical flume and the distance between the gravity center and the flume inlet is 1500 m. The submarine is in a state of equilibrium with its own buoyancy. The power of the submarine is not taken into account, so it has no initial speed and its freedom of motion is not constrained.
In order to study the interactions between different ISWs and submarine, three ISW amplitudes and two submergence depths are used in this part, which include m, m, m and m, m, as shown in Table 1.
| H (m) (m) |
45 | 15 |
|---|---|---|
| 10 | C11 | C12 |
| 20 | C21 | C22 |
| 30 | C31 | C32 |
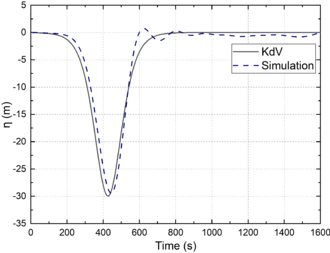
The case C31 was selected to verify the numerical flume established in this paper, and the formation of ISWs was monitored at x=1500m. As can be seen from Figure 6, the wave generation of the numerical flume was highly consistent with that of KdV theory, which met the requirements of numerical simulation.
|
| Figure 6. Numerical result verification |
3.1 Trajectory of submarine motion
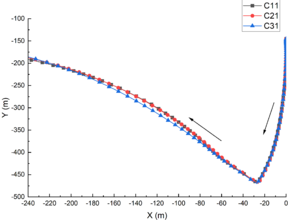
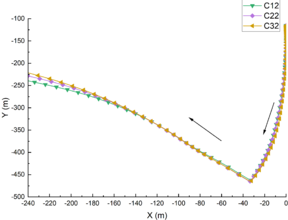
The initial submergence depth of SUBOFF was 45m or 15m below the interface. When the ISWs flow field was formed by the numerical flume, the motion of the submarine was observed. Figure 7 shows the motion trajectory of SUBOFF's center of gravity under different submergence depths. As can be seen from Figure 7, no matter the depth is 45m or 15m, SUBOFF's center of gravity moved in a similar trajectory, moving to the lower left under the influence of the ISWs. And the longitudinal displacement was significantly greater than the lateral displacement. Restricted by the size of the numerical flume, SUBOFF rebounded after impacting the bottom of the flume, and then continued to move to the upper left. At the same depth, the ISWs amplitude had no effect on the trajectory of submarine motion. Different wave amplitudes had no effect on the position of the impact point of SUBOFF, and the trajectory of the submarine basically coincided after rebound.
| ||||
| Figure 7. Trajectory of submarine motion |
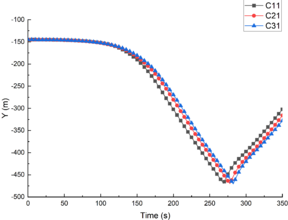
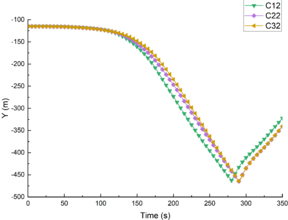
The change of submarine longitudinal position with time is shown in Figure 8. For the first 100s, SUBOFF kept its position unchanged. Because the flow field of ISWs had not reached the zone where the submarine was located, and the submarine was in a state of equilibrium. Then it began to dive under the influence of the ISWs flow field, and finally hit bottom and rebounded. As can be seen from Figure 8, with the increase of ISWs amplitude, the time required for the submarine to reach the bottom was longer, and the time required for C11, C21 and C31 to reach the bottom were 269s, 278s and 282s, respectively. So with the higher ISW amplitude, the submarine longitudinal velocity reduced. According to KdV theory, the ISWs speed decreased with the increase of the ISWs amplitudes, which was the reason for the change of submarine bottoming time. The position of the submarine was 1500m away from the flume inlet, and it took less than 300s for the submarine sink more than 300m. It can be seen that the ISWs can cause serious damage to the submarine.
| ||||
| Figure 8. Change of submarine longitudinal position with time |
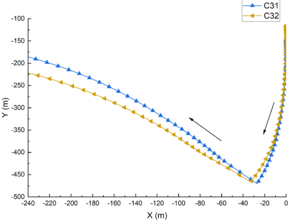
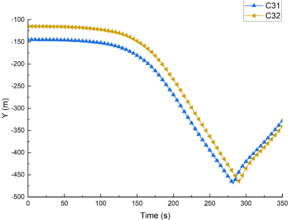
In order to compare the influence of different submergence depth on the submarine motion trajectory, C31 and C32 with a wave amplitude of 30m were selected, as shown in Figure 9. The distance between the submarine and the flume bottom became greater with the decrease of the submergence depth, which lead to the lateral displacement was greater when the submarine hit the bottom, and the longitudinal displacement was smaller after the rebound which was affected by the ISWs. As can be seen from Figure 9(b), as the depth decreased, the time required for the submarine to reach the bottom increased.
| ||||
| Figure 9. Trajectory of submarine motion with different |
It is well known that the submarine will be dragged into the seabed by ISWs, and the impact on the bottom will produce strong load and lead to serious damage to its structure. The data after the rebound on the bottom has little significance. Therefore, this paper focuses on the analysis before the submarine hits the bottom.
3.2 Characteristics of the motion
The motion characteristics of the marine in the flume were studied when the wave amplitude was 20m and the submergence depth was 15m (C22). Figure 10 shows the movement of SUBOFF at six moments before it hits the bottom. The color mark the upper and lower layers of fluid with different densities respectively, and the submarine is below the interface. During the first 100s, the position of the submarine remained basically unchanged. After that, the submarine began to sink, and Figure 10(d) showed obvious sinking of the submarine. At s, it can be seen that the submarine was starting to pitch, the submarine's bow was up. At s, the change of pitching and sinking was obvious. At this time, the ISWs peak has not reached the location of the submarine. The flow field formed by ISWs had a strong influence on the submarine before the peak of the ISW reached the position of the submarine, resulting in not only submarine transverse and longitudinal displacement but also the pitching.
| ||||||||||||
| Figure 10. Submarine motion characteristics at different times |
3.3 Motion parameters
(1) The effect of different ISWs amplitudes
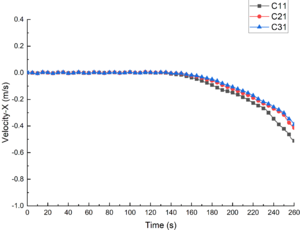
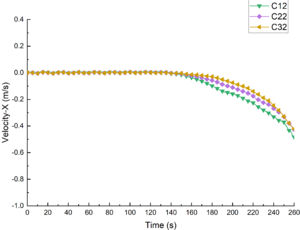
The lateral velocity of the submarine under different ISW amplitudes is shown in Figure 11. After s, the absolute lateral value of velocity increased along the negative -direction. Under the same submergence depth, lateral acceleration decreased with the increase of wave amplitude. When m and s, the lateral velocities of C11, C21 and C31 were -0.51 m/s, -0.41 m/s and -0.39 m/s, respectively. By comparison with Figure 11(a) and Figure 11(b), it is found that the submergence depth has little influence on the lateral velocity variation trend.
| ||||
| Figure 11. Lateral velocity at different ISW amplitudes |
The longitudinal velocity of the submarine under different depths is shown in Figure 12 . Similar to the lateral velocity, the longitudinal velocity increased along the negative y-direction, and the change of longitudinal velocity was one order of magnitude larger than that of the lateral velocity. Before s, the submarine was accelerating longitudinally. After s, the longitudinal velocity began to keep basically stable at about -2.5m/s.
| ||||
| Figure 12. Longitudinal velocity at different ISW amplitudes |
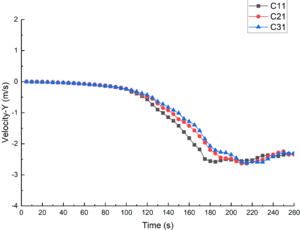
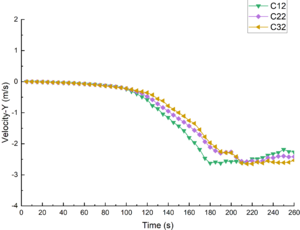
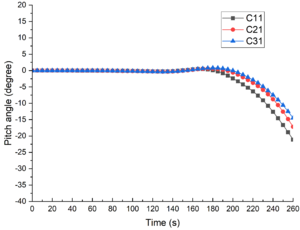
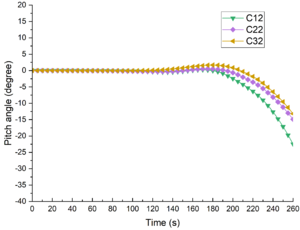
The pitch angle of the submarine under different ISW amplitudes is shown in Figure 13. When the submergence depth was 45m, as shown in Figure 13(a), the submarine basically keeps level without pitching before s; after s, the submarine began to pitch. The pitch angle gradually increased with time, and the pitch angle variation decreased with the increase of ISW amplitudes. When s, the pitch angles of C11, C21 and C31 were -21.10°, -17.16° and -14.50°, respectively. When the submergence depth m, the changes of pitch angle were similar to m.
| ||||
| Figure 13. Pitch angle at different ISW amplitudes |
(2) The effect of submergence depths
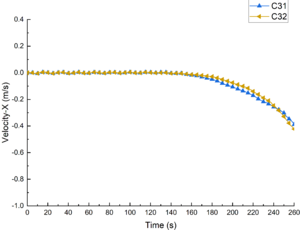
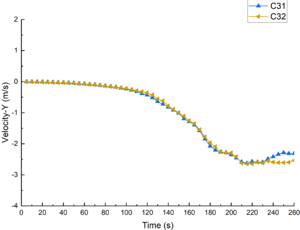
Figure 14 shows the comparison of the submarine velocity under different submergence depths. When the wave amplitude was constant, the influence of the submergence depth on the change of the lateral velocity and longitudinal velocity can be ignored.
| ||||
| Figure 14. Comparison of velocity at different depths |
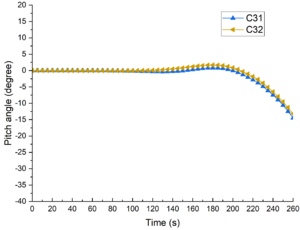
The variations of pitch angle with time at the same wave amplitude but different submergence depths are shown in Figure 15. As shown in the figure, submergence depths had little influence on the variation of pitch angle.
|
| Figure 15. Comparison of pitch angle at different depths |
4. Conclusions
The dynamic response of large submarine induced by ISWs was simulated by establishing the ISWs numerical flume. The flume was a stratified fluid of two layers, and the fluid density varied with the depth which was more in line with the actual ocean. The track of gravity center, variations in lateral, longitudinal and pitch motion are studied. The conclusions of this study are listed as follows:
(1) When the submarine is located under the two-layer interface, the submarine moves to the lower left, then impacts on bottom and rebounds which is affected by ISWs. The submarine motion trajectory and the impact location are not affected by the initial submergence depth.
(2) The ISW amplitude also affects the time for the submarine impacting the flume bottom, and as the ISW amplitude increases, the longer the time is required.
(3) The submarine will move which is affected by ISWs. The longitudinal velocity is bigger than lateral velocity. The motion of the submarine is accompanied by pitching. The influence of submergence depth on the submarine lateral velocity and longitudinal velocity is negligible. Before the submarine reaches the bottom, the horizontal velocity is increasing. The higher the ISW amplitude, the smaller the longitudinal velocity is. The longitudinal velocity also accelerates first, and then the value fluctuation is maintained. In the process of the sinking, the pitch angle gradually becomes larger, and the pitch angle decreases as the ISW amplitude increases. The changes in the pitch angle are not affected by the submergence depth.
Acknowledgments
This work was supported by Natural Science Foundation of Sichuan Province of China No. 2022NSFSC0478, CAFUC Foundation J2022-035 and Foundation of Key Laboratory of Flight Techniques and Flight Safety,CAAC, FZ2020ZZ05.
Conflict of interest statement
The authors declare that there are no conflict of interests, we do not have any possible conflicts of interest.
References
[1] Huang X., Chen Z., Zhao W., et al. An extreme internal solitary wave event observed in the northern South China Sea. Scientific Reports, 6(1):30041, 2016.
[2] Guo C., Chen X. A review of internal solitary wave dynamics in the northern South China Sea. Progress in Oceanography, 121:7-23, 2014.
[3] Cui J., Dong S., Wang Z. Study on applicability of internal solitary wave theories by theoretical and numerical method. Applied Ocean Research, 111:102629, 2021.
[4] Alford M.H., Lien R., Simmons H., et al. Speed and evolution of nonlinear internal waves transiting the South China Sea. Journal of Physical Oceanography, 40(6):1338-1355, 2010.
[5] Chen C.Y., Hsu R.C., Chen H.H., et al. Laboratory observations on internal solitary wave evolution on steep and inverse uniform slopes. Ocean Engineering, 34(1):157-170, 2007.
[6] Zou P.X., Bricker J.D., Uijttewaal W.S.J. The impacts of internal solitary waves on a submerged floating tunnel. Ocean Engineering, 238:109762, 2021.
[7] Wang X., Zhou J., Wang Z., et al. A numerical and experimental study of internal solitary wave loads on semi-submersible platforms. Ocean Engineering, 150:298-308, 2018.
[8] Ding W., Ai C., Jin S., et al. 3D Numerical investigation of forces and flow field around the semi-submersible platform in an internal solitary wave. Water, 12(1):208, 2020.
[9] Chen J., You Y.X., Liu X.D., et al. Numerical simulation of interaction of internal solitary waves with a moving submarine. Chinese Journal of Hydrodynamics, 2010.
[10] Li J., Zhang Q., Chen T. Numerical investigation of internal solitary wave forces on submarines in continuously stratified fluids. Journal of Marine Science and Engineering, 9(12):1374, 2021.
[11] Guan H., Wei G., Hui D.U. Hydrodynamic properties of interactions of three-dimensional internal solitary waves with submarine. Journal of PLA University of Science and Technology (Natural Science Edition), 13(05):577-582, 2012.
[12] Groves N.C., Huang T.T., Chang M.S. Geometric characteristics of DARPA SUBOFF models (DTRC Model Nos. 5470 and 5471). Technical Report (No.DTRC/SHD-1298-01), 1989.
[13] Du H., Wei G., Zeng W.H., et al. Experimental investigation on the kinematics characteristic of submerged slender body under internal solitary wave of depression. Journal of Ship Mechanics, 21(10):1210-1217, 2017.
[14] Cui J., Dong S., Wang Z., et al. Kinematic response of submerged structures under the action of internal solitary waves. Ocean Engineering, 196:106814, 2020.
[15] Koop C.G., Butler G. An investigation of internal solitary waves in a two-fluid system. Journal of Fluid Mechanics, 112:225-251, 1981.
[16] Korteweg D.J., de Vries G. XLI. On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 39(240):422-443, 1895.
[17] Ostrovsky L.A., Stepanyants Y.A. Do internal solitons exist in the ocean?. Reviews of Geophysics, 27(3):293-310, 1989.
[18] Hirt C.W., Nichols B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. Journal of Computational Physics, 39(1):201-225, 1981.
[19] Ma W., Li Y., Ding Y., et al. Numerical investigation of internal wave and free surface wave induced by the DARPA SUBOFF moving in a strongly stratified fluid. Ships and Offshore Structures, 15(6):587-604, 2020.Document information
Published on 05/10/23
Accepted on 07/09/23
Submitted on 25/07/23
Volume 39, Issue 4, 2023
DOI: 10.23967/j.rimni.2023.09.006
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?