(Tag: Visual edit) |
|||
| (86 intermediate revisions by 4 users not shown) | |||
| Line 24: | Line 24: | ||
Email: [mailto:lvthao@dut.udn.vn lvthao@dut.udn.vn] | Email: [mailto:lvthao@dut.udn.vn lvthao@dut.udn.vn] | ||
--> | --> | ||
| + | ==Abstract== | ||
| − | + | The suffusion susceptibility of the soil samples is evaluated through an erosion resistance index. Thanks to existing statistical analyses, the erosion resistance index is estimated from several soil parameters. In actual exploitation, the soil properties with the input parameters related to the grain distribution of the soil… vary greatly from the original design value due to the influence of many factors. One of the factors is the inherent variability. Inherent soil variability is modelled as a random field. The usual problems used to assess the suffusion susceptibility may be not give accurate results or fully evaluate the actual working ability of the ground in each case. This is one of the reasons why dams are still eroded when they are put into use. The paper aims predict erosion resistance index of the earth dam using two-dimensional (2D) Stochastics random field, modelling the initial problem, considering the variability spatial of soil properties, using the assumption of a Normal random field of soil characteristics parameters. The paper shows the predicted results of the variability spatial of erosion resistance index of Phu Vinh dam-Vietnam. Furthermore, the paper also represents the happened probability of suffusion susceptibility at the different zones in the earth dam body. | |
| − | ''' Keywords | + | ''' Keywords''': Internal erosion, suffusion susceptibility, erosion resistance index, numerical simulation, random field |
| − | =1. | + | ==1. Introduction== |
| − | Internal erosion is one of the main causes of instabilities within hydraulic earth structures such as dams, dikes, or levees | + | Internal erosion is one of the main causes of instabilities within hydraulic earth structures such as dams, dikes, or levees [1]. According to Fell and Fry [2], there are four types of internal erosion: concentrated leak erosion, backward erosion, contact erosion and suffusion. Concentrated leak erosion may occur through a crack or hydraulic fracture. Backward erosion mobilizes all the grains in regressive way (i.e., from the downstream part of earth structure to the upstream part) and includes backward erosion piping and global backward erosion. Contact erosion occurs where a coarse soil is in contact with a fine soil. The phenomenon of suffusion corresponds to the process of detachment and then transport of the finest particles within the porous network under seepage flow. The finer fraction eroded and leaving the coarse matrix of the soil will further modify the hydraulic conductivity and mechanical parameters of the soil. This suffusion process may result in an increase of hydraulic conductivity, seepage velocities and hydraulic gradients, possibly accelerating the rate of suffusion [3]. The development of suffusion may cause the incidents of dam including piping and sinkholes. |
| − | In the literature, some researchers assume that suffusion is best represented by its initiation. | + | In the literature, some researchers assume that suffusion is best represented by its initiation. Garner and Fannin [4] take into account the main initiation conditions for suffusion include three components: material susceptibility, critical hydraulic load and critical stress condition. Several methods have been proposed to characterize the initiation of suffusion confronting material susceptibility criteria and hydraulic criteria [5]. |
| − | + | Marot et al. [6] proposed a new analysis based on the energy expended by the seepage flow which is a function of both the flow rate and the pressure gradient. Le et al. [7] performed many the suffusion tests to “final state”. This ‘final state’ is obtained towards the end of each test when the hydraulic conductivity is constant while the rate of erosion decreases. The expended energy <math>E_{\rm flow}</math> is the time integration of the instantaneous power dissipated by the water seepage for the test duration. For the same duration the cumulative eroded dry mass is determined, the erosion resistance index is expressed by: | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> I_\alpha = - \log \,(\hbox{Eroded dry mass/}E_{\rm flow}) </math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(1) | ||
| + | |} | ||
| − | |||
| − | + | Depending on the values of <math> I_\alpha</math> index, Marot et al. [8] proposed six categories of suffusion susceptibility from highly erodible to highly resistant (corresponding susceptibility categories: highly erodible for <math> I_\alpha <2</math>; erodible for <math>2\le I_\alpha < 3</math>; moderately erodible for <math>3\le I_\alpha < 4</math>; moderately resistant for <math>4\le I_\alpha < 5</math>; resistant for <math>5\le I_\alpha < 6</math>; and highly resistant for <math> I_\alpha \ge 6</math>). Since the erosion resistance index <math> I_\alpha</math> has been proven to be intrinsic, i.e., independent of the sample size [9]. Zhang et al. [10] gave a method to assess the suffusion susceptibility of low permeability core soil in compacted dams based on construction data. They showed the one-dimensional (1D) spatial variability of all material parameters, in particular the hydraulic conductivity, the dry unit weight and the grain size distribution which affect the erosion resistance index. However, the suffusion susceptibility of earth dam body through the erosion resistance index needs to be assess the two-dimensional spatial variability. A two-dimensional contour map of the erosion resistance index would provide additional valuable information. | |
| − | + | Phoon and Kulhawy [11] showed the disparate sources of uncertainties. One of the primary sources of geotechnical uncertainties is inherent soil variability. When we repeat the experiment many times at the same location, or at different locations, we always don't get the same result. To suppress or eliminate the influence of this source, we often use a very large number of samples. However, in practice, this implementation is not feasible because the experimental conditions do not allow, or the cost is too great. So, in the current calculation, there is always this random source. The objectives of the paper are to assess the suffusion susceptibility of earth dam considering variability spatial of soil properties. To tackle this objective, the contour map of 2D spatial variability of erosion resistance index of earth dam body is presented. This approach is based on two-dimensional Stochastics random field. | |
| − | + | ==2. Description== | |
| − | ===2.1 | + | ===2.1 Assessment of soil suffusion susceptibility === |
| − | + | Le et al. [7] showed the correlation equation between physical parameters and erosion resistance index <math> I_\alpha</math> for all soils | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>I_{\alpha}= - 13.57 + 0.43 \gamma_d + 0.18 \phi - 0.02 \hbox{ Finer } KL + 0.49 V_{BS} + 189.70 k_i + </math> <math>3.82 \min (H/F) + 0.18 P + 0.28 G_r + 19.51d_5 + 1.06 d_{15} - 0.84 d_{20} + 0.81d_{50} - 0.98 d_{60} - 0.10d_{90}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(1) | ||
| + | |} | ||
| − | + | where: dry unit weight <math>\gamma_d</math>, blue methylene value <math>V_{BS}</math>, internal friction angle <math>\phi</math>, initial hydraulic conductivity <math>k_i</math>, minimum value of ratio H/F, percentage of finer fraction (based on Kenney and Lau’s criteria) <math>\hbox{Finer } KL</math>, gap ratio <math>G_r</math>, <math>d_5</math>, <math>d_{15}</math>, <math>d_{20}</math>, <math>d_{50}</math>, <math>d_{60}</math>, <math>d_{90}</math> (diameters of the 5%, 15%, 20%, 50%, 60%, 90% mass passing, respectively) and <math>P</math> (percentage of finer than 0.063mm) | |
| − | + | For widely graded soils, the correlation of physical parameters with the erosion resistance index: (<math>N=10</math>, <math>R^2 =0.99</math>) | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>I_{\alpha}=-26.34+0.43 \gamma_d + 0.66 \phi - 0.16 \hbox{ Finer } KL + 1.15 V_{BS} + 0.37 P + 6.82 d_5 - 1.26 d_{60}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(2) | ||
| + | |} | ||
| − | + | For gap-graded soils, the correlation of physical parameters with the erosion resistance index: (<math>N=21</math>, <math>R^2 =0.90</math>) | |
| − | + | {| class="formulaSCP" style="width: 100%; text-align: left;" | |
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | style="text-align: center;" | <math>I_{\alpha}=-237.62 + 0.67 \gamma_d + 0.64\phi + 0.09</math> <math> \hbox{ Finer } KL </math> <math> - 0.03 V_{BS} - 1.43 P + 0.63 G_r + 0.76 d_5 -0.97 d_{60} + 0.61 d_{90}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" |(3) | ||
| + | |} | ||
| − | + | ===2.2 Assessment of the relative suffusion potential === | |
| − | + | The erosion resistance index (<math> I_\alpha</math>) is just a material parameter that characterizes the susceptibility of a given soil to suffusion. Hence, it cannot be interpreted as a ‘security factor’ to distinguish between ‘probable occurrence of erosion’ and ‘no erosion’ [10], This distinction requires additionally the estimation of the hydraulic loading. The erosion resistance index is estimated from several soil parameters using 2D Stochastics random field. Therefore, the relative suffusion potential of the earth dam body may be characterized by the 2D contour map of the erosion resistance index <math> I_\alpha</math>. A contour map shows the suffusion susceptibility at locations in the homogeneous earth dam body through the erosion resistance index value <math> I_\alpha</math>. Cross-section of the earth dam will be pointed out with the spatial variability of <math> I_\alpha</math>, may be low of high resistance to suffusion. | |
| − | + | ==3. Numerical simulation== | |
| − | =3. | + | ===3.1 Simulation methodology=== |
| − | + | In this paper, the soil characteristic parameters are modeled as a random field. These parameters are inputted in the model using the two-dimensional (2D) Stochastics random field which is researched in Vanmarcke [12]. In a random finite element method, the spatial variability <math> \gamma</math>, <math> \phi</math>, <math> \hbox{Finer } KL </math>, <math>P</math>, <math>d_5</math>, <math>d_{60}</math> are simulated by a random field with assumed coefficient of variance (cov) <math>cov = 0.05</math> and mapped onto the finite element mesh. This estimation is based on Eq. (2) since all soil samples are widely graded. Among the seven parameters of Eq. (2), the blue methylene value (<math>V_{BS}</math>) was considered constantly <math>V_{BS}=0.5</math> g/100g in the dam. The forecasting result of spatial variability of erosion resistance index with the contour map 2D is showed. | |
| − | + | ===3.2 Numerical results=== | |
| − | + | ====A Case study in Phu Vinh-Quang Binh earth dam==== | |
| − | + | Phu Vinh Reservoir is one of the large reservoirs of Quang Binh-province, Vietnam. Since the project was put into use until now, it has contributed to the benefiting localities to eliminate hunger, reduce poverty, and at the same time make a significant contribution to economic development in Quang Binh province. After 24 years of use, the earth dam has deteriorated. At that time, we were still backward in terms of technological equipment for survey, design and construction of reservoir items, so the construction quality of some items of the reservoir was not up to the requirements of water quality. technical and aesthetic. Phu Vinh-Quang Binh earth dam is homogeneous earth dam, the upstream of the dam is reinforced with anhydrous paving stones and has deteriorated. The top of the dam is 5m wide with mixed soil, currently eroded and degraded. An of cross-section of earth dam body is illustrated in [[#img-1|Figure 1]]. the earth dam body in the [[#img-1|Figure 1]] includes material class (2a), dam crest in location 1a. | |
| − | + | <div id='img-1'></div> | |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:A Cross-Section.jpg|700px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 1'''. A cross-section of Phu Vinh earth dam | ||
| + | |} | ||
| − | |||
| − | |||
| − | + | The data of dam include full grain size distributions with widely graded soil, dry unit weight, internal friction angle, initial hydraulic conductivity, and other parameters with the following assumed average values: dry unit weight <math>\gamma_d =16.9</math> kN/m<sup>3</sup>; internal friction angle <math>\phi =13^0</math>; percentage of fines (%) (based on Kenny & Lau, 1985 criterion) <math>\hbox{Finer } KL =20%</math>; the percentage finer than <math>0.063</math> mm <math>P=24</math>%; <math>d_5 =0.1</math> mm; <math>d_{60} =1</math> mm. The suffusion susceptibility will be estimated through erosion resistance index. | |
| − | </ | + | |
| − | The | + | The result of erosion resistance index with contour map 2D is showed in [[#img-2|Figure 2]]. Several locations in the map pointed out with a low resistance to suffusion (blue color). Some zones with yellow color represent the high resistance to suffusion. The predicted values of Iα lies within the range from 2 to more than 6. These results may be explained by soil spatial variability. According to Zhang et al. [10], they show the one-dimensional spatial variability of erosion resistance index which erosion resistance index is estimated equally for one layer in the dam core. These results may be not given accurate results at different locations. Based on two-dimensional random field model, the two-dimensional spatial variability of erosion resistance index is predicted in the whole dam. |
| − | + | <div id='img-2'></div> | |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"|[[File:Le_2023b_6714_762px-Picture_001.jpg]] | ||
| + | <!--style="text-align: center;padding:10px;"| [[File:Picture 001.jpg|762x762px]]--> | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. Contour map 2D of erosion resistance index | ||
| + | |} | ||
| − | |||
| − | |||
| − | Figure | + | [[#img-3|Figure 3]] shows the histogram plot of erosion resistance index (blue color) with the normal distribution. The probability results are run from five hundred random times with Matlab code. The red curve is the probability of suffusion susceptibility of the earth dam. According to the classification of suffusion susceptibility of Marot et al. [8], the probability of suffusion susceptibility of the earth dam correspond to classification suffusion susceptibility shows in [[#tab-1|Table 1]]. This table shows that 3% is the probability of highly erosion, 6% is erosion, 41% is moderately erodible, 32% is moderately resistant, 14% is resistant and 4% is highly resistant. |
| − | + | ||
| − | Figure 3 | + | <div id='img-3'></div> |
| + | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Le_2023b_5579_733px-Picture_002.jpg]] | ||
| + | <!--style="text-align: center;padding:10px;"| [[File:Picture 002.jpg|733x733px]]--> | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Histogram plot of erosion resistance index and probability of suffusion susceptibility | ||
| + | |} | ||
| − | |||
| − | |||
| − | + | <div class="center" style="font-size: 75%;">'''Table 1'''. Probability of classification of suffusion susceptibility</div> | |
| − | </div> | + | |
| − | <div class=" | + | <div id='tab-1'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | + | |-style="text-align:center" | |
| − | + | ! style="text-align:left;" | Classification of suffusion susceptibility<br> through the Iα based on Marot et al. [8] !! Probability of suffusion <br> susceptibility (forecasting) | |
|- | |- | ||
| − | | style=" | + | | style="vertical-align: top;"|Highly erosion <math> I_\alpha <2</math> |
| − | | style=" | + | | style="vertical-align: top;text-align:center;"|3% |
|- | |- | ||
| − | | style="vertical-align: top;"| | + | | style="vertical-align: top;"|Erosion <math>2\le I_\alpha < 3</math> |
| − | | style="vertical-align: top;"| | + | | style="vertical-align: top;text-align:center"|6% |
|- | |- | ||
| − | | style="vertical-align: top;"| | + | | style="vertical-align: top;"|Moderately erodible <math>3\le I_\alpha < 4</math> |
| − | | style="vertical-align: top;"| | + | | style="vertical-align: top;text-align:center"|41% |
|- | |- | ||
| − | | style="vertical-align: top;"| | + | | style="vertical-align: top;"|Moderately resistant <math>4\le I_\alpha < 5</math> |
| − | | style="vertical-align: top;"| | + | | style="vertical-align: top;text-align:center"|32% |
|- | |- | ||
| − | | style="vertical-align: top;"| | + | | style="vertical-align: top;"|Resistant <math>5\le I_\alpha < 6</math> |
| − | | style="vertical-align: top;"| | + | | style="vertical-align: top;text-align:center"|14% |
|- | |- | ||
| − | | style="vertical-align: top;"|resistant | + | | style="vertical-align: top;"|Highly resistant <math> I_\alpha \ge 6</math> |
| − | | style="vertical-align: top; | + | | style="vertical-align: top;text-align:center"|4% |
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | =4. | + | ==4. Conclusions== |
| − | The result of paper assesses the suffusion susceptibility of the dam body using two-dimensional random field considering soil spatial variability. With illustration of a numerical simulation, the predicted result of spatial variability of erosion resistance index of Phu Vinh, Quang Binh is showed in a contour map 2D. Furthermore, the probability of suffusion susceptibility is also forecasted correspond to classification of suffusion susceptibility. This result demonstrates that the actual state of practice would be to account for the two-dimensional spatial variability | + | The result of paper assesses the suffusion susceptibility of the dam body using two-dimensional random field considering soil spatial variability. With illustration of a numerical simulation, the predicted result of spatial variability of erosion resistance index of Phu Vinh, Quang Binh is showed in a contour map 2D. Furthermore, the probability of suffusion susceptibility is also forecasted correspond to classification of suffusion susceptibility. The forecasted result of classification of suffusion susceptibility from highly erosion to moderately erodible is around 50% and from moderately resistant to highly resistant is around 50%. This result demonstrates that the actual state of practice would be to account for the two-dimensional spatial variability |
| − | + | ==Acknowledgment== | |
| + | |||
| + | This work was supported by The University of Danang, University of Science and Technology. Project Number: T2022-02-53. | ||
==References== | ==References== | ||
| − | [1] Foster | + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> |
| + | |||
| + | [1] Foster M., Fell R., Spanagle M. The statistics of embankment dam failures and accidents. Canadien Geotechnical Journal, 37:1000-1024, 2000. | ||
| − | [2] Fell | + | [2] Fell R., Fry J.J. Erosion in geomechanics applied to dams and levees. ISTE-Wiley, Bonelli S. (Ed.) pp. 1-99, 2013. |
| − | [3] Icold | + | [3] Icold. Internal erosion of existing dams, levees and dykes, and their foundations. Bulletin 164, Internal Erosion Processes and Engineering Assessment, Volume 1, 2013. |
| − | [4] Garner | + | [4] Garner S.J., Fannin R.J. Understanding internal erosion: a decade of research following a sinkhole event. The International Journal on Hydropower and Dams, 17:93-98, 2010. |
| − | [5] Marot | + | [5] Marot D., Benamar A. Suffusion, transport and filtration of fine particles in granular soil. Erosion of Geomaterials, Chapter 2, pp. 39–79, 2012. |
| − | [6] Marot | + | [6] Marot D., Regazzoni P.L., Wahl T. Energy based method for providing soil surface erodibility rankings. Journal of Geotechnical and Geoenvironmental Engineering (ASCE), 48:1772-1787, 2011b. |
| − | [7] Le | + | [7] Le V.T., Marot D., Rochim A., Bendahmane F., Nguyen H.H. Suffusion susceptibility investigation by energy based method and statistical analysis. Canadian Geotechnical Journal, 55(1):57–68, 2018. |
| − | [8] Marot | + | [8] Marot D., Rochim A., Nguyen H.H., Bendahmane F., Sibille L. Assessing the susceptibility of gap graded soils to internal erosion characterization: proposition of a new experimental methodology. Natural Hazards, 83:365–388, 2016. |
| − | [9] Zhong | + | [9] Zhong C., Le V.T., Bendahmane F., Marot D., Yin Z.-Y. Investigation of spatial scale effects on suffusion susceptibility. Journal of Geotechnical and Geoenvironmental Engineering, 144(9), 04018067, 2018. |
| − | [10] Zhang | + | [10] Zhang L., Gelet R., Marot D., Smith M., Konrad J.-M. A method to assess the suffusion susceptibility of low permeability core soils in compacted dams based on construction data. European Journal of Environmental and Civil Engineering, 23(5):626-644, 2019. |
| − | [11] Phoon | + | [11] Phoon K.K, Kulhawy F.H. Characterization of geotechnical variability. Canadian Geotechnical Journal, 36(4):612-624, 1999. |
| − | [12] Vanmarcke | + | [12] Vanmarcke E.H. Probability modeling of soil profiles. Journal of the Geotechnical Engineering Division (ASCE), 103(11):1227–1246, 1977. |
Latest revision as of 10:07, 30 June 2023
Abstract
The suffusion susceptibility of the soil samples is evaluated through an erosion resistance index. Thanks to existing statistical analyses, the erosion resistance index is estimated from several soil parameters. In actual exploitation, the soil properties with the input parameters related to the grain distribution of the soil… vary greatly from the original design value due to the influence of many factors. One of the factors is the inherent variability. Inherent soil variability is modelled as a random field. The usual problems used to assess the suffusion susceptibility may be not give accurate results or fully evaluate the actual working ability of the ground in each case. This is one of the reasons why dams are still eroded when they are put into use. The paper aims predict erosion resistance index of the earth dam using two-dimensional (2D) Stochastics random field, modelling the initial problem, considering the variability spatial of soil properties, using the assumption of a Normal random field of soil characteristics parameters. The paper shows the predicted results of the variability spatial of erosion resistance index of Phu Vinh dam-Vietnam. Furthermore, the paper also represents the happened probability of suffusion susceptibility at the different zones in the earth dam body.
Keywords: Internal erosion, suffusion susceptibility, erosion resistance index, numerical simulation, random field
1. Introduction
Internal erosion is one of the main causes of instabilities within hydraulic earth structures such as dams, dikes, or levees [1]. According to Fell and Fry [2], there are four types of internal erosion: concentrated leak erosion, backward erosion, contact erosion and suffusion. Concentrated leak erosion may occur through a crack or hydraulic fracture. Backward erosion mobilizes all the grains in regressive way (i.e., from the downstream part of earth structure to the upstream part) and includes backward erosion piping and global backward erosion. Contact erosion occurs where a coarse soil is in contact with a fine soil. The phenomenon of suffusion corresponds to the process of detachment and then transport of the finest particles within the porous network under seepage flow. The finer fraction eroded and leaving the coarse matrix of the soil will further modify the hydraulic conductivity and mechanical parameters of the soil. This suffusion process may result in an increase of hydraulic conductivity, seepage velocities and hydraulic gradients, possibly accelerating the rate of suffusion [3]. The development of suffusion may cause the incidents of dam including piping and sinkholes.
In the literature, some researchers assume that suffusion is best represented by its initiation. Garner and Fannin [4] take into account the main initiation conditions for suffusion include three components: material susceptibility, critical hydraulic load and critical stress condition. Several methods have been proposed to characterize the initiation of suffusion confronting material susceptibility criteria and hydraulic criteria [5].
Marot et al. [6] proposed a new analysis based on the energy expended by the seepage flow which is a function of both the flow rate and the pressure gradient. Le et al. [7] performed many the suffusion tests to “final state”. This ‘final state’ is obtained towards the end of each test when the hydraulic conductivity is constant while the rate of erosion decreases. The expended energy is the time integration of the instantaneous power dissipated by the water seepage for the test duration. For the same duration the cumulative eroded dry mass is determined, the erosion resistance index is expressed by:
|
|
(1) |
Depending on the values of index, Marot et al. [8] proposed six categories of suffusion susceptibility from highly erodible to highly resistant (corresponding susceptibility categories: highly erodible for ; erodible for ; moderately erodible for ; moderately resistant for ; resistant for ; and highly resistant for ). Since the erosion resistance index has been proven to be intrinsic, i.e., independent of the sample size [9]. Zhang et al. [10] gave a method to assess the suffusion susceptibility of low permeability core soil in compacted dams based on construction data. They showed the one-dimensional (1D) spatial variability of all material parameters, in particular the hydraulic conductivity, the dry unit weight and the grain size distribution which affect the erosion resistance index. However, the suffusion susceptibility of earth dam body through the erosion resistance index needs to be assess the two-dimensional spatial variability. A two-dimensional contour map of the erosion resistance index would provide additional valuable information.
Phoon and Kulhawy [11] showed the disparate sources of uncertainties. One of the primary sources of geotechnical uncertainties is inherent soil variability. When we repeat the experiment many times at the same location, or at different locations, we always don't get the same result. To suppress or eliminate the influence of this source, we often use a very large number of samples. However, in practice, this implementation is not feasible because the experimental conditions do not allow, or the cost is too great. So, in the current calculation, there is always this random source. The objectives of the paper are to assess the suffusion susceptibility of earth dam considering variability spatial of soil properties. To tackle this objective, the contour map of 2D spatial variability of erosion resistance index of earth dam body is presented. This approach is based on two-dimensional Stochastics random field.
2. Description
2.1 Assessment of soil suffusion susceptibility
Le et al. [7] showed the correlation equation between physical parameters and erosion resistance index for all soils
|
|
(1) |
where: dry unit weight , blue methylene value , internal friction angle , initial hydraulic conductivity , minimum value of ratio H/F, percentage of finer fraction (based on Kenney and Lau’s criteria) , gap ratio , , , , , , (diameters of the 5%, 15%, 20%, 50%, 60%, 90% mass passing, respectively) and (percentage of finer than 0.063mm)
For widely graded soils, the correlation of physical parameters with the erosion resistance index: (, )
|
|
(2) |
For gap-graded soils, the correlation of physical parameters with the erosion resistance index: (, )
|
|
(3) |
2.2 Assessment of the relative suffusion potential
The erosion resistance index () is just a material parameter that characterizes the susceptibility of a given soil to suffusion. Hence, it cannot be interpreted as a ‘security factor’ to distinguish between ‘probable occurrence of erosion’ and ‘no erosion’ [10], This distinction requires additionally the estimation of the hydraulic loading. The erosion resistance index is estimated from several soil parameters using 2D Stochastics random field. Therefore, the relative suffusion potential of the earth dam body may be characterized by the 2D contour map of the erosion resistance index . A contour map shows the suffusion susceptibility at locations in the homogeneous earth dam body through the erosion resistance index value . Cross-section of the earth dam will be pointed out with the spatial variability of , may be low of high resistance to suffusion.
3. Numerical simulation
3.1 Simulation methodology
In this paper, the soil characteristic parameters are modeled as a random field. These parameters are inputted in the model using the two-dimensional (2D) Stochastics random field which is researched in Vanmarcke [12]. In a random finite element method, the spatial variability , , , , , are simulated by a random field with assumed coefficient of variance (cov) and mapped onto the finite element mesh. This estimation is based on Eq. (2) since all soil samples are widely graded. Among the seven parameters of Eq. (2), the blue methylene value () was considered constantly g/100g in the dam. The forecasting result of spatial variability of erosion resistance index with the contour map 2D is showed.
3.2 Numerical results
A Case study in Phu Vinh-Quang Binh earth dam
Phu Vinh Reservoir is one of the large reservoirs of Quang Binh-province, Vietnam. Since the project was put into use until now, it has contributed to the benefiting localities to eliminate hunger, reduce poverty, and at the same time make a significant contribution to economic development in Quang Binh province. After 24 years of use, the earth dam has deteriorated. At that time, we were still backward in terms of technological equipment for survey, design and construction of reservoir items, so the construction quality of some items of the reservoir was not up to the requirements of water quality. technical and aesthetic. Phu Vinh-Quang Binh earth dam is homogeneous earth dam, the upstream of the dam is reinforced with anhydrous paving stones and has deteriorated. The top of the dam is 5m wide with mixed soil, currently eroded and degraded. An of cross-section of earth dam body is illustrated in Figure 1. the earth dam body in the Figure 1 includes material class (2a), dam crest in location 1a.
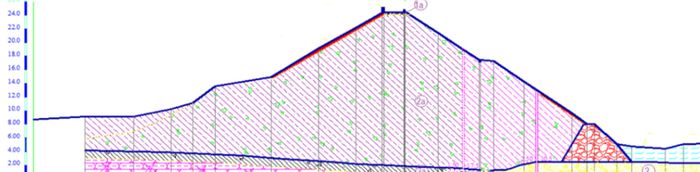
|
| Figure 1. A cross-section of Phu Vinh earth dam |
The data of dam include full grain size distributions with widely graded soil, dry unit weight, internal friction angle, initial hydraulic conductivity, and other parameters with the following assumed average values: dry unit weight kN/m3; internal friction angle ; percentage of fines (%) (based on Kenny & Lau, 1985 criterion) ; the percentage finer than mm %; mm; mm. The suffusion susceptibility will be estimated through erosion resistance index.
The result of erosion resistance index with contour map 2D is showed in Figure 2. Several locations in the map pointed out with a low resistance to suffusion (blue color). Some zones with yellow color represent the high resistance to suffusion. The predicted values of Iα lies within the range from 2 to more than 6. These results may be explained by soil spatial variability. According to Zhang et al. [10], they show the one-dimensional spatial variability of erosion resistance index which erosion resistance index is estimated equally for one layer in the dam core. These results may be not given accurate results at different locations. Based on two-dimensional random field model, the two-dimensional spatial variability of erosion resistance index is predicted in the whole dam.
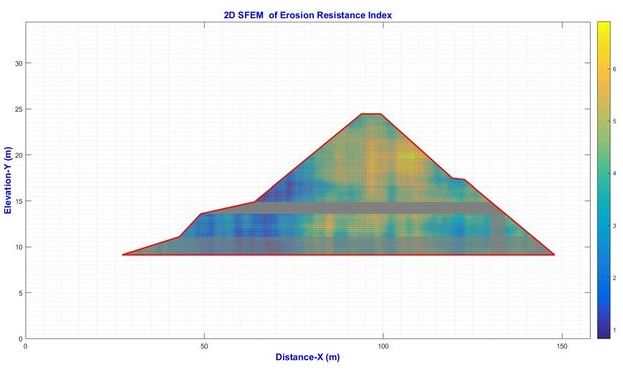
|
| Figure 2. Contour map 2D of erosion resistance index |
Figure 3 shows the histogram plot of erosion resistance index (blue color) with the normal distribution. The probability results are run from five hundred random times with Matlab code. The red curve is the probability of suffusion susceptibility of the earth dam. According to the classification of suffusion susceptibility of Marot et al. [8], the probability of suffusion susceptibility of the earth dam correspond to classification suffusion susceptibility shows in Table 1. This table shows that 3% is the probability of highly erosion, 6% is erosion, 41% is moderately erodible, 32% is moderately resistant, 14% is resistant and 4% is highly resistant.
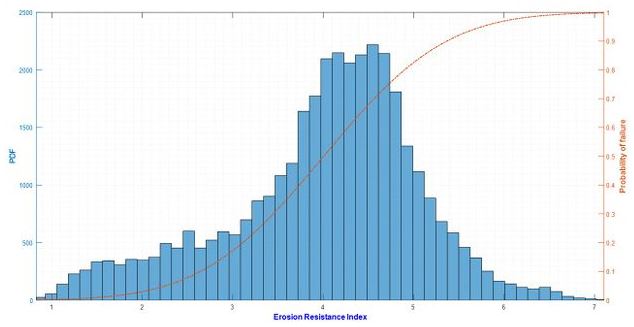
|
| Figure 3. Histogram plot of erosion resistance index and probability of suffusion susceptibility |
| Classification of suffusion susceptibility through the Iα based on Marot et al. [8] |
Probability of suffusion susceptibility (forecasting) |
|---|---|
| Highly erosion | 3% |
| Erosion | 6% |
| Moderately erodible | 41% |
| Moderately resistant | 32% |
| Resistant | 14% |
| Highly resistant | 4% |
4. Conclusions
The result of paper assesses the suffusion susceptibility of the dam body using two-dimensional random field considering soil spatial variability. With illustration of a numerical simulation, the predicted result of spatial variability of erosion resistance index of Phu Vinh, Quang Binh is showed in a contour map 2D. Furthermore, the probability of suffusion susceptibility is also forecasted correspond to classification of suffusion susceptibility. The forecasted result of classification of suffusion susceptibility from highly erosion to moderately erodible is around 50% and from moderately resistant to highly resistant is around 50%. This result demonstrates that the actual state of practice would be to account for the two-dimensional spatial variability
Acknowledgment
This work was supported by The University of Danang, University of Science and Technology. Project Number: T2022-02-53.
References
[1] Foster M., Fell R., Spanagle M. The statistics of embankment dam failures and accidents. Canadien Geotechnical Journal, 37:1000-1024, 2000.
[2] Fell R., Fry J.J. Erosion in geomechanics applied to dams and levees. ISTE-Wiley, Bonelli S. (Ed.) pp. 1-99, 2013.
[3] Icold. Internal erosion of existing dams, levees and dykes, and their foundations. Bulletin 164, Internal Erosion Processes and Engineering Assessment, Volume 1, 2013.
[4] Garner S.J., Fannin R.J. Understanding internal erosion: a decade of research following a sinkhole event. The International Journal on Hydropower and Dams, 17:93-98, 2010.
[5] Marot D., Benamar A. Suffusion, transport and filtration of fine particles in granular soil. Erosion of Geomaterials, Chapter 2, pp. 39–79, 2012.
[6] Marot D., Regazzoni P.L., Wahl T. Energy based method for providing soil surface erodibility rankings. Journal of Geotechnical and Geoenvironmental Engineering (ASCE), 48:1772-1787, 2011b.
[7] Le V.T., Marot D., Rochim A., Bendahmane F., Nguyen H.H. Suffusion susceptibility investigation by energy based method and statistical analysis. Canadian Geotechnical Journal, 55(1):57–68, 2018.
[8] Marot D., Rochim A., Nguyen H.H., Bendahmane F., Sibille L. Assessing the susceptibility of gap graded soils to internal erosion characterization: proposition of a new experimental methodology. Natural Hazards, 83:365–388, 2016.
[9] Zhong C., Le V.T., Bendahmane F., Marot D., Yin Z.-Y. Investigation of spatial scale effects on suffusion susceptibility. Journal of Geotechnical and Geoenvironmental Engineering, 144(9), 04018067, 2018.
[10] Zhang L., Gelet R., Marot D., Smith M., Konrad J.-M. A method to assess the suffusion susceptibility of low permeability core soils in compacted dams based on construction data. European Journal of Environmental and Civil Engineering, 23(5):626-644, 2019.
[11] Phoon K.K, Kulhawy F.H. Characterization of geotechnical variability. Canadian Geotechnical Journal, 36(4):612-624, 1999.
[12] Vanmarcke E.H. Probability modeling of soil profiles. Journal of the Geotechnical Engineering Division (ASCE), 103(11):1227–1246, 1977.Document information
Published on 30/06/23
Accepted on 23/06/23
Submitted on 17/03/23
Volume 39, Issue 2, 2023
DOI: 10.23967/j.rimni.2023.06.007
Licence: CC BY-NC-SA license