| (7 intermediate revisions by one other user not shown) | |||
| Line 204: | Line 204: | ||
{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
|-style="text-align:center" | |-style="text-align:center" | ||
| − | ! Propiedades !! Magnitud y unidades | + | ! style="text-align: left;"| Propiedades !! Magnitud y unidades |
|-style="text-align:center" | |-style="text-align:center" | ||
| Módulo de elasticidad | | Módulo de elasticidad | ||
| <math display="inline">E=</math><math>38000</math> MPa | | <math display="inline">E=</math><math>38000</math> MPa | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Relación de Poisson |
| style="text-align: center;"|<math>v=0.20</math> | | style="text-align: center;"|<math>v=0.20</math> | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Resistencia a tensión |
| style="text-align: center;"|<math display="inline">{f}_{t}=3</math> MPa | | style="text-align: center;"|<math display="inline">{f}_{t}=3</math> MPa | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Energía de fractura |
| style="text-align: center;"|<math display="inline">{G}_{f}=0.06</math> N/mm | | style="text-align: center;"|<math display="inline">{G}_{f}=0.06</math> N/mm | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Ancho de grieta |
| style="text-align: center;"|<math display="inline">h=</math><math>5</math> mm | | style="text-align: center;"|<math display="inline">h=</math><math>5</math> mm | ||
|} | |} | ||
| Line 386: | Line 386: | ||
{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
|-style="text-align:center" | |-style="text-align:center" | ||
| − | ! Modelo !! Factor de ajuste <math display="inline">k</math> | + | ! style="text-align:left"| Modelo !! Factor de ajuste <math display="inline">k</math> |
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Modelo de 5 dientes |
| style="border-top: 1pt solid black;text-align: center;"|<math>k=1.35</math> | | style="border-top: 1pt solid black;text-align: center;"|<math>k=1.35</math> | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Modelo de 10 dientes |
| style="text-align: center;"|<math>k=1.17</math> | | style="text-align: center;"|<math>k=1.17</math> | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Modelo de 20 dientes |
| style="text-align: center;"|<math>k=1.08</math> | | style="text-align: center;"|<math>k=1.08</math> | ||
|} | |} | ||
| Line 462: | Line 462: | ||
{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
|-style="text-align:center" | |-style="text-align:center" | ||
| − | ! Propiedades !! Magnitud y unidades | + | ! style="text-align:left| Propiedades !! Magnitud y unidades |
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Módulo de elasticidad |
| style="text-align: center;"|<math display="inline">E=</math><math>16900</math> MPa | | style="text-align: center;"|<math display="inline">E=</math><math>16900</math> MPa | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Relación de Poisson |
| style="text-align: center;"|<math>v=0.20</math> | | style="text-align: center;"|<math>v=0.20</math> | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Resistencia a tensión |
| style="text-align: center;"|<math display="inline">{f}_{t}=2.4</math> MPa | | style="text-align: center;"|<math display="inline">{f}_{t}=2.4</math> MPa | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Energía de fractura |
| style="text-align: center;"|<math display="inline">{G}_{f}=0.3</math> N/mm | | style="text-align: center;"|<math display="inline">{G}_{f}=0.3</math> N/mm | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Ancho de grieta |
| style="text-align: center;"|<math display="inline">h=</math><math>5</math> mm | | style="text-align: center;"|<math display="inline">h=</math><math>5</math> mm | ||
|} | |} | ||
| Line 542: | Line 542: | ||
{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
|-style="text-align:center" | |-style="text-align:center" | ||
| − | ! Propiedades !! Magnitud y unidades | + | ! style="text-align: left;"| Propiedades !! Magnitud y unidades |
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Módulo de elasticidad |
| style="text-align: center;"|<math display="inline">E=</math><math>20000</math> MPa | | style="text-align: center;"|<math display="inline">E=</math><math>20000</math> MPa | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Relación de Poisson |
| style="text-align: center;"|<math>v=0.20</math> | | style="text-align: center;"|<math>v=0.20</math> | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Resistencia a tensión |
| style="text-align: center;"|<math display="inline">{f}_{t}=2.4</math> MPa | | style="text-align: center;"|<math display="inline">{f}_{t}=2.4</math> MPa | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Energía de fractura |
| style="text-align: center;"|<math display="inline">{G}_{f}=0.113</math> N/mm | | style="text-align: center;"|<math display="inline">{G}_{f}=0.113</math> N/mm | ||
|- | |- | ||
| − | | style="text-align: | + | | style="text-align: left;"|Ancho de grieta |
| style="text-align: center;"|<math display="inline">h=</math><math>5</math> mm | | style="text-align: center;"|<math display="inline">h=</math><math>5</math> mm | ||
|} | |} | ||
| Line 566: | Line 566: | ||
{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:50%;" | {| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:50%;" | ||
|-style="background:white;" | |-style="background:white;" | ||
| − | |style="text-align: center;padding:10px;"| [[File:Fig. 21.png| | + | |style="text-align: center;padding:10px;"| [[File:Fig. 21.png|400px]] |
|- | |- | ||
| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figura 21'''. Diagrama de reacción-desplazamiento para la viga con muesca (sin regularización) | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figura 21'''. Diagrama de reacción-desplazamiento para la viga con muesca (sin regularización) | ||
| Line 651: | Line 651: | ||
[2] Contrafatto L., Cuomo, M. A new thermodynamically consistent continuum model for hardening plasticity coupled with damage. International Journal of Solids and Structures, 39:6241-6271, 2002. | [2] Contrafatto L., Cuomo, M. A new thermodynamically consistent continuum model for hardening plasticity coupled with damage. International Journal of Solids and Structures, 39:6241-6271, 2002. | ||
| − | [3] Belytschko T., Bindeman L.P. Assumed strain stabilization of the 4-node quadrilateral with 1-point quadrature for nonlinear problems | + | [3] Belytschko T., Bindeman L.P. Assumed strain stabilization of the 4-node quadrilateral with 1-point quadrature for nonlinear problems. Computer Methods in Applied Mechanics and Engineering, 88:311–340, 1991. |
[4] Belytschko T., Bachrach W.E. Efficient implementation of the quadrilaterals with high coarse-mesh accuracy. Computer Methods in Applied Mechanics and Engineering, 54:279-301, 1986. | [4] Belytschko T., Bachrach W.E. Efficient implementation of the quadrilaterals with high coarse-mesh accuracy. Computer Methods in Applied Mechanics and Engineering, 54:279-301, 1986. | ||
| − | [5] Amezcua H.R., Ayala A.G. A computationally efficient numerical integration scheme for non-Linear plane-stress/strain FEM applications using one-point constitutive model evaluation. Structural | + | [5] Amezcua H.R., Ayala A.G. A computationally efficient numerical integration scheme for non-Linear plane-stress/strain FEM applications using one-point constitutive model evaluation. Structural Engineering and Mechanics, 85(1):89-104, 2023. DOI:10.12989/SEM.2023.85.1.089 |
[6] Bassa B., Sabourin F., Brunet M. A new nine-node solid-shell finite element using complete 3D constitutive laws. International Journal for Numerical Methods in Engineering, 92(7):589–636, 2012. | [6] Bassa B., Sabourin F., Brunet M. A new nine-node solid-shell finite element using complete 3D constitutive laws. International Journal for Numerical Methods in Engineering, 92(7):589–636, 2012. | ||
Latest revision as of 23:52, 22 June 2023
Resumen
En este artículo se propone una estrategia computacionalmente eficiente para la aproximación del comportamiento no-lineal de estructuras mediante el método de los elementos finitos. Esta propuesta se basa en la ejecución de una serie de análisis lineales en los que la resistencia de los elementos en los que se presenta el daño se degrada de manera secuencial complementándose con un esquema de integración numérica reducida estabilizada para elementos finitos sólidos. Así, la matriz de rigidez solo contiene información en un punto de integración y, en consecuencia, los esfuerzos se calculan en dicho punto. Del mismo modo, la estabilización posibilita que no solamente se utilice integración reducida en los elementos donde se asume que ocurrirá el daño, sino en todos los elementos, garantizando una mayor reducción del costo computacional. En este artículo se aplica esta estrategia de análisis no-lineal basada en análisis lineales secuenciales e integración reducida estabilizada a una serie de ejemplos tanto de validación como de aplicación en los que se discute la calidad en la aproximación y la eficiencia computacional alcanzada. Finalmente, se discuten algunos desarrollos futuros para la estrategia.
Palabras clave: Análisis no-lineal, daño, análisis lineales secuenciales, integración reducida, elementos finitos
Abstract
In this paper, a computationally efficient strategy for the approximation of the non-linear behaviour of structures through the finite element method is proposed. This proposal is based on the execution of a set of linear analyses in which the strength of the elements where the damage occurs is sequentially degraded and, in addition, complemented with a stabilized reduced numerical integration scheme for solid finite elements. Thus, the stiffness matrix only contains information of one integration point and, consequently, the stresses are computed only at that point. Also, due to the stabilization, it is possible to use reduced integration not only in the elements where the damage is assumed to occur, but in all the elements, guaranteeing a greater reduction in the computational cost. In this paper, the strategy of sequentially linear analysis with stabilized reduced integration is applied to several validation as well as application examples in which the quality of the approximation and the computational efficiency achieved are discussed. Finally, some future developments for the strategy are proposed.
Keywords: Non-linear analysis, damage, sequentially linear analysis, reduced integration, finite elements
1. Introducción
En la actualidad, el análisis de estructuras, en el que se considera la aparición y evolución de daño, se está convirtiendo en una tendencia para el ejercicio profesional de todo ingeniero estructurista. Una de las etapas de dicho análisis es la construcción de un modelo matemático que aproxime, de manera suficientemente cercana a los objetivos planteados para dicho análisis, el comportamiento de la estructura. Así, es posible construir modelos matemáticos con consideraciones muy apegadas a la realidad del problema en cuestión, e.g., comportamiento no-lineal de los materiales que componen a la estructura; sin embargo, su solución o aproximación demanda un costo computacional demasiado alto que los deja rezagados a aplicaciones académicas o de investigación.
Un ejemplo de estos modelos matemáticos son los modelos constitutivos basados en la teoría de plasticidad que consideran distintos criterios de fluencia y que están orientados a simular el comportamiento de materiales con diversas características. Para materiales como el concreto y la mampostería, son convenientes los modelos que consideran criterios de falla con resistencias diferentes a tensión y compresión tales como los criterios de Drucker-Prager y Mohr-Coulomb. Adicionalmente, existen modelos constitutivos complejos que combinan las teorías de plasticidad y de daño, lo que los convierte en ideales para simular de una manera muy realista este tipo de materiales cuasi-frágiles, e.g., los modelos constitutivos de Lubliner et al. [1] y Contrafatto y Cuomo [2].
Estos modelos constitutivos complejos han mostrado ser capaces de simular el comportamiento real de estructuras; sin embargo, su aplicación no es eficiente para fines prácticos debido a las siguientes necesidades: programas de computadora que incluyan las implementaciones de los modelos a emplear; que dichos programas incluyan algoritmos robustos y eficientes que permitan aproximar la solución del problema matemático no-lineal; computadoras con buena capacidad de procesamiento y mano de obra especializada para las etapas de pre- y pos-proceso del análisis.
Adicionalmente, el tiempo de cómputo puede ser un factor de mucha consideración especialmente si se requiere la obtención de resultados de manera rápida y eficiente. Por esta razón, resulta conveniente contar con estrategias de aproximación del comportamiento no-lineal de las estructuras que sean computacionalmente eficientes y que, además, demuestren que los resultados obtenidos sean los suficientemente buenos para poder ser empleados de manera cotidiana.
Algunas de estas estrategias se enfocan en la reducción del costo computacional requerido para llevar a cabo análisis no-lineales empleando este tipo de modelos constitutivos complejos. Por ejemplo, las estrategias basadas en formulaciones que emplean integración numérica reducida y estabilizada en elementos finitos sólidos, cuadriláteros y hexaedros. Algunas de estas formulaciones se concentran principalmente en controlar las inconsistencias numéricas generadas por el empleo de integración reducida para la obtención de la matriz de rigidez [3]; o en la posibilidad de emplear mallas más gruesas por el mejoramiento en la representación de la energía de deformación de los modos de deformación lineal en los elementos cuadriláteros [4]. Otros desarrollos, se enfocan en formulaciones que permiten que la evaluación de cierto modelo constitutivo se realice en una cantidad reducida de puntos de integración, disminuyendo así el volumen de cómputo [5]. Adicionalmente, existen desarrollos recientes en los llamados elementos solid-shell, i.e., elementos que combinan las formulaciones de los sólidos con los cascarones para el análisis de problemas en tres dimensiones de estructuras delgadas [6,7].
Otras estrategias buscan la simplificación de los modelos constitutivos mediante el establecimiento de hipótesis o, incluso, la propuesta de nuevos modelos numéricos simplificados cuya aplicación demande menor costo computacional. Por ejemplo, una de estas propuestas consiste en la aplicación de Análisis Lineales Secuenciales (ALS) [8], la cual busca aproximar el comportamiento no-lineal de una estructura mediante una serie de análisis lineales en los que se reduce, siguiendo una ley de ablandamiento, las magnitudes de las propiedades mecánicas del material de los elementos que se dañan. Esta estrategia es computacionalmente eficiente pues, al consistir en una serie de análisis lineales, no es necesario un proceso iterativo para alcanzar la convergencia de la solución en cada análisis.
En este artículo se propone ejecutar los ALS aplicando un modelo de elementos finitos resueltos mediante un esquema de integración reducida estabilizada (IRE). La combinación de estas dos estrategias, ALS-IRE, es naturalmente compatible, pues ambas, de manera independiente, reducen el costo computacional requerido en el análisis no-lineal de estructuras desde distintos enfoques. Del mismo modo, al combinarlas, se generan algunas nuevas ventajas que se discuten a lo largo del artículo. En este documento se incluye la descripción de la propuesta y de su implementación numérica mediante una herramienta computacional independiente y compatible con programas de pre-proceso comerciales. Adicionalmente, se valida la propuesta con ejemplos tomados de la literatura especializada sobre el tema y posteriormente se aplica para mostrar la eficiencia alcanzada en comparación con otras propuestas de análisis no-lineal más robustas. Finalmente, se incluye una breve discusión sobre el potencial de este esquema en trabajos futuros.
2. Integración numérica reducida en el método de elementos finitos
En la formulación isoparamétrica de un elemento finito cuadrilátero, se emplean técnicas de integración numérica en el cálculo de la matriz de rigidez , y cuando se considera un comportamiento no-lineal del material en la evaluación numérica del modelo constitutivo en cuestión
|
|
(1) |
donde es el espesor del elemento, es la matriz de compatibilidad y es la matriz constitutiva para un comportamiento asumido de esfuerzo plano o deformación plana. Además, y son las coordenadas del espacio físico real, y son las del espacio padre de referencia y es el Jacobiano de la transformación. Los términos , y , corresponden a los puntos de muestreo y a los pesos de la cuadratura de Gauss-Legendre empleada para el proceso de integración numérica, respectivamente. Como se puede apreciar en la ec. (1), el costo computacional de este procedimiento es proporcional al número de puntos de integración empleados, i.e., orden de cuadratura. Particularmente, para el elemento finito cuadrilátero de 4 nodos, se identifican dos esquemas de integración numérica: integración completa (IC), correspondiente al uso de una cuadratura de , e integración reducida (IR) que corresponde al empleo de una cuadratura de .
El empleo de cuadraturas de orden inferior al requerido puede generar inestabilidades numéricas como el llamado efecto “reloj de arena”, conocido comúnmente en la literatura especializada por su traducción al idioma inglés como efecto hourglass. El cual consiste en la aparición de modos de deformación espurios o modos hourglass i.e., modos inconsistentes que presentan deformación, pero para los cuales la energía de deformación es nula, . Por lo tanto, la selección de un orden de cuadratura adecuado debe representar una actividad de gran importancia en la ejecución de análisis no-lineales mediante el método de los elementos finitos. En otras palabras, se debe recurrir a un procedimiento de control de efecto hourglass o de estabilización si se quiere tomar ventaja del empleo de IR.
Uno de los métodos más empleados para emplear IR es el desarrollado por Belytschko et al. [3], el cual se basa en la adición de una matriz de rigidez estabilizadora, , a la matriz de rigidez obtenida con IR, (ec. (2)). Desde un punto de vista matemático, la matriz , de rango 2, controla el efecto hourglass debido a la recuperación de rango de 3 a 5 de la matriz , mediante la adición de los términos ignorados cuando se usa IR
|
|
(2) |
donde
|
|
(3) |
En el método original [3], la integral de la ec. (3) se evalúa mediante integración numérica con una cuadratura de , de otra manera resulta ser nula. Esto significa que la matriz de rigidez estabilizada contiene información en los 4 puntos de integración y, consecuentemente, las deformaciones y los esfuerzos se aproximan en estos 4 puntos de integración. Esto es especialmente de consideración cuando se asume un comportamiento no-lineal del material, ya que las evaluaciones del modelo constitutivo en cuestión se realizarán en cada uno de estos 4 puntos de integración, como si se tratara de un esquema de IC. En el trabajo de Belytschko y Bachrach [4] se ha demostrado que este método controla de manera satisfactoria el efecto hourglass y además posibilita, en algunos casos, el empleo de mallas gruesas.
En este artículo, se trabaja con una modificación propuesta al método que consiste en integrar analíticamente la expresión de la ec. (3) con la finalidad de contar con una expresión analítica para la matriz [5]. De esta manera, la matriz de rigidez estabilizada contiene información en un solo punto de integración. La principal ventaja de este esquema de IRE es su eficiencia computacional en análisis no-lineales, debido a que la evaluación de cierto modelo constitutivo solamente se realiza en un punto de integración.
3. Procedimiento de ALS para cargas proporcionales
De acuerdo con Rots [9], el principal objetivo de un procedimiento de ALS es el estudio del fenómeno de fractura en materiales cuasi-frágiles, como el concreto y la mampostería. Este procedimiento aproxima el ablandamiento característico en la correspondiente curva de esfuerzo-deformación a tensión mediante un diagrama dentado, i.e., ley de ablandamiento dentado (Figura 1). Por la naturaleza de la formulación original de ALS, es de esperarse que se subestime el área bajo la curva esfuerzo-deformación del material. Por ello, la formulación de ALS fue mejorada por Rots e Invernizzi [10], quienes propusieron un procedimiento de regularización de malla con el objetivo de minimizar la influencia de ésta en la ejecución de los análisis. Este procedimiento consiste en la inclusión de un factor que modifica la resistencia a tensión y la deformación última del material. En el presente trabajo se implementa este procedimiento en la propuesta de ALS-IRE.

|
| Figura 1. Ablandamiento en curva esfuerzo-deformación [8] |
En el procedimiento original de Rots [8] se plantea una ley de ablandamiento lineal del material el cual se aproxima con forma dentada. Rots et al. [11] propusieron nuevos modelos de ablandamiento, incluyendo uno no-lineal. En el mismo sentido, DeJong et al. [12], Eliáš et al. [13] y Yu et al. [14] propusieron innovadores algoritmos que posibilitan la consideración de cargas no proporcionales en la aplicación de ALS. Esto amplía el campo de aplicación de la estrategia a otros patrones de carga, e.g., etapas de carga de pre-compresión y carga lateral.
En cuanto a los campos de aplicación de la estrategia, Rots [8,9] la aplicó al estudio de construcciones de mampostería histórica y de concreto. Más tarde, Invernizzi et al. [15] y Slobbe et al. [16] la aplicaron al estudio de elementos estructurales de concreto sin refuerzo. Adicionalmente, Pari et al. [17] desarrollaron un modelo robusto que permite el empleo de ALS para el estudio de estructuras de mampostería en 2 y 3 dimensiones, mostrando que su propuesta es capaz de reproducir comportamientos complejos de la mampostería. Existen, incluso, algunos algoritmos para reducir el costo computacional en la aplicación de ALS como los de Pari et al. [18], quienes proponen dos estrategias de solución para reutilizar algunas descomposiciones de la matriz de rigidez realizadas en los análisis lineales previos. De esta manera se toma ventaja de que los cambios en el sistema de ecuaciones del modelo de elementos finitos solo son locales.
A grandes rasgos, el procedimiento de ALS consiste en, como su nombre lo indica, realizar una serie de análisis en los que el comportamiento del material siempre es elástico lineal. Después de cada uno de estos análisis se selecciona el elemento más demandado y se degrada su rigidez. Este procedimiento se repite hasta que los elementos por donde se asume que aparecerán grietas se degradan totalmente. Con este procedimiento de ALS, se logra modelar el fenómeno de snap-back (rebote hacia atrás) comúnmente presente en las curvas de esfuerzo-deformación de materiales cuasi-frágiles, mientras que un análisis no-lineal presenta dificultades para reproducirlos numéricamente.
Este procedimiento inicia con la discretización de la estructura empleando elementos finitos sólidos. En la propuesta original, estos elementos son cuadriláteros de 4 nodos, i.e., de aproximación lineal, para aplicar IR con una cuadratura de en los elementos donde se asume que ocurrirá el daño. Aunque esto es naturalmente extrapolable a elementos hexaedros para análisis tridimensionales. El comportamiento del material se asume elástico-lineal en cada uno de los análisis. Como parámetros iniciales del material, a cada elemento se le asigna un módulo de elasticidad, , una relación de Poisson, , y una resistencia a tensión, . Posteriormente, se sigue el siguiente procedimiento de cargas proporcionales de manera secuencial [10]:
- 1. Se asigna la carga externa como una carga unitaria de referencia.
- 2. Se ejecuta un análisis elástico-lineal de manera convencional.
- 3. A partir de los resultados, se identifica el elemento crítico, i.e., el elemento para el cual el esfuerzo principal de tensión, , es el más cercano su resistencia a tensión actual. De acuerdo con Rots e Invernizzi [10], el criterio del esfuerzo principal de tensión es ampliamente aceptado en el Modo I de la Mecánica de la Fractura para materiales cuasi-frágiles.
- 4. Se calcula el factor de escala, , como un cociente entre la resistencia a tensión actual y el esfuerzo principal de tensión del elemento crítico
|
|
(4) |
- 5. De manera que se pueda construir la curva carga-desplazamiento, se calculan la carga crítica global, como el producto del factor de escala por la carga unitaria de referencia asignada en el paso 1 y, además, se calcula su correspondiente desplazamiento global.
- 6. Se reducen el módulo de elasticidad y la resistencia a tensión del elemento crítico de acuerdo a la curva de ablandamiento dentado (Figura 1) como se describe en la siguiente sección.
- 7. Se repiten los pasos del 2 al 6 con la estructura para la cual el módulo de elasticidad y la resistencia a tensión del elemento crítico fueron reducidas.
- 8. Con todas las configuraciones de encontradas en el paso 5, se construye la curva reacción-desplazamiento.
Finalmente, se traza la malla deformada. De acuerdo con Rots e Invernizzi [10], esta gráfica revela la ubicación de la fractura debido a que la serie de elementos críticos degradados mostrarán las deformaciones más grandes. El resultado de este método depende de la forma en la cual se reduce progresivamente la rigidez y la resistencia del elemento crítico. Esto constituye la esencia del procedimiento. De manera muy simplificada se podría reducir a cero inmediatamente después de que un elemento sea seleccionado como elemento crítico por primera vez. Sin embargo, de acuerdo con Rots [9] esto beneficiaría la dependencia de la malla en la obtención de resultados acertados.
3.1 Ley de ablandamiento dentado
El diagrama de esfuerzo-deformación es definido por el módulo de elasticidad , la resistencia a tensión , la forma del diagrama y la energía de fractura dividida entre el ancho de grieta , representado por el área bajo el diagrama [10]. Por lo tanto, para un diagrama de ablandamiento lineal, la deformación última se expresa tal como aparece en la siguiente ecuación
|
|
(5) |
En el procedimiento descrito en la sección anterior, el diagrama de ablandamiento se reproduce mediante reducciones consecutivas del módulo de elasticidad con la ec. (6) [8]
|
|
(6) |
donde representa el estado actual del diagrama dentado y el factor por el cual se reduce el módulo de elasticidad del elemento crítico. Además, es la cantidad de reducciones que se aplican en total a un solo elemento hasta considerarlo totalmente dañado, i.e., número de dientes. Para evitar problemas numéricos, es recomendable mantener un valor residual muy pequeño para el módulo de elasticidad. La resistencia a tensión reducida, , correspondiente a , se calcula de acuerdo con la envolvente del diagrama de ablandamiento (ec. (7)) [9]
|
|
(7) |
donde
|
|
(8) |
|
|
(9) |
donde es la tangente al diagrama de ablandamiento de esfuerzo deformación. En la Figura 1 se observa un ejemplo de este tipo de curvas para las propiedades del material de la Tabla 1 considerando 10 dientes.
| Propiedades | Magnitud y unidades |
|---|---|
| Módulo de elasticidad | MPa |
| Relación de Poisson | |
| Resistencia a tensión | MPa |
| Energía de fractura | N/mm |
| Ancho de grieta | mm |
En la Figura 1 se aprecia la formación de los dientes en la aproximación por la reducción del módulo de elasticidad. Del mismo modo, se observa la reducción de la resistencia a tensión desde su valor inicial de 3 MPa hasta un valor residual muy cercano a cero. Es de notarse la subestimación que existe sobre la envolvente. Esto sugiere que el resultado del procedimiento es susceptible, entre otros factores, al número de dientes seleccionado.
4. Modelo combinado de ALS con IRE
En este artículo se combina el procedimiento de ALS con la aplicación del esquema IRE descrito anteriormente [5]. Este procedimiento de ALS-IRE es muy atractivo para implementarse, por las siguientes razones:
- Según lo establecido por Rots [8], el procedimiento de ALS obtiene buenas aproximaciones con mallas gruesas. Esta característica se comparte con el esquema de IRE, para la cual se ha probado el enriquecimiento de resultados para mallas gruesas [5].
- En la implementación original de la estrategia de ALS, se utiliza IR sin estabilización en los elementos donde se espera que ocurra el agrietamiento. Esto significa que si el esfuerzo principal de tensión máximo se identifica en el único punto de integración de cierto elemento en la ruta potencial de agrietamiento, la rigidez y la resistencia de ese elemento crítico se degradan. Esta característica es atractiva para el esquema de IRE, en el cual es posible evaluar esfuerzos en un solo punto de integración con estabilidad numérica. Además, todos los elementos que componen la malla se pueden integrar empleando IRE sin problemas numéricos.
- Ambas estrategias tienen el enfoque de ser computacionalmente económicas y eficientes. Por lo cual, al combinarlas, se espera contar una estrategia que sea de aplicación práctica y eficiente, que ofrezca un apoyo para la toma de decisiones rápida que ayuden a la evaluación de la seguridad en estructuras.
4.1 Implementación numérica
Para realizar la implementación numérica del procedimiento de ALS-IRE se seleccionó el lenguaje de programación Python 3.0 [19], especialmente por la gran compatibilidad que ofrece con distintos sistemas operativos. La idea es contar con una herramienta independiente que permita el estudio de problemas con esta estrategia y que, además, pueda continuarse desarrollando para expandir sus aplicaciones con nuevos desarrollos como los mencionados en la sección 3. En la Figura 2 se incluye un diagrama de flujo con el procedimiento implementado. En la etapa de pre-proceso se utiliza el programa GiD [23]. Este es un programa muy utilizado por la comunidad académica y profesional para la generación de mallas de los elementos finitos y para la visualización gráfica de los resultados de cierto análisis. Así, se realizaron los algoritmos necesarios para que el archivo de salida del programa GiD [23] funcione directamente como archivo de entrada para la herramienta desarrollada en este trabajo. Una vez ingresada toda la información, se construye la curva de ablandamiento dentado correspondiente e inicia la etapa de proceso mediante la ejecución de los ALS.Todos los análisis lineales con el método de los elementos finitos se realizan de manera interna en la herramienta desarrollada en el lenguaje de programación Python 3.0 [19]. Finalmente, en la etapa de pos-proceso se construyen tanto los diagramas de reacción-desplazamiento como la configuración de malla deformada al final del análisis.

|
| Figura 2. Diagrama de flujo del programa desarrollado |
4.2 Ejemplos de validación
Como ejemplo de validación, se seleccionó una viga con una muesca estudiada por Rots [8]. La geometría y las dimensiones de esta viga se muestran en la Figura 3.

|
| Figura 3. Geometría de la viga con muesca |
Inicialmente, se construyó la malla de la Figura 4. Se emplearon elementos finitos cuadriláteros de 4 nodos, dispuestos de tal manera que benefician el comienzo de la fisura en la muesca. Para la estrategia original ALS, todos los elementos de la malla se integraron mediante un esquema IC, excepto los elementos sobre la muesca de la viga que se integraron mediante IR sin estabilizar y, para la propuesta de ALS-IRE, todos los elementos se integraron mediante el esquema IRE pero sólo pueden dañarse los elementos sobre la muesca.

|
| Figura 4. Malla empleada en el análisis de la viga con muesca |
Las propiedades mecánicas se seleccionaron según lo establecido por Rots [9] (Tabla 1): módulo de elasticidad MPa, relación de Poisson , resistencia inicial a tensión MPa, y energía de fractura N/mm. Se realizaron tres análisis diferentes considerando 5, 10 y 20 dientes. Por tanto, el factor se tomó como 4, 2 y , para cada uno de estos análisis, respectivamente ((ec. (6)). Los resultados, tanto para ALS como para ALS-IRE, se muestran en las curvas reacción-desplazamiento de las Figuras 5 a 7. En estas figuras, a modo de comparación, se ha añadido una curva de referencia. Esta curva fue obtenida por Rots [20] a partir de un análisis de ablandamiento lineal para una grieta de línea discreta con los mismos parámetros.

|
| Figura 5. Diagrama de reacción-desplazamiento para la viga con muesca (5 dientes) |

|
| Figura 6. Diagrama de reacción-desplazamiento para la viga con muesca (10 dientes) |

|
| Figura 7. Diagrama de reacción-desplazamiento para la viga con muesca (20 dientes) |
Se puede observar que cuanto mayor es el número de dientes, más suave es la envolvente en ambos procedimientos, ALS y ALS-IRE. También se puede apreciar que todas las aproximaciones subestiman la reacción-desplazamiento obtenida numéricamente por Rots [20], pero las aproximadas por ALS-IRE son un poco más cercanas. Esto se podía esperar debido a la subestimación en el diagrama de ablandamiento dentado. Así, resulta conveniente la implementación de un procedimiento de regularización de malla para ajustar este diagrama. Finalmente, todos los resultados son consistentes con los calculados por Rots [8].
En la Figura 8 se muestra la configuración deformada de la viga con muesca al final del análisis. Aquí, se puede apreciar la concentración de las deformaciones de mayor magnitud en los elementos que están sobre la muesca (color rojo).

|
| Figura 8. Configuración deformada de la viga con muesca después del análisis con el modelo ALS-IRE |
5. Procedimiento de regularización de malla
Como se comentó en la sección anterior, a partir de los resultados se puede notar que resulta conveniente incluir un proceso de regularización de malla para minimizar el efecto de la sensibilidad de la malla en el análisis. Por esta razón, Rots e Invernizzi [10] propusieron un procedimiento basado en un factor de ajuste, , que busca compensar la subestimación del área bajo el diagrama de ablandamiento dentado (Figura 9). Así, establecen tres opciones para compensar la subestimación mediante el factor . En la primera, el factor solo se usa para actualizar la resistencia a tensión con la ec. (10) y, en la segunda, el parámetro actualizado es la deformación última con la ec. (11)
|
|
(10) |
|
|
(11) |

|
| Figura 9. Área subestimada en el diagrama de ablandamiento con la aproximación dentada [10] |
Finalmente, en una tercera opción, Rots e Invernizzi [10] proponen actualizar ambos parámetros, i.e., la resistencia a tensión y la deformación última, empleando las ecs. (7) y (8). Este esquema de regularización se muestra en la Figura 10 y el factor de ajuste, , se calcula con la ec. (9). En esta ecuación, es el número de dientes considerado el diagrama
|
|
(12) |
donde
|
|
(13) |

|
| Figura 10. Compensación del área subestimada en el diagrama de ablandamiento con la aproximación dentada [10] |
5.1 Ejemplos de validación
Como ejemplo de validación para el procedimiento de regularización se seleccionó nuevamente la viga con muesca analizada en la sección anterior. Se consideraron los mismos parámetros mecánicos para el material (Tabla 1) y los mismos modelos para 5, 10 y 20 dientes. Para cada caso se calcularon los factores (Tabla 2).
| Modelo | Factor de ajuste |
|---|---|
| Modelo de 5 dientes | |
| Modelo de 10 dientes | |
| Modelo de 20 dientes |
Los resultados de estos análisis se observan en las Figuras 11 a 13. En estas figuras se puede observar que las aproximaciones son más cercanas a la aproximación numérica de Rots [20] que las obtenidas en el apartado anterior sin procedimiento de regularización de malla, especialmente en la aproximación del área bajo la curva. No obstante, se observa una sobreestimación en la reacción de fluencia y una subestimación en la última parte de la curva. Por último, se puede concluir que cuanto mayor es el número de dientes mejor se aproxima.

|
| Figura 11. Diagrama de reacción-desplazamiento para la viga con muesca (5 dientes regularizado) |

|
| Figura 12. Diagrama de reacción-desplazamiento para la viga con muesca (10 dientes regularizado) |

|
| Figura 13. Diagrama de reacción-desplazamiento para la viga con muesca (20 dientes regularizado) |
6. Ejemplos ilustrativos de la propuesta
Se seleccionaron dos ejemplos de aplicación de la estrategia de ALS-IRE, ambos estudiados por Juárez y Ayala [21]. Ambos ejemplos son ideales para ser modelados con esta estrategia pues presentan una falla en el modo I. El primero consiste en una viga cuya sección transversal es variable y, además, presenta dos muescas. En el segundo ejemplo se estudia una viga de sección transversal constante con una sola muesca.
6.1 Viga de sección transversal variable con muescas
El primer ejemplo consiste en una viga de sección variable con una doble muesca de 25 mm de longitud cada una, como se muestra en la Figura 14. Esta viga está totalmente restringida en su extremo izquierdo y libre en el derecho en el que se imponen los desplazamientos. En el trabajo de Juárez y Ayala [21], esta viga fue analizada mediante una formulación de elementos finitos mixtos no lineales con un modelo de daño continuo isotrópico para el material.
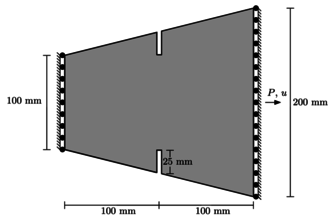
|
| Figura 14. Geometría de la viga de sección transversal variable con muescas [21] |
La malla se construyó empleando únicamente elementos finitos cuadrilaterales de 4 nodos (Figura 15). Todos los elementos de la malla se integraron utilizando este esquema IRE, pero sólo se pueden reducir las propiedades mecánicas de los elementos entre las muescas.

|
| Figura 15. Malla empleada en el análisis de la viga de sección transversal variable con muescas |
Las propiedades mecánicas del material se muestran en la Tabla 3 [21]. Adicionalmente, se consideró un modelo de 10 dientes con un factor .
| Propiedades | Magnitud y unidades |
|---|---|
| Módulo de elasticidad | MPa |
| Relación de Poisson | |
| Resistencia a tensión | MPa |
| Energía de fractura | N/mm |
| Ancho de grieta | mm |
En la Figura 16 se muestran las curvas de reacción-desplazamiento, sin procedimiento de regularización de malla, tanto para ALS como para ALS-IRE. Adicionalmente, se incluye la curva obtenida por Juárez y Ayala [21] a modo de comparación. Aquí se puede observar una clara similitud entre ALS y ALS-IRE. Como era de esperarse de acuerdo a los resultados previos, ambas curvas subestiman el comportamiento aproximado numéricamente [21] ya que no se considera la regularización de la malla.

|
| Figura 16. Diagrama de reacción-desplazamiento para la viga de sección variable con muescas (sin regularización) |
Además, en la Figura 17 se incluyen los resultados considerando el procedimiento de regularización de la malla. El factor calculado es igual a 1.28 y, en consecuencia, la resistencia a la tensión regularizada es de 3.08 MPa y la deformación última regularizada es de 0.064. En la Figura 17 se puede observar que ambos esquemas, ALS y ALS-IRE están más cerca de la aproximación numérica. La diferencia en la forma de las curvas puede explicarse por el hecho de que la falla de la viga de sección variable se rige principalmente por un comportamiento de tensión pura, por lo que la forma de la curva aproximada mediante el procedimiento ALS tiende a parecerse a la línea recta. Esto sugiere la necesidad de emplear un ablandamiento dentado no-lineal.

|
| Figura 17. Diagrama de reacción-desplazamiento para la viga de sección variable con muescas (regularizado) |
Finalmente, en la Figura 18 se muestra la configuración deformada tras el análisis con el modelo ALS-IRE de la viga. Esto es similar a lo reportado en el trabajo de Juárez y Ayala [21].

|
| Figura 18. Configuración deformada de la viga de sección variable con muescas después del análisis con el modelo ALS-IRE |
6.2 Viga de sección transversal constante con muesca
El segundo ejemplo de aplicación consiste en una viga con muesca, mostrada en la Figura 18, que fue ensayada por Kormeling y Reinhardt [22] y analizada numéricamente por Juárez y Ayala [21]. Los ensayos experimentales se realizaron en la Universidad Tecnológica de Delft y tenían como objetivo determinar la energía de fractura del concreto y del concreto modificado con epoxi. Para ello se ensayaron varios especímenes, como el mostrado en la Figura 19.

|
| Figura 19. Geometría de la viga con muesca [21] |
Para el análisis mediante ALS y ALS-IRE, se construyó la malla de la Figura 20. La malla está compuesta únicamente por elementos finitos cuadriláteros de aproximación lineal. Se consideraron las propiedades mecánicas para el material en la Tabla 4. Estas propiedades se seleccionaron según Juárez y Ayala [21] y Kormeling y Reinhardt [22]. Para la aplicación del modelo, se consideraron 20 dientes con un factor .

|
| Figura 20. Malla empleada en el análisis de la viga con muesca |
| Propiedades | Magnitud y unidades |
|---|---|
| Módulo de elasticidad | MPa |
| Relación de Poisson | |
| Resistencia a tensión | MPa |
| Energía de fractura | N/mm |
| Ancho de grieta | mm |
Las curvas de reacción-desplazamiento, sin procedimiento de regularización de malla, tanto para ALS como para ALS-IRE, se muestran en la Figura 21. A efectos de comparación, se ha incluido la curva aproximada numéricamente [20] y las correspondientes de los ensayos experimentales [22]. De los resultados, se puede observar una clara similitud entre ALS, ALS-IRE y los resultados experimentales. Al igual que en el ejemplo anterior, ambas curvas subestiman el comportamiento aproximado numéricamente por Juárez y Ayala [21] ya que no se considera el procedimiento de regularización.

|
| Figura 21. Diagrama de reacción-desplazamiento para la viga con muesca (sin regularización) |
En la Figura 22 se incluyen los resultados de un procedimiento de regularización de la malla. Para esto, el factor es igual a 1.11 y la resistencia a la tensión regularizada es de 2.65 MPa y la deformación última regularizada es de 0.02. A partir de esta figura, se puede observar que ambos esquemas, ALS y ALS-IRE, están más cerca que la aproximación numérica también en el ablandamiento no-lineal de la viga, pero al mismo tiempo se alejan de los resultados experimentales. Finalmente, en la Figura 23 se muestra la configuración deformada resultante del análisis con el modelo ALS-IRE de la viga. Esto es similar a lo reportado en el trabajo de Juárez y Ayala [21] y a lo observado experimentalmente por Kormeling y Reinhardt [22].
 
|
| Figura 22. Diagrama de reacción-desplazamiento para la viga con muesca (regularizado) |

|
| Figura 23. Configuración deformada de la viga con muesca después del análisis con el modelo ALS-IRE |
7. Ley de ablandamiento bilineal
En todos los ejemplos se utilizó una ley de ablandamiento dentado con comportamiento lineal (Figura 1). Siempre que la comparación de los resultados con esta ley de ablandamiento lineal sea contra otra aproximación numérica que también considere un ablandamiento lineal, se obtienen muy buenas aproximaciones. Sin embargo, de acuerdo con lo observado en los ejemplos ilustrativos, especialmente en el de la sección 6.2 que incluye una comparación contra evidencia experimental, la ley de ablandamiento lineal no es adecuada para simular estos comportamientos.
En esta sección, se toma ventaja de la estabilización numérica del procedimiento IRE para calibrar una ley de ablandamiento bilineal. Esto es posible debido a que el procedimiento ALS-IRE permite analizar un solo elemento cuadrilátero de 4 nodos con estabilidad numérica para aproximar el comportamiento del material, i.e., no hay deficiencia de rango en la matriz de rigidez del elemento analizado con integración reducida. En la Figura 24 se observan los resultados de una serie de experimentos en los que se ensayaron elementos de concreto, de diferentes proporciones de mezcla, sometidos a tensión pura [24] y una aproximación bilineal aproximada a dichos resultados experimentales.
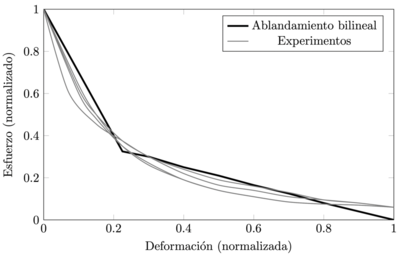
|
| Figura 24. Ablandamiento del concreto sin reforzar sometido a tensión pura [24] |
Con este enfoque, se calibró una ley de ablandamiento bilineal mediante un análisis de un elemento finito cuadrilátero de 4 nodos resuelto con ALS-IRE. En la Figura 25 se incluye dicha calibración y su comparación con la ley de ablandamiento lineal de la Figura 1.

|
| Figura 25. Leyes de ablandamiento en curva esfuerzo-deformación |
Empleando esta ley de ablandamiento bilineal se analizó nuevamente la viga con muesca de la sección 6.2 sin considerar el procedimiento de regularización y solo para el caso ALS-IRE. Se empleó la misma malla y propiedades mecánicas de la Tabla 4. La curva de reacción-desplazamiento se incluye en la Figura 26. Aquí, se puede apreciar una clara mejora en comparación con los resultados obtenidos mediante la ley de ablandamiento lineal (Figuras 21 y 22). La aproximación con la curva obtenida mediante ALS-IRE es más cercana a la serie de experimentos [22]. Del mismo modo, se aprecia que el procedimiento de regularización no es necesario cuando se emplea ALS-IRE y se considera ablandamiento bilineal.

|
| Figura 26. Diagrama de reacción-desplazamiento para la viga con muesca (sin regularizar y con ley de ablandamiento bilineal) |
8. Conclusiones
La estrategia de ALS ha sido muy estudiada en los años recientes, convirtiéndose en una herramienta útil y práctica para la aproximación del comportamiento no-lineal de estructuras en las que, por la gran demanda de volumen de cómputo, no sea viable la aplicación de un modelo constitutivo complejo. La razón principal es que debido a que la estrategia consiste una serie de análisis lineales, no es necesario un procedimiento iterativo para alcanzar la convergencia en cada uno de ellos.
En este artículo se presenta una formulación de IRE aplicada mediante una estrategia de ALS para el estudio de estructuras de materiales cuasi-frágiles. Esta propuesta de ALS-IRE, mostró ser computacionalmente eficiente y, además, obtener resultados satisfactorios en la aproximación en comparación con modelos de análisis no-lineal con formulaciones más robustas.
Una de las características más atractivas de esta propuesta es la posibilidad de emplear IRE en todos los elementos de la malla y no solamente en aquellos donde se asume que se presentará el daño. Esto puede ser atractivo por la reducción del tiempo computacional y por la posibilidad de desarrollos futuros en los que se puede considerar distintas trayectorias de propagación de grietas al no tener la restricción de imponer dicha trayectoria al inicio del análisis.
En la propuesta original de ALS se emplea IR, sin ningún tipo de estabilización, en los elementos en los que se espera que exista daño. Dependiendo del problema a resolver, la matriz de rigidez global puede ser singular, i.e., de rango deficiente, debido al empleo de IR sin estabilización. En la propuesta de ALS-IRE se corrige este problema mediante la inclusión de un procedimiento de estabilización que anula las deficiencias de rango ocasionadas por el uso de IR. Así, debido a la estabilización numérica, como se mostró en la sección 7, es posible calibrar modelos de ablandamiento bilineales para que se ajusten al comportamiento real de cierto material y, a su vez, aproximando de mejor manera los resultados observados en laboratorio.
Del mismo modo, esta propuesta es atractiva de ser mejorada con la inclusión de un algoritmo para cargas no proporcionales y, además, con la inclusión de otros modelos de leyes de ablandamiento, por ejemplo, comportamiento no-lineal y comportamientos distintos para tensión y compresión. Esto puede ampliar el campo de aplicación de la estrategia ALS-IRE y, al mismo tiempo, puede mejorar la calidad en la aproximación a modelar de manera más cercana a la realidad del comportamiento de los materiales.
Agradecimientos
Los autores de este artículo agradecen los patrocinios otorgados por la Dirección General de Asuntos de Personal Académico (DGAPA) de la Universidad Nacional Autónoma de México (UNAM) mediante el proyecto PAPIIT IN104821 “Desarrollo e implementación de una metodología para la evaluación y diseño sísmico de edificios de concreto reforzado basado en resiliencia y control de daño” y al Instituto para la Seguridad de las Construcciones en la Ciudad de México (ISC) mediante el proyecto ISCDF/CEC-04/2022-28 “Metodología simplificada de la evaluación y diseño sísmico de edificios tipo en la CDMX que incluya el control de daño inducido por sismo y el tiempo y costo de recuperación óptimos”. Finalmente, el primer autor de este artículo agradece al Consejo Nacional de Ciencia y Tecnología (CONACyT) por la beca otorgada para realizar sus estudios de doctorado
Referencias
[1] Lubliner J., Oliver J., Oller S., Oñate E. A plastic damage model for concrete. International Journal of Solids and Structures, 25:299-326, 1989.
[2] Contrafatto L., Cuomo, M. A new thermodynamically consistent continuum model for hardening plasticity coupled with damage. International Journal of Solids and Structures, 39:6241-6271, 2002.
[3] Belytschko T., Bindeman L.P. Assumed strain stabilization of the 4-node quadrilateral with 1-point quadrature for nonlinear problems. Computer Methods in Applied Mechanics and Engineering, 88:311–340, 1991.
[4] Belytschko T., Bachrach W.E. Efficient implementation of the quadrilaterals with high coarse-mesh accuracy. Computer Methods in Applied Mechanics and Engineering, 54:279-301, 1986.
[5] Amezcua H.R., Ayala A.G. A computationally efficient numerical integration scheme for non-Linear plane-stress/strain FEM applications using one-point constitutive model evaluation. Structural Engineering and Mechanics, 85(1):89-104, 2023. DOI:10.12989/SEM.2023.85.1.089
[6] Bassa B., Sabourin F., Brunet M. A new nine-node solid-shell finite element using complete 3D constitutive laws. International Journal for Numerical Methods in Engineering, 92(7):589–636, 2012.
[7] Bettaieb A., de Sena J., de Sousa R., Valente R., Habraken A., Duchêne L. On the comparison of two solid-shell formulations based on in-plane reduced and full integration schemes in linear and non-linear applications. Finite Elements in Analysis and Design, 107:44–59, 2015.
[8] Rots J. Sequentially linear continuum model for concrete fracture. Fracture Mechanics of Concrete Structures, 13:831-839, 2001.
[9] Rots J. The role of structural modelling in preserving Amsterdam architectural city heritage. Historical Constructions, pp. 685-696, 2001.
[10] Rots J., Invernizzi S. Regularized sequentially linear saw‐tooth softening model. International Journal for Numerical and Analytical Methods in Geomechanics, 28(7‐8):821-856, 2004.
[11] Rots J., Belleti B., Invernizzi S. Robust modeling of RC structures with an event-by-event strategy. Engineering Fracture Mechanics, 75(3-4):590-614, 2008. DOI:10.1016/j.engfracmech.2007.03.027
[12] DeJong M. Hendriks M., Rots J. Sequentially linear analysis of fracture under non-proportional loading. Engineering Fracture Mechanics, 75(18):5042-5056, 2008. DOI:10.1016/j.engfracmech.2008.07.003
[13] Eliáš J., Frantík P., Vořechovský M. Improved sequentially linear solution procedure. Engineeering Fracture Mechanics, 77(12):2263-2276, 2010. DOI:10.1016/j.engfracmech.2010.05.018
[14] Yu C., Hoogenboom P., Rots J. Incremental sequentially linear analysis to control failure for quasibrittle materials and structures including non-proportional loading. Engineering Fracture Mechanics, 202:332-349, 2018. https://doi.org/10.1016/j.engfracmech.2018.07.036
[15] Invernizzi S., Trovato D., Hendriks M., Van de Graaf A. Sequentially linear modelling of local snap-back in extremely brittle structures. Engineering Structures, 33:1617-1625, 2011. DOI:10.1016/j.engstruct.2011.01.031
[16] Slobbe A., Hendriks M., Rots J. Sequentially linear analysis of shear critical reinforced concrete beams without shear reinforcement. Finite Elements in Analysis and Design, 50:108-124, 2012. DOI:10.1016/j.finel.2011.09.002
[17] Pari M., Van de Graaf A., Hendriks M., Rots J. A multi-surface interface model for sequentially linear methods to analyse masonry structures. Engineering Structures, 238:112-123, 2021. https://doi.org/10.1016/j.engstruct.2021.112123
[18] Pari M., Swart W., Van Gijzen M., Hendriks M., Rots J. Two solution strategies to improve the computational performance of sequentially linear analysis for quasi-brittle structures. Numerical Methods in Engineering, 121(10):2128-2146, 2020. DOI: 10.1002/nme.6302
[19] Van Rossum G., Drake F. Python 3 Reference Manual. Scotts Valley CA, CreateSpace, 2009.
[20] Rots J. The smeared crack model for localized Mode-I tensile fracture. Numerical Models in Fracture Mechanics of Concrete, F.H. Witttmann (editor), Balkema, Rotterdam, pp. 101-114, 1993.
[21] Juárez G., Ayala A.G. Aproximación del proceso de falla en sólidos con elementos finitos mixtos usando modelos de daño continuo. Revista Internacional de Métodos Numéricos para el Cálculo y Diseño en Ingeniería, 26(3):225-232, 2010. http://hdl.handle.net/2117/77528
[22] Kormeling H., Reindhart H. Determination of the fracture energy of normal concrete and epoxy modified concrete. Delft University of Technology, Experiment Report, pp. 5-83, 1983
[23] Coll A., Ribó R., Pasenau M., Escolano E., Perez J., Monros A., Gárate J. GiD v.14 User Manual. www.gidsimulation.com, 2018.
[24] Petersson, P.E. Crack growth and development of fracture zones in plain concrete and similar materials (No. LUTVDG/TVBM--1006/1-174/(1981)). Lund Inst. of Tech. (Sweden), Div. of Building Materials, 1981.Document information
Published on 20/06/23
Accepted on 08/06/23
Submitted on 06/10/22
Volume 39, Issue 2, 2023
DOI: 10.23967/j.rimni.2023.06.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?