An analytical solution to soil consolidation around a pile considering earthquake effect

Latest revision as of 09:22, 9 June 2023

Abstract

In this paper, an analytical solution is developed to investigate soil consolidation around a pile under earthquake loading. The solution is validated using finite element method. The influence of various parameters on excess pore water pressure is analyzed. The results show that excess pore water pressure increases with depth and is positively correlated with ${\textstyle n}$ and ${\textstyle N_{eq}}$ / $N_{1}$ , while negatively correlated with ${\textstyle \eta }$ , ${\textstyle \chi }$ , ${\textstyle k_{v}}$ , and ${\textstyle t_{d}}$ . The values of ${\textstyle \eta }$ , ${\textstyle \chi }$ , ${\textstyle k_{v}}$ , ${\textstyle N_{eq}}$ / $N_{1}$ , and ${\textstyle t_{d}}$ affect excess pore water pressure during and after the earthquake, while the value of ${\textstyle n}$ only affects excess pore water pressure after the earthquake. The growth rate of excess pore water pressure during the earthquake is positively correlated with ${\textstyle n}$ , ${\textstyle \eta }$ , ${\textstyle k_{v}}$ , and ${\textstyle N_{eq}}$ / $N_{1}$ , and negatively correlated with ${\textstyle \chi }$ and ${\textstyle t_{d}}$ . The dissipation rate of excess pore water pressure during the earthquake is positively correlated with ${\textstyle \eta }$ , ${\textstyle \chi }$ , ${\textstyle k_{v}}$ , ${\textstyle N_{eq}}$ / $N_{1}$ , and ${\textstyle t_{d}}$ , and negatively correlated with ${\textstyle n}$ . Additionally, a formula for calculating the reconsolidation settlement of pile-soil foundation after an earthquake is proposed, and the effects of pile and soil parameters on pile-soil foundation reconsolidation settlement are analyzed. The results indicate that reconsolidation settlement can be divided into two stages: rapid settlement stage and slow settlement stage. The total settlement of the foundation is positively correlated with ${\textstyle n}$ , ${\textstyle \eta }$ , and ${\textstyle N_{eq}}$ / $N_{1}$ , while negatively correlated with ${\textstyle \chi }$ , ${\textstyle k_{v}}$ , and ${\textstyle t_{d}}$ .

Keywords: Earthquake, pile-soil foundation, excess pore water pressure, reconsolidation settlement, analytical solution

1. Introduction

The use of pile foundation in high-rise and super high-rise buildings has become increasingly common with the continuous development of modern urbanization [1]. However, frequent earthquakes around the world have raised concerns about the instability of buildings caused by liquefaction and reconsolidation of sandy soil foundations [2,3]. To address this issue, it is necessary to analyze the anti-liquefaction capacity and post-earthquake reconsolidation behavior of pile foundation treatment in sandy soil foundations to provide guidance for the safe and effective application of pile foundation in sandy soils.

After the implementation of pile foundation treatment in sandy soils, the pile and the sand collaboratively bear the upper loading. However, during strong earthquake activity, the pore water pressure inside the saturated sand may increase sharply, leading to a rapid decrease in effective stress and the continuous disappearance of the sand’s bearing capacity [4]. In such cases, the pile foundation can offer better stability and support to reduce the risk of upper structure collapse [5]. Knappett and Madabhushi [6] conducted centrifuge test to analyze the development of excess pore water pressure caused by liquefaction in pile-sandy soil foundation and the post-liquefaction reconsolidation settlement of the foundation. Bao et al. [7] analyzed the earthquake performance and post-earthquake consolidation settlement of multi-layered pile foundation buildings on liquefiable ground using finite element software.

Similarly, other researcher such as Xu et al. [1], Rollins and Strand [8], Chen et al. [9], Hussein and El Naggar [10], Chiou et al. [11], Xu et al. [12], Chen et al. [13] have analyzed the dynamic response of pile-sandy soil foundations under earthquake loading using experimental methods (such as shake table tests) or numerical simulation methods. Xu et al. [1] provided a comprehensive introduction to the existing experimental situations. Although these experimental and numerical simulation results are of great significance in guiding the earthquake design of pile-sandy soil foundations, they also reflect that the current research methods for the earthquake behavior of pile-sandy soil foundation mainly rely on experiments and numerical simulation, lacking analytical model. Compared to experiments and numerical simulations, analytical models are simpler and more convenient for engineering application. Additionally, analytical model can verify the accuracy of experiments and numerical simulations to some extent.

This paper proposes a theoretical model for soil consolidation around a pile considering earthquake effects, using the pile-soil strain compatibility assumption. After analyzing and solving the problem using Fourier transforms, the accuracy of the analytical model is verified using numerical simulations. Based on this, the influence of key parameters in the analytical model on the development and distribution of excess pore water pressure is analyzed using graphical methods. Finally, based on the obtained analytical model for soil consolidation around a pile considering earthquake effects, a calculation formula for reconsolidation settlement of pile-soil foundation is proposed, and the effects of pile and soil parameters on pile-soil foundation reconsolidation settlement are analyzed.

2. Mathematical model

2.1 Model background

Figure 1(a) shows two common types of pile layout: rectangular distribution and triangular distribution. Both types can be utilized to extract the pile-soil element illustrated in Figure 1(b). Furthermore, the pile-soil element can be further depicted on a coordinate axis as shown in Figure 1(c). The radius of the pile is ${\textstyle r_{p}}$ , the influence radius of the pile is denoted as ${\textstyle r_{e}}$ , and the thickness of the pile-soil foundation is represented as ${\textstyle H}$ . Since the pile is an impermeable pile, only vertical drainage of the soil is considered, and the vertical permeability coefficient is ${\textstyle k_{v}}$ . The compressive modulus of the pile and the soil are ${\textstyle E_{p}}$ and ${\textstyle E_{s}}$ , respectively.


Figure 1. Diagram of pile-soil foundation. (a) Pile layout. (b) Pile-soil element. (c) Mathematical model of pile-soil element

2.2 Governing equation

Under earthquake loading, the equilibrium relationship can be expressed as follows:

(1)

where ${\overline {\sigma }}_{s}$ and ${\overline {\sigma }}_{p}$ denote the radial average total stresses of the soil and pile, respectively, and $\sigma$ represents the loading induced by earthquake.

Based on the assumption of equal strain, one can obtain:

(2)

where ${\overline {u}}_{s}$ denote the radial average excess pore water pressure of the soil , and ${\epsilon }_{v}$ is the vertical strain of pile-soil foundation.

Combining Eqs. (1) and (2), the vertical strain rate $\partial {\epsilon }_{v}/\partial t$ is expressed as follows:

(3)

where $\lambda =\pi r_{0}^{2}/\left(\pi r_{\mbox{e}}^{2}\right)$ , and $\chi =E_{p}/E_{s}$ .

The rate of change of total stress $\partial \sigma /\partial t$ is regarded as the rate of excess pore pressure induced by earthquake [14], that is

(4)

where $N_{eq}$ related to magnitude, as shown in Table 1 by Seed and Booker [15]; ${\gamma }^{'}$ is effective unit weight of soil; $N_{l}$ is number of liquefaction cycles; $t_{d}$ is the duration of the earthquake, and $H\left(t\right)=\left\{{\begin{array}{cc}0,&t<0\\1,&t\geq 0\end{array}}\right.$ .

Table 1. The relationship between Magnitude and

[15]

Magnitude	$N_{eq}$
6.5	8
7	12
8	30

The mass conservation equation for the water phase can be obtained using Darcy’s law by

(5)

where ${\textstyle {\gamma }_{w}}$ unit weight of water, 9.8 kN/m³.

Combing Eqs. (3)~(5), one can obtain

(6)

where ${\textstyle \alpha =\left(1-\lambda +\lambda \chi \right)/\left(1-\lambda \right)}$ .

2.3 Solving conditions

The initial excess pore water pressure is

(7)

The top surface of soil is pervious, and the bottoms are impervious. The vertical boundary conditions of soil can be expressed as

(8)

2.4 Normalization

For convenience, normalization is generally conducted to simplify problems to eliminate the influence of measured units. In this model, dimensionless variables or parameters are given as follows:

(9)

Using the dimensionless parameters defined in Eq. (9), Eqs. (6)~(8) in dimensionless form are, respectively, listed below:

(10)

(11)

and

(12)

2.5 Solution of dimensionless excess pore water pressure

Applying the finite Fourier transform to Eqs. (10) and (11) with the boundary conditions of Eq. (12), one can obtain

(13)

and

(14)

where ${\tilde {\overline {U}}}_{s}={\int }_{0}^{1}{\overline {U}}_{s}\sin \left(M_{m}Z\right){d}Z$ , and $M_{m}={\frac {2m-1}{2}}\pi$ .

Eq. (13) is a first-order differential equation that can be solved using the initial condition of Eq. (14). The solution is given by:

{\tilde {\overline {U}}}_{s}=\left\{{\begin{array}{lc}\displaystyle {\frac {N_{eq}}{N_{l}T_{d}}}\displaystyle {\frac {{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_{m}^{4}}}\left(1-{e}^{-\alpha M_{m}^{2}T_{v}}\right),&T_{v}\leq T_{d}\\\displaystyle {\frac {N_{eq}}{N_{l}T_{d}}}\displaystyle {\frac {{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_{m}^{4}}}\left[{e}^{\alpha M_{m}^{2}\left(T_{d}-T_{v}\right)}-{e}^{-\alpha M_{m}^{2}T_{v}}\right],&T_{v}>T_{d}\end{array}}\right.

,

(15)

The general solution of this model can be obtained by applying the inverse finite Fourier transform to Eq. (14), that is

{\overline {U}}_{s}=\left\{{\begin{array}{lc}\displaystyle 2\sum _{m=1}^{\infty }\displaystyle {\frac {N_{eq}}{N_{l}T_{d}}}\displaystyle {\frac {{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_{m}^{4}}}\left(1-{e}^{-\alpha M_{m}^{2}T_{v}}\right)\sin \left(M_{m}Z\right),&T_{v}\leq T_{d}\\\displaystyle 2\sum _{m=1}^{\infty }{\frac {N_{eq}}{N_{l}T_{d}}}{\frac {{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_{m}^{4}}}\left[{e}^{\alpha M_{m}^{2}\left(T_{d}-T_{v}\right)}-{e}^{-\alpha M_{m}^{2}T_{v}}\right]\sin \left(M_{m}Z\right),&T_{v}>T_{d}\end{array}}\right.

(16)

4. Numerical verification

The finite element software COMSOL Multiphysics is used to solve the model numerically to verify the correctness of the analytical model. The parameters used in numerical simulation are given as follows: $r_{p}=0.25$ m, $r_{e}=1{\mbox{ m}}$ , $H=3.75{\mbox{ m}}$ , $k_{v}={10}^{-4}{\mbox{ m}}/{\mbox{s}}$ , $E_{s}=3{\mbox{ MPa}}$ , $E_{p}=150{\mbox{ MPa}}$ , $t_{d}=30{\mbox{ s}}$ , and $N_{eq}/N_{1}=2$ . Figure 2 shows the distribution of excess pore water pressure around a pile simulated by COMSOL Multiphysics. The legend unit in Figure 2 is “Pa”. The data of excess pore water pressure calculated by COMSOL Multiphysics are extracted and compared with the analytical results, as shown in Figure 3. It is found that the numerical results coincide perfectly with the analytical results, which proves the correctness of the analytical solution.


Figure 2. The distribution of excess pore water pressure around a pile by COMSOL Multiphysics ( ${\textstyle t=30}$ s)


Figure 3. Comparison of numerical results and analytical results

5. Excess pore water pressure during earthquake

Figure 4 shows the distribution and development of excess pore water pressure in soil around a pile under different ${\textstyle n}$ values (or influence radius ${\textstyle r_{e}}$ ). Firstly, it can be seen from Figure 4(a) that ${\textstyle n}$ value mainly has an obvious influence on the excess pore water pressure at the bottom of soil. Specifically, the excess pore water pressure increases with the increase of ${\textstyle n}$ value. Figure 4(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the ${\textstyle n}$ value has little influence on the excess pore water pressure in the earthquake stage, but has obvious influence on the excess pore water pressure in the post-earthquake stage. Specifically, the dissipation rate of excess pore water pressure is accelerated with the increase of ${\textstyle n}$ value.



(a)	(b)

Figure 4. Effect of

value on excess pore water pressure. (a) Distribution along depth. (b) Development over time

Figure 5 shows the distribution and development of excess pore water pressure in soil around a pile under different ${\textstyle \eta }$ values (or the thickness of the pile-soil foundation ${\textstyle H}$ ). It can be seen from Figure 5(a) that ${\textstyle \eta }$ value has a significant influence on the excess pore water pressure along the depth direction. At the same depth, the excess pore water pressure increases with the increase of ${\textstyle \eta }$ value. However, it is noted that the increase of excess pore water pressure at the same depth decreases with the increase of ${\textstyle \eta }$ value. Figure 5(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the ${\textstyle \eta }$ value has a significant effect on the excess pore water pressure during and after the earthquake. Firstly, it can be found that the maximum excess pore water pressure generated by earthquake increases with the increase of ${\textstyle \eta }$ value. Then, the growth rate of excess pore water pressure during the earthquake and the dissipation rate of excess pore water pressure after earthquake increase with the increase of ${\textstyle \eta }$ value.



(a)	(b)

Figure 5. Effect of

value on excess pore water pressure. (a) Distribution along depth. (b) Development over time

Figure 6 shows the distribution and development of excess pore water pressure in soil around a pile under different ${\textstyle \chi }$ values (or the compression moduli of the pile ${\textstyle E_{p}}$ ). It can be seen from Figure 6(a) that ${\textstyle \chi }$ value has a significant influence on the excess pore water pressure along the depth direction. At the same depth, the excess pore water pressure decreases with the increase of ${\textstyle \chi }$ value. Moreover, the increase of excess pore water pressure at the same depth decreases with the increase of ${\textstyle \chi }$ value. Figure 6(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the ${\textstyle \chi }$ value has a significant effect on the excess pore water pressure during and after the earthquake. Firstly, it can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of ${\textstyle \chi }$ value. Then, the dissipation rate of excess pore water pressure after earthquake increase with the increase of ${\textstyle \chi }$ value.



(a)	(b)

Figure 6. Effect of

value on excess pore water pressure. (a) Distribution along depth. (b) Development over time

Figure 7 shows the distribution and development of excess pore water pressure in soil around a pile under different ${\textstyle k_{v}}$ . It can be seen from Figure 7(a): when ${\textstyle k_{v}}$ is small, ${\textstyle k_{v}}$ mainly has an obvious influence on the excess pore water pressure at the bottom of soil; when ${\textstyle k_{v}}$ is high, ${\textstyle k_{v}}$ value has a significant influence on the excess pore water pressure along the depth direction. The effect of ${\textstyle k_{v}}$ on the excess pore water pressure shows that the excess pore water pressure decreases with the increase of ${\textstyle k_{v}}$ . Figure 7(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of ${\textstyle k_{v}}$ value. Then, the growth rate of excess pore water pressure during the earthquake and the dissipation rate of excess pore water pressure after earthquake increase with the increase of ${\textstyle k_{v}}$ value.



(a)	(b)

Figure 7. Effect of

on excess pore water pressure. (a) Distribution along depth. (b) Development over time

Figure 8 shows the distribution and development of excess pore water pressure in soil around a pile under different ${\textstyle N_{eq}/N_{1}}$ . It can be seen from Figure 8(a) that the excess pore water pressure increases with the increase of ${\textstyle N_{eq}/N_{1}}$ . Figure 8(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of ${\textstyle N_{eq}/N_{1}}$ value. Then, the growth rate of excess pore water pressure during the earthquake and the dissipation rate of excess pore water pressure after earthquake increase with the increase of ${\textstyle N_{eq}/N_{1}}$ value.



(a)	(b)

Figure 8. Effect of

on excess pore water pressure. (a) Distribution along depth. (b) Development over time

Figure 9 shows the distribution and development of excess pore water pressure in soil around a pile under different ${\textstyle t_{d}}$ . ${\textstyle t_{d}}$ stands for the duration of an earthquake. If the frequency of earthquakes remains constant, a shorter duration implies a higher frequency. It can be seen from Figure 9(a) that the excess pore water pressure decreases with the increase of ${\textstyle t_{d}}$ . Figure 9(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of ${\textstyle t_{d}}$ value. Then, it is noted that the effect of ${\textstyle t_{d}}$ on the excess pore water pressure during the earthquake is obviously greater than that after the earthquake.



(a)	(b)

Figure 9. Effect of

on excess pore water pressure. (a) Distribution along depth. (b) Development over time

6. Reconsolidation settlement of goundation after earthquake

Due to the assumption of equal strain, the reconsolidation settlement of pipe-soil foundation can be calculated by the reconsolidation settlement of soil around the pile. The reconsolidation settlement of soil around the pile can be expressed as follows [4]:

{\begin{array}{c}\displaystyle S\left(T_{v}\right)={\frac {1}{E_{s}}}{\int }_{T_{vd}}^{T_{v}}{\int }_{0}^{H}{\frac {\partial {\gamma }_{w}H{\overline {U}}_{s}}{\partial t}}{d}z{d}t\\\displaystyle ={\frac {{\gamma }_{w}H}{E_{s}}}\sum _{m=1}^{\infty }{\frac {2N_{eq}}{N_{l}T_{vd}}}{\frac {{\left(-1\right)}^{m-1}\left[{e}^{\alpha M_{m}^{2}\left(T_{vd}-T_{v}\right)}-{e}^{-\alpha M_{m}^{2}T_{v}}+{e}^{-\alpha M_{m}^{2}T_{vd}}-1\right]}{\left(1-\lambda \right)\alpha M_{m}^{5}}}\end{array}}

(16)

Figure 10 shows the reconsolidation settlement of foundation after earthquake under different ${\textstyle n}$ values. It can be found that reconsolidation settlement is mainly divided into two stages: one is the rapid settlement stage, in which reconsolidation settlement develops rapidly; then there is the slow settlement stage in which reconsolidation settlement develops slowly. It can be seen from Figure 10 that the larger the ${\textstyle n}$ value is, the slower the settlement rate in the early stage and the faster the settlement rate in the later stage. In general, the total settlement of foundation increases with the increase of ${\textstyle n}$ value.


Figure 10. Effect of n on reconsolidation settlement of foundation after earthquake

Figure 11 shows the reconsolidation settlement of foundation after earthquake under different ${\textstyle \eta }$ values. It can be seen that the total settlement of the foundation increases significantly as the value of ${\textstyle \eta }$ increases.


Figure 11. Effect of ${\textstyle \eta }$ on reconsolidation settlement of foundation after earthquake

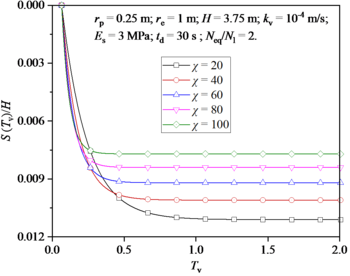
Figure 12 shows the reconsolidation settlement of foundation after earthquake under different ${\textstyle \chi }$ values. It can be seen from Figure 12 that the larger the ${\textstyle \chi }$ value is, the faster the settlement rate in the early stage and the slower the settlement rate in the later stage. In general, the total settlement of foundation decreases with the increase of ${\textstyle \chi }$ value.


Figure 12. Effect of ${\textstyle \chi }$ on reconsolidation settlement of foundation after earthquake

Figure 13 shows the reconsolidation settlement of foundation after earthquake under different ${\textstyle k_{v}}$ values. It can be seen that the total settlement of the foundation decreases significantly as the value of ${\textstyle k_{v}}$ increases.


Figure 13. Effect of ${\textstyle k_{v}}$ on reconsolidation settlement of foundation after earthquake

Figure 14 shows the reconsolidation settlement of foundation after earthquake under different ${\textstyle N_{eq}}$ / $N_{1}$ values. It can be seen that the total settlement of the foundation increases significantly as the value of ${\textstyle N_{eq}}$ / $N_{1}$ increases.


Figure 14. Effect of ${\textstyle N_{eq}}$ / $N_{1}$ on reconsolidation settlement of foundation after earthquake

Figure 15 shows the reconsolidation settlement of foundation after earthquake under different ${\textstyle t_{d}}$ values. It can be seen that the total settlement of the foundation decreases significantly as the value of ${\textstyle t_{d}}$ increases.


Figure 15. Effect of ${\textstyle t_{d}}$ on reconsolidation settlement of foundation after earthquake

7. Conclusions

In this paper, an analytical solution to soil consolidation around a pile considering earthquake effect is proposed, and the accuracy of the analytical model is verified by finite element software. Finally, the effects of soil parameters, pile parameters and earthquake parameters in the analytical model on the excess pore water pressure and reconsolidation settlement after earthquakes are analyzed and discussed. The main conclusions are as follows:

(1) Distribution of excess pore water pressure in soil around the pile: The excess pore water pressure increased with depth, and is positively correlated with ${\textstyle n}$ and ${\textstyle N_{eq}}$ / $N_{1}$ , and negatively correlated with ${\textstyle \eta }$ , ${\textstyle \chi }$ , ${\textstyle k_{v}}$ , and ${\textstyle t_{d}}$ .

(2) Development of excess pore water pressure in soil around the pile: The values of ${\textstyle \eta }$ , ${\textstyle \chi }$ , ${\textstyle k_{v}}$ , ${\textstyle N_{eq}}$ / $N_{1}$ , and ${\textstyle t_{d}}$ affect the excess pore water pressure during and after the earthquake, and the value of ${\textstyle n}$ only obvious affects the excess pore water pressure after the earthquake; The growth rate of excess pore water pressure during the earthquake is positively correlated with ${\textstyle n}$ , ${\textstyle \eta }$ , ${\textstyle k_{v}}$ , and ${\textstyle N_{eq}}$ / $N_{1}$ , and negatively correlated with ${\textstyle \chi }$ and ${\textstyle t_{d}}$ . The dissipation rate of excess pore water pressure during the earthquake is positively correlated with ${\textstyle \eta }$ , ${\textstyle \chi }$ , ${\textstyle k_{v}}$ , ${\textstyle N_{eq}}$ / $N_{1}$ , and ${\textstyle t_{d}}$ , and negatively correlated with ${\textstyle n}$ .

(3) Reconsolidation settlement of foundation after earthquake: Reconsolidation settlement is mainly divided into two stages: rapid settlement stage and slow settlement stage; The total settlement of foundation is positively correlated with ${\textstyle n}$ , ${\textstyle \eta }$ , and ${\textstyle N_{eq}}$ / $N_{1}$ , and negatively correlated with ${\textstyle \chi }$ , ${\textstyle k_{v}}$ , and ${\textstyle t_{d}}$ .

Data Availability Statement

All data, models, and code generated or used during the study appear in the submitted article.

Acknowledgements

This work had been supported by the Guangdong Key Areas R&D Program Projects, China (Grant number: 2020B0101130005), Research Project of Guangdong Power Grid Co. (Grant number: 031000QQ00220012).

References

[1] Xu C., Dou P., Du X., et al. Seismic performance of pile group-structure system in liquefiable and non-liquefiable soil from large-scale shake table tests. Soil Dynamics and Earthquake Engineering, 138, 106299, 2020.

[2] Finn W.D.L, Fujita N. Piles in liquefiable soils: seismic analysis and design issues. Soil Dynamics and Earthquake Engineering, 22(9-12):731-742, 2002.

[3] Cubrinovski M., Bray J.D., De La Torre C., et al. Liquefaction effects and associated damages observed at the Wellington CentrePort from the 2016 Kaikoura earthquake. Bulletin of the New Zealand Society for Earthquake Engineering, 50(2):152-173, 2017.

[4] Pal S., Deb K. Postearthquake reconsolidation settlement of stone column-treated liquefiable sand. International Journal of Geomechanics, 20(10), 04020183, 2020.

[5] Su L., Tang L., Ling X.-Z., et al. Responses of reinforced concrete pile group in two-layered liquefied soils: shake-table investigations. Journal of Zhejiang University-SCIENCE A, 2(16):93-104, 2015.

[6] Knappett J.A., Madabhushi S.P. Liquefaction-induced settlement of pile groups in liquefiable and laterally spreading soils. Journal of Geotechnical and Geoenvironmental Engineering, 134(11):1609-1618, 2008.

[7] Bao X., Ye G., Ye B., et al. Seismic performance of multi-story building with pile foundation in liquefiable ground including post-earthquake consolidation settlement. Advances in Soil Dynamics and Foundation Engineering, pp. 353-362, Shanghai, China, May 26-28 2014.

[8] Rollins K.M., Strand S.R. Downdrag forces due to liquefaction surrounding a pile. Proc. 8th National Conference on Earthquake Engineering, Earthquake Engineering Research Institute, Paper No. 1646, San Francisco, CA, April 18-22 2006.

[9] Chen X., Guan Z., Spencer Jr B.F., et al. A simplified procedure for estimating nonlinear seismic demand of tall piers. Engineering Structures, 174:778-791, 2018.

[10] Hussein A.F., El Naggar M.H. Seismic axial behaviour of pile groups in non-liquefiable and liquefiable soils. Soil Dynamics and Earthquake Engineering, 149, 106853, 2021.

[11] Chiou J.-S., Huang T.-J., Chen C.-L., et al. Shaking table testing of two single piles of different stiffnesses subjected to liquefaction-induced lateral spreading. Engineering Geology, 281, 105956, 2021.

[12] Xu L.-Y., Song C.-X., Chen W.-Y., et al. Liquefaction-induced settlement of the pile group under vertical and horizontal ground motions. Soil Dynamics and Earthquake Engineering, 144, 106709, 2021.

[13] Chen X., Xiang N., Li C. Influence of higher-order modes of slender tall pier bridge columns on the seismic performance of pile foundations. Soil Dynamics and Earthquake Engineering, 142, 106543, 2021.

[14] Xu Z. Calculation of pore pressure of liquefiable sand deposits using gravel drains (in Chinese). Earthquake Engineering and Engineering Vibration, 12(4):88-92, 1992.

[15] Seed H.B., Booker J.R. Stabilization of potentially liquefiable sand deposits using gravel drains. Journal of the Geotechnical Engineering Division, 103(7):757-768, 1977.

Latest revision as of 09:22, 9 June 2023

Abstract

1. Introduction

2. Mathematical model

2.1 Model background

2.2 Governing equation

2.3 Solving conditions

2.4 Normalization

2.5 Solution of dimensionless excess pore water pressure

4. Numerical verification

5. Excess pore water pressure during earthquake

6. Reconsolidation settlement of goundation after earthquake

7. Conclusions

Data Availability Statement

Acknowledgements

References

Document information

Document Score

Share this document

Keywords

claim authorship

@@ Line 105: / Line 105: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>\frac{\partial {\epsilon }_\mbox{v}}{\partial t}=</math><math>-\frac{\left(1-\lambda \right)\frac{\partial {\overline{u}}_\mbox{s}}{\partial t}-\frac{\partial \sigma }{\partial t}}{E_\mbox{s}\left(1-\lambda +\lambda \epsilon \right)}</math>
+| <math>\frac{\partial {\epsilon }_{v}}{\partial t}=</math><math>-\frac{\left(1-\lambda \right)\frac{\partial {\overline{u}}_{s}}{\partial t}-\frac{\partial \sigma }{\partial t}}{E_{s}\left(1-\lambda +\lambda \epsilon \right)}</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (3)
 |}
+where  <math>\lambda =\pi r_0^2/\left(\pi r_\mbox{e}^2\right)</math>, and  <math>\chi =E_{p}/E_{s}</math>.
-where  <math>\lambda =\mbox{π}r_0^2/\left(\mbox{π}r_\mbox{e}^2\right)</math> ; and  <math>\chi =E_\mbox{p}/E_\mbox{s}</math> .
+The rate of change of total stress  <math>\partial \sigma /\partial t</math> is regarded as the rate of excess pore pressure induced by earthquake [14], that is
-The rate of change of total stress  <math>\partial \sigma /\partial t</math> is regarded as the rate of excess pore pressure induced by earthquake<sup>[14]</sup>, that is
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 120: / Line 119: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>\frac{\partial \sigma }{\partial t}=\frac{N_{\mbox{eq}}{\gamma }^{{'}}z}{N_\mbox{l}t_\mbox{d}}H\left(t_\mbox{d}-\right. </math><math>\left. t\right)</math>
+| <math>\frac{\partial \sigma }{\partial t}=\frac{N_{{eq}}{\gamma }^{{'}}z}{N_{l}t_{d}}H\left(t_{d}- t\right)</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (4)
 |}
+where  <math>N_{{eq}}</math> related to magnitude, as shown in [[#tab-1|Table 1]] by Seed and Booker [15];  <math>{\gamma }^{{'}}</math> is effective unit weight of soil;  <math>N_{l}</math> is number of liquefaction cycles;  <math>t_{d}</math> is the duration of the earthquake, and  <math>H\left(t\right)=\left\{ \begin{array}{cc}
-where  <math>N_{\mbox{eq}}</math> related to magnitude, as shown in Table 1 by Seed and Booker (1977)<sup>[15]</sup>.  <math>{\gamma }^{{'}}</math> is effective unit weight of soil;  <math>N_\mbox{l}</math> is number of liquefaction cycles;  <math>t_\mbox{d}</math> is the duration of the earthquake;  <math>H\left(t\right)=\lbrace \begin{array}{cc}
 , & t<0\\
 , & t\geq 0
-\end{array}</math> .
+\end{array}\right.</math>.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div class="center" style="font-size: 75%;">'''Table 1'''. The relationship between Magnitude and <math>N_{{eq}}</math> [15]</div>
-Table 1 The relationship between Magnitude and ''N''<sub>eq</sub><sup>[15]</sup>.</div>
-{| style="width: 62%;margin: 1em auto 0.1em auto;border-collapse: collapse;"
+<div id='tab-1'></div>
-|-
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
-|  style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: center;"|Magnitude
+|-style="text-align:center"
-|  style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: center;"|''N''<sub>eq</sub>
+! Magnitude !! <math>N_{{eq}}</math>
 |-
-|  style="border-top: 1pt solid black;text-align: center;"|6.5
+|  style="text-align: center;"|6.5
-|  style="border-top: 1pt solid black;text-align: center;"|8
+|  style="text-align: center;"|8
 |-
 |  style="text-align: center;"|7
 |  style="text-align: center;"|12
 |-
-|  style="border-bottom: 2pt solid black;text-align: center;"|8
+|  style="text-align: center;"|8
-|  style="border-bottom: 2pt solid black;text-align: center;"|30
+|  style="text-align: center;"|30
 |}
@@ Line 157: / Line 154: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>\frac{\partial {\epsilon }_\mbox{v}}{\partial t}=</math><math>-\frac{k_\mbox{v}}{{\gamma }_\mbox{w}}\frac{{\partial }^2{\overline{u}}_\mbox{s}}{\partial z^2}</math>
+| <math>\frac{\partial {\epsilon }_{v}}{\partial t}=-\frac{k_\mbox{v}}{{\gamma }_{w}}\frac{{\partial }^2{\overline{u}}_{s}}{\partial z^2}</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (5)
 |}
+where  <math display="inline">{\gamma }_{w}</math> unit weight of water, 9.8 kN/m<sup>3</sup>.
-where  <math display="inline">{\gamma }_\mbox{w}</math> unit weight of water, 9.8 kN/m<sup>3</sup>.
+Combing Eqs. (3)~(5), one can obtain
-Combing Eqs. (3) ~ (5), one can obtain
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 172: / Line 168: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>\frac{\partial {\overline{u}}_\mbox{s}}{\partial t}=</math><math>\frac{\alpha k_\mbox{v}E_\mbox{s}}{{\gamma }_\mbox{w}}\frac{{\partial }^2{\overline{u}}_\mbox{s}}{\partial z^2}+</math><math>\frac{1}{1-\lambda }\frac{N_{\mbox{eq}}{\gamma }^{{'}}z}{N_\mbox{l}t_\mbox{d}}H\left(t_\mbox{d}-\right. </math><math>\left. t\right)</math>
+| <math>\frac{\partial {\overline{u}}_{s}}{\partial t}=\frac{\alpha k_{v}E_{s}}{{\gamma }_{w}}\frac{{\partial }^2{\overline{u}}_{s}}{\partial z^2}+</math><math>\frac{1}{1-\lambda }\frac{N_{{eq}}{\gamma }^{{'}}z}{N_{l}t_{d}}H\left(t_{d}- t\right)</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (6)
 |}
+where  <math display="inline">\alpha =\left(1-\lambda +\lambda \chi \right)/\left(1- \lambda \right)</math>.
-where  <math display="inline">\alpha =\left(1-\lambda +\lambda \chi \right)/\left(1-\right. </math><math>\left. \lambda \right)</math> .
+===2.3 Solving conditions===
-====2.3 Solving conditions====
 The initial excess pore water pressure is
@@ Line 189: / Line 184: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>{{\overline{u}}_\mbox{s}\vert }_{t=0}=0</math>
+| <math>{{\overline{u}}_{s}\Bigg| }_{t=0}=0</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (7)
@@ Line 202: / Line 197: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>{{\overline{u}}_\mbox{s}\vert }_{z=0}={\frac{\partial {\overline{u}}_\mbox{s}}{\partial z}\vert }_{z=H}=</math><math>0</math>
+| <math>{{\overline{u}}_{s}\Bigg| }_{z=0}={\frac{\partial {\overline{u}}_{s}}{\partial z}\Bigg| }_{z=H}=</math><math>0</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (8)
 |}
+===2.4 Normalization===
-====2.4 Normalization====
 For convenience, normalization is generally conducted to simplify problems to eliminate the influence of measured units. In this model, dimensionless variables or parameters are given as follows:
@@ Line 217: / Line 211: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>Z=\frac{z}{H},\mbox{ }T_\mbox{v}=\frac{k_\mbox{v}E_\mbox{s}t}{{\gamma }_\mbox{w}H^2},\mbox{ }T_\mbox{d}=</math><math>\frac{k_\mbox{v}E_\mbox{s}t_\mbox{d}}{{\gamma }_\mbox{w}H^2},{\overline{U}}_\mbox{s}=</math><math>\frac{{\overline{u}}_\mbox{s}}{{\gamma }^{{'}}H}.</math>
+| <math>Z=\frac{z}{H},T_{v}=\frac{k_{v}E_{s}t}{{\gamma }_{w}H^2},T_{d}=</math><math>\frac{k_{v}E_{s}t_{d}}{{\gamma }_{w}H^2},{\overline{U}}_{s}=</math><math>\frac{{\overline{u}}_{s}}{{\gamma }^{{'}}H}.</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (9)
@@ Line 223: / Line 217: @@
-Using the dimensionless parameters defined in Eq. (9), Eqs. (6) ~ (8) in dimensionless form are respectively listed below:
+Using the dimensionless parameters defined in Eq. (9), Eqs. (6)~(8) in dimensionless form are, respectively, listed below:
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 230: / Line 224: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>\frac{\partial {\overline{U}}_\mbox{s}}{\partial T_\mbox{v}}=</math><math>\alpha \frac{{\partial }^2{\overline{U}}_\mbox{s}}{\partial Z^2}+</math><math>\frac{1}{1-\lambda }\frac{N_{\mbox{eq}}Z}{N_\mbox{l}T_{\mbox{vd}}}H\left(T_\mbox{d}-\right. </math><math>\left. T_\mbox{v}\right)</math>
+| <math>\frac{\partial {\overline{U}}_{s}}{\partial T_{v}}=</math><math>\alpha \frac{{\partial }^2{\overline{U}}_{s}}{\partial Z^2}+</math><math>\frac{1}{1-\lambda }\frac{N_{{eq}}Z}{N_{l}T_{{vd}}}H\left(T_{d}- T_{v}\right)</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (10)
@@ Line 240: / Line 234: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>{{\overline{U}}_\mbox{s}\vert }_{T_\mbox{v}=0}=0</math>
+| <math>{{\overline{U}}_{s}\Bigg| }_{T_{v}=0}=0</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (11)
 |}
 and
@@ Line 253: / Line 246: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>{{\overline{U}}_\mbox{s}\vert }_{Z=0}={\frac{\partial {\overline{U}}_\mbox{s}}{\partial Z}\vert }_{Z=1}=</math><math>0</math>
+| <math>{{\overline{U}}_{s}\Bigg| }_{Z=0}={\frac{\partial {\overline{U}}_{s}}{\partial Z}\Bigg| }_{Z=1}=</math><math>0</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (12)
 |}
+===2.5 Solution of dimensionless excess pore water pressure===
-====2.5 Solution of Dimensionless Excess Pore Water Pressure====
 Applying the finite Fourier transform to Eqs. (10) and (11) with the boundary conditions of Eq. (12), one can obtain
@@ Line 268: / Line 260: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>\frac{\partial {\tilde{\overline{U}}}_\mbox{s}}{\partial T_\mbox{v}}=</math><math>-\alpha M_m^2{\tilde{\overline{U}}}_\mbox{s}+\frac{1}{1-\lambda }\frac{{\left(-1\right)}^{m-1}}{M_m^2}\frac{N_{\mbox{eq}}}{N_\mbox{l}T_\mbox{d}}H\left(T_\mbox{d}-\right. </math><math>\left. T_\mbox{v}\right)</math>
+| <math>\frac{\partial {\tilde{\overline{U}}}_{s}}{\partial T_{v}}=</math><math>-\alpha M_m^2{\tilde{\overline{U}}}_{s}+\frac{1}{1-\lambda }\frac{{\left(-1\right)}^{m-1}}{M_m^2}\frac{N_{{eq}}}{N_{l}T_{d}}H\left(T_{d}- T_{v}\right)</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (13)
 |}
 and
@@ Line 281: / Line 272: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>{{\overline{U}}_\mbox{s}\vert }_{T_\mbox{v}=0}=0</math>
+| <math>{{\overline{U}}_{s}\Bigg| }_{T_{v}=0}=0</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (14)
 |}
+where  <math>{\tilde{\overline{U}}}_{s}={\int }_0^1{\overline{U}}_{s}\sin\left(M_mZ\right){d}Z</math>,  and <math>M_m=\frac{2m-1}{2}\pi </math>.
-where  <math>{\tilde{\overline{U}}}_\mbox{s}={\int }_0^1{\overline{U}}_\mbox{s}sin\left(M_mZ\right)\mbox{d}Z</math> ,  <math>M_m=\frac{2m-1}{2}\pi </math> .
 Eq. (13) is a first-order differential equation that can be solved using the initial condition of Eq. (14). The solution is given by:
@@ Line 296: / Line 286: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>{\tilde{\overline{U}}}_\mbox{s}=\lbrace \begin{array}{cc}
+| <math>{\tilde{\overline{U}}}_{s}=\left\{ \begin{array}{lc}
-\frac{N_{\mbox{eq}}}{N_\mbox{l}T_\mbox{d}}\frac{{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_m^4}\left(1-\mbox{e}^{-\alpha M_m^2T_\mbox{v}}\right), & T_\mbox{v}\leq T_\mbox{d}\\
+\displaystyle\frac{N_{{eq}}}{N_{l}T_{d}}\displaystyle\frac{{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_m^4}\left(1-{e}^{-\alpha M_m^2T_{v}}\right), & T_{v}\leq T_{d}\\
-\frac{N_{\mbox{eq}}}{N_\mbox{l}T_\mbox{d}}\frac{{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_m^4}\left[\mbox{e}^{\alpha M_m^2\left(T_\mbox{d}-T_\mbox{v}\right)}-\mbox{e}^{-\alpha M_m^2T_\mbox{v}}\right], & T_\mbox{v}>T_\mbox{d}
+\displaystyle\frac{N_{{eq}}}{N_{l}T_{d}}\displaystyle\frac{{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_m^4}\left[{e}^{\alpha M_m^2\left(T_{d}-T_{v}\right)}-{e}^{-\alpha M_m^2T_{v}}\right], & T_{v}>T_{d}\end{array}\right.</math>,
-\end{array}</math> ,
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (15)
@@ Line 312: / Line 301: @@
 {| style="text-align: center; margin:auto;"
 |-
-| <math>{\overline{U}}_\mbox{s}=\lbrace \begin{array}{cc}
+| <math>{\overline{U}}_{s}=\left\{ \begin{array}{lc}
-\sum_{m=1}^{\infty }\frac{N_{\mbox{eq}}}{N_\mbox{l}T_\mbox{d}}\frac{{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_m^4}\left(1-\mbox{e}^{-\alpha M_m^2T_\mbox{v}}\right)sin\left(M_mZ\right), & T_\mbox{v}\leq T_\mbox{d}\\
+\displaystyle 2\sum_{m=1}^{\infty }\displaystyle\frac{N_{{eq}}}{N_{l}T_{d}}\displaystyle\frac{{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_m^4}\left(1-{e}^{-\alpha M_m^2T_{v}}\right)\sin\left(M_mZ\right), & T_{v}\leq T_{d}\\
-\sum_{m=1}^{\infty }\frac{N_{\mbox{eq}}}{N_\mbox{l}T_\mbox{d}}\frac{{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_m^4}\left[\mbox{e}^{\alpha M_m^2\left(T_\mbox{d}-T_\mbox{v}\right)}-\mbox{e}^{-\alpha M_m^2T_\mbox{v}}\right]sin\left(M_mZ\right), & T_\mbox{v}>T_\mbox{d}
+\displaystyle2\sum_{m=1}^{\infty }\frac{N_{{eq}}}{N_{l}T_{d}}\frac{{\left(-1\right)}^{m-1}}{\left(1-\lambda \right)\alpha M_m^4}\left[{e}^{\alpha M_m^2\left(T_{d}-T_{v}\right)}-{e}^{-\alpha M_m^2T_{v}}\right]\sin\left(M_mZ\right), & T_{v}>T_{d}
-\end{array}</math>
+\end{array}\right.</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (16)
 |}
-===4. Numerical Verification===
+==4. Numerical verification==
-The finite element software COMSOL Multiphysics is used to solve the model numerically to verify the correctness of the analytical model. The parameters used in numerical simulation are given as follows:  <math>r_\mbox{p}=0.25\mbox{ m}</math> ,  <math>r_\mbox{e}=1\mbox{ m}</math> ,  <math>H=3.75\mbox{ m}</math> ,  <math>k_\mbox{v}={10}^{-4}\mbox{ }\mbox{m}/\mbox{s}</math> ,  <math>E_\mbox{s}=3\mbox{ MPa}</math> ,  <math>E_\mbox{p}=150\mbox{ MPa}</math> ,  <math>t_\mbox{d}=30\mbox{ s}</math> , and  <math>N_{\mbox{eq}}/N_1=2</math> . Figure 2 shows the distribution of excess pore water pressure around a pile simulated by COMSOL Multiphysics. The legend unit in Figure 2 is “Pa”. The data of excess pore water pressure calculated by COMSOL Multiphysics are extracted and compared with the analytical results, as shown in Figure 3. It is found that the numerical results coincide perfectly with the analytical results, which proves the correctness of the analytical solution.
+The finite element software COMSOL Multiphysics is used to solve the model numerically to verify the correctness of the analytical model. The parameters used in numerical simulation are given as follows:  <math>r_{p}=0.25</math> m,  <math>r_{e}=1\mbox{ m}</math>,  <math>H=3.75\mbox{ m}</math>,  <math>k_{v}={10}^{-4}\mbox{ m}/\mbox{s}</math>,  <math>E_{s}=3\mbox{ MPa}</math>,  <math>E_{p}=150\mbox{ MPa}</math>,  <math>t_{d}=30\mbox{ s}</math>, and  <math>N_{{eq}}/N_1=2</math>. [[#img-2|Figure 2]] shows the distribution of excess pore water pressure around a pile simulated by COMSOL Multiphysics. The legend unit in [[#img-2|Figure 2]] is “Pa”. The data of excess pore water pressure calculated by COMSOL Multiphysics are extracted and compared with the analytical results, as shown in [[#img-3|Figure 3]]. It is found that the numerical results coincide perfectly with the analytical results, which proves the correctness of the analytical solution.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-2'></div>
- [[Image:Review_979873928567-image43-c.png|234px]] </div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
+|-style="background:white;"
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image43-c.png|234px]]
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. The distribution of excess pore water pressure around a pile by COMSOL Multiphysics (<math display="inline">t= 30</math> s)
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 2 The distribution of excess pore water pressure around a pile by COMSOL Multiphysics (''t'' = 30 s).</div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-3'></div>
- [[Image:Review_979873928567-image44.png|300px]] </div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
+|-style="background:white;"
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image44.png|400px]]
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. Comparison of numerical results and analytical results
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 3 Comparison of numerical results and analytical results.</div>
-===5. Excess Pore Water Pressure during Earthquake===
+==5. Excess pore water pressure during earthquake==
-Figure 4 shows the distribution and development of excess pore water pressure in soil around a pile under different ''n'' values (or influence radius ''r''<sub>e</sub>). Firstly, it can be seen from Figure 4(a) that ''n'' value mainly has an obvious influence on the excess pore water pressure at the bottom of soil. Specifically, the excess pore water pressure increases with the increase of ''n'' value. Figure 4(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the ''n'' value has little influence on the excess pore water pressure in the earthquake stage, but has obvious influence on the excess pore water pressure in the post-earthquake stage. Specifically, the dissipation rate of excess pore water pressure is accelerated with the increase of ''n'' value.
+[[#img-4|Figure 4]] shows the distribution and development of excess pore water pressure in soil around a pile under different <math display="inline"> n </math> values (or influence radius <math display="inline">r_e</math>). Firstly, it can be seen from [[#img-4|Figure 4]](a) that <math display="inline"> n </math> value mainly has an obvious influence on the excess pore water pressure at the bottom of soil. Specifically, the excess pore water pressure increases with the increase of <math display="inline"> n </math> value. [[#img-4|Figure 4]](b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the <math display="inline"> n </math> value has little influence on the excess pore water pressure in the earthquake stage, but has obvious influence on the excess pore water pressure in the post-earthquake stage. Specifically, the dissipation rate of excess pore water pressure is accelerated with the increase of <math display="inline"> n </math> value.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-4'></div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
-{|
+|-style="background:white;"
+|align="center" |
+{|style="margin: 0em auto 0.1em auto;width:auto;"
+|+
 |-
-| [[Image:Review_979873928567-image45.png|300px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image45.png|350px]]
-| [[Image:Review_979873928567-image46.png|center|300px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image46.png|center|350px]]
+|-
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a)
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b)
+|}
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. Effect of <math display="inline"> n </math> value on excess pore water pressure. (a) Distribution along depth. (b) Development over time
 |}
-</div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 4 Effect of ''n'' value on excess pore water pressure: (a) distribution along depth; and (b) development over time.</div>
-Figure 5 shows the distribution and development of excess pore water pressure in soil around a pile under different ''η'' values (or the thickness of the pile-soil foundation ''H''). It can be seen from Figure 5(a) that ''η'' value has a significant influence on the excess pore water pressure along the depth direction. At the same depth, the excess pore water pressure increases with the increase of ''η'' value. However, it is noted that the increase of excess pore water pressure at the same depth decreases with the increase of ''η'' value. Figure 5(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the ''η'' value has a significant effect on the excess pore water pressure during and after the earthquake. Firstly, it can be found that the maximum excess pore water pressure generated by earthquake increases with the increase of ''η'' value. Then, the growth rate of excess pore water pressure during the earthquake and the dissipation rate of excess pore water pressure after earthquake increase with the increase of ''η'' value.
+[[#img-5|Figure 5]]  shows the distribution and development of excess pore water pressure in soil around a pile under different <math display="inline"> \eta </math> values (or the thickness of the pile-soil foundation <math display="inline"> H </math>). It can be seen from [[#img-5|Figure 5]](a) that <math display="inline"> \eta </math> value has a significant influence on the excess pore water pressure along the depth direction. At the same depth, the excess pore water pressure increases with the increase of <math display="inline"> \eta </math> value. However, it is noted that the increase of excess pore water pressure at the same depth decreases with the increase of <math display="inline"> \eta </math> value. [[#img-5|Figure 5]](b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the <math display="inline"> \eta </math> value has a significant effect on the excess pore water pressure during and after the earthquake. Firstly, it can be found that the maximum excess pore water pressure generated by earthquake increases with the increase of <math display="inline"> \eta </math> value. Then, the growth rate of excess pore water pressure during the earthquake and the dissipation rate of excess pore water pressure after earthquake increase with the increase of <math display="inline"> \eta </math> value.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-5'></div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
-{|
+|-style="background:white;"
+|align="center" |
+{|style="margin: 0em auto 0.1em auto;width:auto;"
+|+
 |-
-| [[Image:Review_979873928567-image47.png|300px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image47.png|350px]]
-| [[Image:Review_979873928567-image48.png|center|300px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image48.png|center|350px]]
+|-
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a)
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b)
+|}
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. Effect of <math display="inline"> \eta </math> value on excess pore water pressure. (a) Distribution along depth. (b) Development over time
 |}
-</div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 5 Effect of ''η'' value on excess pore water pressure: (a) distribution along depth; and (b) development over time.</div>
-Figure 6 shows the distribution and development of excess pore water pressure in soil around a pile under different ''χ'' values (or the compression moduli of the pile ''E''<sub>p</sub>). It can be seen from Figure 6(a) that ''χ'' value has a significant influence on the excess pore water pressure along the depth direction. At the same depth, the excess pore water pressure decreases with the increase of ''χ'' value. Moreover, the increase of excess pore water pressure at the same depth decreases with the increase of ''χ'' value. Figure 6(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the ''χ'' value has a significant effect on the excess pore water pressure during and after the earthquake. Firstly, it can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of ''χ'' value. Then, the dissipation rate of excess pore water pressure after earthquake increase with the increase of ''χ'' value.
+[[#img-6|Figure 6]]  shows the distribution and development of excess pore water pressure in soil around a pile under different <math display="inline"> \chi </math> values (or the compression moduli of the pile <math display="inline">E_p</math>). It can be seen from [[#img-6|Figure 6]](a) that <math display="inline"> \chi </math> value has a significant influence on the excess pore water pressure along the depth direction. At the same depth, the excess pore water pressure decreases with the increase of <math display="inline"> \chi </math> value. Moreover, the increase of excess pore water pressure at the same depth decreases with the increase of <math display="inline"> \chi </math> value. [[#img-6|Figure 6]](b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the <math display="inline"> \chi </math> value has a significant effect on the excess pore water pressure during and after the earthquake. Firstly, it can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of <math display="inline"> \chi </math> value. Then, the dissipation rate of excess pore water pressure after earthquake increase with the increase of <math display="inline"> \chi </math> value.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-6'></div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
-{|
+|-style="background:white;"
+|align="center" |
+{|style="margin: 0em auto 0.1em auto;width:auto;"
+|+
+|-
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image49.png|350px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image50.png|center|350px]]
 |-
-| [[Image:Review_979873928567-image49.png|300px]]
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a)
-| [[Image:Review_979873928567-image50.png|center|300px]]
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b)
+|}
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 6'''. Effect of <math display="inline"> \chi </math> value on excess pore water pressure. (a) Distribution along depth. (b) Development over time
 |}
-</div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 6 Effect of ''χ'' value on excess pore water pressure: (a) distribution along depth; and (b) development over time.</div>
-Figure 7 shows the distribution and development of excess pore water pressure in soil around a pile under different ''k''<sub>v</sub>. It can be seen from Figure 7(a): when ''k''<sub>v</sub> is small, ''k''<sub>v</sub> mainly has an obvious influence on the excess pore water pressure at the bottom of soil; when ''k''<sub>v</sub> is high, ''k''<sub>v</sub> value has a significant influence on the excess pore water pressure along the depth direction. The effect of ''k''<sub>v</sub> on the excess pore water pressure shows that the excess pore water pressure decreases with the increase of ''k''<sub>v</sub>. Figure 7(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of ''k''<sub>v</sub> value. Then, the growth rate of excess pore water pressure during the earthquake and the dissipation rate of excess pore water pressure after earthquake increase with the increase of ''k''<sub>v</sub> value.
+[[#img-7|Figure 7]] shows the distribution and development of excess pore water pressure in soil around a pile under different <math display="inline">k_v</math>. It can be seen from [[#img-7|Figure 7]](a): when <math display="inline">k_v</math> is small, <math display="inline">k_v</math> mainly has an obvious influence on the excess pore water pressure at the bottom of soil; when <math display="inline">k_v</math> is high, <math display="inline">k_v</math> value has a significant influence on the excess pore water pressure along the depth direction. The effect of <math display="inline">k_v</math> on the excess pore water pressure shows that the excess pore water pressure decreases with the increase of <math display="inline">k_v</math>. [[#img-7|Figure 7]](b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of <math display="inline">k_v</math> value. Then, the growth rate of excess pore water pressure during the earthquake and the dissipation rate of excess pore water pressure after earthquake increase with the increase of <math display="inline">k_v</math> value.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-7'></div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
-{|
+|-style="background:white;"
+|align="center" |
+{|style="margin: 0em auto 0.1em auto;width:auto;"
+|+
 |-
-| [[Image:Review_979873928567-image51.png|300px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image51.png|350px]]
-| [[Image:Review_979873928567-image52.png|center|300px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image52.png|center|350px]]
+|-
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a)
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b)
+|}
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 7'''. Effect of <math display="inline">k_v</math> on excess pore water pressure. (a) Distribution along depth. (b) Development over time
 |}
-</div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 7 Effect of ''k''<sub>v</sub> on excess pore water pressure: (a) distribution along depth; and (b) development over time.</div>
-Figure 8 shows the distribution and development of excess pore water pressure in soil around a pile under different ''N''<sub>eq</sub>/''N''<sub>1</sub>. It can be seen from Figure 8(a) that the excess pore water pressure increases with the increase of ''N''<sub>eq</sub>/''N''<sub>1</sub>. Figure 8(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of ''N''<sub>eq</sub>/''N''<sub>1</sub> value. Then, the growth rate of excess pore water pressure during the earthquake and the dissipation rate of excess pore water pressure after earthquake increase with the increase of ''N''<sub>eq</sub>/''N''<sub>1</sub> value.
+[[#img-8|Figure 8]] shows the distribution and development of excess pore water pressure in soil around a pile under different <math display="inline">N_{eq}/N_1</math>. It can be seen from [[#img-8|Figure 8]](a) that the excess pore water pressure increases with the increase of <math display="inline">N_{eq}/N_1</math>. [[#img-8|Figure 8]](b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of <math display="inline">N_{eq}/N_1</math> value. Then, the growth rate of excess pore water pressure during the earthquake and the dissipation rate of excess pore water pressure after earthquake increase with the increase of <math display="inline">N_{eq}/N_1</math> value.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-8'></div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
-{|
+|-style="background:white;"
+|align="center" |
+{|style="margin: 0em auto 0.1em auto;width:auto;"
+|+
 |-
-| [[Image:Review_979873928567-image53.png|300px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image53.png|350px]]
-| [[Image:Review_979873928567-image54.png|center|300px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image54.png|center|350px]]
+|-
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a)
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b)
+|}
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 8'''. Effect of <math display="inline">N_{eq}/N_1</math> on excess pore water pressure. (a) Distribution along depth. (b) Development over time
 |}
-</div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 8 Effect of ''N''<sub>eq</sub>/''N''<sub>1</sub> on excess pore water pressure: (a) distribution along depth; and (b) development over time.</div>
-Figure 9 shows the distribution and development of excess pore water pressure in soil around a pile under different ''t''<sub>d</sub>. ''t''<sub>d</sub> stands for the duration of an earthquake. If the frequency of earthquakes remains constant, a shorter duration implies a higher frequency. It can be seen from Figure 9(a) that the excess pore water pressure decreases with the increase of ''t''<sub>d</sub>. Figure 9(b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of ''t''<sub>d</sub> value. Then, it is noted that the effect of ''t''<sub>d</sub> on the excess pore water pressure during the earthquake is obviously greater than that after the earthquake.
+[[#img-9|Figure 9]] shows the distribution and development of excess pore water pressure in soil around a pile under different <math display="inline">t_d</math>. <math display="inline">t_d</math> stands for the duration of an earthquake. If the frequency of earthquakes remains constant, a shorter duration implies a higher frequency. It can be seen from [[#img-9|Figure 9]](a) that the excess pore water pressure decreases with the increase of <math display="inline">t_d</math>. [[#img-9|Figure 9]](b) shows the development of excess pore water pressure at the bottom of soil. It can be found that the maximum excess pore water pressure generated by earthquake increases with the decrease of <math display="inline">t_d</math> value. Then, it is noted that the effect of <math display="inline">t_d</math> on the excess pore water pressure during the earthquake is obviously greater than that after the earthquake.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-9'></div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
-{|
+|-style="background:white;"
+|align="center" |
+{|style="margin: 0em auto 0.1em auto;width:auto;"
+|+
 |-
-| [[Image:Review_979873928567-image55.png|300px]]
+|style="text-align: center;padding:10px;"|[[Image:Review_979873928567-image55.png|350px]]
-| [[Image:Review_979873928567-image56.png|center|300px]]
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image56.png|center|350px]]
+|-
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a)
+|style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b)
+|}
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 9'''. Effect of <math display="inline">t_d</math> on excess pore water pressure. (a) Distribution along depth. (b) Development over time
 |}
-</div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 9 Effect of ''t''<sub>d</sub> on excess pore water pressure: (a) distribution along depth; and (b) development over time.</div>
-<span id='_Hlk133318918'></span><span id='_Hlk133323628'></span><span id='_Hlk133327361'></span>
-===6. Reconsolidation Settlement of Foundation after Earthquake===
+==6. Reconsolidation settlement of goundation after earthquake==
-<span id='_GoBack'></span>Due to the assumption of equal strain, the reconsolidation settlement of pipe-soil foundation can be calculated by the reconsolidation settlement of soil around the pile. The reconsolidation settlement of soil around the pile can be expressed as follows<sup>[4]</sup>:
+Due to the assumption of equal strain, the reconsolidation settlement of pipe-soil foundation can be calculated by the reconsolidation settlement of soil around the pile. The reconsolidation settlement of soil around the pile can be expressed as follows [4]:
 {| class="formulaSCP" style="width: 100%; text-align: center;"
@@ Line 434: / Line 462: @@
 |-
 | <math>\begin{array}{c}
-S\left(T_\mbox{v}\right)=\frac{1}{E_\mbox{s}}{\int }_{T_{\mbox{vd}}}^{T_\mbox{v}}{\int }_0^H\frac{\partial {\gamma }_\mbox{w}H{\overline{U}}_\mbox{s}}{\partial t}\mbox{d}z\mbox{d}t\\
+\displaystyle S\left(T_{v}\right)=\frac{1}{E_{s}}{\int }_{T_{{vd}}}^{T_{v}}{\int }_0^H\frac{\partial {\gamma }_{w}H{\overline{U}}_{s}}{\partial t}{d}z{d}t\\
-=\frac{{\gamma }_\mbox{w}H}{E_\mbox{s}}\sum_{m=1}^{\infty }\frac{2N_{\mbox{eq}}}{N_\mbox{l}T_{\mbox{vd}}}\frac{{\left(-1\right)}^{m-1}\left[\mbox{e}^{\alpha M_m^2\left(T_{\mbox{vd}}-T_\mbox{v}\right)}-\mbox{e}^{-\alpha M_m^2T_\mbox{v}}+\mbox{e}^{-\alpha M_m^2T_{\mbox{vd}}}-1\right]}{\left(1-\lambda \right)\alpha M_m^5}
+\displaystyle =\frac{{\gamma }_{w}H}{E_{s}}\sum_{m=1}^{\infty }\frac{2N_{{eq}}}{N_{l}T_{{vd}}}\frac{{\left(-1\right)}^{m-1}\left[{e}^{\alpha M_m^2\left(T_{{vd}}-T_{v}\right)}-{e}^{-\alpha M_m^2T_{v}}+{e}^{-\alpha M_m^2T_{{vd}}}-1\right]}{\left(1-\lambda \right)\alpha M_m^5}
 \end{array}</math>
 |}
@@ Line 442: / Line 470: @@
-Figure 10 shows the reconsolidation settlement of foundation after earthquake under different ''n'' values. It can be found that reconsolidation settlement is mainly divided into two stages: one is the rapid settlement stage, in which reconsolidation settlement develops rapidly; then there is the slow settlement stage in which reconsolidation settlement develops slowly. It can be seen from Figure 10 that the larger the ''n'' value is, the slower the settlement rate in the early stage and the faster the settlement rate in the later stage. In general, the total settlement of foundation increases with the increase of ''n'' value.
+[[#img-10|Figure 10]] shows the reconsolidation settlement of foundation after earthquake under different <math display="inline">n</math> values. It can be found that reconsolidation settlement is mainly divided into two stages: one is the rapid settlement stage, in which reconsolidation settlement develops rapidly; then there is the slow settlement stage in which reconsolidation settlement develops slowly. It can be seen from [[#img-10|Figure 10]] that the larger the <math display="inline">n</math> value is, the slower the settlement rate in the early stage and the faster the settlement rate in the later stage. In general, the total settlement of foundation increases with the increase of <math display="inline">n</math> value.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-10'></div>
- [[Image:Review_979873928567-image58.png|300px]] </div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
+|-style="background:white;"
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image58.png|350px]]
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 10'''. Effect of ''n'' on reconsolidation settlement of foundation after earthquake
+|}
-<div id="_Hlk133319734" class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 10 Effect of ''n'' on reconsolidation settlement of foundation after earthquake.</div>
-Figure 11 shows the reconsolidation settlement of foundation after earthquake under different ''η'' values. It can be seen that the total settlement of the foundation increases significantly as the value of ''η'' increases.
+[[#img-11|Figure 11]] shows the reconsolidation settlement of foundation after earthquake under different <math display="inline">\eta</math>  values. It can be seen that the total settlement of the foundation increases significantly as the value of <math display="inline">\eta</math> increases.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-11'></div>
- [[Image:Review_979873928567-image59.png|300px]] </div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
+|-style="background:white;"
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image59.png|350px]]
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 11'''. Effect of <math display="inline">\eta</math> on reconsolidation settlement of foundation after earthquake
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 11 Effect of ''η'' on reconsolidation settlement of foundation after earthquake.</div>
-Figure 12 shows the reconsolidation settlement of foundation after earthquake under different ''χ'' values. It can be seen from Figure 12 that the larger the ''χ'' value is, the faster the settlement rate in the early stage and the slower the settlement rate in the later stage. In general, the total settlement of foundation decreases with the increase of ''χ'' value.
+[[#img-12|Figure 12]] shows the reconsolidation settlement of foundation after earthquake under different <math display="inline"> \chi </math> values. It can be seen from [[#img-12|Figure 12]] that the larger the <math display="inline"> \chi </math> value is, the faster the settlement rate in the early stage and the slower the settlement rate in the later stage. In general, the total settlement of foundation decreases with the increase of <math display="inline"> \chi </math> value.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-12'></div>
- [[Image:Review_979873928567-image60.png|300px]] </div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
+|-style="background:white;"
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image60.png|350px]]
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 12'''. Effect of <math display="inline"> \chi </math> on reconsolidation settlement of foundation after earthquake
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 12 Effect of ''χ'' on reconsolidation settlement of foundation after earthquake.</div>
-Figure 13 shows the reconsolidation settlement of foundation after earthquake under different ''k''<sub>v</sub> values. It can be seen that the total settlement of the foundation decreases significantly as the value of ''k''<sub>v</sub> increases.
+[[#img-13|Figure 13]] shows the reconsolidation settlement of foundation after earthquake under different <math display="inline">k_v</math> values. It can be seen that the total settlement of the foundation decreases significantly as the value of <math display="inline">k_v</math> increases.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-13'></div>
- [[Image:Review_979873928567-image61.png|300px]] </div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
+|-style="background:white;"
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image61.png|350px]]
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 13'''. Effect of <math display="inline">k_v</math> on reconsolidation settlement of foundation after earthquake
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 13 Effect of ''k''<sub>v</sub>'' ''on reconsolidation settlement of foundation after earthquake.</div>
-Figure 14 shows the reconsolidation settlement of foundation after earthquake under different ''N''<sub>eq</sub>/''N''<sub>1</sub> values. It can be seen that the total settlement of the foundation increases significantly as the value of ''N''<sub>eq</sub>/''N''<sub>1</sub> increases.
+[[#img-14|Figure 14]] shows the reconsolidation settlement of foundation after earthquake under different <math display="inline">N_{eq}</math>/<math>N_1</math> values. It can be seen that the total settlement of the foundation increases significantly as the value of <math display="inline">N_{eq}</math>/<math>N_1</math> increases.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-14'></div>
- [[Image:Review_979873928567-image62.png|300px]] </div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
+|-style="background:white;"
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image62.png|350px]]
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 14'''. Effect of  <math display="inline">N_{eq}</math>/<math>N_1</math> on reconsolidation settlement of foundation after earthquake
+|}
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
-Figure 14 Effect of ''N''<sub>eq</sub>/''N''<sub>1</sub>'' ''on reconsolidation settlement of foundation after earthquake.</div>
-Figure 15 shows the reconsolidation settlement of foundation after earthquake under different ''t''<sub>d</sub> values. It can be seen that the total settlement of the foundation decreases significantly as the value of ''t''<sub>d</sub> increases.
+[[#img-15|Figure 15]] shows the reconsolidation settlement of foundation after earthquake under different <math display="inline">t_d</math> values. It can be seen that the total settlement of the foundation decreases significantly as the value of <math display="inline">t_d</math> increases.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-15'></div>
- [[Image:Review_979873928567-image63.png|300px]] </div>
+{| class="wikitable" style="margin: 0em auto 0.1em auto;border-collapse: collapse;width:auto;"
+|-style="background:white;"
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+|style="text-align: center;padding:10px;"| [[Image:Review_979873928567-image63.png|350px]]
-Figure 15 Effect of ''t''<sub>d</sub> on reconsolidation settlement of foundation after earthquake.</div>
+|-
+| style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 15'''. Effect of <math display="inline">t_d</math> on reconsolidation settlement of foundation after earthquake
+|}
-===7. Conclusions===
+==7. Conclusions==
 In this paper, an analytical solution to soil consolidation around a pile considering earthquake effect is proposed, and the accuracy of the analytical model is verified by finite element software. Finally, the effects of soil parameters, pile parameters and earthquake parameters in the analytical model on the excess pore water pressure and reconsolidation settlement after earthquakes are analyzed and discussed. The main conclusions are as follows:
-(1) Distribution of excess pore water pressure in soil around the pile: The excess pore water pressure increased with depth, and is positively correlated with ''n'' and ''N''<sub>eq</sub>/''N''<sub>1</sub>, and negatively correlated with ''η'', ''χ'', ''k''<sub>v</sub>, and ''t''<sub>d</sub>.
+(1) Distribution of excess pore water pressure in soil around the pile: The excess pore water pressure increased with depth, and is positively correlated with <math display="inline">n</math> and <math display="inline">N_{eq}</math>/<math>N_1</math>, and negatively correlated with <math display="inline">\eta </math>, <math display="inline">\chi</math>, <math display="inline">k_v</math>, and <math display="inline">t_d</math>.
-(2) Development of excess pore water pressure in soil around the pile: The values of ''η'', ''χ'', ''k''<sub>v</sub>, ''N''<sub>eq</sub>/''N''<sub>1</sub> and ''t''<sub>d</sub> affect the excess pore water pressure during and after the earthquake, and the value of ''n'' only obvious affects the excess pore water pressure after the earthquake; The growth rate of excess pore water pressure during the earthquake is positively correlated with ''n'', ''η'', ''k''<sub>v</sub>, and ''N''<sub>eq</sub>/''N''<sub>1</sub>, and negatively correlated with ''χ'' and ''t''<sub>d</sub>; The dissipation rate of excess pore water pressure during the earthquake is positively correlated with ''η'', ''χ'', ''k''<sub>v</sub>, ''N''<sub>eq</sub>/''N''<sub>1</sub> and ''t''<sub>d</sub>, and negatively correlated with ''n''.
+(2) Development of excess pore water pressure in soil around the pile: The values of <math display="inline">\eta </math>, <math display="inline">\chi</math>, <math display="inline">k_v</math>, <math display="inline">N_{eq}</math>/<math>N_1</math>, and <math display="inline">t_d</math> affect the excess pore water pressure during and after the earthquake, and the value of <math display="inline">n</math> only obvious affects the excess pore water pressure after the earthquake; The growth rate of excess pore water pressure during the earthquake is positively correlated with <math display="inline">n</math>, <math display="inline">\eta </math>, <math display="inline">k_v</math>, and <math display="inline">N_{eq}</math>/<math>N_1</math>, and negatively correlated with <math display="inline">\chi</math> and <math display="inline">t_d</math>. The dissipation rate of excess pore water pressure during the earthquake is positively correlated with <math display="inline">\eta </math>, <math display="inline">\chi</math>, <math display="inline">k_v</math>, <math display="inline">N_{eq}</math>/<math>N_1</math>, and <math display="inline">t_d</math>, and negatively correlated with <math display="inline">n</math>.
-(3) Reconsolidation settlement of foundation after earthquake: Reconsolidation settlement is mainly divided into two stages: rapid settlement stage and slow settlement stage; The total settlement of foundation is positively correlated with ''n'', ''η'', and ''N''<sub>eq</sub>/''N''<sub>1</sub>, and negatively correlated with ''χ'', ''k''<sub>v</sub>, and ''t''<sub>d</sub>.<br/>
+(3) Reconsolidation settlement of foundation after earthquake: Reconsolidation settlement is mainly divided into two stages: rapid settlement stage and slow settlement stage; The total settlement of foundation is positively correlated with <math display="inline">n</math>, <math display="inline">\eta </math>, and <math display="inline">N_{eq}</math>/<math>N_1</math>, and negatively correlated with <math display="inline">\chi</math>, <math display="inline">k_v</math>, and <math display="inline">t_d</math>.
 ===Data Availability Statement===
-All data, models, and code generated or used during the study appear in the submitted article.<br/>
+All data, models, and code generated or used during the study appear in the submitted article.
-<span id='_Hlk93324296'></span><span id='_Hlk93324211'></span>
+==Acknowledgements==
-===Acknowledgements===
 This work had been supported by the Guangdong Key Areas R&D Program Projects, China (Grant number: 2020B0101130005), Research Project of Guangdong Power Grid Co. (Grant number: 031000QQ00220012).<br/>
-===References===
+==References==
+<div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;">
-[1] Xu Chengshun, Dou Pengfei, Du Xiuli, et al. Seismic performance of pile group-structure system in liquefiable and non-liquefiable soil from large-scale shake table tests [J]. Soil Dynamics and Earthquake Engineering, 2020, 138, 106299.
+[1] Xu C., Dou P., Du X., et al. Seismic performance of pile group-structure system in liquefiable and non-liquefiable soil from large-scale shake table tests. Soil Dynamics and Earthquake Engineering, 138, 106299, 2020.
-[2] Finn WDL, Fujita N. Piles in liquefiable soils: seismic analysis and design issues [J]. Soil Dynamics and Earthquake Engineering, 2002, 22(9-12), 731-742.
+[2] Finn W.D.L, Fujita N. Piles in liquefiable soils: seismic analysis and design issues. Soil Dynamics and Earthquake Engineering, 22(9-12):731-742, 2002.
-[3] Cubrinovski Misko, Bray Jonathan D, De La Torre Christopher, et al. Liquefaction effects and associated damages observed at the Wellington CentrePort from the 2016 Kaikoura earthquake [J]. Bulletin of the New Zealand Society for Earthquake Engineering, 2017, 50(2), 152-173.
+[3] Cubrinovski M., Bray J.D., De La Torre C., et al. Liquefaction effects and associated damages observed at the Wellington CentrePort from the 2016 Kaikoura earthquake. Bulletin of the New Zealand Society for Earthquake Engineering, 50(2):152-173, 2017.
-[4] Pal Suravi, Deb Kousik. Postearthquake reconsolidation settlement of stone column-treated liquefiable sand [J]. International Journal of Geomechanics, 2020, 20(10), 04020183.
+[4] Pal S., Deb K. Postearthquake reconsolidation settlement of stone column-treated liquefiable sand. International Journal of Geomechanics, 20(10), 04020183, 2020.
-[5] Su Lei, Tang Liang, Ling Xian-zhang, et al. Responses of reinforced concrete pile group in two-layered liquefied soils: shake-table investigations [J]. Journal of Zhejiang University-SCIENCE A, 2015, 2(16), 93-104.
+[5] Su L., Tang L., Ling X.-Z., et al. Responses of reinforced concrete pile group in two-layered liquefied soils: shake-table investigations. Journal of Zhejiang University-SCIENCE A, 2(16):93-104, 2015.
-[6] Knappett JA, Madabhushi SP. Liquefaction-induced settlement of pile groups in liquefiable and laterally spreading soils [J]. Journal of Geotechnical and Geoenvironmental Engineering, 2008, 134(11), 1609-1618.
+[6] Knappett J.A., Madabhushi S.P. Liquefaction-induced settlement of pile groups in liquefiable and laterally spreading soils. Journal of Geotechnical and Geoenvironmental Engineering, 134(11):1609-1618, 2008.
-[7] Bao Xiaohua, Ye Guanlin, Ye Bin, et al. (2014). Seismic Performance of Multi-story Building with Pile Foundation in Liquefiable Ground Including Post-earthquake Consolidation Settlement. [M] Advances in Soil Dynamics and Foundation Engineering, 353-362.
+[7] Bao X., Ye G., Ye B., et al. Seismic performance of multi-story building with pile foundation in liquefiable ground including post-earthquake consolidation settlement.  Advances in Soil Dynamics and Foundation Engineering, pp. 353-362, Shanghai, China, May 26-28 2014.
-[8] Rollins KM, Strand SR. Downdrag forces due to liquefaction surrounding a pile [C]. Proc. 8th National Conference on Earthquake Engineering, Earthquake Engineering Research Institute, 2006.
+[8] Rollins K.M., Strand S.R. Downdrag forces due to liquefaction surrounding a pile. Proc. 8th National Conference on Earthquake Engineering, Earthquake Engineering Research Institute, Paper No. 1646, San Francisco, CA, April 18-22 2006.
-[9] Chen Xu, Guan Zhongguo, Spencer Jr Billie F, et al. A simplified procedure for estimating nonlinear seismic demand of tall piers [J]. Engineering Structures, 2018, 174, 778-791.
+[9] Chen X., Guan Z., Spencer Jr B.F., et al. A simplified procedure for estimating nonlinear seismic demand of tall piers. Engineering Structures, 174:778-791, 2018.
-[10] Hussein A Fouad, El Naggar M Hesham. Seismic axial behaviour of pile groups in non-liquefiable and liquefiable soils [J]. Soil Dynamics and Earthquake Engineering, 2021, 149, 106853.
+[10] Hussein A.F., El Naggar M.H. Seismic axial behaviour of pile groups in non-liquefiable and liquefiable soils. Soil Dynamics and Earthquake Engineering, 149, 106853, 2021.
-[11] Chiou Jiunn-Shyang, Huang Tzu-Jui, Chen Ching-Lin, et al. Shaking table testing of two single piles of different stiffnesses subjected to liquefaction-induced lateral spreading [J]. Engineering Geology, 2021, 281, 105956.
+[11] Chiou J.-S., Huang T.-J., Chen C.-L., et al. Shaking table testing of two single piles of different stiffnesses subjected to liquefaction-induced lateral spreading. Engineering Geology, 281, 105956, 2021.
-[12] Xu Ling-Yu, Song Cheng-Xiang, Chen Wei-Yun, et al. Liquefaction-induced settlement of the pile group under vertical and horizontal ground motions [J]. Soil Dynamics and Earthquake Engineering, 2021, 144, 106709.
+[12] Xu L.-Y., Song C.-X., Chen W.-Y., et al. Liquefaction-induced settlement of the pile group under vertical and horizontal ground motions. Soil Dynamics and Earthquake Engineering, 144, 106709, 2021.
-[13] Chen Xu, Xiang Nailiang, Li Chunxiang. Influence of higher-order modes of slender tall pier bridge columns on the seismic performance of pile foundations [J]. Soil Dynamics and Earthquake Engineering, 2021, 142, 106543.
+[13] Chen X., Xiang N., Li C. Influence of higher-order modes of slender tall pier bridge columns on the seismic performance of pile foundations. Soil Dynamics and Earthquake Engineering, 142, 106543, 2021.
-[14] Xu Zhiying. Calculation of pore pressure of sand foundation in resistance to seismic liquefaction by gravel drainage pile [J]. Earthquake Engineering and Engineering Vibration, 1992, 12(4), 88-92 (in Chinese).
+[14] Xu Z. Calculation of pore pressure of liquefiable sand deposits using gravel drains (in Chinese). Earthquake Engineering and Engineering Vibration, 12(4):88-92, 1992.
-[15] Seed H Bolton, Booker John R. Stabilization of potentially liquefiable sand deposits using gravel drains [J]. Journal of the Geotechnical Engineering Division, 1977, 103(7), 757-768.
+[15] Seed H.B., Booker J.R. Stabilization of potentially liquefiable sand deposits using gravel drains. Journal of the Geotechnical Engineering Division, 103(7):757-768, 1977.