(Tag: Visual edit) |
|||
| Line 1: | Line 1: | ||
| − | + | <big>'''Caracterización de la tenacidad interlaminar en modo I en interfases multidireccionales en un compuesto fabricado por impresión 3D'''</big><big>'''Characterisation of the mode I interlaminar fracture toughness in multidirectional interfaces in a 3D-printed composite'''</big> | |
| − | + | ||
| − | + | ||
| − | <big>'''Caracterización de la tenacidad interlaminar en modo I en interfases multidireccionales en un compuesto fabricado por impresión 3D'''</big> | + | |
| − | + | ||
| − | <big>'''Characterisation of the mode I interlaminar fracture toughness in multidirectional interfaces in a 3D-printed composite'''</big> | + | |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
Revision as of 15:58, 4 June 2023
Caracterización de la tenacidad interlaminar en modo I en interfases multidireccionales en un compuesto fabricado por impresión 3DCharacterisation of the mode I interlaminar fracture toughness in multidirectional interfaces in a 3D-printed composite
Keywords: Toughness, Interlaminar fracture, Multidirectional, 3D printing
1. Introducción
Los compuestos laminados termoplásticos de fibra continua ofrecen una elevada relación rigidez/peso y resistencia/peso, buena resistencia a la corrosión, alta conductividad térmica, etc. Estos materiales compuestos son ampliamente utilizados en diferentes sectores, como la aeronáutica, automoción, deportes, etc. Sin embargo, las técnicas de manufactura convencional de componentes estructurales de material compuesto suelen requerir de elevados tiempos de producción, como las operaciones manuales de apilamiento de capas, y equipos y herramientas de coste elevado, por lo que lotes reducidos de producción resultan económicamente inviables. No obstante, la fabricación aditiva (AM), o impresión 3D, puede ser una alternativa válida para superar estas limitaciones. La primera impresora comercial de material compuesto de fibra continua (cFRP) fue desarrollada por Markforged® en 2014 [1] con un cabezal de impresión de dos extrusores, uno para el filamento de PolyAmide 6 (PA) y otro para el filamento de compuesto de fibra de carbono, vidrio o aramida. Existe un número relativamente elevado de publicaciones científicas acerca de caracterización experimental del material compuesto cFRP fabricado con impresoras 3D Markforged®, pero la mayoría se centran en las propiedades en el plano del laminado. Iragi et al. [2] fue el pionero en caracterizar la tenacidad a la fractura interlaminar en modo I y II para el compuesto cFRP de fibra de carbono de Markforged® (CF/PA), obteniendo una tenacidad a la fractura en modo I mayor que la de modo II, en contra de lo que suele ser habitual para este tipo de materiales. En un trabajo posterior con el mismo material pero utilizando probetas monolíticas delgadas, Santos et al. [3] obtuvieron una tenacidad interlaminar en modo I menor que la de modo II, tanto a iniciación como a propagación. Los valores obtenidos fueron corroborados por un trabajo posterior de Polyzos et al. [4]. Más recientemente, Dang et al. [5] observaron un efecto positivo de la hibridación de cFRP en la tenacidad interlaminar en modo I explorando las combinaciones CF/CF, CF/Kevlar y Kevlar/Kevlar. Estos estudios se centraron en la caracterización de la tenacidad interlaminar en interfases donde la orientación de la fibra es paralela a la dirección de propagación de la grieta. No obstante, la propagación de las grietas interlaminares raramente se da en interfases unidireccionales en aplicaciones reales. Esta comunicación presenta el diseño mediante métodos numéricos de las probetas cFRP CF/PA para la caracterización de la tenacidad interlaminar en modo I en interfases multidireccionales asegurando la correcta propagación de la grieta (sin otros mecanismos de fallo) y la posterior caracterización experimental.
2. Diseño de laminados multidireccionales
El estudio se basó en la combinación de fibra continua de carbono como refuerzo de la matriz polimérica de PolyAmida 6 (CF/PA) de Markforged®. La Tabla 1 presenta el compendio de propiedades mecánicas del compuesto reportadas por Santos et al. [3] e Iragi et al. [2].
2.1. Configuración de laminados y balance de propiedades elásticas a flexión
Para la configuración de los laminados, inicialmente se analizó el comportamiento elástico a flexión de probetas multidireccionales de doble viga en voladizo (DCB) según la norma ISO-15024 [6] con siete combinaciones distintas para las orientaciones de las capas en la interfase. Los ángulos considerados fueron 0, ±15, ±30 y ±45 sin repetición de ángulo en las dos interfases. Para garantizar una apertura simétrica y la propagación de la grieta en modo I, se estableció que la relación de rigideces entre los dos brazos de la probeta debería ser igual o superior a 0.9. Además, se tuvo en cuenta que según Sebaey et al. [7], una mayor rigidez a flexión de los brazos de la probeta dificulta la migración de la grieta y que según Santos et al. [3], la caracterización de la tenacidad a la fractura interlaminar en modo I debe considerar especímenes delgados.
| Propiedad | |
| Modulo elástico longitudinal, E11 (GPa) | 66.5 ± 7.1 |
| Modulo elástico transversal, E22 (GPa) | 6.2 ± 1.1 |
| Coeficiente de Poisson, | 0.39 ± 0.03 |
| Modulo cortante en el plano, G12 (GPa) | 2.1 ± 0.2 |
| Tenacidad a la fractura en modo I, GIc (J/m2) | 1.7 ± 0.1 |
| Tenacidad a la fractura en modo II, GIIc (J/m2) | 2.3 ± 0.1 |
| Resistencia longitudinal a tensión, XT (MPa) | 752 ± 88.6 |
| Resistencia longitudinal a compresión, XC (MPa) | 426 ± 9.7* |
| Resistencia transversal a tensión, YT (MPa) | 49.3 ± 9.9 |
| Resistencia transversal a compresión, YC (MPa) | 66 ± 6.6* |
| Resistencia a cortante, SL (MPa) | 31 ± 0.1 |
| Espesor de la capa, t (mm) | 0.125 |
En la primera configuración de laminado, L1_12_12_θ1_θ2, se consideraron 12 capas en cada brazo de la probeta (3 mm de grosor en total) con una secuencia de apilado simétrica y balanceada para cada brazo y con capas centrales a 0°: [(±θ1/04)s//(±θ2/04)s], donde // indica la posición de la interfase. Dado que con esta configuración no fue posible cumplir el criterio de rigidez homogénea entre los brazos de la probeta, se consideraron nueve configuraciones más con mayor espesor, 4 y 5 mm, pero distribuciones de capas entre brazos no siempre iguales para cumplir con el criterio de la relación de rigideces. En la Tabla 2 se presenta el compendio de las secuencias de apilado de las configuraciones analizas y las diferentes orientaciones de las capas de la interfase que garantizan homogeneidad de rigidez entre brazos de la probeta.
| Codificación | Secuencia de apilado | Ángulos de la interfase (θ1/θ2) |
| L1_12_12_θ1_θ2 | [(±θ1/04)s // (±θ2/04)s] | 0/15, -15/15, -30/30 |
| L2_16_16_θ1_θ2 | [(±θ1/06)s // (±θ2/06)s] | 0/15, -15/15, -30/30, -45/45 |
| L3_15_17_θ1_θ2 | [(±θ1/06)$ // (±θ2/07)$] | 0/30, -15/30, 15/30 |
| L4_15_18_θ1_θ2 | [(±θ1/06)$ // (±θ2/07)s] | 0/45, -15/45, 15/45 |
| L5_16_17_θ1_θ2 | [(±θ1/06)s // (±θ2/07)$] | -30/45, 30/45 |
| L6_20_20_θ1_θ2 | [(±θ1/08)s // (±θ2/08)s] | 0/15, -15/15, -30/30, -45/45 |
| L7_19_21_θ1_θ2 | [(±θ1/08)$ // (±θ2/09)$] | 0/30, -15/30, 15/30 |
| L8_19_22_θ1_θ2 | [(±θ1/08)$ // (±θ2/09)s] | 0/45, -15/45, 15/45 |
| L9_20_21_θ1_θ2 | [(±θ1/08)s // (±θ2/09)$] | -30/45, 30/45 |
2.2. Configuración del modelo numérico
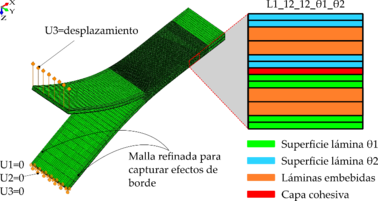
Las probetas DCB multidireccionales (MD-DCB) con las configuraciones de laminado y orientaciones de interfase indicadas en la Tabla 2 se simularon mediante elementos finitos (FE) para analizar la simetría del frente de grieta y el agrietamiento de la matriz en las capas de la interfase durante la propagación de la grieta. Para las simulaciones se usó el programa Abaqus/Standard 6.14. La longitud reducida (menor costo computacional) y ancho de la muestra fueron 100 y 22.5 mm, respectivamente. La probeta fue divida en tres zonas, pre-grieta 50 mm, zona de propagación de grieta 40 mm y zona de unión 10 mm. Para captar con precisión el comportamiento de delaminación, la malla fue refinada en ambos bordes y en la punta de la grieta, como se puede observar en la Figura 2. Cada brazo de viga de la probeta fue modelado con un elemento C3D8I de 0.125 mm en la dirección del espesor para lámina ±θde lámina y dos bloques de láminas embebidas en la dirección de 0°, como se observa en la Figura 1.
Para simular la propagación de la grieta se usaron elementos cohesivos en la zona de propagación según la formulación propuesta por Turon et al. [8] e implementada a través de la subrutina de elemento definido por el usuario (UEL), con un espesor despreciable de 1 μm. Para analizar la aparición de grietas en la matriz que puedan facilitar la migración de plano de la grieta interlaminar o la ramificación de grietas durante el ensayo, se utilizó el criterio de fallo de matriz a tensión (FI) LaRC04 [9] implementado mediante la variable de subrutina estándar, UVARM.
2.3. Resultados de simulación numérica
El índice de fallo (FI) para todos los laminados considerados fueron superior a 1 excepto pare los laminados L6, cuyos índices de fallo fueron menores que la unidad para todas las orientaciones de la interfase consideradas. Por tanto, este laminado es el único a considerar. Para garantizar una campaña experimental posterior, un factor de seguridad igual a 2 fue introducido para todos los laminados que presentaron un valor de FI menor que 1. Por tanto, los especímenes MD-DCB adecuados pare ser fabricados serían el laminado L6 y las interfases 0/15, 15/-15, 30/-30.
3. Fabricación y ensayo de los especímenes MD-DCB
Las muestras fueron manufacturadas en la impresora Markforged MarkTwo®, cuyo software de configuración impone que las muestras DCB sean impresas con cuatro capas de piso, cielo y pared con PA, siguiendo el procedimiento descrito por Santos et al. [3]. Las capas de piso y pared de las muestras impresas, fueron posteriormente retiradas para evitar cualquier influencia en el comportamiento experimental de los ensayos. Las dimensiones de la probeta impresa sin considerar el borde o brim se presentan en la Figura 2. Mediante un disco de corte apropiado, la muestra impresa fue cortada según 175 × 25 × 5 mm (longitud, ancho y espesor) y 50 mm (pre-grieta). Todos los ensayos se realizaron a 23 ± 2°C y 50 ± 5 HR en una máquina universal MTS Insight equipada con una célula de carga de 5 kN bajo control de desplazamiento con una velocidad de 1.5 mm/min durante la carga y de 25 mm/min en la descarga. La velocidad del proceso de carga se modificó ligeramente respecto a lo indicado en la norma ISO-15024 [6] por un comportamiento más apropiado observado en ensayos preliminares. En total se ensayaron seis muestras para cada interfase 0/15, 15/-15 y 30/-30. Durante los ensayos, las probetas se instrumentaron con inclinómetros para poder determinar la tenacidad interlaminar de iniciación y propagación mediante el método J-integral según lo indicado por Sarrado [10].
4. Resultados experimentales y discusión
1.1. Resultados de curvas esfuerzo-desplazamiento
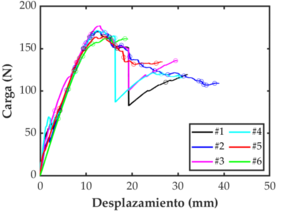
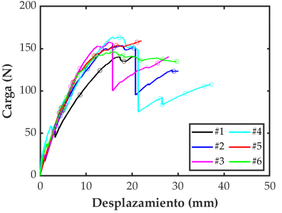
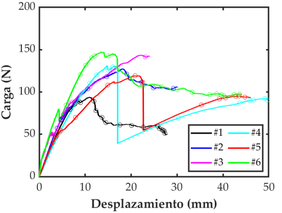
Las curvas de todos los ensayos se presentan en la Figura 3. Las curvas muestras la etapa de carga completa incluyendo caídas de carga, hasta el punto anterior a una propagación de grieta catastrófica. Todas las muestras 0/15 muestran un comportamiento similar al inicio del ensayo (Figura 3a). Así, todos los especímenes fueron considerados para determinar la tenacidad interlaminar de iniciación y propagación en modo I. Las curvas de los especímenes 15/-15 (Figura 3b), muestran menor grado de repetitividad que en el caso de 0/15. La probeta 15/-15-1 muestra menor rigidez que el resto y presenta un comportamiento distinto después de la caída de carga inicial. Por lo tanto, esta probeta no fue considerada para determinar la tenacidad a la fractura de la interfase 15/-15. La Figura 6c muestra las curvas fuerza-desplazamiento para el lote de 30/-30 con un alto grado de variabilidad. Por un lado, las probetas 30/-30-1 y 30/-30-2 experimentaron una propagación limpia y estable a lo largo de todo el ensayo. Por otro lado, las probetas 30/-30-4 y 30/-30-5 mostraron una rigidez similar al inicio del ensayo, pero luego de la caída de carga a los 5 mm de apertura la rigidez de la probeta 30/-30-5 es significativamente menor que el resto del lote. Finalmente, la probeta 30/-30-6 mostro una respuesta de mayor rigidez que el resto de probetas. Por lo tanto, las probetas 30/-30-1, 30/-30-4 y 30/-30-5 no son considerados para la reducción numérica de la tenacidad a la fractura del caso 30/-30.
|
|
| a) 0/15 | b) 15/-15 |
| |
| c) 30/-30 | |
Es importante comentar que sólo en la probeta 30/-30-4 se pudo observar migración de plano, lo cual valida el proceso metodológico desarrollado. La presenta el compendio de valores de la tenacidad a la fractura de todos los casos estudiados. El valor máximo tanto para iniciación como para propagación fue experimentado por el laminado 0/15, 1763 y 2146 J/m2, respectivamente. Los valores de tenacidad a propagación para los casos 15/-15 y 30/-30 son virtualmente los mismos, 1720 y 1758 J/m2, respectivamente, mientras que para iniciación difieren algo más, 870 y 960 J/m2, respectivamente. No obstante, para 15/-15 y 30/-30 los valores de tenacidad son muy similares a los de las probetas unidireccionales obtenidos por Santos et al. [3].
1.2. Análisis de superficie de fractura
La zona de propagación de las muestras post-mortem fueron cortadas cuidadosamente, evitando modificar la superficie de fractura mediante el mismo disco de corte. La superficie fue tratada y observada mediante microscopía electrónica de barrido (SEM) con una aceleración de partículas de 7 kV. El análisis de fractografía de la lámina a 15° de la muestra 0/15 (Figura 4a) revela surcos entre filamentos depositados, áreas con vacíos (burbujas de aire) y algunas fibras sueltas. En la superficie se pueden observar filamentos depositados a 0° y 15° (marcados con línea entre cortada azul), mientras que en la Figura 4b a un mayor número de aumentos se puede observar claramente un entrecruzamiento de estos filamentos. También se puede observar fibras a 15° arrancadas de la resina y roto durante la delaminación, mientras que la resina en la fibra longitudinal muestra deformación plástica. La superficie de fractura de la lámina de 15° de la probeta 15/-15 muestra menos vacíos y fibras rotas (Figura 4c). Se puede observar claramente el entrecruzamiento entre las láminas en la ampliación de la Figura 4d, además de un grupo de fibras orientadas a 15° muestran fragmentación luego de haber sido arrancadas con deformación plástica alrededor de la resina en la zona adyacente. La superficie de fractura de la lámina de 30° de la probeta 30/-30 muestra zonas de resina dominante, como también varias fibras rotas (Figura 4e). El entrecruzamiento entre las láminas se puede observar claramente. El análisis mediante una mayor amplificación en la Figura 4f muestra un área central de fibras de 30° que se han retirado de la superficie. Observando en un plano superior de la imagen, se muestra huellas de fibras desprendidas de la resina y varias fibras rotas.
5. Conclusiones
Las principales conclusiones de este estudio se pueden resumir en:
- Las probetas MD-DCB con similar rigidez a flexión entre los brazos de viga, garantizaron una apertura en modo I puro durante todo el ensayo. Solo uno de los 18 especímenes caracterizados mostró salto de grieta y únicamente al inicio del ensayo.
- La diferencia de los ángulos de orientación de las interfases de las probetas afecta al valor de la tenacidad interlaminar del material y a la repetibilidad del ensayo.
- El análisis de fractografía reveló que la grieta no se propaga a lo largo de un plano uniforme en el largo del ancho de la probeta, de hecho, la morfología de la propagación es similar a una onda entre los finalmente depositados entre las láminas.
Bibliografía
[1] Markforged. Markforged 2019. https://markforged.com/composites/ (accessed May 21, 2023).
[2] M. Iragi, C. Pascual-González, A. Esnaola, C.S. Lopes y L. Aretxabaleta. Ply and interlaminar behaviours of 3D printed continuous carbon fibre-reinforced thermoplastic laminates; effects of processing conditions and microstructure. Additive Manufacturing 2019;30:100884. https://doi.org/10.1016/j.addma.2019.100884.
[3] J.D. Santos, A. Fernández, L. Ripoll y N. Blanco. Experimental Characterization and Analysis of the In-Plane Elastic Properties and Interlaminar Fracture Toughness of a 3D-Printed Continuous Carbon Fiber-Reinforced Composite. Polymers (Basel) 2022;14. https://doi.org/10.3390/polym14030506.
[4] E. Polyzos, A. Katalagarianakis, D. Van Hemelrijck y L. Pyl. Delamination analysis of 3D-printed nylon reinforced with continuous carbon fibers. Additive Manufacturing 2021;46. https://doi.org/10.1016/j.addma.2021.102144.
[5] Z. Dang, J. Cao, A. Pagani y C. Zhang. Fracture toughness determination and mechanism for mode-I interlaminar failure of 3D-printed carbon-Kevlar composites. Composites Communications 2023;39. https://doi.org/10.1016/j.coco.2023.101532.
[6] ISO 15024: Fibre-reinforced plastic composites - Determination of mode i interlaminar fracture toughness, GIC, for unidirectionally reinforced materials. Switzerland, Geneva: International Organization for Standardization; 2001.
[7] T.A. Sebaey, N. Blanco, C.S. Lopes y J. Costa. Numerical investigation to prevent crack jumping in Double Cantilever Beam tests of multidirectional composite laminates. Composites Science and Technology 2011;71:1587–92. https://doi.org/10.1016/j.compscitech.2011.07.002.
[8] A. Turon, P.P. Camanho, J. Costa y C.G. Dávila. A damage model for the simulation of delamination in advanced composites under variable-mode loading. Mechanics of Materials 2006;38:1072–89. https://doi.org/10.1016/j.mechmat.2005.10.003.
[9] S.T. Pinho, C.G. Dávila, P.P. Camanho, L. Iannucci y P. Robinson. Failure Models and Criteria for FRP Under In-Plane or Three-Dimensional Stress States Including Shear Non-linearity. Nasa/Tm-2005-213530 2005:68.
[10] C. Sarrado. Experimental characterization and numerical simulation of composite adhesive joints using the cohesive zone model approach. Tesis Doctoral. 2015; Univesitat de Girona, Girona.
Document information
Published on 26/01/24
Accepted on 18/06/23
Submitted on 21/05/23
Volume 08 - COMUNICACIONES MATCOMP21 (2022) Y MATCOMP23 (2023), Issue Núm. 3 - Caracterización - Daño, Fractura y Fatiga, 2024
DOI: 10.23967/r.matcomp.2024.03.09
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?