Dejan.brkic (talk | contribs) |
Dejan.brkic (talk | contribs) m (Unit change) (Tag: Visual edit) |
||
| (92 intermediate revisions by 3 users not shown) | |||
| Line 2: | Line 2: | ||
| − | < | + | <span id='_Hlk74511807'></span> |
| + | ==Volatility of Natural Gas Prices - Structural Shocks and Influencing Factors== | ||
| − | <big>Ljubiša Stajić<sup>a</sup>, Bojan Đorđević<sup>b</sup>, Silvana Ilić<sup>b</sup> and Dejan Brkić<sup> | + | <big>Ljubiša Stajić<sup>a</sup>, Bojan Đorđević<sup>b</sup>, Silvana Ilić<sup>b</sup> and Dejan Brkić<sup>acd</sup>*</big> |
''<sup>a</sup>Research and Development Center “IRC Alfatec”, Niš, Serbia'' | ''<sup>a</sup>Research and Development Center “IRC Alfatec”, Niš, Serbia'' | ||
| Line 11: | Line 12: | ||
''<sup>c</sup>Faculty of Electronic Engineering, University of Niš, Niš, Serbia'' | ''<sup>c</sup>Faculty of Electronic Engineering, University of Niš, Niš, Serbia'' | ||
| + | |||
| + | ''<sup>d</sup>IT4Innovations, VSB – Technical University of Ostrava, Ostrava, Czechia'' | ||
--> | --> | ||
| + | ==Abstract== | ||
| − | + | The paper examines the primary drivers and factors influencing the volatility of natural gas prices in the world from January 2007 to July 2020. In addition to the narrow dependence between crude oil and natural gas prices, the influence of renewable energy production and coal production on the price of natural gas has been studied. For that purpose, the method of multiple linear regression was used. The results show that the volatility of natural gas prices significantly depends on the type of the shock in the natural gas market, and that the total production of energy from renewable sources, production of coal and natural gas and the price of crude oil have a significant impact on the price of gas. | |
| − | '''Keywords''': Energy | + | '''Keywords''': Energy prices, natural gas, multiple linear regressions, renewable energy, price volatility, energy consumption |
==1. Introduction== | ==1. Introduction== | ||
| − | Natural gas is a mixture of hydrocarbons and methane and | + | Natural gas is a mixture of hydrocarbons and methane and because it mixes easily with air and has a high combustion rate without smoke, soot, and solid residues, it has a significant environmental advantage over conventional fuels such as oil and coal [1]. In the same way that oil replaced coal in industrial production at the beginning of the twentieth century, gas suppressed oil at the beginning of the twenty-first century and became an increasingly common fuel used to start the industry. Due to a fact that natural gas is a much cleaner energy source, this tendency in many developed countries is regulated by law, so some industrial sectors are forced to start their production with the help of natural gas. Given the world’s growing concern about the effects of carbon dioxide emissions from fossil fuels, and the impact on climate change and low carbon content in natural gas compared to other fossil fuels, natural gas has become a major energy source in many economies across the globe. Recent research shows that the consumption of natural gas plays an important role in facilitating economic growth in the both short and long term [2] and that disruptions in the supply of natural gas entail huge economic costs [3-5]. Fluctuations in energy prices are also becoming increasingly important in influencing risk reduction and strategic investments [6]. |
| − | The largest recorded shock demand in the history of global natural gas markets happened in the first half of 2020. Faced with historically mild temperatures during the first months of the year, the COVID-19 pandemic hit the already declining demand for gas. Gas consumption is expected to fall by 4% in 2020, due to successive lower demand for warm winter heating, the implementation of lockdown measures in almost all countries and territories, to slow the spread of the virus and lower activity generated by the macroeconomic crisis caused by the pandemic. Faced with this unprecedented shock, natural gas markets are undergoing strong supply and demand adjustments, resulting in historically low spot prices and high volatility. Demand for natural gas is expected to gradually recover in 2021, but the COVID-19 crisis will have a longer-term impact on natural gas markets, as major medium-term drivers are subject to great uncertainty | + | The largest recorded shock demand in the history of global natural gas markets happened in the first half of 2020. Faced with historically mild temperatures during the first months of the year, the COVID-19 pandemic hit the already declining demand for gas. Gas consumption is expected to fall by 4% in 2020 [7-10], due to successive lower demand for warm winter heating [11], the implementation of lockdown measures in almost all countries and territories, to slow the spread of the virus and lower activity generated by the macroeconomic crisis caused by the pandemic. Faced with this unprecedented shock, natural gas markets are undergoing strong supply and demand adjustments, resulting in historically low spot prices and high volatility. Demand for natural gas is expected to gradually recover in 2021, but the COVID-19 crisis will have a longer-term impact on natural gas markets [12-14], as major medium-term drivers are subject to great uncertainty. |
| − | With the above mentioned, the contribution of our work to literature is that by using multiple linear regression (MLR) [ | + | With the above mentioned, the contribution of our work to literature is that by using multiple linear regression (MLR) [15,16] it can be proved that selected independent variables are important and necessary in determining the dependent variable and that there is a significant relationship and interaction between selected factors and natural gas prices. It can be also proved that fluctuations in natural gas prices are correlated with certain global economic events. This article also shows how the two most significant depressions in recent history - the global economic crisis and COVID-19, have affected the price of natural gas, which can be useful in further research, forecasting prices and consumption in the energy markets, especially when it comes to increased risk of potentially new infectious diseases in the global market soon. |
| − | + | This paper examines the primary drivers and factors influencing the volatility of natural gas prices in the world from January 2007 to July 2020. In addition to the narrow dependence between crude oil and natural gas prices, the influence of renewable energy production and coal production on the price of natural gas has been studied. For that purpose, the method of multiple linear regression was used, as follows. | |
| − | ==2. | + | ==2. Estimation of natural gas prices== |
| − | + | ===2.1 Literature review=== | |
| − | + | Much of the literature on the natural gas market is devoted to examining the relationship between natural gas prices and the crude oil market, suggesting that oil price fluctuations are important determinants of natural gas prices [17-24]. Only a few studies examined the role of supply and demand factors in determining prices in the U.S. natural gas market [25-28]. Some recent studies show that, unlike globally defined crude oil markets, natural gas markets are regionally segmented, suggesting that natural gas prices are formed by regional supply-demand relationships [29]. Following the recent decoupling of the relationship between the crude oil and natural gas markets [30], it is crucial to understand how natural gas prices respond to supply and demand in times of natural gas market shocks, and to identify the relative contribution factors of each. Accordingly, Nick and Thoenes [31] use a structural VAR model to examine price volatility in the German natural gas market. They conclude that supply shocks have a significant impact on the German natural gas market and that temperature, storage and supply shocks lead to relatively short-term effects, while oil and coal price shocks result in more lasting effects on gas prices. The relationship between the prices of natural gas and coal was also investigated by Everts et al. [32]. The study used a basic market price replication model with an analysis of the impact of changes on the individual price drivers such as coal prices or subsidies for renewable energy production. The study showed the fall in electricity prices in Germany in the period 2008-2014 can be attributed to market effects such as a reduction in coal use and gas prices as well as a reduction in electricity demand (50%). Only approximately 30% of price reductions could be directly related to subsidies for energy from renewable sources such as wind and solar energy. Mosquera-López and Nursimulu [33] came to qualitatively similar conclusions. They found that in the short- and medium-term, the main drivers of prices differ and vary in time. In the case of the spot market, determinants of prices were renewable sources and demand for electricity, while in the future markets the main drivers of natural gas prices were the supply and price of coal. Mu [34] identifies demand for natural gas concerning weather conditions as an important factor influencing the movement of gas prices. Hulshof et al. [35] conclude that natural gas prices are mainly determined by the weather conditions and availability of stored quantities, while supply has no significant effect. The availability of natural gas in storage and the outside temperature negatively affected the price of natural gas. They also concluded that the price of natural gas was related to the production of electricity from wind. | |
| − | + | The outbreak of the COVID-19 pandemic has shaken global financial markets, commodity markets, economic activities, employment, and GDP, in almost all countries of the world. Only a few studies have analyzed the effect of this global pandemic on natural gas prices [36-38]. For this reason, there is a need to study the impact of this phenomenon on the volatility of natural gas prices. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| + | ===2.2 Influencing factors=== | ||
| − | + | It is impossible to talk about a single price of natural gas, considering the division of markets in which this energy source is sold. Unlike crude oil, which is traded on stock exchanges and whose prices are uniform worldwide, natural gas prices vary by region. The difference in the price of natural gas is due to different costs of production and transportation, as well as different degrees of liberalization of national natural gas markets. The price of natural gas can be discussed at different levels of the supply chain. The final price of gas at the point of consumption is the sum of the price of production, the price of transportation and the price of local distribution. The price also varies depending on the final consumer, so the industrial sector will usually have a lower price for gas than households do. Thus, in 2007, the average price of natural gas at the level of the European Union was 36% higher for the household sector compared to the industrial sector [39,40]. Another unavoidable factor that contributes to different levels of natural gas prices are taxes that vary from country to country [41,42]. | |
| − | + | The price of natural gas is experiencing a constant escalation in the market, especially during 2009 because of the global financial crisis of 2008, when the price of natural gas in September was US$ 2.99 per 1,05 million kJ. This was followed by market recovery and relative price stability during 2010 and subsequent years [7-10]). | |
| − | [[ | + | However, natural gas prices fell sharply since the beginning of 2020 due to weak demand and abundant supply. European natural gas prices fell to a decade-long low and have fallen by almost 40% since early 2020 [39,40]. U.S. natural gas prices have fallen slightly, in part because they had already been low [25-28]. Price differences between regional benchmarks for natural gas continued to decline, mostly driven by the increasing availability of liquefied natural gas. However, the fall in prices of natural gas and coal is smaller than the price of crude oil, which has fallen by about 65% since January 2020. Natural gas and coal are primarily used for electricity generation and industrial purposes, not for transportation. As such, lockdowns and travel restrictions had less of an impact on demand for these products than for crude oil [43]. |
| − | + | The onset of the COVID-19 pandemic created an unprecedented shock to the global energy system, and gas consumption around the world was significantly affected. Demand for natural gas has fallen in the electricity sector due to lower electricity usage, and in the industrial and commercial sectors due to the shutdown of factories and businesses. The demand for gas among the population did not decrease while people stayed at home. These impacts varied by region. In Europe, gas demand fell by 7% year-on-year during the first five months of 2020 [7-10]. In the first quarter, the decline was driven by mild winters and higher production from renewable sources. However, lockdown measures began to affect gas demand from March on, where May consumption was already 11% lower than in March [7-10]. Natural gas and coal have seen significant reductions in demand, as lockdown measures have reduced industrial activity and electricity consumption, while extremely warm winters have also reduced demand in early 2020. The International Energy Agency estimates that lockdown measures have reduced electricity demand to at least 15% in several major economies, including France, Italy, Spain, and the United Kingdom [7-10]. In the United States, the U.S. Energy Information Administration expects U.S. demand for electricity to fall by about 5%, and a moderate decline in housing use will offset a greater decline in commercial and industrial use - sectors affected by lockdowns [7-10]. | |
| − | + | Natural gas prices are expected to recover from the current low but will still be about 25% lower than in 2019 [7-10]. Demand for natural gas is expected to gradually recover from current low levels after lifting the lockdown but will remain below 2019 levels. Demand for coal is likely to remain weaker, as a part of the ongoing transition from coal to natural gas in global electricity generation. | |
| − | + | Global gas demand could fall by 4% annually in 2020 [7-10]. This would be the largest drop in gas demand ever recorded since the development of the gas industry in the second half of the 20th century. By comparison, gas demand fell by 2% in 2009 due to the global financial crisis. About 75% of demand loss is likely to occur in developed gas markets across Europe, North America, the Commonwealth of Independent States (CIS), and Asia due to lower electricity demand, declining industrial activity, and lower space heating needs in the commercial sector. | |
| − | [[ | + | Production and consumption of natural gas from January 2007 - September 2020 are given in [[#img-1|Figure 1]], production of coal and energy from renewable sources from January 2007 - September 2020 in [[#img-2|Figure 2]], while prices of crude oil and natural gas from January 2007 - September 2020 in [[#img-3|Figure 3]]. |
| − | + | <div id='img-1'></div> | |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 60%;" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | ' | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | = | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | [[ | + | | style="text-align: center;padding:10px;"| [[File:Screenshot 2023-02-14 114205.jpg|396x396px]] |
| − | | [[ | + | |- |
| + | | style="text-align: center;padding:10px;"| [[File:Screenshot 2023-02-14 144232.jpg|396x396px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;"| '''Figure 1'''. Fluctuation of production and consumption of natural gas from January 2007-September 2020. Source: U.S. Energy Information Administration - Monthly Energy Review | ||
|} | |} | ||
| − | < | + | <div id='img-2'></div> |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 60%;" | |
| − | + | ||
| − | {| | + | |
|- | |- | ||
| − | | [[ | + | | style="text-align: center;padding:10px;"| [[File:Screenshot 2023-02-14 143633.jpg|396x396px]] |
| − | | [[ | + | |- |
| + | | style="text-align: center;padding:10px;"| [[File:Screenshot 2023-02-14 144018.jpg|396x396px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;"| '''Figure 2'''. Fluctuation of production of coal and energy from renewable sources from January 2007-September 2020. Source: U.S. Energy Information Administration - Monthly Energy Review | ||
|} | |} | ||
| − | '' | + | <div id='img-3'></div> |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 60%;" | |
| − | + | ||
| − | {| | + | |
|- | |- | ||
| − | | [[Image:Review_988885787501- | + | | style="text-align: center;padding:10px;"| [[Image:Review_988885787501-image5.jpg|396px]] |
| − | | [[Image:Review_988885787501- | + | |- |
| + | | style="text-align: center;padding:10px;"| [[Image:Review_988885787501-image6.jpg|396px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;"| '''Figure 3'''. Fluctuation of prices of crude oil and natural gas from January 2007-September 2020. Source: FRED Graph Observations, and Henry Hub Natural Gas Spot Price, respectively | ||
|} | |} | ||
| − | + | As we can see in [[#img-3|Figure 3]], the market shock caused by the global economic crisis led to a fall in the price of natural gas from 12.69 US$ per 1.05 million kJ of June 2008 to 2.99 US$ in September 2009. Also, the pandemic COVID -19 caused a drop in price from 4.09 US$ (December 2019) to 1.63 US$ per 1.05 million kJ as the price was in June 2020. | |
| − | == | + | ===2.3 Methodology. Multiple linear regression=== |
| − | + | To identify the dependence of natural gas prices on different shocks in the natural gas market, monthly time intervals were used during the period from January 2007 to September 2020. This period was used to cover two major shocks in the natural gas market: the 2008 global economic crisis and the COVID-19 virus pandemic. Monthly data have sufficient frequency to analyze the effects of price dependence and market spillovers over time [43]. As a source of data for total production and total consumption of natural gas in billions of cubic feet, a database published by the EIA (U.S Energy Information Administration) was used. | |
| − | The | + | The price of crude oil (US$ per barrel) is from the Federal Reserve Economic Data - FRED, and for the actual price of natural gas (US$ per 1.05 million kJ) the data published by Henry Hub Natural Gas Spot Price was used. Data on coal production (in thousands of tons) as well as data on energy production from renewable energy sources (RES) in 1.05 million kJ were taken from the EIA. |
| − | + | The Multiple Linear Regression analysis is conducted using a mathematical expression of this model [44] as follows: | |
| − | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | {| class="formulaSCP" style="width: 100%; text-align: center;" | + | |
|- | |- | ||
| | | | ||
| − | {| style=" | + | {| style="margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math | + | | <math>{y}_{i\, }=\, {\beta }_{0\, }+\, {\beta }_{1}{x}_{1i\, }+\, \cdots \, +\, {\beta }_{k}{x}_{ki}\, +{\varepsilon }_{i}</math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(1) |
|} | |} | ||
| − | + | where <math>y</math> is the dependent variable, <math>{\beta }_0</math> the regression constant, <math>x_1</math>, <math>x_2\cdots x_k</math> the independent variables, <math>\varepsilon</math> the standard error i.e., residues and <math>\beta</math> the unknown parameter to be evaluated (regression parameter). | |
| − | where | + | |
Values of the regression parameters with each independent variable show how much the dependent variable changes on average when the observed independent variable increases by one of its units, and all other independent variables remain unchanged. | Values of the regression parameters with each independent variable show how much the dependent variable changes on average when the observed independent variable increases by one of its units, and all other independent variables remain unchanged. | ||
| Line 208: | Line 118: | ||
:* regressors should not be perfectly correlated with each other (linearly dependent). | :* regressors should not be perfectly correlated with each other (linearly dependent). | ||
| − | Sample estimates of unknown parameters are obtained by applying the method of least squares. In the case of models with two independent variables, the following function needs to be minimized | + | Sample estimates of unknown parameters are obtained by applying the method of least squares. In the case of models with two independent variables, the following function needs to be minimized: |
| − | {| class="formulaSCP" style="width: 100%; text-align: center;" | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" |
|- | |- | ||
| | | | ||
| − | {| style=" | + | {| style="margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math | + | | <math>F\left( \hat{b}_{0},\hat{b}_{1},\cdots ,\hat{b}_{k}\right) =\sum _{i=1}^{n}{\epsilon }_{i}^{2}=\sum _{i=1}^{n}{\left( {y}_{i}-\hat{y}_{i}\right) }^{2}=\sum _{i=1}^{n}{\left( \hat{b}_{0}+\hat{b}_{1}\cdot {x}_{1i}+\hat{b}_{k}\cdot {x}_{2i}\right) }^{2}</math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(2) |
|} | |} | ||
| + | where <math>F</math> is the function to be minimized, <math display="inline">\hat{b}_{0},\hat{b}_{1},\cdots,\hat{b}_{k}</math> the estimates of the corresponding coefficients of their standard error (roots of the estimates of their dispersions), <math display="inline">\epsilon</math> the standard error i.e., residues, <math display="inline">{y}_{i}-</math><math>\hat{y}_{i}</math> the difference between the actual and the predicted value of the dependent variable and <math>n</math> the number of variables. | ||
| − | Minimization of the function F is achieved by equalizing its partial derivatives of the first order by parameters, with zero | + | Minimization of the function <math>F</math> is achieved by equalizing its partial derivatives of the first order by parameters, with zero: |
| − | {| class="formulaSCP" style="width: 100%; text-align: center;" | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" |
|- | |- | ||
| | | | ||
| − | {| style=" | + | {| style="margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math | + | | <math>\begin{matrix}\displaystyle\frac{\partial F}{\partial \hat{b}_{0}}=0\\ |
| + | \displaystyle \frac{\partial F}{\partial \hat{b}_{1}}=0\\ | ||
| + | \begin{matrix}\vdots \\ | ||
| + | \displaystyle\frac{\partial F}{\partial \hat{b}_{k}}=0\end{matrix}\end{matrix}</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(3) |
|} | |} | ||
| + | By arranging these equations, a system of normal equations is obtained: | ||
| − | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | |
| − | + | ||
| − | {| class="formulaSCP" style="width: 100%; text-align: center;" | + | |
|- | |- | ||
| | | | ||
| − | {| style=" | + | {| style="margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math | + | | <math>\sum _{i=1}^{n}{y}_{i}=n\cdot \hat{b}_{0}+\hat{b}_{1}\cdot \sum _{i=1}^{n}{x}_{1i}+\ldots +\hat{b}_{k}\cdot \sum _{i=1}^{n}{x}_{ki}</math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(4) |
|} | |} | ||
| − | {| class="formulaSCP" style="width: 100%; text-align: center;" | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" |
|- | |- | ||
| | | | ||
| − | {| style=" | + | {| style="margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math | + | | <math>\sum _{i=1}^{n}{{x}_{1i}\cdot y}_{i}=\hat{b}_{0}\cdot \sum _{i=1}^{n}{x}_{1i}+\hat{b}_{1}\cdot \sum _{i=1}^{n}{x}_{1i}^{2}\ldots +\hat{b}_{k}\cdot \sum _{i=1}^{n}{{x}_{1i}\cdot x}_{ki}</math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(5) |
|} | |} | ||
| + | whose solution yields sample grades <math>{b}_{0}</math>, <math>{b}_1,\cdots , b_k</math>, of unknown parameters <math>\beta_0 ,\cdots, \beta_k</math>. | ||
| − | + | The equations of the observed system can be presented in matrix notation: | |
| − | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | |
| − | + | ||
| − | {| class="formulaSCP" style="width: 100%; text-align: center;" | + | |
|- | |- | ||
| | | | ||
| − | {| style=" | + | {| style="margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math | + | | <math>X'\cdot Y=\left( X'\cdot X\right) \hat{b}</math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(6) |
|} | |} | ||
| + | where <math>X'</math> is transposed matrix of matrix <math>X</math>, follows: | ||
| − | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | |
| − | + | |- | |
| − | + | | | |
| − | + | {| style="margin:auto;width: 100%;" | |
| − | + | |- | |
| − | + | | <math>{X}^{'}\cdot Y=\left[ \begin{matrix}\displaystyle\sum _{i=1}^{n}{Y}_{i}\\ | |
| − | + | \displaystyle\sum _{i=1}^{n}{x}_{1i}\cdot {Y}_{i}\\ | |
| + | \begin{matrix}\vdots \\ \displaystyle\sum _{i=1}^{n}{x}_{ki}\cdot {Y}_{i}\end{matrix}\end{matrix}\right]</math> | ||
| + | |} | ||
| + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(7) | ||
| + | |} | ||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>{X}^{'}\cdot X=\left[ \begin{matrix}n&\displaystyle\sum _{i=1}^{n}{x}_{1i}&\begin{matrix}\ldots &\displaystyle\sum _{i=1}^{n}{x}_{ki}\end{matrix}\\\displaystyle\sum _{i=1}^{n}{x}_{1i}&\displaystyle\sum _{i=1}^{n}{x}_{1i}^{2}&\begin{matrix}\ldots &\displaystyle\sum _{i=1}^{n}{x}_{1i}\cdot {x}_{ki}\end{matrix}\\\begin{matrix}\vdots \\\displaystyle\sum _{i=1}^{n}{x}_{ki}\end{matrix}&\begin{matrix}\vdots \\\displaystyle\sum _{i=1}^{n}{x}_{1i}\cdot {x}_{ki}\end{matrix}&\begin{matrix}\begin{matrix}\ddots \\\ldots \end{matrix}&\begin{matrix}\vdots \\\displaystyle\sum _{i=1}^{n}{x}_{ki}^{2}\end{matrix}\end{matrix}\end{matrix}\right]</math> | ||
| + | |} | ||
| + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(8) | ||
| + | |} | ||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>\hat{b}=\left[ \begin{matrix}\hat{b}_{0}\\\hat{b}_{1}\\\begin{matrix}\vdots \\\hat{b}_{k}\end{matrix}\end{matrix}\right]</math> | ||
| + | |} | ||
| + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(9) | ||
| + | |} | ||
| − | By solving the matrix equation, a solution for the evaluation vector is obtained <math display="inline">\hat{b}</math> | + | By solving the matrix equation, a solution for the evaluation vector is obtained <math display="inline">\hat{b}</math>: |
| − | {| class="formulaSCP" style="width: 100%; text-align: center;" | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" |
|- | |- | ||
| | | | ||
| − | {| style=" | + | {| style="margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math | + | | <math>\hat{b}={\left( X'\cdot X\right) }^{-1}\left( X'\cdot Y\right)</math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(10) |
|} | |} | ||
| + | To test the significance of the estimated regression parameters, it is necessary to know their distributions. In case the model assumptions are met, these parameters have the following distribution: | ||
| − | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | |
| − | + | ||
| − | {| class="formulaSCP" style="width: 100%; text-align: center;" | + | |
|- | |- | ||
| | | | ||
| − | {| style=" | + | {| style="margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math | + | | <math>\hat{b}:N\left( \beta ;{\sigma }^{2}{\left( X'X\right) }^{-1}\right)</math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(11) |
|} | |} | ||
| + | where <math>N</math> is the number of parameters, <math>\beta</math> is the vector of regression population parameters and <math display="inline">\sigma</math> is the accidental error. In that case, testing the significance of the mentioned parameters can be performed using the following distribution: | ||
| − | + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | |
| − | + | ||
| − | {| class="formulaSCP" style="width: 100%; text-align: center;" | + | |
|- | |- | ||
| | | | ||
| − | {| style=" | + | {| style="margin:auto;width: 100%;" |
|- | |- | ||
| − | | <math | + | | <math>T=\displaystyle\frac{\hat{{b}_{j}}}{\sqrt{\displaystyle\frac{{a}_{ii}\cdot \sum _{i=1}^{n}{\epsilon }_{i}^{2}}{n-k-1}}}</math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(12) |
|} | |} | ||
| + | This random variable, in the case of the correct hypothesis <math>H_0 </math> (null hypothesis - which assumes that there is no significant relationship between the dependent and the independent variable), <math>\beta_j</math>, has a <math>T</math> distribution with <math>n-k-1</math> degrees of freedom, where the <math>k</math> is the number of independent variables, аnd <math>a_{ii}</math> is <math>i</math>-th diagonal element of the matrix <math>(X'X)^{-1}</math>. | ||
| − | + | The basic assumption in the formation of a multilinear regression model is the normal distribution of residual variable models. [[#tab-1|Table 1]] shows the minimum and the maximum values of all variables and their standard deviations (Standard Deviation) between the minimum and the maximum values in the observed period. | |
| − | < | + | <div class="center" style="font-size: 75%;">'''Table 1'''. Original variables with parameters from descriptive statistics</div> |
| − | '' | + | <div id='tab-1'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | {| style=" | + | |-style="text-align:center" |
| − | + | ! style="text-align:left;"| Variable !! Minimum !! Maximum !! Mean !! Std. deviation | |
| − | + | |-style="text-align:center" | |
| − | | | + | | style="vertical-align: center;text-align:left;"|Natural Gas Price |
| − | + | | style="vertical-align: center;"|1.63 | |
| − | | | + | | style="vertical-align: center;"|12.69 |
| − | + | | style="vertical-align: center;"|3.95 | |
| − | + | | style="vertical-align: center;"|1.96 | |
| − | | style=" | + | |-style="text-align:center" |
| − | | style=" | + | | style="vertical-align: center;text-align:left;"|Crude Oil Price |
| − | | style=" | + | | style="vertical-align: center;"|16.55 |
| − | | style=" | + | | style="vertical-align: center;"|133.88 |
| − | | style=" | + | | style="vertical-align: center;"|71.73 |
| − | |- | + | | style="vertical-align: center;"|23.73 |
| − | | style="vertical-align: | + | |-style="text-align:center" |
| − | | style="vertical-align: | + | | style="vertical-align: center;text-align:left;"|Natural Gas Production |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|1878.00 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|3.620.71 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|2.603,39 |
| − | |- | + | | style="vertical-align: center;"|426.78 |
| − | | style="vertical-align: | + | |-style="text-align:center" |
| − | | style="vertical-align: | + | | style="vertical-align: center;text-align:left;"|Natural Gas Consumption |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|1460.04 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|3.417.20 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|2192.16 |
| − | |- | + | | style="vertical-align: center;"|450.96 |
| − | | style="vertical-align: | + | |-style="text-align:center" |
| − | | style="vertical-align: | + | | style="vertical-align: center;text-align:left;"|Renew. Eng. Source Prod. - RES |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|483.32 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|1063.77 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|789.28 |
| − | |- | + | | style="vertical-align: center;"|142.78 |
| − | | style="vertical-align: | + | |-style="text-align:center" |
| − | | style="vertical-align: | + | | style="vertical-align: center;text-align:left;"|Coal Production |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|36934.07 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|104389.50 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|77800.98 |
| − | |- | + | | style="vertical-align: center;"|15804.46 |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
|} | |} | ||
| − | + | SPSS (Statistical Package for the Social Sciences) version 23 and XLStat (Statistical Software for Excel) premium software are used to build regression models. | |
| − | + | To assess the quality of the acquired regression models, i.e., to assess the reliability and the impartiality, several econometric tests need to be performed: | |
| − | + | :1. '''Absence of multicollinearity.''' This test uses two determinants: Variance Inflation Factor (VIF) and Tolerance Factor (TOL). If the tolerance value is less than 0.2 or 0.1 and at the same time the VIF value is 10 or more, then multicollinearity is problematic. The problem of multicollinearity does not exist when the values of VIF are <5 and 10, respectively, while the values of TOL are <0.2 and 0.1, respectively. Variables whose VIF values are greater than 10 and TOL> 0.4 indicate a multicollinearity problem and should not be in the model. | |
| − | + | :2. '''Normal distribution of variables in the model.''' It is tested using Shapiro-Wilk and values of two coefficients: asymmetry (Skewness) and flatness (Kurtosis) for which acceptable values of variables are approximately ± 1. | |
| − | + | :3. '''Control of the random error of homoskedasticity or heteroskedasticity.''' Random errors should show the same level of distribution around their mean value. When random variances of errors differ significantly from each other, it is a case of heteroskedasticity. This testing will be performed by Breusch-Pagan (based on testing the dependence of residual variation on the height of all regressors) and White's test (based on comparing the variance of estimators obtained by the method of least squares under conditions of homoskedasticity and heteroskedasticity). | |
| − | ''' | + | :4. '''Autocorrelation of residues is a common occurrence in the case of economic time series.''' The Durbin-Watson test is used to detect autocorrelation. Values of this test can range from 0 to 4. Values greater than 2 indicate negative, while values less than 2 indicate positive autocorrelation. |
| − | + | ===2.4 Results and comments=== | |
| − | + | ||
| − | | | + | Results of the Pearson correlation coefficient (test statistics that measures the statistical relationship between two continuous variables), show a relatively strong statistical relationship between the price of natural gas and the price of crude oil, natural gas production, renewable energy production and coal production, except for gas consumption where the natural gas price relationship is weak. The highest level of positive correlation with the dependent variable is achieved by coal production (0.654), followed by the price of crude oil (0.527), while the gas production (-0.629) and energy production from renewable sources (-0.663) variables are highly correlated, but with the opposite sign. The correlation matrix is given in [[#tab-2|Table 2]]. |
| − | + | ||
| − | + | <div class="center" style="font-size: 75%;">'''Table 2'''. Pearson correlation matrix</div> | |
| − | | | + | |
| − | + | <div id='tab-2'></div> | |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | | | + | |-style="text-align:center" |
| − | + | ! Variable !! (1) !! (2) !! (3) !! (4) !! (5) !! (6) | |
| − | | style=" | + | |-style="text-align:center" |
| − | | style=" | + | | style="vertical-align: center;"|(1) |
| − | | style=" | + | | style="vertical-align: top;"|1.000 |
| − | | style=" | + | | style="vertical-align: top;"|'''0.527''' |
| − | | style=" | + | | style="vertical-align: top;"|'''-0.629''' |
| − | | style=" | + | | style="vertical-align: top;"|-0.264 |
| − | | style=" | + | | style="vertical-align: top;"|'''-0.663''' |
| − | |- | + | | style="vertical-align: top;"|'''0.654''' |
| − | | style="vertical-align: | + | |-style="text-align:center" |
| + | | style="vertical-align: center;"|(2) | ||
| style="vertical-align: top;"|0.527 | | style="vertical-align: top;"|0.527 | ||
| style="vertical-align: top;"|1.000 | | style="vertical-align: top;"|1.000 | ||
| Line 408: | Line 338: | ||
| style="vertical-align: top;"|-0.404 | | style="vertical-align: top;"|-0.404 | ||
| style="vertical-align: top;"|0.635 | | style="vertical-align: top;"|0.635 | ||
| − | |- | + | |-style="text-align:center" |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|(3) |
| style="vertical-align: top;"|-0.629 | | style="vertical-align: top;"|-0.629 | ||
| style="vertical-align: top;"|-0.490 | | style="vertical-align: top;"|-0.490 | ||
| Line 416: | Line 346: | ||
| style="vertical-align: top;"|0.865 | | style="vertical-align: top;"|0.865 | ||
| style="vertical-align: top;"|-0.848 | | style="vertical-align: top;"|-0.848 | ||
| − | |- | + | |-style="text-align:center" |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|(4) |
| style="vertical-align: top;"|-0.264 | | style="vertical-align: top;"|-0.264 | ||
| style="vertical-align: top;"|-0.284 | | style="vertical-align: top;"|-0.284 | ||
| Line 424: | Line 354: | ||
| style="vertical-align: top;"|0.406 | | style="vertical-align: top;"|0.406 | ||
| style="vertical-align: top;"|-0.447 | | style="vertical-align: top;"|-0.447 | ||
| − | |- | + | |-style="text-align:center" |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|(5) |
| style="vertical-align: top;"|-0.663 | | style="vertical-align: top;"|-0.663 | ||
| style="vertical-align: top;"|-0.404 | | style="vertical-align: top;"|-0.404 | ||
| Line 432: | Line 362: | ||
| style="vertical-align: top;"|1.000 | | style="vertical-align: top;"|1.000 | ||
| style="vertical-align: top;"|-0.843 | | style="vertical-align: top;"|-0.843 | ||
| − | |- | + | |-style="text-align:center" |
| − | | style=" | + | | style="vertical-align: center;"|(6) |
| − | | style=" | + | | style="vertical-align: top;"|0.654 |
| − | | style=" | + | | style="vertical-align: top;"|0.635 |
| − | | style=" | + | | style="vertical-align: top;"|-0.848 |
| − | | style=" | + | | style="vertical-align: top;"|-0.447 |
| − | | style=" | + | | style="vertical-align: top;"|-0.843 |
| − | | style=" | + | | style="vertical-align: top;"|1.000 |
| − | + | ||
| − | + | ||
|} | |} | ||
| + | <div class="center" style="font-size: 75%;">(1) Natural Gas Price. (2) Crude Oil Price. (3) Natural Gas Production. (4) Natural Gas Consumption.<br> | ||
| + | (5) Renewable Energy Source Production - RES. (6) Coal Production</div> | ||
| + | <br> | ||
| − | Table | + | [[#tab-3|Table 3]] shows the Skewness and Kurtosis coefficients. Results for all variables are within the acceptable value of ± 1. The value of the Shapiro -Wilk test is also within the acceptable limit values, so it can be concluded that a normal distribution of variables in the model has been achieved. |
| − | '''Table | + | <div class="center" style="font-size: 75%;">'''Table 3'''. Checking the normality of the distribution of dependent variables in the model</div> |
| − | {| style=" | + | <div id='tab-3'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! rowspan='2' style="text-align:left;" |Variables !! colspan='2' | Skewness !! colspan='2' | Kurtosis | ||
|- | |- | ||
| − | + | ! Statistic !! Std. Error !! Statistic !! Std. Error | |
| − | + | |-style="text-align:center" | |
| − | + | | style="vertical-align: center;text-align:left;"|Crude Oil Price | |
| − | + | | style="vertical-align: center;"|0.208 | |
| − | + | | style="vertical-align: center;"|0.190 | |
| − | + | | style="vertical-align: center;"|-0.739 | |
| − | | | + | | style="vertical-align: center;"|0.377 |
| − | | style=" | + | |-style="text-align:center" |
| − | + | | style="vertical-align: center;text-align:left;"|Natural Gas Production | |
| − | + | | style="vertical-align: center;"|0.655 | |
| − | | style=" | + | | style="vertical-align: center;"|0.190 |
| − | | style=" | + | | style="vertical-align: center;"|-0.394 |
| − | | style=" | + | | style="vertical-align: center;"|0.377 |
| − | | style=" | + | |-style="text-align:center" |
| − | |- | + | | style="vertical-align: center;text-align:left;"|Natural Gas Consumption |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|0.636 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|0.190 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|-0.392 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|0.377 |
| − | | style="vertical-align: | + | |-style="text-align:center" |
| − | |- | + | | style="vertical-align: center;text-align:left;"|Ren. Eng. Source Prod. - RES |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|-0.128 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|0.190 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|-0.781 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|0.377 |
| − | | style="vertical-align: | + | |-style="text-align:center" |
| − | |- | + | | style="vertical-align: center;text-align:left;"|Coal Production |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|-0.515 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|0.190 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|-0.694 |
| − | | style="vertical-align: | + | | style="vertical-align: center;"|0.377 |
| − | | style="vertical-align: | + | |-style="text-align:center" |
| − | |- | + | | colspan='5' style="vertical-align: center;"|Shapiro-Wilk: 0,961 |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | |- | + | |
| − | | colspan='5' style=" | + | |
|} | |} | ||
| − | Results of the regression model are given in Table | + | Results of the regression model are given in [[#tab-4|Table 4]]. The value of the coefficient of the multiple correlation (R) serves to determine the quality of the prediction for the independent variable, in this case, Natural gas price. The value of 0.723 represents a good prediction. The value of the multiple determination coefficient (R Square) is relatively high and states that the model explains 52.3% of the dependent variable. The value of the standard error of the estimate (Std. Error of the Estimate) indicates that the set model is accurate, while the Durbin-Watson test indicates a positive autocorrelation (the result is less than 2), which is a good sign for our regression model. |
| − | '''Table | + | <div class="center" style="font-size: 75%;">'''Table 4'''. Multiple correlation, determination, and autocorrelation coefficients</div> |
| − | {| style=" | + | <div id='tab-4'></div> |
| − | |- | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | + | |-style="text-align:center" | |
| − | + | !rowspan='2'| R !! rowspan='2' |R Square !! rowspan='2' |Adjusted R Square !! rowspan='2' |Std. error of the Estimate !! colspan='2' |Change Statistics !! rowspan='2' | Durbin-Watson | |
| − | + | |-style="text-align:center" | |
| − | + | ! R Square Change !! F Change | |
| − | + | |-style="text-align:center" | |
| − | + | | style="vertical-align: center;"|0.723 | |
| − | + | | style="vertical-align: center;"|0.523 | |
| − | + | | style="vertical-align: center;"|0.507 | |
| − | |- | + | | style="vertical-align: center;"|1.37743 |
| − | + | | style="vertical-align: center;"|0.523 | |
| − | + | | style="vertical-align: center;"|34.586 | |
| − | | | + | | style="vertical-align: center;"|0.238 |
| − | + | |-style="text-align:left" | |
| − | | style=" | + | | colspan='7' style="vertical-align: center;"|<div class="left" style="font-size: 90%;">'''Model Summary.''' Predictors: (Constant), Coal Production, Natural Gas Consumption, Oil Price, Renewable Energy Sources </div> |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | | style=" | + | |
| − | |- | + | |
| − | | colspan='7' style=" | + | |
| − | + | <div class="left" style="font-size: 90%;">Production (RES), Natural Gas Production; Dependent Variable: Natural Gas Price</div> | |
|} | |} | ||
| − | The ANOVA method was used to test the null hypothesis on the coefficient of multiple determinations. | + | The ANOVA ('''analysis of variance''') method was used to test the null hypothesis on the coefficient of multiple determinations. '''ANOVA''' is a test of the hypothesis that is appropriate to compare means of a continuous variable in two or more independent comparison groups. The results indicate that the null hypothesis can be rejected, i.e., it makes sense to use this model to explain the dependent variable ([[#tab-5|Table 5]]). |
| − | '''Table | + | <div class="center" style="font-size: 75%;">'''Table 5'''. Estimation of the significance of partial regression coefficients</div> |
| − | {| style=" | + | <div id='tab-5'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | + | |-style="text-align:center" | |
| − | | | + | ! Model !! Sum of Squares !! <math>D_f</math> !! Mean Square !! F !! Sig. |
| − | + | |-style="text-align:center" | |
| − | + | | Regression | |
| − | + | | 328.105 | |
| − | + | | 5 | |
| − | |- | + | | 65.621 |
| − | + | | 34.586 | |
| − | | | + | | 0.000 |
| − | | | + | |-style="text-align:center" |
| − | | | + | |
| − | | | + | |
| − | | style=" | + | |
| − | + | ||
| Residual | | Residual | ||
| 299.776 | | 299.776 | ||
| Line 553: | Line 468: | ||
| | | | ||
| | | | ||
| − | |- | + | |-style="text-align:center" |
| − | + | | Total | |
| − | | | + | | 627.881 |
| − | | | + | | 164 |
| − | | | + | | |
| − | + | | | |
| − | | | + | | |
|} | |} | ||
| − | The significance of partial regression coefficients was determined by performing a T-test. From Table | + | The significance of partial regression coefficients was determined by performing a T-test. From [[#tab-6|Table 6]] it is possible to conclude based on coefficients in the column Sig. to make a unique contribution to the model, i.e., that the statistically significant variables “Crude Oil price” and “RES Production” (the same conclusion can be reached on basis of 95% confidence interval, which only in the case of the mentioned variables does not include 0). As values of the inflation factor of variance - VIF and the tolerance factor - Tol., are within acceptable limits, it can be concluded that all variables can be part of the regression model, so the value of the independent variable Y is the sum of the values of the coefficient B other than zero. |
| − | '''Table | + | <div class="center" style="font-size: 75%;">'''Table 6'''. Estimation of the significance of partial regression coefficients</div> |
| − | {| style=" | + | <div id='tab-6'></div> |
| − | |- | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | + | |-style="text-align:center" | |
| − | | rowspan='2' | + | ! rowspan='2' | !! rowspan='2' |(1) !! rowspan='2' |(2) !! rowspan='2' |(3) !! rowspan='2' |(4) !! rowspan='2' |(5) !! colspan='2' |Collinearity Statistics !! rowspan='2' |(6) !! rowspan='2' |(7) |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | Crude oil price | + | ! style="text-align: center;"|Lower Bound !! style="text-align: center;"|Upper Bound |
| + | |-style="text-align:center" | ||
| + | | style="text-align: left;"|(Constant) | ||
| + | | '''7.568''' | ||
| + | | 2.541 | ||
| + | | | ||
| + | | 2.978 | ||
| + | | 0.003 | ||
| + | | 2.549 | ||
| + | | 12.587 | ||
| + | | | ||
| + | | | ||
| + | |- style="text-align:center" | ||
| + | | style="text-align: left;"| Crude oil price | ||
| style="text-align: center;"|'''0.025''' | | style="text-align: center;"|'''0.025''' | ||
| style="text-align: center;"|0.006 | | style="text-align: center;"|0.006 | ||
| Line 604: | Line 511: | ||
| style="text-align: center;"|1.870 | | style="text-align: center;"|1.870 | ||
|- | |- | ||
| − | | Nat. Gas Production | + | | style="text-align: left;"| Nat. Gas Production |
| style="text-align: center;"|0.000 | | style="text-align: center;"|0.000 | ||
| style="text-align: center;"|0.001 | | style="text-align: center;"|0.001 | ||
| Line 615: | Line 522: | ||
| style="text-align: center;"|4.957 | | style="text-align: center;"|4.957 | ||
|- | |- | ||
| − | | Nat. Gas Consumption | + | | style="text-align: left;"| Nat. Gas Consumption |
| style="text-align: center;"|0.000 | | style="text-align: center;"|0.000 | ||
| style="text-align: center;"|0.000 | | style="text-align: center;"|0.000 | ||
| Line 626: | Line 533: | ||
| style="text-align: center;"|1.262 | | style="text-align: center;"|1.262 | ||
|- | |- | ||
| − | | | + | | Renewable Energy Sources Production - RES |
| style="text-align: center;"|'''-0.007''' | | style="text-align: center;"|'''-0.007''' | ||
| style="text-align: center;"|0.002 | | style="text-align: center;"|0.002 | ||
| Line 637: | Line 544: | ||
| style="text-align: center;"|5.246 | | style="text-align: center;"|5.246 | ||
|- | |- | ||
| − | | style=" | + | | style="btext-align: left;"|Coal Production |
| − | | style=" | + | | style="text-align: center;"|0.000 |
| − | | style=" | + | | style="text-align: center;"|0.000 |
| − | | style=" | + | | style="text-align: center;"|0.018 |
| − | | style=" | + | | style="text-align: center;"|0.130 |
| − | | style=" | + | | style="text-align: center;"|0.897 |
| − | | style=" | + | | style="text-align: center;"|0.000 |
| − | | style=" | + | | style="text-align: center;"|0.000 |
| − | | style=" | + | | style="text-align: center;"|0.162 |
| − | | style=" | + | | style="text-align: center;"|6.168 |
|- | |- | ||
| − | | colspan='10' style=" | + | | colspan='10' style="padding-top:10px;vertical-align: top;"|(1) '''Unstandardized Coefficients B'''. (2) Stand. Coefficients - Std. Error. (3) t – Beta. (4) Sig. (5) 95.0% Confidence Interval for B. (6) Tol. (7) VIF |
|} | |} | ||
| − | Based on Table | + | Based on [[#tab-6|Table 6]], the natural gas price can be estimated using Eq. (13): |
{| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| Line 659: | Line 566: | ||
{| style="margin:auto;width: 100%;" | {| style="margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | '''Y (Natural Gas Price)''' =7 | + | | style="text-align: center;" | '''Y (Natural Gas Price)''' =7.568 + 0.025 (Crude Oil Price) – 0.007 (RES Production) |
|} | |} | ||
| − | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|( | + | | style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(13) |
|} | |} | ||
| + | Based on values in [[#tab-7|Table 7]], it can be concluded that the homogeneity of variances and predictive values deviates from the limit values, so that in this case a pronounced heteroskedasticity exists. | ||
| − | + | <div class="center" style="font-size: 75%;">'''Table 7'''. Heteroskedasticity tests</div> | |
| − | '' | + | <div id='tab-7'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | |
| − | {| style=" | + | |-style="text-align:center" |
| − | |- | + | ! style="text-align:left;"| Heteroskedasticity Test !! Breusch-Pagan !! White |
| − | + | |-style="text-align:center" | |
| − | + | | style="text-align:left;"| Critical value | |
| − | | | + | | 3.8414588 |
| − | + | | 5.9914645 | |
| − | | style=" | + | |-style="text-align:center" |
| − | | | + | | style="text-align:left;"| Observed value R-squared |
| − | | style=" | + | | 16.1229036 |
| − | + | | 20.6487180 | |
| − | | style=" | + | |
| − | | | + | |
| − | | | + | |
|} | |} | ||
| − | As the influence of non-constant variance of errors on the efficiency of estimation by the least | + | As the influence of non-constant variance of errors on the efficiency of estimation by the least square method as well as the validity of its conclusions, depends on several factors including sample size, degree of predictor variation, regressor values and the relationship between error variance and independent variables, it is not possible to reach full general conclusions relating to the consequences produced by heteroskedasticity in this case. Some authors believe that heteroskedasticity is not a big problem in econometric research. One of them is N. Gregori Mankiw who argues that “heteroskedasticity has never been a reason to reject an otherwise good model.” [45]. On the other hand, John Fox [46] points out that “unequal variances of errors should be corrected only if the problem is serious.” As previous tests have led to the conclusion that the regression model in work is good, it can be believed that there is no need to correct the data by applying possible forms of transformation. |
| − | |||
| − | == | + | ==3. Conclusions== |
| − | + | Natural gas is one of the most used non-renewable hydrocarbons. Like almost any non-renewable energy source, it releases carbon dioxide during combustion. The linear model identified that one of the most important factors influencing the prices of natural gas is green energy or energy obtained from renewable sources (solar energy, wind energy, etc.). Namely, the presence of this factor in the model is statistically significant with a high correlation coefficient with the price of natural gas - with a negative sign as the volume of natural gas production. Traditionally, a significant factor is the price of crude oil, which is statistically significant in the model and has a positive high correlation coefficient as well as coal production. | |
| − | + | It is difficult to predict the expected volatility of natural gas prices in the future because factors of influence depend on global crises and shocks as well as on the geopolitical situation in the world. Investors in the natural gas market can use models formulated in this way to make investment decisions. Our findings highlight the importance of including pandemic risk in forecasting global gas supply and demand. The results of the research will help policymakers assess the impact of the COVID-19 pandemic on natural gas price volatility and formulate appropriate plans and strategies to reduce the impact and improve forecasting models that should include pandemics, natural and economic disasters. | |
| − | + | Our proposed method can be used for the prediction of future natural gas prices, in addition to other techniques such as wavelets, time series, symbolic regression [47-49], artificial neural networks [50,51], cointegration technique [52], Monte Carlo [53], etc. | |
| − | == | + | ==Acknowledgements== |
| − | This research has been supported by the Ministry of Education, Science, and Technological Development of the Republic of Serbia. | + | This research has been supported by the Ministry of Education, Science, and Technological Development of the Republic of Serbia. Dejan Brkić acknowledges additional support by the Technology Agency of the Czech Republic through the project CEET—"Center of Energy and Environmental Technologies" TK03020027. |
| − | + | '''Conflicts of interest:''' The authors declare no conflict of interest. All authors have approved the final version of this paper. | |
| − | + | ||
| − | The authors declare no conflict of interest. All authors have approved the final version of this paper. | + | |
==References== | ==References== | ||
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
| + | |||
| + | [1] Petrović N., Bojović N., Petrović M., Jovanović V. A study of the environmental Kuznets curve for transport greenhouse gas emissions in the European Union. Facta Universitatis, Series: Mechanical Engineering, 18(3):513-524, 2020. [https://doi.org/10.22190/FUME171212010P https://doi.org/10.22190/FUME171212010P] | ||
| + | |||
| + | [2] Apergis N., Payne J.E. Natural gas consumption and economic growth: A panel investigation of 67 countries. Applied Energy, 87(8):2759-2763, 2010. [https://doi.org/10.1016/j.apenergy.2010.01.002 https://doi.org/10.1016/j.apenergy.2010.01.002] | ||
| + | |||
| + | [3] Alcarazа C., Villalvazo S. The effect of natural gas shortages on the Mexican economy. Energy Economics, 66:147-153, 2017. [https://doi.org/10.1016/j.eneco.2017.06.006 https://doi.org/10.1016/j.eneco.2017.06.006] | ||
| + | |||
| + | [4] Leahy E., Devitt C., Lyons S., Tol R.S. The cost of natural gas shortages in Ireland. Energy Policy, 46:153-169, 2012. [https://doi.org/10.1016/j.enpol.2012.03.047 https://doi.org/10.1016/j.enpol.2012.03.047] | ||
| + | |||
| + | [5] Brkić D. Serbian gas sector in the spotlight of oil and gas agreement with Russia. Energy Policy, 37(5):1925-1938, 2009. [https://doi.org/10.1016/j.enpol.2009.01.031 https://doi.org/10.1016/j.enpol.2009.01.031] | ||
| + | |||
| + | [6] Henriques I., Sadorsky P. The effect of oil price volatility on strategic investment. Energy Economics, 33(1):79-87, 2011. [https://doi.org/10.1016/j.eneco.2010.09.001 https://doi.org/10.1016/j.eneco.2010.09.001] | ||
| + | |||
| + | [7] IEA (2020), Gas 2020, OECD Publishing, Paris. [https://doi.org/10.1787/df4b275f-en https://doi.org/10.1787/df4b275f-en] (accessed 11 April 2021). | ||
| + | |||
| + | [8] International Gas Union (2020). [https://igu.org/resources/global-gas-report-2020/ https://igu.org/resources/global-gas-report-2020/] (accessed 23 November 2020) | ||
| + | |||
| + | [9] EIA U.S Energy Information Administration ('''2020'''). [https://www.eia.gov/dnav/ng/hist/rngwhhdm.htm https://www.eia.gov/dnav/ng/hist/rngwhhdm.htm] (accessed 26 December 2020). | ||
| + | |||
| + | [10] Worldbank (2020). [https://blogs.worldbank.org/opendata/will-natural-gas-and-coal-prices-recover-coronavirus-covid-19-slump https://blogs.worldbank.org/opendata/will-natural-gas-and-coal-prices-recover-coronavirus-covid-19-slump] (accessed 26 December 2020). | ||
| + | |||
| + | [11] Brkić D., Tanasković T.I. Systematic approach to natural gas usage for domestic heating in urban areas. Energy, 33(12):1738-1753, 2008. [https://doi.org/10.1016/j.energy.2008.08.009 https://doi.org/10.1016/j.energy.2008.08.009] | ||
| + | |||
| + | [12] Nyga-Łukaszewska H., Aruga K. Energy prices and COVID-immunity: The case of crude oil and natural gas prices in the US and Japan. Energies, 13:6300, 2020. [https://doi.org/10.3390/en13236300 https://doi.org/10.3390/en13236300] | ||
| + | |||
| + | [13] Foglia M., Angelini E. Volatility connectedness between clean energy firms and crude oil in the COVID-19 era. Sustainability, 12:9863, 2020. [https://doi.org/10.3390/su12239863 https://doi.org/10.3390/su12239863] | ||
| + | |||
| + | [14] Czech K., Wielechowski M. Is the alternative energy sector COVID-19 resistant? Comparison with the conventional energy sector: Markov-Switching model analysis of stock market indices of energy companies. Energies, 14:988, 2021. [https://doi.org/10.3390/en14040988 https://doi.org/10.3390/en14040988] | ||
| − | [ | + | [15] Vieira P.C., Silva W.T.M. Elastoplastic analysis of steel frames with interaction surfaces in stress resultants obtained for multiple linear regression. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 35(4):46, 2019. [https://doi.org/10.23967/j.rimni.2019.09.009 https://doi.org/10.23967/j.rimni.2019.09.009] |
| − | [ | + | [16] Ambhore N., Kamble D. Experimental investigation of tool wear and induced vibration in turning high hardness AISI52100 steel using cutting parameters and tool acceleration. Facta Universitatis, Series: Mechanical Engineering, 18(4):623-637, 2020. [https://doi.org/10.22190/FUME200116018A https://doi.org/10.22190/FUME200116018A] |
| − | [ | + | [17] Hailemariam A., Smyth R. What drives volatility in natural gas prices? Energy Economics, 71:5-31, 2019. [https://doi.org/10.1016/j.eneco.2019.02.011 https://doi.org/10.1016/j.eneco.2019.02.011] |
| − | [ | + | [18] Caporin M., Fontini F. The long-run oil–natural gas price relationship and the shale gas revolution. Energy Economics, 64:511-519, 2017. [https://doi.org/10.1016/j.eneco.2016.07.024 https://doi.org/10.1016/j.eneco.2016.07.024] |
| − | [ | + | [19] Batten J.A., Ciner C., Lucey B.M. The dynamic linkages between crude oil and natural gas markets. Energy Economics, 62:155-170, 2017. [https://doi.org/10.1016/j.eneco.2016.10.019 https://doi.org/10.1016/j.eneco.2016.10.019] |
| − | [ | + | [20] Hartley P.R., Medlock III K.B. The relationship between crude oil and natural gas prices: The role of the exchange rate. The Energy Journal, 35(2):25-44, 2014. [https://doi.org/10.5547/01956574.35.2.2 https://doi.org/10.5547/01956574.35.2.2] |
| − | [ | + | [21] Brigida M. The switching relationship between natural gas and crude oil. Energy Economics, 43:48-55, 2014. [https://doi.org/10.1016/j.eneco.2014.01.014 https://doi.org/10.1016/j.eneco.2014.01.014] |
| − | [ | + | [22] Atil A., Lahiani A., Nguyen D.K. Asymmetric and nonlinear pass-through of crude oil prices to gasoline and natural gas prices. Energy Policy, 65:567-573, 2014. [https://doi.org/10.1016/j.enpol.2013.09.064 https://doi.org/10.1016/j.enpol.2013.09.064] |
| − | [ | + | [23] Ramberg D.J., Parsons J.E. The weak tie between natural gas and oil prices. The Energy Journal, 33(2):13-35, 2012. [https://doi.org/10.5547/01956574.33.2.2 https://doi.org/10.5547/01956574.33.2.2] |
| − | [ | + | [24] Brown S.P., Yucel M.K. What drives natural gas prices? The Energy Journal, 29(2):45-60, 2008. [https://doi.org/10.5547/ISSN0195-6574-EJ-Vol29-No2-3 https://doi.org/10.5547/ISSN0195-6574-EJ-Vol29-No2-3] |
| − | [ | + | [25] Ji Q., Zhang H.Y., Geng J.B. What drives natural gas prices in the United States? A directed acyclic graph approach. Energy Economics, 69:79-88, 2018. [https://doi.org/10.1016/j.eneco.2017.11.002 https://doi.org/10.1016/j.eneco.2017.11.002] |
| − | [ | + | [26] Wiggins S., Etienne X.L. Turbulent times: Uncovering the origins of US natural gas price fluctuations since deregulation. Energy Economics, 64:196-205, 2017. [https://doi.org/10.1016/j.eneco.2017.03.015 https://doi.org/10.1016/j.eneco.2017.03.015] |
| − | [ | + | [27] Jadidzadeh A., Serletis A. How does the US natural gas market react to demand and supply shocks in the crude oil market? Energy Economics, 63:66-74, 2017. [https://doi.org/10.1016/j.eneco.2017.01.007 https://doi.org/10.1016/j.eneco.2017.01.007] |
| − | [ | + | [28] Mohammadi H. Market integration and price transmission in the US natural gas market: From the wellhead to end use markets. Energy Economics, 33(2):227-235, 2011. [https://doi.org/10.1016/j.eneco.2010.08.011 https://doi.org/10.1016/j.eneco.2010.08.011] |
| − | [ | + | [29] Renou-Maissant P. Toward the integration of European natural gas markets: A time-varying approach. Energy Policy, 51:779-790, 2012. [https://doi.org/10.1016/j.enpol.2012.09.027 https://doi.org/10.1016/j.enpol.2012.09.027] |
| − | [ | + | [30] Krichene N. World crude oil and natural gas: A demand and supply model. Energy Economics, 24(6):557-576, 2002. [https://doi.org/10.1016/S0140-9883(02)00061-0 https://doi.org/10.1016/S0140-9883(02)00061-0] |
| − | [ | + | [31] Nick S., Thoenes S. What drives natural gas prices? -A structural VAR approach. Energy Economics, 45:517-527, 2014. [https://doi.org/10.1016/j.eneco.2014.08.010 https://doi.org/10.1016/j.eneco.2014.08.010] |
| − | [ | + | [32] Everts M., Claus H., Eike B.W. Politics vs markets: How German power prices hit the floor. Journal of World Energy Law and Business, 9(2):116-123, 2016. [https://doi.org/10.1093/jwelb/jww005 https://doi.org/10.1093/jwelb/jww005] |
| − | [ | + | [33] Mosquera-López S., Nursimulu A. Drivers of electricity price dynamics: Comparative analysis of spot and futures markets. Energy Policy, 126:76-87, 2019. [https://doi.org/10.1016/j.enpol.2018.11.020 https://doi.org/10.1016/j.enpol.2018.11.020] |
| − | [ | + | [34] Mu X. Weather, storage, and natural gas price dynamics: Fundamentals and volatility. Energy Economics, 29(1):46-63, 2007. [https://doi.org/10.1016/j.eneco.2006.04.003 https://doi.org/10.1016/j.eneco.2006.04.003] |
| − | [ | + | [35] Hulshof D., Van der Maat J.P., Mulder M. Market fundamentals, competition and natural-gas prices. Energy Policy, 94:480-491, 2016. [https://doi.org/10.1016/j.enpol.2015.12.016 https://doi.org/10.1016/j.enpol.2015.12.016] |
| − | [ | + | [36] Fateh B., Youssef A., Chiao B., Guesmi K. The Impacts of COVID-19 on China’s domestic natural gas market. IAEE Energy Forum, 107-111, 2020. |
| − | [ | + | [37] Meher B.K., Hawaldar I.T., Mohapatra L., Adel M., Sarea A.M. The impact of COVID-19 on price volatility of crude oil and natural gas listed on multi commodity exchange of India. International Journal of Energy Economics and Policy, 10(5):422-431, 2020. [https://doi.org/10.32479/ijeep.10047 https://doi.org/10.32479/ijeep.10047] |
| − | [ | + | [38] Koloshkin E. EU natural gas market in the context of the global economic crisis due to the COVID-19 pandemic (in Russian). Финансовая экономика, 9:45-50, 2020. |
| − | [ | + | [39] Tsemekidi Tzeiranaki S., Bertoldi P., Diluiso F., Castellazzi L., Economidou M., Labanca N., Ribeiro Serrenho T., Zangheri P. Analysis of the EU residential energy consumption: trends and determinants. Energies, 12(6):1065, 2019. [https://doi.org/10.3390/en12061065 https://doi.org/10.3390/en12061065] |
| − | [ | + | [40] Ansari E., Kaufmann, R.K. The effect of oil and gas price and price volatility on rig activity in tight formations and OPEC strategy. Nature Energy, 4(4):321-328, 2019. [https://doi.org/10.1038/s41560-019-0350-1 https://doi.org/10.1038/s41560-019-0350-1] |
| − | [ | + | [41] Dong K., Dong X., Sun R. How did the price and income elasticities of natural gas demand in China evolve from 1999 to 2015? The role of natural gas price reform. Petroleum Science, 16(3):685-700, 2019. [https://doi.org/10.1007/s12182-019-0320-z https://doi.org/10.1007/s12182-019-0320-z] |
| − | [ | + | [42] Drosos D., Skordoulis M., Arabatzis G., Tsotsolas N., Galatsidas S. Measuring industrial customer satisfaction: The case of the natural gas market in Greece. Sustainability, 11(7):1905, 2019. [https://doi.org/10.3390/su11071905 https://doi.org/10.3390/su11071905] |
| − | [ | + | [43] Lin B., Li J. The spillover effects across natural gas and oil markets: Based on the VEC–MGARCH framework. Applied Energy 155:229–241, 2015. [https://doi.org/10.1016/j.apenergy.2015.05.123 https://doi.org/10.1016/j.apenergy.2015.05.123] |
| − | [ | + | [44] Freedman D. Statistical Models: Theory and Practice. Cambridge University Press, 2009. |
| − | [ | + | [45] Mankiw N.G. A quick refresher course in macroeconomics. Journal of Economic Literature, 28:1648, 1990. [https://doi.org/10.3386/w3256 https://doi.org/10.3386/w3256] |
| − | [ | + | [46] Fox J. Applied regression analysis, linear models, and related methods. Sage Publications, pp. 597, 1997. |
| − | [ | + | [47] Praks P., Brkić D. Review of new flow friction equations: Constructing Colebrook’s explicit correlations accurately. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 36(3):41, 2020. [https://doi.org/10.23967/j.rimni.2020.09.001 https://doi.org/10.23967/j.rimni.2020.09.00] |
| − | [ | + | [48] Brkić D., Stajić Z. Excel VBA-based user defined functions for highly precise Colebrook’s pipe flow friction approximations: A comparative overview. Facta Universitatis, Series: Mechanical Engineering, 19(2):253-269, 2021. [https://doi.org/10.22190/FUME210111044B https://doi.org/10.22190/FUME210111044B] |
| − | [ | + | [49] Brkić D., Praks P. Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright ω-function. Mathematics, 7(1):34, 2019. [https://doi.org/10.3390/math7010034 https://doi.org/10.3390/math7010034] |
| − | [ | + | [50] Jin J., Kim J. Forecasting natural gas prices using wavelets, time series, and artificial neural networks. PloS One, 10(11):e0142064, 2015. [https://doi.org/10.1371/journal.pone.0142064 https://doi.org/10.1371/journal.pone.0142064] |
| − | [ | + | [51] Zhang W., Hamori S. Do machine learning techniques and dynamic methods help forecast US natural gas crises? Energies, 13(9):2371, 2020. [https://doi.org/10.3390/en13092371 https://doi.org/10.3390/en13092371] |
| − | [ | + | [52] Ghouri S.S. Forecasting natural gas prices using cointegration technique. OPEC Review, 30(4):249-269, 2006. [https://doi.org/10.1111/j.1468-0076.2006.00171.x https://doi.org/10.1111/j.1468-0076.2006.00171.x] |
| − | [ | + | [53] Han T.-C., Wang C.-M. Shipping bunker cost risk assessment and management during the coronavirus oil shock. Sustainability, 13(9):4998, 2021. [https://doi.org/10.3390/su13094998 https://doi.org/10.3390/su13094998] |
Latest revision as of 14:49, 14 February 2023
Abstract
The paper examines the primary drivers and factors influencing the volatility of natural gas prices in the world from January 2007 to July 2020. In addition to the narrow dependence between crude oil and natural gas prices, the influence of renewable energy production and coal production on the price of natural gas has been studied. For that purpose, the method of multiple linear regression was used. The results show that the volatility of natural gas prices significantly depends on the type of the shock in the natural gas market, and that the total production of energy from renewable sources, production of coal and natural gas and the price of crude oil have a significant impact on the price of gas.
Keywords: Energy prices, natural gas, multiple linear regressions, renewable energy, price volatility, energy consumption
1. Introduction
Natural gas is a mixture of hydrocarbons and methane and because it mixes easily with air and has a high combustion rate without smoke, soot, and solid residues, it has a significant environmental advantage over conventional fuels such as oil and coal [1]. In the same way that oil replaced coal in industrial production at the beginning of the twentieth century, gas suppressed oil at the beginning of the twenty-first century and became an increasingly common fuel used to start the industry. Due to a fact that natural gas is a much cleaner energy source, this tendency in many developed countries is regulated by law, so some industrial sectors are forced to start their production with the help of natural gas. Given the world’s growing concern about the effects of carbon dioxide emissions from fossil fuels, and the impact on climate change and low carbon content in natural gas compared to other fossil fuels, natural gas has become a major energy source in many economies across the globe. Recent research shows that the consumption of natural gas plays an important role in facilitating economic growth in the both short and long term [2] and that disruptions in the supply of natural gas entail huge economic costs [3-5]. Fluctuations in energy prices are also becoming increasingly important in influencing risk reduction and strategic investments [6].
The largest recorded shock demand in the history of global natural gas markets happened in the first half of 2020. Faced with historically mild temperatures during the first months of the year, the COVID-19 pandemic hit the already declining demand for gas. Gas consumption is expected to fall by 4% in 2020 [7-10], due to successive lower demand for warm winter heating [11], the implementation of lockdown measures in almost all countries and territories, to slow the spread of the virus and lower activity generated by the macroeconomic crisis caused by the pandemic. Faced with this unprecedented shock, natural gas markets are undergoing strong supply and demand adjustments, resulting in historically low spot prices and high volatility. Demand for natural gas is expected to gradually recover in 2021, but the COVID-19 crisis will have a longer-term impact on natural gas markets [12-14], as major medium-term drivers are subject to great uncertainty.
With the above mentioned, the contribution of our work to literature is that by using multiple linear regression (MLR) [15,16] it can be proved that selected independent variables are important and necessary in determining the dependent variable and that there is a significant relationship and interaction between selected factors and natural gas prices. It can be also proved that fluctuations in natural gas prices are correlated with certain global economic events. This article also shows how the two most significant depressions in recent history - the global economic crisis and COVID-19, have affected the price of natural gas, which can be useful in further research, forecasting prices and consumption in the energy markets, especially when it comes to increased risk of potentially new infectious diseases in the global market soon.
This paper examines the primary drivers and factors influencing the volatility of natural gas prices in the world from January 2007 to July 2020. In addition to the narrow dependence between crude oil and natural gas prices, the influence of renewable energy production and coal production on the price of natural gas has been studied. For that purpose, the method of multiple linear regression was used, as follows.
2. Estimation of natural gas prices
2.1 Literature review
Much of the literature on the natural gas market is devoted to examining the relationship between natural gas prices and the crude oil market, suggesting that oil price fluctuations are important determinants of natural gas prices [17-24]. Only a few studies examined the role of supply and demand factors in determining prices in the U.S. natural gas market [25-28]. Some recent studies show that, unlike globally defined crude oil markets, natural gas markets are regionally segmented, suggesting that natural gas prices are formed by regional supply-demand relationships [29]. Following the recent decoupling of the relationship between the crude oil and natural gas markets [30], it is crucial to understand how natural gas prices respond to supply and demand in times of natural gas market shocks, and to identify the relative contribution factors of each. Accordingly, Nick and Thoenes [31] use a structural VAR model to examine price volatility in the German natural gas market. They conclude that supply shocks have a significant impact on the German natural gas market and that temperature, storage and supply shocks lead to relatively short-term effects, while oil and coal price shocks result in more lasting effects on gas prices. The relationship between the prices of natural gas and coal was also investigated by Everts et al. [32]. The study used a basic market price replication model with an analysis of the impact of changes on the individual price drivers such as coal prices or subsidies for renewable energy production. The study showed the fall in electricity prices in Germany in the period 2008-2014 can be attributed to market effects such as a reduction in coal use and gas prices as well as a reduction in electricity demand (50%). Only approximately 30% of price reductions could be directly related to subsidies for energy from renewable sources such as wind and solar energy. Mosquera-López and Nursimulu [33] came to qualitatively similar conclusions. They found that in the short- and medium-term, the main drivers of prices differ and vary in time. In the case of the spot market, determinants of prices were renewable sources and demand for electricity, while in the future markets the main drivers of natural gas prices were the supply and price of coal. Mu [34] identifies demand for natural gas concerning weather conditions as an important factor influencing the movement of gas prices. Hulshof et al. [35] conclude that natural gas prices are mainly determined by the weather conditions and availability of stored quantities, while supply has no significant effect. The availability of natural gas in storage and the outside temperature negatively affected the price of natural gas. They also concluded that the price of natural gas was related to the production of electricity from wind.
The outbreak of the COVID-19 pandemic has shaken global financial markets, commodity markets, economic activities, employment, and GDP, in almost all countries of the world. Only a few studies have analyzed the effect of this global pandemic on natural gas prices [36-38]. For this reason, there is a need to study the impact of this phenomenon on the volatility of natural gas prices.
2.2 Influencing factors
It is impossible to talk about a single price of natural gas, considering the division of markets in which this energy source is sold. Unlike crude oil, which is traded on stock exchanges and whose prices are uniform worldwide, natural gas prices vary by region. The difference in the price of natural gas is due to different costs of production and transportation, as well as different degrees of liberalization of national natural gas markets. The price of natural gas can be discussed at different levels of the supply chain. The final price of gas at the point of consumption is the sum of the price of production, the price of transportation and the price of local distribution. The price also varies depending on the final consumer, so the industrial sector will usually have a lower price for gas than households do. Thus, in 2007, the average price of natural gas at the level of the European Union was 36% higher for the household sector compared to the industrial sector [39,40]. Another unavoidable factor that contributes to different levels of natural gas prices are taxes that vary from country to country [41,42].
The price of natural gas is experiencing a constant escalation in the market, especially during 2009 because of the global financial crisis of 2008, when the price of natural gas in September was US$ 2.99 per 1,05 million kJ. This was followed by market recovery and relative price stability during 2010 and subsequent years [7-10]).
However, natural gas prices fell sharply since the beginning of 2020 due to weak demand and abundant supply. European natural gas prices fell to a decade-long low and have fallen by almost 40% since early 2020 [39,40]. U.S. natural gas prices have fallen slightly, in part because they had already been low [25-28]. Price differences between regional benchmarks for natural gas continued to decline, mostly driven by the increasing availability of liquefied natural gas. However, the fall in prices of natural gas and coal is smaller than the price of crude oil, which has fallen by about 65% since January 2020. Natural gas and coal are primarily used for electricity generation and industrial purposes, not for transportation. As such, lockdowns and travel restrictions had less of an impact on demand for these products than for crude oil [43].
The onset of the COVID-19 pandemic created an unprecedented shock to the global energy system, and gas consumption around the world was significantly affected. Demand for natural gas has fallen in the electricity sector due to lower electricity usage, and in the industrial and commercial sectors due to the shutdown of factories and businesses. The demand for gas among the population did not decrease while people stayed at home. These impacts varied by region. In Europe, gas demand fell by 7% year-on-year during the first five months of 2020 [7-10]. In the first quarter, the decline was driven by mild winters and higher production from renewable sources. However, lockdown measures began to affect gas demand from March on, where May consumption was already 11% lower than in March [7-10]. Natural gas and coal have seen significant reductions in demand, as lockdown measures have reduced industrial activity and electricity consumption, while extremely warm winters have also reduced demand in early 2020. The International Energy Agency estimates that lockdown measures have reduced electricity demand to at least 15% in several major economies, including France, Italy, Spain, and the United Kingdom [7-10]. In the United States, the U.S. Energy Information Administration expects U.S. demand for electricity to fall by about 5%, and a moderate decline in housing use will offset a greater decline in commercial and industrial use - sectors affected by lockdowns [7-10].
Natural gas prices are expected to recover from the current low but will still be about 25% lower than in 2019 [7-10]. Demand for natural gas is expected to gradually recover from current low levels after lifting the lockdown but will remain below 2019 levels. Demand for coal is likely to remain weaker, as a part of the ongoing transition from coal to natural gas in global electricity generation.
Global gas demand could fall by 4% annually in 2020 [7-10]. This would be the largest drop in gas demand ever recorded since the development of the gas industry in the second half of the 20th century. By comparison, gas demand fell by 2% in 2009 due to the global financial crisis. About 75% of demand loss is likely to occur in developed gas markets across Europe, North America, the Commonwealth of Independent States (CIS), and Asia due to lower electricity demand, declining industrial activity, and lower space heating needs in the commercial sector.
Production and consumption of natural gas from January 2007 - September 2020 are given in Figure 1, production of coal and energy from renewable sources from January 2007 - September 2020 in Figure 2, while prices of crude oil and natural gas from January 2007 - September 2020 in Figure 3.
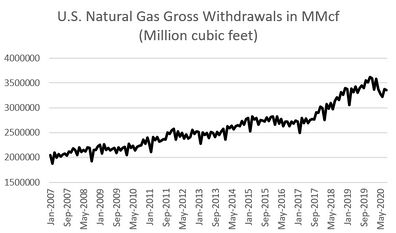
|
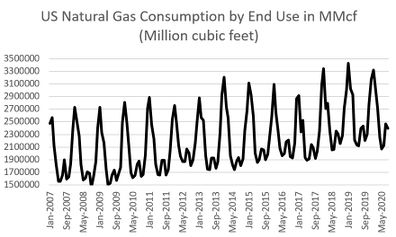
|
| Figure 1. Fluctuation of production and consumption of natural gas from January 2007-September 2020. Source: U.S. Energy Information Administration - Monthly Energy Review |
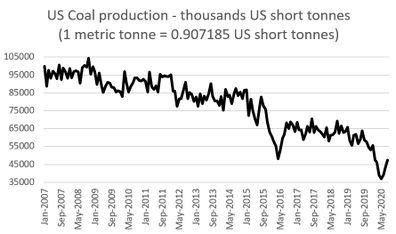
|
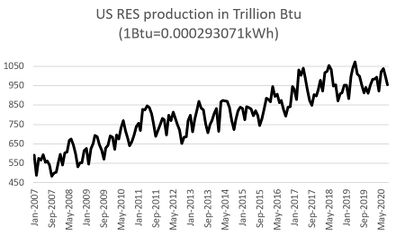
|
| Figure 2. Fluctuation of production of coal and energy from renewable sources from January 2007-September 2020. Source: U.S. Energy Information Administration - Monthly Energy Review |
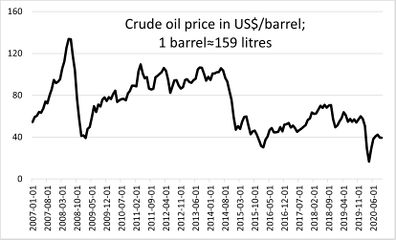
|
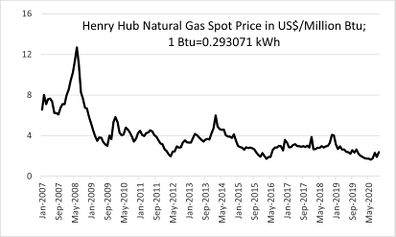
|
| Figure 3. Fluctuation of prices of crude oil and natural gas from January 2007-September 2020. Source: FRED Graph Observations, and Henry Hub Natural Gas Spot Price, respectively |
As we can see in Figure 3, the market shock caused by the global economic crisis led to a fall in the price of natural gas from 12.69 US$ per 1.05 million kJ of June 2008 to 2.99 US$ in September 2009. Also, the pandemic COVID -19 caused a drop in price from 4.09 US$ (December 2019) to 1.63 US$ per 1.05 million kJ as the price was in June 2020.
2.3 Methodology. Multiple linear regression
To identify the dependence of natural gas prices on different shocks in the natural gas market, monthly time intervals were used during the period from January 2007 to September 2020. This period was used to cover two major shocks in the natural gas market: the 2008 global economic crisis and the COVID-19 virus pandemic. Monthly data have sufficient frequency to analyze the effects of price dependence and market spillovers over time [43]. As a source of data for total production and total consumption of natural gas in billions of cubic feet, a database published by the EIA (U.S Energy Information Administration) was used.
The price of crude oil (US$ per barrel) is from the Federal Reserve Economic Data - FRED, and for the actual price of natural gas (US$ per 1.05 million kJ) the data published by Henry Hub Natural Gas Spot Price was used. Data on coal production (in thousands of tons) as well as data on energy production from renewable energy sources (RES) in 1.05 million kJ were taken from the EIA.
The Multiple Linear Regression analysis is conducted using a mathematical expression of this model [44] as follows:
|
|
(1) |
where is the dependent variable, the regression constant, , the independent variables, the standard error i.e., residues and the unknown parameter to be evaluated (regression parameter).
Values of the regression parameters with each independent variable show how much the dependent variable changes on average when the observed independent variable increases by one of its units, and all other independent variables remain unchanged.
In this model, all assumptions apply as in the simple regression model with two additional assumptions, so that the parameter estimates have their desired properties:
- the sample size must be greater than the number of evaluation parameters,
- regressors should not be perfectly correlated with each other (linearly dependent).
Sample estimates of unknown parameters are obtained by applying the method of least squares. In the case of models with two independent variables, the following function needs to be minimized:
|
|
(2) |
where is the function to be minimized, the estimates of the corresponding coefficients of their standard error (roots of the estimates of their dispersions), the standard error i.e., residues, the difference between the actual and the predicted value of the dependent variable and the number of variables.
Minimization of the function is achieved by equalizing its partial derivatives of the first order by parameters, with zero:
|
|
(3) |
By arranging these equations, a system of normal equations is obtained:
|
|
(4) |
|
|
(5) |
whose solution yields sample grades , , of unknown parameters .
The equations of the observed system can be presented in matrix notation:
|
|
(6) |
where is transposed matrix of matrix , follows:
|
|
(7) |
|
|
(8) |
|
|
(9) |
By solving the matrix equation, a solution for the evaluation vector is obtained :
|
|
(10) |
To test the significance of the estimated regression parameters, it is necessary to know their distributions. In case the model assumptions are met, these parameters have the following distribution:
|
|
(11) |
where is the number of parameters, is the vector of regression population parameters and is the accidental error. In that case, testing the significance of the mentioned parameters can be performed using the following distribution:
|
|
(12) |
This random variable, in the case of the correct hypothesis (null hypothesis - which assumes that there is no significant relationship between the dependent and the independent variable), , has a distribution with degrees of freedom, where the is the number of independent variables, аnd is -th diagonal element of the matrix .
The basic assumption in the formation of a multilinear regression model is the normal distribution of residual variable models. Table 1 shows the minimum and the maximum values of all variables and their standard deviations (Standard Deviation) between the minimum and the maximum values in the observed period.
| Variable | Minimum | Maximum | Mean | Std. deviation |
|---|---|---|---|---|
| Natural Gas Price | 1.63 | 12.69 | 3.95 | 1.96 |
| Crude Oil Price | 16.55 | 133.88 | 71.73 | 23.73 |
| Natural Gas Production | 1878.00 | 3.620.71 | 2.603,39 | 426.78 |
| Natural Gas Consumption | 1460.04 | 3.417.20 | 2192.16 | 450.96 |
| Renew. Eng. Source Prod. - RES | 483.32 | 1063.77 | 789.28 | 142.78 |
| Coal Production | 36934.07 | 104389.50 | 77800.98 | 15804.46 |
SPSS (Statistical Package for the Social Sciences) version 23 and XLStat (Statistical Software for Excel) premium software are used to build regression models.
To assess the quality of the acquired regression models, i.e., to assess the reliability and the impartiality, several econometric tests need to be performed:
- 1. Absence of multicollinearity. This test uses two determinants: Variance Inflation Factor (VIF) and Tolerance Factor (TOL). If the tolerance value is less than 0.2 or 0.1 and at the same time the VIF value is 10 or more, then multicollinearity is problematic. The problem of multicollinearity does not exist when the values of VIF are <5 and 10, respectively, while the values of TOL are <0.2 and 0.1, respectively. Variables whose VIF values are greater than 10 and TOL> 0.4 indicate a multicollinearity problem and should not be in the model.
- 2. Normal distribution of variables in the model. It is tested using Shapiro-Wilk and values of two coefficients: asymmetry (Skewness) and flatness (Kurtosis) for which acceptable values of variables are approximately ± 1.
- 3. Control of the random error of homoskedasticity or heteroskedasticity. Random errors should show the same level of distribution around their mean value. When random variances of errors differ significantly from each other, it is a case of heteroskedasticity. This testing will be performed by Breusch-Pagan (based on testing the dependence of residual variation on the height of all regressors) and White's test (based on comparing the variance of estimators obtained by the method of least squares under conditions of homoskedasticity and heteroskedasticity).
- 4. Autocorrelation of residues is a common occurrence in the case of economic time series. The Durbin-Watson test is used to detect autocorrelation. Values of this test can range from 0 to 4. Values greater than 2 indicate negative, while values less than 2 indicate positive autocorrelation.
2.4 Results and comments
Results of the Pearson correlation coefficient (test statistics that measures the statistical relationship between two continuous variables), show a relatively strong statistical relationship between the price of natural gas and the price of crude oil, natural gas production, renewable energy production and coal production, except for gas consumption where the natural gas price relationship is weak. The highest level of positive correlation with the dependent variable is achieved by coal production (0.654), followed by the price of crude oil (0.527), while the gas production (-0.629) and energy production from renewable sources (-0.663) variables are highly correlated, but with the opposite sign. The correlation matrix is given in Table 2.
| Variable | (1) | (2) | (3) | (4) | (5) | (6) |
|---|---|---|---|---|---|---|
| (1) | 1.000 | 0.527 | -0.629 | -0.264 | -0.663 | 0.654 |
| (2) | 0.527 | 1.000 | -0.490 | -0.284 | -0.404 | 0.635 |
| (3) | -0.629 | -0.490 | 1.000 | 0.425 | 0.865 | -0.848 |
| (4) | -0.264 | -0.284 | 0.425 | 1.000 | 0.406 | -0.447 |
| (5) | -0.663 | -0.404 | 0.865 | 0.406 | 1.000 | -0.843 |
| (6) | 0.654 | 0.635 | -0.848 | -0.447 | -0.843 | 1.000 |
(5) Renewable Energy Source Production - RES. (6) Coal Production
Table 3 shows the Skewness and Kurtosis coefficients. Results for all variables are within the acceptable value of ± 1. The value of the Shapiro -Wilk test is also within the acceptable limit values, so it can be concluded that a normal distribution of variables in the model has been achieved.
| Variables | Skewness | Kurtosis | ||
|---|---|---|---|---|
| Statistic | Std. Error | Statistic | Std. Error | |
| Crude Oil Price | 0.208 | 0.190 | -0.739 | 0.377 |
| Natural Gas Production | 0.655 | 0.190 | -0.394 | 0.377 |
| Natural Gas Consumption | 0.636 | 0.190 | -0.392 | 0.377 |
| Ren. Eng. Source Prod. - RES | -0.128 | 0.190 | -0.781 | 0.377 |
| Coal Production | -0.515 | 0.190 | -0.694 | 0.377 |
| Shapiro-Wilk: 0,961 | ||||
Results of the regression model are given in Table 4. The value of the coefficient of the multiple correlation (R) serves to determine the quality of the prediction for the independent variable, in this case, Natural gas price. The value of 0.723 represents a good prediction. The value of the multiple determination coefficient (R Square) is relatively high and states that the model explains 52.3% of the dependent variable. The value of the standard error of the estimate (Std. Error of the Estimate) indicates that the set model is accurate, while the Durbin-Watson test indicates a positive autocorrelation (the result is less than 2), which is a good sign for our regression model.
| R | R Square | Adjusted R Square | Std. error of the Estimate | Change Statistics | Durbin-Watson | |
|---|---|---|---|---|---|---|
| R Square Change | F Change | |||||
| 0.723 | 0.523 | 0.507 | 1.37743 | 0.523 | 34.586 | 0.238 |
Model Summary. Predictors: (Constant), Coal Production, Natural Gas Consumption, Oil Price, Renewable Energy Sources
Production (RES), Natural Gas Production; Dependent Variable: Natural Gas Price
| ||||||
The ANOVA (analysis of variance) method was used to test the null hypothesis on the coefficient of multiple determinations. ANOVA is a test of the hypothesis that is appropriate to compare means of a continuous variable in two or more independent comparison groups. The results indicate that the null hypothesis can be rejected, i.e., it makes sense to use this model to explain the dependent variable (Table 5).
| Model | Sum of Squares | Mean Square | F | Sig. | |
|---|---|---|---|---|---|
| Regression | 328.105 | 5 | 65.621 | 34.586 | 0.000 |
| Residual | 299.776 | 159 | 1.897 | ||
| Total | 627.881 | 164 |
The significance of partial regression coefficients was determined by performing a T-test. From Table 6 it is possible to conclude based on coefficients in the column Sig. to make a unique contribution to the model, i.e., that the statistically significant variables “Crude Oil price” and “RES Production” (the same conclusion can be reached on basis of 95% confidence interval, which only in the case of the mentioned variables does not include 0). As values of the inflation factor of variance - VIF and the tolerance factor - Tol., are within acceptable limits, it can be concluded that all variables can be part of the regression model, so the value of the independent variable Y is the sum of the values of the coefficient B other than zero.
| (1) | (2) | (3) | (4) | (5) | Collinearity Statistics | (6) | (7) | ||
|---|---|---|---|---|---|---|---|---|---|
| Lower Bound | Upper Bound | ||||||||
| (Constant) | 7.568 | 2.541 | 2.978 | 0.003 | 2.549 | 12.587 | |||
| Crude oil price | 0.025 | 0.006 | 0.301 | 4.001 | 0.000 | 0.013 | 0.037 | 0.535 | 1.870 |
| Nat. Gas Production | 0.000 | 0.001 | -0.063 | -0.515 | 0.608 | -0.001 | 0.001 | 0.202 | 4.957 |
| Nat. Gas Consumption | 0.000 | 0.000 | 0.057 | 0.920 | 0.359 | 0.000 | 0.001 | 0.793 | 1.262 |
| Renewable Energy Sources Production - RES | -0.007 | 0.002 | -0.495 | -3.930 | 0.000 | -0.010 | -0.003 | 0.191 | 5.246 |
| Coal Production | 0.000 | 0.000 | 0.018 | 0.130 | 0.897 | 0.000 | 0.000 | 0.162 | 6.168 |
| (1) Unstandardized Coefficients B. (2) Stand. Coefficients - Std. Error. (3) t – Beta. (4) Sig. (5) 95.0% Confidence Interval for B. (6) Tol. (7) VIF | |||||||||
Based on Table 6, the natural gas price can be estimated using Eq. (13):
|
(13) |
Based on values in Table 7, it can be concluded that the homogeneity of variances and predictive values deviates from the limit values, so that in this case a pronounced heteroskedasticity exists.
| Heteroskedasticity Test | Breusch-Pagan | White |
|---|---|---|
| Critical value | 3.8414588 | 5.9914645 |
| Observed value R-squared | 16.1229036 | 20.6487180 |
As the influence of non-constant variance of errors on the efficiency of estimation by the least square method as well as the validity of its conclusions, depends on several factors including sample size, degree of predictor variation, regressor values and the relationship between error variance and independent variables, it is not possible to reach full general conclusions relating to the consequences produced by heteroskedasticity in this case. Some authors believe that heteroskedasticity is not a big problem in econometric research. One of them is N. Gregori Mankiw who argues that “heteroskedasticity has never been a reason to reject an otherwise good model.” [45]. On the other hand, John Fox [46] points out that “unequal variances of errors should be corrected only if the problem is serious.” As previous tests have led to the conclusion that the regression model in work is good, it can be believed that there is no need to correct the data by applying possible forms of transformation.
3. Conclusions
Natural gas is one of the most used non-renewable hydrocarbons. Like almost any non-renewable energy source, it releases carbon dioxide during combustion. The linear model identified that one of the most important factors influencing the prices of natural gas is green energy or energy obtained from renewable sources (solar energy, wind energy, etc.). Namely, the presence of this factor in the model is statistically significant with a high correlation coefficient with the price of natural gas - with a negative sign as the volume of natural gas production. Traditionally, a significant factor is the price of crude oil, which is statistically significant in the model and has a positive high correlation coefficient as well as coal production.
It is difficult to predict the expected volatility of natural gas prices in the future because factors of influence depend on global crises and shocks as well as on the geopolitical situation in the world. Investors in the natural gas market can use models formulated in this way to make investment decisions. Our findings highlight the importance of including pandemic risk in forecasting global gas supply and demand. The results of the research will help policymakers assess the impact of the COVID-19 pandemic on natural gas price volatility and formulate appropriate plans and strategies to reduce the impact and improve forecasting models that should include pandemics, natural and economic disasters.
Our proposed method can be used for the prediction of future natural gas prices, in addition to other techniques such as wavelets, time series, symbolic regression [47-49], artificial neural networks [50,51], cointegration technique [52], Monte Carlo [53], etc.
Acknowledgements
This research has been supported by the Ministry of Education, Science, and Technological Development of the Republic of Serbia. Dejan Brkić acknowledges additional support by the Technology Agency of the Czech Republic through the project CEET—"Center of Energy and Environmental Technologies" TK03020027.
Conflicts of interest: The authors declare no conflict of interest. All authors have approved the final version of this paper.
References
[1] Petrović N., Bojović N., Petrović M., Jovanović V. A study of the environmental Kuznets curve for transport greenhouse gas emissions in the European Union. Facta Universitatis, Series: Mechanical Engineering, 18(3):513-524, 2020. https://doi.org/10.22190/FUME171212010P
[2] Apergis N., Payne J.E. Natural gas consumption and economic growth: A panel investigation of 67 countries. Applied Energy, 87(8):2759-2763, 2010. https://doi.org/10.1016/j.apenergy.2010.01.002
[3] Alcarazа C., Villalvazo S. The effect of natural gas shortages on the Mexican economy. Energy Economics, 66:147-153, 2017. https://doi.org/10.1016/j.eneco.2017.06.006
[4] Leahy E., Devitt C., Lyons S., Tol R.S. The cost of natural gas shortages in Ireland. Energy Policy, 46:153-169, 2012. https://doi.org/10.1016/j.enpol.2012.03.047
[5] Brkić D. Serbian gas sector in the spotlight of oil and gas agreement with Russia. Energy Policy, 37(5):1925-1938, 2009. https://doi.org/10.1016/j.enpol.2009.01.031
[6] Henriques I., Sadorsky P. The effect of oil price volatility on strategic investment. Energy Economics, 33(1):79-87, 2011. https://doi.org/10.1016/j.eneco.2010.09.001
[7] IEA (2020), Gas 2020, OECD Publishing, Paris. https://doi.org/10.1787/df4b275f-en (accessed 11 April 2021).
[8] International Gas Union (2020). https://igu.org/resources/global-gas-report-2020/ (accessed 23 November 2020)
[9] EIA U.S Energy Information Administration (2020). https://www.eia.gov/dnav/ng/hist/rngwhhdm.htm (accessed 26 December 2020).
[10] Worldbank (2020). https://blogs.worldbank.org/opendata/will-natural-gas-and-coal-prices-recover-coronavirus-covid-19-slump (accessed 26 December 2020).
[11] Brkić D., Tanasković T.I. Systematic approach to natural gas usage for domestic heating in urban areas. Energy, 33(12):1738-1753, 2008. https://doi.org/10.1016/j.energy.2008.08.009
[12] Nyga-Łukaszewska H., Aruga K. Energy prices and COVID-immunity: The case of crude oil and natural gas prices in the US and Japan. Energies, 13:6300, 2020. https://doi.org/10.3390/en13236300
[13] Foglia M., Angelini E. Volatility connectedness between clean energy firms and crude oil in the COVID-19 era. Sustainability, 12:9863, 2020. https://doi.org/10.3390/su12239863
[14] Czech K., Wielechowski M. Is the alternative energy sector COVID-19 resistant? Comparison with the conventional energy sector: Markov-Switching model analysis of stock market indices of energy companies. Energies, 14:988, 2021. https://doi.org/10.3390/en14040988
[15] Vieira P.C., Silva W.T.M. Elastoplastic analysis of steel frames with interaction surfaces in stress resultants obtained for multiple linear regression. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 35(4):46, 2019. https://doi.org/10.23967/j.rimni.2019.09.009
[16] Ambhore N., Kamble D. Experimental investigation of tool wear and induced vibration in turning high hardness AISI52100 steel using cutting parameters and tool acceleration. Facta Universitatis, Series: Mechanical Engineering, 18(4):623-637, 2020. https://doi.org/10.22190/FUME200116018A
[17] Hailemariam A., Smyth R. What drives volatility in natural gas prices? Energy Economics, 71:5-31, 2019. https://doi.org/10.1016/j.eneco.2019.02.011
[18] Caporin M., Fontini F. The long-run oil–natural gas price relationship and the shale gas revolution. Energy Economics, 64:511-519, 2017. https://doi.org/10.1016/j.eneco.2016.07.024
[19] Batten J.A., Ciner C., Lucey B.M. The dynamic linkages between crude oil and natural gas markets. Energy Economics, 62:155-170, 2017. https://doi.org/10.1016/j.eneco.2016.10.019
[20] Hartley P.R., Medlock III K.B. The relationship between crude oil and natural gas prices: The role of the exchange rate. The Energy Journal, 35(2):25-44, 2014. https://doi.org/10.5547/01956574.35.2.2
[21] Brigida M. The switching relationship between natural gas and crude oil. Energy Economics, 43:48-55, 2014. https://doi.org/10.1016/j.eneco.2014.01.014
[22] Atil A., Lahiani A., Nguyen D.K. Asymmetric and nonlinear pass-through of crude oil prices to gasoline and natural gas prices. Energy Policy, 65:567-573, 2014. https://doi.org/10.1016/j.enpol.2013.09.064
[23] Ramberg D.J., Parsons J.E. The weak tie between natural gas and oil prices. The Energy Journal, 33(2):13-35, 2012. https://doi.org/10.5547/01956574.33.2.2
[24] Brown S.P., Yucel M.K. What drives natural gas prices? The Energy Journal, 29(2):45-60, 2008. https://doi.org/10.5547/ISSN0195-6574-EJ-Vol29-No2-3
[25] Ji Q., Zhang H.Y., Geng J.B. What drives natural gas prices in the United States? A directed acyclic graph approach. Energy Economics, 69:79-88, 2018. https://doi.org/10.1016/j.eneco.2017.11.002
[26] Wiggins S., Etienne X.L. Turbulent times: Uncovering the origins of US natural gas price fluctuations since deregulation. Energy Economics, 64:196-205, 2017. https://doi.org/10.1016/j.eneco.2017.03.015
[27] Jadidzadeh A., Serletis A. How does the US natural gas market react to demand and supply shocks in the crude oil market? Energy Economics, 63:66-74, 2017. https://doi.org/10.1016/j.eneco.2017.01.007
[28] Mohammadi H. Market integration and price transmission in the US natural gas market: From the wellhead to end use markets. Energy Economics, 33(2):227-235, 2011. https://doi.org/10.1016/j.eneco.2010.08.011
[29] Renou-Maissant P. Toward the integration of European natural gas markets: A time-varying approach. Energy Policy, 51:779-790, 2012. https://doi.org/10.1016/j.enpol.2012.09.027
[30] Krichene N. World crude oil and natural gas: A demand and supply model. Energy Economics, 24(6):557-576, 2002. https://doi.org/10.1016/S0140-9883(02)00061-0
[31] Nick S., Thoenes S. What drives natural gas prices? -A structural VAR approach. Energy Economics, 45:517-527, 2014. https://doi.org/10.1016/j.eneco.2014.08.010
[32] Everts M., Claus H., Eike B.W. Politics vs markets: How German power prices hit the floor. Journal of World Energy Law and Business, 9(2):116-123, 2016. https://doi.org/10.1093/jwelb/jww005
[33] Mosquera-López S., Nursimulu A. Drivers of electricity price dynamics: Comparative analysis of spot and futures markets. Energy Policy, 126:76-87, 2019. https://doi.org/10.1016/j.enpol.2018.11.020
[34] Mu X. Weather, storage, and natural gas price dynamics: Fundamentals and volatility. Energy Economics, 29(1):46-63, 2007. https://doi.org/10.1016/j.eneco.2006.04.003
[35] Hulshof D., Van der Maat J.P., Mulder M. Market fundamentals, competition and natural-gas prices. Energy Policy, 94:480-491, 2016. https://doi.org/10.1016/j.enpol.2015.12.016
[36] Fateh B., Youssef A., Chiao B., Guesmi K. The Impacts of COVID-19 on China’s domestic natural gas market. IAEE Energy Forum, 107-111, 2020.
[37] Meher B.K., Hawaldar I.T., Mohapatra L., Adel M., Sarea A.M. The impact of COVID-19 on price volatility of crude oil and natural gas listed on multi commodity exchange of India. International Journal of Energy Economics and Policy, 10(5):422-431, 2020. https://doi.org/10.32479/ijeep.10047
[38] Koloshkin E. EU natural gas market in the context of the global economic crisis due to the COVID-19 pandemic (in Russian). Финансовая экономика, 9:45-50, 2020.
[39] Tsemekidi Tzeiranaki S., Bertoldi P., Diluiso F., Castellazzi L., Economidou M., Labanca N., Ribeiro Serrenho T., Zangheri P. Analysis of the EU residential energy consumption: trends and determinants. Energies, 12(6):1065, 2019. https://doi.org/10.3390/en12061065
[40] Ansari E., Kaufmann, R.K. The effect of oil and gas price and price volatility on rig activity in tight formations and OPEC strategy. Nature Energy, 4(4):321-328, 2019. https://doi.org/10.1038/s41560-019-0350-1
[41] Dong K., Dong X., Sun R. How did the price and income elasticities of natural gas demand in China evolve from 1999 to 2015? The role of natural gas price reform. Petroleum Science, 16(3):685-700, 2019. https://doi.org/10.1007/s12182-019-0320-z
[42] Drosos D., Skordoulis M., Arabatzis G., Tsotsolas N., Galatsidas S. Measuring industrial customer satisfaction: The case of the natural gas market in Greece. Sustainability, 11(7):1905, 2019. https://doi.org/10.3390/su11071905
[43] Lin B., Li J. The spillover effects across natural gas and oil markets: Based on the VEC–MGARCH framework. Applied Energy 155:229–241, 2015. https://doi.org/10.1016/j.apenergy.2015.05.123
[44] Freedman D. Statistical Models: Theory and Practice. Cambridge University Press, 2009.
[45] Mankiw N.G. A quick refresher course in macroeconomics. Journal of Economic Literature, 28:1648, 1990. https://doi.org/10.3386/w3256
[46] Fox J. Applied regression analysis, linear models, and related methods. Sage Publications, pp. 597, 1997.
[47] Praks P., Brkić D. Review of new flow friction equations: Constructing Colebrook’s explicit correlations accurately. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería, 36(3):41, 2020. https://doi.org/10.23967/j.rimni.2020.09.00
[48] Brkić D., Stajić Z. Excel VBA-based user defined functions for highly precise Colebrook’s pipe flow friction approximations: A comparative overview. Facta Universitatis, Series: Mechanical Engineering, 19(2):253-269, 2021. https://doi.org/10.22190/FUME210111044B
[49] Brkić D., Praks P. Accurate and efficient explicit approximations of the Colebrook flow friction equation based on the Wright ω-function. Mathematics, 7(1):34, 2019. https://doi.org/10.3390/math7010034
[50] Jin J., Kim J. Forecasting natural gas prices using wavelets, time series, and artificial neural networks. PloS One, 10(11):e0142064, 2015. https://doi.org/10.1371/journal.pone.0142064
[51] Zhang W., Hamori S. Do machine learning techniques and dynamic methods help forecast US natural gas crises? Energies, 13(9):2371, 2020. https://doi.org/10.3390/en13092371
[52] Ghouri S.S. Forecasting natural gas prices using cointegration technique. OPEC Review, 30(4):249-269, 2006. https://doi.org/10.1111/j.1468-0076.2006.00171.x
[53] Han T.-C., Wang C.-M. Shipping bunker cost risk assessment and management during the coronavirus oil shock. Sustainability, 13(9):4998, 2021. https://doi.org/10.3390/su13094998Document information
Published on 15/12/21
Accepted on 02/12/21
Submitted on 12/04/21
Volume 37, Issue 4, 2021
DOI: 10.23967/j.rimni.2021.12.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?