| (44 intermediate revisions by 3 users not shown) | |||
| Line 16: | Line 16: | ||
==Corresponding author: [mailto:xym_02@126.com xym_02@126.com]== | ==Corresponding author: [mailto:xym_02@126.com xym_02@126.com]== | ||
--> | --> | ||
| + | ==Abstract== | ||
| − | + | For improving the energy efficiency of hopping robot, an asymmetric spring loaded inverted pendulum hopping model with leg mass is considered. The period orbit problem of two-legged hopping robot is investigated. Firstly, the hybrid dynamic model is constructed. Then the passive hopping gaits are found using quasi-newton optimization method. Secondly, a PD controller is implemented to track the desired pitch trajectory of the body. Through applying control during stance phase, period orbits of the robot with offset body mass is obtained. Finally, the effect of the location of the leg mass and the body mass on hopping performances is investigated. | |
| − | '''Keywords | + | '''Keywords''': Hopping robot, asymmetric, passive dynamics, periodic motion, energy efficiency |
| − | + | ==1. Introduction== | |
| − | Hopping robots use isolated footholds, so it can negotiate uneven terrain. Due to these advantages, it has been studied by many researchers in recent years. Raibert and his coworkers had developed one-legged and two-legged hopping robots [1]based on a spring-loaded inverted pendulum (SLIP) model. These robots had a massless telescopic leg and a point foot. They use a three-part algorithm to control the robot. Since then, many jumping robots such as robots with spring leg[2-5] and robots with multi-joint leg[6-8] are constructed. | + | Hopping robots use isolated footholds, so it can negotiate uneven terrain. Due to these advantages, it has been studied by many researchers in recent years. Raibert and his coworkers had developed one-legged and two-legged hopping robots [1] based on a spring-loaded inverted pendulum (SLIP) model. These robots had a massless telescopic leg and a point foot. They use a three-part algorithm to control the robot. Since then, many jumping robots such as robots with spring leg [2-5] and robots with multi-joint leg [6-8] are constructed. |
| − | The SLIP model is the simplest mathematical model for hopping robot and it captured the basic dynamicbehaviors of the running of many animals<span id='cite-_Ref85573788'></span>[[#_Ref85573788|[9]]]. The control of the SLIP model is very simple because it doesn’t consider the dynamic coupling between the body and the legs. The control strategy based on SLIP model is necessary to be modified in order to successful apply in the control of the real robots[10], so it is necessary to construct a more realistic model similar to the real hopping robots. | + | The SLIP model is the simplest mathematical model for hopping robot and it captured the basic dynamicbehaviors of the running of many animals <span id='cite-_Ref85573788'></span>[[#_Ref85573788|[9]]]. The control of the SLIP model is very simple because it doesn’t consider the dynamic coupling between the body and the legs. The control strategy based on SLIP model is necessary to be modified in order to successful apply in the control of the real robots [10], so it is necessary to construct a more realistic model similar to the real hopping robots. |
| − | In the hopping control, the energy consumption is especially crucial because it directly affects the size of the actuator and in return influences the weight of the robots. So, it is necessary to achieve the hopping gait with minimal power consumption. In this field, there are some remarkable researches on passive hopping. It has been found that using the proper initial conditions, the hopping robots can excuates periodic motion without input torque[11-12]. Papadopoulos and Cherouvim proved that the passive gait is the least energy-consuming gait[2]. Ahmadi and Buehler used hip and leg compliance to realize passive motion [3-4]. Schammass et al exploited the passive dynamics of the system to reduce the energy consumption <span id='cite-_neb2B61CDB5_6B04_4FED_8F96_C3854775F3E0'></span>[[#_neb2B61CDB5_6B04_4FED_8F96_C3854775F3E0|[13]]]. The simulation results shown that the robot including hip compliance reduced approximately 67% of the total energy compared to the robot without hip compliance. Hyon et al used a new gait-searching algorithm to find the passive orbit and proposed two kinds of controllers to realize orbital stabilization [14-16]. | + | In the hopping control, the energy consumption is especially crucial because it directly affects the size of the actuator and in return influences the weight of the robots. So, it is necessary to achieve the hopping gait with minimal power consumption. In this field, there are some remarkable researches on passive hopping. It has been found that using the proper initial conditions, the hopping robots can excuates periodic motion without input torque [11-12]. Papadopoulos and Cherouvim proved that the passive gait is the least energy-consuming gait [2]. Ahmadi and Buehler used hip and leg compliance to realize passive motion [3-4]. Schammass et al exploited the passive dynamics of the system to reduce the energy consumption <span id='cite-_neb2B61CDB5_6B04_4FED_8F96_C3854775F3E0'></span>[[#_neb2B61CDB5_6B04_4FED_8F96_C3854775F3E0|[13]]]. The simulation results shown that the robot including hip compliance reduced approximately 67% of the total energy compared to the robot without hip compliance. Hyon et al used a new gait-searching algorithm to find the passive orbit and proposed two kinds of controllers to realize orbital stabilization [14-16]. |
All of these hopping robots have symmetric configuration with the center of mass (COM) along the geometrical axis of a telescopic leg. In reality, the COM of most animals offsets the hip joint and the weight of the leg can’t be ignored. The offset body-mass offers greater flexibility in the design of hopping robot because the actuator can be placed within the body freely. The asymmetrical body mass configurations have been considered by several scholars [17-23]. Kuswadi et al. proposed an asymmetric model of a single-legged robot and realized a sustained hopping motion. The center of gravity of the model isn’t on the line of action of the actuator [19]. Sayyad et al analyzed a springy-legged offset-mass (SLOM) configuration and proposed an energy compensated model to explore the possibility of a periodic motion [20]. But all these paper doesn’t consider the rotation of the body. Poulakakis et al used a SLIP-embedding control law to control an asymmetric spring loaded inverted pendulum (ASLIP) hopping model, but the leg is assumed to be massless [22-23]. | All of these hopping robots have symmetric configuration with the center of mass (COM) along the geometrical axis of a telescopic leg. In reality, the COM of most animals offsets the hip joint and the weight of the leg can’t be ignored. The offset body-mass offers greater flexibility in the design of hopping robot because the actuator can be placed within the body freely. The asymmetrical body mass configurations have been considered by several scholars [17-23]. Kuswadi et al. proposed an asymmetric model of a single-legged robot and realized a sustained hopping motion. The center of gravity of the model isn’t on the line of action of the actuator [19]. Sayyad et al analyzed a springy-legged offset-mass (SLOM) configuration and proposed an energy compensated model to explore the possibility of a periodic motion [20]. But all these paper doesn’t consider the rotation of the body. Poulakakis et al used a SLIP-embedding control law to control an asymmetric spring loaded inverted pendulum (ASLIP) hopping model, but the leg is assumed to be massless [22-23]. | ||
| Line 35: | Line 36: | ||
This paper is organized as follows. In Section 2, the dynamic model is presented along with its mechanical properties and motion equations. In Section 3, the Poincare mapping is used to analyze the passive periodic hopping motion of the hopping robot and the fix point is obtained using optimization, and the effects of the offset mass and the leg mass on the hopping motion are presented in Section 4. | This paper is organized as follows. In Section 2, the dynamic model is presented along with its mechanical properties and motion equations. In Section 3, the Poincare mapping is used to analyze the passive periodic hopping motion of the hopping robot and the fix point is obtained using optimization, and the effects of the offset mass and the leg mass on the hopping motion are presented in Section 4. | ||
| − | + | ==2. Dynamical model== | |
| − | <span id='cite-_Ref503256883'></span>[[#_Ref503256883| | + | <span id='cite-_Ref503256883'></span>[[#_Ref503256883|Figure 1]] is the simplified model of the ASLIP hopping robot. The hopping robot consists of two parts, a body and a springy telescope leg. The body and the leg is connected by a torsional spring on the hip joint <math>H</math>. In the model, the hip joint doesn’t coincide with the center of mass of the body. The mass of the leg is also taken into account. A coupling between the leg swing motion and the body rotation is introduced, which made the analysis of the dynamics of the robot more complicated. Supposing the position of the center of mass of the leg <math>S_1 </math> and the position of the center of mass of the body <math>S_2 </math> are given by <math>FS_1= \alpha l</math> and <math>HS_2 = \beta l_b</math>, where <math>0<\alpha ,\beta <1</math>. The variable <math>l</math> denotes the length of the leg, <math>theta</math> represents the leg angle with respect to the vertical axis <math>\varphi</math> indicates the body angle with respect to the horizontal axis. Other physical parameters and its values are listed in [[#tab-1|Table 1]]. |
| − | <div class=" | + | <div id='_Ref503256883'></div> |
| − | [[Image:Review_801861383672-image2.png| | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[Image:Review_801861383672-image2.png|344px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 1'''. Model of robot | ||
| + | |} | ||
| − | |||
| − | |||
| − | The hopping motion of the robot is composed of two phases: stance phase and flight phase. The switch from the stance phase to the flight phase is called lift-off, triggered by <math>l\geq l_0</math> . The switch from the flight phase to the stance phase is called touchdown, triggered by <math>zh\leq | + | The hopping motion of the robot is composed of two phases: stance phase and flight phase. The switch from the stance phase to the flight phase is called lift-off, triggered by <math>l\geq l_0</math>. The switch from the flight phase to the stance phase is called touchdown, triggered by <math>zh\leq l_0 \cos(\theta )</math>. We use the event-based subscript to describe the motion during different phases. The subscript <math>st</math> represents the stance phase, <math>fl</math> represents the flight phase, <math>td</math> is the moment at touchdown and <math>l_0</math> is the moment at lift off. |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | |||
| − | |||
| − | < | + | <div class="center" style="font-size: 85%;">'''Table 1'''. Physical parameters</div> |
| − | + | ||
| − | < | + | <div id='tab-1'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! Notation !! Units !! Value | ||
| + | |-style="text-align:center" | ||
| + | | body mass <math>m_b </math> | ||
| + | | kg | ||
| + | | 9 | ||
| + | |-style="text-align:center" | ||
| + | | leg mass <math>m_l </math> | ||
| + | | kg | ||
| + | | 3 | ||
| + | |-style="text-align:center" | ||
| + | | body length <math>l_b </math> | ||
| + | | m | ||
| + | | 0.22 | ||
| + | |-style="text-align:center" | ||
| + | | body inertia <math>J_b</math> | ||
| + | | kg.m<sup>2</sup> | ||
| + | | 0.5 | ||
| + | |-style="text-align:center" | ||
| + | | leg inertia <math>J_L</math> | ||
| + | | kg.m<sup>2</sup> | ||
| + | | 0.11 | ||
| + | |-style="text-align:center" | ||
| + | | leg spring stiffness <math>k_l </math> | ||
| + | | N/m | ||
| + | | 3000 | ||
| + | |-style="text-align:center" | ||
| + | | hip spring stiffness <math>k_h </math> | ||
| + | | Nm/rad | ||
| + | | 10 | ||
| + | |-style="text-align:center" | ||
| + | | natural leg length <math>l_0 </math> | ||
| + | | m | ||
| + | | 0.5 | ||
| + | |-style="text-align:center" | ||
| + | | gravity acceleration <math>g </math> | ||
| + | |m/s<sup>2</sup> | ||
| + | | 9.81 | ||
|} | |} | ||
| − | During the stance phase the leg is in contact with ground at a toe point | + | During the stance phase the leg is in contact with ground at a toe point <math>F </math> (end of the leg). Supposing that the robot does not bounce back nor slip relative to the ground, the leg rotates around the toe. Then the toe can be modeled as a pivot. We choose polar coordinates <math>\boldsymbol{q}_{st}={\left[\begin{array}{ccc} l & \theta & \varphi \end{array}\right]}^T</math>, as the generalized coordinates. Using the Lagrange method [22], the equations of motion is obtained as: |
| − | l & \theta & \varphi | + | |
| − | \end{array}\right]}^T</math> as the generalized coordinates. Using the Lagrange method[22], the equations of motion is obtained as: | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 110: | Line 109: | ||
|} | |} | ||
| + | where <math>\boldsymbol{M}_{st}</math> is the symmetric positive definite inertia matrix during the stance phase, which deponds on the generalized coordinates <math>\boldsymbol{q}_{st}</math>; <math>\boldsymbol{C}_{st}</math> is the matrix containing centrifugal force and Coriolis force during the stance phase, which is a function of <math>\boldsymbol{q}_{st}</math> and <math>{\boldsymbol{\dot{q}}}_{st}</math>; <math>\boldsymbol{G}_{st}</math> is the gravity vector during the stance phase, which is a function of <math>\boldsymbol{q}_{st}</math>; <math>\boldsymbol{K}_{st}</math> is the equivalent driving torque vector of torsion spring during the stance phase, which is related to <math>\boldsymbol{q}_{st}</math>; <math>{\boldsymbol{\tau }}_{st}={\left[\begin{array}{ccc} f & 0 & {\tau }_{st} \end{array}\right]}^T</math>; <math>f</math> is the driving force to the leg, while <math>{\tau }_{st}</math> denotes the hip torque during the stance phase. | ||
| − | + | During the flight phase the leg loses contact with the ground. The COM of the robot moves along the ballistic trajectory and the angular momentum of the robot about the COM is conserved. The length of the leg is assumed to keep constant. We select Cartesian coordinates <math>\boldsymbol{q}_{fl}={\left[\begin{array}{cccc} x_h & z_h & \theta & \phi \end{array}\right]}^T</math> as the generalized coordinates, <math>\left(x_h,z_h\right)</math> is the position of the hip joint. The dynamics is given by: | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | During the flight phase the leg loses contact with the ground. The COM of the robot moves along the ballistic trajectory and the angular momentum of the robot about the COM is conserved. The length of the leg is assumed to keep constant. We select Cartesian coordinates <math>\boldsymbol{q}_{fl}={\left[\begin{array}{cccc} | + | |
| − | x_h & z_h & \theta & \phi | + | |
| − | \end{array}\right]}^T</math> as the generalized coordinates, <math>\left(x_h,z_h\right)</math> is the position of the hip joint. The dynamics is given by: | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 129: | Line 123: | ||
|} | |} | ||
| + | where <math>\boldsymbol{M}_{fl}</math> is the symmetric positive definite inertia matrix during the flight phase, which deponds on the generalized coordinates <math>\boldsymbol{q}_{fl}</math>; <math>\boldsymbol{C}_{fl}</math> is the matrix containing centrifugal force and Coriolis force during the flight phase, which is a function of <math>\boldsymbol{q}_{fl}</math> and <math>{\boldsymbol{\dot{q}}}_{fl}</math>; <math>\boldsymbol{G}_{fl}</math> is the gravity vector during the flight phase, which is a function of <math>\boldsymbol{q}_{fl}</math>; <math>\boldsymbol{K}_{fl}</math> is the equivalent driving torque vector of torsion spring during the flight phase, which is related to <math>\boldsymbol{q}_{fl}</math>; <math>{\boldsymbol{\tau }}_{fl}={\left[\begin{array}{cccc} 0 & 0 & 0 & {\tau }_{fl}\end{array}\right]}^T</math>; <math>{\tau }_{fl}</math> is the hip torque during the flight phase. | ||
| − | + | At touchdown, the leg touches down the ground and inelastic impulse occurs. The generalized displacements keep constant, but the generalized velocities change instantaneously | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | At touchdown, the leg touches down the ground and inelastic impulse occurs. The generalized displacements keep constant, but the generalized velocities change instantaneously | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 146: | Line 137: | ||
|} | |} | ||
| − | + | where the subscript <math>td-</math> and <math>td+</math> represent the moment before and after touchdown respectively. | |
| − | where the subscript | + | |
At lift-off, there are no discontinuous changes of states except for: | At lift-off, there are no discontinuous changes of states except for: | ||
| Line 160: | Line 150: | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (4) | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
|} | |} | ||
| − | |||
It can be seen that during the landing phase, the leg compresses and releases the spring to realize the energy conversion from the above equations. Since the loss caused by friction is not considered, the mechanical energy is conserved. In the flight phase, the mechanical energy of the system is also conserved. At touchdown, the robot legs collide with the ground, which will lead to energy loss. In order to simplify the analysis, the energy loss at touchdown is not considered in this paper. The robot is a complex switching system with multi variables, strong coupling and nonlinearity, so it is impossible to obtain the analytical solution of the trajectory of the system, and can only be solved by numerical calculation. | It can be seen that during the landing phase, the leg compresses and releases the spring to realize the energy conversion from the above equations. Since the loss caused by friction is not considered, the mechanical energy is conserved. In the flight phase, the mechanical energy of the system is also conserved. At touchdown, the robot legs collide with the ground, which will lead to energy loss. In order to simplify the analysis, the energy loss at touchdown is not considered in this paper. The robot is a complex switching system with multi variables, strong coupling and nonlinearity, so it is impossible to obtain the analytical solution of the trajectory of the system, and can only be solved by numerical calculation. | ||
| − | + | ==3. Passive hopping motion== | |
To improve the energy efficiency, firstly we consider the completely passive hopping which means that there is no driving force applied on the robot. A very useful and common method to study the existence and stability of periodic motions is the Poincare map. According to the trajectory of the state variables in the Poincare section, we can find the periodic motion. Through Poincare map, we can transform the existence of the periodic orbits of the hopping robot to the fixed point in the Poincare section. | To improve the energy efficiency, firstly we consider the completely passive hopping which means that there is no driving force applied on the robot. A very useful and common method to study the existence and stability of periodic motions is the Poincare map. According to the trajectory of the state variables in the Poincare section, we can find the periodic motion. Through Poincare map, we can transform the existence of the periodic orbits of the hopping robot to the fixed point in the Poincare section. | ||
| − | The robot has 4 DOF during flight and 3 DOF during stance. For reducing the number of the independent variables, we choose the moment just after touchdown as the Poincare section and state vector is defined as <math>x= | + | The robot has 4 DOF during flight and 3 DOF during stance. For reducing the number of the independent variables, we choose the moment just after touchdown as the Poincare section and state vector is defined as <math>x=\left[\begin{array} {cccccc} l_{td} & \theta^{td} & {\varphi }_{td} & {\dot{l}}_{td} & \dot{\theta }_{td} & \dot{\varphi }_{td} \end{array}\right]^T</math>. For <math>l_{td}=l_0</math> at touchdown, the number of the independent variables reduces to 5. In the process of iteration, let the state vector in the <math>j^{th}</math> step is <math>{\bf x}^j</math>, we can get the state vector <math>{\bf x}^{j+1} </math> in the <math>(j+1)^{th}</math> step after one mapping. This process can be described as a Poincare map <math>x^{j+1}=P\left(x^j\right)</math>. |
| − | l_{td} & \theta | + | |
| − | \end{array}\right] | + | |
| − | For a certain state vector | + | For a certain state vector <math>{\bf x}</math>, the point is called a fixed point if it maps itself through one map, |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 184: | Line 171: | ||
|} | |} | ||
| − | + | Then we build the Poincare map of the hopping robot. The dynamic Eqs. (1) and (2) are rewritten into a standard state-space form. | |
| − | Then we build the Poincare map of the hopping robot. The dynamic | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 192: | Line 178: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{P}_{st}:{\boldsymbol{\dot{x}}}_{st}=\boldsymbol{f}_{st}\left(\boldsymbol{x}_{st},\boldsymbol{u}_{st}\right)</math> | + | | <math>\boldsymbol{P}_{st}:{\boldsymbol{\dot{x}}}_{st}=\boldsymbol{f}_{st}\left(\boldsymbol{x}_{st},\boldsymbol{u}_{st}\right)</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (6) | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
| Line 207: | Line 193: | ||
|} | |} | ||
| − | + | where <math>\boldsymbol{x}_{st}={\left[\boldsymbol{q}_{st}^\mbox{T},{\boldsymbol{\dot{q}}}_{st}^\mbox{T}\right]}^\mbox{T}</math> is the state vector during the stance phase and <math>\boldsymbol{x}_{fl}={\left[\boldsymbol{q}_{fl}^\mbox{T},{\boldsymbol{\dot{q}}}_{fl}^\mbox{T}\right]}^\mbox{T}</math> during the flight phase. Because the number of the state variables between the stance phase and the flight phase is different, we need to construct two mapping between the transitions of these two phases. The mapping is represented by the following equations | |
| − | where <math>\boldsymbol{x}_{st}={\left[\boldsymbol{q}_{st}^\mbox{T},{\boldsymbol{\dot{q}}}_{st}^\mbox{T}\right]}^\mbox{T}</math> is the state vector during the stance phase and <math>\boldsymbol{x}_{fl}={\left[\boldsymbol{q}_{fl}^\mbox{T},{\boldsymbol{\dot{q}}}_{fl}^\mbox{T}\right]}^\mbox{T}</math> during the flight phase. Because the number of the state variables between the stance phase and the flight phase is different, we need to construct two mapping between the transitions of these two phases. The mapping is represented by the following equations | + | |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 215: | Line 200: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | | + | | <math>\boldsymbol{P}_{lo}:\left\{ \begin{array}{l} x_ {h,lo} = - l_{lo}\sin\left({\theta }_{lo}\right)\\ |
| + | z_ {h,lo} = l_{lo}\cos\left({\theta }_{lo}\right)\\ \dot x_ {h,lo} = - \dot l_{lo}\sin\left({\theta }_{lo}\right)-l_{lo}\dot {\theta }_{lo} \cos\left({\theta }_{lo}\right)\\ \dot z_ {h,lo} = \dot l_{lo} \cos\left({\theta }_{lo}\right) -l_{lo} \dot {\theta }_{lo} \sin\left({\theta }_{lo}\right) \end{array}\right.</math> | ||
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (8) | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) | ||
| Line 225: | Line 211: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{P}_{td}:\ | + | | <math>\boldsymbol{P}_{td}:\left\{ \begin{array}{c}l_{td}=l_0\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\\{\dot{l}}_{td}=-{\dot{x}}_{h,td}\sin\left({\theta }_{lo}\right)+{\dot{z}}_{h,td}\cos\left({\theta }_{lo}\right)\end{array}\right.</math> |
| − | l_{td}=l_0\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\mbox{ }\\ | + | |
| − | {\dot{l}}_{td}=-{\dot{x}}_{h,td}sin\left({\theta }_{lo}\right)+{\dot{z}}_{h,td}cos\left({\theta }_{lo}\right) | + | |
| − | \end{array}</math> | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (9) | | style="width: 5px;text-align: right;white-space: nowrap;" | (9) | ||
|} | |} | ||
| + | Combining these four sub-maps, then the whole Poincare mapping is <math>\boldsymbol{P}=\boldsymbol{P}_{st}\circ \boldsymbol{P}_{lo}\circ \boldsymbol{P}_{fl}\circ \boldsymbol{P}_{td}</math>. | ||
| − | + | Since the Poincare map of the hopping robot have been constructed, now we consider the method of finding the fixed point. The Newton-Raphson’s method [15] is commonly used to find the fixed point | |
| − | + | ||
| − | + | ||
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 243: | Line 225: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>x^{j+1}=x^{j+1}+{\left[I-DP(x_j)\right]}^{-1}\left[P(x_j)- | + | | <math>x^{j+1}=x^{j+1}+{\left[I-DP(x_j)\right]}^{-1}\left[P(x_j)- x_j\right]</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (10) | | style="width: 5px;text-align: right;white-space: nowrap;" | (10) | ||
|} | |} | ||
| − | + | where, <math>\bf I</math> is the identity matrix, <math>D\boldsymbol{P}\left(\boldsymbol{x}\right)=\partial \boldsymbol{P}\left(\boldsymbol{x}\right)/\partial \boldsymbol{x}</math> is the jacobian matrix of the Poincare map at <math>{\bf x}^j</math>. | |
| − | where, | + | |
Because the Newton-Raphson’s method demands the initial value of the state vector to be very close to the accurate value of the fixed point, it’s difficult to give the initial value. If the initial value is selected improperly, the algorithm will diverge soon. | Because the Newton-Raphson’s method demands the initial value of the state vector to be very close to the accurate value of the fixed point, it’s difficult to give the initial value. If the initial value is selected improperly, the algorithm will diverge soon. | ||
| Line 266: | Line 247: | ||
| − | Then the problem becomes an unconstrained optimization problem. We can use the quasi-Newton method to find the minimum value of Eq.<span id='cite-_Ref511318234'></span>[[#_Ref511318234|(11)]]. If the minimum value of <math>f(x)</math> is zero, the point | + | Then the problem becomes an unconstrained optimization problem. We can use the quasi-Newton method to find the minimum value of Eq.<span id='cite-_Ref511318234'></span>[[#_Ref511318234|(11)]]. If the minimum value of <math>f(x)</math> is zero, the point <math>{\bf x}</math> is considered as the fixed point. In reality, due to calculation error, the point is considered as the fixed point if <math>f(x)<{10}^{-6}</math>. |
| − | In this paper, quasi Newton method is used to solve the minimum problem | + | In this paper, quasi Newton method is used to solve the minimum problem |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 280: | Line 261: | ||
|} | |} | ||
| + | where <math>\boldsymbol{s}_k=x_{k+1}\mbox{-}x_k</math>, <math>H_k=B_k^{-1}</math>, <math>y_k=\nabla f\left(x_{k+1}\right)\mbox{-}\nabla f\left(x_k\right)</math>, <math>H_{k+1}=H_k-\frac{H_ky_ky_k^TH_k}{y_k^TH_ky_k}+\frac{s_ks_k^T}{y_k^Ts_k}</math>. | ||
| − | + | ==4. The effect of the center of mass of the leg and the body== | |
| − | + | Using the proposed algorithm, passive hopping gaits are found. According to the Hyon [14], all passive running gaits of the ARL monopod robot were unstable except for a vertical hopping. The obtained gaits of our hopping robot are also quasi-period ones, not stable limit cycle. The distance between the COM of the leg and the toe is <math>\alpha l</math>, and the distance between the COM of the body and the hip joint is <math>\beta l_b</math>. The location of the COM of the leg and the body is depend on <math>\alpha</math> and <math>\beta</math>, respectively, we examine the influence of <math>\alpha</math> and <math>\beta</math> on the jumping performance of the robot. | |
| − | + | ===4.1 The effect of the center of mass of the leg=== | |
| − | == | + | Firstly the effect of α is examined when the COM of the body is coincide with hip joint (<math>\beta</math> is zero). The base parameters given in <span id='cite-_Ref511379307'></span>[[#tab-1|Table 1]]. The results are shown in <span id='cite-_Ref511379460'></span>[[#_Ref511379460|Figure 2]]. The location of the COM of the leg is displaced along the leg from the toe to the hip joint, which means that the value of <math>\alpha</math> is between 0 and 1. When <math>\alpha =0</math>, the center of the leg is located in the toe and the model is similar to a two-mass model; when <math>\alpha =1</math>, the center lies in the hip joint and the model is the ARL monopod. In <span id='cite-_Ref511379460'></span>[[#_Ref511379460|Figure 2]] it can be seen that when α increases, the apex height of the COM of the robot and the compression of the leg spring decreases, while the step length increases. The step length reached at the maximum value when <math>\alpha =0.7</math>. The following conclusions can be drawn. If the robot is wanted to have a long jump, the COM of the leg should be close to the hip joint. If the robot is wanted to have a high jump, it should be far away from the hip joint and at the same time the robot should provide greater power by increasing the compression of the spring. |
| − | + | <div id='_Ref511379460'></div> | |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_1330_fig2.png|250px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 2'''. The step length , the apex height and the minimum value of the leg length during stance phase | ||
| + | |} | ||
| − | |||
| − | [[ | + | In [[#img-3|Figure 3]] with the increase of α, the angle of the center of mass at the take-off time (take-off angle) decreases, the horizontal velocity of the center of mass increases, and the vertical velocity decreases. With <math>\alpha =0.9</math> these velocities are approximately equal. The decrease of vertical velocity means the decrease of flight time, but the step size of the robot increases with the increase of horizontal velocity. Due to the dual influence of flight time and horizontal velocity, the robot <math>\alpha =0.7</math>. The maximum step size is reached at 0.7. |
| − | <div class=" | + | <div id='img-3'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_8608_fig3.png|250px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 3'''. The horizontal and vertial velocity of the COM at takeoff | ||
| + | |} | ||
| − | |||
| − | + | During the change of leg centroid, the stance time changed very little and remained around 0.2s ([[#img-4|Figure 4]]). However, as the COM of the leg gets closer to the toe, the total jump time increases and the duty cycle decreases, which means that the time spent by the robot in the take-off phase increases and the gait frequency decreases. Before the next jump, the swing of the leg is controlled more easily. | |
| − | [[File: | + | <div id='img-4'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_7950_fig4.png|250px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 4'''. Bounce period, stance time v.s. <math>\alpha</math> | ||
| + | |} | ||
| − | |||
| − | |||
| − | + | In [[#img-5|Figures 5]] and [[#img-6|6]], it can be seen that with the increase of α, the center of mass of the leg is closer to the hip joint, and the body angle amplitude decreases, but the leg angle amplitude increases. The closer the center of mass of the leg is to the hip joint, the closer the leg swing curve is to the sine curve. When the center of mass of the body is located at the hip joint, the leg swing curve is a sine curve. | |
| − | <div class=" | + | <div id='img-5'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_6031_fig5.png|250px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 5'''. Trajectory of the leg | ||
| + | |} | ||
| − | |||
| − | <div class=" | + | <div id='img-6'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_7763_fig6.png|250px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 6'''. Trajectory of the body | ||
| + | |} | ||
| − | + | ===4.2 The effect of the center of mass of the body=== | |
| − | < | + | Then we investigate the effect of the COM of the body on the hopping performance, it can be expressed by <math display="inline">\beta</math>. The periodic gait of the hopping robot without active control is in [[#img-7|Figure 7]] when the COM of the body doesn’t locate in the hip joint. It shows that there was little change in the angle of the leg and the body, the motion of the robot is a vertical hopping and the robot doesn’t leave the ground, so it is necessary to control the robot in order to get a forward hopping. The control scheme is using the hip actuator to control the pitch angle to track the desired trajectory during the stance phase. A PD (Proportional-Derivative) controller is used to track the desired pitch trajectory [24-26]. |
| − | [[File: | + | <div id='img-7'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_4570_fig7.png|700px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 7'''. Periodic passive hopping gait without active control | ||
| + | |} | ||
| − | |||
| − | |||
| − | < | + | Using the pitch angle of passive hopping of ARL robot as the desired trajectory and computing the limit cycle with the optimization method, the passive gait of the asymmetrical hopping robot is obtained. <span id='cite-_Ref511381050'></span>[[#_Ref511381050|Figures 8]] and [[#img-9|9]] are the posture and the limit cycle during one hoping cycle. It is can be seen that with active control, a satisfactory periodic motion is obtained when the robot has an asymmetric body mass. It can be seen that the toes of the robot collided with the ground in the flight phase. In order to prevent the toes of the robot from contacting the ground in the flight stage, the jumping height of the robot should be increased. |
| − | [[File: | + | <div id='_Ref511381050'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_9300_fig8.png|600px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 8'''. Active periodic gait of the hopping robot when <math display="inline">\alpha =0.7</math>, <math display="inline">\beta =0.13</math> | ||
| + | |} | ||
| − | |||
| − | |||
| − | ==== | + | <div id='img-9'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_3557_fig9.png|300px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 9'''. Limit cycle of the hopping robot | ||
| + | |} | ||
| − | |||
| − | < | + | Although in theory <math display="inline">\beta</math> can be taken in [0,1], <math display="inline">\beta</math> is less than 1 for the following two reasons. The first reason is that it is unable to find fixed point. The second reason is that the minimum length of the leg length at the landing stage is 0, which means that the compression of the spring reaches 100%. In fact, due to the structure of the spring itself, the compression cannot be pressed to the bottom. The above two cases can be increased by improving the control method and increasing the spring stiffness to increase the range of <math display="inline">\beta</math>. As can be seen from [[#img-10|Figure 10]], with the increase of <math display="inline">\alpha</math>, the maximum allowed value of <math display="inline">\beta</math> is small. It shows that the closer the robot leg is to the hip joint, the smaller the allowable eccentricity of the body. |
| − | [[ | + | |
| − | <div id= | + | <div id='img-10'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_4471_fig10.png|250px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 10'''. The maximum allowable value of <math display="inline">\beta</math> v.s. <math display="inline">\alpha</math> | ||
| + | |} | ||
| − | |||
| − | [[ | + | [[#img-11|Figure 11]] shows that with the increase of <math display="inline">\beta</math>, the angle of the center of mass at the take-off decreases, the vertical velocity remains almost unchanged, while the horizontal velocity increases rapidly, and the step size of the robot becomes larger. The farther the body centroid is from the hip joint, the better. Because the change of bounce cycle time is very small, most of the energy provided by the leg spring is transformed into forward movement. However, due to the low centroid height of the robot at the take-off, the maximum height in the flight phase is also low, and the robot toe is easy to collide with the ground. So <math display="inline">\beta</math> cannot be too large. |
| − | <div id= | + | <div id='img-11'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_3775_fig11.png|250px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 11'''. The horizontal and vertical velocity of the center of mass at take-off | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | < | + | As can be seen from [[#img-12|Figure 12]], with the increase of <math display="inline">\beta</math>, the minimum length of the leg in the landing stage decreases rapidly, and the compression amount of the spring changes from 38% to 69%, indicating that the farther the center of mass of the body is from the hip joint, the greater the force required to be provided by the leg spring. It should be considered to increase the stiffness of the spring. |
| − | < | + | |
| − | + | <div id='img-11'></div> | |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_6465_fig12.png|250px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 12'''. Minimum length of legs in landing phase with different of <math display="inline">\beta</math> | ||
| + | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | [[#img-13|Figure 13]] shows that with the increase of <math display="inline">\beta</math>, the center of mass of the body deviates more and more from the hip joint, and the rotation amplitude of the body and legs increases. The closer the body centroid is to the hip joint, the closer the leg swing curve is to the sinusoidal curve. The angle of the body and leg increases at the take-off, correspondingly the take-off angle of the body centroid decreases. Body eccentricity provides a larger take-off range for robot motion. | ||
| + | <div id='img-13'></div> | ||
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | ||
| + | |-style="background:white;" | ||
| + | |align="center" | | ||
{| | {| | ||
| + | |+ | ||
| + | |- | ||
| + | | style="text-align: center;padding:10px;"| [[Image:Review_801861383672-image65.png|258px]] | ||
| + | | style="text-align: center;padding:10px;"| [[Image:Review_801861383672-image66.png|center|276px]] | ||
|- | |- | ||
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(a) |
| − | | | + | |style="text-align: center;font-size: 75%;padding-bottom:10px;"|(b) |
| + | |} | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 13'''. Leg angle and the body angle vs. time | ||
|} | |} | ||
| − | + | [[#img-14|Figure 14]] shows that the greater the body eccentricity, the greater the driving torque required by the robot to drive the body pitching motion in the landing phase, because the swing range of the body in the landing phase also becomes larger. | |
| − | <div class=" | + | <div id='img-14'></div> |
| − | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;width:auto;" | |
| + | |-style="background:white;" | ||
| + | |style="text-align: center;padding:10px;"| [[File:Review_801861383672_2649_fig14.png|250px]] | ||
| + | |- | ||
| + | | style="background:#efefef;text-align:left;padding:10px;font-size: 85%;"| '''Figure 14'''. Influence of body eccentricity ratio on driving torque | ||
| + | |} | ||
| − | + | ==5. Conclusion== | |
| − | + | The period orbit problem of an asymmetric spring loaded inverted pendulum is addressed. The dynamic equations of the two link robot are established. Then the Poincare mapping method is used to turn the solution of the periodic motion of the hopping robot into the solution of the fixed point, and then the optimization method is used to obtain the fixed point of the hip robot. With a PD controller, a period orbit can be obtained. Through investigating the effect of the location of the leg mass and the body mass on the hopping performance, if the robot is wanted to jump longer, the center of mass of the leg and the body should be far away from the hip joint. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ==References== | |
| − | + | ||
| − | + | ||
| − | = | + | |
| − | + | ||
| − | + | ||
| − | == | + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> |
| − | + | [[#cite-_Ref12350684|[1]]] Raibert M.H. Legged robots that balance. The MIT Press, Cambridge, pp. 233, 1986. | |
| − | + | [[#cite-_Ref85575208|[2]]] Zeglin G. The bow leg hopping robot. Carnegie Mellon University, pp. 161, 1999. | |
| − | + | [[#cite-_nebBDB59058_F776_465E_B5AC_AC541DEFCC1F|[3]]] Ahmadi M., Buehler M. A control strategy for stable passive running. Proc. IEEE Conf. Intelligent Robots and Systems, 3:152-157, Pittsburgh, PA, 1995. | |
| − | + | [[#cite-_nebFD2E02D8_1E40_4008_8B88_D2915396DF2B|[4]]] Ahmadi M., Buehler M. Stable control of a simulated one-legged running robot with hip and leg compliance. IEEE Transactions on Robots and Automation, 13(1):96-104, 1997. | |
| − | + | [5] Zeglin G.J. Uniroo-a one legged dynamic hopping robot. Massachusetts Institute of Technology, Thesis, 1991. | |
| − | [5] | + | |
| − | + | [[#cite-_Ref85575246|[6]]] Recovering, storing and releasing energy based on a natural model. 2014. [http://www.festo.com/cms/en_corp/13704.htm http://www.festo.com/cms/en_corp/13704.htm] | |
| − | + | [[#cite-_Ref85575554|[7]]] Hutter M., Remy C.D., Hoepflinger M.A., Siegwart R. ScarlETH: Design and control of a planar running robot. IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, pp. 562-567, 2011. | |
| − | + | [[#cite-_Ref85573788|[8]]] Blickhan B. The spring-mass model for running and hopping. J.Biomechanics, 22(11-12):1217-1227, 1989. | |
| − | + | [[#cite-_Ref85571161|[9]]] Cherouvim N., Papadopoulos E. Single actuator control analysis of a planar 3DOF hopping robot. Robotics: Science and Systems I, Massachusetts Institute of Technology, Cambridge, Massachusetts, June 8-11, 2005. | |
| − | + | [[#cite-_nebF72182DD_0142_4EDA_B461_376335BF0C09|[10]]] Papadopoulos E., Cherouvim N. On increasing energy autonomy for a one-legged hopping robot. Proceedings of the 2004 IEEE International Conference on Robotics and Automation, pp. 4645-4650, 2004. | |
| − | + | [11] François C., Samson C. A new approach to the control of the planar one-legged hopper. International Journal of Robotics Research, 17(11):1150-1166, 1998. | |
| − | [11] | + | |
| − | + | [12] Thompson C.M., Raibert M.H. Passive dynamic running. The First International Symposium on Experimental Robotics I, pp. 74-83, 1989. | |
| − | [12] | + | |
| − | + | [[#cite-_neb2B61CDB5_6B04_4FED_8F96_C3854775F3E0|[13]]] Schammass A., Caurin G.A.P., Valente C.M.O. Control of a one-legged robot with energy savings. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 23(1):41-48, 2001. | |
| − | + | [[#cite-_neb52EE5DEE_BAB6_4DAC_A20D_6AC27787712F|[14]]] Hyon S., Emura T. Quasi-periodic gaits of passive one-legged hopper. IEEE/RSJ International Conference on Intelligent Robots and Systems, 3:2625-2630, Lausanne, Switzerland, 2002. | |
| − | + | [[#cite-_neb7640F6CD_0F2B_4E48_B930_2867006FF860|[15]]] Hyon S., Emura T. Energy-preserving control of a passive one-legged running robot. Advanced Robotics, 18(4):357-381, 2004. | |
| − | + | [[#cite-_Ref12353154|[16]]] Hyon S., Emura T., Ueta T. Delayed feedback control of one-legged passive running robot. Sice 2004 Annual Conference, pp. 949-954, Sapporo, Japan, 2004. | |
| − | + | [[#cite-_nebEDF936BE_0B8E_45AC_99C2_65ECDA8F4FB6|[17]]] Lei B., Wang P., Zha F., Li M., Guo W. Stability analysis of quasi-periodic hopping of a passive one-legged robot with compliant hip joint. IEEE International Conference on Mechatronics and Automation, pp. 623-628, Tianjin, China, 2014. | |
| − | + | [[#cite-_nebE5FC569D_7EF3_45E1_A38F_45D02981FAD7|[18]]] Wei T.E., Nelson G.M., Quinn R.D., Verma H., Garverick S.L. Design of a 5-cm Monopod Hopping Robot. Proceedings 2000 ICRA, Millennium Conference, IEEE International Conference on Robotics and Automation, 3:2828-2833, San Francisco, CA, USA, 2000. | |
| − | + | [[#cite-_neb4A4A8CC9_A46A_4BCF_BC9D_670B4C03FF5A|[19]]] Kuswadi S., Ohnishi A., Takahashi A., Sampei M., Nakaura S. A one linear actuator hopping robot:modeling and control. Advanced Robotics, 17(8):709-737, 2003. | |
| − | + | [[#cite-_neb8F66AAB4_7662_4F92_98D1_63D73F7A88B8|[20]]] Sayyad A., Seth B., Issac K.K. Dynamics and control of a one-legged 2-D SLOM popping robot. 12th IFToMM World Congress, Besançon, 2007. | |
| − | + | [[#cite-_nebE783E321_38AC_4A39_936A_93AB94B9C761|[21]]] Seth B., Seshu S., Shanmuganathan P.V., Vichare V.V., Raj P. Search for initial conditions for sustained hopping of passive springy-leg offset-mass hopping robot. Journal of Dynamic Systems, Measurement, and Control, 129(4):522-526, 2007. | |
| − | + | [[#cite-_Ref17710425|[22]]] Poulakakis I., Grizzle J.W. The spring loaded inverted pendulum as the hybrid zero dynamics of an asymmetric hopper. IEEE Transactions on Automatic Control, 54(8):1779-1793, 2009. | |
| − | + | [23] Poulakakis I. Spring loaded inverted pendulum embedding: Extensions toward the control of compliant running robots. 2010 IEEE International Conference on Robotics and Automation (ICRA), pp. 1050-4729, Anchorage, Alaska, USA, 2010. | |
| − | [23] | + | |
| − | + | [24] Terry P., Piovan G., Byl K. Towards precise control of hoppers: Using high order partial feedback linearization to control the hopping robot FRANK. IEEE 55th Conference on Decision and Control (CDC), pp. 6669-6675, Las Vegas, USA, 2016. | |
| − | [24] | + | |
| − | + | [25] Zou H., Schmiedeler J.P. The effect of asymmetrical body-mass distribution on the stability and dynamics of quadruped bounding. IEEE Transactions on Robotics, 22(4):711-723, 2006. | |
| − | [25] | + | |
| − | + | [26] Nie H., Sun R., Hu L., Su Z., Hu W. Control of a cheetah robot in passive bounding gait. Journal of Bionic Engineering, 13(2):283-291, 2016. | |
| − | [26]. | + | |
Latest revision as of 12:18, 19 January 2023
Abstract
For improving the energy efficiency of hopping robot, an asymmetric spring loaded inverted pendulum hopping model with leg mass is considered. The period orbit problem of two-legged hopping robot is investigated. Firstly, the hybrid dynamic model is constructed. Then the passive hopping gaits are found using quasi-newton optimization method. Secondly, a PD controller is implemented to track the desired pitch trajectory of the body. Through applying control during stance phase, period orbits of the robot with offset body mass is obtained. Finally, the effect of the location of the leg mass and the body mass on hopping performances is investigated.
Keywords: Hopping robot, asymmetric, passive dynamics, periodic motion, energy efficiency
1. Introduction
Hopping robots use isolated footholds, so it can negotiate uneven terrain. Due to these advantages, it has been studied by many researchers in recent years. Raibert and his coworkers had developed one-legged and two-legged hopping robots [1] based on a spring-loaded inverted pendulum (SLIP) model. These robots had a massless telescopic leg and a point foot. They use a three-part algorithm to control the robot. Since then, many jumping robots such as robots with spring leg [2-5] and robots with multi-joint leg [6-8] are constructed.
The SLIP model is the simplest mathematical model for hopping robot and it captured the basic dynamicbehaviors of the running of many animals [9]. The control of the SLIP model is very simple because it doesn’t consider the dynamic coupling between the body and the legs. The control strategy based on SLIP model is necessary to be modified in order to successful apply in the control of the real robots [10], so it is necessary to construct a more realistic model similar to the real hopping robots.
In the hopping control, the energy consumption is especially crucial because it directly affects the size of the actuator and in return influences the weight of the robots. So, it is necessary to achieve the hopping gait with minimal power consumption. In this field, there are some remarkable researches on passive hopping. It has been found that using the proper initial conditions, the hopping robots can excuates periodic motion without input torque [11-12]. Papadopoulos and Cherouvim proved that the passive gait is the least energy-consuming gait [2]. Ahmadi and Buehler used hip and leg compliance to realize passive motion [3-4]. Schammass et al exploited the passive dynamics of the system to reduce the energy consumption [13]. The simulation results shown that the robot including hip compliance reduced approximately 67% of the total energy compared to the robot without hip compliance. Hyon et al used a new gait-searching algorithm to find the passive orbit and proposed two kinds of controllers to realize orbital stabilization [14-16].
All of these hopping robots have symmetric configuration with the center of mass (COM) along the geometrical axis of a telescopic leg. In reality, the COM of most animals offsets the hip joint and the weight of the leg can’t be ignored. The offset body-mass offers greater flexibility in the design of hopping robot because the actuator can be placed within the body freely. The asymmetrical body mass configurations have been considered by several scholars [17-23]. Kuswadi et al. proposed an asymmetric model of a single-legged robot and realized a sustained hopping motion. The center of gravity of the model isn’t on the line of action of the actuator [19]. Sayyad et al analyzed a springy-legged offset-mass (SLOM) configuration and proposed an energy compensated model to explore the possibility of a periodic motion [20]. But all these paper doesn’t consider the rotation of the body. Poulakakis et al used a SLIP-embedding control law to control an asymmetric spring loaded inverted pendulum (ASLIP) hopping model, but the leg is assumed to be massless [22-23].
In this paper, an asymmetric spring loaded inverted pendulum hopping model (ASLIP) is proposed, where the leg mass is considered and the center of mass of the body is not located in the hip joint. The goal is to study of the effect of the offset mass of the body and the mass of the leg on the robot’s hopping performance.
This paper is organized as follows. In Section 2, the dynamic model is presented along with its mechanical properties and motion equations. In Section 3, the Poincare mapping is used to analyze the passive periodic hopping motion of the hopping robot and the fix point is obtained using optimization, and the effects of the offset mass and the leg mass on the hopping motion are presented in Section 4.
2. Dynamical model
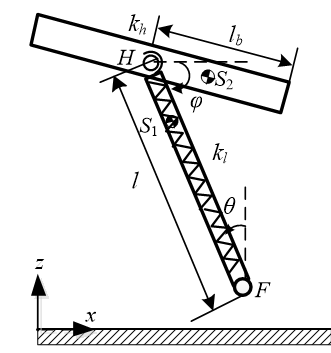
Figure 1 is the simplified model of the ASLIP hopping robot. The hopping robot consists of two parts, a body and a springy telescope leg. The body and the leg is connected by a torsional spring on the hip joint . In the model, the hip joint doesn’t coincide with the center of mass of the body. The mass of the leg is also taken into account. A coupling between the leg swing motion and the body rotation is introduced, which made the analysis of the dynamics of the robot more complicated. Supposing the position of the center of mass of the leg and the position of the center of mass of the body are given by and , where . The variable denotes the length of the leg, represents the leg angle with respect to the vertical axis indicates the body angle with respect to the horizontal axis. Other physical parameters and its values are listed in Table 1.
|
| Figure 1. Model of robot |
The hopping motion of the robot is composed of two phases: stance phase and flight phase. The switch from the stance phase to the flight phase is called lift-off, triggered by . The switch from the flight phase to the stance phase is called touchdown, triggered by . We use the event-based subscript to describe the motion during different phases. The subscript represents the stance phase, represents the flight phase, is the moment at touchdown and is the moment at lift off.
| Notation | Units | Value |
|---|---|---|
| body mass | kg | 9 |
| leg mass | kg | 3 |
| body length | m | 0.22 |
| body inertia | kg.m2 | 0.5 |
| leg inertia | kg.m2 | 0.11 |
| leg spring stiffness | N/m | 3000 |
| hip spring stiffness | Nm/rad | 10 |
| natural leg length | m | 0.5 |
| gravity acceleration | m/s2 | 9.81 |
During the stance phase the leg is in contact with ground at a toe point (end of the leg). Supposing that the robot does not bounce back nor slip relative to the ground, the leg rotates around the toe. Then the toe can be modeled as a pivot. We choose polar coordinates , as the generalized coordinates. Using the Lagrange method [22], the equations of motion is obtained as:
|
|
(1) |
where is the symmetric positive definite inertia matrix during the stance phase, which deponds on the generalized coordinates ; is the matrix containing centrifugal force and Coriolis force during the stance phase, which is a function of and ; is the gravity vector during the stance phase, which is a function of ; is the equivalent driving torque vector of torsion spring during the stance phase, which is related to ; ; is the driving force to the leg, while denotes the hip torque during the stance phase.
During the flight phase the leg loses contact with the ground. The COM of the robot moves along the ballistic trajectory and the angular momentum of the robot about the COM is conserved. The length of the leg is assumed to keep constant. We select Cartesian coordinates as the generalized coordinates, is the position of the hip joint. The dynamics is given by:
|
|
(2) |
where is the symmetric positive definite inertia matrix during the flight phase, which deponds on the generalized coordinates ; is the matrix containing centrifugal force and Coriolis force during the flight phase, which is a function of and ; is the gravity vector during the flight phase, which is a function of ; is the equivalent driving torque vector of torsion spring during the flight phase, which is related to ; ; is the hip torque during the flight phase.
At touchdown, the leg touches down the ground and inelastic impulse occurs. The generalized displacements keep constant, but the generalized velocities change instantaneously
|
|
(3) |
where the subscript and represent the moment before and after touchdown respectively.
At lift-off, there are no discontinuous changes of states except for:
|
|
(4) |
It can be seen that during the landing phase, the leg compresses and releases the spring to realize the energy conversion from the above equations. Since the loss caused by friction is not considered, the mechanical energy is conserved. In the flight phase, the mechanical energy of the system is also conserved. At touchdown, the robot legs collide with the ground, which will lead to energy loss. In order to simplify the analysis, the energy loss at touchdown is not considered in this paper. The robot is a complex switching system with multi variables, strong coupling and nonlinearity, so it is impossible to obtain the analytical solution of the trajectory of the system, and can only be solved by numerical calculation.
3. Passive hopping motion
To improve the energy efficiency, firstly we consider the completely passive hopping which means that there is no driving force applied on the robot. A very useful and common method to study the existence and stability of periodic motions is the Poincare map. According to the trajectory of the state variables in the Poincare section, we can find the periodic motion. Through Poincare map, we can transform the existence of the periodic orbits of the hopping robot to the fixed point in the Poincare section.
The robot has 4 DOF during flight and 3 DOF during stance. For reducing the number of the independent variables, we choose the moment just after touchdown as the Poincare section and state vector is defined as . For at touchdown, the number of the independent variables reduces to 5. In the process of iteration, let the state vector in the step is , we can get the state vector in the step after one mapping. This process can be described as a Poincare map .
For a certain state vector , the point is called a fixed point if it maps itself through one map,
|
|
(5) |
Then we build the Poincare map of the hopping robot. The dynamic Eqs. (1) and (2) are rewritten into a standard state-space form.
|
|
(6) |
|
|
(7) |
where is the state vector during the stance phase and during the flight phase. Because the number of the state variables between the stance phase and the flight phase is different, we need to construct two mapping between the transitions of these two phases. The mapping is represented by the following equations
|
|
(8) |
|
|
(9) |
Combining these four sub-maps, then the whole Poincare mapping is .
Since the Poincare map of the hopping robot have been constructed, now we consider the method of finding the fixed point. The Newton-Raphson’s method [15] is commonly used to find the fixed point
|
|
(10) |
where, is the identity matrix, is the jacobian matrix of the Poincare map at .
Because the Newton-Raphson’s method demands the initial value of the state vector to be very close to the accurate value of the fixed point, it’s difficult to give the initial value. If the initial value is selected improperly, the algorithm will diverge soon.
In this paper we used the optimization algorithm to solve the nonlinear equations. Firstly we transformed the problem into a minimum value problem. Eq. (5) can be rewritten as
|
|
(11) |
Then the problem becomes an unconstrained optimization problem. We can use the quasi-Newton method to find the minimum value of Eq.(11). If the minimum value of is zero, the point is considered as the fixed point. In reality, due to calculation error, the point is considered as the fixed point if .
In this paper, quasi Newton method is used to solve the minimum problem
|
|
(12) |
where , , , .
4. The effect of the center of mass of the leg and the body
Using the proposed algorithm, passive hopping gaits are found. According to the Hyon [14], all passive running gaits of the ARL monopod robot were unstable except for a vertical hopping. The obtained gaits of our hopping robot are also quasi-period ones, not stable limit cycle. The distance between the COM of the leg and the toe is , and the distance between the COM of the body and the hip joint is . The location of the COM of the leg and the body is depend on and , respectively, we examine the influence of and on the jumping performance of the robot.
4.1 The effect of the center of mass of the leg
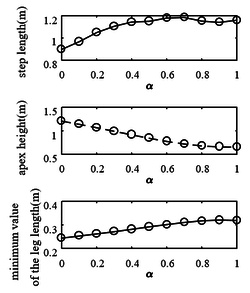
Firstly the effect of α is examined when the COM of the body is coincide with hip joint ( is zero). The base parameters given in Table 1. The results are shown in Figure 2. The location of the COM of the leg is displaced along the leg from the toe to the hip joint, which means that the value of is between 0 and 1. When , the center of the leg is located in the toe and the model is similar to a two-mass model; when , the center lies in the hip joint and the model is the ARL monopod. In Figure 2 it can be seen that when α increases, the apex height of the COM of the robot and the compression of the leg spring decreases, while the step length increases. The step length reached at the maximum value when . The following conclusions can be drawn. If the robot is wanted to have a long jump, the COM of the leg should be close to the hip joint. If the robot is wanted to have a high jump, it should be far away from the hip joint and at the same time the robot should provide greater power by increasing the compression of the spring.
|
| Figure 2. The step length , the apex height and the minimum value of the leg length during stance phase |
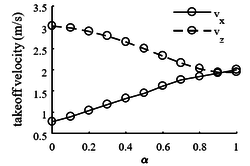
In Figure 3 with the increase of α, the angle of the center of mass at the take-off time (take-off angle) decreases, the horizontal velocity of the center of mass increases, and the vertical velocity decreases. With these velocities are approximately equal. The decrease of vertical velocity means the decrease of flight time, but the step size of the robot increases with the increase of horizontal velocity. Due to the dual influence of flight time and horizontal velocity, the robot . The maximum step size is reached at 0.7.
|
| Figure 3. The horizontal and vertial velocity of the COM at takeoff |
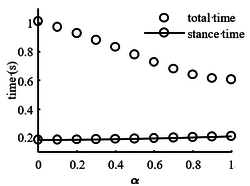
During the change of leg centroid, the stance time changed very little and remained around 0.2s (Figure 4). However, as the COM of the leg gets closer to the toe, the total jump time increases and the duty cycle decreases, which means that the time spent by the robot in the take-off phase increases and the gait frequency decreases. Before the next jump, the swing of the leg is controlled more easily.
|
| Figure 4. Bounce period, stance time v.s. |
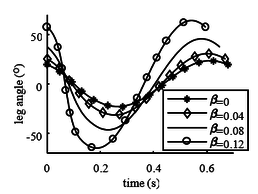
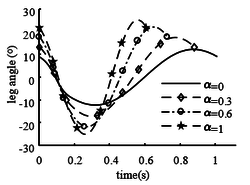
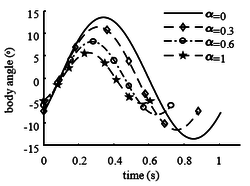
In Figures 5 and 6, it can be seen that with the increase of α, the center of mass of the leg is closer to the hip joint, and the body angle amplitude decreases, but the leg angle amplitude increases. The closer the center of mass of the leg is to the hip joint, the closer the leg swing curve is to the sine curve. When the center of mass of the body is located at the hip joint, the leg swing curve is a sine curve.
|
| Figure 5. Trajectory of the leg |
|
| Figure 6. Trajectory of the body |
4.2 The effect of the center of mass of the body
Then we investigate the effect of the COM of the body on the hopping performance, it can be expressed by . The periodic gait of the hopping robot without active control is in Figure 7 when the COM of the body doesn’t locate in the hip joint. It shows that there was little change in the angle of the leg and the body, the motion of the robot is a vertical hopping and the robot doesn’t leave the ground, so it is necessary to control the robot in order to get a forward hopping. The control scheme is using the hip actuator to control the pitch angle to track the desired trajectory during the stance phase. A PD (Proportional-Derivative) controller is used to track the desired pitch trajectory [24-26].
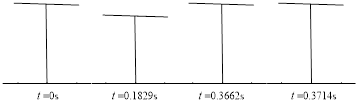
|
| Figure 7. Periodic passive hopping gait without active control |
Using the pitch angle of passive hopping of ARL robot as the desired trajectory and computing the limit cycle with the optimization method, the passive gait of the asymmetrical hopping robot is obtained. Figures 8 and 9 are the posture and the limit cycle during one hoping cycle. It is can be seen that with active control, a satisfactory periodic motion is obtained when the robot has an asymmetric body mass. It can be seen that the toes of the robot collided with the ground in the flight phase. In order to prevent the toes of the robot from contacting the ground in the flight stage, the jumping height of the robot should be increased.
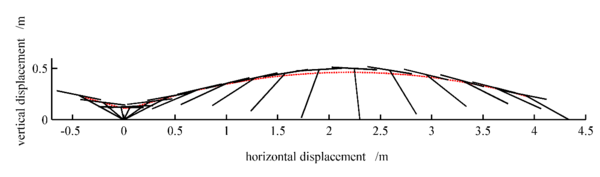
|
| Figure 8. Active periodic gait of the hopping robot when , |
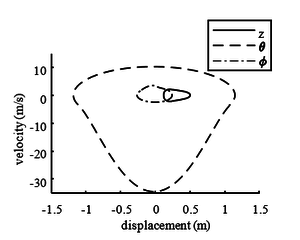
|
| Figure 9. Limit cycle of the hopping robot |
Although in theory can be taken in [0,1], is less than 1 for the following two reasons. The first reason is that it is unable to find fixed point. The second reason is that the minimum length of the leg length at the landing stage is 0, which means that the compression of the spring reaches 100%. In fact, due to the structure of the spring itself, the compression cannot be pressed to the bottom. The above two cases can be increased by improving the control method and increasing the spring stiffness to increase the range of . As can be seen from Figure 10, with the increase of , the maximum allowed value of is small. It shows that the closer the robot leg is to the hip joint, the smaller the allowable eccentricity of the body.
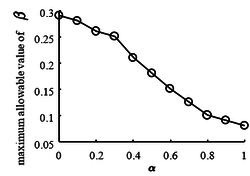
|
| Figure 10. The maximum allowable value of v.s. |
Figure 11 shows that with the increase of , the angle of the center of mass at the take-off decreases, the vertical velocity remains almost unchanged, while the horizontal velocity increases rapidly, and the step size of the robot becomes larger. The farther the body centroid is from the hip joint, the better. Because the change of bounce cycle time is very small, most of the energy provided by the leg spring is transformed into forward movement. However, due to the low centroid height of the robot at the take-off, the maximum height in the flight phase is also low, and the robot toe is easy to collide with the ground. So cannot be too large.
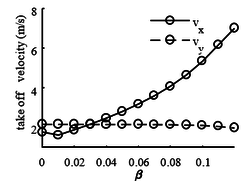
|
| Figure 11. The horizontal and vertical velocity of the center of mass at take-off |
As can be seen from Figure 12, with the increase of , the minimum length of the leg in the landing stage decreases rapidly, and the compression amount of the spring changes from 38% to 69%, indicating that the farther the center of mass of the body is from the hip joint, the greater the force required to be provided by the leg spring. It should be considered to increase the stiffness of the spring.
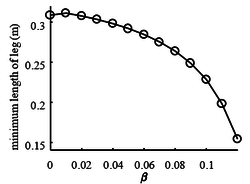
|
| Figure 12. Minimum length of legs in landing phase with different of |
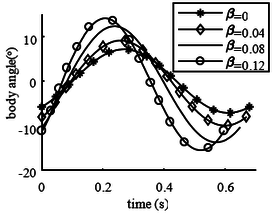
Figure 13 shows that with the increase of , the center of mass of the body deviates more and more from the hip joint, and the rotation amplitude of the body and legs increases. The closer the body centroid is to the hip joint, the closer the leg swing curve is to the sinusoidal curve. The angle of the body and leg increases at the take-off, correspondingly the take-off angle of the body centroid decreases. Body eccentricity provides a larger take-off range for robot motion.
| ||||
| Figure 13. Leg angle and the body angle vs. time |
Figure 14 shows that the greater the body eccentricity, the greater the driving torque required by the robot to drive the body pitching motion in the landing phase, because the swing range of the body in the landing phase also becomes larger.
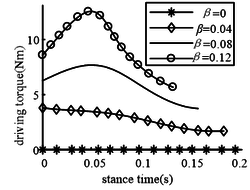
|
| Figure 14. Influence of body eccentricity ratio on driving torque |
5. Conclusion
The period orbit problem of an asymmetric spring loaded inverted pendulum is addressed. The dynamic equations of the two link robot are established. Then the Poincare mapping method is used to turn the solution of the periodic motion of the hopping robot into the solution of the fixed point, and then the optimization method is used to obtain the fixed point of the hip robot. With a PD controller, a period orbit can be obtained. Through investigating the effect of the location of the leg mass and the body mass on the hopping performance, if the robot is wanted to jump longer, the center of mass of the leg and the body should be far away from the hip joint.
References
[1] Raibert M.H. Legged robots that balance. The MIT Press, Cambridge, pp. 233, 1986.
[2] Zeglin G. The bow leg hopping robot. Carnegie Mellon University, pp. 161, 1999.
[3] Ahmadi M., Buehler M. A control strategy for stable passive running. Proc. IEEE Conf. Intelligent Robots and Systems, 3:152-157, Pittsburgh, PA, 1995.
[4] Ahmadi M., Buehler M. Stable control of a simulated one-legged running robot with hip and leg compliance. IEEE Transactions on Robots and Automation, 13(1):96-104, 1997.
[5] Zeglin G.J. Uniroo-a one legged dynamic hopping robot. Massachusetts Institute of Technology, Thesis, 1991.
[6] Recovering, storing and releasing energy based on a natural model. 2014. http://www.festo.com/cms/en_corp/13704.htm
[7] Hutter M., Remy C.D., Hoepflinger M.A., Siegwart R. ScarlETH: Design and control of a planar running robot. IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, CA, USA, pp. 562-567, 2011.
[8] Blickhan B. The spring-mass model for running and hopping. J.Biomechanics, 22(11-12):1217-1227, 1989.
[9] Cherouvim N., Papadopoulos E. Single actuator control analysis of a planar 3DOF hopping robot. Robotics: Science and Systems I, Massachusetts Institute of Technology, Cambridge, Massachusetts, June 8-11, 2005.
[10] Papadopoulos E., Cherouvim N. On increasing energy autonomy for a one-legged hopping robot. Proceedings of the 2004 IEEE International Conference on Robotics and Automation, pp. 4645-4650, 2004.
[11] François C., Samson C. A new approach to the control of the planar one-legged hopper. International Journal of Robotics Research, 17(11):1150-1166, 1998.
[12] Thompson C.M., Raibert M.H. Passive dynamic running. The First International Symposium on Experimental Robotics I, pp. 74-83, 1989.
[13] Schammass A., Caurin G.A.P., Valente C.M.O. Control of a one-legged robot with energy savings. Journal of the Brazilian Society of Mechanical Sciences & Engineering, 23(1):41-48, 2001.
[14] Hyon S., Emura T. Quasi-periodic gaits of passive one-legged hopper. IEEE/RSJ International Conference on Intelligent Robots and Systems, 3:2625-2630, Lausanne, Switzerland, 2002.
[15] Hyon S., Emura T. Energy-preserving control of a passive one-legged running robot. Advanced Robotics, 18(4):357-381, 2004.
[16] Hyon S., Emura T., Ueta T. Delayed feedback control of one-legged passive running robot. Sice 2004 Annual Conference, pp. 949-954, Sapporo, Japan, 2004.
[17] Lei B., Wang P., Zha F., Li M., Guo W. Stability analysis of quasi-periodic hopping of a passive one-legged robot with compliant hip joint. IEEE International Conference on Mechatronics and Automation, pp. 623-628, Tianjin, China, 2014.
[18] Wei T.E., Nelson G.M., Quinn R.D., Verma H., Garverick S.L. Design of a 5-cm Monopod Hopping Robot. Proceedings 2000 ICRA, Millennium Conference, IEEE International Conference on Robotics and Automation, 3:2828-2833, San Francisco, CA, USA, 2000.
[19] Kuswadi S., Ohnishi A., Takahashi A., Sampei M., Nakaura S. A one linear actuator hopping robot:modeling and control. Advanced Robotics, 17(8):709-737, 2003.
[20] Sayyad A., Seth B., Issac K.K. Dynamics and control of a one-legged 2-D SLOM popping robot. 12th IFToMM World Congress, Besançon, 2007.
[21] Seth B., Seshu S., Shanmuganathan P.V., Vichare V.V., Raj P. Search for initial conditions for sustained hopping of passive springy-leg offset-mass hopping robot. Journal of Dynamic Systems, Measurement, and Control, 129(4):522-526, 2007.
[22] Poulakakis I., Grizzle J.W. The spring loaded inverted pendulum as the hybrid zero dynamics of an asymmetric hopper. IEEE Transactions on Automatic Control, 54(8):1779-1793, 2009.
[23] Poulakakis I. Spring loaded inverted pendulum embedding: Extensions toward the control of compliant running robots. 2010 IEEE International Conference on Robotics and Automation (ICRA), pp. 1050-4729, Anchorage, Alaska, USA, 2010.
[24] Terry P., Piovan G., Byl K. Towards precise control of hoppers: Using high order partial feedback linearization to control the hopping robot FRANK. IEEE 55th Conference on Decision and Control (CDC), pp. 6669-6675, Las Vegas, USA, 2016.
[25] Zou H., Schmiedeler J.P. The effect of asymmetrical body-mass distribution on the stability and dynamics of quadruped bounding. IEEE Transactions on Robotics, 22(4):711-723, 2006.
[26] Nie H., Sun R., Hu L., Su Z., Hu W. Control of a cheetah robot in passive bounding gait. Journal of Bionic Engineering, 13(2):283-291, 2016.Document information
Published on 13/01/23
Accepted on 01/01/23
Submitted on 15/10/22
Volume 39, Issue 1, 2023
DOI: 10.23967/j.rimni.2023.01.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?