AinhoaArrese (talk | contribs) m (AinhoaArrese moved page Draft Arrese 189193530 to Review 395874996529) |
m (Marherna moved page Review 395874996529 to Arrese et al 2022a) |
||
| (2 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==ABSTRACT== | ==ABSTRACT== | ||
Latest revision as of 12:46, 10 January 2023
ABSTRACT
In this work, a novel extrapolation procedure to predict the cohesive laws of mode I and II adhesive bonds is presented and numerically validated.
First, starting from the recently proposed flexibility variation based data reduction methods to extract the cohesive laws, new factored expressions are defined with respect to the applied load and the adhesive and adherend thicknesses of the flexibility (C0i), the Integral-J (J0i) and the crack tip displacement (Δ0i) for each fracture mode.
Assuming that every effect associated to the damage is included in the equivalent crack length and according to the polynomial expressions of J0i, C0i and Δ0i with respect to it, invariant relationships between J0i - C0i and Δ0i - C0i are obtained for any given adhesive-adhesive thickness ratio of a given material system and test configuration, both in mode I and mode II.
Finally, an extrapolation procedure based on the calibrated J0i - C0i and Δ0i - C0i curves is presented, which allows estimating the cohesive laws for a wide range of adhesive to adherend ratio of a given material system by processing only load-displacement curve.
KEYWORDS: Adhesive joints; Cohesive law; J-Integral; Mode I; Mode II.
1 Introducción
Unir dos piezas y garantizar que esa unión va a funcionar perfectamente en el campo y condiciones de operación del producto, con un proceso optimizado y viable técnica y económicamente, no es obvio.
Parte de esa complicación proviene de la creciente demanda de productos que van a trabajar en condiciones hostiles de todo tipo (ambientales, esfuerzos, ataques químicos, de ciclo de operación…) y con la necesidad de diversificar, reducir y abaratar materia prima y peso.
Las uniones adhesivas son cada vez más importantes para las industrias de automoción, eólica y aeroespacial [1,2], ya que permiten la producción de estructuras livianas que combinan perfectamente aleaciones metálicas con compuestos de matriz polimérica.
El empleo de adhesivos estructurales en este tipo de uniones, en vez de los sistemas tradicionales, como soldadura, tornillos o remaches, no sólo implican una reducción de peso por la eliminación de estos elementos sino que supone una mejora en las características estructurales [3].
El uso de materiales compuestos y la utilización cada vez más generalizada de adhesivos estructurales frente a otros procesos de unión tradicional implica la necesidad de un conocimiento específico del comportamiento de dichas uniones ante solicitaciones que provocan la separación de las piezas unidas.
Para mejorar los métodos de diseño y modelización de las uniones adhesivas, las propiedades de fractura de los adhesivos deben determinarse de manera confiable experimentalmente, para allanar el camino hacia el desarrollo de herramientas numéricas más precisas para el diseño crítico de dichas juntas.
En este trabajo se pretende desarrollar un nuevo método para la caracterización integral de las uniones adhesivas con la generación de Curvas Maestras (Key Curves) para fractura en modo I y II que permiten obtener las propiedades de los adhesivos con una única probeta para a continuación extrapolar los resultados de una manera sencilla y rápida utilizando únicamente los datos de carga y desplazamiento del ensayo.
2 Metodología
Recientemente se ha propuesto un método de reducción de datos basado en la flexibilidad que permite determinar la tasa de liberación de energía J y el desplazamiento relativo en la punta de grieta Δ tanto modo I y modo II [4, 5] en función del avance de grieta equivalente.
El método basado en la teoría de la viga supone que todos los efectos asociados al desarrollo del daño están incluidos en la longitud de grieta equivalente obtenida a partir de la variación de la flexibilidad.
Se han derivado expresiones analíticas para la flexibilidad C, el desplazamiento relativo en la punta de grieta Δ y la J-Integral, todas ellas función de las propiedades elásticas de los adherentes, la configuración del ensayo, las dimensiones de la sección transversal de las probetas, la carga aplicada y la longitud de grieta equivalente (ae).
Reescribiendo las expresiones de C, la Δ y la J-Integral en forma de una multiplicación de funciones separadas, se definen nuevas expresiones factorizadas con respecto a la carga aplicada y a los espesores de adhesivo y adherente, de la flexibilidad (C0i), la Integral–J (J0i) y el desplazamiento de la punta de la grieta (Δ0i) para cada modo de fractura.
Suponiendo que todos los efectos asociados al daño se incluyen en la longitud de grieta equivalente, y de acuerdo con las expresiones polinómicas de J0i, C0i y Δ0i con respecto a la misma, se obtienen relaciones invariantes entre J0i-C0i y Δ0i-C0i para cualquier relación de espesores adhesivo-adherente de un sistema material y configuración de ensayo determinados, tanto en modo I como en modo II.
Si las curvas invariantes se calibran para un sistema material y una configuración de ensayo determinados, entonces sería posible extrapolar la J y la Δ, y en consecuencia, la ley de cohesiva para diferentes espesores adhesivo-adherente del mismo sistema de materiales y configuración de ensayo procesando únicamente con la curva carga-desplazamiento tanto en modo I como en modo II.
3 Verificación del método propuesto.
Se ha llevado a cabo un análisis de elementos finitos bidimensional para examinar la idoneidad del procedimiento de reducción de datos propuesto para extraer la ley de cohesiva para el ensayo ENF y DCB,
En el ensayo ENF, la luz entre apoyos es 2L = 120 mm y la anchura es w= 25 mm; en la configuración del ensayo DCB, la anchura también es w= 25 mm. En ambos las propiedades elásticas correspondientes al adherente se muestran en la Tabla 1.
Tabla 1. Propiedades del adherente.
| E11 | 144.7 GPa | E22=E33 | 10.6 GPa | G23 | 2.8 GPa |
| G12=G13 | 5.3 GPa | ν12=ν13 | 0.34 | ν23 | 0.4 |
En el modelo desarrollado en ABAQUS se han utilizando elementos de deformación plana 2D de cuatro nodos (CPE4) para el adherente y elementos cohesivos de cuatro nodos (COH2D4) para simular el adhesivo. El efecto de los rodillos de carga y de apoyo no se ha tenido en cuenta en el modelo de ENF.
Debido a que el objetivo es verificar la idoneidad del procedimiento de extrapolación y la precisión de las leyes cohesivas extraídas, una vez calibradas las curvas maestras tanto para modo I como para modo II, se han simulado diferentes configuraciones de probeta, variando tanto el espesor del adherente como del adhesivo y variando a su vez las propiedades cohesivas del adhesivo.
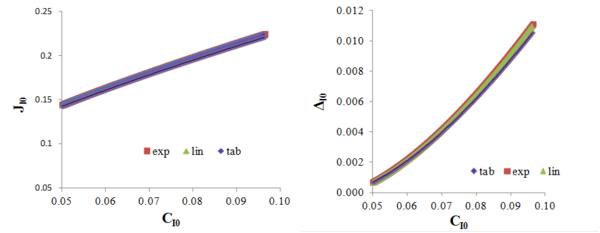
En la Fig.1 se muestran las curvas J0i-C0i y Δ0i-C0i para diferentes ensayos en modo I, donde se mantienen las propiedades del adherente y variando tanto las dimensiones de la probeta como las propiedades cohesivas del adhesivo.
De acuerdo con la Fig. 1, se puede validar numéricamente que las curvas J0I-C0I y Δ0I-C0I son invariantes para un sistema material y una configuración de ensayo determinados. Se han obtenido resultados similares en el caso del ensayo ENF.
Figura 1. Curvas J0I-C0I y Δ0I-C0I.enmodo I.
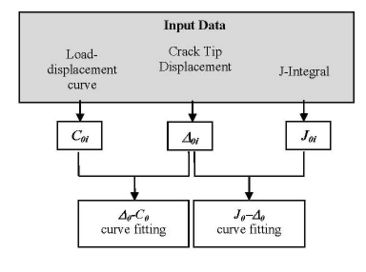
Asumiendo el carácter invariante de las curvas J0I-C0I y Δ0I-C0I, es posible extraer las Curvas Maestras tanto para modo I como para modo II a partir de los datos una única probeta siguiendo el diagrama de flujo que se muestra en la Fig. 2 .
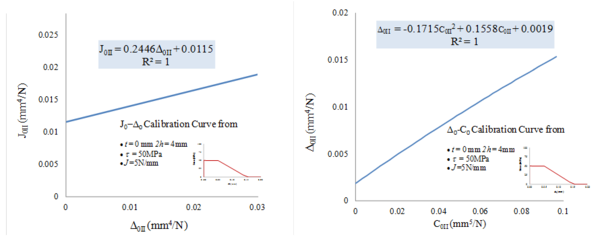
Como ejemplo, en la Fig. 3 se muestran las curvas maestras para el ensayo en modo II.
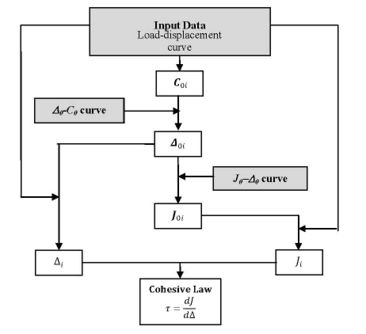
Una vez obtenidas las Curvas Maestras en modo I y Modo II, siguiendo el procedimiento de extrapolación que se muestra en la Fig. 4, se pueden extrapolar los resultados a diferentes configuraciones de probeta procesando únicamente la curva carga desplazamiento.
En las siguientes figuras se muestran los resultados obtenidos aplicando el procedimiento de extrapolación para los diferentes ensayos DCB y ENF.
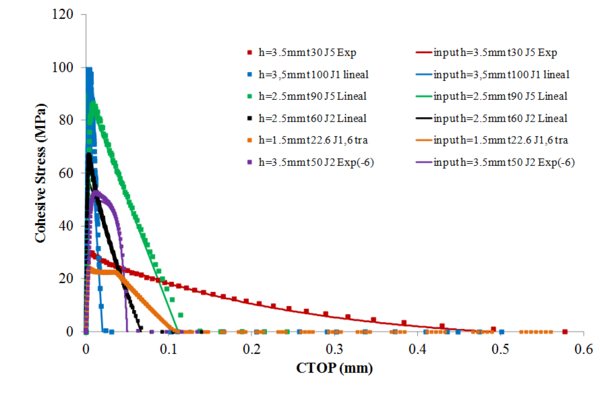
En la Fig.5 se muestran las leyes cohesivas en modo I extrapoladas variando el espesor del adherente desde 1,5 mm a 3,5mm, la tenacidad a la fractura en modo I entre 1000N/m y 5000N/m y la forma de la ley cohesiva.
Figura 5. Leyes cohesivas extrapoladas en modo I.
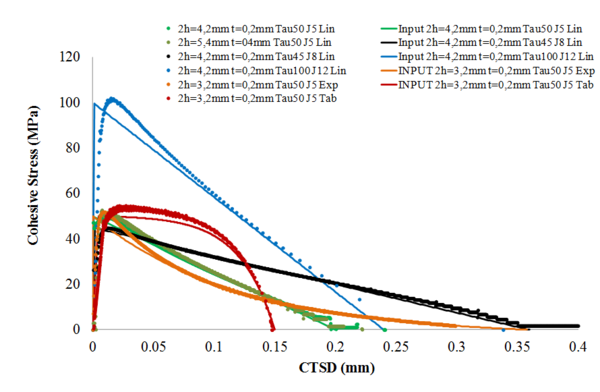
En la Fig. 6 se muestran las leyes cohesivas en modo II extrapoladas variando el espesor del adherente desde 1,5 mm a 2,5mm, el espesor del adhesivo de 0 a 0,4 mm, la tenacidad a la fractura en modo II entre 5000N/m y 12000N/m y la forma de la ley cohesiva.
Figura 6. Leyes cohesivas extrapoladas en modo II.
Según la Figs. 5 y 6, el procedimiento de extrapolación presentado permite estimar la ley cohesiva para un determinado sistema material variando los espesores del adhesivo y del adherente procesando únicamente la curva carga-desplazamiento, calibrando previamente las curvas maestras mediante los datos de ensayo de una única probeta.
4 Conclusiones
Se ha presentado un novedoso método de extrapolación para predecir las leyes cohesivas de modo I y II de uniones adhesivas que permite estimar las leyes cohesivas para un amplio rango de relación adhesivo/adherente de un sistema de materiales y una configuración de ensayo determinados.
5 Agradecimientos
Los autores agradecen a la Universidad del País Vasco (UPV/EHU) la financiación del Grupo de Investigación Mecánica de Materiales GIU 20/060.
6 Referencias
[1] Badwe, N., Mahajan, R., Sieradzki, K., 2016. Interfacial fracture strength and toughness of copper/epoxy-resin interfaces. Acta Materialia 103, 512–518. doi: 10. 1016/j.actamat.2015.10.009 .
[2] Banea, M.D., da Silva, L.F.M., 2009. Adhesively bonded joints in composite materials: an overview. J. Mater. Design Appl. 223 (1), 1–18. doi: 10.1243/14644207 .
[3] T.A Barnes, I.R. Pashby, Journal of Materials Processing Technology. 99, pág. 72-79 (2000). https://doi.org/10.1016/S0924-0136(99)00361-1
[4] A. Arrese, A. Boyano, J. de Gracia, F. Mujika, Composites Science and Technology, 152, pág. 76- 84, (2017) https://doi.org/10.1016/j.compscitech.2017.09.012
[5] A. Arrese, N. Insausti, F. Mujika, M. Perez-Galmés, J. Renart, Composites Science and Technology, 170, pág. 42–50, (2019) https://doi.org/10.1016/j.compscitech.2018.11.031
Document information
Published on 30/07/23
Accepted on 09/01/23
Submitted on 02/05/22
Volume 08 - COMUNICACIONES MATCOMP21 (2022) Y MATCOMP23 (2023), Issue Núm. 1 - Caracterización - Sostenibilidad y Reciclaje, 2023
DOI: 10.23967/r.matcomp.2024.01.13
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?