| (One intermediate revision by the same user not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==1 Introduction== | ==1 Introduction== | ||
| Line 106: | Line 22: | ||
Additionally, the effect of hydrostatic pressure on the tensile failure of fibre reinforced composites is addressed and the generalized strength reduction with increased pressure is shown to be well captured by the models (Figure 2), however, no key differences were observed in the failure mechanisms. | Additionally, the effect of hydrostatic pressure on the tensile failure of fibre reinforced composites is addressed and the generalized strength reduction with increased pressure is shown to be well captured by the models (Figure 2), however, no key differences were observed in the failure mechanisms. | ||
| − | + | [[File:Tavares_et_al_2021a-image6.png|centre|600x600px]] | |
| − | [[ | + | |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 193: | Line 108: | ||
The results of the open-hole tensile tests performed show a very interesting behaviour of the hybrid materials. Notched tensile tests are not only dominated by strength or toughness, but both properties interact and affect the notched strength of the material. It was concluded that the H2 material had the highest notched strength, higher than the non-hybrid T800 baseline, however, the H1 material showed the lowest strength. Analysing the notch sensitivity of these specimens, it is concluded that the H2 material has a very notch insensitive behaviour, being the normalized strength of the 12 mm wide specimens higher than the theoretical notch insensitive limit [2]. The H1 material, although having lower unnotched and notched strengths than the baseline T800, also shows a high notch intensive behaviour, which can be explained by the complex failure mechanisms that occur in the hybrid materials (Figure 6). | The results of the open-hole tensile tests performed show a very interesting behaviour of the hybrid materials. Notched tensile tests are not only dominated by strength or toughness, but both properties interact and affect the notched strength of the material. It was concluded that the H2 material had the highest notched strength, higher than the non-hybrid T800 baseline, however, the H1 material showed the lowest strength. Analysing the notch sensitivity of these specimens, it is concluded that the H2 material has a very notch insensitive behaviour, being the normalized strength of the 12 mm wide specimens higher than the theoretical notch insensitive limit [2]. The H1 material, although having lower unnotched and notched strengths than the baseline T800, also shows a high notch intensive behaviour, which can be explained by the complex failure mechanisms that occur in the hybrid materials (Figure 6). | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;">[[File:Captura de pantalla 2022-12-11 152511.png|centre|600x600px]]</div> |
| − | + | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 209: | Line 123: | ||
From the tensile tests in the unidirectional composites, it was concluded that there was a reduction in strength for the hybrid materials when comparing to the T800 baseline. Additionally, Hybrid 2-1 and Hybrid 1-1 materials had a very similar strength as the HR40 material, being their failure dominated by the failure of the HR40 fibres. The Hybrid 4-1 material with a 12% of HR40 fibres showed the highest strength of the hybrid materials. Additionally, a high non-linear behaviour prior to the failure was observed [2]. This non-linearity is associated with the failure of the HR40 fibres, that have a lower failure strain and that, in this hybrid, did not lead to the failure of the material, as the T800 fibres could support the additional load, due to the higher T800 volume fraction. | From the tensile tests in the unidirectional composites, it was concluded that there was a reduction in strength for the hybrid materials when comparing to the T800 baseline. Additionally, Hybrid 2-1 and Hybrid 1-1 materials had a very similar strength as the HR40 material, being their failure dominated by the failure of the HR40 fibres. The Hybrid 4-1 material with a 12% of HR40 fibres showed the highest strength of the hybrid materials. Additionally, a high non-linear behaviour prior to the failure was observed [2]. This non-linearity is associated with the failure of the HR40 fibres, that have a lower failure strain and that, in this hybrid, did not lead to the failure of the material, as the T800 fibres could support the additional load, due to the higher T800 volume fraction. | ||
| − | |||
| − | |||
From the analysis of the DENT specimens it was concluded that all hybrid materials had a lower fracture toughness than the baseline non-hybrid T800 material. This reduction of fracture toughness was attributed to the addition of the more brittle HR40 fibres without promoting other failure mechanisms with the exception of fibre failure, was seen to be crucial in the increase of the apparent fracture toughness of interply hybrid materials by Danzi [8]. The reduction is fracture toughness was attributed to the low fibre dispersion achieved via the mechanical spreading process used, meaning that the tows of the different fibre types did not successfully combine in the second stage of the process. This was a consequence of the low spreading ratio achieved with the mechanical spreader used. However, higher spreading ratios could not be achieved as it would lead to extensive fibre damage during the manufacturing process and, therefore, a low quality material. | From the analysis of the DENT specimens it was concluded that all hybrid materials had a lower fracture toughness than the baseline non-hybrid T800 material. This reduction of fracture toughness was attributed to the addition of the more brittle HR40 fibres without promoting other failure mechanisms with the exception of fibre failure, was seen to be crucial in the increase of the apparent fracture toughness of interply hybrid materials by Danzi [8]. The reduction is fracture toughness was attributed to the low fibre dispersion achieved via the mechanical spreading process used, meaning that the tows of the different fibre types did not successfully combine in the second stage of the process. This was a consequence of the low spreading ratio achieved with the mechanical spreader used. However, higher spreading ratios could not be achieved as it would lead to extensive fibre damage during the manufacturing process and, therefore, a low quality material. | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Table 2. '''Material properties and test results for the manufactured materials | + | <span style="text-align: center; font-size: 75%;">'''Table 2. '''Material properties and test results for the manufactured materials</span></div> |
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
| Line 261: | Line 173: | ||
|} | |} | ||
| + | [[Image:Tavares_et_al_2021a-image12.png|center|600px]] | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
Latest revision as of 15:32, 11 December 2022
1 Introduction
Fibre-reinforced composites play a fundamental role in aircraft structural applications, however their optimal use is still hampered partly due to the relatively low toughness they exhibit. The tensile failure of UD composites is a catastrophic process due to the propagation of a cluster of broken fibres and hybridization may change this behaviour by changing the failure mechanisms typically observed in composite materials, leading to non-brittle composites [1].
Hybridization in composite materials is the concept of using more than one type of reinforcement or matrix system on the same material. Although hybridization was a large field of study from the invention of carbon fibre until the late 80s, the interest has since then faded away, mainly due to the price reduction of carbon fibres and development of accurate models to predict the failure of non-hybrid composites. In the last years, hybridization, especially fibre hybridization, has become a field of interest mainly due to the possibility of delaying and achieving a more gradual failure of composite materials by controlling the damage mechanisms [1]. However, their behaviour and the mechanisms that drive failure are not yet fully understood. In addition, modelling their complex behaviour is extremely challenging due to the complex interaction between failure mechanisms.
The objective of this work is to analyse and understand the mechanics of deformation and failure of fibre hybrid composites, with focus on fibre dominated failure. To better understand the behaviour of hybrid composites, a combined approach is taken: the development of numerical models to predict the longitudinal failure and the experimental study of the effects of interply and intratow hybridization techniques on the damage mechanisms that control longitudinal failure. For a more in-depth version of this work, the reader is refered to reference [2]
2 Numerical modelling
2.1 3D micromechanical models
Due to the challenging complexity of modelling longitudinal tensile failure of composite materials, sophisticated micromechanical models that account for the different behaviour of its constituents are used. In this work, a 3D finite element micromechanical framework is developed, taking into account the non-linear elastic behaviour of the fibres and their stochastic strength[3], matrix plasticity and damage [4], [5], and interface decohesion. The developed framework is used to analyse simple micromechanical tests such as single fibre fragmentation and fibre push-out tests. The damage mechanisms that control failure in these tests are shown to be accurately represented using the proposed modelling methodology. Furthermore, it is shown that the properties of fibre-matrix interfaces are key in the failure process and their wrong definition leads to the premature failure of the composite material [2]
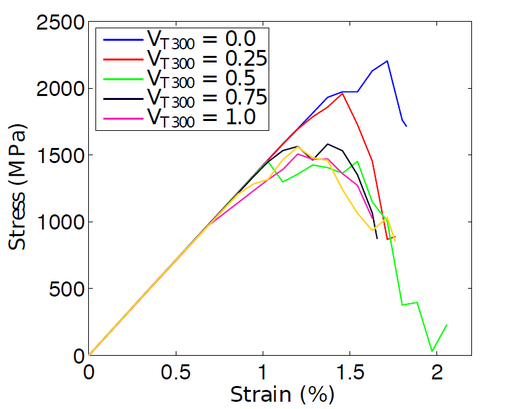
Analyses on both hybrid and non-hybrid composites were also performed to understand the failure process of these materials. For the hybrid composites it is shown that it is possible to obtain a pseudo-ductile behaviour by carefully controlling the hybridizing fibres and their respective fibre volume fractions (Figure 1).
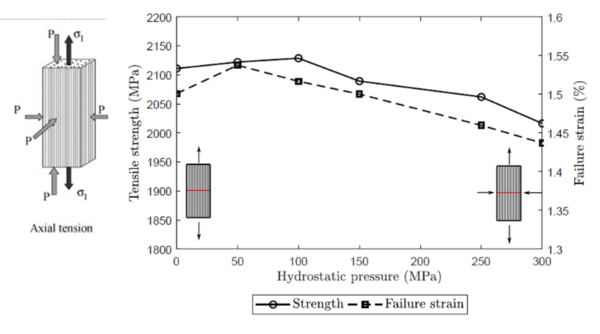
Additionally, the effect of hydrostatic pressure on the tensile failure of fibre reinforced composites is addressed and the generalized strength reduction with increased pressure is shown to be well captured by the models (Figure 2), however, no key differences were observed in the failure mechanisms.
2.2 Spring Element Model (SEM)
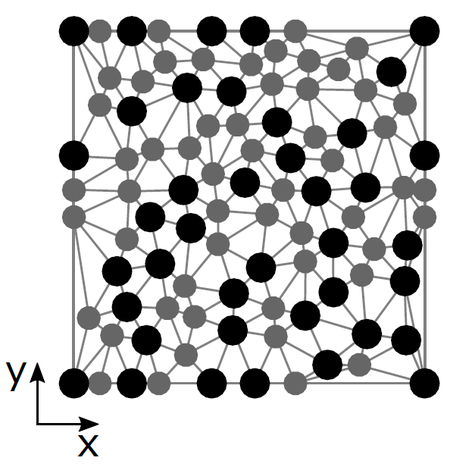
The presented 3D modelling strategy is capable of capturing the complex failure mechanisms of composite materials, however, its computational complexity and cost limit its usability. To circumvent this issue the Spring Element Model is proposed [6], [7]. This is a simplified model focused on longitudinal failure of composite materials that considers a random fibre arrangement of more than one type of fibre, so it can be used to simulate hybrid and non-hybrid composites. The model considers the matrix to be liner elastic and perfectly plastic via shear springs that connect the fibres (Figure 3), which are considered linear elastic up to failure. The fibre strength is considered to be a stochastic property, varying for each fibre element.
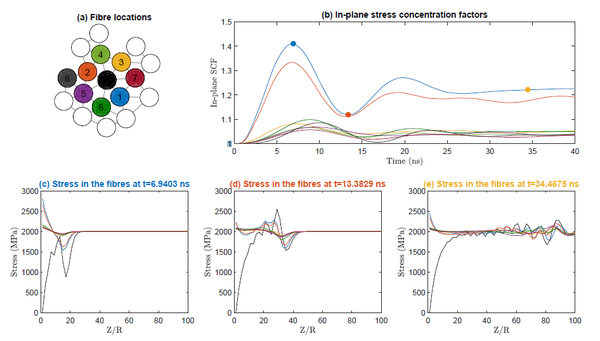
A more complex version of the model that accounts for the dynamics of fibre failure is also proposed [7] and shown to accurately capture the dynamic transient effects that occur when fibres fracture (Figure 4). The Spring Element Model was used to study fibre fracture and cluster formation on non-hybrid materials, however, the numerical results are shown to differ from the experiments as higher fibre break densities at failure are generally predicted [6]. The model is also used to investigate the effect of the microstructure on hybrid composite materials. A high dependence on the fibre dispersion is observed and higher fibre dispersion leads to improved composite performance [2].
3 Experimental work
Alongside the development of the numerical tools to predict failure of hybrid composites, two experimental campaigns on fibre hybrid composites are performed, both on interply and intratow hybrid materials.
3.1 Interply hybridization
Interply hybridization is a hybridization strategy that consists in combining layers of different materials into a single composite laminate. This is the hybridization strategy that leads to the lowest fibre dispersion, however, it is the less challenging to manufacture, as traditional hand layup methods combined with autoclave curing can be used. This hybridization strategy can be combined with the use of thin-ply layers, enabling the control of the failure mechanisms. In this work, interply hybridization is explored by combining thin-ply T800 and HR40 carbon fibre layers with the ThinPreg 80EP-736 resin system by NTPT. The non-hybrid laminas were used to create three different hybrid materials with the following sub-laminate building blocks:
- H1: [T800/HR40/T800] – 120 g/m2;
- H2: [2T800/HR40/2T800] – 220 g/m2.
Additionally, a T800 hybrid material with a areal weight of 100 g/m2 was also manufactured. In his previous work, Danzi [8] concluded that although there is a reduction in the tensile strength of the hybrid materials, when comparing to the baseline T800 material, there is a large increase in their intralaminar fracture toughness. The tensile tests on the hybrid materials suggest the occurrence of stable fragmentation of the HR40 plies, specially on the H2. This was concluded by a post-mortem analysis of the tensile specimens. As for the Double Edge Notched Specimens (DENT) used to determine the fracture toughness, a large difference in the failure mechanisms was observed when comparing the hybrid to the non-hybrid baseline materials.
In this work, hard multidirectional laminates similar to the industry defined baseline (T800) were selected based on previous work developed. Due to the different areal weights and thicknesses of the materials two different layups were defined:
- T800: [45/-45/0/45/-45/90/0]$;
- H1: [45/-45/0/45/-45/90/0]$;
- H2: [45/-45/0/90]$.
Note that each layer of the hybrid materials represent the hybrid sublaminate: [T800/HR40/T800] for the H1 material and [2T800/HR40/2T800] for the H2 material.
Both plain strength tension (Table 1) and open.hole tension tests were performed (Figure 5).
| Material | XT [MPa] | Ex [MPa] | XT /Ex |
| T800 | 839.6 ± 53.4 | 53472.7 | 15.7 |
| H1 | 640.8 ±46.8 | 55078.0 | 11.6 |
| H2 | 875.8 ±86.1 | 58501.2 | 15.0 |
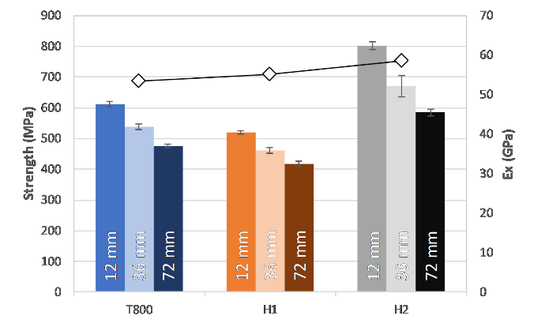
From the plain strength tension tests it is concluded that the H2 material has the highest unnotched strength, however, this material has a higher percentage of 0º layers than the remaining two materials. If we considered the strength normalized by the laminate's longitudinal elastic modulus, the T800 non-hybrid material has the highest normalized strength, meaning that the addition of the brittle HR40 layers to the T800 material leads to a lower unnotched normalized strength of the material.
The results of the open-hole tensile tests performed show a very interesting behaviour of the hybrid materials. Notched tensile tests are not only dominated by strength or toughness, but both properties interact and affect the notched strength of the material. It was concluded that the H2 material had the highest notched strength, higher than the non-hybrid T800 baseline, however, the H1 material showed the lowest strength. Analysing the notch sensitivity of these specimens, it is concluded that the H2 material has a very notch insensitive behaviour, being the normalized strength of the 12 mm wide specimens higher than the theoretical notch insensitive limit [2]. The H1 material, although having lower unnotched and notched strengths than the baseline T800, also shows a high notch intensive behaviour, which can be explained by the complex failure mechanisms that occur in the hybrid materials (Figure 6).
3.2
3.3 Intratow hybridization
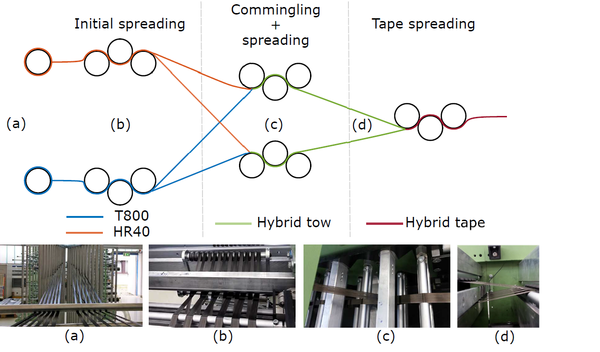
In this work, a strategy to manufacture intratow hybrid materials is also developed and implemented based on the spread-tow technology. T800, high elongation fibres, and HR40, low elongation fibres are used. An UD500 spreading machine from LIBA (now Karl Mayer Technische Textilien GmbH, Naila), at the Airbus Group Innovations Munich, Germany was used. The machine can produce UD tapes up to 500mm wide and combines coated spreading bars with the possibility of adding vibration and temperature to spread the fibres. The machine is divided in three spreading stages (Figure 7). In the first stage, the non-hybrid tows are spread to lower tow thicknesses to improve the commingling process. In the second stage a hybrid tow is formed by overlapping and combing the previously spread non-hybrid tows. Finally, in the last stage, the hybrid tows are combined to create a hybrid tape, which is later infused to produce a composite plate.
Five different materials were produced with different fibre volume fractions of T800 and HR40 fibres (Table 2). UD tensile strength tests and Double Edge Notched Tension (DENT) [9] tests were performed to determine the material’s strength (XT) and fracture toughness (R0).
From the tensile tests in the unidirectional composites, it was concluded that there was a reduction in strength for the hybrid materials when comparing to the T800 baseline. Additionally, Hybrid 2-1 and Hybrid 1-1 materials had a very similar strength as the HR40 material, being their failure dominated by the failure of the HR40 fibres. The Hybrid 4-1 material with a 12% of HR40 fibres showed the highest strength of the hybrid materials. Additionally, a high non-linear behaviour prior to the failure was observed [2]. This non-linearity is associated with the failure of the HR40 fibres, that have a lower failure strain and that, in this hybrid, did not lead to the failure of the material, as the T800 fibres could support the additional load, due to the higher T800 volume fraction.
From the analysis of the DENT specimens it was concluded that all hybrid materials had a lower fracture toughness than the baseline non-hybrid T800 material. This reduction of fracture toughness was attributed to the addition of the more brittle HR40 fibres without promoting other failure mechanisms with the exception of fibre failure, was seen to be crucial in the increase of the apparent fracture toughness of interply hybrid materials by Danzi [8]. The reduction is fracture toughness was attributed to the low fibre dispersion achieved via the mechanical spreading process used, meaning that the tows of the different fibre types did not successfully combine in the second stage of the process. This was a consequence of the low spreading ratio achieved with the mechanical spreader used. However, higher spreading ratios could not be achieved as it would lead to extensive fibre damage during the manufacturing process and, therefore, a low quality material.
| Material | Tape areal weight [g/m2] | % T800 | % HR40 | XT [MPa] | R0 [N/mm] |
| T800 | 100 | 100 | 0 | 2175 | 171.7 |
| Hybrid 4-1 | 138 | 88 | 12 | 1842 | 133.2 |
| Hybrid 2-1 | 141 | 78 | 22 | 1525 | 100.6 |
| Hybrid 1-1 | 93 | 64 | 36 | 1540 | 98.8 |
| HR40 | 63 | 0 | 100 | 1559 | - |
4 Conclusion
This work focused on analysing and understanding the mechanics and mechanisms that control the behaviour of fibre hybrid composite materials. This thematic was tackled using both numerical methods and experimental work.
Two distinct numerical frameworks were developed with different fidelities. The 3D micromechanical framework that takes into account the complex behaviour of both the fibres, matrix and their interfaces was used to analyse the mechanisms that control tensile failure of polymer composites on both hybrid and non-hybrid composites. Furthermore, the effect of hydrostatic pressure in tensile failure was analysed and a reduction in strength with increased pressure was observed. The Spring Element Model was developed to allow the simulation of larger RVEs to better understand the formation of clusters of broken fibres in the fracture process. This model was extended to included the local dynamic effects that occur during fibre fracture. However, key differences between the numerical predictions and experimental results were found, mainly on the fibre break density at failure and the cluster evolution. For the analysed hybrid materials it was concluded that increasing the fibre dispersion leads to improved material performance, implying that improvements can be made by using intratow hybridization.
Additionally, two experimental campaigns on interply and intratow hybrid materials were performed. The combination of hybridization and thin-ply materials in an interply hybridization lead to interesting results. The hybrid materials were seen to be less notch sensitive than their non-hybrid counterparts and an increased notched strength was observed.
Finally, intratow hybrid materials were manufactured, using tow spreading technology to combine non-hybrid tows into a hybrid tape, and tested. However, due to achieving a low fibre dispersion due to manufacturing constraints, no improvement on the analysed material properties due to hybridization was found.
Acknowledgements
The first author would acknowledges the financial support provided by the Portuguese Government’s Fundação para a Ciência e a Tecnologia, under grant SFRH/BD/115872/2016 and the project PTDC/EMS-PRO/4732/2014. The authors would like to thank Airbus Group Innovations (Munich, Germany) for the support on the development of the work on intratow hybrid composites.
References
[1] Y. Swolfs, L. Gorbatikh, and I. Verpoest, “Fibre hybridisation in polymer composites: A review,” Composites Part A: Applied Science and Manufacturing, vol. 67, no. 0, pp. 181–200, 2014, doi: http://dx.doi.org/10.1016/j.compositesa.2014.08.027.
[2] R. P. Tavares, “Mechanics of deformation and failure of fibre hybrid composites,” 2020. Accessed: Sep. 14, 2021. [Online]. Available: https://hdl.handle.net/10216/125975
[3] R. P. Tavares, A. R. Melro, A. Turon, and P. P. Camanho, “Modelling the tensile failure of hybrid polymer composites,” 2016.
[4] A. R. Melro, P. P. Camanho, F. M. Andrade Pires, and S. T. Pinho, “Micromechanical analysis of polymer composites reinforced by unidirectional fibres: Part I – Constitutive modelling,” International Journal of Solids and Structures, vol. 50, no. 11, pp. 1897–1905, 2013, doi: 10.1016/j.ijsolstr.2013.02.009.
[5] A. R. Melro, P. P. Camanho, F. M. Andrade Pires, and S. T. Pinho, “Micromechanical analysis of polymer composites reinforced by unidirectional fibres: Part II – Micromechanical analyses,” International Journal of Solids and Structures, vol. 50, no. 11, pp. 1906–1915, 2013, doi: 10.1016/j.ijsolstr.2013.02.007.
[6] R. P. Tavares, F. Otero, A. Turon, and P. P. Camanho, “Effective simulation of the mechanics of longitudinal tensile failure of unidirectional polymer composites,” International Journal of Fracture, vol. 208, no. 1–2, 2017, doi: 10.1007/s10704-017-0252-9.
[7] R. P. Tavares, F. Otero, J. Baiges, A. Turon, and P. P. Camanho, “A dynamic spring element model for the prediction of longitudinal failure of polymer composites,” Computational Materials Science, vol. 160, 2019, doi: 10.1016/j.commatsci.2018.12.048.
[8] F. Danzi, “Composite failure properties and non-linearity evaluation via statistical micromechanical analysis,” 2018.
[9] G. Catalanotti, A. Arteiro, M. Hayati, and P. P. Camanho, “Determination of the mode I crack resistance curve of polymer composites using the size-effect law,” Engineering Fracture Mechanics, vol. 118, pp. 49–65, Mar. 2014, doi: 10.1016/J.ENGFRACMECH.2013.10.021.
Document information
Published on 13/10/21
Accepted on 06/10/21
Submitted on 29/09/21
Volume 05 - Comunicaciones Matcomp19 (2021), Issue Núm. 4 - Tesis doctorales presentadas al premio AEMAC a la mejor tesis., 2021
DOI: 10.23967/r.matcomp.2021.10.004
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?