(Created page with "== Abstract == Additive manufacturing technologies allow us the creation of 3D objects through layer overlay. This process is faster than other traditional manufacturing proc...") |
|||
| (3 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | ==1 Introducción == |
| − | + | La fabricación aditiva engloba las tecnologías que crean objetos tridimensionales capa a capa. Esta forma de fabricación ha despertado mucho interés por parte de la industria al presentar ventajas frente a los métodos tradicionales de conformado, como la reproducción de casi cualquier geometría, la rapidez desde el diseño a la obtención de la pieza final, la personalización y la competitividad en series cortas. En la tecnología ''Fused Deposition Modeling'' (FDM), la más extendida actualmente, cada capa se construye generalmente mediante hilos de material termoplástico fundido extruidos a través de una boquilla. Los parámetros de fabricación definidos para cada pieza, como la orientación de la pieza respecto a la impresora, las trayectorias de los hilos que forman el relleno de cada capa o su densidad, condicionan sus características finales como el acabado superficial o las propiedades mecánicas [<span id='cite-1'></span>[[#1|1]]]. | |
| − | + | ||
| − | + | ||
| − | == | + | El comportamiento mecánico de una pieza procesada por FDM es complejo, al variar sus propiedades en función de la dirección en la que se miden y del estado de tensión al que se encuentre sometida [<span id='cite-2'></span>[[#2|2]]]. Esto se debe a la fabricación mediante superposición de capas, de manera que las direcciones en las que los hilos se encuentran alineados con las cargas son más resistentes a tracción que a compresión, al contrario que la dirección en la que se apilan las capas (Figura 1). |
| − | < | + | |
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Alonso_et_al_2021a-image5-c.png|120px]] | ||
| + | | [[Image:Alonso_et_al_2021a-image5-c1.png|center|150px]] | ||
| + | |} | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Alonso_et_al_2021a-image6-c.png|138px]] | ||
| + | | [[Image:Alonso_et_al_2021a-image6-c1.png|center|144px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 1.''' Efecto de la tracción y la compresión en las diferentes orientaciones de FDM.</span></div> | ||
| + | |||
| + | Esta característica es la que limita la realización de predicciones del comportamiento mecánico de estas piezas a través de análisis de elementos finitos (FEA). Normalmente estos análisis se llevan a cabo mediante programas comerciales de simulación, los cuales llevan implementados modelos de material que no reproducen la complejidad del comportamiento del material FDM. El desconocimiento existente respecto a cómo se van a comportar las piezas obtenidas por esta tecnología limita las aplicaciones del FDM para la fabricación de piezas funcionales o con responsabilidad estructural. | ||
| + | |||
| + | El objetivo de este trabajo es, por tanto, reducir la incertidumbre respecto al comportamiento mecánico de las piezas fabricadas por FDM a partir de materiales termoplásticos. | ||
| + | |||
| + | Para ello se va a definir una metodología a partir de modelos teóricos de comportamiento de los materiales y de ensayos experimentales de caracterización, que podrá ser implementada en programas de simulación para adaptarlos al material FDM y poder realizar predicciones de su comportamiento. | ||
| + | |||
| + | ==2 Modelo de comportamiento teórico== | ||
| + | |||
| + | El comportamiento mecánico de los materiales se determina a partir de ensayos experimentales que proporcionan las curvas esfuerzo-deformación. Las curvas de comportamiento de los materiales termoplásticos se caracterizan por tener una zona elástica y otra plástica (Figura 2). | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;"> [[Image:Alonso_et_al_2021a-image7-c.png|498px]] </span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 2.''' Curva esfuerzo-deformación de un material termoplástico.</span></div> | ||
| + | |||
| + | Además, los materiales una vez procesados mediante la tecnología FDM presentan tres direcciones principales de comportamiento según la disposición de los hilos del material. Por tanto, para definir este comportamiento se utilizan modelos ortótropos [<span id='cite-3'></span>[[#3|3]],<span id='cite-4'></span>[[#4|4]],<span id='cite-5'></span>[[#5|5]]], que tienen en cuenta las propiedades de cada una de las direcciones, obtenidas mediante ensayos de probetas fabricadas en diferentes planos (Figura 3). | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Alonso_et_al_2021a-image8-c.png|234px]] | ||
| + | | [[Image:Alonso_et_al_2021a-image9-c.png|center|318px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 3.''' Orientaciones de fabricación de las probetas para la caracterización del material.</span></div> | ||
| + | |||
| + | Así, mientras que para la zona elástica del material es más común la definición de modelos ortótropos que tengan en cuenta las diferencias en el comportamiento de las direcciones principales, no lo es para la parte plástica. | ||
| + | |||
| + | Otra característica del comportamiento derivada de la orotropía del material una vez procesado es la diferente respuesta ante esfuerzos de tracción y compresión que deberá tenerse en cuenta a la hora de definir el modelo. | ||
| + | |||
| + | A continuación se van a definir los modelos teóricos de comportamiento, para la parte elástica y para la parte plástica, que tendrán en cuenta todas las variables del comportamiento de los termoplásticos procesados por FDM. | ||
| + | |||
| + | ==='''2.1''' Comportamiento elástico=== | ||
| + | |||
| + | Para modelar la parte elástica o lineal del comportamiento se sigue la ley de Hooke, ecuación (1), que establece que el esfuerzo es proporcional a la deformación. La constante de proporcionalidad entre ambas propiedades es la matriz de rigidez, que es característica de cada material y se construye a partir de las constantes mecánicas del mismo. | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\overline{\epsilon }=\overline{\overline{S}}\overline{\sigma }</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Para el material FDM se utiliza la matriz de rigidez ortótropa, que se define con 9 constantes independientes establecidas a partir de las propiedades mecánicas del material, ecuación (2). En este caso se definirán dos matrices de rigidez, una a tracción y otra a compresión. Así, para modelar la parte elástica será necesaria una caracterización a tracción, a compresión y a cortadura del material, ya que en materiales ortótropos el módulo de cizalladura no se puede obtener a partir de las propiedades a tracción. | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\left[ \begin{matrix}{\epsilon }_{x}\\\\{\epsilon }_{y}\\\\{\epsilon }_{z}\\\\{\gamma }_{yz}\\\\{\gamma }_{xz}\\\\{\gamma }_{xy}\end{matrix}\right] =</math><math>\left[ \begin{matrix}\frac{1}{{E}_{x}}&-\frac{{\nu }_{xy}}{{E}_{x}}&-\frac{{\nu }_{xz}}{{E}_{x}}&0&0&0\\&\frac{1}{{E}_{y}}&-\frac{{\nu }_{yz}}{{E}_{y}}&0&0&0\\&&\frac{1}{{E}_{z}}&0&0&0\\&&&\frac{1}{{G}_{yz}}&0&0\\&sim.&&&\frac{1}{{G}_{xz}}&0\\&&&&&\frac{1}{{G}_{xy}}\end{matrix}\right] \cdot \left[ \begin{matrix}{\sigma }_{x}\\\\{\sigma }_{y}\\\\{\sigma }_{z}\\\\{\tau }_{yz}\\\\{\tau }_{xz}\\\\{\tau }_{xy}\end{matrix}\right]</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Dónde ''ε<sub>i</sub> ''es la deformación longitudinal en la dirección i, ''γ<sub>i</sub>'' la deformación transversal en el plano ij, ''σ<sub>i</sub>'' la tensión normal en la dirección i, ''τ<sub>i</sub>'' la tensión tangencial en el plano ij, ''E<sub>i</sub>'' el módulo de Young en la dirección i, ''ν<sub>ij</sub>'' el coeficiente de Poisson en el plano ij y ''G<sub>ij</sub>'' el módulo de cortadura en el plano ij. | ||
| + | |||
| + | ==='''2.2''' Comportamiento plástico=== | ||
| + | |||
| + | Para modelar la parte plástica se utilizan los criterios de plasticidad, que establecen la condición a partir de la cual tiene lugar la deformación plástica en un material. En la metodología definida en este trabajo se utilizará el criterio de Von Mises, ecuación (3), por ser el que proporciona los resultados más optimizados. | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\sqrt{\, \frac{1}{2}\cdot [{\left( {\sigma }_{1}-{\sigma }_{2}\right) }^{2}+{\left( {\sigma }_{2}-\, {\sigma }_{3}\right) }^{2}+\, {\left( {\sigma }_{3}-{\sigma }_{1}\right) }^{2}]}=</math><math>{\sigma }_{e}\,</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Donde ''σ<sub>i</sub>'' es la tensión principal del tensor de tensiones en la dirección i y ''σ<sub>e</sub>'' el límite elástico. | ||
| + | |||
| + | El comportamiento una vez alcanzado el límite elástico del material se rige a través de la curva de plasticidad que relaciona el esfuerzo frente a la deformación plástica [<span id='cite-6'></span>[[#6|6]]]. Esta curva se obtiene de los ensayos experimentales a rotura a tracción y a compresión, y sus parámetros se pueden definir a través del ajuste de la curva experimental a una función potencial, ecuación (4). | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\sigma =K\cdot {{\epsilon }_{p}\, }^{n}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Dónde ''K'' es un coeficiente de fuerza y ''n'' el exponente de endurecimiento por deformación. | ||
| + | |||
| + | Cada material tendrá un límite elástico y una curva de plasticidad diferente en cada orientación y para cada tipo de esfuerzo, excepto para la dirección XZ a tracción, cuyo comportamiento es frágil y no presenta plasticidad, por lo que para ese caso solo se definirá el límite elástico. | ||
| + | |||
| + | ==3 Caracterización experimental== | ||
| + | |||
| + | Para alimentar el modelo de comportamiento teórico definido es necesaria una caracterización experimental del material una vez procesado. Para ello será necesario mantener los parámetros de impresión constantes durante la fabricación de las probetas. | ||
| + | |||
| + | Como no existe una normativa específica de caracterización de materiales procesados por FDM se han definido las normas más adecuadas para obtener las propiedades mecánicas necesarias para la definición del modelo. | ||
| + | |||
| + | ==='''3.1''' Ensayo de tracción=== | ||
| + | |||
| + | Para los ensayos a tracción se utilizará la norma ASTM D3039 [<span id='cite-7'></span>[[#7|7]]] que emplea probetas rectangulares para evitar zonas de concentración de tensiones [2]. Se ensayarán 5 probetas para cada una de las orientaciones de fabricación (Figura 4). | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Alonso_et_al_2021a-image10-c.png|270px]] | ||
| + | | [[Image:Alonso_et_al_2021a-image11-c.png|center|300px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 4.''' Esquema de las probetas a tracción fabricadas con un relleno ±45º.</span></div> | ||
| + | |||
| + | De este ensayo se obtendrá para cada dirección el módulo de Young (E<sub>x</sub>, E<sub>y</sub>, E<sub>z</sub>), el coeficiente de Poisson (ν<sub>xy</sub>, ν<sub>yz</sub>, ν<sub>xz</sub>), el límite elástico (σ<sub>e-x</sub>, σ<sub>e-y</sub>, σ<sub>e-z</sub>) y la curva de plasticidad. | ||
| + | |||
| + | ==='''3.2''' Ensayo de compresión=== | ||
| + | |||
| + | Para los ensayos a compresión se utilizará la norma ASTM D695 [<span id='cite-8'></span>[[#8|8]]] con probetas prismáticas para una mayor sencillez en su fabricación. Se utilizarán probetas más alargadas para la obtención de las propiedades elásticas (12,7 x 12,7 x 50,8 mm) y más cortas para las propiedades plásticas (12,7 x 12,7 x 25,4 mm). Por la simetría de las probetas, dos de las orientaciones (XY e YZ) serán equivalentes y tendrán, por tanto, las mismas propiedades. Se fabricarán 5 probetas para cada orientación de fabricación (Figura 5). | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Alonso_et_al_2021a-image12-c.png|228px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 5.''' Esquema de las probetas a compresión fabricadas con un relleno ±45º.</span></div> | ||
| + | |||
| + | De este ensayo se obtendrá para cada dirección el módulo de Young (E<sub>x</sub>=E<sub>y</sub>, E<sub>z</sub>), el límite elástico (σ<sub>e-x</sub>=σ<sub>e-y</sub>, σ<sub>e-z</sub>) y la curva de plasticidad a compresión. | ||
| + | |||
| + | ==='''3.3''' Ensayo de cortadura=== | ||
| + | |||
| + | Para obtener los módulos de cortadura de un material ortótropo es necesario hacer un ensayo experimental específico. En este caso se llevará a cabo un ensayo Off-Axis que consiste en la realización de un ensayo a tracción de probetas fabricadas con las fibras inclinadas. Para el material FDM otros autores han utilizado una inclinación de 45º respecto a la dirección principal [3,4,<span id='cite-9'></span>[[#9|9]]], pudiéndose obtener el módulo de cortadura a partir de la ecuación (5). | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{G}_{xy}=\frac{{E}_{1}}{2(1+{\nu }_{12})}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Dónde E<sub>1</sub> y ν<sub>12 </sub>son las constantes obtenidas de la tracción de las probetas Off-Axis. | ||
| + | |||
| + | Para un relleno de ±45º la probeta XY coincidirá con la definida a tracción, por lo que no habría que volver a ensayarla. Además, al utilizar una inclinación de 45º las otras dos orientaciones serían simétricas, pudiendo ensayar únicamente una orientación con una repetitividad de 5 ensayos (Figura 6). | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Alonso_et_al_2021a-image10-c1.png|246px]] | ||
| + | | [[Image:Alonso_et_al_2021a-image13-c.png|center|300px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 6.''' Esquema de las probetas a cortadura fabricadas con un relleno ±45º.</span></div> | ||
| + | |||
| + | De los ensayos off-axis se obtiene el módulo de Young y el coeficiente de Poisson, a partir de los cuales calculamos el módulo de cortadura a través de la ecuación (5). | ||
| + | |||
| + | ==4 Construcción del modelo de cálculo== | ||
| + | |||
| + | Una vez definido el modelo teórico del comportamiento del material FDM y la caracterización necesaria para poder construirlo se procedió con el desarrollo de su implementación en programas comerciales de cálculo mediante elementos finitos. | ||
| + | |||
| + | La incorporación del modelo en estos programas se lleva a cabo a través de la programación de subrutinas que se introducen en el software para ampliar sus opciones de cálculo. En este caso se modificará la parte elástica y la plástica del modelo de material para adaptarlas al comportamiento de los procesados FDM. | ||
| + | |||
| + | ==='''4.1''' Modelo para la parte elástica=== | ||
| + | |||
| + | Para modificar la asignación de las propiedades de la parte elástica del material se utilizan subrutinas que permiten la introducción de la matriz que relaciona el esfuerzo con la deformación. En primer lugar la subrutina obtendrá del cálculo el valor de la tensión media en el punto a asignar, le evaluará y en función del estado de tensión en el que se encuentre trabajando le asignará la matriz de rigidez a tracción o compresión, construidas a partir de las propiedades mecánicas del material. | ||
| + | |||
| + | ==='''4.2''' Modelo para la parte plástica=== | ||
| + | |||
| + | Para definir el comportamiento en la parte plástica del material se utilizan subrutinas que permiten introducir la curva que relaciona el esfuerzo con la deformación plástica, basándose en el criterio de plasticidad de Von Mises. A través de la programación de la subrutina se aplicará este criterio utilizado para materiales isotrópicos a un material con comportamiento ortótropo. | ||
| + | |||
| + | El primer paso de la programación conlleva la definición de las curvas de plasticidad, que se introducirán en la subrutina a través de dos funciones: el esfuerzo en función de la deformación plástica, ecuación (6), y la pendiente de endurecimiento, ecuación (7). | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{\sigma }_{y}={\sigma }_{e}\cdot {\left( 1+E\cdot \frac{{\epsilon }_{p}}{{\sigma }_{e}}\right) }^{n}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) | ||
| + | |} | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">\frac{\partial {\sigma }_{y}}{\partial {\epsilon }_{p}}=</math><math>n\cdot E\cdot {\left( 1+E\cdot \frac{{\epsilon }_{p}}{{\sigma }_{e}}\right) }^{n-1}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) | ||
| + | |} | ||
| + | |||
| + | |||
| + | A continuación se define el criterio de selección de la curva de plasticidad a asignar en cada punto de integración para cada instante, que se realizará evaluando el tensor de tensiones asociado, obtenido del propio cálculo. La subrutina evaluará el valor absoluto de las tensiones de la diagonal del tensor y, en función de la magnitud de estas tensiones, establecerá la dirección o direcciones dominantes en el punto de integración analizado. Una vez determinada la dirección se evaluará el estado de tensión al que está sometido el punto en esa dirección, es decir, tracción si es positivo o compresión si es negativo y, en función de esto, establecerá la curva de plasticidad que va a seguir ese punto en el incremento analizado. Para las situaciones en las que dos o las tres direcciones estén sometidas a la misma tensión se asignará la curva de plasticidad media de las direcciones dominantes. | ||
| + | |||
| + | ==5 Validación== | ||
| + | |||
| + | Una vez definida la metodología se llevó a cabo una validación de la misma a través de ensayos experimentales, con el objetivo de conocer la calidad de las predicciones que proporciona el modelo de simulación definido. | ||
| + | |||
| + | En primer lugar se realizó una caracterización completa del material una vez procesado. En este caso se utilizó una poliamida procesada con los parámetros de impresión de la Tabla 1. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Tabla 1.''' Parámetros de impresión</span></div> | ||
| + | {| style="width: 70%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| + | |- | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">Diámetro del hilo</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">1,50 mm</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">Altura de capa</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">0,20 mm</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">Número de contornos</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">2</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">Relleno</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">±45º</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">Densidad del relleno</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">100%</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">Temperatura de fusión</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">250ºC</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">Temperatura de la cama</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">150ºC</span> | ||
| + | |} | ||
| + | |||
| + | |||
| + | Se realizaron los ensayos a tracción, compresión y cortadura definidos anteriormente para las tres orientaciones, obteniéndose las propiedades mecánicas ortótropas elásticas y plásticas del material (Tabla 2). | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Tabla 2.''' Propiedades mecánicas del material</span></div> | ||
| + | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| + | |- | ||
| + | | style="border-bottom: 1pt solid black;text-align: center;"| | ||
| + | | style="border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"| | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''XY'''</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''YZ'''</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">'''XZ'''</span> | ||
| + | |- | ||
| + | | rowspan='3' style="border: 1pt solid black;"|<span style="text-align: center; font-size: 75%;">Tracción</span> | ||
| + | | style="border: 1pt solid black;"|<span style="text-align: center; font-size: 75%;">'''E''' (MPa)</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">1451,40</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">1480,20</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">1530,40</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;"|<span style="text-align: center; font-size: 75%;">'''ν'''</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">0,45</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">0,40</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">0,45</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;"|<span style="text-align: center; font-size: 75%;">'''σ<sub>e</sub>'''</span><span style="text-align: center; font-size: 75%;"> (MPa)</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">38,06</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">39,32</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">14,98</span> | ||
| + | |- | ||
| + | | rowspan='2' style="border: 1pt solid black;"|<span style="text-align: center; font-size: 75%;">Compresión</span> | ||
| + | | style="border: 1pt solid black;"|<span style="text-align: center; font-size: 75%;">'''E''' (MPa)</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">1447,39</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">1447,39</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">1458,17</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;"|<span style="text-align: center; font-size: 75%;">'''σ<sub>e</sub>'''</span><span style="text-align: center; font-size: 75%;"> (MPa)</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">30,19</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">30,19</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">41,64</span> | ||
| + | |- | ||
| + | | style="border: 1pt solid black;"|<span style="text-align: center; font-size: 75%;">Cortadura</span> | ||
| + | | style="border: 1pt solid black;"|<span style="text-align: center; font-size: 75%;">'''G''' (MPa)</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">499,45</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">497,93</span> | ||
| + | | style="border: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;">497,93</span> | ||
| + | |} | ||
| + | |||
| + | |||
| + | Una vez caracterizado se configuró el modelo de subrutinas con las propiedades y curvas obtenidas de los ensayos. Para la validación se implementaron las subrutinas en el software de simulación Marc (MSC Software) [<span id='cite-10'></span>[[#10|10]]] mediante el lenguaje de programación FORTRAN. | ||
| + | |||
| + | El método de validación consistió en la comparación de los resultados de un ensayo experimental con los obtenidos al realizar la simulación del mismo ensayo, utilizando el modelo desarrollado una vez implementado. | ||
| + | |||
| + | Como ensayo se eligió uno de flexión a tres puntos sobre una probeta rectangular fabricada mediante FDM, por presentar resultados complejos al incluir diferentes estados de tensión en su comportamiento y ser sencillo de ejecutar. Para realizarlo se siguió la norma ASTM D790 [<span id='cite-11'></span>[[#11|11]]] para probetas fabricadas en las tres orientaciones diferentes (Figura 7) e imponiendo un desplazamiento de 22 mm del pisador. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Alonso_et_al_2021a-image10-c2.png|300px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Alonso_et_al_2021a-image14-c.png|600px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 7.''' Disposición de las capas de las probetas a flexión.</span></div> | ||
| + | |||
| + | Se fabricaron y ensayaron tres probetas de cada orientación para obtener repetitividad en los resultados (Figura 8). Después, se realizaron las simulaciones del ensayo para cada orientación utilizando un modelo geométricamente equivalente al experimental y se obtuvieron las curvas carga - desplazamiento de ambos ensayos. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Alonso_et_al_2021a-image15-c.jpeg|300px]] | ||
| + | | [[Image:Alonso_et_al_2021a-image16-c.jpeg|center|300px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 8.''' Ejecución del ensayo experimental a flexión para una probeta XY.</span></div> | ||
| + | |||
| + | En las Figuras 9, 10 y 11 se muestran los resultados de tensiones equivalentes de Von Mises obtenidos de la simulación, junto con la comparación de las gráficas carga - desplazamiento experimentales y simuladas para cada dirección. Tanto en la dirección XY como en la dirección YZ el comportamiento durante el ensayo de las probetas era dúctil. | ||
| + | |||
| + | En la simulación de la orientación XY (Figura 9) se observan contornos simétricos en la zona de tracción y compresión y bajas tensiones en la línea neutra de la probeta. De la comparación de las curvas en esta dirección se aprecia la buena aproximación entre las predicciones y los resultados experimentales. | ||
| + | |||
| + | La orientación YZ (Figura 10) presenta un comportamiento muy similar a la XY tanto en los contornos de tensiones como en las curvas, aunque la predicción del modelo es menos precisa, con un error en la predicción de la carga comprendido entre el 10 y el 15%. | ||
| + | |||
| + | En la simulación de la orientación XZ (Figura 11) se aprecian diferencias significativas respecto a las otras orientaciones en la simulación, al igual que en el ensayo experimental. Los contornos de tensiones simulados presentan una concentración de tensiones en la zona central, donde se produce la rotura. En cuanto a la comparación de las curvas carga - desplazamiento, al llegar a romper la probeta durante el ensayo la simulación es menos precisa, ya que el modelo desarrollado no tiene en cuenta la vida y muerte de elementos. Por tanto, el modelo llega a predecir cuándo rompe la probeta, pero no permite conocer con exactitud la carga en ese instante, proporcionando un error en la predicción de hasta el 35%. | ||
| + | |||
| + | ==6 Conclusiones== | ||
| + | |||
| + | En este trabajo se ha definido una metodología que permite la realización de predicciones del comportamiento mecánico de piezas procesadas por FDM al implementarse en programas de simulación de elementos finitos. Los modelos de material definidos tienen en cuenta el comportamiento ortótropo de estos materiales además de su diferente respuesta ante esfuerzos de tracción y compresión. | ||
| + | |||
| + | El método ha demostrado, mediante una validación experimental, ser capaz de proporcionar una buena aproximación del comportamiento de las piezas así fabricadas. También se han detectado ciertas debilidades en las predicciones en los casos en los que se produce la rotura del componente. | ||
| + | |||
| + | El modelo de simulación permite predecir cómo se va a comportar cualquier componente fabricado por FDM teniendo en cuenta su cuaderno de cargas. Únicamente se requiere la realización de una caracterización completa del material una vez procesado, como la definida en este trabajo. | ||
| + | |||
| + | Esto permite la optimización de parámetros de fabricación de las piezas como la orientación de impresión en función de su comportamiento mecánico final. Además, permite determinar si un componente obtenido por FDM va a soportar las cargas a las que va a ser sometido sin necesidad de ser fabricado y ensayado experimentalmente. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Alonso_et_al_2021a-image18.png|288px]] | ||
| + | | [[Image:Alonso_et_al_2021a-chart1.svg|center|288px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 9.''' Resultados ensayo y simulación para las probetas fabricadas con la orientación XY.</span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Alonso_et_al_2021a-image19.png|288px]] | ||
| + | | [[Image:Alonso_et_al_2021a-chart2.svg|center|288px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 10.''' Resultados ensayo y simulación para las probetas fabricadas con la orientación YZ.</span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | |||
| + | {| | ||
| + | |- | ||
| + | | [[Image:Alonso_et_al_2021a-image20.png|288px]] | ||
| + | | [[Image:Alonso_et_al_2021a-chart3.svg|center|288px]] | ||
| + | |} | ||
| + | </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 11.''' Resultados ensayo y simulación para las probetas fabricadas con la orientación XZ.</span></div> | ||
| + | |||
| + | ==Agradecimientos== | ||
| + | |||
| + | Los autores agradecen el apoyo del ''Instituto para la Competitividad Empresarial de la Junta de Castilla y León'' para la realización del proyecto DEMETER donde se contextualiza esta investigación. | ||
| + | |||
| + | ==Referencias== | ||
| + | |||
| + | <div id="1"></div> | ||
| + | [[#cite-1|[1]]] A. G. Salazar-Martín, M. A. Pérez, ''Materials & Design'', '''141, '''pág. 414-425 (2018). | ||
| + | |||
| + | [https://doi.org/10.1016/j.matdes.2018.01.008 https://doi.org/10.1016/j.matdes.2018.01.008] | ||
| + | |||
| + | <div id="2"></div> | ||
| + | <span style="text-align: center; font-size: 75%;">[[#cite-2|[2]]]</span> <span style="text-align: center; font-size: 75%;">S. H. Ahn, M. Montero, ''Rapid Prototyping'', '''8''', 4, pág. 248-257 (2002).</span> | ||
| + | |||
| + | [https://doi.org/10.1108/13552540210441166 https://doi.org/10.1108/13552540210441166] | ||
| + | |||
| + | <div id="3"></div> | ||
| + | [[#cite-3|[3]]] M. Domingo, Montero, “Aportaciones al conocimiento sobre la fabricación aditiva con la tecnología Fused Deposition Modeling”, (2016). | ||
| + | |||
| + | [https://hdl.handle.net/10803/359388 https://hdl.handle.net/10803/359388] | ||
| + | |||
| + | <div id="4"></div> | ||
| + | [[#cite-4|[4]]] A. Bellini, S. Güçeri, ''Rapid Prototyping Journal'', '''9''', 4, pág. 252-264 (2003). | ||
| + | |||
| + | [https://doi.org/10.1108/13552540310489631 https://doi.org/10.1108/13552540310489631] | ||
| + | |||
| + | <div id="5"></div> | ||
| + | [[#cite-5|[5]]] S. Dev, C. J. Hansen, ''Science in the Age of Experience'', pág. 559-575 (2017). | ||
| + | |||
| + | <div id="6"></div> | ||
| + | [[#cite-6|[6]]] M. Gedeon, “Materion Brush Performance Alloys: Strain Hardening”, ''Technical Tidbits Newsletter'', '''50''' (2013). | ||
| + | |||
| + | <div id="7"></div> | ||
| + | [[#cite-7|[7]]] ASTM D3039, Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials (2017). | ||
| + | |||
| + | [http://www.astm.org/cgi-bin/resolver.cgi?D3039D3039M-17 http://www.astm.org/cgi-bin/resolver.cgi?D3039D3039M-17] | ||
| + | |||
| + | <div id="8"></div> | ||
| + | [[#cite-8|[8]]] ASTM D695, Standard Test Method for Compressive Properties of Rigid Plastics (2015). | ||
| + | |||
| + | [http://www.astm.org/cgi-bin/resolver.cgi?D695-15 http://www.astm.org/cgi-bin/resolver.cgi?D695-15] | ||
| + | |||
| + | <div id="9"></div> | ||
| + | [[#cite-9|[9]]] M. Bertoldi, M. A. Yardimci, ''1998 International Solid Freeform Fabrication Symposium '' (1998). | ||
| + | |||
| + | [http://dx.doi.org/10.26153/tsw/646 http://dx.doi.org/10.26153/tsw/646] | ||
| + | |||
| + | <div id="10"></div> | ||
| + | [[#cite-10|[10]]] MSC Software Corporation, ''Manual de Marc 2010'' | ||
| + | |||
| + | <div id="11"></div> | ||
| + | [[#cite-11|[11]]] ASTM D790, Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials (2017). | ||
| + | |||
| + | [http://www.astm.org/cgi-bin/resolver.cgi?D790-17 http://www.astm.org/cgi-bin/resolver.cgi?D790-17] | ||
Latest revision as of 21:45, 26 November 2022
1 Introducción
La fabricación aditiva engloba las tecnologías que crean objetos tridimensionales capa a capa. Esta forma de fabricación ha despertado mucho interés por parte de la industria al presentar ventajas frente a los métodos tradicionales de conformado, como la reproducción de casi cualquier geometría, la rapidez desde el diseño a la obtención de la pieza final, la personalización y la competitividad en series cortas. En la tecnología Fused Deposition Modeling (FDM), la más extendida actualmente, cada capa se construye generalmente mediante hilos de material termoplástico fundido extruidos a través de una boquilla. Los parámetros de fabricación definidos para cada pieza, como la orientación de la pieza respecto a la impresora, las trayectorias de los hilos que forman el relleno de cada capa o su densidad, condicionan sus características finales como el acabado superficial o las propiedades mecánicas [1].
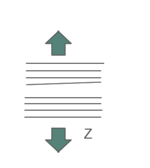
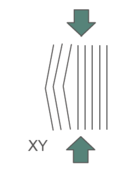
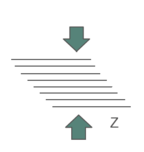
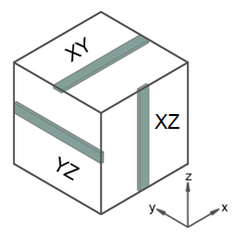
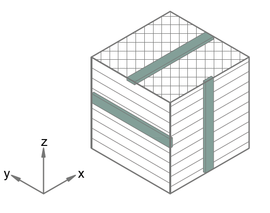
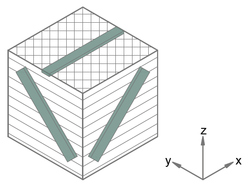
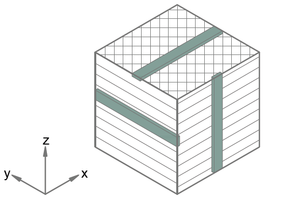
El comportamiento mecánico de una pieza procesada por FDM es complejo, al variar sus propiedades en función de la dirección en la que se miden y del estado de tensión al que se encuentre sometida [2]. Esto se debe a la fabricación mediante superposición de capas, de manera que las direcciones en las que los hilos se encuentran alineados con las cargas son más resistentes a tracción que a compresión, al contrario que la dirección en la que se apilan las capas (Figura 1).
Esta característica es la que limita la realización de predicciones del comportamiento mecánico de estas piezas a través de análisis de elementos finitos (FEA). Normalmente estos análisis se llevan a cabo mediante programas comerciales de simulación, los cuales llevan implementados modelos de material que no reproducen la complejidad del comportamiento del material FDM. El desconocimiento existente respecto a cómo se van a comportar las piezas obtenidas por esta tecnología limita las aplicaciones del FDM para la fabricación de piezas funcionales o con responsabilidad estructural.
El objetivo de este trabajo es, por tanto, reducir la incertidumbre respecto al comportamiento mecánico de las piezas fabricadas por FDM a partir de materiales termoplásticos.
Para ello se va a definir una metodología a partir de modelos teóricos de comportamiento de los materiales y de ensayos experimentales de caracterización, que podrá ser implementada en programas de simulación para adaptarlos al material FDM y poder realizar predicciones de su comportamiento.
2 Modelo de comportamiento teórico
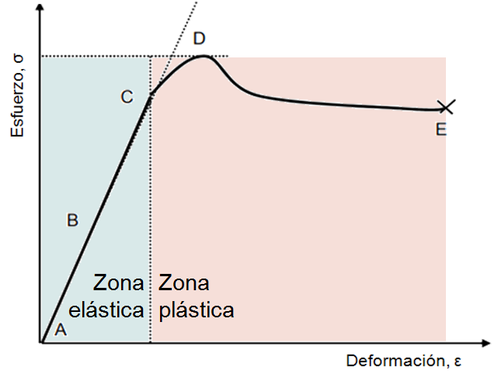
El comportamiento mecánico de los materiales se determina a partir de ensayos experimentales que proporcionan las curvas esfuerzo-deformación. Las curvas de comportamiento de los materiales termoplásticos se caracterizan por tener una zona elástica y otra plástica (Figura 2).
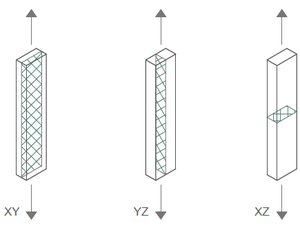
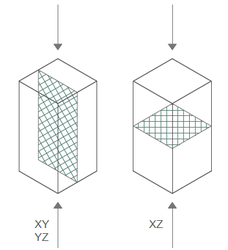
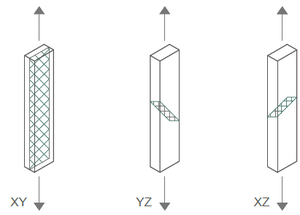
Además, los materiales una vez procesados mediante la tecnología FDM presentan tres direcciones principales de comportamiento según la disposición de los hilos del material. Por tanto, para definir este comportamiento se utilizan modelos ortótropos [3,4,5], que tienen en cuenta las propiedades de cada una de las direcciones, obtenidas mediante ensayos de probetas fabricadas en diferentes planos (Figura 3).
Así, mientras que para la zona elástica del material es más común la definición de modelos ortótropos que tengan en cuenta las diferencias en el comportamiento de las direcciones principales, no lo es para la parte plástica.
Otra característica del comportamiento derivada de la orotropía del material una vez procesado es la diferente respuesta ante esfuerzos de tracción y compresión que deberá tenerse en cuenta a la hora de definir el modelo.
A continuación se van a definir los modelos teóricos de comportamiento, para la parte elástica y para la parte plástica, que tendrán en cuenta todas las variables del comportamiento de los termoplásticos procesados por FDM.
2.1 Comportamiento elástico
Para modelar la parte elástica o lineal del comportamiento se sigue la ley de Hooke, ecuación (1), que establece que el esfuerzo es proporcional a la deformación. La constante de proporcionalidad entre ambas propiedades es la matriz de rigidez, que es característica de cada material y se construye a partir de las constantes mecánicas del mismo.
|
|
(1) |
Para el material FDM se utiliza la matriz de rigidez ortótropa, que se define con 9 constantes independientes establecidas a partir de las propiedades mecánicas del material, ecuación (2). En este caso se definirán dos matrices de rigidez, una a tracción y otra a compresión. Así, para modelar la parte elástica será necesaria una caracterización a tracción, a compresión y a cortadura del material, ya que en materiales ortótropos el módulo de cizalladura no se puede obtener a partir de las propiedades a tracción.
|
|
(2) |
Dónde εi es la deformación longitudinal en la dirección i, γi la deformación transversal en el plano ij, σi la tensión normal en la dirección i, τi la tensión tangencial en el plano ij, Ei el módulo de Young en la dirección i, νij el coeficiente de Poisson en el plano ij y Gij el módulo de cortadura en el plano ij.
2.2 Comportamiento plástico
Para modelar la parte plástica se utilizan los criterios de plasticidad, que establecen la condición a partir de la cual tiene lugar la deformación plástica en un material. En la metodología definida en este trabajo se utilizará el criterio de Von Mises, ecuación (3), por ser el que proporciona los resultados más optimizados.
|
|
(3) |
Donde σi es la tensión principal del tensor de tensiones en la dirección i y σe el límite elástico.
El comportamiento una vez alcanzado el límite elástico del material se rige a través de la curva de plasticidad que relaciona el esfuerzo frente a la deformación plástica [6]. Esta curva se obtiene de los ensayos experimentales a rotura a tracción y a compresión, y sus parámetros se pueden definir a través del ajuste de la curva experimental a una función potencial, ecuación (4).
|
|
(4) |
Dónde K es un coeficiente de fuerza y n el exponente de endurecimiento por deformación.
Cada material tendrá un límite elástico y una curva de plasticidad diferente en cada orientación y para cada tipo de esfuerzo, excepto para la dirección XZ a tracción, cuyo comportamiento es frágil y no presenta plasticidad, por lo que para ese caso solo se definirá el límite elástico.
3 Caracterización experimental
Para alimentar el modelo de comportamiento teórico definido es necesaria una caracterización experimental del material una vez procesado. Para ello será necesario mantener los parámetros de impresión constantes durante la fabricación de las probetas.
Como no existe una normativa específica de caracterización de materiales procesados por FDM se han definido las normas más adecuadas para obtener las propiedades mecánicas necesarias para la definición del modelo.
3.1 Ensayo de tracción
Para los ensayos a tracción se utilizará la norma ASTM D3039 [7] que emplea probetas rectangulares para evitar zonas de concentración de tensiones [2]. Se ensayarán 5 probetas para cada una de las orientaciones de fabricación (Figura 4).
De este ensayo se obtendrá para cada dirección el módulo de Young (Ex, Ey, Ez), el coeficiente de Poisson (νxy, νyz, νxz), el límite elástico (σe-x, σe-y, σe-z) y la curva de plasticidad.
3.2 Ensayo de compresión
Para los ensayos a compresión se utilizará la norma ASTM D695 [8] con probetas prismáticas para una mayor sencillez en su fabricación. Se utilizarán probetas más alargadas para la obtención de las propiedades elásticas (12,7 x 12,7 x 50,8 mm) y más cortas para las propiedades plásticas (12,7 x 12,7 x 25,4 mm). Por la simetría de las probetas, dos de las orientaciones (XY e YZ) serán equivalentes y tendrán, por tanto, las mismas propiedades. Se fabricarán 5 probetas para cada orientación de fabricación (Figura 5).
De este ensayo se obtendrá para cada dirección el módulo de Young (Ex=Ey, Ez), el límite elástico (σe-x=σe-y, σe-z) y la curva de plasticidad a compresión.
3.3 Ensayo de cortadura
Para obtener los módulos de cortadura de un material ortótropo es necesario hacer un ensayo experimental específico. En este caso se llevará a cabo un ensayo Off-Axis que consiste en la realización de un ensayo a tracción de probetas fabricadas con las fibras inclinadas. Para el material FDM otros autores han utilizado una inclinación de 45º respecto a la dirección principal [3,4,9], pudiéndose obtener el módulo de cortadura a partir de la ecuación (5).
|
|
(5) |
Dónde E1 y ν12 son las constantes obtenidas de la tracción de las probetas Off-Axis.
Para un relleno de ±45º la probeta XY coincidirá con la definida a tracción, por lo que no habría que volver a ensayarla. Además, al utilizar una inclinación de 45º las otras dos orientaciones serían simétricas, pudiendo ensayar únicamente una orientación con una repetitividad de 5 ensayos (Figura 6).
De los ensayos off-axis se obtiene el módulo de Young y el coeficiente de Poisson, a partir de los cuales calculamos el módulo de cortadura a través de la ecuación (5).
4 Construcción del modelo de cálculo
Una vez definido el modelo teórico del comportamiento del material FDM y la caracterización necesaria para poder construirlo se procedió con el desarrollo de su implementación en programas comerciales de cálculo mediante elementos finitos.
La incorporación del modelo en estos programas se lleva a cabo a través de la programación de subrutinas que se introducen en el software para ampliar sus opciones de cálculo. En este caso se modificará la parte elástica y la plástica del modelo de material para adaptarlas al comportamiento de los procesados FDM.
4.1 Modelo para la parte elástica
Para modificar la asignación de las propiedades de la parte elástica del material se utilizan subrutinas que permiten la introducción de la matriz que relaciona el esfuerzo con la deformación. En primer lugar la subrutina obtendrá del cálculo el valor de la tensión media en el punto a asignar, le evaluará y en función del estado de tensión en el que se encuentre trabajando le asignará la matriz de rigidez a tracción o compresión, construidas a partir de las propiedades mecánicas del material.
4.2 Modelo para la parte plástica
Para definir el comportamiento en la parte plástica del material se utilizan subrutinas que permiten introducir la curva que relaciona el esfuerzo con la deformación plástica, basándose en el criterio de plasticidad de Von Mises. A través de la programación de la subrutina se aplicará este criterio utilizado para materiales isotrópicos a un material con comportamiento ortótropo.
El primer paso de la programación conlleva la definición de las curvas de plasticidad, que se introducirán en la subrutina a través de dos funciones: el esfuerzo en función de la deformación plástica, ecuación (6), y la pendiente de endurecimiento, ecuación (7).
|
|
(6) |
|
|
(7) |
A continuación se define el criterio de selección de la curva de plasticidad a asignar en cada punto de integración para cada instante, que se realizará evaluando el tensor de tensiones asociado, obtenido del propio cálculo. La subrutina evaluará el valor absoluto de las tensiones de la diagonal del tensor y, en función de la magnitud de estas tensiones, establecerá la dirección o direcciones dominantes en el punto de integración analizado. Una vez determinada la dirección se evaluará el estado de tensión al que está sometido el punto en esa dirección, es decir, tracción si es positivo o compresión si es negativo y, en función de esto, establecerá la curva de plasticidad que va a seguir ese punto en el incremento analizado. Para las situaciones en las que dos o las tres direcciones estén sometidas a la misma tensión se asignará la curva de plasticidad media de las direcciones dominantes.
5 Validación
Una vez definida la metodología se llevó a cabo una validación de la misma a través de ensayos experimentales, con el objetivo de conocer la calidad de las predicciones que proporciona el modelo de simulación definido.
En primer lugar se realizó una caracterización completa del material una vez procesado. En este caso se utilizó una poliamida procesada con los parámetros de impresión de la Tabla 1.
| Diámetro del hilo | 1,50 mm |
| Altura de capa | 0,20 mm |
| Número de contornos | 2 |
| Relleno | ±45º |
| Densidad del relleno | 100% |
| Temperatura de fusión | 250ºC |
| Temperatura de la cama | 150ºC |
Se realizaron los ensayos a tracción, compresión y cortadura definidos anteriormente para las tres orientaciones, obteniéndose las propiedades mecánicas ortótropas elásticas y plásticas del material (Tabla 2).
| XY | YZ | XZ | ||
| Tracción | E (MPa) | 1451,40 | 1480,20 | 1530,40 |
| ν | 0,45 | 0,40 | 0,45 | |
| σe (MPa) | 38,06 | 39,32 | 14,98 | |
| Compresión | E (MPa) | 1447,39 | 1447,39 | 1458,17 |
| σe (MPa) | 30,19 | 30,19 | 41,64 | |
| Cortadura | G (MPa) | 499,45 | 497,93 | 497,93 |
Una vez caracterizado se configuró el modelo de subrutinas con las propiedades y curvas obtenidas de los ensayos. Para la validación se implementaron las subrutinas en el software de simulación Marc (MSC Software) [10] mediante el lenguaje de programación FORTRAN.
El método de validación consistió en la comparación de los resultados de un ensayo experimental con los obtenidos al realizar la simulación del mismo ensayo, utilizando el modelo desarrollado una vez implementado.
Como ensayo se eligió uno de flexión a tres puntos sobre una probeta rectangular fabricada mediante FDM, por presentar resultados complejos al incluir diferentes estados de tensión en su comportamiento y ser sencillo de ejecutar. Para realizarlo se siguió la norma ASTM D790 [11] para probetas fabricadas en las tres orientaciones diferentes (Figura 7) e imponiendo un desplazamiento de 22 mm del pisador.
Se fabricaron y ensayaron tres probetas de cada orientación para obtener repetitividad en los resultados (Figura 8). Después, se realizaron las simulaciones del ensayo para cada orientación utilizando un modelo geométricamente equivalente al experimental y se obtuvieron las curvas carga - desplazamiento de ambos ensayos.
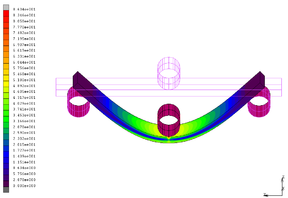
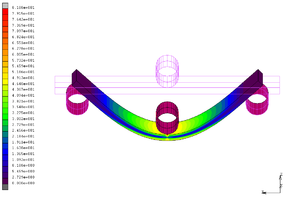
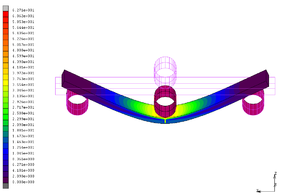
En las Figuras 9, 10 y 11 se muestran los resultados de tensiones equivalentes de Von Mises obtenidos de la simulación, junto con la comparación de las gráficas carga - desplazamiento experimentales y simuladas para cada dirección. Tanto en la dirección XY como en la dirección YZ el comportamiento durante el ensayo de las probetas era dúctil.
En la simulación de la orientación XY (Figura 9) se observan contornos simétricos en la zona de tracción y compresión y bajas tensiones en la línea neutra de la probeta. De la comparación de las curvas en esta dirección se aprecia la buena aproximación entre las predicciones y los resultados experimentales.
La orientación YZ (Figura 10) presenta un comportamiento muy similar a la XY tanto en los contornos de tensiones como en las curvas, aunque la predicción del modelo es menos precisa, con un error en la predicción de la carga comprendido entre el 10 y el 15%.
En la simulación de la orientación XZ (Figura 11) se aprecian diferencias significativas respecto a las otras orientaciones en la simulación, al igual que en el ensayo experimental. Los contornos de tensiones simulados presentan una concentración de tensiones en la zona central, donde se produce la rotura. En cuanto a la comparación de las curvas carga - desplazamiento, al llegar a romper la probeta durante el ensayo la simulación es menos precisa, ya que el modelo desarrollado no tiene en cuenta la vida y muerte de elementos. Por tanto, el modelo llega a predecir cuándo rompe la probeta, pero no permite conocer con exactitud la carga en ese instante, proporcionando un error en la predicción de hasta el 35%.
6 Conclusiones
En este trabajo se ha definido una metodología que permite la realización de predicciones del comportamiento mecánico de piezas procesadas por FDM al implementarse en programas de simulación de elementos finitos. Los modelos de material definidos tienen en cuenta el comportamiento ortótropo de estos materiales además de su diferente respuesta ante esfuerzos de tracción y compresión.
El método ha demostrado, mediante una validación experimental, ser capaz de proporcionar una buena aproximación del comportamiento de las piezas así fabricadas. También se han detectado ciertas debilidades en las predicciones en los casos en los que se produce la rotura del componente.
El modelo de simulación permite predecir cómo se va a comportar cualquier componente fabricado por FDM teniendo en cuenta su cuaderno de cargas. Únicamente se requiere la realización de una caracterización completa del material una vez procesado, como la definida en este trabajo.
Esto permite la optimización de parámetros de fabricación de las piezas como la orientación de impresión en función de su comportamiento mecánico final. Además, permite determinar si un componente obtenido por FDM va a soportar las cargas a las que va a ser sometido sin necesidad de ser fabricado y ensayado experimentalmente.
Agradecimientos
Los autores agradecen el apoyo del Instituto para la Competitividad Empresarial de la Junta de Castilla y León para la realización del proyecto DEMETER donde se contextualiza esta investigación.
Referencias
[1] A. G. Salazar-Martín, M. A. Pérez, Materials & Design, 141, pág. 414-425 (2018).
https://doi.org/10.1016/j.matdes.2018.01.008
[2] S. H. Ahn, M. Montero, Rapid Prototyping, 8, 4, pág. 248-257 (2002).
https://doi.org/10.1108/13552540210441166
[3] M. Domingo, Montero, “Aportaciones al conocimiento sobre la fabricación aditiva con la tecnología Fused Deposition Modeling”, (2016).
https://hdl.handle.net/10803/359388
[4] A. Bellini, S. Güçeri, Rapid Prototyping Journal, 9, 4, pág. 252-264 (2003).
https://doi.org/10.1108/13552540310489631
[5] S. Dev, C. J. Hansen, Science in the Age of Experience, pág. 559-575 (2017).
[6] M. Gedeon, “Materion Brush Performance Alloys: Strain Hardening”, Technical Tidbits Newsletter, 50 (2013).
[7] ASTM D3039, Standard Test Method for Tensile Properties of Polymer Matrix Composite Materials (2017).
http://www.astm.org/cgi-bin/resolver.cgi?D3039D3039M-17
[8] ASTM D695, Standard Test Method for Compressive Properties of Rigid Plastics (2015).
http://www.astm.org/cgi-bin/resolver.cgi?D695-15
[9] M. Bertoldi, M. A. Yardimci, 1998 International Solid Freeform Fabrication Symposium (1998).
http://dx.doi.org/10.26153/tsw/646
[10] MSC Software Corporation, Manual de Marc 2010
[11] ASTM D790, Standard Test Methods for Flexural Properties of Unreinforced and Reinforced Plastics and Electrical Insulating Materials (2017).
Document information
Published on 17/01/21
Accepted on 04/07/19
Submitted on 29/05/19
Volume 05 - Comunicaciones Matcomp19 (2021), Issue Núm. 1 - Comportamiento en servicio – Inspección y reparación., 2021
DOI: 10.23967/r.matcomp.2021.01.012
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?