m (Scipediacontent moved page Draft Content 745785375 to Jose et al 2021a) |
(Tag: Visual edit) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| − | == | + | ==1 Introducción == |
| − | + | Las estructuras sándwich fabricadas con materiales compuestos son ampliamente utilizadas en numerosas aplicaciones industriales debido a su alta relación rigidez/peso específico. Además de las buenas propiedades mecánicas, estos materiales presentan otras propiedades interesantes como la resistencia a la corrosión, que los hacen idóneos para ser utilizados en aplicaciones navales. Su permeabilidad a las ondas electromagnéticas, también los hace idóneos para la protección de antenas y de los radomos de los aviones. Aunque estas estructuras no estan diseñadas para soportar cargas de impacto, durante su vida en servicio, son susceptibles de estar sometidas a impactos de baja y de alta velocidad. Es por ello que la necesidad de estudiar el fenómeno de impacto en este tipo de estructuras para optimizar su comportamiento es latente. | |
| − | + | ||
| − | == | + | El principal incoveniente que presentan estas estructuras es su baja resistencia frente a impactos transversales. Esto sucede porque normalmente las pieles de las que se compone la estructura sándwich son muy delgadas y las deformaciones que presentan los núcleos son muy altas. Ante una carga transversal, se puede producir una indentación permanente o incluso la perforación. Estos daños irreversibles pueden comprometer el comportamiento en servicio de estas estructuras haciendo necesaria su reparación o sustitución. |
| − | < | + | |
| + | En la literatura hay disponibles numerosos estudios del comportamiento frente a impacto de estructuras sándwich. En cuanto a estudios de impacto a baja velocidad, Wang et al. [4] llevaron a cabo un estudio experimental y numérico en paneles fabricados con pieles de tejido de fibra de carbono y nucleo de poliuretano con diferentes proyectiles y energías de impacto, identificando los modos de daño característicos en cada configuración. Mena et al. [1] realizaron un estudio numérico en paneles de fibra de vidrio en una resina fenólica con un núcleo de panel de abeja, en concreto de Nomex, obteniendo un buen ajuste con los datos experimentales. Este modelo es capaz de predecir aspectos como el área dañada producto del impacto y captura efectos como la rotura de fibras en la piel delantera así como la deformación plástica del núcleo. | ||
| + | |||
| + | También se han realizado numerosos estudios de impactos de alta velocidad en estructuras sándwich. Aktay et al. [2] estudiaron el comportamiento de paneles sándwich con pieles de fibra de carbono en una matriz epoxi y núcleo de panel de abeja, en concreto de Nomex, así como de polietirimida. Utilizaron un criterio de fallo 2D para laminados de cinta y realizaron ensayos experimentales a compresión para caracterizar el comportamiento de la espuma. Este modelo predice los modos de fallo del compuesto, sin embargo, el fallo del núcleo presenta algunas limitaciones. Iváñez et al. [7] estudiaron la respuesta a impacto de estructuras sandwich de fibra de vidrio tipo E en matrix poliéster con núcleo de PVC. La comparación de simulaciones numéricas de placas espaciadas frente a la estructura completa con el nucleo revela la mínima influencia de este último en impactos de alta velocidad. | ||
| + | |||
| + | Dentro de este contexto, se propone el desarrollo de un modelo numérico para estudiar el comportamiento de estructuras sándwich de fibra de vidrio tipo E en matrix poliéster con núcleo de PVC en las inmediaciones del límite balístico. Una vez validado el modelo con resultados experimentales de la literatura [7], se procederá al estudio de la influencia del espesor de las pieles en ambas caras. La optimización de este tipo de estructuras fabricándolas de una forma no simétrica, a diferencia de como se hace usualmente constituye un nuevo campo de estudio a explorar. | ||
| + | |||
| + | ==2 Descripción del modelo numérico== | ||
| + | |||
| + | ==='''2.1''' Pieles=== | ||
| + | |||
| + | Para la simulación de las pieles se ha utilizado un modelo numérico 3D. La respuesta constitutiva de las pieles se define mediante un modelo de daño continuo que tiene en cuenta diferentes criterios de fallo asociados a un modelo analítico previamente desarrollado por Alonso et al. [8]. La modelización de las estructuras sándwich se ha llevado a cabo en el software comercial de elementos finitos Abaqus/Explicit mediante una subrutina VUMAT. | ||
| + | |||
| + | Para obtener buenas predicciones de la respuesta mecánica de las pieles el modelo de daño continuo se combina con los criterios de daño que están basados en los propuestos por Hashin [9] y Chang-Chang [10] pero ligeramente modificados para adaptarlos al modelo teórico de Alonso et al. [8]. La evolución del daño se implementa por medio de una función de ablandamiento que se controla a través de la energía de fractura en cada dirección. La respuesta mecánica se considera elástico-lineal hasta el inicio del daño y después viene dada por: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="vertical-align: top;margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>\epsilon ={S}_{d}\sigma</math> | ||
| + | |} | ||
| + | | style="vertical-align: top;width: 5px;text-align: right;white-space: nowrap;"|(1) | ||
| + | |} | ||
| + | |||
| + | |||
| + | donde <math display="inline">{S}_{d}</math> es la matriz de flexibilidad. En notación de Voigt, la ecuación (1) se escribe de la siguiente forma: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>\left( \begin{matrix}{\epsilon }_{11}\\{\epsilon }_{22}\\\begin{matrix}{\epsilon }_{33}\\{\gamma }_{12}\\\begin{matrix}{\gamma }_{23}\\{\gamma }_{13}\end{matrix}\end{matrix}\end{matrix}\right) =</math><math>\left( \begin{matrix}{C}_{n}&{0}_{3x3}\\{0}_{3x3}&{C}_{s}\end{matrix}\right) \left( \begin{matrix}{\sigma }_{11}\\{\sigma }_{22}\\\begin{matrix}{\sigma }_{33}\\{\sigma }_{12}\\\begin{matrix}{\sigma }_{23}\\{\sigma }_{13}\end{matrix}\end{matrix}\end{matrix}\right)</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(2) | ||
| + | |} | ||
| + | |||
| + | |||
| + | donde <math display="inline">{C}_{n}</math> y <math display="inline">{C}_{s}</math> son dos submatrices que dependen de las propiedades del material y se definen a continuación: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>{C}_{n}=\left( \begin{matrix}\frac{1}{{E}_{11}(1-{d}_{1})}&-\frac{{\nu }_{21}}{{E}_{22}}&-\frac{{\nu }_{31}}{{E}_{22}}\\-\frac{{\nu }_{11}}{{E}_{11}}&\frac{1}{{E}_{22}(1-{d}_{2})}&-\frac{{\nu }_{32}}{{E}_{33}}\\-\frac{{\nu }_{13}}{{E}_{11}}&-\frac{{\nu }_{23}}{{E}_{22}}&\frac{1}{{E}_{33}(1-{d}_{3})}\end{matrix}\right)</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(3) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>{C}_{s}=\left( \begin{matrix}\frac{1}{{G}_{12}(1-{d}_{4})}&0&0\\0&\frac{1}{{G}_{23}(1-{d}_{5})}&0\\0&0&\frac{1}{{G}_{13}(1-{d}_{6})}\end{matrix}\right)</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(4) | ||
| + | |} | ||
| + | |||
| + | |||
| + | donde <math display="inline">{E}_{ij}</math>, <math display="inline">{\nu }_{ij}</math>, <math display="inline">{G}_{ij}</math> y <math display="inline">{d}_{k}</math> para <math display="inline">(i=</math><math>1,\, 2,\, 3)</math>, <math display="inline">(j=1,\, 2,\, 3)</math> y <math display="inline">(k=</math><math>1,\, 2,\, 3,\, 4,\, 5,\, 6)</math> son los módulos de Young, los coeficientes de Poisson, los módulos de cortadura y las variables de daño respectivamente. Estas últimas variables de daño están formuladas en deformaciones de tal forma que proporcionen una caída lineal a partir del inicio del daño. | ||
| + | |||
| + | Los diferentes criterios que se han utilizado para activar las distintas variables de daño, modificando así la rigidez del material en cada dirección son las siguientes: | ||
| + | |||
| + | :* Rotura de fibras en las direcciones 11 y 22, <math display="inline">{(d}_{1}\, y\, {d}_{2}</math>) : | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>{\left( \frac{{\sigma }_{11}}{{X}_{11i}}\right) }^{2}+{\left( \frac{{\sigma }_{12}}{{S}_{12}}\right) }^{2}+</math><math>{\left( \frac{{\sigma }_{13}}{{S}_{13}}\right) }^{2}=1</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(5) | ||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>{\left( \frac{{\sigma }_{22}}{{X}_{22i}}\right) }^{2}+{\left( \frac{{\sigma }_{12}}{{S}_{12}}\right) }^{2}+</math><math>{\left( \frac{{\sigma }_{13}}{{S}_{13}}\right) }^{2}=1</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(6) | ||
| + | |} | ||
| + | |||
| + | |||
| + | donde los denominadores son las tensiones máximas en sus respectivas direcciones y <math display="inline">(i=</math><math>c,\, t)</math> contempla efectos de tensión y compresión ya que se tiene en cuenta el fenómeno de cierre de grietas. | ||
| + | |||
| + | :* Rotura de matriz en el plano, <math display="inline">{(d}_{4}</math>): | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>{\left( \frac{{\sigma }_{12}}{{S}_{12s}}\right) }^{2}=1</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(7) | ||
| + | |} | ||
| + | |||
| + | |||
| + | donde <math display="inline">{S}_{12s}</math> es distinto de <math display="inline">{S}_{12}</math> en (5) y (6) porque se considera que la tensión máxima para el fallo de fibras, <math display="inline">{S}_{12}</math>, es distinto a la tensión máxima para el fallo de matriz <math display="inline">{S}_{12s}</math>. | ||
| + | |||
| + | :* Compresión en la dirección 33, <math display="inline">{(d}_{3}</math>): | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>{\left( \frac{{\sigma }_{33}}{{X}_{33}}\right) }^{2}=1</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(8) | ||
| + | |} | ||
| + | |||
| + | |||
| + | :* Rotura de fibra y matriz en las direcciones 13 y 23, <math display="inline">{(d}_{5}\, y\, {d}_{6}</math>): | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>{\left( \frac{{\sigma }_{13}}{{S}_{13s}}\right) }^{2}+{\left( \frac{{\sigma }_{23}}{{S}_{23s}}\right) }^{2}=</math><math>1</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(9) | ||
| + | |} | ||
| + | |||
| + | |||
| + | donde el criterio de iniciación (9) sirve para activar dos funciones de daño, aunque a partir del momento en el que se cumple (9), <math display="inline">{d}_{5}\, y\, {d}_{6}</math> pueden evolucionar independientemente. | ||
| + | |||
| + | Además de este modelo continuo de daño, la unión entre láminas (cada 0.6 mm) en las pieles se ha modelado mediante el uso de elementos cohesivos. | ||
| + | |||
| + | ==='''2.2''' Núcleo=== | ||
| + | |||
| + | El modelo constitutivo del núcleo de espuma PVC se ha modelado mediante el uso del módulo de espumas de fácil compactación disponible en Abaqus. Este módulo es el que mejor se ajusta al comportamiento de este tipo de espumas [7]. Para ello se ha elegido la opción de endurecimiento isótropo y se han tomado los valores experimentales obtenidos por Iváñez et al. [7] en ensayos de compresión uniaxiales. La curva tensión-deformación se observa en la Figura 1 donde se identifican tres zonas. Una primera zona elástica-lineal hasta alcanzar el valor del límite elástico, <math display="inline">{\sigma }_{y}</math> . Una segunda zona donde la tensión no aumenta a pesar del incremento de deformación debido al colapso de las células en el interior de la espuma. Y una tercera zona que se alcanza con tensiones de compresión muy altas, que se denomina de densificación donde la tensión se incrementa con una pendiente diferente a la elástica inicial. Mediante la introducción de <math display="inline">{\sigma }_{y}=</math><math>2.63\, MPa</math>, <math display="inline">{\sigma }_{d}=9.31\, MPa</math>, <math display="inline">{\epsilon }_{y}=</math><math>0.0302</math>, <math display="inline">{\epsilon }_{d1}=0.4813</math>, <math display="inline">{\epsilon }_{d2}=</math><math>0.9</math> y del coeficiente de Poisson <math display="inline">\nu =0.3</math> la curva queda determinada. Estos valores han sido obtenidos de la literatura para esta espuma [7]. | ||
| + | [[File:Jose_et_al_2021a-image5.png|centre|600x600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 1.''' Curva tensión-deformación del modelo constitutivo utilizado para modelar el núcleo de PVC [7].</span></div> | ||
| + | |||
| + | ==='''2.3''' Definición del modelo numérico=== | ||
| + | |||
| + | Para la definición del modelo numérico en Abaqus/Explicit se han utilizado dos tipos de elementos. Por un lado, para las pieles y el núcleo se han utilizado elementos trilineales de integración reducida (C3D8R), con un total de 502695 elementos. Cada lámina, tiene un espesor igual a 0.6 mm y el núcleo tiene un espesor de 30 mm. Para la unión entre láminas se han utilizado elementos cohesivos (COH3D8), con un total de 111710 elementos. Cada unión cohesiva entre láminas tiene un espesor de 0.01 mm. Se ha utilizado un gradiente ascendente desde el punto de impacto hacia los bordes para asegurar un mallado más fino en las inmediaciones del impacto. La Figura 2 muestra la configuración final del mallado. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;">[[File:Captura de pantalla 2022-11-26 200406.png|centre|484x484px]]</div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 2.''' Configuración final de la malla utilizada.</span></div> | ||
| + | |||
| + | Debido a que en la fase de densificación se pueden alcanzar deformaciones muy altas (del orden del 90%), se ha utilizado una deformación equivalente como criterio para la eliminación de elementos dentro de la espuma. Cuando la deformación equivalente descrita en la ecuación (10) alcanza la unidad el elemento se elimina. | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;border-collapse: collapse;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="margin:auto;width: 100%;" | ||
| + | |- | ||
| + | | <math>{\epsilon }_{eq}=\sqrt{{\epsilon }_{11}^{2}+{\epsilon }_{22}^{2}+{\epsilon }_{33}^{2}+{\gamma }_{12}^{2}+{\gamma }_{23}^{2}+{\gamma }_{13}^{2}}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(10) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Además, se ha definido un coeficiente de fricción dependiente de la velocidad de deslizamiento. Los elementos tienen control de hourglass activado (enhanced). | ||
| + | |||
| + | ==3 Validación== | ||
| + | |||
| + | Uno de los aspectos fundamentales que un modelo numérico para impactos de alta velocidad debe cumplir es la predicción del límite balístico, así como de las velocidades residuales. Para verificar que el modelo numérico funciona correctamente, se han comparado las predicciones de la velocidad residual del modelo con los datos experimentales obtenidos de la literatura [6]. Esta validación se ha limitado al límite balístico y sus inmediaciones ya que el estudio de optimización se va a realizar en ese entorno por ser el punto de mayor interés de cara a la seguridad de la estructura. La comparación de los resultados experimentales [6] con los numéricos puede verse en la Figura 3. | ||
| + | [[File:Jose_et_al_2021a-image7.png|centre|600x600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 3.''' Velocidad de impacto vs Velocidad de salida experimentales y numéricas.</span></div> | ||
| + | |||
| + | La Figura 3 permite afirmar que existe una buena correspondencia entre los valores proporcionados por el modelo numérico y los valores experimentales [6] en las inmediaciones del límite balístico por lo que se da por validado el modelo numérico. El límite balístico experimental es 344 <math display="inline">m{s}^{-1}</math> mientras que el numérico es 310 <math display="inline">m{s}^{-1}</math>, por lo que el modelo numérico subestima ligeramente el límite balístico con un error del 9.9 %. A la vista de estos resultados y con el modelo validado se puede proceder a realizar el estudio de optimización. | ||
| + | |||
| + | ==4 Optimización de la distribución de láminas== | ||
| + | |||
| + | Con el objetivo de definir la configuración óptima para la distribución de láminas en las caras frontal y posterior se han definido 8 configuraciones con la nomenclatura indicada a continuación. Se han utilizado un total de 10 láminas en todos los casos analizados. Las configuraciones se identifican gracias a un código <math display="inline">(i-</math><math>j)</math> siendo <math display="inline">i</math> y <math display="inline">j</math> el número de láminas en las caras delantera y trasera respectivamente. A modo de ejemplo en la Figura 4 se muestra una imagen representativa de uno de los estudios realizados correspondiente a la configuración 6-4, impactada a 330 <math display="inline">m{s}^{-1}</math> en la cual se produce perforación. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;">[[File:Captura de pantalla 2022-11-26 200446.png|centre|442x442px]]</div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 4.''' Vista del proceso de penetración en una estructura sándwich con una configuración tipo 6-4 impactada a 330 </span> <math display="inline">m{s}^{-1}</math></div> | ||
| + | |||
| + | En la Figura 4 se puede apreciar que se produce bastante flexión en las láminas de la parte trasera. Este fenómeno es más acusado cuanto más disminuye el número de láminas en dicha cara. | ||
| + | |||
| + | Las configuraciones estudiadas se han probado con dos velocidades de impacto cercanas al límite balístico, como se puede ver en las Figuras 5 y 6. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;"> [[Image:Jose_et_al_2021a-image9.png|426px]] </span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 5.''' Velocidad residual para una velocidad de impacto de 330 </span> <math display="inline">m{s}^{-1}</math><span style="text-align: center; font-size: 75%;"> con las distintas configuraciones.</span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;"> [[Image:Jose_et_al_2021a-image10.png|426px]] </span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 6.''' Velocidad residual para una velocidad de impacto de 350 </span> <math display="inline">m{s}^{-1}</math><span style="text-align: center; font-size: 75%;"> con las distintas configuraciones.</span></div> | ||
| + | |||
| + | En las Figuras 5 y 6, la representación de las velocidades residuales frente a la misma velocidad de impacto con distintas configuraciones reflejan una tendencia. Desde la configuración 8-2 hasta la 5-5 el valor de la velocidad residual sufre pequeñas variaciones pero se puede decir que permanece aproximadamente constante para ambos casos. Para entender estas pequeñas variaciones habría que cuantificar la energía que se absorbe por cada mecanismo de fallo. Sin embargo, a partir de la configuración 5-5 hasta la 1-9 se produce un claro descenso de la velocidad residual conforme se aumenta el número de láminas en la cara trasera y se disminuye en la delantera. Este comportamiento es más acusado para el caso de la Figura 5. | ||
| + | |||
| + | Este comportamiento puede tener su explicación en los fenómenos de flexión apreciables en la Figura 4. Al estar las láminas de la cara delantera pegadas al núcleo, este contribuye a disminuir la flexión de dichas láminas. Por el contrario, las láminas de la cara trasera no se encuentran con esta resistencia adicional por lo que la flexión es mayor en ellas. Debido a estas condiciones de contorno, en la cara delantera las láminas fallan localmente por compresión mientras que en la cara trasera fallan por tensión, lo cual requiere más energía. Por este motivo, por lo menos para las velocidades estudiadas, parece más efectiva una configuración que refuerce más la cara trasera en detrimento de la delantera. Con esto se consigue rigidizar más la cara trasera que no tiene ningún elemento de apoyo detrás. | ||
| + | |||
| + | En cuanto a la configuración óptima, harían falta más estudios a distintas velocidades para poder afirmar una en concreto. Con las simulaciones realizadas se puede afirmar que el comportamiento frente a impactos a altas velocidades en el entorno del límite balístico mejora a medida que se añaden láminas en la cara trasera. | ||
| + | |||
| + | ==5 Conclusiones== | ||
| + | |||
| + | Este trabajo se ha centrado en la simulación de impactos a alta velocidad en estructuras sándwich compuestas por pieles de fibra de vidrio tipo E en una matriz poliéster y un núcleo de PVC. Se ha hecho uso de un modelo de daño continuo 3D mediante una subrutina VUMAT para la simulación de las pieles y del módulo de espumas de fácil compactación de Abaqus para el núcleo. | ||
| + | |||
| + | Después de realizar la validación del modelo numérico con resultados experimentales [6], se han estudiado diferentes configuraciones para la distribución de las láminas en las caras delantera y trasera. Obviamente el número de láminas ha sido siempre el mismo, para poder estudiar la mejor configuración utilizando el mismo material dándole un sentido en términos económicos. | ||
| + | |||
| + | A la vista de los resultados obtenidos se puede concluir que para configuraciones que acumulan muchas láminas en la cara delantera hasta una configuración equilibrada (5-5) no hay diferencias muy significativas en las velocidades residuales. Sin embargo, para configuraciones que acumulan más láminas en la cara trasera, la velocidad residual disminuye significativamente. Esto puede deberse a los efectos de flexión que se producen en las láminas de la cara trasera al no tener ningún material detrás que las sustenten. | ||
| + | |||
| + | ==Agradecimientos== | ||
| + | |||
| + | Los autores agradecen al Ministerio de Economía y Empresa el apoyo prestado para la realización de este trabajo a través del proyecto “Estudio del comportamiento frente a impacto y post-impacto de palas de aerogenerador fabricadas de estructuras sándwich” (2018/00086/001). | ||
| + | |||
| + | ==Referencias== | ||
| + | |||
| + | [<span style="text-align: center; font-size: 75%;">1</span>] C. Mena, A. Zinno, ''Composite Structures,'' '''106''', pág. 326-339 (2012). [https://doi.org/10.1016/j.compstruct.2013.06.010 https://doi.org/10.1016/j.compstruct.2013.06.010] | ||
| + | |||
| + | [2] L. Aktay, A.F. Johnson, ''Computational Materials Science,'' '''32''', pág. 252-260 (2005). [https://doi.org/10.1016/j.commatsci.2004.09.044 https://doi.org/10.1016/j.commatsci.2004.09.044] | ||
| + | |||
| + | [3] M. Ghalami-Choobar, M. Sadighi, ''Aerospace Science and Technology,'' '''32''', pág. 142-152 (2014). [https://doi.org/10.1016/j.ast.2013.12.005 https://doi.org/10.1016/j.ast.2013.12.005] | ||
| + | |||
| + | [4] J. Wang, A.M. Waas, ''Composite Structures,'' '''96''', pág. 298-311 (2013). [https://doi.org/10.1016/j.compstruct.2012.09.002 https://doi.org/10.1016/j.compstruct.2012.09.002] | ||
| + | |||
| + | [5] S.L. Lopatnikov, B.A Gama, ''International Journal of Impact Engineering,'' '''30''', pág. 421-445 (2004). [https://doi.org/10.1016/S0734-743X(03)00066-6 https://doi.org/10.1016/S0734-743X(03)00066-6] | ||
| + | |||
| + | [6] B. Buitrago, S.K. García-Castillo, ''Composite Structures,'' '''64''', pág. 1052-1054 (2010). [https://doi.org/10.1016/j.compstruct.2011.03.028 https://doi.org/10.1016/j.compstruct.2011.03.028] | ||
| + | |||
| + | [7] I. Iváñez, C. Santiuste, ''Composite Structures,'' '''93''', pág. 2392-2399 (2011). 10.1016/j.matlet.2010.02.007 | ||
| + | |||
| + | [8] L.Alonso, S.K. García-Castillo, ''Materials Letters,'' '''143''', pág. 292-300 (2018). [https://doi.org/10.1016/j.compositesb.2018.01.030 https://doi.org/10.1016/j.compositesb.2018.01.030] | ||
| + | |||
| + | [9] Z. Hashin, ''Journal of Applied Mechanics,'' '''47''', pág. 329-334 (1980). 10.1115/1.3153664 | ||
| + | |||
| + | [10] F. Chang, K.A Chang, ''Journal of Composite Materials,'' '''21''', pág. 834-855 (1987). 10.1177/002199838702100904 | ||
| + | |||
| + | [11] Systemes D. Abaqus 6.14 User's manual, (2014). | ||
Latest revision as of 20:10, 26 November 2022
1 Introducción
Las estructuras sándwich fabricadas con materiales compuestos son ampliamente utilizadas en numerosas aplicaciones industriales debido a su alta relación rigidez/peso específico. Además de las buenas propiedades mecánicas, estos materiales presentan otras propiedades interesantes como la resistencia a la corrosión, que los hacen idóneos para ser utilizados en aplicaciones navales. Su permeabilidad a las ondas electromagnéticas, también los hace idóneos para la protección de antenas y de los radomos de los aviones. Aunque estas estructuras no estan diseñadas para soportar cargas de impacto, durante su vida en servicio, son susceptibles de estar sometidas a impactos de baja y de alta velocidad. Es por ello que la necesidad de estudiar el fenómeno de impacto en este tipo de estructuras para optimizar su comportamiento es latente.
El principal incoveniente que presentan estas estructuras es su baja resistencia frente a impactos transversales. Esto sucede porque normalmente las pieles de las que se compone la estructura sándwich son muy delgadas y las deformaciones que presentan los núcleos son muy altas. Ante una carga transversal, se puede producir una indentación permanente o incluso la perforación. Estos daños irreversibles pueden comprometer el comportamiento en servicio de estas estructuras haciendo necesaria su reparación o sustitución.
En la literatura hay disponibles numerosos estudios del comportamiento frente a impacto de estructuras sándwich. En cuanto a estudios de impacto a baja velocidad, Wang et al. [4] llevaron a cabo un estudio experimental y numérico en paneles fabricados con pieles de tejido de fibra de carbono y nucleo de poliuretano con diferentes proyectiles y energías de impacto, identificando los modos de daño característicos en cada configuración. Mena et al. [1] realizaron un estudio numérico en paneles de fibra de vidrio en una resina fenólica con un núcleo de panel de abeja, en concreto de Nomex, obteniendo un buen ajuste con los datos experimentales. Este modelo es capaz de predecir aspectos como el área dañada producto del impacto y captura efectos como la rotura de fibras en la piel delantera así como la deformación plástica del núcleo.
También se han realizado numerosos estudios de impactos de alta velocidad en estructuras sándwich. Aktay et al. [2] estudiaron el comportamiento de paneles sándwich con pieles de fibra de carbono en una matriz epoxi y núcleo de panel de abeja, en concreto de Nomex, así como de polietirimida. Utilizaron un criterio de fallo 2D para laminados de cinta y realizaron ensayos experimentales a compresión para caracterizar el comportamiento de la espuma. Este modelo predice los modos de fallo del compuesto, sin embargo, el fallo del núcleo presenta algunas limitaciones. Iváñez et al. [7] estudiaron la respuesta a impacto de estructuras sandwich de fibra de vidrio tipo E en matrix poliéster con núcleo de PVC. La comparación de simulaciones numéricas de placas espaciadas frente a la estructura completa con el nucleo revela la mínima influencia de este último en impactos de alta velocidad.
Dentro de este contexto, se propone el desarrollo de un modelo numérico para estudiar el comportamiento de estructuras sándwich de fibra de vidrio tipo E en matrix poliéster con núcleo de PVC en las inmediaciones del límite balístico. Una vez validado el modelo con resultados experimentales de la literatura [7], se procederá al estudio de la influencia del espesor de las pieles en ambas caras. La optimización de este tipo de estructuras fabricándolas de una forma no simétrica, a diferencia de como se hace usualmente constituye un nuevo campo de estudio a explorar.
2 Descripción del modelo numérico
2.1 Pieles
Para la simulación de las pieles se ha utilizado un modelo numérico 3D. La respuesta constitutiva de las pieles se define mediante un modelo de daño continuo que tiene en cuenta diferentes criterios de fallo asociados a un modelo analítico previamente desarrollado por Alonso et al. [8]. La modelización de las estructuras sándwich se ha llevado a cabo en el software comercial de elementos finitos Abaqus/Explicit mediante una subrutina VUMAT.
Para obtener buenas predicciones de la respuesta mecánica de las pieles el modelo de daño continuo se combina con los criterios de daño que están basados en los propuestos por Hashin [9] y Chang-Chang [10] pero ligeramente modificados para adaptarlos al modelo teórico de Alonso et al. [8]. La evolución del daño se implementa por medio de una función de ablandamiento que se controla a través de la energía de fractura en cada dirección. La respuesta mecánica se considera elástico-lineal hasta el inicio del daño y después viene dada por:
|
|
(1) |
donde es la matriz de flexibilidad. En notación de Voigt, la ecuación (1) se escribe de la siguiente forma:
|
|
(2) |
donde y son dos submatrices que dependen de las propiedades del material y se definen a continuación:
|
|
(3) |
|
|
(4) |
donde , , y para , y son los módulos de Young, los coeficientes de Poisson, los módulos de cortadura y las variables de daño respectivamente. Estas últimas variables de daño están formuladas en deformaciones de tal forma que proporcionen una caída lineal a partir del inicio del daño.
Los diferentes criterios que se han utilizado para activar las distintas variables de daño, modificando así la rigidez del material en cada dirección son las siguientes:
- Rotura de fibras en las direcciones 11 y 22, ) :
|
|
(5) |
|
|
(6) |
donde los denominadores son las tensiones máximas en sus respectivas direcciones y contempla efectos de tensión y compresión ya que se tiene en cuenta el fenómeno de cierre de grietas.
- Rotura de matriz en el plano, ):
|
|
(7) |
donde es distinto de en (5) y (6) porque se considera que la tensión máxima para el fallo de fibras, , es distinto a la tensión máxima para el fallo de matriz .
- Compresión en la dirección 33, ):
|
|
(8) |
- Rotura de fibra y matriz en las direcciones 13 y 23, ):
|
|
(9) |
donde el criterio de iniciación (9) sirve para activar dos funciones de daño, aunque a partir del momento en el que se cumple (9), pueden evolucionar independientemente.
Además de este modelo continuo de daño, la unión entre láminas (cada 0.6 mm) en las pieles se ha modelado mediante el uso de elementos cohesivos.
2.2 Núcleo
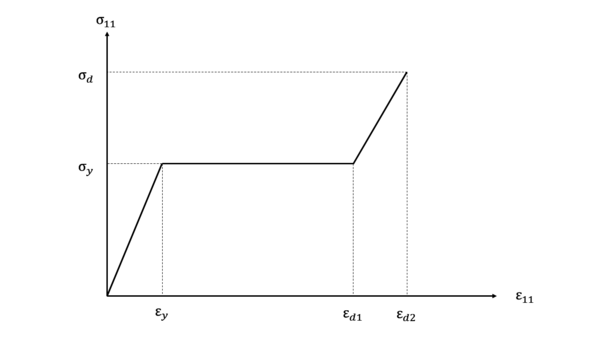
El modelo constitutivo del núcleo de espuma PVC se ha modelado mediante el uso del módulo de espumas de fácil compactación disponible en Abaqus. Este módulo es el que mejor se ajusta al comportamiento de este tipo de espumas [7]. Para ello se ha elegido la opción de endurecimiento isótropo y se han tomado los valores experimentales obtenidos por Iváñez et al. [7] en ensayos de compresión uniaxiales. La curva tensión-deformación se observa en la Figura 1 donde se identifican tres zonas. Una primera zona elástica-lineal hasta alcanzar el valor del límite elástico, . Una segunda zona donde la tensión no aumenta a pesar del incremento de deformación debido al colapso de las células en el interior de la espuma. Y una tercera zona que se alcanza con tensiones de compresión muy altas, que se denomina de densificación donde la tensión se incrementa con una pendiente diferente a la elástica inicial. Mediante la introducción de , , , , y del coeficiente de Poisson la curva queda determinada. Estos valores han sido obtenidos de la literatura para esta espuma [7].
2.3 Definición del modelo numérico
Para la definición del modelo numérico en Abaqus/Explicit se han utilizado dos tipos de elementos. Por un lado, para las pieles y el núcleo se han utilizado elementos trilineales de integración reducida (C3D8R), con un total de 502695 elementos. Cada lámina, tiene un espesor igual a 0.6 mm y el núcleo tiene un espesor de 30 mm. Para la unión entre láminas se han utilizado elementos cohesivos (COH3D8), con un total de 111710 elementos. Cada unión cohesiva entre láminas tiene un espesor de 0.01 mm. Se ha utilizado un gradiente ascendente desde el punto de impacto hacia los bordes para asegurar un mallado más fino en las inmediaciones del impacto. La Figura 2 muestra la configuración final del mallado.
Debido a que en la fase de densificación se pueden alcanzar deformaciones muy altas (del orden del 90%), se ha utilizado una deformación equivalente como criterio para la eliminación de elementos dentro de la espuma. Cuando la deformación equivalente descrita en la ecuación (10) alcanza la unidad el elemento se elimina.
|
|
(10) |
Además, se ha definido un coeficiente de fricción dependiente de la velocidad de deslizamiento. Los elementos tienen control de hourglass activado (enhanced).
3 Validación
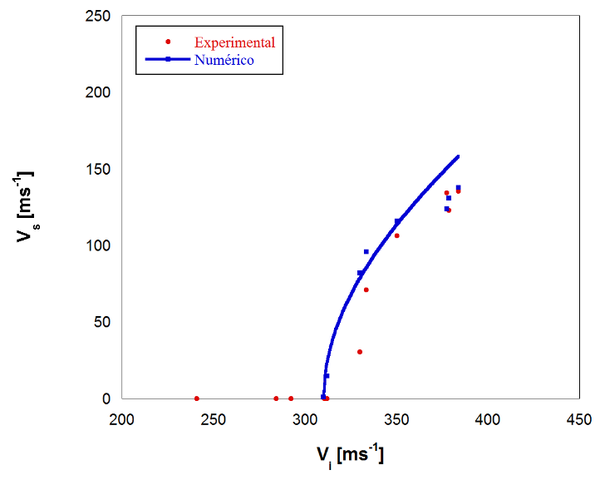
Uno de los aspectos fundamentales que un modelo numérico para impactos de alta velocidad debe cumplir es la predicción del límite balístico, así como de las velocidades residuales. Para verificar que el modelo numérico funciona correctamente, se han comparado las predicciones de la velocidad residual del modelo con los datos experimentales obtenidos de la literatura [6]. Esta validación se ha limitado al límite balístico y sus inmediaciones ya que el estudio de optimización se va a realizar en ese entorno por ser el punto de mayor interés de cara a la seguridad de la estructura. La comparación de los resultados experimentales [6] con los numéricos puede verse en la Figura 3.
La Figura 3 permite afirmar que existe una buena correspondencia entre los valores proporcionados por el modelo numérico y los valores experimentales [6] en las inmediaciones del límite balístico por lo que se da por validado el modelo numérico. El límite balístico experimental es 344 mientras que el numérico es 310 , por lo que el modelo numérico subestima ligeramente el límite balístico con un error del 9.9 %. A la vista de estos resultados y con el modelo validado se puede proceder a realizar el estudio de optimización.
4 Optimización de la distribución de láminas
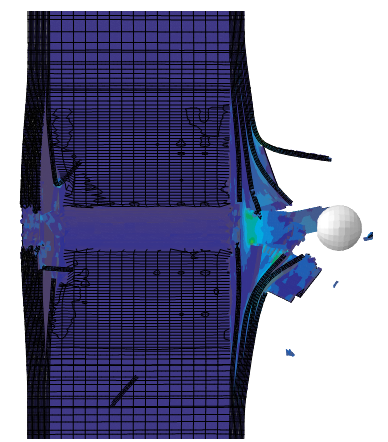
Con el objetivo de definir la configuración óptima para la distribución de láminas en las caras frontal y posterior se han definido 8 configuraciones con la nomenclatura indicada a continuación. Se han utilizado un total de 10 láminas en todos los casos analizados. Las configuraciones se identifican gracias a un código siendo y el número de láminas en las caras delantera y trasera respectivamente. A modo de ejemplo en la Figura 4 se muestra una imagen representativa de uno de los estudios realizados correspondiente a la configuración 6-4, impactada a 330 en la cual se produce perforación.
En la Figura 4 se puede apreciar que se produce bastante flexión en las láminas de la parte trasera. Este fenómeno es más acusado cuanto más disminuye el número de láminas en dicha cara.
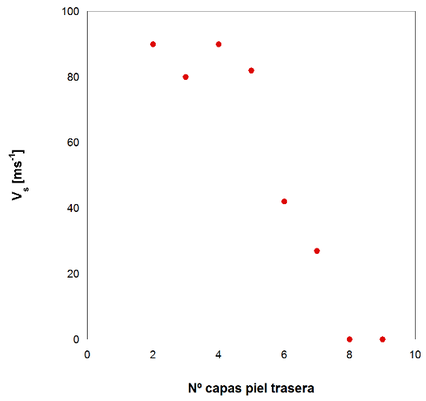
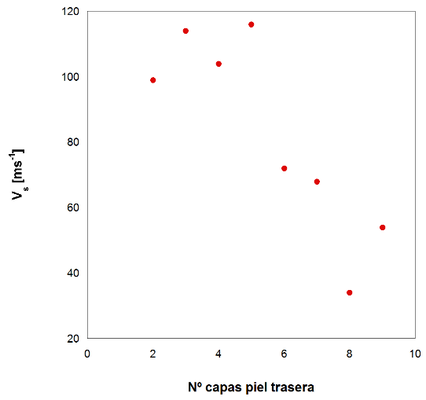
Las configuraciones estudiadas se han probado con dos velocidades de impacto cercanas al límite balístico, como se puede ver en las Figuras 5 y 6.
En las Figuras 5 y 6, la representación de las velocidades residuales frente a la misma velocidad de impacto con distintas configuraciones reflejan una tendencia. Desde la configuración 8-2 hasta la 5-5 el valor de la velocidad residual sufre pequeñas variaciones pero se puede decir que permanece aproximadamente constante para ambos casos. Para entender estas pequeñas variaciones habría que cuantificar la energía que se absorbe por cada mecanismo de fallo. Sin embargo, a partir de la configuración 5-5 hasta la 1-9 se produce un claro descenso de la velocidad residual conforme se aumenta el número de láminas en la cara trasera y se disminuye en la delantera. Este comportamiento es más acusado para el caso de la Figura 5.
Este comportamiento puede tener su explicación en los fenómenos de flexión apreciables en la Figura 4. Al estar las láminas de la cara delantera pegadas al núcleo, este contribuye a disminuir la flexión de dichas láminas. Por el contrario, las láminas de la cara trasera no se encuentran con esta resistencia adicional por lo que la flexión es mayor en ellas. Debido a estas condiciones de contorno, en la cara delantera las láminas fallan localmente por compresión mientras que en la cara trasera fallan por tensión, lo cual requiere más energía. Por este motivo, por lo menos para las velocidades estudiadas, parece más efectiva una configuración que refuerce más la cara trasera en detrimento de la delantera. Con esto se consigue rigidizar más la cara trasera que no tiene ningún elemento de apoyo detrás.
En cuanto a la configuración óptima, harían falta más estudios a distintas velocidades para poder afirmar una en concreto. Con las simulaciones realizadas se puede afirmar que el comportamiento frente a impactos a altas velocidades en el entorno del límite balístico mejora a medida que se añaden láminas en la cara trasera.
5 Conclusiones
Este trabajo se ha centrado en la simulación de impactos a alta velocidad en estructuras sándwich compuestas por pieles de fibra de vidrio tipo E en una matriz poliéster y un núcleo de PVC. Se ha hecho uso de un modelo de daño continuo 3D mediante una subrutina VUMAT para la simulación de las pieles y del módulo de espumas de fácil compactación de Abaqus para el núcleo.
Después de realizar la validación del modelo numérico con resultados experimentales [6], se han estudiado diferentes configuraciones para la distribución de las láminas en las caras delantera y trasera. Obviamente el número de láminas ha sido siempre el mismo, para poder estudiar la mejor configuración utilizando el mismo material dándole un sentido en términos económicos.
A la vista de los resultados obtenidos se puede concluir que para configuraciones que acumulan muchas láminas en la cara delantera hasta una configuración equilibrada (5-5) no hay diferencias muy significativas en las velocidades residuales. Sin embargo, para configuraciones que acumulan más láminas en la cara trasera, la velocidad residual disminuye significativamente. Esto puede deberse a los efectos de flexión que se producen en las láminas de la cara trasera al no tener ningún material detrás que las sustenten.
Agradecimientos
Los autores agradecen al Ministerio de Economía y Empresa el apoyo prestado para la realización de este trabajo a través del proyecto “Estudio del comportamiento frente a impacto y post-impacto de palas de aerogenerador fabricadas de estructuras sándwich” (2018/00086/001).
Referencias
[1] C. Mena, A. Zinno, Composite Structures, 106, pág. 326-339 (2012). https://doi.org/10.1016/j.compstruct.2013.06.010
[2] L. Aktay, A.F. Johnson, Computational Materials Science, 32, pág. 252-260 (2005). https://doi.org/10.1016/j.commatsci.2004.09.044
[3] M. Ghalami-Choobar, M. Sadighi, Aerospace Science and Technology, 32, pág. 142-152 (2014). https://doi.org/10.1016/j.ast.2013.12.005
[4] J. Wang, A.M. Waas, Composite Structures, 96, pág. 298-311 (2013). https://doi.org/10.1016/j.compstruct.2012.09.002
[5] S.L. Lopatnikov, B.A Gama, International Journal of Impact Engineering, 30, pág. 421-445 (2004). https://doi.org/10.1016/S0734-743X(03)00066-6
[6] B. Buitrago, S.K. García-Castillo, Composite Structures, 64, pág. 1052-1054 (2010). https://doi.org/10.1016/j.compstruct.2011.03.028
[7] I. Iváñez, C. Santiuste, Composite Structures, 93, pág. 2392-2399 (2011). 10.1016/j.matlet.2010.02.007
[8] L.Alonso, S.K. García-Castillo, Materials Letters, 143, pág. 292-300 (2018). https://doi.org/10.1016/j.compositesb.2018.01.030
[9] Z. Hashin, Journal of Applied Mechanics, 47, pág. 329-334 (1980). 10.1115/1.3153664
[10] F. Chang, K.A Chang, Journal of Composite Materials, 21, pág. 834-855 (1987). 10.1177/002199838702100904
[11] Systemes D. Abaqus 6.14 User's manual, (2014).
Document information
Published on 17/01/21
Accepted on 04/07/19
Submitted on 29/05/19
Volume 05 - Comunicaciones Matcomp19 (2021), Issue Núm. 1 - Comportamiento en servicio – Inspección y reparación., 2021
DOI: 10.23967/r.matcomp.2021.01.003
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?