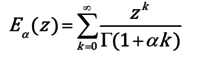(Tag: Visual edit) |
|||
| Line 66: | Line 66: | ||
| | | | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
| − | + | |[[File:Captura de pantalla 2022-06-23 194658.png|center|200px]] | |
| − | |[[File:Captura de pantalla 2022-06-23 194658.png| | + | |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (3) | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
Latest revision as of 20:14, 19 November 2022
1 Introduction
Vehicles lightweight is one of the most important topics considered in the automotive industry. In this sense, composite materials are an efficient alternative to metals, and therefore, the automotive industry is making a great effort in order to reduce costs and increase productivity for the manufacturing process of these materials.
The use of Non-Crimp Fabrics (NCF), in which the unidirectional (UD) fibres with several orientations are transversally stitched, facilitates the automation of manufacturing processes by increasing their productivity [1]. Furthermore, the probability of fibre orientation errors is reduced, together with the better in plane properties compared with woven fabrics (there is no fibre crimps) and better interlaminar prop- erties (the layers are stitched together).
Due to the high manufacturing rates and reduced manufacturing cost margin needed, the best positioned manufacturing methods are the LCM processes in which there is a compression phase, such as WCM or CRTM [2, 9]. In such cases, the dry fibre preform is compressed during the process, so it is essential to know the material compression behaviour in order to select and optimise the manufacturing process by means of numerical process simulation techniques.
The force acting on the mould surface is the sum of the pressure generated by the resin and the reaction generated by the preform compaction. The relative importance of each of these contributions depends on the viscosity of the resin, preform (type of fibre, roving, fabric, fibre volume), the dimensions and geometry of the part and the compression parameters. Even if the viscosity of the resin has been the subject of numerous studies, the mechanical response of the preforms has received less attention. In such cases, the most common material response has been considered as linear elastic behaviour. Nevertheless, most of the publications in recent years have shown that this behaviour is viscoelastic [3, 4].
The objective of this study is to model the stress relaxation of 50k wet carbon fibre reinforced NCFs while subjected to maximum compaction in function of the compression velocity. To do so, based on the experience of previous works [5, 10], a fractional viscoelastic model is used for 3 different compression velocities.
2 Materials and experimental setup
A 0/90 oriented 50k and 610 g/m2 density carbon fibre NCF with 150 140 mm2 dimensions has been used to obtain the preforms. The tests have been performed in an Instron universal test machine with a 100 kN load cell. In order to compress the preform in an homogeneous way, an aluminium plate with dimensions 151×140×3 mm3 is placed over the preforms, so that a 300 Pa pressure is applied which permits a similar initial deformation of the samples. To measure the deformation induced in the samples, the aluminium plate displacement is measured in two different locations by using 2 laser sensors, as it can be seen in the setup shown in Fig. 1.
In the initial stage of the test, due to the weight of the aluminium plate, the preform has a initial thickness e0 of 7 mm. Then, the preform is compacted until the maximum thickness of compaction is reached. The level of maximum compaction is maintained for some fixed tc time. In this study, 3 different compaction velocities levels have been analysed, corresponding to 1 m/min, 5 m/min and 10 m/min.
In Fig. 2 the thickness and load profiles are shown. As stated before, in this study only the phase of maximum compression is studied, where the force decreases due to the material relaxation.
3 Fractional viscoelastic model
In order to characterise the viscoelastic material behaviour of a preform submitted to a constant compaction level, fractional models have been used [5–7, 10]. These models generalise the classical models based on elastic elements (linear springs) and viscous elements (linear dashpots), which model the elastic and pure viscous character, respectively, by the use of Scott-Blair elements of α order. For α = 0 and α = 1, perfectly elastic an viscous elements are obtained, respectively. Thus, extending the method used for classical mechanical models, based on springs and dashpots, the following fractional standard linear solid (FSLS) model is used to establish the relationship between the force in time F(t) with the thickness in time e(t):
|
|
(1) |
where τ, k0, k∞ are material parameters and Dα is the fractional derivative operator of order α with respect to time [8]. The relaxation force Frel(t) corresponding to a constant maximum compaction thickness e0(t), imposed at t = 0 is obtained by integrating Eq. 1, which yields:
|
|
(2) |
where τ is the material relaxation time and Eα is the α-order Mittag-Leffler function, which is defined as [8]:
|
|
(3) |
For the particular case where α = 1, Eq. 2 yields the exponential classical relaxation response:
|
|
(4) |
4 Numerical experimental correlation
In Fig. 3, the experimetal curves corresponding to the compression tests for 3 different compression velocities are shown. For all these tests, the maximum compression has been maintained until Force is stabilised.
Figs. 4-6 show the experimental-numerical correlation for the 3 different compaction velocities, until the force is stabilised. The force relaxation levels are 35%, 34% and 39% for preforms compression velocites of 1 m/min, 5 m/min and 10 m/min, respectively.
As it has been previously stated, fractional models are able to model relaxation phenomena in a more accurate way than classical exponential models [10].
Table 1 gathers the fractional models parameters after identification from the experimental tests for different vf fibre volumes and né number of fabric layers. The model’s parameters, F0 and F∞ represent the compression force at the beginning and end of the maximum compression stage, respectively. The relaxation time τ indicates the way in which the force decreases due to material’s relaxation. In this sense, it can be observed that the relaxation time remains constant for all the compression velocities. Finally, the derivative order α remains constant for the smallest compression velocities and increases for the bigest compaction velocity, which suggests that the derivation order is not an intrinsic material parameter and thus depends on the strain rate.
| Test | v | F0 | F∞ | τ | α |
| number | [m/min] | [N] | [s] | [s] | |
| T1 | 1 | 469.11 | 300.94 | 1.5 | 0.53 |
| T2 | 5 | 1652.93 | 1087.98 | 1.5 | 0.53 |
| T3 | 10 | 3730.84 | 2291.92 | 1.5 | 0.65 |
5 Conclusion
In this work, the relaxation of a wet 50k carbon fibre reinforced NCF has been modelled by fractional models while it is subjected to maximum compaction for 3 different compression velocities.
For all the cases, compared with classical exponential models, the fractional model is able to correctly predict the material relaxation. Concerning the model’s parameters, the relaxation times remain constant for all the compression velocities. However, the fractional derivative order remains constant for the smallest compression velocities and increases as the compression velocity is increased, which suggests the fractional derivative order dependence on the compression velocity and therefore is not an intrinsic material parameter as has been found in previous works of the authors.
As a future work, based on the ability of fractional models to predict correctly the material relaxation during the preform compression process, a model for the material’s thickness recovery after the unloading stage will be developed, in order to optimise the manufacturing of LCM processes.
Acknowledgements
The authors gratefully acknowledge the financial support of this research work provided by Fagor Arrasate S.Coop., Diputación foral de Gipuzkoa (OF 144/2014), and Gobierno Vasco (Programa Predoctoral de Formación de Personal Investigador No Doctor PRE_2014_1_402).
References
[1] J. Yang L. Li, Y. Zhao and J. Zhang. An experimental investigation of compaction behavior of carbon non-crimp fabris for liquid composite molding. Journal of Materials Science, 50:2960–2972 (2015).
[2] K. Friedrich and A.A. Y Aljamid. Manufacturing aspects of advanced polymer composites for automotive applications. Applied Composite Materials, 20(2):107–128 (2013).
[3] A.A. Somashekar, S. Bickerton, and D. Y Bhattacharyya. An experimental investigation of non- elastic deformation of fibrous reinforcements in composite manufacturing. Composites: Part A, 37:858–867, 2006.
[4] S. Bickerton, M.J. Buntain, and A.A. Somashekar. The viscoelastic compression behaviour of liquid composite molding preforms. Composites Part A, 34:431–444, 2003.
[5] L. Aretxabaleta, M. Baskaran, A. Aizpuru, M. Mateos, and J. Aurrekoetxea. Modelado del comportamiento a compresión de tejidos NCF para automoción. In Actas del XI congreso nacional de materiales compuestos, 2015.
[6] R.C. Koeller. Applications of fractional calculus to the theory of viscoelasticity. Journal of Applied Mechanics, 51(2):299–307, 1984.
[7] F. Mainardi. Fractional Calculus and Waves in Linear Viscoelasticity. Imperial Collegue Press, 2010.
[8] I. Podlubny. Fractional Differential Equations. Academic Press, 1999.
[9] M. Baskaran,Optimización del proceso de Compression Resin Transfer Moulding (CRTM) mediante técnicas experimentales y simulación, 2017.
[10] M. Mateos, M. Baskaran, A. Aizpuru, L. Aretxabaleta, J. Aurrekoetxea, The compression behaviour of Non-Crimp Fabrics Composites for Automotive Applications, 17th European Conference on Composite Materials Munich, Germany, 2016.
Document information
Published on 23/06/22
Accepted on 23/06/22
Submitted on 23/06/22
Volume 04 - Comunicaciones Matcomp19 (2020), Issue Núm. 2 - Procesos de Fabricación y Técnicas de Unión, 2022
DOI: 10.23967/r.matcomp.2022.06.037
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?