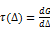(Tag: Visual edit) |
|||
| Line 1: | Line 1: | ||
| − | == | + | ==1 Introducción == |
Se presenta un nuevo modelo para la determinación de la ley cohesiva en modo II de uniones adhesivas de pequeño espesor. La tasa de liberación de energía G en función del avance de grieta Δa se determina mediante el método de reducción de datos denominado Beam Theory including Bending Rotation effects (BTBR) [<span id='cite-1'></span>[[#1|1]]]. Mediante este método, la longitud de grieta para cada punto del ensayo se determina mediante la variación de flexibilidad. El desplazamiento relativo de cortadura en la punta de grieta Δ se determina en función del avance de grieta equivalente, asumiendo que el desarrollo de la Zona de Proceso de Fractura (FPZ) es análogo al avance de grieta. Finalmente, se representa G en función de Δ y se determina la ley cohesiva τ = τ (Δ) mediante derivación numérica.. | Se presenta un nuevo modelo para la determinación de la ley cohesiva en modo II de uniones adhesivas de pequeño espesor. La tasa de liberación de energía G en función del avance de grieta Δa se determina mediante el método de reducción de datos denominado Beam Theory including Bending Rotation effects (BTBR) [<span id='cite-1'></span>[[#1|1]]]. Mediante este método, la longitud de grieta para cada punto del ensayo se determina mediante la variación de flexibilidad. El desplazamiento relativo de cortadura en la punta de grieta Δ se determina en función del avance de grieta equivalente, asumiendo que el desarrollo de la Zona de Proceso de Fractura (FPZ) es análogo al avance de grieta. Finalmente, se representa G en función de Δ y se determina la ley cohesiva τ = τ (Δ) mediante derivación numérica.. | ||
| − | == | + | ==2 Metodología == |
===La Fig. 1 muestra la configuración del ensayo de flexión en tres puntos con entalla final (ENF) de acuerdo a BTBR=== | ===La Fig. 1 muestra la configuración del ensayo de flexión en tres puntos con entalla final (ENF) de acuerdo a BTBR=== | ||
| Line 10: | Line 10: | ||
[[Image:Arrese_et_al_2018a-image5-c.png|534px]] </div> | [[Image:Arrese_et_al_2018a-image5-c.png|534px]] </div> | ||
| − | Figura 1. Configuración del ensayo ENF de acuerdo a BTBR. | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> |
| + | <span style="text-align: center; font-size: 75%;">'''Figura 1.''' Configuración del ensayo ENF de acuerdo a BTBR.</span></div> | ||
==La integral-J es equivalente a la tasa de liberación de energía G para un cuerpo elástico. [<span id='cite-2'></span>[[#2|2]]] == | ==La integral-J es equivalente a la tasa de liberación de energía G para un cuerpo elástico. [<span id='cite-2'></span>[[#2|2]]] == | ||
| Line 27: | Line 28: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Figura 2. '''Zona de proceso de Fractura</span> | + | <span style="text-align: center; font-size: 75%;">'''Figura 2. '''Zona de proceso de Fractura.</span></div> |
De acuerdo a la teoría clásica de vigas Δ puede expresarse de la siguiente forma: | De acuerdo a la teoría clásica de vigas Δ puede expresarse de la siguiente forma: | ||
| Line 45: | Line 46: | ||
[[Image:Arrese_et_al_2018a-image12-c.png|336px]] () | [[Image:Arrese_et_al_2018a-image12-c.png|336px]] () | ||
| − | == | + | ==3 Procedimiento Experimental == |
==='''3.1''' Material === | ==='''3.1''' Material === | ||
| Line 77: | Line 78: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Figura 4.''' Evolución de la longitud de grieta </span></div> | + | <span style="text-align: center; font-size: 75%;">'''Figura 4.''' Evolución de la longitud de grieta. </span></div> |
Teniendo la longitud de de grieta inicial y la longitud de grieta para cada punto del ensayo, es posible obtener la curva-R, la cual representa la evolución de G respecto al avance de grieta, Fig. 5. | Teniendo la longitud de de grieta inicial y la longitud de grieta para cada punto del ensayo, es posible obtener la curva-R, la cual representa la evolución de G respecto al avance de grieta, Fig. 5. | ||
| Line 91: | Line 92: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Figura 6.''' Curva </span>G-Δ<span style="text-align: center; font-size: 75%;">.</span></div> | + | <span style="text-align: center; font-size: 75%;">'''Figura 6.''' Curva.</span>G-Δ<span style="text-align: center; font-size: 75%;">.</span></div> |
Para evitar el ruido excesivo de los datos experimentales, los datos los datos G-Δ se aproximan a la función logística de la Eq (3). La función F (Δ) se ajusta a los datos experimentales mediante un ajuste lineal por regiones. Fig. 7 muestra los datos experimentales obtenidos de la Eq. (3) y la curva ajustada. Con el fin de evaluar la precisión del ajuste, los datos experimentales y la función logística aproximada se representan en la Fig. 8. | Para evitar el ruido excesivo de los datos experimentales, los datos los datos G-Δ se aproximan a la función logística de la Eq (3). La función F (Δ) se ajusta a los datos experimentales mediante un ajuste lineal por regiones. Fig. 7 muestra los datos experimentales obtenidos de la Eq. (3) y la curva ajustada. Con el fin de evaluar la precisión del ajuste, los datos experimentales y la función logística aproximada se representan en la Fig. 8. | ||
| Line 97: | Line 98: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Figura 7.''' La función F(Δ)</span></div> | + | <span style="text-align: center; font-size: 75%;">'''Figura 7.''' La función F.(Δ)</span></div> |
[[File:Arrese_et_al_2018a-image19-c.png|centre|600x600px]] | [[File:Arrese_et_al_2018a-image19-c.png|centre|600x600px]] | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | <span style="text-align: center; font-size: 75%;">'''Figura 8.''' (G-G<sub>ini</sub>)/(G<sub>ss</sub>-G<sub>ini</sub>) experimental y aproximada </span></div> | + | <span style="text-align: center; font-size: 75%;">'''Figura 8.''' (G-G<sub>ini</sub>)/(G<sub>ss</sub>-G<sub>ini</sub>) experimental y aproximada. </span></div> |
Reemplazando los valores de F (Δ) y sus derivadas obtenidas por diferenciación numérica en la Eq. (4), se obtiene la ley cohesiva. | Reemplazando los valores de F (Δ) y sus derivadas obtenidas por diferenciación numérica en la Eq. (4), se obtiene la ley cohesiva. | ||
| Line 113: | Line 114: | ||
<span style="text-align: center; font-size: 75%;">'''Figura 9.''' Ley cohesiva de la probeta S1.</span></div> | <span style="text-align: center; font-size: 75%;">'''Figura 9.''' Ley cohesiva de la probeta S1.</span></div> | ||
| − | == | + | ==4 Conclusiones== |
En el presente trabajo se propone un nuevo método para la determinación de la ley cohesiva en modo II para uniones adhesivas de pequeño espesor. | En el presente trabajo se propone un nuevo método para la determinación de la ley cohesiva en modo II para uniones adhesivas de pequeño espesor. | ||
Revision as of 18:28, 20 October 2022
1 Introducción
Se presenta un nuevo modelo para la determinación de la ley cohesiva en modo II de uniones adhesivas de pequeño espesor. La tasa de liberación de energía G en función del avance de grieta Δa se determina mediante el método de reducción de datos denominado Beam Theory including Bending Rotation effects (BTBR) [1]. Mediante este método, la longitud de grieta para cada punto del ensayo se determina mediante la variación de flexibilidad. El desplazamiento relativo de cortadura en la punta de grieta Δ se determina en función del avance de grieta equivalente, asumiendo que el desarrollo de la Zona de Proceso de Fractura (FPZ) es análogo al avance de grieta. Finalmente, se representa G en función de Δ y se determina la ley cohesiva τ = τ (Δ) mediante derivación numérica..
2 Metodología
La Fig. 1 muestra la configuración del ensayo de flexión en tres puntos con entalla final (ENF) de acuerdo a BTBR
La integral-J es equivalente a la tasa de liberación de energía G para un cuerpo elástico. [2]

|
()
En la aproximación propuesta se asume que el desarrollo de la FPZ es análogo al avance de grieta equivalente Δa, relacionado con la variación de la flexibilidad.
De acuerdo a la teoría clásica de vigas Δ puede expresarse de la siguiente forma:
donde
La relación G=G(Δ) se aproxima a una función logística de la siguiente forma:
F(Δ) se determina mediante un ajuste lineal por regiones de los datos experimentales. Finalmente la ley cohesiva se obtiene median derivación numérica.
3 Procedimiento Experimental
3.1 Material
Para la fabricación de las probetas se han utilizado probetas unidireccionales fabricadas a partir de prepregs de carbono/epoxi T6T/F593 proporcionados por Hexcel Composites con 16 capas unidireccionales que han sido delaminadas completamente. Los adherentes fruto de la delaminación completa han sido unidas por el adhesivo Loctite 9644 Hysol.
Las dimensiones nominales de la probeta son 3 mm de espesor y 16mm de ancho. La grieta inicial se genera mediante un inserto de teflón.
Los ensayos se han realizado en una maquina de ensayo universal MTS-Insight 10 con célula de carga de 10kN
3.2 Ensayos Preliminares
Las propiedades elásticas Ef and G13, se han determinado mediante el procedimiento propuesto por Mujika [3], siendo el modulo de flexión 107GPa y el modulo de cortadura 3 GPa.
El desplazamiento de la probeta (δspec) se determina de las curvas carga desplazamiento. El desplazamiento experimental (δexp) es la suma del desplazamiento de la probeta y el desplazamiento debido a la flexibilidad del sistema.
La flexibilidad del sistema se determina experimentalmente siendo su valor promedio Cs = 1/15•10-3 mm/N.
3.3 Resultados
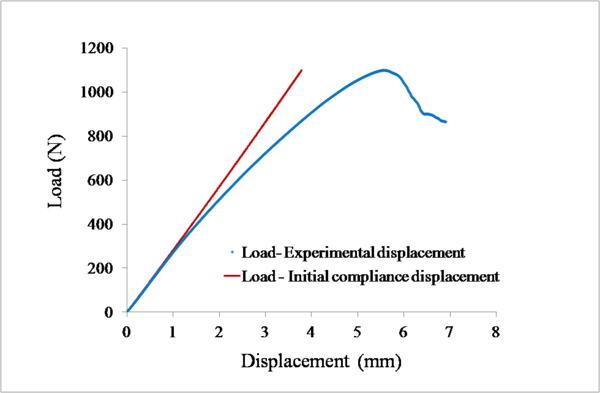
En la Figura 3 se muestra la curva experimental carga desplazamiento correspondiente a la probeta S1.
Una vez determinada la longitud de grieta para cada punto del ensayo, la longitud de grieta inicial se determina como promedio de los valores en el rango de carga donde la longitud de grieta se mantiene constante, tal y como se aprecia en la Fig. 4. Por lo tanto, la iniciación del daño local está relacionada con el primer punto donde el avance de grieta es distinto de cero.
Teniendo la longitud de de grieta inicial y la longitud de grieta para cada punto del ensayo, es posible obtener la curva-R, la cual representa la evolución de G respecto al avance de grieta, Fig. 5.
De acuerdo a la Eq. (2) el desplazamiento de cortadura en la punta de grieta puede ser determinado para cada punto del ensayo sustituyendo el correspondiente avance de grieta. La Fig 6. muestra la curva G¸Ç_ë?Δ que corresponde a la probeta S1.
Para evitar el ruido excesivo de los datos experimentales, los datos los datos G-Δ se aproximan a la función logística de la Eq (3). La función F (Δ) se ajusta a los datos experimentales mediante un ajuste lineal por regiones. Fig. 7 muestra los datos experimentales obtenidos de la Eq. (3) y la curva ajustada. Con el fin de evaluar la precisión del ajuste, los datos experimentales y la función logística aproximada se representan en la Fig. 8.
Reemplazando los valores de F (Δ) y sus derivadas obtenidas por diferenciación numérica en la Eq. (4), se obtiene la ley cohesiva.
La Fig. 9 muestra la ley cohesiva de la probeta S1
4 Conclusiones
En el presente trabajo se propone un nuevo método para la determinación de la ley cohesiva en modo II para uniones adhesivas de pequeño espesor.
La aproximación propuesta, se basa en la correlación entre la tasa de liberación de energía desarrollada (G) en función del desplazamiento de cortadura de la punta de grieta (Δ).
La Curva de Resistencia se determina obteniendo G en función del avance de grieta cuya determinación se basa en la variación de la flexibilidad de la probeta debido al avance del daño.
El desplazamiento de cortadura de la punta de la grieta se determina en función del avance de grieta equivalente suponiendo que el desarrollo de la Zona de Proceso de Fractura es análogo a un avance grieta.
Finalmente, representando la tasa de liberación de energía y el desplazamiento de cortadura de la grieta determinados, y mediante un ajuste a una función logística de la curva G-Δ y la ley cohesiva experimental se determina por diferenciación numérica.
Mediante el método propuesto se ha evaluado una unión realizada con LOCTITE HYSOL 9644. La resistencia cohesiva obtenida es del orden de 34 MPa,
El método propuesto proporciona una manera sencilla de obtener la ley cohesiva en modo II utilizando únicamente datos de desplazamiento y carga proporcionados por la máquina de ensayo universal, sin necesidad de ninguna medición de desplazamiento externo y sin asumir ninguna forma de la ley cohesiva.
Agradecimientos
Los autores agradecen a la Universidad del País Vasco (UPV/EHU) la financiación del Grupo de Investigación Mecánica de Materiales GIU 16/51 en la convocatoria de 2016.
Referencias
1 [?] A. Arrese, N. Carbajal, G. Vargas, F. Mujika F. A new method for determining mode II R-curve by the End-Notched flexure test. Engineering Fracture Mechanics, 77, 2010, p.77-20.
2 [?] Anderson TL. Fracture Mechanics. Fundamentals and applications. 2005
3 [?] Mujika F. On the effect of shear and local deformation in three point bending tests. Polymer testing 2007;26:869-77
Document information
Published on 14/10/18
Accepted on 14/10/18
Submitted on 14/10/18
Volume 02 - Comunicaciones Matcomp17 (2018), Issue Núm. 4 - Comportamiento en servicio de los materiales compuestos (2), 2018
DOI: 10.23967/r.matcomp.2018.10.016
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?