m (Scipediacontent moved page Draft Content 696569811 to Bonhomme et al 2018a)
 
(One intermediate revision by one other user not shown)
Line 1: Line 1:
−
== Abstract ==
+
== 1 Introducción ==
 +
El refuerzo de resinas con partículas es un campo de gran  interés con objeto de mejorar las propiedades mecánicas de las matrices utilizadas en distintas aplicaciones.
  
−
In this work the mechanical behaviour of a epoxy resin reinforced with small particles has been studied. This study has been carried out by means of Finite Element Modelling (FEM).
+
Partículas como por ejemplo el óxido de grafeno (GO) se utilizan como refuerzo en matrices poliméricas para formar nanocomposites con resultados prometedores. Diferentes autores han estudiado la variación de las propiedades mecánicas de estos compuestos utilizando diferentes tipos de GO [1-4].
−
A number of models have been prepared with different volume fractions of particles and different particle geometry. The particles had different thickness to surface ratios.
+
−
These particles were randomly distributed in the matrix with main surfaces parallel to the loading direction.
+
−
In this study it was found that, as the thickness to surface ratio decreases, the stiffening effect of the particles is more effective. This behaviour was observed for all volume fractions studied.
+
−
On the other hand, in mechanical tests carried out in parallel experimental programs it was observed that the addition of degassers and reducers of surface tension in the manufacture of the test pieces had an appreciable effect on the final mechanical properties. Due to this, the influence of the porosity on the aparent elastic modulus of the resins was also modelled.
+
  
−
== Full document ==
+
Una importante línea de trabajo en la actualidad se centra en determinar la proporción óptima de refuerzo con objeto de mejorar las propiedades mecánicas [5-8]
−
<pdf>Media:Draft_Content_696569811native-articles-175.pdf</pdf>
+
 
 +
La utilización de partículas con relaciones de aspecto muy pequeñas hace que las técnicas clásicas de modelización por elementos finitos tengan un límite por las limitaciones geométricas de los elementos utilizados.
 +
 
 +
En este trabajo se estudió el comportamiento mecánico de una resina epoxi reforzada con partículas mediante cálculo por elementos finitos. Se han modelizado compuestos con diferentes contenidos de partículas y diferentes geometrías de dichas partículas.
 +
 
 +
Por otra parte, se llevó a cabo un programa experimental de manera paralela en el que se observó que la adición de desgasificantes y reductores de tensión superficial en la fabricación de las probetas tenía un efecto apreciable sobre las propiedades de las probetas ensayadas. Debido a esto se estudió también la influencia de la porosidad sobre el módulo elástico aparente de las resinas. Este estudio puede permitir, junto con otras técnicas analíticas, estimar el contenido en porosidad de las probetas.
 +
 
 +
Todos los modelos de elementos finitos desarrollados en este estudio se llevaron a acabo con un programa de cálculo por elementos finitos ANSYS<sup>®</sup>.
 +
 
 +
En primer lugar se prepararon modelos de resina reforzados con partículas con distintas relaciones de aspecto. Estas partículas, con forma de paralelepípedo se distribuyeron aleatoriamente en el interior de la matriz con sus caras principales paralelas. Estos estudios se realizaron para distintas fracciones volumétricas de refuerzo.
 +
 
 +
Posteriormente se estudió la influencia de la porosidad sobre el módulo elástico aparente de las resinas.
 +
 
 +
==2 Materiales==
 +
 
 +
En la tabla 1 se muestran las propiedades mecánicas de los materiales individuales utilizados en la modelización por elementos finitos.
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
<span style="text-align: center; font-size: 75%;">'''Tabla 1.''' Materiales modelizados</span></div>
 +
 
 +
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;"
 +
|-
 +
|  style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">Propiedad</span>
 +
|  style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Valor</span>
 +
|-
 +
|  style="border-top: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">Densidad de la resina (g/cm<sup>3</sup>)</span>
 +
|  style="border-top: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">1,1</span>
 +
|-
 +
|  style="text-align: right;"|<span style="text-align: center; font-size: 75%;">Densidad de las partículas (g/cm<sup>3</sup>)</span>
 +
|  style="text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">2,2</span>
 +
|-
 +
|  style="text-align: right;"|<span style="text-align: center; font-size: 75%;">Módulo elástico de la resina (MPa)</span>
 +
|  style="text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">2.144</span>
 +
|-
 +
|  style="border-bottom: 2pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">Módulo elástico de las partículas (GPa)</span>
 +
|  style="border-bottom: 2pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">1.050</span>
 +
|}
 +
 
 +
 
 +
==3 Modelos de Elementos Finitos==
 +
 
 +
==='''3.1''' Efecto de la geometría de las partículas===
 +
 
 +
Con objeto de estudiar la influencia del espesor de las partículas en el efecto reforzante, se prepararon modelos 3D. Se definió la relación de aspecto ''k'' como el espesor de la partícula dividido por el área de la misma:
 +
 
 +
{| class="formulaSCP" style="width: 100%; text-align: center;"
 +
|-
 +
|
 +
{| style="text-align: center; margin:auto;"
 +
|-
 +
| <math display="inline">k=\frac{Espesor}{\acute{A}rea}</math>
 +
|}
 +
| style="width: 5px;text-align: right;white-space: nowrap;" | (1)
 +
|}
 +
 
 +
 
 +
En primer lugar se prepararon modelos de resina reforzados con partículas con distintas relaciones de aspecto (diferentes relaciones espesor/superficie). Estas partículas, con forma de paralelepípedo se distribuyeron mediante una función aleatoria en el interior de la matriz con sus caras principales paralelas y orientadas en la dirección de la solicitación para obtener el mayor efecto reforzante.
 +
 
 +
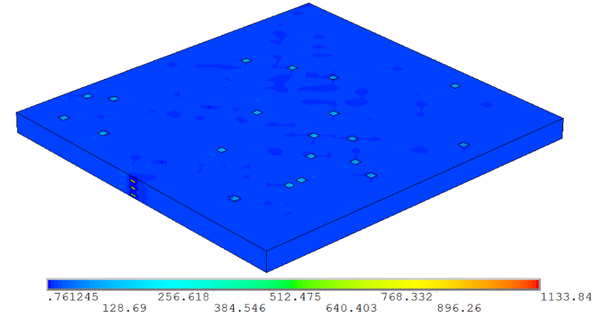
En estos modelos se aplicó una deformación lineal y se calculó el módulo elástico aparente. En las figuras 1 y 2 se muestran dos de los modelos analizados.
 +
 
 +
Estos estudios se realizaron para distintas fracciones volumétricas de refuerzo. En la tabla 2 se muestran los resultados obtenidos.
 +
[[File:Bonhomme_et_al_2018a-image5.png|centre|600x600px]]
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
<span style="text-align: center; font-size: 75%;">'''Figura 1.''' Tensiones de Von Mises para 3% en peso de partículas con geometría ''k''=0,5.</span></div>
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
'' [[Image:Bonhomme_et_al_2018a-image6.png|600px]] ''</div>
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
<span style="text-align: center; font-size: 75%;">'''Figura 2.''' Tensiones de Von Mises para 3% en peso de partículas con geometría ''k''=0,125.</span></div>
 +
 
 +
Como se puede ver en la tabla 2, a medida que disminuye la relación de aspecto de las partículas, su efecto rigidizador se incrementa. La técnica de modelización por elementos finitos mediante elementos brick tiene un límite, como se comentó anteriormente, por las limitaciones geométricas de dichos elementos.
 +
 
 +
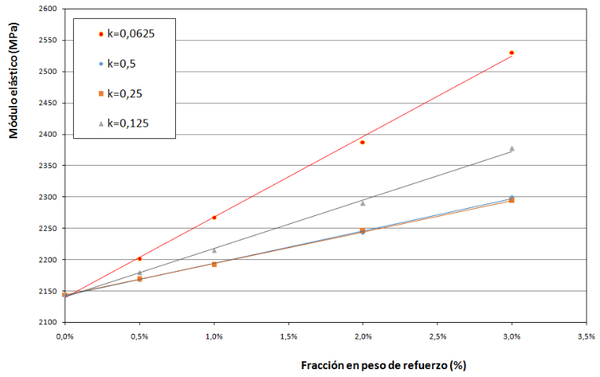
En la figura 3 se pueden ver los resultados obtenidos anteriormente representados de forma gráfica.
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
<span style="text-align: center; font-size: 75%;">'''Tabla 2.''' Módulo elástico de los distintos modelos en función de la fracción en peso y la geometría de las partículas </span></div>
 +
 
 +
{| style="width: 86%;margin: 1em auto 0.1em auto;border-collapse: collapse;"
 +
|-
 +
|  style="border-top: 2pt solid black;text-align: right;"|
 +
|  colspan='4'  style="border-top: 2pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Módulo elástico (MPa)</span>
 +
|-
 +
|  style="border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">Fracción en peso de partículas</span>
 +
|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">''k''=0,5</span>
 +
|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">''k''=0,25</span>
 +
|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">''k''=0,125</span>
 +
|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">''k''=0,0625</span>
 +
|-
 +
|  style="border-top: 1pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">0,0%</span>
 +
|  style="border-top: 1pt solid black;text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2144,0</span>
 +
|  style="border-top: 1pt solid black;text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2144,0</span>
 +
|  style="border-top: 1pt solid black;text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2144,0</span>
 +
|  style="border-top: 1pt solid black;text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2144,0</span>
 +
|-
 +
|  style="text-align: right;"|<span style="text-align: center; font-size: 75%;">0,5%</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2167,7</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2168,5</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2178,7</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2201,5</span>
 +
|-
 +
|  style="text-align: right;"|<span style="text-align: center; font-size: 75%;">1,0%</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2192,7</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2191,5</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2214,5</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2267,2</span>
 +
|-
 +
|  style="text-align: right;"|<span style="text-align: center; font-size: 75%;">2,0%</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2243,2</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2245,5</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2289,5</span>
 +
|  style="text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2387,0</span>
 +
|-
 +
|  style="border-bottom: 2pt solid black;text-align: right;"|<span style="text-align: center; font-size: 75%;">3,0%</span>
 +
|  style="border-bottom: 2pt solid black;text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2299,0</span>
 +
|  style="border-bottom: 2pt solid black;text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2294,0</span>
 +
|  style="border-bottom: 2pt solid black;text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2377,0</span>
 +
|  style="border-bottom: 2pt solid black;text-align: right;vertical-align: bottom;"|<span style="text-align: center; font-size: 75%;">2530,2</span>
 +
|}
 +
[[File:Bonhomme_et_al_2018a-image8.png|centre|600x600px]]
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
<span style="text-align: center; font-size: 75%;">'''Figura 3.''' Módulo elástico de las resinas para distintos factores geométricos ''k'' y distintas fracciones en peso de partículas reforzantes.</span></div>
 +
 
 +
==='''3.2''' Efecto de la porosidad. ===
 +
 
 +
En el programa experimental desarrollado paralelamente a este estudio se observó que la adición de desgasificantes y reductores de tensión superficial en la fabricación de probetas tenía un efecto apreciable sobre las propiedades mecánicas finales del compuesto.
 +
 
 +
Debido a esto se estudió también con modelos de elementos finitos la influencia de la porosidad sobre las propiedades mecánicas de las resinas.
 +
 
 +
Este estudio se llevó a cabo con una resina epoxi de módulo elástico E=3.176 MPa.
 +
 
 +
Para estudiar este efecto se prepararon modelos de elementos finitos 3D en los que se introdujeron huecos mediante una función aleatoria simulando la porosidad del material con distintas fracciones volumétricas. Posteriormente se aplicó una deformación al modelo y se calculó el módulo elástico aparente.
 +
 
 +
Inicialmente se realizaron modelos con distintos tamaños de elemento con objeto de estudiar la influencia del tamaño en los resultados finales. En las figuras 3 y 4 se muestran imágenes de estos modelos para tamaños de poro de 0,296 mm<sup>3</sup> y 0,125 mm<sup>3</sup>.
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
[[Image:Bonhomme_et_al_2018a-image9.png|480px]] </div>
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
<span style="text-align: center; font-size: 75%;">'''Figura 3.''' Modelo de la resina con huecos de tamaño 0,296 mm3.</span></div>
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
[[Image:Bonhomme_et_al_2018a-image10.png|474px]] </div>
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
<span style="text-align: center; font-size: 75%;">'''Figura 4.''' Modelo de la resina con huecos de tamaño 0,125 mm3.</span></div>
 +
 
 +
Con este primer estudio se comprobó que para fracciones volumétricas de poros equivalentes, el distinto tamaño de los poros prácticamente no tenía ninguna influencia sobre el módulo elástico aparente.
 +
 
 +
Seguidamente se prepararon modelos con distintas fracciones volumétricas de poros para ver su influencia sobre los resultados finales.
 +
 
 +
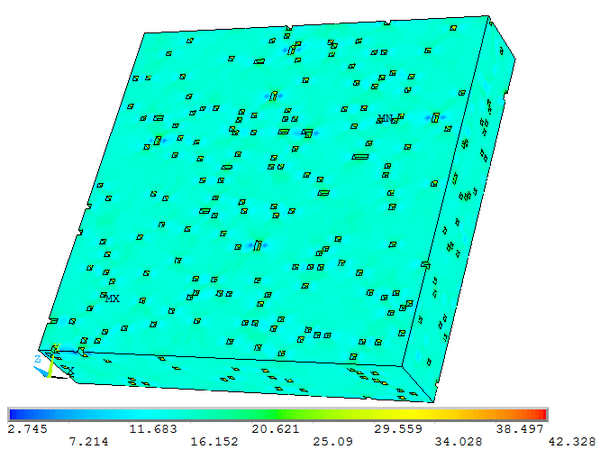
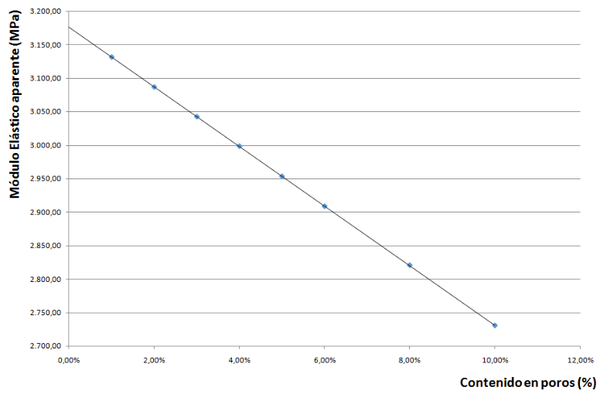
En la figura 5 se muestra uno de los modelos de elementos finitos. En la figura 6 se muestra la relación ente el módulo elástico aparente y la fracción volumétrica de poros. Como se puede observar, esta relación es lineal.
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
[[Image:Bonhomme_et_al_2018a-image11.png|600px]] </div>
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
<span style="text-align: center; font-size: 75%;">'''Figura 5.''' Tensiones de Von Mises. Modelo con fracción volumétrica de poros 3%.</span></div>
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
[[Image:Bonhomme_et_al_2018a-image12.png|600px]] </div>
 +
 
 +
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
 +
<span style="text-align: center; font-size: 75%;">'''Figura 6.''' Módulo elástico en función de la fracción volumétrica de poros.</span></div>
 +
 
 +
==4 Conclusiones==
 +
 
 +
En este trabajo se estudió el comportamiento mecánico de una resina epoxi reforzada con partículas mediante cálculo numérico por elementos finitos.
 +
 
 +
En los estudios realizados se ha observado que a media que disminuye la relación entre el espesor y el área de la partícula el efecto rigidizador de las partículas es más efectivo. Este efecto es independiente de la fracción volumétrica de refuerzo.
 +
 
 +
Se observó también que el aumento del módulo elástico es prácticamente lineal respecto a la fracción volumétrica de partículas de refuerzo.
 +
 
 +
En ensayos experimentales se observó que la adición de desgasificantes y reductores de tensión superficial en la fabricación de las probetas tenía un efecto apreciable sobre las propiedades mecánicas finales.
 +
 
 +
Los estudios de la influencia de la porosidad sobre el módulo elástico aparente demostraron una relación lineal con la fracción volumétrica de poros.
 +
 
 +
==5 Referencias==
 +
 
 +
[1] R. Wanga, Z. Li, W. Liu, et al. Attapulgite–graphene oxide hybrids as thermal and mechanical reinforcements for epoxy composites, Composites Science and Technology, '''87''', pág. 29–35 (2013)
 +
 
 +
[2] S. Chandrasekaran, N. Sato, F. Tölle, et al. Fracture toughness and failure mechanism of graphene based epoxy composites, Composites Science and Technology, '''97''', pág. 90–99 (2014)
 +
 
 +
[3] J.A. King, D.R. Klimek, I. Miskioglu, et al. Mechanical properties of graphene nanoplatelet/epoxy composites, Journal of Composite Materials, '''49''', 6, pág. 659–668 (2015)
 +
 
 +
[4] Y.J. Wan, L.C. Tang, L.X. Gong, et al. Grafting of epoxy chains onto graphene oxide for epoxy composites with improved mechanical and thermal properties, Carbon, '''69''', pág. 467–480 (2014)
 +
 
 +
[5] M.M. Shokrieh, M. Esmkhani, Z. Shokrieh, et al. Stiffness prediction of graphene nanoplatelet/epoxy nanocomposites by a combined molecular dynamics–micromechanics method. Computational Material Science, '''92''', pág. 444–450 (2014)
 +
 
 +
[6] M.M. Shokrieh, M. Esmkhani, H.R. Shahverdi, et al. Effect of graphene nanosheets (GNS) and graphite nanoplatelets (GNP) on the mechanical properties of epoxy nanocomposites. Science of Advanced Materials, '''5''', pág. 260–266 (2013)
 +
 
 +
[7] B. Karimi, B. Ramezanzadeh, A comparative study on the effect of ultrathin luminescent graphene oxide quantum dot (GOQD) and graphene oxide (GO) nanosheets on the interfacial interactive and mechanical properties of an epoxy composite, Journal of Colloid and Interface Science,  '''493''', pág. 62–76 (2017)
 +
 
 +
[8] Z.S. Pour, M. Ghaemy, Polymer grafted graphene oxide: for improved dispersion in epoxy resin and enhancement of mechanical properties of nanocomposite. Composites Science and Technololy, '''136''', pág.145–157 (2016)

Latest revision as of 12:28, 16 October 2022

1 Introducción

El refuerzo de resinas con partículas es un campo de gran interés con objeto de mejorar las propiedades mecánicas de las matrices utilizadas en distintas aplicaciones.

Partículas como por ejemplo el óxido de grafeno (GO) se utilizan como refuerzo en matrices poliméricas para formar nanocomposites con resultados prometedores. Diferentes autores han estudiado la variación de las propiedades mecánicas de estos compuestos utilizando diferentes tipos de GO [1-4].

Una importante línea de trabajo en la actualidad se centra en determinar la proporción óptima de refuerzo con objeto de mejorar las propiedades mecánicas [5-8]

La utilización de partículas con relaciones de aspecto muy pequeñas hace que las técnicas clásicas de modelización por elementos finitos tengan un límite por las limitaciones geométricas de los elementos utilizados.

En este trabajo se estudió el comportamiento mecánico de una resina epoxi reforzada con partículas mediante cálculo por elementos finitos. Se han modelizado compuestos con diferentes contenidos de partículas y diferentes geometrías de dichas partículas.

Por otra parte, se llevó a cabo un programa experimental de manera paralela en el que se observó que la adición de desgasificantes y reductores de tensión superficial en la fabricación de las probetas tenía un efecto apreciable sobre las propiedades de las probetas ensayadas. Debido a esto se estudió también la influencia de la porosidad sobre el módulo elástico aparente de las resinas. Este estudio puede permitir, junto con otras técnicas analíticas, estimar el contenido en porosidad de las probetas.

Todos los modelos de elementos finitos desarrollados en este estudio se llevaron a acabo con un programa de cálculo por elementos finitos ANSYS®.

En primer lugar se prepararon modelos de resina reforzados con partículas con distintas relaciones de aspecto. Estas partículas, con forma de paralelepípedo se distribuyeron aleatoriamente en el interior de la matriz con sus caras principales paralelas. Estos estudios se realizaron para distintas fracciones volumétricas de refuerzo.

Posteriormente se estudió la influencia de la porosidad sobre el módulo elástico aparente de las resinas.

2 Materiales

En la tabla 1 se muestran las propiedades mecánicas de los materiales individuales utilizados en la modelización por elementos finitos.

Tabla 1. Materiales modelizados
Propiedad Valor
Densidad de la resina (g/cm3) 1,1
Densidad de las partículas (g/cm3) 2,2
Módulo elástico de la resina (MPa) 2.144
Módulo elástico de las partículas (GPa) 1.050


3 Modelos de Elementos Finitos

3.1 Efecto de la geometría de las partículas

Con objeto de estudiar la influencia del espesor de las partículas en el efecto reforzante, se prepararon modelos 3D. Se definió la relación de aspecto k como el espesor de la partícula dividido por el área de la misma:

(1)


En primer lugar se prepararon modelos de resina reforzados con partículas con distintas relaciones de aspecto (diferentes relaciones espesor/superficie). Estas partículas, con forma de paralelepípedo se distribuyeron mediante una función aleatoria en el interior de la matriz con sus caras principales paralelas y orientadas en la dirección de la solicitación para obtener el mayor efecto reforzante.

En estos modelos se aplicó una deformación lineal y se calculó el módulo elástico aparente. En las figuras 1 y 2 se muestran dos de los modelos analizados.

Estos estudios se realizaron para distintas fracciones volumétricas de refuerzo. En la tabla 2 se muestran los resultados obtenidos.

Bonhomme et al 2018a-image5.png
Figura 1. Tensiones de Von Mises para 3% en peso de partículas con geometría k=0,5.
Bonhomme et al 2018a-image6.png
Figura 2. Tensiones de Von Mises para 3% en peso de partículas con geometría k=0,125.

Como se puede ver en la tabla 2, a medida que disminuye la relación de aspecto de las partículas, su efecto rigidizador se incrementa. La técnica de modelización por elementos finitos mediante elementos brick tiene un límite, como se comentó anteriormente, por las limitaciones geométricas de dichos elementos.

En la figura 3 se pueden ver los resultados obtenidos anteriormente representados de forma gráfica.

Tabla 2. Módulo elástico de los distintos modelos en función de la fracción en peso y la geometría de las partículas
Módulo elástico (MPa)
Fracción en peso de partículas k=0,5 k=0,25 k=0,125 k=0,0625
0,0% 2144,0 2144,0 2144,0 2144,0
0,5% 2167,7 2168,5 2178,7 2201,5
1,0% 2192,7 2191,5 2214,5 2267,2
2,0% 2243,2 2245,5 2289,5 2387,0
3,0% 2299,0 2294,0 2377,0 2530,2
Bonhomme et al 2018a-image8.png
Figura 3. Módulo elástico de las resinas para distintos factores geométricos k y distintas fracciones en peso de partículas reforzantes.

3.2 Efecto de la porosidad.

En el programa experimental desarrollado paralelamente a este estudio se observó que la adición de desgasificantes y reductores de tensión superficial en la fabricación de probetas tenía un efecto apreciable sobre las propiedades mecánicas finales del compuesto.

Debido a esto se estudió también con modelos de elementos finitos la influencia de la porosidad sobre las propiedades mecánicas de las resinas.

Este estudio se llevó a cabo con una resina epoxi de módulo elástico E=3.176 MPa.

Para estudiar este efecto se prepararon modelos de elementos finitos 3D en los que se introdujeron huecos mediante una función aleatoria simulando la porosidad del material con distintas fracciones volumétricas. Posteriormente se aplicó una deformación al modelo y se calculó el módulo elástico aparente.

Inicialmente se realizaron modelos con distintos tamaños de elemento con objeto de estudiar la influencia del tamaño en los resultados finales. En las figuras 3 y 4 se muestran imágenes de estos modelos para tamaños de poro de 0,296 mm3 y 0,125 mm3.

Bonhomme et al 2018a-image9.png
Figura 3. Modelo de la resina con huecos de tamaño 0,296 mm3.
Bonhomme et al 2018a-image10.png
Figura 4. Modelo de la resina con huecos de tamaño 0,125 mm3.

Con este primer estudio se comprobó que para fracciones volumétricas de poros equivalentes, el distinto tamaño de los poros prácticamente no tenía ninguna influencia sobre el módulo elástico aparente.

Seguidamente se prepararon modelos con distintas fracciones volumétricas de poros para ver su influencia sobre los resultados finales.

En la figura 5 se muestra uno de los modelos de elementos finitos. En la figura 6 se muestra la relación ente el módulo elástico aparente y la fracción volumétrica de poros. Como se puede observar, esta relación es lineal.

Bonhomme et al 2018a-image11.png
Figura 5. Tensiones de Von Mises. Modelo con fracción volumétrica de poros 3%.
Bonhomme et al 2018a-image12.png
Figura 6. Módulo elástico en función de la fracción volumétrica de poros.

4 Conclusiones

En este trabajo se estudió el comportamiento mecánico de una resina epoxi reforzada con partículas mediante cálculo numérico por elementos finitos.

En los estudios realizados se ha observado que a media que disminuye la relación entre el espesor y el área de la partícula el efecto rigidizador de las partículas es más efectivo. Este efecto es independiente de la fracción volumétrica de refuerzo.

Se observó también que el aumento del módulo elástico es prácticamente lineal respecto a la fracción volumétrica de partículas de refuerzo.

En ensayos experimentales se observó que la adición de desgasificantes y reductores de tensión superficial en la fabricación de las probetas tenía un efecto apreciable sobre las propiedades mecánicas finales.

Los estudios de la influencia de la porosidad sobre el módulo elástico aparente demostraron una relación lineal con la fracción volumétrica de poros.

5 Referencias

[1] R. Wanga, Z. Li, W. Liu, et al. Attapulgite–graphene oxide hybrids as thermal and mechanical reinforcements for epoxy composites, Composites Science and Technology, 87, pág. 29–35 (2013)

[2] S. Chandrasekaran, N. Sato, F. Tölle, et al. Fracture toughness and failure mechanism of graphene based epoxy composites, Composites Science and Technology, 97, pág. 90–99 (2014)

[3] J.A. King, D.R. Klimek, I. Miskioglu, et al. Mechanical properties of graphene nanoplatelet/epoxy composites, Journal of Composite Materials, 49, 6, pág. 659–668 (2015)

[4] Y.J. Wan, L.C. Tang, L.X. Gong, et al. Grafting of epoxy chains onto graphene oxide for epoxy composites with improved mechanical and thermal properties, Carbon, 69, pág. 467–480 (2014)

[5] M.M. Shokrieh, M. Esmkhani, Z. Shokrieh, et al. Stiffness prediction of graphene nanoplatelet/epoxy nanocomposites by a combined molecular dynamics–micromechanics method. Computational Material Science, 92, pág. 444–450 (2014)

[6] M.M. Shokrieh, M. Esmkhani, H.R. Shahverdi, et al. Effect of graphene nanosheets (GNS) and graphite nanoplatelets (GNP) on the mechanical properties of epoxy nanocomposites. Science of Advanced Materials, 5, pág. 260–266 (2013)

[7] B. Karimi, B. Ramezanzadeh, A comparative study on the effect of ultrathin luminescent graphene oxide quantum dot (GOQD) and graphene oxide (GO) nanosheets on the interfacial interactive and mechanical properties of an epoxy composite, Journal of Colloid and Interface Science, 493, pág. 62–76 (2017)

[8] Z.S. Pour, M. Ghaemy, Polymer grafted graphene oxide: for improved dispersion in epoxy resin and enhancement of mechanical properties of nanocomposite. Composites Science and Technololy, 136, pág.145–157 (2016)

Back to Top
GET PDF

Document information

Published on 14/10/18
Accepted on 14/10/18
Submitted on 14/10/18

Volume 02 - Comunicaciones Matcomp17 (2018), Issue Núm. 4 - Comportamiento en servicio de los materiales compuestos (2), 2018
DOI: 10.23967/r.matcomp.2018.10.013
Licence: Other

Document Score

0

Views 1
Recommendations 0

Share this document

Keywords

• •

claim authorship

Are you one of the authors of this document?

I am an author