(Tag: Visual edit) |
|||
| Line 1: | Line 1: | ||
| − | + | <span id="_GoBack"></span> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <span | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==1 Scope of the study== | ==1 Scope of the study== | ||
| Line 80: | Line 10: | ||
Four resins mixtures of rigid and flexible epoxy resins were considered in this project: | Four resins mixtures of rigid and flexible epoxy resins were considered in this project: | ||
| − | '''Table 1''' | + | '''Table 1.''' Resin system combinations |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 133: | Line 63: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | '''Figure 2.1 | + | '''Figure 2.1.''' Fibre orientation.</div> |
Each material was modelled as an equivalent homogeneous orthotropic shell. From the symmetry of the layout, the longitudinal and transversal Young’s moduli are equal and determined from the tests. The shear modulus was approximated to be twice the longitudinal modulus. This ratio was obtained in previous studies of a similar material <span id='cite-_Ref454200055'></span>[[#_Ref454200055|[2]]]. The Poisson ratio was considered to be 0.76 for all materials <span id='cite-_Ref454200055'></span>[[#_Ref454200055|[2]]]. Its influence in the results is negligible. This way, the only parameter related to stiffness to be determined by test is the longitudinal Young’s modulus. | Each material was modelled as an equivalent homogeneous orthotropic shell. From the symmetry of the layout, the longitudinal and transversal Young’s moduli are equal and determined from the tests. The shear modulus was approximated to be twice the longitudinal modulus. This ratio was obtained in previous studies of a similar material <span id='cite-_Ref454200055'></span>[[#_Ref454200055|[2]]]. The Poisson ratio was considered to be 0.76 for all materials <span id='cite-_Ref454200055'></span>[[#_Ref454200055|[2]]]. Its influence in the results is negligible. This way, the only parameter related to stiffness to be determined by test is the longitudinal Young’s modulus. | ||
| Line 159: | Line 89: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | '''Figure | + | '''Figure 2.2. '''Hinge geometry</div> |
Following figure shows the boundary conditions applied to the FEM for its initial folding manoeuvre: | Following figure shows the boundary conditions applied to the FEM for its initial folding manoeuvre: | ||
| Line 167: | Line 97: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | '''Figure | + | '''Figure 2.3. '''Boundary conditions.</div> |
==3 Results== | ==3 Results== | ||
| Line 177: | Line 107: | ||
The tensile tests were carried out until fracture. The following table shows the measured average Young’s modulus at the linear part of the stress-strain curve, and the ultimate strength: | The tensile tests were carried out until fracture. The following table shows the measured average Young’s modulus at the linear part of the stress-strain curve, and the ultimate strength: | ||
| − | '''Table 2 | + | '''Table 2.''' Average Young´s modulus and material strength |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 209: | Line 139: | ||
The following table shows the average calculated modulus of elasticity. | The following table shows the average calculated modulus of elasticity. | ||
| − | <span id='_Ref449517066'></span><span id='_Ref449516901'></span>'''Table 3 | + | <span id='_Ref449517066'></span><span id='_Ref449516901'></span>'''Table 3. '''Average bending stiffness coefficient and calculated Young´s modulus |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 239: | Line 169: | ||
Next table shows the obtained average damping ratio <math display="inline">\xi</math> , natural frequency <math display="inline">{f}_{n}</math> and corresponding Rayleigh’s model <math display="inline">\beta</math> coefficient for each material. | Next table shows the obtained average damping ratio <math display="inline">\xi</math> , natural frequency <math display="inline">{f}_{n}</math> and corresponding Rayleigh’s model <math display="inline">\beta</math> coefficient for each material. | ||
| − | '''Table 4 | + | '''Table 4. '''Average damping ratio, natural frequency and Rayleigh’s model <math display="inline">\mathit{\boldsymbol{\beta }}</math> coefficient. |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 284: | Line 214: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | '''Figure 31 | + | '''Figure 31. '''Creep tests results.</div> |
====3.1.5 Termal Stability Tests==== | ====3.1.5 Termal Stability Tests==== | ||
| Line 301: | Line 231: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | [[Image:Nieto_et_al_2018b-image9.png| | + | [[Image:Nieto_et_al_2018b-image9.png|473x473px]] </div> |
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | '''Figure 32 | + | '''Figure 32. '''Analysis sequence.</div> |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;">[[File:Nieto_et_al_2018b-image10.png|centre|473x473px]]'''Figure 33 (cont’d).''' Analysis sequence.</div> |
| − | + | ||
<span id='_Toc453862589'></span> | <span id='_Toc453862589'></span> | ||
| Line 429: | Line 358: | ||
<span id='_Ref453834890'></span> | <span id='_Ref453834890'></span> | ||
| − | '''Table 6''': Results summary for the hinges ( <math display="inline">\xi</math> approach) | + | '''Table 6''': Results summary for the hinges ( <math display="inline">\xi</math> approach) |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 466: | Line 395: | ||
| − | '''Table '''6''' (cont’d): '''Results summary ( <math display="inline">\mathit{\boldsymbol{\xi }}</math> approach) | + | '''Table '''6''' (cont’d): '''Results summary ( <math display="inline">\mathit{\boldsymbol{\xi }}</math> approach) |
{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | {| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;" | ||
| Line 517: | Line 446: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| − | '''Figure 4. 1 | + | '''Figure 4. 1. '''Thor mission booms and magnetometer stowed configuration.</div> |
The following conclusions were obtained: | The following conclusions were obtained: | ||
| Line 531: | Line 460: | ||
<div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
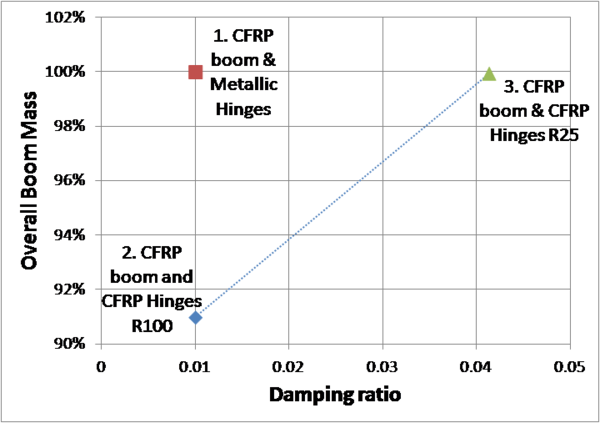
| − | '''Figure 4. 2 | + | '''Figure 4. 2. '''Mass/damping comparison for booms with similar behaviour and other possible intermediate solutions (in dashed line)-</div> |
Additionally, a potential pointing accuracy improvement of the application has been outlined, due to its simpler design compared to the boom with metallic hinges. | Additionally, a potential pointing accuracy improvement of the application has been outlined, due to its simpler design compared to the boom with metallic hinges. | ||
Revision as of 11:34, 12 October 2022
1 Scope of the study
This study aims to verify if a mixture of rigid and flexible epoxy resins, reinforced with carbon fibres, could change its mechanical properties (stiffness and damping) by changing the resins proportion. If so, this fact could be used to improve the performances of some space applications.
Once these materials were characterised experimentally, the stiffness and damping properties obtained from the tests were used in finite element simulations to study the effect of the different matrix mixes in a potential space application: the deployment of a tubular tape-spring composite hinge.
2 Materials and methods
Four resins mixtures of rigid and flexible epoxy resins were considered in this project:
Table 1. Resin system combinations
| Material Reference | Material label | Rigid resin (%) | Flexible resin (%) |
| 1 | R25 | 25 | 75 |
| 2 | R50 | 50 | 50 |
| 3 | R75 | 75 | 25 |
| 4 | R100 | 100 | 0 |
These resins mixtures were reinforced using different layers of carbon fibre plain fabric to manufacture the test coupons, depending on the type of test performed on the coupon.A series of tests were conducted in order to determine the materials properties:
- Stiffness was characterised through the Young’s modulus in both axial tensile tests and four-point bending tests:
- Axial tensile tests are designed to measure the tensile modulus of elasticity. A universal test machine has been used.
- The objective of the four-point bending tests is to measure the bending modulus of elasticity. A universal test machine with adequate test fixtures has been used.
- For measuring the damping, the amplitude decay logarithm increment method was used and the critical damping ratio and an equivalent Rayleigh stiffness-proportional damping model coefficient [1] were obtained.
- The pre-load loss was also investigated through creep tests in which the capability of the material for bearing a constant load for a long time is verified. In these tests, the coupons are bent 180 degrees with a radius of 20 mm. The applied load was maintained constant and the position of the tip of the coupon was registered over time.
- The thermal stability at high temperatures was verified by applying the following cycle: 20 °C to 150 °C, heat up rate 1 °C/min, and dwell 60 minutes at 150 °C.
Once these materials were characterised, they were used in finite element simulations to study the deployment of a tubular tape-spring composite hinge. MSC/Marc finite element software was used for the analyses.
The four considered materials had the same laminate layout (2 layers ±45, with a total thickness of 0.22 mm). The following image shows the overall geometry of the model and the fibre orientation (±45) with respect to the hinge longitudinal axis.
Each material was modelled as an equivalent homogeneous orthotropic shell. From the symmetry of the layout, the longitudinal and transversal Young’s moduli are equal and determined from the tests. The shear modulus was approximated to be twice the longitudinal modulus. This ratio was obtained in previous studies of a similar material [2]. The Poisson ratio was considered to be 0.76 for all materials [2]. Its influence in the results is negligible. This way, the only parameter related to stiffness to be determined by test is the longitudinal Young’s modulus.
On the other hand, damping is perhaps the most unrealistic part of any dynamic model. The mechanisms by which a structure dissipates mechanical energy are not well understood and, consequently, damping models are distant approximations. Different damping models can be found in bibliography, all giving different results. Usually, the only feature that can be demanded to a damping model is the overall loss of energy that produces to be correct. The damping model used in the simulations was the Rayleigh’s proportional damping model with only stiffness proportional coefficient [1]. Two approaches were considered:
- 1) ‘ approach’: Assuming that the parameter found in damping tests is a material property and, thus, has the same value in all conditions (for any geometry made with the tested material).
- 2) ‘ approach’: Assuming that the critical damping ratio found in damping tests is a material property and consequently it has the same value in all conditions (for any geometry made with the tested material). For this assumption, and due to the fact that only the Rayleigh’s parameters can be introduced in MSC/Marc software, the following equivalence is established: being the natural frequency of the tubular tape-spring hinge model. This approach was only carried out for the materials labelled as R100 and R25.
The finite element model took into account the following issues:
- Material linear behaviour.
- Damping is modelled with Rayleigh’s model, considering only the stiffness term.
- Large displacements.
- Implicit numeric solver.
The four hinges had the same geometry which is shown below:
Following figure shows the boundary conditions applied to the FEM for its initial folding manoeuvre:
3 Results
3.1 Materials Tests Results
3.1.1 Axial Tensile Test
The tensile tests were carried out until fracture. The following table shows the measured average Young’s modulus at the linear part of the stress-strain curve, and the ultimate strength:
Table 2. Average Young´s modulus and material strength
| Material
(rigid resin percentage) |
Young's modulus (GPa) | Strength (MPa) |
| 100 | 6.02 | 172 |
| 75 | 1.38 | 151 |
| 50 | 0.55 | 112 |
| 25 | 0.27 | 53 |
3.1.2 Four Point Bendings Test
The following table shows the average calculated modulus of elasticity.
Table 3. Average bending stiffness coefficient and calculated Young´s modulus
| Material (rigid resin percentage) | Average stiffness (N·mm-1) | Young’s modulus (GPa) |
| 100 | 17.10 | 6.75 |
| 75 | 15.29 | 6.04 |
| 50 | 10.74 | 4.24 |
| 25 | 5.04 | 1.99 |
3.1.3 Damping test
Next table shows the obtained average damping ratio , natural frequency and corresponding Rayleigh’s model coefficient for each material.
Table 4. Average damping ratio, natural frequency and Rayleigh’s model coefficient.
| Material
(rigid resin percentage) |
Damping ratio | Natural frequency (Hz) | Rayleigh’s coefficient (s·rad-1)
|
| 100 | 0.010 | 262.84 | 1.20E-05 |
| 75 | 0.014 | 241.93 | 1.84E-05 |
| 50 | 0.023 | 229.65 | 3.17E-05 |
| 25 | 0.038 | 224.61 | 5.38E-05 |
3.1.4 Creeps Test
The coupons with 100% and 50% rigid resin respectively collapsed after only one day. It was found out that the designed test rig did not maintain a constant load over the coupon, contrary to what could be thought. As the material creeps and its stiffness is reduced, the change in the coupon shape increases the moment at the critical point, which in turn increases the deformation, and so on, which can cause the collapse of the coupon. Creep test methodology must be reviewed for avoiding the increasing of the coupon stress.
Two coupons (75% and 25% rigid resin respectively) survived the objective time of 30 days. Next figure shows the evolution of the coupon tip height along the time.
3.1.5 Termal Stability Tests
No effect on the samples was visually detected neither during the heat up ramp nor the 150 ºC dwell. After the 60 min at 150 ºC all of them presented a similar behaviour to the sample at room temperature. After the test, visual inspection showed no failures, defects or micro-cracking in the coupons.
3.2 Potential Space Application
The material properties obtained in the material characterisation tests were used to simulate the tubular tape-spring composite hinge.
The folding simulation was carried out in two stages. A tape-spring hinge has a high bending stiffness in the fully deployed configuration. Therefore, to reproduce the folding a hinge without imposing very large strains, the process begins by pinching and flattening the hinge between two rigid surfaces. Then, the folding itself is produced.
Once the hinge is completely folded, the system is stable after a short period of time. The deployment simulation starts when one of the pivot points is released.
3.3 Approach3.3
β
{\textstyle {\mathit {\boldsymbol {\beta }}}}
Approach
Table 5 shows a summary of the simulations results for the β approach.
Table 5: Results summary (β approach)
| Hinge | Max. Angular velocity | Max. Reaction torque at the embedment | Reaction torque at the embedment at 180° | Min. Reaction torque at the embedment (before 150°) | Max. Von Mises stress | Deployment time |
| (rad/s) | (Nm) | (Nm) | (Nm) | (MPa) | (s) | |
| R100 | 28.3 | 11.6 | 1.00 | 0.082 | 718 | 0.259 |
| R75 | 33.9 | 10.4 | 0.90 | 0.072 | 644 | 0.274 |
| R50 | 21.7 | 8.2 | 0.64 | 0.054 | 464 | 0.321 |
| R25 | 17.8 | 3.5 | 0.31 | 0.0247 | 220 | 0.465 |
Table 5 (cont’d): Results summary (β approach)
| Hinge | Bending Modulus | Max. strain energy | Kinetic energy at 0° | Dissipated energy at 0° | Energy ratio at 0° (Dissipated energy / Max. strain energy) |
| (GPa) | (J) | (J) | (J) | - | |
| R100 | 6.75 | 0.670 | 0.584 | 0.068 | 0.102 |
| R75 | 6.04 | 0.602 | 0.537 | 0.055 | 0.091 |
| R50 | 4.24 | 0.433 | 0.377 | 0.047 | 0.11 |
| R25 | 1.99 | 0.205 | 0.183 | 0.019 | 0.093 |
The energy ratio shown in
Table 5 compares the dissipated energy with the initial strain energy before deployment (last column data). This value is approximately constant in the four simulations with the different material models and does not follow any understandable rule. This is a contradiction with what is found in the damping tests (the higher the flexible epoxy resin percentage, the higher the ratio of dissipated energy with respect to the total energy). It has been thought that the origin of this contradictory result is the assumed hypothesis that the Rayleigh’s damping model parameter is a material constant that can characterise the damping behaviour of the material in all conditions. So, this hypothesis should be verified.
3.4 Approach3.4
ξ
{\textstyle {\mathit {\boldsymbol {\xi }}}}
Approach
The same folding and deployment manoeuvres were simulated with the R100 and R25 materials but following the approach. Following table shows the results obtained in terms of relevant deployment features for the considered models.
Table 6: Results summary for the hinges ( approach)
| Hinge | Max. Angular velocity
(rad/s) |
Max. Reaction torque at the embedment
(Nm) |
Reaction torque at the embedment at 180°
(Nm) |
Min. Reaction torque at the embedment
(before 150°) (Nm) |
Deployment time
(s) |
| R100 | 28.3 | 11.1 | 1.07 | 0.067 | 0.263 |
| R25 | 12.6 | 3.36 | 0.32 | 0.026 | 0.475 |
Table 6 (cont’d): Results summary ( approach)
| Hinge | Bending Modulus | Max. strain energy | Kinetic energy at 0° | Dissipated energy at 0° | Energy ratio at 0° (Dissipated energy / Max. strain energy) |
| (GPa) | (J) | (J) | (J) | - | |
| R100 | 6.75 | 0.67 | 0.567 | 0.0831 | 0.124 |
| R25 | 1.99 | 0.205 | 0.173 | 0.031 | 0.151 |
These results show a substantial increase of the energy ratio shown in the last column when the percentage of flexible resin increases, which is reasonable and shows very promising results for this space application.
4 Weight and Cost Study
A coarse comparison between the weight, performance and manufacturing and assembly costs of a full CFRP deployable boom with integrated slotted hinges with different epoxy resins and the same structure with traditional metallic hinges was done for a typical space application. Possible future Thor ESA mission was selected, which contains several booms. Two of them are part of the magnetometer and their design was studied. The magnetometer contains two 6.3 meter long boom deployed from three segments. Following figure shows a spacecraft image and the stowed booms on the spacecraft.
The following conclusions were obtained:
- The use of CFRP slotted hinges made with 100% rigid epoxy resin can reduce the weight of the boom (9% for the considered boom) and its cost (to 64%) compared to the solution with metallic hinges for the same mechanical requirements.
- The use of CFRP slotted hinges made with 25% rigid epoxy and 75% flexible epoxy can maintain the weight of the boom, reduce its cost (to 64%) compared to the solution with metallic hinges and additionally increase its damping properties to values where the dynamic effects of the environmental loads, deployment manoeuvre and deployed loads can be mitigated.
- Additional weight can be saved at the expense of a reduction in damping (but still being more damped that a metallic hinge solution), as it is shown in the following figure:
Additionally, a potential pointing accuracy improvement of the application has been outlined, due to its simpler design compared to the boom with metallic hinges.
5 Conclusions
The results of this project have proven that the concept of a material which properties (stiffness and damping) can be tuned for the intended application is feasible: a carbon fibre reinforced mixture of rigid and flexible epoxy resins changes its stiffness and its damping capacity as the proportions of the resins in the mixture changes.
Both properties are strongly related (one increases when the other decreases), but it is likely possible to find compromise points between them that improve a specific space application. In particular, it is thought that a CFRP slotted hinge can be developed with this material and its stiffness and damping properties can be adapted to a specific mechanical requirement.
Additionally, it has been shown that a space application such the one presented in the present study would be improved in terms of weight and cost if CFRP slotted hinges were used.
Next intended steps for this activity are to further investigate on the material behaviour and its damping modelling, and to develop, manufacture and test a breadboard of a space application where its advantages can be demonstrated.
Acknowledgements
This activity is carried out in the scope of the ESA Innovation Triangle Initiative - CN 4000114438/15/NL/CBi/GM.
Referencias
[1] Jia, Junbo. Essentials of Applied Dynamic Analysis. Springer, 2014. ISBN: 978-3-642-37002-1.
[2] Mallikarachchi, H.M. Yasitha Chinthaka. Thin-walled composite deployable booms with tape-spring hinges. Ph.D. Thesis. University of Cambridge, 2011.
Document information
Published on 29/04/18
Accepted on 29/04/18
Submitted on 29/04/18
Volume 02 - Comunicaciones Matcomp17 (2018), Issue Num. 2 - Aplicaciones y compuestos multifuncionales, 2018
DOI: 10.23967/r.matcomp.2018.04.011
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?