m (Mcserna moved page Draft Serna Moreno 364944830 to Review 447512806113) |
(Versión con pequeñas correcciones de formato realizadas por el equipo editorial de la revista) (Tag: Visual edit) |
||
| (10 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==1 Introducción== | ==1 Introducción== | ||
| Line 123: | Line 87: | ||
| − | Uno de los principales resultados del trabajo proviene de la complejidad para describir la evolución tensión-deformación en la última etapa en relación a las propiedades iniciales del material. En el caso de cargas cíclicas de tracción, la respuesta mecánica en las Etapas I y II sigue el patrón de un daño progresivo. Sin embargo, un modelo de daño basado en una variable (''ξ'' en la Ecuación 2) no podría describir la evolución completa de tres etapas. Siguiendo la hipótesis y las observaciones experimentales de otros investigadores [17-19], durante el proceso pseudodúctil de laminados ±45° no se considera daño ni fluencia en las fibras. En consecuencia, la evolución no lineal dependería únicamente de lo que suceda en las direcciones tangencial y transversal a la fibra. Usando el cálculo tradicional de rigidez a nivel de capa de la Teoría Clásica de Placas Laminadas (CLPT) [28], la propuesta es actualizar las propiedades elásticas de la matriz durante el proceso de carga, reduciendo el módulo de elasticidad transversal | + | Uno de los principales resultados del trabajo proviene de la complejidad para describir la evolución tensión-deformación en la última etapa en relación a las propiedades iniciales del material. En el caso de cargas cíclicas de tracción, la respuesta mecánica en las Etapas I y II sigue el patrón de un daño progresivo. Sin embargo, un modelo de daño basado en una variable (''ξ'' en la Ecuación 2) no podría describir la evolución completa de tres etapas. Siguiendo la hipótesis y las observaciones experimentales de otros investigadores [17-19], durante el proceso pseudodúctil de laminados ±45° no se considera daño ni fluencia en las fibras. En consecuencia, la evolución no lineal dependería únicamente de lo que suceda en las direcciones tangencial y transversal a la fibra. Usando el cálculo tradicional de rigidez a nivel de capa de la Teoría Clásica de Placas Laminadas (CLPT) [28], la propuesta es actualizar las propiedades elásticas de la matriz durante el proceso de carga, reduciendo el módulo de elasticidad transversal ''E''<sub>2</sub> y el módulo de cortadura en el plano ''G''<sub>12</sub>. Para ello, se define la variable de daño interno ''ξ'' que puede tomar valores entre cero y uno [22]. En la Ecuación 2 la matriz constitutiva '''Q''' a nivel de capa se expresa en las direcciones principales del material. De acuerdo con la CLPT, una vez que la matriz constitutiva se expresa en las direcciones globales ''x'' (longitudinal) e ''y'' (transversal) en el plano utilizando el ángulo actualizado 𝜃''<sub>f</sub>'', se puede ensamblar la matriz '''ABD'''. En este caso, la matriz '''A''' indica la rigidez en el plano, la matriz '''B''' indica el acople entre esfuerzos en el plano y momentos y la matriz '''D''' indica la rigidez flexión-torsión. Si definimos la matriz de flexibilidad como '''S''' = ('''ABD''')<sup>−1</sup>, la pendiente secante ''ss<sub>A</sub>'' se puede estimar con la Ecuación 3 teniendo en cuenta el espesor ℎ de la muestra. Esto da una aproximación de la rigidez longitudinal aparente que tiene en cuenta la reducción de las propiedades de la matriz inicial y el ángulo actualizado de las fibras. |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 272: | Line 236: | ||
| − | La reducción de la rigidez durante el ensayo está relacionada con la energía disipada. En un ensayo LUR, para un cierto ciclo, el área parcial bajo la curva de tensión-deformación durante la carga se puede definir como <math display="inline">{w}_{P}</math>. Esto se puede relacionar con la energía total almacenada desde el comienzo del proceso <math display="inline">{w}_{T}</math> por medio de la magnitud porcentual | + | La reducción de la rigidez durante el ensayo está relacionada con la energía disipada. En un ensayo LUR, para un cierto ciclo, el área parcial bajo la curva de tensión-deformación durante la carga se puede definir como <math display="inline">{w}_{P}</math>. Esto se puede relacionar con la energía total almacenada desde el comienzo del proceso <math display="inline">{w}_{T}</math> por medio de la magnitud porcentual ''pw'' (Ecuación 4). Por lado, en la Ecuación 5, ''pss'' se define como el porcentaje de reducción de la pendiente secante experimental <math display="inline">{ss}_{Exp}</math> con respecto al valor inicial <math display="inline">{ss}_{0}</math>. La pendiente secante inicial se obtiene a partir de la evolución tensión-deformación antes del primer ciclo LUR. |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
Latest revision as of 09:48, 20 June 2022
1 Introducción
La pseudoductilidad puede definirse como la capacidad del material compuesto para soportar una gran deformación antes del fallo final. El fenómeno ha suscitado un gran interés [1-5] debido a la capacidad de evitar el comportamiento inherentemente frágil de los polímeros reforzados con fibras, lo que abre la posibilidad de una detección temprana de daños que conduzca a una estructura más segura. En la bibliografía se proponen varias alternativas que conduzcan a un comportamiento pseudo-dúctil, como la utilización de laminados angle-ply con distintas orientaciones [1,3,6], la fragmentación de capas [2], las arquitecturas de "brick and mortar" [7,8] o hibridación de capas delgadas [4,9-13]. Además, se proponen diferentes tipos de ensayo para analizar el potencial de los materiales compuestos con comportamiento pseudoductil, por ejemplo, su respuesta a altas velocidades de deformación [13] o la disminución de la sensibilidad a los agujeros [9,14].
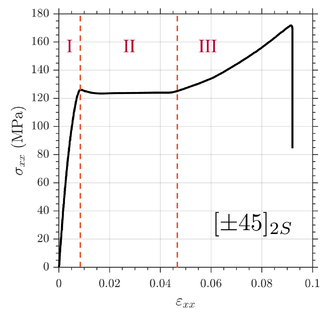
Centrándose en los laminados angle-ply de matriz polimérica reforzados con fibra de carbono (CFRP), las secuencias de apilamiento con orientaciones de capas simétricas a ±45° bajo cargas uniaxiales presentan un comportamiento promovido por la respuesta a cortadura de la matriz que da como resultado una respuesta de tensión-deformación altamente no lineal [1,15-20]. En el caso de que el laminado esté sometido a cargas uniaxiales de tracción y contenga un número bajo de capas, se pueden observar tres etapas bien diferenciadas (Fig 1): una etapa inicial con una relación tensión-deformación prácticamente lineal (Etapa I), seguida de una meseta en la que la deformación crece sin aumentar el nivel de tensión (Etapa II), y una última región que presenta un endurecimiento por deformación aparente hasta el fallo final (Etapa III). Esta respuesta no-lineal es el resultado del proceso de daño y cambios microestructurales de la matriz (que favorecen su plastificación) combinados con la tendencia a la reorientación de las fibras en la dirección de la carga. El proceso de daño de la matriz puede entenderse mejor siguiendo el trabajo de Sket et al [16], en el que se realizan ensayos de tracción en laminados [±45]2S observando la generación de grietas en cada etapa mediante tomografía de rayos X. Asimismo, la degradación de la respuesta a cortadura se confirma mediante ensayos de tracción cíclica con laminados [±45]2S en las investigaciones de Herakovich et al [17] o Troty et al [18], en las que además se indica la importancia de tener en cuenta la reorientación de las fibras en los modelos constitutivos.
Figura 1. Respuesta típica de un laminado [±45]2Ssometido a tracción monotónica uniaxial [21,22].
Con la intención de analizar el potencial pseudo-dúctil de los laminados ±45° de CFRP, a parte de los ensayos los ensayos uniaxiales de tracción hay algunos estudios en la literatura científica bajo diferentes escenarios de carga [20,23]. El trabajo de Cui et al [20] realiza ensayos uniaxiales de compresión en laminados [±45]4S en los que se promueve un nivel significativo de reorientación de las fibras lejos de la dirección de carga. Otra observación importante es la dependencia de la respuesta mecánica del laminado con la velocidad de deformación. Debido a esto, bajo la consideración de las fibras como un constituyente frágil, se señala que la matriz debe ser el principal contribuyente a la respuesta pseudo-dúctil debido a los importantes efectos viscoelásticos. Mientras tanto, uno de los trabajos previos de los autores [23] destaca los efectos pseudo-dúctiles en un laminado [±45]6S bajo ensayos de flexión de tres puntos. Se necesita un gran número de capas para evitar el acoplamiento flexión-torsión y promover la respuesta pseudodúctil. Gracias a las deformaciones medidas mediante técnicas de Correlación de Imagen Digital (DIC), se pueden observar simultáneamente diferentes grados de pseudo-ductilidad en distintas posiciones a lo largo del espesor.
En este artículo se resume el trabajo realizado en la referencia [22] y se analizan las principales decisiones tomadas. La investigación se centra en la respuesta pseudodúctil de laminados de CFRP en configuraciones [±45]2S sometidos a cargas cíclicas de tracción uniaxial y en secuencias [±45]4S ante cargas uniaxiales monotónicas de compresión. Para comprender mejor el proceso pseudodúctil ante cargas de tracción, se trabaja en [22] con ensayos de carga-descarga-recarga (LUR) para verificar si la energía recuperada en cada ciclo se puede utilizar para estimar la pérdida de la rigidez aparente. Además, la investigación desarrollada en [22] sienta las bases para la descripción del fenómeno de pseudo-ductilidad en compresión, ya que hasta la fecha los efectos no se habían examinado en profundidad en la literatura para laminados angle-ply sometidos a compresión uniaxial.
2 Material e instalación experimental
Se trabaja con laminados simétricos a ±45°, compuestos por capas de fibras de carbono unidireccionales IMA-12K preimpregnadas con la resina epoxi M21E de Hexcel® [24]. El prepreg tiene un contenido de resina del 34% en peso, mientras que el gramaje de fibra y la densidad de las fibras son de 268 g/m2 y 1,79 g/cm3 respectivamente, lo que da como resultado una fracción volumétrica de fibras del 59,2%. Cada capa de preimpregnado presenta un comportamiento elástico lineal ortótropo cuyas propiedades promedio en el plano, en las direcciones principales del material, se han determinado en investigaciones previas [21,25,26]. La Tabla 1 muestra los módulos de elasticidad y cortadura en el plano en direcciones principales del material a un nivel de carga anterior al primer ciclo LUR, así como los coeficientes de Poisson mayor y menor.
| (GPa) | (GPa) | (GPa) | ||
| 177.56 | 11.84 | 7.76 | 0.39 | 0.03 |
Para los ensayos de tracción uniaxial LUR, se estudian laminados [±45]2S debido a que el bajo número de capas permite obtener una curva tensión-deformación con tres etapas bien delimitadas (Fig. 1). Sin embargo, en los ensayos de compresión uniaxial se considera la configuración [±45]4S para cumplir con las limitaciones impuestas para evitar la inestabilidad de la probeta. El espesor nominal de una capa es Δ = 0,25 mm, de manera que se considera que el espesor total de cada laminado es h = 2 mm en el [±45]2S y h = 4 mm en el [±45]4S. Tras emplear la técnica de laminación manual, el proceso de fabricación continúa aplicando un ciclo de curado de 7 bar a 180⁰ durante 120 min [24] mediante una prensa de platos calientes LabEcon 300 del Grupo Fontijne Grotnes. Así se fabrican placas de 300 mm x 300 mm, a partir de las cuales se mecanizan probetas prismáticas rectangulares que se protegen con tacos poliméricos reforzados con fibra de vidrio de 3 mm de espesor. La zona de ensayo en las probetas [±45]2S tienen un largo nominal de 100 mm y un ancho nominal de 30 mm, mientras que en las probetas [±45]4S se deja una zona libre para el ensayo de 15 mm x 15 mm. En los ensayos se emplean mordazas neumáticas en una máquina electromecánica servocontrolada de la empresa Microtest con una capacidad de carga máxima de 50 kN. Durante la carga, se utiliza un sistema DIC LaVision StrainMaster para la medición óptica de campo completo de desplazamientos y deformaciones. Además, para adquirir deformaciones locales, se emplean rosetas de galgas extensométricas de Kyowa de 5 mm de longitud y un extensómetro de MTS que promedia la medición de la deformación longitudinal en una franja de 25 mm. En cuanto a los ensayos de compresión uniaxial, se diseña ad-hoc un dispositivo antipandeo basado en la norma D695 Modificada [27], que aquí se propone incluya una ventana que permita la inspección visual mediante DIC (Fig. 2). Además, se añade una ranura en la parte trasera del aparato que permite pegar una roseta de deformación en la cara posterior de la probeta para controlar la aparición de inestabilidades. De esta forma, la presencia de curvaturas debidas al pandeo se refleja en la diferencia entre las medidas de deformación en cada una de las superficies instrumentadas.
3 Resultados
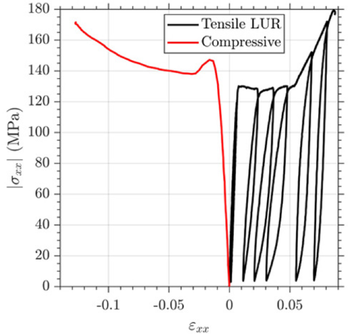
En la Fig 3 se muestra la respuesta mecánica de los laminados [±45]4S y [±45]2S ante cargas uniaxiales de compresión monotónica y de tracción cíclica, respectivamente. En el caso de los ensayos LUR, ocho han sido los cilcos de carga-descarga-recarga programados. Ambos casos de carga presentan una evolución tensión-deformación con tres etapas, con una primera evolución lineal seguida de una meseta y un endurecimiento por deformación final. En la Fig 3 las variables y son la deformación y tensión en la dirección en la dirección de la carga, respectivamente. Gracias a la utilización de las técnicas DIC, se observan campos de deformación longitudinal y transversal no uniformes en los pasos de carga intermedios de la meseta. Esta deformación no uniforme es debida a procesos de localización de deformaciones asociados a los cambios dimensionales en dirección perpendicular a la carga.
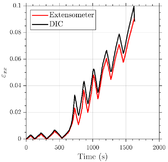
Teniendo en cuenta los campos de deformación no uniformes observados tras la primera etapa lineal, para mostrar la respuesta tensión-deformación global (Fig. 3) se ha optado por representar la deformación longitudinal media obtenida en la región de interés mediante DIC y/o el extensómetro. Como la tensión aplicada se calcula utilizando el área de la sección transversal inicial, la intención es tratar de evitar las diferencias locales entre las deformaciones tomadas en diferentes posiciones de la zona de medida durante la etapa no-lineal. En el caso de los ensayos de tracción cíclica, el programa de carga-descarga-recarga se hizo en base a los desplazamientos medidos por el extensómetro. Para comprobar si los resultados obtenidos por el extensómetro son adecuados para este fin, se propuso en los ensayos LUR comparar las deformaciones longitudinales medias obtenidas mediante DIC y el extensómetro. Algunos efectos locales no pueden evitarse por completo porque las medidas del extensómetro y del DIC tuvieron que adquirirse en diferentes posiciones. Téngase en cuenta que la longitud total de la región de ensayo en la muestra LUR es de 100 mm, sobre la que se colocó el extensómetro en una longitud de 25 mm. Por su parte, las observaciones del DIC se realizaron en un área contigua de 40 x 25 mm2 para evitar la obstrucción del extensómetro en las fotografías (Fig 4a). La Fig 4b muestra la medición promedio de mediante DIC en una galga virtual con una longitud de 40 mm, lo que se compara con el valor obtenido del extensómetro. Se observa una buena correspondencia en la Etapa I, aunque se inicia una cierta diferencia en la meseta que se asocia a que las medidas no se obtienen exactamente en las mismas regiones durante una etapa con campos de deformación no homogéneos. Sin embargo, estas discrepancias locales no afectan significativamente a los resultados y conclusiones del trabajo.

|
(b) |

(a) |
La respuesta aparentemente pseudo-dúctil es el resultado de un proceso de daño de la matriz y ciertos cambios microestructurales en la misma que favorecen su plastificación, combinados con la reorientación de las fibras. Durante el proceso de carga, es posible calcular el ángulo de fibra actualizado a partir del ángulo inicial y de las deformaciones longitudinal y transversal a la dirección de la carga mediante la Ecuación 1 [15,17].
|
|
(1) |
Uno de los principales resultados del trabajo proviene de la complejidad para describir la evolución tensión-deformación en la última etapa en relación a las propiedades iniciales del material. En el caso de cargas cíclicas de tracción, la respuesta mecánica en las Etapas I y II sigue el patrón de un daño progresivo. Sin embargo, un modelo de daño basado en una variable (ξ en la Ecuación 2) no podría describir la evolución completa de tres etapas. Siguiendo la hipótesis y las observaciones experimentales de otros investigadores [17-19], durante el proceso pseudodúctil de laminados ±45° no se considera daño ni fluencia en las fibras. En consecuencia, la evolución no lineal dependería únicamente de lo que suceda en las direcciones tangencial y transversal a la fibra. Usando el cálculo tradicional de rigidez a nivel de capa de la Teoría Clásica de Placas Laminadas (CLPT) [28], la propuesta es actualizar las propiedades elásticas de la matriz durante el proceso de carga, reduciendo el módulo de elasticidad transversal E2 y el módulo de cortadura en el plano G12. Para ello, se define la variable de daño interno ξ que puede tomar valores entre cero y uno [22]. En la Ecuación 2 la matriz constitutiva Q a nivel de capa se expresa en las direcciones principales del material. De acuerdo con la CLPT, una vez que la matriz constitutiva se expresa en las direcciones globales x (longitudinal) e y (transversal) en el plano utilizando el ángulo actualizado 𝜃f, se puede ensamblar la matriz ABD. En este caso, la matriz A indica la rigidez en el plano, la matriz B indica el acople entre esfuerzos en el plano y momentos y la matriz D indica la rigidez flexión-torsión. Si definimos la matriz de flexibilidad como S = (ABD)−1, la pendiente secante ssA se puede estimar con la Ecuación 3 teniendo en cuenta el espesor ℎ de la muestra. Esto da una aproximación de la rigidez longitudinal aparente que tiene en cuenta la reducción de las propiedades de la matriz inicial y el ángulo actualizado de las fibras.
|
|
(2) |
|
|
(3) |
Para juzgar si la no-linealidad de la matriz o la realineación de las fibras son dominantes en la respuesta pseudo-dúctil observada, a continuación se muestra el efecto de la variable separada de la influencia de la variable ξ. Con esta intención, en los ensayos LUR sobre laminados [±45]2S se analizan la influencia de la variable daño y el ángulo actualizado en la estimación de la pendiente secante empleando el CLPT para cada ciclo de carga-descarga. La Tabla 2 muestra la pendiente secante experimental frente al valor estimado de forma analítica (Ecuación 3) considerando la variable daño pero sin reorientación de fibras. Por su parte, la Tabla 3 enumera la influencia del ángulo actualizado en la estimación analítica de sin reducir las propiedades de la matriz. A pesar del hecho de que la reorientación de las fibras juega un papel no despreciable en el aumento de la rigidez efectiva del laminado durante todas las etapas, la aparente evolución tensión-deformación global está impulsada por la disminución de las propiedades de la matriz.
| Etapa I | Etapa II | Etapa III | ||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |
| (GPa) | 26.7 | 24.9 | 23.3 | 9.7 | 7.5 | 7.1 | 11.1 | 15.3 |
| (GPa) | 45.0 | 45.0 | 45.0 | 45.0 | 45.0 | 45.0 | 45.0 | 45.0 |
| ξ (%) | 1.3 | 9.5 | 16.4 | 69.7 | 78.2 | 80.6 | 71.6 | 62.7 |
| (GPa) | 26.6 | 24.6 | 22.9 | 8.9 | 6.5 | 5.8 | 8.4 | 10.9 |
| Etapa I | Etapa II | Etapa III | ||||||
| C1 | C2 | C3 | C4 | C5 | C6 | C7 | C8 | |
| (GPa) | 26.7 | 24.9 | 23.3 | 9.7 | 7.5 | 7.1 | 11.1 | 15.3 |
| (GPa) | 44.9 | 44.8 | 44.7 | 43.7 | 42.9 | 42.2 | 41.0 | 40.0 |
| ξ (%) | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| (GPa) | 27.1 | 27.2 | 27.3 | 28.7 | 30.0 | 31.2 | 33.4 | 35.3 |
La reducción de la rigidez durante el ensayo está relacionada con la energía disipada. En un ensayo LUR, para un cierto ciclo, el área parcial bajo la curva de tensión-deformación durante la carga se puede definir como . Esto se puede relacionar con la energía total almacenada desde el comienzo del proceso por medio de la magnitud porcentual pw (Ecuación 4). Por lado, en la Ecuación 5, pss se define como el porcentaje de reducción de la pendiente secante experimental con respecto al valor inicial . La pendiente secante inicial se obtiene a partir de la evolución tensión-deformación antes del primer ciclo LUR.
|
|
(4) |
|
|
(5) |
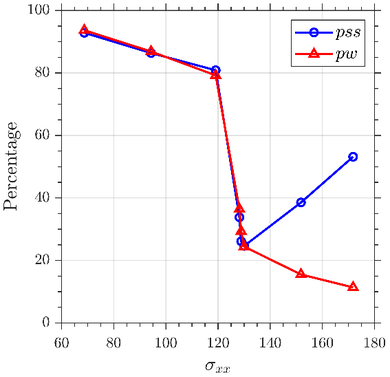
En la Figura 5 se han representado ambos porcentajes, pw y pss, frente a la tensión aplicada al comienzo de cada ciclo. Se puede observar que existe una correlación entre la reducción de la rigidez y la energía disipada en las dos primeras etapas de la respuesta tensión-deformación, pero la correlación ya no es válida en la tercera etapa. La Etapa III sigue un patrón diferente con un remonte de la rigidez que sugiere transformaciones microestructurales de la resina durante la Etapa II [29]. Estos cambios microestructurales se producen en la Etapa II debido a los procesos de localización de deformaciones tanto a tracción como a compresión, que se observan cualitativa y cuantitativamente gracias a los campos de deformaciones DIC (Fig 6). Efectos locales sobre el ancho de la sección de estrechamiento a tracción y de ensanchamiento a compresión, que se extiende por toda la longitud de la zona de medida a un determinado nivel de tensión aplicada. Se espera que este proceso promueva reordenamientos moleculares en la matriz que induzcan la última etapa del endurecimiento por deformación. En particular, en la Figura 6 se puede intuir el aumento en el ancho del área de la sección transversal a lo largo de la región de interés a partir del campo de deformación transversal que se muestra en un paso de carga intermedio en la Etapa II. A pesar de las restricciones visuales impuestas por la apertura del dispositivo antipandeo, se observa un "frente de deformación" que se extiende por la región de medición.
Figura 6. Ensayo de compresión en un laminado [±45]4S. Mapa de deformación transversal , a un nivel intermedio de carga en la etapa de meseta.
4 Conclusiones
La respuesta mecánica pseudo-dúctil de laminados CFRP simétricos con capas dispuestas a ±45° se estudia mediante ensayos de compresión uniaxial en laminados [±45]4S y ensayos de tracción uniaxial cíclica en secuencias de apilamiento [±45]2S. Ambos presentan una respuesta tensión-deformación con una primera evolución lineal seguida de una respuesta no-lineal con una última etapa de endurecimiento por deformación. Bajo ambos casos de carga, la respuesta mecánica en las Etapas I y II podría seguir el patrón de un daño progresivo con una reducción de la rigidez relacionada con la energía disipada. Sin embargo, un modelo de daño con un parámetro no podría describir la evolución completa de tres etapas. Además, existe una correlación entre la reducción de la rigidez y la energía disipada en las dos primeras etapas de la respuesta tensión-deformación, pero la correlación ya no es válida en la tercera etapa. La Etapa III sigue un patrón diferente con un aumento de rigidez que sugiere transformaciones microestructurales de la resina durante la Etapa II. Estos cambios microestructurales se producen en la Etapa II debido a los procesos de localización de deformaciones tanto a tracción como a compresión, que se observan cualitativa y cuantitativamente gracias a los campos de deformaciones DIC.
Agradecimientos
La publicación forma parte del proyecto PDC2021-121154-I00, financiado por MCIN/AEI/10.13039/501100011033 y por la Unión Europea ‘‘NextGenerationEU/PRTR’’. Asimismo, debe agradecerse las subvenciones de la Junta de Castilla-La Mancha por el proyecto regional SBPLY/19/180501/0000170 y al Ministerio de Economía y Competitividad de España junto con el Fondo Europeo de Desarrollo Regional por el proyecto nacional DPI2016-77715-R. El segundo autor también agradece el apoyo brindado por la Universidad de Castilla-La Mancha (UCLM) y el Fondo Europeo de Desarrollo Regional (FEDER) en el marco de la subvención 2020/3771. Ambos autores quisieran agradecer a la empresa Airbus por proporcionar el material utilizado en la preparación de los especímenes.
Referencias
[1] Fuller JD, Wisnom MR. Compos Part A Appl Sci Manuf 2015;69:64–71.
[2] Fuller JD, Jalalvand M, Wisnom MR. Compos Struct 2016;142:155–166.
[3] Fuller JD, Wisnom MR. Compos Sci Technol 2015;112:8–15.
[4] Jalalvand M, Czél G, Wisnom MR. Compos Part A Appl Sci Manuf 2015;69:83–93.
[5] University of Bristol and Imperial College London. High Performance Ductile Composite Technology research project: http://hiperduct.ac.uk/ (Accessed at 10/04/2021).
[6] Fuller JD, Wisnom MR. Compos Part A Appl Sci Manuf 2018;107:31–38.
[7] Pimenta S, Robinson P. Compos Sci Technol 2014;104:111–124.
[8] De Luca F, Clancy AJ, Carrero NR, Anthony DB, De Luca HG, Shaffer MSP, Mater Horiz 2018;5:668–674.
[9] Fotouhi M, Jalalvand M, Wisnom MR. Compos Part A Appl Sci Manuf 2018;110:29–44.
[10] Czél G, Wisnom MR. Compos Part A Appl Sci Manuf 2013;52:23–30.
[11] Jalalvand M, Czél G, Wisnom MR. Compos Part A Appl Sci Manuf 2015;74:123–131.
[12] Fotouhi M, Jalalvand M, Wisnom MR. Compos Sci Technol 2017;152:101–110.
[13] Fotouhi M, Fuller J, Longana M, Jalalvand M, Wisnom MR. Compos Struct 2019;215:365–376.
[14] Czél G, Rev T, Jalalvand M, Fotouhi M, Longana ML, Nixon-Pearso OJ, Wisnom MR. Compos Part A Appl Sci Manuf 2018;104:151–164.
[15] Wisnom MR. The effect of fibre rotation in 45 tension tests on measured shear properties. Compos 1995;26:25–32.
[16] Sket F, Rodríguez-Hortalá M, Molina-Aldareguía JM, Llorca J, Maire E, Requena E. Mater Sci Technol 2014;31(5):587–593.
[17] Herakovich CT, Schroedter RD, Gasser A, Guitard L. Compos Sci Technol 2000;60(15):2781–2789.
[18] Totry E, Molina-Aldareguía JM, González C, LLorca J. Compos Sci Technol 2019;70(6):970–980.
[19] Van Paepegem W, De Baere I, Degrieck J. Compos Sci Technol 2006;66(10):1455–1464.
[20] Cui H, Thomson D, Pellegrino A, Wiegand J, Petrinic N. Compos Sci Technol 2016:135:106–115.
[21] Horta Muñoz S. Complexity of the structural response of fibre reinforced polymer matrix composites. PhD Thesis 2020. URI: http://hdl.handle.net/10578/28223.
[22] Serna Moreno MC, Horta Muñoz S, Composites Part B 233 (2022) 109631.
[23] Serna Moreno MC, Horta Muñoz S, Romero Gutiérrez A, Rappold C, Martínez Vicente JL, Morales-Rodríguez PA, López Cela JJ. Compos Sci Technol 2018;156:8–18.
[24] Hexcel®. HexPly® M21 DataSheet. Available online at: https://www.hexcel.com/Resources/DataSheets/Prepreg (Accessed at 10/04/2021).
[25] Serna Moreno MC, Romero Gutiérrez A, Martínez Vicente JL. Compos Struct 2016;136:706–711.
[26] Serna Moreno MC, Romero Gutiérrez A, Martínez Vicente JL. Compos Struct 2016;146:62–68.
[27] ASTM D695-15. Standard Test Method for Compressive Properties of Rigid Plastics. American Society for Testing and Materials, 2015.
[28] Staab GH. Laminar Composites. 2nd edition. Elsevier; 2015.
[29] Sui XM, Tiwari M, Greenfeld I, Khalfin RL, Meeuw H, Fiedler B, Wagner HD. Express Polym Lett 2019;13(11):993–1003.
Document information
Published on 16/10/22
Accepted on 20/06/22
Submitted on 03/05/22
Volume 07 - COMUNICACIONES MATCOMP21 (2022), Issue Núm. 2 - Aplicaciones Industriales - Caracterización, 2022
DOI: 10.23967/r.matcomp.2022.10.006
Licence: Other