m (Scipediacontent moved page Draft Content 611054450 to Olay et al 2021a) |
|||
| Line 1: | Line 1: | ||
| − | |||
| − | |||
| − | == | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> |
| − | < | + | C. Bertorello<sup>a</sup>, J. Viña<sup>a</sup>, S. Sánchez<sup>b</sup>, V. Mollón<sup>a</sup>, </div> |
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | J. Bonhomme<sup>b</sup>, I. Viña<sup>b</sup>, A. Argüelles<sup>b</sup></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;"><sup>a</sup>Departamento de Ciencia de los Materiales e Ingniería Metalúrgica. Edificio Departamental Este, Campus Universitario, 33203 Gijón</span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;"><sup>b</sup>Departamento de Construcción e Ingeniería de Fabricación, Edificio Departamental Oeste, Campus Universitario, 33203 Gijón</span></div> | ||
| + | |||
| + | {| style="width: 87%;border-collapse: collapse;" | ||
| + | |- | ||
| + | | colspan='2' style="vertical-align: top;"|<big>Caracterización dinámica simétrica y asimétrica a fractura en modo III de composites epoxi-fibra de carbono unidireccional</big> | ||
| + | |- | ||
| + | | style="border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:Olay_et_al_2021a-image1.png|54px]] </span> | ||
| + | | style="vertical-align: top;"| | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Historia del artículo:</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Recibido 22 de Mayo de 2019</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">En la versión revisada 20 de Junio de 2019</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Aceptado 5 de Julio de 2019</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Accesible online 15 de Abril de 2021</span> | ||
| + | | rowspan='4' style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">En el presente trabajo se muestran los resultados obtenidos tras ensayar a fatiga en modo III un material compuesto de resina epoxi con refuerzo de fibra de carbono unidireccional. Para la ejecución de los ensayos se ha empleado un dispositivo de ensayo que ha sido diseñado previamente y cuya validez ha sido comprobada. La novedad de este trabajo radica en que es la primera vez que se lleva a cabo un estudio de fatiga a fractura según modo III en este tipo de materiales. Además esta fatiga se ha relizado de dos maneras distintas. En primer lugar, se ha cargado en una dirección hasta alcanzar un cierto ángulo y volviendo casi hasta el punto de inicio</span><span style="text-align: center; font-size: 75%;"> y, en segundo lugar, se ha cargado tanto en una dirección como en la contraria. De ahí que el primer caso se denomine fatiga asimétrica y en el segundo, fatiga simétrica. Los resultados obtenidos son distintos puesto que el caso de carga es, en ambos casos, sustancialmente diferente. En ambos casos se ha llevado a cabo un análisis estadístico de los resultados con objeto de poder constrastar mas adecuadamente las diferencias existentes.</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Palabras clave:</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Fatiga</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Fractura modo III</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Compuesto unidireccional</span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;vertical-align: top;"| | ||
| + | |- | ||
| + | | colspan='2' style="vertical-align: top;"|<big>Symmetrical and asymmetric dynamic characterization to fracture in mode III of epoxy composites-unidirectional carbon fiber </big> | ||
| + | |- | ||
| + | | style="border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;"> [[Image:Olay_et_al_2021a-image2.png|54px]] </span> | ||
| + | | style="vertical-align: top;"| | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;border-bottom: 1pt solid black;vertical-align: top;"|<span style="text-align: center; font-size: 75%;">Keywords:</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Fatigue</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Mode III fracture</span> | ||
| + | |||
| + | <span style="text-align: center; font-size: 75%;">Unidirectional Composite</span> | ||
| + | | rowspan='2' style="vertical-align: top;"|<span style="text-align: center; font-size: 75%;">The present work shows the results obtained after rehearsing fatigue in mode III a material composed of epoxy resin with unidirectional carbon fiber reinforcement. For the execution of the tests and has used a test device that has been previously designed and whose validity has been proven. The novelty of this work is that it is the first time that a study of fatigue to fracture is carried out according to mode III in this type of materials.In addition, this fatigue has been made in two different ways. First, it has been loaded in one direction until reaching a certain angle and returning almost to the starting point and, secondly, it has been loaded both in one direction and in the opposite. Hence the first case is called asymmetric fatigue and in the second, symmetrical fatigue. The results obtained are different since the case of loading is, in both cases, substantially different.In both cases, a statistical analysis of the results has been carried out in order to be able to compare the existing differences more properly. </span> | ||
| + | |- | ||
| + | | style="border-top: 1pt solid black;vertical-align: top;"| | ||
| + | |} | ||
| + | |||
| + | |||
| + | <br/> | ||
| + | |||
| + | ==1 Introducción== | ||
| + | |||
| + | En los últimos años se ha llegado a la conclusión, tanto por parte de la industria consumidora de materiales compuestos laminares, como de los distintos grupos de investigación de que uno de los fallos más comunes que ocurren en laminados consiste en la formación y, posterior crecimiento de grietas a lo largo de las distintas láminas que constituyen el material. Este fenómeno, que ha recibido el nombre de deslaminación, es tremendamente complicado de detectar en una estructura en funcionamiento, e incluso, no tiene por qué provocar la rotura catastrófica del elemento. Es más, en muchos casos, lo degrada de manera paulatina provocando pandeos locales y/o permitiendo la entrada de la humedad hasta el mismo centro del laminado. Todo esto provoca una disminución evidente de la vida a fatiga de las piezas. | ||
| + | |||
| + | Una cuestión complicada de analizar es como se produce el avance de la deslaminación, es decir, bajo qué estado tensional se encuentra una pieza en servicio que determina el crecimiento de las grietas en su interior. Todo el mundo académico, investigador y empresarial que se dedica a este tipo de material conoce que el frente de una grieta puede encontrase sometido a cualquiera de los tres modos fundamentales de fractura e, incluso a las distintas combinaciones que pueden existir de ellos. Los modos básicos I y II han sido estudiados ampliamente en los últimos años tanto estática como dinámicamente y su combinación modo I/II también ha sido motivo de importantes análisis. En lo referente al modo III los estudios han sido menores. La principal razón es que durante muchos años todos los dispositivos diseñados para analizar el comportamiento de estos materiales frente a este modo implicaban un componente importante de modo II. Este es el motivo por el que, probablemente, existen más estudios del modo mixto II/III que del modo III puro. | ||
| + | |||
| + | Inicialmente se comenzó a estudiar el modo III con el método conocido como Split Cantilever Beam (SCB) [1,2]. Este método emplea una probeta con una geometría similar a la Double Cantilever Beam usada en el modo I. Este método ofreció buenos resultados, aunque puede llegar a inducir sobrecargas irregulares sobre la probeta. Por tal motivo se procedió a una modificación del sistema cono objeto de disminuir, en la medida de lo posible, los momentos torsores durante el ensayo. Así surge el ensayo Simplified Split Cantilever Beam (SSCB) [2]. Los trabajos realizados con este método muestran más estabilidad que en el ensayo SCB, pero el porcentaje de modo II, aunque es minoritario, no puede considerarse como despreciable. También se desarrolló el Modified Split Cantilever Beam (MSCB) [3,4] que supuso una mejora importante puesto que se alcanzaron valores superiores al 95% de modo III. Pero, sin duda, el método de ensayo que ha concitado mayor número de seguidores es el Edge Crack Torsion (ECT) [5-7]. En este ensayo se consiguen unos altos porcentajes de modo III, aunque éstos varían del centro a los extremos de la probeta. Una modificación de este método lo constituye el Six-Point Edge Crack Torsion (6ECT) en el que se aplican dos cargas adicionales que permiten el análisis de la fase de crecimiento de la deslaminación [8]. | ||
| + | |||
| + | Posteriormente han ido surgiendo varios métodos más pero su éxito ha sido más bien discreto aunque todos ellos han realizado una importante aportación al conocimiento. Finalmente se ha presentado el método Longitudinal Half Fixed Beam (LHFB) [9]. Este método cuenta con una desventaja importante que es que precisa de una máquina de ensayos capaz de aplicar un par torsor, pero también tiene una ventaja grande como es que el modo III está asegurado al, prácticamente 100%, a lo largo de todo el frente de la probeta. Otra ventaja importante es que si la máquina de ensayos es dinámica permite analizar el comportamiento de los laminados bajo cargas dinámicas en modo III. Tal como se ha demostrado previamente, el modo III puro se obtiene cuando la carga se aplica a una distancia de 1 mm del frente de grieta, incrementándose el porcentaje de modo II conforme la carga se distancia del citado frente. Por ese motivo y con objeto de no caer en la discusión de si el estudio realizado a fatiga es en modo III puro o con un porcentaje de modo II, durante este estudio sólo se hablará de la iniciación y no del crecimiento. | ||
| + | |||
| + | ==2 Procedimiento experimental== | ||
| + | |||
| + | El dispositivo LHFB [23] fue utilizado en este trabajo para ensayar probetas con una geometría típica DCB (Double Cantilever Beam) obtenidas a partir de un laminado. Este laminado fue fabricado empleando un preimpregnado MTM45-1/IM7 (12k) - 134g/m<sup>2</sup> con un 32% en peso de resina. La MTM45-1 es una resina de tipo epoxi con temperatura de curado flexible, altas propiedades mecánicas y tenacidad que puede ser empleada en sistemas de infusión y para curado en bolsa de vacío o en autoclave. Por su parte la fibra de carbono IM7 es una fibra continua, de alta resistencia y alta deformación obtenida a partir de poliacrilonitrilo (PAN). Esta fibra ha sido tratada superficialmente con objeto de mejorar su adherencia a la matriz. | ||
| + | |||
| + | La carga dinámica fue aplicada a una distancia de 1 mm del frente de grieta, dado que en esta situación, tal como se ha demostrado previamente [10], el porcentaje de modo II existente es despreciable, en comparación con el modo III. La frecuencia utilizada ha sido de 4 Hz. | ||
| + | |||
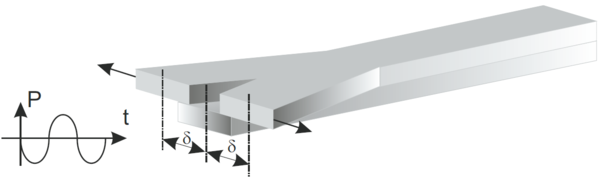
| + | El dispositivo LHFB se acopló a una máquina servohidráulica axial-torsional Walter+Bai (Figura 1) que permitió aplicar dos tipos de esfuerzo de torsión senoidal. Uno de ellos consistente en aplicar un par en una dirección y volver a un par mínimo en la misma dirección, utilizando un coeficiente de asimetría de 0.1 y el otro consistente en aplicar la mitad del par anterior en una dirección y, posteriormente en la contraria y así sucesivamente. En ambos casos el par aplicado se mantiene constante durante todo el ensayo. Este par se ha aplicado, en un caso en una dirección y en otro, de valor la mitad, y aplicado en las dos direcciones contrarias, generando un ángulo máximo inicial de valor θ que ha ido aumentado ligeramente conforme aumentaba el número de ciclos (Figura 2). | ||
| + | |||
| + | La configuración de los laminados era simétrica y con las fibras unidireccionales, empleando una lámina de 15μm de espesor Tygavac RF-260-R en el plano medio como un inserto que hizo el efecto de iniciador de la deslaminación. Las dimensiones de la probeta DCB utilizada en este estudio fueron: longitud = 200mm, ancho = 10mm y espesor = 6mm. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Olay_et_al_2021a-image5.jpeg|600px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 1.''' Equipo de ensayo</span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Olay_et_al_2021a-image6.png|600px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Olay_et_al_2021a-image7.png|600px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 2.''' Detalle de los dos tipos de aplicación de la carga</span></div> | ||
| + | |||
| + | ==3 Resultados== | ||
| + | |||
| + | Se han realizado ensayos con distintos pares torsores aplicados sobre el brazo móvil, empleándose para la obtención de los valores de la tasa de relajación de energía la Teoría de Timoshenko de vigas cortas. | ||
| + | |||
| + | Según esta teoría, el desplazamiento total será: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{\delta }_{T}={\delta }_{flexi\grave{o}n}+{\delta }_{cortante}=</math><math>\frac{P{L}^{3}}{3E{I}_{z}}+\frac{3PL}{2bhG}</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Y la tasa de liberación de energía será: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">G=\frac{1}{b}\left( \frac{{P}^{2}{L}^{2}}{2E{I}_{z}}+\frac{3{P}^{2}}{4bhG}\right)</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Donde P: carga aplicada | ||
| + | |||
| + | E: módulo de Young | ||
| + | |||
| + | L: longitud de la probeta | ||
| + | |||
| + | b: ancho de la probeta | ||
| + | |||
| + | h: espesor de la probeta | ||
| + | |||
| + | Aplicando esta formulación a las probetas ensayadas se obtiene la figura 3 donde se muestran los resultados obtenidos con todas las probetas ensayadas. | ||
| + | |||
| + | Se ha considerado que se produce el fallo a fatiga cuando se produce una deslaminación completa. Bajo este modo de fractura, el proceso de crecimiento del proceso de fractura, es inestable y ocurre de manera prácticamente simultánea al proceso de iniciación de la grieta. | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Olay_et_al_2021a-image8.png|600px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">a)</span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | [[Image:Olay_et_al_2021a-image9.png|600px]] </div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">b)</span></div> | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 3'''. Resultados bajo solicitación a fatiga cuando es sometido a carga en un solo sentido R=0,1 o en ambos sentidos del movimiento R=-1, para una probabilidad de rotura del 5% (a) y del 50% (b).</span></div> | ||
| + | |||
| + | Para poder realizar una interpretación adecuada del comportamiento a fatiga de un material compuesto es conveniente realizar un análisis estadístico de la muestra obtenida, dada su relativamente alta dispersión. En este trabajo se ha utilizado un modelo basado en una distribución de Weibull propuesto por Castillo et al. [11], que ya ha sido utilizado con éxito en este tipo de materiales, pero en otro modo de fractura. Este modelo permite obtener todo el campo de vida a fatiga a partir de una muestra representativa de datos experimentales. | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| + | |- | ||
| + | | | ||
| + | {| style="text-align: center; margin:auto;" | ||
| + | |- | ||
| + | | <math display="inline">{P}_{f}=F\left( N;G\right) =1-exp\left[ \left( \frac{log\left( N/{N}_{0}\right) \cdot log\left( {G}_{max}/{G}_{0}\right) -\lambda }{\delta }\right) \right]</math> | ||
| + | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) | ||
| + | |} | ||
| + | |||
| + | |||
| + | Con <math display="inline">log\left( N/{N}_{0}\right) \cdot log\left( {G}_{max}/{G}_{0}\right) \geq \lambda</math> | ||
| + | |||
| + | Donde N es la vida a fatiga medida en ciclos, G el rango de solicitación, P<sub>f</sub>, la probabilidad de fallo y G<sub>0</sub>, N<sub>0</sub>¸7·R� β, λ y δ son los parámetros a estimar, con el siguiente significado: | ||
| + | |||
| + | N<sub>0</sub>: valor umbral o número límite de ciclos | ||
| + | |||
| + | G<sub>0</sub>: energía de fractura límite | ||
| + | |||
| + | β: parámetro de forma de la distribución de Weibull | ||
| + | |||
| + | λ: parámetro que fija la posición de la curva límite o de la probabilidad nula | ||
| + | |||
| + | δ: parámetro de escala. | ||
| + | |||
| + | La figura 3 muestra las curvas percentiles para el material ensayado y para ambos casos de carga o para los dos modos de aplicación del par, que corresponden con las probabilida-des de rotura a fatiga del 5 (figura 3.a) y del 50% (figura 3.b), de acuerdo con el modelo de Weibull, representando la ener-gía de fractura máxima frente al número de ciclos requeridos para la iniciación de la grieta a fatiga. Se puede apreciar la enorme diferencia en el comportamiento para ambos tipos de solicitación, siendo el material mucho más resistente a fatiga cuando se carga en un solo sentido que cuando se aplica la mitad de la carga en ambos sentidos. Por lo que se refiere al límite de fatiga, para el 5% es de 180 J/m<sup>2</sup> para la carga en un sentido y de 35 J/m<sup>2</sup> si se carga en ambos sentidos, mientras que para el 50% los valores son, respectivamente, 200 y 40 J/m<sup>2</sup>. En ambos casos, el valor del límite de fatiga cuando la carga es en ambos sentidos es un 20% del obtenido cuando la carga es el doble pero en un único sentido. | ||
| + | |||
| + | ==4 Fractografía== | ||
| + | |||
| + | Se ha realizado un estudio fractográfico de la superficie de fractura de probetas que previamente habían sido ensayadas empleando el dispositivo LHFB, usando un JEOL 6610LV Scanning Electron Microscopy (SEM). | ||
| + | |||
| + | El análisis se ha desarrollado tanto en la zona próxima al inserto como en zonas más internas con objeto de intentar encontrar rasgos típicos de la fractura en modo III [10, 5], así como particularidades correspondientes al ensayo de fatiga bajo este modo de carga. | ||
| + | |||
| + | En la figura 4 se puede ver una fractura plana en una zona próxima al inserto en una probeta ensayada a fatiga siempre en el mismo sentido, en ella se pueden observar los dientes de sierra [10] característicos de este modo de fractura en régimen estático. | ||
| + | |||
| + | [[Image:Olay_et_al_2021a-image10.png|600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 4.''' Micrografía de la zona cercana al inserto en una probeta ensayada a fatiga aplicando la carga siempre en la misma dirección, con presencia de dientes de sierra.</span></div> | ||
| + | |||
| + | En la figura 5 se puede apreciar, en imágenes obtenidas de una probeta ensayada con la carga aplicada siempre en la misma dirección, la presencia de las escamas y de las fibras rotas típicas también de la fractografía estática. | ||
| + | |||
| + | [[Image:Olay_et_al_2021a-image11.png|600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 5.''' Micrografía de una probeta ensayada a fatiga aplicando la carga siempre en la misma dirección, con presencia de escamas y fibras rotas.</span></div> | ||
| + | |||
| + | En la figura 6 se puede apreciar la aparición de camas de resina en las probetas ensayadas con cargas aplicadas siem-pre en la misma dirección. Se trata de un rasgo fractográfico específico de las superficies fatigadas en modo III. | ||
| + | |||
| + | [[Image:Olay_et_al_2021a-image12.png|600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 6.''' Micrografía de una probeta ensayada a fatiga aplicando la carga siempre en la misma dirección, con presencia de camas de resina.</span></div> | ||
| + | |||
| + | En la figura 7 se muestra una fractografía de la superficie de fractura de una probeta en la que la carga se ha aplicado en las dos direcciones opuestas. Se ha observado la existencia de una cama de resina continua que con el paso del tiempo se va desconchando y desprendiendo dejando unos vacíos con las fibras perfectamente a la vista y el inicio de la creación de una nueva cama de resina. | ||
| + | |||
| + | [[Image:Olay_et_al_2021a-image13.png|600px]] | ||
| + | |||
| + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| + | <span style="text-align: center; font-size: 75%;">'''Figura 7.''' SEM de la superficie de fractura de una probeta ensayada con la carga aplicada en los dos sentidos, donde se aprecia la cama de resina y aparición de desconches.</span></div> | ||
| + | |||
| + | ==5 Conclusiones== | ||
| + | |||
| + | A lo largo del estudio presentado se ha podido confirmar la validez del dispositivo LHFB para poder realizar ensayos de fatiga en modo III, tanto si las cargas son aplicadas en un único sentido como si lo son aplicadas en dos sentidos contrarios. La dificultad que presenta es la necesidad de contar con una máquina de ensayos que permita la aplicación de esfuerzos de torsión. | ||
| + | |||
| + | El modelo estadístico de regresión empleado en la evaluación de los resultados experimentales basado en una distribución de Weibull, permite obtener información adicional al resultado del ensayo de fatiga como es la estimación de la resistencia a fatiga para cargas diferentes de las empleadas en el ensayo. Asimismo se ha podido constatar una muy importante diferencia en el comportamiento del material si la carga actúa en un único sentido o la mitad de la carga se aplica en dos sentidos opuestos. En este último caso esta diferencia se puede cuantificar en una disminución del límite de fatiga de un 20% frente al límite obtenido cuando la carga de aplica en un solo sentido. | ||
| + | |||
| + | El análisis fractográfico presentado permite principalmente dos conclusiones: | ||
| + | |||
| + | :* En el caso de que la carga sea aplicada en un solo sentido la morfología es muy similar a la existente en el caso fractura en modo III estática, con la salvedad de la aparición de unas importantes acumulaciones de resina a las que se ha dado el nombre de camas de resina. | ||
| + | |||
| + | :* En el caso de que la carga sea aplicada en dos sentidos opuestos, la morfología no tiene ninguna similitud con la existente en el caso de fractura en modo III estática. Al igual que en el caso de carga aplicada en un único sentido, aparecen camas de resina pero con alguna particularidad. Estas son más anchas lo cual es lógico porque el área barrido en mayor y también se van desconchando en trozos relativamente grandes, cosa que no ocurre en el otro caso de carga. | ||
| + | |||
| + | ==6 Agradecimientos== | ||
| + | |||
| + | Los autores agradecen el apoyo económico dado para la realización del presente trabajo por el Ministerio de Ciencia, Innovación y Universidades a través de proyecto RTI2018-095290-B-I00. | ||
| + | |||
| + | ==Referencias== | ||
| + | |||
| + | [1] S.L.Donaldson, ''Composites Science and Technology'', '''32''', 225-249 (1988). | ||
| + | |||
| + | [2] S.F.Hwang, C.L.Hu, ''Polymer Composites'', '''22''', 57-64 (2001). | ||
| + | |||
| + | [3] A.Szekrényes, ''International Journal of Mechanical Sciences'', '''51''', 682-693 (2009). | ||
| + | |||
| + | [4] M.R.Khoshravan, M.Moslemi, ''Engineering Fracture Mechanics'', '''127''', 267-279 (2014). | ||
| + | |||
| + | [5] X.Li, A.Carlsson, P.Davies, ''Composites Science and Technology'', '''69''', 1279-1286 (2004). | ||
| + | |||
| + | [6] A.B.de Morais, A.B.Pereira, M.F.S.F.de Moura, A.G.Magalhaes, ''Composites Science and Technology'', 69, 670-676 (2009). | ||
| + | |||
| + | [7] M.W.Czabaj, J.G.Ratcliffe, B.D.Davidson, ''Engineering Fracture Mechanics'', '''120''', 1-14 (2014). | ||
| + | |||
| + | [8] A.B.de Morais, A.B.Pereira,, M.F.S.F.de Moura, ''Composites Part A'', '''42''', 1793-1799 (2011). | ||
| + | |||
| + | [9] A.López-Menéndez, J.Viña, A. Argüelles, S. Rubiera, S., ''Journal of Composite Materials, '' '''50''', 3973-3980 (2016). | ||
| + | |||
| + | [10] A.López-Menéndez, J.Viña, A.Argüelles, I.Viña, S.Rubiera, ''Engineering Fracture Mechanics'', '''173''', 55-63 (2017). | ||
| + | |||
| + | [11] E.Castillo, A.F.Canteli, ''International Journal of Fatigue'', '''107''', 117-137 (2001). | ||
Revision as of 15:04, 7 May 2022
1 Introducción
En los últimos años se ha llegado a la conclusión, tanto por parte de la industria consumidora de materiales compuestos laminares, como de los distintos grupos de investigación de que uno de los fallos más comunes que ocurren en laminados consiste en la formación y, posterior crecimiento de grietas a lo largo de las distintas láminas que constituyen el material. Este fenómeno, que ha recibido el nombre de deslaminación, es tremendamente complicado de detectar en una estructura en funcionamiento, e incluso, no tiene por qué provocar la rotura catastrófica del elemento. Es más, en muchos casos, lo degrada de manera paulatina provocando pandeos locales y/o permitiendo la entrada de la humedad hasta el mismo centro del laminado. Todo esto provoca una disminución evidente de la vida a fatiga de las piezas.
Una cuestión complicada de analizar es como se produce el avance de la deslaminación, es decir, bajo qué estado tensional se encuentra una pieza en servicio que determina el crecimiento de las grietas en su interior. Todo el mundo académico, investigador y empresarial que se dedica a este tipo de material conoce que el frente de una grieta puede encontrase sometido a cualquiera de los tres modos fundamentales de fractura e, incluso a las distintas combinaciones que pueden existir de ellos. Los modos básicos I y II han sido estudiados ampliamente en los últimos años tanto estática como dinámicamente y su combinación modo I/II también ha sido motivo de importantes análisis. En lo referente al modo III los estudios han sido menores. La principal razón es que durante muchos años todos los dispositivos diseñados para analizar el comportamiento de estos materiales frente a este modo implicaban un componente importante de modo II. Este es el motivo por el que, probablemente, existen más estudios del modo mixto II/III que del modo III puro.
Inicialmente se comenzó a estudiar el modo III con el método conocido como Split Cantilever Beam (SCB) [1,2]. Este método emplea una probeta con una geometría similar a la Double Cantilever Beam usada en el modo I. Este método ofreció buenos resultados, aunque puede llegar a inducir sobrecargas irregulares sobre la probeta. Por tal motivo se procedió a una modificación del sistema cono objeto de disminuir, en la medida de lo posible, los momentos torsores durante el ensayo. Así surge el ensayo Simplified Split Cantilever Beam (SSCB) [2]. Los trabajos realizados con este método muestran más estabilidad que en el ensayo SCB, pero el porcentaje de modo II, aunque es minoritario, no puede considerarse como despreciable. También se desarrolló el Modified Split Cantilever Beam (MSCB) [3,4] que supuso una mejora importante puesto que se alcanzaron valores superiores al 95% de modo III. Pero, sin duda, el método de ensayo que ha concitado mayor número de seguidores es el Edge Crack Torsion (ECT) [5-7]. En este ensayo se consiguen unos altos porcentajes de modo III, aunque éstos varían del centro a los extremos de la probeta. Una modificación de este método lo constituye el Six-Point Edge Crack Torsion (6ECT) en el que se aplican dos cargas adicionales que permiten el análisis de la fase de crecimiento de la deslaminación [8].
Posteriormente han ido surgiendo varios métodos más pero su éxito ha sido más bien discreto aunque todos ellos han realizado una importante aportación al conocimiento. Finalmente se ha presentado el método Longitudinal Half Fixed Beam (LHFB) [9]. Este método cuenta con una desventaja importante que es que precisa de una máquina de ensayos capaz de aplicar un par torsor, pero también tiene una ventaja grande como es que el modo III está asegurado al, prácticamente 100%, a lo largo de todo el frente de la probeta. Otra ventaja importante es que si la máquina de ensayos es dinámica permite analizar el comportamiento de los laminados bajo cargas dinámicas en modo III. Tal como se ha demostrado previamente, el modo III puro se obtiene cuando la carga se aplica a una distancia de 1 mm del frente de grieta, incrementándose el porcentaje de modo II conforme la carga se distancia del citado frente. Por ese motivo y con objeto de no caer en la discusión de si el estudio realizado a fatiga es en modo III puro o con un porcentaje de modo II, durante este estudio sólo se hablará de la iniciación y no del crecimiento.
2 Procedimiento experimental
El dispositivo LHFB [23] fue utilizado en este trabajo para ensayar probetas con una geometría típica DCB (Double Cantilever Beam) obtenidas a partir de un laminado. Este laminado fue fabricado empleando un preimpregnado MTM45-1/IM7 (12k) - 134g/m2 con un 32% en peso de resina. La MTM45-1 es una resina de tipo epoxi con temperatura de curado flexible, altas propiedades mecánicas y tenacidad que puede ser empleada en sistemas de infusión y para curado en bolsa de vacío o en autoclave. Por su parte la fibra de carbono IM7 es una fibra continua, de alta resistencia y alta deformación obtenida a partir de poliacrilonitrilo (PAN). Esta fibra ha sido tratada superficialmente con objeto de mejorar su adherencia a la matriz.
La carga dinámica fue aplicada a una distancia de 1 mm del frente de grieta, dado que en esta situación, tal como se ha demostrado previamente [10], el porcentaje de modo II existente es despreciable, en comparación con el modo III. La frecuencia utilizada ha sido de 4 Hz.
El dispositivo LHFB se acopló a una máquina servohidráulica axial-torsional Walter+Bai (Figura 1) que permitió aplicar dos tipos de esfuerzo de torsión senoidal. Uno de ellos consistente en aplicar un par en una dirección y volver a un par mínimo en la misma dirección, utilizando un coeficiente de asimetría de 0.1 y el otro consistente en aplicar la mitad del par anterior en una dirección y, posteriormente en la contraria y así sucesivamente. En ambos casos el par aplicado se mantiene constante durante todo el ensayo. Este par se ha aplicado, en un caso en una dirección y en otro, de valor la mitad, y aplicado en las dos direcciones contrarias, generando un ángulo máximo inicial de valor θ que ha ido aumentado ligeramente conforme aumentaba el número de ciclos (Figura 2).
La configuración de los laminados era simétrica y con las fibras unidireccionales, empleando una lámina de 15μm de espesor Tygavac RF-260-R en el plano medio como un inserto que hizo el efecto de iniciador de la deslaminación. Las dimensiones de la probeta DCB utilizada en este estudio fueron: longitud = 200mm, ancho = 10mm y espesor = 6mm.
3 Resultados
Se han realizado ensayos con distintos pares torsores aplicados sobre el brazo móvil, empleándose para la obtención de los valores de la tasa de relajación de energía la Teoría de Timoshenko de vigas cortas.
Según esta teoría, el desplazamiento total será:
|
|
(1) |
Y la tasa de liberación de energía será:
|
|
(2) |
Donde P: carga aplicada
E: módulo de Young
L: longitud de la probeta
b: ancho de la probeta
h: espesor de la probeta
Aplicando esta formulación a las probetas ensayadas se obtiene la figura 3 donde se muestran los resultados obtenidos con todas las probetas ensayadas.
Se ha considerado que se produce el fallo a fatiga cuando se produce una deslaminación completa. Bajo este modo de fractura, el proceso de crecimiento del proceso de fractura, es inestable y ocurre de manera prácticamente simultánea al proceso de iniciación de la grieta.
Para poder realizar una interpretación adecuada del comportamiento a fatiga de un material compuesto es conveniente realizar un análisis estadístico de la muestra obtenida, dada su relativamente alta dispersión. En este trabajo se ha utilizado un modelo basado en una distribución de Weibull propuesto por Castillo et al. [11], que ya ha sido utilizado con éxito en este tipo de materiales, pero en otro modo de fractura. Este modelo permite obtener todo el campo de vida a fatiga a partir de una muestra representativa de datos experimentales.
|
|
(3) |
Con
Donde N es la vida a fatiga medida en ciclos, G el rango de solicitación, Pf, la probabilidad de fallo y G0, N0¸7·R�? β, λ y δ son los parámetros a estimar, con el siguiente significado:
N0: valor umbral o número límite de ciclos
G0: energía de fractura límite
β: parámetro de forma de la distribución de Weibull
λ: parámetro que fija la posición de la curva límite o de la probabilidad nula
δ: parámetro de escala.
La figura 3 muestra las curvas percentiles para el material ensayado y para ambos casos de carga o para los dos modos de aplicación del par, que corresponden con las probabilida-des de rotura a fatiga del 5 (figura 3.a) y del 50% (figura 3.b), de acuerdo con el modelo de Weibull, representando la ener-gía de fractura máxima frente al número de ciclos requeridos para la iniciación de la grieta a fatiga. Se puede apreciar la enorme diferencia en el comportamiento para ambos tipos de solicitación, siendo el material mucho más resistente a fatiga cuando se carga en un solo sentido que cuando se aplica la mitad de la carga en ambos sentidos. Por lo que se refiere al límite de fatiga, para el 5% es de 180 J/m2 para la carga en un sentido y de 35 J/m2 si se carga en ambos sentidos, mientras que para el 50% los valores son, respectivamente, 200 y 40 J/m2. En ambos casos, el valor del límite de fatiga cuando la carga es en ambos sentidos es un 20% del obtenido cuando la carga es el doble pero en un único sentido.
4 Fractografía
Se ha realizado un estudio fractográfico de la superficie de fractura de probetas que previamente habían sido ensayadas empleando el dispositivo LHFB, usando un JEOL 6610LV Scanning Electron Microscopy (SEM).
El análisis se ha desarrollado tanto en la zona próxima al inserto como en zonas más internas con objeto de intentar encontrar rasgos típicos de la fractura en modo III [10, 5], así como particularidades correspondientes al ensayo de fatiga bajo este modo de carga.
En la figura 4 se puede ver una fractura plana en una zona próxima al inserto en una probeta ensayada a fatiga siempre en el mismo sentido, en ella se pueden observar los dientes de sierra [10] característicos de este modo de fractura en régimen estático.
En la figura 5 se puede apreciar, en imágenes obtenidas de una probeta ensayada con la carga aplicada siempre en la misma dirección, la presencia de las escamas y de las fibras rotas típicas también de la fractografía estática.
En la figura 6 se puede apreciar la aparición de camas de resina en las probetas ensayadas con cargas aplicadas siem-pre en la misma dirección. Se trata de un rasgo fractográfico específico de las superficies fatigadas en modo III.
En la figura 7 se muestra una fractografía de la superficie de fractura de una probeta en la que la carga se ha aplicado en las dos direcciones opuestas. Se ha observado la existencia de una cama de resina continua que con el paso del tiempo se va desconchando y desprendiendo dejando unos vacíos con las fibras perfectamente a la vista y el inicio de la creación de una nueva cama de resina.
5 Conclusiones
A lo largo del estudio presentado se ha podido confirmar la validez del dispositivo LHFB para poder realizar ensayos de fatiga en modo III, tanto si las cargas son aplicadas en un único sentido como si lo son aplicadas en dos sentidos contrarios. La dificultad que presenta es la necesidad de contar con una máquina de ensayos que permita la aplicación de esfuerzos de torsión.
El modelo estadístico de regresión empleado en la evaluación de los resultados experimentales basado en una distribución de Weibull, permite obtener información adicional al resultado del ensayo de fatiga como es la estimación de la resistencia a fatiga para cargas diferentes de las empleadas en el ensayo. Asimismo se ha podido constatar una muy importante diferencia en el comportamiento del material si la carga actúa en un único sentido o la mitad de la carga se aplica en dos sentidos opuestos. En este último caso esta diferencia se puede cuantificar en una disminución del límite de fatiga de un 20% frente al límite obtenido cuando la carga de aplica en un solo sentido.
El análisis fractográfico presentado permite principalmente dos conclusiones:
- En el caso de que la carga sea aplicada en un solo sentido la morfología es muy similar a la existente en el caso fractura en modo III estática, con la salvedad de la aparición de unas importantes acumulaciones de resina a las que se ha dado el nombre de camas de resina.
- En el caso de que la carga sea aplicada en dos sentidos opuestos, la morfología no tiene ninguna similitud con la existente en el caso de fractura en modo III estática. Al igual que en el caso de carga aplicada en un único sentido, aparecen camas de resina pero con alguna particularidad. Estas son más anchas lo cual es lógico porque el área barrido en mayor y también se van desconchando en trozos relativamente grandes, cosa que no ocurre en el otro caso de carga.
6 Agradecimientos
Los autores agradecen el apoyo económico dado para la realización del presente trabajo por el Ministerio de Ciencia, Innovación y Universidades a través de proyecto RTI2018-095290-B-I00.
Referencias
[1] S.L.Donaldson, Composites Science and Technology, 32, 225-249 (1988).
[2] S.F.Hwang, C.L.Hu, Polymer Composites, 22, 57-64 (2001).
[3] A.Szekrényes, International Journal of Mechanical Sciences, 51, 682-693 (2009).
[4] M.R.Khoshravan, M.Moslemi, Engineering Fracture Mechanics, 127, 267-279 (2014).
[5] X.Li, A.Carlsson, P.Davies, Composites Science and Technology, 69, 1279-1286 (2004).
[6] A.B.de Morais, A.B.Pereira, M.F.S.F.de Moura, A.G.Magalhaes, Composites Science and Technology, 69, 670-676 (2009).
[7] M.W.Czabaj, J.G.Ratcliffe, B.D.Davidson, Engineering Fracture Mechanics, 120, 1-14 (2014).
[8] A.B.de Morais, A.B.Pereira,, M.F.S.F.de Moura, Composites Part A, 42, 1793-1799 (2011).
[9] A.López-Menéndez, J.Viña, A. Argüelles, S. Rubiera, S., Journal of Composite Materials, 50, 3973-3980 (2016).
[10] A.López-Menéndez, J.Viña, A.Argüelles, I.Viña, S.Rubiera, Engineering Fracture Mechanics, 173, 55-63 (2017).
[11] E.Castillo, A.F.Canteli, International Journal of Fatigue, 107, 117-137 (2001).
Document information
Published on 15/04/21
Accepted on 04/07/19
Submitted on 21/05/19
Volume 05 - Comunicaciones Matcomp19 (2021), Issue Núm. 2 - Caracterización analítica, numérica y experimental de los materiales compuestos. Materiales multifuncionales. Comportamiento de componentes estructurales., 2021
DOI: 10.23967/r.matcomp.2021.04.005
Licence: Other
Share this document
Keywords
claim authorship
Are you one of the authors of this document?