Revision as of 10:21, 3 May 2022

Ensayos numéricos de uniones adhesivas composite-composite para la determinación de la tenacidad a la fractura
Historia del artículo: Recibido 5 de Mayo 2017 En la versión revisada 5 de Mayo 2017 Aceptado 31 de Mayo 2017 Accesible online 21 de Junio 2017	En la actualidad el uso de uniones adhesivas entre componentes de material compuesto se ha incrementado notablemente en estructuras aeronáuticas primarias. Por ello es fundamental disponer de herramientas numéricas y ensayos experimentales que predigan los modos y cargas de fallo en este tipo de uniones. Usualmente, la evaluación de la calidad de una unión adhesiva se realiza mediante el ensayo de fractura interlaminar DCB (G1c), sin embargo, son conocidas las limitaciones que conlleva este procedimiento. En este trabajo se presentan algunos de los resultados de la investigación llevada a cabo sobre dos ensayos alternativos para determinar la calidad de una unión adhesiva. Estos ensayos están basados en el ensayo clásico de pelado sobre laminados de carbono. La simulación numérica, que se lleva a cabo usando el código de elementos finitos Abaqus®, incluye un modelo de iniciación y propagación del daño en el adhesivo. Los resultados numéricos se comparan con medidas experimentales provenientes de una extensa campaña de ensayos en laboratorio. Uno de los objetivos del modelo ha consistido en verificar la viabilidad de utilizar estos ensayos para evaluar el valor de G1c.
Palabras clave: Tenacidad a a la fractura FEM Cargas de pelado Grietas de interfase Ensayo In-Situ
Numerical analysis of composite-composite bonded joints. Fracture toughness determination
Keywords: Fracture toughness FEM Peeling loads Interface cracks In-Situ Test	Nowadays, the use of composite materials in primary structures has considerably increased, in particular in what refers to primary structures and bonded joints. Thus, numerical tools and experimental tests have to be implemented in order to understand failure modes and critical loads in this kind of structures. Usually, bonded joints quality is tested based on the interlaminar fracture test DCB (G1c). Nevertheless, these tests have some limitations. The aim of the present study is to create a feasible and accurate numerical model which allows the quality of a bonded joint as function of the peeling load to be determined. The idea is then an actual alternative to offer in-situ test by means of a transportable and easy to use device. In this study, a research analyzing two tests able to identify the quality of a bonded joints, as an alternative to the interlaminar fracture test, based on a classic peeling test on carbon laminates, is presented. The numerical simulation is based on a Finite Element Analysis using the commercial software Abaqus®. Onset and propagation of adhesive damage is taken into account by means of a cohesive zone model. A virtual test of the peeling test is done and its behavior is compared with the experimental results from an extensive laboratory test campaign. Numerical results will allow us to verify the feasibility to compute the value of G1c from experimental results.

1 Introducción

El uso de los materiales compuestos en estructuras primarias se ha incrementado notablemente en los últimos años sobre todo en las industrias aeronáutica y de automoción. Esto se traduce en la necesidad de tener caracterizado el comportamiento mecánico y los principales mecanismos de fallo de una manera precisa y fiable. Para ello se requieren herramientas numéricas y experimentales que predigan las cargas y modos de fallo de estas estructuras.

En particular, los procesos de delaminación o la evaluación de la calidad del encolado en uniones adhesivas en materiales compuestos reforzados con fibras de carbono (CFRP), pueden ser evaluadas correctamente mediante simulaciones numéricas [7–9,12]. En éstas, la tenacidad a la fractura (G_c), asociada a los diferentes modos de propagación del fallo, es el parámetro principal para caracterizar el modelo de daño elegido. Existen varias propuestas de ensayos experimentales para determinarla, algunos de ellas han derivado en normas técnicas [1-3]. Sin embargo, existen aún cuestiones que no están del todo resueltas y algunos inconvenientes que deben ser solventados [4].

En este estudio se presenta una nueva configuración de ensayo de pelado, que permite la evaluación in-situ de la tenacidad.

1.1 Ensayo de tenacidad a la fractura en modo I

Para determinar la tenacidad a la fractura en modo I, el ensayo más extendido es el ensayo sobre probeta tipo Double Cantilever Beam (DCB). Este ensayo puede utilizarse para determinar la tenacidad a la fractura interlaminar (con la grieta propagándose entre dos láminas del compuesto [1]) o para determinar la tenacidad de un adhesivo (cuando la grieta se propaga entre dos laminados unidos con dicho adhesivo [2]), y se da en términos de la tasa de liberación de energía (G). El esquema del ensayo y sus características se encuentra normalizado en [1-3]. A partir de la curva carga vs. desplazamiento del ensayo se calcula la tenacidad a la fractura usando la ecuación (1).

donde: A (J) es el área por debajo de curva carga-desplazamiento (energía para propagar la grieta), b (mm) es el ancho de la probeta, y a (mm) es la longitud que se ha propagado la grieta.

Este ensayo es el ensayo de referencia en la actualidad, y las principales ventajas son su sencillez y que, si la grieta se propaga a lo largo del plano de simetría de un laminado, G_c = G_1c. El principal inconveniente está en la necesidad de medir la longitud que va creciendo la grieta durante ensayo, lo cual puede no ser fácil con métodos normalizados [3]. Por otro lado, no es aplicable directamente en algunos casos como son laminados no simétricos o muy delgados.

1.2 Ensayo de pelado (Climbing drum peel)

Una alternativa al ensayo DCB para calcular la tenacidad a la fractura en materiales compuestos es el denominado “Climbing Drum Peel” CDP [5]. Este ensayo fue originalmente concebido para evaluar la resistencia de una unión adhesiva entre un adherente flexible y otro rígido o entre revestimiento y el núcleo en paneles tipo sándwich.

La Figura 1 muestra un esquema del funcionamiento de este ensayo, que consiste en enrollar un laminado de pequeño espesor (a pelar) usando un tambor con dos diámetros. Inicialmente se parte de una probeta con una pregrieta. En el radio menor del tambor (r₁ en la Figura 1) se fija el extremo del laminado a pelar, y en el diámetro exterior (r₂ en la Figura 1) se fija un feje. El extremo del fleje (B en la Figura 1) se ancla; al aplicar una tracción en el extremo opuesto de la probeta (A en la Figura 1) inicialmente se produce un plegado del laminado contra el tambor y posteriormente, alcanzado el valor apropiado de la carga, la propagación de la grieta. Una vez alcanzada la longitud de grieta suficiente, durante la descarga se produce el desliado del laminado a pelar.

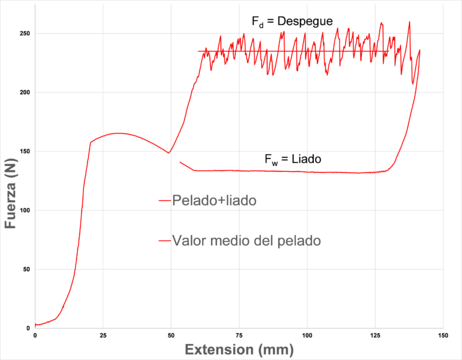
La Figura 2 muestra la curva de obtenida de un ensayo CDP. En ella se diferencian dos niveles de carga característicos: uno asociado al liado del laminado a pelar (F_w, que se puede medir durante la fase de descarga del ensayo) y otro asociado al despegue (F_d, que se mide durante la fase de carga del ensayo cuando la grieta crece).

La evaluación de la tenacidad se realiza por medio de la ecuación (2), [5,6].

donde: F_d (N) es la fuerza de pelado, F_w (N)es la fuerza de liado y b (mm) es el ancho de la probeta.

La propia configuración del ensayo y la cinemática impuesta dan lugar a una propagación estable de la grieta y no es necesario, a diferencia del DCB, medir la longitud de la propagación del daño, lo que se traduce en un ensayo más fácil de analizar. Por otro lado, la tenacidad que se evalúa no es directamente la asociada a un modo I de fractura, sino que existe cierta mixicidad a causa de posibles deslizamientos relativos en la interfaz entre el laminado a pelar y el resto de la probeta.

1.3 Nueva propuesta de ensayo de pelado (Horizontal Drum Peel)

Los procedimientos presentados en las secciones anteriores son procedimientos que están aceptados para evaluar la calidad de una unión adhesiva o la resistencia interlaminar de un CFRP. En ambos casos se precisa de una máquina universal de ensayos para aplicar la carga, lo que los hace inviables para su aplicación in-situ. Dado el interés de este tipo de aplicaciones, se planteó el objetivo de diseñar una nueva configuración que no requiriera la necesidad de medir la posición del vértice de la grieta, que permitiera la realización de los ensayos sobre los componentes estructurales directamente y con una gestión de las medidas del ensayo sencilla.

En la Figura 3 se muestra un esquema de la propuesta de ensayo, a la que se ha denominado “Horizontal Drum Peel” (HDP).

El principio mecánico es la aplicación de un par de rotación directamente al tambor, que se mide mediante una/s célula/s de carga. La tenacidad a la fractura (G_c) se calcula por medio de la ecuación (3).

donde, M_d es el momento de pelado, M_wes el Momento de liado, t_p es espesor del laminado, y D_t es el diámetro del tambor. Esta expresión se puede traducir en términos de fuerza liado (F_w) o despegue (F_d) por medio de las ecuaciones (4) y (5).

Durante la realización del ensayo se constata que la lámina se separa del tambor (Figura 4), y se obtienen curvas (Figura 11) de aspecto parecido a las del CDP (Figuras 2 y 12) pero con niveles de carga (F_d) muy inferiores.

Para dilucidar la contribución de los distintos parámetros geométricos y comprender la cinemática asociada a la propuesta de ensayo se ha desarrollado un modelo numérico de Elementos Finitos. Pueden consultarse otros detalles sobre este ensayo en [6].

2 Modelo numérico de Elementos Finitos

Se han realizado modelos de elementos finitos de los ensayos CDP y HDP con el software “Abaqus”. Se trata de modelos bidimensionales de tensión plana. El tambor se modela por medio de una superficie analítica rígida con un nodo central que gobierna los movimientos (traslaciones y giros). Se consideran la no linealidad geométrica y las interacciones de contacto entre tambor-laminado y laminado a pelar-laminado grueso. La iniciación y propagación del daño se tiene en cuenta mediante el uso de elementos cohesivos COH2D4 de “Abaqus”, [7], con una ley de tracción-separación bilineal y la propuesta de Benzeggah-Kenane [8] con η=2.0, Figura 5.

La Figura 6 presenta un esquema del modelo y la curva numérica obtenida en un ensayo HDP. En dicha curva se distinguen dos tramos característicos: el primero se corresponde con el liado de la pregrieta, y el segundo con el pelado o propagación de la grieta propiamente dicho.

3 Momento y radio crítico

Numéricamente también se constata una separación entre el tambor y el laminado a pelar. Al imponer una rotación en el extremo del laminado se obtiene una distribución de flectores constante a lo largo del tramo de pregrieta. Si los momentos aplicados van aumentando se alcanza un momento crítico (M_crit) a partir del cual la grieta crece; en esta situación el momento (y la curvatura del tramo) se mantiene constante. El modo de fallo es predominantemente modo I y el M_crites función de la rigidez del laminado (EI) y de las propiedades del adhesivo. La Figura 7 muestra un esquema del concepto de radio y momento crítico y de su evolución en función de la rotación.

En la Tablas 1 y 2 se presentan las características de los materiales modelados y los valores de los radios y momentos criticos obtenidos usando FEM, además se incluyen los valores de los radios usando la fórmula analítica que aparece en la Figura 7 en función de las propiedades de los laminados y de los diferentes espesores de la lámina a pelar.

Se observa que a menores espesores del laminado a pelar, aparecen diferencias más significativas entre los resultados FEM y la solución analítica debido a la mayor contribución de los grandes desplazamientos debido a la flexibilidad del laminado.

Como conclusión, se puede afirmar que salvo que la suma del diámetro del tambor y el semiespesor del laminado a pelar coincida con el correspondiente R_crit, siempre se producirá separación. No obstante, siempre que el patrón de esta separación se mantenga, no es necesario medir el avance de la grieta (pues coincidirá con lo que ha avanzado el tambor), y además el modo de fallo será predominantemente modo I.

4 Virtual testing

En paralelo con el análisis numérico presentado en esta comunicación, se ha realizado una amplia campaña de ensayos tanto para el CDP como para el HDP, [6], que ha permitido correlacionar los resultados numéricos con medidas experimentales.

4.1 Selección de los parámetros geométricos y materiales para el HDP y CDP

El diámetro del tambor y las células de carga para el prototipo HDP fabricado fueron seleccionadas a partir de estudios paramétricos para diferentes configuraciones de espesor y laminados. En la Tabla 3 se resumen dichos resultados.

Según las Tablas 1-3, podemos afirmar que a mayor diferencia entre el radio del tambor y R_crit, mayor será la separación entre el laminado a pelar y el propio tambor, y las tensiones de flexión serán menores. En base a estos resultados y teniendo en cuenta que a mayores diámetros de tambor más fácil es el manejo de la máquina, se recomienda para t<1 mm, un rango de diámetro de tambor entre 150 mm y 200 mm.

En este caso particular se decidió un valor de D_t = 190 mm, y se seleccionaron dos células de carga de 5 N.m cada una.

Para el caso del CDP se usaron las dos configuraciones disponibles en el laboratorio, cuyos datos geométricos se resumen en la Tabla 4.

Se han ensayado dos configuraciones, una con un laminado unidireccional y otra con un tejido. Las propiedades nominales de los materiales se resumen en la Tabla 5 y en la Tabla 6.

4.2 Resumen de resultados y Comparación numérico experimental

En este apartado se presentan las curvas numéricas para la evaluación de G_c, en los ensayos HDP y CDP para las diversas configuraciones analizadas. En ellas se analiza la influencia de las propiedades de los materiales y los espesores del laminado a pelar en los resultados.

Para verificar la fiabilidad de los modelos numéricos, las Figuras 8 y 9 muestran una comparación entre los resultados numéricos para en ensayo CDP y para el HDP en un laminado unidireccional y para un tejido, con sus correspondientes ensayos experimentales en laboratorio. A la vista de los resultados y la comparación entre valores de Tenacidad podemos concluir que la herramienta numérica es representativa de la realidad experimental, tanto cualitativa como cuantitativamente.

Para el ensayo HDP (Figura 9) se comprueba comparando los modelos que siempre se produce separación entre el laminado a pelar y el tambor, tal como hemos concluido en el Apartado 4. La Figura 10 es una fotografía del ensayo en un instante determinado, superpuesta a dicha imagen se ha incluido la deformada obtenida con el modelo numérico (en verde). Una vez alcanzado el M_crit en el vértice de la grieta, el patrón de propagación se mantiene constante, creciendo la grieta lo mismo que el se ha trasladado el tambor.

La Figura 11 es un resumen de las curvas numéricas carga vs desplazamiento del tambor para el ensayo HDP. En la Figura 11 se muestran también los valores obtenidos de la tenacidad para cada caso. En ella se determina con claridad la carga de liado y la de despegue, y a partir de ellas se calcula la tenacidad.

De manera análoga, en la Figura 12 se presentan las curvas numéricas para el ensayo CDP (que se ha utilizado de referencia para comparación entre ensayos). Los valores de la tenacidad se muestran superpuestos. En la simulación del ensayo CDP se ha procedido igual que en el laboratorio: una primera parte donde no hay grieta inicial y se procede a la propagación y una segunda parte que se descarga con una grieta ya creada, con lo que el mismo ensayo determina la carga de liado (durante la descarga) y la carga de pelado (durante la propagación).

5 Conclusiones

Las conclusiones más relevantes del estudio son:

• Los resultados numéricos del MEF y su comprobación experimental muestran la fiabilidad del modelo desarrollado y nos permiten usarlo como herramienta de comparación.

• Se valida la idea de evaluar la calidad de un encolado por medio de un ensayo de pelado más simple.

• Existe una separación de la lamina a pelar y el útil de ensayo, no afectando al modo de fractura y estando asociado al concepto de momento/radio crítico.

• El modelo numérico es robusto y suficientemente fiable para representar la realidad de los ensayos, como muestra de ello la correlación numérica-experimental del “Virtual Testing”.

Agradecimientos

Este trabajo ha sido financiado por el proyecto de excelencia TEP-1207 de la Junta de Andalucía y agradece el apoyo por parte de cátedra AIRBUS GROUP.

Referencia

[1] AITM 1-0005.”Fibre reinforced plastics - Determination of interlaminar fracture toughness energy - Mode I - G_1c”.

[2] AITM 1-0053.”Carbon fiber reinforced plastics. Determination of fracture toughness energy of bonded joints. Mode I. GIC test”.

[3] ISO-15024. “Fibre-reinforced plastic composites-determination of mode Iinterlaminar fracture toughness, GIc, for unidirectionally reinforced materials”.

[4] F. Daghia, C. Cluzel. “The Climbing Drum peel Test: An alternative to the Double Cantilever Beam for the determination of fracture toughness of monolithic laminates”. Elsevier, composites. Part A nº78, pg. 70-83.

[5] ASTM-D1781. “Standar test method for climbing drum peel for adhesives”

[6] M. M. Castro, J.Cañas, G. Santacruz, J. Justo, A. Cañas. “Evaluación experimental de la calidad de una unión encolada composite-composite mediante ensayos de pelado”. MATCOMP 17.

[7] Dávila, C.G., Camanho, P.P., and Turón, A. “Cohesive Elements for Shells” .NASA/TP-2007-214869, 2007.

[8] Benzeggagh, M.L., and Kenane, M., "Measurement of Mixed-Mode Delamination Fracture Toughness of Unidirectional Glass/Epoxy Composites with Mixed-Mode Bending Apparatus," Comp. Sci. Tech., 56 (4), pp. 439-449, 1996.

[9] L. Távara. “Damage initiation and propagation in composite materials. Boundary element analysis using weak interface and cohesive zone models”. PhD Thesis. Universidad de Sevilla: Sevilla 2010.

[10] L. Távara, V. Mantič, E. Graciani, F. París. “BEM analysis of crack onset and propagation along fibre-matrix interface under transverse tension using a linear elastic-brittle interface model”. Engineering Analysis with Boundary Elements, 35: 207-202, 2011.

[11] Hibbitt, Karlsson and Serensen. "ABAQUS/STANDARD. User’s Guide and Theoretical Manual", Version 6.8, 2008.

[12] Una de nuestras referencias del run-out