Revision as of 13:18, 22 April 2022 (view source) Jugoncan (talk | contribs) (Tag: Visual edit) ← Older edit	Latest revision as of 13:26, 22 April 2022 (view source) Jugoncan (talk | contribs) m (Jugoncan moved page Draft Gonzalez Cantero 569981957 to Review 447360982606)
(No difference)

---

Latest revision as of 13:26, 22 April 2022

1. Introducción

El uso de los materiales compuestos en los distintos componentes de la estructura de las aeronaves se ha visto incrementa considerablemente en las últimas décadas. Este hecho introdujo nuevas necesidades de simulación así como un incremento significativo del conocimiento sobre el comportamiento de los materiales compuestos. El conocimiento adquirido en el comportamiento de este tipo de materiales ha permitido realizar diseños optimizados para las distintas estructuras, pudiendo obtener valores precisos de las cargas máximas que son capaces de obtener.

Sin embargo, el diseño de los materiales compuestos presenta una complejidad adicional debido los propios procesos de fabricación, donde se pueden introducir distintos defectos o distorsiones geométricas que pueden afectar a la funcionalidad del propio componente y a la resistencia del mismo. Entre estos defectos podemos encontrar arrugas introducidas durante el conformado, especialmente en componentes con curvaturas complejas, problemas de porosidad debido a compactaciones deficientes o problemas de inyección, o distorsión tras el curado de estos materiales, entre otros muchos.

Es por ello que las necesidades de simulación están ampliando sus horizontes para centrarse no sólo en el comportamiento elástico y la resistencia del material, sino también para ser capaces de predecir el comportamiento de los componentes durante el proceso de fabricación, la generación de defectos y el efecto que puedan tener esos defectos.

De esta forma, hay bastantes estudios así como software específicos centrados en la simulación de los distintos pasos de fabricación: conformado, inyección o infusión, compactación, curado, así como la simulación de los posteriores pasos de recanteado y mecanizado de las piezas y el montaje final con otros componentes.

Este artículo se centra principalmente en la distorsión tras el curado, aplicado particularmente a material compuesto con resina epoxy termoestable. Airbus ha desarrollado herramientas internas basadas en subrutinas de Abaqus que han sido utilizadas en la simulaciones presentadas en este artículo. También se contemplaron software comerciales, aunque no cumplían los requisitos necesarios para la simulación al no considerar todos los efectos necesarios, particularmente en lo relativo a geometrías en forma de cajón cilíndrico/cónico.

En el artículo se presenta el proceso de simulación completo desde la caracterización completa del material a la simulación de un componente real en el avión y la validación experimental de la misma. Como caso de simulación se ha considerado un componente de alta complejidad como es la Sección 19 del A350.

2. Caracterización y modelado del material

Durante el curado de una resina termoestable se producen reacciones físico-químicas que producen cambios volumétricos y de rigidez en la resina. Al encontrarnos en un material no homogéneo con la presencia de las fibras, la contracción de la resina va a provocar que una lámina tenga una contracción ortotrópica, donde para una lámina con fibras unidireccionales la dirección de la fibra apenas presentará contracción mientras que las otras dos direcciones sí que llegarán a mostrarla, o en el caso de una lámina con fibra en varias direcciones (tejidos y NCF) se tendrá contracción principalmente en el espesor.

De esta forma, centrándonos en láminas con fibras unidireccionales, podemos diferenciar dos tipos de distorsión por curado según las dos direcciones en la que se observa una contracción significativa de la lámina:

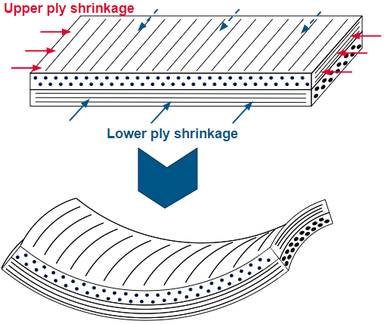
• Warpage, debido principalmente a la contracción en dirección 2 de la lámina (dirección en el plano perpendicular a la fibra), donde asimetrías en un laminado considerando que la dirección 1 presenta una contracción mínima van a presentar una deformada por flexión del laminado. Ver Figura 1.

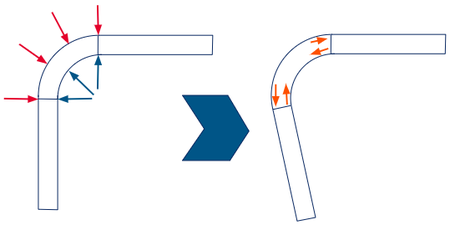
• Spring-in, debido principalmente a la contracción en dirección 3 de la lámina. Esta deformada se presenta en laminados con curvatura. Considerando un laminado cuasi-isotrópico, de forma que como conjunto las direcciones en el plano no presentan apenas deformación, al deformarse en el espesor no se produce una contracción homogéneo, lo que conlleva cambios de forma en el laminado. En particular, al contraerse más en el espesor, y como se observa en la Figura 2, las capas en radios exteriores van a intentar moverse hacia radios interiores que tienen una longitud menos, por lo que se van a comprimir y van a empujar los brazos del angular representado. Por otro lado, las capas en radios interiores se van a mover a radios mayores con longitudes mayores, tensionándose y tirando de los brazos de la L. En definitiva, el efecto final resulta en una flexión que cierra el angular y disminuye el ángulo entre ambos brazos.

Dentro de la contracción propia de la resina, que es la principal causante de estos dos mecanismos de deformación, además se puede diferenciar dos sub-mecanismos debido a las causas físico-químicas de la contracción de la resina. Wisnom et al. [1] presentado ambos mecanismos de contracción, el primero basado en la contracción térmica debido a los cambios de temperatura durante el curado, principalmente en el enfriamiento, y el segundo basado en la contracción química de la resina durante el proceso de curado, donde la formación de las cadenas poliméricas provocan importantes cambios volumétricos. Ambos efectos térmico y químico son importantes por igual, y suponen generalmente cada uno alrededor del 50% de la deformada total de la pieza.

Wisnom et al. además presenta otros mecanismos afectando la deformada final de la pieza, como son la interacción con el útil, bien sea por fricción o por las fuerzas introducidas durante la expansión del útil al calentarse, o elementos de bajo orden como la compactación, distorsión de fibras, zonas ricas en resina, etc.

Sin embargo, modelar la contracción de la resina no es útil por sí sólo, ya que las propiedades mecánicas de la resina también cambian durante el curado, por lo que las tensiones que se van a absorber debido a la contracción química de la resina van a depender a su vez de la rigidez en cada instante de la resina que depende a su vez del grado de curado y la temperatura. Además, se añade la complejidad de los flujos de resina durante la fase líquida de la misma, o el comportamiento viscoelástico durante la fase rubbery que van a relajar las tensiones absorbidas.

Como se puede ver, la complejidad del modelado aumenta significativamente, y es por ello por lo que se recurre a modelos Cure Hardening Instantaneously Linear Elastic (CHILE), donde se aproxima la resina en todo momento como un material lineal y elástico, como bien han utilizado varios autores [2,3].

Por ello, para el material de interés se ha realizado una caracterización en detalle de las distintas propiedades de interés:

• Cinética de curado, mediante caracterización DSC, para poder determinar la evolución del grado de curado con el tiempo dependiendo de la temperatura en cada instante del ciclo de curado. Incluye caracterización del grado de curado de gelificación y la temperatura de transición vítrea, Tg.

• Evolución del módulo de rigidez de la resina, mediante ensayo DMA aplicado a especímenes con varios grados de curado.

• Coeficiente de expansión térmica, mediante ensayo TMA. Se obtienen a grandes rasgos dos coeficientes principales: uno para la fase sólida del material y otro para la fase rubbery, cuya transición depende de la Tg del material.

• Contracción química, mediante reología, que suele presentar un comportamiento lineal con el grado de curado de la resina.

Tras la caracterización se ha llevado a cabo una aproximación mediante distintos modelos matemáticos de las distintas propiedades del material y se han introducido dentro de subrutinas de Abaqus que son usadas durante la simulación. Esta subrutina ha sido validada en ambos modos de deformación, warpage y spring-in, con elementos simples tales como paneles planos asimétricos o angulares.

La subrutina incluye, en conjunto con las propiedades de la resina anteriormente descritas, propiedades de la fibra. Ambos materiales son enlazados matemáticamente mediante modelos micromecánicos que permiten obtener las propiedades de la lámina a partir de sus constituyentes, como el presentado por Bogetti et al. [4], e incluso considerando el caso de interleaf de resina que está presente en algunos materiales comerciales, como en el modelo presentado por Frerich et al. [5].

3. Generación del modelo FEM y simulación

La simulación en elementos finitos de la Sección 19 del A350 se ha llevado a cabo mediante la utilización de elementos sólidos utilizando la definición de secciones sólidas de tipo composite, de forma que varias capas del laminado pueden son modeladas en un único elemento. La elección de los elementos sólidos radica en la necesidad de modelar la contracción en el espesor para ser capaces de predecir el spring-in. No obstante, Graciani et al. [6] están estudiando metodologías de simulación que permiten modelar el efecto de la contracción en el espesor mediante modificaciones de las propiedades en el plano, lo que permitiría simplificar significativamente la complejidad de la malla y reducir los tiempos de simulación.

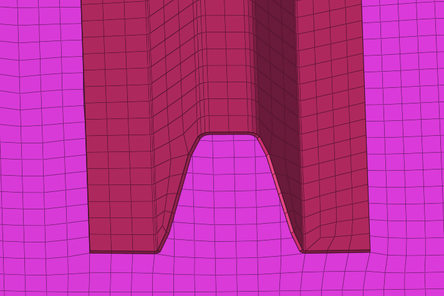
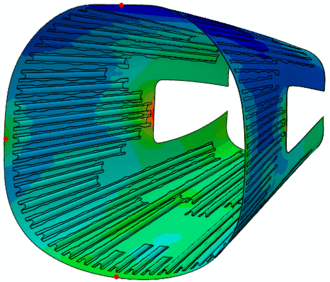
Se ha utilizado una malla de 5mm de tamaño, con una refinado de la misma en las zonas angulares de alta curvatura, y se ha utilizado un único elemento en el espesor debido al gran tamaño del componente. Para ser capaces de predecir la flexión del componente con alta precisión mediante un único elemento en el espesor se han utilizado elementos de modos incompatibles. Además, los distintos elementos cocurados (rigidizadores) han sido modelados mediante una malla de elementos coincidentes como se puede ver en la Figura 3, despreciando cualquier deslizamiento que pueda haber durante el curado.

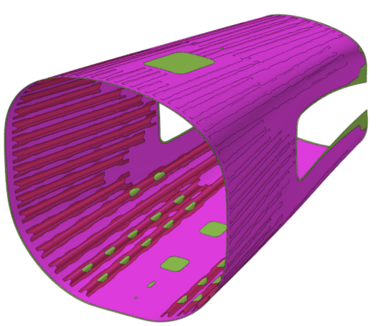
Por último, se han identificado las zonas de recanteado, tal y como se observa en la Figura 4, para la posterior simulación del proceso de mecanizado.

La principal particularidad de la simulación se centra en la alta importancia de la interacción pieza-útil. Debido la geometría de cajón cerrado de la pieza, las capas a 90º (donde la fibra sigue la dirección circunferencial) no presentan una continuidad completa de la fibra y se requieren solapes para compensarlo. Por otro lado, al ser fabricado sobre útil macho, la expansión del útil durante la fase de calentamiento va a provocar que todo el componente se tensione, y al curarse las tensiones van a ser absorbidas como tensiones residuales y en parte liberadas tras el desmoldeo de la pieza, teniendo un efecto significativo sobre la distorsión geométrica de la pieza. Sin embargo, la presencia de los solapes va a provocar deslizamientos entre capas que relajan esas tensiones, por lo que el modelado de este efecto de deslizamiento tiene una importancia alta. Para ello, se ha realizado una modificación de las propiedades de las fibras en ciertas capas para modelar este efecto de relajación mediante un módulo inferior. Esta modificación es totalmente empírica y ha sido calibrado con la fabricación de demostradores pequeña escala.

Una vez realizada la malla y con las propiedades material modeladas mediante subrutinas, la simulación se ha llevado a cabo mediante el modelado y mallado del útil, la definición de contactos entre ambos para considerar la interacción pieza-útil, y la definición de steps de simulación en los que se ha incluido el ciclo de curado y de presión introducidos sobre la pieza real.

4. Resultados y validación

Tras la simulación en Abaqus mediante el modelado indicado anteriormente se ha obtenido la deformada final de la pieza tras el curado, como puede observarse en la Figura 5, así como la modificación de dicha deformada tras el recanteado, como puede observarse en la Figura 6.

Ambas deformadas han podido ser validadas mediante dos métodos distintos:

• Mediciones de la pieza in-situ. Requiere una simulación adicional de los puntos de apoyo y el efecto de la gravedad sobre la pieza, intentando analizar a priori qué porcentaje de la distorsión es debido a la gravedad y qué porcentaje a la propia distorsión de curado, de forma que la comparativa sea representativa.

• Mediciones de cargas de actuadores en la estación de mecanizado, que dependen altamente de la geometría de la pieza. De forma similar, requiere una simulación adicional de los puntos de apoyo, los actuadores y el efecto de la gravedad sobre la pieza.

5. Conclusiones y desarrollos futuros

La simulación de los procesos de fabricación de materiales compuestos aporta un valor añadido significativo a las simulaciones tradicionales, al permitir predecir defectos y de esta forma poder afectar al diseño del proceso de fabricación de forma anticipada, reduciendo el número de intentos prueba-error físicos y de esta forma reduciendo significativamente los costes de desarrollo de nuevos componentes y el desperdicio de material.

En el artículo principal se ha presentado la metodología de simulación del proceso de curado, siendo capaces de obtener con una alta precisión la geometría final de la pieza. Se ha mostrado los parámetros más importantes a tener en cuenta durante la simulación, y se ha aplicado a un componente real de gran escala como es la Sección 19 del A350.

El curado de materiales compuestos es el proceso que cuenta con un nivel de madurez superior dentro de todo el ciclo de fabricación, siendo capaces de obtener la geometría deformada con una alta precisión, y aplicarlo a un proceso de compensación de útil mediante distintas iteraciones de simulación para ser capaz de compensarlo en las piezas que así lo requieran.

Sin embargo, todavía quedan puntos que requieren investigaciones y desarrollos adicionales. Este es el caso mostrado de los cajones cerrados, donde el deslizamiento entre capas en solapes juega un papel importante y, aunque el modelado empírico realizado ha mostrado buenos resultados, requeriría un análisis en detalle para ser capaces de capturar el efecto del tamaño de los solapes, distancia entre solapes, etc.

Además, debido al comportamiento viscoelástico de la resina, se puede añadir en ciertos casos la necesidad de modelar dicho comportamiento para tener en cuenta la relajación de la resina cuando se tienen ciclos de curado más largos o cortos, así como para suplir las necesidades de simulación de ciclos de post-curado, donde se pueden introducir cargar al componente y los efectos viscoelásticos juegan un papel importante.

Por último, aunque no menos importante, uno de los puntos más buscados por la industria es la realización de simulaciones end-to-end, donde se sea capaz de simular el proceso completo de fabricación, comenzando por conformado, incluyendo infusión/inyección en materiales de fibra seca o compactación en prepreg, hasta el curado, mecanizado y ensamblado del componente final, y ser capaces de enlazar todas las simulaciones de forma que se pueda incluir, por ejemplo, las distorsiones de fibra de un conformado dentro del curado, o los volumen de fibra obtenidos tras un conformado en una simulación de inyección y en el curado, y de esta forma tener visibilidad del proceso completo.

Referencias:

[1] M.R. Wisnom, M. Gigliotti, N. Ersoy, M. Campbell, K.D. Potter. Mechanisms generating residual stresses and distortion during manufacture of polymer-matrix composite structures. Composites: Part A 37, 522-529 (2006).

[2] S.R. White, H.T. Hahn. Process modeling of composite materials: Residual stress development during cure. Part II. Experimental validation. Journal of Composite Materials 26, 2423–2453 (1992).

[3] G. Fernlund, A. Osooly, A. Poursartip, R. Vaziri, R. Courdji, K. Nelson, P. George, L. Hendrickson, J. Griffiith. Finite element based prediction of process-induced deformation of autoclaved composite structures using 2D process analysis and 3D structural analysis. Composite Structures 62, 223–234 (2003).

[4] T.A. Bogetti, J.W. Gillespie. Process-Induced Stress and Deformation in Thick-Section Thermoset Composite Laminates. Journal of Composite Materials 26, 626-660 (1992).

[5] T. Frerich, C. Brauner, J. Jendrny, A.S. Hermann. Modeling the influence of interleaf-layers in composite materials on elastic properties, thermal expansion and chemical shrinkage. Journal of Composite Materials 53(17), 2415-2428 (2019).

[6] E. Graciani, A. Blázquez, J. Justo, F. París. Modelling thermal deformations in curved Composite laminates using standard shell finite Elements. Proceedings of ECCM17 - 17th European Conference on Composite Materials, Munich, Germany, 26-30th June 2016.