m (Gstinoco moved page Draft Tinoco Guerrero 234551248 to Review 300670986669) |
|||
| Line 9: | Line 9: | ||
One of the greatest challenges in the area of applied mathematics continues to be the design of numerical methods capable of approximating the solution of partial differential equations quickly and accurately. One of the most important equations, due to the hydraulic and transport applications it has, and the large number of difficulties that it usually presents when solving it numerically is the Diffusion Equation. | One of the greatest challenges in the area of applied mathematics continues to be the design of numerical methods capable of approximating the solution of partial differential equations quickly and accurately. One of the most important equations, due to the hydraulic and transport applications it has, and the large number of difficulties that it usually presents when solving it numerically is the Diffusion Equation. | ||
| − | In the present work, a Method of Lines applied to the numerical solution of the said equation in irregular regions is presented using a scheme of Generalized Finite Differences. A series of tests and numerical results are presented, which show the accuracy of the proposed method. | + | In the present work, a Method of Lines applied to the numerical solution of the said equation in irregular regions is presented using a scheme of Generalized Finite Differences. The second-order finite difference method uses a central node and 8 neighbor points in order to address the spatial approximation. A series of tests and numerical results are presented, which show the accuracy of the proposed method. |
'''keywords''' Generalized Finite Differences, Method of Lines, Diffusion Equation, Irregular Regions | '''keywords''' Generalized Finite Differences, Method of Lines, Diffusion Equation, Irregular Regions | ||
| Line 17: | Line 17: | ||
When a substance is been transported with a speed equal to zero, i.e. no flow moves it, then, according to the transport equation <span id='citeF-1'></span>[[#cite-1|[1]]], the initial profile of the substance should remain the same as time goes by, maintaining the substance concentration at each point in the fluid. | When a substance is been transported with a speed equal to zero, i.e. no flow moves it, then, according to the transport equation <span id='citeF-1'></span>[[#cite-1|[1]]], the initial profile of the substance should remain the same as time goes by, maintaining the substance concentration at each point in the fluid. | ||
| − | However, in practice, this does not happen due to molecular diffusion; this is due to the molecules are in constant motion, causing collisions and rebounds in different directions. The molecules will tend to separate, or diffuse, within the flow. In general, this movement moves from areas with a higher density of molecules to areas with a lower density | + | However, in practice, this does not happen due to molecular diffusion; this is due to the molecules are in constant motion, causing collisions and rebounds in different directions. The molecules will tend to separate, or diffuse, within the flow. In general, this movement moves from areas with a higher density of molecules to areas with a lower density; this is called ''diffusion'' and can be described by a well-known Partial Differential Equation: |
| − | + | ||
| − | + | ||
<span id="eq-1"></span> | <span id="eq-1"></span> | ||
| Line 27: | Line 25: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>\frac{\partial u}{\partial t} = \nu \nabla ^2 u </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (1) | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) | ||
| Line 34: | Line 32: | ||
where <math display="inline">\nu </math> represents the diffusion coefficient, which tells how easy a substance diffuses in a medium. | where <math display="inline">\nu </math> represents the diffusion coefficient, which tells how easy a substance diffuses in a medium. | ||
| − | + | In the past years, many people have worked in different methods to achieve good numerical solutions to this equation, involving a great variety of modern and classical techniques. Nevertheless, even though a large number of numerical methods have been proposed to solve it, a large number of these have a rather limited application to real world scenarios since they are designed for regular regions. | |
| − | + | This is due to the fact that the spatial discretization of the diffusion equation imposes bounds on the time step size in order to achieve numerical stability. However, the use of semidiscretization schemes allows to overcome many stability issues by using well known and widely used one step methods for ordinary initial value problems. For example, in <span id='citeF-2'></span>[[#cite-2|[2]]], a Method of Lines, involving solutions with ''a'' Runge-Kutta method, is presented along with its stability analysis; the results presented show that it is possible to use this kind of methods to compute numerical solutions of the equation, yet, the regions where the method is tested are unidimensional regions. On the side of the Generalized Finite Difference methods, Ureña <span id='citeF-3'></span>[[#cite-3|[3]]] presents a scheme to achieve numerical solutions using this method; the results presented in this work show that it is possible to solve different Partial Differential Equations using finite differences over non-regular clouds of points; this work presents that the solutions obtained with this method satisfactorily match with the exact solution of the proposed tests. Some other authors, like P. W. Li et al <span id='citeF-4'></span><span id='citeF-5'></span><span id='citeF-6'></span><span id='citeF-7'></span><span id='citeF-8'></span><span id='citeF-9'></span>[[#cite-4|[4,5,6,7,8,9]]], and Q. Wang <span id='citeF-10'></span>[[#cite-10|[10]]] have addressed a large number of applications. Nevertheless, the computational cost of the method as proposed in the aforementioned papers is high, since for each node of the cloud, it is required to take up to twenty-six support nodes, even in 2D problems, which increases the computational cost of the implementation. | |
| − | + | ||
| − | | | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | | | + | |
| − | + | ||
| − | + | On the other hand, in <span id='citeF-11'></span><span id='citeF-12'></span><span id='citeF-13'></span><span id='citeF-14'></span><span id='citeF-15'></span>[[#cite-11|[11,12,13,14,15]]], some variations of the presented generalized finite difference method for several transport equations, which produce satisfactory numerical solutions using a low-cost implementation for the spatial discretization, were presented. Even though, the use of several straightforward time integration schemes remained as an important issue to take into account. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <span id= | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | <span id= | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
For the case of interest of this work, it is important to obtain an approximation in generalized finite differences, for the spatial part, to the solution of the problem | For the case of interest of this work, it is important to obtain an approximation in generalized finite differences, for the spatial part, to the solution of the problem | ||
| Line 126: | Line 54: | ||
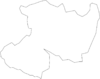
Where <math display="inline">\Omega </math> is a simply connected planar domain, and its boundary, <math display="inline">\partial \Omega </math>, is a positively oriented Jordan polygon, as the domain shown in Figure [[#img-1|1]]. | Where <math display="inline">\Omega </math> is a simply connected planar domain, and its boundary, <math display="inline">\partial \Omega </math>, is a positively oriented Jordan polygon, as the domain shown in Figure [[#img-1|1]]. | ||
| − | |||
| − | |||
<div id='img-1'></div> | <div id='img-1'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig01.png|100px|Example of an Ω domain.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figure 1:''' Example of an <math>\Omega </math> domain. | | colspan="1" | '''Figure 1:''' Example of an <math>\Omega </math> domain. | ||
|} | |} | ||
| + | |||
| + | On the other hand, for the temporal discretization, a Method of Lines (MOL) is proposed <span id='citeF-16'></span>[[#cite-16|[16]]]. The basic idea of the MOL is to solve a time-dependent Partial Differential Equation (PDE) by discretizing the spatial derivatives and then, integrating the semi-discretized problem as an Ordinary Differential Equations (ODE) system. | ||
==2 Proposed Scheme== | ==2 Proposed Scheme== | ||
| − | + | In order to apply a MOL for the case of diffusion equation | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 152: | Line 80: | ||
it is possible to discretize the spatial derivatives applying a generalized finite differences method, for that it is convenient to considerate the approximation to the second order linear operator | it is possible to discretize the spatial derivatives applying a generalized finite differences method, for that it is convenient to considerate the approximation to the second order linear operator | ||
| − | <span id="eq- | + | <span id="eq-2"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 160: | Line 88: | ||
| style="text-align: center;" | <math>Lu = Au_{xx} + Bu_{xy} + Cu_{yy} + Du_{x} + Eu_{y} + Fu, </math> | | style="text-align: center;" | <math>Lu = Au_{xx} + Bu_{xy} + Cu_{yy} + Du_{x} + Eu_{y} + Fu, </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (2) |
|} | |} | ||
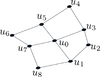
| − | where <math display="inline">A</math>, <math display="inline">B</math>, <math display="inline">C</math>, <math display="inline">D</math>, <math display="inline">E</math>, and <math display="inline">F</math> are given functions. Within an arbitrary distribution of nodes, as the one presented on Figure [[#img-2|2]], it is possible to approximate its value at a node <math display="inline">p_0 = (x_0,y_0)</math> using values of <math display="inline">u</math> at some neighbor nodes <math display="inline">p_i = (x_i, y_i)</math>, <math display="inline">i~=~1,2,\dots ,q</math> <span id='citeF- | + | where <math display="inline">A</math>, <math display="inline">B</math>, <math display="inline">C</math>, <math display="inline">D</math>, <math display="inline">E</math>, and <math display="inline">F</math> are given functions. Within an arbitrary distribution of nodes, as the one presented on Figure [[#img-2|2]], it is possible to approximate its value at a node <math display="inline">p_0 = (x_0,y_0)</math> using values of <math display="inline">u</math> at some neighbor nodes <math display="inline">p_i = (x_i, y_i)</math>, <math display="inline">i~=~1,2,\dots ,q</math> <span id='citeF-12'></span>[[#cite-12|[12]]]. For this work, a finite difference scheme is applied at the node <math display="inline">p_0</math>, which can be written as a linear combination as |
| − | <span id="eq- | + | <span id="eq-3"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 173: | Line 101: | ||
| style="text-align: center;" | <math>L_0 = \Gamma _0 u(p_0) + \Gamma _1 u(p_1) + ... + \Gamma _q u(p_q) = \sum _{i=0}^{q}\Gamma _i u(p_i). </math> | | style="text-align: center;" | <math>L_0 = \Gamma _0 u(p_0) + \Gamma _1 u(p_1) + ... + \Gamma _q u(p_q) = \sum _{i=0}^{q}\Gamma _i u(p_i). </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (3) |
|} | |} | ||
| Line 181: | Line 109: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig02.png|100px|Arbitrary distribution of p₀ and its neighbors.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figure 2:''' Arbitrary distribution of <math>p_0</math> and its | + | | colspan="1" | '''Figure 2:''' Arbitrary distribution of <math>p_0</math> and its neighbors. |
|} | |} | ||
| − | According to <span id='citeF- | + | According to <span id='citeF-17'></span><span id='citeF-18'></span>[[#cite-17|[17,18]]], a finite difference scheme <math display="inline">L_0</math> is consistent with the linear operator <math display="inline">L</math> if the local truncation error <math display="inline">\tau </math> satisfies that |
| − | <span id="eq- | + | <span id="eq-4"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 196: | Line 124: | ||
| style="text-align: center;" | <math>\tau = \left[Lu\right]_{p_{0}} - [L_{0}u]_{p_{0}} \to 0 </math> | | style="text-align: center;" | <math>\tau = \left[Lu\right]_{p_{0}} - [L_{0}u]_{p_{0}} \to 0 </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (4) |
|} | |} | ||
as <math display="inline">p_{1}</math>, <math display="inline">p_{2}</math>, <math display="inline">\dots </math>, <math display="inline">p_{q} \to p_{0}</math>. | as <math display="inline">p_{1}</math>, <math display="inline">p_{2}</math>, <math display="inline">\dots </math>, <math display="inline">p_{q} \to p_{0}</math>. | ||
| − | Using the six first terms of Taylor's series expansion, up to second order, of the consistency condition ([[#eq- | + | Using the six first terms of Taylor's series expansion, up to second order, of the consistency condition ([[#eq-4|4]]), it is possible to obtain the system |
| − | <span id="eq- | + | <span id="eq-5"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 211: | Line 139: | ||
| style="text-align: center;" | <math>\left( \begin{array}{lclc}1 & 1 & ... & 1\\ 0 & \Delta x_1 & ... & \Delta x_q\\ 0 & \Delta y_1 & ... & \Delta y_q\\ 0 & (\Delta x_1)^2 & ... & (\Delta x_q)^2\\ 0 & \Delta x_1\Delta y_1 & ... & \Delta x_q \Delta y_q\\ 0 & (\Delta y_1)^2 & ... & (\Delta y_q)^2\\ \end{array} \right) \left( \begin{array}{l}\Gamma _0\\ \Gamma _1\\ \Gamma _2\\ .\\ .\\ .\\ \Gamma _q\\ \end{array} \right) = \left( \begin{array}{l}F(p_0)\\ D(p_0)\\ E(p_0)\\ 2A(p_0)\\ B(p_0)\\ 2C(p_0)\\ \end{array} \right), </math> | | style="text-align: center;" | <math>\left( \begin{array}{lclc}1 & 1 & ... & 1\\ 0 & \Delta x_1 & ... & \Delta x_q\\ 0 & \Delta y_1 & ... & \Delta y_q\\ 0 & (\Delta x_1)^2 & ... & (\Delta x_q)^2\\ 0 & \Delta x_1\Delta y_1 & ... & \Delta x_q \Delta y_q\\ 0 & (\Delta y_1)^2 & ... & (\Delta y_q)^2\\ \end{array} \right) \left( \begin{array}{l}\Gamma _0\\ \Gamma _1\\ \Gamma _2\\ .\\ .\\ .\\ \Gamma _q\\ \end{array} \right) = \left( \begin{array}{l}F(p_0)\\ D(p_0)\\ E(p_0)\\ 2A(p_0)\\ B(p_0)\\ 2C(p_0)\\ \end{array} \right), </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) |
|} | |} | ||
| − | where <math display="inline">\Delta x_{i} = x_{i} - x_{0}</math> and <math display="inline">\Delta y_{i} = y_{i} - y_{0}</math>. In order to solve this linear system, it is possible to separate the first equation of the system ([[#eq- | + | where <math display="inline">\Delta x_{i} = x_{i} - x_{0}</math> and <math display="inline">\Delta y_{i} = y_{i} - y_{0}</math>. In order to solve this linear system, it is possible to separate the first equation of the system ([[#eq-5|5]]) |
| − | <span id="eq- | + | <span id="eq-6"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 224: | Line 152: | ||
| style="text-align: center;" | <math>\sum _{i=0}^{q}\Gamma _{i} - F(p_0) = 0 </math> | | style="text-align: center;" | <math>\sum _{i=0}^{q}\Gamma _{i} - F(p_0) = 0 </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (6) |
|} | |} | ||
and then, the problem defined by | and then, the problem defined by | ||
| − | <span id="eq- | + | <span id="eq-7"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 237: | Line 165: | ||
| style="text-align: center;" | <math>\left( \begin{array}{lcl}\Delta x_1 & ... & \Delta x_q\\ \Delta y_1 & ... & \Delta y_q\\ (\Delta x_1)^2 & ... & (\Delta x_q)^2\\ \Delta x_1\Delta y_1 & ... & \Delta x_q \Delta y_q\\ (\Delta y_1)^2 & ... & (\Delta y_q)^2\\ \end{array} \right) \left( \begin{array}{l}\Gamma _1\\ \Gamma _2\\ .\\ .\\ .\\ \Gamma _q\\ \end{array} \right) = \left( \begin{array}{l}D(p_0)\\ E(p_0)\\ 2A(p_0)\\ B(p_0)\\ 2C(p_0)\\ \end{array} \right), </math> | | style="text-align: center;" | <math>\left( \begin{array}{lcl}\Delta x_1 & ... & \Delta x_q\\ \Delta y_1 & ... & \Delta y_q\\ (\Delta x_1)^2 & ... & (\Delta x_q)^2\\ \Delta x_1\Delta y_1 & ... & \Delta x_q \Delta y_q\\ (\Delta y_1)^2 & ... & (\Delta y_q)^2\\ \end{array} \right) \left( \begin{array}{l}\Gamma _1\\ \Gamma _2\\ .\\ .\\ .\\ \Gamma _q\\ \end{array} \right) = \left( \begin{array}{l}D(p_0)\\ E(p_0)\\ 2A(p_0)\\ B(p_0)\\ 2C(p_0)\\ \end{array} \right), </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (7) |
|} | |} | ||
| − | can be solved using the reduced Cholesky factorization of its normal equations, as in <span id='citeF- | + | can be solved using the reduced Cholesky factorization of its normal equations, as in <span id='citeF-19'></span>[[#cite-19|[19]]], namely |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 262: | Line 190: | ||
|} | |} | ||
| − | The value of <math display="inline">\Gamma _0</math> is then obtained from ([[#eq- | + | The value of <math display="inline">\Gamma _0</math> is then obtained from ([[#eq-6|6]]) assuming, for the case of the diffusion equation, <math display="inline">F(p_0) = 0</math>. |
| − | Now, the scheme defined by ([[#eq- | + | Now, the scheme defined by ([[#eq-7|7]]) can be used to approximate the linear operator |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 277: | Line 205: | ||
taking <math display="inline">A = C = \nu </math>, and <math display="inline">B = D = E = 0</math>. The resulting <math display="inline">\Gamma _{i}</math> coefficients, define the Finite-Difference Scheme | taking <math display="inline">A = C = \nu </math>, and <math display="inline">B = D = E = 0</math>. The resulting <math display="inline">\Gamma _{i}</math> coefficients, define the Finite-Difference Scheme | ||
| − | <span id="eq- | + | <span id="eq-8"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 283: | Line 211: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>\frac{\partial }{\partial t}u_{i}(t) = \sum _{j=0}^{q}\Gamma _{j}u_{j}(t), </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (8) |
|} | |} | ||
| − | for diffusion equation, where | + | for diffusion equation, where <math display="inline">u_{i}(t)</math> is the approximation to the solution in the point <math display="inline">p_{i} = (x_{i}, y_{i})</math>, and <math display="inline">p_j</math> are the corresponding neighbor nodes of <math display="inline">p_i</math>. |
An important issue to be taken into account is the number of neighbors, <math display="inline">q</math>, to use in the scheme. In this paper, 8 neighbor points were taken into account following the stencil shown in Figure [[#img-3|3]]. | An important issue to be taken into account is the number of neighbors, <math display="inline">q</math>, to use in the scheme. In this paper, 8 neighbor points were taken into account following the stencil shown in Figure [[#img-3|3]]. | ||
| Line 295: | Line 223: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig03.png|100px|Centered stencil used in the scheme.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| colspan="1" | '''Figure 3:''' Centered stencil used in the scheme. | | colspan="1" | '''Figure 3:''' Centered stencil used in the scheme. | ||
|} | |} | ||
| − | Once a discretization of the spatial operator is obtained, the | + | Once a discretization of the spatial operator is obtained, following the idea presented in <span id='citeF-1'></span>[[#cite-1|[1]]], the semi-discretized PDE can be rewritten as a linear ODE system in time, |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 307: | Line 235: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> \frac{\partial | + | | style="text-align: center;" | <math> \frac{\partial }{\partial t}u_{i}(t) = \sum _{j=0}^{8}\Gamma _{j}u_{j}(t), i = 1,\dots ,m, </math> |
|} | |} | ||
|} | |} | ||
| − | + | where <math display="inline">m</math> is the total amount of grid points. | |
| − | + | There exist several ways to approximate the solution of this ODE system, for example, it is possible to use a forward Euler method as | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 320: | Line 248: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> \frac{u_{i}^{k+1} - u_{i}^{k}}{\Delta t} = \sum _{j=0}^{8}\Gamma _{j}u_{j}^{k}, </math> |
|} | |} | ||
|} | |} | ||
| − | where | + | nevertheless, this kind of implementations has proven to be ''conditionally stable'' and, in some cases, the stability conditions are difficult to accomplish. |
| + | |||
| + | Another way to solve this system is the Method of Lines, where each <math display="inline">u_i(t)</math> is solved for a fixed grid node <math display="inline">p_i = (x_i, y_i)</math>, ''i.e.'' it is solved by “lines”. As we are now dealing with a set of ODEs, it is possible to use a Runge-Kutta method, to solve the ODE on each line in order to obtain a stable and accurate results. | ||
| + | |||
| + | In the present work it is propose to use Runge-Kutta <span id='citeF-20'></span>[[#cite-20|[20]]] of 2nd, 3rd, and 4th order, as follows: | ||
| + | |||
| + | ==Second order Runge-Kutta method== | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 331: | Line 265: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> u_{i}^{k} = u_{i}^{k-1} + \frac{\Delta t}{2}\left(r_1 + r_2\right), </math> |
|} | |} | ||
|} | |} | ||
| + | |||
| + | where | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 340: | Line 276: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> r_2 = | + | | style="text-align: center;" | <math>r_1 = u_{i}^{k-1},</math> |
| + | |- | ||
| + | | style="text-align: center;" | <math> r_2 = u_{i}^{k-1}+ \frac{\Delta t}{2} (r_1).</math> | ||
| + | |- | ||
| + | | style="text-align: center;" | <math> u_i^{k-1} = \sum _{j=0}^{8}\Gamma _{j}u_{j}^{k-1} </math> | ||
|} | |} | ||
|} | |} | ||
| − | ==Third order Runge-Kutta== | + | ==Third order Runge-Kutta method== |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 351: | Line 291: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> u_{i}^{k} = u_{i}^{k-1} + \frac{\Delta t}{6}\left(r_1 + 4r_2 + r_3\right), </math> |
|} | |} | ||
|} | |} | ||
| Line 362: | Line 302: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>r_1 = u_{i}^{k-1},</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | + | | style="text-align: center;" | <math> r_2 = u_{i}^{k-1} + \frac{\Delta t}{2} (r_1),</math> | |
| − | + | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> r_3 = u_{i}^{k-1} + \Delta t (2r_2-r_1),</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> u_i^{k-1} = \sum _{j=0}^{8}\Gamma _{j}u_{j}^{k-1} </math> |
|} | |} | ||
|} | |} | ||
| − | ==Fourth order Runge-Kutta== | + | ==Fourth order Runge-Kutta method== |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 391: | Line 319: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> u_{i}^{k} = u_{i}^{k-1} + \frac{\Delta t}{6}\left(r_1 + 2r_2 + 2r_3 + r_4\right), </math> |
|} | |} | ||
|} | |} | ||
| Line 402: | Line 330: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math>r_1 = u_{i}^{k-1},</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | + | | style="text-align: center;" | <math> r_2 = u_{i}^{k-1} + \frac{\Delta t}{2} (r_1),</math> | |
| − | + | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> r_3 = u_{i}^{k-1} + \frac{\Delta t}{2} (r_2),</math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | + | | style="text-align: center;" | <math> r_4 = u_{i}^{k-1} + \Delta t (r_3),</math> | |
| − | + | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> u_i^{k-1} = \sum _{j=0}^{8}\Gamma _{j}u_{j}^{k-1} </math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
|} | |} | ||
| Line 437: | Line 346: | ||
==3 Numerical tests== | ==3 Numerical tests== | ||
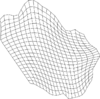
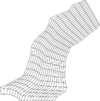
| − | To show the performance of the proposed scheme, the problem of obtaining a numerical solution to diffusion equation on | + | To show the performance of the proposed scheme, the problem of obtaining a numerical solution to diffusion equation on four different regions was proposed. The first region, denoted as A, corresponds to the unitary square, for comparison reasons, and the other three regions, denoted as B, C, and D, are non-rectangular planar domains. All the regions were scaled to fit on <math display="inline">[0,1]\times [0,1]</math>, and meshed with <math display="inline">21\times{21}</math> nodes, following a variational procedure implemented in UNAMalla <span id='citeF-21'></span>[[#cite-21|[21]]], then they were subdivided to obtain meshes with <math display="inline">41\times{41}</math> nodes. The meshes for with <math display="inline">21\times{21}</math> nodes for each region can be seen on Figure [[#img-4|4]] |
| − | |||
| − | |||
<div id='img-4'></div> | <div id='img-4'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig11.png|100px|Meshes of the test regions with 21×21 nodes.]] |
| − | |[[Image: | + | |[[Image:Review_300670986669-fig08.png|100px|]] |
| + | |[[Image:Review_300670986669-fig09.png|100px|]] | ||
| + | |[[Image:Review_300670986669-fig10.png|100px|]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | ( | + | | (4) Meshes of the test regions with <math>21\times{21}</math> nodes. |
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | < | + | |
| − | {| class=" | + | For all the regions, two different test were performed: |
| + | |||
| + | '''Test 1.''' Following the same idea as In <span id='citeF-22'></span>[[#cite-22|[22]]], where a well-know diffusion problem is presented, the initial and boundary conditions were taken from the closed form solution: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| − | | | + | | |
| − | | | + | {| style="text-align: left; margin:auto;width: 100%;" |
| − | | | + | |- |
| + | | style="text-align: center;" | <math> g(x, y, t) = e^{(-2\pi ^2\nu t)}\cos (\pi x)\cos (\pi y). </math> | ||
| + | |} | ||
|} | |} | ||
| − | + | '''Test 2.''' For comparison purposes, one of the test presented in <span id='citeF-23'></span>[[#cite-23|[23]]], was also taken into account; in this case the initial and boundary conditions were taken from the closed form solution: | |
| − | + | ||
| − | + | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 469: | Line 379: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;" | <math> g(x, y, t) = e^{(-2\pi ^2\nu t)}\sin (\pi x + \pi y). </math> |
|} | |} | ||
|} | |} | ||
| − | The time interval <math display="inline">[0,1]</math> was subdivided with different discretizations, the number of time steps was chosen to satisfy the classical Courant condition <span id='citeF- | + | The time interval <math display="inline">[0,1]</math> was subdivided with different discretizations, the number of time steps was chosen to satisfy the classical Courant condition <span id='citeF-24'></span>[[#cite-24|[24]]]: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 499: | Line 409: | ||
where <math display="inline">U_{i,j}^k</math> and <math display="inline">u_{i,j}^k</math> are the approximated and theoretical solutions, respectively, at the <math display="inline">i,j</math>-th grid node, and <math display="inline">A_{i,j}</math> is the area of the polygon defined by the points <math display="inline">P_{i+1,j}</math>, <math display="inline">P_{i,j+1}</math>, <math display="inline">P_{i-1,j}</math> and <math display="inline">P_{i,j-1}</math>. | where <math display="inline">U_{i,j}^k</math> and <math display="inline">u_{i,j}^k</math> are the approximated and theoretical solutions, respectively, at the <math display="inline">i,j</math>-th grid node, and <math display="inline">A_{i,j}</math> is the area of the polygon defined by the points <math display="inline">P_{i+1,j}</math>, <math display="inline">P_{i,j+1}</math>, <math display="inline">P_{i-1,j}</math> and <math display="inline">P_{i,j-1}</math>. | ||
| − | + | Figure [[#img-5|5]] presents a comparison of the numerical results obtained with the proposed scheme using the second order Runge-Kutta approximation and the exact solutions for the test region A at time <math display="inline">t = 0.66</math>s. The approximation is presented on the left, and the exact solution on the right. | |
| + | |||
| + | <div id='img-5'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[Image:Review_300670986669-fig13.png|600px|]] | ||
| + | |[[Image:Review_300670986669-fig14.png|600px|Comparison between numerical results (left) and exact solution (right) for test region A. Test 1 (Top) and Test 2 (Bottom).]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="2" | '''Figure 5:''' Comparison between numerical results (left) and exact solution (right) for test region A. Test 1 (Top) and Test 2 (Bottom). | ||
| + | |} | ||
| + | |||
| + | In a similar way, Figures [[#img-6|6]], [[#img-7|7]], and [[#img-8|8]] present the respective comparisons for the regions B, C, and D. | ||
<div id='img-6'></div> | <div id='img-6'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig15.png|600px|]] |
| + | |[[Image:Review_300670986669-fig16.png|600px|Comparison between numerical results (left) and exact solution (right) for test region B. Test 1 (Top) and Test 2 (Bottom).]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figure 6:''' Comparison between numerical results (left) and exact solution (right) for test region B. Test 1 (Top) and Test 2 (Bottom). |
|} | |} | ||
| + | |||
<div id='img-7'></div> | <div id='img-7'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig17.png|600px|]] |
| + | |[[Image:Review_300670986669-fig18.png|600px|Comparison between numerical results (left) and exact solution (right) for test region C. Test 1 (Top) and Test 2 (Bottom).]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figure 7:''' Comparison between numerical results (left) and exact solution (right) for test region C. Test 1 (Top) and Test 2 (Bottom). |
|} | |} | ||
| + | |||
<div id='img-8'></div> | <div id='img-8'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig19.png|600px|]] |
| + | |[[Image:Review_300670986669-fig20.png|600px|Comparison between numerical results (left) and exact solution (right) for test region D. Test 1 (Top) and Test 2 (Bottom).]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figure 8:''' Comparison between numerical results (left) and exact solution (right) for test region D. Test 1 (Top) and Test 2 (Bottom). |
|} | |} | ||
| + | |||
| + | Figures [[#img-9|9]] to [[#img-12|12]] present the maximum value of the error <math display="inline">\| e^k\| _2</math> computed for all the regions. For each Figure, both test were performed in the regions meshed with <math display="inline">21\times{21}</math> nodes and <math display="inline">41\times{41}</math> nodes. | ||
| + | |||
<div id='img-9'></div> | <div id='img-9'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig21.png|100px|]] |
| + | |[[Image:Review_300670986669-fig22.png|100px|Maximum \| e<sup>k</sup>\| ₂ computed for Test region A with 21×21 nodes (Left) and 41×41 nodes (Right).]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figure 9:''' Maximum <math>\| e^k\| _2</math> computed for Test region A with <math>21\times{21}</math> nodes (Left) and <math>41\times{41}</math> nodes (Right). |
|} | |} | ||
| − | |||
| − | |||
<div id='img-10'></div> | <div id='img-10'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig23.png|100px|]] |
| + | |[[Image:Review_300670986669-fig24.png|100px|Maximum \| e<sup>k</sup>\| ₂ computed for Test region B with 21×21 nodes (Left) and 41×41 nodes (Right).]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figure 10:''' Maximum <math>\| e^k\| _2</math> computed for Test region B with <math>21\times{21}</math> nodes (Left) and <math>41\times{41}</math> nodes (Right). |
|} | |} | ||
| + | |||
<div id='img-11'></div> | <div id='img-11'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig25.png|100px|]] |
| + | |[[Image:Review_300670986669-fig26.png|100px|Maximum \| e<sup>k</sup>\| ₂ computed for Test region C with 21×21 nodes (Left) and 41×41 nodes (Right).]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figure 11:''' Maximum <math>\| e^k\| _2</math> computed for Test region C with <math>21\times{21}</math> nodes (Left) and <math>41\times{41}</math> nodes (Right). |
|} | |} | ||
| + | |||
<div id='img-12'></div> | <div id='img-12'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_300670986669-fig27.png|100px|]] |
| + | |[[Image:Review_300670986669-fig28.png|100px|Maximum \| e<sup>k</sup>\| ₂ computed for Test region D with 21×21 nodes (Left) and 41×41 nodes (Right).]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan=" | + | | colspan="2" | '''Figure 12:''' Maximum <math>\| e^k\| _2</math> computed for Test region D with <math>21\times{21}</math> nodes (Left) and <math>41\times{41}</math> nodes (Right). |
| − | + | ||
| − | < | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | + | ==4 Conclusions== | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | The numerical results show that the proposed method of Lines applied to the diffusion equation produces satisfactory numerical solutions. In the tests carried out, no spurious oscillations or instabilities were perceived. In addition, the results show that it is not necessary to “work more” by using higher Runge-Kutta methods; this scheme accomplishes better results when second-order Runge-Kutta is used to solve the Ordinary Differential Equations system. | |
| + | It is possible to appreciate that with the presented discretizations, even with the fourth-order Runge-Kutta method, acceptable numerical results can be obtained. Additionally, the numerical results in shown on Figures [[#img-9|9]] to [[#img-12|12]] show that a refinement of the spatial mesh can improve the approximations carried out with the method; as expected in these kinds of methods. It is worth mentioning that, for all the tests, a minimum number of time steps was used, taking into account the classical theory for the diffusion equation, which makes the computational cost of this method low, since it does not require making very small temporary discretizations, as in other cases. | ||
| − | + | Furthermore, the proposed scheme can produce stable results for non-standard initial conditions on highly irregular regions. For example, on the following videos | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | * https://youtu.be/soUxe5uUY_U | |
| + | * https://youtu.be/479YeBjqmSs | ||
| + | solutions of the diffusion equation are presented on domains that are geometrical approximations to real geographical locations, where the boundary conditions are fixed as <math display="inline">0</math> and the initial condition is stated as: | ||
| − | {| | + | {| class="formulaSCP" style="width: 100%; text-align: left;" |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | |
| − | | style=" | + | {| style="text-align: left; margin:auto;width: 100%;" |
| − | + | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;" | <math> g(x,y) = \begin{cases} 1 & x,y \hbox{ in } [0.35, 0.65]\\ 0 & \hbox{ All the other cases.} \end{cases} </math> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
|} | |} | ||
| − | + | It is possible to see that even for these conditions on these regions, the scheme produce stable results that show the expected behavior. | |
| − | + | ||
| − | It | + | |
| − | + | An important remark is that, even when in this work structured convex grids were used, the development of the method doesn't take into account a particular data structure, ''i.e.'' this method can be used not only on structured meshes but also as a meshless method, that would be developed as future work. | |
==5 Acknowledgments== | ==5 Acknowledgments== | ||
| − | We want to thank AULA CIMNE-Morelia and CIC-UMSNH for the financial support for this work. | + | We want to thank AULA CIMNE-Morelia and CIC-UMSNH for the financial support for this work. Thanks to Universidad Vasco de Quiroga for lending the facilities to perform the final part of the work done for the paper. |
Special thanks to the ``Laboratorio de Matemáticas Aplicadas'' of the ``Facultad de Ciencias Físico-Matemáticas'' at ``Universidad Michoacana de San Nicolás de Hidalgo'' for lending their computational infrastructure. | Special thanks to the ``Laboratorio de Matemáticas Aplicadas'' of the ``Facultad de Ciencias Físico-Matemáticas'' at ``Universidad Michoacana de San Nicolás de Hidalgo'' for lending their computational infrastructure. | ||
| + | |||
| + | The authors would also like to thank the reviewers for their valuable feedback and suggestions to improve the present work. | ||
===BIBLIOGRAPHY=== | ===BIBLIOGRAPHY=== | ||
| Line 802: | Line 527: | ||
<div id="cite-2"></div> | <div id="cite-2"></div> | ||
| − | '''[[#citeF-2|[2]]]''' | + | '''[[#citeF-2|[2]]]''' Bukhari Manshoor and Hamidon Salleh nad Amir Khalid and Muhammed Abdelfattah Sayed Abdelaal. (2021) "Method of Lines and Runge-Kutta Method in Solving Partial Differential Equation for Heat Equation", Volume 3. Journal of Complex Flow 1 21 - 25 |
<div id="cite-3"></div> | <div id="cite-3"></div> | ||
| − | '''[[#citeF-3|[3]]]''' | + | '''[[#citeF-3|[3]]]''' Francisco Ureña Prieto and Juan José Benito Muñoz and Luis Gavete Corvinos. (2011) "Application of the generalized finite difference method to solve the advection–diffusion equation", Volume 235. Journal of Computational and Applied Mathematics 1849 - 1855 |
<div id="cite-4"></div> | <div id="cite-4"></div> | ||
| − | '''[[#citeF-4|[4]]]''' | + | '''[[#citeF-4|[4]]]''' Li, Po-Wei and Fan, Chia-Ming and Grabski, Jakub Krzysztof. (2021) "A meshless generalized finite difference method for solving shallow water equations with the flux limiter technique", Volume 131. Elsevier. Engineering Analysis with Boundary Elements 159–173 |
<div id="cite-5"></div> | <div id="cite-5"></div> | ||
| − | '''[[#citeF-5|[5]]]''' | + | '''[[#citeF-5|[5]]]''' Zhang, Ting and Lin, Zhen-Huan and Huang, Guan-Yi and Fan, Chia-Ming and Li, Po-Wei. (2020) "Solving Boussinesq equations with a meshless finite difference method", Volume 198. Elsevier. Ocean Engineering 106957 |
<div id="cite-6"></div> | <div id="cite-6"></div> | ||
| − | '''[[#citeF-6|[6]]]''' | + | '''[[#citeF-6|[6]]]''' Fu, Zhuo-Jia and Tang, Zhuo-Chao and Zhao, Hai-Tao and Li, Po-Wei and Rabczuk, Timon. (2019) "Numerical solutions of the coupled unsteady nonlinear convection-diffusion equations based on generalized finite difference method", Volume 134. Springer. The European Physical Journal Plus 6 1–20 |
<div id="cite-7"></div> | <div id="cite-7"></div> | ||
| − | '''[[#citeF-7|[7]]]''' | + | '''[[#citeF-7|[7]]]''' Zhang, Ting and Ren, Yu-Fei and Yang, Zhi-Qiang and Fan, Chia-Ming and Li, Po-Wei. (2016) "Application of generalized finite difference method to propagation of nonlinear water waves in numerical wave flume", Volume 123. Elsevier. Ocean Engineering 278–290 |
<div id="cite-8"></div> | <div id="cite-8"></div> | ||
| − | '''[[#citeF-8|[8]]]''' | + | '''[[#citeF-8|[8]]]''' Li, Po-Wei and Fan, Chia-Ming. (2017) "Generalized finite difference method for two-dimensional shallow water equations", Volume 80. Elsevier. Engineering Analysis with Boundary Elements 58–71 |
<div id="cite-9"></div> | <div id="cite-9"></div> | ||
| − | '''[[#citeF-9|[9]]]''' | + | '''[[#citeF-9|[9]]]''' Fu, Zhuo-Jia and Zhang, Jin and Li, Po-Wei and Zheng, Jin-Hai. (2020) "A semi-Lagrangian meshless framework for numerical solutions of two-dimensional sloshing phenomenon", Volume 112. Elsevier. Engineering Analysis with Boundary Elements 58–67 |
<div id="cite-10"></div> | <div id="cite-10"></div> | ||
| − | '''[[#citeF-10|[10]]]''' Michael B. Abbott and Andrew D. McCowan and Ian R. Warren. (1984) "Accuracy of Short-Wave Numerical Models", Volume 110. Journal of Hydraulic Engineering 10 1287 - 1301 | + | '''[[#citeF-10|[10]]]''' Wang, Qiang and Kim, Pyeoungkee and Qu, Wenzhen. (2022) "A Hybrid Localized Meshless Method for the Solution of Transient Groundwater Flow in Two Dimensions", Volume 10. Mathematics 3 |
| + | |||
| + | <div id="cite-11"></div> | ||
| + | '''[[#citeF-11|[11]]]''' Francisco Javier Domínguez-Mota and Sanzon Mendoza-Armenta and José Gerardo Tinoco-Ruiz. (2011) "Finite Difference Schemes Satisfying an Optimality Condition". IMACS Series in Computational and Applied Mathematics: MASCOT 2010 | ||
| + | |||
| + | <div id="cite-12"></div> | ||
| + | '''[[#citeF-12|[12]]]''' Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz. (2015) "Numerical Solution of Advection Equations Using Structured Grids on Plane Irregular Regions With a Finite Differences Scheme", Volume 1. Boletín de la Sociedad Mexicana de Computación Científica y Sus Aplicaciones 3 29 - 32 | ||
| + | |||
| + | <div id="cite-13"></div> | ||
| + | '''[[#citeF-13|[13]]]''' José Gerardo Tinoco-Ruiz and Francisco Javier Domínguez-Mota and Gerardo Tinoco-Guerrero and Pablo Michel Fernández-Valdés and Sanzon Mendoza-Armenta. (2013) "Numerical Solution of Differential Equations in Irregular Plane Regions Using Quality Structured Convex Grids", Volume 4. International Journal of Modeling, Simulation and Scientific Computing 2 | ||
| + | |||
| + | <div id="cite-14"></div> | ||
| + | '''[[#citeF-14|[14]]]''' Francisco Javier Domínguez-Mota and Juan Salvador Lucas-Martínez and Gerardo Tinoco-Guerrero. (2020) "A Generalized Finite-Differences Scheme Used in Modeling of a Direct and an Inverse Problem of Advection-Difussion", Volume 33. International Journal of Applied Mathematics 4 599 - 608 | ||
| + | |||
| + | <div id="cite-15"></div> | ||
| + | '''[[#citeF-15|[15]]]''' Chávez-Negrete, C and Domínguez-Mota, FJ and Santana-Quinteros, D. (2018) "Numerical solution of Richards' equation of water flow by generalized finite differences", Volume 101. Elsevier. Computers and Geotechnics 168–175 | ||
| + | |||
| + | <div id="cite-16"></div> | ||
| + | '''[[#citeF-16|[16]]]''' William Schiesser. (1991) "The Numerical Method of Lines". San Diego : Academic Press | ||
| + | |||
| + | <div id="cite-17"></div> | ||
| + | '''[[#citeF-17|[17]]]''' John C. Strikwerda. (2004) "Finite Difference Schemes and Partial Differential Equations". Society for Industrial and Applied Mathematics | ||
| + | |||
| + | <div id="cite-18"></div> | ||
| + | '''[[#citeF-18|[18]]]''' J. W. Thomas. (1995) "Numerical Partial Differential Equations: Finite Difference Methods", Volume 2. Springer | ||
| + | |||
| + | <div id="cite-19"></div> | ||
| + | '''[[#citeF-19|[19]]]''' Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz. (2020) "A Study of the Stability for a Generalized Finite-Difference Scheme Applied to the Advection-Diffusion Equation", Volume 176. Mathematics and Computer in Simulations 301 - 311 | ||
| + | |||
| + | <div id="cite-20"></div> | ||
| + | '''[[#citeF-20|[20]]]''' J. C. Butcher. (1969) "Conference on the Numerical Solution of Differential Equations", Volume 109. Springer 133 - 139 | ||
| + | |||
| + | <div id="cite-21"></div> | ||
| + | '''[[#citeF-21|[21]]]''' UNAMalla. (2011) "An Automatic Package for Numerical Grid Generation" | ||
| + | |||
| + | <div id="cite-22"></div> | ||
| + | '''[[#citeF-22|[22]]]''' José Gerardo Tinoco-Ruiz and Francisco Javier Domínguez-Mota and Juan Salvador Lucas-Martínez and Gerardo Tinoco-Guerrero. (2019) "Study of the Stability of a Generalized Finite Difference Scheme Applied to the Diffusion Equation in Irregular 2D Space Regions Using Convex Grids". IMACS Series in Computational and Applied Mathematics: MASCOT 2018 | ||
| + | |||
| + | <div id="cite-23"></div> | ||
| + | '''[[#citeF-23|[23]]]''' L.M. Sánchez and F. Ureña and J.J. Benito and L. Gavete. (2009) "Resolución de la ecuación de Difusión en 2-D y 3-D utilizando diferencias finitas generalizadas. Consistencia y Estabilidad". XXI Congreso de Ecuaciones Diferenciales y Aplicaciones 1 - 8 | ||
| + | |||
| + | <div id="cite-24"></div> | ||
| + | '''[[#citeF-24|[24]]]''' Michael B. Abbott and Andrew D. McCowan and Ian R. Warren. (1984) "Accuracy of Short-Wave Numerical Models", Volume 110. Journal of Hydraulic Engineering 10 1287 - 1301 | ||
Revision as of 18:27, 20 April 2022
Abstract
One of the greatest challenges in the area of applied mathematics continues to be the design of numerical methods capable of approximating the solution of partial differential equations quickly and accurately. One of the most important equations, due to the hydraulic and transport applications it has, and the large number of difficulties that it usually presents when solving it numerically is the Diffusion Equation.
In the present work, a Method of Lines applied to the numerical solution of the said equation in irregular regions is presented using a scheme of Generalized Finite Differences. The second-order finite difference method uses a central node and 8 neighbor points in order to address the spatial approximation. A series of tests and numerical results are presented, which show the accuracy of the proposed method.
keywords Generalized Finite Differences, Method of Lines, Diffusion Equation, Irregular Regions
1 Introduction
When a substance is been transported with a speed equal to zero, i.e. no flow moves it, then, according to the transport equation [1], the initial profile of the substance should remain the same as time goes by, maintaining the substance concentration at each point in the fluid.
However, in practice, this does not happen due to molecular diffusion; this is due to the molecules are in constant motion, causing collisions and rebounds in different directions. The molecules will tend to separate, or diffuse, within the flow. In general, this movement moves from areas with a higher density of molecules to areas with a lower density; this is called diffusion and can be described by a well-known Partial Differential Equation:
|
|
(1) |
where represents the diffusion coefficient, which tells how easy a substance diffuses in a medium.
In the past years, many people have worked in different methods to achieve good numerical solutions to this equation, involving a great variety of modern and classical techniques. Nevertheless, even though a large number of numerical methods have been proposed to solve it, a large number of these have a rather limited application to real world scenarios since they are designed for regular regions.
This is due to the fact that the spatial discretization of the diffusion equation imposes bounds on the time step size in order to achieve numerical stability. However, the use of semidiscretization schemes allows to overcome many stability issues by using well known and widely used one step methods for ordinary initial value problems. For example, in [2], a Method of Lines, involving solutions with a Runge-Kutta method, is presented along with its stability analysis; the results presented show that it is possible to use this kind of methods to compute numerical solutions of the equation, yet, the regions where the method is tested are unidimensional regions. On the side of the Generalized Finite Difference methods, Ureña [3] presents a scheme to achieve numerical solutions using this method; the results presented in this work show that it is possible to solve different Partial Differential Equations using finite differences over non-regular clouds of points; this work presents that the solutions obtained with this method satisfactorily match with the exact solution of the proposed tests. Some other authors, like P. W. Li et al [4,5,6,7,8,9], and Q. Wang [10] have addressed a large number of applications. Nevertheless, the computational cost of the method as proposed in the aforementioned papers is high, since for each node of the cloud, it is required to take up to twenty-six support nodes, even in 2D problems, which increases the computational cost of the implementation.
On the other hand, in [11,12,13,14,15], some variations of the presented generalized finite difference method for several transport equations, which produce satisfactory numerical solutions using a low-cost implementation for the spatial discretization, were presented. Even though, the use of several straightforward time integration schemes remained as an important issue to take into account.
For the case of interest of this work, it is important to obtain an approximation in generalized finite differences, for the spatial part, to the solution of the problem
|
|
Where is a simply connected planar domain, and its boundary, , is a positively oriented Jordan polygon, as the domain shown in Figure 1.
|
| Figure 1: Example of an domain. |
On the other hand, for the temporal discretization, a Method of Lines (MOL) is proposed [16]. The basic idea of the MOL is to solve a time-dependent Partial Differential Equation (PDE) by discretizing the spatial derivatives and then, integrating the semi-discretized problem as an Ordinary Differential Equations (ODE) system.
2 Proposed Scheme
In order to apply a MOL for the case of diffusion equation
|
|
it is possible to discretize the spatial derivatives applying a generalized finite differences method, for that it is convenient to considerate the approximation to the second order linear operator
|
|
(2) |
where , , , , , and are given functions. Within an arbitrary distribution of nodes, as the one presented on Figure 2, it is possible to approximate its value at a node using values of at some neighbor nodes , [12]. For this work, a finite difference scheme is applied at the node , which can be written as a linear combination as
|
|
(3) |
where are adequate weighs.

|
| Figure 2: Arbitrary distribution of and its neighbors. |
According to [17,18], a finite difference scheme is consistent with the linear operator if the local truncation error satisfies that
|
|
(4) |
as , , , .
Using the six first terms of Taylor's series expansion, up to second order, of the consistency condition (4), it is possible to obtain the system
|
|
(5) |
where and . In order to solve this linear system, it is possible to separate the first equation of the system (5)
|
|
(6) |
and then, the problem defined by
|
|
(7) |
can be solved using the reduced Cholesky factorization of its normal equations, as in [19], namely
|
|
where
|
|
The value of is then obtained from (6) assuming, for the case of the diffusion equation, .
Now, the scheme defined by (7) can be used to approximate the linear operator
|
|
taking , and . The resulting coefficients, define the Finite-Difference Scheme
|
|
(8) |
for diffusion equation, where is the approximation to the solution in the point , and are the corresponding neighbor nodes of .
An important issue to be taken into account is the number of neighbors, , to use in the scheme. In this paper, 8 neighbor points were taken into account following the stencil shown in Figure 3.
|
| Figure 3: Centered stencil used in the scheme. |
Once a discretization of the spatial operator is obtained, following the idea presented in [1], the semi-discretized PDE can be rewritten as a linear ODE system in time,
|
|
where is the total amount of grid points.
There exist several ways to approximate the solution of this ODE system, for example, it is possible to use a forward Euler method as
|
|
nevertheless, this kind of implementations has proven to be conditionally stable and, in some cases, the stability conditions are difficult to accomplish.
Another way to solve this system is the Method of Lines, where each is solved for a fixed grid node , i.e. it is solved by “lines”. As we are now dealing with a set of ODEs, it is possible to use a Runge-Kutta method, to solve the ODE on each line in order to obtain a stable and accurate results.
In the present work it is propose to use Runge-Kutta [20] of 2nd, 3rd, and 4th order, as follows:
Second order Runge-Kutta method
|
|
where
|
|
Third order Runge-Kutta method
|
|
where
|
|
Fourth order Runge-Kutta method
|
|
where
|
|
in all the cases, represents the time level.
3 Numerical tests
To show the performance of the proposed scheme, the problem of obtaining a numerical solution to diffusion equation on four different regions was proposed. The first region, denoted as A, corresponds to the unitary square, for comparison reasons, and the other three regions, denoted as B, C, and D, are non-rectangular planar domains. All the regions were scaled to fit on , and meshed with nodes, following a variational procedure implemented in UNAMalla [21], then they were subdivided to obtain meshes with nodes. The meshes for with nodes for each region can be seen on Figure 4
|

|

|
|
| (4) Meshes of the test regions with nodes. |
For all the regions, two different test were performed:
Test 1. Following the same idea as In [22], where a well-know diffusion problem is presented, the initial and boundary conditions were taken from the closed form solution:
|
|
Test 2. For comparison purposes, one of the test presented in [23], was also taken into account; in this case the initial and boundary conditions were taken from the closed form solution:
|
|
The time interval was subdivided with different discretizations, the number of time steps was chosen to satisfy the classical Courant condition [24]:
|
|
where and are the spatial steps on each grid, taken from the meshes with nodes, and .
The norm of the quadratic error, at a th time level, can be computed as
|
|
where and are the approximated and theoretical solutions, respectively, at the -th grid node, and is the area of the polygon defined by the points , , and .
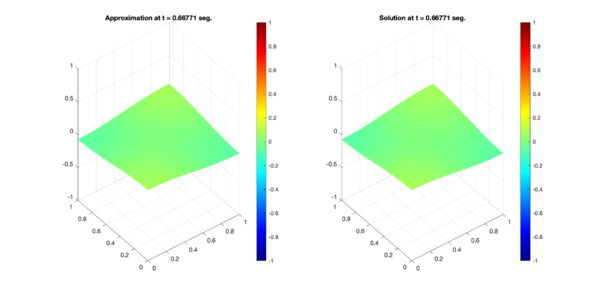
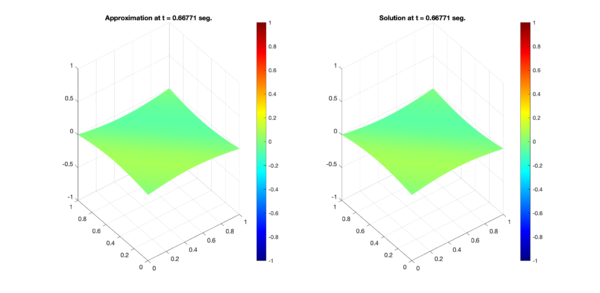
Figure 5 presents a comparison of the numerical results obtained with the proposed scheme using the second order Runge-Kutta approximation and the exact solutions for the test region A at time s. The approximation is presented on the left, and the exact solution on the right.
|
|
| Figure 5: Comparison between numerical results (left) and exact solution (right) for test region A. Test 1 (Top) and Test 2 (Bottom). | |
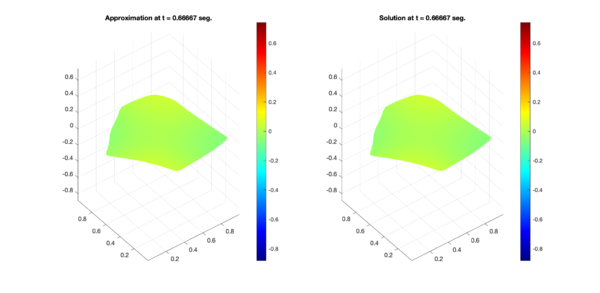
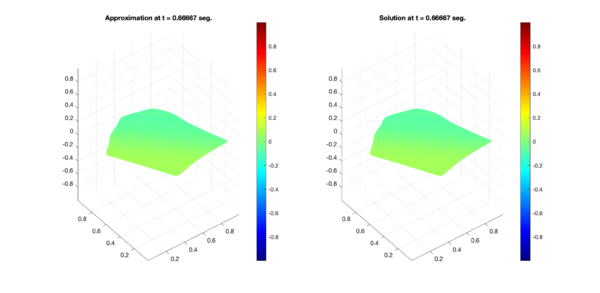
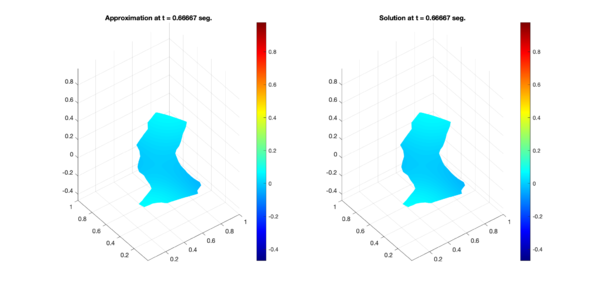
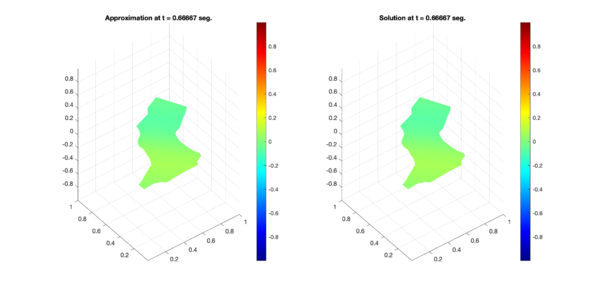
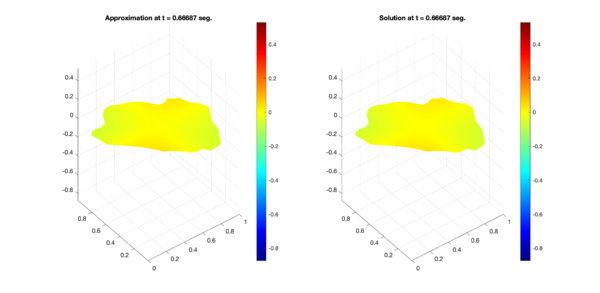
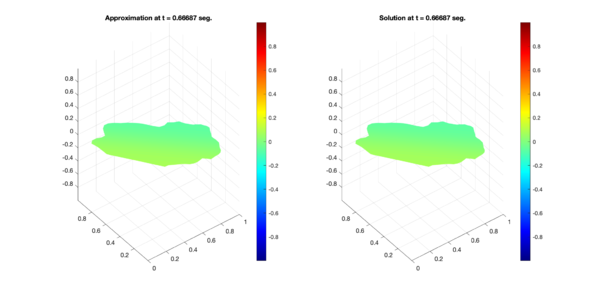
In a similar way, Figures 6, 7, and 8 present the respective comparisons for the regions B, C, and D.
|
|
| Figure 6: Comparison between numerical results (left) and exact solution (right) for test region B. Test 1 (Top) and Test 2 (Bottom). | |
|
|
| Figure 7: Comparison between numerical results (left) and exact solution (right) for test region C. Test 1 (Top) and Test 2 (Bottom). | |
|
|
| Figure 8: Comparison between numerical results (left) and exact solution (right) for test region D. Test 1 (Top) and Test 2 (Bottom). | |
Figures 9 to 12 present the maximum value of the error computed for all the regions. For each Figure, both test were performed in the regions meshed with nodes and nodes.

|

|
| Figure 9: Maximum computed for Test region A with nodes (Left) and nodes (Right). | |

|

|
| Figure 10: Maximum computed for Test region B with nodes (Left) and nodes (Right). | |

|

|
| Figure 11: Maximum computed for Test region C with nodes (Left) and nodes (Right). | |

|

|
| Figure 12: Maximum computed for Test region D with nodes (Left) and nodes (Right). | |
4 Conclusions
The numerical results show that the proposed method of Lines applied to the diffusion equation produces satisfactory numerical solutions. In the tests carried out, no spurious oscillations or instabilities were perceived. In addition, the results show that it is not necessary to “work more” by using higher Runge-Kutta methods; this scheme accomplishes better results when second-order Runge-Kutta is used to solve the Ordinary Differential Equations system.
It is possible to appreciate that with the presented discretizations, even with the fourth-order Runge-Kutta method, acceptable numerical results can be obtained. Additionally, the numerical results in shown on Figures 9 to 12 show that a refinement of the spatial mesh can improve the approximations carried out with the method; as expected in these kinds of methods. It is worth mentioning that, for all the tests, a minimum number of time steps was used, taking into account the classical theory for the diffusion equation, which makes the computational cost of this method low, since it does not require making very small temporary discretizations, as in other cases.
Furthermore, the proposed scheme can produce stable results for non-standard initial conditions on highly irregular regions. For example, on the following videos
solutions of the diffusion equation are presented on domains that are geometrical approximations to real geographical locations, where the boundary conditions are fixed as and the initial condition is stated as:
|
|
It is possible to see that even for these conditions on these regions, the scheme produce stable results that show the expected behavior.
An important remark is that, even when in this work structured convex grids were used, the development of the method doesn't take into account a particular data structure, i.e. this method can be used not only on structured meshes but also as a meshless method, that would be developed as future work.
5 Acknowledgments
We want to thank AULA CIMNE-Morelia and CIC-UMSNH for the financial support for this work. Thanks to Universidad Vasco de Quiroga for lending the facilities to perform the final part of the work done for the paper.
Special thanks to the ``Laboratorio de Matemáticas Aplicadas of the ``Facultad de Ciencias Físico-Matemáticas at ``Universidad Michoacana de San Nicolás de Hidalgo for lending their computational infrastructure.
The authors would also like to thank the reviewers for their valuable feedback and suggestions to improve the present work.
BIBLIOGRAPHY
[1] Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz and Juan Salvador Lucas-Martínez. (2018) "Aproximación de la Ecuación de Advección en Regiones Irregulares Utilizando un Método de Líneas y Diferencias Finitas Generalizadas", Volume 2. Revista Mexicana de Métodos Numéricos 2
[2] Bukhari Manshoor and Hamidon Salleh nad Amir Khalid and Muhammed Abdelfattah Sayed Abdelaal. (2021) "Method of Lines and Runge-Kutta Method in Solving Partial Differential Equation for Heat Equation", Volume 3. Journal of Complex Flow 1 21 - 25
[3] Francisco Ureña Prieto and Juan José Benito Muñoz and Luis Gavete Corvinos. (2011) "Application of the generalized finite difference method to solve the advection–diffusion equation", Volume 235. Journal of Computational and Applied Mathematics 1849 - 1855
[4] Li, Po-Wei and Fan, Chia-Ming and Grabski, Jakub Krzysztof. (2021) "A meshless generalized finite difference method for solving shallow water equations with the flux limiter technique", Volume 131. Elsevier. Engineering Analysis with Boundary Elements 159–173
[5] Zhang, Ting and Lin, Zhen-Huan and Huang, Guan-Yi and Fan, Chia-Ming and Li, Po-Wei. (2020) "Solving Boussinesq equations with a meshless finite difference method", Volume 198. Elsevier. Ocean Engineering 106957
[6] Fu, Zhuo-Jia and Tang, Zhuo-Chao and Zhao, Hai-Tao and Li, Po-Wei and Rabczuk, Timon. (2019) "Numerical solutions of the coupled unsteady nonlinear convection-diffusion equations based on generalized finite difference method", Volume 134. Springer. The European Physical Journal Plus 6 1–20
[7] Zhang, Ting and Ren, Yu-Fei and Yang, Zhi-Qiang and Fan, Chia-Ming and Li, Po-Wei. (2016) "Application of generalized finite difference method to propagation of nonlinear water waves in numerical wave flume", Volume 123. Elsevier. Ocean Engineering 278–290
[8] Li, Po-Wei and Fan, Chia-Ming. (2017) "Generalized finite difference method for two-dimensional shallow water equations", Volume 80. Elsevier. Engineering Analysis with Boundary Elements 58–71
[9] Fu, Zhuo-Jia and Zhang, Jin and Li, Po-Wei and Zheng, Jin-Hai. (2020) "A semi-Lagrangian meshless framework for numerical solutions of two-dimensional sloshing phenomenon", Volume 112. Elsevier. Engineering Analysis with Boundary Elements 58–67
[10] Wang, Qiang and Kim, Pyeoungkee and Qu, Wenzhen. (2022) "A Hybrid Localized Meshless Method for the Solution of Transient Groundwater Flow in Two Dimensions", Volume 10. Mathematics 3
[11] Francisco Javier Domínguez-Mota and Sanzon Mendoza-Armenta and José Gerardo Tinoco-Ruiz. (2011) "Finite Difference Schemes Satisfying an Optimality Condition". IMACS Series in Computational and Applied Mathematics: MASCOT 2010
[12] Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz. (2015) "Numerical Solution of Advection Equations Using Structured Grids on Plane Irregular Regions With a Finite Differences Scheme", Volume 1. Boletín de la Sociedad Mexicana de Computación Científica y Sus Aplicaciones 3 29 - 32
[13] José Gerardo Tinoco-Ruiz and Francisco Javier Domínguez-Mota and Gerardo Tinoco-Guerrero and Pablo Michel Fernández-Valdés and Sanzon Mendoza-Armenta. (2013) "Numerical Solution of Differential Equations in Irregular Plane Regions Using Quality Structured Convex Grids", Volume 4. International Journal of Modeling, Simulation and Scientific Computing 2
[14] Francisco Javier Domínguez-Mota and Juan Salvador Lucas-Martínez and Gerardo Tinoco-Guerrero. (2020) "A Generalized Finite-Differences Scheme Used in Modeling of a Direct and an Inverse Problem of Advection-Difussion", Volume 33. International Journal of Applied Mathematics 4 599 - 608
[15] Chávez-Negrete, C and Domínguez-Mota, FJ and Santana-Quinteros, D. (2018) "Numerical solution of Richards' equation of water flow by generalized finite differences", Volume 101. Elsevier. Computers and Geotechnics 168–175
[16] William Schiesser. (1991) "The Numerical Method of Lines". San Diego : Academic Press
[17] John C. Strikwerda. (2004) "Finite Difference Schemes and Partial Differential Equations". Society for Industrial and Applied Mathematics
[18] J. W. Thomas. (1995) "Numerical Partial Differential Equations: Finite Difference Methods", Volume 2. Springer
[19] Gerardo Tinoco-Guerrero and Francisco Javier Domínguez-Mota and José Gerardo Tinoco-Ruiz. (2020) "A Study of the Stability for a Generalized Finite-Difference Scheme Applied to the Advection-Diffusion Equation", Volume 176. Mathematics and Computer in Simulations 301 - 311
[20] J. C. Butcher. (1969) "Conference on the Numerical Solution of Differential Equations", Volume 109. Springer 133 - 139
[21] UNAMalla. (2011) "An Automatic Package for Numerical Grid Generation"
[22] José Gerardo Tinoco-Ruiz and Francisco Javier Domínguez-Mota and Juan Salvador Lucas-Martínez and Gerardo Tinoco-Guerrero. (2019) "Study of the Stability of a Generalized Finite Difference Scheme Applied to the Diffusion Equation in Irregular 2D Space Regions Using Convex Grids". IMACS Series in Computational and Applied Mathematics: MASCOT 2018
[23] L.M. Sánchez and F. Ureña and J.J. Benito and L. Gavete. (2009) "Resolución de la ecuación de Difusión en 2-D y 3-D utilizando diferencias finitas generalizadas. Consistencia y Estabilidad". XXI Congreso de Ecuaciones Diferenciales y Aplicaciones 1 - 8
[24] Michael B. Abbott and Andrew D. McCowan and Ian R. Warren. (1984) "Accuracy of Short-Wave Numerical Models", Volume 110. Journal of Hydraulic Engineering 10 1287 - 1301
Document information
Published on 14/06/22
Accepted on 07/06/22
Submitted on 19/09/21
Volume 38, Issue 2, 2022
DOI: 10.23967/j.rimni.2022.06.003
Licence: CC BY-NC-SA license