| Line 219: | Line 219: | ||
|} | |} | ||
| − | + | The values presented in [[#tab-1|Table 1]] provide the input parameters (constants) to measure the amount of greenhouse gas emissions proposed in this work. | |
==4. Proposed Methodology== | ==4. Proposed Methodology== | ||
Revision as of 14:37, 13 January 2022
Abstract
Logistic distribution involves many costs for organizations. Therefore, opportunities for optimization in this respect are always welcome. The purpose of this work is to present a methodology to provide a solution to a complexity task of optimization in Multi-objective Optimization for Green Vehicle Routing Problem (MOOGVRP). The methodology, illustrated using a case study (employee transport problem) and instances from the literature, was divided into three stages: Stage 1, “data treatment”, where the asymmetry of the routes to be formed and other particular features were addressed; Stage 2, “metaheuristic approaches” (hybrid or non-hybrid), used comparatively, more specifically: NSGA-II (Non-dominated Sorting Genetic Algorithm II), MOPSO (Multi-Objective Particle Swarm Optimization), which were compared with the new approaches proposed by the authors, CWNSGA-II (Clarke and Wright’s Savings with the Non-dominated Sorting Genetic Algorithm II) and CWTSNSGA-II (Clarke and Wright’s Savings, Tabu Search and Non-dominated Sorting Genetic Algorithm II); and, finally, Stage 3, “analysis of the results”, with a comparison of the algorithms. Using the same parameters as the current solution, an optimization of 5.2% was achieved for Objective Function 1 (OF; minimization of CO emissions) and 11.4% with regard to Objective Function 2 (OF; minimization of the difference in demand), with the proposed CWNSGA-II algorithm showing superiority over the others for the approached problem. Furthermore, a complementary scenario was tested, meeting the constraints required by the company concerning time limitation. For the instances from the literature, the CWNSGA-II and CWTSNSGA-II algorithms achieved superior results.
Keywords: Multi-objective green vehicle routing problem, green logistics, meta-heuristic procedures, case study, instances from the literature
1. Introduction
Traffic congestion in large urban centers is a cause for concern because it results in economic losses, lower productivity at the global level and a negative impact on the environment. A basic logistic management issue is defining configurations of distribution to meet demand points economically, offering increasingly better qualified levels of service in terms of ability to meet demand in progressively shorter time intervals [1].
The Vehicle Routing Problem (VRP), proposed by Dantzig and Ramser [2], is of great importance in terms of effective logistic distribution [3]. In this context, we can find in the literature a number of works that address the optimization of fuel consumption [4], CO emissions [5,6], both of these cases simultaneously [7] and other approaches [8,9]. To complement the VRP, the Green VRP analyzes routing activities while taking environmental aspects into consideration [10,11,12].
In recent decades, there has been an increase in the number of publications related to the VRP. At the same time, computational power has evolved in terms of performance, contributing to and stimulating the growth in research and development in this field. Even so, it remains difficult to find an exact solution to large problems, and it is often necessary to resort to heuristic and metaheuristic procedures [13].
Heuristic and metaheuristic algorithms are alternative procedures with regard to exact methods because of the latter’s high computational cost. Heuristic methods seek to achieve results to problems quickly, but do not guarantee that the solutions they provide are optimal solutions. On the other hand, metaheuristic methods do not usually “cling” to local optima in the search for global optimization [1].
Meanwhile, the field of Multi-Objective Optimization (MOO) addresses the process of optimizing two or more conflicting objectives simultaneously, subject to constraints [14]. Thus, the objective of a MOO problem is to find non-dominated solutions and quantify the trade-offs in satisfaction between the different established objectives [15,16].
The proposal of the Multi-objective Optimization for Green Vehicle Routing Problem (MOOGVRP) is to combine the VRP, MOO techniques and environmental considerations to generate economically and environmentally feasible routing. In this context, many researchers have adapted their solution procedures to attend to issues related to factors such as cost, travel time, CO emissions, fuel consumption, reverse logistics and environmental impacts [17,18,19].
To address the theme of the Green VRP, the classification proposed by Lin et al. [17] was used. Therefore, the Green VRP was classified as: Green VRP (GVRP), Pollution Routing Problem (PRP) and VRP in Reverse Logistics (VRPRL). GVRP addresses the optimization of energy consumption in transport and reduced fuel consumption. The PRP is used to choose a vehicle routing scheme with lower pollution levels, particularly the reduction of Greenhouse Gases (GHG). It can also include broader goals that reflect environmental costs. The VRPRL concentrates on aspects of reverse logistic distribution, which in turn is divided into four subcategories: Selective Pickups with Pricing, Waste Collection, End-of-life Goods Collection, and Simultaneous Distribution and Collection.
In the literature, we can highlight some works on the proposed theme in recent years. Those that were most instrumental in inspiring the development of the present study are described below, ordered by year of publication. Govindan et al. [20] presented the two-echelon location–routing problem with time-windows (2E-LRPTW), applied in a case study to address perishable food distribution. The authors used multi-objective particle swarm optimization (MOPSO), adapted multi-objective variable neighbourhood search (AMOVNS) and the multi-objective hybrid approach.
Through multi-objective route based fuel consumption vehicle routing problems (MRFCVRPs), Psychas et al. [21] used the Pareto Front (PF), applied to parallel multi-start non-dominated sorting differential evolution algorithms (PMS-NSDEs) to minimize the cost of the route, travel time and fuel consumption. A design of a Forward/Reverse Logistics Network with Environmental Considerations was proposed by Rabbani et al. [22]. The authors compared two metaheuristic procedures, NSGA-ӀӀ and MOPSO, with the former presenting the best performance.
Gupta et al. [23], presented a shortest path evolutionary algorithm applied to the green multi-objective multi-attribute VRP (G-MoMaVRP), considering time windows, pickup and delivery, heterogeneous fleets of vehicles and traffic congestions. Tests were performed in the literature and some real case studies were conducted in Singapore. Hassanzadeh and Rasti-Barzoki [24] presented a bi-objective mathematical model, taking into consideration production programming and vehicle routing in order to minimize the consumption of resources and delayed deliveries. The model can also reduce CO emissions. For this purpose, a new Genetic Algorithm (GA) was developed, the variable neighborhood search based non-dominated sorting genetic algorithm II (VNSGA-II).
With the green open location-routing problem (G-OLRP), a Mixed Integer Linear Programming (MILP) problem, Toro et al. [11] used the ε-constraint algorithm with a view to minimizing costs, fuel consumption and CO emissions. Finally, the authors realized a need for other approaches to calculate fuel consumption.
Abad et al. [4] presented a general application for the bi-objective model for pickup and delivery PRP with integration and consolidation shipments in a crossdocking system. As a solution procedure, the non-dominated ranking genetic algorithm (NRGA), NSGA-II and MOPSO were used. The algorithms were treated with a view to minimizing costs and fuel consumption. The main contribution lies in the use of cross-docking, which can be applied during loading, sorting or unloading. Gong et al. [19] treated the new closed-loop supply chain logistics network of the vehicle routing problem with simultaneous pickups and deliveries (VRPSPD) dominated by the remanufacturer, where they presented the bee evolutionary algorithm guiding nondominated sorting genetic algorithm II (BEG-NSGA-II) to solve it with three goals in mind: to minimize fuel consumption, minimize waiting time and minimize the distance to delivery. The problem was applied in the context of logistic distribution and generic tests were conducted. The effectiveness of the proposed algorithm was verified in comparison with the traditional NSGA-II.
Liu et al. [25] presented the green vehicle routing optimization problem (GVROP), a MILP. For this purpose, the authors used the Hybrid Quantum Immune Algorithm. Wang et al. [26] presented Recycling Vehicle Routing Optimization in Two-Echelon Reverse Logistics Networks, and to solve it the authors used an algorithm based on the Clarke and Wright (CW) savings method, along with the NSGA-II (CW_NSGA-II). In this context of reverse logistics, applied to a case in China, it was possible to minimize costs and the number of vehicles.
Erdelic and Caric [1] proposed a study on the Electric Vehicle Routing Problem, a variation on GVRP. Finally, Wang et al. [27] presented a hyper-heuristic approach to the Location-Routing Problem of Cold Chain Logistics (LRPCCL), considering fuel consumption. The authors sought to minimize the total cost of LRPCCL (including the cost of fuel consumption) and minimize vehicle distribution time.
The aim of this work is to present a methodology to solve a MOOGVRP, illustrated through an employee transport problem and instances from the literature where it was considered two objective functions (environmental issues and also balancing work between the routes) ensuring savings and satisfaction for the users. In this context, a multi-objective approach, could aid the complex decision-making process in order to achieve the intended objectives. The main contribution of this work lies in the methodology proposed for the MOOGVRP, which was divided into three stages: Stage 1, “data treatment”, where the asymmetry of the routes to be formed and other particular features were addressed; Stage 2, “metaheuristic approaches” (hybrid or non-hybrid), used comparatively, more specifically: NSGA-II (Non-dominated Sorting Genetic Algorithm II), MOPSO (Multi-Objective Particle Swarm Optimization), which were compared with the new approaches proposed by the authors, CWNSGA-II (Clarke and Wright’s Savings with the Non-dominated Sorting Genetic Algorithm II) and CWTSNSGA-II (Clarke and Wright’s Savings, Tabu Search and Non-dominated Sorting Genetic Algorithm II); and, finally, Stage 3, “analysis of the results”, with a comparison of the algorithms. The multi-objective approach was applied to a case study, with a view to minimizing the distance travelled (and the consequent minimization of fuel consumption and CO2 emissions), in addition to the homogenization of demand, which is achieved by minimizing the difference between the demand for each route and the average demand considering all the routes, in terms of absolute value. Furthermore, the asymmetry of distances/real travel times is also considered here instead of the usual symmetrical Euclidean distances. Environmental considerations are included in all these aspects, treated as a mechanism for conscious decision making.
The work is structured into six sections. Following this introduction, Section 2 contains a description of the problem to be studied, describing the methodology used and contains correlated works, while in Section 3 the theoretical foundations for the development of the study are presented. The methodology and data treatment for the case study are addressed in Section 4. Section 5 contains the results, with the conclusion of the study presented in Section 6.
2. Characterization of the problem
The case study used to illustrate the methodology employed to solve a MOOGVRP is the process of transporting passengers (employees) to a company.
The municipality of São José dos Pinhais, located in Paraná State, Brazil, is home to a passenger transport company, whose main business is transporting employees from “home to work” and vice-versa. This transport is usually done in shifts, at the times when employees begin and end their shifts. The first shift is from 6:00h to 14:00h, the second from 14:00h to 22:00h, and the third from 22:00h to 6:00h the following morning. Finally, the fourth shift is office hours. Therefore, there are 8 groups of routes (4 four shifts, from home to work and back) that have to be travelled.
The length of each group of routes varies according to employee demand. In the initial context, the company uses minibuses with room for 31 passengers, with this division and definition of routes restricted to this capacity and the addresses of the employees that travel this route. It should be highlighted that there is a time limit of one and a half hours for the employees to remain on the bus. This deadline is not currently being met on most of the routes used by the company for all the shifts.
The group of routes selected for analysis is that of the employees on the first shift and their journey from “home to work”. In this group of routes, 8 vehicles are currently used, transporting 199 employees who live in Curitiba, the capital of Paraná State, and municipalities in its metropolitan region (São José dos Pinhais, Campina Grande do Sul, Quatro Barras and Colombo) to the company, which is located in São José do Pinhais.
It should also be highlighted that there is an agreement that employees may be obliged to walk up to 250 meters from their homes to access the transport service. This could mean considerable savings in terms of distance travelled on each line if it were used to its full potential. However, the fact is that for the groups of routes in question, the time that the journey is made begins between four and five o’clock in the morning. This makes it unsafe for many users to walk a longer distance to access the service, due to the location of their homes and because many of the employees are women.
Some considerations regarding the company should be highlighted in addition to those already described. There is no time window. It would be preferable for the journey not to last longer than one hour and thirty minutes (90 minutes). The capacity of the bus is limited to 31 passengers plus the driver. There are no restrictions that preclude certain addresses from belonging to the same route. No provisions were made for the routes to have to be balanced, i.e., with approximately the same demand. The company has autonomy to use the routes in the way that is most convenient for it, and the routes are mostly asymmetrical because in the municipalities in question there are many one-way streets.
3. Theoretical foundation
This section contains a brief presentation of the main concepts and algorithms that provide the foundation for the present study.
3.1 Vehicle routing problem
In the literature, some mathematical approaches to solving the VRP can be found, such as those proposed by Fisher and Jaikumar [28] and Subramanian et al. [29]. According to Lin et al. [17], the VRP is a problem with very wide-ranging applications in the fields of distribution and logistics management, such as newspaper distribution [30], and numerous other possible applications.
3.2 Clark and Wright savings algorithm (C&W Savings)
The Clarke and Wright algorithm, proposed in 1964 [31], is also known as the C&W Savings Heuristic or C&W Savings. This is one of the classic heuristic algorithms used for routing construction [26].
3.3 Tabu search
According to Ferreira et al. [30], Glover [32] is considered the father of the Tabu Search (TS) metaheuristic due to the author’s numerous publications in this context. TS explores solutions in the solution space beyond the local optima. The method follows the premise of local search, where it generates moves at each iteration through neighborhood solutions. The move transforms one solution into another and the neighborhood is a set of solutions that enable a set of possible moves.
3.4 Multi-objective optimization
Multi-Objective Optimization (MOO) is a process that optimizes two or more conflicting objectives simultaneously, subject to constraints [33]. When addressing the problem of minimization, the mathematical model is defined as in Eqs.(1) to (5),
|
|
(1) |
|
|
(2) |
|
|
(3) |
|
|
(4) |
|
|
(5) |
where is the -dimension decision variable vector, and correspond to the -dimensional objective vector, is the set of -dimensional inequality constraints, is the set of -dimensional inequality constraints. In Eq.(1), the space addresses the image of , thus referred to as the feasible region for the objective function space. The constraints presented in Eqs.(2) and (3) define the space of the decision variables in of the feasible region and any point of as a feasible solution. In Eq.(4) there is the decision variable domain and, finally, in Eq.(5), the objective function domain [27].
There now follows a brief description of the hypervolume, which addresses a metric to evaluate the PF in MOO problems.
3.4.1 Hypervolume
According to Deb [34], with the calculation of the hypervolume, it is possible to estimate the proximity of the solutions in relation to the optimal PF. The procedure involves calculating the volume of the covered region between the points of the solutions on the PF and a certain reference point. Thus, the sum of the hypercubes formed by the non-dominated solutions is obtained. This procedure is used when the optimal PF is not known. It aids the measurement of the quality of a solution in comparison with other solutions and, thus, the greater the hypervolume, the better the solution will be.
3.5 NSGA II algorithm
The Genetic Algorithm (GA), developed by Holland [35] in the nineteen sixties, has been widely used in applications with multi-objectives. The Non-dominated Sorting Genetic Algorithm II (NSGA-II), proposed by Deb et al. [36], is a multi-objective GA that classifies solutions through the concept of Pareto dominance. The differential of this algorithm occurs through “Elitism”, which guarantees the preservation of good solutions in the search process, and also through the application of the Fast-non-dominated-sorting (FNS) procedure, in which the classification of the population at different levels through the use of Pareto dominance occurs.
3.6 MOPSO algorithm
According to Abad et al. [4], Multi-objective particle swarm optimization (MOPSO), proposed by Coello [37], has proved to be highly efficient and is widely used in the literature to solve optimization problems. The three steps of this algorithm are initialization, unloaded sorting and crowding distance (CD). Equations (6) and (7), below, show the speed and updating of the particle position
|
|
(6) |
|
|
(7) |
where, and are uniform random numbers; and are constants that specify the acceleration of particles to pBest and gBest, and w is the inertial weight. To calculate the inertial weight, the linear distribution proposed by Kennedy et al. [38] can be used, as shown in (8), where and address, respectively, the maximum and minimum amount of inertia
|
|
(8) |
3.7 Utility theory
According to Poterba and Rotemberg [39], the fundamental property of Utility Theory is that the Monetary Utility Function (UF) of a Decision Maker (DM) is that it is indifferent between two alternatives if they yield the same expected utility.
Therefore, can be configured for the lowest utility value and for the highest utility value. All other utilities must lie within this interval. This procedure facilitates the definition of the relative utility of all the results from the worst to the best. Finally, when using a UF in a decision analysis process, it must be adapted to the preferences and values of the DM.
3.8 Environmental considerations
Here, the environmental considerations related to GHG emissions are addressed. According to Carvalho [40], it is possible to observe the average CO emissions from urban transport through the different modes of transport, as shown in Table 1.
| Mode | Carbon emissions per kilometer [kg of CO/km] |
|---|---|
| Underground | 3.16 |
| Bus | 1.28 |
| Car | 0.19 |
| Motorcycle | 0.07 |
| Heavy vehicles | 1.28 |
The values presented in Table 1 provide the input parameters (constants) to measure the amount of greenhouse gas emissions proposed in this work.
4. Proposed Methodology
The proposed methodology for the study consisted of three stages, as shown in Figure 1.
4.1 Stage 1: Data “Treatment”
The data treatment used to obtain the data used in the solution of the proposed case study is presented in this section. It should be highlighted that R software was used along with Google Maps to collect the times and also the distances. The site that was used makes available some modes of transport as a reference, namely car, public transport, walking, bicycle and plane. For the present study, the “car” was used as a reference for the data collection in the software as it is closest to the reality of the activity, given that the route is covered by a bus (as already mentioned in Section 2).
In all, there are 199 employees to be picked up at 184 collection points on eight routes. As the route selected was the first shift, the “depot” for the problem will be the bus garage at the beginning of the route. The employees’ addresses will be the points to be visited and the company will be the return to the “depot”. With this approach to the problem, the solution will be feasible in the applied context. The proposed routing is shown in schematic form in Figure 2.
Table 2 contains a summary of the current situation using data obtained through Google Maps, considering the respective route (line), the number of passengers, the vehicle occupancy rate, the journey time to pick up the employees (here, the time spent from the garage to the first collection point is not considered) and the total distance of the corresponding journey. Table 2 also shows a difference in vehicle occupancy rates of over 40%, as well as discrepancies in the time and distance of the journeys.
| Reference | Passengers | Occupation [%] | Collection Time [min] | Total Distance [km] |
| Line 1 | 26 | 83.8 | 93 | 108 |
| Line 2 | 31 | 100.0 | 127 | 93 |
| Line 3 | 32 | 103.2 | 112 | 77 |
| Line 4 | 20 | 64.5 | 102 | 56 |
| Line 5 | 27 | 87.1 | 106 | 77 |
| Line 6 | 18 | 58.0 | 93 | 79 |
| Line 7 | 30 | 96.7 | 112 | 94 |
| Line 8 | 18 | 58.1 | 117 | 82 |
Therefore, the Objective Functions (OFs) used in this case study to optimize the employee transport process are, as already mentioned, “OF1: minimization of CO2 emissions” and “OF2: absolute minimization of the demands of each route in relation to the average demand”.
4.2 Stage 2: Metaheuristic Approaches
Here, a description is given of the multi-objective metaheuristic procedures used in the study.
4.2.1 NSGA-II
The NSGA-II algorithm, presented in Section 3.5, will be applied to the MOOGVRP in the cases study in question and the instances from the literature. For the case study, the parameters used, after several preliminary experiments, were: population = 100; vehicle capacity = 31 (passengers); number of iterations = 100; percentage of crossover = 0.5; percentage of mutation = 0.1; and maximum journey time = 127 min.
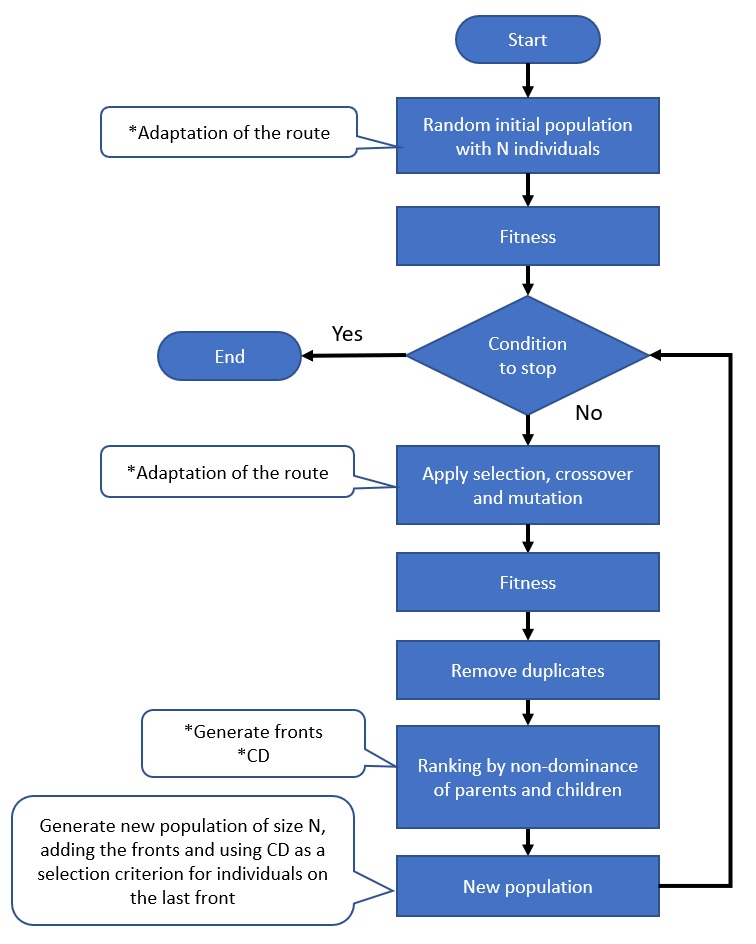
The formation of the route in the initial solution is random. To make the crossover, first of all, the VRP was transformed into a Traveling Salesman Problem (TSP), and then a random cut was made of one point between the second and second-last gene. The chromosome was then adapted through mutation to contain all the addresses on the route as a TSP. Finally, the TSP was “transformed” into a VRP making the “distribution” of the chromosome according to the “maximum travel time” along with “vehicle capacity” to validate the routes. Thus, the creation of a new route (chromosome) will be feasible. A flowchart of the implemented NSGA-II algorithm is shown in Figure 3.
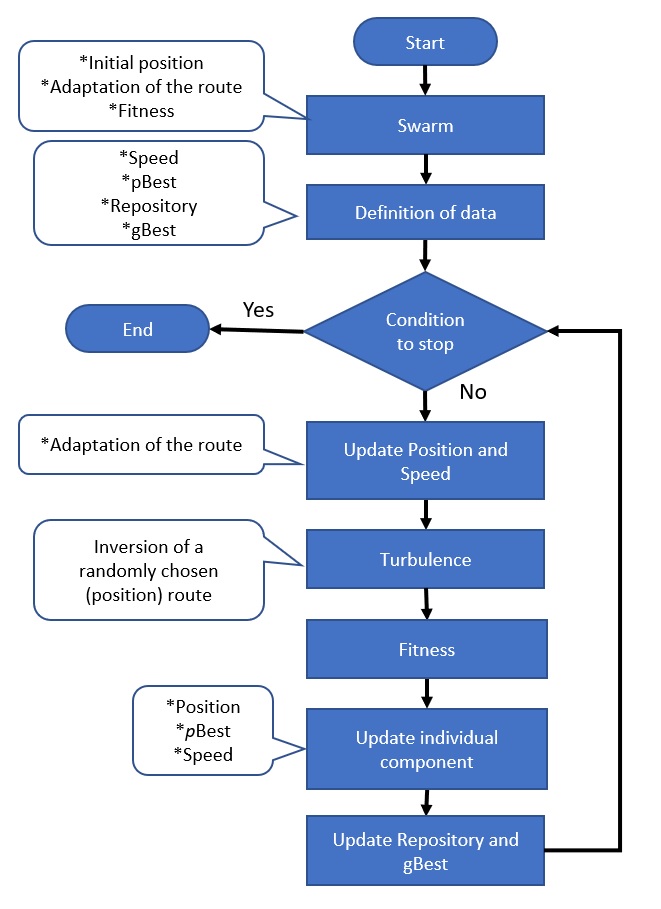
4.2.2 MOPSO
The MOPSO algorithm, presented in Section 3.6, will be applied to the MOOGVRP in the case in question and the instances from the literature. The parameters and procedures for the case study will be the same as those presented in Section 4.2.1 (NSGA-II). Furthermore, for the calculation of speed and position, Equations (6) and (7) were selected, in accordance with the recommendations from the literature [4]: acceleration constant or cognition rate C1 and C2 = 1; inertial weight W through Equation (8); Wmax = 1 and Wmin = 0.2.
It should be observed that the positions (routes) were simplified for the TSP and, following the calculation procedures of Equations (6) and (7), were readapted for the VRP. It was established that the velocity vector can contain up to N changes, where N is the number of addresses to be visited, in addition to the depot.
As the pBest particle, the evolution of the particle itself was considered. The gBest particle is the random choice of a particle from the repository. In the repository, the updated PF at each iteration is found. It should be highlighted that all the routes were validated by the capacity of the vehicle (bus). A flowchart of the MOPSO algorithm is shown in Figure 4.
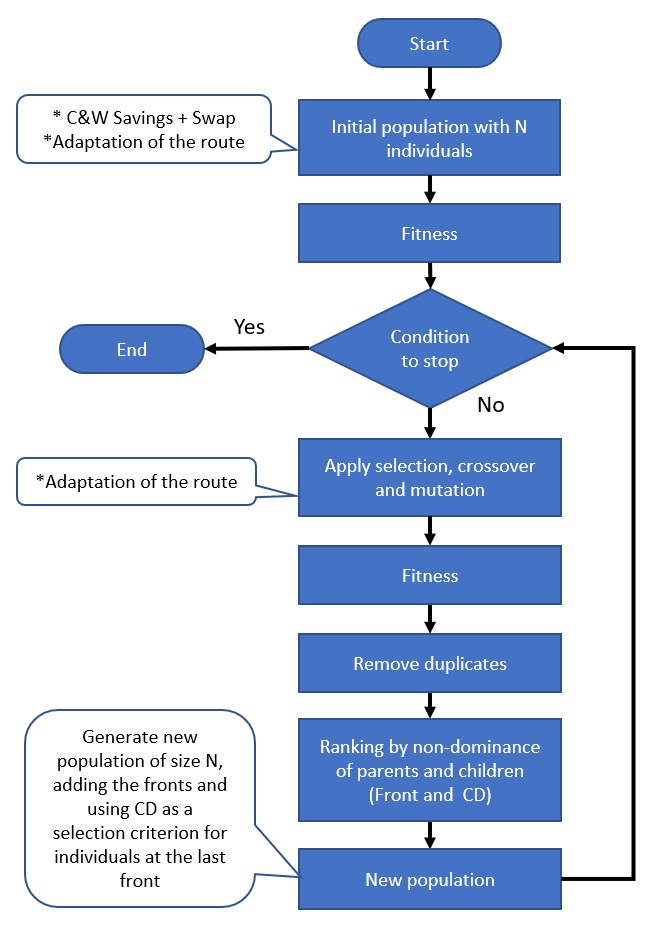
4.2.3 CWNSGA-II Hybrid Algorithm
The proposed procedure of the Hybrid Algorithm of Clarke and Wright’s Savings and the Non-dominated Sorting Genetic Algorithm II (CWNSGA-II) is presented here. The C&W algorithm was described in Section 3.2, and the NSGA-II in Section 3.5. In the literature, correlated works can be found, such as that of Wang et al. [26], with the authors using the C&W as a procedure in the generation of the initial population. Here, the C&W was applied and a swap operation was used to achieve the established number of the population to form the initial population. The parameters and procedures are the same as those presented in 4.2.1 (NSGA-II) in the solution of the proposed case study. A flowchart of the CWNSGA-II algorithm is presented in Figure 5. The innovation is in the hybridization of the algorithms.
4.2.4 CWTSNSGA-II Hybrid Algorithm
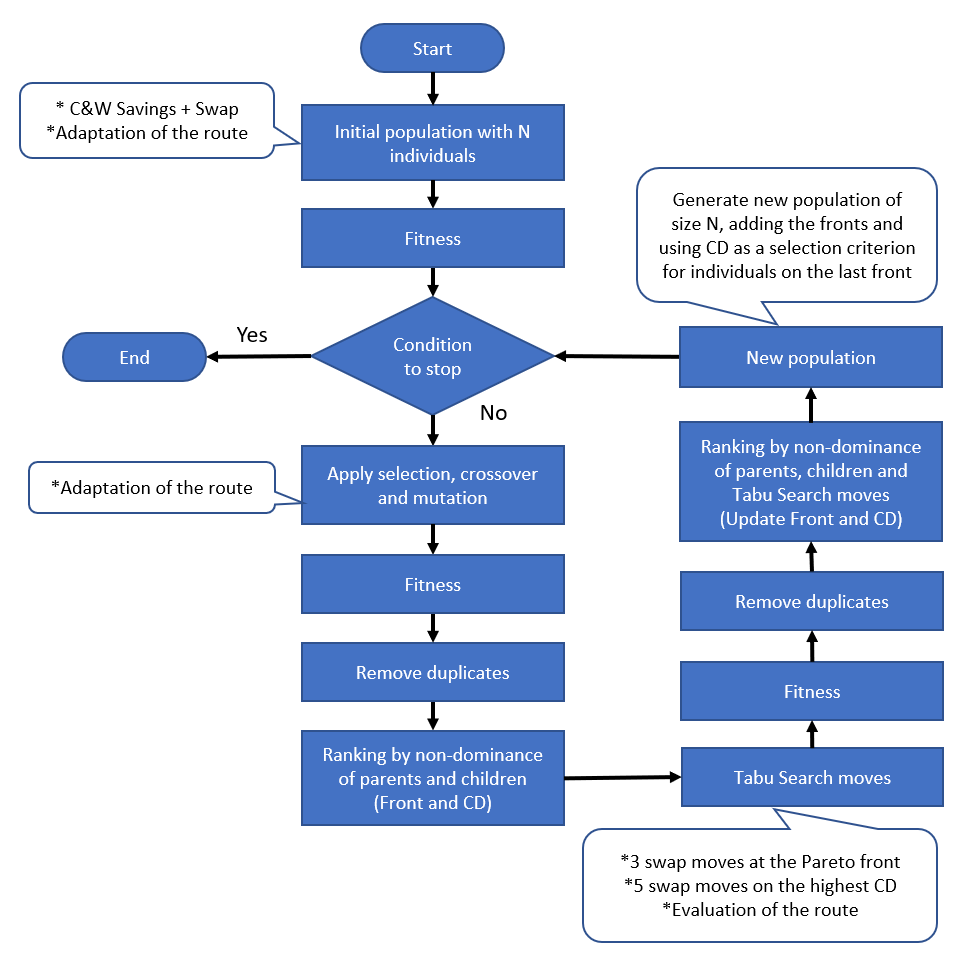
The proposed procedure of the Hybrid Algorithm of Clarke & Wright’s Savings, Tabu Search and the Non-dominated Sorting Genetic Algorithm II (CWTSNSGA-II) is presented. The C&W algorithm was described in Section 3.2, the TS in Section 3.3 and the NSGA-II in Section 3.5. The parameters and procedures are the same as those presented in 4.2.3 (CWNSGA-II).
The differential (innovation) of the CWTSNSGA-II is in the loop (Figure 6), as it follows the same procedures as the NSGA-II, in addition to a number of TS moves, calculates fitness, removes duplicate solutions, updates the PF and CD and generates a new population. The TS moves are swaps on the PF and in the highest value solution of CD, to increase the number of solutions close to the PF and identify isolated solutions. Thus, the algorithm considerably improves its population at each iteration. A flowchart of the CWTSNSGA-II algorithm is shown in Figure 7. A commented illustration of the stages in the iterations of this procedure is presented in Figure 7.
4.3 Stage 4: Analysis of the Results
In order to analyse the results, we generically call “algorithm x” each one of the algorithms used here. Initially, we consider the Pareto Frontier (PF) resulting from the “algorithm x”. The “algoritm x” was executed three times and the obtained PF forms the data for calculating the hyprvolume of this partial analysis. Thus, the PF that has the highest hypervolume value will be the reference solution for the “algorithm x”. Then, with the best solution from each algorithm, all of them were evaluated and compared according to their hypervolume, and the most adequate solution was selected. Finally, the best route was selected according to the Utility Function [24, 34].
5. Results and Discussion
In this section, the results that were obtained using the techniques proposed in Section 4 are presented, analyzed and discussed. To test the results of the case study, as well as the instances from the literature, Matlab R2016b software was used, installed in a notebook with an Intel® Core™ i7-7500U processor CPU @ 2.7GHz 2.90GHZ, and 16.00 GB of RAM, with a 64-bit operational system.
5.1 Case Study: Employee Transport
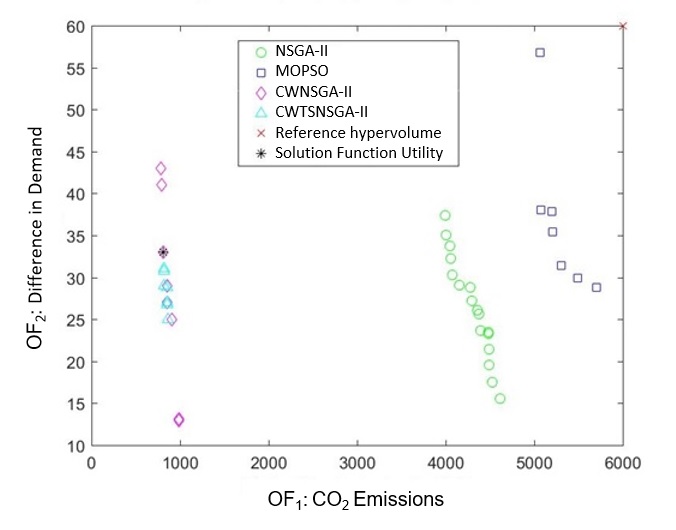
Figure 8 contains a graph with the Pareto Fronts obtained as a result of the techniques that were employed (NSGA-II; MOPSO; CWNSGA-II and CWTSNSGA-II) to solve the case study. The randomly selected reference point can also be seen here, point = (6000; 60), for the calculation of the hypervolume and the solution for the Utility Function, point = (808.19; 33.0), which will be presented later in the article.
The result of the evaluation of the Pareto fronts is presented in Table 3. Note that the higher the value of the hypervolume, the better the set of solutions will be. Therefore, the calculation of the hypervolume strengthens the dominance of the solution of the CWNSGA-II algorithm compared with the CWTSNSGA-II, NSGA-II and MOPSO, in this case the value being 2.4 billion a.u. It should be highlighted that the values of the hypervolumes were high because the demand points (addresses) are far from each other, since the area includes the entire city of Curitiba and its metropolitan region (neighbouring municipalities of Curitiba).
| Algorithm | Hypervolume |
| NSGA-II | 823,170,000 |
| MOPSO | 262,310,000 |
| CWNSGA-II | 2,423,900,000 |
| CWTSNSGA-II | 1,813,000,000 |
A comparison of the current situation and the solutions proposed to the company is presented in Table 4. Thus, the information obtained through the objective functions can be seen, more specifically the routes obtained from the PF, CO2 emissions (OF1), distance traveled, fuel consumption, travel time, number of vehicles used and difference in demand (OF2).
| Solution (route) | Emissions in Kilograms [kg] of CO2/km | Distance traveled [km] | Fuel consumption [l] | Journey time [min] | No. of vehicles | Difference in demand |
| Current | 852.4 | 666.0 | 256.1 | 862 | 8 | 37.2 |
| VRP 1 | 787.5 | 615.2 | 236.6 | 869 | 8 | 43.0 |
| VRP 2 | 790.2 | 617.4 | 237.4 | 863 | 8 | 41.0 |
| VRP 3 | 808.1 | 631.4 | 242.8 | 896 | 8 | 33.0 |
| VRP 4 | 850.4 | 664.4 | 255.5 | 925 | 8 | 29.0 |
| VRP 5 | 857.6 | 670.0 | 257.6 | 940 | 8 | 27.0 |
| VRP 6 | 910.1 | 711.0 | 273.4 | 940 | 8 | 25.0 |
| VRP 7 | 983.0 | 768.0 | 295.3 | 978 | 9 | 22.0 |
| VRP 8 | 988.1 | 772.0 | 296.9 | 984 | 9 | 22.0 |
The Utility Function was then applied to the dominant PF resulting from the CWNSGA-II algorithm. For this procedure, the decision maker was asked to attribute weights to each objective function. The decision maker then attributed 70% importance to the first objective function and 30% to the second one. Finally, Solution 3, with coordinates (808.1; 33.0), presented the greatest Utility Function and was the solution proposed for this case study. The optimization level was 5.2% for OF1 (minimum CO2 emission) and 11.4% for OF2 (minimum difference in demand).
The optimized solution uses the same number of vehicles (buses) as the solution adopted by the company and was better in terms of CO2 emissions, distance, fuel consumption and difference in demand. In other words, it was more balanced in the number of passengers assigned to the buses. It was worse in terms of travel time. On the other hand, the buses that are not often idle can meet the fluctuations in demand more efficiently. The comparison of the current solution (left-hand side) and the optimized solution (right) is shown in the form of a graph in Figure 9.
5.2 Meeting the Requirements of the Case Study
So far it has been shown how much the solution can improve considering the same parameters currently used by the company, which are a maximum of 127 minutes of travel time and 31 seats in the vehicles. This section has already considered the maximum travel time requirement requested by the company, which is 90 minutes. The technique used will be the CWNSGA-II algorithm, as it has shown the best performance so far. The other parameters are the same as in Section 4.2.3.
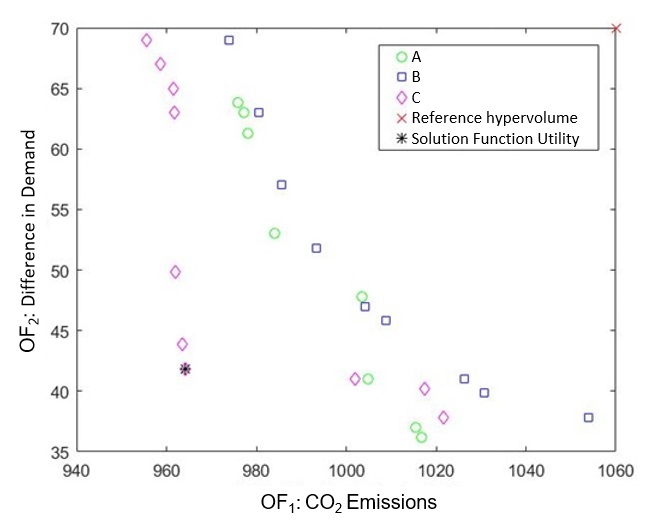
Initially, three rounds were performed (A, B and C), with variations in the initial populations in each round, using the CWNSGA-II technique. The computational time was 8.9, 9.1 and 9.0 seconds. The hypervolumes obtained were 22,390,000; 18,918,000 and 29,347,000 a.u., respectively. Consequently, the C set of solutions (front) was the one that presented the largest hypervolume and will be the analysed solution.
Figure 10 contains a graph with the Pareto fronts obtained using the CWNSGA-II technique for the solution of this case study in the ideal version. The reference point selected by the authors is also presented, point = (1060; 70), for the calculation of the hypervolume, and the solution for the Utility Function, point = (964.1; 41.8), the solution of round C, which will be presented below. In the current case, with more vehicles, the situation is different and there is more space for analysis.
Table 5 contains information obtained through the objective functions, in other words, the routes from the PF, CO2 emissions (OF1), distance traveled, fuel consumption, travel time, number of vehicles used and difference in demand (OF2).
| Solution (route) | Emissions in Kilograms [kg] of CO2/km | Distance traveled [km] | Fuel consumption [l] | Journey time [min] | No. of vehicles | Difference in demand |
| Current | 852.4 | 666 | 256.1 | 862 | 8 | 37.2 |
| VRP 1 | 955.5 | 746.5 | 287.1 | 931 | 12 | 69.0 |
| VRP 2 | 958.7 | 749.0 | 288.1 | 930 | 12 | 67.0 |
| VRP 3 | 961.5 | 751.2 | 288.9 | 934 | 12 | 65.0 |
| VRP 4 | 961.7 | 751.3 | 289.0 | 936 | 12 | 63.0 |
| VRP 5 | 962.1 | 751.6 | 289.1 | 947 | 12 | 49.8 |
| VRP 6 | 963.5 | 752.7 | 289.5 | 956 | 12 | 43.8 |
| VRP 7 | 964.1 | 753.2 | 289.7 | 962 | 12 | 41.8 |
| VRP 8 | 1,002.0 | 782.8 | 301.1 | 988 | 12 | 41.0 |
| VRP 9 | 1,017.5 | 794.9 | 305.7 | 1003 | 12 | 40.2 |
| VRP 10 | 1,021.6 | 798.1 | 307.0 | 1005 | 12 | 37.8 |
Note that complying with up to 90 minutes of travel time will mean adding 4 buses. Therefore, it would be preferable to use a minibus or van to avoid idle capacity. Although apparently unfeasible, due to the need for more vehicles and drivers, this is the proposal, and it is for the company to decide which proposal is the most appropriate. A comparison between the current solution with 8 vehicles (left side) and the optimized solution with 12 vehicles (right) is shown in Figure 11 in graphic form.
5.3 Instances from the Literature
The algorithms presented in this work (NSGA-II; MOPSO; CWNSGA-II and CWTSNSGA-II) were applied to a set of instances from the literature. For the case of the MOOGVRP, a set of 27 instances of the CVRP (more specifically, Augerat’s Set A), with the dimension varying from 32 to 80 cities (considering the depot), standard vehicle capacity of 100 units, and 5 to 10 routes in the solutions, available at [41] http://neo.lcc.uma.es/vrp/vrp-instances/capacitated-vrp-instances/.
To evaluate the algorithms presented in this work through instances from the literature, the same parameters of Hassanzadeh and Rasti-Barzoki [24] were used regarding the number of iterations, population and/or particle size, percentage of crossover and percentage of mutation; and Abad et al. [4] for the cognition rate. The assigned parameters are shown in Table 6.
| Parameter | Level |
| Iterations | 100 |
| Population/Particle | 60 |
| Crossover | 0.7 |
| Mutation | 0.3 |
| C1 and C2 | 1 |
The OFs that were used are the same as in the case study, i.e., “minimization of CO2 emissions” and “absolute minimization of the demands of each route in relation to the average demand”. To evaluate the instances, three simulations were performed and the response with the greatest hypervolume was selected (presented in Section 3.4.1).
The results of the tests with the instances from the literature are synthesized in Figure 12. Table 7 shows the mean and standard deviation of the analyzed data. The CWNSGA-II and CWTSNSGA-II presented better results than the NSGA-II and MOPSO.
| Criterion | NSGA-II | MOPSO | CWNSGA-II | CWTSNSGA-II | |
| Hypervolume | Mean | 5,061.9 | 1,376.6 | 9,299.2 | 9,485.1 |
| S.D. | 3,481.9 | 1,344.1 | 7,088.6 | 7,098.9 | |
6. Conclusions
This work presents a new approach to a complexity task of optimization in a MOOGVRP that can be used in logistic distribution problems in general. The use of the methodology is illustrated here through a case study that addresses employee transport.
It should be highlighted that to collect the data for the case study, the asymmetry of distances traveled was considered and, consequently, the travel times, instead of the usual Euclidean (symmetric) distances.
Use was then made of the hybrid algorithms of the NSGA-II with C&W Savings (CWNSGA-II), as well as NSGA-II with C&W and TS (CWTSNSGA-II). The hybridization of these algorithms is the main contribution of this work. In the CWNSGA-II algorithm, the initial solution was obtained through the application of the C&W with a TSP, making swap moves until a number of individuals for the initial population were generated and then adapting the TSP to the VRP. The differential of the CWTSNSGA-II, is in the loop shown in Figure 6, which follows the same procedures as the CWNSGA-II and a certain number of TS moves: it calculates fitness, excludes duplicates, updates the PF, CD and generates a new population. The TS moves are swaps on the PF and in the solution with the highest CD value to expand the number of solutions close to the PF and diversify isolated solutions. Therefore, the algorithm improves its population considerably at each iteration.
Comparative tests of the algorithms were performed through hypervolume (the bigger, the better). Afterwards, the utility function was used to choose the best solutions, supported by the weights assigned by the decision maker.
The case study restricted its routes in relation to time, which was one of the main problems that were faced. Using the same parameters as the current solution, an optimization of 5.2% was achieved for OF1 (minimum CO2 emissions) and 11.4% for OF2 (minimum difference in demand). Here the proposed CWNSGA-II algorithm proved to be superior to the others. A scenario considering a time limit of 90 minutes per vehicle was also tested, and for adequate practical implementation, it was concluded that it would be necessary to add 4 vehicles to the current fleet.
In this context, multi-objective optimization was helpful in the conflict between minimizing CO2 emission and minimizing difference in demand. Thus, regarding OF1 it was possible to stratify distance travelled, fuel consumption and travel time. CO2 emission represents the environmental concerns that transformed this problem into a MOOGVRP. The FO2, difference in demand, contributes to the homogenization of occupied vehicle capacity. The environmental concerns, currently with high values, are treated here as a mechanism for conscious decision making. This is why OF1 had a greater weight.
Finally, with regard to the instances from the literature, the CWTSNSGA-II algorithm had the best performance compared with the other techniques.
For future works, we suggest that some statistical tests, like Wilcoxon or Kruskall-Wallis or others, be done with the results contained in Table 7. Also, the mathematical model for Green Vehicle Routing Problem could be constructed based on the presented general model (1) to (5), in Section 3.4. Besides, there remain many opportunities with a view to exploring applications and techniques regarding works related to the MOOGVRP. In this context, the intention is to develop more scenarios, developing new multi-objective metaheuristic algorithms in addition to hybrid versions, always seeking to improve results and achieve scientific advances through new techniques. Finally, the Taylor&Francis, IEEEXplore, ACM Digital library, Wiley, Elsevier, Springer, MDPI, and Hindawi databases and others could be used for further research.
Acknowledgments
This study was partly funded by PUCPR and the Coordination for the Improvement of Higher Education Personnel - Brazil (CAPES; 1st author) and by the National Council for Scientific and Technological Development – Brazil (CNPq; 2nd author).
References
[1] Erdelic T., Caric T., A Survey on the Electric Vehicle Routing Problem: Variants and Solution Approaches. Journal of Advanced Transportation, 2019:1-48, 2019.
[2] Dantzig G. B., Ramser J.H., The truck dispatching problem. Management Science, 6:80-91, 1959.
[3] Validi S., Bhattacharya A., Byrne P.J., A solution method for a two-layer sustainable supply chain distribution model. Computers & Operations Research, 54: 204–217, 2015.
[4] Abad H.K.E.A., Vahdani B., Sharifi M., Etebari F., A bi-objective model for pickup and delivery pollution-routing problem with integration and consolidation shipments in cross-docking system. J. Clean. Prod., 193:784–801, 2018.
[5] Ebrahimi S.B., A stochastic multi-objective location-allocation-routing problem for tire supply chain considering sustainability aspects and quantity discounts. J. Clean. Prod., 198:704–720, 2018.
[6] Fathollahi-Fard A.M., Hajiaghaei-Keshteli M.H.K., Tavakkoli-Moghaddam R., A Bi-objective green home health care routing problem. J. Clean. Prod., 200:423–443, 2018.
[7] Amer H., Salman N., Hawes M., Chaqfeh M., Mihaylova L., Mayfield M., An improved simulated annealing technique for enhanced mobility in smart cities. Sensors (Switzerland), 16:1-23, 2016.
[8] Ghezavati V.R., Beigi M., Solving a bi-objective mathematical model for location-routing problem with time windows in multi-echelon reverse logistics using metaheuristic procedure. Journal of Industrial Engineering International., 12:469–483, 2016.
[9] Fu P., Li H., Wang X., Luo J., Zhan S.L., Zuo C., Multiobjective Location Model Design Based on Government Subsidy in the Recycling of CDW. Math. Probl. Eng., 2017.
[10] Sawik B., Faulin J., Pérez-Bernabeu E., A Multicriteria Analysis for the Green VRP: A Case Discussion for the Distribution Problem of a Spanish Retailer. Transportation Research Procedia, 22:305-313, 2017.
[11] Toro E.M., Franco J.F., Echeverri M.G., Guimarães F.G., A multi-objective model for the green capacitated location-routing problem considering environmental impact. Computers and Industrial Engineering, 110:114–125, 2017.
[12] Soleimani H., Chaharlang Y., Ghaderi H., Collection and distribution of returned-remanufactured products in a vehicle routing problem with pickup and delivery considering sustainable and green criteria. Journal of Cleaner Production, 172:960-970, 2018.
[13] Braekers K., Ramaekers K., Nieuwenhuyse I.V., The vehicle routing problem: State of the art classification and review. Computers & Industrial Engineering, 99:300-313, 2016.
[14] Kumar R.S., Kondapaneni K., Dixit V., Goswami A., Thakur L.S., Tiwari M.K., Multi-objective modeling of production and pollution routing problem with time window: A self-learning particle swarm optimization approach. Computers and Industrial Engineering, 99:29–40, 2016.
[15] Ehrgott M., Wang J.Y.T., Raith A., Van Houtte C., A bi-objective cyclist route choice model. Transp. Res. Part A Policy Pract., 46:652–663, 2012.
[16] Steiner M.T.A., Datta D., Steiner Neto P.J., Scarpin C.T., Figueira J.R., Multi-objective optimization in partitioning the healthcare system of Parana State in Brazil. Omega, 52:53-64, 2015.
[17] Lin C., Choy K.L., Ho G.T.S., Chung S.H., Lam H.Y., Survey of Green Vehicle Routing Problem: Past and future trends. Expert Systems with Applications, 41:1118-1138, 2014.
[18] Norouzi N., Sadegh-Amalnick M., Tavakkoli-Moghaddam R., Modified particle swarm optimization in a time-dependent vehicle routing problem: minimizing fuel consumption. Optimization Letters, 11:121–134, 2017.
[19] Gong X., Deng Q., Gong X., Zhang L., Wang H., Xie H., A Bee Evolutionary Algorithm for multiobjective Vehicle Routing Problem with Simultaneous Pickup and Delivery. Math. Probl. Eng., 1–21, 2018.
[20] Govindan K., Jafarian A., Khodaverdi R., Devika K., Two-echelon multiple-vehicle location-routing problem with time windows for optimization of sustainable supply chain network of perishable food. Int. J. Prod. Econ., 152:9–28, 2014.
[21] Psychas I.D., Marinaki M., Marinakis Y., Migdalas A., Non-dominated sorting differential evolution algorithm for the minimization of route based fuel consumption multiobjective vehicle routing problems. Energy Syst., 8:785–814, 2016.
[22] Rabbani M., Saravi N.A., Farrokhi-Asl H., Design of a forward/reverse logistics network with environmental considerations. Int. J. Supply Oper. Manag., 4:115–132, 2017.
[23] Gupta A., Heng C.K., Ong Y.S., Tan P.S., Zhang A.N., A generic framework for multi-criteria decision support in eco-friendly urban logistics systems. Expert Systems with Applications, 71:288-300, 2017.
[24] Hassanzadeh A., Rasti-Barzoki M., Minimizing total resource consumption and total tardiness penalty in a resource allocation supply chain scheduling and vehicle routing problem. Applied Soft Computing, 58:307–323, 2017.
[25] Liu X.H., Shan M.Y., Zhang R.L., Zhang L.H., Green Vehicle Routing Optimization Based on Carbon Emission and Multiobjective Hybrid Quantum Immune Algorithm. Math. Probl. Eng., 1–9, 2018.
[26] Wang Y., Peng S., Assogba K., Liu Y., Wang H., Xu M., Wang Y., Implementation of cooperation for recycling vehicle routing optimization in two-echelon reverse logistics networks. Sustain, 10, 2018.
[27] Wang Z., Leng L., Wang S., Li G., Zhao Y., A Hyperheuristic Approach for Location-Routing Problem of Cold Chain Logistics considering Fuel Consumption. Computational Intelligence and Neuroscience, 2020:1-17, 2020.
[28] Fisher M.L., Jaikumar R., A generalized assignment heuristic for vehicle routing. Networks, 11(2):109-124, 1981.
[29] Subramanian A., Penna P.H.V., Ochi L.S., Souza M.J.F., Um algoritmo heurístico baseado em iterated local search para problemas de roteamento de veículos. In: Lopes H.S., Rodrigues L.C.A., Steiner M.T.A., (eds.) Meta-Heurísticas em Pesquisa Operacional. Ed. Omnipax, Curitiba, PR, 2013.
[30] Ferreira J.C., Steiner M.T.A., Guersola M.S., A Vehicle Routing Problem Solved Through Some Metaheuristics Procedures: A Case Study. IEEE Latin America Transactions, 15(5), 2017.
[31] Clarke G., Wright J.W., Scheduling of vehicles from a central depot to a number of delivery points. Operations Research, 12(4):568–582, 1964.
[32] Glover F., Future paths for integer programming and links to artificial intelligence. Computers an Operational Research, 13(5):533-549, 1986.
[33] Demir E., Bektas T., Laporte G., A review of recent research on green road freight transportation. European Journal of Operational Research, 237:775–793, 2014.
[34] Deb K., Multi-objective optimization using evolutionary algorithms. [S.l.]: John Wiley & Sons, Inc, 2001.
[35] Holland J.H., Adaptation in natural and artificial systems. Ann Arbor: University of Michigan Press, 1975.
[36] Deb K., Pratap A., Aguarwal S., Meyarivan T., A fast and elitist multiobjective genetic algorithm: NSGA-II. IEEE transactions on evolutionary computation, 6(2):182–197, 2002.
[37] Coello C.A., MOPSO: a proposal for multiple objective particle swarm optimization. Proceedings of the 2002 Congress on Evolutionary Computation, 2:1051-1056, 2000.
[38] Kennedy J., Eberhart R.C., Shi Y., Swarm Intelligence. Kaufmann, San Francisco, 1:700-720, 2001.
[39] Poterba J.M., Rotemberg J., Money in the Utility Function: An Empirical Implementation. Creative Media Partners: LLC, 2018.
[40] Carvalho C.H.R., 1606: Texto para discussão. Emissões relativas de poluentes do transporte motorizado de passageiros nos grandes centros urbanos brasileiros. Instituto de Pesquisa Econômica Aplicada (IPEA), Brasília, april 2011.
[41] NEO. Networking and Emerging Optimization. Capacitated VRP Instances. In: < http://neo.lcc.uma.es/vrp/vrp-instances/capacitated-vrp-instances/ >. Accessed in: june 3, 2019.
Document information
Published on 14/01/22
Accepted on 10/01/22
Submitted on 17/04/21
Volume 38, Issue 1, 2022
DOI: 10.23967/j.rimni.2022.01.001
Licence: CC BY-NC-SA license