(Created page with "==El potencial del aprendizaje hebbiano en la clasificación supervisada== '''Fernando Aguilar-Canto Carlos Brito-Loeza''' ==Resumen== A pesar de tener un sustento bioló...") |
|||
| (34 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
| − | + | =1 Introducción= | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
La Regla de Hebb es un modelo teórico de plasticidad sináptica propuesto originalmente el trabajo de Donald Hebb <span id='citeF-1'></span>[[#cite-1|[1]]], aunque, como observa <span id='citeF-2'></span>[[#cite-2|[2]]], autores como Konorski <span id='citeF-3'></span>[[#cite-3|[3]]] y Ramón y Cajal <span id='citeF-4'></span>[[#cite-4|[4]]] ya habían concebido ideas semejantes. Unas décadas después, las ideas de Hebb recibieron confirmación experimental al observarse que su conjetura modelaba al fenómeno de Potenciación a Largo Plazo (''Long-Term Potentiation'', LTP), el cual fue descrita por primera vez en los trabajos de Terje Lmo y Timothy Bliss <span id='citeF-5'></span><span id='citeF-6'></span>[[#cite-5|[5,6]]]. | La Regla de Hebb es un modelo teórico de plasticidad sináptica propuesto originalmente el trabajo de Donald Hebb <span id='citeF-1'></span>[[#cite-1|[1]]], aunque, como observa <span id='citeF-2'></span>[[#cite-2|[2]]], autores como Konorski <span id='citeF-3'></span>[[#cite-3|[3]]] y Ramón y Cajal <span id='citeF-4'></span>[[#cite-4|[4]]] ya habían concebido ideas semejantes. Unas décadas después, las ideas de Hebb recibieron confirmación experimental al observarse que su conjetura modelaba al fenómeno de Potenciación a Largo Plazo (''Long-Term Potentiation'', LTP), el cual fue descrita por primera vez en los trabajos de Terje Lmo y Timothy Bliss <span id='citeF-5'></span><span id='citeF-6'></span>[[#cite-5|[5,6]]]. | ||
| Line 21: | Line 11: | ||
La discusión que se plantea en este artículo es diferente: dadas redes neuronales generales, ¿es preferible disponer de aprendizaje hebbiano sobre aprendizaje basado en el gradiente? Una de las acusadas ventajas que disponen las reglas basadas en Hebb se refieren a la capacidad de implementarse en tiempo real <span id='citeF-13'></span>[[#cite-13|[13]]], pero su principal desventaja es que por lo general no alcanzan el desempeño otorgado por las reglas basadas en el gradiente y en algunos casos la diferencia es muy aguda <span id='citeF-14'></span>[[#cite-14|[14]]]. | La discusión que se plantea en este artículo es diferente: dadas redes neuronales generales, ¿es preferible disponer de aprendizaje hebbiano sobre aprendizaje basado en el gradiente? Una de las acusadas ventajas que disponen las reglas basadas en Hebb se refieren a la capacidad de implementarse en tiempo real <span id='citeF-13'></span>[[#cite-13|[13]]], pero su principal desventaja es que por lo general no alcanzan el desempeño otorgado por las reglas basadas en el gradiente y en algunos casos la diferencia es muy aguda <span id='citeF-14'></span>[[#cite-14|[14]]]. | ||
| − | ¿Por qué un algoritmo biológicamente inspirado no alcanza los resultados de clasificación | + | ¿Por qué un algoritmo biológicamente inspirado no alcanza los resultados de clasificación de un algoritmo aparentemente artificial? Divisamos cinco posibles razones principales por las que esto ocurra: |
<ol> | <ol> | ||
| Line 37: | Line 27: | ||
En este artículo, trataremos de aproximarnos a las preguntas anteriormente planteadas. La aproximación que haremos será referente a la última posible respuesta que se planteó, indicando que la arquitectura que se maneja es insuficiente para resolver los problemas de clasificación. Hemos visto que dada una arquitectura arbitraria, el descenso del gradiente suele obtener mejores resultados. Sin embargo, ¿existirá una arquitectura apropiada para la regla de Hebb con la que se puedan obtener los resultados que se observan con métodos basados en el gradiente? Este acercamiento que se dará será de corte principalmente teórico, pero se mostrará una implementación de las ideas abordadas. | En este artículo, trataremos de aproximarnos a las preguntas anteriormente planteadas. La aproximación que haremos será referente a la última posible respuesta que se planteó, indicando que la arquitectura que se maneja es insuficiente para resolver los problemas de clasificación. Hemos visto que dada una arquitectura arbitraria, el descenso del gradiente suele obtener mejores resultados. Sin embargo, ¿existirá una arquitectura apropiada para la regla de Hebb con la que se puedan obtener los resultados que se observan con métodos basados en el gradiente? Este acercamiento que se dará será de corte principalmente teórico, pero se mostrará una implementación de las ideas abordadas. | ||
| − | + | =2 Preliminares teóricos= | |
La descripción matemática de la Regla de Hebb estará principalmente basada en <span id='citeF-21'></span>[[#cite-21|[21]]], salvo donde se indique. Por simplicidad, partiremos del modelo de tasa de disparo para representar a la actividad de cada neurona individual. De manera alternativa, se pueden utilizar ''spikes'' (potenciales de acción) para modelar la actividad neuronal, como se realiza en <span id='citeF-19'></span>[[#cite-19|[19]]]. Sea <math display="inline">y \in D \subset \mathbb{R}^{+} </math> la actividad de una neurona (usualmente postsináptica) que recibe un vector de señales aferentes <math display="inline">\mathbf{x} = (x_1,\cdots ,x_m)</math>, las cuales pueden tener origen sensorial (datos de sensores o de bases) o de otras neuronas. El conjunto <math display="inline">D</math> puede ser discreto (<math display="inline">\{ 0,1\} </math>), un intervalo continuo (<math display="inline">[0,1]</math>), o bien el mismo conjunto de los números reales no negativos. La actividad (tasa de disparo) está modelada por la siguiente ecuación diferencial | La descripción matemática de la Regla de Hebb estará principalmente basada en <span id='citeF-21'></span>[[#cite-21|[21]]], salvo donde se indique. Por simplicidad, partiremos del modelo de tasa de disparo para representar a la actividad de cada neurona individual. De manera alternativa, se pueden utilizar ''spikes'' (potenciales de acción) para modelar la actividad neuronal, como se realiza en <span id='citeF-19'></span>[[#cite-19|[19]]]. Sea <math display="inline">y \in D \subset \mathbb{R}^{+} </math> la actividad de una neurona (usualmente postsináptica) que recibe un vector de señales aferentes <math display="inline">\mathbf{x} = (x_1,\cdots ,x_m)</math>, las cuales pueden tener origen sensorial (datos de sensores o de bases) o de otras neuronas. El conjunto <math display="inline">D</math> puede ser discreto (<math display="inline">\{ 0,1\} </math>), un intervalo continuo (<math display="inline">[0,1]</math>), o bien el mismo conjunto de los números reales no negativos. La actividad (tasa de disparo) está modelada por la siguiente ecuación diferencial | ||
| Line 48: | Line 38: | ||
| style="text-align: center;" | <math>\tau _y \frac{dy}{dt} = -y + a(\mathbf{w} \cdot \mathbf{x}), </math> | | style="text-align: center;" | <math>\tau _y \frac{dy}{dt} = -y + a(\mathbf{w} \cdot \mathbf{x}), </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| − | donde <math display="inline">\mathbf{w} = (w_1,\dots ,w_m)</math> representa el vector de pesos de las entradas, y la constante satisface <math display="inline">\tau _y \approx 0</math>. Para | + | donde <math display="inline">\mathbf{w} = (w_1,\dots ,w_m)</math> representa el vector de pesos de las entradas, y la constante satisface <math display="inline">\tau _y \approx 0</math>. Para linealizar la ecuación, se suele tomar <math display="inline">\tau _y = 0</math>, lo cual lo convierte en el modelo estándar de red neuronal artificial y de esta forma se trabajará en este artículo. <math display="inline">a: \mathbb{R} \rightarrow D</math> representa a la función de activación y en este caso se tomará por la función identidad cuando utilicemos <math display="inline">D = \mathbb{R}^{+}</math> o sigmoide si <math display="inline">D = [0,1]</math>. Para fines prácticos, en este artículo se tomará a la función de activación como la identidad. |
| − | + | ==2.1 Regla de Hebb Simple== | |
Un modelo sencillo de la Regla de Hebb ha sido llamado como Simple o Básico y tiene como objetivo encapsular a las propiedades esenciales de la conjetura hebbiana, resumidas por Shatz <span id='citeF-22'></span>[[#cite-22|[22]]] como ``''cells that fire together, wire together''''. La regla de Hebb Simple está dada por | Un modelo sencillo de la Regla de Hebb ha sido llamado como Simple o Básico y tiene como objetivo encapsular a las propiedades esenciales de la conjetura hebbiana, resumidas por Shatz <span id='citeF-22'></span>[[#cite-22|[22]]] como ``''cells that fire together, wire together''''. La regla de Hebb Simple está dada por | ||
| Line 64: | Line 54: | ||
| style="text-align: center;" | <math>\tau _w \frac{d\mathbf{w}}{dt} = \mathbf{x} y. </math> | | style="text-align: center;" | <math>\tau _w \frac{d\mathbf{w}}{dt} = \mathbf{x} y. </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 79: | Line 69: | ||
| style="text-align: center;" | <math>\mathbf{w}(t+1) = \mathbf{w}(t) + \alpha \mathbf{x}(t) y(t), </math> | | style="text-align: center;" | <math>\mathbf{w}(t+1) = \mathbf{w}(t) + \alpha \mathbf{x}(t) y(t), </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (1) |
|} | |} | ||
donde <math display="inline">\alpha >0</math> es la tasa de aprendizaje y <math display="inline">\mathbf{w}(0)</math> puede tomarse como <math display="inline"> \mathbf{0}</math>, aunque también puede recibir una inicialización aleatoria, la cual es una opción que evita la inactividad total que podría tener una interneurona si los pesos fueran todos inicializados en cero. | donde <math display="inline">\alpha >0</math> es la tasa de aprendizaje y <math display="inline">\mathbf{w}(0)</math> puede tomarse como <math display="inline"> \mathbf{0}</math>, aunque también puede recibir una inicialización aleatoria, la cual es una opción que evita la inactividad total que podría tener una interneurona si los pesos fueran todos inicializados en cero. | ||
| − | + | =3 Resultados teóricos= | |
En esta sección, probaremos algunos resultados sobre la regla de Hebb relacionados con la clasificación supervisada, la cual es un tema relevante puesto que en general dada una red arbitraria y de inicialización en ceros, una red de entrenamiento hebbiano no supera a una red neuronal con entrenamiento por descenso de gradiente como se muestra en <span id='citeF-14'></span>[[#cite-14|[14]]]. Esto quiere decir, que si definimos a nuestro ''dataset'' como <math display="inline">\{ (\mathbf{x}(i), y(i)) \} _{i=1}^{n}</math> (<math display="inline">y(i) \in \{ 0,\dots ,k \} </math>) y a <math display="inline">\hat{y}= NN_{\mathbf{w}}(\mathbf{x}) </math> como la salida de una red neuronal de una capa, el entrenamiento hebbiano no converge a algún mínimo de la función <math display="inline">L(\mathbf{w}) = \sum _{i=1}^{n} \mathbf{1}_{y(i)\neq NN_{\mathbf{w}}(\mathbf{x}(i))}</math>, como sí lo hacen los enfoques basados en el gradiente. No obstante, eso no significa que no exista una arquitectura competente capaz de efectuar adecuadamente el aprendizaje hebbiano. | En esta sección, probaremos algunos resultados sobre la regla de Hebb relacionados con la clasificación supervisada, la cual es un tema relevante puesto que en general dada una red arbitraria y de inicialización en ceros, una red de entrenamiento hebbiano no supera a una red neuronal con entrenamiento por descenso de gradiente como se muestra en <span id='citeF-14'></span>[[#cite-14|[14]]]. Esto quiere decir, que si definimos a nuestro ''dataset'' como <math display="inline">\{ (\mathbf{x}(i), y(i)) \} _{i=1}^{n}</math> (<math display="inline">y(i) \in \{ 0,\dots ,k \} </math>) y a <math display="inline">\hat{y}= NN_{\mathbf{w}}(\mathbf{x}) </math> como la salida de una red neuronal de una capa, el entrenamiento hebbiano no converge a algún mínimo de la función <math display="inline">L(\mathbf{w}) = \sum _{i=1}^{n} \mathbf{1}_{y(i)\neq NN_{\mathbf{w}}(\mathbf{x}(i))}</math>, como sí lo hacen los enfoques basados en el gradiente. No obstante, eso no significa que no exista una arquitectura competente capaz de efectuar adecuadamente el aprendizaje hebbiano. | ||
| − | De esta forma, de la ecuación ([[#eq-3| | + | De esta forma, de la ecuación ([[#eq-3|1]]) observamos que, con la base de datos definida, |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 97: | Line 87: | ||
| style="text-align: center;" | <math>\mathbf{w}_{j}(n) = \sum _{i=1}^{n} \mathbf{x}(n) y_{j}(n). </math> | | style="text-align: center;" | <math>\mathbf{w}_{j}(n) = \sum _{i=1}^{n} \mathbf{x}(n) y_{j}(n). </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 109: | Line 99: | ||
| style="text-align: center;" | <math>NN_{\mathbf{w}}(\mathbf{x}) = \arg \max _{ j \in \{ 1,\dots ,k\} } y_j </math> | | style="text-align: center;" | <math>NN_{\mathbf{w}}(\mathbf{x}) = \arg \max _{ j \in \{ 1,\dots ,k\} } y_j </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| − | + | ==3.1 Red hebbiana infinita== | |
| − | Comenzaremos nuestra descripción con una red hebbiana construida de la siguiente forma: a cada valor del espacio vectorial <math display="inline">\mathbf{z} \in D^m \subset \mathbb{R}^m</math>, le daremos una representación geométrica de la siguiente forma: consideremos una nueva capa de neuronas <math display="inline">r_{\mathbf{ | + | Comenzaremos nuestra descripción con una red hebbiana construida de la siguiente forma: a cada valor del espacio vectorial <math display="inline">\mathbf{z} \in D^m \subset \mathbb{R}^m</math>, le daremos una representación geométrica de la siguiente forma: consideremos una nueva capa de neuronas <math display="inline">r_{\mathbf{z}}</math> dada por |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 121: | Line 111: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>r_{\mathbf{z}}(\mathbf{x}) = \begin{cases}1 & |\mathbf{z}-\mathbf{x}| = 0 \\ 0 & |\mathbf{z}-\mathbf{x}| \neq 0 \end{cases} </math> | + | | style="text-align: center;" | <math>r_{\mathbf{z}}(\mathbf{x}) = \begin{cases}1, & |\mathbf{z}-\mathbf{x}| = 0 \\ 0, & |\mathbf{z}-\mathbf{x}| \neq 0 \end{cases} </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 137: | Line 127: | ||
| style="text-align: center;" | <math>y_j = \sum _{\mathbf{z}} w_{j,r_{\mathbf{z}}} r_{\mathbf{z}}(\mathbf{x}). </math> | | style="text-align: center;" | <math>y_j = \sum _{\mathbf{z}} w_{j,r_{\mathbf{z}}} r_{\mathbf{z}}(\mathbf{x}). </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
Primeramente, demostraremos la existencia de un minimizador global para posteriormente probar que la regla de Hebb induce a uno. | Primeramente, demostraremos la existencia de un minimizador global para posteriormente probar que la regla de Hebb induce a uno. | ||
| − | Proposición 1: Sea <math display="inline">g: D^m \rightarrow \{ 0,\dots ,k\} </math> definida para cada valor <math display="inline">\mathbf{a} = (a_1,\dots ,a_m)</math> como | + | '''Proposición 1''': Sea <math display="inline">g: D^m \rightarrow \{ 0,\dots ,k\} </math> definida para cada valor <math display="inline">\mathbf{a} = (a_1,\dots ,a_m)</math> como |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 149: | Line 139: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>g(\mathbf{a}) = \arg \max _{ j \in \{ 1,\dots ,k\} } \sum _{i=1}^{ | + | | style="text-align: center;" | <math>g(\mathbf{a}) = \arg \max _{ j \in \{ 1,\dots ,k\} } \sum _{i=1}^{n} v(x_{1}(n) = a_1, \dots , x_{m}(i) = a_m, y_j (n) = 1), </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 163: | Line 153: | ||
| style="text-align: center;" | <math>g = \arg \min _{f \in \mathcal{F}} \sum _{i=1}^{n} \mathbf{1}_{y(i) \neq f(\mathbf{x}(i))} </math> | | style="text-align: center;" | <math>g = \arg \min _{f \in \mathcal{F}} \sum _{i=1}^{n} \mathbf{1}_{y(i) \neq f(\mathbf{x}(i))} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 177: | Line 167: | ||
|} | |} | ||
| − | Hagamos <math display="inline">g^{\star }(\mathbf{x}) = g^{*}(\mathbf{x}) </math> para <math display="inline">\mathbf{x} \neq \mathbf{a}</math> y para <math display="inline">\mathbf{x} = \mathbf{a}</math>, tomemos <math display="inline">g^{\star }(\mathbf{a}) = \sum v(x_{1}(i) = a_1,\dots , x_{m}(i)=a_m, y_{j} = 1)</math>. Entonces la función cuenta con menor error que <math display="inline">g^{*}</math>, lo cual contradice su minimalidad. | + | Hagamos <math display="inline">g^{\star \star }(\mathbf{x}) = g^{*}(\mathbf{x}) </math> para <math display="inline">\mathbf{x} \neq \mathbf{a}</math> y para <math display="inline">\mathbf{x} = \mathbf{a}</math>, tomemos <math display="inline">g^{\star \star }(\mathbf{a}) = \sum v(x_{1}(i) = a_1,\dots , x_{m}(i)=a_m, y_{j} = 1)</math>. Entonces la función cuenta con menor error que <math display="inline">g^{*}</math>, lo cual contradice su minimalidad. <math display="inline"> \square </math> |
Finalmente probaremos que la red hebbiana infinita <math display="inline">H:D^m \rightarrow \{ 0,\dots ,k\} </math> es un minimizador global para la función de costo previamente definida: | Finalmente probaremos que la red hebbiana infinita <math display="inline">H:D^m \rightarrow \{ 0,\dots ,k\} </math> es un minimizador global para la función de costo previamente definida: | ||
| − | Teorema 1: Sea <math display="inline">H:D^m \rightarrow \{ 0,\dots ,k\} </math> una red hebbiana infinita con <math display="inline">D = \{ 0,1\} </math>. Entonces | + | '''Teorema 1''': Sea <math display="inline">H:D^m \rightarrow \{ 0,\dots ,k\} </math> una red hebbiana infinita con <math display="inline">D = \{ 0,1\} </math>. Entonces |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 190: | Line 180: | ||
| style="text-align: center;" | <math>H = \arg \min _{f \in \mathcal{F}} \sum _{i=1}^{n} \mathbf{1}_{y(i) \neq f(\mathbf{x}(i))} </math> | | style="text-align: center;" | <math>H = \arg \min _{f \in \mathcal{F}} \sum _{i=1}^{n} \mathbf{1}_{y(i) \neq f(\mathbf{x}(i))} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 221: | Line 211: | ||
|} | |} | ||
| − | siguiéndose el resultado por la Proposición 1. | + | siguiéndose el resultado por la Proposición 1. <math display="inline"> \square </math> |
A pesar de que la prueba de los anteriores resultados es relativamente directa, las consecuencias son importantes en el contexto de la regla de Hebb simple. A ''grosso modo'', establece que si disponemos de recursos ilimitados, es posible diseñar una red neuronal de aprendizaje hebbiano que minimice global la suma de los errores totales que se cometen. La idea básica resultó ser en crear una capa de representación con todos los valores posibles de entrada y la regla de Hebb cuenta cuántos elementos de la base de datos arrojan dichos valores y realiza una actualización hebbiana cuando encuentra uno. | A pesar de que la prueba de los anteriores resultados es relativamente directa, las consecuencias son importantes en el contexto de la regla de Hebb simple. A ''grosso modo'', establece que si disponemos de recursos ilimitados, es posible diseñar una red neuronal de aprendizaje hebbiano que minimice global la suma de los errores totales que se cometen. La idea básica resultó ser en crear una capa de representación con todos los valores posibles de entrada y la regla de Hebb cuenta cuántos elementos de la base de datos arrojan dichos valores y realiza una actualización hebbiana cuando encuentra uno. | ||
| Line 234: | Line 224: | ||
| style="text-align: center;" | <math>\mathcal{B} = \{ (0,0),(1,0),(2,0),\cdots ,(127,0),(128,1), \cdots ,(254,1),(255,1) \} . </math> | | style="text-align: center;" | <math>\mathcal{B} = \{ (0,0),(1,0),(2,0),\cdots ,(127,0),(128,1), \cdots ,(254,1),(255,1) \} . </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 248: | Line 238: | ||
<span style="text-align: center; font-size: 75%;">([[#fnc-1|<sup>1</sup>]]) También podemos distinguir los estados iluminado / poco iluminado para evitar pensar en el gris.</span> | <span style="text-align: center; font-size: 75%;">([[#fnc-1|<sup>1</sup>]]) También podemos distinguir los estados iluminado / poco iluminado para evitar pensar en el gris.</span> | ||
| − | + | ==3.2 <span id='lb-3.2'></span>m-celdas== | |
| − | Una posible forma en | + | Una posible forma en que se pueden tratar de minimizar los efectos de la red hebbiana infinita en términos prácticos (los seres infinitos pueden ejecutarla sin problemas) consiste en crear dividir a los datos de la capa de representación en <math display="inline">m</math>-celdas (mejor conocidas en la literatura como <math display="inline">k</math>-celdas, pero en esta caso <math display="inline">k = m</math>), que es el enfoque que se trató en el artículo de <span id='citeF-14'></span>[[#cite-14|[14]]], logrando resultados experimentales comparables con otros métodos de clasificación estándares o incluso mejores para datos sintéticos. En esta sección, intentaremos brindar un mejor sustento matemático sobre por qué el método funciona y finalmente lo aplicaremos en datos no sintéticos. |
En general la idea de las <math display="inline">m</math>-celdas se reduce a dividir al espacio <math display="inline">\mathbb{R}^m</math> primero en un espacio compacto donde se asume que viven los datos y después se subdividen en <math display="inline">m</math>-celdas de radio <math display="inline">\delta </math>. Cada celda se puede entender como una neurona que recibe datos y se activa si los datos de entrada pertenecen a la <math display="inline">m</math>-celda. Estas celdas forman la capa de representación que se describió en la red hebbiana infinita. Posteriormente, estas celdas se conectan con las neuronas de salida y en la conexión de las celdas con las neuronas de salida se aplica aprendizaje hebbiano. | En general la idea de las <math display="inline">m</math>-celdas se reduce a dividir al espacio <math display="inline">\mathbb{R}^m</math> primero en un espacio compacto donde se asume que viven los datos y después se subdividen en <math display="inline">m</math>-celdas de radio <math display="inline">\delta </math>. Cada celda se puede entender como una neurona que recibe datos y se activa si los datos de entrada pertenecen a la <math display="inline">m</math>-celda. Estas celdas forman la capa de representación que se describió en la red hebbiana infinita. Posteriormente, estas celdas se conectan con las neuronas de salida y en la conexión de las celdas con las neuronas de salida se aplica aprendizaje hebbiano. | ||
| Line 256: | Line 246: | ||
La siguiente proposición establece que es posible aproximarnos a la medida de Lebesgue <math display="inline">\mu </math> de un conjunto abierto y acotado utilizando un número finito de <math display="inline">m</math>-celdas. La notación que se usará para las celdas es <math display="inline">I_i (\delta )</math> si tiene el índice <math display="inline">i</math> y radio <math display="inline">\delta </math>, o bien <math display="inline">I_{\mathbf{x}} (\delta ) = \prod _{i=1}^{m} (x_i - \delta ,x_i + \delta ) </math>. | La siguiente proposición establece que es posible aproximarnos a la medida de Lebesgue <math display="inline">\mu </math> de un conjunto abierto y acotado utilizando un número finito de <math display="inline">m</math>-celdas. La notación que se usará para las celdas es <math display="inline">I_i (\delta )</math> si tiene el índice <math display="inline">i</math> y radio <math display="inline">\delta </math>, o bien <math display="inline">I_{\mathbf{x}} (\delta ) = \prod _{i=1}^{m} (x_i - \delta ,x_i + \delta ) </math>. | ||
| − | Proposición 2: Sea <math display="inline">U \subset \mathbb{R}^m </math> un conjunto abierto y acotado, y <math display="inline">\varepsilon > 0</math>. Entonces existe <math display="inline">\delta{>0}</math> tal que existen <math display="inline">d</math> <math display="inline">m</math>-celdas de radio <math display="inline">\delta </math> tales que | + | '''Proposición 2''': Sea <math display="inline">U \subset \mathbb{R}^m </math> un conjunto abierto y acotado, y <math display="inline">\varepsilon > 0</math>. Entonces existe <math display="inline">\delta{>0}</math> tal que existen <math display="inline">d</math> <math display="inline">m</math>-celdas de radio <math display="inline">\delta </math> tales que |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 265: | Line 255: | ||
| style="text-align: center;" | <math>\Big|\mu (U) - \mu \big(\bigcup _{i=1}^{d} I_{i}(\delta ) \big)\Big|< \varepsilon{.} </math> | | style="text-align: center;" | <math>\Big|\mu (U) - \mu \big(\bigcup _{i=1}^{d} I_{i}(\delta ) \big)\Big|< \varepsilon{.} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 277: | Line 267: | ||
| style="text-align: center;" | <math>A = \{ \mathbf{x} \in U : x_i \in \mathbb{Q}, i = 1,\dots , m \} </math> | | style="text-align: center;" | <math>A = \{ \mathbf{x} \in U : x_i \in \mathbb{Q}, i = 1,\dots , m \} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 289: | Line 279: | ||
| style="text-align: center;" | <math>U = \bigcup _{i=1}^{\infty } I_{i}(\delta _i). </math> | | style="text-align: center;" | <math>U = \bigcup _{i=1}^{\infty } I_{i}(\delta _i). </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 316: | Line 306: | ||
| style="text-align: center;" | <math>\Big|\mu (U) - \mu \big(\bigcup _{i=1}^{c} I_{i}(\delta _i) \big)\Big|< \frac{\varepsilon }{2}. </math> | | style="text-align: center;" | <math>\Big|\mu (U) - \mu \big(\bigcup _{i=1}^{c} I_{i}(\delta _i) \big)\Big|< \frac{\varepsilon }{2}. </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 328: | Line 318: | ||
| style="text-align: center;" | <math>\hat{\delta _{j}} = a_j \prod _{i\neq j} b_{i} \delta , </math> | | style="text-align: center;" | <math>\hat{\delta _{j}} = a_j \prod _{i\neq j} b_{i} \delta , </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 340: | Line 330: | ||
| style="text-align: center;" | <math>I_{i}( \hat{\delta _{j}}) = \bigcup _{i=1}^{d_{j}^{m}} I_{\mathbf{x}_i} (\delta{).} </math> | | style="text-align: center;" | <math>I_{i}( \hat{\delta _{j}}) = \bigcup _{i=1}^{d_{j}^{m}} I_{\mathbf{x}_i} (\delta{).} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 352: | Line 342: | ||
| style="text-align: center;" | <math>\Big|\mu ( I_{i}(\delta _j) ) - \mu \big(\bigcup _{i=1}^{d_{j}^{m}} I_{\mathbf{x}_i} (\delta ) \big)\Big|< \frac{\varepsilon }{2c} </math> | | style="text-align: center;" | <math>\Big|\mu ( I_{i}(\delta _j) ) - \mu \big(\bigcup _{i=1}^{d_{j}^{m}} I_{\mathbf{x}_i} (\delta ) \big)\Big|< \frac{\varepsilon }{2c} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| Line 364: | Line 354: | ||
| style="text-align: center;" | <math>\Big|\mu (U) - \mu \big(\bigcup _{i=1}^{d} I_{i}(\delta ) \big)\Big|< \varepsilon{.} </math> | | style="text-align: center;" | <math>\Big|\mu (U) - \mu \big(\bigcup _{i=1}^{d} I_{i}(\delta ) \big)\Big|< \varepsilon{.} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| + | |||
| + | <math display="inline"> \square </math> | ||
De manera similar al último argumento, podemos fragmentar por completo al espacio <math display="inline">\mathbb{R}^m</math> de tal forma que se aproxime tanto como se puedan a las <math display="inline">m</math>-celdas encontradas en la prueba anterior. De este modo, al reducir <math display="inline">\delta </math> hemos de encontrar una clasificación más fina que permita obtener resultados más precisos. | De manera similar al último argumento, podemos fragmentar por completo al espacio <math display="inline">\mathbb{R}^m</math> de tal forma que se aproxime tanto como se puedan a las <math display="inline">m</math>-celdas encontradas en la prueba anterior. De este modo, al reducir <math display="inline">\delta </math> hemos de encontrar una clasificación más fina que permita obtener resultados más precisos. | ||
| Line 380: | Line 372: | ||
| style="text-align: center;" | <math>L(\mathbf{w}) = | \mu (U) - \mu (V_{\mathbf{w}}) | </math> | | style="text-align: center;" | <math>L(\mathbf{w}) = | \mu (U) - \mu (V_{\mathbf{w}}) | </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
donde <math display="inline">U</math> es el conjunto abierto donde cada <math display="inline">\mathbf{x} \in U</math> si y sólo si pertenece a la clase <math display="inline">j</math> y <math display="inline">V_{\mathbf{w}}</math> es el conjunto tal que para toda <math display="inline">\mathbf{x} \in V_{\mathbf{w}}</math>, <math display="inline">NN_{\mathbf{w}}(\mathbf{x}) = j</math>. Este error se puede reducir tanto como se desee: | donde <math display="inline">U</math> es el conjunto abierto donde cada <math display="inline">\mathbf{x} \in U</math> si y sólo si pertenece a la clase <math display="inline">j</math> y <math display="inline">V_{\mathbf{w}}</math> es el conjunto tal que para toda <math display="inline">\mathbf{x} \in V_{\mathbf{w}}</math>, <math display="inline">NN_{\mathbf{w}}(\mathbf{x}) = j</math>. Este error se puede reducir tanto como se desee: | ||
| − | Teorema 2: Supongamos que el problema de clasificación se puede separar en conjuntos abiertos y acotados. Para cada <math display="inline">\varepsilon > 0</math>, existe una división del espacio <math display="inline">E^m</math> en <math display="inline">m</math>-celdas de tamaño <math display="inline">\delta </math> tales que <math display="inline">L(\mathbf{w}) < \varepsilon </math>. | + | '''Teorema 2''': Supongamos que el problema de clasificación se puede separar en conjuntos abiertos y acotados. Para cada <math display="inline">\varepsilon > 0</math>, existe una división del espacio <math display="inline">E^m</math> en <math display="inline">m</math>-celdas de tamaño <math display="inline">\delta </math> tales que <math display="inline">L(\mathbf{w}) < \varepsilon </math>. |
Usando la Proposición 1, es posible hallar una partición del espacio en <math display="inline">k</math>-celdas de tamaño <math display="inline">\delta </math> tal que | Usando la Proposición 1, es posible hallar una partición del espacio en <math display="inline">k</math>-celdas de tamaño <math display="inline">\delta </math> tal que | ||
| Line 396: | Line 388: | ||
| style="text-align: center;" | <math>\Big|\mu (U) - \mu \Big(\bigcup _{i=1}^{d} I_{i}(\delta ) \Big)\Big|< \frac{\varepsilon }{k}. </math> | | style="text-align: center;" | <math>\Big|\mu (U) - \mu \Big(\bigcup _{i=1}^{d} I_{i}(\delta ) \Big)\Big|< \frac{\varepsilon }{k}. </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | | + | | style="width: 5px;text-align: right;white-space: nowrap;" | |
|} | |} | ||
| − | Como cada <math display="inline">I_{i}(\delta ) \subset U</math>, para cada <math display="inline">\mathbf{x} \in I_{i}(\delta )</math>, <math display="inline">NN_{\mathbf{w}}(\mathbf{x}) = j</math>, por lo que <math display="inline">L(\mathbf{w}) < \frac{\varepsilon }{k}</math>. Tomando las <math display="inline">k</math> clases, tenemos que <math display="inline">L(\mathbf{w}) < \varepsilon </math>. (En principio cada <math display="inline">\delta </math> de cada partición puede ser diferente, pero podemos seleccionar uno usando una técnica similar a la que aparece en la prueba de la Proposición 2). | + | Como cada <math display="inline">I_{i}(\delta ) \subset U</math>, para cada <math display="inline">\mathbf{x} \in I_{i}(\delta )</math>, <math display="inline">NN_{\mathbf{w}}(\mathbf{x}) = j</math>, por lo que <math display="inline">L(\mathbf{w}) < \frac{\varepsilon }{k}</math>. Tomando las <math display="inline">k</math> clases, tenemos que <math display="inline">L(\mathbf{w}) < \varepsilon </math>. (En principio cada <math display="inline">\delta </math> de cada partición puede ser diferente, pero podemos seleccionar uno usando una técnica similar a la que aparece en la prueba de la Proposición 2). <math display="inline"> \square </math> |
En la práctica, la bondad de este resultado (poder minimizar al costo tanto como se quiera) está afectado por varios factores. Primeramente, la superposición de los datos supone un problema, como ya se ha mencionado previamente. Además, cuando tomamos celdas con menor <math display="inline">\delta </math> si bien aumentamos la precisión el conjunto de clasificación, se produce un sobreajuste al aparecer celdas sin asignación que pueden aparecer en el conjunto de entrenamiento. Sin embargo, nuevamente este problema puede resolverse con una mayor cantidad de datos. El otro problema recae en la definición de <math display="inline">m</math>-celdas para dimensiones grandes de <math display="inline">m</math>, requiere de definir una cantidad creciente de celdas. Estos dos problemas son análogos a los dos problemas de la red hebbiana infinita, pero al menos aparecen atenuados y en bajas dimensiones son perfectamente implementables, como se verá a continuación. | En la práctica, la bondad de este resultado (poder minimizar al costo tanto como se quiera) está afectado por varios factores. Primeramente, la superposición de los datos supone un problema, como ya se ha mencionado previamente. Además, cuando tomamos celdas con menor <math display="inline">\delta </math> si bien aumentamos la precisión el conjunto de clasificación, se produce un sobreajuste al aparecer celdas sin asignación que pueden aparecer en el conjunto de entrenamiento. Sin embargo, nuevamente este problema puede resolverse con una mayor cantidad de datos. El otro problema recae en la definición de <math display="inline">m</math>-celdas para dimensiones grandes de <math display="inline">m</math>, requiere de definir una cantidad creciente de celdas. Estos dos problemas son análogos a los dos problemas de la red hebbiana infinita, pero al menos aparecen atenuados y en bajas dimensiones son perfectamente implementables, como se verá a continuación. | ||
| − | + | =4 Resultados experimentales= | |
| − | En <span id='citeF-14'></span>[[#cite-14|[14]]] se implementó el algoritmo de <math display="inline">m</math>-celdas para datos sintéticos y se comparó con métodos estándares como la regresión logística y kNN. En esta ocasión, probaremos su desempeño frente a redes neuronales con métodos basados en el gradiente y utilizando un ''dataset'' no sintético, el cual es la base de datos Iris para la clasificación de flores del género ''Iris'' a partir de datos biométricos <span id='citeF-23'></span>[[#cite-23|[23]]]. En este caso, para entrenamiento se utilizarán únicamente dos dimensiones en cierta medida separables: longitud y ancho de pétalo (véase figura [[#img-1|1]]). | + | En <span id='citeF-14'></span>[[#cite-14|[14]]] se implementó el algoritmo de <math display="inline">m</math>-celdas para datos sintéticos y se comparó con métodos estándares como la regresión logística y kNN. En esta ocasión, probaremos su desempeño frente a redes neuronales con métodos basados en el gradiente y utilizando un ''dataset'' no sintético, el cual es la base de datos Iris para la clasificación de flores del género ''Iris'' a partir de datos biométricos <span id='citeF-23'></span>[[#cite-23|[23]]]. En este caso, para entrenamiento de las m-celdas se utilizarán únicamente dos dimensiones en cierta medida separables: longitud y ancho de pétalo (véase figura [[#img-1|1]]), longitud de sépalo y ancho de pétalo (figura [[#img-2|2]]), y finalmente longitud de sépalo y longitud de pétalo (figura [[#img-3|3]]). |
<div id='img-1'></div> | <div id='img-1'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[Image:Draft_Aguilar Canto_823313646-iris2.png|216px|Gráfico de | + | |[[Image:Draft_Aguilar Canto_823313646-iris2.png|216px|Gráfico de las variables longitud y ancho de pétalo del dataset Iris.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 1:''' Gráfico de | + | | colspan="1" | '''Figura 1:''' Gráfico de las variables longitud y ancho de pétalo del dataset Iris. |
|} | |} | ||
| − | + | <div id='img-2'></div> | |
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Review_687888297298_5827_Unknown-28.png|216px|Gráfico de las variables longitud de sépalo y ancho de pétalo del dataset Iris.]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" | '''Figura 2:''' Gráfico de las variables longitud de sépalo y ancho de pétalo del dataset Iris. | ||
| + | |} | ||
| − | === | + | <div id='img-3'></div> |
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Review_687888297298_4841_Unknown-29.png|216px|Gráfico de dos variables del dataset Iris.]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" | '''Figura 3:''' Gráfico de las variables longitud de sépalo y longitud de pétalo del dataset Iris. | ||
| + | |} | ||
| − | |||
| − | + | Como se puede ver, las tres clases del ''dataset'' son en gran medida separables, aunque existe cierto traslape entre las clases ''I. versicolor'' e ''I. virginica''. Se tiene un total de 150 datos, de los cuales 75 se utilizaron para entrenamiento, 30 para validación y 45 para prueba. | |
| − | + | ==4.1 Descenso de Gradiente== | |
| + | |||
| + | Para contrastar al descenso de gradiente con el aprendizaje hebbiano, se utilizó un esquema de redes neuronales de alimentación hacia adelante (''Feedforward Neural Networks'' o FNNs). El entrenamiento se realizó con la función de costo de entropía cruzada categórica a 15 épocas y se utilizó al optimizador Adam <span id='citeF-24'></span>[[#cite-24|[24]]], uno de los métodos basados en el gradiente más recientes y ampliamente utilizados en la actualidad para redes neuronales. Para este caso, se utilizaron las cuatro dimensiones de los datos. Por ende, se tomarán 4 unidades de entrada y 3 de salida, correspondiente a cada clase. | ||
| + | |||
| + | Ese enfoque se estudió de dos maneras: por medio de redes neuronales con arquitectura fija y mediante una optimización hiperparamétrica. Las arquitecturas fijas fueron <math display="inline">(50)</math>, <math display="inline">(50, 50)</math> y <math display="inline">(50, 50, 50)</math>, donde cada vector representa el número de neuronas en cada capa intermedia (oculta): es decir la primera arquitectura (Modelo 1) cuenta con 50 neuronas en una capa intermedia, la segunda 50 en la primera capa oculta y 50 en la segunda (Modelo 2), mientras que el Modelo 3 cuenta con 50 neuronas en tres capas intermedias. | ||
| + | |||
| + | El modelo 1 tardó 1.586 s y alcanzó una exactitud sobre el conjunto de prueba de 0.967, 0.853 en el conjunto de entrenamiento y 0.822 en el conjunto de validación. Por su parte, el modelo 2 logró la misma exactitud sobre el conjunto de prueba, 0.987 en el conjunto de prueba y 0.911 en el conjunto de validación durando 1.489 segundos, mientras que el modelo 3 obtuvo 0.933 en el conjunto de prueba, 0.973 en el conjunto de entrenamiento y 0.866 en la validación, durando 1.733 s. La figura [[#img-4|4]] representa las curvas de aprendizaje de los tres modelos. | ||
<div id='img-2'></div> | <div id='img-2'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
|- | |- | ||
| − | |[[ | + | |[[File:Review_687888297298_8820_Unknown-27.png|216px|Evolución de la exactitud de los tres modelos base en 15 épocas]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura | + | | colspan="1" | '''Figura 4:''' Evolución de la exactitud de los tres modelos base en 15 épocas. |
|} | |} | ||
| − | |||
| − | + | Para realizar una exploración sobre el espacio de las FNNs (optimización hiperparamétrica), se utilizó la heurística de evolución descrita en <span id='citeF-25'></span>[[#cite-25|[25]]], utilizando la variante A con constantes <math display="inline">\mu = 9</math>, <math display="inline">M = 4</math>, <math display="inline">T = 3</math> y <math display="inline">k = 10</math>, así como quince generaciones. | |
| + | |||
| + | La optimización hiperparamétrica arrojó como arquitectura con máxima validación a <math display="inline">(50, 10, 10, 10)</math>, la cual logró 0.967 de exactitud en el conjunto de prueba, 0.853 en el conjunto de entrenamiento y 0.889 en el conjunto de validación. El esquema de evolución queda patente en la figura [[#img-5|5]]. En la figura [[#img-6|6]] podemos apreciar la evolución del número de redes neuronales por cada generación que participa en el proceso de evolución. | ||
| + | |||
| + | |||
| + | |||
| + | <div id='img-5'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Review_687888297298_2693_Unknown-33.png|216px|Evolución de la exactitud con 15 generaciones.]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" | '''Figura 5:''' Evolución de la exactitud con 15 generaciones. | ||
| + | |} | ||
| + | |||
| + | |||
| + | |||
| + | <div id='img-6'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Review_687888297298_7009_Unknown-32.png|216px|Número de individuos por generación.]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" | '''Figura 6:''' Número de individuos por generación. Se incluyen generaciones donde se da un decremento. | ||
| + | |} | ||
| + | |||
| + | ==4.2 <span id='lb-4.2'></span>Algoritmo de m-celdas== | ||
| + | En el caso de las <math display="inline">m</math>-celdas, se tomaron celdas de tamaño <math display="inline">\frac{1}{s}</math> y únicamente se tomaron dos dimensiones por simplicidad. Los resultados principales se resumen en la tablas [[#table-1|1]], [[#table-2|2]], [[#table-3|3]] y se obtuvieron al variar <math display="inline">s</math>. Los mejores resultados se obtuvieron al utilizar las variables de los pétalos (longitud y ancho), donde si seleccionamos la máxima exactitud sobre el conjunto de validación, obtenemos 0.967 de exactitud sobre el conjunto de prueba, aunque para <math display="inline">s = 3</math> se obtiene una clasificación perfecta. Los tiempos de ejecución fueron considerablemente más bajos: 0.00072 para la primera combinación de variables, 0.00055 para la segunda y 0.001 para la tercera. Las otras combinaciones de variables en general no resultaron lo suficientemente apropiadas, pero el uso del conjunto de validación nos puede ayudar a seleccionar el par de variables más significativo, aunque una opción más apropiada sería considerar a todas las varibles. | ||
{| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;" | {| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;" | ||
| − | |+ style="font-size: 75%;" |<span id='table-1'></span>Tabla. 1 Resultados de clasificación utilizando el algoritmo de <math>m</math>-celdas con aprendizaje hebbiano y diferentes valores de <math>s</math>. | + | |+ style="font-size: 75%;" |<span id='table-1'></span>Tabla. 1 Resultados de clasificación utilizando el algoritmo de <math>m</math>-celdas con aprendizaje hebbiano y diferentes valores de <math>s</math> con las variables longitud y ancho de pétalo. |
|- style="border-top: 2px solid;" | |- style="border-top: 2px solid;" | ||
| style="border-right: 2px solid;" | <math display="inline">s</math> | | style="border-right: 2px solid;" | <math display="inline">s</math> | ||
| style="border-left: 2px solid;" | Entrenamiento | | style="border-left: 2px solid;" | Entrenamiento | ||
| − | | Prueba | + | | style="border-left: 2px solid;" | Validación |
| + | | style="border-left: 2px solid;" | Prueba | ||
|- style="border-top: 2px solid;" | |- style="border-top: 2px solid;" | ||
| style="border-right: 2px solid;" | <math display="inline">1</math> | | style="border-right: 2px solid;" | <math display="inline">1</math> | ||
| style="border-left: 2px solid;" | <math>0.893</math> | | style="border-left: 2px solid;" | <math>0.893</math> | ||
| − | | <math>0. | + | | style="border-left: 2px solid;"| <math>0.933</math> |
| + | | style="border-left: 2px solid;"| <math>0.9</math> | ||
|- | |- | ||
| style="border-right: 2px solid;" | <math>2</math> | | style="border-right: 2px solid;" | <math>2</math> | ||
| style="border-left: 2px solid;" | <math>0.947</math> | | style="border-left: 2px solid;" | <math>0.947</math> | ||
| − | | <math>0. | + | | style="border-left: 2px solid;"| <math>0.956</math> |
| + | | style="border-left: 2px solid;"|<math>0.967</math> | ||
|- | |- | ||
| style="border-right: 2px solid;" | <math>3</math> | | style="border-right: 2px solid;" | <math>3</math> | ||
| − | | style="border-left: 2px solid;" | <math> | + | | style="border-left: 2px solid;" | <math>0.973</math> |
| − | | <math>0. | + | | style="border-left: 2px solid;"| <math>0.933</math> |
| + | | style="border-left: 2px solid;"| <math>1</math> | ||
|- | |- | ||
| style="border-right: 2px solid;" | <math>4</math> | | style="border-right: 2px solid;" | <math>4</math> | ||
| style="border-left: 2px solid;" | <math>0.987</math> | | style="border-left: 2px solid;" | <math>0.987</math> | ||
| − | | <math>0. | + | | style="border-left: 2px solid;"| <math>0.933</math> |
| + | | style="border-left: 2px solid;"| <math>0.966</math> | ||
|- | |- | ||
| style="border-right: 2px solid;" | <math>5</math> | | style="border-right: 2px solid;" | <math>5</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.973</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.8</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.933</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>6</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.986</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.911</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.867</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>7</math> | ||
| style="border-left: 2px solid;" | <math>0.987</math> | | style="border-left: 2px solid;" | <math>0.987</math> | ||
| − | | <math>0.973</math> | + | | style="border-left: 2px solid;" | <math>0.867</math> |
| + | | style="border-left: 2px solid;" | <math>0.867</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>8</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.987</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.8</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.633</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>9</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.987</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.756</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.756</math> | ||
| + | |- style="border-bottom: 2px solid;" | ||
| + | | style="border-right: 2px solid;" | <math>10</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.987</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.756</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.6</math> | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | {| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;" | ||
| + | |+ style="font-size: 75%;" |<span id='table-2'></span>Tabla. 2 Resultados de clasificación utilizando el algoritmo de <math>m</math>-celdas con aprendizaje hebbiano y diferentes valores de <math>s</math> con las variables longitud de sépalo y ancho de pétalo. | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-right: 2px solid;" | <math display="inline">s</math> | ||
| + | | style="border-left: 2px solid;" | Entrenamiento | ||
| + | | style="border-left: 2px solid;" | Validación | ||
| + | | style="border-left: 2px solid;" | Prueba | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-right: 2px solid;" | <math display="inline">1</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.84</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.867</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.833</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>2</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.947</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.867</math> | ||
| + | | style="border-left: 2px solid;"|<math>0.933</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>3</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.973</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.867</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.9</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>4</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.973</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.689</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.767</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>5</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.973</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.667</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.667</math> | ||
|- | |- | ||
| style="border-right: 2px solid;" | <math>6</math> | | style="border-right: 2px solid;" | <math>6</math> | ||
| − | | style="border-left: 2px solid;" | <math> | + | | style="border-left: 2px solid;" | <math>0.973</math> |
| − | | <math> | + | | style="border-left: 2px solid;"| <math>0.644</math> |
| + | | style="border-left: 2px solid;"| <math>0.7</math> | ||
|- | |- | ||
| style="border-right: 2px solid;" | <math>7</math> | | style="border-right: 2px solid;" | <math>7</math> | ||
| − | | style="border-left: 2px solid;" | <math> | + | | style="border-left: 2px solid;" | <math>0.973</math> |
| − | | <math>0. | + | | style="border-left: 2px solid;" | <math>0.667</math> |
| + | | style="border-left: 2px solid;" | <math>0.633</math> | ||
|- | |- | ||
| style="border-right: 2px solid;" | <math>8</math> | | style="border-right: 2px solid;" | <math>8</math> | ||
| − | | style="border-left: 2px solid;" | <math> | + | | style="border-left: 2px solid;" | <math>0.973</math> |
| − | | <math>0. | + | | style="border-left: 2px solid;" | <math>0.511</math> |
| + | | style="border-left: 2px solid;" | <math>0.533</math> | ||
|- | |- | ||
| style="border-right: 2px solid;" | <math>9</math> | | style="border-right: 2px solid;" | <math>9</math> | ||
| − | | style="border-left: 2px solid;" | <math> | + | | style="border-left: 2px solid;" | <math>0.973</math> |
| − | | <math> | + | | style="border-left: 2px solid;" | <math>0.511</math> |
| + | | style="border-left: 2px solid;" | <math>0.533</math> | ||
|- style="border-bottom: 2px solid;" | |- style="border-bottom: 2px solid;" | ||
| style="border-right: 2px solid;" | <math>10</math> | | style="border-right: 2px solid;" | <math>10</math> | ||
| − | | style="border-left: 2px solid;" | <math> | + | | style="border-left: 2px solid;" | <math>0.973</math> |
| − | | <math> | + | | style="border-left: 2px solid;" | <math>0.511</math> |
| + | | style="border-left: 2px solid;" | <math>0.533</math> | ||
|} | |} | ||
| − | + | {| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;" | |
| + | |+ style="font-size: 75%;" |<span id='table-3'></span>Tabla. 3 Resultados de clasificación utilizando el algoritmo de <math>m</math>-celdas con aprendizaje hebbiano y diferentes valores de <math>s</math> con las variables longitud de pétalo y longitud de sépalo. | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-right: 2px solid;" | <math display="inline">s</math> | ||
| + | | style="border-left: 2px solid;" | Entrenamiento | ||
| + | | style="border-left: 2px solid;" | Validación | ||
| + | | style="border-left: 2px solid;" | Prueba | ||
| + | |- style="border-top: 2px solid;" | ||
| + | | style="border-right: 2px solid;" | <math display="inline">1</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.813</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.822</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.9</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>2</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.88</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.867</math> | ||
| + | | style="border-left: 2px solid;"|<math>1</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>3</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.96</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.911</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.767</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>4</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.96</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.933</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.966</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>5</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.96</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.556</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.667</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>6</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.986</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.644</math> | ||
| + | | style="border-left: 2px solid;"| <math>0.633</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>7</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.987</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.733</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.667</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>8</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.987</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.511</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.567</math> | ||
| + | |- | ||
| + | | style="border-right: 2px solid;" | <math>9</math> | ||
| + | | style="border-left: 2px solid;" | <math>1.0</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.422</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.533</math> | ||
| + | |- style="border-bottom: 2px solid;" | ||
| + | | style="border-right: 2px solid;" | <math>10</math> | ||
| + | | style="border-left: 2px solid;" | <math>1.0</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.4</math> | ||
| + | | style="border-left: 2px solid;" | <math>0.533</math> | ||
| + | |||
| + | |} | ||
| + | |||
| + | |||
| + | Por otro lado, en las tablas observamos cómo al reducir el tamaño de <math display="inline">\delta </math>, obtenemos mejores resultados de clasificación en el conjunto de entrenamiento, dando confirmación experimental del Teorema 2, pero al reducirse el tamaño de las vecindades también dejamos fuera a los datos que no son de entrenamiento, por lo que las exactitudes sobre los conjuntos de prueba y validación se reducen, tendiendo a <math display="inline">\frac{1}{3} </math>. La primera tabla también está representada en la figura [[#img-7|7]]. | ||
| + | |||
| + | |||
| + | |||
| + | <div id='img-7'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[File:Review_687888297298_8754_Captura de Pantalla 2021-12-20 a la(s) 23.54.29.png|216px|Gráfico de las exactitudes del algoritmo de m-celdas con las variables longitud y ancho de pétalo del dataset Iris.]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" | '''Figura 7:''' Gráfico de las exactitudes del algoritmo de m-celdas con las variables longitud y ancho de pétalo del dataset Iris. | ||
| + | |} | ||
| − | + | =5 Conclusiones= | |
Los resultados observados con las <math display="inline">m</math>-celdas dan sustento a la hipótesis de que la arquitectura tiene una influencia crucial en las redes neuronales con aprendizaje hebbiano, a pesar de que sea un método poco práctico de implementar para dimensiones mayores. En este caso se implementó para <math display="inline">m = 2</math>, siendo posible ya que se puede no utilizar toda la información de una base de datos, aunque no siempre parece posible lograr resultados de clasificación correctos utilizando pocas dimensiones o reduciéndolas. | Los resultados observados con las <math display="inline">m</math>-celdas dan sustento a la hipótesis de que la arquitectura tiene una influencia crucial en las redes neuronales con aprendizaje hebbiano, a pesar de que sea un método poco práctico de implementar para dimensiones mayores. En este caso se implementó para <math display="inline">m = 2</math>, siendo posible ya que se puede no utilizar toda la información de una base de datos, aunque no siempre parece posible lograr resultados de clasificación correctos utilizando pocas dimensiones o reduciéndolas. | ||
| − | En este caso, para la base de datos de iris, se pudieron observar | + | En este caso, para la base de datos de iris, se pudieron observar resultados similares pero significativamente más rápidos que los que arroja el optimizador Adam (una versión moderna del descenso del gradiente), incluso utilizando un esquema de evolución. Esto supone una primera victoria de los métodos basados en Hebb frente al enfoque predominante y es respaldado por los resultados teóricos. Dichos resultados empíricos también son comparables con otros algoritmos de clasificación modernos, como los aplicados en <span id='citeF-26'></span>[[#cite-26|[26]]]. |
No obstante, el optimismo debe tomarse con cautela. Para mayores dimensiones, parece complicada la ejecución del algoritmo de <math display="inline">m</math>-celdas y el refinamiento del radio <math display="inline">\delta </math> requiere de una mayor capacidad de cómputo. De esta forma, quizá sólo se pueda aspirar a celdas burdas para dimensiones medianas, pero parece imposible manejar <math display="inline">m = 20 \times 20</math>, que es el caso de las imágenes. | No obstante, el optimismo debe tomarse con cautela. Para mayores dimensiones, parece complicada la ejecución del algoritmo de <math display="inline">m</math>-celdas y el refinamiento del radio <math display="inline">\delta </math> requiere de una mayor capacidad de cómputo. De esta forma, quizá sólo se pueda aspirar a celdas burdas para dimensiones medianas, pero parece imposible manejar <math display="inline">m = 20 \times 20</math>, que es el caso de las imágenes. | ||
| Line 501: | Line 677: | ||
==Disponibilidad de código y datos== | ==Disponibilidad de código y datos== | ||
| − | El código principal se puede obtener de https://github.com/Pherjev/hebbian-m-cells/blob/master/HebbMNIST.ipynb. La base de datos se obtuvo directamente de la librería <code>sklearn</code>. | + | El código principal se puede obtener de https://github.com/Pherjev/hebbian-m-cells/blob/master/HebbMNIST-2.ipynb. La base de datos se obtuvo directamente de la librería <code>sklearn</code>. |
| − | + | ==BIBLIOGRAFÍA== | |
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
Latest revision as of 03:34, 5 January 2022
1 Introducción
La Regla de Hebb es un modelo teórico de plasticidad sináptica propuesto originalmente el trabajo de Donald Hebb [1], aunque, como observa [2], autores como Konorski [3] y Ramón y Cajal [4] ya habían concebido ideas semejantes. Unas décadas después, las ideas de Hebb recibieron confirmación experimental al observarse que su conjetura modelaba al fenómeno de Potenciación a Largo Plazo (Long-Term Potentiation, LTP), el cual fue descrita por primera vez en los trabajos de Terje Lmo y Timothy Bliss [5,6].
Computacionalmente, la regla de Hebb señala un método paramétrico de aprendizaje de redes neuronales que ha recibido cierto sustento biológico. Posterior al planteamiento original de la regla de Hebb simple se han propuesto otras reglas de aprendizaje más próximas a experimentos más recientes, como es el caso de la regla BCM [7] o la regla STDP (véase [8] para una formulación), o tratan de resolver problemas computacionales concretos como es el caso de la regla de Oja [9]. Sin embargo, a pesar de los avances, los algoritmos de redes neuronales (incluyendo las profundas) usualmente se entrenan utilizando métodos basados en el gradiente y retropropagación.
¿Qué ventajas proporciona disponer de un aprendizaje basado en el conocimiento disponible de la plasticidad frente a los métodos “artificiales”? ¿Por qué en la actualidad se han descartado a los métodos basados en la regla de Hebb frente a los métodos basados en el gradiente? Estas preguntas forman parte de la discusión general existente entre hasta qué punto se debe tratar de emular a los sistemas biológicos para crear inteligencia artificial, generalmente enmarcado en la discusión del conexionismo contra el enfoque simbólico de la Inteligencia Artificial (véase, por ejemplo [10] para una breve discusión de la situación actual del debate en un área concreto). En este caso, sin embargo, tenemos un caso donde dos enfoques conexionistas entran en debate sobre la forma en que deben aprender las neuronas, siendo en apariencia el modelo basado en el gradiente el de mayor éxito hasta ahora.
No es la primera vez que dos modelos conexionistas entran en conflicto sobre el nivel de plausibilidad biológica que se necesita para alcanzar los resultados. Por ejemplo, en cuestiones relacionadas con la arquitectura, los modelos de redes neuronales profundas han sido señalados por tener un alto grado de abstracción con respecto a las neuronas biológicas [11], siendo modelos como HMAX (véase [12]) preferidos por algunos autores por tener una construcción más relacionada con los experimentos en la Corteza Visual.
La discusión que se plantea en este artículo es diferente: dadas redes neuronales generales, ¿es preferible disponer de aprendizaje hebbiano sobre aprendizaje basado en el gradiente? Una de las acusadas ventajas que disponen las reglas basadas en Hebb se refieren a la capacidad de implementarse en tiempo real [13], pero su principal desventaja es que por lo general no alcanzan el desempeño otorgado por las reglas basadas en el gradiente y en algunos casos la diferencia es muy aguda [14].
¿Por qué un algoritmo biológicamente inspirado no alcanza los resultados de clasificación de un algoritmo aparentemente artificial? Divisamos cinco posibles razones principales por las que esto ocurra:
- Los modelos de aprendizaje por plasticidad están incompletos. Como se ha mencionado anteriormente, los experimentos y otros datos nos han permitido perfeccionar la regla de aprendizaje sináptica que se tiene. No obstante, la misma puede no estar suficientemente bien comprendida. Un posible elemento faltante es el tercer factor que es mencionado por [15] referente a los moduladores de la plasticidad (como es el caso de los neurotransmisores). Este aspecto ha sido abordado por trabajos como [16] y ha sido explorado computacionalmente en problemas de IA por [17] para la base de datos MNIST, obteniendo resultados mejores que la aplicación directa de la regla de Hebb. El problema es que tales intentos no muestran mejores resultados que los trabajos que utilizan retropropagación. Esto puede deberse a que las reglas de aprendizaje tratan de diseñar una forma de aproximarse a los pesos adecuados, mientras que los métodos basados en el gradiente directamente buscan dichos pesos óptimos.
- La retropropagación es biológicamente inspirada. Como si fuera una convergencia evolutiva, es posible que hayamos partido de una definición matemática para encontrar un algoritmo presente en la naturaleza. Este tema es ampliamente discutido en [18]. Sin embargo, podemos ver de manera rápida que el aprendizaje de redes neuronales artificiales actual difiere del aprendizaje de seres humanos, debido a que por lo regular no se implementa en tiempo real.
- El modelo de actividad neuronal es simple. Es posible que no se haya tomado un modelo conveniente para la actividad de las neuronas y dependamos de incluir este factor (y otros como las células gliales, la maduración de las neuronas, etcétera). Una solución en este sentido es el desarrollo de las redes neuronales pulsantes (Spiking Neural Networks o SNN, véase por ejemplo [19]). Sin embargo, incluso la adición de reglas de plasticidad avanzadas con STDP (como [8]) no logran alcanzar los resultados logrados por otros modelos como los basados en el gradiente.
- La evolución juega un gran papel. ¿Y si los valores de pesos como por ejemplo los kernels de convolución de la corteza visual están mediados por mecanismos diferentes a la plasticidad para su desarrollo? Esta pregunta requiere de una respuesta en el área de biología pero la cuestión que se plantea aquí es que la evolución puede ser determinante para el aprendizaje hebbiano pueda ajustarse adecuadamente. Sin embargo, a nivel algorítmico, implementar un esquema de evolución para los pesos parece ser excesivo.
- La arquitectura es inadecuada. Posiblemente el éxito del aprendizaje profundo reside en su arquitectura compuesta por múltiples capas convolucionales y millones de parámetros, que se acercan de alguna manera a la realidad del cerebro, el cual está compuesto por un número astronómico de neuronas. Al parecer, incluso un modelo simple pero con una gran cantidad de parámetros suena suficiente e incluso mejor que un modelo pequeño pero con aspectos más basados en la biología, puesto que obvian el aspecto fundamental que es la inclusión de millones de neuronas. Para resolver este problema, en conjunto con los puntos anteriores 2 y 4, en [13] planteamos una red convolucional con pesos pre-entrenados y aprendizaje hebbiano en la capa final, obteniendo resultados cercanos a los logrados utilizando algoritmos recientes basados en el gradiente. Sin embargo, si bien los resultados se acercaron a lo logrado por los métodos basados en el gradiente, no fue posible superarlos.
En apariencia, los esfuerzos por generar algoritmos biológicamente más plausibles para modelos conexionistas parecen acercarse asintóticamente a los resultados logrados vía descenso del gradiente pero sin lograr aún un resultado contundente que los supere. Esto no quiere decir que las propuestas estén mal fundadas, ya que pueden incluir otras ventajas como el aprendizaje en tiempo real. Sin embargo, la pregunta sigue abierta y no creemos que una solución no exista puesto que los seres humanos somos capaces de realizar tales actividades de reconocimiento de imágenes sin dificultad. No obstante, incluso esta idea puede estar mal fundada ya que los modelos de redes profundas pueden superar a la exactitud humana como clama el artículo de [20]. De esta manera, es posible que los algoritmos puedan estar sobrecalificados para tareas específicas y disponer de una buena aproximación a los mismos con arquitecturas convenientes puede llegar a ser una solución conveniente y no tratar de aspirar a entender cómo las redes biológicas logran una mayor capacidad de clasificación.
En este artículo, trataremos de aproximarnos a las preguntas anteriormente planteadas. La aproximación que haremos será referente a la última posible respuesta que se planteó, indicando que la arquitectura que se maneja es insuficiente para resolver los problemas de clasificación. Hemos visto que dada una arquitectura arbitraria, el descenso del gradiente suele obtener mejores resultados. Sin embargo, ¿existirá una arquitectura apropiada para la regla de Hebb con la que se puedan obtener los resultados que se observan con métodos basados en el gradiente? Este acercamiento que se dará será de corte principalmente teórico, pero se mostrará una implementación de las ideas abordadas.
2 Preliminares teóricos
La descripción matemática de la Regla de Hebb estará principalmente basada en [21], salvo donde se indique. Por simplicidad, partiremos del modelo de tasa de disparo para representar a la actividad de cada neurona individual. De manera alternativa, se pueden utilizar spikes (potenciales de acción) para modelar la actividad neuronal, como se realiza en [19]. Sea la actividad de una neurona (usualmente postsináptica) que recibe un vector de señales aferentes , las cuales pueden tener origen sensorial (datos de sensores o de bases) o de otras neuronas. El conjunto puede ser discreto (), un intervalo continuo (), o bien el mismo conjunto de los números reales no negativos. La actividad (tasa de disparo) está modelada por la siguiente ecuación diferencial
|
|
donde representa el vector de pesos de las entradas, y la constante satisface . Para linealizar la ecuación, se suele tomar , lo cual lo convierte en el modelo estándar de red neuronal artificial y de esta forma se trabajará en este artículo. representa a la función de activación y en este caso se tomará por la función identidad cuando utilicemos o sigmoide si . Para fines prácticos, en este artículo se tomará a la función de activación como la identidad.
2.1 Regla de Hebb Simple
Un modelo sencillo de la Regla de Hebb ha sido llamado como Simple o Básico y tiene como objetivo encapsular a las propiedades esenciales de la conjetura hebbiana, resumidas por Shatz [22] como ``cells that fire together, wire together''. La regla de Hebb Simple está dada por
|
|
Es regla lograr representar bien la idea básica, puesto que si , entonces aumenta (y el aumento es mayor si ambos tienen alta actividad), pero si uno es 0, entonces no se produce ningún cambio. Por ejemplo, si , entonces representan encendidos simultáneos que se traducen en un aumento.
Utilizando el método de Euler podemos discretizar a la regla de Hebb para su implementación:
|
|
(1) |
donde es la tasa de aprendizaje y puede tomarse como , aunque también puede recibir una inicialización aleatoria, la cual es una opción que evita la inactividad total que podría tener una interneurona si los pesos fueran todos inicializados en cero.
3 Resultados teóricos
En esta sección, probaremos algunos resultados sobre la regla de Hebb relacionados con la clasificación supervisada, la cual es un tema relevante puesto que en general dada una red arbitraria y de inicialización en ceros, una red de entrenamiento hebbiano no supera a una red neuronal con entrenamiento por descenso de gradiente como se muestra en [14]. Esto quiere decir, que si definimos a nuestro dataset como () y a como la salida de una red neuronal de una capa, el entrenamiento hebbiano no converge a algún mínimo de la función , como sí lo hacen los enfoques basados en el gradiente. No obstante, eso no significa que no exista una arquitectura competente capaz de efectuar adecuadamente el aprendizaje hebbiano.
De esta forma, de la ecuación (1) observamos que, con la base de datos definida,
|
|
En este caso, redefinimos si y si , teniendo una capa de salida de neuronas. se refiere a los pesos de la -ésima neurona de salida y las entradas. Asimismo, es posible definir , que se refiere a los pesos después de un entrenamiento supervisado. Adicionalmente, añadiremos una capa de clasificación, de tal forma que
|
|
3.1 Red hebbiana infinita
Comenzaremos nuestra descripción con una red hebbiana construida de la siguiente forma: a cada valor del espacio vectorial , le daremos una representación geométrica de la siguiente forma: consideremos una nueva capa de neuronas dada por
|
|
Esta capa debe distinguirse de la capa de entrada, consistente en neuronas. En su lugar, está conformada por todos los valores posibles que puede tener. Esto quiere decir que la capa de neuronas tiene valores posibles, lo cual es un número potencialmente grande incluso si , e infinito si lo es. A pesar de lo anterior, dicha capa infinita nos servirá como punto de partida y como un modelo teórico de la importancia de la Regla de Hebb. En términos especulativos, dicha capa puede ser imaginada como la inteligencia de un ser infinito. No obstante, en algún momento tendremos que reducir la dimensionalidad de capa infinita, puesto que no nos interesa estudiar la inteligencia de los seres metafísicos sino de los existentes en el mundo discreto.
La capa de salida para la red hebbiana infinita, la podemos definir expandiendo el concepto de producto punto:
|
|
Primeramente, demostraremos la existencia de un minimizador global para posteriormente probar que la regla de Hebb induce a uno.
Proposición 1: Sea definida para cada valor como
|
|
donde es una función de verdad binaria. Sea . Entonces
|
|
Notemos que . Por lo tanto, existe minimizador global. Supongamos que . Entonces existe tal que y
|
|
Hagamos para y para , tomemos . Entonces la función cuenta con menor error que , lo cual contradice su minimalidad.
Finalmente probaremos que la red hebbiana infinita es un minimizador global para la función de costo previamente definida:
Teorema 1: Sea una red hebbiana infinita con . Entonces
|
|
Sea . Entonces
|
|
de donde vemos que
|
|
siguiéndose el resultado por la Proposición 1.
A pesar de que la prueba de los anteriores resultados es relativamente directa, las consecuencias son importantes en el contexto de la regla de Hebb simple. A grosso modo, establece que si disponemos de recursos ilimitados, es posible diseñar una red neuronal de aprendizaje hebbiano que minimice global la suma de los errores totales que se cometen. La idea básica resultó ser en crear una capa de representación con todos los valores posibles de entrada y la regla de Hebb cuenta cuántos elementos de la base de datos arrojan dichos valores y realiza una actualización hebbiana cuando encuentra uno.
Por situar un ejemplo, podemos tomar una base de datos consistente en los siguientes datos:
|
|
El primer elemento de cada vector representa a la entrada y el segundo a la etiqueta . Para dar una interpretación a esta base de datos hipotética, podemos entender a la entrada como una tonalidad en escala de grises y la salida como negro si y blanco si 1. Este problema de clasificación puede resolverse de manera simple con cualquier algoritmo y el la red hebbiana infinita no es la excepción. La segunda capa de la red (representación) estará formada por cada posible valor de , en este caso 255 neuronas. Finalmente el aprendizaje hebbiano se da en la última capa, compuesta por una neurona que clasifica el negro y que clasifica el blanco. Notemos que (y ) para porque para los primeros datos tenemos y para pero a partir de 127 observamos , por lo que para pero . De esta forma, el error el conjunto de entrenamiento será 1, ya que cada valor posible que puede tomar está perfectamente clasificado. Aún más, si suministramos datos difusos, por ejemplo con repetidos varias veces, la red tenderá por el valor más repetido.
No obstante, este ejemplo de juguete muestra algunas de las desventajas propias del método. La primera es la acusada falta de datos, que tiene repercusiones sobre el conjunto de prueba. Si, por ejemplo utilizamos un conjunto de entrenamiento con los datos pares de y un conjunto de prueba con los impares, el error en el conjunto de entrenamiento será 0 pero cerca de la mitad de los datos del conjunto de prueba serán incorrectamente clasificados, ya que no se suministran los ejemplos concretos y por lo tanto todos los pesos están en 0.
Este problema puede pensarse que se puede resolver suministrando aún más datos, pero aparece otro problema en la práctica, que es la explosión combinatoria en la capa de representación. Supongamos ahora que queremos clasificar 7 colores RGB. Entonces tenemos valores posibles, lo cual es una gran cantidad de neuronas incluso para algunos organismos vivos. Una posible solución reside en compactar a la representación reduciendo la dimensión al redondear a unos cuantos valores, lo cual también reduce el problema del conjunto de prueba mencionado previamente. Sin embargo, el problema persiste: si quisiéramos clasificar 10 imágenes en un espacio de que es un caso reducido de MNIST y de entrada binaria, necesitamos un total de neuronas de representación, es decir, más neuronas que las existentes en los cerebros humanos (). Reducir imágenes de caracteres a un tamaño de es incluso excesivo y una reducción mayor simplemente no se puede clasificar fácilmente. Este caso se complica cuando consideramos imágenes RGB de objetos. Por lo tanto, este enfoque es irrealizable en la práctica computacional y en la biología misma, donde formas más eficientes toman lugar.
A pesar de las dos desventajas agudas, el objetivo del Teorema 1 es probar que la existencia de una arquitectura en el que el aprendizaje hebbiano logre una minimización perfecta (global) de la función de costo suma de los errores. Esto responde de alguna manera a la pregunta fundamental planteada en este artículo, señalando que el principal problema del aprendizaje hebbiano recae en la necesidad de hallar una arquitectura conveniente para su ejecución. Al menos sabemos que existe una arquitectura donde opera perfectamente, quizá exista una arquitectura intermedia que resuelva el problema de clasificación de manera efectiva y eficiente.
(1) También podemos distinguir los estados iluminado / poco iluminado para evitar pensar en el gris.
3.2 m-celdas
Una posible forma en que se pueden tratar de minimizar los efectos de la red hebbiana infinita en términos prácticos (los seres infinitos pueden ejecutarla sin problemas) consiste en crear dividir a los datos de la capa de representación en -celdas (mejor conocidas en la literatura como -celdas, pero en esta caso ), que es el enfoque que se trató en el artículo de [14], logrando resultados experimentales comparables con otros métodos de clasificación estándares o incluso mejores para datos sintéticos. En esta sección, intentaremos brindar un mejor sustento matemático sobre por qué el método funciona y finalmente lo aplicaremos en datos no sintéticos.
En general la idea de las -celdas se reduce a dividir al espacio primero en un espacio compacto donde se asume que viven los datos y después se subdividen en -celdas de radio . Cada celda se puede entender como una neurona que recibe datos y se activa si los datos de entrada pertenecen a la -celda. Estas celdas forman la capa de representación que se describió en la red hebbiana infinita. Posteriormente, estas celdas se conectan con las neuronas de salida y en la conexión de las celdas con las neuronas de salida se aplica aprendizaje hebbiano.
La siguiente proposición establece que es posible aproximarnos a la medida de Lebesgue de un conjunto abierto y acotado utilizando un número finito de -celdas. La notación que se usará para las celdas es si tiene el índice y radio , o bien .
Proposición 2: Sea un conjunto abierto y acotado, y . Entonces existe tal que existen -celdas de radio tales que
|
|
El conjunto de -celdas abiertas de tamaño arbitrario forman una base del espacio con la topología de los conjuntos abiertos. Consideremos el conjunto
|
|
Para cada existe tal que . Consideremos si . Entonces . Así, tenemos una unión contable de -celdas. En particular, los elementos pueden tomarse disjuntos ya que si , podemos definir como la unión de otras -celdas, o aproximarse tan bien como se desee, según el procedimiento que se expone al final de esta prueba. Reindexando y ordenando de mayor a menor :
|
|
Por lo tanto,
|
|
Entonces, como es acotado, y para existe tal que
|
|
Ahora, falta aproximar . Para cada tomemos una aproximación racional de con radio . Notemos que si entonces
|
|
de donde, para
|
|
donde es una partición de de tamaño . De esta forma,
|
|
Así, por la desigualdad del triángulo y tomando
|
|
De manera similar al último argumento, podemos fragmentar por completo al espacio de tal forma que se aproxime tanto como se puedan a las -celdas encontradas en la prueba anterior. De este modo, al reducir hemos de encontrar una clasificación más fina que permita obtener resultados más precisos.
Para poder realizar clasificación apropiadamente, debemos asumir que los datos se pueden separar en vecindades o conjuntos abiertos, lo cual siempre es posible para cualquier dispersión, pero idealmente los datos deben no estar intercalados entre sí para su correcto funcionamiento en el conjunto de prueba. Este problema también se observa si las distribuciones de los datos coinciden y se superponen, pero en general el conjunto de entrenamiento puede sobreajustarse y resolver el problema en el mismo.
Dado que estamos considerando espacios continuos como , utilizando el supuesto de separación de datos en conjuntos abiertos, definiremos el error como
|
|
donde es el conjunto abierto donde cada si y sólo si pertenece a la clase y es el conjunto tal que para toda , . Este error se puede reducir tanto como se desee:
Teorema 2: Supongamos que el problema de clasificación se puede separar en conjuntos abiertos y acotados. Para cada , existe una división del espacio en -celdas de tamaño tales que .
Usando la Proposición 1, es posible hallar una partición del espacio en -celdas de tamaño tal que
|
|
Como cada , para cada , , por lo que . Tomando las clases, tenemos que . (En principio cada de cada partición puede ser diferente, pero podemos seleccionar uno usando una técnica similar a la que aparece en la prueba de la Proposición 2).
En la práctica, la bondad de este resultado (poder minimizar al costo tanto como se quiera) está afectado por varios factores. Primeramente, la superposición de los datos supone un problema, como ya se ha mencionado previamente. Además, cuando tomamos celdas con menor si bien aumentamos la precisión el conjunto de clasificación, se produce un sobreajuste al aparecer celdas sin asignación que pueden aparecer en el conjunto de entrenamiento. Sin embargo, nuevamente este problema puede resolverse con una mayor cantidad de datos. El otro problema recae en la definición de -celdas para dimensiones grandes de , requiere de definir una cantidad creciente de celdas. Estos dos problemas son análogos a los dos problemas de la red hebbiana infinita, pero al menos aparecen atenuados y en bajas dimensiones son perfectamente implementables, como se verá a continuación.
4 Resultados experimentales
En [14] se implementó el algoritmo de -celdas para datos sintéticos y se comparó con métodos estándares como la regresión logística y kNN. En esta ocasión, probaremos su desempeño frente a redes neuronales con métodos basados en el gradiente y utilizando un dataset no sintético, el cual es la base de datos Iris para la clasificación de flores del género Iris a partir de datos biométricos [23]. En este caso, para entrenamiento de las m-celdas se utilizarán únicamente dos dimensiones en cierta medida separables: longitud y ancho de pétalo (véase figura 1), longitud de sépalo y ancho de pétalo (figura 2), y finalmente longitud de sépalo y longitud de pétalo (figura 3).
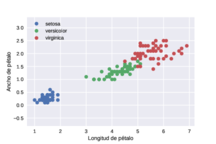
|
| Figura 1: Gráfico de las variables longitud y ancho de pétalo del dataset Iris. |

|
| Figura 2: Gráfico de las variables longitud de sépalo y ancho de pétalo del dataset Iris. |

|
| Figura 3: Gráfico de las variables longitud de sépalo y longitud de pétalo del dataset Iris. |
Como se puede ver, las tres clases del dataset son en gran medida separables, aunque existe cierto traslape entre las clases I. versicolor e I. virginica. Se tiene un total de 150 datos, de los cuales 75 se utilizaron para entrenamiento, 30 para validación y 45 para prueba.
4.1 Descenso de Gradiente
Para contrastar al descenso de gradiente con el aprendizaje hebbiano, se utilizó un esquema de redes neuronales de alimentación hacia adelante (Feedforward Neural Networks o FNNs). El entrenamiento se realizó con la función de costo de entropía cruzada categórica a 15 épocas y se utilizó al optimizador Adam [24], uno de los métodos basados en el gradiente más recientes y ampliamente utilizados en la actualidad para redes neuronales. Para este caso, se utilizaron las cuatro dimensiones de los datos. Por ende, se tomarán 4 unidades de entrada y 3 de salida, correspondiente a cada clase.
Ese enfoque se estudió de dos maneras: por medio de redes neuronales con arquitectura fija y mediante una optimización hiperparamétrica. Las arquitecturas fijas fueron , y , donde cada vector representa el número de neuronas en cada capa intermedia (oculta): es decir la primera arquitectura (Modelo 1) cuenta con 50 neuronas en una capa intermedia, la segunda 50 en la primera capa oculta y 50 en la segunda (Modelo 2), mientras que el Modelo 3 cuenta con 50 neuronas en tres capas intermedias.
El modelo 1 tardó 1.586 s y alcanzó una exactitud sobre el conjunto de prueba de 0.967, 0.853 en el conjunto de entrenamiento y 0.822 en el conjunto de validación. Por su parte, el modelo 2 logró la misma exactitud sobre el conjunto de prueba, 0.987 en el conjunto de prueba y 0.911 en el conjunto de validación durando 1.489 segundos, mientras que el modelo 3 obtuvo 0.933 en el conjunto de prueba, 0.973 en el conjunto de entrenamiento y 0.866 en la validación, durando 1.733 s. La figura 4 representa las curvas de aprendizaje de los tres modelos.

|
| Figura 4: Evolución de la exactitud de los tres modelos base en 15 épocas. |
Para realizar una exploración sobre el espacio de las FNNs (optimización hiperparamétrica), se utilizó la heurística de evolución descrita en [25], utilizando la variante A con constantes , , y , así como quince generaciones.
La optimización hiperparamétrica arrojó como arquitectura con máxima validación a , la cual logró 0.967 de exactitud en el conjunto de prueba, 0.853 en el conjunto de entrenamiento y 0.889 en el conjunto de validación. El esquema de evolución queda patente en la figura 5. En la figura 6 podemos apreciar la evolución del número de redes neuronales por cada generación que participa en el proceso de evolución.

|
| Figura 5: Evolución de la exactitud con 15 generaciones. |

|
| Figura 6: Número de individuos por generación. Se incluyen generaciones donde se da un decremento. |
4.2 Algoritmo de m-celdas
En el caso de las -celdas, se tomaron celdas de tamaño y únicamente se tomaron dos dimensiones por simplicidad. Los resultados principales se resumen en la tablas 1, 2, 3 y se obtuvieron al variar . Los mejores resultados se obtuvieron al utilizar las variables de los pétalos (longitud y ancho), donde si seleccionamos la máxima exactitud sobre el conjunto de validación, obtenemos 0.967 de exactitud sobre el conjunto de prueba, aunque para se obtiene una clasificación perfecta. Los tiempos de ejecución fueron considerablemente más bajos: 0.00072 para la primera combinación de variables, 0.00055 para la segunda y 0.001 para la tercera. Las otras combinaciones de variables en general no resultaron lo suficientemente apropiadas, pero el uso del conjunto de validación nos puede ayudar a seleccionar el par de variables más significativo, aunque una opción más apropiada sería considerar a todas las varibles.
| Entrenamiento | Validación | Prueba | |
| Entrenamiento | Validación | Prueba | |
| Entrenamiento | Validación | Prueba | |
Por otro lado, en las tablas observamos cómo al reducir el tamaño de , obtenemos mejores resultados de clasificación en el conjunto de entrenamiento, dando confirmación experimental del Teorema 2, pero al reducirse el tamaño de las vecindades también dejamos fuera a los datos que no son de entrenamiento, por lo que las exactitudes sobre los conjuntos de prueba y validación se reducen, tendiendo a . La primera tabla también está representada en la figura 7.

|
| Figura 7: Gráfico de las exactitudes del algoritmo de m-celdas con las variables longitud y ancho de pétalo del dataset Iris. |
5 Conclusiones
Los resultados observados con las -celdas dan sustento a la hipótesis de que la arquitectura tiene una influencia crucial en las redes neuronales con aprendizaje hebbiano, a pesar de que sea un método poco práctico de implementar para dimensiones mayores. En este caso se implementó para , siendo posible ya que se puede no utilizar toda la información de una base de datos, aunque no siempre parece posible lograr resultados de clasificación correctos utilizando pocas dimensiones o reduciéndolas.
En este caso, para la base de datos de iris, se pudieron observar resultados similares pero significativamente más rápidos que los que arroja el optimizador Adam (una versión moderna del descenso del gradiente), incluso utilizando un esquema de evolución. Esto supone una primera victoria de los métodos basados en Hebb frente al enfoque predominante y es respaldado por los resultados teóricos. Dichos resultados empíricos también son comparables con otros algoritmos de clasificación modernos, como los aplicados en [26].
No obstante, el optimismo debe tomarse con cautela. Para mayores dimensiones, parece complicada la ejecución del algoritmo de -celdas y el refinamiento del radio requiere de una mayor capacidad de cómputo. De esta forma, quizá sólo se pueda aspirar a celdas burdas para dimensiones medianas, pero parece imposible manejar , que es el caso de las imágenes.
Sin embargo, a pesar de las limitaciones del método propuesto debemos señalar que el logro obtenido tanto a nivel teórico como práctico señala la existencia de una red en donde el aprendizaje hebbiano opera apropiadamente. Esto puede darnos esperanzas para sospechar la existencia de una red óptima en el que el aprendizaje hebbiano no sólo funcione adecuadamente sino que la red sea eficiente para su implementación práctica en dimensiones altas. Tal red puede tener una estructura convolucional y disponer de millones de parámetros. En el trabajo previo de [13] se ha tratado de dar dicha aproximación. Quizá otros componentes como el tercer factor sean necesarios para lograr el delicado balance entre eficacia y eficiencia.
Disponibilidad de código y datos
El código principal se puede obtener de https://github.com/Pherjev/hebbian-m-cells/blob/master/HebbMNIST-2.ipynb. La base de datos se obtuvo directamente de la librería sklearn.
BIBLIOGRAFÍA
[1] Hebb, Donald Olding. (1949) "The Organisation of Behaviour: a neuropsychological theory". John Wiley & Sons-Chapman & Hall
[2] Markram, Henry and Gerstner, Wulfram and Sjöström, Per Jesper. (2012) "Spike-timing-dependent plasticity: a comprehensive overview", Volume 4. Frontiers. Frontiers in synaptic neuroscience 2
[3] Konorski, Jerzi. (1948) "Conditioned Reflexes and Neuron Organizaion". Cambridge University Press
[4] Ramón y Cajal, Santiago. (1894) "The Croonian lecture: la fine structure des centres nerveux", Volume 4. Proceedings of the Royal Society of London B Biology Sciences 444-468
[5] Lmo, Terje. (1966) "Frequency potentiation of excitatory synaptic activity in dentate area of hippocampal formation". Blackwell Science. Acta Physiologica Scandinavica 128
[6] Bliss, Tim VP and Lmo, Terje. (1973) "Long-lasting potentiation of synaptic transmission in the dentate area of the anaesthetized rabbit following stimulation of the perforant path", Volume 232. Wiley Online Library. The Journal of Physiology 2 331–356
[7] Bienenstock, Elie L and Cooper, Leon N and Munro, Paul W. (1982) "Theory for the development of neuron selectivity: orientation specificity and binocular interaction in visual cortex", Volume 2. Soc Neuroscience. Journal of Neuroscience 1 32–48
[8] Diehl, Peter U and Cook, Matthew. (2015) "Unsupervised learning of digit recognition using spike-timing-dependent plasticity", Volume 9. Frontiers. Frontiers in computational neuroscience 99
[9] Oja, Erkki. (1982) "Simplified neuron model as a principal component analyzer", Volume 15. Springer. Journal of mathematical biology 3 267–273
[10] Hitzler, Pascal and Bianchi, Federico and Ebrahimi, Monireh and Sarker, Md Kamruzzaman. (2020) "Neural-symbolic integration and the Semantic Web", Volume 11. IOS Press. Semantic Web 1 3–11
[11] Cichy, Radoslaw M and Kaiser, Daniel. (2019) "Deep neural networks as scientific models", Volume 23. Elsevier. Trends in cognitive sciences 4 305–317
[12] Liu, Chang and Sun, Fuchun. (2015) "HMAX model: A survey". IEEE. 2015 International Joint Conference on Neural Networks (IJCNN) 1–7
[13] Aguilar Canto, Fernando Javier. (2020) "Convolutional Neural Networks with Hebbian-Based Rules in Online Transfer Learning". Springer. Mexican International Conference on Artificial Intelligence 35–49
[14] Aguilar Canto, Fernando Javier. (2020) "Eficacia de diferentes reglas hebbianas en el Aprendizaje Supervisado: Efficacy of different Hebbian rules in Supervised Learning", Volume 7. Tecnología Educativa Revista CONAIC 1 92–97
[15] Kumierz, ukasz and Isomura, Takuya and Toyoizumi, Taro. (2017) "Learning with three factors: modulating Hebbian plasticity with errors", Volume 46. Elsevier. Current opinion in neurobiology 170–177
[16] Foncelle, Alexandre and Mendes, Alexandre and Jedrzejewska-Szmek, Joanna and Valtcheva, Silvana and Berry, Hugues and Blackwell, Kim T and Venance, Laurent. (2018) "Modulation of spike-timing dependent plasticity: towards the inclusion of a third factor in computational models", Volume 12. Frontiers. Frontiers in Computational Neuroscience 49
[17] Holca-Lamarre, Raphaël and Lücke, Jörg and Obermayer, Klaus. (2017) "Models of acetylcholine and dopamine signals differentially improve neural representations", Volume 11. Frontiers. Frontiers in computational neuroscience 54
[18] Lillicrap, Timothy P and Santoro, Adam and Marris, Luke and Akerman, Colin J and Hinton, Geoffrey. (2020) "Backpropagation and the brain", Volume 21. Nature Publishing Group. Nature Reviews Neuroscience 6 335–346
[19] Kozdon, Katarzyna and Bentley, Peter. (2018) "The evolution of training parameters for spiking neural networks with hebbian learning". MIT Press. Artificial Life Conference Proceedings 276–283
[20] He, Kaiming and Zhang, Xiangyu and Ren, Shaoqing and Sun, Jian. (2015) "Delving deep into rectifiers: Surpassing human-level performance on imagenet classification". Proceedings of the IEEE international conference on computer vision 1026–1034
[21] Dayan, Peter and Abbott, Laurence F. (2001) "Theoretical neuroscience: computational and mathematical modeling of neural systems". Computational Neuroscience Series
[22] Bliss, Tim VP and Lmo, Terje. (2010) "The developing brain", Volume 267. Sci. Am
[23] Fisher, Ronald A and Marshall, Michael. (1936) "Iris data set", Volume 440. RA Fisher, UC Irvine Machine Learning Repository 87
[24] Kingma, Diederik P and Ba, Jimmy. (2014) "Adam: A method for stochastic optimization". arXiv preprint arXiv:1412.6980
[25] Canto, Fernando Javier Aguilar. (2020) "Redes neuronales evolutivas con modelos de Lotka-Volterra.", Volume 149. Res. Comput. Sci. 8 1179–1194
[26] Wu, Yuanyuan and He, Jing and Ji, Yimu and Huang, Guangli and Yao, Haichang and Zhang, Peng and Xu, Wen and Guo, Mengjiao and Li, Youtao. (2019) "Enhanced classification models for iris dataset", Volume 162. Elsevier. Procedia Computer Science 946–954
Document information
Published on 27/12/21
Submitted on 31/10/21
Licence: CC BY-NC-SA license
Share this document
claim authorship
Are you one of the authors of this document?