Revision as of 05:13, 19 December 2021 (view source) Gstinoco (talk | contribs) ← Older edit		Latest revision as of 05:14, 19 December 2021 (view source) Gstinoco (talk | contribs)
Line 163:		Line 163:
	|}		|}
−	===2.1 El problema de minimización global y el diferencial de J===	+	==2.1 El problema de minimización global y el diferencial de J==
	El problema de minimización global o sin restricciones asociado con los problemas de búsqueda en línea descritos es		El problema de minimización global o sin restricciones asociado con los problemas de búsqueda en línea descritos es

---

Latest revision as of 05:14, 19 December 2021

1 Introducción

En optimización, la estrategia de búsqueda en línea es uno de los enfoques iterativos básicos para encontrar un mínimo local ${\textstyle \displaystyle v^{*}}$ de una función objetivo ${\textstyle \displaystyle f:\mathbb {R} ^{n}\to \mathbb {R} }$. El enfoque de búsqueda en línea primero supone conocida una aproximación previa ${\textstyle u}$ para ${\textstyle v^{*}}$ y encuentra una dirección de descenso ${\textstyle w}$ a lo largo de la cual la función objetivo ${\textstyle \displaystyle f}$ será minimizada y entonces esto determinará qué tan lejos ${\textstyle u}$ debe moverse a lo largo de esa dirección. Este tamaño de paso está asociado con un mínimo local de la restricción de ${\textstyle f}$ a la recta de búsqueda. Al problema de encontrar este tamaño de paso se le llama un problema de búsqueda en línea, es decir, es un problema de minimización con restricciones de la forma

${\displaystyle \left\{{\begin{array}{c}Min{\hbox{ }}f(v)\\{\hbox{sujeto a }}v=u-\rho w,\forall \rho \in \mathbb {R} ;u,w\in \mathbb {R} ^{n},\end{array}}\right.}$

que también se puede escribir como

${\displaystyle Min_{\rho \in \mathbb {R} }{\hbox{ }}f(u-\rho w).}$

(1)

Aquí la recta de búsqueda es la recta que pasa por ${\textstyle u}$ y tiene (por conveniencia, para nuestras posteriores aplicaciones) la dirección ${\textstyle -w}$. Como ya se dijo, una de las áreas donde surgen problemas de búsqueda en línea son los métodos iterativos para minimizar localmente una función ${\textstyle f:\mathbb {R} ^{n}\rightarrow \mathbb {R} }$ sin restricciones. En cada iteración ${\textstyle i}$ debe resolverse un problema de búsqueda en línea de la forma (1), para ${\textstyle u}$ y ${\textstyle w}$ conocidos. Si denotamos con ${\textstyle \rho _{i}}$ a la solución del problema de búsqueda en línea de la iteración ${\textstyle i}$, se toma a ${\textstyle v_{i}=u-\rho _{i}w}$ como la nueva aproximación para el mínimo de ${\textstyle f}$. La solución de los problemas de búsqueda en línea se puede aproximar por una variedad de métodos numéricos [1], entre ellos el método de Newton. Si definimos ${\textstyle g(\rho )=f(u-\rho w)}$ entonces la solución del problema (1) es equivalente a la solución del problema en ${\textstyle \mathbb {R} }$

${\displaystyle Min_{\rho \in \mathbb {R} }{\hbox{ }}g(\rho ).}$

Para resolver este problema buscamos los valores donde la derivada de ${\textstyle g}$ se hace cero, es decir, resolvemos (por el método de Newton) la ecuación

${\displaystyle g'(\rho ^{*})=0.}$

Tenemos que

${\displaystyle g'(\rho )=-Df(u-\rho w;w)=-\nabla f(u-\rho w)\cdot w,}$

donde ${\textstyle Df(v;w)}$ denota la derivada direccional de ${\textstyle f}$ en ${\textstyle v}$ en la dirección de ${\textstyle w}$. Así que por comodidad definimos

${\displaystyle H(\rho )=-g'(\rho )=Df(u-\rho w;w)=\nabla f(u-\rho w)\cdot w}$

y resolvemos la ecuación

${\displaystyle H(\rho ^{*})=0,}$

para lo cual, dada una aproximación inicial ${\textstyle \rho _{0}}$, se construyen sucesivas aproximaciones de acuerdo a

${\displaystyle \rho _{i+1}=\rho _{i}-{\frac {H(\rho _{i})}{H^{\prime }(\rho _{i})}},i=0,1,2,....}$

En este trabajo extenderemos estas ideas para aplicar el método de Newton a un problema de búsqueda en línea pero donde los elementos ${\textstyle u}$ y ${\textstyle w}$ aunque conocidos, pertenecen al espacio de Hilbert ${\textstyle (L^{2})^{3}}$ y no a ${\textstyle \mathbb {R} ^{n}}$. En este contexto, este artículo es una continuación o extensión de lo expuesto en [2].

2 Descripción del problema

Los problemas de búsqueda en línea en que estamos interesados aquí son del tipo

${\displaystyle \left\{{\begin{array}{c}{\hbox{Encontrar }}\mathbf {\rho ^{*}} \in \mathbb {R} ,{\hbox{ tal que }}\\J(\mathbf {u} -\rho ^{*}\mathbf {w} )\leq J(\mathbf {u} -\rho \mathbf {w} ),\forall \rho \in \mathbb {R} ,\end{array}}\right.}$

(2)

con ${\textstyle \mathbf {u} }$ y ${\textstyle \mathbf {w} }$ fijos en ${\textstyle (L^{2}(0,T))^{3}}$, y donde el funcional de nuestro interés ${\textstyle J:(L^{2}(0,T))^{3}\longrightarrow \mathbb {R} }$ es

${\displaystyle J(\mathbf {v} )={\frac {\eta }{2}}\int \limits _{0}^{T}\Vert \mathbf {v} \Vert ^{2}dt+{\frac {k}{2}}||\mathbf {y} (T)-\mathbf {y} _{T}||^{2},}$

(3)

donde ${\textstyle k,\eta >0}$ y ${\textstyle ||.||}$ la norma euclideana canónica, donde ${\textstyle \mathbf {v} }$ es una función vectorial, ${\textstyle \mathbf {v} =(v_{1}(t),v_{2}(t),v_{3}(t))^{T}}$, ${\textstyle \Vert \mathbf {v} \Vert ^{2}=v_{1}^{2}+v_{2}^{2}+v_{3}^{2}}$ y la función vectorial ${\textstyle \mathbf {y} =(y_{1},y_{2},y_{3})^{T}}$ es la solución del siguiente problema de valor inicial que modela la dinámica de un circuito de tres juntas de Josephson acopladas inductivamente, [3]:

${\displaystyle \left\{{\begin{array}{c}\gamma _{1}{\frac {dy_{1}}{dt}}+\kappa _{1}(y_{1}-y_{2})+\operatorname {sen} y_{1}=i_{1}+v_{1},{\hbox{ en }}(0,T),\\\gamma _{2}{\frac {dy_{2}}{dt}}+\kappa _{1}(y_{2}-y_{1})+\kappa _{2}(y_{2}-y_{3})+\operatorname {sen} y_{2}=i_{2}+v_{2},{\hbox{ en }}(0,T),\\\gamma _{3}{\frac {dy_{3}}{dt}}+\kappa _{2}(y_{3}-y_{2})+\operatorname {sen} y_{3}=i_{3}+v_{3},{\hbox{ en }}(0,T),\\\mathbf {y} (0)=\mathbf {y} _{0}.\end{array}}\right.}$

(4)

En (3)-(4), ${\textstyle \mathbf {y} _{0}}$ y ${\textstyle \mathbf {y} _{T}}$ son estados inicial y final conocidos, respectivamente. En [3] y en [4] se dan los siguientes valores factibles para los parámetros involucrados en este sistema y con los cuales se harán los experimentos numéricos mas adelante:

${\displaystyle \gamma _{1}=0.7,{\hbox{ }}\gamma _{2}=1.1,{\hbox{ }}\gamma _{3}=0.7,{\hbox{ }}i_{1}=1,{\hbox{ }}i_{2}=0.8,{\hbox{ }}i_{3}=-1,}$ ${\displaystyle {\hbox{ }}\kappa _{1}=\kappa _{2}=0.1.}$

2.1 El problema de minimización global y el diferencial de J

El problema de minimización global o sin restricciones asociado con los problemas de búsqueda en línea descritos es

${\displaystyle \left\{{\begin{array}{c}{\hbox{Encontrar }}v^{*}\in (L^{2}(0,T))^{3},{\hbox{tal que }}\\J(v^{*})\leq J(v),\forall v\in (L^{2}(0,T))^{3},\end{array}}\right.}$

el cual, (junto con (3)-(4)) corresponde a un problema de control cuyo objetivo es llevar la dinámica del sistema del estado ${\textstyle \mathbf {y} _{0}}$ al estado ${\textstyle \mathbf {y} _{T}}$. Este tipo de problemas de control pueden resolverse usando un algoritmo de gradiente conjugado como los discutidos en el Capítulo 2 de [5] y el Capítulo 3 de [6], donde también se menciona el concepto de Frechet-diferenciabilidad adecuado para minimizar funcionales en espacios de Hilbert. A continuación damos una definción y un teorema básicos para resolver el problema que nos ocupa.

Definición. Sea ${\textstyle V}$ un espacio de Hilbert. Un funcional ${\textstyle J}$ sobre ${\textstyle V}$ es Frechet-diferenciable si, para todo ${\textstyle v,w\in V}$, existe ${\textstyle DJ(v)\in V'}$, la derivada o el diferencial de ${\textstyle J}$ en ${\textstyle v}$, tal que

${\displaystyle J(v+w)-J(v)=\langle DJ(v),w\rangle +\Vert w\Vert \epsilon (v,w),}$

con ${\textstyle \langle .,.\rangle }$ denotando par de dualidad, y ${\textstyle \epsilon (v,w)}$ tendiendo a cero cuando ${\textstyle \Vert w\Vert }$ tiende a cero.

Teorema. Si ${\textstyle J}$ está definido como en (3) entonces es Frechet-diferenciable y su diferencial ${\textstyle DJ(\mathbf {v} )}$ es

${\displaystyle DJ(\mathbf {v} )=\eta \mathbf {v} +\mathbf {p} ,}$

(5)

donde ${\textstyle \mathbf {p} }$ se obtiene al resolver el sistema (versión matricial de (4)) :

${\displaystyle \left\lbrace {\begin{array}{c}\Gamma {\dfrac {d\mathbf {y} }{dt}}+K\mathbf {y} +\operatorname {sen} \mathbf {y} =\left({\begin{array}{ccc}i_{1}+v_{1}\\i_{2}+v_{2}\\i_{3}+v_{3}\\\end{array}}\right){\hbox{ en }}(0,T),\\\mathbf {y} (0)=\mathbf {y} _{0},\end{array}}\right.}$

(6)

y después el sistema adjunto

${\displaystyle \left\lbrace {\begin{array}{c}-\Gamma {\dfrac {d\mathbf {p} }{dt}}+K\mathbf {p} +C(\mathbf {y} )\;\mathbf {p} =0{\hbox{ en }}(0,T),\\\Gamma \mathbf {p} (T)=k(\mathbf {y} (T)-\mathbf {y} _{T}),\end{array}}\right.}$

(7)

donde ${\textstyle C(\mathbf {y} )}$ es una matriz diagonal de 3x3 para la cual la entrada iésima de la diagonal es ${\textstyle cos(y_{i})}$.

De este teorema resulta que ${\textstyle DJ(\mathbf {u} -\rho \mathbf {w} )=\eta (\mathbf {u} -\rho \mathbf {w} )+\mathbf {p} }$, con ${\textstyle \mathbf {p} }$ solución de (7) una vez que ${\textstyle \mathbf {y} (t)}$ es solución del sistema (6) tomando ${\textstyle \mathbf {v} =\mathbf {u} -\rho \mathbf {w} }$.

La demostración de este teorema, y de los resultados que se mencionan a continuación pueden consultarse en [7].

3 Metodología de solución

Para resolver por el método de Newton nuestro problema de búsqueda en línea (2) definimos

${\displaystyle g(\rho )=J(\mathbf {u} -\rho \mathbf {w} ),}$

(8)

entonces el problema se reduce a encontrar raíces para ${\textstyle g'}$ (un problema de ${\textstyle \mathbb {R} }$ en ${\textstyle \mathbb {R} }$), las cuales aproximaremos con la iteración de Newton

${\displaystyle \rho _{i+1}=\rho _{i}-{\dfrac {g'(\rho _{i})}{g''(\rho _{i})}};g''(\rho _{i})\neq 0,}$

para lo cual debemos conocer ${\textstyle g'}$ y ${\textstyle g''}$. Para describir ${\textstyle g'(\rho )}$ en términos de ${\textstyle DJ}$ necesitamos el siguiente teorema:

Teorema. Sea ${\textstyle J}$ un funcional Frechet-diferenciable sobre ${\textstyle V}$ y ${\textstyle g}$ como en (8). Entonces

${\displaystyle g'(\rho )={\dfrac {d}{d\rho }}J(\mathbf {u} -\rho \mathbf {w} )=-\langle DJ(\mathbf {u} -\rho \mathbf {w} ),\mathbf {w} \rangle {.}}$

Así que la ecuación que tenemos que resolver para ${\textstyle \rho }$ es

${\displaystyle g'(\rho )=-\langle DJ(\mathbf {u} -\rho \mathbf {w} ),\mathbf {w} \rangle =0.}$

Como la iteración de Newton es

${\displaystyle \rho _{i+1}=\rho _{i}-{\dfrac {g'(\rho _{i})}{g''(\rho _{i})}},}$

aún nos falta encontrar una expresión para ${\textstyle g''(\rho )}$. Como estamos trabajando en ${\textstyle (L^{2}(0,T))^{3}}$, los pares de dualidad coinciden con el producto interno gracias al teorema de representación de Riesz. Dado que ya conocemos el representante de la transformación ${\textstyle DJ(v)}$ (ver (5)), podemos escribir

${\displaystyle g'(\rho )=-(\eta (\mathbf {u} -\rho \mathbf {w} )+\mathbf {p} ,\mathbf {w} )=-\int _{0}^{T}(\eta (\mathbf {u} -\rho \mathbf {w} )+\mathbf {p} )\cdot \mathbf {w} {\hbox{ dt}},}$

(9)

donde ${\textstyle \mathbf {p} }$ se obtiene resolviendo

${\displaystyle \left\{{\begin{array}{c}\gamma _{1}{\frac {dy_{1\rho }}{dt}}+\kappa _{1}(y_{1\rho }-y_{2\rho })+\operatorname {sen} y_{1\rho }=i_{1}+u_{1}-\rho w_{1}{\hbox{ en }}(0,T),\\\gamma _{2}{\frac {dy_{2\rho }}{dt}}+\kappa _{1}(y_{2\rho }-y_{1\rho })+\kappa _{2}(y_{2\rho }-y_{3\rho })+\operatorname {sen} y_{2\rho }=i_{2}+u_{2}-\rho w_{2}{\hbox{ en }}(0,T),\\\gamma _{3}{\frac {dy_{3\rho }}{dt}}+\kappa _{2}(y_{3\rho }-y_{2\rho })+\operatorname {sen} y_{3\rho }=i_{3}+u_{3}-\rho w_{3}{\hbox{ en }}(0,T),\\\mathbf {y} (0)=\mathbf {y} _{0}.\end{array}}\right.}$

y luego el problema

${\displaystyle \left\lbrace {\begin{array}{c}-\Gamma {\dfrac {d\mathbf {p} _{\rho }}{dt}}+K\mathbf {p} _{\rho }+\left({\begin{array}{ccc}\cos y_{1\rho }&0&0\\0&\cos y_{2\rho }&0\\0&0&\cos y_{3\rho }\\\end{array}}\right)\mathbf {p} _{\rho }=0{\hbox{ en }}(0,T),\\\Gamma \mathbf {p} _{\rho }(T)=k(\mathbf {y} _{\rho }(T)-\mathbf {y} _{T}).\end{array}}\right.}$

Para calcular ${\textstyle g''(\rho )={\dfrac {dg'}{d\rho }}}$, por la regla de Leibniz para la diferenciación bajo el signo integral tenemos, a partir de (9) que:

${\displaystyle {\frac {dg'(\rho )}{d\rho }}=-\int _{0}^{T}{\dfrac {\partial }{\partial \rho }}(\eta (\mathbf {u} -\rho \mathbf {w} )+\mathbf {p} )\cdot \mathbf {w} {\hbox{ dt }},}$

lo cual nos da

${\displaystyle g''(\rho )=\int _{0}^{T}\left[\eta \mathbf {w} -{\dot {\mathbf {p} }}_{\rho }\right]\cdot \mathbf {w} {\hbox{ dt }},}$

que denotaremos como

${\displaystyle g''(\rho )=\langle D^{2}J(\mathbf {u} -\rho \mathbf {w} )\mathbf {w} ,\mathbf {w} \rangle }$

y donde ${\textstyle {\dot {\mathbf {p} }}_{\rho }}$ se obtiene resolviendo

${\displaystyle \left\lbrace {\begin{array}{c}\Gamma {\dfrac {d{\dot {\mathbf {y} }}_{\rho }}{dt}}+K{\dot {\mathbf {y} }}_{\rho }+\left({\begin{array}{ccc}\cos y_{1\rho }&0&0\\0&\cos y_{2\rho }&0\\0&0&\cos y_{3\rho }\\\end{array}}\right){\dot {\mathbf {y} }}_{\rho }=\left({\begin{array}{ccc}-w_{1}\\-w_{2}\\-w_{3}\\\end{array}}\right){\hbox{ en }}(0,T),\\{\dot {\mathbf {y} }}_{\rho }(0)=0\end{array}}\right.}$

y luego el problema

${\displaystyle \left\lbrace {\begin{array}{c}-\Gamma {\dfrac {d{\dot {\mathbf {p} }}_{\rho }}{dt}}+K{\dot {\mathbf {p} }}_{\rho }+\left({\begin{array}{ccc}\cos y_{1\rho }&0&0\\0&\cos y_{2\rho }&0\\0&0&\cos y_{3\rho }\\\end{array}}\right){\dot {\mathbf {p} }}_{\rho }=\\\left({\begin{array}{ccc}\operatorname {sen} y_{1\rho }\;{\dot {y}}_{1\rho }&0&0\\0&\operatorname {sen} y_{2\rho }\;{\dot {y}}_{2\rho }&0\\0&0&\operatorname {sen} y_{3\rho }\;{\dot {y}}_{3\rho }\\\end{array}}\right)\mathbf {p} _{\rho }{\hbox{ en }}(0,T),\\\Gamma {\dot {\mathbf {p} }}_{\rho }(T)=k{\dot {\mathbf {y} }}_{\rho }(T).\end{array}}\right.}$

Con ésto el método de Newton para aproximar ${\textstyle \rho ^{*}}$ queda

${\displaystyle \rho _{i+1}=\rho _{i}-{\dfrac {g'(\rho _{i})}{g''(\rho _{i})}}}$ ${\displaystyle \rho _{i+1}=\rho _{i}-{\dfrac {-\langle DJ(\mathbf {u} -\rho \mathbf {w} ),\mathbf {w} \rangle }{\langle D^{2}J(\mathbf {u} -\rho \mathbf {w} )\mathbf {w} ,\mathbf {w} \rangle }}}$ ${\displaystyle \rho _{i+1}=\rho _{i}+{\dfrac {\langle DJ(\mathbf {u} -\rho \mathbf {w} ),\mathbf {w} \rangle }{\langle D^{2}J(\mathbf {u} -\rho \mathbf {w} )\mathbf {w} ,\mathbf {w} \rangle }}.}$

4 Discretización del problema de búsqueda en línea

La idea principal es sustituir el espacio ${\textstyle L^{2}(0,T)}$ por un espacio de funciones más práctico. A grandes rasgos este espacio será el de las funciones lineales por pedazos en (0,T), que además ofrecen la ventaja de poder ser representadas computacionalmente por eneadas de números.

Para describir esto con mayor precisión, comenzamos haciendo una partición uniforme del intervalo ${\textstyle (0,T)}$ con

• ${\textstyle N}$ número de subintervalos de la partición uniforme.
• ${\textstyle h={\frac {T}{N}}}$ tamaño de cada subintervalo.
• ${\textstyle tt}$ un vector de ${\textstyle N+1}$ puntos espaciados uniformemente en el intervalo ${\textstyle (0,T)}$ de la forma

${\displaystyle tt=[0,\cdots ,tt_{N}].}$

Con ${\textstyle tt_{i}=i*h,i=0,1,2,\cdots ,N}$, esto significa que en el arreglo ${\textstyle tt}$ se almacena la partición en el tiempo.

Dada esta partición, una función ${\textstyle f(t)}$ en ${\textstyle L^{2}(0,T)}$ puede ser aproximada por la función lineal por pedazos ${\textstyle f_{h}(t)}$ cuyo valor en ${\textstyle t_{i}}$ es ${\textstyle f_{h}(t_{i})=f(t_{i})}$. En la figura 1 se muestra una ${\textstyle f}$ y su aproximación lineal ${\textstyle f_{h}}$ por pedazos, con ${\textstyle N=10}$. Note que entonces una función ${\textstyle f}$ puede ser representada computacionalmente por dos ${\textstyle (N+1)}$-eadas:

${\displaystyle f\approx \left\lbrace {\begin{array}{c}(tt_{0}=0,\cdots ,tti,\cdots ,tt_{N})\\(f(0),\cdots ,f(tt_{i}),\cdots ,f(tt_{N})).\\\end{array}}\right.}$

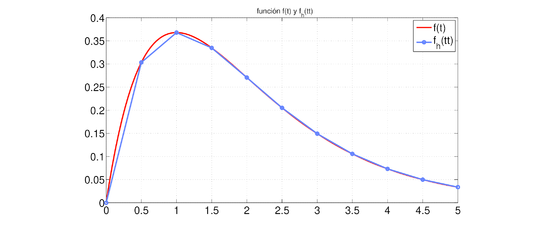
Figura 1: Función ${\displaystyle f(t)=t\exp(-t)}$ y ${\displaystyle f_{h}(tt)=tt\exp(-tt),}$ con ${\displaystyle N=10,T=5}$ y ${\displaystyle h=0.5}$.

Con esto, está claro que podemos aproximar las funciones ${\textstyle \mathbf {v} }$ en ${\textstyle (L^{2}(0,T))^{3}}$ por triadas de funciones lineales por pedazos, es decir por matrices de la forma

${\textstyle \mathbf {v} (t)\approx (v_{1},v_{2},v_{3})(tt)=\left({\begin{array}{ccc}v_{1}(0)&\cdots &v_{1}(tt_{N})\\v_{2}(0)&\cdots &v_{2}(tt_{N})\\v_{3}(0)&\cdots &v_{3}(tt_{N})\\\end{array}}\right),}$

mientras que las funciones ${\textstyle \mathbf {u} }$ de nuestra teoría quedarían aproximada o representadas por la matriz

${\displaystyle \mathbf {u} =\left({\begin{array}{ccc}u_{1}(0)&\cdots &u_{1}(tt_{N})\\u_{2}(0)&\cdots &u_{2}(tt_{N})\\u_{3}(0)&\cdots &u_{3}(tt_{N})\\\end{array}}\right),}$

y las funciones ${\textstyle \mathbf {w} }$ de nuestra teoría quedarían aproximadas o representadas por la matriz

${\displaystyle \mathbf {w} =\left({\begin{array}{ccc}w_{1}(0)&\cdots &w_{1}(tt_{N})\\w_{2}(0)&\cdots &w_{2}(tt_{N})\\w_{3}(0)&\cdots &w_{3}(tt_{N})\\\end{array}}\right).}$

También a partir de ahora, estaremos usando la notación ${\textstyle \mathbf {v} ^{n}}$ para denotar el valor de la función ${\textstyle \mathbf {v} }$, lineal por pedazos, en el tiempo ${\textstyle nh}$. Esta notación también aplica para las funciones ${\textstyle \mathbf {y} }$ y ${\textstyle \mathbf {p} }$, es decir, con ${\textstyle \mathbf {y} ^{n}}$ denotamos el valor de la función ${\textstyle \mathbf {y} }$ en el tiempo ${\textstyle nh}$ y similarmente para ${\textstyle \mathbf {p} }$. Esto se resume en decir que en este capítulo damos los valores de ${\textstyle \mathbf {u} }$ y ${\textstyle \mathbf {w} }$ en la partición ${\textstyle tt}$ y debemos minimizar una version discreta del funcional, para lo cual es necesario encontrar los valores aproximados de

${\displaystyle \mathbf {y} \approx (y_{1},y_{2},y_{3})(tt)=\left({\begin{array}{ccc}y_{1}(0)&\cdots &y_{1}(tt_{N})\\y_{2}(0)&\cdots &y_{2}(tt_{N})\\y_{3}(0)&\cdots &y_{3}(tt_{N})\\\end{array}}\right),}$

y de

${\displaystyle \mathbf {p} \approx (p_{1},p_{2},y_{3})(tt)=\left({\begin{array}{ccc}p_{1}(0)&\cdots &p_{1}(tt_{N})\\p_{2}(0)&\cdots &p_{2}(tt_{N})\\p_{3}(0)&\cdots &p_{3}(tt_{N})\\\end{array}}\right)}$

en la partición ${\textstyle tt}$. En lo que sigue detallamos cómo hacemos todas estas discretizaciones.

4.1 Discretización del Funcional

El funcional ${\textstyle J}$ de (3) lo aproximamos por

${\displaystyle J^{h}(\mathbf {v} )={\frac {\eta h}{2}}\sum _{n=1}^{N}||\mathbf {v} ^{n}||^{2}+{\frac {k}{2}}||\mathbf {y} ^{N}-\mathbf {y} _{T}||^{2},}$

con ${\textstyle ||\mathbf {v} ^{n}||^{2}=|v_{1}^{n}|^{2}+|v_{2}^{n}|^{2}+|v_{3}^{n}|^{2}}$. Aquí ${\textstyle \mathbf {y} ^{N}}$ es la aproximación de ${\textstyle \mathbf {y} }$ en el tiempo ${\textstyle N}$ ${\textstyle (tt_{N}=Nh)}$, que mas adelante especificamos cómo calcular.

4.2 Discretización del SEDO

Aproximamos el sistema (6) por un esquema de Euler explícito que luce como sigue:

${\displaystyle \left\lbrace {\begin{array}{c}{\hbox{Dado }}\mathbf {y} ^{0}=\mathbf {y} _{0},\\\\{\hbox{ para }}n=0,...,N-1{\hbox{ resolver }}\\\\\mathbf {y} ^{n+1}=\mathbf {y} ^{n}-h\Gamma ^{-1}K\mathbf {y} ^{n}-h\Gamma ^{-1}\left({\begin{array}{ccc}\operatorname {sen} y_{1}^{n}\\\operatorname {sen} y_{2}^{n}\\\operatorname {sen} y_{3}^{n}\\\end{array}}\right)+h\Gamma ^{-1}\left({\begin{array}{ccc}i_{1}+v_{1}^{n}\\i_{2}+v_{2}^{n}\\i_{3}+v_{3}^{n}\end{array}}\right).\end{array}}\right.}$

4.3 Discretización del SEDO Adjunto

El sistema adjunto (7) lo aproximamos por

${\displaystyle \left\lbrace {\begin{array}{c}\mathbf {p} ^{N}=k\Gamma ^{-1}(\mathbf {y} ^{N}-\mathbf {y} _{T}),\\\\{\hbox{ para }}n=N-1,...,0{\hbox{ resolver }}\\\\\mathbf {p} ^{n}=\mathbf {p} ^{n+1}-h\Gamma ^{-1}K\mathbf {p} ^{n+1}-h\Gamma ^{-1}\left({\begin{array}{ccc}\cos y_{1}^{n}&0&0\\0&\cos y_{2}^{n}&0\\0&0&\cos y_{3}^{n}\\\end{array}}\right)\;\mathbf {p} ^{n+1}.\\\end{array}}\right.}$

4.4 Discretización del Producto interno

Las discretizaciones mencionadas implican que estamos considerando el siguiente producto interno

${\displaystyle (\mathbf {u} ,\mathbf {w} )_{h}=h\sum _{n=1}^{N}\mathbf {u} ^{n}\cdot \mathbf {w} ^{n},\forall \mathbf {u} ,\mathbf {w} \in (\mathbb {R} ^{3})^{N}.}$

4.5 Discretización de g'(ρ) y g(ρ)

Para resolver la ecuación ${\textstyle g(\rho ^{*})=0}$ con el método de Newton se requiere el conocimiento de ${\textstyle g'(\rho )}$ que estará dada en los nuevos espacios vectoriales por

${\displaystyle g'(\rho )=-h\eta \sum _{n=1}^{N}[\mathbf {u} ^{n}-\rho \mathbf {w} ^{n}+\mathbf {p} _{\rho }^{n}]\cdot \mathbf {w} ^{n},}$

donde ${\textstyle \mathbf {p} _{\rho }^{n}}$ se obtiene resolviendo

${\displaystyle \left\lbrace {\begin{array}{c}{\hbox{Dado }}\mathbf {y} _{\rho }^{0}=\mathbf {y} _{\rho }(0),\\\\{\hbox{ para }}n=0,...,N-1{\hbox{ resolver }}\\\\\mathbf {y} _{\rho }^{n+1}=\mathbf {y} _{\rho }^{n}-h\Gamma ^{-1}K\mathbf {y} _{\rho }^{n}-h\Gamma ^{-1}\left({\begin{array}{ccc}\operatorname {sen} y_{\rho {1}}^{n}\\\operatorname {sen} y_{\rho {2}}^{n}\\\operatorname {sen} y_{\rho {3}}^{n}\\\end{array}}\right)+h\Gamma ^{-1}\left({\begin{array}{ccc}i_{1}+u_{1}^{n}-\rho w_{1}^{n}\\i_{2}+u_{2}^{n}-\rho w_{2}^{n}\\i_{3}+u_{3}^{n}-\rho w_{3}^{n}\\\end{array}}\right).\\\end{array}}\right.}$

y luego resolviendo

${\displaystyle \left\lbrace {\begin{array}{c}\mathbf {p} _{\rho }^{N}=k\Gamma ^{-1}(\mathbf {y} _{\rho }^{N}-\mathbf {y} _{T}),\\\\{\hbox{ para }}n=N-1,...,0{\hbox{ resolver }}\\\\\mathbf {p} _{\rho }^{n}=\mathbf {p} _{\rho }^{n+1}-h\Gamma ^{-1}K\mathbf {p} _{\rho }^{n+1}-h\Gamma ^{-1}\left({\begin{array}{ccc}\cos y_{\rho {1}}^{n+1}&0&0\\0&\cos y_{\rho {2}}^{n+1}&0\\0&0&\cos y_{\rho {3}}^{n+1}\\\end{array}}\right)\;\mathbf {p} _{\rho }^{n+1}.\\\end{array}}\right.}$

y para

${\displaystyle g''(\rho )=h\sum _{n=1}^{N}[\eta \mathbf {w} ^{n}-{\overset {\cdot }{\mathbf {p} }}_{\rho }^{n}]\cdot \mathbf {w} ^{n},}$

con ${\textstyle {\overset {\cdot }{\mathbf {p} }}_{\rho }^{n},}$ obtenido al resolver

${\displaystyle \left\{{\begin{array}{c}{\overset {\cdot }{\mathbf {y} }}_{\rho }^{0}=\mathbf {0} ,\\{\hbox{para }}n=0,....,N-1{\hbox{ resolver}}\\{\overset {\cdot }{\mathbf {y} }}_{\rho }^{n+1}={\overset {\cdot }{\mathbf {y} ^{n}}}_{\rho }-h\Gamma ^{-1}K{\overset {\cdot }{\mathbf {y} }}_{\rho }{n}-h\Gamma ^{-1}\left({\begin{array}{c}\cos y_{1\rho }^{n}\\\cos y_{2\rho }^{n}\\\cos y_{3\rho }^{n}\end{array}}\right){\overset {\cdot }{\mathbf {y} ^{n}}}_{\rho }-h\Gamma ^{-1}\left({\begin{array}{c}w_{1}^{n}\\w_{2}^{n}\\w_{3}^{n}\end{array}}\right),\end{array}}\right.}$

y luego resolver

${\displaystyle \left\{{\begin{array}{c}{\overset {\cdot }{\mathbf {p} }}_{\rho }^{N}=k\Gamma ^{-1}{\overset {\cdot }{\mathbf {y} }}_{\rho }^{N},\\{\hbox{para }}n=N-1,....,0{\hbox{ resolver}}\\{\overset {\cdot }{\mathbf {p} }}_{\rho }^{n}={\overset {\cdot }{\mathbf {p} }}_{\rho }^{n+1}+h\Gamma ^{-1}K{\overset {\cdot }{\mathbf {p} }}_{\rho }^{n+1}\\\\+h\Gamma ^{-1}\left({\begin{array}{ccc}\cos y_{1\rho }^{n}&0&0\\0&\cos y_{2\rho }^{n}&0\\0&0&\cos y_{3\rho }^{n}\end{array}}\right){\overset {\cdot }{\mathbf {p} }}_{\rho }^{n+1}\\\\-\left({\begin{array}{ccc}{\overset {\cdot }{y}}_{1\rho }^{n}\operatorname {sen} y_{1\rho }^{n}&0&0\\0&{\overset {\cdot }{y}}_{2\rho }^{n}\operatorname {sen} y_{2\rho }^{n}&0\\0&0&{\overset {\cdot }{y}}_{3\rho }^{n}\operatorname {sen} y_{3\rho }^{n}\end{array}}\right)\mathbf {p} _{\rho }^{n+1}\mathbf {.} \end{array}}\right.}$

Con esto podemos ya aplicar el método de Newton para resolver la versión discreta de ${\textstyle g'(\rho )=0}$: Dado ${\textstyle \rho ^{0}}$, iterar con

${\displaystyle \rho ^{m+1}=\rho ^{m}-{\frac {g'(\rho ^{m})}{g''(\rho ^{m})}}.}$

Usamos el criterio de paro ${\textstyle {\dfrac {\vert \rho ^{m+1}-\rho ^{m}\vert }{\vert \rho ^{m+1}\vert }}<\varepsilon }$, para ${\textstyle \varepsilon }$ pequeño dado.

5 Experimentación computacional

5.1 Ejemplo 1

En este ejemplo tomamos ${\textstyle u_{1}(t)=t\exp(-t)}$, ${\textstyle u_{2}(t)=t^{3}}$, ${\textstyle u_{3}(t)=0}$ y ${\textstyle w_{1}(t)=\exp(-t)/10}$, ${\textstyle w_{2}(t)=3t-t^{3}}$ y ${\textstyle w_{3}(t)=0}$. Se tomaron los valores siguientes para los parámetros en la iteración de Newton y en la discretización de los problemas involucrados:

• ${\textstyle T=16}$; ${\textstyle k=1.0e-3}$; ${\textstyle \rho ^{0}=0}$; ${\textstyle h=T/500}$; ${\textstyle \eta =1}$.
• ${\textstyle \mathbf {y} _{0}=[1.2514;0.7456;-0.9753]}$; ${\textstyle \mathbf {y} _{T}=[7.4207;6.4958;-0.3236]}$.

Dadas las funciones ${\textstyle \mathbf {u} =(t\exp(-t),t^{3},0)}$ y ${\textstyle \mathbf {w} =(\exp(-t)/10,3t-t^{3},0)}$, minimizamos con el método de Newton el funcional ${\textstyle J(\mathbf {u} (t)-\rho \mathbf {w} (t))}$ sobre ${\textstyle \rho }$ y en 3 iteraciones se obtuvo el valor ${\textstyle \rho ^{*}=-1.017}$. La gráfica del funcional ${\textstyle J}$ restringido a la recta ${\textstyle \mathbf {v} =\mathbf {u} -\rho \mathbf {w} }$ se muestra en la Figura 2.

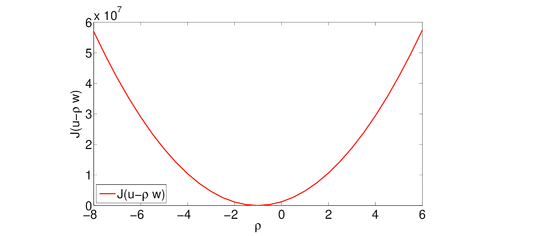
Figura 2: Funcional ${\displaystyle J(\mathbf {u} (t)-\rho \mathbf {w} (t))}$ para las funciones ${\displaystyle \mathbf {u} }$ y ${\displaystyle \mathbf {w} }$ del ejemplo 1.

5.2 Ejemplo 2

En este ejemplo tomamos ${\textstyle u_{1}(t)=-(t-2)\exp(-t)}$, ${\textstyle u_{2}(t)=3t^{2}+1}$, ${\textstyle u_{3}(t)=(t-1)^{2}+1}$ y ${\textstyle w_{1}(t)=t^{3}+t-1}$, ${\textstyle w_{2}(t)={\dfrac {1}{3}}t^{3}-t}$, ${\textstyle w_{3}(t)=\exp(-t)/10}$. Tanto para la discretización de los problemas involucrados como para las iteraciones de Newton se tomaron los valores siguientes:

• ${\textstyle T=12}$; ${\textstyle k=1.0e-3}$; ${\textstyle \rho ^{0}=0.5}$; ${\textstyle h=T/500}$; ${\textstyle \eta =1}$.
• ${\textstyle \mathbf {y} _{0}=[0.1992;0.1187;-0.1552]}$; ${\textstyle \mathbf {y} _{T}=[0.1810;0.0338;-0.0515]}$.

Dadas las funciones ${\textstyle \mathbf {u} =(-(t-2)\exp(-t),3t^{2}+1,(t-1)^{2}+1)}$ y ${\textstyle \mathbf {w} =(t^{3}+t-1,{\frac {1}{3}}t^{3}-t,\exp(-t)/10)}$, minimizamos con el método de Newton el funcional ${\textstyle J(\mathbf {u} (t)-\rho \mathbf {w} (t))}$ sobre ${\textstyle \rho }$ y en 6 iteraciones se obtuvo el valor ${\textstyle \rho ^{*}=0.084}$. La gráfica del funcional ${\textstyle J}$ restringido a la recta ${\textstyle \mathbf {v} =\mathbf {u} -\rho \mathbf {w} }$ se muestra en la Figura 3.

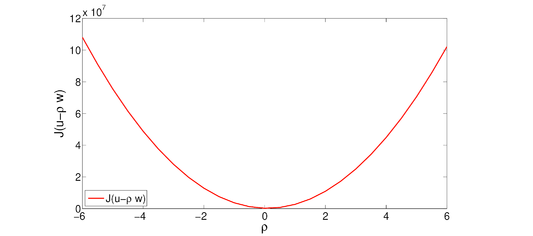
Figura 3: Funcional ${\displaystyle J(\mathbf {u} (t)-\rho \mathbf {w} (t))}$ para las funciones ${\displaystyle \mathbf {u} }$ y ${\displaystyle \mathbf {w} }$ del ejemplo 2.

6 Conclusiones

No contamos con un ejemplo para el cual se conozca la solución exacta, así que nuestra validación se basa en el desempeño del método en ejemplos como los dos mostrados, dado que es posible tener una visualización suficientemente detallada del funcional ${\textstyle J}$ restringido a la "recta" que pasa por ${\textstyle \mathbf {u} }$ y tiene dirección ${\textstyle \mathbf {w} }$. De acuerdo a estos ejemplos se puede concluir que el método de Newton produce resultados excelentes. En este trabajo el objetivo no es comparar el método de Newton con otros métodos, sino verificar que este tipo de problemas se pueden resolver aceptablemente utilizando el método de Newton; sin embargo en trabajos futuros esperamos considerar otros métodos y hacer tal comparación, por ejemplo, con los métodos que no utilizan derivadas. También podemos mencionar que los resultados presentados aquí se aplicarán próximamente para resolver el problema de minimización global asociado con el problema de control, el cual, como se conocen el estado inicial del que se parte y el estado final al que se quiere llegar, podrá considerarse como un caso de validación de la metodología expuesta en el presente trabajo.

BIBLIOGRAFÍA

[1] R. P. Brent (2002) Algorithms for minimization without derivatives. New York: Courier Dover Publications.

[2] J. López, L. H. Juárez (2019) Método de Newton para Problemas de Búsqueda en Línea en ${\textstyle L^{2}}$. Journal of Basic Sciences. Vol. 5, Num. 13.

[3] Y. Braiman, B. Neschke, N. Nair, N. Ima, and R. Glowinski. (2016) Memory States in Small Arrays of Josephson Junctions, PHYSICAL REVIEW E (94), 052223: 1-13.

[4] J. D. Rezac, N. Imam and Y. Braiman, (2017) Parameter optimization for transitions between memory states in small arrays of Josephson junctions, PHYSICA A (474), 267-281.

[5] R. Glowinski (2015) Variational Methods for the Numerical Solution of Nonlinear Elliptic Problems, Philadelphia: SIAM.

[6] R. Glowinski (2003) Finite element methods for incompressible viscous flow. In Handbook of Numerical Analysis, Vol. IX, P.G. Ciarlet & J.L. Lions, eds., 3-1176, Amsterdam: Elsevier.

[7] C. N. Cortazar (2020) Método de Newton para búsquedas en línea en el espacio ${\textstyle (L^{2})^{3}}$. Tesis de Maestría. Universidad Juárez Autónoma de Tabasco.