Latest revision as of 13:37, 30 August 2021

Resumo

A análise de estruturas no domínio da frequência vem ganhando campo nas últimas décadas, primeiramente, em virtude do desenvolvimento computacional e estratégias para avaliar a Transformada Discreta de Fourier com mais eficiência. As vantagens em se avaliar a resposta no domínio da frequência é que não há necessidade de conhecer as condições iniciais, e pode se avaliar a resposta para sistemas com propriedades dependentes da frequência com maior precisão, por exemplo, interação solo-estrutura. Este trabalho tem como objetivo avaliar a resposta dinâmica de um sistema estrutural discreto no domínio da frequência mediante as curvas de ressonância por meio do Método do Balanço Harmônico HBM. A resposta é avaliada na fase permanente para ações e/ou cargas harmônicas para sistemas dotados de amortecimento viscoso tipo proporcional e não proporcional. As propriedades do sistema, como massa e rigidez, são tomadas como constantes. Para os modelos desenvolvidos e analisados neste estudo são apresentados os respectivos espectros de resposta em frequência e histórico de deslocamento no tempo por meio do HBM. As respostas do sistema obtidas por intermédio do HBM são comparadas com outros dois métodos também baseados no domínio da frequência (ImFT e Pseudo-Forças), permitindo, então, avaliar as amplitudes e frequências críticas do sistema.

Palavras-chave: Análise dinâmica, domínio da frequência, espectro de resposta

Abstract

The analysis of structures in the frequency domain has been gaining ground in the last decades, first, because of the computational development and strategies to evaluate the Discrete Fourier Transform more efficiently. The advantages of evaluating the frequency response are that there is no need to know the initial conditions, and the response to systems with frequency-dependent properties can be evaluated more accurately, eg, soil-structure interaction. This work aims to evaluate the dynamic response of a discrete structural system in the frequency domain through the resonance curves using the Harmonic Balance Method HBM. The response is evaluated in the permanent phase for actions and / or harmonic loads for systems with proportional and non-proportional viscous damping. The properties of the system, such as mass and rigidity, are taken as constants. For the models developed and analyzed in this study are presented the respective spectra of frequency response and history of displacement in time through the HBM. The system responses obtained through the HBM are compared with two other methods also based on the frequency domain (ImFT and PseudoForces), allowing to evaluate the amplitudes and critical frequencies of the system.

Keywords: Dynamic analysis, response structural, domain frequency, analysis harmonics of structures

1. Introdução

A análise de estruturas no domínio da frequência vem ganhando campo nas últimas décadas, primeiramente, em virtude do desenvolvimento computacional. A resposta no domínio da frequência permite obter um espectro de resposta associado, neste caso, às propriedades do sistema, como massa, rigidez, amortecimento e excitação dinâmica. Em alguns casos a resposta em frequência, que é caracterizada pela curva de ressonância, pode ser obtida indiretamente por meio da análise no tempo Galvão [7] e Silva [13], o que leva a um grande esforço computacional para estruturas com vários graus de liberdade.

Estendendo a formulação para o domínio da frequência, é possível avaliar quais são as frequências críticas e suas respectivas amplitudes, porém se sabe que esta amplitude está associada à resposta na fase permanente, dependendo da excitação dinâmica e do modelo de amortecimento adotado. Na Figura 1 é apresentado um sistema dinâmico discreto qualquer e suas respectivas propriedades, também a resposta no domínio frequência e no domínio do tempo.

Figura 1. Exemplo: Histórico de resposta (tempo) e espectro de resposta (Freq.), SDOF

Entre as soluções possíveis ou alternativas para obter a resposta em frequência, temos os métodos baseados na superposição modal e os métodos baseados em linearização equivalente, ambos abordados de uma forma implícita; uma abordagem diferenciada, porém não nova, que consiste em fazer uso do Método do Balanço Harmônico ou Balanço Harmônico Linearizado para obter a resposta no domínio da frequência.

A transformação da equação de equilíbrio da análise dinâmica por meio de elementos finitos para o domínio da frequência, é feita pelo método do balanço harmônico clássico, seguindo a formulação apresentada por Pasquetti [9].

Após a transformação e mudança de variável temporal, a solução da equação de equilíbrio implica duas soluções possíveis: via Newton-Raphson e/ou incremento de frequência e linearização Bernárdez [1] e Childs [3].

2. Resposta em frequência

A resposta em frequência está associada a sistemas lineares invariantes no tempo sob excitação harmônica ou periódica, considerando sua resposta no regime permanente. A importância da resposta em frequência consiste no fato de que sinais periódicos podem ser decompostos ou representados por uma combinação de harmônicos.

Os métodos de análise baseados na resposta em frequência são, talvez, os mais utilizados em ambientes industriais, pois permitem avaliar a resposta de um sistema na presença de incertezas em razão da utilização e/ou operação.

A avalição do comportamento dinâmico de estruturas no domínio da frequência dependerá basicamente das propriedades ortogonais dos modos. O conceito de modos normais em sistemas estruturais dinâmicos é associado às frequências naturais (ou fundamentais) de um sistema linear, no qual a existência destes modos possibilita a introdução de coordenadas normais que proporcionam o desacoplamento do sistema. Nesse contexto, podemos citar os trabalhos desenvolvidos por Claret et al. [4] e Ribeiro [10].

Tendo em vista que algumas propriedades são não ortogonalizáveis, tal como o amortecimento não proporcional dos dependentes da frequência, faz-se necessário, então, um método no qual sua resposta seja avaliada no domínio da frequência de forma implícita, ou seja, a resposta e dada por meio de operações matriciais que envolvam a linearização do sistema, obtendo a resposta em coordenadas físicas, como o método das Pseudo-Forças de Ferreira [6] e Soares [14], e o método do balanço harmônico, linearizado por Muñoz et al. [8].

Logo, a resposta do sistema no domínio da frequência é definida em relação aos termos associados à amplitude ${\textstyle U}$ e à fase ${\textstyle \phi }$. Observa-se que nos métodos de redução da ordem da equação do equilíbrio dinâmico e da linearização do sistema, por mais que se dê a mudança da variável temporal, a resposta do sistema é dada no domínio do tempo. Para a proposta de obter a resposta tanto no domínio da frequência quanto no tempo para sistemas dotados de amortecimento proporcional e/ou não proporcional, faz-se uso do Método do Balanço Harmônico por meio de duas soluções possíveis: via Newton-Raphson e/ou solução incremental de frequência ${\textstyle \omega }$ e solução linear em termos de amplitudes modais ${\textstyle \left(A,B\right)}$.

2.1 Método do balanço harmônico

Umas das técnicas geralmente utilizadas para obter soluções aproximadas para equações diferenciais é o Método do Balanço Harmônico. Este método permite gerar soluções periódicas aproximadas a partir de uma série de Fourier truncada Pasquetti [9].

O método do balanço harmônico consiste na aproximação dos deslocamentos na fase permanente por meio da combinação de harmônicos, tal como dado pela expressão:

onde ${\textstyle \,{A}_{n}}$ e ${\textstyle {B}_{n}}$ são os vetores das componentes das amplitudes modais no enésimo harmônico e ${\textstyle N}$ é o número de harmônicos usados na aproximação, tendo a equação de equilíbrio dinâmica dada pela equação (2)

Submetendo a estrutura a uma excitação harmônica com uma frequência de excitação ${\textstyle \omega }$ que multiplica o vetor de forças de referência ${\textstyle p}$, o equilíbrio dinâmico é dado por:

onde ${\textstyle F}$ e ${\textstyle \omega }$ são a amplitude e a frequência da excitação harmônica.

Com base nos trabalhos publicados por Muñoz et al. [8] e Pasquetti [9], sendo o caso de uma análise linear a equação (3), se faz necessário apenas o segundo termo do somatório.

O vetor de deslocamento, portanto, é aproximado por:

Substituindo a equação (4) e suas respectivas derivadas na equação (3) obtém-se:

Simplificando a equação (5) tem-se:

Considerando ${\textstyle Fp=\,{F}_{0}}$, a equação (6) pode ser reescrita como um sistema de equações que iguala os coeficientes das funções harmônicas, como:

Os componentes trigonométricos de cada harmônico podem ser reduzidos a:

A equação (6) pode ser escrita de uma forma mais compacta, tal como:

onde:

sendo a frequência de excitação ${\textstyle \omega }$ e o vetor de amplitudes modais ${\textstyle {\overline {A}}}$ as variáveis a serem determinadas.

Muñoz et al. [8] salientam que, apesar de uma análise linear, o sistema de equações é não linear, portanto é necessário o emprego de um método de solução ou de controle para solução de sistemas de equações não lineares.

2.1.1 Solução via Newton-Raphson

Como observado, temos a solução da equação de equilíbrio dinâmico reduzida à solução de um sistema de equações lineares; este, porém, apresenta um número de incógnitas superior às equações de equilíbrio fornecidas, recorrendo ao método de Galerkin para ortogonalizar o resíduo no intervalo de ${\textstyle \left[0,{\frac {2\pi }{\omega }}\right]}$ e obter a solução das equações algébricas.

O sistema resultante ${\textstyle G\left(A,B,\omega \right)=0}$, apresenta duas equações e duas variáveis dependentes ${\textstyle A}$ e ${\textstyle B}$ com uma variável independente ${\textstyle \omega }$.

A solução recai em um dado valor de ${\textstyle \omega }$. Podemos, então, aplicar Newton-Raphson para um par de valores iniciais ${\textstyle {\left({A}^{0},{B}^{0}\right)}^{T}}$, convergindo para uma solução aproximada da resposta permanente do sistema,

onde a matriz Jacobiana ${\textstyle {G}_{A,B}}$ será:

A amplitude da resposta harmônica é derivada dos coeficientes ${\textstyle \left(A,B\right)}$

enquanto o ângulo fase entre a resposta e a excitação é uma função de ${\textstyle \mathrm {{tan}^{-1}} \,\left({\frac {B}{A}}\right)}$ para um domínio ${\textstyle \left[0,\pi \right]}$

O sinal de menos do ângulo de fase em todo o intervalo indicará um atraso da resposta em relação à excitação.

2.1.2 Solução incremental e linear

Como observa-se na equação (9), e em sua forma reduzida na equação (8), uma das soluções possíveis consiste basicamente em realizar incrementos de frequências ${\textstyle \omega }$. Neste caso a variável independente, onde o vetor de amplitudes modais ${\textstyle {\overline {A}}}$ é determinado pela inversão da matriz ${\textstyle {\overline {K}}\left(\omega \right)}$, sendo, então, ${\textstyle \omega }$ já estabelecido dentro do ciclo interativo, logo.

A curva de ressonância é obtida a partir do vetor de amplitudes modais ${\textstyle {\overline {A}}}$, sendo este avaliado a cada incremento de frequência ${\textstyle \omega }$. O vetor de amplitudes modais é avaliado pela sua normal.

É a solução para cada incremento de ${\textstyle \omega }$, e o mesmo também assume posições distintas dentro do vetor de amplitudes modais ${\textstyle {\overline {A}}}$, por exemplo. Este depende das dimensões das matrizes envolvidas, logo:

sendo ${\textstyle i=1\ldots n}$, para os ${\textstyle n}$ respectivos graus de liberdade, e ${\textstyle j=}$${\displaystyle 0\ldots {\omega }_{n}}$ avaliado para cada incremento de frequência.

Podemos ainda associar a resposta com o ângulo fase ou simplesmente fase da resposta do espectro, a partir de uma frequência discreta ${\textstyle \omega }$, como mostrado na equação (14) e/ou na forma matricial.

A fase no método do balanço harmônico consiste em uma parte real ${\textstyle {A}_{i,j}}$ e a parte imaginária de ${\textstyle {B}_{2+i,j}}$. É possível avaliar então a relação entre amplitude ${\textstyle \left|u\right|}$ e a fase ${\textstyle \phi }$ em relação à frequência ${\textstyle \omega }$, como mostra a equação (18).

Tem-se, então, que a mudança na amplitude e na fase não é fixa, mas, sim, dependente das características dinâmicas do sistema e da frequência de entrada ${\textstyle \omega }$.

Para o caso de análise linear, a solução incremental e linear, baseada na inversão da matriz ${\textstyle {\overline {K}}_{\omega }}$ reduz significativamente o tempo de processamento e também dispensa a necessidade de avaliar os valores iniciais ${\textstyle \left({A}^{0},{B}^{0}\right)}$. As duas soluções apresentadas foram implementadas gerando, respectivamente, a mesma resposta na frequência. Verifica-se que, caso não se realize o incremento de frequência ${\textstyle \omega }$, ambas as soluções são indeterminadas.

3. Matriz de amortecimento

Em sistemas em que o amortecimento é considerado distribuído pela estrutura de forma semelhante à massa e à rigidez, ele é dito proporcional ou de Rayleigh. Sistemas com amortecimento proporcional utilizam técnicas de transformação modal para desacoplar as equações de equilíbrio dinâmicas. Assim, a resposta em coordenadas físicas pode ser obtida pela superposição da resposta em coordenadas modais, tanto no domínio do tempo quanto no da frequência Clough et al. [5].

Já em sistemas com características mais complexas de amortecimento, a matriz de amortecimento não é mais proporcional à massa e rigidez do sistema. Diz-se, então, que o amortecimento é não proporcional.

O amortecimento não proporcional é representado por uma matriz que não é ortogonal à matriz modal. Uma das técnicas utilizadas para desacoplar as equações de equilíbrio dinâmica, como dado por Rubinstein et al. [11], consiste em utilizar modos complexos, porém o problema de autovalor e autovetor para este caso é duas vezes maior que o convencional, e os modos complexos dificultam a interpretação física da resposta do sistema.

Conforme Santolin [12], pode-se resolver os sistemas dotados de amortecimento não proporcional por meio do método das Pseudo-Forças. Neste método, os termos da matriz de amortecimento responsáveis pelo acoplamento das equações são transferidos para o segundo membro da equação e tratados como Pseudo-Forças. Assim, o primeiro termo permanece desacoplado, como ocorre no sistema de amortecimento proporcional.

4. Resposta na fase permanente

A resposta associada ao sistema na fase permanente nos remete ao modelo de excitação dinâmica a ser adotado ou combinado. Em virtude do uso do método do balanço harmônico, para cada incremento de frequência ${\textstyle \omega }$ interessa obter a respectiva amplitude correspondente à excitação para alcançar a solução do sistema em razão das amplitudes modais.

Uma forma de corresponder à excitação dinâmica dada no domínio do tempo, é por intermédio da periodização do carregamento. O método a ser empregado aqui é o mesmo utilizado por Camargo [2] e Ribeiro [10] na formulação da ImFT, que consiste em fazer uso da transformada discreta de Fourier e periodizar o vetor de cargas de referência. Os parâmetros, associados à excitação no domínio da frequência, necessitam, por exemplo, do tempo estendido ${\textstyle {T}_{0}}$ e o número de termos ${\textstyle N}$, onde se deseja avaliar a resposta em frequência. O vetor de incremento de frequências ${\textstyle \omega }$ será, então, associado a uma respectiva amplitude dada pela ${\textstyle FFT\left(p\right)}$, quando o vetor de amplitudes modais ${\textstyle {\overline {A}}}$ apresentam a solução do sistema para o equilíbrio dinâmico. A excitação adotada neste trabalho é uma excitação harmônica, dada por uma combinação linear de seno e cosseno com a mesma frequência, tal como ${\textstyle p\left(t\right)=}$${\displaystyle b\mathrm {sin} \,\left(\omega t\right)}$.

5. Exemplos

A seguir são avaliadas as respostas de sistemas estruturais discretos, representados por suas respectivas matrizes de massa, rigidez e amortecimento, estando o sistema excitado por um carregamento e/ou ação harmônica. São apresentados três modelos para análise, variando entre si a matriz de amortecimento e, então, comparando-se a resposta no tempo com os métodos baseados no domínio da frequência supracitados.

Os espectros de respostas foram obtidos pelo método do balanço harmônico, assim como o histórico de deslocamento para ambos os modelos. O critério de comparação do histórico de deslocamento com os demais métodos depende, respectivamente, do tipo de amortecimento, e optou-se para sistemas dotados de amortecimento proporcional comparar a resposta com a ImFT Ribeiro [10], e para sistemas dotados de amortecimento não proporcional com a Pseudo-Forças Santolin [12].

5.1 Modelo 1

O sistema estrutural discreto apresentado na Figura 2 é tratado como Shear Building, sendo analisado por Clough et al. [5] e Santolin [12], e será submetido a um carregamento harmônico a fim de obter e verificar quais são as frequências e as amplitudes críticas.

O sistema apresenta os seguintes coeficientes para a matriz de massa ${\textstyle M}$ e rigidez ${\textstyle K}$:

Na matriz de amortecimento ${\textstyle C}$ será assumido um amortecimento de ${\textstyle 5\%}$ para os modos 1 e 3, resultando, desta forma, em uma matriz de amortecimento proporcional em coordenadas físicas

No vetor de forças de referência adota-se um carregamento harmônico, dado

com incidência sobre o grau de liberdade ${\textstyle {u}_{1}}$, como mostra a Figura 2.

Serão desenvolvidas neste Modelo 1 duas análises: a primeira com ${\textstyle p\left(t\right)}$ assumindo ${\textstyle \omega =}$${\displaystyle {\omega }_{crit}}$, e uma segunda análise com base no trabalho publicado por Santolin [12], assumindo ${\textstyle p\left(t\right)=}$${\displaystyle 100\mathrm {sin} \,\left(\omega t\right)}$ com ${\textstyle \omega =}$${\displaystyle 5,0}$, atuando de modo pertinente a excitar a estrutura.

Figura 2. Modelo estrutural discreto 1

Já os parâmetros associados à discretização do tempo e frequência de amostragem são: intervalo de tempo ${\textstyle \Delta t=}$${\displaystyle 0,01}$ segundos, tempo de análise de ${\textstyle 3,0}$ segundos. Para obter o espectro de resposta, os parâmetros foram definidos ${\textstyle N=}$${\displaystyle 1024}$ e a frequência de amostragem ${\textstyle {F}_{s}=100}$. As respectivas frequências naturais foram obtidas a partir da solução do problema de autovalor e autovetor, pois será utilizada para comparar com as obtidas pelo espectro de resposta, onde ${\textstyle {\omega }_{1}=}$${\displaystyle 14,52\,rad/s}$, ${\textstyle {\omega }_{2}=31,05\,rad/s}$ e ${\textstyle {\omega }_{3}=}$${\displaystyle 46,09\,rad/s}$.

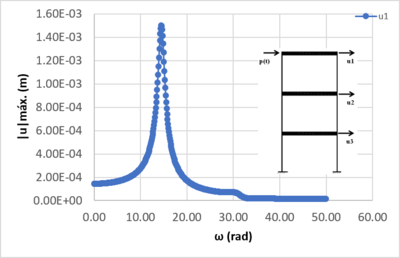
Na Figura 3 temos a resposta no domínio da frequência e/ou espectro de resposta via HBM. Como é possível verificar, as amplitudes críticas coincidem respectivamente com as frequências naturais do sistema.

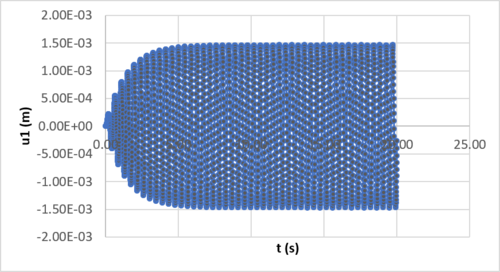
Já para a Figura 4 temos o histórico de deslocamento avaliado pela ImFT, também se comparou a resposta no tempo por algoritmo de integração direta via método de Newmark. O propósito desta avaliação e garantir que as soluções desenvolvidas venham ao convergir para a mesma resposta, sendo os resultados satisfatórios.

Verifica-se que as amplitudes obtidas no espectro de resposta, refere-se a amplitude da resposta na fase permanente do sistema, isto quando assume-se ${\textstyle \omega =}$${\displaystyle {\omega }_{n}}$, caso contrário a resposta deverá ser avaliada a partir das amplitudes modais.

Logo, a partir da Figura 5 temos então a apresentação das respostas no domínio da frequência e no tempo para os modelos adaptados de Clough et al. [5] e Santolin [12].

Figura 3. Espectro de resposta para o grau de liberdade ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {1}}}}$

Figura 4. Histórico de resposta (tempo) para ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {1}}}}$ via ImFT com ${\textstyle {\mathit {\boldsymbol {\omega }}}=}$${\displaystyle {\mathit {\boldsymbol {\omega }}}_{\mathit {\boldsymbol {crit}}}}$

Observa-se nas Figuras 3 e 4 que as amplitudes são idênticas quando assume-se que ${\textstyle \omega =}$${\displaystyle {\omega }_{n}}$, tendo, assim, as respectivas amplitudes críticas ${\textstyle \left|{u}_{crit}\right|}$, o que mostra a convergências de valores para ambos os métodos.

A resposta a um carregamento harmônico monta o vetor de forças de referência assumindo ${\textstyle p\left(t\right)=}$${\displaystyle 100\mathrm {sin} \,\left(\omega t\right)}$, tal como apresentado por Santolin [12] via ImFT, atuando de modo pertinente a excitar a estrutura, ou seja, agindo durante todo o período definido pela análise, logo:

Figura 5. Espectro de resposta via HBM para ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {1}}}}$, ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {2}}}}$ e ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {3}}}}$

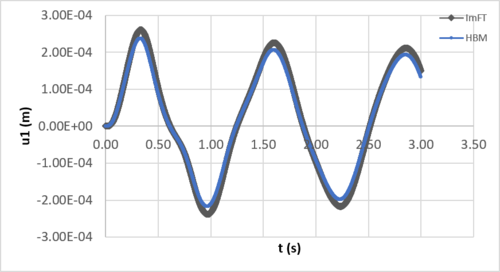
A Figura 6 mostra o histórico de resposta para o grau de liberdade ${\textstyle {u}_{1}}$, comparando-o com o ImFT e HBM para um sistema dotado de amortecimento do tipo proporcional.

Figura 6. Histórico de resposta (tempo) para ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {1}}}}$ via ImFTe HBM

5.2 Modelo 2

O modelo 2 consiste em um sistema com as mesmas propriedades atribuídas ao modelo 1, porém sendo acrescentado um amortecedor discreto ao primeiro grau de liberdade ${\textstyle {u}_{1}}$, onde, ${\textstyle {c}_{1}=}$${\displaystyle 20,0\,kN\cdot s/m}$, como observa-se na Figura 7. Desta forma, o problema não pode ser mais avaliado utilizando técnicas de superposição modal. A solução agora fica basicamente restringida ao uso do método do balanço harmônico e da Pseudo-Forças.

Figura 7. Modelo estrutural discreto 2

As matrizes de massa e rigidez são as mesmas apresentadas no modelo 1; logo a matriz de amortecimento, levando em consideração a inclusão de um amortecedor discreto, é dado por:

A inclusão do amortecedor discreto faz com que se some o valor de ${\textstyle {c}_{1}}$ ao termo ${\textstyle {C}_{1,1}}$ da matriz de amortecimento.

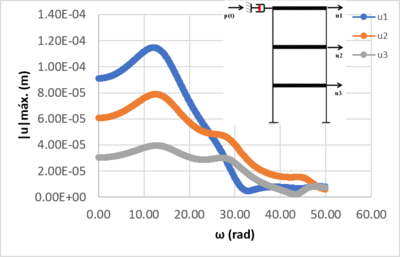
Na Figura 8, é possível observar uma mudança no espectro de resposta devido a inclusão deste amortecedor junto ao ponto de excitação, fazendo com que as amplitudes sejam menores que as apresentadas no modelo 1. Também é possível verificar que as faixas de frequências que podem ser assumidas críticas para o sistema estão à esquerda de ${\textstyle {\omega }_{1}}$ ou seja a primeira frequência natural. Já para os demais graus de liberdade esta condição não é aplicável, pois é facilmente verificada junto à ${\textstyle {\omega }_{2}}$ e ${\textstyle {\omega }_{3}}$ as amplitudes apresentam picos, assumindo uma amplitude crítica.

Figura 8. Espectro de resposta via HBM para ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {1}}}}$, ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {2}}}}$ e ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {3}}}}$

Na Figura 8 temos a resposta no domínio da frequência e/ou espectro de resposta via HBM para um sistema dotado de amortecimento do tipo não proporcional.

A Figura 9 mostra a resposta no tempo para o grau de liberdade ${\textstyle {u}_{1}}$, comparando-o com a Pseudo-Forças e HBM para um sistema dotado de amortecimento do tipo não proporcional.

Figura 9. Histórico de resposta (tempo) para ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {1}}}}$ via Pseudo-Forças e HBM

5.3 Modelo 3

No modelo 3 o grau de liberdade ${\textstyle {u}_{1}}$ segue como no modelo 1, porém são adicionados amortecedores discretos ${\textstyle {c}_{2}}$ e ${\textstyle {c}_{3}}$, como observa-se na Figura 10, onde se pretende avaliar a influência que o amortecedor pode trazer em relação à amplitude máxima avaliada pelo espectro de resposta.

Figura 10. Modelo estrutural discreto 3

Os amortecedores discretos ${\textstyle {c}_{2}=10\,kN\cdot s/m}$ e ${\textstyle {c}_{3}=}$${\displaystyle 20\,kN\cdot s/m}$, sendo a matriz de amortecimento do sistema, apresentada junto a expressão 24.

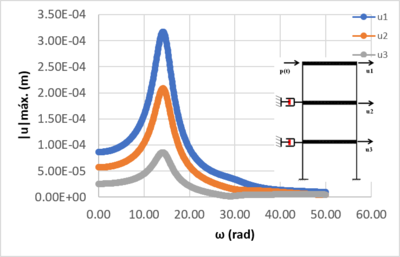
Na Figura 11 temos o espectro de resposta via HBM para o modelo 3.

Figura 11. Espectro de resposta via HBM para ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {1}}}}$, ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {2}}}}$ e ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {3}}}}$

Ao observar os espectros de respostas gerados via HBM e comparar as Figuras 8 8 e 11, verifica-se que os amortecedores discretos a serem inseridos no sistema se tornam mais eficientes sobre o grau de liberdade ou posição onde incide a excitação dinâmica. Tal conclusão é verificada em razão das amplitudes dos deslocamentos geradas pelo espectro de resposta.

A Figura 12 mostra a resposta para o grau de liberdade ${\textstyle {u}_{1}}$, comparando-o com a Pseudo-Forças e HBM para um sistema dotado de amortecimento do tipo não proporcional.

Figura 12. Histórico de resposta (tempo) para ${\textstyle {\mathit {\boldsymbol {u}}}_{\mathit {\boldsymbol {1}}}}$ via Pseudo-Forças e HBM

6. Conclusões

Ao se proceder uma análise harmônica, o HBM apresenta resultados satisfatórios ao se avaliar a resposta em uma frequência discreta ${\textstyle \omega }$. Com isso, podemos obter facilmente a amplitude dos deslocamentos ${\textstyle \left|u\right|}$ associada às propriedades do sistema.

O HBM permitiu, dentro da mesma solução, obter a resposta tanto no domínio do tempo quanto no domínio da frequência, tanto para sistemas dotados de amortecimento proporcional ou não proporcional. O histórico de deslocamento dado via HBM e comparado com os demais métodos (ImFT e Pseudo-Forças), apresentou resultados satisfatórios tanto em amplitude quanto em fase.

Quanto à inclusão dos dissipadores de energia, neste caso amortecimento discreto, pode-se avaliar que o mesmo tem influência significativa na resposta do sistema em relação à amplitude crítica. Ao avaliar a resposta no domínio do tempo, porém, temos que o melhor modelo de amortecimento a ser adotado é aquele distribuído de forma homogênea no sistema.

Agradecimentos

Os autores agradecem à CAPES, PROPEC e UFOP.

Referências