On the robustness of the multigrid method combining ILU and Partial Weight applied in an orthotropic diffusion problem

Latest revision as of 14:43, 6 July 2021

Abstract

This paper proposes an efficient and robust algorithm for solving a physical orthotropy problem. The algorithm is based on choosing the most efficient restriction operator and on an incomplete LU decomposition suited for each orthotropy direction. Local Fourier Analysis (LFA) is carried out in order to increase the efficiency of the multigrid method. Pure diffusion with orthotropy aligned to the coordinate axis x is the model considered. Equations are discretized by Finite Difference Method with uniform grid and second-order numerical scheme. Problems are solved with geometric multigrid method, correction scheme, V-cycle and standard coarsening ratio. The asymptotic convergence factor is calculated for different multigrid components, such as restriction operators, prolongation operators and solvers. Based on the optimum components obtained by LFA, we carried out experiments to analyze the complexity and computational cost of the algorithm proposed. The main conclusion is that the methodology proposed is efficient for the resolution of problems with strong orthotropy.

Keywords: Physical orthotropy, multigrid components, diffusion, local Fourier analysis

1. Introduction

Computational Fluid Dynamics (CFD) is a branch of Computational Science that studies numerical methods used for simulating fluid flow problems. It is known that these methods usually have a high computational cost. In general, this happens as the problems that have to be solved require the resolution of algebraic equation systems whose coefficient matrices are large and sparse [1].

Linear systems are obtained by discretizing the mathematical model, which consists in approximating, through algebraic equations, each term of the mathematical model for each grid node or point. This process leads to an algebraic equation system of the form

,

(1)

where $A\in {R^{NxN}}$ is the coefficient matrix, ${\textstyle T\in {R^{N}}}$ is the variable of interest and ${\textstyle b\in {R^{N}}}$ is the independent vector.

In CFD, the methods that are traditionally employed in this process are: Finite Difference Method (FDM) [2], Finite Volume Method (FVM) [3] and Finite Element Method (FEM) [4].

The algebraic equation system given by Eq. (1) can be solved using direct or iterative methods. In this work, iterative methods were employed due to the aforementioned characteristics of linear systems in CFD (sparse and large coefficients matrices), for which iterative methods are recommended. The multigrid method is one of the most effective methods to accelerate the convergence of iterative methods when solving linear or nonlinear systems, isotropic or anisotropic problems, among others [5-7].

Anisotropic problems are fairly common in Engineering and appear in many phenomena, such as when a material has different heat conduction behaviors in different directions. In this case, the coefficients of the differential equations are distinct among themselves and generate what is called physical anisotropy. Anisotropies can also appear from discretization of grids with different spacing in each direction, for instance, boundary layer problems. This is called geometric anisotropy [5,6]. The efficiency of the multigrid method has not yet been fully achieved for problems with strong anisotropy, either physical or geometric [8].

Physical anisotropic convection problems have been investigated by Rabi and de Lemos [9], who discretized two-dimensional pure diffusion, pure advection and advection-diffusion equations by applying the finite volume method. The multigrid method was employed using correction scheme and V- and W-cycles. The authors presented a study on the different speed ranges, number of grids, number of smoothing steps at each grid level and different solvers. They concluded that there was a significant reduction in the computational effort required for increasing the values of the components of the advection velocity.

Wienands and Joppich [10] presented an in-depth study on the Local Fourier Analysis (LFA) and its application on several problems, including anisotropic problems. The authors calculated the convergence factor of the multigrid method for an anisotropic diffusion equation with different solvers and restriction and prolongation operators.

Johannsen [11] solved an anisotropic diffusion problem using finite volume method for discretizing the equations and 9-point incomplete LU (ILU) decomposition for solving the systems of linear equations. The author employed LFA to demonstrate the superior smoothing properties of ILU.

Oliveira et al. [8] evaluated geometric anisotropy for different grids and aspect ratios. They also assessed some components of the multigrid method, such as: solvers, type of restriction, number of levels and number of inner iterations, among several coarsening algorithms. They concluded that Partial Weighting (PW) had a good performance.

Vinogradova and Krukier [12] solved a three-dimensional advection-diffusion problem with intermediate anisotropy using FDM for discretizing equations and ILU for the resolution of the linear systems. They concluded that the proposed methodology is efficient, however, the coefficients of the mixed derivatives present limitations, which is a disadvantage and has no physical significance.

Vassoler-Rutz et al. [13] analyzed the effect of physical anisotropy on the multigrid method for two anisotropic diffusion problems. They used FAS scheme, V-cycle as well as Modified Strongly Implicit (MSI) and Gauss-Seidel (GS) solvers. They concluded that, for strong anisotropies, the complexity order of the multigrid method is not suitable.

Several works on the implementation of the multigrid method found in the literature demonstrate that the choice of the multigrid components is crucial for the convergence or not of the method. Trottenberg et al. [6] state that this choice is difficult and thus small changes can considerably improve convergence. In this sense, LFA can help this choice as it allows to predict the performance of the multigrid method, since it provides estimates of the convergence rates based on the variation of the multigrid method components.

Pinto et al. [14] solved an anisotropic diffusion problem using ILU in triangular grids. They used LFA to highlight the good smoothing properties of the solver and the asymptotic convergence of the multigrid.

Franco et al. [15] performed LFA in transient problems and obtained the critical value of the parameter that represents the level of space-time anisotropy for 1D and 2D Fourier equations.

Oliveria et al. [16] solved an 2D anisotropic diffusion equation. The equation was discretized by the Finite Difference Method (FDM) and Central Differencing Scheme (CDS). Correction Scheme (CS). An xy-zebra-GS smoother was proposed, which proved to be efficient and robust for the different anisotropy coefficients. They concluded that, the convergence factors calculated empirically and by LFA are in agreement.

A particular case of anisotropy is denominated orthotropy, which happens when the anisotropy occurs in orthogonal directions. In this work, an efficient and robust method for solving physical orthotropy problems using LFA is proposed. A two-dimensional diffusion mathematical model is considered, in which physical orthotropy appears in the coefficients and it will be denominated diffusion orthotropy. Equations were discretized using FDM with second-order central difference scheme.

The asymptotic convergence factor ( ${\textstyle \rho _{loc}}$ ) of the multigrid method was calculated by assessing the ILU solver in different directions [7] as well as several restriction and prolongation operators. The results obtained via LFA were used to assess the influence of the diffusion orthotropy on the computational cost and took into account the CPU time and number of operations in each V-cycle and at the restriction step.

The remainder of this work is organized as follows: section 2 presents the mathematical and numerical models; section 3 discusses considerations regarding the LFA used; section 4 presents the results of the convergence analysis and complexity analysis; and section 5 presents the conclusion.

2. Mathematical and Numerical Models

For the problem presented below, the calculus domain used is given by ${\textstyle {0}\leq {x}\leq {1}}$ , ${\textstyle {0}\leq {y}\leq {1}}$ and the discretization of the equations is done using a uniform grid with a number of points given by ${\textstyle N=N_{x}.N_{y}}$ , where ${\textstyle N_{x}}$ and ${\textstyle N_{y}}$ are the number of points in the directions $x$ and $y$ , respectively, including the boundaries.

2.1. Mathematical Model and Discretization

A model that exemplifies physical and geometric anisotropy for a two-dimensional diffusion equation is given by Trottenberg et al. (2001) as shown below,

(2)

where $g=\cos(\alpha )$ , $w=sen\,(\alpha )$ , $0\leq \alpha \leq {\frac {\pi }{2}}$ and $0<\varepsilon <<1$ or $\varepsilon >>1$ .

For $\alpha ={\frac {\pi }{2}}$ , it is considered that the expression given by Eq. (2) is aligned with the axis of the coordinate y, so it becomes

(3)

From here, the diffusion orthotropic problem will be assessed by means of the two-dimensional diffusion equation given by Eq. (4) [5,6]

(4)

where T is the temperature, ${\textstyle T_{xx}}$ is the second derivative of T as a function of ${\textstyle x}$ , ${\textstyle T_{yy}}$ is the second derivative as a function of ${\textstyle y}$ and ${\textstyle \varepsilon >0}$ .

The source term S and the analytical solution T are given by

and

.

(5)

Eq. (4) was discretized using FDM with CDS, resulting in

,

(6)

where $T$ is the unknown of the system.

Figure 1(b) depicts the notation of the grid points in Figure 1(a). The points P (central), W (west), E (east), N (north) and S (south) in Figure 1(b) correspond to the points ${\textstyle (i,j),(i-1,j),(i+1,j),(i,j+1),(i,j-1)}$ in Figure 1(a), respectively.

Figure 1. Points of a uniform two-dimensional grid

The classic 5-point finite difference is not convergent for cases of general anisotropy, such as the example given by the full tensor

.

Therefore, this methodology cannot be generalized to any type of anisotropic problem. In this paper, we analyze a specific case of anisotropy given by the tensor

,

which represents a case of orthotropy.

The discretization of Eq. (4) results in Eq. (6), and for the inner points, considering ${\textstyle h_{x}^{}={\frac {1}{N_{x}^{}-1}}}$ and ${\textstyle h_{y}^{}={\frac {1}{N_{y}^{}-1}}}$

,

.

(7)

For the boundaries north, south, east and west, ${\textstyle {{a}_{P}}=1}$ , ${{a}_{W}}={{a}_{E}}={{a}_{N}}={{a}_{S}}=0$ .

2.2. Multigrid Method and Computational Details

The multigrid method accelerates the convergence rate of iterative methods. It consists in employing a group of grids with different refinement levels. At each refinement level of the grid, the more oscillatory errors are smoothed, and only low frequency errors remain. After passing to another grid, the remaining low frequency errors become more oscillatory. The efficiency of this process, called smoothing, depends on the choice of a suitable solver.

For employing multigrid, besides a solver with good smoothing properties, grid transfer operators are required (restriction and prolongation).

In [8] and [17], restriction through partial weighting in the directions x and y, henceforth denoted by ${\text{P}}{{\text{W}}_{\text{x}}}$ and ${\text{P}}{{\text{W}}_{\text{y}}}$ , respectively, applied in problems involving geometric anisotropy was proposed. These operators are given in stencil notation as

:

,

:

.

(8)

In this work, such restriction was combined with 7-point incomplete LU decomposition (henceforth denoted by ILU). According to [18], this decomposition has a better convergence factor than 5-point incomplete LU decomposition for orthotropic problems.

In Eq. (4), discretized using FDM, the stencil for the 5-point Laplacian operator is given by

.

(9)

The ${\mbox{ILU}}$ decomposition of the same operator will be given by

,

(10)

note that in this case, ${\textstyle b=f=0}$ .

Thus, the ${\mbox{ILU}}$ decomposition is represented by:

,

(11)

where ${{L}_{h}}$ is the stencil of a lower triangular matrix, ${{U}_{h}}$ is the stencil of an upper triangular matrix and ${{R}_{h}}$ is the residual matrix.

The iterative process for solving Eq. (4) can be:

,

${{L}_{h}}\,{{y}^{m}}={{r}^{m}}\,$ ,

${{U}_{h}}\,{{\sigma }^{m}}={{y}^{m}}$ ,

${{T}^{m+1}}={{T}^{m}}+{{\sigma }^{m}}$ .

(12)

Depending on the ordination of the grid points, different directions can be obtained for the ${\mbox{ILU}}$ decomposition. In lexicographical order, ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ [18], is given by

{{L}_{h}}={{\left[{\begin{matrix}0&0&0\\\gamma &\delta &0\\0&\alpha &\beta \\\end{matrix}}\right]}_{h}},{{U}_{h}}={{\left[{\begin{matrix}\zeta &\eta &0\\0&\delta &\mu \\0&0&0\\\end{matrix}}\right]}_{h}},{{R}_{h}}={{\left[{\begin{matrix}{{p}_{2}}&0&0&0&{}\\{}&0&{{p}_{3}}&0&{}\\{}&0&0&0&{{p}_{1}}\\\end{matrix}}\right]}_{h}}

.

(13)

Another example of ordination for ${\mbox{ILU}}$ , ${\textstyle {\mbox{ILU}}_{\mbox{NE}}}$ [18], is given by

.

${{L}_{h}}={{\left[{\begin{matrix}\zeta &0&0\\\gamma &\delta &0\\0&\alpha &0\\\end{matrix}}\right]}_{h}},{{U}_{h}}={{\left[{\begin{matrix}0&\eta &0\\0&\delta &\mu \\0&0&\beta \\\end{matrix}}\right]}_{h}},{{R}_{h}}={{\left[{\begin{matrix}{{p}_{1}}&{}&{}\\0&0&0\\0&{{p}_{3}}&0\\0&0&0\\{}&{}&{{p}_{2}}\\\end{matrix}}\right]}_{h}}$ .

(14)

The linear system given by Eq. (1) was solved using geometric multigrid method [5,6] with correction scheme (CS), V-cycle and zero initial guess.

The coarsening ratio is given by $r=2$ (standard coarsening) [18]. The grid transfer operators employed were: Injection Restriction (INJ), Half Weighting (HW), Full Weighting (FW) [6], Partial Weighting in ${\textstyle x}$ ( ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ ), Partial Weighting in ${\textstyle y}$ ( ${\textstyle {\mbox{PW}}_{\mbox{y}}}$ ) as well as prolongation by bilinear interpolation and 7-point interpolation. The systems of equations obtained by means of discretization were resolved using 7-point ILU solvers in different directions ( ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ , ${\textstyle {\mbox{ILU}}_{\mbox{NE}}}$ , among others).

The stop criterion used to interrupt the iterative process is based on the nondimensionlized residual norm. The residual of the system of algebraic equation is defined by

,

(15)

where $T^{m}$ is the solution of the unknown in the iteration $m$ .

Considering ${{L}^{m}}={{\left\|r_{}^{m}\right\|}_{1}}$ and ${{L}^{0}}={{\left\|R_{}^{0}\right\|}_{1}}$ , if ${\frac {{L}^{m}}{{L}^{0}}}\leq tol$ the iterative process is interrupted if $tol={{10}^{-10}}$ .

Double precision arithmetic was used for the simulations. The numerical codes were implemented in the Fortran 2003 language, using the Intel 9.1 Visual Fortran application. All numerical results were obtained in a computer with Intel Core i7 2.66 GHz processor, 16 GB RAM and Windows 8 operating system, 64-bit version.

3. Local Fourier analysis

LFA allows to predict the performance of the multigrid method as it supplies estimates of the convergence rate of its components. Therefore, LFA becomes a powerful tool in quantitative analysis and in the research of efficient multigrid methods.

In order to perform the LFA, general discrete linear operators with constant coefficients are considered, which are defined in an infinite grid $G_{h}$ , where the influence of the boundaries can be dismissed [6].

Consider the grid functions of the form of

, with

,

(16)

where $x$ varies in the infinite grid $G_{h}$ and $\theta$ is a parameter that characterize the frequency of the function concerning to grid $G_{h}$ .

For $-\pi \leq \theta <\pi$ , every function of the grid ${{\phi }_{h}}\left(\theta ,x\right)$ are eigenfunctions of a discrete operator that can be written as a stencil.

Thus,

,

(17)

where

(18)

and ${{s}_{k}}$ is the stencil notation of the operator, were $k\in \{(-1,-1),\,(-1,0),(-1,1),...,(1,-1),(1,0),(1,1)\}$ for the 5-point stencil.

In order to smooth as well as to analyze the two grids, it is necessary to distinguish between components of low and high frequency of $G_{h}$ and $G_{2h}$ .

It is known that [6] only

with

,

(19)

are visible in $G_{h}$ .

For each ${\textstyle {\bar {\theta }}\in \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)\times \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)}$ , three other frequency components ${{\phi }_{h}}\left(\theta ,x\right)$ with ${\textstyle \theta \in [-\pi ,\pi )\times [-\pi ,\pi )}$ coincide in $G_{2h}$ with ${{\phi }_{h}}\left({\bar {\theta }},x\right)$ and are not visible in $G_{2h}$ . Therefore, the low- and high-frequency components are defined as follows:

$\phi$ is a low-frequency component $\Leftrightarrow \theta \in {{T}^{low}}=\left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)\times \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)$

$\phi$ is a high-frequency component $\Leftrightarrow \theta \in {{T}^{high}}=\left[-\pi ,\pi \right)\times \left[-\pi ,\pi \right)\backslash \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)\times \left[-{\frac {\pi }{2}},{\frac {\pi }{2}}\right)$ (Figure 2).

Figure 2. Low- (inner white area) and high-frequency (hatched area) areas

Considering the frequencies

,

(20)

the correction operator of the coarse grid is given by $K_{h}^{2h}$ ans is represented by a 4x4 matrix ${\hat {K}}_{h}^{2h}$ , as follows

{\hat {K}}_{h}^{2h}\left(\theta \right)={{\hat {I}}_{h}}-\left({\hat {I}}_{2h}^{h}\left(\theta \right)\right){{\left({\hat {L}}_{2h}^{}\left(2\theta \right)\right)}^{-1}}{{\left({\hat {I}}_{h}^{2h}\left(\theta \right)\right)}_{y}}{\hat {L}}_{h}^{}\left(\theta \right)

with

,

(21)

where ${\hat {I}}_{h}^{}$ is represented by a 4x4 identity matrix.

${{\hat {L}}_{h}}(\theta )$ is the 4x4 matrix:

{{\hat {L}}_{h}}=\left({\begin{matrix}{{\tilde {L}}_{h}}({{\theta }^{(0,0)}})&{}&{}&{}\\{}&{{\tilde {L}}_{h}}({{\theta }^{(1,1)}})&{}&{}\\{}&{}&{{\tilde {L}}_{h}}({{\theta }^{(1,0)}})&{}\\{}&{}&{}&{{\tilde {L}}_{h}}({{\theta }^{(0,1)}})\\\end{matrix}}\right)

,

(22)

where ${{\tilde {L}}_{h}}$ are eigenvalues, evaluated by ${{\tilde {L}}_{h}}(\theta )=\sum \limits _{\kappa }{{{s}_{\kappa }}{{e}^{i{{\theta }^{\alpha }}\kappa }}}$ , and ${{s}_{\kappa }}\in R$ are stencil coefficients [7].

The discrete Laplace operator given by Eq. (9) is represented by:

{{\hat {L}}_{h}}=\left({\begin{matrix}{{\tilde {L}}_{1}}&{}&{}&{}\\{}&{{\tilde {L}}_{2}}&{}&{}\\{}&{}&{{\tilde {L}}_{3}}&{}\\{}&{}&{}&{{\tilde {L}}_{4}}\\\end{matrix}}\right)

,

(23)

where ${{\tilde {L}}_{1}}=(2+2\varepsilon )-2(\varepsilon \cos({{\theta }_{1}})+\cos({{\theta }_{2}}))$ , ${{\tilde {L}}_{2}}=(2+2\varepsilon )-2(\varepsilon \cos({{\bar {\theta }}_{1}})+\cos({{\bar {\theta }}_{2}}))$ , ${{\tilde {L}}_{3}}=(2+2\varepsilon )-2(\varepsilon \cos({{\bar {\theta }}_{1}})+\cos({{\theta }_{2}}))$ and ${{\tilde {L}}_{4}}=(2+2\varepsilon )-2(\varepsilon \cos({{\theta }_{1}})+\cos({{\bar {\theta }}_{2}}))$ .

The restriction operator ${\hat {I}}_{h}^{2h}(\theta )$ is a 1x4 matrix, and is given by:

{\hat {I}}_{h}^{2h}=\left({\begin{matrix}{\tilde {I}}_{h}^{2h}\left({{\theta }^{(0,0)}}\right)&{\tilde {I}}_{h}^{2h}\left({{\theta }^{(1,1)}}\right)&{\tilde {I}}_{h}^{2h}\left({{\theta }^{(1,0)}}\right)&{\tilde {I}}_{h}^{2h}\left({{\theta }^{(0,1)}}\right)\\\end{matrix}}\right)

,

(24)

For the ${\mbox{INJ}}$ restricion operator, ${\overset {}{\mathop {{\tilde {I}}_{h}^{2h}}}}\,\left({{\theta }^{\alpha }}\right)=1$ , for the ${\mbox{HW}}$ restriction operator, ${\overset {}{\mathop {{\tilde {I}}_{h}^{2h}}}}\,\left({{\theta }^{\alpha }}\right)={\frac {1}{4}}(2+\cos {{\bar {\theta }}_{1}}+\cos {{\bar {\theta }}_{2}})$ , for the ${\mbox{FW}}$ restriction operator, ${\overset {}{\mathop {{\tilde {I}}_{h}^{2h}}}}\,\left({{\theta }^{\alpha }}\right)={\frac {1}{4}}(1+\cos {{\bar {\theta }}_{1}})(1+\cos {{\bar {\theta }}_{2}})$ , for the ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ (see Eq.(8)), ${\overset {}{\mathop {{\tilde {I}}_{h}^{2h}}}}\,\left({{\theta }^{\alpha }}\right)={\frac {1}{2}}(1+\cos {{\bar {\theta }}_{1}})$ and for the ${\textstyle {\mbox{PW}}_{\mbox{y}}}$ (see Eq.(8)), ${\overset {}{\mathop {{\tilde {I}}_{h}^{2h}}}}\,\left({{\theta }^{\alpha }}\right)={\frac {1}{2}}(1+\cos {{\bar {\theta }}_{2}})$ .

The prolongation operator ${\hat {I}}_{2h}^{h}(\theta )$ is a 4x1 matrix, and is given by:

{\hat {I}}_{2h}^{h}\left(\theta \right)=\left({\begin{matrix}{\overset {}{\mathop {{\tilde {I}}_{2h}^{h}}}}\,\left({{\theta }^{(0,0)}}\right)\\{\overset {}{\mathop {{\tilde {I}}_{2h}^{h}}}}\,\left({{\theta }^{(1,1)}}\right)\\{\overset {}{\mathop {{\tilde {I}}_{2h}^{h}}}}\,\left({{\theta }^{(1,0)}}\right)\\{\overset {}{\mathop {{\tilde {I}}_{2h}^{h}}}}\,\left({{\theta }^{(0,1)}}\right)\\\end{matrix}}\right)

,

(25)

For the bilinear prolongation operator, ${\overset {}{\mathop {{\tilde {I}}_{2h}^{h}}}}\,\left({{\theta }^{\alpha }}\right)=(1+\cos {{\bar {\theta }}_{1}})(1+\cos {{\bar {\theta }}_{2}})$ and for the 7-point prolongation operator, ${\overset {}{\mathop {{\tilde {I}}_{2h}^{h}}}}\,\left({{\theta }^{\alpha }}\right)=\left(1+\cos {{\bar {\theta }}_{1}}+\cos {{\bar {\theta }}_{2}}+\cos({{\bar {\theta }}_{1}}-{{\bar {\theta }}_{2}})\right)$ [10].

The operator of the grid coarse ${{\left({{\hat {L}}_{2h}}(2\theta )\right)}^{-1}}$ is a 1x1 matrix, and for the discrete Laplace operators, ${{\tilde {L}}_{2h}}$ is represented by ${{\tilde {L}}_{2h}}\,(2\theta )=\sum \limits _{k}{{{s}_{k,2h}}{{e}^{i2\,\theta \,k}}}$ or ${{\tilde {L}}_{2h}}={\frac {(2+2\varepsilon )-2(\varepsilon \cos(2{{\theta }_{1}})+\cos(2{{\theta }_{2}}))}{2{{h}^{2}}}}$ .

A representation for the operator of two grids ${\textstyle M_{h}^{2h}}$ can be obtained by a matrix ${\hat {M}}_{h}^{2h}(\theta )$ of the form

,

(26)

where ${\hat {K}}_{h}^{2h}(\theta )$ is given by Eq. (21) and ${{\hat {S}}_{h}}(\theta )$ is a 4x4 matrix and represents the smoothing operator ${{S}_{h}}(\theta )$ given by:

{{\hat {S}}_{h}}=\left({\begin{matrix}{{\tilde {S}}_{h}}({{\theta }^{(0,0)}})&{}&{}&{}\\{}&{{\tilde {S}}_{h}}({{\theta }^{(1,1)}})&{}&{}\\{}&{}&{{\tilde {S}}_{h}}({{\theta }^{(1,0)}})&{}\\{}&{}&{}&{{\tilde {S}}_{h}}({{\theta }^{(0,1)}})\\\end{matrix}}\right)

.

(27)

In order to perform the LFA using the ${\textstyle {\mbox{ILU}}}$ solver, the smoothing operator ${{S}_{h}}$ , according to [6], is given by

,

(28)

with

.

(29)

where ${{\lambda }_{h}}(\theta )=1$ , for ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ , $\lambda _{h}^{R}(\theta )\,={{p}_{1}}{{e}^{i(2{{\theta }_{1}}-{{\theta }_{2}})}}+{{p}_{3}}+{{p}_{2}}{{e}^{i(-2{{\theta }_{1}}+{{\theta }_{2}})}}$ and for ${\textstyle {\mbox{ILU}}_{\mbox{NE}}}$ , $\lambda _{h}^{R}(\theta )\,={{p}_{1}}{{e}^{i(-{{\theta }_{1}}+2{{\theta }_{2}})}}+{{p}_{3}}+{{p}_{2}}{{e}^{i({{\theta }_{1}}-2{{\theta }_{2}})}}.$ .

The asymptotic convergence factor $\rho \left(M_{h}^{2h}\right)$ can be calculated by

,

(30)

where $\Lambda =\left\{\theta \in {{T}^{low}}:\,{{\tilde {L}}_{h}}(\theta )=0\,\,{\text{or}}\,\,{{\tilde {L}}_{2h}}(\theta )=0\right\}$ and $\rho \left({\hat {M}}_{h}^{2h}(\theta )\right)$ is the spectral radius of the 4x4 matrix ${\hat {M}}_{h}^{2h}(\theta )$ .

In this work, LFA was used to determine the asymptotic convergence factor of the multigrid method ${\bigl (}\rho \left(M_{h}^{2h}\right)={{\rho }_{loc}}{\bigr )}$ combining ${\mbox{ILU}}$ solvers in several directions (such as ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ and ${\textstyle {\mbox{ILU}}_{\mbox{NE}}}$ ), ${\mbox{FW}}$ , HW, INJ, ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ and ${\textstyle {\mbox{PW}}_{\mbox{y}}}$ restriction operators and bilinear and 7-point prolongation operators.

4. Numerical results

An orthotropic diffusion equation was solved using 7-point ILU solver in different directions. Several restriction operators and two prolongation operators were employed. We proposed an algorithm that presents the lowest asymptotic convergence factor values and the lowest computational cost for the multigrid method.

Equation (4) was assessed for $\varepsilon ={{10}^{\kappa }}$ and $\varepsilon ={{10}^{-\kappa }}$ , with $\kappa \in \mathrm {K} =\{0,\,\,1,\,\,2,\,\,3,\,\,4,\,\,5,\,\,6,\,\,7\}$ . When $\varepsilon ={{10}^{\kappa }}$ or $\varepsilon ={{10}^{-\kappa }}$ in this work, there is symmetric orthotropy. For instance, $\varepsilon ={{10}^{2}}$ is an orthotropy symmetric to $\varepsilon ={{10}^{-2}}$ .

Section 4.1 presents the convergence analysis by means of LFA. Only the optimum components obtained via LFA will be used in the complexity analysis in section 4.2.

4.1. Convergence Analysis

Figure 3 depicts ${{\rho }_{loc}}$ , given by Eq. (30), with ${\textstyle {\mbox{ILU}}}$ in the EN, NE, ES, SE directions, ${\mbox{FW}}$ restriction, bilinear prolongation, number of inner iterations $v=2$ , $\varepsilon ={{10}^{\kappa }}$ and $\varepsilon ={{10}^{-\kappa }}$ , with $\kappa \in K$ .

Figure 3.

versus orthotropy coefficients

with

in different directions.

It is noticed that for $0<\varepsilon <<1$ , ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ has a good performance. For $\varepsilon >>1$ , ${\mbox{ILU}}_{\mbox{NE}}$ also has a good performance, that is, ${{\rho }_{loc}}<<1$ . By using ${\textstyle {\mbox{ILU}}}$ solvers in the ES and SE directions, the multigrid method did not present a good performance for any of the orthotropy coefficients studied.

For the analyses presented below, tests were carried out using only the solvers that had the best performances in previous analysis.

Figure 4 presents ${{\rho }_{loc}}$ using as solvers, ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ for $0<\varepsilon <<1$ and ${\textstyle {\mbox{ILU}}_{\mbox{NE}}}$ for $\varepsilon >>1$ ; $\nu =2$ ; ${\mbox{FW}}$ restriction; 7-point and bilinear prolongation; $\varepsilon ={{10}^{\kappa }}$ and $\varepsilon ={{10}^{-\kappa }}$ , with $\kappa \in K$ .

Figure 4.

versus orthotropy coefficients

with different interpolation operators.

It can be observed that the restriction|prolongation combinations ${\mbox{FW}}$ |bilinear and ${\mbox{FW}}$ |7-points had a good performance ${\bigl (}{{\rho }_{loc}}<<1{\bigr )}$ and presented very similar convergence factors.

Bilinear prolongation operator was used in the following analysis as it is easy to program and demands fewer memory resources. The asymptotic convergence factors were compared with different restriction operators.

Figure 5 presents ${{\rho }_{loc}}$ using as solvers, ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ for $0<\varepsilon <<1$ and ${\textstyle {\mbox{ILU}}_{\mbox{NE}}}$ for $\varepsilon >>1$ ; $\nu =2$ ; ${\mbox{FW}}$ , HW, INJ, ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ and ${\textstyle {\mbox{PW}}_{\mbox{y}}}$ restriction; bilinear prolongation; $\varepsilon ={{10}^{\kappa }}$ and $\varepsilon ={{10}^{-\kappa }}$ , with $\kappa \in K$ .

Figure 5.

versus orthotropy coefficients

with different restriction operators.

Figure 5 demonstrates that for $\varepsilon ={{10}^{\kappa }}$ and $\varepsilon ={{10}^{-\kappa }}$ , with $\kappa \in K$ (symmetric orthotropies), ${{\rho }_{loc}}$ presents very similar values. It is noted that for orthotropic problems ${\bigl (}\kappa \neq 0{\bigr )}$ , the lowest values for ${{\rho }_{loc}}$ are achieved with ${\mbox{FW}}$ and ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ restriction, which show very similar values.

Based on the results presented, we propose Algorithm 1, which combines ILU solver in different directions, with ${\mbox{FW}}$ and ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ restrictions. The algorithm is presented below. The abbreviation REST, used in the algorithm represents any of the restrictions ( ${\mbox{FW}}$ or ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ ) previously defined.

Algorithm 1.
_______________________________________________________

if $\varepsilon >1$ then

Apply

smoothing with REST restriction

else if

then

Apply

smoothing with

restriction

else

Apply

REST restriction

end if
_______________________________________________________

Remark 1: Pinto et al. [14] solved an anisotropic diffusion problem using ILU in triangular grids and several anisotropies not aligned with x or y. The authors noted that ILU_NE and ILU_EN were efficient for some of the anisotropies, making it is possible to adapt this algorithm to an alternating form so it will work well for any anisotropy.

Remark 2: One of the biggest problems in the literature is the numerical resolution of the Navier-Stokes equation. Depending on its numerical formulation (simplec, projections [19]), a great computational effort is required at the numerical solution of the continuity equation, which can be represented by Poisson’s equation. Moreover, the algorithm depends on the mesh sweep and is independent of the complexity of the proposed problem equation. Therefore, this algorithm can be adapted to certain orthotropic problems with a certain degree of complexity.

Next, the asymptotic convergence factor ${{\rho }_{loc}}$ , calculated by LFA, and the empiric asymptotic convergence factor $\rho _{h}$ , for different orthotropy coefficients, are presented.

Figure 6 shows Algorithm 1 with REST ${\textstyle ={\mbox{PW}}_{\mbox{x}}}$ , $\nu =2$ and bilinear prolongation.

Figure 6.

and

versus orthotropy coefficients

.

It is observed that $\rho _{loc}\approx \rho _{h}<<1$ for every orthotropy coefficients assessed. Furthermore, ${{\rho }_{loc}}$ calculated by LFA is in accordance with $\rho _{h}$ calculated experimentally.

Figure 7 depicts the numerical asymptotic convergence factor ${{\rho }_{loc}}$ calculated by LFA and the experimental asymptotic convergence factor $\rho _{h}$ , for different orthotropy coefficients for different grids. Algorithm 1 with REST = ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ , $\nu =2$ and bilinear prolongation was used. As the grid becomes more refined, $\rho _{h}\rightarrow \rho _{loc}$ for every orthotropy coefficient analyzed, what demonstrates the robustness of the methodology assessed.

Figure 7.

and

versus orthotropy coefficients

for different number of grid points.

Some of the data presented in Figure 7 can be better visualized in Table 1.

Table 1.

and

for some orthotropy coefficients

and different number of grid points.

$\varepsilon$	$\rho _{h}$ $(N=513\times 513)$	$\rho _{h}$ $(N=1025\times 1025)$	$\rho _{h}$ $(N=2049\times 2049)$	$\rho _{l}oc$
$10^{-5}$	$4.181939\times {{10}^{-4}}$	$0.006544947$	$0.01993340$	$0.02943536$
$10^{-4}$	$0.01569827$	$0.025212810$	$0.02806990$	$0.02943000$
$10^{-3}$	$0.02748596$	$0.028578500$	$0.02884448$	$0.022941390$
$10^{-2}$	$0.02858316$	$0.028703710$	$0.02874592$	$0.02921000$
$10^{-1}$	$0.02683346$	$0.026852440$	$0.02685995$	$0.02725823$

Next section presents the complexity analysis of multigrid. For the analysis, multigrid was built with the components that had the best convergence factors according to LFA. In addition, a comparison between partial weighting and full weighting will be presented.

4.2. Complexity Analysis

In order to assess the effect of the number of unknowns on CPU time, optimum components obtained via LFA were used. Figures 8(a) and 8(b) show, for ${\mbox{FW}}$ and ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ restrictions, respectively, that for the isotropic problem ${\bigl (}\varepsilon =1{\bigr )}$ , the ${\textstyle t_{CPU}}$ is not lower. As the problem becomes more orthotropic ${\bigl (}0<\varepsilon <<1\,\,\,{\text{or}}\,\,\,\varepsilon >>1{\bigr )}$ , the $t_{CPU}$ decreases for every N value assessed. For every orthotropy coefficient assessed, the $t_{CPU}$ with ${\mbox{FW}}$ restriction is very similar to the $t_{CPU}$ with ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ restriction, that is, ${\textstyle t_{CPU}\left(FW\right)\approx t_{CPU}\left({\mbox{PW}}_{\mbox{x}}\right)}$ .

It is also observed for symmetric orthotropies ${\bigl (}\varepsilon ={{10}^{-\kappa }}\,\,\,{\text{and}}\,\,\,\varepsilon ={{10}^{\kappa }}{\bigr )}$ with $\kappa \in \{1,2,3,4\}$ , that the values of $t_{CPU}$ obtained are extremely similar.


Figure 8. CPU time versus number of nodes (N).

In order to assess the performance of the multigrid method with different anisotropy coefficients, a curve adjustment of the form ${{t}_{CPU}}=c{{N}^{p}}$ [20] was made, where $p$ represents the complexity order of the solver, N is the number of grid points and $N$ $c$ is a constant that depends on the method. The closer the value of $p$ is to one, the better the performance of the method used. Ideally, multigrid presents $p=1$ , what means that the CPU time grows linearly with the increase of N. Results are shown in Table 2 for both restrictions assessed $N$ ( ${\mbox{FW}}$ and ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ ).

One can observe in Table 2 that, for every orthotropy employed, the multigrid method has a good performance, since $p\approx 1$ in every case. These results prove the efficiency and robustness of Algorithm 1, proposed in this work.

Table 2. Complexity order

for different orthotropy coefficients

.

$\varepsilon$	${\textstyle p({\mbox{PW}}_{\mbox{x}})}$	${\textstyle p({\mbox{FW}})}$
$10^{-4}$	$1.07747$	$1.07733$
$10^{-2}$	$1.05023$	$1.05894$
$1$	$1.05940$	$1.04380$
$10^{2}$	$1.07255$	$1.06199$
$10^{4}$	$1.07627$	$1.07775$

The values obtained for the convergence factor, presented in section 4.1, and for the complexity order concerning to the ${\text{PW}}_{x}$ and ${\mbox{FW}}$ restriction operators (Table 2) are quite similar and thus insufficient to decide which one results in a more efficient algorithm.

To complement the analysis, the number of arithmetical operations performed in each V-cycle and at the restriction step for each one of the operators was assessed.

These arithmetical operations concern to floating-point operations (flops) performed during the iterative process and are not affect by the hardware used. Each addition, multiplication and division operation correspond to 1 flop.

Tests were carried out for $N_{10}=10$ ( $N_{10}$ is the number of points of the finest grid, considering a problem whose maximum number of levels is $L_{\text{max}}=10$ ) and for some values of $\varepsilon$ . Table 3 presents the ratio between number of flops of a V-cycle and number of points of the finest grid $N_{10}$ . Table 4 shows the ratio between number of flops performed in each restriction and the number of points of the finest grid $N_{10}$ .

Table 3. Ratio between number of flops of a V-cycle and the number of points of the finest grid.

$\varepsilon$	${\textstyle {\mbox{flops}}({\text{V-cycle}}\|{\mbox{PW}}_{\mbox{x}})/N_{10}}$	${\textstyle {\mbox{flops}}({\text{V-cycle}}\|{\mbox{FW}})/N_{10}}$
$10^{-2}$	$1510.221554$	$1543.296057$
$10^{-1}$	$1798.299366$	$1837.988770$
$1$	$2368.277388$	$2126.896785$
$10^{1}$	$1860.997604$	$1900.687008$
$10^{2}$	$1564.958717$	$1598.033220$

Table 4. Ratio between number of flops of the restriction and number of points of the finest grid.

$\varepsilon$	${\textstyle {\mbox{flops}}({\mbox{PW}}_{\mbox{x}})/N_{10}}$	${\textstyle {\mbox{flops}}({\mbox{FW}})/N_{10}}$
$10^{-2}$	$11.57607615$	$44.65057942$
$10^{-1}$	$13.89129130$	$53.58069530$
$1$	$18.37833483$	$62.02688007$
$10^{1}$	$13.89129137$	$53.58069530$
$10^{2}$	$11.57607615$	$44.65057942$

According to Table 3, the multigrid cycle that requires the lowest number of flops is the cone with ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ operator, except for the isotropic case ${\bigl (}\varepsilon =1{\bigr )}$ . Considering only the restriction step, results presented in Table 4 show a great advantage of the ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ operator over the ${\mbox{FW}}$ operator regarding the number of flops performed. For every case, the number of flops for ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ is roughly 75% lower than the number of flops for ${\mbox{FW}}$ .

Remark 3: 75% of the reduction in the number of operations in the restriction was expected. However, this has little impact on the total cost of the cycle, which shows the great concentration of operations in the execution of the solver.

The remaining orthotropy coefficients assessed showed similar performances to those presented in Figure 5 and Tables 3 and 4, what confirms the efficiency and robustness of the algorithm proposed, in addition to the low computational cost with the use of the ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ operator.

5. Conclusions

- For the ${\mbox{ILU}}$ directions assessed (EN, NE, ES, SE) for standard multigrid method ( ${\mbox{FW}}$ restriction operator and bilinear prolongation), it is concluded that $\rho _{loc}\approx 0.02$ when using ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ for $0<\varepsilon <<1$ and ${\textstyle {\mbox{ILU}}_{\mbox{NE}}}$ for $\varepsilon >>1$ .

- With ${\mbox{FW}}$ restriction, ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ for $0<\varepsilon <<1$ and ${\mbox{ILU}}_{\mbox{NE}}$ for $\varepsilon >>1$ , results showed that the 7-point and bilinear prolongation operators presented a similar performance, and for every value of $\varepsilon$ assessed, $\rho _{loc}<<1$ was obtained.

- With bilinear interpolation, ${\textstyle {\mbox{ILU}}_{\mbox{EN}}}$ for $0<\varepsilon <<1$ and ${\mbox{ILU}}_{\mbox{NE}}$ for $\varepsilon >>1$ , the lowest values of ${{\rho }_{loc}}$ are obtained with ${\mbox{FW}}$ and ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ restriction operators, and the values of ${{\rho }_{loc}}$ with these operators are very similar.

- Using Algorithm 1, ${{\rho }_{loc}}\approx {{\rho }_{h}}<<1$ for every orthotropy coefficient assessed and ${{\rho }_{h}}\to {{\rho }_{loc}}$ as the grid becomes more refined.

- The ${\textstyle t_{CPU}\left({\mbox{FW}}\right)\approx t_{CPU}\left({\mbox{PW}}_{\mbox{x}}\right)}$ for every value of $\varepsilon$ assessed.

- The complexity order $p$ of the multigrid method with Algorithm 1 is close to one for every orthotropy assessed. For $\varepsilon ={{10}^{-4}}$ , for example, $p=1.07747$ with this algorithm.

- The computational cost of multigrid depends on the number of flops of the restriction in a V-cycle. Using Algorithm 1 with ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ restriction, the computational cost is 75% lower than with ${\mbox{FW}}$ restriction.

- The Algorithm 1 with ${\textstyle {\mbox{PW}}_{\mbox{x}}}$ restriction proposed in this work is efficient, robust and has low computational cost.

Acknowledgements

The authors would like to acknowledge the Graduate Program in Numerical Methods for Engineering (PPGMNE) of the Federal University of Parana (UFPR). The first author would like to thank the Federal Institute of Education, Science and Technology of Santa Catarina (IFSC) for the financial support.

References

[1] Thekale T. Gradl, Klamroth K., Rüde U. Optimizing the number of multigrid cycles in the full multigrid algorithm. Numerical Linear Algebra with Applications, Vol. 17, 199–210, 2010.

[2] Pletcher R.H., Tannehill J.C., Anderson D.A. Computational fluid mechanics and heat Transfer. 3ª ed. CRC Press, USA, 2013.

[3] G.H. Golub, J.M. Ortega, Scientific Computing and Differential Equations: an Introduction to Numerical Methods, Academic Press, 1992.

[4] Y. Saad, Iterative Methods for Sparse Linear Systems, 2ªed., PWS, Philadelphia, 2003.

[5] W.L. Briggs, V.E. Henson, S.F. Mccormick, A Multigrid Tutorial, 2ª ed., SIAM, USA, 2000.

[6] U. Trottenberg, C. Oosterlee, A. Schüller, Multigrid, Academic Press, England, 2001.

[7] P. Wesseling, An Introduction to Multigrid Methods, John Wiley & Sons, England, 1992.

[8] F. Oliveira, M.A.V. Pinto, C.H. Marchi, L.K. Araki. Optimized partial semicoarsening multigrid algorithm for heat diffusion problems and anisotropic grids. Applied Mathematical Modelling, Vol. 36 (2012) 4665–4676.

[9] J.A. Rabi, M.J.S. de Lemos. Optimization of convergence acceleration in multigrid numerical solutions of conductive-convective problems. Applied Mathematics and Computational, Vol. 124 (2001) 215-226.

[10] R. Wienands, W. Joppich, Practical Fourier Analysis for Multigrid Methods, CRC Press, USA, 2005.

[11] K. Johannsen. A robust 9-point ILU smoother for anisotropic problems, IWR Preprint, University of Heidelberg, 2005.

[12] S.A. Vinogradova, L.A. Krukier, The use of incomplete LU decomposition in modeling convection-diffusion processes in an anisotropic medium. Mathematical Models and Computer Simulations, Vol. 5 (2013) 190-197.

[13] G. Vassoler-Rutz, M.A.V. Pinto, R. Suero, Comparison of the physical anisotropy of multigrid method for two-dimensional diffusion equation, in: Proceedings of COBEM, Rio de Janeiro, Brazil, (2015) 6-11.

[14] M.A. V. Pinto, C. Rodrigo, F.J. Gaspar, C.W. Oosterlee. On the robustness of ILU smoothers on triangular grids, Applied Numerical Mathematics, Vol. 106 (2016), 37-52.

[15] S.R. Franco, F.J. Gaspar, M.A.V. Pinto, C. Rodrigo. Multigrid method based on a space-time approach with standard coarsening for parabolic problems. Applied Mathematics and Computation, Vol. 317 (2018) 25-34.

[16] M.L. Oliveira, M.A. V. Pinto, S.F.T. Gonçalves, G. Vassoler-Rutz. On the Robustness of the xy-Zebra-Gauss-Seidel Smoother on an Anisotropic Diffusion Problem. CMES., Vol.117 (2018) 251-270.

[17] F. Oliveira. Effect of Two-Dimensional Anisotropic Meshes on the Performance of the Geometric Multigrid Method. Tese de doutorado, UFPR, 2010. In portuguese.

[18] P. Wesseling, C.W. Oosterlee. Geometric Multigrid with Applications to Computational Fluid Dynamics. Journal of Computation and Applied Mathematics, Vol. 128 (2001) 311-334.

[19] J.L. Guermond, P. Minev, Jie Shen. An overview of prejection methods for incompressible flows. Computer Methods in Apllied Mechanics and Engineering, Vol. 195 (2006) 6011-6045.

[20] R.L. Burden, J.D. Faires, Numerical Analysis, 9ª ed., Cengage Learning, USA, 2010.

Latest revision as of 14:43, 6 July 2021

Abstract

1. Introduction

2. Mathematical and Numerical Models

2.1. Mathematical Model and Discretization

2.2. Multigrid Method and Computational Details

3. Local Fourier analysis

4. Numerical results

4.1. Convergence Analysis

4.2. Complexity Analysis

5. Conclusions

Acknowledgements

References

Document information

Document Score

Share this document

Keywords

@@ Line 1: / Line 1: @@
-<!-- metadata commented in wiki content
+== Abstract ==
+This paper proposes an efficient and robust algorithm for solving a physical orthotropy problem. The algorithm is based on choosing the most efficient restriction operator and on an incomplete LU decomposition suited for each orthotropy direction. Local Fourier Analysis (LFA) is carried out in order to increase the efficiency of the multigrid method. Pure diffusion with orthotropy aligned to the coordinate axis ''x'' is the model considered''.'' Equations are discretized by Finite Difference Method with uniform grid and second-order numerical scheme. Problems are solved with geometric multigrid method, correction scheme, V-cycle and standard coarsening ratio. The asymptotic convergence factor is calculated for different multigrid components, such as restriction operators, prolongation operators and solvers. Based on the optimum components obtained by LFA, we carried out experiments to analyze the complexity and computational cost of the algorithm proposed. The main conclusion is that the methodology proposed is efficient for the resolution of problems with strong orthotropy.
+'''Keywords''': Physical orthotropy, multigrid components, diffusion, local Fourier analysis
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+==1. Introduction ==
-On the robustness of multigrid method combining ILU and Partial Weight </div>
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+Computational Fluid Dynamics (CFD) is a branch of Computational Science that studies numerical methods used for simulating fluid flow problems. It is known that these methods usually have a high computational cost. In general, this happens as the problems that have to be solved require the resolution of algebraic equation systems whose coefficient matrices are large and sparse [1].
-on anisotropic diffusion problem</div>
-==Grazielli Vassoler Rutz==
+Linear systems are obtained by discretizing the mathematical model, which consists in approximating, through algebraic equations, each term of the mathematical model for each grid node or point. This process leads to an algebraic equation system of the form
-grazielli.vassoler[mailto:@ @]ifsc.edu.br
-Federal Institute of Santa Catarina - Campus Chapecó.
-Federal University of Paraná.
-Rua Nereu Ramos, 3450D, 89.813-000, Chapecó, Santa Catarina, Brazil.
-==Marcio Augusto Villela Pinto==
-[mailto:marcio_villela@ufpr.br marcio_villela@ufpr.br]
-Federal University of Paraná.
-Department of Mechanical Engineering (DEMEC), 81.531-980, Curitiba, Paraná, Brasil.
-==Simone de Fátima Tomazzoni Gonçalves==
-[mailto:simone.tg@ufpr.br simone.tg@ufpr.br]
-Federal University of Paraná.
-Department of Mechanical Engineering (DEMEC), 81.531-980, Curitiba, Paraná, Brasil.
--->
-Abstract: In this work it is proposed an efficient and robust algorithm for the solution of a physical anisotropy problem. This algorithm is based on the choice of the most efficient restriction operator and on an incomplete LU decomposition suited for each anisotropy direction. Local Fourier analysis is carried out in order to assist the project of an efficient multigrid method. The model considered is pure diffusion with anisotropy aligned to the coordinate axis ''x. ''Finite difference method with uniform grid and second-order numerical scheme is used for the discretization of equations. Problems are solved with geometric multigrid method, correction scheme, V-cycle and standard coarsening ratio. The asymptotic convergence factor is calculated for different multigrid components, such as restriction operators, prolongation operators and solvers. Based on the optimum components obtained by LFA, experiments are carried out for the analysis of complexity and computational cost for the algorithm proposed. The main conclusion is that the methodology proposed is efficient for the resolution of problems with strong anisotropy.
-Keywords: Physical anisotropy; Multigrid components; Diffusion; Local Fourier analysis.
-== <br />1. Introduction ==
-Computational Fluid Dynamics (CFD) is a branch of Computational Science that studies numerical methods for the simulation of fluid flows problems. It is known that these methods usually require a high computational cost. In general, this happens because the problems that have to be solved require the resolution of algebraic equation systems whose coefficients matrices are large and sparse [1].
-Linear systems are obtained with discretization of the mathematical model, which consists in approximating, through algebraic equations, each term of the mathematical model for each grid node or point. This process leads to an algebraic equation system of the form
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
-|<math>AT=b</math>
+|<math>AT=b</math>,
 |  style="text-align: right;width: 5px;text-align: right;white-space: nowrap;"|(1)
 |}
@@ Line 55: / Line 21: @@
 </math> is the independent vector.
-In CFD, the methods traditionally employed in this process are: Finite Difference Method (FDM) [2], Finite Volume Method (FVM) [3] and Finite Element Method (FEM) [4].
+In CFD, the methods that are traditionally employed in this process are: Finite Difference Method (FDM) [2], Finite Volume Method (FVM) [3] and Finite Element Method (FEM) [4].
-The algebraic equation system given by Eq. (1) can be solved using direct or iterative methods. In this work, iterative methods were employed due to the aforementioned characteristics of linear systems in CFD (sparse and large coefficients matrices), for which iterative methods are recommended. The multigrid method is one of the most effective methods to accelerate the convergence of iterative methods for the resolution of linear or nonlinear systems, isotropic or anisotropic problems, among others [5-7].
+The algebraic equation system given by Eq. (1) can be solved using direct or iterative methods. In this work, iterative methods were employed due to the aforementioned characteristics of linear systems in CFD (sparse and large coefficients matrices), for which iterative methods are recommended. The multigrid method is one of the most effective methods to accelerate the convergence of iterative methods when solving linear or nonlinear systems, isotropic or anisotropic problems, among others [5-7].
-Anisotropic problems are fairly common in Engineering and appear in many phenomena, such as in the case of a material with different heat conduction behaviors for different directions. In this case, the coefficients of the differential equations are distinct among themselves and generate, what is called, physical anisotropy. Anisotropies can also appear from discretization of grids with different spacing in each direction, for instance, boundary layer problems. This is called geometric anisotropy [5,6]. The efficiency of the multigrid method has not yet been fully achieved for problems with strong anisotropy, either physical or geometric [8].
+Anisotropic problems are fairly common in Engineering and appear in many phenomena, such as when a material has different heat conduction behaviors in different directions. In this case, the coefficients of the differential equations are distinct among themselves and generate what is called physical anisotropy. Anisotropies can also appear from discretization of grids with different spacing in each direction, for instance, boundary layer problems. This is called geometric anisotropy [5,6]. The efficiency of the multigrid method has not yet been fully achieved for problems with strong anisotropy, either physical or geometric [8].
-Physical anisotropy problems have been investigated by Rabi and de Lemos [9], who discretized the two-dimensional advection-diffusion equation combining null and constant coefficients. Finite volume method was used in the discretization of the equations. Multigrid method was employed using correction scheme, Gauss-Seidel solver and V- and W-cycles. The authors presented a study of the different speed ranges (null and constant), number of grids, number of smoothing steps at each grid level and different solvers. They concluded that there was a significant reduction in the computational effort when the speed range values were increased.
+Physical anisotropic convection problems have been investigated by Rabi and de Lemos [9], who discretized two-dimensional pure diffusion, pure advection and advection-diffusion equations by applying the finite volume method. The multigrid method was employed using correction scheme and V- and W-cycles. The authors presented a study on the different speed ranges, number of grids, number of smoothing steps at each grid level and different solvers. They concluded that there was a significant reduction in the computational effort required for increasing the values of the components of the advection velocity.
-Wienands and Joppich [10] presented an in-depth study on the Local Fourier Analysis (LFA) and its application on several problems, which included anisotropic problems. The authors calculated the convergence factor of the multigrid method for the anisotropic diffusion equation with different solvers and restriction and prolongation operators.
+Wienands and Joppich [10] presented an in-depth study on the Local Fourier Analysis (LFA) and its application on several problems, including anisotropic problems. The authors calculated the convergence factor of the multigrid method for an anisotropic diffusion equation with different solvers and restriction and prolongation operators.
-Johannsen [11] solved an anisotropic diffusion problem using finite volume method for discretizing the equations and 9-point incomplete LU (ILU) decomposition method for solving the linear equations systems. The author employed LFA to demonstrate the superior smoothing properties of ILU.
+Johannsen [11] solved an anisotropic diffusion problem using finite volume method for discretizing the equations and 9-point incomplete LU (ILU) decomposition for solving the systems of linear equations. The author employed LFA to demonstrate the superior smoothing properties of ILU.
-Oliveira et al. [8] assessed geometric anisotropy for different grids and aspect ratios. They also assessed some components of the multigrid method, such as: solvers, type of restriction, number of levels and number of inner iterations, among several coarsening algorithms. They concluded that Partial Weighting (PW) had a good performance.
+Oliveira et al. [8] evaluated geometric anisotropy for different grids and aspect ratios. They also assessed some components of the multigrid method, such as: solvers, type of restriction, number of levels and number of inner iterations, among several coarsening algorithms. They concluded that Partial Weighting (PW) had a good performance.
-Vinogradova and Krukier [12] solved a three-dimensional advection-diffusion problem with intermediate anisotropy using FDM for the discretization of the equations and ILU for the resolution of the linear equation systems. They concluded that the proposed methodology is efficient, but it has the disadvantage of having limitations in the coefficients of the mixed derivatives, which has no physical meaning.
+Vinogradova and Krukier [12] solved a three-dimensional advection-diffusion problem with intermediate anisotropy using FDM for discretizing equations and ILU for the resolution of the linear systems. They concluded that the proposed methodology is efficient, however, the coefficients of the mixed derivatives present limitations, which is a disadvantage and has no physical significance.
-Vassoler-Rutz et al. [11] analyzed the effect of physical anisotropy on multigrid method for two anisotropic diffusion problems. They used FAS scheme, V-cycle, and Modified Strongly Implicit (MSI) and Gauss-Seidel (GS) solvers. They concluded that, for strong anisotropies, the complexity order of the multigrid method is not suitable.
+Vassoler-Rutz et al. [13] analyzed the effect of physical anisotropy on the multigrid method for two anisotropic diffusion problems. They used FAS scheme, V-cycle as well as Modified Strongly Implicit (MSI) and Gauss-Seidel (GS) solvers. They concluded that, for strong anisotropies, the complexity order of the multigrid method is not suitable.
-Several works on the implementation of the multigrid method found in the literature demonstrate that the choice of the multigrid components is crucial for the convergence or not of the method. Trottenberg et al. [6] state that these choices are difficult and thus small changes can considerably improve convergence. In this sense, LFA can assist these choices as it allows to predict the performance of the multigrid method, since it provides estimates of the converge rates based on the variation of the multigrid method components.
+Several works on the implementation of the multigrid method found in the literature demonstrate that the choice of the multigrid components is crucial for the convergence or not of the method. Trottenberg et al. [6] state that this choice is difficult and thus small changes can considerably improve convergence. In this sense, LFA can help this choice as it allows to predict the performance of the multigrid method, since it provides estimates of the convergence rates based on the variation of the multigrid method components.
-Pinto et al. [14] solved the anisotropic diffusion problem using ILU in triangular grids. They used LFA to show the good smoothing properties of the solver and the asymptotic convergence of the multigrid.
+Pinto et al. [14] solved an anisotropic diffusion problem using ILU in triangular grids. They used LFA to highlight the good smoothing properties of the solver and the asymptotic convergence of the multigrid.
-Franco et al. [13] performed LFA in transient problems and obtained the critical value of the parameter that represents the level of space-time anisotropy for the 1D and 2D Fourier equations.
+Franco et al. [15] performed LFA in transient problems and obtained the critical value of the parameter that represents the level of space-time anisotropy for 1D and 2D Fourier equations.
-In this work, an efficient and robust method for solving physical anisotropy problems using LFA is proposed. A two-dimensional diffusion mathematical model is considered, in which physical anisotropy appears in the coefficients and it will be denominated diffusion anisotropy. Equations were discretized using FDM with second-order central difference scheme.
+Oliveria et al. [16] solved an 2D anisotropic diffusion equation. The equation was discretized by the Finite Difference Method (FDM) and Central Differencing Scheme (CDS). Correction Scheme (CS). An xy-zebra-GS smoother was proposed, which proved to be efficient and robust for the different anisotropy coefficients. They concluded that, the convergence factors calculated empirically and by LFA are in agreement.
+A particular case of anisotropy is denominated orthotropy, which happens when the anisotropy occurs in orthogonal directions. In this work, an efficient and robust method for solving physical orthotropy problems using LFA is proposed. A two-dimensional diffusion mathematical model is considered, in which physical orthotropy appears in the coefficients and it will be denominated diffusion orthotropy. Equations were discretized using FDM with second-order central difference scheme.
 The asymptotic convergence factor (<math display="inline">\rho_{loc}
-</math>) of the multigrid method was calculated through assessment of the ILU solver in different directions [7] and several restriction and prolongation operators. The results obtained by means of LFA were used to assess the influence of physical anisotropy on computational cost by means of CPU time and number of operations in each V-cycle and at the restriction step.
+</math>) of the multigrid method was calculated by assessing the ILU solver in different directions [7] as well as several restriction and prolongation operators. The results obtained via LFA were used to assess the influence of the diffusion orthotropy on the computational cost and took into account the CPU time and number of operations in each V-cycle and at the restriction step.
-The remainder of this work is organized as follows: section 2 presents the mathematical and numerical models. Section 3 discusses considerations regarding the LFA used. Section 4 presents the results of the convergence analysis and complexity analysis. Section 5 presents the conclusion.
+The remainder of this work is organized as follows: section 2 presents the mathematical and numerical models; section 3 discusses considerations regarding the LFA used; section 4 presents the results of the convergence analysis and complexity analysis; and section 5 presents the conclusion.
 == 2. Mathematical and Numerical Models ==
 For the problem presented below, the calculus domain used is given by  <math display="inline">{0}\leq{x}\leq{1}
 </math>, <math display="inline">{0}\leq{y}\leq{1}
-</math>and the discretization of the equations is done using a uniform grid with a number of points given by  <math display="inline">N=N_{x}.N_{y}
+</math> and the discretization of the equations is done using a uniform grid with a number of points given by  <math display="inline">N=N_{x}.N_{y}
 </math> , where <math display="inline">N_x
 </math> and  <math display="inline">N_y
-</math> are the number of points in the directions ''x'' and ''y'', respectively, including the boundaries.
+</math> are the number of points in the directions <math>x</math> and <math>y</math>, respectively, including the boundaries.
 ===2.1. Mathematical Model and Discretization===
-The diffusion anisotropy problem will be assessed through the two-dimension diffusion equation given by Eq. (2) [5,6]
+A model that exemplifies physical and geometric anisotropy for a two-dimensional diffusion equation is given by Trottenberg et al. (2001) as shown below,
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 103: / Line 72: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>\begin{cases} \varepsilon T_{xx}-T_{yy}=S \\ T(0,y)=T(x,0)=T(x,1)=T(1,y)=0 \end{cases}
+| <math display="block">-\left| {{g}^{2}}+\varepsilon \,{{w}^{2}} \right|\,{{u}_{xx}}+2\left( 1-\varepsilon  \right)g\,w\,{{u}_{xy}}-\left| {{w}^{2}}+\varepsilon \,{{g}^{2}} \right|\,{{u}_{yy}}=S
 </math>
 |}
@@ Line 109: / Line 78: @@
 |}
+where <math>g=\cos (\alpha )
+</math>, <math>w=sen\,(\alpha )
+</math>, <math>0\le \alpha \le \frac{\pi }{2}
+</math> and <math>0<\varepsilon <<1
+</math> or <math> \varepsilon >>1
+</math>.
+For <math>\alpha =\frac{\pi }{2}
+</math>, it is considered that the expression given by Eq. (2) is aligned with the axis of the coordinate ''y'', so it becomes
+{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;width: 100%;"
+|-
+| <math display="block">-\varepsilon \,{{u}_{xx}}-\,{{u}_{yy}}=S.
+</math>
+|}
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(3)
+|}
+From here, the diffusion orthotropic problem will be assessed by means of the two-dimensional diffusion equation given by Eq. (4) [5,6]
+{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;width: 100%;"
+|-
+| <math display="block">\left\{ \begin{align}
+  & -\varepsilon {{T}_{xx}}-\,{{T}_{yy}}=S \\
+ & T\left( 0,y \right)=T\left( x,0 \right)=T\left( x,1 \right)=T\left( 1,y \right)=0 \\
+\end{align} \right.
+</math>
+|}
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(4)
+|}
 where ''T'' is the temperature, <math display="inline">T_{xx}
@@ Line 124: / Line 131: @@
 | <math display="inline">S=2\left[ \varepsilon \left( 1-6{{x}^{2}} \right){{y}^{2}}\left( 1-{{y}^{2}} \right)+\left( 1-6{{y}^{2}} \right){{x}^{2}}\left( 1-{{x}^{2}} \right) \right]</math> and <math display="inline">T(x,y)=({{x}^{2}}-{{x}^{4}})({{y}^{4}}-{{y}^{2}})</math>.
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(3)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(5)
 |}
+Eq. (4) was discretized using FDM with CDS, resulting in
-Eq. (2) was discretized using FDM with CDS, resulting in
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
 |<math>{{a}_{P}}{{T}_{P}}+{{a}_{W}}{{T}_{W}}+{{a}_{N}}{{T}_{N}}+{{a}_{E}}{{T}_{E}}+{{a}_{S}}{{T}_{S}}={{b}_{P}}</math>,
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(4)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(6)
 |}
-where <math>T</math> is the system unknown.
+where <math>T</math> is the unknown of the system.
-Fig. 1(b) depicts the notation of the grid points in Fig. 1(a). The points P (central), W (west), E (east), N (north) and S (south) in Fig. 1(b) correspond to the points <math display="inline">(i,j),(i-1,j),(i+1,j),(i,j+1),(i,j-1)</math> in Fig. 1(a), respectively.
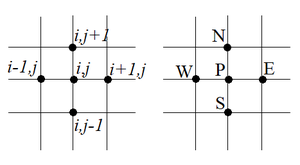
+[[#img-1|Figure 1]](b) depicts the notation of the grid points in [[#img-1|Figure 1]](a). The points P (central), W (west), E (east), N (north) and S (south) in [[#img-1|Figure 1]](b) correspond to the points <math display="inline">(i,j),(i-1,j),(i+1,j),(i,j+1),(i,j-1)</math> in [[#img-1|Figure 1]](a), respectively.
+<div id='img-1'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"| [[File:2345.png|thumb|centre]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 1'''. Points of a uniform two-dimensional grid
+|}
+The classic 5-point finite difference is not convergent for cases of general anisotropy, such as the example given by the full tensor
-               [[File:Figura1Grazielli.png|centre|thumb]]
-<nowiki>               </nowiki><span id="_Ref428667097"></span><span id="_Ref428707178"></span>
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
 |
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-|Figure 1: Points of a uniform two-dimensional grid.
+| <math>\left( \begin{matrix}
+      {{k}_{11}} & {{k}_{12}}  \\
+      {{k}_{21}} & {{k}_{22}}  \\
+   \end{matrix} \right)
+   </math>.
 |}
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |
 |}
-The discretization of Eq. (2) results in Eq. (4), and for the inner points, considering <math display="inline">h_{x}^{{}}=\frac{1}{N_{x}^{{}}-1}</math> and <math display="inline">h_{y}^{{}}=\frac{1}{N_{y}^{{}}-1}</math>.
+Therefore, this methodology cannot be generalized to any type of anisotropic problem. In this paper, we analyze a specific case of anisotropy given by the tensor
+{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
+|-
+|
+{| style="text-align: center; margin:auto;width: 100%;"
+|-
+| <math>\left( \begin{matrix}
+     \varepsilon  & 0  \\
+& 1  \\
+  \end{matrix} \right)
+  </math>,
+|}
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |
+|}
+which represents a case of orthotropy.
+The discretization of Eq. (4) results in Eq. (6), and for the inner points, considering <math display="inline">h_{x}^{{}}=\frac{1}{N_{x}^{{}}-1}</math> and <math display="inline">h_{y}^{{}}=\frac{1}{N_{y}^{{}}-1}</math>
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 161: / Line 199: @@
 | <math>{{a}_{P}}=\left( \frac{2\varepsilon }{h_{x}^{2}}+\frac{2}{h_{y}^{2}} \right)</math>, <math>{{a}_{W}}={{a}_{E}}=-\frac{\varepsilon }{h_{x}^{2}},  {{a}_{N}}={{a}_{S}}=-\frac{1}{h_{y}^{2}} </math>, <math>{{b}_{P}}={{S}_{P}}</math>.
 |}
-| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(5)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(7)
 |}
 For the boundaries north, south, east and west,<math display="inline">{{a}_{P}}=1  </math>, <math>{{a}_{W}}={{a}_{E}}={{a}_{N}}={{a}_{S}}=0</math>.
-===2.2. Multigrid method and computational details===
+===2.2. Multigrid Method and Computational Details===
-The multigrid method accelerates the convergence rate of iterative methods. It consists in employing a group of grids with different refinement levels. At each grid refinement level, the more oscillatory errors are smoothed, and only low frequency errors remain. After passing to another grid, the remaining low frequency errors become more oscillatory. The efficiency of this process, called smoothing, depends on the choice of a suitable solver.
+The multigrid method accelerates the convergence rate of iterative methods. It consists in employing a group of grids with different refinement levels. At each refinement level of the grid, the more oscillatory errors are smoothed, and only low frequency errors remain. After passing to another grid, the remaining low frequency errors become more oscillatory. The efficiency of this process, called smoothing, depends on the choice of a suitable solver.
 For employing multigrid, besides a solver with good smoothing properties, grid transfer operators are required (restriction and prolongation).
-In [8] and [16], restriction through partial weighting in the directions <math>x</math> and <math>y</math>, henceforth denoted by  <math display="inline">{\mbox{PW}}_\mbox{x}</math> and <math display="inline">{\mbox{PW}}_\mbox{y},</math> respectively, applied in problems involving geometric anisotropy was proposed. These operators, are given in stencil notation as
+In [8] and [17], restriction through partial weighting in the directions ''x'' and ''y'', henceforth denoted by <math>\text{P}{{\text{W}}_{\text{x}}}
+</math> and <math>\text{P}{{\text{W}}_{\text{y}}}
+</math>, respectively, applied in problems involving geometric anisotropy was proposed. These operators are given in stencil notation as
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 179: / Line 219: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>\text{P}{{\text{W}}_{\text{x}}}</math> : <math display="inline">I_{h}^{2h}=\frac{1}{4}\left( \begin{matrix}
+| <math>\text{P}{{\text{W}}_{\text{x}}}</math> : <math display="inline">I_{h}^{2h}=\frac{1}{4}{{\left[ \begin{matrix}
 & 0 & 0  \\
 & 2 & 1  \\
 & 0 & 0  \\
-\end{matrix} \right)
+\end{matrix} \right]}_{h}}
-</math>, <math>\text{P}{{\text{W}}_{\text{y}}}</math> : <math>I_{h}^{2h}=\frac{1}{4}\left( \begin{matrix}
+</math>, <math>\text{P}{{\text{W}}_{\text{y}}}</math> : <math>I_{h}^{2h}=\frac{1}{4}{{\left[ \begin{matrix}
 & 1 & 0  \\
 & 2 & 0  \\
 & 1 & 0  \\
-\end{matrix} \right)</math>.
+\end{matrix} \right]}_{h}}
+</math>.
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(6)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(8)
 |}
-In this work, such restriction was combined with 7-point incomplete LU decomposition (henceforth denoted by <math>\mbox{ILU}</math>). According to [17], this decomposition has a better convergence factor than 5-point incomplete LU decomposition for anisotropic problems.
+In this work, such restriction was combined with 7-point incomplete LU decomposition (henceforth denoted by ILU). According to [18], this decomposition has a better convergence factor than 5-point incomplete LU decomposition for orthotropic problems.
-In Eq. (2), discretized using FDM, the stencil for 5-point Laplacian operator is given by
+In Eq. (4), discretized using FDM, the stencil for the 5-point Laplacian operator is given by
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 205: / Line 247: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>{{L}_{h}}={{\left( \begin{matrix}
+| <math>{{L}_{h}}={{\left[ \begin{matrix}
 & -1 & 0  \\
     -\varepsilon  & 2+2\varepsilon  & -\varepsilon   \\
 & -1 & 0  \\
-\end{matrix} \right)}_{h}}
+\end{matrix} \right]}_{h}}
 </math>.
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(7)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(9)
 |}
-The <math>\mbox{ILU}</math> decomposition of this same operator will be given by
+The <math>\mbox{ILU}</math> decomposition of the same operator will be given by
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 222: / Line 264: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>{{L}_{h}}={{\left( \begin{matrix}
+| <math>{{L}_{h}}={{\left[ \begin{matrix}
     f & g & 0  \\
     c & d & q  \\
 & a & b  \\
-\end{matrix} \right)}_{h}}
+\end{matrix} \right]}_{h}}
 </math>,
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(8)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(10)
 |}
@@ Line 242: / Line 285: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>{{\overset{{}}{\mathop{L}}\,}_{h}}={{\overset{\hat{\ }}{\mathop{L}}\,}_{h}}{{\overset{\hat{\ }}{\mathop{U}}\,}_{h}}-{{R}_{h}}</math>,
+| <math>{{\overset{{}}{\mathop{L}}\,}_{h}}={{L}_{h}}{{U}_{h}}-{{R}_{h}}</math>,
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(9)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(11)
 |}
-where <math>{{\overset{\hat{\ }}{\mathop{L}}\,}_{h}}</math>   is a lower triangular matrix,   <math>{{\overset{\hat{\ }}{\mathop{U}}\,}_{h}}</math> is an upper triangular matrix and  <math>{{R}_{h}}</math> is the residual matrix.
+where <math>{{L}_{h}}</math>   is the stencil of a lower triangular matrix, <math>{{U}_{h}}</math> is the stencil of an upper triangular matrix and  <math>{{R}_{h}}</math> is the residual matrix.
 The iterative process for solving Eq. (4) can be:
@@ Line 258: / Line 301: @@
 |<math>{{r}^{m}}=b-A{{T}^{m}}</math>,
-<math>{{\overset{\hat{\ }}{\mathop{L}}\,}_{h}}{{y}^{m}}={{r}^{m}}\,</math>,
+<math>{{L}_{h}}\,{{y}^{m}}={{r}^{m}}\,</math>,
-<math>{{\overset{\hat{\ }}{\mathop{U}}\,}_{h}}\,{{\sigma }^{m}}={{y}^{m}}</math>,
+<math>{{U}_{h}}\,{{\sigma }^{m}}={{y}^{m}}</math>,
 <math>{{T}^{m+1}}={{T}^{m}}+{{\sigma }^{m}}</math>.
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(10)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(12)
 |}
-Depending on the ordination of the grid points, different directions can be obtained for the <math>\mbox{ILU}</math> decomposition. In lexicographical order,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> [17], is given by
+Depending on the ordination of the grid points, different directions can be obtained for the <math>\mbox{ILU}</math> decomposition. In lexicographical order,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> [18], is given by
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 274: / Line 317: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>{{\overset{\hat{\ }}{\mathop{L}}\,}_{h}}={{\left( \begin{matrix}
+| <math>{{L}_{h}}={{\left[ \begin{matrix}
 & 0 & 0  \\
     \gamma  & \delta  & 0  \\
 & \alpha  & \beta   \\
-\end{matrix} \right)}_{h}}, {{\overset{\hat{\ }}{\mathop{U}}\,}_{h}}={{\left( \begin{matrix}
+\end{matrix} \right]}_{h}}, {{U}_{h}}={{\left[ \begin{matrix}
     \zeta  & \eta  & 0  \\
 & \delta  & \mu   \\
 & 0 & 0  \\
-\end{matrix} \right)}_{h}}, {{R}_{h}}={{\left( \begin{matrix}
+\end{matrix} \right]}_{h}}, {{R}_{h}}={{\left[ \begin{matrix}
     {{p}_{2}} & 0 & 0 & 0 & {}  \\
     {} & 0 & {{p}_{3}} & 0 & {}  \\
     {} & 0 & 0 & 0 & {{p}_{1}}  \\
-\end{matrix} \right)}_{h}}
+\end{matrix} \right]}_{h}}
 </math>.
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(11)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(13)
 |}
-Another example of ordination for <math>\mbox{ILU}</math>,  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> [17], is given by
+Another example of ordination for <math>\mbox{ILU}</math>,  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> [18], is given by
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 302: / Line 344: @@
 |-
 | .
-<math>{{\overset{\hat{\ }}{\mathop{L}}\,}_{h}}={{\left( \begin{matrix}
+<math>{{L}_{h}}={{\left[ \begin{matrix}
     \zeta  & 0 & 0  \\
     \gamma  & \delta  & 0  \\
 & \alpha  & 0  \\
-\end{matrix} \right)}_{h}}, {{\overset{\hat{\ }}{\mathop{U}}\,}_{h}}={{\left( \begin{matrix}
+\end{matrix} \right]}_{h}}, {{U}_{h}}={{\left[ \begin{matrix}
 & \eta  & 0  \\
 & \delta  & \mu   \\
 & 0 & \beta   \\
-\end{matrix} \right)}_{h}}, {{R}_{h}}={{\left( \begin{matrix}
+\end{matrix} \right]}_{h}}, {{R}_{h}}={{\left[ \begin{matrix}
     {{p}_{1}} & {} & {}  \\
 & 0 & 0  \\
@@ Line 316: / Line 358: @@
 & 0 & 0  \\
     {} & {} & {{p}_{2}}  \\
-\end{matrix} \right)}_{h}}
+\end{matrix} \right]}_{h}}
 </math>.
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(12)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(14)
 |}
+The linear system given by Eq. (1) was solved using geometric multigrid method [5,6] with correction scheme (CS), V-cycle and zero initial guess.
-The linear equation system given by Eq. (1) was solved using the geometric multigrid method [5,6] with correction scheme (CS), V-cycle and zero initial estimate.
+The coarsening ratio is given by <math>r=2</math> (standard coarsening) [18]. The grid transfer operators employed were: Injection Restriction (INJ), Half Weighting (HW), Full Weighting (FW) [6], Partial Weighting in <math display="inline">x</math> (<math display="inline">{\mbox{PW}}_\mbox{x}</math> ), Partial Weighting in <math display="inline">y</math> (<math display="inline">{\mbox{PW}}_\mbox{y}</math>) as well as prolongation by bilinear interpolation and 7-point interpolation. The systems of equations obtained by means of discretization were resolved using 7-point ILU solvers in different directions (<math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math>, <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math>, among others).
-The coarsening ratio is given by <math>r=2</math> (standard coarsening) [17]. The grid transfer operators employed were: Injection Restriction (INJ), Half Weighting (HW), Full Weighting (<math>\mbox{FW}</math>) (see [6]), Partial Weighting in <math display="inline">x</math> (<math display="inline">{\mbox{PW}}_\mbox{x}</math> ), Partial Weighting in <math display="inline">y</math> (<math display="inline">{\mbox{PW}}_\mbox{y}</math>) and prolongation by bilinear interpolation and 7-point interpolation. The equation systems obtained by means of discretization were resolved using 7-point <math>\mbox{ILU}</math> solvers in different directions (<math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math>, <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math>, among others).
+The stop criterion used to interrupt the iterative process is based on the nondimensionlized residual norm. The residual of the system of algebraic equation is defined by
-The stop criterion used to interrupt the iterative process is based on the non-dimensional residual norm. The residual of the algebraic equation system is defined by
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 337: / Line 379: @@
 | <math display="inline">{{r}^{m}}=b-A{{T}^{m}}</math>,
 |}
-| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(13)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(15)
 |}
 where  <math>T^m</math> is the solution of the unknown in the iteration <math>m</math>.
-Considering  <math>{{L}^{m}}={{\left\| r_{{}}^{m} \right\|}_{1}}</math> and  <math>{{L}^{0}}={{\left\| r_{{}}^{0} \right\|}_{1}}</math> , if  <math>\frac{{{L}^{m}}}{{{L}^{0}}}\le tol</math> the iterative process is interrupted if  <math>tol={{10}^{-10}}</math> .
+Considering  <math>{{L}^{m}}={{\left\| r_{{}}^{m} \right\|}_{1}}</math> and  <math>{{L}^{0}}={{\left\| R_{{}}^{0} \right\|}_{1}}</math>, if  <math>\frac{{{L}^{m}}}{{{L}^{0}}}\le tol</math> the iterative process is interrupted if  <math>tol={{10}^{-10}}</math>.
 Double precision arithmetic was used for the simulations. The numerical codes were implemented in the Fortran 2003 language, using the Intel 9.1 Visual Fortran application. All numerical results were obtained in a computer with Intel Core i7 2.66 GHz processor, 16 GB RAM and Windows 8 operating system, 64-bit version.
-== 3. Local Fourier Analysis ==
+== 3. Local Fourier analysis ==
-LFA allows to predict the performance of the multigrid method as it supplies estimates of the convergence rate of its components. Therefore, LFA becomes a powerful tool in quantitative analysis and for the project of efficient multigrid methods.
-In order to perform the LFA, general discrete linear operators with constant coefficients are considered, which are defined in an infinite grid  <math>G_h</math> , where the influence of the boundaries can be dismissed [6].
+LFA allows to predict the performance of the multigrid method as it supplies estimates of the convergence rate of its components. Therefore, LFA becomes a powerful tool in quantitative analysis and in the research of efficient multigrid methods.
+In order to perform the LFA, general discrete linear operators with constant coefficients are considered, which are defined in an infinite grid <math>G_h</math> , where the influence of the boundaries can be dismissed [6].
 Consider the grid functions of the form of
@@ Line 360: / Line 403: @@
 | <math display="inline">{{\phi }_{h}}\left( \theta ,x \right)={{e}^{{i\theta x}/{h}\;}}</math> , with  <math display="inline">\theta =({{\theta }_{1}},{{\theta }_{2}})\in {{R}^{2}}</math> ,
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(14)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(16)
 |}
 where <math>x</math> varies in the infinite grid  <math>G_h</math> and  <math>\theta</math> is a parameter that characterize the frequency of the function concerning to grid  <math>G_h</math> .
-For  <math>-\pi \le \theta <\pi </math> , every function of the grid  <math>{{\phi }_{h}}\left( \theta ,x \right)</math> are eigenfunctions of a discrete operator that can be written by a stencil.
+For  <math>-\pi \le \theta <\pi </math> , every function of the grid  <math>{{\phi }_{h}}\left( \theta ,x \right)</math> are eigenfunctions of a discrete operator that can be written as a stencil.
 Thus,
@@ Line 374: / Line 417: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>{{L}_{h}}\,{{\phi }_{h}}\left( \theta ,x \right)=\overset{\tilde{\ }}{\mathop{{{L}_{h}}(}}\,\,\theta )\,{{\phi }_{h}}\left( \theta ,x \right)</math>,
+| <math>{{L}_{h}}\,{{\phi }_{h}}\left( \theta ,x \right)={{\tilde{L}}_{h}}(\theta ){{\phi }_{h}}\left( \theta ,x \right)</math>,
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(15)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(17)
 |}
@@ Line 386: / Line 429: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>{{L}_{h}}\,(\theta )={{\left[ {{s}_{k}} \right]}_{h}}, \overset{\tilde{\ }}{\mathop{{{L}_{h}}}}\,\,(\theta )=\sum\limits_{k}{{{s}_{k}}{{e}^{i\,\theta \,k}}}</math> and <math display="inline">{s}_{k}</math> is the stencil notation of the operator.
+| <math>{{L}_{h}}\,(\theta )={{\left[ {{s}_{k}} \right]}_{h}},  {{\tilde{L}}_{h}}(\theta )=\sum\limits_{k}{{{s}_{k}}{{e}^{i\,\theta \,k}}}</math>
 |}
-| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(16)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(18)
 |}
-For the smoothing and the analysis of two grids, it necessary to distinguish components of high and low frequency of  <math>G_h</math> in relation to  <math>G_{2h}</math> .
+and <math>{{s}_{k}}</math> is the stencil notation of the operator, were <math>k\in \{(-1,-1),\,(-1,0),(-1,1),...,(1,-1),(1,0),(1,1)\}</math> for  the 5-point stencil.
-It is known that [6] only if
+In order to smooth as well as to analyze the two grids, it is necessary to distinguish between components of low and high frequency of <math>G_h</math> and  <math>G_{2h}</math> .
+It is known that [6] only
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 402: / Line 447: @@
 | <math>{{\phi }_{h}}\left( \theta ,x \right)</math> with <math display="inline">-\frac{\pi }{2}\le \theta <\frac{\pi }{2}</math>,
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(17)
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(19)
 |}
@@ Line 410: / Line 455: @@
 For each  <math display="inline">\bar{\theta }\in \left[ -\frac{\pi }{2},\frac{\pi }{2} \right)\times \left[ -\frac{\pi }{2},\frac{\pi }{2} \right)</math>, three other frequency components  <math>{{\phi }_{h}}\left( \theta ,x \right)</math> with  <math display="inline">\theta \in [-\pi ,\pi )\times [-\pi ,\pi )</math> coincide in  <math>G_{2h}</math> with  <math>{{\phi }_{h}}\left( \bar{\theta },x \right)</math> and are not visible in  <math>G_{2h}</math> . Therefore, the low- and high-frequency components are defined as follows:
-<math>\varphi</math> is a low-frequency component<math>\Leftrightarrow \theta \in {{T}^{low}}=\left[ -\frac{\pi }{2},\frac{\pi }{2} \right)\times \left[ -\frac{\pi }{2},\frac{\pi }{2} \right)</math>
+<math>\phi</math> is a low-frequency component<math>\Leftrightarrow \theta \in {{T}^{low}}=\left[ -\frac{\pi }{2},\frac{\pi }{2} \right)\times \left[ -\frac{\pi }{2},\frac{\pi }{2} \right)</math>
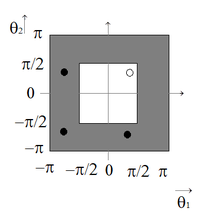
-<math>\varphi</math> is a high-frequency component<math>\Leftrightarrow \theta \in {{T}^{high}}=\left[ -\pi ,\pi  \right)\times \left[ -\pi ,\pi  \right)\backslash \left[ -\frac{\pi }{2},\frac{\pi }{2} \right)\times \left[ -\frac{\pi }{2},\frac{\pi }{2} \right)</math>. See Fig. 2.
+<math>\phi</math> is a high-frequency component<math>\Leftrightarrow \theta \in {{T}^{high}}=\left[ -\pi ,\pi  \right)\times \left[ -\pi ,\pi  \right)\backslash \left[ -\frac{\pi }{2},\frac{\pi }{2} \right)\times \left[ -\frac{\pi }{2},\frac{\pi }{2} \right)</math> ([[#img-2|Figure 2]]).
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-2'></div>
-<span style="text-align: center; font-size: 75%;"> [[Image:draft_Vassoler Rutz_344011008-image93.png|288px]] </span></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
-<span id='_Ref428218644'></span><span id='_Toc428200463'></span><span id='_Toc428200508'></span><span id='_Toc429758843'></span><span id='_Ref466666326'></span>
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
-|
+|style="padding:10px;"| [[File:234.png|200px|centre|thumb]]
-{| style="text-align: center; margin:auto;width: 100%;"
+|- style="text-align: center; font-size: 75%;"
-|-
+| colspan="1" style="padding:10px;"| '''Figure 2'''. Low- (inner white area) and high-frequency (hatched area) areas
-|Figure 2: Low- (inner white area) and high-frequency (hatched area) areas.
-|}
 |}
 Considering the frequencies
@@ Line 436: / Line 477: @@
    & {{\theta }_{i}}+\pi \,,\,\,\,\text{if}\,\,{{\theta }_{i}}<0 \\
   & {{\theta }_{i}}-\pi \,,\,\,\,\text{if}\,\,{{\theta }_{i}}\ge 0\,\,\, \\
-\end{align} \right.</math>.
+\end{align} \right.</math>,
 |}
-| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(18)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(20)
 |}
-The operator  <math>K_{h}^{2h}</math> is represented by a 4x4 matrix  <math>\hat{K}_{h}^{2h}</math> , as follows
+the correction operator of the coarse grid is given by <math>K_{h}^{2h}</math> ans is represented by a 4x4 matrix  <math>\hat{K}_{h}^{2h}</math> , as follows
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
@@ Line 449: / Line 490: @@
 | <math>\hat{K}_{h}^{2h}\left( \theta  \right)={{\hat{I}}_{h}}-\left( \hat{I}_{2h}^{h}\left( \theta  \right) \right){{\left( \hat{L}_{2h}^{{}}\left( 2\theta  \right) \right)}^{-1}}{{\left( \hat{I}_{h}^{2h}\left( \theta  \right) \right)}_{y}}\hat{L}_{h}^{{}}\left( \theta  \right)</math> with <math>\theta \in {{T}^{low}}</math>,
 |}
-| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(19)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(21)
 |}
-where  <math>\hat{I}_{h}^{{}}</math> is represented by a 4x4 identity matrix,  <math>{{\hat{L}}_{h}}(\theta )</math> is the 4x4 matrix, <math>\hat{I}_{h}^{2h}(\theta )</math>  is a 1x4 matrix,  <math>\hat{I}_{2h}^{h}(\theta )</math> is a 4x1 matrix and  <math>{{\left( {{{\hat{L}}}_{2h}}(2\theta ) \right)}^{-1}}</math> is a 1x1 matrix.
+where  <math>\hat{I}_{h}^{{}}</math> is represented by a 4x4 identity matrix.
-A representation for <math display="inline">M_{h}^{2h}</math> can be obtained by a matrix  <math>\hat{M}_{h}^{2h}(\theta )</math> of the form
+<math>{{\hat{L}}_{h}}(\theta )</math> is the 4x4 matrix:
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 461: / Line 502: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>\hat{M}_{h}^{2h}:={{({{\hat{S}}_{h}}(\theta ))}^{{{v}_{2}}}}\hat{K}_{h}^{2h}(\theta )\,{{({{\hat{S}}_{h}}(\theta ))}^{{{v}_{1}}}}</math>,
+| <math>{{\hat{L}}_{h}}=\left( \begin{matrix}
+   {{{\tilde{L}}}_{h}}({{\theta }^{(0,0)}}) & {} & {} & {}  \\
+   {} & {{{\tilde{L}}}_{h}}({{\theta }^{(1,1)}}) & {} & {}  \\
+   {} & {} & {{{\tilde{L}}}_{h}}({{\theta }^{(1,0)}}) & {}  \\
+   {} & {} & {} & {{{\tilde{L}}}_{h}}({{\theta }^{(0,1)}})  \\
+\end{matrix} \right)
+</math> ,
 |}
-| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(20)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(22)
 |}
-where <math>\hat{K}_{h}^{2h}(\theta )</math> is given by Eq. (19) and <math>{{\hat{S}}_{h}}(\theta )</math> is a 4x4 matrix and represents <math>{{S}_{h}}(\theta )</math>.
+where <math>{{\tilde{L}}_{h}}</math> are eigenvalues, evaluated by <math>{{\tilde{L}}_{h}}(\theta )=\sum\limits_{\kappa }{{{s}_{\kappa }}{{e}^{i{{\theta }^{\alpha }}\kappa }}}</math>, and <math>{{s}_{\kappa }}\in R</math> are stencil coefficients [7].
-Let it be
+The discrete Laplace operator given by Eq. (9) is represented by:
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
 |
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>\Lambda =\left\{ \theta \in \left[ -\frac{\pi }{2},\frac{\pi }{2} \right)\times \left[ -\frac{\pi }{2},\frac{\pi }{2} \right):\,{{\overset{\tilde{\ }}{\mathop{L}}\,}_{h}}(\theta )=0\,\,\text{or}\,\,{{\overset{\tilde{\ }}{\mathop{L}}\,}_{2h}}(\theta )=0 \right\}</math>.
+| <math>{{\hat{L}}_{h}}=\left( \begin{matrix}
+   {{{\tilde{L}}}_{1}} & {} & {} & {}  \\
+   {} & {{{\tilde{L}}}_{2}} & {} & {}  \\
+   {} & {} & {{{\tilde{L}}}_{3}} & {}  \\
+   {} & {} & {} & {{{\tilde{L}}}_{4}}  \\
+\end{matrix} \right)
+</math>,
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(21)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(23)
 |}
-The asymptotic convergence factor <math>\rho \left( M_{h}^{2h} \right)</math> can be calculated by
+where <math>{{\tilde{L}}_{1}}=(2+2\varepsilon )-2(\varepsilon \cos ({{\theta }_{1}})+\cos ({{\theta }_{2}}))</math>, <math>{{\tilde{L}}_{2}}=(2+2\varepsilon )-2(\varepsilon \cos ({{\bar{\theta }}_{1}})+\cos ({{\bar{\theta }}_{2}}))</math>, <math>{{\tilde{L}}_{3}}=(2+2\varepsilon )-2(\varepsilon \cos ({{\bar{\theta }}_{1}})+\cos ({{\theta }_{2}}))
+</math> and <math>{{\tilde{L}}_{4}}=(2+2\varepsilon )-2(\varepsilon \cos ({{\theta }_{1}})+\cos ({{\bar{\theta }}_{2}}))</math>.
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
+The restriction operator <math>\hat{I}_{h}^{2h}(\theta )
+</math> is a 1x4 matrix, and is given by:
+{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
 |
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-|<math>\rho \left( M_{h}^{2h} \right)=\sup \left\{ \rho \left( \hat{M}_{h}^{2h}(\theta ) \right):\,\,\theta \in {{T}^{low}},\,\,\theta \notin \Lambda  \right\}</math>,
+| <math>\hat{I}_{h}^{2h}=\left( \begin{matrix}
+   \tilde{I}_{h}^{2h}\left( {{\theta }^{(0,0)}} \right) & \tilde{I}_{h}^{2h}\left( {{\theta }^{(1,1)}} \right) & \tilde{I}_{h}^{2h}\left( {{\theta }^{(1,0)}} \right) & \tilde{I}_{h}^{2h}\left( {{\theta }^{(0,1)}} \right)  \\
+\end{matrix} \right)
+</math>,
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(22)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(24)
 |}
-where <math>\rho \left( \hat{M}_{h}^{2h}(\theta ) \right)</math> is the spectral radius of the 4x4 matrix <math>\hat{M}_{h}^{2h}(\theta )</math>.
+For the <math>\mbox{INJ}</math> restricion operator,  <math>\overset{{}}{\mathop{\tilde{I}_{h}^{2h}}}\,\left( {{\theta }^{\alpha}} \right)=1</math>, for the <math>\mbox{HW}</math> restriction operator, <math>\overset{{}}{\mathop{\tilde{I}_{h}^{2h}}}\,\left( {{\theta }^{\alpha}} \right)=\frac{1}{4}(2+\cos {{\bar{\theta }}_{1}}+\cos {{\bar{\theta }}_{2}})</math>, for the <math>\mbox{FW}</math> restriction operator, <math>\overset{{}}{\mathop{\tilde{I}_{h}^{2h}}}\,\left( {{\theta }^{\alpha}} \right)=\frac{1}{4}(1+\cos {{\bar{\theta }}_{1}})(1+\cos {{\bar{\theta }}_{2}})</math>, for the  <math display="inline">{\mbox{PW}}_\mbox{x}</math> (see Eq.(8)), <math>\overset{{}}{\mathop{\tilde{I}_{h}^{2h}}}\,\left( {{\theta }^{\alpha}} \right)=\frac{1}{2}(1+\cos {{\bar{\theta }}_{1}})</math> and for the  <math display="inline">{\mbox{PW}}_\mbox{y}</math> (see Eq.(8)), <math>\overset{{}}{\mathop{\tilde{I}_{h}^{2h}}}\,\left( {{\theta }^{\alpha}} \right)=\frac{1}{2}(1+\cos {{\bar{\theta }}_{2}})</math>.
-In this work, LFA was used to determine the asymptotic convergence factor of the multigrid method <math>\bigl(\rho \left( M_{h}^{2h} \right)={{\rho }_{loc}}\bigr)</math> combining <math>\mbox{ILU}</math> solvers in several directions (such as  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> and  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math>), <math>\mbox{FW}</math>, HW, INJ,  <math display="inline">{\mbox{PW}}_\mbox{x}</math> and  <math display="inline">{\mbox{PW}}_\mbox{y}</math> restriction operators and bilinear and 7-point prolongation operators.
-For the <math>\mbox{FW}</math> restriction operator, <math>\overset{\tilde{\ }}{\mathop{I_{h}^{2h}}}\,\left( {{\theta }^{\alpha }} \right)=\frac{1}{4}(1+\cos {{\bar{\theta }}_{1}})(1+\cos {{\bar{\theta }}_{2}})</math>, for the  <math display="inline">{\mbox{PW}}_\mbox{x}</math>, <math>\overset{\tilde{\ }}{\mathop{I_{h}^{2h}}}\,\left( {{\theta }^{\alpha }} \right)=\frac{1}{2}(1+\cos {{\bar{\theta }}_{1}})</math> and for the  <math display="inline">{\mbox{PW}}_\mbox{y}</math>, <math>\overset{\tilde{\ }}{\mathop{I_{h}^{2h}}}\,\left( {{\theta }^{\alpha }} \right)=\frac{1}{2}(1+\cos {{\bar{\theta }}_{2}})</math>. For the other restriction operators, see [4].
-For the bilinear prolongation operator, <math>\overset{\tilde{\ }}{\mathop{I_{2h}^{h}}}\,\left( {{\theta }^{\alpha }} \right)=(1+\cos {{\bar{\theta }}_{1}})(1+\cos {{\bar{\theta }}_{2}})</math> and for the 7-point prolongation operator, <math>\overset{\tilde{\ }}{\mathop{I_{2h}^{h}}}\,\left( {{\theta }^{\alpha }} \right)=\left( 1+\cos {{{\bar{\theta }}}_{1}}+\cos {{{\bar{\theta }}}_{2}}+\cos ({{{\bar{\theta }}}_{1}}-{{{\bar{\theta }}}_{2}}) \right)</math> [10].
-In order to perform the LFA using the  <math display="inline">\mbox{ILU}</math> solver, the eigenfunctions of <math>{{L}_{h}}</math>, <math>{{\overset{\hat{\ }}{\mathop{L}}\,}_{h}}</math>, <math>{{\overset{\hat{\ }}{\mathop{U}}\,}_{h}}</math> and <math>{{R}_{h}}</math> are given by
+The prolongation operator <math>\hat{I}_{2h}^{h}(\theta )</math> is a 4x1 matrix, and is given by:
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 507: / Line 561: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>{{\lambda }_{h}}(\theta ),\,\,\,\lambda _{h}^{L}(\theta ),\,\,\,\lambda _{h}^{U}(\theta )\,\,\text{e}\,\,\,\lambda _{h}^{R}(\theta )\,\,\,</math> with  <math>-\pi \le \theta <\pi </math>.
+| <math>\hat{I}_{2h}^{h}\left( \theta  \right)=\left( \begin{matrix}
+   \overset{{}}{\mathop{\tilde{I}_{2h}^{h}}}\,\left( {{\theta }^{(0,0)}} \right)  \\
+   \overset{{}}{\mathop{\tilde{I}_{2h}^{h}}}\,\left( {{\theta }^{(1,1)}} \right)  \\
+   \overset{{}}{\mathop{\tilde{I}_{2h}^{h}}}\,\left( {{\theta }^{(1,0)}} \right)  \\
+   \overset{{}}{\mathop{\tilde{I}_{2h}^{h}}}\,\left( {{\theta }^{(0,1)}} \right)  \\
+\end{matrix} \right)
+</math>,
 |}
-| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(23)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(25)
 |}
-The smoothing operator <math>{{S}_{h}}</math>, according to [6], is given by
+For the bilinear prolongation operator, <math>\overset{{}}{\mathop{\tilde{I}_{2h}^{h}}}\,\left( {{\theta }^{\alpha}} \right)=(1+\cos {{\bar{\theta }}_{1}})(1+\cos {{\bar{\theta }}_{2}})</math> and for the 7-point prolongation operator, <math>\overset{{}}{\mathop{\tilde{I}_{2h}^{h}}}\,\left( {{\theta }^{\alpha}} \right)=\left( 1+\cos {{{\bar{\theta }}}_{1}}+\cos {{{\bar{\theta }}}_{2}}+\cos ({{{\bar{\theta }}}_{1}}-{{{\bar{\theta }}}_{2}}) \right)</math> [10].
+The operator of the grid coarse <math>{{\left( {{{\hat{L}}}_{2h}}(2\theta ) \right)}^{-1}}</math> is a 1x1 matrix, and for the discrete Laplace operators, <math>{{\tilde{L}}_{2h}}</math> is represented by <math>{{\tilde{L}}_{2h}}\,(2\theta )=\sum\limits_{k}{{{s}_{k,2h}}{{e}^{i2\,\theta \,k}}}</math>or <math>{{\tilde{L}}_{2h}}=\frac{(2+2\varepsilon )-2(\varepsilon \cos (2{{\theta }_{1}})+\cos (2{{\theta }_{2}}))}{2{{h}^{2}}}</math>.
+A representation for the operator of two grids <math display="inline">M_{h}^{2h}</math> can be obtained by a matrix  <math>\hat{M}_{h}^{2h}(\theta )</math> of the form
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 519: / Line 583: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-| <math>{{S}_{h}}\phi (\theta ,x)={{\overset{\tilde{\ }}{\mathop{S}}\,}_{h}}\phi (\theta ,x)</math>, <math>-\pi \le \theta <\pi </math>,
+| <math>\hat{M}_{h}^{2h}:={{({{\hat{S}}_{h}}(\theta ))}^{{{v}_{2}}}}\hat{K}_{h}^{2h}(\theta )\,{{({{\hat{S}}_{h}}(\theta ))}^{{{v}_{1}}}}</math>,
 |}
-| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(24)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(26)
 |}
-with
+where <math>\hat{K}_{h}^{2h}(\theta )</math> is given by Eq. (21) and <math>{{\hat{S}}_{h}}(\theta )</math> is a 4x4 matrix and represents the smoothing operator  <math>{{S}_{h}}(\theta )</math> given by:
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
 |
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-|<math>{{\overset{\tilde{\ }}{\mathop{S}}\,}_{h}}(\theta ):=\frac{\lambda _{h}^{L}(\theta )\lambda _{h}^{U}(\theta )-\lambda (\theta )}{\lambda _{h}^{L}(\theta )\lambda _{h}^{U}(\theta )}=\frac{\lambda _{h}^{R}(\theta )}{{{\lambda }_{h}}(\theta )+\lambda _{h}^{R}(\theta )}</math>.
+| <math>{{\hat{S}}_{h}}=\left( \begin{matrix}
+   {{{\tilde{S}}}_{h}}({{\theta }^{(0,0)}}) & {} & {} & {}  \\
+   {} & {{{\tilde{S}}}_{h}}({{\theta }^{(1,1)}}) & {} & {}  \\
+   {} & {} & {{{\tilde{S}}}_{h}}({{\theta }^{(1,0)}}) & {}  \\
+   {} & {} & {} & {{{\tilde{S}}}_{h}}({{\theta }^{(0,1)}})  \\
+\end{matrix} \right)</math>.
 |}
-|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(25)
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(27)
 |}
-For  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math>, <math>\lambda _{h}^{R}(\theta )\,={{p}_{1}}{{e}^{i(2{{\theta }_{1}}-{{\theta }_{2}})}}+{{p}_{3}}+{{p}_{2}}{{e}^{i(-2{{\theta }_{1}}+{{\theta }_{2}})}}</math> and for  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math>, <math>\lambda _{h}^{R}(\theta )\,={{p}_{1}}{{e}^{i(-{{\theta }_{1}}+2{{\theta }_{2}})}}+{{p}_{3}}+{{p}_{2}}{{e}^{i({{\theta }_{1}}-2{{\theta }_{2}})}}.</math>
+In order to perform the LFA using the  <math display="inline">\mbox{ILU}</math> solver, the smoothing operator <math>{{S}_{h}}</math>, according to [6], is given by
-== 4. Numerical Results ==
-In this work, the anisotropic diffusion equation was solved using 7-point <math>\mbox{ILU}</math> solver in different directions. Several restriction operators and two prolongation operators were employed. It is proposed an algorithm that presents the lowest asymptotic convergence factor values and the lowest computational cost for the multigrid method.
-Eq. (2) was assessed for <math>\varepsilon ={{10}^{\kappa }}</math>  and <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in \Kappa =\{0,\,\,1,\,\,2,\,\,3,\,\,4,\,\,5,\,\,6,\,\,7\}</math>. When <math>\varepsilon ={{10}^{\kappa }}</math> or <math>\varepsilon ={{10}^{-\kappa }}</math> in this work, there is symmetric anisotropy. For instance, <math>\varepsilon ={{10}^{2 }}</math> is an anisotropy symmetric to  <math>\varepsilon ={{10}^{-2}}</math>.
-Section 4.1 presents the convergence analysis by means of LFA. Only the optimum components obtained by LFA will be used in the complexity analysis in section 4.2.
-===4.1. Convergence Analysis===
-Fig. 3 depicts <math>{{\rho }_{loc}}</math>, given by Eq. (22), with <math display="inline">\mbox{ILU}</math> in the EN, NE, ES, SE directions, <math>\mbox{FW}</math> restriction, bilinear prolongation, number of inner iterations <math>v=2</math>, <math>\varepsilon ={{10}^{\kappa }}</math> and  <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in K</math>.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
- [[Image:draft_Vassoler Rutz_344011008-image153.jpeg|390px]] </div>
 {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
@@ Line 558: / Line 613: @@
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-|Figure 3: <math>{{\rho }_{loc}}</math> ''versus'' anisotropy coefficients <math>\bigl(\varepsilon\bigr)</math> with  <math display="inline">\mbox{ILU}</math> in different directions.
+| <math>{{S}_{h}}\phi (\theta ,x)={{\tilde{S}}_{h}}\phi (\theta ,x)</math>, <math>-\pi \le \theta <\pi </math>,
 |}
+| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;" |(28)
 |}
-It is noticed that for <math>0<\varepsilon<<1</math>,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> has a good performance and for <math>\varepsilon>>1</math>, <math>{\mbox{ILU}}_{\mbox{NE}}</math> has a good performance as well, that is, <math>{{\rho }_{loc}}<<1</math>. By using  <math display="inline">\mbox{ILU}</math> solvers in the ES and SE directions, the multigrid did not present a good performance for any of the anisotropy coefficients studied.
+with
-For the analyses presented below, tests were carried out using only the solvers that had the best performances in the previous analysis.
+{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
-Fig. 4 presents <math>{{\rho }_{loc}}</math> using as solvers,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for <math>0<\varepsilon<<1</math> and  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> for <math>\varepsilon>>1</math>; <math>\nu =2</math>; <math>\mbox{FW}</math> restriction; 7-point and bilinear prolongation; <math>\varepsilon ={{10}^{\kappa }}</math> and  <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in K</math>.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
- [[Image:draft_Vassoler Rutz_344011008-image166.jpeg|396px]] </div><span id="_GoBack"></span>
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
 |
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-|Figure 4: <math>{{\rho }_{loc}}</math> ''versus'' anisotropy coefficients <math>\bigl(\varepsilon\bigr)</math> with different interpolation operators.
+|<math>{{\tilde{S}}_{h}}(\theta ):=\frac{\lambda _{h}^{R}(\theta )}{{{\lambda }_{h}}(\theta )+\lambda _{h}^{R}(\theta )}</math>.
 |}
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(29)
 |}
-It is observed that the restriction|prolongation combinations <math>\mbox{FW}</math>|bilinear and <math>\mbox{FW}</math>|7-points had a good performance <math>\bigl({{\rho }_{loc}}<<1\bigr)</math> and presented very similar convergence factors.
+where <math>{{\lambda }_{h}}(\theta )=1</math>, for <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math>, <math>\lambda _{h}^{R}(\theta )\,={{p}_{1}}{{e}^{i(2{{\theta }_{1}}-{{\theta }_{2}})}}+{{p}_{3}}+{{p}_{2}}{{e}^{i(-2{{\theta }_{1}}+{{\theta }_{2}})}}</math> and for <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math>, <math>\lambda _{h}^{R}(\theta )\,={{p}_{1}}{{e}^{i(-{{\theta }_{1}}+2{{\theta }_{2}})}}+{{p}_{3}}+{{p}_{2}}{{e}^{i({{\theta }_{1}}-2{{\theta }_{2}})}}.</math>.
-Bilinear prolongation operator was used in the following analysis as it is easy to program and demands fewer memory resources. The asymptotic convergence factors were compared with different restriction operators.
+The asymptotic convergence factor <math>\rho \left( M_{h}^{2h} \right)</math> can be calculated by
-Fig. 5 presents'' ''<math>{{\rho }_{loc}}</math> using as solvers,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for <math>0<\varepsilon<<1</math> and  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> for <math>\varepsilon>>1</math>; <math>\nu =2</math>; <math>\mbox{FW}</math>, HW, INJ,  <math display="inline">{\mbox{PW}}_\mbox{x}</math> and  <math display="inline">{\mbox{PW}}_\mbox{y}</math> restriction; bilinear prolongation; <math>\varepsilon ={{10}^{\kappa }}</math> and  <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in K</math>.
+{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
- [[Image:draft_Vassoler Rutz_344011008-image171.jpeg|414px]] </div>
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
 |
 {| style="text-align: center; margin:auto;width: 100%;"
 |-
-|Figure 5: <math>{{\rho }_{loc}}</math> ''versus'' anisotropy coefficients <math>\bigl(\varepsilon\bigr)</math> with different restriction operators.
+|<math>\rho \left( M_{h}^{2h} \right)=\sup \left\{ \rho \left( \hat{M}_{h}^{2h}(\theta ) \right):\,\,\theta \in {{T}^{low}},\,\,\theta \notin \Lambda  \right\}</math>,
 |}
+|  style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(30)
 |}
-Fig. 5 shows that for <math>\varepsilon ={{10}^{\kappa }}</math> and  <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in K</math> (symmetric anisotropies), <math>{{\rho }_{loc}}</math> presents very similar values. It is noted that for anisotropic problems <math>\bigl(\kappa\neq0\bigr)</math>, the lowest values for <math>{{\rho }_{loc}}</math> are achieved with <math>\mbox{FW}</math> and  <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction, which present very similar values.
+where <math>\Lambda =\left\{ \theta \in {{T}^{low}}:\,{{{\tilde{L}}}_{h}}(\theta )=0\,\,\text{or}\,\,{{{\tilde{L}}}_{2h}}(\theta )=0 \right\}</math> and <math>\rho \left( \hat{M}_{h}^{2h}(\theta ) \right)</math> is the spectral radius of the 4x4 matrix <math>\hat{M}_{h}^{2h}(\theta )</math>.
-Based on the results shown, it is proposed Algorithm 1, which combines <math>\mbox{ILU}</math> solver in different directions with <math>\mbox{FW}</math> and  <math display="inline">{\mbox{PW}}_\mbox{x}</math> restrictions. The algorithm will be presented now. The abbreviation '''REST''', used in the algorithm, represents any of the restrictions (<math>\mbox{FW}</math> or  <math display="inline">{\mbox{PW}}_\mbox{x}</math>) previously defined.
-Algorithm 1:
+In this work, LFA was used to determine the asymptotic convergence factor of the multigrid method  <math>\bigl(\rho \left( M_{h}^{2h} \right)={{\rho }_{loc}}\bigr)</math> combining <math>\mbox{ILU}</math> solvers in several directions (such as  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> and  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math>), <math>\mbox{FW}</math>, HW, INJ,  <math display="inline">{\mbox{PW}}_\mbox{x}</math> and  <math display="inline">{\mbox{PW}}_\mbox{y}</math> restriction operators and bilinear and 7-point prolongation operators.
-_____________________________________________________________________________________
+== 4. Numerical results==
-if <math>\varepsilon >1</math> then
+An orthotropic diffusion equation was solved using 7-point ILU solver in different directions. Several restriction operators and two prolongation operators were employed. We proposed an algorithm that presents the lowest asymptotic convergence factor values and the lowest computational cost for the multigrid method.
-Apply  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> smoothing with '''REST '''restriction
+Equation (4) was assessed for <math>\varepsilon ={{10}^{\kappa }}</math>  and <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in \Kappa =\{0,\,\,1,\,\,2,\,\,3,\,\,4,\,\,5,\,\,6,\,\,7\}</math>. When <math>\varepsilon ={{10}^{\kappa }}</math> or <math>\varepsilon ={{10}^{-\kappa }}</math> in this work, there is symmetric orthotropy. For instance, <math>\varepsilon ={{10}^{2 }}</math> is an orthotropy symmetric to  <math>\varepsilon ={{10}^{-2}}</math>.
-else if <math>\varepsilon =1</math> then
+Section 4.1 presents the convergence analysis by means of LFA. Only the optimum components obtained via LFA will be used in the complexity analysis in section 4.2.
-Apply  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> smoothing with <math>\mbox{FW}</math> restriction
+===4.1. Convergence Analysis===
-else
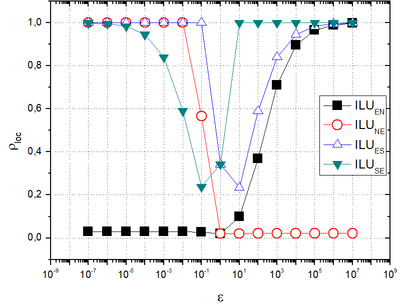
+[[#img-3|Figure 3]] depicts <math>{{\rho }_{loc}}</math>, given by Eq. (30), with <math display="inline">\mbox{ILU}</math> in the EN, NE, ES, SE directions, <math>\mbox{FW}</math> restriction, bilinear prolongation, number of inner iterations <math>v=2</math>, <math>\varepsilon ={{10}^{\kappa }}</math> and  <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in K</math>.
-Apply  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> '''REST '''restriction
+<div id='img-3'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"|  [[File:Review 644666424766 2434 Fig3.png|400px|centre|thumb]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 3'''. <math>{{\rho }_{loc}}</math> ''versus'' orthotropy coefficients <math>\bigl(\varepsilon\bigr)</math> with  <math display="inline">\mbox{ILU}</math> in different directions.
+|}
-end if
-_____________________________________________________________________________________
+It is noticed that for <math>0<\varepsilon<<1</math>,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> has a good performance. For <math>\varepsilon>>1</math>, <math>{\mbox{ILU}}_{\mbox{NE}}</math> also has a good performance, that is, <math>{{\rho }_{loc}}<<1</math>. By using  <math display="inline">\mbox{ILU}</math> solvers in the ES and SE directions, the multigrid method did not present a good performance for any of the orthotropy coefficients studied.
-Next, it is presented the asymptotic convergence factor <math>{{\rho }_{loc}}</math>, calculated by LFA, and the empiric asymptotic convergence factor <math>\rho_h</math>, for different anisotropy coefficients.
+For the analyses presented below, tests were carried out using only the solvers that had the best performances in previous analysis.
-Fig. 6 shows Algorithm 1 with '''REST''' <math display="inline">={\mbox{PW}}_\mbox{x}</math> ,<math>\nu=2</math> and bilinear prolongation.
+[[#img-|Figure 4]] presents <math>{{\rho }_{loc}}</math> using as solvers,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for <math>0<\varepsilon<<1</math> and  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> for <math>\varepsilon>>1</math>; <math>\nu =2</math>; <math>\mbox{FW}</math> restriction; 7-point and bilinear prolongation; <math>\varepsilon ={{10}^{\kappa }}</math> and  <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in K</math>.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-4'></div>
- [[Image:draft_Vassoler Rutz_344011008-image187.jpeg|420px]] </div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
 |-
-|
+|style="padding:10px;"| [[File:Fig4.png|400px|centre|thumb]]
-{| style="text-align: center; margin:auto;width: 100%;"
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 4'''. <math>{{\rho }_{loc}}</math> ''versus'' orthotropy coefficients <math>\bigl(\varepsilon\bigr)</math> with different interpolation operators.
+|}
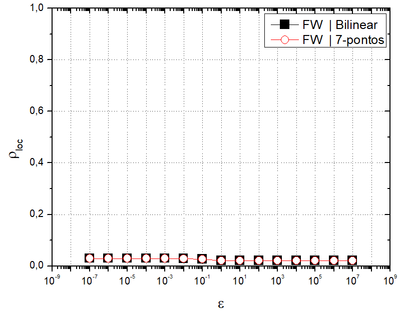
+It can be observed that the restriction|prolongation combinations <math>\mbox{FW}</math>|bilinear and <math>\mbox{FW}</math>|7-points had a good performance <math>\bigl({{\rho }_{loc}}<<1\bigr)</math> and presented very similar convergence factors.
+Bilinear prolongation operator was used in the following analysis as it is easy to program and demands fewer memory resources. The asymptotic convergence factors were compared with different restriction operators.
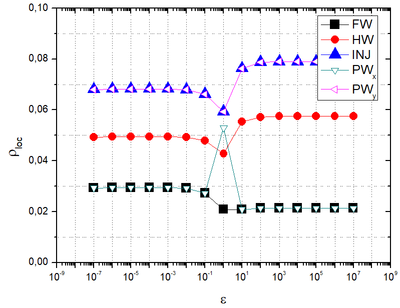
+[[#img-5|Figure 5]] presents'' ''<math>{{\rho }_{loc}}</math> using as solvers,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for <math>0<\varepsilon<<1</math> and  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> for <math>\varepsilon>>1</math>; <math>\nu =2</math>; <math>\mbox{FW}</math>, HW, INJ,  <math display="inline">{\mbox{PW}}_\mbox{x}</math> and  <math display="inline">{\mbox{PW}}_\mbox{y}</math> restriction; bilinear prolongation; <math>\varepsilon ={{10}^{\kappa }}</math> and  <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in K</math>.
+<div id='img-5'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
 |-
-|Figure 6: <math>{{\rho }_{loc}}</math> and <math>\rho_h</math> versus anisotropy coefficients <math>\bigl(\varepsilon\bigr)</math>.
+|style="padding:10px;"|  [[File:Fig5.png|400px|centre|thumb]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 5'''. <math>{{\rho }_{loc}}</math> ''versus'' orthotropy coefficients <math>\bigl(\varepsilon\bigr)</math> with different restriction operators.
 |}
+[[#img-5|Figure 5]] demonstrates that for <math>\varepsilon ={{10}^{\kappa }}</math> and  <math>\varepsilon ={{10}^{-\kappa }}</math>, with <math>\kappa \in K</math> (symmetric orthotropies), <math>{{\rho }_{loc}}</math> presents very similar values. It is noted that for orthotropic problems <math>\bigl(\kappa\neq0\bigr)</math>, the lowest values for <math>{{\rho }_{loc}}</math> are achieved with <math>\mbox{FW}</math> and  <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction, which show very similar values.
+Based on the results presented, we propose [[#algorithm-1|Algorithm 1]], which combines ILU solver in different directions, with <math>\mbox{FW}</math> and <math display="inline">{\mbox{PW}}_\mbox{x}</math> restrictions. The algorithm is presented below. The abbreviation '''REST''', used in the algorithm represents any of the restrictions (<math>\mbox{FW}</math> or  <math display="inline">{\mbox{PW}}_\mbox{x}</math>) previously defined.
+<div id='algorithm-1'></div>
+<div class="left" style="font-size: 85%;">
+'''Algorithm 1.'''<br />
+_______________________________________________________
+if <math>\varepsilon >1</math> then
+:Apply  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> smoothing with '''REST '''restriction
+::else if <math>\varepsilon =1</math> then
+:Apply  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> smoothing with <math>\mbox{FW}</math> restriction
+::else
+:Apply  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> '''REST '''restriction
+end if<br />
+_______________________________________________________
+</div>
+'''Remark 1:''' Pinto et al. [14] solved an anisotropic diffusion problem using ILU in triangular grids and several anisotropies not aligned with ''x'' or ''y''. The authors noted that ILU<sub>NE</sub> and ILU<sub>EN</sub> were efficient for some of the anisotropies, making it is possible to adapt this algorithm to an alternating form so it will work well for any anisotropy.
+'''Remark 2:'''   One of the biggest problems in the literature is the numerical resolution of the Navier-Stokes equation. Depending on its numerical formulation (simplec, projections [19]), a great computational effort is required at the numerical solution of the continuity equation, which can be represented by Poisson’s equation. Moreover, the algorithm depends on the mesh sweep and is independent of the complexity of the proposed problem equation. Therefore, this algorithm can be adapted to certain orthotropic problems with a certain degree of complexity.
+Next, the asymptotic convergence factor <math>{{\rho }_{loc}}</math>, calculated by LFA, and the empiric asymptotic convergence factor <math>\rho_h</math>, for different orthotropy coefficients, are presented.
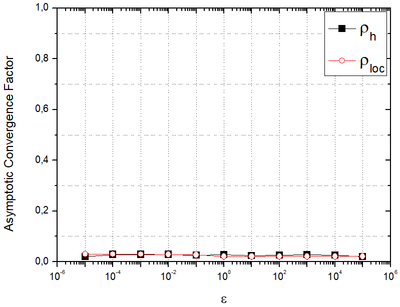
+[[#img-6|Figure 6]] shows [[#algorithm-1|Algorithm 1]] with '''REST''' <math display="inline">={\mbox{PW}}_\mbox{x}</math> , <math>\nu =2</math> and bilinear prolongation.
+<div id='img-6'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
+|-
+|style="padding:10px;"| [[File:Fig6.png|400px|centre|thumb]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding:10px;"| '''Figure 6'''. <math>{{\rho }_{loc}}</math> and <math>\rho_h</math> versus orthotropy coefficients <math>\bigl(\varepsilon\bigr)</math>.
 |}
-It is observed that <math>\rho_{loc} \approx \rho_{h} <<1</math>  for every anisotropy coefficients assessed. Moreover, <math>{{\rho }_{loc}}</math> calculated by LFA is in accordance with <math>\rho_h</math> calculated experimentally.
-Fig. 7 depicts the numerical asymptotic convergence factor <math>{{\rho }_{loc}}</math> calculated by LFA and the experimental asymptotic convergence factor <math>\rho_h</math>, for different anisotropy coefficients for different grids. Algorithm 1 with  '''REST''' = <math display="inline">{\mbox{PW}}_\mbox{x}</math> , <math>\nu=2</math> and bilinear prolongation was used. As the grid  becomes more refined, <math>\rho_{h} \rightarrow\rho_{loc} </math> for every anisotropy coefficient analyzed, what demonstrates the robustness of the methodology assessed.
+It is observed that <math>\rho_{loc} \approx \rho_{h} <<1</math>  for every orthotropy coefficients assessed. Furthermore, <math>{{\rho }_{loc}}</math> calculated by LFA is in accordance with <math>\rho_h</math> calculated experimentally.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
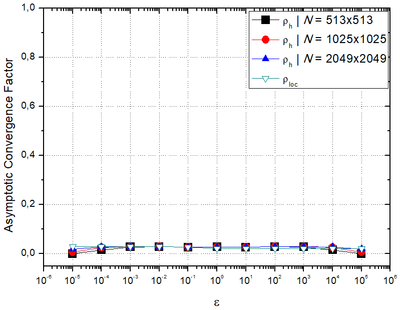
+[[#img-7|Figure 7]] depicts the numerical asymptotic convergence factor <math>{{\rho }_{loc}}</math> calculated by LFA and the experimental asymptotic convergence factor <math>\rho_h</math>, for different orthotropy coefficients for different grids. [[#algorithm-1|Algorithm 1]] with  '''REST''' = <math display="inline">{\mbox{PW}}_\mbox{x}</math>, <math>\nu=2</math> and bilinear prolongation was used. As the grid  becomes more refined, <math>\rho_{h} \rightarrow\rho_{loc} </math> for every orthotropy coefficient analyzed, what demonstrates the robustness of the methodology assessed.
- [[Image:draft_Vassoler Rutz_344011008-image193.jpeg|408px]] </div>
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
+<div id='img-7'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
 |-
-|
+|style="padding:10px;"|  [[File:Fig7.png|400px|thumb|centre]]
-{| style="text-align: center; margin:auto;width: 100%;"
+|- style="text-align: center; font-size: 75%;"
-|-
+| colspan="1" style="padding:10px;"| '''Figure 7'''. <math>{{\rho }_{loc}}</math> and <math>\rho_h</math> versus orthotropy coefficients <math>\bigl(\varepsilon\bigr)</math> for different number of grid points.
-|Figure 7: <math>{{\rho }_{loc}}</math> and <math>\rho_h</math> versus anisotropy coefficients <math>\bigl(\varepsilon\bigr)</math> for different number of grid points.
 |}
+Some of the data presented in [[#img-7|Figure 7]] can be better visualized in [[#tab-1|Table 1]].
+<div class="center" style="font-size: 75%;">
+'''Table 1'''. <math>{{\rho }_{loc}}</math> and <math>\rho_h</math> for some orthotropy coefficients <math>\bigl(\varepsilon\bigr)</math> and different number of grid points.</div>
+<div id='tab-1'></div>
+{| style="width: 76%;margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;"
+|-
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" |<math>\varepsilon</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math>\rho_h</math>  <math>(N=513\times 513)</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math>\rho_h</math> <math>(N=1025\times 1025)</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math>\rho_h</math> <math>(N=2049\times 2049)</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math>\rho_loc</math>
+|-
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<math>10^{-5}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>4.181939\times {{10}^{-4}}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.006544947</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.01993340</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.02943536</math>
+|-
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<span style="text-align: center; font-size: 75%;"> </span><math>10^{-4}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.01569827</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.025212810</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.02806990</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.02943000</math>
+|-
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math>10^{-3}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<math>0.02748596</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<math>0.028578500</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<math>0.02884448</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<math>0.022941390</math>
+|-
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" |<math>10^{-2}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.02858316</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.028703710</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.02874592</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.02921000</math>
+|-
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math>10^{-1}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.02683346</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.026852440</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.02685995</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>0.02725823</math>
 |}
-Next section presents the complexity analysis of multigrid. For the analysis, multigrid was built with the components that had the best convergence factors, according to LFA. In addition, a comparison between partial weighting and full weighting will be presented.
+Next section presents the complexity analysis of multigrid. For the analysis, multigrid was built with the components that had the best convergence factors according to LFA. In addition, a comparison between partial weighting and full weighting will be presented.
 ===4.2. Complexity Analysis===
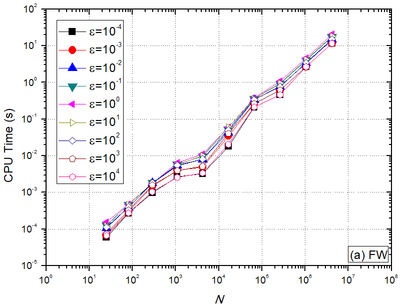
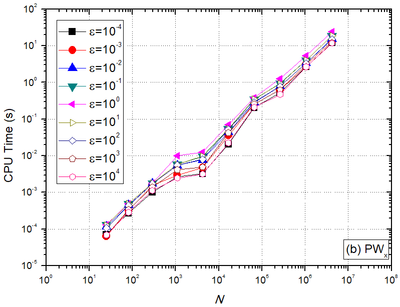
-In order to assess the effect of the number of unknowns on CPU time, optimum components obtained by LFA were used. Figures 8 (a) and 8 (b) show, for <math>\mbox{FW}</math> and  <math display="inline">{\mbox{PW}}_\mbox{x}</math> restrictions respectively, that for the anisotropic problem <math>\bigl(\varepsilon=1\bigr)</math>, the <math display="inline">t_{CPU}</math> is not lower. As the problem becomes more anisotropic <math>\bigl(0<\varepsilon<<1\,\,\,\text{or}\,\,\,\varepsilon>>1\bigr) </math>, the <math>t_{CPU}</math> decreases for every ''N ''value assessed. For every anisotropy coefficient assessed, the <math>t_{CPU}</math> with <math>\mbox{FW}</math> restriction is very similar to the <math>t_{CPU}</math> with <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction, that is,  <math display="inline">t_{CPU}\left(FW\right)\approx t_{CPU}\left({\mbox{PW}}_\mbox{x}\right)</math> .
+In order to assess the effect of the number of unknowns on CPU time, optimum components obtained via LFA were used. [[#img-8|Figures 8]](a) and [[#img-8|8]](b) show, for <math>\mbox{FW}</math> and  <math display="inline">{\mbox{PW}}_\mbox{x}</math> restrictions, respectively, that for the isotropic problem <math>\bigl(\varepsilon=1\bigr)</math>, the <math display="inline">t_{CPU}</math> is not lower. As the problem becomes more orthotropic <math>\bigl(0<\varepsilon<<1\,\,\,\text{or}\,\,\,\varepsilon>>1\bigr) </math>, the <math>t_{CPU}</math> decreases for every ''N'' value assessed. For every orthotropy coefficient assessed, the <math>t_{CPU}</math> with <math>\mbox{FW}</math> restriction is very similar to the <math>t_{CPU}</math> with <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction, that is,  <math display="inline">t_{CPU}\left(FW\right)\approx t_{CPU}\left({\mbox{PW}}_\mbox{x}\right)</math>.
-It is also observed for symmetric anisotropies <math>\bigl(\varepsilon ={{10}^{-\kappa }}\,\,\,\text{and}\,\,\,\varepsilon ={{10}^{\kappa }}\bigr)</math> with <math>\kappa\in\{1,2,3,4\}</math>, that the values of <math>t_{CPU}</math> obtained are extremely similar.
+It is also observed for symmetric orthotropies <math>\bigl(\varepsilon ={{10}^{-\kappa }}\,\,\,\text{and}\,\,\,\varepsilon ={{10}^{\kappa }}\bigr)</math> with <math>\kappa\in\{1,2,3,4\}</math>, that the values of <math>t_{CPU}</math> obtained are extremely similar.
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+<div id='img-8'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
-{|
 |-
-| [[Image:draft_Vassoler Rutz_344011008-image206.jpeg|288px]]
+|style="padding:10px;"|  [[File:Fig8 a.png|400px|thumb]]
-| [[Image:draft_Vassoler Rutz_344011008-image207.jpeg|center|282px]]
+|style="padding-right:15px;"|[[File:Fig8 b.png|400px|thumb]]
-|}
+|- style="text-align: center; font-size: 75%;"
-</div>
+| colspan="2" style="padding:10px;"| '''Figure 8'''. CPU time versus number of nodes (''N'').
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
-|-
-|
-{| style="text-align: center; margin:auto;width: 100%;"
-|-
-|Figure 8: CPU time versus number of nodes (''N'').
-|}
 |}
-In order to assess the performance of the multigrid with different anisotropy coefficients, a curve adjustment of the form <math>{{t}_{CPU}}=c{{N}^{p}}</math> [18] was made, where ''p ''represents the complexity order of the solver, ''N'' is the number of grid points and ''c ''is a constant that depends on the method. The closer the value of ''p ''is to one, the better the performance of method used. Ideally, multigrid presents <math>p=1</math>, what means that the CPU time grows linearly with the increase of ''N''. Results are shown in Table 1 for both restrictions assessed (<math>\mbox{FW}</math> and  <math display="inline">{\mbox{PW}}_\mbox{x}</math>).
-One can observe in Tab. 1 that, for every anisotropy employed, the multigrid method has a good performance, since <math>p\approx1</math> in every case. These results prove the efficiency and robustness of Algorithm 1, proposed in this work.
+In order to assess the performance of the multigrid method with different anisotropy coefficients, a curve adjustment of the form <math>{{t}_{CPU}}=c{{N}^{p}}</math> [20] was made, where <math>p</math> represents the complexity order of the solver, ''N'' is the number of grid points and<math>N</math> <math>c</math> is a constant that depends on the method. The closer the value of <math>p</math> is to one, the better the performance of the method used. Ideally, multigrid presents <math>p=1</math>, what means that the CPU time grows linearly with the increase of ''N''. Results are shown in [[#tab-2|Table 2]] for both restrictions assessed<math>N</math> (<math>\mbox{FW}</math> and  <math display="inline">{\mbox{PW}}_\mbox{x}</math>).
-<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+One can observe in [[#tab-2|Table 2]] that, for every orthotropy employed, the multigrid method has a good performance, since <math>p\approx1</math> in every case. These results prove the efficiency and robustness of [[#algorithm-1|Algorithm 1]], proposed in this work.
-{| style="width: 76%;margin: 1em auto 0.1em auto;border-collapse: collapse;"
+<div class="center" style="font-size: 75%;">
+'''Table 2'''. Complexity order <math>\bigl(p\bigr)</math> for different'' ''orthotropy coefficients <math>\bigl(\varepsilon\bigr)</math>.</div>
+<div id='tab-2'></div>
+{| style="width: 66%;margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;"
 |-
 | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" |<math>\varepsilon</math>
@@ Line 690: / Line 830: @@
 | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>1.07733</math>
 |-
-| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<span style="text-align: center; font-size: 75%;"> </span><math>10^{-2}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<math>10^{-2}</math>
 | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>1.05023</math>
 | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>1.05894</math>
@@ Line 705: / Line 845: @@
 | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>1.07627</math>
 | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>1.07775</math>
-|}</div>
+|}
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
-|-
-|
-{| style="text-align: center; margin:auto;width: 100%;"
-|-
-|Table 1. Complexity order <math>\bigl(p\bigr)</math> for different'' ''anisotropy coefficients <math>\bigl(\varepsilon\bigr)</math>.
-|}
-|}
-The values obtained for the convergence factor, presented in section 4.1, and for the complexity order concerning to the <math>\text{PW}_x</math> and <math>\mbox{FW}</math> restriction operators (Tab. 1)  are quite similar and thus, insufficient to decide which one results in a more efficient algorithm.
+The values obtained for the convergence factor, presented in section 4.1, and for the complexity order concerning to the <math>\text{PW}_x</math> and <math>\mbox{FW}</math> restriction operators ([[#tab-2|Table 2]]) are quite similar and thus insufficient to decide which one results in a more efficient algorithm.
 To complement the analysis, the number of arithmetical operations performed in each V-cycle and at the restriction step for each one of the operators was assessed.
-These arithmetical operations concern to floating point operations (flops) performed during the iterative process and are not affect by the hardware used. Each addition, multiplication and division operation correspond to 1 flop.
+These arithmetical operations concern to floating-point operations (flops) performed during the iterative process and are not affect by the hardware used. Each addition, multiplication and division operation correspond to 1 flop.
-Tests were carried out for <math>N_{10}=10</math> (<math>N_{10}</math> is the number of points of the finest grid, considering a problem whose maximum number of levels is <math>L_{\text{max}}=10</math>) and for some values of <math>\varepsilon</math>. Tab. 2 presents the ratio between number of flops of a V-cycle and number of points of the finest grid <math>N_{10}</math>. Tab. 3 shows the ratio between number of flops performed in each restriction and the number of points of the finest grid <math>N_{10}</math>.<div class="center" style="width: auto; margin-left: auto; margin-right: auto;">
+Tests were carried out for <math>N_{10}=10</math> (<math>N_{10}</math> is the number of points of the finest grid, considering a problem whose maximum number of levels is <math>L_{\text{max}}=10</math>) and for some values of <math>\varepsilon</math>. [[#tab-3|Table 3]] presents the ratio between number of flops of a V-cycle and number of points of the finest grid <math>N_{10}</math>. [[#tab-4|Table 4]] shows the ratio between number of flops performed in each restriction and the number of points of the finest grid <math>N_{10}</math>.
-{| style="width: 76%;margin: 1em auto 0.1em auto;border-collapse: collapse;"
+<div class="center" style="font-size: 75%;">
+'''Table 3'''. Ratio between number of flops of a V-cycle and the number of points of the finest grid.</div>
+<div id='tab-3'></div>
+{| style="width: 76%;margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;"
 |-
 | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" |<math>\varepsilon</math>
@@ Line 749: / Line 884: @@
 | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |'''<math>1564.958717</math>'''
 | style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>1598.033220</math>
-|}</div>
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
-|-
-|
-{| style="text-align: center; margin:auto;width: 100%;"
-|-
-|Table 2. Ratio between number of flops of a V-cycle and the number of points of the finest grid.
-|}
 |}
-{| style="width: 76%;margin: 1em auto 0.1em auto;border-collapse: collapse;"
+<div class="center" style="font-size: 75%;">
+'''Table 4'''. Ratio between number of flops of the restriction and number of points of the finest grid.</div>
+<div id='tab-4'></div>
+{| style="width: 76%;margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;"
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;"|<math>\varepsilon</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" |<math>\varepsilon</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;"| <math display="inline">\mbox{flops}({\mbox{PW}}_\mbox{x})/N_{10}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math display="inline">\mbox{flops}({\mbox{PW}}_\mbox{x})/N_{10}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;"| <math display="inline">\mbox{flops}(\mbox{FW})/N_{10}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math display="inline">\mbox{flops}(\mbox{FW})/N_{10}</math>
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>10^{-2}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<math>10^{-2}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|'''<math>11.57607615</math>'''
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |'''<math>11.57607615</math>'''
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|<math>44.65057942</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>44.65057942</math>
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<span style="text-align: center; font-size: 75%;"> </span><math>10^{-1}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<span style="text-align: center; font-size: 75%;"> </span><math>10^{-1}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|'''<math>13.89129130</math>'''
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |'''<math>13.89129130</math>'''
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|<math>53.58069530</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>53.58069530</math>
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;"| <math>1</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math>1</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|'''<math>18.37833483</math>'''
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |'''<math>18.37833483</math>'''
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;"|<math>62.02688007</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;" |<math>62.02688007</math>
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;"|<math>10^{1}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" |<math>10^{1}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|'''<math>13.89129137</math>'''
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |'''<math>13.89129137</math>'''
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|<math>53.58069530</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>53.58069530</math>
 |-
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;"| <math>10^{2}</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;width: 25%;" | <math>10^{2}</math>
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|'''<math>11.57607615</math>'''
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |'''<math>11.57607615</math>'''
-|  style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;"|<math>44.65057942</math>
+| style="border-top: 1pt solid black;border-bottom: 1pt solid black;text-align: center;vertical-align: top;" |<math>44.65057942</math>
-|}
-{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;"
-|-
-|
-{| style="text-align: center; margin:auto;width: 100%;"
-|-
-|Table 3. Ratio between number of flops of the restriction and number of points of the finest grid.
-|}
 |}
-According to Tab. 2, the multigrid cycle that requires the lowest number of flops is the cycle with  <math display="inline">{\mbox{PW}}_\mbox{x}</math> operator, except for the isotropic case <math>\bigl(\varepsilon=1\bigr)</math>. Considering only the restriction step, results presented in Tab. 3 show a great advantage of the  <math display="inline">{\mbox{PW}}_\mbox{x}</math> operator over the <math>\mbox{FW}</math> operator regarding the number of flops performed. For every case, the number of flops for  <math display="inline">{\mbox{PW}}_\mbox{x}</math> is roughly 75% lower than the number of flops for <math>\mbox{FW}</math>.
-The remaining anisotropy coefficients assessed showed similar performances to those presented in Fig. 5 and Tables 2 and 3, what confirms the efficiency and robustness of the algorithm proposed, in addition to the low computational cost with the use of the  <math display="inline">{\mbox{PW}}_\mbox{x}</math> operator.
+According to [[#tab-3|Table 3]], the multigrid cycle that requires the lowest number of flops is the cone with  <math display="inline">{\mbox{PW}}_\mbox{x}</math> operator, except for the isotropic case <math>\bigl(\varepsilon=1\bigr)</math>. Considering only the restriction step, results presented in [[#tab-4|Table 4]] show a great advantage of the  <math display="inline">{\mbox{PW}}_\mbox{x}</math> operator over the <math>\mbox{FW}</math> operator regarding the number of flops performed. For every case, the number of flops for  <math display="inline">{\mbox{PW}}_\mbox{x}</math> is roughly 75% lower than the number of flops for <math>\mbox{FW}</math>.
+'''Remark 3:''' 75% of the reduction in the number of operations in the restriction was expected. However, this has little impact on the total cost of the cycle, which shows the great concentration of operations in the execution of the solver.
+The remaining orthotropy coefficients assessed showed similar performances to those presented in [[#img-5|Figure 5]] and [[#tab-3|Tables 3]] and [[#tab-4|4]], what confirms the efficiency and robustness of the algorithm proposed, in addition to the low computational cost with the use of the <math display="inline">{\mbox{PW}}_\mbox{x}</math> operator.
 == 5. Conclusions ==
-- Among the <math>\mbox{ILU}</math> directions assessed (EN, NE, ES, SE) for standard multigrid (<math>\mbox{FW}</math> restriction operator and bilinear prolongation), it is concluded that  <math display="inline">{\rho }_{loc}\approx 0.02</math> when using  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for <math>0<\varepsilon<<1</math> and  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> for <math>\varepsilon>>1</math><span style="text-align: center; font-size: 75%;">.</span>
-- With <math>\mbox{FW}</math> restriction,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for  <math>0<\varepsilon<<1</math> and <math>{\mbox{ILU}}_{\mbox{NE}}</math> for <math>\varepsilon>>1</math>, it can be concluded that the 7-point and bilinear prolongation operators presented a similar performance, and for every value of  <math>\varepsilon</math> assessed, <math>\rho_{loc}<<1</math> was obtained.
+- For the  <math>\mbox{ILU}</math> directions assessed (EN, NE, ES, SE) for standard multigrid method (<math>\mbox{FW}</math> restriction operator and bilinear prolongation), it is concluded that <math>\rho_{loc}\approx0.02</math> when using  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for <math>0<\varepsilon<<1</math> and  <math display="inline">{\mbox{ILU}}_{\mbox{NE}}</math> for <math>\varepsilon>>1</math><span style="text-align: center; font-size: 75%;">.</span>
-- With bilinear interpolation, <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for <math>0<\varepsilon<<1</math> and <math>{\mbox{ILU}}_{\mbox{NE}}</math>for  <math>\varepsilon>>1</math>, it can be stated that the lowest values of <math>{{\rho }_{loc}}</math> are obtained with <math>\mbox{FW}</math> and <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction operators, and that the values of <math>{{\rho }_{loc}}</math> with these operators are very similar.
+- With <math>\mbox{FW}</math> restriction,  <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for <math>0<\varepsilon<<1</math> and <math>{\mbox{ILU}}_{\mbox{NE}}</math> for <math>\varepsilon>>1</math>, results showed that the 7-point and bilinear prolongation operators presented a similar performance, and for every value of <math>\varepsilon</math> assessed, <math>\rho_{loc}<<1</math> was obtained.
-- Using Algorithm 1, <math>{{\rho }_{loc}}\approx{{\rho }_{h}}<<1</math>  for every anisotropy coefficient assessed and <math>{{\rho }_{h}}\rightarrow{{\rho }_{loc}}</math> as the grid becomes more refined.
+- With bilinear interpolation, <math display="inline">{\mbox{ILU}}_{\mbox{EN}}</math> for <math>0<\varepsilon <<1</math> and <math>{\mbox{ILU}}_{\mbox{NE}}</math> for  <math>\varepsilon>>1</math>, the lowest values of  <math>{{\rho }_{loc}}</math> are obtained with <math>\mbox{FW}</math> and <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction operators, and the values of  <math>{{\rho }_{loc}}</math> with these operators are very similar.
-- The  <math display="inline">t_{CPU}\left(\mbox{FW}\right)\approx t_{CPU}\left({\mbox{PW}}_\mbox{x}\right)</math> for every value of   assessed.
+- Using [[#algorithm-1|Algorithm 1]], <math>{{\rho }_{loc}}\approx{{\rho }_{h}}<<1</math>  for every orthotropy coefficient assessed and <math>{{\rho }_{h}}\to {{\rho }_{loc}}</math> as the grid becomes more refined.
-- The complexity order <math>p</math> of the multigrid method with Algorithm 1 is close to one for every anisotropy assessed. For <math>\varepsilon=10^{-4}</math>, for example, <math>p=1.07747</math> with this algorithm.
+- The  <math display="inline">t_{CPU}\left(\mbox{FW}\right)\approx t_{CPU}\left({\mbox{PW}}_\mbox{x}\right)</math> for every value of <math>\varepsilon</math> assessed.
-- The computational cost of multigrid depends on the number of flops of the restriction in a V-cycle. Using Algorithm 1 with  <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction, the computational cost is 75% lower than with <math>\mbox{FW}</math> restriction.
+- The complexity order <math>p</math> of the multigrid method with [[#algorithm-1|Algorithm 1]] is close to one for every orthotropy assessed. For <math>\varepsilon ={{10}^{-4}}</math>, for example, <math>p=1.07747</math> with this algorithm.
-- The Algorithm 1 with  <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction proposed in this work is efficient, robust and has low computational cost.
+- The computational cost of multigrid depends on the number of flops of the restriction in a V-cycle. Using [[#algorithm-1|Algorithm 1]] with  <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction, the computational cost is 75% lower than with <math>\mbox{FW}</math> restriction.
+- The [[#algorithm-1|Algorithm 1]] with  <math display="inline">{\mbox{PW}}_\mbox{x}</math> restriction proposed in this work is efficient, robust and has low computational cost.
+== Acknowledgements ==
+The authors would like to acknowledge the Graduate Program in Numerical Methods for Engineering (PPGMNE) of the Federal University of Parana (UFPR). The first author would like to thank the Federal Institute of Education, Science and Technology of Santa Catarina (IFSC) for the financial support.
 ==References==
+<div class="auto" style="width: auto; margin-left: auto; margin-right: auto;font-size: 85%;">
-:[1] T. Gradl, K. Klamroth, U. Rüde, U. Optimizing the number of multigrid cycles in the full multigrid algorithm. Numerical Linear Algebra with Applications. Vol. 17 (2010) 199–210.
+[1] Thekale T. Gradl, Klamroth K.,  Rüde U. Optimizing the number of multigrid cycles in the full multigrid algorithm. Numerical Linear Algebra with Applications, Vol. 17, 199–210,  2010.
-:[2] R. H. Pletcher, J. C. Tannehill, D. A. Anderson, Computational Fluid Mechanics and Heat Transfer, 3ª ed. CRC Press, USA, 2013.
+[2] Pletcher R.H.,  Tannehill J.C.,  Anderson D.A. Computational fluid mechanics and heat Transfer. 3ª ed. CRC Press, USA, 2013.
-:[3] G. H. Golub, J. M. Ortega, Scientific Computing and Differential Equations: an Introduction to Numerical Methods, Academic Press, 1992.
+[3] G.H. Golub, J.M. Ortega, Scientific Computing and Differential Equations: an Introduction to Numerical Methods, Academic Press, 1992.
-:[4] Y. Saad, Iterative Methods for Sparse Linear Systems, 2ªed., PWS, Philadelphia, 2003.
+[4] Y. Saad, Iterative Methods for Sparse Linear Systems, 2ªed., PWS, Philadelphia, 2003.
-:[5] W. L. Briggs, V.E. Henson, S.F. Mccormick, A Multigrid Tutorial, 2ª ed., SIAM, USA, 2000.
+[5] W.L. Briggs, V.E. Henson, S.F. Mccormick, A Multigrid Tutorial, 2ª ed., SIAM, USA, 2000.
-:[6] U. Trottenberg, C. Oosterlee, A. Schüller, Multigrid, Academic Press, England, 2001.
+[6] U. Trottenberg, C. Oosterlee, A. Schüller, Multigrid, Academic Press, England, 2001.
-:[7] P. Wesseling, An Introduction to Multigrid Methods, John Wiley & Sons, England, 1992.
+[7] P. Wesseling, An Introduction to Multigrid Methods, John Wiley & Sons, England, 1992.
-:[8] F. Oliveira, M. A. V. Pinto, C. H. Marchi, L. K. Araki. Optimized partial semicoarsening multigrid algorithm for heat diffusion problems and anisotropic grids. Applied Mathematical Modelling. Vol. 36 (2012) 4665–4676.
+[8] F. Oliveira, M.A.V. Pinto, C.H. Marchi, L.K. Araki. Optimized partial semicoarsening multigrid algorithm for heat diffusion problems and anisotropic grids. Applied Mathematical Modelling, Vol. 36 (2012) 4665–4676.
-:[9] J. A. Rabi, M. J. S. de Lemos. Optimization of convergence acceleration in multigrid numerical solutions of conductive-convective problems. Applied Mathematics and Computational. Vol. 124 (2001) 215-226.
+[9] J.A. Rabi, M.J.S. de Lemos. Optimization of convergence acceleration in multigrid numerical solutions of conductive-convective problems. Applied Mathematics and Computational, Vol. 124 (2001) 215-226.
-:[10] R. Wienands, W. Joppich, Practical Fourier Analysis for Multigrid Methods, CRC Press, USA, 2005.
+[10] R. Wienands, W. Joppich, Practical Fourier Analysis for Multigrid Methods, CRC Press, USA, 2005.
-:[11] K. Johannsen. A robust 9-point ILU smoother for anisotropic problems, IWR Preprint, University of Heidelberg, 2005.
+[11] K. Johannsen. A robust 9-point ILU smoother for anisotropic problems, IWR Preprint, University of Heidelberg, 2005.
-:[12] S. A. Vinogradova, L. A. Krukier, The use of incomplete LU decomposition in modeling convection-diffusion processes in an anisotropic medium. Mathematical Models and Computer Simulations. Vol. 5 (2013) 190-197.
+[12] S.A. Vinogradova, L.A. Krukier, The use of incomplete LU decomposition in modeling convection-diffusion processes in an anisotropic medium. Mathematical Models and Computer Simulations, Vol. 5 (2013) 190-197.
-:[13] G. Vassoler-Rutz, M. A. V. Pinto, R. Suero, Comparison of the physical anisotropy of multigrid method for two-dimensional diffusion equation, in: Proceedings of COBEM, Rio de Janeiro, Brazil, Dezembro 6-11.
+[13] G. Vassoler-Rutz, M.A.V. Pinto, R. Suero, Comparison of the physical anisotropy of multigrid method for two-dimensional diffusion equation, in: Proceedings of COBEM, Rio de Janeiro, Brazil, (2015) 6-11.
-:[14] M. A. V. Pinto, C. Rodrigo, F. J. Gaspar, C.W. Oosterlee. On the robustness of ILU smoothers on triangular grids, Applied Numerical Mathematics. Vol. 106 (2016), 37-52.
+[14] M.A. V. Pinto, C. Rodrigo, F.J. Gaspar, C.W. Oosterlee. On the robustness of ILU smoothers on triangular grids, Applied Numerical Mathematics, Vol. 106 (2016), 37-52.
-:[15] S. R. Franco, F. J. Gaspar, M. A. V. Pinto, C. Rodrigo. Multigrid method based on a space-time approach with standard coarsening for parabolic problems. Applied Mathematics and Computation. Vol. 317 (2018) 25-34.
+[15] S.R. Franco, F.J. Gaspar, M.A.V. Pinto, C. Rodrigo. Multigrid method based on a space-time approach with standard coarsening for parabolic problems. Applied Mathematics and Computation, Vol. 317 (2018) 25-34.
-:[16] F. Oliveira. Effect of Two-Dimensional Anisotropic Meshes on the Performance of the Geometric Multigrid Method. Tese de doutorado, UFPR, 2010. ''In portuguese''.
+[16] M.L. Oliveira, M.A. V. Pinto, S.F.T. Gonçalves, G. Vassoler-Rutz. On the Robustness of the xy-Zebra-Gauss-Seidel Smoother on an Anisotropic Diffusion Problem. CMES., Vol.117 (2018) 251-270.
-:[17] P. Wesseling, C. W. Oosterlee. Geometric Multigrid with Applications to Computational Fluid Dynamics. Journal of Computation and Applied Mathematics. Vol. 128 (2001) 311-334.
+[17] F. Oliveira. Effect of Two-Dimensional Anisotropic Meshes on the Performance of the Geometric Multigrid Method. Tese de doutorado, UFPR, 2010. ''In portuguese''.
-:[18] R. L. Burden, J.D. Faires, Numerical Analysis, 9ª ed., Cengage Learning, USA, 2010.
+[18] P. Wesseling, C.W. Oosterlee. Geometric Multigrid with Applications to Computational Fluid Dynamics. Journal of Computation and Applied Mathematics, Vol. 128 (2001) 311-334.
+[19] J.L. Guermond, P. Minev, Jie Shen. An overview of prejection methods for incompressible flows. Computer Methods in Apllied Mechanics and Engineering, Vol. 195 (2006)  6011-6045.
+[20] R.L. Burden, J.D. Faires, Numerical Analysis, 9ª ed., Cengage Learning, USA, 2010.
+</div>