| (7 intermediate revisions by the same user not shown) | |||
| Line 42: | Line 42: | ||
==2. The micro-macro LaTIn based Domain Decomposition Method== | ==2. The micro-macro LaTIn based Domain Decomposition Method== | ||
| − | Let us consider a laminate composite ( | + | Let us consider a laminate composite ([[#img-1|Figure 1]]) occupying the domain <math display="inline">\Omega </math> bounded by <math display="inline">\partial \Omega </math> in the current configuration, and consisting of <math display="inline">N_P</math> plies. Each ply <math display="inline">P</math> is connected to an adjacent ply <math display="inline">P' </math> through the interface <math display="inline">{\Gamma _{PP'}}</math>. The structure is subjected to an external surface traction field <math display="inline">{\underline{F}_d}</math> on the part <math display="inline">{\partial \Omega _{F_d}}</math> and to a displacement field <math display="inline">{\underline{U}_d}</math> on the complementary part <math display="inline">{\partial \Omega _{U_d}}</math>. The body force per unit of mass is written <math display="inline">{\underline{f}_d}</math>. The relevant quantities are described in reference to the undeformed configuration using the index <math display="inline">\cdot _\mathit{0}</math>. The geometrically nonlinear evolution is handled through a total Lagrangian formulation and delamination (damageable interfaces) is modeled using CZM and unilateral contact conditions. For the sake of simplicity, an extensive description of the CZM is found in <span id='citeF-24'></span>[[#cite-24|[24]]], while <span id='citeF-25'></span>[[#cite-25|[25]]] describe contact inequalities. |
| − | To propose the partitioned problem, the whole domain <math display="inline">\Omega </math> is split into subdomains which are connected by interfaces with mechanical behaviors. Two possibilities are considered: “material” interfaces between plies with localized non-linearities (damage, contact) that are compatible with the mesomodeling, and “numerical” interfaces (the perfect ones) within the plies to conceive smaller problems that are suited for parallelism, as schematized in | + | To propose the partitioned problem, the whole domain <math display="inline">\Omega </math> is split into subdomains which are connected by interfaces with mechanical behaviors. Two possibilities are considered: “material” interfaces between plies with localized non-linearities (damage, contact) that are compatible with the mesomodeling, and “numerical” interfaces (the perfect ones) within the plies to conceive smaller problems that are suited for parallelism, as schematized in [[#img-1|Figure 1]]. A subdomain <math display="inline">{S^{\quad }_\mathit{0}}</math> defined in the undeformed domain <math display="inline">{\Omega _{S_\mathit{0}}}</math> is connected to an adjacent undeformed subdomain <math display="inline">{{S'}_\mathit{0}}</math> through an undeformed interface <math display="inline">{\Gamma _{S_\mathit{0}{S'}_\mathit{0}}}=\partial {\Omega _{S_\mathit{0}}}\cap \partial {\Omega _{S_\mathit{0}'}}</math>. The surface entity <math display="inline">{\Gamma _{S_\mathit{0}{S'}_\mathit{0}}}</math> applies force distributions <math display="inline">{\underline{F}_{{S^{\quad }_\mathit{0}}}}</math>, <math display="inline">{\underline{F}_{S_\mathit{0}'}}</math> and displacement distributions <math display="inline">{\underline{W}_{{S^{\quad }_\mathit{0}}}}</math>, <math display="inline">{\underline{W}_{{S'}_\mathit{0}}}</math> to <math display="inline">{S^{\quad }_\mathit{0}}</math> and <math display="inline">{{S'}_\mathit{0}}</math> respectively ([[#img-2|Figure 2]]). Let us define <math display="inline">{\Gamma _{S_\mathit{0}}}= \cup _{{{S'}_\mathit{0}}\in {\mathbf{E}}} {\Gamma _{S_\mathit{0}{S'}_\mathit{0}}}</math>. For a subdomain <math display="inline">{S^{\quad }_\mathit{0}}</math> such that <math display="inline">{\Gamma _{S_\mathit{0}}}\cap ({\partial \Omega _{F_{d_\mathit{0}}}}\cup {\partial \Omega _{U_{d_\mathit{0}}}}) \neq \emptyset </math>, the boundary condition <math display="inline">({\underline{F}_{d_\mathit{0}}},{\underline{U}_{d_\mathit{0}}})</math> is applied through a boundary interface <math display="inline">{\Gamma _{{S}_{d_\mathit{0}}}}</math>. |
| Line 52: | Line 52: | ||
|style="padding:10px;"|[[Image:Draft_Saavedra_368043899-reference_pb.png|700px|The reference problem, the mesomodel and its partitioning <span id='citeF-18'></span>[[#cite-18|[18]]]] | |style="padding:10px;"|[[Image:Draft_Saavedra_368043899-reference_pb.png|700px|The reference problem, the mesomodel and its partitioning <span id='citeF-18'></span>[[#cite-18|[18]]]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" style="padding-bottom:10px;"| '''Figure 1 | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 1'''. The reference problem, the mesomodel and its partitioning <span id='citeF-18'></span>[[#cite-18|[18]]] |
|} | |} | ||
| Line 60: | Line 60: | ||
|style="padding:10px;"|[[Image:Draft_Saavedra_368043899-sst_v2.png|540px|Subdomains and interfaces <span id='citeF-16'></span>[[#cite-16|[16]]]] | |style="padding:10px;"|[[Image:Draft_Saavedra_368043899-sst_v2.png|540px|Subdomains and interfaces <span id='citeF-16'></span>[[#cite-16|[16]]]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" style="padding-bottom:10px;"| '''Figure 2 | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 2'''. Subdomains and interfaces <span id='citeF-16'></span>[[#cite-16|[16]]] |
|} | |} | ||
| Line 196: | Line 196: | ||
===2.2 Discretization=== | ===2.2 Discretization=== | ||
| − | To solve both equations' sets of the multiscale algorithm, interfaces and subdomains are discretized in space using classical finite elements. At an interface <math display="inline">{\Gamma _{S_\mathit{0}{S'}_\mathit{0}}}</math>, the displacements <math display="inline">{\underline{W}_{{S^{\quad }_\mathit{0}}}}</math> and forces <math display="inline">{\underline{F}_{{S^{\quad }_\mathit{0}}}}</math> belong to the approximation spaces <math display="inline">{\mathcal{W}_{{S^{\quad }_\mathit{0}}{{S'}_\mathit{0}},h}}</math> and <math display="inline">{\mathcal{F}_{{S^{\quad }_\mathit{0}}{{S'}_\mathit{0}},h}}</math>. These spaces are chosen such that the bilinear form (in the sense of the interface mechanical work) is non-degenerate. Additionally, a wrong discretization for <math display="inline">{\mathcal{F}_{{S^{\quad }_\mathit{0}}{{S'}_\mathit{0}},h}}</math> could generate spurious oscillating modes leading to numerical instability. These inconveniences can be evaded using a common space for the displacements and forces and including a local refinement of the mesh near the boundary (over-discretization) of the subdomains (approximation space <math display="inline">{\mathcal{U}_{S_\mathit{0}}}</math>). Two manners are possible: to increase the number of elements (<math display="inline">h</math>-version) or to use a higher degree of approximation (<math display="inline">p</math>-version) for the field <math display="inline">{\underline{u}_{{S^{\quad }_\mathit{0}}}}</math> near to the interface, as illustrated in | + | To solve both equations' sets of the multiscale algorithm, interfaces and subdomains are discretized in space using classical finite elements. At an interface <math display="inline">{\Gamma _{S_\mathit{0}{S'}_\mathit{0}}}</math>, the displacements <math display="inline">{\underline{W}_{{S^{\quad }_\mathit{0}}}}</math> and forces <math display="inline">{\underline{F}_{{S^{\quad }_\mathit{0}}}}</math> belong to the approximation spaces <math display="inline">{\mathcal{W}_{{S^{\quad }_\mathit{0}}{{S'}_\mathit{0}},h}}</math> and <math display="inline">{\mathcal{F}_{{S^{\quad }_\mathit{0}}{{S'}_\mathit{0}},h}}</math>. These spaces are chosen such that the bilinear form (in the sense of the interface mechanical work) is non-degenerate. Additionally, a wrong discretization for <math display="inline">{\mathcal{F}_{{S^{\quad }_\mathit{0}}{{S'}_\mathit{0}},h}}</math> could generate spurious oscillating modes leading to numerical instability. These inconveniences can be evaded using a common space for the displacements and forces and including a local refinement of the mesh near the boundary (over-discretization) of the subdomains (approximation space <math display="inline">{\mathcal{U}_{S_\mathit{0}}}</math>). Two manners are possible: to increase the number of elements (<math display="inline">h</math>-version) or to use a higher degree of approximation (<math display="inline">p</math>-version) for the field <math display="inline">{\underline{u}_{{S^{\quad }_\mathit{0}}}}</math> near to the interface, as illustrated in [[#img-3|Figure 3]] <span id='citeF-27'></span>[[#cite-27|[27]]]. Classically, the code MULTI has considered linear elements <math display="inline">\mathcal{P}_1</math> with local <math display="inline">h</math>-refinement along the subdomain's boundary, while the spaces <math display="inline">{\mathcal{W}_{{S^{\quad }_\mathit{0}}{{S'}_\mathit{0}},h}}</math> and <math display="inline">{\mathcal{F}_{{S^{\quad }_\mathit{0}}{{S'}_\mathit{0}},h}}</math> are piecewise constant functions <math display="inline">\mathcal{P}_0</math>. |
In this work, the <math display="inline">p</math>-refinement is also explored. Indeed, it is here proposed to use the second order approximation for <math display="inline">{\underline{u}_{{S^{\quad }_\mathit{0}}}}</math> not only in the boundary but in the whole subdomain. | In this work, the <math display="inline">p</math>-refinement is also explored. Indeed, it is here proposed to use the second order approximation for <math display="inline">{\underline{u}_{{S^{\quad }_\mathit{0}}}}</math> not only in the boundary but in the whole subdomain. | ||
| Line 205: | Line 205: | ||
|[[Image:Review_265042547183_2078_Fig3.png|600px|Modification of the classical approximations of the inter-force and local displacement along the edge of a subdomain: h-and p-versions <span id='citeF-13'></span>[[#cite-13|[13]]]] | |[[Image:Review_265042547183_2078_Fig3.png|600px|Modification of the classical approximations of the inter-force and local displacement along the edge of a subdomain: h-and p-versions <span id='citeF-13'></span>[[#cite-13|[13]]]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" style="padding-bottom:10px;"| '''Figure 3 | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 3'''. Modification of the classical approximations of the inter-force and local displacement along the edge of a subdomain: <math>h</math>-and <math>p</math>-versions <span id='citeF-13'></span>[[#cite-13|[13]]] |
|} | |} | ||
| Line 212: | Line 212: | ||
This section analyses the influence of the subdomains' discretization for three different problems: bending, buckling and delamination. The following three meshes <math display="inline">{\mathcal{U}_{S_\hbox{0}}}</math> are considered: | This section analyses the influence of the subdomains' discretization for three different problems: bending, buckling and delamination. The following three meshes <math display="inline">{\mathcal{U}_{S_\hbox{0}}}</math> are considered: | ||
| − | * <math display="inline">i</math>-version: linear six-node wedge elements of equal size in the whole subdomain (“initial” version without local over discretization, | + | * <math display="inline">i</math>-version: linear six-node wedge elements of equal size in the whole subdomain (“initial” version without local over discretization, ([[#img-3|Figure 3]]); |
| − | * <math display="inline">h</math>-version: linear six-node wedge elements, where the elements along the subdomain's boundary are divided into three four-node tetrahedral elements as shown in | + | * <math display="inline">h</math>-version: linear six-node wedge elements, where the elements along the subdomain's boundary are divided into three four-node tetrahedral elements as shown in [[#img-4|Figure 4]] (local <math display="inline">h</math> over discretization); |
* <math display="inline">p</math>-version: quadratic fifteen-node wedge elements of equal size in the whole subdomain (global <math display="inline">p</math> over discretization). | * <math display="inline">p</math>-version: quadratic fifteen-node wedge elements of equal size in the whole subdomain (global <math display="inline">p</math> over discretization). | ||
| Line 223: | Line 223: | ||
|[[Image:Review_265042547183_2934_Fig4.png|600px|before and after local h-refinement: a) wedge element b) mesh of the subdomain's boundary (the inner mesh remains unchanged)]] | |[[Image:Review_265042547183_2934_Fig4.png|600px|before and after local h-refinement: a) wedge element b) mesh of the subdomain's boundary (the inner mesh remains unchanged)]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" style="padding-bottom:10px;"| '''Figure 4 | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 4'''. before and after local <math>h</math>-refinement. (a) Wedge element. (b) Mesh of the subdomain's boundary (the inner mesh remains unchanged) |
|} | |} | ||
| Line 232: | Line 232: | ||
====3.1.1 Isotropic material==== | ====3.1.1 Isotropic material==== | ||
| − | It is considered an elastic modulus <math display="inline">E=210</math> [GPa] and a poisson coefficient <math display="inline">\nu=0.3</math> [-]. The geometry is partitioned into <math display="inline">64</math> identical subdomains and <math display="inline">184</math> interfaces ( | + | It is considered an elastic modulus <math display="inline">E=210</math> [GPa] and a poisson coefficient <math display="inline">\nu=0.3</math> [-]. The geometry is partitioned into <math display="inline">64</math> identical subdomains and <math display="inline">184</math> interfaces ([[#img-5|Figure 5]]); each subdomain has length <math display="inline">L_{sst}=20</math> [mm], width <math display="inline">a_{sst}= 15</math> [mm] and thickness <math display="inline">h_{sst}= 4</math> [mm]. Five meshes are considered: two different initial discretization with their respective <math display="inline">h</math>-refinement while the last one is a <math display="inline">p</math>-version. Each subdomain has <math display="inline">n_x</math>(<math display="inline">n_y</math>,<math display="inline">n_z</math>) elements in the <math display="inline">x</math>(<math display="inline">y</math>,<math display="inline">z</math>)-direction, respectively, as shown in [[#table-1|Table 1]] as well as the total number of elements and the total degrees of freedom used for each mesh. In order to estimate the solution's error ([[#table-1|Table 1]]), the maximum vertical displacement is compared with the theoretical elastic curve <span id='citeF-28'></span>[[#cite-28|[28]]]. |
<div id='img-5'></div> | <div id='img-5'></div> | ||
| Line 239: | Line 239: | ||
|[[Image:Review_265042547183_5579_Fig5.png|600px|Partitioning of the geometry (bending problem with isotropic material)]] | |[[Image:Review_265042547183_5579_Fig5.png|600px|Partitioning of the geometry (bending problem with isotropic material)]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" style="padding-bottom:10px;"| '''Figure 5 | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 5'''. Partitioning of the geometry (bending problem with isotropic material) |
|} | |} | ||
| + | <div class="center" style="font-size: 75%;">'''Table 1'''. Results according to the discretization (bending problem with isotropic material); '''+''' ratio respect to simulation (b.1)</div> | ||
| + | |||
| + | <div id='tab-1'></div> | ||
{| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size: 85%;" | {| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size: 85%;" | ||
| − | |||
|- style="border-top: 2px solid;" | |- style="border-top: 2px solid;" | ||
| style="border-left: 2px solid;" | mesh | | style="border-left: 2px solid;" | mesh | ||
| Line 304: | Line 306: | ||
|} | |} | ||
| − | In | + | In [[#img-6|Figure 6a]], theoretical and numerical displacements of the neutral line are compared. As naturally expected, when increasing the number of linear elements in the thickness, the solution's error decreases, but the dof and the computational cost increase. However, it is important to notice that for the <math display="inline">h</math>-refinements (a.2) and (b.2), the displacement's error and calculation time increase ([[#table-1|Table 1]]) while the convergence rate decrease respect to the corresponding <math display="inline">i</math>-versions (a.1) and (b.1). Even after 1000 iterations, the iterative LaTIn error for mesh (a.2) is twice the detention criteria. This phenomena could be explained by the fact that <math display="inline">h</math>-version has only a localized refinement along the edge of a subdomain, while the element's size inside the subdomain remains the same as the <math display="inline">i</math>-version. This choice could induce different stiffness through a subdomain, implying additional difficulties to transfer informationn between subdomains. |
| − | Finally, the mesh (d) (<math display="inline">p</math>-version) is twice more accurate, has 73% less dof and is 19,3% more quickly than mesh (b.1). Differences in the computation time ( | + | Finally, the mesh (d) (<math display="inline">p</math>-version) is twice more accurate, has 73% less dof and is 19,3% more quickly than mesh (b.1). Differences in the computation time ([[#table-1|Table 1]]) are mainly related to the mesh size, because convergence rates are similar, as shown in [[#img-6|Figure 6b]]. |
<div id='img-6a'></div> | <div id='img-6a'></div> | ||
| Line 314: | Line 316: | ||
|[[Image:Review_265042547183_4713_Fig6.png|700px|]] | |[[Image:Review_265042547183_4713_Fig6.png|700px|]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" style="padding-bottom:10px;"| '''Figure 6 | + | | colspan="2" style="padding-bottom:10px;"| '''Figure 6'''. Bending problem with isotropic material. (a) Deflection. (b) Evolution of the iterative LaTIn error |
|} | |} | ||
====3.1.2 Orthotropic material==== | ====3.1.2 Orthotropic material==== | ||
| − | The precedent problem is now studied considering a composite laminate made of four plies <math display="inline">[0^o,90^o]_S</math>, each 1 [mm] a thick. A <math display="inline">0^o</math>-layer is transversely isotropic with the following elastic properties: <math display="inline">E_1=165</math> [GPa], <math display="inline">E_2=E_3=9</math> [GPa], <math display="inline">\nu _{12}=\nu _{13}=0.3</math> [-], <math display="inline">\nu _{23}=0.5</math> [-], <math display="inline">G_{12}=G_{13}=5.6</math> [GPa] and <math display="inline">G_{23}=2.8</math> [GPa]. The geometry is divided into 256 identical subdomains of <math display="inline">L_{sst}=20</math> [mm], <math display="inline">a_{sst}= 15</math> [mm] and <math display="inline">h_{sst}= 1</math> [mm], generating 736 interfaces. Therefore, for each ply there is one subdomain in the <math display="inline">z</math>-direction (four in total through the thickness). | + | The precedent problem is now studied considering a composite laminate made of four plies <math display="inline">[0^o,90^o]_S</math>, each 1 [mm] a thick. A <math display="inline">0^o</math>-layer is transversely isotropic with the following elastic properties: <math display="inline">E_1=165</math> [GPa], <math display="inline">E_2=E_3=9</math> [GPa], <math display="inline">\nu _{12}=\nu _{13}=0.3</math> [-], <math display="inline">\nu _{23}=0.5</math> [-], <math display="inline">G_{12}=G_{13}=5.6</math> [GPa] and <math display="inline">G_{23}=2.8</math> [GPa]. The geometry is divided into 256 identical subdomains of <math display="inline">L_{sst}=20</math> [mm], <math display="inline">a_{sst}= 15</math> [mm] and <math display="inline">h_{sst}= 1</math> [mm], generating 736 interfaces. Therefore, for each ply there is one subdomain in the <math display="inline">z</math>-direction (four in total through the thickness). [[#table-2|Table 2]] compares the different discretizations. |
| + | <div class="center" style="font-size: 75%;">'''Table 2'''. Results according to the discretization (bending problem with an orthotropic material); '''+''' ratio respect to simulation (b.1)</div> | ||
| + | <div id='table-2'></div> | ||
{| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size: 85%;" | {| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size: 85%;" | ||
| − | |||
|- style="border-top: 2px solid;" | |- style="border-top: 2px solid;" | ||
| style="border-left: 2px solid;" | mesh | | style="border-left: 2px solid;" | mesh | ||
| Line 369: | Line 372: | ||
|} | |} | ||
| − | In | + | In [[#img-7|Figure 7a]] is observed that the vertical displacement of the neutral axis is similar except for simulations (a.1) and (a.2). In these two cases, the iterative LaTIn error ([[#img-7|Figure 7b]]) is twice the detention criteria, even after 1000 iterations. Using the <math display="inline">p</math>-version mesh (c), the LaTIn error is less than <math display="inline">10^{-5}</math> in only 68 iteraciones, less than half of the iterations made by the curve (b.1) to converge. If the upper stresses <math display="inline">\sigma _{xx}</math> are compared respect to the theoretical ones ([[#img-8|Figure 8]]), it is possible to confirm that (a.1), (a.2) and (b.2) do not fit the desired solution. |
<div id='img-7a'></div> | <div id='img-7a'></div> | ||
| Line 377: | Line 380: | ||
| [[Image:Review_265042547183_6563_Fig7.png|700px]] | | [[Image:Review_265042547183_6563_Fig7.png|700px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" style="padding-bottom:10px;"| '''Figure 7 | + | | colspan="2" style="padding-bottom:10px;"| '''Figure 7'''. Bending problem with orthotropic material. (a) Deflection. (b) Evolution of the iterative LaTIn error |
|} | |} | ||
| − | + | [[#table-2|Table 2]] compares calculation time, total number of elements and total dof. It is verified that using <math display="inline">p</math>-version, mesh (c), it is possible to obtain the same results as in (b.1) but consuming only 54.2% of the time, even considering that the number of dof increases in a 50%. This is explained because (c) has the best convergence rate ([[#img-7|Figure 7b]]). | |
<div id='img-8a'></div> | <div id='img-8a'></div> | ||
| Line 388: | Line 391: | ||
| [[Image:Review_265042547183_4572_Fig8.png|700px]] | | [[Image:Review_265042547183_4572_Fig8.png|700px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" style="padding-bottom:10px;"| '''Figure 8 | + | | colspan="2" style="padding-bottom:10px;"| '''Figure 8'''. Results for the orthotropic material: normal stresses <math>\sigma _{xx}</math> |
|} | |} | ||
| Line 395: | Line 398: | ||
===3.2 Buckling=== | ===3.2 Buckling=== | ||
| − | The problem to be addressed is a slender 3D beam built-in at both ends, with one of them subjected to a negative displacement <math display="inline">\underline{u}_d</math> to produce uniaxial compression, while a perpendicular perturbation <math display="inline">\underline{F}_d</math> induces buckling out of the plane ( | + | The problem to be addressed is a slender 3D beam built-in at both ends, with one of them subjected to a negative displacement <math display="inline">\underline{u}_d</math> to produce uniaxial compression, while a perpendicular perturbation <math display="inline">\underline{F}_d</math> induces buckling out of the plane ([[#img-9|Figure 9a]]). The structure has the following geometry: length <math display="inline">L=10</math> [mm] (<math display="inline">x</math>-direction), width <math display="inline">a=1</math> [mm] (<math display="inline">y</math>-direction) and thickness <math display="inline">h=0.1</math> [mm] (<math display="inline">z</math>-direction). The properties of the material are <math display="inline">E= 135</math> [GPa] and <math display="inline"> \nu = 0.3 </math> [-]. The geometry is divided into 100 subdomains and 156 perfect interfaces, therefore, each subdomain has <math display="inline">L_{sst}=0.2</math> [mm], width <math display="inline">a_{sst}= 0.5</math> [mm] and thickness <math display="inline">h_{sst}= 0.1</math> [mm]. Three meshes are considered, the first two are linear without over discretization (<math display="inline">i</math>-version), while the mesh (c) is a <math display="inline">p</math>-refinement. More details of the meshes and their results are shown in [[#table-3|Table 3]]. |
| + | <div class="center" style="font-size: 75%;">'''Table 3'''. Results according to the discretization (buckling problem); '''+''' ratio respect to simulation (b)</div> | ||
| + | <div id='table-3'></div> | ||
{| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size: 85%;" | {| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size: 85%;" | ||
| − | |||
|- style="border-top: 2px solid;" | |- style="border-top: 2px solid;" | ||
| style="border-left: 2px solid;" | mesh | | style="border-left: 2px solid;" | mesh | ||
| Line 431: | Line 435: | ||
|} | |} | ||
| − | The simulation was performed in 1000 steps. | + | The simulation was performed in 1000 steps. [[#img-9|Figure 9a]] shows the initial configuration and the final deformation at the last time step. The evolution of the compression axial load (<math display="inline">P/P_{crit}</math>) is obtained as a function of the transverse displacement in <math display="inline">x=L/2</math>, as shown in [[#img-9|Figure 9b]]. |
It is noticed that simulations (a) and (b) has respectively <math display="inline">8.68%</math> and <math display="inline">2.61%</math> of error in the critical load when the transverse displacement over <math display="inline">L_0</math> is 0.005 [-], while mesh (c) is the closest (only <math display="inline">1.46 %</math> of error at the same point). In addition, the time spent for mesh (c) is only the <math display="inline">2.9 %</math> used in (b). | It is noticed that simulations (a) and (b) has respectively <math display="inline">8.68%</math> and <math display="inline">2.61%</math> of error in the critical load when the transverse displacement over <math display="inline">L_0</math> is 0.005 [-], while mesh (c) is the closest (only <math display="inline">1.46 %</math> of error at the same point). In addition, the time spent for mesh (c) is only the <math display="inline">2.9 %</math> used in (b). | ||
| Line 440: | Line 444: | ||
|[[Image:Review_265042547183_1362_Fig9.png|700px|(a) The initial configuration and the final deformation after the last time step (b) the load-displacement curve ]] | |[[Image:Review_265042547183_1362_Fig9.png|700px|(a) The initial configuration and the final deformation after the last time step (b) the load-displacement curve ]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" style="padding-bottom:10px;"| '''Figure 9 | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 9'''. (a) The initial configuration and the final deformation after the last time step. (b) The load-displacement curve |
|} | |} | ||
===3.3 Delamination=== | ===3.3 Delamination=== | ||
| − | In this section we study the effect of discretization when problems involve CZM. The example to be simulated is a 3D double cantilever beam (DCB), whose length is <math display="inline">L=20</math> [mm] (<math display="inline">x</math>-direction), width <math display="inline">a=2</math> [mm] (<math display="inline">y</math>-direction), thickness <math display="inline">h=1</math> [mm] (<math display="inline">z</math>-direction) and pre-crack <math display="inline">a_0=10</math> [mm] located at the end of the beam along the <math display="inline">x</math>-direction ( | + | In this section we study the effect of discretization when problems involve CZM. The example to be simulated is a 3D double cantilever beam (DCB), whose length is <math display="inline">L=20</math> [mm] (<math display="inline">x</math>-direction), width <math display="inline">a=2</math> [mm] (<math display="inline">y</math>-direction), thickness <math display="inline">h=1</math> [mm] (<math display="inline">z</math>-direction) and pre-crack <math display="inline">a_0=10</math> [mm] located at the end of the beam along the <math display="inline">x</math>-direction ([[#img-11|Figure 11a]]). The properties of the material are <math display="inline">E= 135</math> [GPa] and <math display="inline"> \nu = 0.3 </math> [-]; the cohesive interface parameters are <math display="inline">k_n=100\cdot 10^3</math> [N/mm<math display="inline">^3</math>], <math display="inline">\alpha=1</math> [-], <math display="inline">Y_c=0.4</math> [N/mm] and <math display="inline">n=0.5</math> [-]. |
| − | + | ||
| − | + | ||
| + | The geometry is divided into 160 subdomains and 324 interfaces such as each subdomain has <math display="inline">L_{sst}=0.5</math> [mm], width <math display="inline">a_{sst}= 1</math> [mm] and thickness <math display="inline">h_{sst}= 0.5</math> [mm]. Four meshes were considered (see details in [[#table-4|Table 4]]) and the simulation was performed in 50 time steps. | ||
| + | <div class="center" style="font-size: 75%;">'''Table 4'''. Results according to the discretization (DCB problem); '''+''' ratio respect to simulation (a)</div> | ||
| + | <div id='table-1'></div> | ||
{| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size: 85%;" | {| class="floating_tableSCP wikitable" style="text-align: center; margin: 1em auto;min-width:50%;font-size: 85%;" | ||
| − | |||
|- style="border-top: 2px solid;" | |- style="border-top: 2px solid;" | ||
| style="border-left: 2px solid;" | mesh | | style="border-left: 2px solid;" | mesh | ||
| Line 483: | Line 487: | ||
|} | |} | ||
| − | Results are compared to the theoretical solution <span id='citeF-29'></span>[[#cite-29|[29]]] in | + | Results are compared to the theoretical solution <span id='citeF-29'></span>[[#cite-29|[29]]] in [[#img-10|Figure 10]]. It is possible to observe three areas: the first is the bending mode (without delamination); the second zone appears for the crack's propagation (softening curve) and the third one is the second bending mode (when the beam has been completely delaminated). For bending, mesh (b) with three non-linear elements in the thickness is satisfactory, but it does not correctly represent delamination due to the visible zigzag. If the discretization (c) is studied, with a greater number of elements in the <math display="inline">y</math>-direction, the entire curve is correctly predicted, but the time used for the calculation is double that used for the linear discretization (a). The lack of accuracy in the response of mesh (b) could be related to the fact that the forces calculated to evaluate damage are performed at the interfaces which are discretize by constant functions <math display="inline">\mathcal{P}_0</math> ([[#img-3|Figure 3]]), although subdomains have finite elements of higher order. [[#img-11|Figure 11]] shows the crack's front at the beginning of the propagation. |
<div id='img-10'></div> | <div id='img-10'></div> | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;max-width: 80%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;max-width: 80%;" | ||
|- | |- | ||
| − | |[[Image:Review_265042547183_8931_Fig10.png| | + | |[[Image:Review_265042547183_8931_Fig10.png|700px|The load-displacement curve of the DCB test]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" style="padding-bottom:10px;"| '''Figure 10 | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 10'''. The load-displacement curve of the DCB test |
|} | |} | ||
| Line 496: | Line 500: | ||
{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;max-width: 80%;" | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;max-width: 80%;" | ||
|- | |- | ||
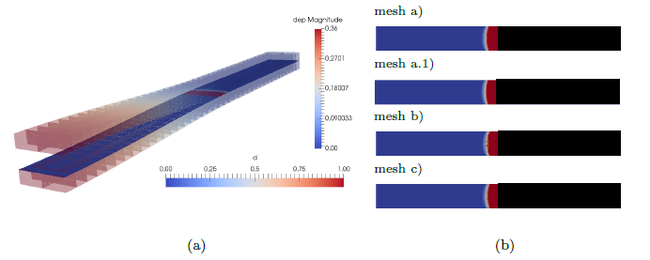
| − | |[[Image:Review_265042547183_2690_Fig11.png| | + | |[[Image:Review_265042547183_2690_Fig11.png|650px|DCB problem: (a) subdomains and interfaces (b) crack's front after the 11<sup>th</sup> step where pre-crack is in black and d is the damage variable ranging from 0 (healthy point) to 1 (completely damaged interface point)]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" style="padding-bottom:10px;"| '''Figure 11 | + | | colspan="1" style="padding-bottom:10px;"| '''Figure 11'''. DCB problem. (a) Subdomains and interfaces. (b) Crack's front after the 11<math>^{th}</math> step where pre-crack is in black and d is the damage variable ranging from 0 (healthy point) to 1 (completely damaged interface point) |
|} | |} | ||
| Line 517: | Line 521: | ||
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | [[#citeF-1|[1]]] Herakovich C.T. Mechanics of composites: A historical review. Mechanics Research Communications, 1: 1 - 20, 2012. | + | [[#citeF-1|[1]]] Herakovich C.T. Mechanics of composites: A historical review. Mechanics Research Communications, 1:1-20, 2012. |
<div id="cite-2"></div> | <div id="cite-2"></div> | ||
Latest revision as of 13:39, 6 July 2021
Abstract
This article is focused on the study of a micro-macro LaTIn based Domain Decomposition Method (LaTIn-DDM) for the prediction of the nonlinear behavior of slender composite structures subjected to bending, buckling and delamination. Previous studies have shown that an adequate selection of the iterative parameters (search directions and macroscopic space) allow to improve the convergence rate and ensure scalability (i.e. number of iterations is independent of the number of subdomains) of the iterative schema. To obtain precise solutions, only the size reduction of the subdomains' discretization has been addressed (-refinement), disregarding the option of increasing the polynomial degree of the finite elements (-refinement) and ignoring their underlying effects on the information's transmission through the interfaces between subdomains. In this work and using linear and quadratic finite elements, and refinements on the subdomains and local -refinement only along the edges of the subdomains were investigated. It is conclude that the -refinement in the whole subdomain not only enables to reach more exact solutions than using global or local -refinement, but also the convergence rate is improved. These enhancements allow more complex simulations but using less degrees of freedom and less calculation time, even up to 97% faster.
Keywords: Domain decomposition method, quadratic finite elements, composites, delamination, buckling
1. Introduction
Since the middle of the last century, composite materials have been widely used in several industrial applications, showing advantages over materials such as steel and aluminum due to their specific properties. Furthermore, scientists and engineers have made efforts to understand their behavior and to predict them [1,2]. The usage of models which are defined at micro-length scales would be ideal, but numerical complexity and computational limitations (memory and time) appear when simulations are performed [3]. Instead, Domain Decomposition Methods (DDM) [4,5,6] are suitable to face these issues taking advantage of the power of parallel and distributed computations (high performance computing). By partitioning the structure into smaller subdomains connected by interfaces, these algorithms lead with local problems defined in each subdomain and a condensed interface problem. Then computational limitations are overcome because they are numerically cheaper and adapted to the parallel architecture of hardwares. The scalability of these methods (i.e. convergence rate does not depends on the number of subdomains) is often managed using a coarse problem ensuring a global communication between subdomains (i.e. a second calculation's scale) [7,8,9].
The LaTIn method [10] is in principle a non-incremental schema to solve non-linear problems; however its extension as a multiscale mixed DDM has been easily done [11]. Contact [12], crack propagation [13,14,15], buckling-delamination interaction [16,17] and heterogeneous structures [11] are among the different nonlinear and complex problems solved with this method. It distinguishes the no-linear equations defined on the subdomains from the non-linear ones defined on the interfaces, in order to define two groups of partial solutions over which a fixed point is applied to reach the intersection of them at convergence. This algorithm is configured with two search directions linking the force to the displacement distributions on the interfaces (i.e. mixed or Robin conditions). The LaTIn method aims to improve its convergence rate by introducing a second space scale at the interface level (classically called the “macroscopic problem” in contrast to the local problems solved in each subdomain which are called “microscopic problems”). For this reason, the global equilibrium over the structure is enforced in a few interface's unknowns by defining a macroscopic basis of the interface's displacements. Additionally, the Robin conditions need to be optimized (large-wavelength components converge rapidly whereas small-wavelength components converge slowly) as shown in [18,19,20].
Delamination is one of the main degradation mechanisms of laminated composite materials. This phenomenon is generally initiated by large interlaminar stresses and can be accelerated under geometric instabilities as buckling, leading eventually to a structural failure. For simulating the buckling-delamination interaction in composite laminates, the work of [18] uses the mesoscopic scale defining two constituents: the plies (3D elements) and the interfaces (2D elements), which are naturally linked to the domain partitioning. The geometrically nonlinear evolution is handled through a total Lagrangian formulation as proposed by [16], while delamination is modeled using a Cohesive Zone Model (CZM) which are based on damage mechanics [21]. Conditions of unilateral contact are considered to avoid interpenetration between delaminated surfaces.
The simulations previously carried out need a large amount of degrees of freedom (dof) to correctly capture the different local and global phenomena. Until now, the strategy has privileged to use sufficiently refined meshes (-refinement), but this has implyied expensive computations. The other classical technique to reach more exact solutions rather than dividing elements into smaller ones is to increase the polynomial degree of the finite element approximation (-refinement), as proposed in [22,23] for problems using direct solvers (without parallel computations). Therefore, this work studies the influence of the -refinement not only on the accuracy of the results, but also on the iterative solver (LaTIn-DDM). The numerical implementation is made using the C++ research code MULTI developed at the Laboratoire de Mécanique et Technologies de Cachan1 using MPI and METIS libraries for the parallel assignments.
This work proposes to use second order finite elements in the LaTIn-DDM and to study their effects on the convergence rate and on the calculation time with respect to the LaTIn-DDM previously defined in [18]. To achieve this goal, Section 2 shows the general aspects of the multiscale strategy, then the reference problem, the domain partitioning, governing equations and the multiscale iterative algorithm are detailed. Subsequently, in Section 3, different - and -refinements are compared in 3D beam problems: bending, buckling and delamination. Finally, the conclusions and ongoing work are presented in Section 4.
(1) LMT-Cachan (ENS Paris-Saclay/CNRS/Université Paris-Saclay)
2. The micro-macro LaTIn based Domain Decomposition Method
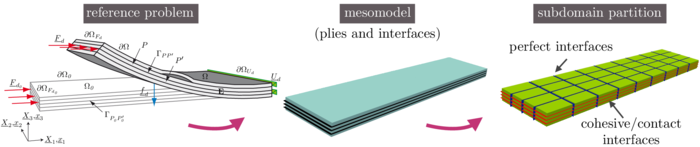
Let us consider a laminate composite (Figure 1) occupying the domain bounded by in the current configuration, and consisting of plies. Each ply is connected to an adjacent ply through the interface . The structure is subjected to an external surface traction field on the part and to a displacement field on the complementary part . The body force per unit of mass is written . The relevant quantities are described in reference to the undeformed configuration using the index . The geometrically nonlinear evolution is handled through a total Lagrangian formulation and delamination (damageable interfaces) is modeled using CZM and unilateral contact conditions. For the sake of simplicity, an extensive description of the CZM is found in [24], while [25] describe contact inequalities.
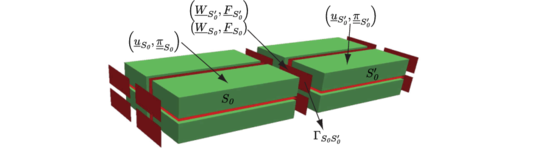
To propose the partitioned problem, the whole domain is split into subdomains which are connected by interfaces with mechanical behaviors. Two possibilities are considered: “material” interfaces between plies with localized non-linearities (damage, contact) that are compatible with the mesomodeling, and “numerical” interfaces (the perfect ones) within the plies to conceive smaller problems that are suited for parallelism, as schematized in Figure 1. A subdomain defined in the undeformed domain is connected to an adjacent undeformed subdomain through an undeformed interface . The surface entity applies force distributions , and displacement distributions , to and respectively (Figure 2). Let us define . For a subdomain such that , the boundary condition is applied through a boundary interface .
|
| Figure 1. The reference problem, the mesomodel and its partitioning [18] |
|
| Figure 2. Subdomains and interfaces [16] |
The purpose of the method is to find the subdomain fields (displacement) and (second Piola-Kirchhoff stress), and the interface fields (displacement) and (inter-forces), where the index ranges over all subdomains. After partitioning, the governing equations are separated into two groups:
1. Non-linear equations in subdomains and macroscopic admissibility of interfaces, whose solutions are elements of the manifold :
- non-linear kinematic admissibility of the subdomains:
|
|
(1) |
|
|
(2) |
- non-linear static admissibility of the subdomains:
|
|
(3) |
where .
- behavior of the subdomains:
|
|
(4) |
where is the stored energy function per unit of undeformed volume. For this work, has been used.
- macroscopic admissibility of the interfaces (after the linearization of the previous equations), which is a partial verification of the action-reaction principle:
|
|
(5) |
where the subspace of interface macroscopic admissible displacements is a parameter described in Section 2.1.
2. Local (non-linear) equations in the interfaces whose solutions belong to the manifold :
- constitutive equation where is the interface displacement gap.
- boundary behavior . The relation can be made explicit for:
- Perfect interface:
- Cohesive interface:
- Unilateral contact interface:
where is the unit normal to and is the corresponding tangential projection operator.
The algorithm consists in seeking the interface solution alternatively in these two spaces: first, one finds a solution in , then a solution in . In order for the two problems to be well-posed, two search directions and , which link the solutions and during the iterative process, are introduced. The converged interface solution is such that . A complete description of this iterative method can be found in [16].
In order to evaluate the convergence, a criterion based on the verification of the constitutive laws of the interfaces quantities issued from the admissibility stage has been implemented, as proposed by [26].
2.1 Separation of the micro-macro scales
The definition of the macroscopic quantities is done through an orthogonal projector for each interface , such as the macroscopic fields are and . Consequently, the microscopic spaces, and , are orthogonal to the macroscopic spaces, and , with respect to the inner product , so the scales can be uncoupled with respect to the interface virtual work as follows:
|
|
(6) |
|
|
(7) |
In order to ensure the scalability of the iterative scheme, a global linear coarse grid problem 5 has been introduced. It is fully characterized by the set of interface macroscopic spaces which is a parameter of the method as well as its dual . Usually, a common macroscopic basis for both the traction and displacement macroscopic fields is chosen so that the uniqueness of the micro-macro descomposition is ensured. Classically, the macroscopic space contain at least the affine part of the interface displacements; this corresponds to verify the balance of the first moments of forces at the interface. However, if complex structures are involved, the geometry and its partitioning degrade the convergence rate. To palliate this problem, [18] propose to find an optimized search direction instead to enrich the macroscopic space.
In this paper, simulations have been carried out using the standard linear macroscopic space and the local search direction previously used in [16].
2.2 Discretization
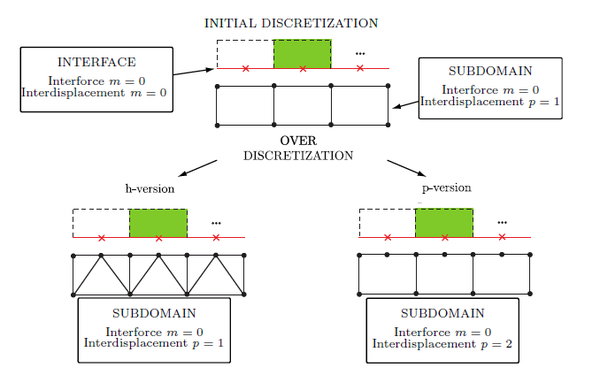
To solve both equations' sets of the multiscale algorithm, interfaces and subdomains are discretized in space using classical finite elements. At an interface , the displacements and forces belong to the approximation spaces and . These spaces are chosen such that the bilinear form (in the sense of the interface mechanical work) is non-degenerate. Additionally, a wrong discretization for could generate spurious oscillating modes leading to numerical instability. These inconveniences can be evaded using a common space for the displacements and forces and including a local refinement of the mesh near the boundary (over-discretization) of the subdomains (approximation space ). Two manners are possible: to increase the number of elements (-version) or to use a higher degree of approximation (-version) for the field near to the interface, as illustrated in Figure 3 [27]. Classically, the code MULTI has considered linear elements with local -refinement along the subdomain's boundary, while the spaces and are piecewise constant functions .
In this work, the -refinement is also explored. Indeed, it is here proposed to use the second order approximation for not only in the boundary but in the whole subdomain.
|
| Figure 3. Modification of the classical approximations of the inter-force and local displacement along the edge of a subdomain: -and -versions [13] |
3. Influence of the discretization on the LaTIn-DDM
This section analyses the influence of the subdomains' discretization for three different problems: bending, buckling and delamination. The following three meshes are considered:
- -version: linear six-node wedge elements of equal size in the whole subdomain (“initial” version without local over discretization, (Figure 3);
- -version: linear six-node wedge elements, where the elements along the subdomain's boundary are divided into three four-node tetrahedral elements as shown in Figure 4 (local over discretization);
- -version: quadratic fifteen-node wedge elements of equal size in the whole subdomain (global over discretization).
For all cases, the approximation functions of the interfaces are . Displacements, convergence rate and time are used to compare the refinements.
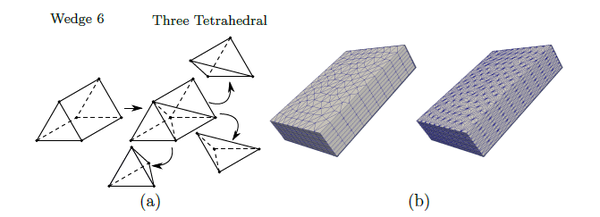
|
| Figure 4. before and after local -refinement. (a) Wedge element. (b) Mesh of the subdomain's boundary (the inner mesh remains unchanged) |
3.1 Bending
The problem consists of a thin 3D beam whose length is [mm] (-direction), width is [mm] (-direction) and thickness is [mm] (-direction). Regarding the boundary conditions, the cantilever beam is embedded at one end and subjected to a surface load [N/m] on its upper face. Here, the hypothesis of small displacements is considered. First an isotropic material is studied, then an orthotropic one is analysed to study the influence of material heterogeneities.
3.1.1 Isotropic material
It is considered an elastic modulus [GPa] and a poisson coefficient [-]. The geometry is partitioned into identical subdomains and interfaces (Figure 5); each subdomain has length [mm], width [mm] and thickness [mm]. Five meshes are considered: two different initial discretization with their respective -refinement while the last one is a -version. Each subdomain has (,) elements in the (,)-direction, respectively, as shown in Table 1 as well as the total number of elements and the total degrees of freedom used for each mesh. In order to estimate the solution's error (Table 1), the maximum vertical displacement is compared with the theoretical elastic curve [28].

|
| Figure 5. Partitioning of the geometry (bending problem with isotropic material) |
| mesh | discretization | -- | total | total dof | time+ | displ. |
| / element | elements | error [mm] | ||||
| a.1) | / wedge 6 | -- | ||||
| a.2) | / wedge 6 | -- | ||||
| b.1) | / wedge 6 | -- | ||||
| b.2) | / wedge 6 | -- | ||||
| c) | / wedge 15 | -- |
In Figure 6a, theoretical and numerical displacements of the neutral line are compared. As naturally expected, when increasing the number of linear elements in the thickness, the solution's error decreases, but the dof and the computational cost increase. However, it is important to notice that for the -refinements (a.2) and (b.2), the displacement's error and calculation time increase (Table 1) while the convergence rate decrease respect to the corresponding -versions (a.1) and (b.1). Even after 1000 iterations, the iterative LaTIn error for mesh (a.2) is twice the detention criteria. This phenomena could be explained by the fact that -version has only a localized refinement along the edge of a subdomain, while the element's size inside the subdomain remains the same as the -version. This choice could induce different stiffness through a subdomain, implying additional difficulties to transfer informationn between subdomains.
Finally, the mesh (d) (-version) is twice more accurate, has 73% less dof and is 19,3% more quickly than mesh (b.1). Differences in the computation time (Table 1) are mainly related to the mesh size, because convergence rates are similar, as shown in Figure 6b.
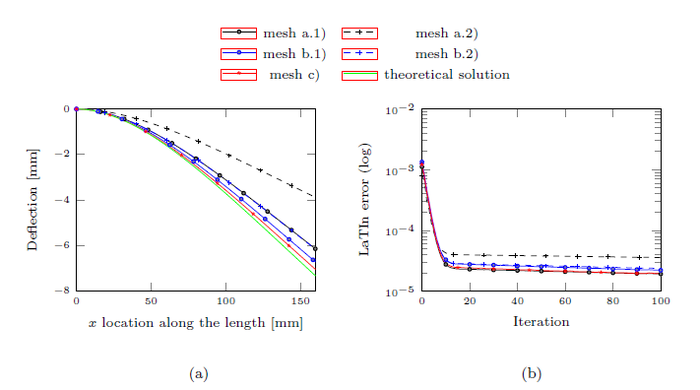
| |
| Figure 6. Bending problem with isotropic material. (a) Deflection. (b) Evolution of the iterative LaTIn error | |
3.1.2 Orthotropic material
The precedent problem is now studied considering a composite laminate made of four plies , each 1 [mm] a thick. A -layer is transversely isotropic with the following elastic properties: [GPa], [GPa], [-], [-], [GPa] and [GPa]. The geometry is divided into 256 identical subdomains of [mm], [mm] and [mm], generating 736 interfaces. Therefore, for each ply there is one subdomain in the -direction (four in total through the thickness). Table 2 compares the different discretizations.
| mesh | disc. / element | -- | total elements | total dof | time+ |
| a.1) | / wedge 6 | -- | |||
| a.2) | / wedge 6 | -- | |||
| b.1) | / wedge 6 | -- | |||
| b.2) | / wedge 6 | -- | |||
| c) | / wedge 15 | -- |
In Figure 7a is observed that the vertical displacement of the neutral axis is similar except for simulations (a.1) and (a.2). In these two cases, the iterative LaTIn error (Figure 7b) is twice the detention criteria, even after 1000 iterations. Using the -version mesh (c), the LaTIn error is less than in only 68 iteraciones, less than half of the iterations made by the curve (b.1) to converge. If the upper stresses are compared respect to the theoretical ones (Figure 8), it is possible to confirm that (a.1), (a.2) and (b.2) do not fit the desired solution.
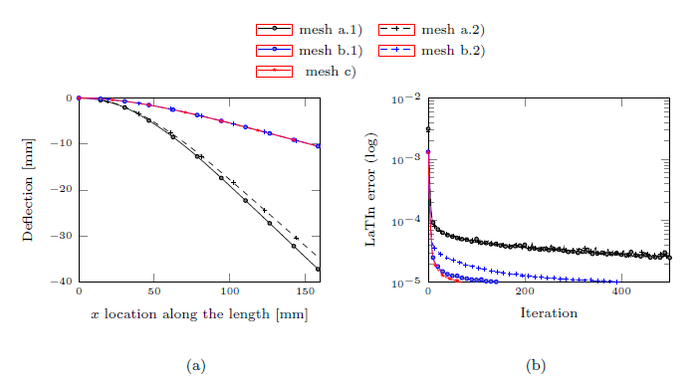
| |
| Figure 7. Bending problem with orthotropic material. (a) Deflection. (b) Evolution of the iterative LaTIn error | |
Table 2 compares calculation time, total number of elements and total dof. It is verified that using -version, mesh (c), it is possible to obtain the same results as in (b.1) but consuming only 54.2% of the time, even considering that the number of dof increases in a 50%. This is explained because (c) has the best convergence rate (Figure 7b).
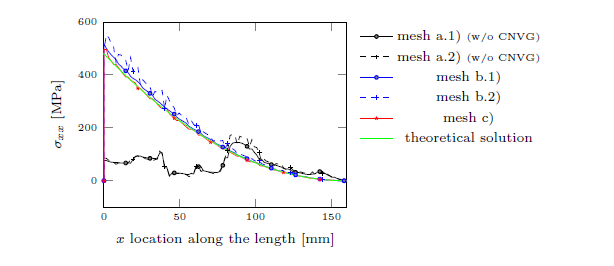
| |
| Figure 8. Results for the orthotropic material: normal stresses | |
Similar to the precedent example, the local -version does not ensure better results. Therefore, the meshes considered for the next examples will be and -versions.
3.2 Buckling
The problem to be addressed is a slender 3D beam built-in at both ends, with one of them subjected to a negative displacement to produce uniaxial compression, while a perpendicular perturbation induces buckling out of the plane (Figure 9a). The structure has the following geometry: length [mm] (-direction), width [mm] (-direction) and thickness [mm] (-direction). The properties of the material are [GPa] and [-]. The geometry is divided into 100 subdomains and 156 perfect interfaces, therefore, each subdomain has [mm], width [mm] and thickness [mm]. Three meshes are considered, the first two are linear without over discretization (-version), while the mesh (c) is a -refinement. More details of the meshes and their results are shown in Table 3.
| mesh | disc. / element | -- | total elements | total dof | time+ |
| a) | / wedge 6 | -- | |||
| b) | / wedge 6 | -- | |||
| c) | / wedge 15 | -- |
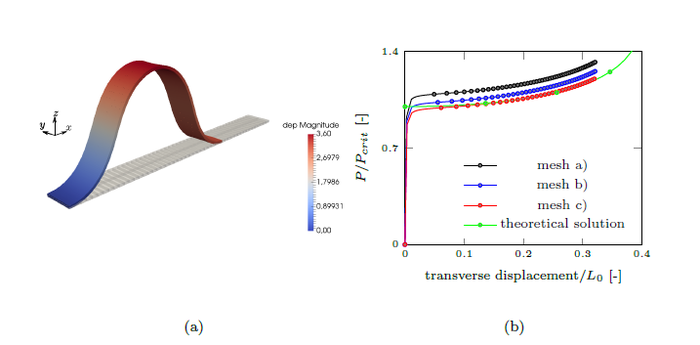
The simulation was performed in 1000 steps. Figure 9a shows the initial configuration and the final deformation at the last time step. The evolution of the compression axial load () is obtained as a function of the transverse displacement in , as shown in Figure 9b.
It is noticed that simulations (a) and (b) has respectively and of error in the critical load when the transverse displacement over is 0.005 [-], while mesh (c) is the closest (only of error at the same point). In addition, the time spent for mesh (c) is only the used in (b).
|
| Figure 9. (a) The initial configuration and the final deformation after the last time step. (b) The load-displacement curve |
3.3 Delamination
In this section we study the effect of discretization when problems involve CZM. The example to be simulated is a 3D double cantilever beam (DCB), whose length is [mm] (-direction), width [mm] (-direction), thickness [mm] (-direction) and pre-crack [mm] located at the end of the beam along the -direction (Figure 11a). The properties of the material are [GPa] and [-]; the cohesive interface parameters are [N/mm], [-], [N/mm] and [-].
The geometry is divided into 160 subdomains and 324 interfaces such as each subdomain has [mm], width [mm] and thickness [mm]. Four meshes were considered (see details in Table 4) and the simulation was performed in 50 time steps.
| mesh | disc. / element | -- | total elements | total dof | time+ |
| a) | / wedge 6 | -- | |||
| b) | / wedge 15 | -- | |||
| c) | / wedge 15 | -- |
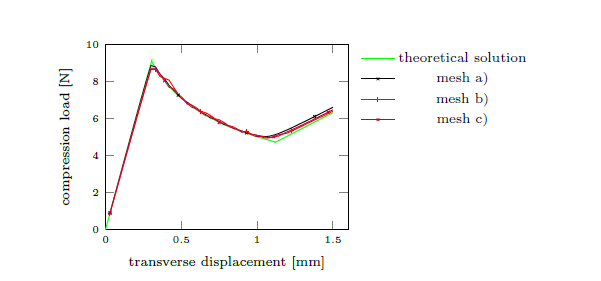
Results are compared to the theoretical solution [29] in Figure 10. It is possible to observe three areas: the first is the bending mode (without delamination); the second zone appears for the crack's propagation (softening curve) and the third one is the second bending mode (when the beam has been completely delaminated). For bending, mesh (b) with three non-linear elements in the thickness is satisfactory, but it does not correctly represent delamination due to the visible zigzag. If the discretization (c) is studied, with a greater number of elements in the -direction, the entire curve is correctly predicted, but the time used for the calculation is double that used for the linear discretization (a). The lack of accuracy in the response of mesh (b) could be related to the fact that the forces calculated to evaluate damage are performed at the interfaces which are discretize by constant functions (Figure 3), although subdomains have finite elements of higher order. Figure 11 shows the crack's front at the beginning of the propagation.
|
| Figure 10. The load-displacement curve of the DCB test |
4. Conclusions
In this article, the influence of the discretization on a micro-macro LaTIn-based Domain Decomposition Method have been investigated. Three subdomains's discretizations have been analyzed: initial linear mesh without localized over discretization on the boundary (-version); linear mesh with local -refinement on the boundary; and -version with quadratic elements on the whole subdomain.
Bending results show that the -refinement on the boundary elements increase the calculation time and decrease the convergence rate with respect to the meshes without over discretization (so-called initial version). The best results were obtained when using -refinement on the whole subdomain, reaching even 97% faster simulations for the buckling example.
However, -refinement is not enough to well represent delamination due to the polynomial degree used for the approximation space of the interfaces. Therefore, to have a correct representation of the phenomenon, a greater number of elements are required in the crack's front (-direction). A posible solution will be to use linear or higher order finite elements for the interfaces' discretization.
Acknowledgements
K. Saavedra acknowledges the financial support from CONICYT, FONDECYT Initiation into research project No 11130623. J. Fernández acknowledges the financial support from CONICYT-PFCHA, National Doctorat 2017, No 21171988. The authors also wish to thanks LMT-Cachan (ENS Paris-Saclay/CNRS/Université Paris-Saclay) for enabling to use the research code MULTI.
References
[1] Herakovich C.T. Mechanics of composites: A historical review. Mechanics Research Communications, 1:1-20, 2012.
[2] LLorca J., González C., Molina-Aldareguía J.M., Lópes CS. Multiscale modeling of composites: toward virtual testing... and beyond. JOM, 65(2):215-225, 2013.
[3] Okereke M.I., Akpoyomare A.I., Bingley M.S. Virtual testing of advanced composites, cellular materials and biomaterials: A review. Composites Part B: Engineering, 60:637-662, 2014.
[4] Mandel J. Balancing Domain Decomposition. Communications in Numerical Methods in Engineering, 9:233-241, 1993.
[5] Farhat C., Roux F.-X. A method of finite element tearing and interconnecting and its parallel solution algorithm. International Journal for Numerical Methods in Engineering, 32:1205-1227, 1991.
[6] Roux F.-X. A FETI-2LM method for non-matching grids. Domain Decomposition Methods in Science and Engineering XVIII, 121-128, 2009.
[7] Gosselet P., Rey C. Non-overlapping domain decomposition methods in structural mechanics. Archives of Computational Methods in Engineering, 13:515-572, 2006.
[8] Klawonn A., Radtke P., Rheinbach O. FETI-DP Methods with an Adaptive Coarse Space. SIAM Journal on Numerical Analysis, 53(1):297-320, 2015.
[9] Haferssas R., Jolivet P., Nataf F. A robust coarse space for Optimized Schwarz methods SORAS-GenEO-2, C. R. Math. Acad. Sci, 353:959-963, 2015.
[10] Ladeveze P. Nonlinear computational structural mechanics: new approaches and non-incremental methods of calculation. Springer-Verlag, 1999.
[11] Ladeveze P., Loiseau O., Dureisseix D. A micro-macro and parallel computational strategy for highly heterogeneous structures. International Journal for Numerical Methods in Engineering, 52(1-2):121-138, 2001.
[12] Roulet V., Champaney L., Boucard P.-A. A parallel strategy for the multiparametric analysis of structures with large contact and friction surfaces. Advances in Engineering Software, 42(6):347-358, 2011.
[13] Guidault P.-A., Allix O., Champaney L., Cornuault C. A multiscale extended finite element method for crack propagation. Computer Methods in Applied Mechanics and Engineering, 197(5):381-399, 2008.
[14] Kerfriden P., Allix O., Gosselet P. A three-scale domain decomposition method for the 3D analysis of debonding in laminates. Computational Mechanics, 44(3):343-362, 2009.
[15] Saavedra Flores E.I, Saavedra K., Hinojosa J., Chandra Y., Das R. Multi-scale modelling of rolling shear failure in cross-laminated timber structures by homogenisation and cohesive zone models. International Journal of Solids and Structures, 81:219-232, 2016.
[16] Saavedra K., Allix O, Gosselet P. On a multiscale strategy and its optimization for the simulation of combined delamination and buckling. International Journal for Numerical Methods in Engineering, 91(7):772-798, 2012.
[17] Allix O., Gosselet P., Kerfriden P., Saavedra K. Virtual delamination testing through non-linear multi-scale computational methods: some recent progress. Computers, Materials & Continua, 32(2):107-132, 2012.
[18] Saavedra K., Allix O., Gosselet P., Hinojosa J., Viard A. An enhanced nonlinear multi-scale strategy for the simulation of buckling and delamination on 3D composite plates. Computer Methods in Applied Mechanics and Engineering, 317:952-969, 2017.
[19] Dubois O., Gander M.J. Domain Decomposition Methods in Science and Engineering XVIII, Springer, 177-184, 2009.
[20] Negrello C., Gosselet P., Rey C. A new impedance accounting for short‐ and long‐range effects in mixed substructured formulations of nonlinear problems. International Journal for Numerical Methods in Engineering, 14(7):675-693, 2018.
[21] Mosler J., Scheider I. A thermodynamically and variationally consistent class of damagetype cohesive models. Journal of the Mechanics and Physics of Solids, 59(8):1647-1668, 2011.
[22] Babuska I., Szabo B. On the rates of convergence of the finite element method. International Journal for Numerical Methods in Engineering, 18(3):323-341, 1982.
[23] Babuska I., Suri M. The p-and hp versions of the finite element method, an overview. Computer Methods in Applied Mechanics and Engineering, 80(1-3):5-26, 1990.
[24] Allix O., Léveque D., Perret L. Identification and forecast of delamination in composite laminates by an interlaminar interface model. Composites Science and Technology, 58(5):671-678, 1998.
[25] Duvant G., Lions J.L. Inequalities in Mechanics and Physics. Vol. 219, Springer Science & Business Media, 2012.
[26] Allix O., Kerfriden P., Gosselet P. On the control of the load increments for a proper description of multiple delamination in a domain decomposition framework. International Journal for Numerical Methods in Engineering, 83(11):1518-1540, 2010.
[27] Ladeveze P., Nouy A., Loiseau O. A multiscale computational approach for contact problems. Computer Methods in Applied Mechanics and Engineering, 191(43):4869-4891, 2002.
[28] Timoshenko S. Theory of Elastic Stability, McGraw-Hill Education, 1970.
[29] Kanninen MF. An augmented double cantilever beam model for studying crack propagation and arrest. International Journal of Fracture, 9(1):83-92, 1973.
Document information
Published on 13/03/19
Accepted on 27/02/19
Submitted on 03/06/18
Volume 35, Issue 1, 2019
DOI: 10.23967/j.rimni.2019.02.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?