Determining the micro film of hexyl alcohol in laminar condition on a rotating drum

Latest revision as of 10:59, 2 July 2021

Abstract

In this research, the free surface of micro film of hexyl alcohol on a partially submerged rotating drum has been predicted using CFD (computational fluid dynamics) and compared with experimental data and analytical solution. The trend of has been found very comparable with experimental and analytical solution. A Matlab code was used to model the flow and film dynamics. Computationally it was an unsteady state problem and semi-steady state was achieved. No surfactant was present on the surface. The speed of the moving rotating drum was set a rpm. With the increase of rotating drum, the minimum film thickness increases with rpm (for ${\textstyle \alpha _{o}}$ = 47 $^{0}$ and for ${\textstyle \alpha _{o}}$ = 58 $^{0}$ ).

Keywords: Liquid film, cfd, vof, moving surface, hexyl alcohol

1. Introduction

This paper presents a two-dimensional (not a 3D as performed in [1]) computational CFD model describing an unsteady state thin liquid hexyl alcohol film on the RD adjacent to the surface of a partially submerged rotating drum (RD). The liquid film was modeled by volume of fluid, VOF [2]. A RD submerged in a fluid picks up fluid on the outer surface of the RD (Figure 1). Few parameters e.g. $D_{\mathit {rd,\rho ,\sigma ,\mu ,\alpha _{o}}}$ , and rpm influence the free surface as well (refer to list of symbols). These properties form various nondimensional numbers, e.g., Ca, We, Re, Fr (refer to list of symbols) . Solving complete Navier-Stokes equation with VOF as performed here would allow predicting the free surface provided numerical error is minimized. However, VOF has limitation like all other free surface modeling approaches.

Literature review suggests that there is limited focus [3,4,5,6,7] on this topic and only a few correlations are available based on the experimental or analytical simplification [8,9,10]. The surface area of the liquid film and the amount of fluid being carried by an RD are important parameters for design purpose (e.g. cooling of final molasses in a sugar factory [10,11,12] and pharmaceutical drug delivery of solid oral dosage forms film coatings [13,14,15].

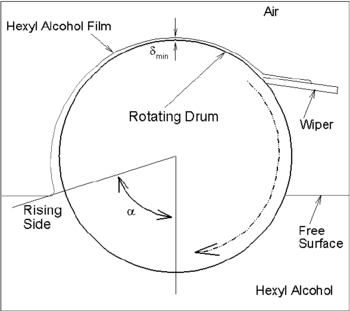
Figure 1. Schematic diagram of the thin film on a partially-submerged rotating drum

The dynamics of liquid film on a straight plate [16] is relatively easy compared to the investigation performed here. Prediction of dynamic contact line [17] is still under investigation. This paper will particularly focus when a wiper is used to wipe the film of hexyl alcohol. The prime motivation of this investigation is that there is published experimental data for hexyl alcohol which occur at ${\textstyle \alpha }$ =180 $^{0}$ (Figure 1). There is no accurate measuring technique available to measure the film thickness [18], even though, the experimental effort has been lifted. Most of the studies avoided curved moving plane movement [19,20] in detail.

After the computational domain and model equation, this paper will continue with the computational results compared with the experimental and analytical solution of [8,9]. This article assumes that there is no foam [21] formation near RD and no vaporization [22] on the liquid film.

2. Computation Domain

The computational domain of an RD rotating anti-clockwise on a free liquid surface is shown in Figure 2. Various boundary conditions are shown in Table 1.

Table 1. List of BC for the model

Serial	Location	Boundary
1	RD wall	Moving wall with rpm
2	Top surface of the tank	Outflow
3	Walls of the tank	Wall-no slip
4	Scrap of fluid	Pressure outlet

The amount of film leaves the pressure outlet BC, is forced to enter into the left entrance (pressure inlet) of the domain to keep the liquid level same.

Figure 2. Various conditions (BC) at the boundary for a partially submerged rotating drum rotating on a free liquid surface in the tank [boundary D

=130 mm, H

=365.555 mm, W

=800 mm, H

=134.445 mm]

The stagnant free liquid surface is located at ${\textstyle \alpha =\alpha _{o}}$ . By varying H $_{a}$ the initial ${\textstyle \alpha _{o}}$ can be changed. An arc of 225 degrees RD is modeled.

3. Computational Model

A Volume of Fluid [2] approach is used to model the free the surface of the liquid film (vof is based on the Continuum Surface Force, CSF, [23]).

The continuity equation for the 2D case is governed by Eq.(1)

(1)

The momentum equation for x (horizontal direction) is given by Eq.(2)

{\begin{array}{l}{\begin{array}{l}\rho \left({{\frac {\partial u}{\partial t}}+u{\frac {\partial u}{\partial x}}+v{\frac {\partial u}{\partial y}}}\right)=-{\frac {\partial p}{\partial x}}\\+\mu \left({{\frac {{\partial ^{2}}u}{\partial {x^{2}}}}+{\frac {{\partial ^{2}}u}{\partial {y^{2}}}}}\right)+{F_{stx}}\end{array}}\end{array}}

(2)

The momentum equation for y (vertical direction) is given by Eq.(3)

{\begin{array}{l}{\begin{array}{c}{\begin{array}{l}\rho \left({{\frac {\partial v}{\partial t}}+u{\frac {\partial v}{\partial x}}+v{\frac {\partial v}{\partial y}}}\right)=-{\frac {\partial p}{\partial y}}+\\\mu \left({{\frac {{\partial ^{2}}v}{\partial {x^{2}}}}+{\frac {{\partial ^{2}}v}{\partial {y^{2}}}}}\right)+{F_{sty}}-{\dot {m}}{g_{y}}\end{array}}\end{array}}\end{array}}

(3)

The Reynolds stress is solved by Realizable models [24] which are two equation models (Eq.(4) and Eq.(5)) and can be described as:

{\begin{array}{l}{\begin{array}{l}{\begin{array}{l}{\begin{array}{l}{\frac {\partial \left(\rho \varepsilon \right)}{\partial t}}+{\frac {\partial \left(\rho \varepsilon u\right)}{\partial x}}+{\frac {\partial \left(\rho \varepsilon v\right)}{\partial y}}=\;{\frac {\partial }{\partial x}}\left[\left(\mu +{\frac {\mu _{t}}{\sigma _{\varepsilon }}}\right){\frac {\partial \varepsilon }{\partial x}}\right]+\end{array}}\\{\frac {\partial }{\partial y}}\left[\left(\mu +{\frac {\mu _{t}}{\sigma _{\varepsilon }}}\right){\frac {\partial \varepsilon }{\partial y}}\right]+\;\rho C_{1}S\varepsilon \end{array}}\\-\rho C_{2}{\frac {\varepsilon ^{2}}{k+{\sqrt {\nu \varepsilon }}}}\end{array}}\end{array}}

(4)

{\begin{array}{l}{\begin{array}{l}{\begin{array}{l}{\begin{array}{l}{\frac {\partial \left(\rho \varepsilon \right)}{\partial t}}+{\frac {\partial \left(\rho \varepsilon u\right)}{\partial x}}+{\frac {\partial \left(\rho \varepsilon v\right)}{\partial y}}=\;{\frac {\partial }{\partial x}}\left[\left(\mu +{\frac {\mu _{t}}{\sigma _{\varepsilon }}}\right){\frac {\partial \varepsilon }{\partial x}}\right]+\end{array}}\\{\frac {\partial }{\partial y}}\left[\left(\mu +{\frac {\mu _{t}}{\sigma _{\varepsilon }}}\right){\frac {\partial \varepsilon }{\partial y}}\right]+\;\rho C_{1}S\varepsilon \end{array}}\\-\rho C_{2}{\frac {\varepsilon ^{2}}{k+{\sqrt {\nu \varepsilon }}}}\end{array}}\end{array}}

(5)

${\textstyle G_{k}}$ is the generation of turbulent kinetic energy [25]. The constants are ${\textstyle \sigma _{k}}$ =1.0, ${\textstyle C_{\mu }}$ =0.09, ${\textstyle C_{2}}$ =1.9, ${\textstyle C1=max(0.43,\;{\frac {\eta }{\eta {+5}}})}$ , where ${\textstyle \eta ={\frac {S\kappa }{\varepsilon }}}$ , ${\textstyle S}$ is the magnitude of vorticity. The unstable [26] nature of the wave demands tiny time step for the film dynamics to predict.

The computational modeling parameters were chosen after verification [27]. Quadrilateral mesh [28], higher order discretization, PISO [29] pressure- velocity coupling, geometric reconstruction [30] for VOF, and smooth wall (K $_{s}$ =0, Cs =0.5) were used in the CFD [31,32] calculations. For VOF, a modified discretization is used [33]. The minimum film thickness ( ${\textstyle \alpha }$ = 180 $^{0}$ ) as determined theoretically by Eq.(6) offered by [8]:

(6)

For no backflow condition [34], a solution is given by Eq.(7).

(7)

The introduction of ${\textstyle \left({\frac {\mu U_{o}}{\sigma }}\right)^{\frac {1}{6}}=\left(Ca\right)^{\frac {1}{6}}}$ in (7) has a striking similarity as found here [8]. As the rotating drum increases, the ${\textstyle \left({\frac {\mu U_{o}}{\sigma }}\right)^{\frac {1}{6}}}$ approaches to unity. The aspect ratio of the mesh near the wall was 1.08, so gradually the size was reduced. All the calculations presented in the journal were double precision and took nearly 8 days to complete one set of calculation. The mesh was refined few times to confirm that the solutions were less dependent on the size and shape of the mesh.

4. Results

Figure 3 shows the ${\textstyle \delta _{min}}$ as function of rpm for ${\textstyle \alpha _{o}}$ = 47 $^{0}$ from three different sources, e.g., analytical solution without the CF (Eq.(6)), analytical solution with CF (Eq.(7)) and CFD [35] solution. Apparently, the analytical solution without the CF is very close to the CFD [36,37] prediction. In all three lots, the trend is the same. From Eqs.(6) and (7), the ${\textstyle \delta _{min}}$ varies with is relationship of rpm ( ${\textstyle \delta _{min}\infty rpm^{0.50}}$ ), for the CFD results it varies as ${\textstyle \delta _{min}\infty rpm^{0.47}}$ . The properties of the hexyl alcohol are the same for all three sources ( ${\textstyle \sigma }$ =0.00384 N/m, ${\textstyle \rho }$ =812 kg/m3, ${\textstyle \mu }$ =0.00392 kg/m/s). In the original paper of [8,9], the precise properties of hexyl alcohol was not reported.

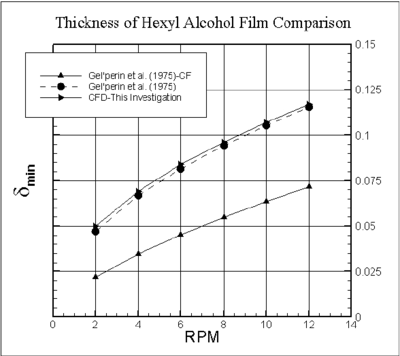
Figure 3. A minimum film thickness for hexyl alcohol as a function of rpm of the drum for

47

There are few important aspects to highlight here. Firstly, the loss of liquid at the pressure outlet BC (Figure 2) is compensated by the same amount of liquid injection at the pressure inlet BC which is far away from the RD so there is little impact on the film dynamics of the inflow on the RD. It was expected though for a laminar condition when the plunging [38,39,40] the point is avoided (no drop passes the wiper and falls on the receiving tank), there would be a steady state solution which is found to be wrong. Secondly, because of the plunging point is avoided; there is less complicate in terms of numerical instability. Thirdly, as the 10 plunging point is avoided, there is no consequence of entrained air in the form of bubbles from the plunging point which would disturb the stability of the solution. Fourthly, in the real wiper (Figure 1), it would not cause the surface completely free from hexyl alcohol

before plunging into the liquid bath and also the surface property would change because of the erosion and the friction between the RD and the wiper would cause heat (maybe negligible).

Several steps were taken to minimise the instability. The unsteady calculations were started to a smaller value, Grid and time step are linked through the Courant condition. So grid was refined locally few times. During the solver iterations, the time step is changed to alter the instability.

To model the wall roughness effects, two parameters are needed to specify. In the current scenario, a smooth wall is considered to avoid more issues and so the Roughness Height I set to be zero and a default value of roughness constant is chosen.

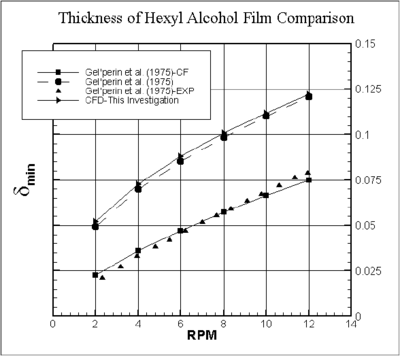
Figure 4. A minimum liquid film thickness for hexyl alcohol as a function of rotating speed of the drum for

58

Again striking similarities have been found for ${\textstyle \alpha _{o}}$ = 58 $^{0}$ as shown in Figure 4. There are four plots in Figure 4, e.g., two analytical solutions (Eqs.(6) and (7)), CFD solutions and experimental data. The trend of variation of ${\textstyle \delta _{min}}$ has been proved the same in CFD, experimental and analytical results. In CFD results, ${\textstyle \delta _{min}}$ varies with rpm by ${\textstyle \delta _{min}=rpm^{0.48}}$ . Surprisingly again, Eq.(6) and CFD results are close and away from the Eq.(7) and experimental data by a factor 1/CF. The proportionality constant in CFD prediction for this case is only 4% a way from the critical prediction.

5. Conclusions

The problem of determining a thin film on a RD and the minimum film thickness are investigated using CFD for a partially-submerged rotating drum. The analytical solution is too simplified to determine the ${\textstyle \delta _{min}}$ and CFD is needed to understand the dynamics of liquid film. A no-slip boundary condition was considered on the RD wall and the meniscus free surface was predicted using VOF. CFD investigation shows that ${\textstyle \delta _{min}}$ increases with, same as experimental dd analytical solution. Because plunging end of RD was avoided by using a wiper, convergence behavior was quite stable.

All the 12 case of the simulations shown in this paper were for isothermal conditions [41], a terms used for this is called 'cold modeling'. It is possible to extend the model developed for the non-isothermal condition were the physical properties would change as a function of temperature. It is possible to extend the model developed for non-isothermal conditions were the physical properties would change as a function of temperature. If crystallization does occur and vaporization takes place, an equivalent sink/source term to be added in the model equations to account the mass/momentum/energy transfer and it would be more complicated. For the higher rate crystallization, the back flow will be miminised. From CFD point of the view, viscous film hold up is less complicated to predict. For a partial crystallization of the film would between Eqs.(6) and (7).

6 List of Symbols

Table. 2 Notations with units and values

Symbols	Description	Unit
${\textstyle P}$	Pressure	N/m $^{2}$
${\textstyle u,\;v}$	Velocity components	m/s
${\textstyle u'',\;v''}$	Velocity fluctuating components	m/s
${\textstyle H_{a}}$	Air height in the top of the bath	m
${\textstyle H_{l}}$	Liquid level	m
${\textstyle R_{rd}}$	Rotating drum Reynolds number	-
${\textstyle x,\;y}$	Two directions of the Cartesian co-ordinates	m
${\textstyle C_{s}}$	Wall roughness constant	-
${\textstyle K_{s}}$	Wall roughness height	m
${\textstyle \kappa }$	Turbulent kinetic energy	m $^{2}$ /s $^{2}$
${\textstyle \in }$	Turbulent Dissipation Rate	m $^{2}$ /s $^{3}$
${\textstyle D_{rd}}$	Diameter of the rotating drum	m
${\textstyle RPM}$	Revolution per minute	rev/min
${\textstyle W_{t}}$	Width of tank	m
${\textstyle \sigma }$	Surface tension	N/m
${\textstyle \mu }$	Viscosity	kg/m/s
${\textstyle \rho }$	Density	kg/m $^{3}$
${\textstyle \omega }$	rad/sec	1/s
${\textstyle \alpha }$	Angular location of tip	deg
${\textstyle \alpha _{o}}$	Initial angular location	deg
${\textstyle U_{o}}$	Velocity Scale	m/s
${\textstyle U_{t}}$	Tangitial velocity	m/s
${\textstyle Fr}$	Froude number	-
${\textstyle Re}$	Reynoulds number	-
${\textstyle We}$	Weber number

References

[1] Evans P.P., Schwartz L.W., Roy R.V. Three-dimensional solutions for coating flow on a rotating horizontal cylinder: Theory and experiment. Physics of Fluids, 17:072102/1–072102/20, 2005.

[2] Hirt C.W., Nichols B.D. Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys., 39:201–225, 1981.

[3] Duffy B.R., Wilson S.K. Thin-film and curtain flows on the outside of a rotating horizontal cylinder. Journal of Fluid Mechanics, 394:29–49, 1999.

[4] Khan M.N.H., Fletcher C., Evans G., He Q. CFD modeling of free surface and entrainment of buoyant particles from free surface for sumberged jet systems. American Society of Mechanical Engineers, Heat Transfer Division, (Publication) HTD.

[5] Moffatt K. Behaviour of a Viscous Film on the Outer Surface of a Rotating Cylinder. J. Mec., 16:651–673, 1977.

[6] Moffatt K. Viscous and Resistive Eddies Near Sharp Corner. Journal of Fluid Mechanics, 18:1–18, 1964.

[7] Nikolov A.D., Wasan D.T. A novel method for studying the dynamic behavior of both plane-parallel and curved thin liquid films. Colloids and Surfaces A: Physicochemical and Engineering Aspects, 123-124:375–381, 1997.

[8] Gelpérin N.I., Nosov, G. A., Makotkin, A.V. Determinating the thickness of liquid film holdup on a rotating drum surface. Chemical and Petroleum Engineering, 11:230–233, 1975.

[9] Gelpérin, N.I., Nosov G.A., Makotkin A.V. Thickness of a liquid film covering the surface of a rotating drum. Khimicheskoe i Neftyanoe Mashinostroenie, pp. 18–20, 1975.

[10] Butler K., White E.T., Wright P. G. Pickup layer thickness on a horizontal rotating drum. In Chemeca 90: The Eighteenth Australasian Chemical Engineering Conference, Processing Pacific Re- sources, 1990.

[11] Korn O. Cyclone Dryer: A pneumatic dryer with increased solid residence time. Drying Technology, 19:1925, 2001.

[12] Jullienne L.M.S.A., Munsamy S. Assessment Of Final Molasses Coolers. Proceedings of The South African Sugar Technologists' Association - June 1981.

[13] Harting R., Johnston K., Petersen S. Correlating in vitro degradation and drug release kinetics of biopolymer-based drug delivery systems. International Journal of Biobased Plastics, 1:8–21, 2019.

[14] Macha I.J., Karacan I., Ben-Nissan B., Cazalbou S., Müller W.H. Development of antimicrobial composite coatings for drug release in dental, orthopaedic and neural prostheses applications. SN Applied Sciences, 1:68, 2019.

[15] Bisharat L., Barker S.A., Narbad A., Craig D.Q. In vitro drug release from acetylated high amylose starch-zein films for oral colon-specific drug delivery. International journal of pharmaceutics, 556:311–319, 2019.

[16] Cox R.G. Dynamics of the spreading of liquids on a solid surface. Part 1. Viscous flow. Journal of Fluid Mechanics, 168:169–194, 1986.

[17] Shikhmurzaev Y.D. Mathematical modeling of wetting hydrodynamic. Fluid Dynamics Research, 13:45–64, 1994.

[18] Gongxia G., Xiao L., Ding C., Xiayi H., Ardi H., Hallvard S., Zhiwu L. A study of film thickness and hydrodynamic entrance length in liquid laminar film flow along a vertical tube. AICHE Journal, 64:2078–2088, 2018.

[19] Wilkinson W.L. Entrainment of air by a solid surface entering a liquid/air interface. Chemical Engineering Science, 30:1227–1230, 1975.

[20] Evans P.L., Schwartz L.W., Roy R.V. Steady and unsteady solutions for coating flow on a rotating horizontal cylinder: Two-dimensional theoretical and numerical modeling. Physics of Fluids, 16:2742– 2756, 2004.

[21] Saeid N.H., Hasan N., Ali M.H.B.H.M. Effect of the metallic foam heat sink shape on the mixed convection jet impingement cooling of a horizontal surface. Journal of Porous Media, 21:295–309, 2018.

[22] Rashid H., Hasan N., Iskandar M.N.M. Accurate modeling of evaporation and enthalpy of vapor phase in CO2 absorption by amine based solution. Separation Science and Technology (Philadelphia), 49:1326–1334, 2014.

[23] Brackbill J.U. A continuum method for modeling surface tension. Journal of Computational Physics, 100:335–354, 1992.

[24] Shih T.-H., Liou W.W., Shabbir A., Yang Z., Zhu J. A New k-Epsilon eddy viscosity model for high Reynolds number turbulent flows. Computers and Fluids, 24:227–238, 1995.

[25] Hinze J.O. Turbulence, McGraw-Hill series in mechanical engineering, McGraw-Hill College, 1975.

[26] Bontozoglou V. Papapolymerou G.P. Laminar film flow down a wavy incline. International Journal of Multiphase Flow, 23:69–79, 1997.

[27] Roache P.J. Verification and validation in computational science and engineering. Hermosa Publishers, Albuquerque, pp. 446, 1998.

[28] Zhalehrajabi E., Rahmanian N., Hasan N. Effects of mesh grid and turbulence models on heat transfer coefficient in a convergent divergent nozzle. Asia-Pacific Journal of Chemical Engineering, 9:265–271, 2014.

[29] Ferzieger J.H., Peric M. Computational Methods for Fluid Dynamics. In null, New York City, USA, Springer, 1996.

[30] Youngs D.L. Time-dependent multi-material flow with large fluid distortion. Numerical Methods for Fluid Dynamics. Academic Press, 1982.

[31] Witt P., Khan M.N.H., Brooks G. CFD modelling of heat transfer in supersonic nozzles for magnesium production. TMS Annual Meeting. pp. 123–132. 2007.

[32] Naser J., Alam F., Khan M.N.H. Evaluation of a proposed dust ventilation/collection system in an underground mine crushing plant. Proceedings of the 16th Australasian Fluid Mechanics Conference, 16AFMC. pp. 1411–1414. 2007.

[33] Muzaferija S., Peric M., Sames P., Schellin T. A two-fluid Navier-Stokes solver to simulate water entry. National Academy Press, pp. 277–289. 1998.

[34] Hasan N., Naser J. Determining the thickness of liquid film in laminar condition on a rotating drum surface using CFD. Chemical Engineering Science, 64:919–924, 2009.

[35] Versteeg H.K., Malalasekera W. An introduction to computational fluid dynamics: The Finite Volume Method. Boston, Massachusetts, United States, Addison-Wesley, 1996.

[36] Khan M.N.H., Fletcher C., Evans G., He Q. CFD analysis of the mixing zone for a submerged jet system. Proceedings of the ASME Fluids Engineering Division Summer Meeting, volume 1, pp. 29–34. 2003.

[37] Geoffrey B., Hasan N., Witt P. Design of supersonic nozzles for ultra-rapid quenching of metallic Vapours. TMS Annual Meeting, pp. 699–709, 2006.

[38] Rodriguez D.J., Shedd T.A. Entrainment of gas in the liquid film of horizontal, annular, two-phase flow. International Journal of Multiphase Flow, 30:565–583, 2004.

[39] Buonopane R.A., Gutoff E.B., Rimore M.M.T. Effect of plunging tape surface properties on air entrainment velocity. AIChE Journal, 32:682–683, 1986.

[40] Burley R.W., Jolly P.S.R. Entrainment of air into liquids by a high speed continuous solid surface. Chemical Engineering Science, 39:1357–1372, 1984.

[41] Rashid H., Hasan N., Iskandar M.N.M. Temperature peak analysis and its effect on absorption column for CO2 capture process at different operating conditions. Chemical Product and Process Modeling, 9:105–115, 2014.

Author biography

Christ Trang has a bachelor in chemical Engineering. Her interests include Multiphase (nucleation, separation), Optimization (converging-diverging nozzle), Biomedical (nasal drug delivery), Environmental (Tsunami, Flood, Safety, Pollution in City), Maritime, Nanoparticle, Offshore Stability, Turbo machinery, Hydraulics Design, Casting Design.