| (123 intermediate revisions by 3 users not shown) | |||
| Line 1: | Line 1: | ||
| − | ==Análisis de vigas sobre fundación flexible empleando funciones de Green Analysis of beams on elastic foundations using Green's functions== | + | <!--==Análisis de vigas sobre fundación flexible empleando funciones de Green Analysis of beams on elastic foundations using Green's functions== |
'''Juan Camilo Molina-Villegas<sup>a,b</sup>, Jorge Eliecer Ballesteros Ortega<sup>b</sup>, Andrés Camilo Quintero Toro<sup>a</sup>''' | '''Juan Camilo Molina-Villegas<sup>a,b</sup>, Jorge Eliecer Ballesteros Ortega<sup>b</sup>, Andrés Camilo Quintero Toro<sup>a</sup>''' | ||
| − | + | --> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
==Resumen== | ==Resumen== | ||
| − | Las vigas sobre fundación flexible representan un modelo básico dentro del análisis estructural, las cuales suelen emplearse para modelar vigas de cimentación, pilas, muros de contención y estructuras más complejas que tengan algún tipo de estos elementos. Para el análisis de estas, usualmente se emplea el método de elementos finitos <span id='citeF-1'></span>[[#cite-1|[1]]], el cual produce una solución aproximada del problema; y el método de rigidez con funciones de Green <span id='citeF-2'></span>[[#cite-2|[2 | + | Las vigas sobre fundación flexible representan un modelo básico dentro del análisis estructural, las cuales suelen emplearse para modelar vigas de cimentación, pilas, muros de contención y estructuras más complejas que tengan algún tipo de estos elementos. Para el análisis de estas, usualmente se emplea el método de elementos finitos <span id='citeF-1'></span>[[#cite-1|[1]]], el cual produce una solución aproximada del problema; y el método de rigidez con funciones de Green <span id='citeF-2'></span>[[#cite-2|[2]]], el cual produce una solución exacta del mismo. |
En este artículo se presenta una metodología 100 % basada en el empleo de las funciones de Green (respuesta ante una fuerza puntual unitaria), para obtener la respuesta exacta de las vigas sobre fundación flexible. La principal ventaja de esta formulación es su menor costo computacional comparado con las citadas alternativas, además que la respuesta puede expresarse solo por medio de sumas e integrales, las cuales se pueden realizar fácilmente de forma numérica. | En este artículo se presenta una metodología 100 % basada en el empleo de las funciones de Green (respuesta ante una fuerza puntual unitaria), para obtener la respuesta exacta de las vigas sobre fundación flexible. La principal ventaja de esta formulación es su menor costo computacional comparado con las citadas alternativas, además que la respuesta puede expresarse solo por medio de sumas e integrales, las cuales se pueden realizar fácilmente de forma numérica. | ||
| Line 15: | Line 11: | ||
Por completez, también se presentan una gran variedad de funciones de Green para vigas sobre fundación flexible finitas e infinitas con diferentes condiciones de frontera, así como algunos ejemplos con la implementación de la metodología propuesta. | Por completez, también se presentan una gran variedad de funciones de Green para vigas sobre fundación flexible finitas e infinitas con diferentes condiciones de frontera, así como algunos ejemplos con la implementación de la metodología propuesta. | ||
| − | Beams on elastic foundation are basic elements within structural analysis, which are used to model foundation beams, foundation piles, retaining walls, and more complex structures that include some of these elements. For their analysis, the finite element method is usually used <span id='citeF-1'></span>[[#cite-1|[1]]], which produces an approximate solution of the problem; and the Green's function stiffness method <span id='citeF-2'></span>[[#cite-2|[2 | + | '''Palabras clave''': Funciones de Green, vigas sobre fundación flexible, pilas, campos de desplazamiento |
| + | |||
| + | ==Abstract== | ||
| + | |||
| + | Beams on elastic foundation are basic elements within structural analysis, which are used to model foundation beams, foundation piles, retaining walls, and more complex structures that include some of these elements. For their analysis, the finite element method is usually used <span id='citeF-1'></span>[[#cite-1|[1]]], which produces an approximate solution of the problem; and the Green's function stiffness method <span id='citeF-2'></span>[[#cite-2|[2]]], which produces an exact solution. This article presents a methodology 100% based on the use of Green function's (response to a unit point force), to obtain the exact response of beams on elastic foundation. The main advantage of this formulation is its computational low cost compared to the aforementioned alternatives, and even for a large number of problems, it can be expressed only by means of sums and integrals, which can be easily performed numerically. | ||
Also, a great variety of Green function's for finite and infinite beams on elastic foundations with different boundary conditions are also presented, as well as some examples with the implementation of the proposed methodology. | Also, a great variety of Green function's for finite and infinite beams on elastic foundations with different boundary conditions are also presented, as well as some examples with the implementation of the proposed methodology. | ||
| − | ''' | + | '''Keywords''': Green’s functions, beams on elastic foundation, piles, displacement field |
| − | ==1 Introducción== | + | ==1. Introducción== |
En mecánica, se define como función de Green, al campo de desplazamiento en un medio ante la acción de una fuerza puntual unitaria. En general, para casos tridimensionales, dicha fuerza unitaria puede estar ubicada en cualquier punto y dirección del medio, y el campo de desplazamiento será vectorial y tendrá también tres componentes escalares. El concepto de función de Green puede fácilmente extenderse a cualquier problema físico en el cual la fuerza puntual será reemplazada por una fuente o acción puntual unitaria, mientras que el campo de desplazamiento será reemplazado por el campo de la variable dependiente principal para el problema. Por ejemplo, en transferencia de calor, la función de Green será el campo de temperatura debido a la acción de una fuente de calor puntual unitaria. | En mecánica, se define como función de Green, al campo de desplazamiento en un medio ante la acción de una fuerza puntual unitaria. En general, para casos tridimensionales, dicha fuerza unitaria puede estar ubicada en cualquier punto y dirección del medio, y el campo de desplazamiento será vectorial y tendrá también tres componentes escalares. El concepto de función de Green puede fácilmente extenderse a cualquier problema físico en el cual la fuerza puntual será reemplazada por una fuente o acción puntual unitaria, mientras que el campo de desplazamiento será reemplazado por el campo de la variable dependiente principal para el problema. Por ejemplo, en transferencia de calor, la función de Green será el campo de temperatura debido a la acción de una fuente de calor puntual unitaria. | ||
| − | Por si solas, las funciones de Green juegan un papel muy importante en la solución de problemas físicos, puesto que presentan la solución a problemas fundamentales. Por ejemplo, en el famoso problema de Boussinesq, la función de Green es el campo de desplazamiento en un semiespacio (espacio semi-infinito) tridimensional ante la acción de una fuerza puntual unitaria en su superficie. En textos como <span id='citeF- | + | Por si solas, las funciones de Green juegan un papel muy importante en la solución de problemas físicos, puesto que presentan la solución a problemas fundamentales. Por ejemplo, en el famoso problema de Boussinesq, la función de Green es el campo de desplazamiento en un semiespacio (espacio semi-infinito) tridimensional ante la acción de una fuerza puntual unitaria en su superficie. En textos como <span id='citeF-3'></span>[[#cite-3|[3,4,5]]], se presentan las principales funciones de Green empleadas en la física clásica, en <span id='citeF-6'></span>[[#cite-6|[6]]] se presenta un compendio de las principales funciones de Green empleadas en la geotecnia, para sismología y elastodinámica sus principales funciones de Green son presentadas en <span id='citeF-7'></span>[[#cite-7|[7]]], para transferencia de calor en <span id='citeF-8'></span>[[#cite-8|[8]]], mientras que aquellas propias de los problemas de difusión se presentan en <span id='citeF-9'></span>[[#cite-9|[9]]]. |
| − | Además de lo anterior, las funciones de Green son la base de algunos métodos numéricos de contorno o frontera, los cuales permiten resolver problemas diferentes a aquellos para los cuales fueron definidas dichas funciones, es decir, problemas con diferentes condiciones de cargas o fuentes y de frontera. Entre estos métodos numéricos destacan el método directo de elementos de frontera <span id='citeF- | + | Además de lo anterior, las funciones de Green son la base de algunos métodos numéricos de contorno o frontera, los cuales permiten resolver problemas diferentes a aquellos para los cuales fueron definidas dichas funciones, es decir, problemas con diferentes condiciones de cargas o fuentes y de frontera. Entre estos métodos numéricos destacan el método directo de elementos de frontera <span id='citeF-10'></span>[[#cite-10|[10,11,12]]], el método indirecto de elementos de frontera <span id='citeF-13'></span>[[#cite-13|[13,14]]], y el método de rigidez con funciones de Green <span id='citeF-2'></span>[[#cite-2|[2]]]. |
| − | Las vigas sobre fundación flexible representan un modelo básico dentro del análisis estructural, las cueles suelen emplearse para modelar vigas de cimentación, pilas, muros de contención y estructuras más complejas que tengan algún tipo de estos elementos. Pese a que en la actualidad existen | + | Las vigas sobre fundación flexible representan un modelo básico dentro del análisis estructural, las cueles suelen emplearse para modelar vigas de cimentación, pilas, muros de contención y estructuras más complejas que tengan algún tipo de estos elementos. Pese a que en la actualidad existen diversos métodos para el análisis de estas estructuras, los cuales van desde soluciones tabuladas para gran cantidad de condiciones de frontera y carga <span id='citeF-15'></span>[[#cite-15|[15]]], la solución directa de los problemas de valor en la frontera gobernantes empleando métodos clásicos de ecuaciones diferenciales <span id='citeF-16'></span>[[#cite-16|[16]]], hasta el método de elementos finitos <span id='citeF-1'></span>[[#cite-1|[1]]] o de rigidez con funciones de Green <span id='citeF-2'></span>[[#cite-2|[2]]] e incluso hay sitios web para su análisis (https://www.buildingsguide.com/calculators/structural/BOEF), es posible empleando solo las funciones de Green obtener su solución. |
| − | En este artículo se presenta una metodología | + | En este artículo se presenta una metodología basada en las funciones de Green para el análisis de vigas sobre fundación flexible, en la cual el problema de valor en la frontera gobernante para cada problema es resuelto por medio de la superposición o suma de la respuesta ante cargas puntuales. Pese a que el presente procedimiento tiene similitudes conceptuales con aquel propuesto por Dinev <span id='citeF-17'></span>[[#cite-17|[17]]] los autores creen que la formulación en términos de funciones de Green es más ingenieril y además al presentarse gran variedad de estas funciones para diferentes condiciones de frontera, hace más fácil su implementación para vigas sobre fundación flexible de uno o varios tramos. |
| − | ==2 Ecuación diferencial gobernante y convenciones== | + | ==2. Ecuación diferencial gobernante y convenciones== |
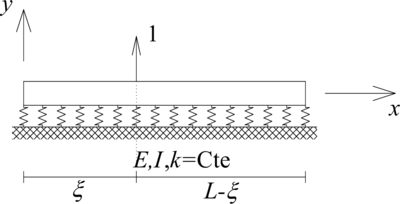
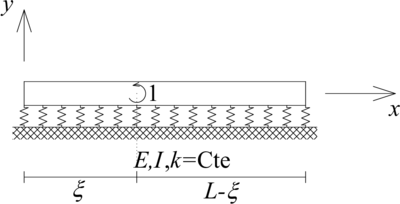
| − | La ecuación diferencial que gobierna el desplazamiento de una viga sobre fundación flexible ( | + | La ecuación diferencial que gobierna el desplazamiento de una viga sobre fundación flexible ([[#img-1|Figura 1]]), formada por una viga de material elástico lineal homogéneo, de sección transversal constante y apoyada sobre un medio flexible con rigidez por unidad de longitud constante, es (ver <span id='citeF-2'></span>[[#cite-2|[2]]] para una deducción paso a paso): |
<span id="eq-1"></span> | <span id="eq-1"></span> | ||
| Line 48: | Line 48: | ||
|} | |} | ||
| − | + | donde: | |
<math display="inline">E</math>: Módulo de elasticidad del material de la viga. | <math display="inline">E</math>: Módulo de elasticidad del material de la viga. | ||
| Line 58: | Line 58: | ||
<math display="inline">v(x)</math>: Campo de desplazamiento en dirección del eje <math display="inline">y</math> de la viga. | <math display="inline">v(x)</math>: Campo de desplazamiento en dirección del eje <math display="inline">y</math> de la viga. | ||
| − | <math display="inline">q(x)</math>: Fuerza externa por unidad de longitud en dirección del eje | + | <math display="inline">q(x)</math>: Fuerza externa por unidad de longitud en dirección del eje <math display="inline">y</math> que actúa sobre la viga. |
| − | {| | + | |
| + | <div id='img-1'></div> | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-Figura01.png|420px|Viga sobre fundación flexible sometida a carga externa distribuida.)]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 1 | + | | colspan="1" style="padding:10px;"| '''Figura 1'''. Viga sobre fundación flexible sometida a carga externa distribuida |
|} | |} | ||
| − | Por facilidad en su solución, es usual dividir [[#eq-1|(1)]] entre <math display="inline">EI</math>, obteniéndose: | + | |
| + | |||
| + | Por facilidad en su solución, es usual dividir la ecuación [[#eq-1|(1)]] entre <math display="inline">EI</math>, obteniéndose: | ||
<span id="eq-2"></span> | <span id="eq-2"></span> | ||
| Line 78: | Line 82: | ||
|} | |} | ||
| − | + | donde <math display="inline">\lambda =\sqrt[4]{\dfrac{k}{4EI}}</math>. | |
Además de la fuerza externa por unidad de longitud <math display="inline">q(x)</math>, la viga también se encuentra sometida a la fuerza distribuida que el suelo ejerce sobre esta, la cual es proporcional al desplazamiento en cada de esta y se calcula como: | Además de la fuerza externa por unidad de longitud <math display="inline">q(x)</math>, la viga también se encuentra sometida a la fuerza distribuida que el suelo ejerce sobre esta, la cual es proporcional al desplazamiento en cada de esta y se calcula como: | ||
| Line 93: | Line 97: | ||
|} | |} | ||
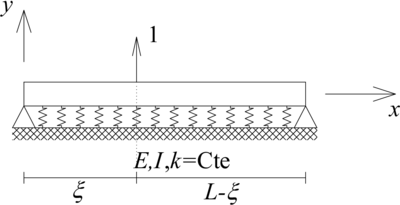
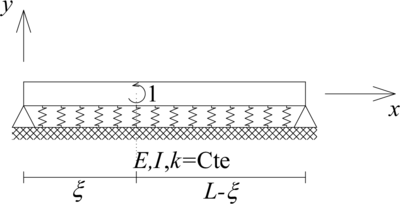
| − | En este punto es importante resaltar que pese a que las ecuaciones [[#eq-1|(1)]] y [[#eq-2|(2)]] están escritas en términos de la fuerza externa por unidad de longitud <math display="inline">(q(x))</math> sobre la viga, es decir, una carga distribuida, incluso fuerzas y momentos puntuales se pueden expresar de esta manera. Como ejemplo se tiene que la carga externa puntual aplicada a la viga sobre fundación flexible presentada en | + | En este punto es importante resaltar que pese a que las ecuaciones [[#eq-1|(1)]] y [[#eq-2|(2)]] están escritas en términos de la fuerza externa por unidad de longitud <math display="inline">(q(x))</math> sobre la viga, es decir, una carga distribuida, incluso fuerzas y momentos puntuales se pueden expresar de esta manera. Como ejemplo, se tiene que la carga externa puntual aplicada a la viga sobre fundación flexible presentada en la [[#img-1|Figura 2a]] se define por medio de la siguiente función: |
<span id="eq-4"></span> | <span id="eq-4"></span> | ||
| Line 106: | Line 110: | ||
|} | |} | ||
| − | + | donde <math display="inline">\delta ()</math> es la función delta de Dirac, cuyas principales propiedades se presentan en <span id='citeF-4'></span>[[#cite-4|[4]]]. <div id='img-2b'></div> | |
| − | + | ||
<div id='img-2'></div> | <div id='img-2'></div> | ||
| − | {| | + | <div id='img-2a'></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | |[[Image: | + | | style="text-align: center;padding:10px;"|[[Image:Review_921349416580-Figura02a.png|400px|Fuerza puntual.]] |
| − | |[[Image: | + | | style="text-align: center;padding:10px;"| [[Image:Review_921349416580-Figura02b.png|400px|Momento puntual.Vigas sobre fundación flexible sometidas a fuerzas y momentos puntuales.]] |
| + | |- | ||
| + | | style="text-align: center;font-size: 75%;"|(a) | ||
| + | | style="text-align: center;font-size: 75%;"|(b) | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="2" style="padding:10px;"| '''Figura 2'''. Vigas sobre fundación flexible sometidas a fuerzas y momentos puntuales. (a) Fuerza puntual. (b) Momento puntual | ||
| + | |} | ||
| + | |||
| + | <!--{| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 100%;max-width: 100%;" | ||
| + | |- | ||
| + | |[[Image:Review_921349416580-Figura02b.png|420px|Momento puntual.Vigas sobre fundación flexible sometidas a fuerzas y momentos puntuales.]] | ||
| + | |[[Image:Review_921349416580-Figura02a.png|420px|Fuerza puntual.]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | |||
| (b) Momento puntual. | | (b) Momento puntual. | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura | + | | colspan="2" | '''Figura a:''' Fuerza puntual. |
| − | |} | + | |}--> |
| − | Mientras que para el caso del momento externo puntual presentado en la | + | |
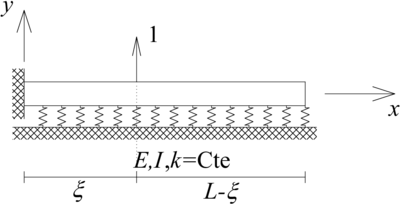
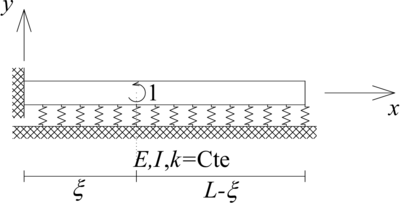
| + | Mientras que para el caso del momento externo puntual presentado en la [[#img-2b|Figura 2b]], la función <math display="inline">q(x)</math> se define a partir de [[#eq-4|(4)]] como (ver la [[#img-3|Figura 3]] para una explicación): | ||
<span id="eq-5"></span> | <span id="eq-5"></span> | ||
| Line 127: | Line 143: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>q(x,\xi )=\lim _{\Delta \xi \rightarrow 0} \left[\dfrac{M}{\Delta \xi } \delta (x-\xi{-\Delta}\xi ) -\dfrac{M}{\Delta \xi } \delta (x-\xi ) \right] = | + | | style="text-align: center;" | <math>q(x,\xi )=\lim _{\Delta \xi \rightarrow 0} \left[\dfrac{M}{\Delta \xi } \delta (x-\xi{-\Delta}\xi ) -\dfrac{M}{\Delta \xi } \delta (x-\xi ) \right] = </math> |
|- | |- | ||
| − | | style="text-align: center;" | <math> =M\dfrac{\partial \delta (x-\xi )}{\partial \xi } </math> | + | | style="text-align: center;" | <math>\qquad \qquad \qquad \qquad M \lim _{\Delta \xi \rightarrow 0} \dfrac{\delta (x-\xi{-\Delta}\xi )-\delta (x-\xi )}{\Delta \xi } = M\dfrac{\partial \delta (x-\xi )}{\partial \xi } </math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (5) | | style="width: 5px;text-align: right;white-space: nowrap;" | (5) | ||
| Line 135: | Line 151: | ||
<div id='img-3'></div> | <div id='img-3'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 50%;" |
|- | |- | ||
| − | |[[Image: | + | |style="text-align: center;padding:10px;"|[[Image:Review_921349416580-Figura05.png|420px|Definición de un momento puntual como el caso límite de dos fuerzas puntuales muy cercanas entre si.)]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 3 | + | | colspan="1" style="padding:10px;"| '''Figura 3'''. Definición de un momento puntual como el caso límite de dos fuerzas puntuales muy cercanas entre si |
|} | |} | ||
| + | |||
De otra parte, a partir del campo de desplazamiento, es posible obtener los campos de fuerzas internas en la viga como: <span id="eq-6"></span> | De otra parte, a partir del campo de desplazamiento, es posible obtener los campos de fuerzas internas en la viga como: <span id="eq-6"></span> | ||
| Line 151: | Line 168: | ||
|- | |- | ||
| style="text-align: center;" | <math>M(x)=EI \dfrac{d^2 v}{dx^2}(x) </math> | | style="text-align: center;" | <math>M(x)=EI \dfrac{d^2 v}{dx^2}(x) </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (6a) |
|- | |- | ||
| style="text-align: center;" | <math> V(x)=-EI \dfrac{d^3 v}{dx^3}(x) </math> | | style="text-align: center;" | <math> V(x)=-EI \dfrac{d^3 v}{dx^3}(x) </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (6b) |
|} | |} | ||
|} | |} | ||
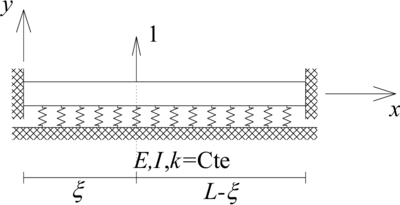
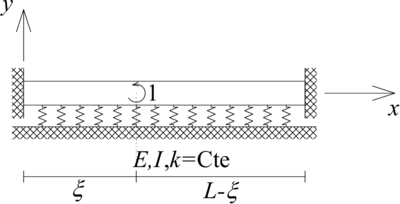
| − | + | donde <math display="inline">M(x)</math> es el campo de momento flector y <math display="inline">V(x)</math> es el campo de fuerza cortante, cuya convención positiva se presenta en la [[#img-4|Figura 4]]. | |
| − | + | ||
| − | <math display="inline">M(x)</math> | + | |
| − | + | <div id='img-4'></div> | |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| − | |[[Image: | + | |style="text-align: center;padding:10px;"| [[Image:Review_921349416580-Figura03.png|420px|Convención positiva de las fuerzas internas.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 4 | + | | colspan="1" style="padding:10px;"| '''Figura 4'''. Convención positiva de las fuerzas internas |
|} | |} | ||
| − | ==3 Funciones de Green para vigas sobre fundación flexible== | + | ==3. Funciones de Green para vigas sobre fundación flexible== |
===3.1 Fuerzas puntuales=== | ===3.1 Fuerzas puntuales=== | ||
| − | En las | + | En las [[#img-5|Figuras 5]] y [[#img-6|6]] se presentan los modelos de las vigas sobre fundación flexible finitas e infinitas para los cuales se definirán las funciones de Green a emplear en este artículo, todas las cuales son solución de la siguiente ecuación diferencial: |
<span id="eq-7"></span> | <span id="eq-7"></span> | ||
| Line 187: | Line 202: | ||
|} | |} | ||
| − | + | donde <math display="inline">G_{yy}(x,\xi )</math> es la función de Green del problema en particular, es decir, el desplazamiento en dirección <math display="inline">y</math> del punto <math display="inline">x</math>, debido a la aplicación de una fuerza puntual unitaria en dirección <math display="inline">y</math> en el punto <math display="inline">\xi </math>. | |
| − | La ecuación [[#eq-7|(7)]] es un caso particular de [[#eq-2|(2)]], en la cual en lugar de <math display="inline">v(x,\xi )</math> se ha empleado <math display="inline">G_{yy}(x,\xi )</math> y para definir la función de la carga externa se ha empleado [[#eq-4|(4)]] con <math display="inline">F=1</math>. <div id='img-5a'></div> | + | La ecuación [[#eq-7|(7)]] es un caso particular de la ecuación [[#eq-2|(2)]], en la cual en lugar de <math display="inline">v(x,\xi )</math> se ha empleado <math display="inline">G_{yy}(x,\xi )</math> y para definir la función de la carga externa se ha empleado la ecuación [[#eq-4|(4)]] con <math display="inline">F=1</math>. |
| + | |||
| + | <div id='img-5a'></div> | ||
<div id='img-5b'></div> | <div id='img-5b'></div> | ||
<div id='img-5c'></div> | <div id='img-5c'></div> | ||
<div id='img-5d'></div> | <div id='img-5d'></div> | ||
<div id='img-5'></div> | <div id='img-5'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-FigGyyLibreLibre.png|400px|Libre - libre.]] |
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-FigGyySimplementeApoyada.png|400px|Simplemente apoyada.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) Libre - libre | + | | (a) Libre - libre |
| − | | (b) Simplemente apoyada | + | | (b) Simplemente apoyada |
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-FigGyyEmpotradaLibre.png|400px|Empotrada - libre.]] |
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-FigGyyEmpotradaEmpotrada.png|400px|Empotrada - empotrada.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (c) Empotrada - libre | + | | (c) Empotrada - libre |
| − | | (d) Empotrada - empotrada | + | | (d) Empotrada - empotrada |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 5 | + | | colspan="2" style="padding:10px;"| '''Figura 5'''. Vigas sobre fundación flexible finitas con diferentes condiciones de frontera y sometidas a fuerzas puntuales unitarias transversales |
|} | |} | ||
| + | |||
<div id='img-6'></div> | <div id='img-6'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"|[[Image:Review_921349416580-FigGyyInfinita.png|400px]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 6 | + | | colspan="1" style="padding:10px;"| '''Figura 6'''. Viga sobre fundación flexible infinita sometida a una fuerza puntual unitaria |
|} | |} | ||
====3.1.1 Viga sobre fundación flexible finita libre - libre==== | ====3.1.1 Viga sobre fundación flexible finita libre - libre==== | ||
| − | La función de Green para la viga sobre fundación flexible finita, con ambos extremos libres y presentada en la | + | La función de Green para la viga sobre fundación flexible finita, con ambos extremos libres y presentada en la [[#img-5a|Figura 5a]], es la solución del siguiente problema de valor en la frontera: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 228: | Line 246: | ||
|- | |- | ||
| style="text-align: center;" | <math>\frac{\partial ^4 G_{yy}^{LL}}{\partial x^4}(x,\xi )+4\lambda ^4 G_{yy}^{LL}(x,\xi )=\frac{\delta (x-\xi )}{EI} </math> | | style="text-align: center;" | <math>\frac{\partial ^4 G_{yy}^{LL}}{\partial x^4}(x,\xi )+4\lambda ^4 G_{yy}^{LL}(x,\xi )=\frac{\delta (x-\xi )}{EI} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (8a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> EI \dfrac{\partial ^2 G_{yy}^{LL}}{\partial ^2 | + | | style="text-align: center;padding-top:5px;" | <math> EI \dfrac{\partial ^2 G_{yy}^{LL}}{\partial x^2}(0,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (8b) |
|- | |- | ||
| − | | style="text-align: center;" | <math> -EI \dfrac{\partial ^3 G_{yy}^{LL}}{\partial ^ | + | | style="text-align: center;padding-top:5px" | <math> -EI \dfrac{\partial ^3 G_{yy}^{LL}}{\partial x^2}(0,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (8c) |
|- | |- | ||
| − | | style="text-align: center;" | <math> EI \dfrac{\partial ^2 G_{yy}^{LL}}{\partial ^2 | + | | style="text-align: center;padding-top:5px" | <math> EI \dfrac{\partial ^2 G_{yy}^{LL}}{\partial x^2}(L,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (8d) |
|- | |- | ||
| − | | style="text-align: center;" | <math> -EI \dfrac{\partial ^3 G_{yy}^{LL}}{\partial ^3 | + | | style="text-align: center;padding-top:5px" | <math> -EI \dfrac{\partial ^3 G_{yy}^{LL}}{\partial x^3}(L,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (8e) |
|} | |} | ||
|} | |} | ||
| − | + | donde las dos <math display="inline">L</math> que acompañan al nombre de la función de Green hacen referencia a que cada uno de los extremos es <math display="inline">L</math>ibre. | |
Cada uno de los tramos de esta función de Green se definen como: | Cada uno de los tramos de esta función de Green se definen como: | ||
| Line 259: | Line 277: | ||
|} | |} | ||
| − | + | donde | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 267: | Line 285: | ||
|- | |- | ||
| style="text-align: center;" | <math>G_{yy}^{LL1}(x,\xi )=\dfrac{A(x,\xi )}{4EI\lambda ^3\left[\sin ^2(\lambda L)-\sinh ^2(\lambda L)\right]} </math> | | style="text-align: center;" | <math>G_{yy}^{LL1}(x,\xi )=\dfrac{A(x,\xi )}{4EI\lambda ^3\left[\sin ^2(\lambda L)-\sinh ^2(\lambda L)\right]} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (10a) |
|- | |- | ||
| style="text-align: center;" | <math> G_{yy}^{LL2}(x,\xi )=\dfrac{B(x,\xi )}{4EI\lambda ^3\left[\sin ^2(\lambda L)-\sinh ^2(\lambda L)\right]} </math> | | style="text-align: center;" | <math> G_{yy}^{LL2}(x,\xi )=\dfrac{B(x,\xi )}{4EI\lambda ^3\left[\sin ^2(\lambda L)-\sinh ^2(\lambda L)\right]} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (10b) |
|} | |} | ||
|} | |} | ||
| Line 303: | Line 321: | ||
| style="text-align: center;" | <math> +\sinh (\lambda L)\left\{\cos (\lambda \xi )\sinh[\lambda(L-\xi)](\lambda \xi )\cosh[\lambda(L-\xi)]\right\} </math> | | style="text-align: center;" | <math> +\sinh (\lambda L)\left\{\cos (\lambda \xi )\sinh[\lambda(L-\xi)](\lambda \xi )\cosh[\lambda(L-\xi)]\right\} </math> | ||
|} | |} | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;" | (13) | ||
|} | |} | ||
| Line 312: | Line 331: | ||
| style="text-align: center;" | <math>B(x,\xi )=A(\xi ,x) </math> | | style="text-align: center;" | <math>B(x,\xi )=A(\xi ,x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (14) |
|} | |} | ||
| Line 322: | Line 341: | ||
| style="text-align: center;" | <math>G_{yy}^{LL2}(x,\xi )=G_{yy}^{LL1}(\xi ,x) </math> | | style="text-align: center;" | <math>G_{yy}^{LL2}(x,\xi )=G_{yy}^{LL1}(\xi ,x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) |
|} | |} | ||
====3.1.2 Viga sobre fundación flexible finita simplemente apoyada==== | ====3.1.2 Viga sobre fundación flexible finita simplemente apoyada==== | ||
| − | La función de Green para la viga sobre fundación flexible finita con ambos extremos | + | La función de Green para la viga sobre fundación flexible finita con ambos extremos con apoyos simples, presentada en la [[#img-5b|Figura 5b]], es la solución del siguiente problema de valor en la frontera: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 335: | Line 354: | ||
|- | |- | ||
| style="text-align: center;" | <math>\frac{\partial ^4 G_{yy}^{SS}}{\partial x^4}(x,\xi )+4\lambda ^4 G_{yy}^{SS}(x,\xi )=\frac{\delta (x-\xi )}{EI} </math> | | style="text-align: center;" | <math>\frac{\partial ^4 G_{yy}^{SS}}{\partial x^4}(x,\xi )+4\lambda ^4 G_{yy}^{SS}(x,\xi )=\frac{\delta (x-\xi )}{EI} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (16a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> G_{yy}^{SS}(0,\xi )=0 </math> | + | | style="text-align: center;padding-top:7px;" | <math> G_{yy}^{SS}(0,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (16b) |
|- | |- | ||
| − | | style="text-align: center;" | <math> EI \dfrac{\partial ^2 G_{yy}^{SS}}{\partial ^2 | + | | style="text-align: center;padding-top:7px;" | <math> EI \dfrac{\partial ^2 G_{yy}^{SS}}{\partial x^2}(0,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (16c) |
|- | |- | ||
| − | | style="text-align: center;" | <math> G_{yy}^{SS}(L,\xi )=0 </math> | + | | style="text-align: center;padding-top:7px;" | <math> G_{yy}^{SS}(L,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (16d) |
|- | |- | ||
| − | | style="text-align: center;" | <math> EI \dfrac{\partial ^2 G_{yy}^{SS}}{\partial ^2 | + | | style="text-align: center;padding-top:7px;" | <math> EI \dfrac{\partial ^2 G_{yy}^{SS}}{\partial x^2}(L,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (16e) |
|} | |} | ||
|} | |} | ||
| − | + | donde las dos <math display="inline">S</math> que acompañan al nombre de la función de Green hacen referencia a que cada uno de los extremos es un apoyo <math display="inline">S</math>imple. | |
Cada uno de los tramos de esta función de Green se definen como: | Cada uno de los tramos de esta función de Green se definen como: | ||
| − | <span id="eq- | + | <span id="eq-17"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 363: | Line 382: | ||
| style="text-align: center;" | <math>G_{yy}^{SS}(x,\xi )= \begin{cases}G_{yy}^{SS1} (x,\xi ) & 0 < x \leq \xi \\ G_{yy}^{SS2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>G_{yy}^{SS}(x,\xi )= \begin{cases}G_{yy}^{SS1} (x,\xi ) & 0 < x \leq \xi \\ G_{yy}^{SS2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (17) |
|} | |} | ||
| − | + | donde | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 374: | Line 393: | ||
|- | |- | ||
| style="text-align: center;" | <math>G_{yy}^{SS1}(x,\xi )=\dfrac{C(x,\xi )}{4EI\lambda ^3\left[\cos (2\lambda L)-\cosh (2\lambda L) \right]} </math> | | style="text-align: center;" | <math>G_{yy}^{SS1}(x,\xi )=\dfrac{C(x,\xi )}{4EI\lambda ^3\left[\cos (2\lambda L)-\cosh (2\lambda L) \right]} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (18a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> G_{yy}^{SS2}(x,\xi )=\dfrac{D(x,\xi )}{4EI\lambda ^3\left[\cos (2\lambda L)-\cosh (2\lambda L) \right]} </math> | + | | style="text-align: center;padding-top:7px;" | <math> G_{yy}^{SS2}(x,\xi )=\dfrac{D(x,\xi )}{4EI\lambda ^3\left[\cos (2\lambda L)-\cosh (2\lambda L) \right]} </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (18b) |
|} | |} | ||
|} | |} | ||
| Line 388: | Line 407: | ||
| style="text-align: center;" | <math>C(x,\xi )= \left\{\sin[\lambda(2L-\xi)]\sinh (\lambda \xi )-\sinh[\lambda(2L-\xi)]\sin (\lambda \xi )\right\} \left[\sin (\lambda x)\cosh (\lambda x)+\cos (\lambda x)\sinh (\lambda x)\right]</math> | | style="text-align: center;" | <math>C(x,\xi )= \left\{\sin[\lambda(2L-\xi)]\sinh (\lambda \xi )-\sinh[\lambda(2L-\xi)]\sin (\lambda \xi )\right\} \left[\sin (\lambda x)\cosh (\lambda x)+\cos (\lambda x)\sinh (\lambda x)\right]</math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> +\left\{\cosh[\lambda(2L-\xi)]\cos (\lambda \xi )-\cos[\lambda(2L-\xi)]\cosh (\lambda \xi )\right\} \left[\sin (\lambda x)\cosh (\lambda x)-\cos (\lambda x)\sinh (\lambda x)\right] </math> | + | | style="text-align: center;padding-top:5px;" | <math> +\left\{\cosh[\lambda(2L-\xi)]\cos (\lambda \xi )-\cos[\lambda(2L-\xi)]\cosh (\lambda \xi )\right\} \left[\sin (\lambda x)\cosh (\lambda x)-\cos (\lambda x)\sinh (\lambda x)\right] </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (19) |
|} | |} | ||
| Line 400: | Line 419: | ||
| style="text-align: center;" | <math>D(x,\xi )=C(\xi ,x) </math> | | style="text-align: center;" | <math>D(x,\xi )=C(\xi ,x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (20) |
|} | |} | ||
| Line 410: | Line 429: | ||
| style="text-align: center;" | <math>G_{yy}^{SS2}(x,\xi )=G_{yy}^{SS1}(\xi ,x) </math> | | style="text-align: center;" | <math>G_{yy}^{SS2}(x,\xi )=G_{yy}^{SS1}(\xi ,x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) |
|} | |} | ||
====3.1.3 Viga sobre fundación flexible finita empotrada - libre==== | ====3.1.3 Viga sobre fundación flexible finita empotrada - libre==== | ||
| − | La función de Green para la viga sobre fundación flexible finita con su extremo inicial <math display="inline">(x=0)</math> empotrado y su extremo final <math display="inline">(x=L)</math> libre, presentada en la | + | La función de Green para la viga sobre fundación flexible finita con su extremo inicial <math display="inline">(x=0)</math> empotrado y su extremo final <math display="inline">(x=L)</math> libre, presentada en la [[#img-5c|Figura 5c]], es la solución del siguiente problema de valor en la frontera: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 423: | Line 442: | ||
|- | |- | ||
| style="text-align: center;" | <math>\frac{\partial ^4 G_{yy}^{EL}}{\partial x^4}(x,\xi )+4\lambda ^4 G_{yy}^{EL}(x,\xi )=\frac{\delta (x-\xi )}{EI} </math> | | style="text-align: center;" | <math>\frac{\partial ^4 G_{yy}^{EL}}{\partial x^4}(x,\xi )+4\lambda ^4 G_{yy}^{EL}(x,\xi )=\frac{\delta (x-\xi )}{EI} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (22a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> G_{yy}^{EL}(0,\xi )=0 </math> | + | | style="text-align: center;padding-top:7px;" | <math> G_{yy}^{EL}(0,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (22b) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \dfrac{\partial G_{yy}^{EL}}{\partial x}(0,\xi )=0 </math> | + | | style="text-align: center;padding-top:7px;" | <math> \dfrac{\partial G_{yy}^{EL}}{\partial x}(0,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (22c) |
|- | |- | ||
| − | | style="text-align: center;" | <math> EI \dfrac{\partial ^2 G_{yy}^{EL}}{\partial ^2 | + | | style="text-align: center;padding-top:7px;" | <math> EI \dfrac{\partial ^2 G_{yy}^{EL}}{\partial x^2}(L,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (22d) |
|- | |- | ||
| − | | style="text-align: center;" | <math> -EI \dfrac{\partial ^3 G_{yy}^{EL}}{\partial ^3 | + | | style="text-align: center;padding-top:7px;" | <math> -EI \dfrac{\partial ^3 G_{yy}^{EL}}{\partial x^3}(L,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (22e) |
|} | |} | ||
|} | |} | ||
| − | + | donde la <math display="inline">E</math> del primer supeindice del nombre hace referencia a que el extremo inicial es <math display="inline">E</math>mpotrado y la <math display="inline">L</math> a que el extremo final es <math display="inline">L</math>ibre. | |
Cada uno de los tramos de esta función de Green se definen como: | Cada uno de los tramos de esta función de Green se definen como: | ||
| − | <span id="eq- | + | <span id="eq-23"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 451: | Line 470: | ||
| style="text-align: center;" | <math>G_{yy}^{EL}(x,\xi )= \begin{cases}G_{yy}^{EL1}(x,\xi ) & 0 < x \leq \xi \\ G_{yy}^{EL2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>G_{yy}^{EL}(x,\xi )= \begin{cases}G_{yy}^{EL1}(x,\xi ) & 0 < x \leq \xi \\ G_{yy}^{EL2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) |
|} | |} | ||
| − | + | donde | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 462: | Line 481: | ||
|- | |- | ||
| style="text-align: center;" | <math>G_{yy}^{EL1}(x,\xi )=\dfrac{E(x,\xi )}{4EI\lambda ^3\left[\cos ^2(\lambda L)+\cosh ^2(\lambda L)\right]} </math> | | style="text-align: center;" | <math>G_{yy}^{EL1}(x,\xi )=\dfrac{E(x,\xi )}{4EI\lambda ^3\left[\cos ^2(\lambda L)+\cosh ^2(\lambda L)\right]} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (24a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> G_{yy}^{EL2}(x,\xi )=\dfrac{F(x,\xi )}{4EI\lambda ^3\left[\cos ^2(\lambda L)+\cosh ^2(\lambda L)\right]} </math> | + | | style="text-align: center;padding-top:7px;" | <math> G_{yy}^{EL2}(x,\xi )=\dfrac{F(x,\xi )}{4EI\lambda ^3\left[\cos ^2(\lambda L)+\cosh ^2(\lambda L)\right]} </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (24b) |
|} | |} | ||
|} | |} | ||
| Line 476: | Line 495: | ||
| style="text-align: center;" | <math>E(x,\xi )=2E_1(\xi )\sin (\lambda x)\sinh (\lambda x)+E_2(\xi )\left[\sin (\lambda x)\cosh (\lambda x)-\cos (\lambda x)\sinh (\lambda x)\right] </math> | | style="text-align: center;" | <math>E(x,\xi )=2E_1(\xi )\sin (\lambda x)\sinh (\lambda x)+E_2(\xi )\left[\sin (\lambda x)\cosh (\lambda x)-\cos (\lambda x)\sinh (\lambda x)\right] </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (25) |
|} | |} | ||
| Line 486: | Line 505: | ||
| style="text-align: center;" | <math>E_1(\xi )=\sinh (\lambda L)\sin (\lambda \xi )\sinh[\lambda(L-\xi)] -\sin (\lambda L)\sinh (\lambda \xi )\sin[\lambda (L-\xi)]</math> | | style="text-align: center;" | <math>E_1(\xi )=\sinh (\lambda L)\sin (\lambda \xi )\sinh[\lambda(L-\xi)] -\sin (\lambda L)\sinh (\lambda \xi )\sin[\lambda (L-\xi)]</math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> +\sin (\lambda \xi )\cosh (\lambda \xi )+\cos (\lambda \xi )\sinh (\lambda \xi ) </math> | + | | style="text-align: center;padding-top:7px;" | <math> +\sin (\lambda \xi )\cosh (\lambda \xi )+\cos (\lambda \xi )\sinh (\lambda \xi ) </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (26) |
|} | |} | ||
| Line 498: | Line 517: | ||
| style="text-align: center;" | <math>E_2(\xi )=\sin (\lambda L)\left\{\cosh (\lambda \xi )\sin[\lambda (L-\xi)+\sinh(\lambda \xi )\cos[\lambda (L-\xi)] \right\}</math> | | style="text-align: center;" | <math>E_2(\xi )=\sin (\lambda L)\left\{\cosh (\lambda \xi )\sin[\lambda (L-\xi)+\sinh(\lambda \xi )\cos[\lambda (L-\xi)] \right\}</math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> | + | | style="text-align: center;padding-top:7px;" | <math> -\sinh (\lambda L) \left\{\sin (\lambda \xi )\cosh[\lambda (L-\xi)]+\cos(\lambda \xi )\sinh[\lambda(L-\xi)]\right\} -2\cos (\lambda \xi )\cosh (\lambda \xi ) </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (27) |
|} | |} | ||
| Line 510: | Line 529: | ||
| style="text-align: center;" | <math>F(x,\xi )=E(\xi ,x) </math> | | style="text-align: center;" | <math>F(x,\xi )=E(\xi ,x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (28) |
|} | |} | ||
| Line 520: | Line 539: | ||
| style="text-align: center;" | <math>G_{yy}^{EL2}(x,\xi )=G_{yy}^{EL1}(\xi ,x) </math> | | style="text-align: center;" | <math>G_{yy}^{EL2}(x,\xi )=G_{yy}^{EL1}(\xi ,x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (29) |
|} | |} | ||
====3.1.4 Viga sobre fundación flexible finita doblemente empotrada==== | ====3.1.4 Viga sobre fundación flexible finita doblemente empotrada==== | ||
| − | La función de Green para la viga sobre fundación flexible finita doblemente empotrada presentada en la | + | La función de Green para la viga sobre fundación flexible finita doblemente empotrada presentada en la [[#img-5d|Figura 5d]], es la solución del siguiente problema de valor en la frontera: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 533: | Line 552: | ||
|- | |- | ||
| style="text-align: center;" | <math>\frac{\partial ^4 G_{yy}^{EE}}{\partial x^4}(x,\xi )+4\lambda ^4 G_{yy}^{EE}(x,\xi )=\frac{\delta (x-\xi )}{EI} </math> | | style="text-align: center;" | <math>\frac{\partial ^4 G_{yy}^{EE}}{\partial x^4}(x,\xi )+4\lambda ^4 G_{yy}^{EE}(x,\xi )=\frac{\delta (x-\xi )}{EI} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (30a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> G_{yy}^{EE}(0,\xi )=0 </math> | + | | style="text-align: center;padding-top:7px;" | <math> G_{yy}^{EE}(0,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (30b) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \dfrac{\partial G_{yy}^{EE}}{\partial x}(0,\xi )=0 </math> | + | | style="text-align: center;padding-top:7px;" | <math> \dfrac{\partial G_{yy}^{EE}}{\partial x}(0,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (30c) |
|- | |- | ||
| − | | style="text-align: center;" | <math> G_{yy}^{EE}(L,\xi )=0 </math> | + | | style="text-align: center;padding-top:7px;" | <math> G_{yy}^{EE}(L,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (30d) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \dfrac{\partial G_{yy}^{EE}}{\partial x}(L,\xi )=0 </math> | + | | style="text-align: center;padding-top:7px;" | <math> \dfrac{\partial G_{yy}^{EE}}{\partial x}(L,\xi )=0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (30e) |
|} | |} | ||
|} | |} | ||
| − | + | donde las dos <math display="inline">E</math> que acompañan al nombre de la función de Green hacen referencia a que cada uno de los extremos es un apoyo <math display="inline">E</math>mpotrado. | |
Cada uno de los tramos de esta función de Green se definen como: | Cada uno de los tramos de esta función de Green se definen como: | ||
| − | <span id="eq- | + | <span id="eq-31"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 561: | Line 580: | ||
| style="text-align: center;" | <math>G_{yy}^{EE}(x,\xi )= \begin{cases}G_{yy}^{EE1}(x,\xi ) & 0 < x \leq \xi \\ G_{yy}^{EE2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>G_{yy}^{EE}(x,\xi )= \begin{cases}G_{yy}^{EE1}(x,\xi ) & 0 < x \leq \xi \\ G_{yy}^{EE2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (31) |
|} | |} | ||
| − | + | donde | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 572: | Line 591: | ||
|- | |- | ||
| style="text-align: center;" | <math>G_{yy}^{EE1}(x,\xi )=\dfrac{H(x,\xi )}{4EI \lambda ^3 [\sin ^2(\lambda L)-\sinh ^2(\lambda L)]} </math> | | style="text-align: center;" | <math>G_{yy}^{EE1}(x,\xi )=\dfrac{H(x,\xi )}{4EI \lambda ^3 [\sin ^2(\lambda L)-\sinh ^2(\lambda L)]} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (32a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> G_{yy}^{EE2}(x,\xi )=\dfrac{J(x,\xi )}{4EI \lambda ^3 [\sin ^2(\lambda L)-\sinh ^2(\lambda L)]} </math> | + | | style="text-align: center;padding-top:7px;" | <math> G_{yy}^{EE2}(x,\xi )=\dfrac{J(x,\xi )}{4EI \lambda ^3 [\sin ^2(\lambda L)-\sinh ^2(\lambda L)]} </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (32b) |
|} | |} | ||
|} | |} | ||
| Line 586: | Line 605: | ||
| style="text-align: center;" | <math>H(\xi )=2\sin (\lambda x)\sinh (\lambda x)H_1(\xi )+[\sin (\lambda x)\cosh (\lambda x)-\cos (\lambda x)\sinh (\lambda x)]H_2(\xi ) </math> | | style="text-align: center;" | <math>H(\xi )=2\sin (\lambda x)\sinh (\lambda x)H_1(\xi )+[\sin (\lambda x)\cosh (\lambda x)-\cos (\lambda x)\sinh (\lambda x)]H_2(\xi ) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (33) |
|} | |} | ||
| Line 596: | Line 615: | ||
| style="text-align: center;" | <math>H_1(\xi )=\sin (\lambda L)\sinh (\lambda \xi )\sin[\lambda (L-\xi)]-\sin(\lambda \xi )\sinh (\lambda L)\sinh[\lambda (L-\xi)] </math> | | style="text-align: center;" | <math>H_1(\xi )=\sin (\lambda L)\sinh (\lambda \xi )\sin[\lambda (L-\xi)]-\sin(\lambda \xi )\sinh (\lambda L)\sinh[\lambda (L-\xi)] </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (34) |
|} | |} | ||
| Line 608: | Line 627: | ||
| style="text-align: center;" | <math> +\sinh (\lambda L)\{ \sin (\lambda \xi )\cosh[\lambda (L-\xi)]+\cos(\lambda \xi )\sinh[\lambda (L-\xi)]\} </math> | | style="text-align: center;" | <math> +\sinh (\lambda L)\{ \sin (\lambda \xi )\cosh[\lambda (L-\xi)]+\cos(\lambda \xi )\sinh[\lambda (L-\xi)]\} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (35) |
|} | |} | ||
| Line 618: | Line 637: | ||
| style="text-align: center;" | <math>J(x,\xi )=H(\xi ,x) </math> | | style="text-align: center;" | <math>J(x,\xi )=H(\xi ,x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (36) |
|} | |} | ||
| Line 628: | Line 647: | ||
| style="text-align: center;" | <math>G_{yy}^{EE2}(x,\xi )=G_{yy}^{EE1}(\xi ,x) </math> | | style="text-align: center;" | <math>G_{yy}^{EE2}(x,\xi )=G_{yy}^{EE1}(\xi ,x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (37) |
|} | |} | ||
====3.1.5 Viga sobre fundación flexible infinita==== | ====3.1.5 Viga sobre fundación flexible infinita==== | ||
| − | La función de Green para la viga sobre fundación flexible infinita presentada en la | + | La función de Green para la viga sobre fundación flexible infinita presentada en la [[#img-6|Figura 6]], se define como: |
| − | <span id="eq- | + | <span id="eq-38"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 641: | Line 660: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>G_{yy}(x,\xi )= \begin{cases}G_{yy}^1(x,\xi ) & -\infty < x \leq \xi \\ G_{yy}^2(x,\xi ) \qquad & \xi \leq x < +\infty \end{cases} </math> | + | | style="text-align: center;" | <math>G_{yy}(x,\xi )= \begin{cases}G_{yy}^1(x,\xi ) & -\infty < x \leq \xi \\[.3cm] G_{yy}^2(x,\xi ) \qquad & \xi \leq x < +\infty \end{cases} </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (38) |
|} | |} | ||
| + | |||
| + | Donde: | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 653: | Line 674: | ||
| style="text-align: center;" | <math>G_{yy}^1(x,\xi )=\dfrac{\exp[+\lambda (x-\xi)]\{ \cos[\lambda (x-\xi)]-\sin[\lambda(x-\xi)] \}}{8EI\lambda ^3} </math> | | style="text-align: center;" | <math>G_{yy}^1(x,\xi )=\dfrac{\exp[+\lambda (x-\xi)]\{ \cos[\lambda (x-\xi)]-\sin[\lambda(x-\xi)] \}}{8EI\lambda ^3} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (39) |
|} | |} | ||
| Line 663: | Line 684: | ||
| style="text-align: center;" | <math>G_{yy}^2(x,\xi )=\dfrac{\exp[-\lambda (x-\xi)]\{ \cos[\lambda (x-\xi)]+\sin[\lambda(x-\xi)]\} }{8EI\lambda ^3} </math> | | style="text-align: center;" | <math>G_{yy}^2(x,\xi )=\dfrac{\exp[-\lambda (x-\xi)]\{ \cos[\lambda (x-\xi)]+\sin[\lambda(x-\xi)]\} }{8EI\lambda ^3} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (40) |
|} | |} | ||
| Line 675: | Line 696: | ||
| style="text-align: center;" | <math>G_{yy}(x,\xi )=\dfrac{\exp (-\lambda |x-\xi |)[ \cos (\lambda |x-\xi |)+\sin (\lambda |x-\xi |)]}{8EI\lambda ^3} \qquad -\infty{<}x<+\infty </math> | | style="text-align: center;" | <math>G_{yy}(x,\xi )=\dfrac{\exp (-\lambda |x-\xi |)[ \cos (\lambda |x-\xi |)+\sin (\lambda |x-\xi |)]}{8EI\lambda ^3} \qquad -\infty{<}x<+\infty </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (41) |
|} | |} | ||
===3.2 Momentos puntuales=== | ===3.2 Momentos puntuales=== | ||
| − | En las | + | En las [[#img-7|Figuras 7]] y [[#img-8|8]] se presentan las vigas sobre fundación flexible finitas e infinitas para las cuales se definirán las funciones de Green debidas a la aplicación de un momento puntual unitario, todas las cuales se pueden obtener directamente a partir de sus contrapartes debidas a fuerzas puntuales unitarias presentadas en la sección [[#3.1 Fuerzas puntuales|3.1]] empleando la representación de un momento como el limite de dos fuerzas puntuales muy cercanas presentado anteriormente. |
| + | <div id='img-7a'></div> | ||
<div id='img-7b'></div> | <div id='img-7b'></div> | ||
<div id='img-7c'></div> | <div id='img-7c'></div> | ||
<div id='img-7d'></div> | <div id='img-7d'></div> | ||
<div id='img-7'></div> | <div id='img-7'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-FigGyqLibreLibre.png|400px|Libre - libre finita.]] |
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-FigGyqSimplementeApoyada.png|400px|Simplemente apoyada.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) Libre - libre finita | + | | (a) Libre - libre finita |
| − | | (b) Simplemente apoyada | + | | (b) Simplemente apoyada |
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-FigGyqEmpotradaLibre.png|400px|Empotrada - libre.]] |
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-FigGyqEmpotradaEmpotrada.png|400px|Empotrada - libre infinita.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (c) Empotrada - libre | + | | (c) Empotrada - libre |
| − | | (d) Empotrada - libre infinita | + | | (d) Empotrada - libre infinita |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 7 | + | | colspan="2" style="padding:10px;" | '''Figura 7'''. Vigas sobre fundación flexible finitas con diferentes condiciones de frontera y sometidas a momentos puntuales unitarios |
|} | |} | ||
| + | |||
<div id='img-8'></div> | <div id='img-8'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" |
|- | |- | ||
| − | |[[Image: | + | |[[Image:Review_921349416580-FigGyqInfinita.png|400px|Viga sobre fundación flexible infinita sometida a un momento puntual unitario.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 8 | + | | colspan="1" style="padding:10px;"| '''Figura 8'''. Viga sobre fundación flexible infinita sometida a un momento puntual unitario |
|} | |} | ||
====3.2.1 Viga sobre fundación flexible finita libre - libre==== | ====3.2.1 Viga sobre fundación flexible finita libre - libre==== | ||
| − | A partir de [[#eq-9|(9)]], la función de Green para la viga sobre fundación flexible finita con ambos extremos libres presentada en la | + | A partir de la ecuación [[#eq-9|(9)]], la función de Green para la viga sobre fundación flexible finita con ambos extremos libres presentada en la [[#img-7a|Figura 7a]], se define como: |
| − | <span id="eq- | + | <span id="eq-42"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 721: | Line 744: | ||
| style="text-align: center;" | <math>G_{y \theta }^{LL}(x,\xi )=\dfrac{G_{yy}^{LL}}{\partial \xi }(x,\xi ) </math> | | style="text-align: center;" | <math>G_{y \theta }^{LL}(x,\xi )=\dfrac{G_{yy}^{LL}}{\partial \xi }(x,\xi ) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (42) |
|} | |} | ||
| Line 733: | Line 756: | ||
| style="text-align: center;" | <math>G_{y\theta }^{LL}(x,\xi )= \begin{cases}G_{y\theta }^{LL1}(x,\xi )=\dfrac{G_{yy}^{LL1}}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^{LL2}(x,\xi )=\dfrac{G_{yy}^{LL2}}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>G_{y\theta }^{LL}(x,\xi )= \begin{cases}G_{y\theta }^{LL1}(x,\xi )=\dfrac{G_{yy}^{LL1}}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^{LL2}(x,\xi )=\dfrac{G_{yy}^{LL2}}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (43) |
|} | |} | ||
====3.2.2 Viga sobre fundación flexible finita simplemente apoyada==== | ====3.2.2 Viga sobre fundación flexible finita simplemente apoyada==== | ||
| − | A partir de [[#eq- | + | A partir de la ecuación [[#eq-17|(17)]], la función de Green para la viga sobre fundación flexible finita simplemente apoyada presentada en la [[#img-7b|Figura 7b]], se define como: |
| − | <span id="eq- | + | <span id="eq-44"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 748: | Line 771: | ||
| style="text-align: center;" | <math>G_{y \theta }^{SS}(x,\xi )=\dfrac{G_{yy}^{SS}}{\partial \xi }(x,\xi ) </math> | | style="text-align: center;" | <math>G_{y \theta }^{SS}(x,\xi )=\dfrac{G_{yy}^{SS}}{\partial \xi }(x,\xi ) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (44) |
|} | |} | ||
| Line 760: | Line 783: | ||
| style="text-align: center;" | <math>G_{y\theta }^{SS}(x,\xi )= \begin{cases}G_{y\theta }^{SS1}(x,\xi )=\dfrac{G_{yy}^{SS1}}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^{SS2}(x,\xi )=\dfrac{G_{yy}^{SS2}}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>G_{y\theta }^{SS}(x,\xi )= \begin{cases}G_{y\theta }^{SS1}(x,\xi )=\dfrac{G_{yy}^{SS1}}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^{SS2}(x,\xi )=\dfrac{G_{yy}^{SS2}}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (45) |
|} | |} | ||
====3.2.3 Viga sobre fundación flexible finita empotrada - libre==== | ====3.2.3 Viga sobre fundación flexible finita empotrada - libre==== | ||
| − | A partir de [[#eq- | + | A partir de la ecuación [[#eq-23|(23)]], la función de Green para la viga sobre fundación flexible finita simplemente apoyada presentada en la [[#img-7c|Figura 7c]], se define como: |
| − | <span id="eq- | + | <span id="eq-46"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 775: | Line 798: | ||
| style="text-align: center;" | <math>G_{y \theta }^{EL}(x,\xi )=\dfrac{G_{yy}^{EL}}{\partial \xi }(x,\xi ) </math> | | style="text-align: center;" | <math>G_{y \theta }^{EL}(x,\xi )=\dfrac{G_{yy}^{EL}}{\partial \xi }(x,\xi ) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (46) |
|} | |} | ||
| Line 787: | Line 810: | ||
| style="text-align: center;" | <math>G_{y\theta }^{EL}(x,\xi )= \begin{cases}G_{y\theta }^{EL1}(x,\xi )=\dfrac{G_{yy}^{EL1}}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^{EL2}(x,\xi )=\dfrac{G_{yy}^{EL2}}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>G_{y\theta }^{EL}(x,\xi )= \begin{cases}G_{y\theta }^{EL1}(x,\xi )=\dfrac{G_{yy}^{EL1}}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^{EL2}(x,\xi )=\dfrac{G_{yy}^{EL2}}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (47) |
|} | |} | ||
====3.2.4 Viga sobre fundación flexible finita doblemente empotrada==== | ====3.2.4 Viga sobre fundación flexible finita doblemente empotrada==== | ||
| − | A partir de [[#eq- | + | A partir de la ecuación [[#eq-31|(31)]], la función de Green para la viga sobre fundación flexible finita simplemente apoyada presentada en la [[#img-7d|Figura 7d]], se define como: |
| − | <span id="eq- | + | <span id="eq-48"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 802: | Line 825: | ||
| style="text-align: center;" | <math>G_{y \theta }^{EE}(x,\xi )=\dfrac{G_{yy}^{EE}}{\partial \xi }(x,\xi ) </math> | | style="text-align: center;" | <math>G_{y \theta }^{EE}(x,\xi )=\dfrac{G_{yy}^{EE}}{\partial \xi }(x,\xi ) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (48) |
|} | |} | ||
| Line 814: | Line 837: | ||
| style="text-align: center;" | <math>G_{y\theta }^{EE}(x,\xi )= \begin{cases}G_{y\theta }^{EE1}(x,\xi )=\dfrac{G_{yy}^{EE1}}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^{EE2}(x,\xi )=\dfrac{G_{yy}^{EE2}}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>G_{y\theta }^{EE}(x,\xi )= \begin{cases}G_{y\theta }^{EE1}(x,\xi )=\dfrac{G_{yy}^{EE1}}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^{EE2}(x,\xi )=\dfrac{G_{yy}^{EE2}}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (49) |
|} | |} | ||
====3.2.5 Viga sobre fundación flexible infinita==== | ====3.2.5 Viga sobre fundación flexible infinita==== | ||
| − | A partir de [[#eq- | + | A partir de la ecuación [[#eq-38|(38)]], la función de Green para la viga sobre fundación flexible finita simplemente apoyada presentada en la [[#img-8|Figura 8]], se define como: |
| − | <span id="eq- | + | <span id="eq-50"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 829: | Line 852: | ||
| style="text-align: center;" | <math>G_{y \theta }(x,\xi )=\dfrac{G_{yy}}{\partial \xi }(x,\xi ) </math> | | style="text-align: center;" | <math>G_{y \theta }(x,\xi )=\dfrac{G_{yy}}{\partial \xi }(x,\xi ) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (50) |
|} | |} | ||
| Line 841: | Line 864: | ||
| style="text-align: center;" | <math>G_{y\theta }(x,\xi )= \begin{cases}G_{y\theta }^1(x,\xi )=\dfrac{G_{yy}^1}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^2(x,\xi )=\dfrac{G_{yy}^2}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>G_{y\theta }(x,\xi )= \begin{cases}G_{y\theta }^1(x,\xi )=\dfrac{G_{yy}^1}{\partial \xi }(x,\xi ) & 0 < x \leq \xi \\[0.3cm] G_{y\theta }^2(x,\xi )=\dfrac{G_{yy}^2}{\partial \xi }(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (51) |
|} | |} | ||
| − | ==4 Solución de vigas sobre fundación flexible empleando funciones de Green== | + | ==4. Solución de vigas sobre fundación flexible empleando funciones de Green== |
| − | Antes de comenzar con la explicación de esta metodología es necesario tener claro que todas las cargas externas aplicadas en una viga sobre fundación flexible pueden obtenerse como un operador lineal de cargas puntuales unitarias, en particular sumas, integrales o derivadas ponderadas por un número o función. Para facilitar la explicación de este concepto, se empleará como ejemplo la viga sobre fundación flexible presentada en la | + | Antes de comenzar con la explicación de esta metodología es necesario tener claro que todas las cargas externas aplicadas en una viga sobre fundación flexible pueden obtenerse como un operador lineal de cargas puntuales unitarias, en particular sumas, integrales o derivadas ponderadas por un número o función. Para facilitar la explicación de este concepto, se empleará como ejemplo la viga sobre fundación flexible presentada en la [[#img-9|Figura 9]]. |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | <div id='img-9'></div> |
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;" | ||
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-Figura06.png|400px|Viga sobre fundación flexible sometida a cargas externas distribuidas y puntuales.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 9 | + | | colspan="1" style="padding:10px;"| '''Figura 9'''. Viga sobre fundación flexible sometida a cargas externas distribuidas y puntuales |
|} | |} | ||
| + | |||
| + | |||
La carga puntual <math display="inline">F</math> se expresa como el producto de una fuerza puntual unitaria por el factor <math display="inline">F</math>, es decir, se encuentra definida por la siguiente función (ver la ecuación [[#eq-4|(4)]] para una explicación): | La carga puntual <math display="inline">F</math> se expresa como el producto de una fuerza puntual unitaria por el factor <math display="inline">F</math>, es decir, se encuentra definida por la siguiente función (ver la ecuación [[#eq-4|(4)]] para una explicación): | ||
| Line 862: | Line 888: | ||
| style="text-align: center;" | <math>q_1(\xi )=F \cdot \delta (\xi{-}x_4) </math> | | style="text-align: center;" | <math>q_1(\xi )=F \cdot \delta (\xi{-}x_4) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (52) |
|} | |} | ||
| Line 873: | Line 899: | ||
|- | |- | ||
| style="text-align: center;" | <math>q_2(\xi )=FY_1 \cdot \delta (\xi ) </math> | | style="text-align: center;" | <math>q_2(\xi )=FY_1 \cdot \delta (\xi ) </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (53a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> q_3(\xi )=FY_2 \cdot \delta (\xi{-}x_2) </math> | + | | style="text-align: center;padding-top:7px;"| " | <math> q_3(\xi )=FY_2 \cdot \delta (\xi{-}x_2) </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (53b) |
|} | |} | ||
|} | |} | ||
| − | + | donde <math display="inline">FY_1</math> y <math display="inline">FY_2</math> son respectivamente los valores de las reacciones en los puntos 1 y 2, las cuales son positivas en dirección del eje <math display="inline">y</math>. | |
Por su parte, los momentos puntuales debidos al momento externo <math display="inline">M</math> y la reacción a momento en el punto 1, se expresan respectivamente como: | Por su parte, los momentos puntuales debidos al momento externo <math display="inline">M</math> y la reacción a momento en el punto 1, se expresan respectivamente como: | ||
| Line 890: | Line 916: | ||
|- | |- | ||
| style="text-align: center;" | <math>q_4(\xi )=M \cdot \dfrac{\partial \delta (\xi{-}r)}{\partial r}(r=x_5) </math> | | style="text-align: center;" | <math>q_4(\xi )=M \cdot \dfrac{\partial \delta (\xi{-}r)}{\partial r}(r=x_5) </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (54a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> q_5(\xi )=M_1 \cdot \dfrac{\partial \delta (\xi{-}r)}{\partial r}(r=0) </math> | + | | style="text-align: center;padding-top:7px;" | <math> q_5(\xi )=M_1 \cdot \dfrac{\partial \delta (\xi{-}r)}{\partial r}(r=0) </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (54b) |
|} | |} | ||
|} | |} | ||
| − | + | donde <math display="inline">M_1</math> es la reacción a momento en el punto 1 y <math display="inline">r</math> es una variable auxiliar muda o temporal. | |
Mientras que la carga distribuida se expresa como: | Mientras que la carga distribuida se expresa como: | ||
| Line 908: | Line 934: | ||
| style="text-align: center;" | <math>q(\xi )=\int _{x_1}^{x_3} q(x)\delta (x-\xi )dx </math> | | style="text-align: center;" | <math>q(\xi )=\int _{x_1}^{x_3} q(x)\delta (x-\xi )dx </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (55) |
|} | |} | ||
| − | Ahora que es claro que cualquier carga puntual o distribuida puede expresarse como un operador lineal de cargas puntuales, se debe seleccionar una función de Green cuya viga sobre fundación flexible cumpla o pueda cumplir, por medio de la aplicación de fuerzas o momentos puntuales, todas condiciones de frontera y compatibilidad de la viga sobre fundación flexible en estudio. Para este problema la función de Green que más se acomoda es aquella de la viga empotrada libre presentada en la | + | Ahora que es claro que cualquier carga puntual o distribuida puede expresarse como un operador lineal de cargas puntuales, se debe seleccionar una función de Green cuya viga sobre fundación flexible cumpla o pueda cumplir, por medio de la aplicación de fuerzas o momentos puntuales, todas condiciones de frontera y compatibilidad de la viga sobre fundación flexible en estudio. Para este problema la función de Green que más se acomoda es aquella de la viga empotrada libre presentada en la [[#img-5c|Figura 5c]]. Una vez seleccionada la función de Green, la viga que la define debe hacerse equivalente a aquella en estudio, lo cual se logra a partir de la aplicación de cargas distribuidas y/o puntuales (todas ellas expresables como un operador lineal de cargas puntuales) y del cumplimiento de condiciones de frontera y/o compatibilidad. En este caso es claro que para que la estructura presentada en la [[#img-5c|Figura 5c]] sea equivalente a aquella de la [[#img-9|Figura 9]] debe cumplirse que el desplazamiento en el punto 2 sea cero, es decir, <math display="inline">v_2=v(x_2)=0</math>, condición de compatibilidad empleada para obtener el valor de la reacción <math display="inline">FY_2</math> que es desconocido, la cual se expresa en términos de las funciones de Green <math display="inline">G^{EL}_{yy}(z,\xi )</math> y <math display="inline">G^{EL}_{y\theta }(z,\xi )</math>, así como empleando el principio de superposición, como: |
| − | <span id="eq- | + | <span id="eq-56"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 921: | Line 947: | ||
| style="text-align: center;" | <math>v_2=v(x_2)=0=FY_2 \cdot G_{yy}^{EL1}(x_2,x_2)+F \cdot G_{yy}^{EL1}(x_2,x_4)+M \cdot G_{y\theta }^{EL1}(x_2,x_5) </math> | | style="text-align: center;" | <math>v_2=v(x_2)=0=FY_2 \cdot G_{yy}^{EL1}(x_2,x_2)+F \cdot G_{yy}^{EL1}(x_2,x_4)+M \cdot G_{y\theta }^{EL1}(x_2,x_5) </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> +\int _{x_1}^{x_2} q(\xi )G_{yy}^{EL2}(x_2,\xi )d\xi{+\int}_{x_2}^{x_3} q(\xi )G_{yy}^{EL1}(x_2,\xi )d\xi </math> | + | | style="text-align: center;padding-top:7px;" | <math> +\int _{x_1}^{x_2} q(\xi )G_{yy}^{EL2}(x_2,\xi )d\xi{+\int}_{x_2}^{x_3} q(\xi )G_{yy}^{EL1}(x_2,\xi )d\xi </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (56) |
|} | |} | ||
| − | Cuyos términos se explican a continuación: | + | Cuyos términos se explican a continuación:<br> |
| + | |||
<math display="inline">FY_2 \cdot G_{yy}^{EL1}(x_2,x_2)</math>: Desplazamiento en <math display="inline">x=x_2</math> debido a la fuerza puntual <math display="inline">FY_2</math> ubicada en <math display="inline">x=x_2</math>. | <math display="inline">FY_2 \cdot G_{yy}^{EL1}(x_2,x_2)</math>: Desplazamiento en <math display="inline">x=x_2</math> debido a la fuerza puntual <math display="inline">FY_2</math> ubicada en <math display="inline">x=x_2</math>. | ||
| Line 938: | Line 965: | ||
<math display="inline">\int _{x_2}^{x_3} q(\xi )G_{yy}^{EL1}(x_2,\xi )d\xi </math>: Desplazamiento en <math display="inline">x=x_2</math> debido a la carga distribuida <math display="inline">q(\xi )</math> ubicada entre <math display="inline">x=x_2</math> y <math display="inline">x=x_3</math>. | <math display="inline">\int _{x_2}^{x_3} q(\xi )G_{yy}^{EL1}(x_2,\xi )d\xi </math>: Desplazamiento en <math display="inline">x=x_2</math> debido a la carga distribuida <math display="inline">q(\xi )</math> ubicada entre <math display="inline">x=x_2</math> y <math display="inline">x=x_3</math>. | ||
| − | En este punto es importante recordarle al lector que <math display="inline">G_{yy}^{EL1}(x,\xi )</math> corresponde al desplazamiento antes de la fuerza puntual unitaria, mientras que <math display="inline">G_{yy}^{EL2}(x,\xi )</math> corresponde a aquel después de esta. | + | <br> |
| + | En este punto, es importante recordarle al lector que <math display="inline">G_{yy}^{EL1}(x,\xi )</math> corresponde al desplazamiento antes de la fuerza puntual unitaria, mientras que <math display="inline">G_{yy}^{EL2}(x,\xi )</math> corresponde a aquel después de esta. | ||
| − | Como siguiente paso, una vez obtenidas todas las condiciones de compatibilidad, se resuelve el sistema lineal de ecuaciones que ellas | + | Como siguiente paso, una vez obtenidas todas las condiciones de compatibilidad, se resuelve el sistema lineal de ecuaciones que ellas forman, de lo cual se obtiene el valor de aquellas reacciones puntuales diferentes a aquellas que también ocurrirían en la viga sobre fundación flexible empleada para definir la función de Green ([[#img-10|Figura 10]]). En este ejemplo esto equivale a obtener el único valor de <math display="inline">FY_2</math> que cumple [[#eq-56|(56)]]. |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | |
| + | <div id='img-10'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 60%;" | ||
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"|[[Image:Review_921349416580-Figura07.png|400px|Aplicación de las cargas externas de la viga sobre fundación flexible a analizar sobre aquella empleada para la definición de la función de Green empleada en la solución.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 10 | + | | colspan="1" style="padding:10px;"| '''Figura 10'''. Aplicación de las cargas externas de la viga sobre fundación flexible a analizar sobre aquella empleada para la definición de la función de Green empleada en la solución |
|} | |} | ||
| + | |||
| + | |||
Una vez obtenidas las reacciones que hacen que se cumplan las condiciones de compatibilidad y/o frontera, es necesario calcular el campo de desplazamiento en cada uno de los tramos de la viga sobre fundación flexible, lo cual se realiza de nuevo empleando el principio de superposición. Para este ejemplo el campo de desplazamiento tiene 6 tramos y se define como: | Una vez obtenidas las reacciones que hacen que se cumplan las condiciones de compatibilidad y/o frontera, es necesario calcular el campo de desplazamiento en cada uno de los tramos de la viga sobre fundación flexible, lo cual se realiza de nuevo empleando el principio de superposición. Para este ejemplo el campo de desplazamiento tiene 6 tramos y se define como: | ||
| Line 956: | Line 988: | ||
| style="text-align: center;" | <math>v(x)= \begin{cases}v_1(x) & 0<x \leq x_1 \\ v_2(x) & x_1 \leq x \leq x_2 \\ v_3(x) & x_2 \leq x \leq x_3 \\ v_4(x) & x_3 \leq x \leq x_4 \\ v_5(x) & x_4 \leq x \leq x_5 \\ v_6(x) & x_5 \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>v(x)= \begin{cases}v_1(x) & 0<x \leq x_1 \\ v_2(x) & x_1 \leq x \leq x_2 \\ v_3(x) & x_2 \leq x \leq x_3 \\ v_4(x) & x_3 \leq x \leq x_4 \\ v_5(x) & x_4 \leq x \leq x_5 \\ v_6(x) & x_5 \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (57) |
|} | |} | ||
| Line 968: | Line 1,000: | ||
| style="text-align: center;" | <math>v_1(x)=FY_2 \cdot G_{yy}^{EL1}(x,x_2)+F \cdot G_{yy}^{EL1}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) +\int _{x_1}^{x_3} q(\xi )G_{yy}^{EL1}(x,\xi )d\xi </math> | | style="text-align: center;" | <math>v_1(x)=FY_2 \cdot G_{yy}^{EL1}(x,x_2)+F \cdot G_{yy}^{EL1}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) +\int _{x_1}^{x_3} q(\xi )G_{yy}^{EL1}(x,\xi )d\xi </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (58) |
|} | |} | ||
| Line 978: | Line 1,010: | ||
| style="text-align: center;" | <math>v_2(x)=FY_2 \cdot G_{yy}^{EL1}(x,x_2)+F \cdot G_{yy}^{EL1}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) </math> | | style="text-align: center;" | <math>v_2(x)=FY_2 \cdot G_{yy}^{EL1}(x,x_2)+F \cdot G_{yy}^{EL1}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> +\int _{x_1}^{x} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi{+\int}_{x}^{x_3} q(\xi )G_{yy}^{EL1}(x,\xi )d\xi </math> | + | | style="text-align: center;padding:7px;" | <math> +\int _{x_1}^{x} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi{+\int}_{x}^{x_3} q(\xi )G_{yy}^{EL1}(x,\xi )d\xi </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (59) |
|} | |} | ||
| Line 990: | Line 1,022: | ||
| style="text-align: center;" | <math>v_3(x)=FY_2 \cdot G_{yy}^{EL2}(x,x_2)+F \cdot G_{yy}^{EL1}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) </math> | | style="text-align: center;" | <math>v_3(x)=FY_2 \cdot G_{yy}^{EL2}(x,x_2)+F \cdot G_{yy}^{EL1}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> +\int _{x_1}^{x} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi{+\int}_{x}^{x_3} q(\xi )G_{yy}^{EL1}(x,\xi )d\xi </math> | + | | style="text-align: center;padding:7px;" | <math> +\int _{x_1}^{x} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi{+\int}_{x}^{x_3} q(\xi )G_{yy}^{EL1}(x,\xi )d\xi </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (60) |
|} | |} | ||
| Line 1,002: | Line 1,034: | ||
| style="text-align: center;" | <math>v_4(x)=FY_2 \cdot G_{yy}^{EL2}(x,x_2)+F \cdot G_{yy}^{EL1}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) +\int _{x_1}^{x_3} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi </math> | | style="text-align: center;" | <math>v_4(x)=FY_2 \cdot G_{yy}^{EL2}(x,x_2)+F \cdot G_{yy}^{EL1}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) +\int _{x_1}^{x_3} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (61) |
|} | |} | ||
| Line 1,012: | Line 1,044: | ||
| style="text-align: center;" | <math>v_5(x)=FY_2 \cdot G_{yy}^{EL2}(x,x_2)+F \cdot G_{yy}^{EL2}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) +\int _{x_1}^{x_3} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi </math> | | style="text-align: center;" | <math>v_5(x)=FY_2 \cdot G_{yy}^{EL2}(x,x_2)+F \cdot G_{yy}^{EL2}(x,x_4)+M \cdot G_{y\theta }^{EL1}(x,x_5) +\int _{x_1}^{x_3} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (62) |
|} | |} | ||
| Line 1,022: | Line 1,054: | ||
| style="text-align: center;" | <math>v_6(x)=FY_2 \cdot G_{yy}^{EL2}(x,x_2)+F \cdot G_{yy}^{EL2}(x,x_4)+M \cdot G_{y\theta }^{EL2}(x,x_5) +\int _{x_1}^{x_3} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi </math> | | style="text-align: center;" | <math>v_6(x)=FY_2 \cdot G_{yy}^{EL2}(x,x_2)+F \cdot G_{yy}^{EL2}(x,x_4)+M \cdot G_{y\theta }^{EL2}(x,x_5) +\int _{x_1}^{x_3} q(\xi )G_{yy}^{EL2}(x,\xi )d\xi </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (63) |
|} | |} | ||
| − | Por último, a partir del campo de desplazamiento calculado anteriormente y empleando [[#eq-3|(3)]] y [[#eq-6|(6)]] se calculan los campos de la fuerza que el suelo ejerce sobre la viga, de momento flector y fuerza cortante respectivamente como: | + | Por último, a partir del campo de desplazamiento calculado anteriormente y empleando las ecuaciones [[#eq-3|(3)]] y [[#eq-6|(6)]] se calculan los campos de la fuerza que el suelo ejerce sobre la viga, de momento flector y fuerza cortante respectivamente como: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,034: | Line 1,066: | ||
| style="text-align: center;" | <math>f_S(x)= \begin{cases}f_S^1(x)=-kv_1(x) & 0<x \leq x_1 \\ f_S^2(x)=-kv_2(x) & x_1 \leq x \leq x_2 \\ f_S^3(x)=-kv_3(x) & x_2 \leq x \leq x_3 \\ f_S^4(x)=-kv_4(x) & x_3 \leq x \leq x_4 \\ f_S^5(x)=-kv_5(x) & x_4 \leq x \leq x_5 \\ f_S^6(x)=-kv_6(x) \qquad & x_5 \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>f_S(x)= \begin{cases}f_S^1(x)=-kv_1(x) & 0<x \leq x_1 \\ f_S^2(x)=-kv_2(x) & x_1 \leq x \leq x_2 \\ f_S^3(x)=-kv_3(x) & x_2 \leq x \leq x_3 \\ f_S^4(x)=-kv_4(x) & x_3 \leq x \leq x_4 \\ f_S^5(x)=-kv_5(x) & x_4 \leq x \leq x_5 \\ f_S^6(x)=-kv_6(x) \qquad & x_5 \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (64) |
|} | |} | ||
| Line 1,044: | Line 1,076: | ||
| style="text-align: center;" | <math>M(x)=EI\dfrac{d^2 v}{dx^2}(x)= \begin{cases}M_1(x)=EI\dfrac{d^2 v_1}{dx^2}(x) & 0<x \leq x_1 \\[0.2cm] M_2(x)=EI\dfrac{d^2 v_2}{dx^2}(x) & x_1 \leq x \leq x_2 \\[0.2cm] M_3(x)=EI\dfrac{d^2 v_3}{dx^2}(x) & x_2 \leq x \leq x_3 \\[0.2cm] M_4(x)=EI\dfrac{d^2 v_4}{dx^2}(x) & x_3 \leq x \leq x_4 \\[0.2cm] M_5(x)=EI\dfrac{d^2 v_5}{dx^2}(x) & x_4 \leq x \leq x_5 \\[0.2cm] M_6(x)=EI\dfrac{d^2 v_6}{dx^2}(x) \qquad & x_5 \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>M(x)=EI\dfrac{d^2 v}{dx^2}(x)= \begin{cases}M_1(x)=EI\dfrac{d^2 v_1}{dx^2}(x) & 0<x \leq x_1 \\[0.2cm] M_2(x)=EI\dfrac{d^2 v_2}{dx^2}(x) & x_1 \leq x \leq x_2 \\[0.2cm] M_3(x)=EI\dfrac{d^2 v_3}{dx^2}(x) & x_2 \leq x \leq x_3 \\[0.2cm] M_4(x)=EI\dfrac{d^2 v_4}{dx^2}(x) & x_3 \leq x \leq x_4 \\[0.2cm] M_5(x)=EI\dfrac{d^2 v_5}{dx^2}(x) & x_4 \leq x \leq x_5 \\[0.2cm] M_6(x)=EI\dfrac{d^2 v_6}{dx^2}(x) \qquad & x_5 \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (65) |
|} | |} | ||
| Line 1,054: | Line 1,086: | ||
| style="text-align: center;" | <math>V(x)=-EI\dfrac{d^3 v}{dx^3}(x)= \begin{cases}V_1(x)=-EI\dfrac{d^3 v_1}{dx^3}(x) & 0<x \leq x_1 \\[0.2cm] V_2(x)=-EI\dfrac{d^3 v_2}{dx^3}(x) & x_1 \leq x \leq x_2 \\[0.2cm] V_3(x)=-EI\dfrac{d^3 v_3}{dx^3}(x) & x_2 \leq x \leq x_3 \\[0.2cm] V_4(x)=-EI\dfrac{d^3 v_4}{dx^3}(x) & x_3 \leq x \leq x_4 \\[0.2cm] V_5(x)=-EI\dfrac{d^3 v_5}{dx^3}(x) & x_4 \leq x \leq x_5 \\[0.2cm] V_6(x)=-EI\dfrac{d^3 v_6}{dx^3}(x) \qquad & x_5 \leq x < L \end{cases} </math> | | style="text-align: center;" | <math>V(x)=-EI\dfrac{d^3 v}{dx^3}(x)= \begin{cases}V_1(x)=-EI\dfrac{d^3 v_1}{dx^3}(x) & 0<x \leq x_1 \\[0.2cm] V_2(x)=-EI\dfrac{d^3 v_2}{dx^3}(x) & x_1 \leq x \leq x_2 \\[0.2cm] V_3(x)=-EI\dfrac{d^3 v_3}{dx^3}(x) & x_2 \leq x \leq x_3 \\[0.2cm] V_4(x)=-EI\dfrac{d^3 v_4}{dx^3}(x) & x_3 \leq x \leq x_4 \\[0.2cm] V_5(x)=-EI\dfrac{d^3 v_5}{dx^3}(x) & x_4 \leq x \leq x_5 \\[0.2cm] V_6(x)=-EI\dfrac{d^3 v_6}{dx^3}(x) \qquad & x_5 \leq x < L \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (66) |
|} | |} | ||
| − | ==5 Ejemplos== | + | ==5. Ejemplos== |
===5.1 Viga sobre fundación flexible simplemente apoyada sometida a una carga externa sinusoidal=== | ===5.1 Viga sobre fundación flexible simplemente apoyada sometida a una carga externa sinusoidal=== | ||
| − | Resolver la viga sobre fundación flexible presentada en la | + | Resolver la viga sobre fundación flexible presentada en la [[#img-11|Figura 11]] empleando la función de Green de la [[#img-5b|Figura 5b]]. |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | |
| + | <div id='img-11'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 50%;" | ||
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"|[[Image:Review_921349416580-FiguraEjemplo1.png|420px|Viga sobre fundación flexible simplemente apoyada sometida a una carga externa sinusoidal.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 11 | + | | colspan="1" style="padding:10px;"| '''Figura 11'''. Viga sobre fundación flexible simplemente apoyada sometida a una carga externa sinusoidal |
|} | |} | ||
| − | |||
| − | |||
| − | + | ====<u>Solución</u>==== | |
| − | + | '''Funciones de Green a emplear''' | |
| − | + | Como se indicó en el enunciado, la función de Green a emplear en la solución de este problema es <math display="inline">G_{yy}^{SS}(x,\xi )</math>, la cual se presenta en la ecuación [[#eq-17|(17)]]. | |
| − | <span id="eq- | + | '''Cálculo del campo de desplazamiento''' |
| + | |||
| + | La carga externa distribuida sobre la viga está definida por medio de la siguiente función: | ||
| + | |||
| + | <span id="eq-67"></span> | ||
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,086: | Line 1,122: | ||
| style="text-align: center;" | <math>q(x)=-Q\sin \left(\pi \dfrac{x}{L} \right)\qquad 0<x<L </math> | | style="text-align: center;" | <math>q(x)=-Q\sin \left(\pi \dfrac{x}{L} \right)\qquad 0<x<L </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (67) |
|} | |} | ||
Ahora, debido a que la viga sobre fundación flexible empleada para la función de Green tiene los mismos tramos, condiciones de frontera y de continuidad que aquella a analizar, su campo de desplazamiento se obtiene de forma inmediata solo mediante la siguiente integral: | Ahora, debido a que la viga sobre fundación flexible empleada para la función de Green tiene los mismos tramos, condiciones de frontera y de continuidad que aquella a analizar, su campo de desplazamiento se obtiene de forma inmediata solo mediante la siguiente integral: | ||
| − | <span id="eq- | + | <span id="eq-68"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,101: | Line 1,137: | ||
| style="text-align: center;" | <math> =-\dfrac{QL^4}{EI}\dfrac{1}{4(\lambda L)^4+\pi ^4}\sin \left(\pi \dfrac{x}{L} \right)\qquad 0<x<L </math> | | style="text-align: center;" | <math> =-\dfrac{QL^4}{EI}\dfrac{1}{4(\lambda L)^4+\pi ^4}\sin \left(\pi \dfrac{x}{L} \right)\qquad 0<x<L </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (68) |
|} | |} | ||
La cual se puede entender como el cálculo del desplazamiento en un punto <math display="inline">x</math> de la viga sobre fundación flexible como la suma del desplazamiento en dicho punto debido a la carga externa <math display="inline">q(\xi )</math> aplicada en cada uno de sus puntos <math display="inline">(0<\xi{<}L)</math>. | La cual se puede entender como el cálculo del desplazamiento en un punto <math display="inline">x</math> de la viga sobre fundación flexible como la suma del desplazamiento en dicho punto debido a la carga externa <math display="inline">q(\xi )</math> aplicada en cada uno de sus puntos <math display="inline">(0<\xi{<}L)</math>. | ||
| − | + | '''Cálculo del campo de la fuerza que el suelo ejerce sobre la viga y de fuerzas internas''' | |
| − | A partir de [[#eq-3|(3)]] y [[#eq-6|(6)]] la fuerza que el suelo ejerce sobre la viga y las fuerzas internas en esta se calculan respectivamente como: | + | A partir de las ecuaciones [[#eq-3|(3)]] y [[#eq-6|(6)]], la fuerza que el suelo ejerce sobre la viga y las fuerzas internas en esta se calculan respectivamente como: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,116: | Line 1,152: | ||
|- | |- | ||
| style="text-align: center;" | <math>f_S(x)=-kv(x)=\dfrac{kQL^4}{EI}\dfrac{1}{4(\lambda L)^4+\pi ^4}\sin \left(\pi \dfrac{x}{L} \right) \qquad 0<x<L </math> | | style="text-align: center;" | <math>f_S(x)=-kv(x)=\dfrac{kQL^4}{EI}\dfrac{1}{4(\lambda L)^4+\pi ^4}\sin \left(\pi \dfrac{x}{L} \right) \qquad 0<x<L </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (69a) |
|- | |- | ||
| − | | style="text-align: center;" | <math>M(x)=EI\dfrac{d^2 v}{dx^2}(x)=QL^2\dfrac{\pi ^2}{4(\lambda L)^4+\pi ^4}\sin \left(\pi \dfrac{x}{L} \right) \qquad 0<x<L </math> | + | | style="text-align: center;padding:7px;" | <math> M(x)=EI\dfrac{d^2 v}{dx^2}(x)=QL^2\dfrac{\pi ^2}{4(\lambda L)^4+\pi ^4}\sin \left(\pi \dfrac{x}{L} \right) \qquad 0<x<L </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (69b) |
|- | |- | ||
| − | | style="text-align: center;" | <math>V(x)=-EI\dfrac{d^3 v}{dx^3}(x)=-QL\dfrac{\pi ^3}{4(\lambda L)^4+\pi ^4}\cos \left(\pi \dfrac{x}{L} \right) \qquad 0<x<L </math> | + | | style="text-align: center;padding:7px;" | <math> V(x)=-EI\dfrac{d^3 v}{dx^3}(x)=-QL\dfrac{\pi ^3}{4(\lambda L)^4+\pi ^4}\cos \left(\pi \dfrac{x}{L} \right) \qquad 0<x<L </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (69c) |
|} | |} | ||
|} | |} | ||
| Line 1,132: | Line 1,168: | ||
===5.2 Viga sobre fundación flexible empotrada - libre sometida a una carga distribuida constante=== | ===5.2 Viga sobre fundación flexible empotrada - libre sometida a una carga distribuida constante=== | ||
| − | Resolver la viga sobre fundación flexible presentada en la | + | Resolver la viga sobre fundación flexible presentada en la [[#img-12|Figura 12]] empleando: a) la función de Green empotrada libre presentada en la sección [[#3.1.3 Viga sobre fundación flexible finita empotrada - libre|3.1.3]] y b) la función de Green de libre-libre presentada en la sección [[#3.1.1 Viga sobre fundación flexible finita libre - libre|3.1.1]]. |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | |
| + | <div id='img-12'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 40%;" | ||
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"| [[Image:Review_921349416580-Figura3Ejemplo2.png|360px|Viga sobre fundación flexible empotrada-libre sometida a una carga externa distribuida constante.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 12 | + | | colspan="1" style="padding:10px;"| '''Figura 12'''. Viga sobre fundación flexible empotrada-libre sometida a una carga externa distribuida constante |
|} | |} | ||
| − | |||
| − | ==Definición de la carga externa | + | ====<u>'''Solución'''</u>==== |
| + | |||
| + | '''Definición de la carga externa''' | ||
La carga externa que actúa sobre la viga está definida por la siguiente función: | La carga externa que actúa sobre la viga está definida por la siguiente función: | ||
| Line 1,152: | Line 1,191: | ||
| style="text-align: center;" | <math>q(x)=-Q \qquad 0<x<L </math> | | style="text-align: center;" | <math>q(x)=-Q \qquad 0<x<L </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (70) |
|} | |} | ||
| − | ====5.2.1 Solución empleando la función de Green de la viga sobre fundación flexible empotrada libre ( | + | ====5.2.1 Solución empleando la función de Green de la viga sobre fundación flexible empotrada libre ([[#img-5c|Figura 5c]])==== |
| − | + | '''Funciones de Green a emplear''' | |
| − | Para esta alternativa la función de Green a emplear es <math display="inline">G_{yy}^{EL}(x,\xi )</math>, la cual se presenta en la ecuación [[#eq- | + | Para esta alternativa la función de Green a emplear es <math display="inline">G_{yy}^{EL}(x,\xi )</math>, la cual se presenta en la ecuación [[#eq-23|(23)]]. |
| − | + | '''Cálculo del campo de desplazamiento''' | |
| − | + | Debido a que la viga de la función de Green que a emplear tienen las mismas condiciones de frontera que aquella a analizar, su campo de desplazamiento se calcula como: | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,172: | Line 1,211: | ||
| style="text-align: center;" | <math>v(x)=\int _0^L G_{yy}^{EL}(x,\xi )q(\xi )d\xi =\int _0^{x} G_{yy}^{EL2}(x,\xi )q(\xi )d\xi{+\int}_x^L G_{yy}^{EL1}(x,\xi ) q(\xi )d\xi </math> | | style="text-align: center;" | <math>v(x)=\int _0^L G_{yy}^{EL}(x,\xi )q(\xi )d\xi =\int _0^{x} G_{yy}^{EL2}(x,\xi )q(\xi )d\xi{+\int}_x^L G_{yy}^{EL1}(x,\xi ) q(\xi )d\xi </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> =-Q\left[\int _0^{x} G_{yy}^{ | + | | style="text-align: center;" | <math> =-Q\left[\int _0^{x} G_{yy}^{EL2}(x,\xi )d\xi{+\int}_x^L G_{yy}^{EL1}(x,\xi ) d\xi \right] </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (71) |
|} | |} | ||
El cual luego de realizar las integrales respectivas, da como resultado: | El cual luego de realizar las integrales respectivas, da como resultado: | ||
| − | <span id="eq- | + | <span id="eq-72"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,187: | Line 1,226: | ||
| style="text-align: center;" | <math>v(x)=-\dfrac{Q}{4EI\lambda ^4} \dfrac{f(x)}{\cos (2\lambda L)+\cosh (2\lambda L)+2} \qquad 0<x<L </math> | | style="text-align: center;" | <math>v(x)=-\dfrac{Q}{4EI\lambda ^4} \dfrac{f(x)}{\cos (2\lambda L)+\cosh (2\lambda L)+2} \qquad 0<x<L </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (72) |
|} | |} | ||
| − | + | donde | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,199: | Line 1,238: | ||
| style="text-align: center;" | <math>f(x)=\sin (\lambda x)\sinh[\lambda(2L-x)]-\sin[\lambda(2L-x)]\sinh (\lambda x)+2\cos (\lambda x)\cosh (\lambda x)+\cos (\lambda x)\cosh[\lambda (2L-x)] </math> | | style="text-align: center;" | <math>f(x)=\sin (\lambda x)\sinh[\lambda(2L-x)]-\sin[\lambda(2L-x)]\sinh (\lambda x)+2\cos (\lambda x)\cosh (\lambda x)+\cos (\lambda x)\cosh[\lambda (2L-x)] </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>+\cos[\lambda(2L-x)]\cosh (\lambda x)-2-\cos (2\lambda L)-\cosh (2\lambda L) </math> | + | | style="text-align: center;padding-top:7px;" | <math>+\cos[\lambda(2L-x)]\cosh (\lambda x)-2-\cos (2\lambda L)-\cosh (2\lambda L) </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (73) |
|} | |} | ||
'''Cálculo del campo de la fuerza que el suelo ejerce sobre la viga y de fuerzas internas''' | '''Cálculo del campo de la fuerza que el suelo ejerce sobre la viga y de fuerzas internas''' | ||
| − | A partir de [[#eq-3|(3)]] y empleando [[#eq- | + | A partir de la ecuación [[#eq-3|(3)]] y empleando la ecuación [[#eq-72|(72)]] se tiene que la fuerza que el suelo hace sobre la viga es: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,213: | Line 1,252: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>f_S(x)=\dfrac{Q}{4EI\lambda ^4} \dfrac{ | + | | style="text-align: center;" | <math>f_S(x)=\dfrac{Q \cdot k}{4EI\lambda ^4} \dfrac{f(x)}{\cos (2\lambda L)+\cosh (2\lambda L)+2} \qquad 0<x<L </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (74) |
|} | |} | ||
| − | Mientras que reemplazando [[#eq- | + | Mientras que, reemplazando la ecuación [[#eq-72|(72)]] en la ecuación [[#eq-6|(6)]], se obtiene que los campos de momento flector y fuerza cortante son respectivamente: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,225: | Line 1,264: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>M(x)=\dfrac{g(x)}{2\lambda ^2[\cos (2\lambda L)+\cosh (2\lambda L)+2]} | + | | style="text-align: center;" | <math>M(x)=\dfrac{g(x)}{2\lambda ^2[\cos (2\lambda L)+\cosh (2\lambda L)+2]} 0<x<L </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (75.a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> V(x)=\dfrac{h(x)}{\lambda [\cos (2\lambda L)+\cosh (2\lambda L)+2]} | + | | style="text-align: center;" | <math> V(x)=\dfrac{h(x)}{\lambda [\cos (2\lambda L)+\cosh (2\lambda L)+2]} 0<x<L </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (75.b) |
|} | |} | ||
|} | |} | ||
| − | + | donde | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,242: | Line 1,281: | ||
| style="text-align: center;" | <math>g(x)=Q \{ 2\sin (\lambda L)\sin[\lambda(L-x)]\cosh (\lambda x) -2\sin (\lambda L)\cos[\lambda (L-x)]\sinh (\lambda x)+3\sin (\lambda x)\sinh (\lambda x)</math> | | style="text-align: center;" | <math>g(x)=Q \{ 2\sin (\lambda L)\sin[\lambda(L-x)]\cosh (\lambda x) -2\sin (\lambda L)\cos[\lambda (L-x)]\sinh (\lambda x)+3\sin (\lambda x)\sinh (\lambda x)</math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> -\sin (\lambda x)\sinh[\lambda (2L-x)]-\cos(\lambda x)\cosh (\lambda x) +\cos (\lambda x)\cosh[\lambda (2L-x)]\} | + | | style="text-align: center;" | <math> -\sin (\lambda x)\sinh[\lambda (2L-x)]-\cos(\lambda x)\cosh (\lambda x) +\cos (\lambda x)\cosh[\lambda (2L-x)]\} </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (76) |
|} | |} | ||
| − | + | y | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,254: | Line 1,293: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>h(x)=Q\{ -\sin (\lambda x)\cosh (\lambda x)+\sin[\lambda(2L-x)]\cosh (\lambda x)-\cos (\lambda x)\sinh (\lambda x) +\cos (\lambda x)\sinh[\lambda (2L-x)] </math> | + | | style="text-align: center;" | <math>h(x)=Q\{ -\sin (\lambda x)\cosh (\lambda x)+\sin[\lambda(2L-x)]\cosh (\lambda x)-\cos (\lambda x)\sinh (\lambda x) +\cos (\lambda x)\sinh[\lambda (2L-x)] \} </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (77) |
|} | |} | ||
| − | ====5.2.2 Solución empleando la función de Green de la viga sobre fundación flexible libre libre ( | + | ====5.2.2 Solución empleando la función de Green de la viga sobre fundación flexible libre libre ([[#img-5a|Figura 5a]])==== |
| − | + | '''Funciones de Green a emplear''' | |
Para la solución de este problema se emplearán las siguientes funciones de Green: | Para la solución de este problema se emplearán las siguientes funciones de Green: | ||
| − | |||
| − | <math display="inline">G_{y\theta }^{LL}(x,\xi )</math>: Campo de desplazamientos de la viga sobre fundación flexible libre-libre sometida a un momento puntual unitario presentada en la | + | <math display="inline">G_{yy}^{LL}(x,\xi )</math>: Campo de desplazamientos de la viga sobre fundación flexible libre-libre sometida a una carga puntual unitaria presentada en la [[#img-5a|Figura 5a]] y cuyo valor se presenta en la ecuación [[#eq-17|(17)]]. |
| + | |||
| + | <math display="inline">G_{y\theta }^{LL}(x,\xi )</math>: Campo de desplazamientos de la viga sobre fundación flexible libre-libre sometida a un momento puntual unitario presentada en la [[#img-7a|Figura 7a]] y cuyo valor se presenta en la ecuación [[#eq-44|(44)]]. | ||
| + | |||
| + | <math display="inline">G_{\theta y}^{LL}(x,\xi )</math>: Campo de rotaciones de la viga sobre fundación flexible libre-libre sometida a una carga puntual unitaria presentada en la [[#img-5a|Figura 5a]]. | ||
| − | <math display="inline">G_{\theta | + | <math display="inline">G_{\theta \theta }(x,\xi )</math>: Campo de rotaciones de la viga sobre fundación flexible libre-libre sometida a un momento puntual unitario presentada en la [[#img-7a|Figura 7a]]. |
| − | |||
En este punto es importante resaltar que debido a que <math display="inline">G_{\theta y}^{LL}(x,\xi )</math>, <math display="inline">G_{y\theta }^{LL}(x,\xi )</math> y <math display="inline">G_{\theta \theta }^{LL}(x,\xi )</math> son derivadas de <math display="inline">G_{yy}^{LL}(x,\xi )</math>, en realidad es posible indicar que lo es necesario emplear está última, mientras que los tramos de las primeras se definen como: | En este punto es importante resaltar que debido a que <math display="inline">G_{\theta y}^{LL}(x,\xi )</math>, <math display="inline">G_{y\theta }^{LL}(x,\xi )</math> y <math display="inline">G_{\theta \theta }^{LL}(x,\xi )</math> son derivadas de <math display="inline">G_{yy}^{LL}(x,\xi )</math>, en realidad es posible indicar que lo es necesario emplear está última, mientras que los tramos de las primeras se definen como: | ||
| Line 1,280: | Line 1,321: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>G_{\theta y}^{LL}(x,\xi )=\dfrac{\partial G_{yy}^{LL}}{\partial x}(x,\xi )= \begin{cases}G_{\theta y}^{LL1}(x,\xi ) (x,\xi ) & 0 < x \leq \xi \\ G_{\theta y}^{LL2}(x,\xi )(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | + | | style="text-align: center;" | <math>G_{\theta y}^{LL}(x,\xi )=\dfrac{\partial G_{yy}^{LL}}{\partial x}(x,\xi )= \begin{cases}G_{\theta y}^{LL1}(x,\xi ) (x,\xi ) & 0 < x \leq \xi \\[.25cm] G_{\theta y}^{LL2}(x,\xi )(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> |
|} | |} | ||
|} | |} | ||
| Line 1,289: | Line 1,330: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>G_{y\theta }^{LL}(x,\xi )=\dfrac{\partial G_{yy}^{LL}}{\partial \xi }(x,\xi )= \begin{cases}G_{y\theta }^{LL1}(x,\xi ) & 0 < x \leq \xi \\ G_{y\theta }^{LL2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | + | | style="text-align: center;" | <math>G_{y\theta }^{LL}(x,\xi )=\dfrac{\partial G_{yy}^{LL}}{\partial \xi }(x,\xi )= \begin{cases}G_{y\theta }^{LL1}(x,\xi ) & 0 < x \leq \xi \\[.25cm] G_{y\theta }^{LL2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> |
|} | |} | ||
|} | |} | ||
| Line 1,298: | Line 1,339: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>G_{\theta \theta }^{LL}(x,\xi )=\dfrac{\partial ^2 G_{yy}^{LL}}{\partial x \partial \xi }(x,\xi )= \begin{cases}G_{\theta \theta }^{LL1}(x,\xi ) & 0 < x \leq \xi \\ G_{\theta \theta }^{LL2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> | + | | style="text-align: center;" | <math>G_{\theta \theta }^{LL}(x,\xi )=\dfrac{\partial ^2 G_{yy}^{LL}}{\partial x \partial \xi }(x,\xi )= \begin{cases}G_{\theta \theta }^{LL1}(x,\xi ) & 0 < x \leq \xi \\[.25cm] G_{\theta \theta }^{LL2}(x,\xi ) \qquad & \xi \leq x < L \end{cases} </math> |
|} | |} | ||
|} | |} | ||
| Line 1,310: | Line 1,351: | ||
<li>Segunda derivada derivada (o momento flector) igual a cero en <math display="inline">x=L</math>. </li> | <li>Segunda derivada derivada (o momento flector) igual a cero en <math display="inline">x=L</math>. </li> | ||
<li>Tercera derivada (o fuerza cortante) igual a cero en <math display="inline">x=L</math>. </li> | <li>Tercera derivada (o fuerza cortante) igual a cero en <math display="inline">x=L</math>. </li> | ||
| − | |||
</ol> | </ol> | ||
| − | |||
| − | + | Las cuales cuales no coinciden con aquellas que posee la viga sobre fundación flexible a estudiar ([[#img-12|Figura 12]]). | |
| − | Para poder hacer cumplir las condiciones de frontera del problema real, a la viga sobre fundación flexible libre-libre no solo se le debe agregar el efecto de la carga distribuida sino también aquel del momento y fuerza puntuales debidos al empotramiento en el extremo izquierdo de esta, así como el cumplimiento de las condiciones de desplazamiento y rotaciones nulos en <math display="inline">x=0</math> ( | + | '''Cálculo del campo de desplazamiento''' |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | |
| + | Para poder hacer cumplir las condiciones de frontera del problema real, a la viga sobre fundación flexible libre-libre no solo se le debe agregar el efecto de la carga distribuida sino también aquel del momento y fuerza puntuales debidos al empotramiento en el extremo izquierdo de esta, así como el cumplimiento de las condiciones de desplazamiento y rotaciones nulos en <math display="inline">x=0</math> ([[#img-13|Figura 13]]). | ||
| + | |||
| + | <div id='img-13'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 50%;" | ||
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"|[[Image:Review_921349416580-Figura4Ejemplo2.png|360px|Viga sobre fundación flexible en voladizo sometida a una carga externa distribuida constante.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 13 | + | | colspan="1" style="padding:10px;"| '''Figura 13'''. Viga sobre fundación flexible en voladizo sometida a una carga externa distribuida constante. |
|} | |} | ||
| + | |||
| + | |||
Con base en lo anterior, las dos ecuaciones a emplear para obtener el valor de las reacciones de la viga sobre fundación flexible son: | Con base en lo anterior, las dos ecuaciones a emplear para obtener el valor de las reacciones de la viga sobre fundación flexible son: | ||
| Line 1,332: | Line 1,377: | ||
|- | |- | ||
| style="text-align: center;" | <math>v(0)=0=FY_1G_{yy}^{LL2}(0,0)+M_1G_{y\theta }^{LL2}(0,0)-Q\int _0^L G_{yy}^{LL1}(0,\xi )d\xi </math> | | style="text-align: center;" | <math>v(0)=0=FY_1G_{yy}^{LL2}(0,0)+M_1G_{y\theta }^{LL2}(0,0)-Q\int _0^L G_{yy}^{LL1}(0,\xi )d\xi </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (78a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \dfrac{dv}{dx}(0)=0=FY_1G_{\theta y}^{LL2}(0,0)+M_1G_{\theta \theta }^{LL2}(0,0)-Q\int _0^L G_{\theta y}^{LL1}(0,\xi )d\xi </math> | + | | style="text-align: center;padding-top:7px;" | <math> \dfrac{dv}{dx}(0)=0=FY_1G_{\theta y}^{LL2}(0,0)+M_1G_{\theta \theta }^{LL2}(0,0)-Q\int _0^L G_{\theta y}^{LL1}(0,\xi )d\xi </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (78b) |
|} | |} | ||
|} | |} | ||
| − | De cuya solución se obtiene: <span id="eq- | + | De cuya solución se obtiene: <span id="eq-79"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,347: | Line 1,392: | ||
|- | |- | ||
| style="text-align: center;" | <math>FY_1=-\dfrac{Q}{\lambda } \dfrac{\sin (2\lambda L)+\sinh (2\lambda L)}{\cos (2\lambda L)+\cosh (2\lambda L)+2} </math> | | style="text-align: center;" | <math>FY_1=-\dfrac{Q}{\lambda } \dfrac{\sin (2\lambda L)+\sinh (2\lambda L)}{\cos (2\lambda L)+\cosh (2\lambda L)+2} </math> | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (79a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> M_1=\dfrac{Q}{2\lambda ^2} \dfrac{\cos (2\lambda L)-\cosh (2\lambda L)}{\cos (2\lambda L)+\cosh (2\lambda L)+2} </math> | + | | style="text-align: center;padding-top:7px;" | <math> M_1=\dfrac{Q}{2\lambda ^2} \dfrac{\cos (2\lambda L)-\cosh (2\lambda L)}{\cos (2\lambda L)+\cosh (2\lambda L)+2} </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (79b) |
|} | |} | ||
|} | |} | ||
| Line 1,363: | Line 1,408: | ||
| style="text-align: center;" | <math>v(x)=FY_1G_{yy}^{LL2}(x,0)+M_1G_{y\theta }^{LL2}(x,0)-Q\left[\int _0^x G_{yy}^{LL2}(0,\xi )d\xi{+\int}_x^L G_{yy}^{LL1}(0,\xi )d\xi \right] </math> | | style="text-align: center;" | <math>v(x)=FY_1G_{yy}^{LL2}(x,0)+M_1G_{y\theta }^{LL2}(x,0)-Q\left[\int _0^x G_{yy}^{LL2}(0,\xi )d\xi{+\int}_x^L G_{yy}^{LL1}(0,\xi )d\xi \right] </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (80) |
|} | |} | ||
| − | El cual luego de realizar las integrales y usando [[#eq- | + | El cual luego de realizar las integrales y usando la ecuación [[#eq-79|(79)]], da como resultado: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,375: | Line 1,420: | ||
| style="text-align: center;" | <math>v(x)=-\dfrac{Q}{4EI\lambda ^4} \dfrac{f(x)}{\cos (2\lambda L)+\cosh (2\lambda L)+2} \qquad 0<x<L </math> | | style="text-align: center;" | <math>v(x)=-\dfrac{Q}{4EI\lambda ^4} \dfrac{f(x)}{\cos (2\lambda L)+\cosh (2\lambda L)+2} \qquad 0<x<L </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (81) |
|} | |} | ||
| − | + | donde | |
| − | <span id="eq- | + | <span id="eq-82"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,390: | Line 1,435: | ||
| style="text-align: center;" | <math>+\cos[\lambda(2L-x)]\cosh (\lambda x)-2-\cos (2\lambda L)-\cosh (2\lambda L) </math> | | style="text-align: center;" | <math>+\cos[\lambda(2L-x)]\cosh (\lambda x)-2-\cos (2\lambda L)-\cosh (2\lambda L) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (82) |
|} | |} | ||
| − | + | '''Cálculo del campo de la fuerza que el suelo ejerce sobre la viga y de fuerzas internas''' | |
| − | Dado que el campo de desplazamiento presentado en [[#eq- | + | Dado que el campo de desplazamiento presentado en la ecuación [[#eq-82|(82)]] es igual al presentado en la ecuación [[#eq-72|(72)]] la fuerza que el suelo ejerce sobre la viga y las fuerzas internas en esta serán también iguales con ambas alternativas. |
Desde el siguiente enlace se puede descargar el código de Python con la solución de este ejemplo: | Desde el siguiente enlace se puede descargar el código de Python con la solución de este ejemplo: | ||
| Line 1,403: | Line 1,448: | ||
===5.3 Viga sobre fundación flexible libre - libre sometida a cargas puntuales y distribuidas así como a momento puntual=== | ===5.3 Viga sobre fundación flexible libre - libre sometida a cargas puntuales y distribuidas así como a momento puntual=== | ||
| − | Resolver la viga sobre fundación flexible presentada en la | + | Resolver la viga sobre fundación flexible presentada en la [[#img-14|Figura 14]] empleando la función de Green libre-libre presentada en la sección [[#3.1.1 Viga sobre fundación flexible finita libre - libre|3.1.1]]. |
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | |
| + | <div id='img-14'></div> | ||
| + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 55%;" | ||
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"|[[Image:Review_921349416580-Figura1Ejemplo3.png|420px|Viga sobre fundación flexible simplemente libre libre sometida a cargas puntuales y distribuidas así como a momento puntual.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" | '''Figura 14 | + | | colspan="1" style="padding:10px;"| '''Figura 14'''. Viga sobre fundación flexible simplemente libre libre sometida a cargas puntuales y distribuidas, así como a momento puntual |
|} | |} | ||
| + | |||
| + | |||
'''Funciones de Green a emplear''' | '''Funciones de Green a emplear''' | ||
| − | Para la solución de este ejercicio se emplearán las funciones de Green <math display="inline">G_{yy}^{LL}(x,\xi )</math> y <math display="inline">G_{y\theta }^{LL}(x,\xi )</math>, las cuales se presentan en las ecuaciones [[#eq-9|(9)]] y [[#eq- | + | Para la solución de este ejercicio se emplearán las funciones de Green <math display="inline">G_{yy}^{LL}(x,\xi )</math> y <math display="inline">G_{y\theta }^{LL}(x,\xi )</math>, las cuales se presentan en las ecuaciones [[#eq-9|(9)]] y [[#eq-42|(42)]], respectivamente. |
| − | + | '''Cálculo del campo de desplazamiento''' | |
El campo de desplazamiento de la viga sobre fundación flexible tiene 4 tramos, los cuales se definen como: | El campo de desplazamiento de la viga sobre fundación flexible tiene 4 tramos, los cuales se definen como: | ||
| − | <span id="eq- | + | <span id="eq-83"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,426: | Line 1,475: | ||
| style="text-align: center;" | <math>v(x)= \begin{cases}v_1(x) & 0 < x \leq 1\hbox{ m} \\ v_2(x) & 1\hbox{ m} \leq x \leq 4\hbox{ m} \\ v_3(x) & 4\hbox{ m} \leq x \leq 5\hbox{ m} \\ v_4(x) & 5\hbox{ m} \leq x < 10\hbox{ m} \end{cases} </math> | | style="text-align: center;" | <math>v(x)= \begin{cases}v_1(x) & 0 < x \leq 1\hbox{ m} \\ v_2(x) & 1\hbox{ m} \leq x \leq 4\hbox{ m} \\ v_3(x) & 4\hbox{ m} \leq x \leq 5\hbox{ m} \\ v_4(x) & 5\hbox{ m} \leq x < 10\hbox{ m} \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (83) |
|} | |} | ||
| Line 1,438: | Line 1,487: | ||
| style="text-align: center;" | <math>v_1(x)=-250G_{yy}^{LL1}(x,1)-100G_{y\theta }^{LL1}(x,4)-200\int _5^{10}G_{yy}^{LL1}(x,\xi )d\xi </math> | | style="text-align: center;" | <math>v_1(x)=-250G_{yy}^{LL1}(x,1)-100G_{y\theta }^{LL1}(x,4)-200\int _5^{10}G_{yy}^{LL1}(x,\xi )d\xi </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (84) |
|} | |} | ||
| − | <span id="eq- | + | <span id="eq-85"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,451: | Line 1,500: | ||
| style="text-align: center;" | <math> -1.716465\times 10^{-3}\cos (\lambda x)\cosh (\lambda x) </math> | | style="text-align: center;" | <math> -1.716465\times 10^{-3}\cos (\lambda x)\cosh (\lambda x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (85) |
|} | |} | ||
| Line 1,461: | Line 1,510: | ||
| style="text-align: center;" | <math>v_2(x)=-250G_{yy}^{LL2}(x,1)-100G_{y\theta }^{LL1}(x,4)-200\int _5^{10}G_{yy}^{LL1}(x,\xi )d\xi </math> | | style="text-align: center;" | <math>v_2(x)=-250G_{yy}^{LL2}(x,1)-100G_{y\theta }^{LL1}(x,4)-200\int _5^{10}G_{yy}^{LL1}(x,\xi )d\xi </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (86) |
|} | |} | ||
| − | <span id="eq- | + | <span id="eq-87"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,474: | Line 1,523: | ||
| style="text-align: center;" | <math> +1.952791\times 10^{-3}\cos (\lambda x)\sinh (\lambda x) -1.595276\times 10^{-3}\cos (\lambda x)\cosh (\lambda x) </math> | | style="text-align: center;" | <math> +1.952791\times 10^{-3}\cos (\lambda x)\sinh (\lambda x) -1.595276\times 10^{-3}\cos (\lambda x)\cosh (\lambda x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (87) |
|} | |} | ||
| Line 1,484: | Line 1,533: | ||
| style="text-align: center;" | <math>v_3(x)=-250G_{yy}^{LL2}(x,1)-100G_{y\theta }^{LL2}(x,4)-200\int _5^{10}G_{yy}^{LL1}(x,\xi )d\xi </math> | | style="text-align: center;" | <math>v_3(x)=-250G_{yy}^{LL2}(x,1)-100G_{y\theta }^{LL2}(x,4)-200\int _5^{10}G_{yy}^{LL1}(x,\xi )d\xi </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (88) |
|} | |} | ||
| − | <span id="eq- | + | <span id="eq-89"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,497: | Line 1,546: | ||
| style="text-align: center;" | <math> -2.305245\times 10^{-4}\cos (\lambda x)\sinh (\lambda x) +4.693530\times 10^{-4}\cos (\lambda x)\cosh (\lambda x) </math> | | style="text-align: center;" | <math> -2.305245\times 10^{-4}\cos (\lambda x)\sinh (\lambda x) +4.693530\times 10^{-4}\cos (\lambda x)\cosh (\lambda x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (89) |
|} | |} | ||
| Line 1,507: | Line 1,556: | ||
| style="text-align: center;" | <math>v_4(x)=-250G_{yy}^{LL2}(x,1)-100G_{y\theta }^{LL2}(x,4)-200\int _5^{x}G_{yy}^{LL2}(x,\xi )d\xi -200\int _x^{10}G_{yy}^{LL1}(x,\xi )d\xi </math> | | style="text-align: center;" | <math>v_4(x)=-250G_{yy}^{LL2}(x,1)-100G_{y\theta }^{LL2}(x,4)-200\int _5^{x}G_{yy}^{LL2}(x,\xi )d\xi -200\int _x^{10}G_{yy}^{LL1}(x,\xi )d\xi </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (90) |
|} | |} | ||
| − | <span id="eq- | + | <span id="eq-91"></span> |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
|- | |- | ||
| Line 1,522: | Line 1,571: | ||
| style="text-align: center;" | <math> -3.636363\times 10^{-3} </math> | | style="text-align: center;" | <math> -3.636363\times 10^{-3} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (91) |
|} | |} | ||
| − | Como resumen de lo anterior, en la | + | Como resumen de lo anterior, en la [[#img-15|Figura 15]] se presenta la gráfica del campo de desplazamiento en toda la viga. |
| + | |||
| + | <div id='img-15a'></div> | ||
<div id='img-15b'></div> | <div id='img-15b'></div> | ||
<div id='img-15'></div> | <div id='img-15'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;" |
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"|[[Image:Review_921349416580-CampoDesplazamientoDefinitivoEjemplo3.png|400px|Campo de desplazamiento.]] |
| − | |[[Image: | + | |style="padding:10px;"|[[Image:Review_921349416580-CampoFuerzaSueloVigaDefinitivoEjemplo3.png|400px|Campo de la fuerza que el suelo le ejerce a la viga.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) Campo de desplazamiento | + | | (a) Campo de desplazamiento |
| − | | (b) Campo de la fuerza que el suelo le ejerce a la viga | + | | (b) Campo de la fuerza que el suelo le ejerce a la viga |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 15 | + | | colspan="2" style="padding:10px;"| '''Figura 15'''. Campos de desplazamiento y fuerza que el suelo ejerce sobre la viga |
|} | |} | ||
| + | |||
'''Cálculo de la fuerza distribuida que el suelo realiza sobre la viga''' | '''Cálculo de la fuerza distribuida que el suelo realiza sobre la viga''' | ||
| Line 1,547: | Line 1,599: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>f_S(x)= \begin{cases}f_S^1(x) & 0 < x \leq 1\hbox{ m} \\ f_S^2(x) & 1\hbox{ m} \leq x \leq 4\hbox{ m} \\ f_S^3(x) & 4\hbox{ m} \leq x \leq 5\hbox{ m} \\ f_S^4(x) & 5\hbox{ m} \leq x < 10\hbox{ m} \end{cases} </math> | + | | style="text-align: center;" | <math>f_S(x)=-kv(x)= \begin{cases}f_S^1(x) & 0 < x \leq 1\hbox{ m} \\ f_S^2(x) & 1\hbox{ m} \leq x \leq 4\hbox{ m} \\ f_S^3(x) & 4\hbox{ m} \leq x \leq 5\hbox{ m} \\ f_S^4(x) & 5\hbox{ m} \leq x < 10\hbox{ m} \end{cases} </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (92) |
|} | |} | ||
| − | + | donde | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,561: | Line 1,613: | ||
| style="text-align: center;" | <math>f_S^1(x)=- 18.696111\sin (\lambda x)\cosh (\lambda x)-18.696111\cos (\lambda x)\sinh (\lambda x) +94.405583\cos (\lambda x)\cosh (\lambda x) </math> | | style="text-align: center;" | <math>f_S^1(x)=- 18.696111\sin (\lambda x)\cosh (\lambda x)-18.696111\cos (\lambda x)\sinh (\lambda x) +94.405583\cos (\lambda x)\cosh (\lambda x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (93) |
|} | |} | ||
| Line 1,573: | Line 1,625: | ||
| style="text-align: center;" | <math> -107.403483\cos (\lambda x)\sinh (\lambda x)+87.740186\cos (\lambda x)\cosh (\lambda x) </math> | | style="text-align: center;" | <math> -107.403483\cos (\lambda x)\sinh (\lambda x)+87.740186\cos (\lambda x)\cosh (\lambda x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (94) |
|} | |} | ||
| Line 1,585: | Line 1,637: | ||
| style="text-align: center;" | <math> +12.678850\cos (\lambda x)\sinh (\lambda x)-25.814414\cos (\lambda x)\cosh (\lambda x) </math> | | style="text-align: center;" | <math> +12.678850\cos (\lambda x)\sinh (\lambda x)-25.814414\cos (\lambda x)\cosh (\lambda x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (95) |
|} | |} | ||
| Line 1,597: | Line 1,649: | ||
| style="text-align: center;" | <math> +89.783516\cos[\lambda (x-5)]\sinh[\lambda (x-5)]-93.986929\cos[\lambda (x-5)]\cosh[\lambda (x-5)]+ 200 </math> | | style="text-align: center;" | <math> +89.783516\cos[\lambda (x-5)]\sinh[\lambda (x-5)]-93.986929\cos[\lambda (x-5)]\cosh[\lambda (x-5)]+ 200 </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (96) |
|} | |} | ||
| Line 1,607: | Line 1,659: | ||
{| style="text-align: left; margin:auto;width: 100%;" | {| style="text-align: left; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | style="text-align: center;" | <math>\sum FY =-250-200 \cdot 5+\int _0^{10} f_S(x)dx \approx 0 | + | | style="text-align: center;" | <math>\sum FY =-250-200 \cdot 5+\int _0^{10} f_S(x)dx \approx 0</math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (97a) |
|- | |- | ||
| − | | style="text-align: center;" | <math> \sum M_1=-250 \cdot 1-100-200 \cdot 7.5+\int _0^{10} f_S(x)\cdot x dx \approx 0 | + | | style="text-align: center;padding-top:7px;" | <math> \sum M_1=-250 \cdot 1-100-200 \cdot 7.5+\int _0^{10} f_S(x)\cdot x dx \approx 0 </math> |
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (97b) |
|} | |} | ||
|} | |} | ||
| − | + | '''Cálculo de los campos de fuerzas internas''' | |
A continuación se calculan las fuerzas internas en la viga a partir de su campo de desplazamiento. | A continuación se calculan las fuerzas internas en la viga a partir de su campo de desplazamiento. | ||
| Line 1,621: | Line 1,673: | ||
<u>Campo de momento flector</u> | <u>Campo de momento flector</u> | ||
| − | A partir del campo de desplazamiento y empleando [[#eq-6.a|( | + | A partir del campo de desplazamiento y empleando la ecuación [[#eq-6.a|(6a)]], el campo de momento flector se calcula como: |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,630: | Line 1,682: | ||
| style="text-align: center;" | <math>M(x)=EI\dfrac{d^2 v}{dx^2}(x)= \begin{cases}M_1(x) & 0 < x \leq 1\hbox{ m} \\ M_2(x) & 1\hbox{ m} \leq x < 4\hbox{ m} \\ M_3(x) & 4\hbox{ m} < x \leq 5\hbox{ m} \\ M_4(x) & 5\hbox{ m} \leq x < 10\hbox{ m} \end{cases} </math> | | style="text-align: center;" | <math>M(x)=EI\dfrac{d^2 v}{dx^2}(x)= \begin{cases}M_1(x) & 0 < x \leq 1\hbox{ m} \\ M_2(x) & 1\hbox{ m} \leq x < 4\hbox{ m} \\ M_3(x) & 4\hbox{ m} < x \leq 5\hbox{ m} \\ M_4(x) & 5\hbox{ m} \leq x < 10\hbox{ m} \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (98) |
|} | |} | ||
| − | + | donde | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,642: | Line 1,694: | ||
| style="text-align: center;" | <math>M_1(x)=236.013957\sin (\lambda x)\sinh (\lambda x) - 46.740277\sin (\lambda x)\cosh (\lambda x) + 46.740277\cos (\lambda x)\sinh (\lambda x) </math> | | style="text-align: center;" | <math>M_1(x)=236.013957\sin (\lambda x)\sinh (\lambda x) - 46.740277\sin (\lambda x)\cosh (\lambda x) + 46.740277\cos (\lambda x)\sinh (\lambda x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (99) |
|} | |} | ||
| Line 1,652: | Line 1,704: | ||
| style="text-align: center;" | <math>M_2(x)=219.350465\sin (\lambda x)\sinh (\lambda x) - 268.508707\sin (\lambda x)\cosh (\lambda x) - 286.781862\cos (\lambda x)\sinh (\lambda x) </math> | | style="text-align: center;" | <math>M_2(x)=219.350465\sin (\lambda x)\sinh (\lambda x) - 268.508707\sin (\lambda x)\cosh (\lambda x) - 286.781862\cos (\lambda x)\sinh (\lambda x) </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> +249.66668430318\cos (\lambda x)\cosh (\lambda x) </math> | + | | style="text-align: center;padding-top:7px;" | <math> +249.66668430318\cos (\lambda x)\cosh (\lambda x) </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (100) |
|} | |} | ||
| Line 1,664: | Line 1,716: | ||
| style="text-align: center;" | <math>M_3(x)=-64.536036\sin (\lambda x)\sinh (\lambda x) + 31.697125\sin (\lambda x)\cosh (\lambda x) - 223.877936\cos (\lambda x)\sinh (\lambda x) </math> | | style="text-align: center;" | <math>M_3(x)=-64.536036\sin (\lambda x)\sinh (\lambda x) + 31.697125\sin (\lambda x)\cosh (\lambda x) - 223.877936\cos (\lambda x)\sinh (\lambda x) </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> +183.146701\cos (\lambda x)\cosh (\lambda x) </math> | + | | style="text-align: center;padding-top:7px;" | <math> +183.146701\cos (\lambda x)\cosh (\lambda x) </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (101) |
|} | |} | ||
| Line 1,676: | Line 1,728: | ||
| style="text-align: center;" | <math>M_4(x)=-234.967314\sin=[\lambda (x-5)]\sinh[\lambda (x-5)] +224.458790\sin[\lambda (x-5)]\cosh[\lambda (x-5)]</math> | | style="text-align: center;" | <math>M_4(x)=-234.967314\sin=[\lambda (x-5)]\sinh[\lambda (x-5)] +224.458790\sin[\lambda (x-5)]\cosh[\lambda (x-5)]</math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> +6.135067\cos[\lambda (x-5)]\sinh[\lambda (x-5)] -12.625633\cos[\lambda (x-5)]\cosh[\lambda (x-5)] </math> | + | | style="text-align: center;padding-top:7px;" | <math> +6.135067\cos[\lambda (x-5)]\sinh[\lambda (x-5)] -12.625633\cos[\lambda (x-5)]\cosh[\lambda (x-5)] </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (102) |
|} | |} | ||
| − | De forma gráfica, el campo de momento flector se presenta en la | + | De forma gráfica, el campo de momento flector se presenta en la [[#img-16|Figura 16]]. |
<u>Campo de fuerza cortante</u> | <u>Campo de fuerza cortante</u> | ||
| − | Mientras que el campo de fuerza cortante se calcula a partir del campo de desplazamiento como (ver [[#eq-6.b|( | + | Mientras que el campo de fuerza cortante se calcula a partir del campo de desplazamiento como (ver ecuación [[#eq-6.b|(6b)]]): |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,694: | Line 1,746: | ||
| style="text-align: center;" | <math>V(x)=-EI\dfrac{d^3 v}{dx^3}(x)= \begin{cases}V_1(x) & 0 < x < 1\hbox{ m} \\ V_2(x) & 1\hbox{ m} < x \leq 4\hbox{ m} \\ V_3(x) & 4\hbox{ m} \leq x \leq 5\hbox{ m} \\ V_4(x) & 5\hbox{ m} \leq x < 10\hbox{ m} \end{cases} </math> | | style="text-align: center;" | <math>V(x)=-EI\dfrac{d^3 v}{dx^3}(x)= \begin{cases}V_1(x) & 0 < x < 1\hbox{ m} \\ V_2(x) & 1\hbox{ m} < x \leq 4\hbox{ m} \\ V_3(x) & 4\hbox{ m} \leq x \leq 5\hbox{ m} \\ V_4(x) & 5\hbox{ m} \leq x < 10\hbox{ m} \end{cases} </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (103) |
|} | |} | ||
| − | + | donde | |
{| class="formulaSCP" style="width: 100%; text-align: left;" | {| class="formulaSCP" style="width: 100%; text-align: left;" | ||
| Line 1,706: | Line 1,758: | ||
| style="text-align: center;" | <math>V_1(x)=41.805775\sin (\lambda x)\sinh (\lambda x) - 105.548650\sin (\lambda x)\cosh (\lambda x) - 105.548650\cos (\lambda x)\sinh (\lambda x) </math> | | style="text-align: center;" | <math>V_1(x)=41.805775\sin (\lambda x)\sinh (\lambda x) - 105.548650\sin (\lambda x)\cosh (\lambda x) - 105.548650\cos (\lambda x)\sinh (\lambda x) </math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (104) |
|} | |} | ||
| Line 1,716: | Line 1,768: | ||
| style="text-align: center;" | <math>V_2(x)=-8.172003\sin (\lambda x)\sinh (\lambda x) + 13.557825\sin (\lambda x)\cosh (\lambda x) - 209.750846\cos (\lambda x)\sinh (\lambda x) </math> | | style="text-align: center;" | <math>V_2(x)=-8.172003\sin (\lambda x)\sinh (\lambda x) + 13.557825\sin (\lambda x)\cosh (\lambda x) - 209.750846\cos (\lambda x)\sinh (\lambda x) </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> + 248.333492\cos (\lambda x)\cosh (\lambda x) </math> | + | | style="text-align: center;padding-top:7px;" | <math> + 248.333492\cos (\lambda x)\cosh (\lambda x) </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (105) |
|} | |} | ||
| Line 1,728: | Line 1,780: | ||
| style="text-align: center;" | <math>V_3(x)=-114.296642\sin (\lambda x)\sinh (\lambda x) + 110.767087\sin (\lambda x)\cosh (\lambda x) - 53.044302\cos (\lambda x)\sinh (\lambda x) </math> | | style="text-align: center;" | <math>V_3(x)=-114.296642\sin (\lambda x)\sinh (\lambda x) + 110.767087\sin (\lambda x)\cosh (\lambda x) - 53.044302\cos (\lambda x)\sinh (\lambda x) </math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> + 85.945872\cos (\lambda x)\cosh (\lambda x) </math> | + | | style="text-align: center;padding-top:7px;" | <math> + 85.945872\cos (\lambda x)\cosh (\lambda x) </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (106) |
|} | |} | ||
| Line 1,740: | Line 1,792: | ||
| style="text-align: center;" | <math>V_4(x)=-97.637337\sin[\lambda (x-5)]\sinh[\lambda (x-5)] + 99.434222\sin[\lambda (x-5)]\cosh[\lambda (x-5)]</math> | | style="text-align: center;" | <math>V_4(x)=-97.637337\sin[\lambda (x-5)]\sinh[\lambda (x-5)] + 99.434222\sin[\lambda (x-5)]\cosh[\lambda (x-5)]</math> | ||
|- | |- | ||
| − | | style="text-align: center;" | <math> +110.72693z\cos[\lambda (x-5)]\sinh[\lambda (x-5)] -103.124708\cos[\lambda (x-5)]\cosh[\lambda (x-5)] </math> | + | | style="text-align: center;padding-top:7px;" | <math> +110.72693z\cos[\lambda (x-5)]\sinh[\lambda (x-5)] -103.124708\cos[\lambda (x-5)]\cosh[\lambda (x-5)] </math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (107) |
|} | |} | ||
| − | Como resumen de los anteriores resultados, en la | + | Como resumen de los anteriores resultados, en la [[#img-16|Figura 16]] se presenta de forma gráfica el campo de fuerza cortante en toda la viga. |
| + | |||
| + | <div id='img-16a'></div> | ||
<div id='img-16b'></div> | <div id='img-16b'></div> | ||
<div id='img-16'></div> | <div id='img-16'></div> | ||
| − | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: | + | {| class="floating_imageSCP" style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;" |
|- | |- | ||
| − | |[[Image: | + | |style="padding:10px;"|[[Image:Review_921349416580-CampoMomentoFlectorDefinitivoEjemplo3.png|450px|Momento flector.]] |
| − | |[[Image: | + | |style="padding:10px;"|[[Image:Review_921349416580-CampoCortanteDefinitivoEjemplo3.png|450px|Fuerza cortante.]] |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | (a) Momento flector | + | | (a) Momento flector |
| − | | (b) Fuerza cortante | + | | (b) Fuerza cortante |
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="2" | '''Figura 16 | + | | colspan="2" style="padding:10px;"| '''Figura 16'''. Campos de fuerzas internas |
|} | |} | ||
| + | |||
| + | |||
Desde el siguiente enlace se puede descargar el código de Python con la solución de este ejemplo: | Desde el siguiente enlace se puede descargar el código de Python con la solución de este ejemplo: | ||
| Line 1,770: | Line 1,826: | ||
<li>Se presenta una metodología basada 100% en las funciones de Green para el análisis de vigas sobre fundación flexible, con la cual se pueden calcular de forma exacta los campos de desplazamiento, momento flector, fuerza cortante y fuerza que el suelo ejerce sobre la viga. </li> | <li>Se presenta una metodología basada 100% en las funciones de Green para el análisis de vigas sobre fundación flexible, con la cual se pueden calcular de forma exacta los campos de desplazamiento, momento flector, fuerza cortante y fuerza que el suelo ejerce sobre la viga. </li> | ||
<li>Una vez implementado de forma numérica, el procedimiento presentado permite analizar de forma muy eficiente vigas sobre fundación flexible. </li> | <li>Una vez implementado de forma numérica, el procedimiento presentado permite analizar de forma muy eficiente vigas sobre fundación flexible. </li> | ||
| − | <li>Pese a que las funciones de Green más eficientes para resolver un determinado problema son aquellas que comparten las mismas condiciones de frontera (homogéneas) del problema en estudio, es posible su empleo para resolver problemas con diferentes condiciones de frontera. Esto se demuestra en el ejemplo | + | <li>Pese a que las funciones de Green más eficientes para resolver un determinado problema son aquellas que comparten las mismas condiciones de frontera (homogéneas) del problema en estudio, es posible su empleo para resolver problemas con diferentes condiciones de frontera. Esto se demuestra en el ejemplo 5.2.2 y le da mucha generalidad al procedimiento. </li> |
| + | <li>Se presentan varias funciones de Green para vigas sobre fundación flexible finitas e infinitas con diferentes condiciones de frontera, lo cual permite la implementación del método propuesto para gran cantidad e vigas sobre fundación flexible. </li> | ||
<li>Se presentan tres ejemplos con la solución de igual número de vigas sobre fundación flexible empleando la metodología presentada en este artículo, las cuales son la respuesta exacta de cada problema pues cumplen sus ecuaciones diferenciales gobernantes (equilibrio de cada punto), condiciones de frontera y equilibrio de toda la viga. </li> | <li>Se presentan tres ejemplos con la solución de igual número de vigas sobre fundación flexible empleando la metodología presentada en este artículo, las cuales son la respuesta exacta de cada problema pues cumplen sus ecuaciones diferenciales gobernantes (equilibrio de cada punto), condiciones de frontera y equilibrio de toda la viga. </li> | ||
</ol> | </ol> | ||
| − | === | + | ==Referencias== |
| + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> | ||
<div id="cite-1"></div> | <div id="cite-1"></div> | ||
| − | + | [[#citeF-1|[1]]] Reddy J.N. An introduction to the finite element method. McGraw-Hill, New York, Volume 1221, 2004. | |
| + | |||
| + | <div id=cite-2></div> | ||
| + | [[#citeF-2|[2]]] Molina-Villegas J.C., Giraldo H.N.D., Ochoa A.F.A. Analytical formulation of the stiffness method for 2D reticular structures using Green functions. Revista Internacional de Metodos Numericos para Calculo y Diseno en Ingenieria, 36:3, 2020. | ||
| − | <div id= | + | <div id=cite-3></div> |
| − | + | [[#citeF-3|[3]]] Stakgold I., Hols M.J. Green's functions and boundary value problems. John Wiley & Sons, Volume 99, 2011. | |
| − | <div id= | + | <div id=cite-4></div> |
| − | + | [[#citeF-4|[4]]] Duffy D.G. Green's functions with applications. CRC Press, 2015. | |
| − | <div id= | + | <div id=cite-5></div> |
| − | + | [[#citeF-5|[5]]] Rother T. Green's functions in classical physics. Springer, Volume 938, 2017. | |
| − | <div id= | + | <div id=cite-6></div> |
| − | + | [[#citeF-6|[6]]] Podio-Guidugli P., Favata A. Elasticity for geotechnicians: A modern exposition of Kelvin, Boussinesq, Flamant, Cerruti, Melan, and Mindlin problems. Springer, Volume 204, 2014. | |
| − | <div id= | + | <div id=cite-7></div> |
| − | + | [[#citeF-7|[7]]] Kausel E. Fundamental solutions in elastodynamics: a compendium. Cambridge University Press, 2006. | |
| − | <div id= | + | <div id=cite-8></div> |
| − | + | [[#citeF-8|[8]]] Cole K., Beck J., Haji-Sheikh A., Litkouhi B. Heat conduction using Greens functions. CRC Press, 2010. | |
| − | <div id= | + | <div id=cite-9></div> |
| − | + | [[#citeF-9|[9]]] Mandelis A. Diffusion-wave fields: mathematical methods and Green functions. Springer Science & Business Media, 2013. | |
| − | <div id= | + | <div id=cite-10></div> |
| − | + | [[#citeF-10|[10]]] Beer G. Programming the boundary element method. John Wiley & Sons, Inc., 2000. | |
| − | <div id= | + | <div id=cite-11></div> |
| − | + | [[#citeF-11|[11]]] Brebbia C.A., Dominguez J. Boundary elements: an introductory course. WIT press, 1994. | |
| − | <div id= | + | <div id=cite-12></div> |
| − | + | [[#citeF-12|[12]]] Katsikadelis J.T. Boundary elements: theory and applications. Elsevier, 2002. | |
| − | <div id= | + | <div id=cite-13></div> |
| − | + | [[#citeF-13|[13]]] Rodriguez-Castellanos A., Flores E., Sánchez-Sesma F.J., Ortiz-Aleman C., Nava-Flores M., Martin R. Indirect boundary element method applied to fluid–solid interfaces. Soil Dynamics and Earthquake Engineering, 31(3):470–477, 2011. | |
| − | <div id= | + | <div id=cite-14></div> |
| − | + | [[#citeF-14|[14]]] Sánchez-Sesma F.J., Ramos-Martinez J., Campillo M. An indirect boundary element method applied to simulate the seismic response of alluvial valleys for incident P, S and Rayleigh waves. Earthquake Engineering & Structural Dynamics, 22(4):279–295, 1993. | |
| − | <div id= | + | <div id=cite-15></div> |
| − | + | [[#citeF-15|[15]]] Young W.C., Budynas R.G., Sadegh A.M. Roark's formulas for stress and strain. McGraw-Hill Education, 2012. | |
| − | <div id= | + | <div id=cite-16></div> |
| − | + | [[#citeF-16|[16]]] Hetényi M. Beams on elastic foundation: theory with applications in the fields of civil and mechanical engineering. University of Michigan, 1971. | |
| − | <div id= | + | <div id=cite-17></div> |
| − | + | [[#citeF-17|[17]]] Dinev D. Analytical solution of beam on elastic foundation by singularity functions. Engineering Mechanics, 19(6):381–392, 2012. | |
| + | </div> | ||
Latest revision as of 14:22, 29 June 2021
Resumen
Las vigas sobre fundación flexible representan un modelo básico dentro del análisis estructural, las cuales suelen emplearse para modelar vigas de cimentación, pilas, muros de contención y estructuras más complejas que tengan algún tipo de estos elementos. Para el análisis de estas, usualmente se emplea el método de elementos finitos [1], el cual produce una solución aproximada del problema; y el método de rigidez con funciones de Green [2], el cual produce una solución exacta del mismo.
En este artículo se presenta una metodología 100 % basada en el empleo de las funciones de Green (respuesta ante una fuerza puntual unitaria), para obtener la respuesta exacta de las vigas sobre fundación flexible. La principal ventaja de esta formulación es su menor costo computacional comparado con las citadas alternativas, además que la respuesta puede expresarse solo por medio de sumas e integrales, las cuales se pueden realizar fácilmente de forma numérica.
Por completez, también se presentan una gran variedad de funciones de Green para vigas sobre fundación flexible finitas e infinitas con diferentes condiciones de frontera, así como algunos ejemplos con la implementación de la metodología propuesta.
Palabras clave: Funciones de Green, vigas sobre fundación flexible, pilas, campos de desplazamiento
Abstract
Beams on elastic foundation are basic elements within structural analysis, which are used to model foundation beams, foundation piles, retaining walls, and more complex structures that include some of these elements. For their analysis, the finite element method is usually used [1], which produces an approximate solution of the problem; and the Green's function stiffness method [2], which produces an exact solution. This article presents a methodology 100% based on the use of Green function's (response to a unit point force), to obtain the exact response of beams on elastic foundation. The main advantage of this formulation is its computational low cost compared to the aforementioned alternatives, and even for a large number of problems, it can be expressed only by means of sums and integrals, which can be easily performed numerically.
Also, a great variety of Green function's for finite and infinite beams on elastic foundations with different boundary conditions are also presented, as well as some examples with the implementation of the proposed methodology.
Keywords: Green’s functions, beams on elastic foundation, piles, displacement field
1. Introducción
En mecánica, se define como función de Green, al campo de desplazamiento en un medio ante la acción de una fuerza puntual unitaria. En general, para casos tridimensionales, dicha fuerza unitaria puede estar ubicada en cualquier punto y dirección del medio, y el campo de desplazamiento será vectorial y tendrá también tres componentes escalares. El concepto de función de Green puede fácilmente extenderse a cualquier problema físico en el cual la fuerza puntual será reemplazada por una fuente o acción puntual unitaria, mientras que el campo de desplazamiento será reemplazado por el campo de la variable dependiente principal para el problema. Por ejemplo, en transferencia de calor, la función de Green será el campo de temperatura debido a la acción de una fuente de calor puntual unitaria.
Por si solas, las funciones de Green juegan un papel muy importante en la solución de problemas físicos, puesto que presentan la solución a problemas fundamentales. Por ejemplo, en el famoso problema de Boussinesq, la función de Green es el campo de desplazamiento en un semiespacio (espacio semi-infinito) tridimensional ante la acción de una fuerza puntual unitaria en su superficie. En textos como [3,4,5], se presentan las principales funciones de Green empleadas en la física clásica, en [6] se presenta un compendio de las principales funciones de Green empleadas en la geotecnia, para sismología y elastodinámica sus principales funciones de Green son presentadas en [7], para transferencia de calor en [8], mientras que aquellas propias de los problemas de difusión se presentan en [9].
Además de lo anterior, las funciones de Green son la base de algunos métodos numéricos de contorno o frontera, los cuales permiten resolver problemas diferentes a aquellos para los cuales fueron definidas dichas funciones, es decir, problemas con diferentes condiciones de cargas o fuentes y de frontera. Entre estos métodos numéricos destacan el método directo de elementos de frontera [10,11,12], el método indirecto de elementos de frontera [13,14], y el método de rigidez con funciones de Green [2].
Las vigas sobre fundación flexible representan un modelo básico dentro del análisis estructural, las cueles suelen emplearse para modelar vigas de cimentación, pilas, muros de contención y estructuras más complejas que tengan algún tipo de estos elementos. Pese a que en la actualidad existen diversos métodos para el análisis de estas estructuras, los cuales van desde soluciones tabuladas para gran cantidad de condiciones de frontera y carga [15], la solución directa de los problemas de valor en la frontera gobernantes empleando métodos clásicos de ecuaciones diferenciales [16], hasta el método de elementos finitos [1] o de rigidez con funciones de Green [2] e incluso hay sitios web para su análisis (https://www.buildingsguide.com/calculators/structural/BOEF), es posible empleando solo las funciones de Green obtener su solución.
En este artículo se presenta una metodología basada en las funciones de Green para el análisis de vigas sobre fundación flexible, en la cual el problema de valor en la frontera gobernante para cada problema es resuelto por medio de la superposición o suma de la respuesta ante cargas puntuales. Pese a que el presente procedimiento tiene similitudes conceptuales con aquel propuesto por Dinev [17] los autores creen que la formulación en términos de funciones de Green es más ingenieril y además al presentarse gran variedad de estas funciones para diferentes condiciones de frontera, hace más fácil su implementación para vigas sobre fundación flexible de uno o varios tramos.
2. Ecuación diferencial gobernante y convenciones
La ecuación diferencial que gobierna el desplazamiento de una viga sobre fundación flexible (Figura 1), formada por una viga de material elástico lineal homogéneo, de sección transversal constante y apoyada sobre un medio flexible con rigidez por unidad de longitud constante, es (ver [2] para una deducción paso a paso):
|
|
(1) |
donde:
: Módulo de elasticidad del material de la viga.
: Momento de inercia respecto al eje de la sección transversal de la viga.
: Constante de rigidez por unidad de longitud del suelo de soporte de la viga.
: Campo de desplazamiento en dirección del eje de la viga.
: Fuerza externa por unidad de longitud en dirección del eje que actúa sobre la viga.
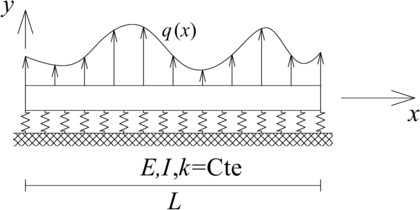
|
| Figura 1. Viga sobre fundación flexible sometida a carga externa distribuida |
Por facilidad en su solución, es usual dividir la ecuación (1) entre , obteniéndose:
|
|
(2) |
donde .
Además de la fuerza externa por unidad de longitud , la viga también se encuentra sometida a la fuerza distribuida que el suelo ejerce sobre esta, la cual es proporcional al desplazamiento en cada de esta y se calcula como:
|
|
(3) |
En este punto es importante resaltar que pese a que las ecuaciones (1) y (2) están escritas en términos de la fuerza externa por unidad de longitud sobre la viga, es decir, una carga distribuida, incluso fuerzas y momentos puntuales se pueden expresar de esta manera. Como ejemplo, se tiene que la carga externa puntual aplicada a la viga sobre fundación flexible presentada en la Figura 2a se define por medio de la siguiente función:
|
|
(4) |
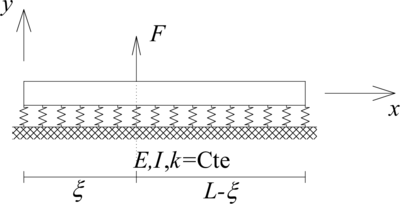
|
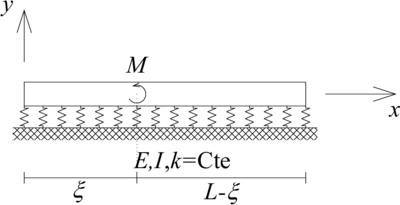
|
| (a) | (b) |
| Figura 2. Vigas sobre fundación flexible sometidas a fuerzas y momentos puntuales. (a) Fuerza puntual. (b) Momento puntual | |
Mientras que para el caso del momento externo puntual presentado en la Figura 2b, la función se define a partir de (4) como (ver la Figura 3 para una explicación):
|
|
(5) |
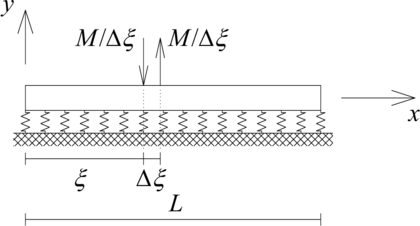
|
| Figura 3. Definición de un momento puntual como el caso límite de dos fuerzas puntuales muy cercanas entre si |
De otra parte, a partir del campo de desplazamiento, es posible obtener los campos de fuerzas internas en la viga como:
|
donde es el campo de momento flector y es el campo de fuerza cortante, cuya convención positiva se presenta en la Figura 4.

|
| Figura 4. Convención positiva de las fuerzas internas |
3. Funciones de Green para vigas sobre fundación flexible
3.1 Fuerzas puntuales
En las Figuras 5 y 6 se presentan los modelos de las vigas sobre fundación flexible finitas e infinitas para los cuales se definirán las funciones de Green a emplear en este artículo, todas las cuales son solución de la siguiente ecuación diferencial:
|
|
(7) |
donde es la función de Green del problema en particular, es decir, el desplazamiento en dirección del punto , debido a la aplicación de una fuerza puntual unitaria en dirección en el punto .
La ecuación (7) es un caso particular de la ecuación (2), en la cual en lugar de se ha empleado y para definir la función de la carga externa se ha empleado la ecuación (4) con .
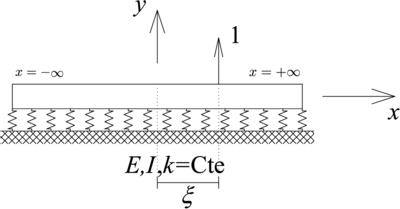
|
| Figura 6. Viga sobre fundación flexible infinita sometida a una fuerza puntual unitaria |
3.1.1 Viga sobre fundación flexible finita libre - libre
La función de Green para la viga sobre fundación flexible finita, con ambos extremos libres y presentada en la Figura 5a, es la solución del siguiente problema de valor en la frontera:
|
donde las dos que acompañan al nombre de la función de Green hacen referencia a que cada uno de los extremos es ibre.
Cada uno de los tramos de esta función de Green se definen como:
|
|
(9) |
donde
|
|
|
(11) |
|
|
(12) |
|
|
(13) |
|
|
(14) |
|
|
(15) |
3.1.2 Viga sobre fundación flexible finita simplemente apoyada
La función de Green para la viga sobre fundación flexible finita con ambos extremos con apoyos simples, presentada en la Figura 5b, es la solución del siguiente problema de valor en la frontera:
|
donde las dos que acompañan al nombre de la función de Green hacen referencia a que cada uno de los extremos es un apoyo imple.
Cada uno de los tramos de esta función de Green se definen como:
|
|
(17) |
donde
|
|
|
(19) |
|
|
(20) |
|
|
(21) |
3.1.3 Viga sobre fundación flexible finita empotrada - libre
La función de Green para la viga sobre fundación flexible finita con su extremo inicial empotrado y su extremo final libre, presentada en la Figura 5c, es la solución del siguiente problema de valor en la frontera:
|
donde la del primer supeindice del nombre hace referencia a que el extremo inicial es mpotrado y la a que el extremo final es ibre.
Cada uno de los tramos de esta función de Green se definen como:
|
|
(23) |
donde
|
|
|
(25) |
|
|
(26) |
|
|
(27) |
|
|
(28) |
|
|
(29) |
3.1.4 Viga sobre fundación flexible finita doblemente empotrada
La función de Green para la viga sobre fundación flexible finita doblemente empotrada presentada en la Figura 5d, es la solución del siguiente problema de valor en la frontera:
|
donde las dos que acompañan al nombre de la función de Green hacen referencia a que cada uno de los extremos es un apoyo mpotrado.
Cada uno de los tramos de esta función de Green se definen como:
|
|
(31) |
donde
|
|
|
(33) |
|
|
(34) |
|
|
(35) |
|
|
(36) |
|
|
(37) |
3.1.5 Viga sobre fundación flexible infinita
La función de Green para la viga sobre fundación flexible infinita presentada en la Figura 6, se define como:
|
|
(38) |
Donde:
|
|
(39) |
|
|
(40) |
La cual se puede escribir en un solo tramo desde a como:
|
|
(41) |
3.2 Momentos puntuales
En las Figuras 7 y 8 se presentan las vigas sobre fundación flexible finitas e infinitas para las cuales se definirán las funciones de Green debidas a la aplicación de un momento puntual unitario, todas las cuales se pueden obtener directamente a partir de sus contrapartes debidas a fuerzas puntuales unitarias presentadas en la sección 3.1 empleando la representación de un momento como el limite de dos fuerzas puntuales muy cercanas presentado anteriormente.
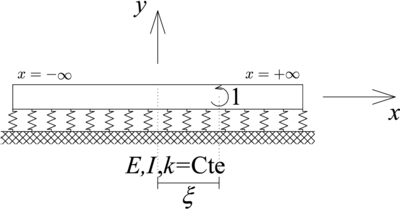
|
| Figura 8. Viga sobre fundación flexible infinita sometida a un momento puntual unitario |
3.2.1 Viga sobre fundación flexible finita libre - libre
A partir de la ecuación (9), la función de Green para la viga sobre fundación flexible finita con ambos extremos libres presentada en la Figura 7a, se define como:
|
|
(42) |
Y sus tramos se definen como:
|
|
(43) |
3.2.2 Viga sobre fundación flexible finita simplemente apoyada
A partir de la ecuación (17), la función de Green para la viga sobre fundación flexible finita simplemente apoyada presentada en la Figura 7b, se define como:
|
|
(44) |
Y sus tramos se definen como:
|
|
(45) |
3.2.3 Viga sobre fundación flexible finita empotrada - libre
A partir de la ecuación (23), la función de Green para la viga sobre fundación flexible finita simplemente apoyada presentada en la Figura 7c, se define como:
|
|
(46) |
Y sus tramos se definen como:
|
|
(47) |
3.2.4 Viga sobre fundación flexible finita doblemente empotrada
A partir de la ecuación (31), la función de Green para la viga sobre fundación flexible finita simplemente apoyada presentada en la Figura 7d, se define como:
|
|
(48) |
Y sus tramos se definen como:
|
|
(49) |
3.2.5 Viga sobre fundación flexible infinita
A partir de la ecuación (38), la función de Green para la viga sobre fundación flexible finita simplemente apoyada presentada en la Figura 8, se define como:
|
|
(50) |
Y sus tramos se definen como:
|
|
(51) |
4. Solución de vigas sobre fundación flexible empleando funciones de Green
Antes de comenzar con la explicación de esta metodología es necesario tener claro que todas las cargas externas aplicadas en una viga sobre fundación flexible pueden obtenerse como un operador lineal de cargas puntuales unitarias, en particular sumas, integrales o derivadas ponderadas por un número o función. Para facilitar la explicación de este concepto, se empleará como ejemplo la viga sobre fundación flexible presentada en la Figura 9.
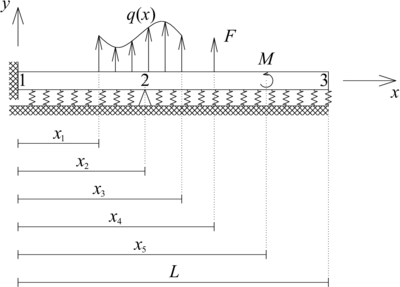
|
| Figura 9. Viga sobre fundación flexible sometida a cargas externas distribuidas y puntuales |
La carga puntual se expresa como el producto de una fuerza puntual unitaria por el factor , es decir, se encuentra definida por la siguiente función (ver la ecuación (4) para una explicación):
|
|
(52) |
Algo similar ocurre con las fuerzas puntuales debidas a las reacciones verticales que ocurren en los puntos 1 y 2, las cuales se definen respectivamente como:
|
donde y son respectivamente los valores de las reacciones en los puntos 1 y 2, las cuales son positivas en dirección del eje .
Por su parte, los momentos puntuales debidos al momento externo y la reacción a momento en el punto 1, se expresan respectivamente como:
|
donde es la reacción a momento en el punto 1 y es una variable auxiliar muda o temporal.
Mientras que la carga distribuida se expresa como:
|
|
(55) |
Ahora que es claro que cualquier carga puntual o distribuida puede expresarse como un operador lineal de cargas puntuales, se debe seleccionar una función de Green cuya viga sobre fundación flexible cumpla o pueda cumplir, por medio de la aplicación de fuerzas o momentos puntuales, todas condiciones de frontera y compatibilidad de la viga sobre fundación flexible en estudio. Para este problema la función de Green que más se acomoda es aquella de la viga empotrada libre presentada en la Figura 5c. Una vez seleccionada la función de Green, la viga que la define debe hacerse equivalente a aquella en estudio, lo cual se logra a partir de la aplicación de cargas distribuidas y/o puntuales (todas ellas expresables como un operador lineal de cargas puntuales) y del cumplimiento de condiciones de frontera y/o compatibilidad. En este caso es claro que para que la estructura presentada en la Figura 5c sea equivalente a aquella de la Figura 9 debe cumplirse que el desplazamiento en el punto 2 sea cero, es decir, , condición de compatibilidad empleada para obtener el valor de la reacción que es desconocido, la cual se expresa en términos de las funciones de Green y , así como empleando el principio de superposición, como:
|
|
(56) |
Cuyos términos se explican a continuación:
: Desplazamiento en debido a la fuerza puntual ubicada en .
: Desplazamiento en debido a la fuerza puntual ubicada en .
: Desplazamiento en debido al momento puntual ubicado en .
: Desplazamiento en debido a la carga distribuida ubicada entre y .
: Desplazamiento en debido a la carga distribuida ubicada entre y .
En este punto, es importante recordarle al lector que corresponde al desplazamiento antes de la fuerza puntual unitaria, mientras que corresponde a aquel después de esta.
Como siguiente paso, una vez obtenidas todas las condiciones de compatibilidad, se resuelve el sistema lineal de ecuaciones que ellas forman, de lo cual se obtiene el valor de aquellas reacciones puntuales diferentes a aquellas que también ocurrirían en la viga sobre fundación flexible empleada para definir la función de Green (Figura 10). En este ejemplo esto equivale a obtener el único valor de que cumple (56).
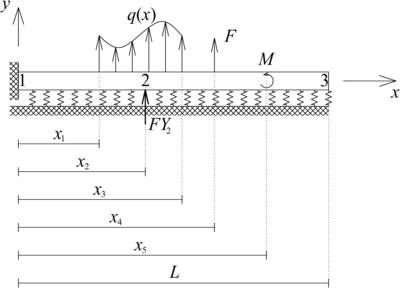
|
| Figura 10. Aplicación de las cargas externas de la viga sobre fundación flexible a analizar sobre aquella empleada para la definición de la función de Green empleada en la solución |
Una vez obtenidas las reacciones que hacen que se cumplan las condiciones de compatibilidad y/o frontera, es necesario calcular el campo de desplazamiento en cada uno de los tramos de la viga sobre fundación flexible, lo cual se realiza de nuevo empleando el principio de superposición. Para este ejemplo el campo de desplazamiento tiene 6 tramos y se define como:
|
|
(57) |
Mientras que cada uno de sus valores se calcula como:
|
|
(58) |
|
|
(59) |
|
|
(60) |
|
|
(61) |
|
|
(62) |
|
|
(63) |
Por último, a partir del campo de desplazamiento calculado anteriormente y empleando las ecuaciones (3) y (6) se calculan los campos de la fuerza que el suelo ejerce sobre la viga, de momento flector y fuerza cortante respectivamente como:
|
|
(64) |
|
|
(65) |
|
|
(66) |
5. Ejemplos
5.1 Viga sobre fundación flexible simplemente apoyada sometida a una carga externa sinusoidal
Resolver la viga sobre fundación flexible presentada en la Figura 11 empleando la función de Green de la Figura 5b.
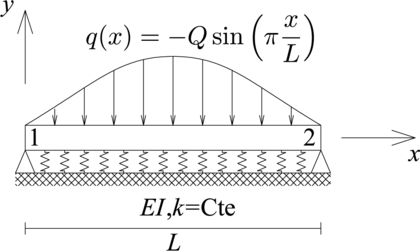
|
| Figura 11. Viga sobre fundación flexible simplemente apoyada sometida a una carga externa sinusoidal |
Solución
Funciones de Green a emplear
Como se indicó en el enunciado, la función de Green a emplear en la solución de este problema es , la cual se presenta en la ecuación (17).
Cálculo del campo de desplazamiento
La carga externa distribuida sobre la viga está definida por medio de la siguiente función:
|
|
(67) |
Ahora, debido a que la viga sobre fundación flexible empleada para la función de Green tiene los mismos tramos, condiciones de frontera y de continuidad que aquella a analizar, su campo de desplazamiento se obtiene de forma inmediata solo mediante la siguiente integral:
|
|
(68) |
La cual se puede entender como el cálculo del desplazamiento en un punto de la viga sobre fundación flexible como la suma del desplazamiento en dicho punto debido a la carga externa aplicada en cada uno de sus puntos .
Cálculo del campo de la fuerza que el suelo ejerce sobre la viga y de fuerzas internas
A partir de las ecuaciones (3) y (6), la fuerza que el suelo ejerce sobre la viga y las fuerzas internas en esta se calculan respectivamente como:
|
Desde el siguiente enlace se puede descargar el código de Python con la solución de este ejemplo:
https://drive.google.com/file/d/18ee0fR2uzRQFk79DYxLziZwbhIHquAgS
5.2 Viga sobre fundación flexible empotrada - libre sometida a una carga distribuida constante
Resolver la viga sobre fundación flexible presentada en la Figura 12 empleando: a) la función de Green empotrada libre presentada en la sección 3.1.3 y b) la función de Green de libre-libre presentada en la sección 3.1.1.
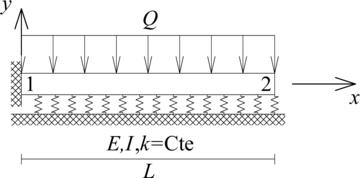
|
| Figura 12. Viga sobre fundación flexible empotrada-libre sometida a una carga externa distribuida constante |
Solución
Definición de la carga externa
La carga externa que actúa sobre la viga está definida por la siguiente función:
|
|
(70) |
5.2.1 Solución empleando la función de Green de la viga sobre fundación flexible empotrada libre (Figura 5c)
Funciones de Green a emplear
Para esta alternativa la función de Green a emplear es , la cual se presenta en la ecuación (23).
Cálculo del campo de desplazamiento
Debido a que la viga de la función de Green que a emplear tienen las mismas condiciones de frontera que aquella a analizar, su campo de desplazamiento se calcula como:
|
|
(71) |
El cual luego de realizar las integrales respectivas, da como resultado:
|
|
(72) |
donde
|
|
(73) |
Cálculo del campo de la fuerza que el suelo ejerce sobre la viga y de fuerzas internas
A partir de la ecuación (3) y empleando la ecuación (72) se tiene que la fuerza que el suelo hace sobre la viga es:
|
|
(74) |
Mientras que, reemplazando la ecuación (72) en la ecuación (6), se obtiene que los campos de momento flector y fuerza cortante son respectivamente:
|
donde
|
|
(76) |
y
|
|
(77) |
5.2.2 Solución empleando la función de Green de la viga sobre fundación flexible libre libre (Figura 5a)
Funciones de Green a emplear
Para la solución de este problema se emplearán las siguientes funciones de Green:
: Campo de desplazamientos de la viga sobre fundación flexible libre-libre sometida a una carga puntual unitaria presentada en la Figura 5a y cuyo valor se presenta en la ecuación (17).
: Campo de desplazamientos de la viga sobre fundación flexible libre-libre sometida a un momento puntual unitario presentada en la Figura 7a y cuyo valor se presenta en la ecuación (44).
: Campo de rotaciones de la viga sobre fundación flexible libre-libre sometida a una carga puntual unitaria presentada en la Figura 5a.
: Campo de rotaciones de la viga sobre fundación flexible libre-libre sometida a un momento puntual unitario presentada en la Figura 7a.
En este punto es importante resaltar que debido a que , y son derivadas de , en realidad es posible indicar que lo es necesario emplear está última, mientras que los tramos de las primeras se definen como:
|
|
|
|
|
|
Para resolver este problema se debe tener en cuenta que solo integrando la función de Green libre-libre multiplicada por la carga externa que actúa sobre la viga, se obtiene una solución que cumplirá las mismas condiciones de frontera homogéneas que la función de Green posee, es decir:
- Segunda derivada derivada (o momento flector) igual a cero en .
- Tercera derivada (o fuerza cortante) igual a cero en .
- Segunda derivada derivada (o momento flector) igual a cero en .
- Tercera derivada (o fuerza cortante) igual a cero en .
Las cuales cuales no coinciden con aquellas que posee la viga sobre fundación flexible a estudiar (Figura 12).
Cálculo del campo de desplazamiento
Para poder hacer cumplir las condiciones de frontera del problema real, a la viga sobre fundación flexible libre-libre no solo se le debe agregar el efecto de la carga distribuida sino también aquel del momento y fuerza puntuales debidos al empotramiento en el extremo izquierdo de esta, así como el cumplimiento de las condiciones de desplazamiento y rotaciones nulos en (Figura 13).
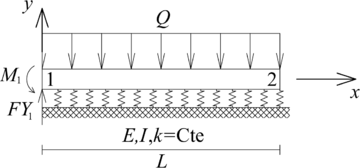
|
| Figura 13. Viga sobre fundación flexible en voladizo sometida a una carga externa distribuida constante. |
Con base en lo anterior, las dos ecuaciones a emplear para obtener el valor de las reacciones de la viga sobre fundación flexible son:
|
De cuya solución se obtiene:
|
Con lo cual, se tiene que el campo de desplazamiento ahora se calcula como:
|
|
(80) |
El cual luego de realizar las integrales y usando la ecuación (79), da como resultado:
|
|
(81) |
donde
|
|
(82) |
Cálculo del campo de la fuerza que el suelo ejerce sobre la viga y de fuerzas internas
Dado que el campo de desplazamiento presentado en la ecuación (82) es igual al presentado en la ecuación (72) la fuerza que el suelo ejerce sobre la viga y las fuerzas internas en esta serán también iguales con ambas alternativas.
Desde el siguiente enlace se puede descargar el código de Python con la solución de este ejemplo:
https://drive.google.com/file/d/1_i-gzT1M8_PfHonABU7wzhmksbqhUeIi
5.3 Viga sobre fundación flexible libre - libre sometida a cargas puntuales y distribuidas así como a momento puntual
Resolver la viga sobre fundación flexible presentada en la Figura 14 empleando la función de Green libre-libre presentada en la sección 3.1.1.
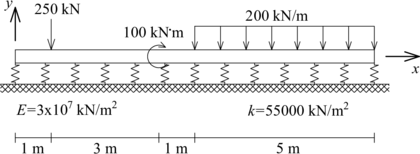
|
| Figura 14. Viga sobre fundación flexible simplemente libre libre sometida a cargas puntuales y distribuidas, así como a momento puntual |
Funciones de Green a emplear
Para la solución de este ejercicio se emplearán las funciones de Green y , las cuales se presentan en las ecuaciones (9) y (42), respectivamente.
Cálculo del campo de desplazamiento
El campo de desplazamiento de la viga sobre fundación flexible tiene 4 tramos, los cuales se definen como:
|
|
(83) |
Donde cada uno de estos se calcula como:
|
|
(84) |
|
|
(85) |
|
|
(86) |
|
|
(87) |
|
|
(88) |
|
|
(89) |
|
|
(90) |
|
|
(91) |
Como resumen de lo anterior, en la Figura 15 se presenta la gráfica del campo de desplazamiento en toda la viga.
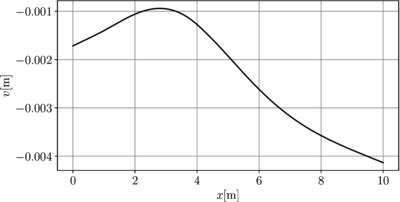
|
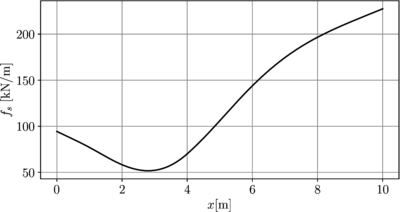
|
| (a) Campo de desplazamiento | (b) Campo de la fuerza que el suelo le ejerce a la viga |
| Figura 15. Campos de desplazamiento y fuerza que el suelo ejerce sobre la viga | |
Cálculo de la fuerza distribuida que el suelo realiza sobre la viga
A partir del campo de desplazamiento es fácil calcular la fuerza que el suelo le hace a la viga como , es decir:
|
|
(92) |
donde
|
|
(93) |
|
|
(94) |
|
|
(95) |
|
|
(96) |
Como revisión de los anteriores resultados a continuación se realizará la revisión del equilibrio vertical y rotacional respecto al nodo 1 de toda la viga:
|
Cálculo de los campos de fuerzas internas
A continuación se calculan las fuerzas internas en la viga a partir de su campo de desplazamiento.
Campo de momento flector
A partir del campo de desplazamiento y empleando la ecuación (6a), el campo de momento flector se calcula como:
|
|
(98) |
donde
|
|
(99) |
|
|
(100) |
|
|
(101) |
|
|
(102) |
De forma gráfica, el campo de momento flector se presenta en la Figura 16.
Campo de fuerza cortante
Mientras que el campo de fuerza cortante se calcula a partir del campo de desplazamiento como (ver ecuación (6b)):
|
|
(103) |
donde
|
|
(104) |
|
|
(105) |
|
|
(106) |
|
|
(107) |
Como resumen de los anteriores resultados, en la Figura 16 se presenta de forma gráfica el campo de fuerza cortante en toda la viga.
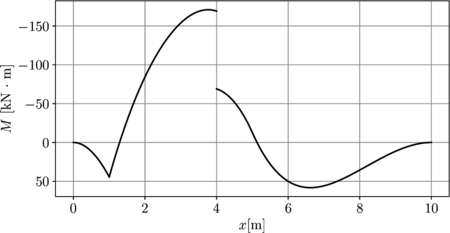
|
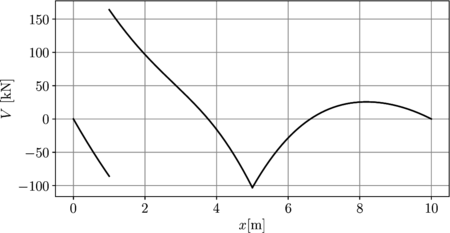
|
| (a) Momento flector | (b) Fuerza cortante |
| Figura 16. Campos de fuerzas internas | |
Desde el siguiente enlace se puede descargar el código de Python con la solución de este ejemplo:
https://drive.google.com/file/d/1OVWDyO10_n7tHrZyyISo-OOYUmVrB8bn
6 Conclusiones
Las principales conclusiones de este artículo son:
- Se presenta una metodología basada 100% en las funciones de Green para el análisis de vigas sobre fundación flexible, con la cual se pueden calcular de forma exacta los campos de desplazamiento, momento flector, fuerza cortante y fuerza que el suelo ejerce sobre la viga.
- Una vez implementado de forma numérica, el procedimiento presentado permite analizar de forma muy eficiente vigas sobre fundación flexible.
- Pese a que las funciones de Green más eficientes para resolver un determinado problema son aquellas que comparten las mismas condiciones de frontera (homogéneas) del problema en estudio, es posible su empleo para resolver problemas con diferentes condiciones de frontera. Esto se demuestra en el ejemplo 5.2.2 y le da mucha generalidad al procedimiento.
- Se presentan varias funciones de Green para vigas sobre fundación flexible finitas e infinitas con diferentes condiciones de frontera, lo cual permite la implementación del método propuesto para gran cantidad e vigas sobre fundación flexible.
- Se presentan tres ejemplos con la solución de igual número de vigas sobre fundación flexible empleando la metodología presentada en este artículo, las cuales son la respuesta exacta de cada problema pues cumplen sus ecuaciones diferenciales gobernantes (equilibrio de cada punto), condiciones de frontera y equilibrio de toda la viga.
Referencias
[1] Reddy J.N. An introduction to the finite element method. McGraw-Hill, New York, Volume 1221, 2004.
[2] Molina-Villegas J.C., Giraldo H.N.D., Ochoa A.F.A. Analytical formulation of the stiffness method for 2D reticular structures using Green functions. Revista Internacional de Metodos Numericos para Calculo y Diseno en Ingenieria, 36:3, 2020.
[3] Stakgold I., Hols M.J. Green's functions and boundary value problems. John Wiley & Sons, Volume 99, 2011.
[4] Duffy D.G. Green's functions with applications. CRC Press, 2015.
[5] Rother T. Green's functions in classical physics. Springer, Volume 938, 2017.
[6] Podio-Guidugli P., Favata A. Elasticity for geotechnicians: A modern exposition of Kelvin, Boussinesq, Flamant, Cerruti, Melan, and Mindlin problems. Springer, Volume 204, 2014.
[7] Kausel E. Fundamental solutions in elastodynamics: a compendium. Cambridge University Press, 2006.
[8] Cole K., Beck J., Haji-Sheikh A., Litkouhi B. Heat conduction using Greens functions. CRC Press, 2010.
[9] Mandelis A. Diffusion-wave fields: mathematical methods and Green functions. Springer Science & Business Media, 2013.
[10] Beer G. Programming the boundary element method. John Wiley & Sons, Inc., 2000.
[11] Brebbia C.A., Dominguez J. Boundary elements: an introductory course. WIT press, 1994.
[12] Katsikadelis J.T. Boundary elements: theory and applications. Elsevier, 2002.
[13] Rodriguez-Castellanos A., Flores E., Sánchez-Sesma F.J., Ortiz-Aleman C., Nava-Flores M., Martin R. Indirect boundary element method applied to fluid–solid interfaces. Soil Dynamics and Earthquake Engineering, 31(3):470–477, 2011.
[14] Sánchez-Sesma F.J., Ramos-Martinez J., Campillo M. An indirect boundary element method applied to simulate the seismic response of alluvial valleys for incident P, S and Rayleigh waves. Earthquake Engineering & Structural Dynamics, 22(4):279–295, 1993.
[15] Young W.C., Budynas R.G., Sadegh A.M. Roark's formulas for stress and strain. McGraw-Hill Education, 2012.
[16] Hetényi M. Beams on elastic foundation: theory with applications in the fields of civil and mechanical engineering. University of Michigan, 1971.
[17] Dinev D. Analytical solution of beam on elastic foundation by singularity functions. Engineering Mechanics, 19(6):381–392, 2012.
Document information
Published on 29/06/21
Accepted on 29/06/21
Submitted on 25/01/21
Volume 37, Issue 2, 2021
DOI: 10.23967/j.rimni.2021.06.002
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?