| (59 intermediate revisions by 2 users not shown) | |||
| Line 1: | Line 1: | ||
<!-- metadata commented in wiki content | <!-- metadata commented in wiki content | ||
| − | |||
<div id="_GoBack" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | <div id="_GoBack" class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | ||
| Line 18: | Line 17: | ||
Correios eletrônicos: [mailto:miguel_angelo05@yahoo.com.br miguel_angelo05@yahoo.com.br], [mailto:paulorocha@em.ufop.br paulorocha@em.ufop.br], [mailto:katia.silva@ufop.edu.br katia.silva@ufop.edu.br], [mailto:ramsilveira@yahoo.com.br ramsilveira@yahoo.com.br] | Correios eletrônicos: [mailto:miguel_angelo05@yahoo.com.br miguel_angelo05@yahoo.com.br], [mailto:paulorocha@em.ufop.br paulorocha@em.ufop.br], [mailto:katia.silva@ufop.edu.br katia.silva@ufop.edu.br], [mailto:ramsilveira@yahoo.com.br ramsilveira@yahoo.com.br] | ||
| − | + | --> | |
==Resumo== | ==Resumo== | ||
| − | Neste trabalho tem-se como objetivo realizar análises elástico-lineares a partir de um programa computacional destinado à implementação numérica do Modelo de Bielas e Tirantes, utilizando-se uma formulação baseada no Método dos Elementos Finitos (MEF). Com este modelo é possível analisar o comportamento de elementos estruturais como blocos de fundação, consolos curtos e sapatas rígidas e realizar o dimensionamento das armaduras de aço, representar os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por | + | Neste trabalho tem-se como objetivo realizar análises elástico-lineares a partir de um programa computacional destinado à implementação numérica do Modelo de Bielas e Tirantes, utilizando-se uma formulação baseada no Método dos Elementos Finitos (MEF). Com este modelo é possível analisar o comportamento de elementos estruturais como blocos de fundação, consolos curtos e sapatas rígidas e realizar o dimensionamento das armaduras de aço, representar os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por Montoya et al. [1], além de modelar numericamente via MEF uma viga-parede com uma grande abertura, desenvolvida por Schlaich et al. [2]. Com o fim de validar as implementações numéricas, os resultados foram comparados com modelagens numéricas realizadas com o auxílio do software ANSYS 17 e com expressões normativas. |
| − | '''Palavras–chave:''' Modelo de | + | '''Palavras–chave:''' Modelo de bielas e tirantes, elementos finitos, blocos de fundação, consolos curtos, vigas-parede, sapatas rígidas |
| − | + | ||
==Abstract== | ==Abstract== | ||
| − | The main objective of this work was to perform elastic-linear analysis through computational program and numerical approach from strut-and-tie model, using a formulation based on Finite Element Method (FEM). In this model, it is possible to analyze the behavior of structural elements such as foundation blocks, wall beams, short consoles; to demosntrate the values of tensions, deformations, and displacements in the region of a beam represented by the Model of cranks developed by | + | The main objective of this work was to perform elastic-linear analysis through computational program and numerical approach from strut-and-tie model, using a formulation based on Finite Element Method (FEM). In this model, it is possible to analyze the behavior of structural elements such as foundation blocks, wall beams, short consoles; to demosntrate the values of tensions, deformations, and displacements in the region of a beam represented by the Model of cranks developed by Montoya et al. [1]; besides numerically modeling a wall beam via FEM with a large aperture, developed by Schlaich et al. [2]. In order to validate the numerical implementations, the results were compared with numerical modeling performed with the aid of the software ANSYS 17 and normative expressions. |
'''Keywords''': Strut-and-tie model, finite elements, foundation block, short consoles, wall beams and rigid shoes | '''Keywords''': Strut-and-tie model, finite elements, foundation block, short consoles, wall beams and rigid shoes | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==1. Introdução== | ==1. Introdução== | ||
| Line 42: | Line 34: | ||
A concepção de projetos estruturais estabelece três propósitos: economia, tempo e segurança. Para atingir o equilíbrio entre esses fatores há uma ampla quantidade de materiais e métodos disponíveis no mercado, que são abordados em vários temas de pesquisas por todo o mundo. Tratando-se dos elementos estruturais, o aço e o concreto são os materiais mais utilizados, visto que, se completam quando trabalham em conjunto. Muitas vezes em uma análise estrutural o projetista é forçado a propor uma solução simplificada para um problema que requer uma análise mais específica, devido aos prazos reduzidos impostos pelo mercado. Esse fato pode acarretar um superdimensionamento dos elementos estruturais gerando um gasto excessivo de materiais ou até mesmo levar o sistema estrutural à ruptura. | A concepção de projetos estruturais estabelece três propósitos: economia, tempo e segurança. Para atingir o equilíbrio entre esses fatores há uma ampla quantidade de materiais e métodos disponíveis no mercado, que são abordados em vários temas de pesquisas por todo o mundo. Tratando-se dos elementos estruturais, o aço e o concreto são os materiais mais utilizados, visto que, se completam quando trabalham em conjunto. Muitas vezes em uma análise estrutural o projetista é forçado a propor uma solução simplificada para um problema que requer uma análise mais específica, devido aos prazos reduzidos impostos pelo mercado. Esse fato pode acarretar um superdimensionamento dos elementos estruturais gerando um gasto excessivo de materiais ou até mesmo levar o sistema estrutural à ruptura. | ||
| − | O Método dos Elementos Finitos (MEF), concebido na década de 50, vem sendo utilizado com grande sucesso na engenharia estrutural. Existe uma infinidade de softwares com poderosos pós-processadores e com os mais avançados modelos construtivos para o tratamento do concreto armado | + | O Método dos Elementos Finitos (MEF), concebido na década de 50, vem sendo utilizado com grande sucesso na engenharia estrutural. Existe uma infinidade de softwares com poderosos pós-processadores e com os mais avançados modelos construtivos para o tratamento do concreto armado [3]. Em uma modelagem utilizando o MEF é necessário que se faça um levantamento dos parâmetros a serem considerados e uma análise cuidadosa da aplicação dos carregamentos e das condições de contorno, para que se possa realizar um estudo preciso e confiável dos resultados obtidos. |
| − | O Modelo de Bielas e Tirantes surge como uma alternativa para solucionar casos específicos em que não se aplica a hipótese de Bernoulli ou hipótese das seções planas. Este procedimento permite identificar as regiões da estrutura que exibem comportamento diferenciado em relação às distribuições de tensões e deformações. | + | O Modelo de Bielas e Tirantes surge como uma alternativa para solucionar casos específicos em que não se aplica a hipótese de Bernoulli ou hipótese das seções planas. Este procedimento permite identificar as regiões da estrutura que exibem comportamento diferenciado em relação às distribuições de tensões e deformações. |
| − | + | O estudo levou em consideração que os materiais se comportam de maneira elástico-linear. Nesse caso, após sofrer deformações, a estrutura tende a retornar ao seu estado original quando o carregamento externo for cessado. Além disso, há uma relação linear entre as componentes de tensão e deformação do material, conhecida como módulo de elasticidade [4]. Nessa pesquisa será utilizada a formulação isoparamétrica do Método dos Elementos Finitos, na qual as funções de forma dos elementos são dadas no sistema local de coordenadas naturais e [5]. | |
| − | O estudo levou em consideração que os materiais se comportam de maneira elástico-linear. Nesse caso, após sofrer deformações, a estrutura tende a retornar ao seu estado original quando o carregamento externo for cessado. Além disso, há uma relação linear entre as componentes de tensão e deformação do material, conhecida como módulo de elasticidade | + | |
O trabalho tem como objetivo realizar análises elástico-lineares de elementos especiais em concreto armado, a partir do Modelo de Bielas e Tirantes utilizando-se uma formulação baseada no Método dos Elementos Finitos (MEF). Para tal desenvolveu-se um programa computacional, em liguagem FORTRAN 90, adotando-se elementos finitos triangulares, conhecidos como Constant Strain Triangle (CST), sendo os resultados numéricos obtidos comparados com modelagens feitas com auxílio do software ANSYS 17. | O trabalho tem como objetivo realizar análises elástico-lineares de elementos especiais em concreto armado, a partir do Modelo de Bielas e Tirantes utilizando-se uma formulação baseada no Método dos Elementos Finitos (MEF). Para tal desenvolveu-se um programa computacional, em liguagem FORTRAN 90, adotando-se elementos finitos triangulares, conhecidos como Constant Strain Triangle (CST), sendo os resultados numéricos obtidos comparados com modelagens feitas com auxílio do software ANSYS 17. | ||
| − | Com este modelo foi possível analisar o comportamento de elementos estruturais como blocos de fundação, consolos curtos, sapatas rígidas, representar os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por | + | Com este modelo foi possível analisar o comportamento de elementos estruturais como blocos de fundação, consolos curtos, sapatas rígidas, representar os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por Montoya et al. [1], além de modelar numericamente via MEF uma viga-parede com uma grande abertura, desenvolvida por Schlaich et al. [2]. Por fim, com o objetivo de verificar que é possível projetar as armaduras de aço de estruturas de concreto usando o Método dos Elementos Finitos, realizou-se o dimensionamento de alguns elementos estruturais via MEF e os resultados foram comparados com respostas obtidas a partir de expressões normativas encontradas na literatura. |
==2. Modelo de bielas e tirantes== | ==2. Modelo de bielas e tirantes== | ||
| Line 56: | Line 47: | ||
===2.1 Conceitos=== | ===2.1 Conceitos=== | ||
| − | O Modelo de Bielas e Tirantes tem como princípio a idealização de que a força do pilar se concentra em algumas regiões do bloco de fundação até chegar às estacas. São formadas zonas de concreto comprimidas (bielas), como Mörsch idealizou no caso das vigas. Na Figura 1 mostram-se as regiões comprimidas do concreto em um bloco submetido a uma força vertical. Este modelo foi comprovado ao se resolver um bloco análogo utilizando o Método dos Elementos Finitos | + | O Modelo de Bielas e Tirantes tem como princípio a idealização de que a força do pilar se concentra em algumas regiões do bloco de fundação até chegar às estacas. São formadas zonas de concreto comprimidas (bielas), como Mörsch idealizou no caso das vigas. Na [[#img-1|Figura 1]] mostram-se as regiões comprimidas do concreto em um bloco submetido a uma força vertical. Este modelo foi comprovado ao se resolver um bloco análogo utilizando o Método dos Elementos Finitos [6], que pode ser visto na [[#img-2|Figura 2]], comprovando a formação das bielas comprimidas. |
| − | + | <div id='img-1'></div> | |
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| Line 64: | Line 55: | ||
| colspan="1" style="padding:10px;"| '''Figura 1'''. Modelo idealizado da formação de bielas | | colspan="1" style="padding:10px;"| '''Figura 1'''. Modelo idealizado da formação de bielas | ||
|} | |} | ||
| − | + | <div id='img-2'></div> | |
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| Line 75: | Line 66: | ||
Logo, o Método de Bielas e Tirantes consiste em admitir que um bloco possui um funcionamento estrutural básico similar à de uma treliça espacial, constituído por barras comprimidas e inclinadas (bielas), formada pelo concreto comprimido e responsáveis pela transmissão do carregamento dos pilares para as estacas e barras tracionadas (tirantes), representadas pelas armaduras principais. | Logo, o Método de Bielas e Tirantes consiste em admitir que um bloco possui um funcionamento estrutural básico similar à de uma treliça espacial, constituído por barras comprimidas e inclinadas (bielas), formada pelo concreto comprimido e responsáveis pela transmissão do carregamento dos pilares para as estacas e barras tracionadas (tirantes), representadas pelas armaduras principais. | ||
| − | Os modelos e conceitos apresentados são embasados em ensaios relatados na bibliografia, e pode-se dizer que se iniciaram com os estudos de | + | Os modelos e conceitos apresentados são embasados em ensaios relatados na bibliografia, e pode-se dizer que se iniciaram com os estudos de Hobbs & Stein [7], que analisaram o comportamento de blocos sobre duas estacas de forma analítica e experimental, em setenta modelos em escala 1:3 e de Blévot & Frémy [8], ensaiando 100 blocos em suas análises. |
===2.2 Método de Blévot & Frémy para blocos de fundação=== | ===2.2 Método de Blévot & Frémy para blocos de fundação=== | ||
| − | A partir dos resultados obtidos pelos ensaios realizados por | + | A partir dos resultados obtidos pelos ensaios realizados por Blévot & Frémy [8], deu-se origem a um processo de cálculo para a armadura longitudinal (tirante) e verificação da tensão de compressão na biela, sendo similar ao processo de Biela e Tirante, mas se difere na definição da seção da biela. Este processo tem sido de grande utilidade nas construções brasileiras, apesar da ABNT NBR 6118 [9] não citá-lo explicitamente. |
Portanto, o Método de Blévot & Frémy, também entendido como o de Biela e Tirante, consiste no cálculo das armaduras tracionadas e verificação da tensão nas bielas de compressão que se desenvolvem no interior do bloco, devendo ser feita junto à base do pilar e junto à cabeça da estaca. | Portanto, o Método de Blévot & Frémy, também entendido como o de Biela e Tirante, consiste no cálculo das armaduras tracionadas e verificação da tensão nas bielas de compressão que se desenvolvem no interior do bloco, devendo ser feita junto à base do pilar e junto à cabeça da estaca. | ||
| − | A tensão nas bielas na base do pilar é verificada pela relação entre as áreas da seção transversal do pilar ( <math> | + | A tensão nas bielas na base do pilar é verificada pela relação entre as áreas da seção transversal do pilar (<math>{A}_{{pilar}}^{}</math>) e da biela (<math>{A}_{{biela}}^{P}</math>) na base do pilar. Dividindo-se a força na biela pela área da biela (<math>{A}_{{biela}}^{P}</math>) tem-se a tensão normal na biela junto ao pilar (<math>\sigma_{{c,biela,P}}</math>): |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 90: | Line 81: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math> | + | | <math>\sigma_{c,biela,P} = \frac{N_d}{{A}_{pilar}sin^2\alpha}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(1) | | style="width: 5px;text-align: right;white-space: nowrap;"|(1) | ||
|} | |} | ||
| − | + | De maneira análoga, a tensão nas bielas junto à estaca pode ser verificada pela relação entre as áreas da seção transversal da estaca (<math>{A}_{{estaca}}^{}</math>) e da biela (<math>{A}_{{biela}}^{e}</math>) junto à estaca. Dividindo-se o valor da força atuante na biela (<math>{F}_{b}^{}</math>), pela área da seção transversal da biela (<math>{A}_{{biela}}^{e}</math>) tem-se a tensão normal na biela junto à estaca (<math>\sigma_{{c,biela,e}}</math>): | |
| − | De maneira análoga, a tensão nas bielas junto à estaca pode ser verificada pela relação entre as áreas da seção transversal da estaca ( <math> | + | |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 103: | Line 93: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math> | + | | <math>\sigma_{c,biela,e} = \frac{N_d}{2{A}_{estaca}sin^2\alpha}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(2) | | style="width: 5px;text-align: right;white-space: nowrap;"|(2) | ||
|} | |} | ||
| − | + | A armadura principal de tração (<math>{A}_{s}^{}</math>), no Estado Limite Último (ELU), pode ser calculada em função da força atuante na armadura (<math>{F}_{t}^{}</math>) e a resistência de cálculo ao escoamento do aço (<math>{f}_{{yd}}^{}</math>). Como <math>{F}_{t}{{ = A}}_{s}{f}_{{yd}}</math>, realizando manipulações matemáticas, tem-se que a armadura principal de tração (<math>{A}_{s}^{}</math>) é dada por: | |
| − | A armadura principal de tração ( <math> | + | |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 116: | Line 105: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math> | + | |<math>{A}_{s}{ = }\frac{{N}_{d}}{{3,6}}\frac{{a}}{{f}_{{yd}}{ d}}\left({1 - }\frac{{a}_{0}}{{2a}}\right)</math> |
|} | |} | ||
| style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(3) | | style="text-align: center;width: 5px;text-align: right;white-space: nowrap;"|(3) | ||
| Line 123: | Line 112: | ||
===2.3 Método de bielas e tirantes para consolos curtos=== | ===2.3 Método de bielas e tirantes para consolos curtos=== | ||
| − | O comportamento estrutural dos consolos curtos e muito curtos se difere das vigas, pois não se pode levar em consideração a hipótese da teoria clássica de flexão. Para analisar sua capacidade resistente ou realizar seu dimensionamento, não se podem utilizar os modelos de cálculo de vigas que levam em consideração a hipótese da manutenção das seções planas após sofrerem deformações. Mesmo em considerações que o material seja homogêneo, isotrópico e elástico perfeito, as tensões normais não variam de forma linear ao longo da sua altura e as tensões tangenciais e as normais aos planos ortogonais e essa seção não podem ser desprezadas. Além disso, após a fissuração do concreto ocorre a redução da rigidez do consolo e outros mecanismos. Desta forma, o projeto desses elementos estruturais deve ser feito obedecendo a recomendações específicas | + | O comportamento estrutural dos consolos curtos e muito curtos se difere das vigas, pois não se pode levar em consideração a hipótese da teoria clássica de flexão. Para analisar sua capacidade resistente ou realizar seu dimensionamento, não se podem utilizar os modelos de cálculo de vigas que levam em consideração a hipótese da manutenção das seções planas após sofrerem deformações. Mesmo em considerações que o material seja homogêneo, isotrópico e elástico perfeito, as tensões normais não variam de forma linear ao longo da sua altura e as tensões tangenciais e as normais aos planos ortogonais e essa seção não podem ser desprezadas. Além disso, após a fissuração do concreto ocorre a redução da rigidez do consolo e outros mecanismos. Desta forma, o projeto desses elementos estruturais deve ser feito obedecendo a recomendações específicas Fernandes & El Debs [10]. |
| − | Segundo a ABNT NBR-9062 [11], os consolos são calculados seguindo intervalos da razão entre a distância da força aplicada até a face do pilar ( <math> | + | Segundo a ABNT NBR-9062 [11], os consolos são calculados seguindo intervalos da razão entre a distância da força aplicada até a face do pilar (<math>a</math>) e a altura útil do consolo (<math>d</math>), sendo que os consolos curtos (<math>0,5 \le a/d \le 1,0</math>) possuem metodologia de cálculo realizado com base no Modelo de Bielas e Tirantes. |
| − | + | ||
| − | + | ||
| + | O Modelo de Bielas e Tirantes para consolos curtos consiste em idealizar o comportamento do concreto, nos trechos descontínuos, por meio das bielas (compressão) e tirantes (tração), com suas posições definidas a partir do fluxo de tensões. Os elementos são conectados por nós, idealizando uma treliça. Sendo assim, o dimensionamento utilizando esse método consiste em verificar a resistência à compressão em uma seção fictícia da biela e calcular a área da armadura do tirante em função da tensão de escoamento do aço. O modelo clássico consiste no equilíbrio de forças e momentos no esquema de treliça apresentado na [[#img-3|Figura 3]]. | ||
| + | <div id='img-3'></div> | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
|style="padding:10px;"| [[Image:review_LIMA_2017a-image23.png|192px]] | |style="padding:10px;"| [[Image:review_LIMA_2017a-image23.png|192px]] | ||
|- style="text-align: center; font-size: 75%;" | |- style="text-align: center; font-size: 75%;" | ||
| − | | colspan="1" style="padding:10px;"| '''Figura 3'''. Modelo de análise e características geométricas de Consolo curto - Leonhardt & Mönnig adaptado por EL | + | | colspan="1" style="padding:10px;"| '''Figura 3'''. Modelo de análise e características geométricas de Consolo curto - Leonhardt & Mönnig adaptado por EL Debs |
|} | |} | ||
| Line 144: | Line 133: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math> | + | | <math>{A}_{{stir}}{ = }\frac{{V}_{d}}{{f}_{{yd}}}{ }\frac{{a}}{{0,9 d}}{ + 1,2 }\frac{{H}_{d}}{{f}_{{yd}}}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(4) | | style="width: 5px;text-align: right;white-space: nowrap;"|(4) | ||
| Line 150: | Line 139: | ||
| − | Por meio de manipulações matemáticas e realizando o equilíbrio de momentos em relação ao ponto C, determina-se que a tensão de compressão na biela ( <math>{ | + | Por meio de manipulações matemáticas e realizando o equilíbrio de momentos em relação ao ponto C, determina-se que a tensão de compressão na biela (<math>{{\sigma}}_{{cd}}</math>) é calculada pela Equação (5), limitando-se o valor da tensão na biela em <math>{{\beta f}}_{{cd}}</math>. |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 157: | Line 146: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>{\ | + | | <math>{{\sigma}}_{{cd}}{ = }\frac{{V}_{d}}{{0,18 b d}}\sqrt{{\left({0,9}\right)}^{2}{+}{\left(\frac{{a}}{{d}}\right)}^{2}}\leq {{\beta f}}_{{cd}}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(5) | | style="width: 5px;text-align: right;white-space: nowrap;"|(5) | ||
| Line 163: | Line 152: | ||
| − | Adota-se <math> | + | Adota-se <math>{\beta =1}</math> no caso de forças diretas e <math>{\beta =0,85}</math> para forças indiretas. |
==3. Formulação via Método dos Elementos Finitos== | ==3. Formulação via Método dos Elementos Finitos== | ||
| Line 171: | Line 160: | ||
O Método dos Elementos Finitos tem como principal finalidade a discretização de uma seção transversal ou de um dado elemento estrutural ao longo do seu domínio. Para isso, podem ser utilizados elementos planos bidimensionais, a saber: o elementos CST (triangular com três nós), elemento quadrilateral com quatro nós, elemento quadrilateral com oito nós ou por fim o elemento quadrilateral com nove nós pertencente à família de Lagrange, além de outros elementos finitos. Em determinados problemas de sólidos com geometrias não regulares, podem ser utilizados os elementos finitos tridimensionais. Dentre eles, podem-se citar os elementos finitos tetraédricos ou hexaédricos. Assim sendo, a ideia central do método é transformar o problema real ou elemento contínuo, em elemento discreto. Daí, transforma-se o problema em um sistema de equações lineares ou não lineares. | O Método dos Elementos Finitos tem como principal finalidade a discretização de uma seção transversal ou de um dado elemento estrutural ao longo do seu domínio. Para isso, podem ser utilizados elementos planos bidimensionais, a saber: o elementos CST (triangular com três nós), elemento quadrilateral com quatro nós, elemento quadrilateral com oito nós ou por fim o elemento quadrilateral com nove nós pertencente à família de Lagrange, além de outros elementos finitos. Em determinados problemas de sólidos com geometrias não regulares, podem ser utilizados os elementos finitos tridimensionais. Dentre eles, podem-se citar os elementos finitos tetraédricos ou hexaédricos. Assim sendo, a ideia central do método é transformar o problema real ou elemento contínuo, em elemento discreto. Daí, transforma-se o problema em um sistema de equações lineares ou não lineares. | ||
| − | Segundo | + | Segundo Chandrupatla & Belegundu [12] a formulação de elementos finitos bidimensionais segue etapas usadas nos problemas unidimensionais. Os deslocamentos, os valores de componentes de força de superfície e de força de corpo distribuídas são funções das posições indicadas por (<math>x, y</math>). A relação entre as tensões e deformações é dada pela Equação (6): |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 185: | Line 174: | ||
===3.2 Modelagem pelo Método dos Elementos Finitos=== | ===3.2 Modelagem pelo Método dos Elementos Finitos=== | ||
| − | Uma região bidimensional é dividida em triângulos de lados retos. Esses triângulos que em sua totalidade formam a região analisada são chamados de elementos. As componentes do deslocamento de um nó j qualquer são consideradas como <math>\boldsymbol{Q}_{\boldsymbol{2j-1}}</math> na direção x e <math>\boldsymbol{Q}_{\boldsymbol{2j}}</math> na direção y. O vetor de deslocamento global da estrutura é indicado por: | + | Uma região bidimensional é dividida em triângulos de lados retos. Esses triângulos que em sua totalidade formam a região analisada são chamados de elementos. As componentes do deslocamento de um nó j qualquer são consideradas como <math>\boldsymbol{Q}_{\boldsymbol{2j-1}}</math> na direção <math>{x}</math> e <math>\boldsymbol{Q}_{\boldsymbol{2j}}</math> na direção y. O vetor de deslocamento global da estrutura é indicado por: |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 196: | Line 185: | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(7) | | style="width: 5px;text-align: right;white-space: nowrap;"|(7) | ||
|} | |} | ||
| − | |||
As conectividades ou incidências de um elemento referem-se aos nós que formam um elemento, adotando o sentido anti-horário para estabelecer uma sequência para identificar os seus nós. O vetor de deslocamento no sistema local é indicado como: | As conectividades ou incidências de um elemento referem-se aos nós que formam um elemento, adotando o sentido anti-horário para estabelecer uma sequência para identificar os seus nós. O vetor de deslocamento no sistema local é indicado como: | ||
| Line 210: | Line 198: | ||
|} | |} | ||
| − | + | Os deslocamentos nos pontos dentro de um elemento precisam ser representados em termos dos deslocamentos nodais do elemento. O Método dos Elementos Finitos usa o conceito de funções de forma no desenvolvimento sistemático dessas interpolações. Para o CST (Constant Strain Triangle), as funções de forma são lineares sobre o elemento. As funções de forma <math>{N}_{1}</math>, <math>{N}_{2}</math> e <math>{N}_{3}</math> correspondem aos nós 1, 2 e 3 do elemento. A função <math>{N}_{1}</math> assume o valor unitário no nó 1, e se reduz linearmente para os nós 2 e 3. Os valores de <math>{N}_{1}</math> definem uma superfície plana <math>{N}_{2}</math> e <math>{N}_{3}</math> são representadas por superfícies semelhantes com valores unitários nos nós 2 e 3, respectivamente, e caindo para zero nas arestas opostas, como mostrado na [[#img-4|Figura 4]]. Sendo assim, qualquer combinação linear dessas funções de forma também representa uma superfície plana. | |
| − | Os deslocamentos nos pontos dentro de um elemento precisam ser representados em termos dos deslocamentos nodais do elemento. O Método dos Elementos Finitos usa o conceito de funções de forma no desenvolvimento sistemático dessas interpolações. Para o CST (Constant Strain Triangle), as funções de forma são lineares sobre o elemento. As funções de forma <math> | + | <div id='img-4'></div> |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| Line 241: | Line 213: | ||
|} | |} | ||
| + | |||
| + | Em particular <math>{N}_{1} + {N}_{2}+ {N}_{3}</math> representa um plano com altura um nos nós 1, 2 e 3 que é paralelo ao triângulo 123. <math>{N}_{1}</math>, <math>{N}_{2}</math> e <math>{N}_{3}</math> não são linearmente independentes. As funções de forma independentes são representadas pelas coordenadas naturais <math>\eta</math> e <math>\xi</math>, como: | ||
| + | |||
| + | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| + | |- | ||
| + | | style="text-align: center;white-space: nowrap;"|<math>{N}_{1}{ = \xi}</math> | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(9.1) | ||
| + | |- | ||
| + | | style="text-align: center;white-space: nowrap;"|<math>{N}_{2}{ = \eta}</math> | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(9.2) | ||
| + | |- | ||
| + | | style="text-align: center;white-space: nowrap;"|<math>{N}_{3}{ = 1 - \xi - \eta}</math> | ||
| + | | style="width: 5px;text-align: right;white-space: nowrap;"|(9.3) | ||
| + | |} | ||
Os deslocamentos dos elementos são escritos usando as funções de forma e os valores nodais do campo de deslocamento desconhecido. | Os deslocamentos dos elementos são escritos usando as funções de forma e os valores nodais do campo de deslocamento desconhecido. | ||
| Line 249: | Line 235: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>{ | + | | <math>{{u = N}}_{1}{{ q}}_{1}{{ + N}}_{2}{{ q}}_{3}{{ + N}}_{3}{{ q}}_{5}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(10.1) | | style="width: 5px;text-align: right;white-space: nowrap;"|(10.1) | ||
| Line 256: | Line 242: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>{ | + | | <math>{{v = N}}_{1}{{ q}}_{2}{{ + N}}_{2}{{ q}}_{4}{{ + N}}_{{3 }}{{ q}}_{6}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(10.2) | | style="width: 5px;text-align: right;white-space: nowrap;"|(10.2) | ||
|} | |} | ||
| − | + | sendo <math>{N}_{1}</math>, <math>{N}_{2}</math> e <math>{N}_{3}</math> expressos pelas Equações (9.1), (9.2) e (9.3), as Equações (10.1) e (10.2) ficam representadas, na forma simplificada, por: | |
| − | + | ||
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 274: | Line 259: | ||
|} | |} | ||
| + | As coordenadas <math>{x}</math> e <math>{y}</math> também podem ser representadas em termos de coordenadas nodais pelo uso das mesmas funções de forma. Essa é a chamada representação isoparamétrica. As representações isoparamétricas relacionam as coordenadas cartesianas <math>{x}</math> e <math>{y}</math> às coordenadas naturais <math>\eta</math> e <math>\xi</math>. | ||
| − | + | Na avaliação das deformações específicas, as derivadas parciais de <math>{u}</math> e <math>{v}</math> devem ser tomadas com relação a <math>{x}</math> e <math>{y}</math>. Pelas representações isoparamétricas verifica-se que <math>{u}</math>, <math>{v}</math>, <math>{x}</math> e <math>{y}</math> são funções de <math>\eta</math> e <math>\xi</math>. Logo, podem ser representadas por: | |
| − | + | ||
| − | Na avaliação das deformações específicas, as derivadas parciais de <math> | + | |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 284: | Line 268: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math> | + | | <math>{u = u}\left[{x}\left({\xi ,\eta}\right){, y}\left({\xi ,\eta}\right)\right]</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(12.1) | | style="width: 5px;text-align: right;white-space: nowrap;"|(12.1) | ||
| Line 291: | Line 275: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math> | + | | <math>{v = v}\left[{x}\left({\xi ,\eta}\right){, y}\left({\xi ,\eta}\right)\right]</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(12.2) | | style="width: 5px;text-align: right;white-space: nowrap;"|(12.2) | ||
|} | |} | ||
| − | |||
Usando-se a regra da cadeia para derivadas de u, obtém-se a matriz quadrada (2x2) denotada como Jacobiana de transformação, logo: | Usando-se a regra da cadeia para derivadas de u, obtém-se a matriz quadrada (2x2) denotada como Jacobiana de transformação, logo: | ||
| Line 304: | Line 287: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{J} | + | | <math>\boldsymbol{J}{ }=\left[\begin{array}{cc} |
| − | \frac{\partial | + | \displaystyle \frac{\partial {x}}{\partial {\xi}} & \displaystyle\frac{\partial {y}}{\partial {\xi}}\\ |
| − | \frac{\partial | + | \displaystyle\frac{\partial {x}}{\partial {\eta}} & \displaystyle\frac{\partial {y}}{\partial {\eta}} |
\end{array}\right]</math> | \end{array}\right]</math> | ||
|} | |} | ||
| Line 312: | Line 295: | ||
|} | |} | ||
| − | + | Realizando-se as derivadas da matriz Jacobiana e algumas manipulações matemáticas chegam-se às relações deformação específica-deslocamento, que pela definição de <math>x_{ij}</math> e <math>y_{ij}</math> demonstra-se que <math>y_{ij} = -y_{ij}</math> e <math>y_{ij} = y_{ik}-y_{jk}</math>, podendo ser escrita, de forma sucinta, da seguinte forma: | |
| − | Realizando-se as derivadas da matriz Jacobiana e algumas manipulações matemáticas chegam-se às relações deformação específica-deslocamento, que pela definição de | + | |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 324: | Line 306: | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(14) | | style="width: 5px;text-align: right;white-space: nowrap;"|(14) | ||
|} | |} | ||
| − | |||
A energia potencial do sistema é dada por: | A energia potencial do sistema é dada por: | ||
| Line 333: | Line 314: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{\pi }\, = | + | | <math>\boldsymbol{\pi }\, =\frac{1}{2}\hat{\underset{A}{\int }}\mbox{ }{\boldsymbol{\epsilon }}^T\mbox{ }\boldsymbol{D\, \epsilon }~\mbox{t dA }-</math><math>\mbox{ }\hat{\underset{A}{\int \mbox{ }}}\boldsymbol{u}^\boldsymbol{T}\boldsymbol{f}\mbox{ t dA}\, -</math><math>\mbox{ }\int_L^{}\mbox{ }\boldsymbol{u}^\boldsymbol{T}\boldsymbol{T}~\mbox{t dL}\, -</math><math>\sum_i\mbox{ }\boldsymbol{u}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{P}_\boldsymbol{i}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(15) | | style="width: 5px;text-align: right;white-space: nowrap;"|(15) | ||
|} | |} | ||
| − | + | sendo que os termos correspondem à energia de deformação do elemento, força de corpo, força de superfície e carregamento pontual, respectivamente. Por meio de triangulação, a energia potencial total pode ser escrita da seguinte forma, sendo que <math>{U}_{e}</math> representa a energia de deformação do elemento. | |
| − | + | ||
{| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;margin: 1em auto 0.1em auto;width: 100%;text-align: center;" | ||
| Line 346: | Line 326: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math>\boldsymbol{\pi }\, =\, \sum_e\, | + | | <math>\boldsymbol{\pi }\, =\, \sum_e\, {U}_{e}-</math><math>\sum_e\hat{\underset{\Alpha}{\, \int }}{ }\boldsymbol{u}^\boldsymbol{T}\boldsymbol{\, f}~\, {t dA}\, -</math><math>\sum_e\hat{\underset{L}{\, \int }}\, \boldsymbol{u}^\boldsymbol{T}\boldsymbol{T}~{ t dL}-</math><math>\sum_i\boldsymbol{\, }\boldsymbol{u}_\boldsymbol{i}^\boldsymbol{T}\boldsymbol{~}\boldsymbol{P}_\boldsymbol{i}\boldsymbol{~}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(16) | | style="width: 5px;text-align: right;white-space: nowrap;"|(16) | ||
|} | |} | ||
| − | + | A matriz de rigidez do elemento é obtida por meio da energia de deformação do elemento. Substituindo-se a Equação (14) na energia de deformação do elemento, tem-se: | |
| − | A matriz de rigidez do elemento é obtida por meio da energia de deformação do elemento. Substituindo-se a Equação 14 na energia de deformação do elemento, tem-se: | + | |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 359: | Line 338: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math> | + | | <math>{U}_{e}{ = }\frac{{1}}{{2}}\hat{\underset{e}{{ }\int }}{ }\boldsymbol{q}^\boldsymbol{T}\boldsymbol{B}^\boldsymbol{T}\boldsymbol{D\, B\, q\, }{ t dA}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(17) | | style="width: 5px;text-align: right;white-space: nowrap;"|(17) | ||
|} | |} | ||
| − | + | Considerando a espessura do elemento (<math>{t}_{e}</math>) e discretizando com triângulos a área a ser analisada, a matriz de rigidez do elemento pode ser obtida a partir da Equação (17), e é dada por: | |
| − | Considerando a espessura do elemento ( | + | |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 372: | Line 350: | ||
{| style="text-align: center; margin:auto;width: 100%;" | {| style="text-align: center; margin:auto;width: 100%;" | ||
|- | |- | ||
| − | | <math> | + | | <math>{K}_{e}{ = }\boldsymbol{B}^\boldsymbol{T}\boldsymbol{D\, B}{{ t}}_{e}{{ A}}_{e}</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;"|(18) | | style="width: 5px;text-align: right;white-space: nowrap;"|(18) | ||
|} | |} | ||
| − | + | Considerando-se a energia de deformação, os termos de força, as condições de contorno e realizando-se as modificações de rigidez e forças, a Equação (16) fica definida como: | |
| − | Considerando-se a energia de deformação, os termos de força, as condições de contorno e realizando-se as modificações de rigidez e forças, a | + | |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 390: | Line 367: | ||
|} | |} | ||
| + | sendo que <math>\boldsymbol{K}</math> refere-se à matriz de rigidez da estrutura analisada, <math>\boldsymbol{Q}</math> ao vetor de deslocamentos nodais da estrutura e <math>\boldsymbol{F}</math> ao vetor de cargas globais aplicadas. | ||
| − | + | Como as deformações específicas são constantes em um elemento CST, as suas componentes de tensões também permanecem constantes. Os valores das tensões devem ser calculados para cada elemento, usando as relações de deformação específica-deslocamento do elemento. Substituindo-se a Equação (14) na Equação (6), tem-se que a tensão em cada elemento é dada por: | |
| − | + | ||
| − | Como as deformações específicas são constantes em um elemento CST, as suas componentes de tensões também permanecem constantes. Os valores das tensões devem ser calculados para cada elemento, usando as relações de deformação específica-deslocamento do elemento. Substituindo-se a | + | |
{| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | {| class="formulaSCP" style="width: 100%;width: 100%;text-align: center;" | ||
| Line 405: | Line 381: | ||
|} | |} | ||
| − | + | A conectividade será utilizada para extrair os deslocamentos nodais do elemento <math>\boldsymbol{q}</math> do vetor de deslocamentos globais <math>\boldsymbol{Q}</math>. Para fim de interpolação, as tensões obtidas pela Equação (20) podem ser usadas como um valor referente ao centroide do elemento analisado. Finalmente, vale ressaltar que as tensões principais e suas direções principais são determinadas a partir das relações do Círculo de Mohr. | |
| − | A conectividade será utilizada para extrair os deslocamentos nodais do elemento <math>\boldsymbol{q}</math> do vetor de deslocamentos globais <math>\boldsymbol{Q}</math> . Para fim de interpolação, as tensões obtidas pela | + | |
==4. Aplicações== | ==4. Aplicações== | ||
| Line 412: | Line 387: | ||
===4.1 Introdução=== | ===4.1 Introdução=== | ||
| − | Neste capítulo são mostradas as aplicações do presente trabalho, representando de forma numérica o Modelo de Bielas e Tirantes. Inicialmente realizou-se a análise, representando os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por | + | Neste capítulo são mostradas as aplicações do presente trabalho, representando de forma numérica o Modelo de Bielas e Tirantes. Inicialmente realizou-se a análise, representando os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por Montoya et al. [1], além de modelar numericamente via MEF uma viga-parede com uma grande abertura, desenvolvida por Schlaich et al. [2]. E por fim analisou-se um consolo curto, um bloco de fundação sob duas estacas de concreto e uma sapata rígida, realizando seus dimensionamentos via MEF e comparando com resultados de expressões normativas e exemplos clássicos encontrados na literatura. Menciona-se ainda que todos os resultados das análises realizadas pelo programa computacional desenvolvido são comparados com resultados determinados por meio da utilização do software ANSYS 17. |
Vale ressaltar que em todos os exemplos analisados neste trabalho foi necessário um maior refinamento de malha, em virtude, da utilização do elemento finito plano adotado, Constant Strain Triangle (CST), que no ANSYS 17 corresponde ao elemento sólido “Plane 182”. Esse elemento apresenta campos de deslocamentos menos refinados que os elementos quadrilaterais com quatro nós, ou elementos lineares e que o elemento quadrilateral com nove nós conhecido na literatura como elemento parabólico. Com isso, realizou-se um maior refinamento da malha utilizada com os elementos CST e assim foi possível obter bons resultados, mesmo utilizando um elemento mais simples que os demais. | Vale ressaltar que em todos os exemplos analisados neste trabalho foi necessário um maior refinamento de malha, em virtude, da utilização do elemento finito plano adotado, Constant Strain Triangle (CST), que no ANSYS 17 corresponde ao elemento sólido “Plane 182”. Esse elemento apresenta campos de deslocamentos menos refinados que os elementos quadrilaterais com quatro nós, ou elementos lineares e que o elemento quadrilateral com nove nós conhecido na literatura como elemento parabólico. Com isso, realizou-se um maior refinamento da malha utilizada com os elementos CST e assim foi possível obter bons resultados, mesmo utilizando um elemento mais simples que os demais. | ||
| Line 418: | Line 393: | ||
===4.2 Modelo desenvolvido por Montoya=== | ===4.2 Modelo desenvolvido por Montoya=== | ||
| − | O modelo desenvolvido por | + | O modelo desenvolvido por Montoya et al. [1] foi implementado analisando-se o comportamento das tensões de compressão nas bielas de uma viga fletida, a partir da discretização da região correspondente ([[#img-5|Figura 5]]a), submetida a um carregamento de superfície igual a 0,797 kN/cm², e não de todo o elemento estrutural. |
| − | {| style=" | + | Na [[#img-5|Figura 5]]b mostram-se as propriedades geométricas da região analisada, sendo submetida a um carregamento pontual <math>\mbox{V}_{\mbox{sd}}\mbox{= 600 kN}</math> aplicado no ponto C. Utilizou-se o modelo de cálculo I da ABNT NBR 6118 [9] para a definição dos ângulos <math>\alpha </math> e <math>\beta </math> , com <math>\alpha \mbox{=50°}</math> e <math>\beta \mbox{=45°}</math> . A seção transversal da região analisada é igual a 40 x 25 cm, com altura útil (d) igual a 36 cm e com (d’) igual a 4 cm. |
| + | <div id='img-5'></div> | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | | style=" | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image65.png|294px]] |
| − | + | | style="text-align: center;vertical-align: top;padding:10px;"|[[Image:review_LIMA_2017a-image66.png|228px]] | |
| − | + | |- | |
| − | | style="vertical-align: top; | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | '''Figura | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="2" style="padding:10px;"| '''Figura 5'''. (a) Região da viga analisada pelo Modelo de Montoya. (b) Modelo de Montoya (cm) | ||
|} | |} | ||
| − | |||
| − | |||
Em relação às propriedades físicas dos materiais, foram utilizados módulo de elasticidade (E) igual a 2800 kN/cm², coeficiente de Poisson ( <math display="inline">\mbox{ν}</math> ) igual a 0,25 e o concreto com resistência característica à compressão ( <math display="inline">\mbox{f}_{\mbox{ck}}</math> ) igual a 30MPa. | Em relação às propriedades físicas dos materiais, foram utilizados módulo de elasticidade (E) igual a 2800 kN/cm², coeficiente de Poisson ( <math display="inline">\mbox{ν}</math> ) igual a 0,25 e o concreto com resistência característica à compressão ( <math display="inline">\mbox{f}_{\mbox{ck}}</math> ) igual a 30MPa. | ||
| − | Com auxílio do software ANSYS 17 a região analisada foi mapeada, gerando uma malha com 1200 elementos finitos triangulares (CST) e 641 nós, representada pela Figura 6. | + | Com auxílio do software ANSYS 17 a região analisada foi mapeada, gerando uma malha com 1200 elementos finitos triangulares (CST) e 641 nós, representada pela [[#img-6|Figura 6]]. |
É importante informar que em todas as aplicações realizadas, o programa ANSYS serviu como um gerador de malha, ou seja, os dados da malha gerada no ANSYS, coordenadas nodais e elementos com as suas respectivas incidências, foram inseridos como dados de entrada no programa computacional desenvolvido. | É importante informar que em todas as aplicações realizadas, o programa ANSYS serviu como um gerador de malha, ou seja, os dados da malha gerada no ANSYS, coordenadas nodais e elementos com as suas respectivas incidências, foram inseridos como dados de entrada no programa computacional desenvolvido. | ||
| + | <div id='img-6'></div> | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:review_LIMA_2017a-image74.png|270px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding:10px;"| '''Figura 6'''. Malha mapeada pelo modelo de Montaya – Ansys | ||
| + | |} | ||
| − | |||
| − | |||
| − | + | As [[#img-7|Figuras 7]]a, 7b e 7c permitem observar as configurações deformadas da região comprimida quando estão submetidas às três tensões principais <math display="inline">{\mbox{σ}}_\mbox{1}</math>, <math display="inline">{\mbox{σ}}_\mbox{2}</math> e <math display="inline">{\mbox{σ}}_\mbox{3}</math>, respectivamente. Os valores das tensões encontrados na escala de referência das figuras são dados em kN/cm². | |
| − | + | <div id='img-7'></div> | |
| − | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | |
| − | + | ||
| − | + | ||
| − | {| style=" | + | |
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image78.png|288px]] |
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image80.png|288px]] |
| + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image82.png|282px]] | ||
|- | |- | ||
| − | | | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | '''Figura | + | | style="text-align: center;font-size: 75%;"|(c) |
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="3" style="padding:10px;"| '''Figura 7'''. (a) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{1}</math>. (b) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{2}</math>. (c) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{3}</math> | ||
|} | |} | ||
| − | Nas Tabelas 1, 2, 3, 4 e 5 apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e a partir do software ANSYS 17. Percebe-se que a precisão obtida pelas simulações numéricas é satisfatória tanto para as tensões elementares ( <math display="inline">{\mbox{σ}}_\mbox{x}</math> , <math display="inline">{\mbox{σ}}_\mbox{y}</math> e <math display="inline">{\mbox{τ}}_{\mbox{xy}}</math> ) quanto para as tensões principais ( <math display="inline">{\mbox{σ}}_\mbox{1}</math> , <math display="inline">{\mbox{σ}}_\mbox{2}</math> ). | + | Nas [[#tab-1|Tabelas 1]], [[#tab-2|2]], [[#tab-3|3]], [[#tab-4|4]] e [[#tab-5|5]] apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e a partir do software ANSYS 17. Percebe-se que a precisão obtida pelas simulações numéricas é satisfatória tanto para as tensões elementares ( <math display="inline">{\mbox{σ}}_\mbox{x}</math> , <math display="inline">{\mbox{σ}}_\mbox{y}</math> e <math display="inline">{\mbox{τ}}_{\mbox{xy}}</math> ) quanto para as tensões principais ( <math display="inline">{\mbox{σ}}_\mbox{1}</math> , <math display="inline">{\mbox{σ}}_\mbox{2}</math> ). |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 1 | + | '''Tabela 1'''. Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{x}</math> (kN/cm²)'''</div> |
| − | + | <div id='tab-1'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 515: | Line 496: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 2 | + | '''Tabela 2'''. Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{y}</math> (kN/cm²)</div> |
| − | + | <div id='tab-2'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 570: | Line 551: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 3 | + | '''Tabela 3'''. Tensões <math display="inline">{\boldsymbol{\tau }}_{\boldsymbol{xy}}</math> (kN/cm²)'''</div> |
| − | + | <div id='tab-3'></div> | |
{| style="width: 100%;border-collapse: collapse;" | {| style="width: 100%;border-collapse: collapse;" | ||
|- | |- | ||
| Line 625: | Line 606: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 4 | + | '''Tabela 4'''. Tensões '<math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{1}</math> (kN/cm²)</div> |
| − | + | <div id='tab-4'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 680: | Line 661: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 5 | + | '''Tabela 5'''. Tensões '<math>{\boldsymbol{\sigma }}_2</math> ' (kN/cm²)</div> |
| − | + | <div id='tab-5'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 735: | Line 716: | ||
| − | Comparando as tensões <math display="inline">{\mbox{σ}}_\mbox{1}</math> positivas com a resistência à tração do concreto ( <math display="inline">{\mbox{0,1 f}}_{\mbox{ck}}</math> ), verifica-se que há formação de fissuras em algumas regiões específicas na viga. A Tabela 6 comprova esse fato, pois há valores de tensão que ultrapassam 0,30 kN/cm², correspondente à resistência do concreto à tração. | + | Comparando as tensões <math display="inline">{\mbox{σ}}_\mbox{1}</math> positivas com a resistência à tração do concreto ( <math display="inline">{\mbox{0,1 f}}_{\mbox{ck}}</math> ), verifica-se que há formação de fissuras em algumas regiões específicas na viga. A [[#tab-6|Tabela 6]] comprova esse fato, pois há valores de tensão que ultrapassam 0,30 kN/cm², correspondente à resistência do concreto à tração. |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 6 | + | '''Tabela 6'''. Verificação das tensões de fissuras (kN/cm²)</div> |
| − | + | <div id='tab-6'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 792: | Line 773: | ||
| − | Nas | + | Nas [[#img-8|Figura 8]]a e 8b mostram-se comparações gráficas entre os deslocamentos nodais obtidos a partir do programa desenvolvido nesta pesquisa e dos resultados encontrados com auxílio do software ANSYS 17. Neste caso, é possível verificar a precisão entre os resultados dos deslocamentos nas duas direções dos eixos de referências (x e y), validando dessa forma a implementação numérica desenvolvida. |
| − | + | <div id='img-8'></div> | |
| − | {| style=" | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image93.png|300px]] |
| − | + | | style="text-align: center;vertical-align: top;padding:10px;"| [[Image:review_LIMA_2017a-image94.png|300px]] | |
| − | + | |- | |
| − | | style="text-align: center; | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | '''Figura | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="2" style="padding:10px;"| '''Figura 8'''. (a) Deslocamentos nodais em ''x''. (b) Deslocamentos nodais em ''y'' | ||
|} | |} | ||
| − | |||
===4.3 Representação numérica do Modelo de Schäfer & Schläich=== | ===4.3 Representação numérica do Modelo de Schäfer & Schläich=== | ||
| − | Neste exemplo é analisado numericamente o modelo de | + | Neste exemplo é analisado numericamente o modelo de Schäfer & Schläich [2] que corresponde a uma viga-parede com abertura submetida a um carregamento pontual. Na [[#img-9|Figura 9]] se apresenta de forma detalhada a viga-parede, que está sujeita à carga de 800 kN. Neste exemplo, o concreto apresenta um módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25. |
| − | + | <div id='img-9'></div> | |
| − | {| style="width: | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | | + | |style="padding:10px;"| [[Image:review_LIMA_2017a-image95.png|312px]] |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | '''Figura 9 | + | | colspan="1" style="padding:10px;"| '''Figura 9'''. Viga-parede Modelo de Schäfer & Schläich |
|} | |} | ||
| − | A viga-parede foi discretizada no software ANSYS 17, gerando-se uma malha livre com 414 elementos finitos triangulares (CST) e 249 nós, conforme mostrado na Figura 10. | + | A viga-parede foi discretizada no software ANSYS 17, gerando-se uma malha livre com 414 elementos finitos triangulares (CST) e 249 nós, conforme mostrado na [[#img-10|Figura 10]]. |
| − | + | <div id='img-10'></div> | |
| − | {| style="width: | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | | + | |style="padding:10px;"| [[Image:review_LIMA_2017a-image96.png|258px]] |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | '''Figura 10 | + | | colspan="1" style="padding:10px;"| '''Figura 10'''. Malha livre da Viga-parede – Ansys |
|} | |} | ||
| − | Com auxílio do ANSYS 17 verifica-se o comportamento e as deformações da viga-parede submetida às tensões principais ( <math display="inline">{\mbox{σ}}_\mbox{1}</math> , <math display="inline">{\mbox{σ}}_\mbox{2}</math> e <math display="inline">{\mbox{σ}}_\mbox{3}</math> ). Essas configurações deformadas são mostradas nas Figuras | + | Com auxílio do ANSYS 17 verifica-se o comportamento e as deformações da viga-parede submetida às tensões principais (<math display="inline">{\mbox{σ}}_\mbox{1}</math>, <math display="inline">{\mbox{σ}}_\mbox{2}</math> e <math display="inline">{\mbox{σ}}_\mbox{3}</math>). Essas configurações deformadas são mostradas nas [[#img-11|Figuras 11]]a, [[#img-11|11]]b e [[#img-11|11]]c, respectivamente, cujas escalas de referências encontram-se em kN/cm². |
| − | {| style=" | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image97.png|258px]] |
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image99.png|264px]] |
| + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image101.png|240px]] | ||
|- | |- | ||
| − | | | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | '''Figura | + | | style="text-align: center;font-size: 75%;"|(c) |
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="3" style="padding:10px;"| '''Figura 11'''. (a) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{1}</math>. (b) Tensão principal <math>{\boldsymbol{\sigma }}_2</math>. (c) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_3</math> | ||
|} | |} | ||
| − | Refinando a malha utilizada, aumentando o número de elementos finitos de forma excessiva, obtendo uma nova malha com 26496 elementos finitos triangulares (CST) e com 13584 nos, é possível visualizar as regiões comprimidas que formam as bielas na viga-parede, representadas na cor azul na Figura 12, demonstrando assim a concentração de tensões de compressão em algumas regiões da viga-parede. | + | Refinando a malha utilizada, aumentando o número de elementos finitos de forma excessiva, obtendo uma nova malha com 26496 elementos finitos triangulares (CST) e com 13584 nos, é possível visualizar as regiões comprimidas que formam as bielas na viga-parede, representadas na cor azul na [[#img-12|Figura 12]], demonstrando assim a concentração de tensões de compressão em algumas regiões da viga-parede. |
| − | + | <div id='img-12'></div> | |
| − | {| style="width: | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | | + | |style="padding:10px;"| [[Image:review_LIMA_2017a-image103.png|234px]] |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | '''Figura 12 | + | | colspan="1" style="padding:10px;"| '''Figura 12'''. Representação vetorial das tensões na viga-parede com a malha refinada Ansys |
|} | |} | ||
| − | Nas Tabelas 7, 8, 9, 10 e 11 apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e o software ANSYS 17. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas. | + | Nas [[#tab-7|Tabelas 7]], [[#tab-8|8]], [[#tab-9|9]], [[#tab-10|10]] e [[#tab-11|11]] apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e o software ANSYS 17. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas. |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 7 | + | '''Tabela 7'''. Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{x}</math> (kN/cm²)</div> |
| − | + | <div id='tab-7'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 907: | Line 891: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 8 | + | '''Tabela 8'''. Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{y}</math> (kN/cm²)</div> |
| − | + | <div id='tab-8'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 962: | Line 946: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 9 | + | '''Tabela 9'''. Tensões <math display="inline">{\boldsymbol{\tau }}_{\boldsymbol{xy}}</math> (kN/cm²)</div> |
| − | + | <div id='tab-9'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,017: | Line 1,001: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 10 | + | '''Tabela 10'''. Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{1}</math> (kN/cm²)</div> |
| − | + | <div id='tab-10'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,072: | Line 1,056: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size:75%;"> |
| − | '''Tabela 11 | + | '''Tabela 11'''. Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{2}</math> (kN/cm²)</div> |
| − | + | <div id='tab-11'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size:85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,127: | Line 1,111: | ||
| − | Nas | + | Nas [[#img-13|Figura 13]]a e [[#img-13|13]]b mostram-se comparações gráficas entre os deslocamentos nodais obtidos por meio do programa desenvolvido e os resultados fornecidos a partir do software ANSYS 17, sendo os nós localizados na parte inferior da viga-parede. |
| − | + | <div id='img-13'></div> | |
| − | {| style=" | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image108.png|252px]] |
| − | + | | style="text-align: center;vertical-align: top;padding:10px;"| [[Image:review_LIMA_2017a-image109.png|246px]] | |
| − | + | |- | |
| − | | style="text-align: center;vertical-align: top; | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | '''Figura | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="2" style="padding:10px;"| '''Figura 13'''. (a) Deslocamento em ''x''. (b) Deslocamento em ''y'' | ||
|} | |} | ||
===4.4 Sapata rígida === | ===4.4 Sapata rígida === | ||
| − | A sapata rígida em análise cujas dimensões são mostradas na Figura 14 está submetida a um carregamento pontual igual a 800 kN. Neste exemplo o concreto apresenta um módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25. | + | A sapata rígida em análise cujas dimensões são mostradas na [[#img-14|Figura 14]] está submetida a um carregamento pontual igual a 800 kN. Neste exemplo o concreto apresenta um módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25. |
| − | + | <div id='img-1'></div> | |
| − | {| style="width: | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | | + | |style="padding:10px;"| [[Image:review_LIMA_2017a-image110.png|324px]] |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | '''Figura 14 | + | | colspan="1" style="padding:10px;"| '''Figura 14'''. Dimensões da sapata rígida (cm) |
|} | |} | ||
| − | Em sua modelagem, a sapata foi dividida em duas áreas para que o Software ANSYS 17 pudesse gerar a malha. A parte superior foi mapeada de forma livre e a parte inferior, correspondente à fôrma, foi mapeada de forma estruturada, realizando três análises distintas dividindo a parte inferior em 10, 20 e 25 divisões com o fim de se comparar eventuais alterações nos resultados numéricos. As respectivas malhas geradas no software ANSYS 17, são mostradas nas Figuras | + | Em sua modelagem, a sapata foi dividida em duas áreas para que o Software ANSYS 17 pudesse gerar a malha. A parte superior foi mapeada de forma livre e a parte inferior, correspondente à fôrma, foi mapeada de forma estruturada, realizando três análises distintas dividindo a parte inferior em 10, 20 e 25 divisões com o fim de se comparar eventuais alterações nos resultados numéricos. As respectivas malhas geradas no software ANSYS 17, são mostradas nas [[#img-15|Figuras 15]]a, [[#img-15|15]]b e [[#img-15|15]]c. No primeiro caso analisado, a malha gerada apresenta 164 elementos finitos triangulares (CST) e 111 nós. A segunda malha gerada apresenta 272 elementos finitos triangulares (CST) e com 170 nós. Já a malha final apresenta 329 elementos finitos triangulares (CST) e com 201 nós. |
| − | + | <div id='img-15'></div> | |
| − | {| style=" | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image111.png|252px]] |
| − | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image112.png|246px]] | |
| − | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image113.png|246px]] | |
| − | | style="text-align: center; | + | |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | '''Figura | + | | style="text-align: center;font-size: 75%;"|(c) |
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="3" style="padding:10px;"| '''Figura 15'''. (a) Malha da sapata rígida – 10 divisões. (b) Malha da sapata rígida – 20 divisões. (c) Malha da sapata rígida - 25 divisões | ||
|} | |} | ||
| − | A malha com 25 divisões apresentou melhores resultados em suas análises, podendo observar o comportamento e as deformações da sapata rígida nas Figuras | + | A malha com 25 divisões apresentou melhores resultados em suas análises, podendo observar o comportamento e as deformações da sapata rígida nas [[#img-16|Figuras 16]]a, [[#img-16|16]]b e [[#img-16|16]]c, cujas escalas de referências encontram-se em kN/cm². Na Figura 16d, mostra-se, de forma vetorial, a transferência dos esforços internos. |
| − | + | <div id='img-16'></div> | |
| − | {| style=" | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image114.png|276px]] |
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image116.png|276px]] |
| + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image118.png|264px]] | ||
| + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image120.png|264px]] | ||
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | '''Figura | + | | style="text-align: center;font-size: 75%;"|(c) |
| − | + | | style="text-align: center;font-size: 75%;"|(d) | |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | + | | colspan="4" style="padding:10px;"| '''Figura 16'''. (a) Tensão principal <math>{\boldsymbol{\sigma }}_\boldsymbol{1}</math>. (b) Tensão principal <math>{\boldsymbol{\sigma }}_\boldsymbol{2}</math>. (c) Tensão principal <math>{\boldsymbol{\sigma }}_\boldsymbol{3}</math>. (d) Representação vetorial das tensões no bloco de fundação – Ansys | |
|} | |} | ||
| − | Nas Tabelas 12, 13, 14, 15 e 16, apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e por meio do software ANSYS 17 para a sapata com 25 divisões na parte inferior. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas. | + | Nas [[#tab-12|Tabelas 12]], [[#tab-13|13]], [[#tab-14|14]], [[#tab-15|15]] e [[#tab-16|16]], apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e por meio do software ANSYS 17 para a sapata com 25 divisões na parte inferior. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas. |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 12 | + | '''Tabela 12'''. - Tensões <math>{\boldsymbol{\sigma }}_\boldsymbol{x}</math> (kN/cm²)'''</div> |
| − | + | <div id='tab-12'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,241: | Line 1,227: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 13 | + | '''Tabela 13'''. Tensões <math>{\boldsymbol{\sigma }}_\boldsymbol{y}</math> (kN/cm²)</div> |
| − | + | <div id='tab-13'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,296: | Line 1,282: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 14 | + | '''Tabela 14'''. Tensões <math>{\boldsymbol{\tau }}_{\boldsymbol{xy}}</math> (kN/cm²)</div> |
| − | + | <div id='tab-14'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,351: | Line 1,337: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 15 | + | '''Tabela 15'''. Tensões <math>{\boldsymbol{\sigma }}_\boldsymbol{1}</math> (kN/cm²)</div> |
| − | + | <div id='tab-15'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,406: | Line 1,392: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 16 | + | '''Tabela 16'''. Tensões <math>{\boldsymbol{\sigma }}_\boldsymbol{2}</math> (kN/cm²)</div> |
| − | + | <div id='tab-16'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,461: | Line 1,447: | ||
| − | Em relação aos deslocamentos nodais, as | + | Em relação aos deslocamentos nodais, as [[#img-17|Figura 17]]a e [[#tab-17|17]]b mostram as comparações gráficas entre os deslocamentos na parte inferior da sapata rígida obtida por meio do programa desenvolvido e pelos resultados determinados via software ANSYS 17, utilizando um maior número de nós entre as simulações realizadas. |
| − | + | <div id='tab-17'></div> | |
| − | {| style="width: | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image126.png|246px]] |
| − | + | | style="text-align: center;vertical-align: top;padding:10px;"| [[Image:review_LIMA_2017a-image127.png|252px]] | |
| − | + | |- | |
| − | | style="text-align: center;vertical-align: top; | + | | style="text-align: center;font-size: 75%;"|(a) |
| + | | style="text-align: center;font-size: 75%;"|(b) | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="2" style="padding:10px;"| '''Figura 17'''. (a) Deslocamento em ''x''. (b) Deslocamento em ''y'' | ||
|} | |} | ||
===4.4 Consolo curto=== | ===4.4 Consolo curto=== | ||
| − | O consolo curto analisado, cujas dimensões são mostradas na Figura | + | O consolo curto analisado, cujas dimensões são mostradas na [[#img-18|Figura 18]]a, está submetido a um carregamento pontual igual a 400 kN. Nesta aplicação, o concreto apresenta módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25. O consolo curto foi discretizado pelo software ANSYS 17, gerando uma malha livre com 223 elementos finitos triangulares (CST) e com 139 nós, conforme mostrado na [[#img-18|Figura 18]]b. |
| − | {| style=" | + | <div id='img-18'></div> |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| − | | style="text-align: center;vertical-align: top; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image128.png|150px]] |
| + | | style="text-align: center;vertical-align: top;padding:10px;"| [[Image:review_LIMA_2017a-image129.png|138px]] | ||
| + | |- | ||
| + | | style="text-align: center;font-size: 75%;"|(a) | ||
| + | | style="text-align: center;font-size: 75%;"|(b) | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="2" style="padding:10px;"| '''Figura 18'''. (a) Dimensões do consolo curto (cm). (b) Malha livre do consolo curto Ansys | ||
| + | |} | ||
| − | |||
| − | |||
| − | '''Figura | + | As configurações deformadas do elemento em análise submetido às tensões principais (<math display="inline">{\mbox{σ}}_\mbox{1}</math>, <math display="inline">{\mbox{σ}}_\mbox{2}</math> e <math display="inline">{\mbox{σ}}_\mbox{3}</math>) são mostradas nas [[#img-19|Figuras 19]]a, [[#img-19|19]]b e [[#img-19|19]]c, respectivamente. |
| + | <div id='img-19'></div> | ||
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image130.png|120px]] | ||
| + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image132.png|114px]] | ||
| + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image134.png|114px]] | ||
| + | |- | ||
| + | | style="text-align: center;font-size: 75%;"|(a) | ||
| + | | style="text-align: center;font-size: 75%;"|(b) | ||
| + | | style="text-align: center;font-size: 75%;"|(c) | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="3" style="padding:10px;"| '''Figura 19'''. (a) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{1}</math>. (b) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_2</math>. (c) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{3}</math> | ||
|} | |} | ||
| − | + | Logo é possível visualizar a transferência dos esforços internos por meio de uma representação vetorial mostrada na [[#img-20|Figura 20]], determinando as regiões tracionadas e comprimidas do consolo curto. | |
| − | + | <div id='img-20'></div> | |
| − | {| style=" | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | | + | |style="padding:10px;"| [[Image:review_LIMA_2017a-image136.png|120px]] |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | + | | colspan="1" style="padding:10px;"| '''Figura 20'''. Representação vetorial das tensões no consolo curto – Ansys | |
| − | | | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|} | |} | ||
| − | + | Nas [[#tab-17|Tabelas 17]], [[#tab-18|18]], [[#tab-19|19]], [[#tab-20|20]] e [[#tab-21|21]] apresentam-se comparações entre os resultados numéricos determinados pelo programa computacional desenvolvido e a partir do software ANSYS 17. | |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto; | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | + | '''Tabela 17'''. Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{x}</math> (kN/cm²)</div> | |
| − | + | <div id='tab-17'></div> | |
| − | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" | |
| − | ''' | + | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | {| style="width: 100%;border-collapse: collapse;" | + | |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,567: | Line 1,560: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 18 - Tensões | + | '''Tabela 18 - Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{y}</math> (kN/cm²)</div> |
| − | + | <div id='tab-18'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,622: | Line 1,615: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 19 | + | '''Tabela 19'''. Tensões <math display="inline">{\boldsymbol{\tau }}_{\boldsymbol{xy}}</math> (kN/cm²)</div> |
| − | + | <div id='tab-19'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,677: | Line 1,670: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 20 | + | '''Tabela 20'''. Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{1}</math> (kN/cm²)</div> |
| − | + | <div id='tab-20'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,732: | Line 1,725: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 21 | + | '''Tabela 21'''. Tensões <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{2}</math> (kN/cm²)</div> |
| − | + | <div id='tab-21'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,787: | Line 1,780: | ||
| − | Nas Figuras | + | Nas [[#img-21|Figuras 21]]a e [[#img-21|21]]b mostram-se comparações gráficas entre os deslocamentos nodais obtidos a partir do programa desenvolvido e os resultados do ANSYS 17, sendo os nós referentes à parte superior do consolo curto. Lembrando que nessa região ficam localizadas as armaduras de tração. |
| − | + | <div id='img-1'></div> | |
| − | {| style=" | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
| + | |- | ||
| + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image141.png|258px]] | ||
| + | | style="text-align: center;vertical-align: top;padding:10px;"| [[Image:review_LIMA_2017a-image142.png|264px]] | ||
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | | style="text-align: center; | + | | colspan="2" style="padding:10px;"| '''Figura 21'''. (a) Deslocamento em ''x''. (b) Deslocamento em ''y'' |
| − | + | ||
| − | '''Figura | + | |
|} | |} | ||
| − | Por fim, realizou-se o dimensionamento do consolo curto e os resultados foram comparados com as respostas determinadas pelo presente trabalho que é baseado no Método dos Elementos Finitos, sendo os valores das tensões elementares extraídos da modelagem numérica realizada. Para a realização do dimensionamento, considerou-se a altura útil do consolo igual a <math display="inline">\mbox{d}</math> | + | Por fim, realizou-se o dimensionamento do consolo curto e os resultados foram comparados com as respostas determinadas pelo presente trabalho que é baseado no Método dos Elementos Finitos, sendo os valores das tensões elementares extraídos da modelagem numérica realizada. Para a realização do dimensionamento, considerou-se a altura útil do consolo igual a <math display="inline">\mbox{d} =31</math>cm, <math display="inline">\mbox{d'} =4</math>cm, a distância entre o ponto de aplicação da carga e a face do pilar igual <math display="inline">\mbox{a}</math> =15,5cm e <math display="inline">\mbox{f}_{\mbox{yd} =43,47}</math>kN/cm<math>^2</math>. Na [[#tab-22|Tabela 22]] mostra-se a boa aproximação entre os resultados encontrados. |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 22 | + | '''Tabela 22'''. Área de Aço (cm²)</div> |
| − | + | <div id='tab-22'></div> | |
| − | {| style=" | + | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:65%;" |
|- | |- | ||
| − | | style="border-top: 2pt solid black;border-bottom: | + | | style="border-top: 2pt solid black;border-bottom: 2pt solid black;text-align: center;"|'''Resultado Normativo''' |
| − | | style="border-top: 2pt | + | | style="border-top: 2pt solid black;border-bottom: 2pt solid black;text-align: center;"|'''Presente Trabalho''' |
| − | | style="border-top: 2pt | + | | style="border-top: 2pt solid black;border-bottom: 2pt solid black;text-align: center;"|'''Presente Trabalho/ Resultado Normativo''' |
|- | |- | ||
| − | | style="border-top: 1pt solid black;border-bottom: 2pt | + | | style="border-top: 1pt solid black;border-bottom: 2pt solid black;text-align: center;"|5,11 |
| − | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-bottom: 2pt | + | | style="border-top: 1pt solid black;border-left: 1pt solid black;border-bottom: 2pt solid black;text-align: center;"|4,64 |
| − | | style="border-top | + | | style="border-top: 1pt solid black;border-bottom: 2pt solid black;text-align: center;"|0,91 |
|} | |} | ||
===4.5 Bloco de fundação sob duas estacas de concreto=== | ===4.5 Bloco de fundação sob duas estacas de concreto=== | ||
| − | O bloco de fundação com duas estacas está submetido a um carregamento pontual igual a 1500 kN, suas dimensões são mostradas na Figura | + | O bloco de fundação com duas estacas está submetido a um carregamento pontual igual a 1500 kN, suas dimensões são mostradas na [[#img-22|Figura 22]]a. Considerou-se neste exemplo que o concreto apresenta módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25. Por sua vez, o bloco de fundação foi discretizado com quatro malhas distintas, sendo apresentados os resultados das análises realizadas com a malha estruturada de 328 elementos finitos triangulares (CST) e 202 nós mostrada na [[#img-22|Figura 22]]b. |
| − | + | <div id='img-22'></div> | |
| − | {| style="width: | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image147.png|216px]] |
| − | + | | style="text-align: center;vertical-align: top;padding:10px;"| [[Image:review_LIMA_2017a-image148.png|228px]] | |
| − | + | |- | |
| − | | style="text-align: center;vertical-align: top; | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | '''Figura | + | |- style="text-align: center; font-size: 75%;" |
| + | | colspan="2" style="padding:10px;"| '''Figura 22'''. (a) Dimensões do bloco de (cm). (b) Malha do bloco de fundação – Ansys | ||
|} | |} | ||
| − | Com auxílio do software ANSYS 17 é possível observar o comportamento e as deformações do bloco de fundação. Essas configurações deformadas são mostradas nas Figuras | + | Com auxílio do software ANSYS 17 é possível observar o comportamento e as deformações do bloco de fundação. Essas configurações deformadas são mostradas nas [[#img-23|Figuras 23]]a, [[#img-23|23]]b e [[#img-23|23]]c, respectivamente, cujas escalas de referências encontram-se em kN/cm². Na [[#img-23|Figura 23]]d, mostra-se, de forma vetorial, as tensões de tração e compressão no bloco de fundação. |
| − | + | <div id='img-23'></div> | |
| − | {| style=" | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image149.png|198px]] |
| − | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image150.png|198px]] | |
| − | + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image152.png|186px]] | |
| − | | style="text-align: center; | + | | style="text-align: center;padding:10px;"|[[Image:review_LIMA_2017a-image154.png|192px]] |
| − | + | ||
| − | + | ||
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | '''Figura | + | | style="text-align: center;font-size: 75%;"|(c) |
| − | + | | style="text-align: center;font-size: 75%;"|(d) | |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | + | | colspan="3" style="padding:10px;"| '''Figura 23'''. (a) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{1}</math>. (b) Tensão principal <math display="inline">{\boldsymbol{\sigma }}_\boldsymbol{2}</math>. (c) Tensão principal <math>{\boldsymbol{\sigma }}_\boldsymbol{3}</math>. (d) Representação vetorial de tensões no bloco de fundação – Ansys | |
|} | |} | ||
| − | Nas Tabelas 23, 24, 25, 26 e 27, apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e do software ANSYS 17. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas. | + | Nas [[#tab-23|Tabelas 23]], [[#tab-24|24]], [[#tab-25|25]], [[#tab-26|26]] e [[#tab-27|27]], apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e do software ANSYS 17. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas. |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 23 | + | '''Tabela 23'''. Tensões <math>{\boldsymbol{\sigma }}_\boldsymbol{x}</math> (kN/cm²)</div> |
| − | + | <div id='tab-23'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,908: | Line 1,901: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 24 | + | '''Tabela 24'''. Tensões <math>{\boldsymbol{\sigma }}_\boldsymbol{y}</math> (kN/cm²)</div> |
| − | + | <div id='tab-24'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 1,963: | Line 1,956: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 25 | + | '''Tabela 25'''. Tensões <math>{\boldsymbol{\tau }}_{\boldsymbol{xy}}</math> (kN/cm²)</div> |
| − | + | <div id='tab-25'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 2,018: | Line 2,011: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 26 | + | '''Tabela 26'''. Tensões <math>{\boldsymbol{\sigma }}_\boldsymbol{1}</math> (kN/cm²)</div> |
| − | + | <div id='tab-26'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 2,073: | Line 2,066: | ||
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 27 | + | '''Tabela 27'''. Tensões <math>{\boldsymbol{\sigma }}_\boldsymbol{2}</math> (kN/cm²)</div> |
| − | + | <div id='tab-27'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;"|'''Elemento''' | ||
| Line 2,128: | Line 2,121: | ||
| − | Nas Figuras | + | Nas [[#img-23|Figuras 24]]a e [[#img-23|24]]b mostram-se comparações gráficas entre os deslocamentos nodais obtidos a partir do programa desenvolvido e os resultados obtidos via ANSYS 17, sendo os nós referentes à parte inferior do bloco de fundação, localizados entre as duas estacas de concreto. |
| − | + | <div id='img-24'></div> | |
| − | {| style=" | + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" |
| + | |- | ||
| + | | style="text-align: center;padding:10px;"| [[Image:review_LIMA_2017a-image159.png|258px]] | ||
| + | | style="text-align: center;vertical-align: top;padding:10px;"| [[Image:review_LIMA_2017a-image160.png|252px]] | ||
|- | |- | ||
| − | | style="text-align: center; | + | | style="text-align: center;font-size: 75%;"|(a) |
| − | + | | style="text-align: center;font-size: 75%;"|(b) | |
| − | + | |- style="text-align: center; font-size: 75%;" | |
| − | | style="text-align: center; | + | | colspan="2" style="padding:10px;"| '''Figura 24'''. (a) Deslocamento em ''x''. (b) Deslocamento em ''y'' |
| − | + | ||
| − | '''Figura | + | |
|} | |} | ||
| − | Por fim, encontrou-se a área de aço da armadura tracionada a partir do Método de Blévot & Frémy e os resultados foram confrontados com respostas obtidas a partir do Método dos Elementos Finitos para as quatro malhas analisadas. Para a realização do dimensionamento, considerou-se: | + | Por fim, encontrou-se a área de aço da armadura tracionada a partir do Método de Blévot & Frémy e os resultados foram confrontados com respostas obtidas a partir do Método dos Elementos Finitos para as quatro malhas analisadas. Para a realização do dimensionamento, considerou-se: <math display="inline">h =25</math> cm, <math>\mbox{d'} =4</math>cm, <math>\mbox{a}_\mbox{0} =40</math>cm, <math>\mbox{a} =60</math>cm e <math display="inline">\mbox{f}_{\mbox{yd}} =43,47</math> kN/cm². Os resultados são mostrados na [[#tab-28|Tabela 28]], verificando uma melhora na aproximação dos resultados com o refinamento da malha. |
| − | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;"> | + | <div class="center" style="width: auto; margin-left: auto; margin-right: auto;font-size: 75%;"> |
| − | '''Tabela 28 | + | '''Tabela 28'''. Área de Aço (cm²)</div> |
| − | + | <div id='tab-28'></div> | |
| − | {| style="width: 100%;border-collapse: collapse;" | + | {| style="width: 100%;border-collapse: collapse;font-size: 85%;" |
|- | |- | ||
| style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|'''Bloco de Fundação''' | | style="border-top: 2pt solid black;border-bottom: 1pt solid black;border-right: 1pt solid black;text-align: center;"|'''Bloco de Fundação''' | ||
| Line 2,180: | Line 2,174: | ||
O objetivo principal prático da pesquisa desenvolvida foi dimensionar as armaduras de aço tracionadas em alguns elementos estruturais estudados, utilizando como base um programa computacional implementado em linguagem FORTRAN com formulação baseada no Método dos Elementos Finitos e realiza um comparativo com algumas prescrições normativas vigentes, com o intuito de verificar a precisão dessas respostas. | O objetivo principal prático da pesquisa desenvolvida foi dimensionar as armaduras de aço tracionadas em alguns elementos estruturais estudados, utilizando como base um programa computacional implementado em linguagem FORTRAN com formulação baseada no Método dos Elementos Finitos e realiza um comparativo com algumas prescrições normativas vigentes, com o intuito de verificar a precisão dessas respostas. | ||
| − | Na análise feita por meio do modelo desenvolvido por | + | Na análise feita por meio do modelo desenvolvido por Montoya el al. [1], verificaram-se também de forma numérica via Método dos Elementos Finitos, diversos pontos em que há o surgimento de trincas, visto que, os valores de tensões obtidos ultrapassaram a resistência à tração do concreto. |
| − | Com relação à análise da viga-parede verificou-se a formação das bielas e tirantes a partir da representação vetorial, comprovando dessa forma as regiões comprimidas e tracionadas do elemento estrutural. | + | Com relação à análise da viga-parede verificou-se a formação das bielas e tirantes a partir da representação vetorial, comprovando dessa forma as regiões comprimidas e tracionadas do elemento estrutural. |
Em relação ao dimensionamento, em duas aplicações (consolos curtos e bloco de fundação) verificou-se boa aproximação ao serem comparados os resultados numéricos com a metodologia desenvolvida por Blévot & Frémy. | Em relação ao dimensionamento, em duas aplicações (consolos curtos e bloco de fundação) verificou-se boa aproximação ao serem comparados os resultados numéricos com a metodologia desenvolvida por Blévot & Frémy. | ||
| − | Para a análise realizada no bloco de fundação, verificou-se que o refinamento na malha de elementos finitos proporcionou maior aproximação entre o valor de área de aço calculado numericamente e o resultado determinado a partir do método clássico desenvolvido por | + | Para a análise realizada no bloco de fundação, verificou-se que o refinamento na malha de elementos finitos proporcionou maior aproximação entre o valor de área de aço calculado numericamente e o resultado determinado a partir do método clássico desenvolvido por Blévot & Frémy [8]. |
==Referências== | ==Referências== | ||
| − | [1] | + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> |
| + | |||
| + | [1] Montoya, P.J., Meseger, A.G., Cabré, F.M. Hormigón Armado. 13 ed. Editorial Gustavo Gili, Barcelona, 1991. | ||
| + | |||
| + | [2] Schlaich, J., Schafer, K. Consistent Design of Structural Concrete Using Strut and Tie Model. 5º Colóquio sobre comportamento e Projeto de estruturas. PUC, Rio de Janeiro, 1988. | ||
| + | |||
| + | [3] Souza, R.A. Análise, dimensionamento e verificação de elementos especiais em concreto armado utilizando o método dos elementos finitos e o método das bielas. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 2006. | ||
| − | [ | + | [4] Fontes, F.F. Análise Estrutural de elementos lineares segundo a NBR 6118:2003. Dissertação de Mestrado, Escola de Engenharia de São Carlos. USP, São Carlos, 2005. |
| − | [ | + | [5] Vicente, W.M., Oliveira, W. C. Análise de Tensões em Placas Circulares Utilizando elementos Finitos Axissimétricos. Trabalho Final de Graduação de Engenharia Mecânica, Universidade Federal de Itajubá, Itajubá, 2009. |
| − | [ | + | [6] Delalibera, R.G. Estudo experimental e analítico de blocos sobre estacas submetidos a momento e normal. Qualificação de Doutorado, Escola de Engenharia de São Carlos, USP, São Carlos, 2005. |
| − | [ | + | [7] Hobbs, N.B., Stein, P. An investigation into the stress distribution in pile caps with some notes on design. Proceedings of the Institution of Civil Engineers, 1957. |
| − | [ | + | [8] Blévot, J., Frémy, R. Semelles sur piex. Analles d’ Institut Techique du Bâtiment et des Travaux Publlics. Paris, 1967. |
| − | [ | + | [9] NBR-6118. Projeto de Estruturas de Concreto – Procedimento, ABNT – Associação Brasileira de Normas Técnicas, Rio de Janeiro, Brasil, 2014. |
| − | [ | + | [10] Fernandes, R. M., EL DEBS, M.K. Análise da capacidade resistente de consolos de concreto armado considerando a contribuição da armadura de costura. Cadernos de Engenharia de Estruturas da UFSCar, 2005. |
| − | [ | + | [11] NBR-9062. Projeto e execução de estruturas de concreto pré-moldado, ABNT – Associação Brasileira de Normas Técnicas, Rio de Janeiro, Brasil, 2006. |
| − | [ | + | [12] Chandrupatla, T.R., Belegundu, A.D. Elementos Finitos. Pearson Education do Brasil, São Paulo, 2014. |
| − | |||
| − | + | </div> | |
Latest revision as of 15:10, 11 June 2021
Resumo
Neste trabalho tem-se como objetivo realizar análises elástico-lineares a partir de um programa computacional destinado à implementação numérica do Modelo de Bielas e Tirantes, utilizando-se uma formulação baseada no Método dos Elementos Finitos (MEF). Com este modelo é possível analisar o comportamento de elementos estruturais como blocos de fundação, consolos curtos e sapatas rígidas e realizar o dimensionamento das armaduras de aço, representar os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por Montoya et al. [1], além de modelar numericamente via MEF uma viga-parede com uma grande abertura, desenvolvida por Schlaich et al. [2]. Com o fim de validar as implementações numéricas, os resultados foram comparados com modelagens numéricas realizadas com o auxílio do software ANSYS 17 e com expressões normativas.
Palavras–chave: Modelo de bielas e tirantes, elementos finitos, blocos de fundação, consolos curtos, vigas-parede, sapatas rígidas
Abstract
The main objective of this work was to perform elastic-linear analysis through computational program and numerical approach from strut-and-tie model, using a formulation based on Finite Element Method (FEM). In this model, it is possible to analyze the behavior of structural elements such as foundation blocks, wall beams, short consoles; to demosntrate the values of tensions, deformations, and displacements in the region of a beam represented by the Model of cranks developed by Montoya et al. [1]; besides numerically modeling a wall beam via FEM with a large aperture, developed by Schlaich et al. [2]. In order to validate the numerical implementations, the results were compared with numerical modeling performed with the aid of the software ANSYS 17 and normative expressions.
Keywords: Strut-and-tie model, finite elements, foundation block, short consoles, wall beams and rigid shoes
1. Introdução
A concepção de projetos estruturais estabelece três propósitos: economia, tempo e segurança. Para atingir o equilíbrio entre esses fatores há uma ampla quantidade de materiais e métodos disponíveis no mercado, que são abordados em vários temas de pesquisas por todo o mundo. Tratando-se dos elementos estruturais, o aço e o concreto são os materiais mais utilizados, visto que, se completam quando trabalham em conjunto. Muitas vezes em uma análise estrutural o projetista é forçado a propor uma solução simplificada para um problema que requer uma análise mais específica, devido aos prazos reduzidos impostos pelo mercado. Esse fato pode acarretar um superdimensionamento dos elementos estruturais gerando um gasto excessivo de materiais ou até mesmo levar o sistema estrutural à ruptura.
O Método dos Elementos Finitos (MEF), concebido na década de 50, vem sendo utilizado com grande sucesso na engenharia estrutural. Existe uma infinidade de softwares com poderosos pós-processadores e com os mais avançados modelos construtivos para o tratamento do concreto armado [3]. Em uma modelagem utilizando o MEF é necessário que se faça um levantamento dos parâmetros a serem considerados e uma análise cuidadosa da aplicação dos carregamentos e das condições de contorno, para que se possa realizar um estudo preciso e confiável dos resultados obtidos.
O Modelo de Bielas e Tirantes surge como uma alternativa para solucionar casos específicos em que não se aplica a hipótese de Bernoulli ou hipótese das seções planas. Este procedimento permite identificar as regiões da estrutura que exibem comportamento diferenciado em relação às distribuições de tensões e deformações. O estudo levou em consideração que os materiais se comportam de maneira elástico-linear. Nesse caso, após sofrer deformações, a estrutura tende a retornar ao seu estado original quando o carregamento externo for cessado. Além disso, há uma relação linear entre as componentes de tensão e deformação do material, conhecida como módulo de elasticidade [4]. Nessa pesquisa será utilizada a formulação isoparamétrica do Método dos Elementos Finitos, na qual as funções de forma dos elementos são dadas no sistema local de coordenadas naturais e [5].
O trabalho tem como objetivo realizar análises elástico-lineares de elementos especiais em concreto armado, a partir do Modelo de Bielas e Tirantes utilizando-se uma formulação baseada no Método dos Elementos Finitos (MEF). Para tal desenvolveu-se um programa computacional, em liguagem FORTRAN 90, adotando-se elementos finitos triangulares, conhecidos como Constant Strain Triangle (CST), sendo os resultados numéricos obtidos comparados com modelagens feitas com auxílio do software ANSYS 17.
Com este modelo foi possível analisar o comportamento de elementos estruturais como blocos de fundação, consolos curtos, sapatas rígidas, representar os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por Montoya et al. [1], além de modelar numericamente via MEF uma viga-parede com uma grande abertura, desenvolvida por Schlaich et al. [2]. Por fim, com o objetivo de verificar que é possível projetar as armaduras de aço de estruturas de concreto usando o Método dos Elementos Finitos, realizou-se o dimensionamento de alguns elementos estruturais via MEF e os resultados foram comparados com respostas obtidas a partir de expressões normativas encontradas na literatura.
2. Modelo de bielas e tirantes
2.1 Conceitos
O Modelo de Bielas e Tirantes tem como princípio a idealização de que a força do pilar se concentra em algumas regiões do bloco de fundação até chegar às estacas. São formadas zonas de concreto comprimidas (bielas), como Mörsch idealizou no caso das vigas. Na Figura 1 mostram-se as regiões comprimidas do concreto em um bloco submetido a uma força vertical. Este modelo foi comprovado ao se resolver um bloco análogo utilizando o Método dos Elementos Finitos [6], que pode ser visto na Figura 2, comprovando a formação das bielas comprimidas.
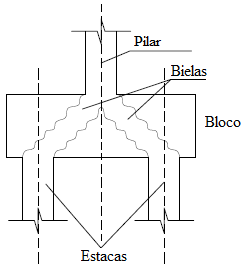
|
| Figura 1. Modelo idealizado da formação de bielas |
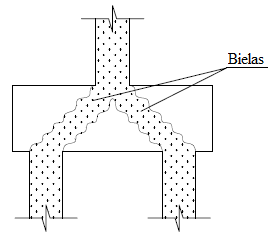
|
| Figura 2. Modelo desenvolvido por elementos finitos |
Logo, o Método de Bielas e Tirantes consiste em admitir que um bloco possui um funcionamento estrutural básico similar à de uma treliça espacial, constituído por barras comprimidas e inclinadas (bielas), formada pelo concreto comprimido e responsáveis pela transmissão do carregamento dos pilares para as estacas e barras tracionadas (tirantes), representadas pelas armaduras principais.
Os modelos e conceitos apresentados são embasados em ensaios relatados na bibliografia, e pode-se dizer que se iniciaram com os estudos de Hobbs & Stein [7], que analisaram o comportamento de blocos sobre duas estacas de forma analítica e experimental, em setenta modelos em escala 1:3 e de Blévot & Frémy [8], ensaiando 100 blocos em suas análises.
2.2 Método de Blévot & Frémy para blocos de fundação
A partir dos resultados obtidos pelos ensaios realizados por Blévot & Frémy [8], deu-se origem a um processo de cálculo para a armadura longitudinal (tirante) e verificação da tensão de compressão na biela, sendo similar ao processo de Biela e Tirante, mas se difere na definição da seção da biela. Este processo tem sido de grande utilidade nas construções brasileiras, apesar da ABNT NBR 6118 [9] não citá-lo explicitamente.
Portanto, o Método de Blévot & Frémy, também entendido como o de Biela e Tirante, consiste no cálculo das armaduras tracionadas e verificação da tensão nas bielas de compressão que se desenvolvem no interior do bloco, devendo ser feita junto à base do pilar e junto à cabeça da estaca.
A tensão nas bielas na base do pilar é verificada pela relação entre as áreas da seção transversal do pilar () e da biela () na base do pilar. Dividindo-se a força na biela pela área da biela () tem-se a tensão normal na biela junto ao pilar ():
|
|
(1) |
De maneira análoga, a tensão nas bielas junto à estaca pode ser verificada pela relação entre as áreas da seção transversal da estaca () e da biela () junto à estaca. Dividindo-se o valor da força atuante na biela (), pela área da seção transversal da biela () tem-se a tensão normal na biela junto à estaca ():
|
|
(2) |
A armadura principal de tração (), no Estado Limite Último (ELU), pode ser calculada em função da força atuante na armadura () e a resistência de cálculo ao escoamento do aço (). Como , realizando manipulações matemáticas, tem-se que a armadura principal de tração () é dada por:
|
|
(3) |
2.3 Método de bielas e tirantes para consolos curtos
O comportamento estrutural dos consolos curtos e muito curtos se difere das vigas, pois não se pode levar em consideração a hipótese da teoria clássica de flexão. Para analisar sua capacidade resistente ou realizar seu dimensionamento, não se podem utilizar os modelos de cálculo de vigas que levam em consideração a hipótese da manutenção das seções planas após sofrerem deformações. Mesmo em considerações que o material seja homogêneo, isotrópico e elástico perfeito, as tensões normais não variam de forma linear ao longo da sua altura e as tensões tangenciais e as normais aos planos ortogonais e essa seção não podem ser desprezadas. Além disso, após a fissuração do concreto ocorre a redução da rigidez do consolo e outros mecanismos. Desta forma, o projeto desses elementos estruturais deve ser feito obedecendo a recomendações específicas Fernandes & El Debs [10].
Segundo a ABNT NBR-9062 [11], os consolos são calculados seguindo intervalos da razão entre a distância da força aplicada até a face do pilar () e a altura útil do consolo (), sendo que os consolos curtos () possuem metodologia de cálculo realizado com base no Modelo de Bielas e Tirantes.
O Modelo de Bielas e Tirantes para consolos curtos consiste em idealizar o comportamento do concreto, nos trechos descontínuos, por meio das bielas (compressão) e tirantes (tração), com suas posições definidas a partir do fluxo de tensões. Os elementos são conectados por nós, idealizando uma treliça. Sendo assim, o dimensionamento utilizando esse método consiste em verificar a resistência à compressão em uma seção fictícia da biela e calcular a área da armadura do tirante em função da tensão de escoamento do aço. O modelo clássico consiste no equilíbrio de forças e momentos no esquema de treliça apresentado na Figura 3.
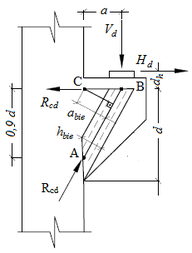
|
| Figura 3. Modelo de análise e características geométricas de Consolo curto - Leonhardt & Mönnig adaptado por EL Debs |
A armadura do tirante é determinada realizando o equilíbrio de momento em relação ao ponto A, resultando na seguinte equação:
|
|
(4) |
Por meio de manipulações matemáticas e realizando o equilíbrio de momentos em relação ao ponto C, determina-se que a tensão de compressão na biela () é calculada pela Equação (5), limitando-se o valor da tensão na biela em .
|
|
(5) |
Adota-se no caso de forças diretas e para forças indiretas.
3. Formulação via Método dos Elementos Finitos
3.1 Introdução
O Método dos Elementos Finitos tem como principal finalidade a discretização de uma seção transversal ou de um dado elemento estrutural ao longo do seu domínio. Para isso, podem ser utilizados elementos planos bidimensionais, a saber: o elementos CST (triangular com três nós), elemento quadrilateral com quatro nós, elemento quadrilateral com oito nós ou por fim o elemento quadrilateral com nove nós pertencente à família de Lagrange, além de outros elementos finitos. Em determinados problemas de sólidos com geometrias não regulares, podem ser utilizados os elementos finitos tridimensionais. Dentre eles, podem-se citar os elementos finitos tetraédricos ou hexaédricos. Assim sendo, a ideia central do método é transformar o problema real ou elemento contínuo, em elemento discreto. Daí, transforma-se o problema em um sistema de equações lineares ou não lineares.
Segundo Chandrupatla & Belegundu [12] a formulação de elementos finitos bidimensionais segue etapas usadas nos problemas unidimensionais. Os deslocamentos, os valores de componentes de força de superfície e de força de corpo distribuídas são funções das posições indicadas por (). A relação entre as tensões e deformações é dada pela Equação (6):
|
|
(6) |
3.2 Modelagem pelo Método dos Elementos Finitos
Uma região bidimensional é dividida em triângulos de lados retos. Esses triângulos que em sua totalidade formam a região analisada são chamados de elementos. As componentes do deslocamento de um nó j qualquer são consideradas como na direção e na direção y. O vetor de deslocamento global da estrutura é indicado por:
|
|
(7) |
As conectividades ou incidências de um elemento referem-se aos nós que formam um elemento, adotando o sentido anti-horário para estabelecer uma sequência para identificar os seus nós. O vetor de deslocamento no sistema local é indicado como:
|
|
(8) |
Os deslocamentos nos pontos dentro de um elemento precisam ser representados em termos dos deslocamentos nodais do elemento. O Método dos Elementos Finitos usa o conceito de funções de forma no desenvolvimento sistemático dessas interpolações. Para o CST (Constant Strain Triangle), as funções de forma são lineares sobre o elemento. As funções de forma , e correspondem aos nós 1, 2 e 3 do elemento. A função assume o valor unitário no nó 1, e se reduz linearmente para os nós 2 e 3. Os valores de definem uma superfície plana e são representadas por superfícies semelhantes com valores unitários nos nós 2 e 3, respectivamente, e caindo para zero nas arestas opostas, como mostrado na Figura 4. Sendo assim, qualquer combinação linear dessas funções de forma também representa uma superfície plana.
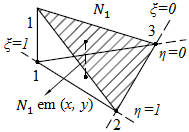
|
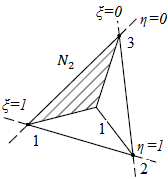
|
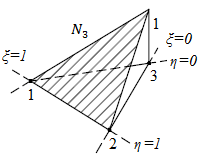
|
| (a) | (b) | (c) |
| Figura 4. Representação das funções de forma no nó 1 (a), nó 2 (b) e nó 3 (c) | ||
Em particular representa um plano com altura um nos nós 1, 2 e 3 que é paralelo ao triângulo 123. , e não são linearmente independentes. As funções de forma independentes são representadas pelas coordenadas naturais e , como:
| (9.1) | |
| (9.2) | |
| (9.3) |
Os deslocamentos dos elementos são escritos usando as funções de forma e os valores nodais do campo de deslocamento desconhecido.
|
|
(10.1) | |
|
|
(10.2) |
sendo , e expressos pelas Equações (9.1), (9.2) e (9.3), as Equações (10.1) e (10.2) ficam representadas, na forma simplificada, por:
|
|
(11) |
As coordenadas e também podem ser representadas em termos de coordenadas nodais pelo uso das mesmas funções de forma. Essa é a chamada representação isoparamétrica. As representações isoparamétricas relacionam as coordenadas cartesianas e às coordenadas naturais e .
Na avaliação das deformações específicas, as derivadas parciais de e devem ser tomadas com relação a e . Pelas representações isoparamétricas verifica-se que , , e são funções de e . Logo, podem ser representadas por:
|
|
(12.1) | |
|
|
(12.2) |
Usando-se a regra da cadeia para derivadas de u, obtém-se a matriz quadrada (2x2) denotada como Jacobiana de transformação, logo:
|
|
(13) |
Realizando-se as derivadas da matriz Jacobiana e algumas manipulações matemáticas chegam-se às relações deformação específica-deslocamento, que pela definição de e demonstra-se que e , podendo ser escrita, de forma sucinta, da seguinte forma:
|
|
(14) |
A energia potencial do sistema é dada por:
|
|
(15) |
sendo que os termos correspondem à energia de deformação do elemento, força de corpo, força de superfície e carregamento pontual, respectivamente. Por meio de triangulação, a energia potencial total pode ser escrita da seguinte forma, sendo que representa a energia de deformação do elemento.
|
|
(16) |
A matriz de rigidez do elemento é obtida por meio da energia de deformação do elemento. Substituindo-se a Equação (14) na energia de deformação do elemento, tem-se:
|
|
(17) |
Considerando a espessura do elemento () e discretizando com triângulos a área a ser analisada, a matriz de rigidez do elemento pode ser obtida a partir da Equação (17), e é dada por:
|
|
(18) |
Considerando-se a energia de deformação, os termos de força, as condições de contorno e realizando-se as modificações de rigidez e forças, a Equação (16) fica definida como:
|
|
(19) |
sendo que refere-se à matriz de rigidez da estrutura analisada, ao vetor de deslocamentos nodais da estrutura e ao vetor de cargas globais aplicadas.
Como as deformações específicas são constantes em um elemento CST, as suas componentes de tensões também permanecem constantes. Os valores das tensões devem ser calculados para cada elemento, usando as relações de deformação específica-deslocamento do elemento. Substituindo-se a Equação (14) na Equação (6), tem-se que a tensão em cada elemento é dada por:
|
|
(20) |
A conectividade será utilizada para extrair os deslocamentos nodais do elemento do vetor de deslocamentos globais . Para fim de interpolação, as tensões obtidas pela Equação (20) podem ser usadas como um valor referente ao centroide do elemento analisado. Finalmente, vale ressaltar que as tensões principais e suas direções principais são determinadas a partir das relações do Círculo de Mohr.
4. Aplicações
4.1 Introdução
Neste capítulo são mostradas as aplicações do presente trabalho, representando de forma numérica o Modelo de Bielas e Tirantes. Inicialmente realizou-se a análise, representando os valores de tensões, deformações e deslocamentos na região de uma viga representada como o Modelo de Bielas desenvolvido por Montoya et al. [1], além de modelar numericamente via MEF uma viga-parede com uma grande abertura, desenvolvida por Schlaich et al. [2]. E por fim analisou-se um consolo curto, um bloco de fundação sob duas estacas de concreto e uma sapata rígida, realizando seus dimensionamentos via MEF e comparando com resultados de expressões normativas e exemplos clássicos encontrados na literatura. Menciona-se ainda que todos os resultados das análises realizadas pelo programa computacional desenvolvido são comparados com resultados determinados por meio da utilização do software ANSYS 17.
Vale ressaltar que em todos os exemplos analisados neste trabalho foi necessário um maior refinamento de malha, em virtude, da utilização do elemento finito plano adotado, Constant Strain Triangle (CST), que no ANSYS 17 corresponde ao elemento sólido “Plane 182”. Esse elemento apresenta campos de deslocamentos menos refinados que os elementos quadrilaterais com quatro nós, ou elementos lineares e que o elemento quadrilateral com nove nós conhecido na literatura como elemento parabólico. Com isso, realizou-se um maior refinamento da malha utilizada com os elementos CST e assim foi possível obter bons resultados, mesmo utilizando um elemento mais simples que os demais.
4.2 Modelo desenvolvido por Montoya
O modelo desenvolvido por Montoya et al. [1] foi implementado analisando-se o comportamento das tensões de compressão nas bielas de uma viga fletida, a partir da discretização da região correspondente (Figura 5a), submetida a um carregamento de superfície igual a 0,797 kN/cm², e não de todo o elemento estrutural.
Na Figura 5b mostram-se as propriedades geométricas da região analisada, sendo submetida a um carregamento pontual aplicado no ponto C. Utilizou-se o modelo de cálculo I da ABNT NBR 6118 [9] para a definição dos ângulos e , com e . A seção transversal da região analisada é igual a 40 x 25 cm, com altura útil (d) igual a 36 cm e com (d’) igual a 4 cm.
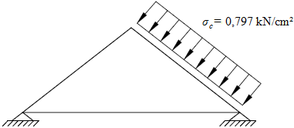
|
|
| (a) | (b) |
| Figura 5. (a) Região da viga analisada pelo Modelo de Montoya. (b) Modelo de Montoya (cm) | |
Em relação às propriedades físicas dos materiais, foram utilizados módulo de elasticidade (E) igual a 2800 kN/cm², coeficiente de Poisson ( ) igual a 0,25 e o concreto com resistência característica à compressão ( ) igual a 30MPa.
Com auxílio do software ANSYS 17 a região analisada foi mapeada, gerando uma malha com 1200 elementos finitos triangulares (CST) e 641 nós, representada pela Figura 6.
É importante informar que em todas as aplicações realizadas, o programa ANSYS serviu como um gerador de malha, ou seja, os dados da malha gerada no ANSYS, coordenadas nodais e elementos com as suas respectivas incidências, foram inseridos como dados de entrada no programa computacional desenvolvido.
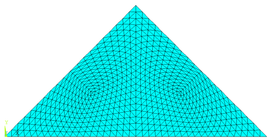
|
| Figura 6. Malha mapeada pelo modelo de Montaya – Ansys |
As Figuras 7a, 7b e 7c permitem observar as configurações deformadas da região comprimida quando estão submetidas às três tensões principais , e , respectivamente. Os valores das tensões encontrados na escala de referência das figuras são dados em kN/cm².
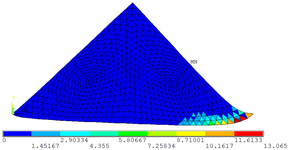
|
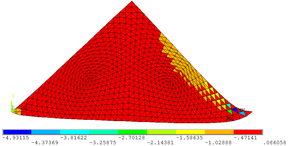
|
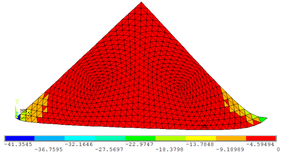
|
| (a) | (b) | (c) |
| Figura 7. (a) Tensão principal . (b) Tensão principal . (c) Tensão principal | ||
Nas Tabelas 1, 2, 3, 4 e 5 apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e a partir do software ANSYS 17. Percebe-se que a precisão obtida pelas simulações numéricas é satisfatória tanto para as tensões elementares ( , e ) quanto para as tensões principais ( , ).
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | -0,7552 | -0,3896 | -0,8807 | -0,4279 | -0,9961 | -0,5038 | -1,1000 | -0,6030 | -1,1890 | -0,7143 |
| ANSYS | -0,7552 | -0,3896 | -0,8807 | -0,4279 | -0,9961 | -0,5038 | -1,0996 | -0,6030 | -1,1892 | -0,7143 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0001 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0004 | 1,0000 | 0,9998 | 1,0000 |
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | -0,6156 | -0,3985 | -0,5535 | -0,4054 | -0,4849 | -0,3993 | -0,4118 | -0,3782 | -0,3364 | -0,3435 |
| ANSYS | -0,6156 | -0,3985 | -0,5535 | -0,4054 | -0,4849 | -0,3993 | -0,4118 | -0,3782 | -0,3364 | -0,3435 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0000 | 0,9999 | 1,0000 | 1,0000 | 0,9999 | 1,0000 | 1,0000 | 0,9999 | 1,0000 |
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | -0,1374 | -0,4087 | -0,1107 | -0,4096 | -0,0990 | -0,4069 | -0,1009 | -0,4040 | -0,1150 | -0,4031 |
| ANSYS | -0,1374 | -0,4088 | -0,1107 | -0,4096 | -0,0990 | -0,4069 | -0,1009 | -0,4040 | -0,1150 | -0,4031 |
| Presente Trabalho/ ANSYS | 1,0002 | 0,9999 | 0,9996 | 1,0000 | 1,0000 | 1,0000 | 1,0005 | 1,0000 | 0,9999 | 0,9999 |
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | -0,5313 | 0,0147 | -0,5196 | -0,0069 | -0,4664 | -0,0413 | -0,3973 | -0,0713 | -0,3212 | -0,0852 |
| ANSYS | -0,5313 | 0,0147 | -0,5196 | -0,0069 | -0,4664 | -0,0413 | -0,3973 | -0,0713 | -0,3212 | -0,0852 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0002 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | -0,8395 | -0,8028 | -0,9146 | -0,8264 | -1,0150 | -0,8618 | -1,1140 | -0,9100 | -0,1204 | -0,9726 |
| ANSYS | -0,8395 | -0,8028 | -0,9147 | -0,8264 | -1,0150 | -0,8618 | -1,1140 | -0,9100 | -0,1204 | -0,9726 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0000 | 0,9999 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 |
Comparando as tensões positivas com a resistência à tração do concreto ( ), verifica-se que há formação de fissuras em algumas regiões específicas na viga. A Tabela 6 comprova esse fato, pois há valores de tensão que ultrapassam 0,30 kN/cm², correspondente à resistência do concreto à tração.
| Elemento | 18 | 19 | 20 | 200 | 201 | 202 | 203 | 204 | 205 | 206 |
| Presente Trabalho | 0,0155 | 0,0028 | 0,0147 | 0,0871 | 2,021 | 3,025 | 2,41 | 3,791 | 2,818 | 4,7445 |
| ANSYS | 0,0155 | 0,0028 | 0,0147 | 0,0871 | 2,0205 | 3,0251 | 2,4103 | 3,7912 | 2,8178 | 4,7452 |
| Ocorrência de Trincas | NÃO | NÃO | NÃO | NÃO | SIM | SIM | SIM | SIM | SIM | SIM |
Nas Figura 8a e 8b mostram-se comparações gráficas entre os deslocamentos nodais obtidos a partir do programa desenvolvido nesta pesquisa e dos resultados encontrados com auxílio do software ANSYS 17. Neste caso, é possível verificar a precisão entre os resultados dos deslocamentos nas duas direções dos eixos de referências (x e y), validando dessa forma a implementação numérica desenvolvida.
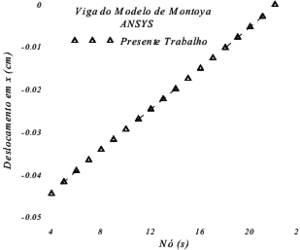
|

|
| (a) | (b) |
| Figura 8. (a) Deslocamentos nodais em x. (b) Deslocamentos nodais em y | |
4.3 Representação numérica do Modelo de Schäfer & Schläich
Neste exemplo é analisado numericamente o modelo de Schäfer & Schläich [2] que corresponde a uma viga-parede com abertura submetida a um carregamento pontual. Na Figura 9 se apresenta de forma detalhada a viga-parede, que está sujeita à carga de 800 kN. Neste exemplo, o concreto apresenta um módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25.
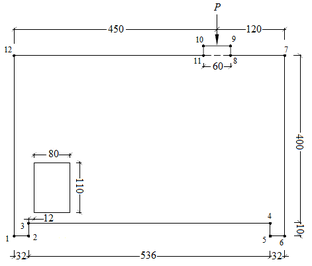
|
| Figura 9. Viga-parede Modelo de Schäfer & Schläich |
A viga-parede foi discretizada no software ANSYS 17, gerando-se uma malha livre com 414 elementos finitos triangulares (CST) e 249 nós, conforme mostrado na Figura 10.
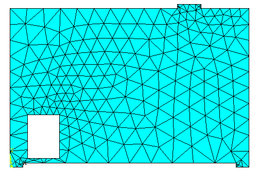
|
| Figura 10. Malha livre da Viga-parede – Ansys |
Com auxílio do ANSYS 17 verifica-se o comportamento e as deformações da viga-parede submetida às tensões principais (, e ). Essas configurações deformadas são mostradas nas Figuras 11a, 11b e 11c, respectivamente, cujas escalas de referências encontram-se em kN/cm².
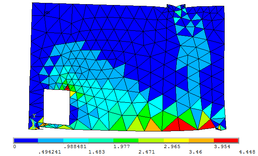
|
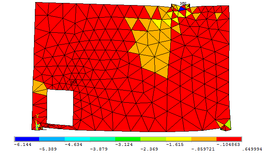
|
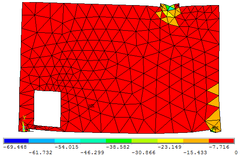
|
| (a) | (b) | (c) |
| Figura 11. (a) Tensão principal . (b) Tensão principal . (c) Tensão principal | ||
Refinando a malha utilizada, aumentando o número de elementos finitos de forma excessiva, obtendo uma nova malha com 26496 elementos finitos triangulares (CST) e com 13584 nos, é possível visualizar as regiões comprimidas que formam as bielas na viga-parede, representadas na cor azul na Figura 12, demonstrando assim a concentração de tensões de compressão em algumas regiões da viga-parede.
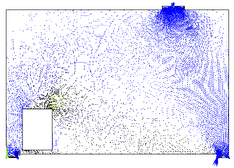
|
| Figura 12. Representação vetorial das tensões na viga-parede com a malha refinada Ansys |
Nas Tabelas 7, 8, 9, 10 e 11 apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e o software ANSYS 17. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas.
| Elemento | 1 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 414 |
| Presente Trabalho | -0,3167 | 1,0030 | -0,1158 | -0,1362 | -0,3266 | 0,0105 | -0,3654 | 0,5519 | -3,8440 | -3,9420 |
| ANSYS | -0,3167 | 1,0035 | -0,1158 | -0,1362 | -0,3266 | 0,0105 | -0,3654 | 0,5519 | -3,8442 | -3,9423 |
| Presente Trabalho/ ANSYS | 1,0001 | 0,9995 | 1,0004 | 1,0001 | 0,9999 | 0,9998 | 1,0000 | 1,0000 | 0,9999 | 0,9999 |
| Elemento | 1 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 414 |
| Presente Trabalho | -0,0766 | -0,0818 | -0,5528 | -2,8170 | -2,3570 | 0,1902 | 0,1591 | 0,3279 | -4,7240 | -3,1630 |
| ANSYS | -0,0766 | -0,0818 | -0,5528 | -2,8169 | -2,3570 | 0,1902 | 0,1591 | 0,3279 | -4,7244 | -3,1627 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0003 | 1,0001 | 1,0000 | 0,9999 | 1,0001 |
| Elemento | 1 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 414 |
| Presente Trabalho | -0,7080 | -0,2509 | -0,3003 | 1,6410 | -0,5192 | -0,5483 | -0,7349 | -0,6071 | -3,9740 | -4,3650 |
| ANSYS | -0,7080 | -0,2510 | -0,3003 | 1,6406 | -0,5192 | -0,5483 | -0,7349 | -0,6071 | -3,9744 | -4,3650 |
| Presente Trabalho/ ANSYS | 1,0001 | 0,9998 | 1,0000 | 1,0002 | 1,0000 | 1,0000 | 0,9999 | 1,0000 | 0,9999 | 1,0000 |
| Elemento | 1 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 414 |
| Presente Trabalho | 0,5215 | 1,0590 | 0,0371 | 0,6420 | -0,2016 | 0,6559 | 0,6772 | 1,0570 | -0,2857 | 0,8299 |
| ANSYS | 0,5215 | 1,0587 | 0,0371 | 0,6420 | -0,2016 | 0,6559 | 0,6772 | 1,0573 | -0,2857 | 0,8299 |
| Presente Trabalho/ ANSYS | 1,0001 | 1,0003 | 1,0001 | 1,0000 | 1,0002 | 0,9999 | 1,0001 | 0,9997 | 1,0002 | 1,0000 |
| Elemento | 1 | 50 | 100 | 150 | 200 | 250 | 300 | 350 | 400 | 414 |
| Presente Trabalho | -0,9147 | -0,1370 | -0,7057 | -3,5950 | -2,4820 | -0,4553 | -0,8835 | -0,1775 | -8,2830 | -7,9350 |
| ANSYS | -0,9147 | -0,1370 | -0,7057 | -3,5950 | -2,4820 | -0,4553 | -0,8835 | -0,1775 | -8,2830 | -7,9348 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0002 | 1,0001 | 1,0000 | 1,0000 | 1,0001 | 1,0000 | 1,0001 | 1,0000 | 1,0000 |
Nas Figura 13a e 13b mostram-se comparações gráficas entre os deslocamentos nodais obtidos por meio do programa desenvolvido e os resultados fornecidos a partir do software ANSYS 17, sendo os nós localizados na parte inferior da viga-parede.

|

|
| (a) | (b) |
| Figura 13. (a) Deslocamento em x. (b) Deslocamento em y | |
4.4 Sapata rígida
A sapata rígida em análise cujas dimensões são mostradas na Figura 14 está submetida a um carregamento pontual igual a 800 kN. Neste exemplo o concreto apresenta um módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25.
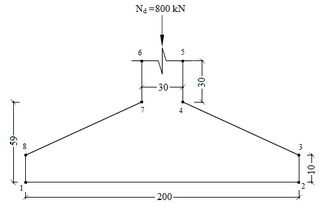
|
| Figura 14. Dimensões da sapata rígida (cm) |
Em sua modelagem, a sapata foi dividida em duas áreas para que o Software ANSYS 17 pudesse gerar a malha. A parte superior foi mapeada de forma livre e a parte inferior, correspondente à fôrma, foi mapeada de forma estruturada, realizando três análises distintas dividindo a parte inferior em 10, 20 e 25 divisões com o fim de se comparar eventuais alterações nos resultados numéricos. As respectivas malhas geradas no software ANSYS 17, são mostradas nas Figuras 15a, 15b e 15c. No primeiro caso analisado, a malha gerada apresenta 164 elementos finitos triangulares (CST) e 111 nós. A segunda malha gerada apresenta 272 elementos finitos triangulares (CST) e com 170 nós. Já a malha final apresenta 329 elementos finitos triangulares (CST) e com 201 nós.
|
|
|
| (a) | (b) | (c) |
| Figura 15. (a) Malha da sapata rígida – 10 divisões. (b) Malha da sapata rígida – 20 divisões. (c) Malha da sapata rígida - 25 divisões | ||
A malha com 25 divisões apresentou melhores resultados em suas análises, podendo observar o comportamento e as deformações da sapata rígida nas Figuras 16a, 16b e 16c, cujas escalas de referências encontram-se em kN/cm². Na Figura 16d, mostra-se, de forma vetorial, a transferência dos esforços internos.
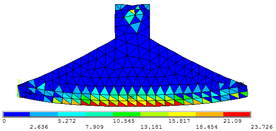
|
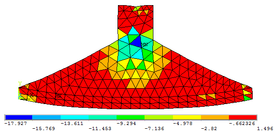
|
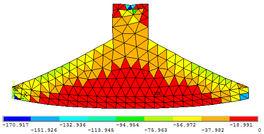
|
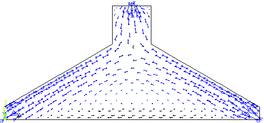
|
| (a) | (b) | (c) | (d) |
| Figura 16. (a) Tensão principal . (b) Tensão principal . (c) Tensão principal . (d) Representação vetorial das tensões no bloco de fundação – Ansys | |||
Nas Tabelas 12, 13, 14, 15 e 16, apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e por meio do software ANSYS 17 para a sapata com 25 divisões na parte inferior. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas.
| Elemento | 1 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 329 |
| Presente Trabalho | -21,38 | 5,2410 | 23,300 | -16,370 | -26,26 | -22,84 | -30,280 | -1,7730 | -2,2510 | -31,9300 |
| ANSYS | -21,384 | 5,2406 | 23,301 | -16,372 | -26,260 | -22,837 | -30,280 | -1,7731 | -2,2509 | -31,9250 |
| Presente Trabalho/ ANSYS | 0,9998 | 1,0001 | 1,0000 | 0,9999 | 1,0000 | 1,0001 | 1,0000 | 0,9999 | 1,0000 | 1,0002 |
| Elemento | 1 | 40 | 80 | 120 | 160 | 200 | 240 | 180 | 320 | 329 |
| Presente Trabalho | -23,550 | 0,4340 | 1,1660 | -2,8400 | -4,9580 | -9,6150 | -8,6300 | -15,700 | -4,7820 | -15,1900 |
| ANSYS | -23,555 | 0,4340 | 1,1661 | -2,8401 | -4,9584 | -9,6153 | -8,6303 | -15,703 | -4,7821 | -15,1900 |
| Presente Trabalho/ ANSYS | 0,9998 | 1,0000 | 0,9999 | 1,0000 | 0,9999 | 1,0000 | 1,0000 | 0,9998 | 1,0000 | 1,0000 |
| Elemento | 1 | 40 | 80 | 120 | 160 | 200 | 240 | 180 | 320 | 329 |
| Presente Trabalho | 24,970 | -0,4914 | 2,4540 | 4,1260 | -11,510 | 5,7290 | 15,950 | 5,6540 | -6,6560 | 25,5700 |
| ANSYS | 24,969 | -0,4914 | 24,538 | 4,1257 | -11,511 | 5,7293 | 15,947 | 5,6545 | -66,562 | 25,5710 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0001 | 1,0000 | 1,0001 | 0,9999 | 1,0000 | 1,0002 | 1,0000 | 1,0000 | 1,00000 |
| Elemento | 1 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 329 |
| Presente Trabalho | 2,5240 | 5,2900 | 23,570 | -1,6810 | 0,0732 | -7,4780 | -0,1815 | 0,2332 | 3,2590 | 3,3480 |
| ANSYS | 2,5236 | 5,2903 | 23,570 | -16,814 | 0,0732 | -7,4781 | -0,1815 | 0,2332 | 3,2590 | 3,3479 |
| Presente Trabalho/ ANSYS | 1,0002 | 0,9999 | 1,0000 | 0,1000 | 1,0000 | 1,0000 | 1,0001 | 0,9999 | 1,0000 | 1,0000 |
| Elemento | 1 | 40 | 80 | 120 | 160 | 200 | 240 | 280 | 320 | 329 |
| Presente Trabalho | -47,460 | 0,3843 | 0,8974 | -17,530 | -31,290 | -24,970 | -38,730 | -17,710 | -10,290 | -47,4600 |
| ANSYS | -47,462 | 0,3843 | 0,8974 | -17,530 | -31,292 | -24,974 | -38,729 | -17,709 | -10,292 | -47,4620 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9999 | 0,9998 | 1,0000 | 1,0001 | 0,9998 | 1,0000 |
Em relação aos deslocamentos nodais, as Figura 17a e 17b mostram as comparações gráficas entre os deslocamentos na parte inferior da sapata rígida obtida por meio do programa desenvolvido e pelos resultados determinados via software ANSYS 17, utilizando um maior número de nós entre as simulações realizadas.

|

|
| (a) | (b) |
| Figura 17. (a) Deslocamento em x. (b) Deslocamento em y | |
4.4 Consolo curto
O consolo curto analisado, cujas dimensões são mostradas na Figura 18a, está submetido a um carregamento pontual igual a 400 kN. Nesta aplicação, o concreto apresenta módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25. O consolo curto foi discretizado pelo software ANSYS 17, gerando uma malha livre com 223 elementos finitos triangulares (CST) e com 139 nós, conforme mostrado na Figura 18b.
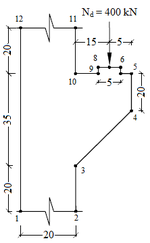
|
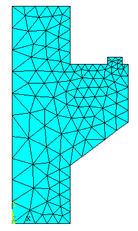
|
| (a) | (b) |
| Figura 18. (a) Dimensões do consolo curto (cm). (b) Malha livre do consolo curto Ansys | |
As configurações deformadas do elemento em análise submetido às tensões principais (, e ) são mostradas nas Figuras 19a, 19b e 19c, respectivamente.
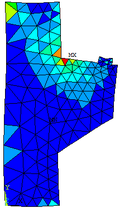
|
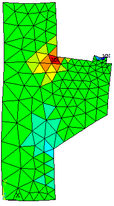
|
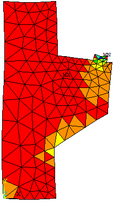
|
| (a) | (b) | (c) |
| Figura 19. (a) Tensão principal . (b) Tensão principal . (c) Tensão principal | ||
Logo é possível visualizar a transferência dos esforços internos por meio de uma representação vetorial mostrada na Figura 20, determinando as regiões tracionadas e comprimidas do consolo curto.
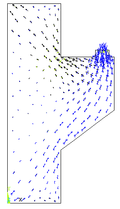
|
| Figura 20. Representação vetorial das tensões no consolo curto – Ansys |
Nas Tabelas 17, 18, 19, 20 e 21 apresentam-se comparações entre os resultados numéricos determinados pelo programa computacional desenvolvido e a partir do software ANSYS 17.
| Elemento | 10 | 30 | 50 | 70 | 90 | 110 | 130 | 150 | 170 | 200 |
| Presente Trabalho | 5,3280 | 8,7690 | -6,1200 | 3,0680 | -11,290 | -4,3290 | -0,7243 | 14,700 | 3,8040 | 15,9100 |
| ANSYS | 5,3283 | 8,7687 | -6,1197 | 3,0675 | -11,295 | -4,3285 | -0,7243 | 14,699 | 3,8043 | 15,9080 |
| Presente Trabalho/ ANSYS | 0,9999 | 1,0000 | 1,0000 | 1,0002 | 0,9996 | 1,0001 | 1,0000 | 1,0001 | 0,9999 | 1,0001 |
| Elemento | 10 | 30 | 50 | 70 | 90 | 110 | 130 | 150 | 170 | 200 |
| Presente Trabalho | 17,540 | -93,230 | -8,4660 | -0,4384 | -12,800 | -17,730 | -16,790 | -1,3020 | -24,540 | 2,0090 |
| ANSYS | 17,536 | -93,228 | -8,4661 | -0,4384 | -12,799 | -17,732 | -16,790 | -1,3024 | -24,541 | 2,0092 |
| Presente Trabalho/ ANSYS | 1,0002 | 1,0000 | 1,0000 | 1,0001 | 1,0001 | 0,9999 | 1,0000 | 0,9997 | 1,0000 | 0,9999 |
| Elemento | 10 | 30 | 50 | 70 | 90 | 110 | 130 | 150 | 170 | 200 |
| Presente Trabalho | - 7,415 | 1,372 | -12,960 | - 3,417 | -14,01 | - 8,805 | - 3,796 | - 4,128 | -13,000 | - 9,3750 |
| ANSYS | - 7,415 | 1,371 | -12,959 | - 3,416 | -14,012 | - 8,804 | - 3,795 | - 4,127 | -12,999 | - 9,3747 |
| Presente Trabalho/ ANSYS | 0,9999 | 1,0002 | 1,0001 | 1,0001 | 0,9999 | 1,0000 | 1,0001 | 1,0001 | 1,0001 | 1,0000 |
| Elemento | 10 | 30 | 50 | 70 | 90 | 110 | 130 | 150 | 170 | 200 |
| Presente Trabalho | 12,890 | 8,7870 | 5,7190 | 5,1550 | 1,9850 | 0,0349 | 0,1274 | 15,700 | 8,8630 | 20,6300 |
| ANSYS | 12,889 | 8,7871 | 5,7192 | 5,1546 | 1,9850 | 0,0349 | 0,1274 | 15,701 | 8,8627 | 20,6280 |
| Presente Trabalho/ ANSYS | 1,0001 | 1,0000 | 1,0000 | 1,0001 | 1,0000 | 0,9999 | 1,0000 | 0,9999 | 1,0000 | 1,0001 |
| Elemento | 10 | 30 | 50 | 70 | 90 | 110 | 130 | 150 | 170 | 200 |
| Presente Trabalho | -45,300 | -93,250 | -20,310 | -2,5250 | -26,080 | -22,100 | -17,640 | -2,3040 | -29,600 | -2,7110 |
| ANSYS | -45,298 | -93,246 | -20,305 | -2,5255 | -26,079 | -22,096 | -17,641 | -2,3043 | -29,599 | -2,7109 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0000 | 1,0002 | 0,9998 | 1,0000 | 1,0002 | 0,9999 | 0,9999 | 1,0000 | 1,0000 |
Nas Figuras 21a e 21b mostram-se comparações gráficas entre os deslocamentos nodais obtidos a partir do programa desenvolvido e os resultados do ANSYS 17, sendo os nós referentes à parte superior do consolo curto. Lembrando que nessa região ficam localizadas as armaduras de tração.

|

|
| (a) | (b) |
| Figura 21. (a) Deslocamento em x. (b) Deslocamento em y | |
Por fim, realizou-se o dimensionamento do consolo curto e os resultados foram comparados com as respostas determinadas pelo presente trabalho que é baseado no Método dos Elementos Finitos, sendo os valores das tensões elementares extraídos da modelagem numérica realizada. Para a realização do dimensionamento, considerou-se a altura útil do consolo igual a cm, cm, a distância entre o ponto de aplicação da carga e a face do pilar igual =15,5cm e kN/cm. Na Tabela 22 mostra-se a boa aproximação entre os resultados encontrados.
| Resultado Normativo | Presente Trabalho | Presente Trabalho/ Resultado Normativo |
| 5,11 | 4,64 | 0,91 |
4.5 Bloco de fundação sob duas estacas de concreto
O bloco de fundação com duas estacas está submetido a um carregamento pontual igual a 1500 kN, suas dimensões são mostradas na Figura 22a. Considerou-se neste exemplo que o concreto apresenta módulo de elasticidade igual a 2800 kN/cm² e coeficiente de Poisson igual a 0,25. Por sua vez, o bloco de fundação foi discretizado com quatro malhas distintas, sendo apresentados os resultados das análises realizadas com a malha estruturada de 328 elementos finitos triangulares (CST) e 202 nós mostrada na Figura 22b.
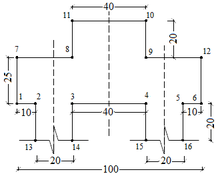
|

|
| (a) | (b) |
| Figura 22. (a) Dimensões do bloco de (cm). (b) Malha do bloco de fundação – Ansys | |
Com auxílio do software ANSYS 17 é possível observar o comportamento e as deformações do bloco de fundação. Essas configurações deformadas são mostradas nas Figuras 23a, 23b e 23c, respectivamente, cujas escalas de referências encontram-se em kN/cm². Na Figura 23d, mostra-se, de forma vetorial, as tensões de tração e compressão no bloco de fundação.

|
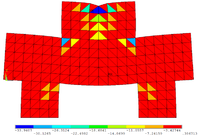
|

|

|
| (a) | (b) | (c) | (d) |
| Figura 23. (a) Tensão principal . (b) Tensão principal . (c) Tensão principal . (d) Representação vetorial de tensões no bloco de fundação – Ansys | |||
Nas Tabelas 23, 24, 25, 26 e 27, apresentam-se comparações entre os resultados numéricos obtidos por meio do programa computacional desenvolvido e do software ANSYS 17. Neste caso, percebe-se também excelente aproximação entre as simulações numéricas realizadas.
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | -15,420 | -22,870 | -12,000 | -46,660 | -2,0900 | -22,540 | -7,0360 | 5,9950 | 27,660 | 58,5300 |
| ANSYS | -15,417 | -22,870 | -11,995 | -46,665 | -2,0905 | -22,538 | -7,0356 | 5,9951 | 27,660 | 58,5320 |
| Presente Trabalho/ ANSYS | 1,0002 | 1,0000 | 1,0004 | 0,9999 | 0,9998 | 1,0001 | 1,0001 | 1,0000 | 1,0000 | 1,0000 |
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | -7,5970 | -59,470 | -74,980 | -216,30 | -21,670 | -29,710 | -27,160 | -18,920 | -15,220 | 0,5455 |
| ANSYS | -7,5974 | -59,474 | -74,979 | -216,26 | -21,666 | -29,715 | -27,161 | -18,916 | -15,221 | 0,5455 |
| Presente Trabalho/ ANSYS | 0,9999 | 0,9999 | 1,0000 | 1,0002 | 1,0002 | 0,9998 | 1,0000 | 1,0002 | 0,9999 | 1,0001 |
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | 2,8870 | -29,430 | -12,660 | 48,170 | 15,420 | 27,870 | 16,820 | 6,8850 | 26,970 | 11,7500 |
| ANSYS | 2,8874 | -29,435 | -12,662 | 48,165 | 15,424 | 27,872 | 16,820 | 6,8846 | 26,971 | 11,7460 |
| Presente Trabalho/ ANSYS | 0,9999 | 0,9998 | 0,9998 | 1,0001 | 0,9997 | 0,9999 | 1,0000 | 1,0001 | 1,0000 | 1,0003 |
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | -6,6470 | -6,5110 | -9,5450 | -33,940 | 6,3890 | 1,9750 | 2,5020 | 7,7710 | 40,670 | 60,8200 |
| ANSYS | -6,6467 | -6,5111 | -9,5453 | -33,941 | 6,3890 | 1,9754 | 2,5019 | 7,7711 | 40,674 | 60,8200 |
| Presente Trabalho/ ANSYS | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 1,0000 | 0,9998 | 1,0000 | 1,0000 | 0,9999 | 1,0000 |
| Elemento | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 |
| Presente Trabalho | -16,370 | -75,830 | -77,430 | -229,00 | -30,150 | -54,230 | -36,700 | -20,690 | -28,240 | -1,7430 |
| ANSYS | -16,367 | -75,832 | -77,429 | -228,99 | -30,146 | -54,229 | -36,698 | -20,692 | -28,236 | -1,7435 |
| Presente Trabalho/ ANSYS | 1,0002 | 1,0000 | 1,0000 | 1,0000 | 1,0001 | 1,0000 | 1,0001 | 0,9999 | 1,0001 | 0,9997 |
Nas Figuras 24a e 24b mostram-se comparações gráficas entre os deslocamentos nodais obtidos a partir do programa desenvolvido e os resultados obtidos via ANSYS 17, sendo os nós referentes à parte inferior do bloco de fundação, localizados entre as duas estacas de concreto.

|

|
| (a) | (b) |
| Figura 24. (a) Deslocamento em x. (b) Deslocamento em y | |
Por fim, encontrou-se a área de aço da armadura tracionada a partir do Método de Blévot & Frémy e os resultados foram confrontados com respostas obtidas a partir do Método dos Elementos Finitos para as quatro malhas analisadas. Para a realização do dimensionamento, considerou-se: cm, cm, cm, cm e kN/cm². Os resultados são mostrados na Tabela 28, verificando uma melhora na aproximação dos resultados com o refinamento da malha.
| Bloco de Fundação | Blévot & Frémy | Presente Trabalho | Presente Trabalho/ Blévot & Frémy |
| 328 elementos | 18,25 | 16,35 | 0,90 |
| 360 elementos | 18,25 | 16,91 | 0,92 |
| 392 elementos | 18,25 | 18,17 | 0,99 |
| 654 elementos | 18,25 | 18,46 | 1,01 |
5. Conclusão
Em todas as aplicações realizadas, observou-se uma ótima convergência entre os resultados numéricos obtidos com o programa computacional implementado e as respostas encontradas por meio do software ANSYS 17. Logo, verifica-se que a implementação desenvolvida foi bem sucedida, contribuindo com valores precisos de tensões elementares, tensões principais e deslocamentos das estruturas planas com comportamento elástico-linear.
O objetivo principal prático da pesquisa desenvolvida foi dimensionar as armaduras de aço tracionadas em alguns elementos estruturais estudados, utilizando como base um programa computacional implementado em linguagem FORTRAN com formulação baseada no Método dos Elementos Finitos e realiza um comparativo com algumas prescrições normativas vigentes, com o intuito de verificar a precisão dessas respostas.
Na análise feita por meio do modelo desenvolvido por Montoya el al. [1], verificaram-se também de forma numérica via Método dos Elementos Finitos, diversos pontos em que há o surgimento de trincas, visto que, os valores de tensões obtidos ultrapassaram a resistência à tração do concreto.
Com relação à análise da viga-parede verificou-se a formação das bielas e tirantes a partir da representação vetorial, comprovando dessa forma as regiões comprimidas e tracionadas do elemento estrutural.
Em relação ao dimensionamento, em duas aplicações (consolos curtos e bloco de fundação) verificou-se boa aproximação ao serem comparados os resultados numéricos com a metodologia desenvolvida por Blévot & Frémy.
Para a análise realizada no bloco de fundação, verificou-se que o refinamento na malha de elementos finitos proporcionou maior aproximação entre o valor de área de aço calculado numericamente e o resultado determinado a partir do método clássico desenvolvido por Blévot & Frémy [8].
Referências
[1] Montoya, P.J., Meseger, A.G., Cabré, F.M. Hormigón Armado. 13 ed. Editorial Gustavo Gili, Barcelona, 1991.
[2] Schlaich, J., Schafer, K. Consistent Design of Structural Concrete Using Strut and Tie Model. 5º Colóquio sobre comportamento e Projeto de estruturas. PUC, Rio de Janeiro, 1988.
[3] Souza, R.A. Análise, dimensionamento e verificação de elementos especiais em concreto armado utilizando o método dos elementos finitos e o método das bielas. Revista Internacional de Métodos Numéricos para Cálculo y Diseño en Ingeniería. 2006.
[4] Fontes, F.F. Análise Estrutural de elementos lineares segundo a NBR 6118:2003. Dissertação de Mestrado, Escola de Engenharia de São Carlos. USP, São Carlos, 2005.
[5] Vicente, W.M., Oliveira, W. C. Análise de Tensões em Placas Circulares Utilizando elementos Finitos Axissimétricos. Trabalho Final de Graduação de Engenharia Mecânica, Universidade Federal de Itajubá, Itajubá, 2009.
[6] Delalibera, R.G. Estudo experimental e analítico de blocos sobre estacas submetidos a momento e normal. Qualificação de Doutorado, Escola de Engenharia de São Carlos, USP, São Carlos, 2005.
[7] Hobbs, N.B., Stein, P. An investigation into the stress distribution in pile caps with some notes on design. Proceedings of the Institution of Civil Engineers, 1957.
[8] Blévot, J., Frémy, R. Semelles sur piex. Analles d’ Institut Techique du Bâtiment et des Travaux Publlics. Paris, 1967.
[9] NBR-6118. Projeto de Estruturas de Concreto – Procedimento, ABNT – Associação Brasileira de Normas Técnicas, Rio de Janeiro, Brasil, 2014.
[10] Fernandes, R. M., EL DEBS, M.K. Análise da capacidade resistente de consolos de concreto armado considerando a contribuição da armadura de costura. Cadernos de Engenharia de Estruturas da UFSCar, 2005.
[11] NBR-9062. Projeto e execução de estruturas de concreto pré-moldado, ABNT – Associação Brasileira de Normas Técnicas, Rio de Janeiro, Brasil, 2006.
[12] Chandrupatla, T.R., Belegundu, A.D. Elementos Finitos. Pearson Education do Brasil, São Paulo, 2014.
Document information
Published on 28/05/19
Accepted on 02/05/19
Submitted on 02/08/17
Volume 35, Issue 2, 2019
DOI: 10.23967/j.rimni.2019.05.001
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?