m (Onate moved page Review 936278190463 to V. D. dos Santos et al 2020a) |
|||
| (2 intermediate revisions by the same user not shown) | |||
| Line 36: | Line 36: | ||
Esta pesquisa se beneficiou da plataforma de intercâmbio fornecida pelo projeto SuFoRun (Marie Sklodowska Curie Grant Agreement No. 691149). | Esta pesquisa se beneficiou da plataforma de intercâmbio fornecida pelo projeto SuFoRun (Marie Sklodowska Curie Grant Agreement No. 691149). | ||
--> | --> | ||
| − | + | ==Resumo== | |
| − | + | ||
| − | + | ||
A aplicação de técnicas de pesquisa operacional em problemas de planejamento florestal contribuiu substancialmente para a melhoria da eficiência econômica e ecológica do manejo, tanto de florestas plantadas como nativas. Modelos de planejamento florestal abordam problemas em diferentes níveis hierárquicos, que envolvem diferentes horizontes de planejamento e complexidade de solução. Este artigo traz uma perspectiva histórica do desenvolvimento de modelos de planejamento florestal nas últimas cinco décadas com ênfase no planejamento operacional. A gênese da aplicação de técnicas de pesquisa operacional na área florestal se dá nas publicações do início da década de 60 intensificando-se nas décadas de 80 e 90 com a rápida evolução da capacidade computacional. A partir da década de 90, os trabalhos começaram a ser diferenciados conforme o nível hierárquico do planejamento florestal abrangido em estratégico, tático e operacional. Enquanto os níveis estratégico e tático abordam decisões de longo e médio prazo, o nível operacional trata de decisões de curto prazo, tipicamente envolvendo a alocação do maquinário de colheita e transporte de produtos florestais. Desta forma, este nível hierárquico se caracteriza por alta complexidade nos modelos de planejamento e relevância econômica ao manejo florestal. Se conclui que apesar do crescente número de publicações tratando do planejamento florestal, o nível operacional de planejamento ainda está sub-representado e são necessários esforços para integrar decisões nos diferentes níveis hierárquicos de planejamento. | A aplicação de técnicas de pesquisa operacional em problemas de planejamento florestal contribuiu substancialmente para a melhoria da eficiência econômica e ecológica do manejo, tanto de florestas plantadas como nativas. Modelos de planejamento florestal abordam problemas em diferentes níveis hierárquicos, que envolvem diferentes horizontes de planejamento e complexidade de solução. Este artigo traz uma perspectiva histórica do desenvolvimento de modelos de planejamento florestal nas últimas cinco décadas com ênfase no planejamento operacional. A gênese da aplicação de técnicas de pesquisa operacional na área florestal se dá nas publicações do início da década de 60 intensificando-se nas décadas de 80 e 90 com a rápida evolução da capacidade computacional. A partir da década de 90, os trabalhos começaram a ser diferenciados conforme o nível hierárquico do planejamento florestal abrangido em estratégico, tático e operacional. Enquanto os níveis estratégico e tático abordam decisões de longo e médio prazo, o nível operacional trata de decisões de curto prazo, tipicamente envolvendo a alocação do maquinário de colheita e transporte de produtos florestais. Desta forma, este nível hierárquico se caracteriza por alta complexidade nos modelos de planejamento e relevância econômica ao manejo florestal. Se conclui que apesar do crescente número de publicações tratando do planejamento florestal, o nível operacional de planejamento ainda está sub-representado e são necessários esforços para integrar decisões nos diferentes níveis hierárquicos de planejamento. | ||
| − | '''Palavras-chave:''' Planejamento florestal | + | '''Palavras-chave:''' Planejamento florestal, planejamento operacional, otimização |
| − | + | ==Abstract== | |
| − | + | ||
The application of operations research techniques has led to a substantial improvement in the economic and ecologic efficiency of forest management, both for planted and natural forests. Forest planning addresses problems in different hierarchical levels that involve specific planning horizons and formulation complexity. This study proposes an historical perspective on the development of forest planning models in the last five decades, with a focus on the operational level. The emergence of operations research applied to forest planning problems can be dated back to the 60’s, with an intensification of this line of research on the 80’s and 90’s, accompanying the fast development on the available computing power. In the 90’s, forest planning problems started to be classified according to hierarchical levels in strategic, tactical and operational. While the strategic and tactical levels address decisions on the long- and medium-term, the operational level deals with short-term decisions, typically involving harvesting machinery allocation and transportation of forest products. In this sense, the operational planning is characterized by a high level of complexity of the planning models and economic importance to forest management. We conclude that despite the increasing number of publications related to forest planning, the operational level remains underrepresented and efforts to integrate decisions across the different hierarchical levels of forest planning are required. | The application of operations research techniques has led to a substantial improvement in the economic and ecologic efficiency of forest management, both for planted and natural forests. Forest planning addresses problems in different hierarchical levels that involve specific planning horizons and formulation complexity. This study proposes an historical perspective on the development of forest planning models in the last five decades, with a focus on the operational level. The emergence of operations research applied to forest planning problems can be dated back to the 60’s, with an intensification of this line of research on the 80’s and 90’s, accompanying the fast development on the available computing power. In the 90’s, forest planning problems started to be classified according to hierarchical levels in strategic, tactical and operational. While the strategic and tactical levels address decisions on the long- and medium-term, the operational level deals with short-term decisions, typically involving harvesting machinery allocation and transportation of forest products. In this sense, the operational planning is characterized by a high level of complexity of the planning models and economic importance to forest management. We conclude that despite the increasing number of publications related to forest planning, the operational level remains underrepresented and efforts to integrate decisions across the different hierarchical levels of forest planning are required. | ||
| − | '''Keywords:''' Forest planning | + | '''Keywords:''' Forest planning, operational planning, optimization |
| − | == | + | ==1. Introdução== |
| − | + | O planejamento é parte fundamental no desenvolvimento das empresas, independente do ramo de atuação. Bateman e Snell [1] dividem o planejamento em três níveis hierárquicos: estratégico, tático e operacional. Estes níveis diferem basicamente em termos de horizonte de planejamento e tipo de trabalho desenvolvido. | |
O planejamento no nível estratégico compreende os altos executivos da organização, responsáveis pela definição dos objetivos, metas e planos e tomada de decisões quanto às questões de longo prazo da empresa, como: sua sobrevivência, crescimento e eficácia geral. O planejamento no nível tático, é utilizado para traduzir os objetivos gerais e as estratégias da alta diretoria em objetivos e atividades mais específicos sendo que o principal desafio neste nível é promover um contato eficiente e eficaz entre o nível estratégico e o nível operacional. O nível tático é uma conexão entre o alto escalão e o escalão gerencial; é neste nível que se decidem as atitudes a serem tomadas, a médio prazo, a fim de atingir os objetivos traçados no nível estratégico. No planejamento operacional, o processo é de uma menor amplitude temporal, onde o foco é trabalhar junto aos funcionários não administrativos, O nível operacional, por sua vez, envolve o escalão gerencial e as equipes de ação da empresa, pois abrange o agendamento de ações pontuais de curto prazo que devem ser tomadas para suprir as demandas levantadas. O nível operacional trabalha com o cenário criado pelos níveis anteriores, tendo a sua disposição o que o nível estratégico projetou e o nível tático implementou. Neste nível são implementados os planos específicos definidos no planejamento tático. | O planejamento no nível estratégico compreende os altos executivos da organização, responsáveis pela definição dos objetivos, metas e planos e tomada de decisões quanto às questões de longo prazo da empresa, como: sua sobrevivência, crescimento e eficácia geral. O planejamento no nível tático, é utilizado para traduzir os objetivos gerais e as estratégias da alta diretoria em objetivos e atividades mais específicos sendo que o principal desafio neste nível é promover um contato eficiente e eficaz entre o nível estratégico e o nível operacional. O nível tático é uma conexão entre o alto escalão e o escalão gerencial; é neste nível que se decidem as atitudes a serem tomadas, a médio prazo, a fim de atingir os objetivos traçados no nível estratégico. No planejamento operacional, o processo é de uma menor amplitude temporal, onde o foco é trabalhar junto aos funcionários não administrativos, O nível operacional, por sua vez, envolve o escalão gerencial e as equipes de ação da empresa, pois abrange o agendamento de ações pontuais de curto prazo que devem ser tomadas para suprir as demandas levantadas. O nível operacional trabalha com o cenário criado pelos níveis anteriores, tendo a sua disposição o que o nível estratégico projetou e o nível tático implementou. Neste nível são implementados os planos específicos definidos no planejamento tático. | ||
| − | No caso do Planejamento Florestal não é diferente, isto porque no nível estratégico, as decisões envolvem alternativas para atender os objetivos de manejo à longo prazo, considerando períodos de 40 a 100 anos no futuro | + | No caso do Planejamento Florestal não é diferente, isto porque no nível estratégico, as decisões envolvem alternativas para atender os objetivos de manejo à longo prazo, considerando períodos de 40 a 100 anos no futuro [2]. Por exemplo, decisões referentes à áreas de plantio e épocas de colheita de cada talhão. O nível tático ocupa-se em viabilizar o acesso a esses talhões e preparar os talhões para colheita, envolvendo atividades a serem desenvolvidas de 10 a 20 anos no futuro. Enquanto no nível operacional o cenário já está criado, conhecem-se os talhões que podem ser colhidos, as estradas de acesso estão prontas, recebem-se as demandas por produtos florestais e deve-se, então, decidir quais frentes de corte serão designadas a cada talhão e para quais centros consumidores serão enviados os produtos florestais colhidos, considerando períodos de uma semana a 1 ano no futuro [2]. |
De acordo com [3], a classificação hierárquica para o planejamento florestal foi introduzida por Paredes no final da década de 80, porém, somente com Weintraub e Cholaky [4], no início da década de 90, é que os conceitos hierárquicos foram finalmente aplicados ao planejamento florestal, separando as atividades do planejamento em estratégico, tático e operacional. | De acordo com [3], a classificação hierárquica para o planejamento florestal foi introduzida por Paredes no final da década de 80, porém, somente com Weintraub e Cholaky [4], no início da década de 90, é que os conceitos hierárquicos foram finalmente aplicados ao planejamento florestal, separando as atividades do planejamento em estratégico, tático e operacional. | ||
| − | + | O objetivo deste trabalho é apresentar uma revisão histórica, de forma cronológica, das abordagens de Planejamento Florestal constantes na literatura especializada. As pesquisas e publicações sobre o assunto iniciaram na década de 60, ampliadas a cada década, atingindo resultados cada vez mais precisos e satisfatórios. Entre os trabalhos mais recentes sobre o Planejamento Florestal, foram selecionados os que tratam dos Níveis Tático e Operacional. | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ==2. Uma perspectiva histórica do planejamento florestal== | |
| − | + | ||
| − | + | Partindo desta breve descrição das características fundamentais dos problemas que envolvem o Planejamento Florestal, em seus diversos níveis, segue uma revisão cronológica dos trabalhos, artigos e livros que foram publicados ao longo das últimas décadas sobre a Otimização no Planejamento Florestal, com ênfase no nível Operacional especialmente na última década. Adicionalmente, uma consulta relacionada ao número de publicações na área de planejamento florestal foi realizada usando o banco de dados Web of Science ([https://www.webofknowledge.com https://www.webofknowledge.com]). A consulta foi realizada usando as palavras-chave “forest AND optimization” no tópico de pesquisa ou “forest AND optimal OR forest AND planning OR forest AND optimization OR forest AND heuristic” para o título das publicações. Foi considerado o período de 1960 – 2019 e filtrando apenas publicações na área florestal, ambiental e econômica. Subsequentemente se aplicou um filtro com a palavra-chave “OPERATION” para selecionar estudos relacionados ao nível operacional ([[#img-1|Figura 1]]). | |
| − | + | ||
| − | + | <div id='img-1'></div> | |
| + | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
| + | |- | ||
| + | |style="padding:10px;"| [[Image:Review_936278190463-image1.png|522px]] | ||
| + | |- style="text-align: center; font-size: 75%;" | ||
| + | | colspan="1" style="padding-bottom:10px;"| '''Figura 1'''. Número de publicações envolvendo problemas de planejamento florestal (Fonte: O Autor, 2019) | ||
| + | |} | ||
| − | FIGURE 1: Number of publications involving forest planning issues. | + | <!--FIGURE 1: Number of publications involving forest planning issues.--> |
A gênese deste ramo de pesquisa está na década de 60 com a publicação dos trabalhos de Curtis [5], Loucks [6] e Leak [7] no ''Journal of Forestry'', além do trabalho de Nautiyal e Pearse [8] no ''Forest'' ''Science''. No início da década de 70 destaca-se o trabalho de Pnevmaticos e Mann [9], em que os autores utilizaram Programação Dinâmica (PD) na otimização da colheita. | A gênese deste ramo de pesquisa está na década de 60 com a publicação dos trabalhos de Curtis [5], Loucks [6] e Leak [7] no ''Journal of Forestry'', além do trabalho de Nautiyal e Pearse [8] no ''Forest'' ''Science''. No início da década de 70 destaca-se o trabalho de Pnevmaticos e Mann [9], em que os autores utilizaram Programação Dinâmica (PD) na otimização da colheita. | ||
| − | Entretanto, os trabalhos de Navon [10], o Serviço Florestal Norte Americano, e Ware e Clutter [11], da Universidade da Georgia e em colaboração com a indústria de celulose do sul dos EUA, marcaram a arrancada da utilização da Programação Linear (PL) no planeamento florestal com maior intensidade. O primeiro trabalho apresentou o sistema Timber RAM (''Timber Resource Allocation Method'') e deu origem a uma série de sistemas usados pelo Serviço Florestal Norte Americano, entre os quais figuram o FORPLAN | + | Entretanto, os trabalhos de Navon [10], o Serviço Florestal Norte Americano, e Ware e Clutter [11], da Universidade da Georgia e em colaboração com a indústria de celulose do sul dos EUA, marcaram a arrancada da utilização da Programação Linear (PL) no planeamento florestal com maior intensidade. O primeiro trabalho apresentou o sistema Timber RAM (''Timber Resource Allocation Method'') e deu origem a uma série de sistemas usados pelo Serviço Florestal Norte Americano, entre os quais figuram o FORPLAN [12] e o SPECTRUM [13]. |
No final da década de 70 foi desenvolvido um dos trabalhos mais importantes nesta área de pesquisa. Foram os autores Johnson e Scheurman [14] que publicaram no Forest Science – Monograph 18, o que pode ser considerado um dos trabalhos mais citados no estudo do Planejamento Florestal com a utilização de Pesquisa Operacional (521 citações até a presente data). Foi neste trabalho que os autores classificaram o que se havia sido desenvolvido até então nos dois modelos padrão para Otimização no Planejamento Florestal Estratégico, sempre buscando decidir quando, onde e quando atuar (plantio, desbaste, poda, colheita, etc.). Esses modelos foram nomeados como Tipo I e Tipo II. O modelo Tipo I, que inclui o formato apresentado por Loucks [6], trabalha com um controle geográfico da floresta e com um número maior de variáveis. Já o modelo Tipo II, que inclui o formato apresentado por Nautiyal e Pearse [8], não trabalha com controle geográfico da floresta, porém apresenta um número reduzido de variáveis. Nestes trabalhos seminais, os objetivos tipicamente maximizavam a produção de madeira ou critérios econômicos como o valor presente líquido e o valor esperado da terra. As principais restrições aplicadas estavam relacionadas à regulação da floresta, visando criar áreas balanceadas por classe de idade e produtividade. Adicionalmente limites de utilização de área e volume, bem como o controle do fluxo de madeira colhida foram utilizados. | No final da década de 70 foi desenvolvido um dos trabalhos mais importantes nesta área de pesquisa. Foram os autores Johnson e Scheurman [14] que publicaram no Forest Science – Monograph 18, o que pode ser considerado um dos trabalhos mais citados no estudo do Planejamento Florestal com a utilização de Pesquisa Operacional (521 citações até a presente data). Foi neste trabalho que os autores classificaram o que se havia sido desenvolvido até então nos dois modelos padrão para Otimização no Planejamento Florestal Estratégico, sempre buscando decidir quando, onde e quando atuar (plantio, desbaste, poda, colheita, etc.). Esses modelos foram nomeados como Tipo I e Tipo II. O modelo Tipo I, que inclui o formato apresentado por Loucks [6], trabalha com um controle geográfico da floresta e com um número maior de variáveis. Já o modelo Tipo II, que inclui o formato apresentado por Nautiyal e Pearse [8], não trabalha com controle geográfico da floresta, porém apresenta um número reduzido de variáveis. Nestes trabalhos seminais, os objetivos tipicamente maximizavam a produção de madeira ou critérios econômicos como o valor presente líquido e o valor esperado da terra. As principais restrições aplicadas estavam relacionadas à regulação da floresta, visando criar áreas balanceadas por classe de idade e produtividade. Adicionalmente limites de utilização de área e volume, bem como o controle do fluxo de madeira colhida foram utilizados. | ||
| Line 109: | Line 106: | ||
No final da década de 90 surgiram alguns trabalhos interessantes como o de Laroze [44] que apresenta um método de Busca Tabu aliado a PL para otimizar o traçamento das toras a nível de floresta e a dissertação de mestrado de Nobre [45] defendida na Universidade Federal de Lavras, onde a autora desenvolve uma heurística nomeada de ‘Heurística da Razão-R’ para o gerenciamento florestal. Neste mesmo ano, outros dois trabalhos apresentaram contribuições muito significativas. O primeiro foi o de Boston e Bettinger [46], que utilizam três heurísticas diferentes para resolver o problema de agendamento da colheita com restrições espaciais: Simulação de Monte Carlo, ''Simulated Annealing'' e Busca Tabu. A solução de cada uma das três heurísticas foi comparada à solução ótima obtida a partir de PLIM e as heurísticas ''Simulated Annealing'' e Busca Tabu apresentaram desempenho superior à Simulação de Monte Carlo. Este trabalho se destaca por ter utilizado mais de dez padrões de corte diferentes na otimização, tornando a complexidade do problema superior aos problemas com poucos padrões de corte. O segundo trabalho, desenvolvido pela equipe do professor Weintraub, no Chile, e publicado por Epstein et al. [47], é uma referência no âmbito do Planejamento Florestal. Conforme dito anteriormente, esta equipe desenvolveu cinco sistemas de gestão específicos para cada setor do Planejamento Florestal. O sistema MEDFOR para o nível de planejamento estratégico e o sistema OPTIMED para o nível tático. Para o Planejamento Operacional foram desenvolvidos três sistemas de gestão: o PLANEX que realiza o planejamento da malha viária e a alocação do maquinário e dos veículos de transporte; o OPTICORT que faz o agendamento da colheita e designa os padrões de corte para cada talhão, além da frente de corte que deverá atuar nos períodos da colheita; e o ASICAM que realiza o agendamento da frota de transporte. Em particular, o OPTICORT consiste em um módulo de PL combinado com um algoritmo de geração de colunas que, na verdade, é um gerador de padrões de corte tipo ''branch-and-bound''. Porém, a partir da ramificação e avaliação iterativa de uma árvore de alternativas, são acrescentadas opções às soluções ótimas encontradas pelo módulo de PL. | No final da década de 90 surgiram alguns trabalhos interessantes como o de Laroze [44] que apresenta um método de Busca Tabu aliado a PL para otimizar o traçamento das toras a nível de floresta e a dissertação de mestrado de Nobre [45] defendida na Universidade Federal de Lavras, onde a autora desenvolve uma heurística nomeada de ‘Heurística da Razão-R’ para o gerenciamento florestal. Neste mesmo ano, outros dois trabalhos apresentaram contribuições muito significativas. O primeiro foi o de Boston e Bettinger [46], que utilizam três heurísticas diferentes para resolver o problema de agendamento da colheita com restrições espaciais: Simulação de Monte Carlo, ''Simulated Annealing'' e Busca Tabu. A solução de cada uma das três heurísticas foi comparada à solução ótima obtida a partir de PLIM e as heurísticas ''Simulated Annealing'' e Busca Tabu apresentaram desempenho superior à Simulação de Monte Carlo. Este trabalho se destaca por ter utilizado mais de dez padrões de corte diferentes na otimização, tornando a complexidade do problema superior aos problemas com poucos padrões de corte. O segundo trabalho, desenvolvido pela equipe do professor Weintraub, no Chile, e publicado por Epstein et al. [47], é uma referência no âmbito do Planejamento Florestal. Conforme dito anteriormente, esta equipe desenvolveu cinco sistemas de gestão específicos para cada setor do Planejamento Florestal. O sistema MEDFOR para o nível de planejamento estratégico e o sistema OPTIMED para o nível tático. Para o Planejamento Operacional foram desenvolvidos três sistemas de gestão: o PLANEX que realiza o planejamento da malha viária e a alocação do maquinário e dos veículos de transporte; o OPTICORT que faz o agendamento da colheita e designa os padrões de corte para cada talhão, além da frente de corte que deverá atuar nos períodos da colheita; e o ASICAM que realiza o agendamento da frota de transporte. Em particular, o OPTICORT consiste em um módulo de PL combinado com um algoritmo de geração de colunas que, na verdade, é um gerador de padrões de corte tipo ''branch-and-bound''. Porém, a partir da ramificação e avaliação iterativa de uma árvore de alternativas, são acrescentadas opções às soluções ótimas encontradas pelo módulo de PL. | ||
| − | A partir do ano 2000 as publicações na área florestal se expandiram. Este período começa com a publicação de três teses de doutorado, duas defendidas na Universidade Federal de Viçosa | + | A partir do ano 2000 as publicações na área florestal se expandiram. Este período começa com a publicação de três teses de doutorado, duas defendidas na Universidade Federal de Viçosa [48,49] e uma defendida na Universidade Federal do Paraná [50]. |
Em sua tese, Chichorro [48] apresenta uma metodologia de análise estrutural do gerenciamento florestal com a finalidade de otimizar a colheita de multiprodutos da madeira. | Em sua tese, Chichorro [48] apresenta uma metodologia de análise estrutural do gerenciamento florestal com a finalidade de otimizar a colheita de multiprodutos da madeira. | ||
| Line 177: | Line 174: | ||
Em sua tese de doutorado, Santana [72], apresenta uma metodologia para o traçamento e a alocação de toras de eucalipto com a utilização de técnicas de Geração de Colunas e PD. O autor conclui que a abordagem proposta foi eficiente pois encontrou soluções ótimas em menos de 5 minutos em oitos cenários estudados. Para o autor, a quantidade de árvores derrubadas para atender determinada carteira de pedidos foi minimizada, gerando menor desperdício. | Em sua tese de doutorado, Santana [72], apresenta uma metodologia para o traçamento e a alocação de toras de eucalipto com a utilização de técnicas de Geração de Colunas e PD. O autor conclui que a abordagem proposta foi eficiente pois encontrou soluções ótimas em menos de 5 minutos em oitos cenários estudados. Para o autor, a quantidade de árvores derrubadas para atender determinada carteira de pedidos foi minimizada, gerando menor desperdício. | ||
| − | == | + | ==3. Discussão e considerações finais== |
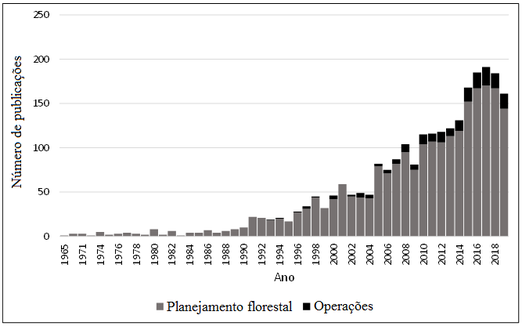
| − | Analisando trabalhos desenvolvidos nas últimas cinco décadas, percebe-se que o assunto do Planejamento Florestal é amplo e de grande importância acadêmica e econômica. Se observou que houve um crescimento exponencial no número de publicações na área de planejamento florestal durante este período (Figura 1). Nota-se que diversos trabalhos foram desenvolvidos no âmbito dos níveis estratégico e tático de planejamento, o que construiu a base de conhecimento para os pesquisadores e empresários da área florestal. O desenvolvimento destes modelos de planejamento contribuiu para uma maior eficiência no manejo de florestal tanto plantadas como nativas. Adicionalmente, aplicações de pesquisa operacional se adequaram às demandas sociais ao decorrer do tempo, como a inclusão de serviços ecossistêmicos, restrições de adjacência e criação de habitat para a vida silvestre a partir da década de 90, acompanhando o surgimento de questões relacionadas à sustentabilidade e biodiversidade no mesmo período (por exemplo a conferência das Nações Unidas sobre o Meio Ambiente). | + | Analisando trabalhos desenvolvidos nas últimas cinco décadas, percebe-se que o assunto do Planejamento Florestal é amplo e de grande importância acadêmica e econômica. Se observou que houve um crescimento exponencial no número de publicações na área de planejamento florestal durante este período ([[#img-1|Figura 1]]). Nota-se que diversos trabalhos foram desenvolvidos no âmbito dos níveis estratégico e tático de planejamento, o que construiu a base de conhecimento para os pesquisadores e empresários da área florestal. O desenvolvimento destes modelos de planejamento contribuiu para uma maior eficiência no manejo de florestal tanto plantadas como nativas. Adicionalmente, aplicações de pesquisa operacional se adequaram às demandas sociais ao decorrer do tempo, como a inclusão de serviços ecossistêmicos, restrições de adjacência e criação de habitat para a vida silvestre a partir da década de 90, acompanhando o surgimento de questões relacionadas à sustentabilidade e biodiversidade no mesmo período (por exemplo a conferência das Nações Unidas sobre o Meio Ambiente). |
Com o aumento na complexidade dos modelos de planejamento causados pela inclusão destes critérios de manejo adicionais e o poder computacional limitado, diversos métodos heurísticos foram adaptados aos problemas de planejamento florestal, com destaque para a Busca Tabu, ''Simulated Annealing'' e o Algoritmo Genético. Com o rápido aumento do poder computacional durante as últimas décadas, cada vez mais soluções exatas foram desenvolvidas, principalmente com a aplicação de programação linear inteira e programação linear inteira mista. | Com o aumento na complexidade dos modelos de planejamento causados pela inclusão destes critérios de manejo adicionais e o poder computacional limitado, diversos métodos heurísticos foram adaptados aos problemas de planejamento florestal, com destaque para a Busca Tabu, ''Simulated Annealing'' e o Algoritmo Genético. Com o rápido aumento do poder computacional durante as últimas décadas, cada vez mais soluções exatas foram desenvolvidas, principalmente com a aplicação de programação linear inteira e programação linear inteira mista. | ||
| Line 185: | Line 182: | ||
Apesar do rápido desenvolvimento nos métodos de solução e o poder computacional, o planejamento operacional se mantém sub-representado na literatura. O nível operacional envolve uma série de variáveis que devem ser avaliadas durante a otimização, como a escolha dos talhões a serem colhidos, a designação das frentes de corte, o transporte dos produtos colhidos, o atendimento das demandas dos produtos, entre outros. Além disso, este nível exige que respostas sejam encontradas em janelas de tempo curtas. Por isso, os trabalhos desenvolvidos focam em uma ou mais variáveis envolvidas neste nível hierárquico. Desta forma, os modelos apresentam natureza combinatória e um grande nível de complexidade para modelos com um longo horizonte de planejamento. Desta forma, a harmonização deste nível hierárquico com o planejamento estratégico e tático permanece limitada. Ainda, avanços recentes no tratamento de incertezas em modelos de otimização foram aplicados a problemas no nível operacional de forma limitada. Em conclusão, esforços futuros no estudo de pesquisa operacional aplicada a problemas de planejamento florestal necessita um maior foco no nível operacional e esforços buscando harmonizar este com o nível estratégico e tático são essenciais, uma vez que soluções ótimas em um nível não se traduzem necessariamente em soluções ótimas para os demais. Com uma integração no planejamento, se pode garantir a eficiência do manejo florestal e assegurar que os objetivos do manejo sejam alcançados. | Apesar do rápido desenvolvimento nos métodos de solução e o poder computacional, o planejamento operacional se mantém sub-representado na literatura. O nível operacional envolve uma série de variáveis que devem ser avaliadas durante a otimização, como a escolha dos talhões a serem colhidos, a designação das frentes de corte, o transporte dos produtos colhidos, o atendimento das demandas dos produtos, entre outros. Além disso, este nível exige que respostas sejam encontradas em janelas de tempo curtas. Por isso, os trabalhos desenvolvidos focam em uma ou mais variáveis envolvidas neste nível hierárquico. Desta forma, os modelos apresentam natureza combinatória e um grande nível de complexidade para modelos com um longo horizonte de planejamento. Desta forma, a harmonização deste nível hierárquico com o planejamento estratégico e tático permanece limitada. Ainda, avanços recentes no tratamento de incertezas em modelos de otimização foram aplicados a problemas no nível operacional de forma limitada. Em conclusão, esforços futuros no estudo de pesquisa operacional aplicada a problemas de planejamento florestal necessita um maior foco no nível operacional e esforços buscando harmonizar este com o nível estratégico e tático são essenciais, uma vez que soluções ótimas em um nível não se traduzem necessariamente em soluções ótimas para os demais. Com uma integração no planejamento, se pode garantir a eficiência do manejo florestal e assegurar que os objetivos do manejo sejam alcançados. | ||
| − | + | ==Referências== | |
| − | == | + | <div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;"> |
| − | [1] Bateman | + | [1] Bateman T.S., Snell S.A. Administração: construindo vantagem competitiva. Atlas, São Paulo, 1998. |
| − | [2] Bettinger | + | [2] Bettinger P., Boston K., Siry J.P., Grebner D.L. Forest management and planning. Academic Press, Burlington, 2009. |
| − | [3] Andersson | + | [3] Andersson S. Approaches to integrated strategic/tactical forest planning. Department of Forest Resource Management and Geomatics, Licentiate Thesis, Swedish University of Agricultural Science, Umea, 2005. |
| − | [4] Weintraub A., Cholaky A. A | + | [4] Weintraub A., Cholaky A. A hierarchical approach to forest planning. For. Sci., 37:439-460, 1991. |
[5] Curtis F.H. Linear programming in the management of a forestry property. J. For., 60:611-616, 1962. | [5] Curtis F.H. Linear programming in the management of a forestry property. J. For., 60:611-616, 1962. | ||
| Line 201: | Line 198: | ||
[6] Loucks D.P. The development of an optimal program for sustained-yield management. J. For., 62:485-490, 1964. | [6] Loucks D.P. The development of an optimal program for sustained-yield management. J. For., 62:485-490, 1964. | ||
| − | [7] Leak W.B. Estimating maximum allowable timber yields by linear programming | + | [7] Leak W.B. Estimating maximum allowable timber yields by linear programming: A case study. J. For., 65:644-646, 1964. |
| − | [8] Nautiyal J.C., Pearse P.H. Optimizing the conversion to sustained-yield | + | [8] Nautiyal J.C., Pearse P.H. Optimizing the conversion to sustained-yield: A programming solution. For. Sci., 13:131-139, 1967. |
[9] Pnevmaticos S.M., Mann S.H. Dynamic programming in tree bucking. For. Prod. J., 22(2):26-30, 1972. | [9] Pnevmaticos S.M., Mann S.H. Dynamic programming in tree bucking. For. Prod. J., 22(2):26-30, 1972. | ||
| Line 211: | Line 208: | ||
[11] Ware G.O., Clutter J.L., A mathematical programming system for the management of industrial forests. For. Sci., 17(3):428-445, 1971. | [11] Ware G.O., Clutter J.L., A mathematical programming system for the management of industrial forests. For. Sci., 17(3):428-445, 1971. | ||
| − | [12] Iverson, D.C., Alston, R.M. | + | [12] Iverson, D.C., Alston, R.M. The genesis of FORPLAN a historical and analytical review of Forest Service planning models. USDA Forest Service General Technical Report, INT-214, 1986. |
[13] USDA Forest Service, Spectrum User’s Guide. Ecosystem Management Analysis Center, Fort Collins, CO. 1995. | [13] USDA Forest Service, Spectrum User’s Guide. Ecosystem Management Analysis Center, Fort Collins, CO. 1995. | ||
| Line 245: | Line 242: | ||
[28] Sessions J., Olsen E., Garland J. Tree bucking for optimal stand value with log allocation constraints. For. Sci., 35(1):271-276, 1989. | [28] Sessions J., Olsen E., Garland J. Tree bucking for optimal stand value with log allocation constraints. For. Sci., 35(1):271-276, 1989. | ||
| − | [29] Carnieri | + | [29] Carnieri C. Planejamento florestal otimizado via redes de manejo. Tese (Doutorado em Engenharia Elétrica), Universidade Estadual de Campinas, Campinas, 1989. |
| − | [30] Von Gadow | + | [30] Von Gadow K., Bredenkamp B.V. Forest management. Academica, Pretoria, 1992. |
| − | [31] Hof | + | [31] Hof J. Coactive forest management. Academic Press, London, 1993. |
| − | [32] Hof | + | [32] Hof J., Bevers M. Apatial optimization for managed ecosystems. Columbia University Press, New York, 1998. |
| − | [33] Rodriguez L.C.E Gerenciamento da | + | [33] Rodriguez L.C.E Gerenciamento da produção florestal. ESALQ, Doc. Flor., 13:1-41, 1991. |
| − | [34] Lockwood C., Moore T. Harvest scheduling with spatial constraints: a simulated annealing approach. Can. J. For. Res, 23(3):468-478. 1993. | + | [34] Lockwood C., Moore T. Harvest scheduling with spatial constraints: a simulated annealing approach. Can. J. For. Res., 23(3):468-478. 1993. |
[35] Hof J.G., Joyce L.A. A mixed integer linear programming approach for spatially optimizing wildlife and timber in managed forest ecosystems. For. Sci., 39:816-834, 1993. | [35] Hof J.G., Joyce L.A. A mixed integer linear programming approach for spatially optimizing wildlife and timber in managed forest ecosystems. For. Sci., 39:816-834, 1993. | ||
| Line 261: | Line 258: | ||
[36] Weintraub A., Jones G., Magendzo A., Meacham M., Kirby M. A heuristic system to solve mixed-integer Forest planning models. Oper. Res., 42(6):1010-1024, 1994. | [36] Weintraub A., Jones G., Magendzo A., Meacham M., Kirby M. A heuristic system to solve mixed-integer Forest planning models. Oper. Res., 42(6):1010-1024, 1994. | ||
| − | [37] Oliveira, E. B. Um sistema computadorizado de prognose do crescimento e produção de Pinus taeda L., com critérios quantitativos para a avaliação técnica e econômica de regimes de manejo. Tese (Doutorado em Ciências Florestais) | + | [37] Oliveira, E.B. Um sistema computadorizado de prognose do crescimento e produção de Pinus taeda L., com critérios quantitativos para a avaliação técnica e econômica de regimes de manejo. Tese (Doutorado em Ciências Florestais), Universidade Federal do Paraná, Curitiba, 1995. |
| − | [38] Ogweno | + | [38] Ogweno D.C.O. Integrated optimization of operational and tactical planning for log production. Thesis (PhD in Forestry), University of Canterbury, 1995. |
| − | [39] Stape J. L. Planejamento global e normatização de procedimentos operacionais da talhadia simples em Eucalyptus. Série Técnica IPEF, 11(30):51-62, 1997. | + | [39] Stape J.L. Planejamento global e normatização de procedimentos operacionais da talhadia simples em Eucalyptus. Série Técnica IPEF, 11(30):51-62, 1997. |
[40] Laroze A.J., Greber B.J. Using Tabu search to generate stand-level, rule-based bucking patterns. For. Sci., 43(2):157-169, 1997. | [40] Laroze A.J., Greber B.J. Using Tabu search to generate stand-level, rule-based bucking patterns. For. Sci., 43(2):157-169, 1997. | ||
| − | [41] Leite | + | [41] Leite H.G. Conversão de árvores em multiprodutos da madeira utilizando programação dinâmica. Tese (Doutorado em Ciência Florestal), Universidade Federal de Viçosa, Viçosa, 1993. |
| − | [42] Andrade V. C. L., Leite H. G. Um método para quantificar multiprodutos de árvores individuais na unidade estere. Rev. Árvore, 22(3):299-306, 1998. | + | [42] Andrade V.C.L., Leite H.G. Um método para quantificar multiprodutos de árvores individuais na unidade estere. Rev. Árvore, 22(3):299-306, 1998. |
[43] Murphy G. Allocation of stands and cutting patterns to logging crews using tabu search heuristics. J. For. Eng., 9(1):31–37, 1998. | [43] Murphy G. Allocation of stands and cutting patterns to logging crews using tabu search heuristics. J. For. Eng., 9(1):31–37, 1998. | ||
| Line 277: | Line 274: | ||
[44] Laroze A.J. A linear programming, tabu search method for solving forest-level bucking optimization problems. For. Sci., 45(1):108-116, 1999. | [44] Laroze A.J. A linear programming, tabu search method for solving forest-level bucking optimization problems. For. Sci., 45(1):108-116, 1999. | ||
| − | [45] Nobre, S.R. A heurística da Razão-R aplicada a problemas de gestão florestal. Dissertação (Mestrado em Administração Rural) | + | [45] Nobre, S.R. A heurística da Razão-R aplicada a problemas de gestão florestal. Dissertação (Mestrado em Administração Rural), Universidade Federal de Lavras, Lavras, 1999. |
[46] Boston K., Bettinger P. An analysis of Monte Carlo integer programming, simulated annealing, and tabu search heuristics for solving spatial harvest scheduling problems. For. Sci., 45(2):292–301, 1999. | [46] Boston K., Bettinger P. An analysis of Monte Carlo integer programming, simulated annealing, and tabu search heuristics for solving spatial harvest scheduling problems. For. Sci., 45(2):292–301, 1999. | ||
| − | [47] Epstein R., Morales R., Serón J., Weintraub A. Use of OR | + | [47] Epstein R., Morales R., Serón J., Weintraub A. Use of OR systems in the Chilean forest industries. Interfaces, 29(1):7-29, 1999. |
| − | [48] Chichorro | + | [48] Chichorro J.F. Análise estrutural e econômica de multiprodutos da madeira. Tese (Doutorado em Ciência Florestal), Universidade Federal de Viçosa, Viçosa, 2000. |
| − | [49] Rodrigues | + | [49] Rodrigues F.L. Metaheurística e sistema de suporte à decisão no gerenciamento de recursos florestais. Tese (Doutorado em Ciência Florestal), Universidade Federal de Viçosa, Viçosa, 2001. |
| − | [50] Arce | + | [50] Arce J.E. Um sistema de análise, simulação e otimização do sortimento florestal em função da demanda por multiprodutos e dos custos de transporte. Tese (Doutorado em Ciências Florestais), Universidade Federal do Paraná, Curitiba, 2000. |
| − | [51] Rodrigues F.L., Leite H.G., Santos H.N., Souza A.L. Solução de problemas de | + | [51] Rodrigues F.L., Leite H.G., Santos H.N., Souza A.L. Solução de problemas de planejamento florestal com restrições de inteireza utilizando busca tabu. Rev. Árvore, 27(5):701-713, 2003. |
| − | [52] Rodrigues F. L., Leite H.G., Santos H.N., Souza A.L., Silva G.F. Metaheurística | + | [52] Rodrigues F.L., Leite H.G., Santos H.N., Souza A.L., Silva G.F. Metaheurística algoritmo genético para solução de problemas de planejamento florestal com restrições de integridade. Rev. Árvore, 28(2):233-245, 2004. |
| − | [53] Rodrigues F. L., Leite H.G., Santos H.N., Souza A.L., Ribeiro C.A.A.S. Metaheurística | + | [53] Rodrigues F.L., Leite H.G., Santos H.N., Souza A.L., Ribeiro C.A.A.S. Metaheurística simulated annealing para solução de problemas de planejamento florestal com restrições de integridade. Rev. Árvore, 28(2):247-256, 2004. |
| − | [54] Rodrigues F. L., Silva G.F., Leite H.G., Xavier A.C., Pezzopane J.E.M. Um modelo de | + | [54] Rodrigues F.L., Silva G.F., Leite H.G., Xavier A.C., Pezzopane J.E.M. Um modelo de regulação florestal e suas implicações na formulação e solução de problemas com restrições de recobrimento. Rev. Árvore, 30(5):769-778, 2006. |
| − | [55] Falcão A.O., Borges J.G. Heurísticas para a integração de níveis | + | [55] Falcão A.O., Borges J.G. Heurísticas para a integração de níveis estratégico e operacional da gestão florestal em problemas de grande dimensão. Scientia Forestalis, 63:94-102, 2003. |
| − | [56] Soares T.S., Vale A.B. do, Leite H.G., Machado C.C. Otimização de | + | [56] Soares T.S., Vale A.B. do, Leite H.G., Machado C.C. Otimização de multiprodutos em povoamentos florestais. Rev. Árvore, 27(6):811-820, 2003. |
| − | [57] Arce J. E., Macdonagh P., Friedl R. A. Geração de padrões ótimos de corte através de algoritmos de traçamento aplicados a fustes individuais. Rev. Árvore, 28(2):207-217, 2004. | + | [57] Arce J.E., Macdonagh P., Friedl R.A. Geração de padrões ótimos de corte através de algoritmos de traçamento aplicados a fustes individuais. Rev. Árvore, 28(2):207-217, 2004. |
| − | [58] Souza, D. O. Algoritmos | + | [58] Souza, D.O. Algoritmos genéticos aplicados ao planejamento do transporte principal de Madeira. Dissertação (Mestrado em Engenharia Florestal), Universidade Federal do Paraná, Curitiba, 2004. |
| − | [59] Mitchel, S.A. Operational forest harvest scheduling optimization: a mathematical model and solution strategy. Tese (Doutorado em Engenharia de Produção) | + | [59] Mitchel, S.A. Operational forest harvest scheduling optimization: a mathematical model and solution strategy. Tese (Doutorado em Engenharia de Produção), Universidade de Auckland, Auckland, 2004. |
| − | [60] Malinovski R. A., Malinovski R. A., Malinovski J. R. Análise das variáveis de influência na produtividade das máquinas de colheita de madeira em função das características físicas do terreno, do povoamento e do planejamento operacional florestal. Rev. Flor., 36(2):169-182, 2006. | + | [60] Malinovski R.A., Malinovski R.A., Malinovski J.R. Análise das variáveis de influência na produtividade das máquinas de colheita de madeira em função das características físicas do terreno, do povoamento e do planejamento operacional florestal. Rev. Flor., 36(2):169-182, 2006. |
[61] Bettinger P., Boston K., Sessions J. Intensifying a heuristic forest harvest scheduling search procedure with 2-opt decision choices. Can. J. For. Res., 29(11):1784-1792, 1999. | [61] Bettinger P., Boston K., Sessions J. Intensifying a heuristic forest harvest scheduling search procedure with 2-opt decision choices. Can. J. For. Res., 29(11):1784-1792, 1999. | ||
| Line 313: | Line 310: | ||
[62] Murray A.T., Church R.L. Heuristic solution approaches to operational forest planning problems. OR Spektrum, 17:193-203, 1995. | [62] Murray A.T., Church R.L. Heuristic solution approaches to operational forest planning problems. OR Spektrum, 17:193-203, 1995. | ||
| − | [63] Yoshimoto A., Brodie J. D., Sessions J. A new heuristic to solve spatially constrained long-term harvest scheduling problems. For. Sci., 40(3):365-396, 1994. | + | [63] Yoshimoto A., Brodie J.D., Sessions J. A new heuristic to solve spatially constrained long-term harvest scheduling problems. For. Sci., 40(3):365-396, 1994. |
[64] Augustynczik A.L.D., Arce J.E., Silva A.C.L. Spatial forest harvest planning considering maximum operational areas. Cerne, 21(4):649-656, 2015. | [64] Augustynczik A.L.D., Arce J.E., Silva A.C.L. Spatial forest harvest planning considering maximum operational areas. Cerne, 21(4):649-656, 2015. | ||
| Line 319: | Line 316: | ||
[65] Augustynczik, A.L.D., Arce J.E., Yousefpour R., Silva, A.C.L. Promoting harvesting stands connectivity and its economic implications in Brazilian forest plantations applying integer linear programming and simulated annealing. For. Pol. and Econ., 73:120-129, 2016. | [65] Augustynczik, A.L.D., Arce J.E., Yousefpour R., Silva, A.C.L. Promoting harvesting stands connectivity and its economic implications in Brazilian forest plantations applying integer linear programming and simulated annealing. For. Pol. and Econ., 73:120-129, 2016. | ||
| − | [66] Santos P.A.V.H., Silva A.C.L., Arce J.E., Augustynczik A.L.D. A | + | [66] Santos P.A.V.H., Silva A.C.L., Arce J.E., Augustynczik A.L.D. A mathematical model for the integrated optimization of harvest and transport scheduling of forest products. Forests, 10(12):1110, 2019. |
| − | [67] Gomide L. R., Arce J. E., Silva, A. C. L. Uso do | + | [67] Gomide L.R., Arce J.E., Silva, A.C.L. Uso do algoritmo genético no planejamento florestal considerando seus operadores de seleção. Cerne, 15(4):460-467, 2009. |
[68] Diaz-Balteiro L., González-Pachón J., Romero C. Measuring systems sustainability with multi-criteria methods: A critical review. Eur. J. Oper. Res., 258:607-616, 2017. | [68] Diaz-Balteiro L., González-Pachón J., Romero C. Measuring systems sustainability with multi-criteria methods: A critical review. Eur. J. Oper. Res., 258:607-616, 2017. | ||
| − | [69] Pascual A., Pukkala T., Rodríguez F., De-Miguel S. Using spatial optimization to create dynamic harvest blocks from LiDAR-based small interpretation units. | + | [69] Pascual A., Pukkala T., Rodríguez F., De-Miguel S. Using spatial optimization to create dynamic harvest blocks from LiDAR-based small interpretation units. Forests, 7(10):220, 2016. |
[70] Álvarez-Miranda E., Garcia-Gonzalo J., Pais C., Weintraub A. A multicriteria stochastic optimization framework for sustainable forest decision making under uncertainty. For. Pol. and Econ., 103:112-122, 2019. | [70] Álvarez-Miranda E., Garcia-Gonzalo J., Pais C., Weintraub A. A multicriteria stochastic optimization framework for sustainable forest decision making under uncertainty. For. Pol. and Econ., 103:112-122, 2019. | ||
| Line 331: | Line 328: | ||
[71] Banhara, J.R., Rodriguez L.C.E., Seixas F., Moreira J.M.M.A.P., Silva L.M.S., Nobre S.R., Cogswell A. Agendamento otimizado da colheita de madeira de eucaliptos sob restrições operacionais, espaciais e climáticas. Scientia Forestalis, 38(85):85-95, 2010. | [71] Banhara, J.R., Rodriguez L.C.E., Seixas F., Moreira J.M.M.A.P., Silva L.M.S., Nobre S.R., Cogswell A. Agendamento otimizado da colheita de madeira de eucaliptos sob restrições operacionais, espaciais e climáticas. Scientia Forestalis, 38(85):85-95, 2010. | ||
| − | [72] Santana, C. J. O. Traçamento e | + | [72] Santana, C.J.O. Traçamento e alocação ótima de toras de eucalipto por geração de colunas e programação dinâmica. Tese (Doutorado em Engenharia Florestal), Universidade Federal do Paraná, Curitiba, 2013. |
| + | </div> | ||
Latest revision as of 12:22, 27 May 2021
Resumo
A aplicação de técnicas de pesquisa operacional em problemas de planejamento florestal contribuiu substancialmente para a melhoria da eficiência econômica e ecológica do manejo, tanto de florestas plantadas como nativas. Modelos de planejamento florestal abordam problemas em diferentes níveis hierárquicos, que envolvem diferentes horizontes de planejamento e complexidade de solução. Este artigo traz uma perspectiva histórica do desenvolvimento de modelos de planejamento florestal nas últimas cinco décadas com ênfase no planejamento operacional. A gênese da aplicação de técnicas de pesquisa operacional na área florestal se dá nas publicações do início da década de 60 intensificando-se nas décadas de 80 e 90 com a rápida evolução da capacidade computacional. A partir da década de 90, os trabalhos começaram a ser diferenciados conforme o nível hierárquico do planejamento florestal abrangido em estratégico, tático e operacional. Enquanto os níveis estratégico e tático abordam decisões de longo e médio prazo, o nível operacional trata de decisões de curto prazo, tipicamente envolvendo a alocação do maquinário de colheita e transporte de produtos florestais. Desta forma, este nível hierárquico se caracteriza por alta complexidade nos modelos de planejamento e relevância econômica ao manejo florestal. Se conclui que apesar do crescente número de publicações tratando do planejamento florestal, o nível operacional de planejamento ainda está sub-representado e são necessários esforços para integrar decisões nos diferentes níveis hierárquicos de planejamento.
Palavras-chave: Planejamento florestal, planejamento operacional, otimização
Abstract
The application of operations research techniques has led to a substantial improvement in the economic and ecologic efficiency of forest management, both for planted and natural forests. Forest planning addresses problems in different hierarchical levels that involve specific planning horizons and formulation complexity. This study proposes an historical perspective on the development of forest planning models in the last five decades, with a focus on the operational level. The emergence of operations research applied to forest planning problems can be dated back to the 60’s, with an intensification of this line of research on the 80’s and 90’s, accompanying the fast development on the available computing power. In the 90’s, forest planning problems started to be classified according to hierarchical levels in strategic, tactical and operational. While the strategic and tactical levels address decisions on the long- and medium-term, the operational level deals with short-term decisions, typically involving harvesting machinery allocation and transportation of forest products. In this sense, the operational planning is characterized by a high level of complexity of the planning models and economic importance to forest management. We conclude that despite the increasing number of publications related to forest planning, the operational level remains underrepresented and efforts to integrate decisions across the different hierarchical levels of forest planning are required.
Keywords: Forest planning, operational planning, optimization
1. Introdução
O planejamento é parte fundamental no desenvolvimento das empresas, independente do ramo de atuação. Bateman e Snell [1] dividem o planejamento em três níveis hierárquicos: estratégico, tático e operacional. Estes níveis diferem basicamente em termos de horizonte de planejamento e tipo de trabalho desenvolvido.
O planejamento no nível estratégico compreende os altos executivos da organização, responsáveis pela definição dos objetivos, metas e planos e tomada de decisões quanto às questões de longo prazo da empresa, como: sua sobrevivência, crescimento e eficácia geral. O planejamento no nível tático, é utilizado para traduzir os objetivos gerais e as estratégias da alta diretoria em objetivos e atividades mais específicos sendo que o principal desafio neste nível é promover um contato eficiente e eficaz entre o nível estratégico e o nível operacional. O nível tático é uma conexão entre o alto escalão e o escalão gerencial; é neste nível que se decidem as atitudes a serem tomadas, a médio prazo, a fim de atingir os objetivos traçados no nível estratégico. No planejamento operacional, o processo é de uma menor amplitude temporal, onde o foco é trabalhar junto aos funcionários não administrativos, O nível operacional, por sua vez, envolve o escalão gerencial e as equipes de ação da empresa, pois abrange o agendamento de ações pontuais de curto prazo que devem ser tomadas para suprir as demandas levantadas. O nível operacional trabalha com o cenário criado pelos níveis anteriores, tendo a sua disposição o que o nível estratégico projetou e o nível tático implementou. Neste nível são implementados os planos específicos definidos no planejamento tático.
No caso do Planejamento Florestal não é diferente, isto porque no nível estratégico, as decisões envolvem alternativas para atender os objetivos de manejo à longo prazo, considerando períodos de 40 a 100 anos no futuro [2]. Por exemplo, decisões referentes à áreas de plantio e épocas de colheita de cada talhão. O nível tático ocupa-se em viabilizar o acesso a esses talhões e preparar os talhões para colheita, envolvendo atividades a serem desenvolvidas de 10 a 20 anos no futuro. Enquanto no nível operacional o cenário já está criado, conhecem-se os talhões que podem ser colhidos, as estradas de acesso estão prontas, recebem-se as demandas por produtos florestais e deve-se, então, decidir quais frentes de corte serão designadas a cada talhão e para quais centros consumidores serão enviados os produtos florestais colhidos, considerando períodos de uma semana a 1 ano no futuro [2].
De acordo com [3], a classificação hierárquica para o planejamento florestal foi introduzida por Paredes no final da década de 80, porém, somente com Weintraub e Cholaky [4], no início da década de 90, é que os conceitos hierárquicos foram finalmente aplicados ao planejamento florestal, separando as atividades do planejamento em estratégico, tático e operacional.
O objetivo deste trabalho é apresentar uma revisão histórica, de forma cronológica, das abordagens de Planejamento Florestal constantes na literatura especializada. As pesquisas e publicações sobre o assunto iniciaram na década de 60, ampliadas a cada década, atingindo resultados cada vez mais precisos e satisfatórios. Entre os trabalhos mais recentes sobre o Planejamento Florestal, foram selecionados os que tratam dos Níveis Tático e Operacional.
2. Uma perspectiva histórica do planejamento florestal
Partindo desta breve descrição das características fundamentais dos problemas que envolvem o Planejamento Florestal, em seus diversos níveis, segue uma revisão cronológica dos trabalhos, artigos e livros que foram publicados ao longo das últimas décadas sobre a Otimização no Planejamento Florestal, com ênfase no nível Operacional especialmente na última década. Adicionalmente, uma consulta relacionada ao número de publicações na área de planejamento florestal foi realizada usando o banco de dados Web of Science (https://www.webofknowledge.com). A consulta foi realizada usando as palavras-chave “forest AND optimization” no tópico de pesquisa ou “forest AND optimal OR forest AND planning OR forest AND optimization OR forest AND heuristic” para o título das publicações. Foi considerado o período de 1960 – 2019 e filtrando apenas publicações na área florestal, ambiental e econômica. Subsequentemente se aplicou um filtro com a palavra-chave “OPERATION” para selecionar estudos relacionados ao nível operacional (Figura 1).
|
| Figura 1. Número de publicações envolvendo problemas de planejamento florestal (Fonte: O Autor, 2019) |
A gênese deste ramo de pesquisa está na década de 60 com a publicação dos trabalhos de Curtis [5], Loucks [6] e Leak [7] no Journal of Forestry, além do trabalho de Nautiyal e Pearse [8] no Forest Science. No início da década de 70 destaca-se o trabalho de Pnevmaticos e Mann [9], em que os autores utilizaram Programação Dinâmica (PD) na otimização da colheita.
Entretanto, os trabalhos de Navon [10], o Serviço Florestal Norte Americano, e Ware e Clutter [11], da Universidade da Georgia e em colaboração com a indústria de celulose do sul dos EUA, marcaram a arrancada da utilização da Programação Linear (PL) no planeamento florestal com maior intensidade. O primeiro trabalho apresentou o sistema Timber RAM (Timber Resource Allocation Method) e deu origem a uma série de sistemas usados pelo Serviço Florestal Norte Americano, entre os quais figuram o FORPLAN [12] e o SPECTRUM [13].
No final da década de 70 foi desenvolvido um dos trabalhos mais importantes nesta área de pesquisa. Foram os autores Johnson e Scheurman [14] que publicaram no Forest Science – Monograph 18, o que pode ser considerado um dos trabalhos mais citados no estudo do Planejamento Florestal com a utilização de Pesquisa Operacional (521 citações até a presente data). Foi neste trabalho que os autores classificaram o que se havia sido desenvolvido até então nos dois modelos padrão para Otimização no Planejamento Florestal Estratégico, sempre buscando decidir quando, onde e quando atuar (plantio, desbaste, poda, colheita, etc.). Esses modelos foram nomeados como Tipo I e Tipo II. O modelo Tipo I, que inclui o formato apresentado por Loucks [6], trabalha com um controle geográfico da floresta e com um número maior de variáveis. Já o modelo Tipo II, que inclui o formato apresentado por Nautiyal e Pearse [8], não trabalha com controle geográfico da floresta, porém apresenta um número reduzido de variáveis. Nestes trabalhos seminais, os objetivos tipicamente maximizavam a produção de madeira ou critérios econômicos como o valor presente líquido e o valor esperado da terra. As principais restrições aplicadas estavam relacionadas à regulação da floresta, visando criar áreas balanceadas por classe de idade e produtividade. Adicionalmente limites de utilização de área e volume, bem como o controle do fluxo de madeira colhida foram utilizados.
Além dos trabalhos acima mencionados, no final da década de 70 mais dois importantes trabalhos foram publicados. No primeiro, os autores Deadman e Goulding [15] apresentam um sistema de inventário florestal nomeado de MARVL (Method for Assessment of Recoverable Volume by Log types). No segundo, os autores Johnson et al. [16] publicaram um manual do sistema de suporte à decisão nomeado MUSYC (Multiple Use Sustained Yield scheduling Calculation).
No Brasil, foi apenas no começo da década de 80 que Borges [17] publicou sua dissertação de mestrado na UFPR, buscando maximizar o volume de madeira serrada utilizando funções polinomiais de modo a obter de cada árvore o número máximo de peças serradas com as maiores dimensões. Neste mesmo ano a UFPR fundou a FUPEF (Fundação de Pesquisas Florestais do Paraná).
Na década de 80, os trabalhos de destaque adicionaram questões relacionadas à utilização aos modelos tradicionais de planejamento. Os problemas de planejamento neste período se destacam pelo surgimento de restrições relacionas à otimização da estrutura do sortimento florestal. Nesse sentido, modelos foram criados buscando padrões ótimos de traçamento de toras e a utilização de técnicas de programação dinâmica para a resolução de modelos de planejamento cada vez mais complexos e de natureza combinatória. Se manteve o foco nos objetivos econômicos e de produção de madeira, com a introdução de restrições relacionadas à utilização de toras e a demanda por diferentes produtos florestais.
Na década de 80 também foram publicados alguns livros que apresentam uma boa introdução ao assunto de Planejamento Florestal utilizando Pesquisa Operacional. Entre as publicações destacam-se as obras de Clutter [18], Leuschener [19] e Davis e Johnson [20]. Porém, duas obras publicadas nessa década são consideradas referência no assunto, pois além de apresentarem uma boa fundamentação teórica expõem uma variedade de exemplos práticos que ilustram cada um dos métodos e problemas abordados. As obras de referência são dos autores Dykstra [21] e Buongiorno e Gilless [22] que são utilizados como livro-texto de disciplinas da área de Planejamento Florestal em diversos cursos de graduação e pós-graduação. Cabe ressaltar que os autores Buongiorno e Gilles lançaram em 2003 uma atualização do livro de 1987, sob o título Decision Methods for Forest Resource Management.
Ainda na década de 80 publicaram-se alguns outros trabalhos interessantes sobre o Planejamento Florestal. Entre eles destacam-se os seguintes autores e trabalhos: Faaland e Briggs [23], que utilizaram PD para resolver o problema do corte ótimo de árvores em produtos serrados; Taube Netto [24], que apresenta um modelo de PL para planejamento de florestas de eucalipto nomeado de PLANFLOR; Eng et al. [25], que utilizaram PD e PL e geraram os padrões de corte por meio do método de decomposição de DANTZIG-WOLFE; Mendoza e Bare [26], que utilizam a técnica de geração de colunas para gerar o conjunto de padrões de corte; Weintraub et al. [27], que fazem uma ampla abordagem sobre o Planejamento Florestal Estratégico; e próximo ao final da década de 80 foi publicado o trabalho de Sessions et al. [28], no qual os autores utilizam heurísticas para gerar os padrões de corte.
No final da década de 80, um importante trabalho realizado no Brasil foi a tese de Carnieri [29], desenvolvida junto ao Departamento de Engenharia de Sistemas da Universidade Estadual de Campinas. Neste trabalho o autor desenvolveu um método de otimização do planejamento florestal por meio de Redes de Manejo. O autor apresentou duas alternativas de solução do problema utilizando PL ou Relaxação Lagrangeana. Como resultado, este trabalho apresentou redução significativa na utilização da memória computacional, viabilizando a utilização de microcomputadores em problemas de planejamento florestal de longo prazo. Ao final de seu trabalho o autor cita que, apesar de ter desenvolvido o método para problemas de longo prazo, ele acredita que o mesmo pode ser adaptado para problemas de curto prazo como definições de tipos de veículos de transporte ou locais de pátios de estocagem, por exemplo.
Durante a década de 90 e a primeira década do século 20, foram desenvolvidos novos métodos de solução aos problemas de traçamento e surgiram tentativas para integrar diferentes níveis hierárquicos de planejamento. Adicionalmente, problemas de planejamento envolvendo considerações espaciais e o agendamento da colheita florestal ganharam notoriedade. Particularmente, grande parte da literatura se dedicou ao tratamento de restrições de adjacência e criação de habitats para a vida silvestre. Os modelos tradicionais lidando com restrições de adjacência foram classificados como URM (Unit Restriction Model) e ARM (Area Restriction Model) [2]. O primeiro se refere às restrições que proíbem que talhões adjacentes sejam colhidos em um mesmo período, ao passo que o segundo permite a colheita de talhões adjacentes, desde um limite de área máximo seja respeitado. Estes modelos também possuem natureza combinatória e de difícil resolução, o que levou ao rápido desenvolvimento de diferentes métodos heurísticos para sua resolução, similarmente aos problemas de otimização do sortimento.
Na década de 90 destacam-se dezenas de trabalhos na área do Planejamento Florestal e algumas obras como Von Gadow e Bredenkamp [30], Hof [31] e Hof e Bevers [32]. No início da década, Rodriguez [33] publicou um modelo básico de tomada de decisão no Gerenciamento da Produção Florestal, no qual trabalha com a determinação da idade ótima de corte, a maximização do incremento médio anual e a determinação da maturidade financeira, utilizando PL no Planejamento Estratégico de modelos Tipo I e Tipo II [14].
Na sequência surgiram três trabalhos interessantes utilizando técnicas diferentes para a otimização do Planejamento Florestal, o de Lockwood e Moore [34] que apresenta a utilização da metaheurística Simulated Annealing no agendamento da colheita da madeira com restrições espaciais; o de Hof e Joyce [35] que também considera restrições espaciais na colheita florestal e utiliza Programação Linear Inteira Mista (PLIM) para otimizar; o de Weintraub et al. [36] que apresenta uma heurística para otimizar modelos de Planejamento Florestal em nível hierárquico Tático, considerando restrições de integridade.
No Brasil, a tese de doutorado de Oliveira [37], realizada em conjunto com a EMBRAPA/CNPF (Empresa Brasileira de Pesquisa Agropecuária – Centro Nacional de Pesquisas em Florestas), apresenta o desenvolvimento do SISPINUS, um sistema para prognose do crescimento e da produção de Pinus spp. no Sul do Brasil, visando avaliar os regimes de manejo. Cabe ressaltar que este sistema não é alimentado com informações de demanda. No mesmo ano, Ogweno [38] publica a sua tese na University of Canterbury, trabalhando com uma proposta de otimização integrada da colheita de madeira nos níveis Tático e Operacional do Planejamento Florestal.
O trabalho de Stape [39] envolve o Planejamento Operacional, mas com a finalidade de determinar técnicas para otimizar o método de colheita conhecido como talhadia. Neste trabalho o autor apresenta alguns fatores que podem interferir na qualidade da talhadia simples e como combatê-los afim de aumentar a produtividade da floresta. Neste mesmo ano, Laroze e Greber [40] publicaram um trabalho que, semelhante ao publicado em 1993, busca gerar os padrões de corte para a colheita, porém desta vez utilizando o método de Busca Tabu.
Os trabalhos de Leite [41] e Andrade e Leite [42] apresentam um método capaz de quantificar os multiprodutos que podem ser obtidos de árvores individuais a partir de uma unidade estere (uma unidade estere equivale ao volume aparente de madeira contido numa pilha com formato cúbico e 1,00 m de aresta). Este é um dos primeiros trabalhos do Brasil que considera a colheita de multiprodutos e busca otimizá-la. Neste mesmo ano, Murphy [43] publicou um trabalho que utiliza busca tabu para otimizar a geração de padrões de corte e também a alocação das frentes de corte em relação aos talhões que serão colhidos.
No final da década de 90 surgiram alguns trabalhos interessantes como o de Laroze [44] que apresenta um método de Busca Tabu aliado a PL para otimizar o traçamento das toras a nível de floresta e a dissertação de mestrado de Nobre [45] defendida na Universidade Federal de Lavras, onde a autora desenvolve uma heurística nomeada de ‘Heurística da Razão-R’ para o gerenciamento florestal. Neste mesmo ano, outros dois trabalhos apresentaram contribuições muito significativas. O primeiro foi o de Boston e Bettinger [46], que utilizam três heurísticas diferentes para resolver o problema de agendamento da colheita com restrições espaciais: Simulação de Monte Carlo, Simulated Annealing e Busca Tabu. A solução de cada uma das três heurísticas foi comparada à solução ótima obtida a partir de PLIM e as heurísticas Simulated Annealing e Busca Tabu apresentaram desempenho superior à Simulação de Monte Carlo. Este trabalho se destaca por ter utilizado mais de dez padrões de corte diferentes na otimização, tornando a complexidade do problema superior aos problemas com poucos padrões de corte. O segundo trabalho, desenvolvido pela equipe do professor Weintraub, no Chile, e publicado por Epstein et al. [47], é uma referência no âmbito do Planejamento Florestal. Conforme dito anteriormente, esta equipe desenvolveu cinco sistemas de gestão específicos para cada setor do Planejamento Florestal. O sistema MEDFOR para o nível de planejamento estratégico e o sistema OPTIMED para o nível tático. Para o Planejamento Operacional foram desenvolvidos três sistemas de gestão: o PLANEX que realiza o planejamento da malha viária e a alocação do maquinário e dos veículos de transporte; o OPTICORT que faz o agendamento da colheita e designa os padrões de corte para cada talhão, além da frente de corte que deverá atuar nos períodos da colheita; e o ASICAM que realiza o agendamento da frota de transporte. Em particular, o OPTICORT consiste em um módulo de PL combinado com um algoritmo de geração de colunas que, na verdade, é um gerador de padrões de corte tipo branch-and-bound. Porém, a partir da ramificação e avaliação iterativa de uma árvore de alternativas, são acrescentadas opções às soluções ótimas encontradas pelo módulo de PL.
A partir do ano 2000 as publicações na área florestal se expandiram. Este período começa com a publicação de três teses de doutorado, duas defendidas na Universidade Federal de Viçosa [48,49] e uma defendida na Universidade Federal do Paraná [50].
Em sua tese, Chichorro [48] apresenta uma metodologia de análise estrutural do gerenciamento florestal com a finalidade de otimizar a colheita de multiprodutos da madeira.
No mesmo ano, mas em Curitiba, a tese defendida por Arce [49] apresenta um sistema capaz de analisar, simular e otimizar o sortimento florestal em função das demandas por multiprodutos e levando em consideração os custos de transporte. Nesta tese, o autor elencou os métodos matemáticos mais utilizados até o momento para solucionar os problemas de traçamento de árvores e de alocação de toras:
- 1) Programação Linear com ou sem variáveis inteiras e binárias;
- 2) Programação Dinâmica;
- 3) Algoritmos de Geração de Colunas;
- 4) Otimização em Redes;
- 5) Sistemas especialistas (Expert Systems);
- 6) Busca Tabu.
O sistema desenvolvido pelo autor é composto por dois módulos principais: O módulo gerador dos padrões de corte (MGPC) e o módulo global de otimização (MGOS) do sortimento. O MGPC utiliza um algoritmo heurístico que identifica os cortes potenciais que devem ser avaliados ao longo do fuste, e um algoritmo baseado na PD, que determina a combinação ótima de produtos que maximiza a receita do fuste. O MGOS é formulado como um problema de PLIM submetido a restrições para o volume de madeira, quantidade de produtos e para as demandas, em cada talhão. O autor comenta ainda que a eficiência do sistema poderia ser medida pelos seguintes critérios:
- 1) Redução dos resíduos comerciais de madeira;
- 2) Aumento no valor total da madeira traçada e baldeada devido ao sortimento e aos custos de transporte otimizados;
- 3) Redução dos custos de classificação na floresta devido à simulação e controle dos produtos a retirar por talhão e;
- 4) Alguma combinação dos fatores mencionados.
No ano seguinte, Rodrigues [49] apresentou em sua tese o Sysflor, um sistema de suporte à tomada de decisão em planejamento florestal. Este mesmo autor publicou, em conjunto com outros autores, mais quatro trabalhos sobre o Planejamento Florestal nos anos seguintes. Nos três primeiros trabalhos foram tratados problemas de Planejamento Florestal com restrições de Integridade, cada um com uma metaheurística diferente. No primeiro trabalho, Rodrigues et al. [51] utilizam Busca Tabu, enquanto que no segundo trabalho, Rodrigues et al. [52] utilizam Algoritmo Genético e no terceiro trabalho, Rodrigues et al. [53] utilizam Simulated Annealing. Após esta sequência, o autor ainda publicou o trabalho Rodrigues et al. [54] no qual apresentam um modelo de regulação florestal e apresentam as implicações em problemas de Planejamento Florestal com restrições de recobrimento.
No trabalho de Falcão e Borges [55], estes pesquisadores portugueses apresentam heurísticas com a proposta de integração entre os níveis estratégico e operacional do Planejamento Florestal. No entanto, o trabalho possui um foco maior sobre os aspectos do Planejamento Estratégico. No trabalho são apresentados dois cenários com Horizontes de Planejamento longos, 70 anos e 25 anos.
Em seu trabalho, Soares et al. [56] apresentam uma metodologia de otimização voltada à colheita de multiprodutos florestais, os autores ressaltam que “até o momento não se tem conhecimento, na literatura brasileira, da utilização da programação dinâmica na definição do tamanho ideal de toras a serem colhidas em povoamentos florestais” ([56] p. 812). Eles propõem então uma metodologia de trabalho onde, inicialmente, decidem quais tamanhos de toras são mais rentáveis para as finalidades escolhidas (celulose, energia ou serraria) e em seguida buscam otimizar o lucro com a comercialização destes produtos. Porém, os autores consideraram que todas a madeira colhida seria comercializada, sem considerar restrições de demanda e zerando a perda de material.
Em Arce et al. [57], os autores desenvolveram uma metodologia para otimizar o traçamento de fustes de árvores, utilizando um algoritmo heurístico e PD em dois módulos distintos: o primeiro módulo utiliza um algoritmo heurístico que identifica os cortes potenciais; o segundo módulo utiliza um algoritmo com base na PD que determina a combinação ótima de produtos, com o objetivo de maximizar o valor. Os autores ressaltam que “a maneira como é conduzido o traçamento das árvores obtidas na colheita ou corte raso é fundamental para estabelecer as quantidades de cada um dos diferentes tipos de produtos que podem ser obtidos da floresta. Porém, esta tarefa é executada quase exclusivamente pelo motosserrista, com base na sua intuição, o que pode comprometer a rentabilidade do negócio florestal” ([57], p.207).
Em sua dissertação de mestrado, Souza [58] desenvolveu um modelo de Algoritmo Genético de modo a permitir que os tomadores de decisão pudessem determinar o período de intervenção das frentes de corte nos talhões e o fluxo de madeira entre os talhões e as fábricas, minimizando o custo de atividades relacionadas à colheita e ao transporte principal de madeira. O autor desenvolveu oito variedades de Algoritmos Genéticos e comparou os resultados obtidos com a solução de um modelo de PLIM. Foram consideradas restrições de demanda e oferta de cada produto florestal, restrições de produtividade por frente de corte, restrições de volume de madeira cortada e a capacidade de transporte dos produtos florestais e restrições que regulam o controle de estoque (Mínimo, Máximo e Corrente).
Um trabalho de grande relevância é a tese de Mitchell [59] apresentada na Escola de Engenharia de Produção da Universidade de Auckland, Nova Zelândia. Nesta tese o autor apresenta um modelo matemático que busca otimizar o Planejamento Operacional Florestal focando no agendamento da colheita da madeira. Segundo o autor, uma das etapas mais complexas no Planejamento Operacional é o Agendamento das Frentes de Corte. Para subsidiar este processo foram desenvolvidas soluções conhecidas como OHS (Operational Harvesting Scheduling). Ele frisa que um bom OHS atenderá às demandas colhendo os talhões mais próximos dos Centros Consumidores e que a solução de um OHS completo deve produzir, no mínimo, as seguintes respostas:
- 1) As agendas para as equipes de colheita por unidade de tempo;
- 2) Os volumes e os produtos que serão produzidos em cada período;
- 3) Como a produção será alocada para os clientes.
O autor também destaca que as estimativas de produção para um talhão podem ser geradas por meio de três formas:
- 1) Informações de produções de um talhão similar;
- 2) Estimativas de produção por produto, geradas por um inventário que considera a qualidade dos fustes;
- 3) Sistemas computacionais que simulam o processamento das árvores e geram estimativas por classe diamétrica.
Os autores Malinovski et al. [60] apresentaram um trabalho de análise das variáveis que podem influenciar na produtividade das Frentes de Corte. Neste trabalho, os autores buscaram identificar e sugerir as principais variáveis física do terreno, do povoamento e do planejamento que podem influenciar na produtividade. Eles também identificaram os principais tipos de máquinas utilizadas na atividade florestal no Brasil e buscaram correlações entre cada máquina e as variáveis apresentadas. Na acepção dos autores, uma adequada predição da produtividade é de suma importância para que sejam realizados orçamentos adequados para as atividades de colheita de madeira nas empresas. É importante ressaltar que os autores identificaram 37 variáveis de influência na produtividade das Frentes de Corte e os 10 tipos de máquinas mais utilizados na produção florestal brasileira. Fizeram a correlação entre estas variáveis e as diferentes máquinas. Ao final do trabalho eles esclarecem que “a interação entre as variáveis de influência de produtividade e as máquinas refletem a complexidade da atividade de planejamento e dimensionamentos das atividades de colheita de madeira” ([60], p.182).
Durante o período 1990-2010 houve uma intensificação no desenvolvimento de soluções heurísticas para vários problemas de planejamento florestal, especialmente relacionadas ao planejamento operacional. Isto ocorreu devido às dimensões do problema gerado e à estrutura das restrições [61]. Destacam-se à aplicação da busca tabu, algoritmo genético e simulated annealing, especialmente na resolução de problemas combinatórios envolvendo restrições espaciais e problemas de traçamento ([62]; [63]). Heurísticas se tornaram necessárias devido à grande complexidade gerado pelos problemas combinatórios aliada a limitada capacidade computacional para resolvê-los.
O mesmo continua a ser desenvolvido em trabalhos recentes como Augustynczik et al. [64] e Augustynczik et al. [65]. No primeiro trabalho os autores restringiram o planejamento utilizando as restrições de áreas máximas operacionais enquanto que no segundo trabalho os autores aliaram PLIM e Simulated Annealing buscando mostrar o impacto econômico que o planejamento e a promoção da colheita produz em plantações florestais brasileiras. Mais recentemente, em Santos et al. [66] os autores descrevem um modelo de Programação Linear Inteira (PILP) que busca otimizar de forma integrada o planejamento da colheita e da distribuição dos produtos de madeira.
Em Gomide et al. [67], os autores apresentam um estudo comparativo ente os Operadores de Seleção de Algoritmos Genéticos (Roleta, Torneio, Elitista e Bi-Classista) no Planejamento Florestal de um modelo do Tipo I [14]. Os autores demonstram no trabalho que o operador de seleção roleta apresentou o melhor desempenho, com desvio percentual em relação à solução ótima de apenas 0,90%.
Os modelos de planejamento introduzidos durante as últimas décadas se caracterizaram por um crescente interesse em modelos com múltiplos objetivos e agentes de decisão, buscando-se conciliar objetivos relacionados à produção e qualidade ambiental. Cada vez mais serviços ecossistêmicos são considerados, como a promoção de biodiversidade, sequestro de carbono e qualidade da água [68] e se observa um aumento na aplicação de técnicas de Compromise Programming e Goal Programming (Programação por Metas). Mais recentemente, a incorporação de dados provenientes de sistemas de sensoriamento remoto [69] e o tratamento de incertezas relacionadas aos dados do modelo de otimização se tornam cada vez mais frequentes, com a aplicação de métodos de programação estocástica [70].
Em Banhara et al. [71], os autores objetivaram aprimorar as técnicas de Planejamento Operacional da colheita de eucalipto utilizando um modelo de PLIM e Goal Programming sob restrições operacionais, espaciais e ambientais. Inicialmente, os autores resolveram o problema proposto sem nenhuma das restrições, depois adicionaram uma restrição apenas, combinaram duas a duas e por fim modelaram com as três simultaneamente, produzindo 8 cenários diferentes.
Em sua tese de doutorado, Santana [72], apresenta uma metodologia para o traçamento e a alocação de toras de eucalipto com a utilização de técnicas de Geração de Colunas e PD. O autor conclui que a abordagem proposta foi eficiente pois encontrou soluções ótimas em menos de 5 minutos em oitos cenários estudados. Para o autor, a quantidade de árvores derrubadas para atender determinada carteira de pedidos foi minimizada, gerando menor desperdício.
3. Discussão e considerações finais
Analisando trabalhos desenvolvidos nas últimas cinco décadas, percebe-se que o assunto do Planejamento Florestal é amplo e de grande importância acadêmica e econômica. Se observou que houve um crescimento exponencial no número de publicações na área de planejamento florestal durante este período (Figura 1). Nota-se que diversos trabalhos foram desenvolvidos no âmbito dos níveis estratégico e tático de planejamento, o que construiu a base de conhecimento para os pesquisadores e empresários da área florestal. O desenvolvimento destes modelos de planejamento contribuiu para uma maior eficiência no manejo de florestal tanto plantadas como nativas. Adicionalmente, aplicações de pesquisa operacional se adequaram às demandas sociais ao decorrer do tempo, como a inclusão de serviços ecossistêmicos, restrições de adjacência e criação de habitat para a vida silvestre a partir da década de 90, acompanhando o surgimento de questões relacionadas à sustentabilidade e biodiversidade no mesmo período (por exemplo a conferência das Nações Unidas sobre o Meio Ambiente).
Com o aumento na complexidade dos modelos de planejamento causados pela inclusão destes critérios de manejo adicionais e o poder computacional limitado, diversos métodos heurísticos foram adaptados aos problemas de planejamento florestal, com destaque para a Busca Tabu, Simulated Annealing e o Algoritmo Genético. Com o rápido aumento do poder computacional durante as últimas décadas, cada vez mais soluções exatas foram desenvolvidas, principalmente com a aplicação de programação linear inteira e programação linear inteira mista.
Apesar do rápido desenvolvimento nos métodos de solução e o poder computacional, o planejamento operacional se mantém sub-representado na literatura. O nível operacional envolve uma série de variáveis que devem ser avaliadas durante a otimização, como a escolha dos talhões a serem colhidos, a designação das frentes de corte, o transporte dos produtos colhidos, o atendimento das demandas dos produtos, entre outros. Além disso, este nível exige que respostas sejam encontradas em janelas de tempo curtas. Por isso, os trabalhos desenvolvidos focam em uma ou mais variáveis envolvidas neste nível hierárquico. Desta forma, os modelos apresentam natureza combinatória e um grande nível de complexidade para modelos com um longo horizonte de planejamento. Desta forma, a harmonização deste nível hierárquico com o planejamento estratégico e tático permanece limitada. Ainda, avanços recentes no tratamento de incertezas em modelos de otimização foram aplicados a problemas no nível operacional de forma limitada. Em conclusão, esforços futuros no estudo de pesquisa operacional aplicada a problemas de planejamento florestal necessita um maior foco no nível operacional e esforços buscando harmonizar este com o nível estratégico e tático são essenciais, uma vez que soluções ótimas em um nível não se traduzem necessariamente em soluções ótimas para os demais. Com uma integração no planejamento, se pode garantir a eficiência do manejo florestal e assegurar que os objetivos do manejo sejam alcançados.
Referências
[1] Bateman T.S., Snell S.A. Administração: construindo vantagem competitiva. Atlas, São Paulo, 1998.
[2] Bettinger P., Boston K., Siry J.P., Grebner D.L. Forest management and planning. Academic Press, Burlington, 2009.
[3] Andersson S. Approaches to integrated strategic/tactical forest planning. Department of Forest Resource Management and Geomatics, Licentiate Thesis, Swedish University of Agricultural Science, Umea, 2005.
[4] Weintraub A., Cholaky A. A hierarchical approach to forest planning. For. Sci., 37:439-460, 1991.
[5] Curtis F.H. Linear programming in the management of a forestry property. J. For., 60:611-616, 1962.
[6] Loucks D.P. The development of an optimal program for sustained-yield management. J. For., 62:485-490, 1964.
[7] Leak W.B. Estimating maximum allowable timber yields by linear programming: A case study. J. For., 65:644-646, 1964.
[8] Nautiyal J.C., Pearse P.H. Optimizing the conversion to sustained-yield: A programming solution. For. Sci., 13:131-139, 1967.
[9] Pnevmaticos S.M., Mann S.H. Dynamic programming in tree bucking. For. Prod. J., 22(2):26-30, 1972.
[10] Navon, D.I., Timber RAM: a long-range planning method for commercial timber lands under multiple-use management. USDA Forest Service Research Paper, PNW-70, 1971.
[11] Ware G.O., Clutter J.L., A mathematical programming system for the management of industrial forests. For. Sci., 17(3):428-445, 1971.
[12] Iverson, D.C., Alston, R.M. The genesis of FORPLAN a historical and analytical review of Forest Service planning models. USDA Forest Service General Technical Report, INT-214, 1986.
[13] USDA Forest Service, Spectrum User’s Guide. Ecosystem Management Analysis Center, Fort Collins, CO. 1995.
[14] Johnson K.N., Scheurman H.L. Techniques for prescribing optimal timber harvest and investment under different objectives: discussion and synthesis. For. Sci., 31(Monograph 18), 1977.
[15] Deadman M. W., Goulding C. J. A method for assessment of recoverable volume by log types. N. Z. J. For. Sci., 9(2):225-239, 1979.
[16] Johnson, K.N., Jones, D., Daniel, B. A user’s guide to multiple use sustained yield scheduling calculation (MUSYC). Fort Collins: Department of Agriculture, Forest Service, Timber Management, 1979.
[17] Borges, J. F. Seccionamento do fuste de Pinus taeda L. para obtenção do volume de madeira serrada através da função de forma polinomial. Dissertação (Mestrado em Ciências Florestais) – Universidade Federal do Paraná, Curitiba, 1981.
[18] Clutter, J.L. Timber management: A quantitative approach. John Wiley & Sons Inc., New York, 1983.
[19] Leuschener, W.A. Introduction to Forest Resource Management. John Wiley & Sons, New York, 1984.
[20] Davis, L.S., Johnson, K.N. Forest Management. McGraw-Hill, New York, 1987.
[21] Dykstra, D.P. Mathematical programming for natural resource management. McGraw-Hill, New York, 1984.
[22] Buongiorno, J., Gilless K. Forest management and economics: a primer in quantitative methods. Macmillan, New York, 1987.
[23] Faaland B., Briggs D. Log bucking and lumber manufacturing using dynamic programming. Management Sci., 30(2):245-257, 1984.
[24] Taube Netto M. Um modelo de programação linear para planejamento de florestas de eucalipto. Pesqui. Oper., 4(1):19-39, 1984.
[25] Eng G., Daellenbach H.G., Whyte A.G.D. Bucking tree-length stems optimally. Can. J. For. Res., 16(5):1030-1035, 1986.
[26] Mendoza G.A., Bare B.B. A two-stage decision model for log bucking and allocation. For. Prod. J., 36(10): 70-74, 1986.
[27] Weintraub A., Guitard S., Hohn V. Strategic planning in Forest industries. Eur. J. Oper. Res., 24:152-162, 1986.
[28] Sessions J., Olsen E., Garland J. Tree bucking for optimal stand value with log allocation constraints. For. Sci., 35(1):271-276, 1989.
[29] Carnieri C. Planejamento florestal otimizado via redes de manejo. Tese (Doutorado em Engenharia Elétrica), Universidade Estadual de Campinas, Campinas, 1989.
[30] Von Gadow K., Bredenkamp B.V. Forest management. Academica, Pretoria, 1992.
[31] Hof J. Coactive forest management. Academic Press, London, 1993.
[32] Hof J., Bevers M. Apatial optimization for managed ecosystems. Columbia University Press, New York, 1998.
[33] Rodriguez L.C.E Gerenciamento da produção florestal. ESALQ, Doc. Flor., 13:1-41, 1991.
[34] Lockwood C., Moore T. Harvest scheduling with spatial constraints: a simulated annealing approach. Can. J. For. Res., 23(3):468-478. 1993.
[35] Hof J.G., Joyce L.A. A mixed integer linear programming approach for spatially optimizing wildlife and timber in managed forest ecosystems. For. Sci., 39:816-834, 1993.
[36] Weintraub A., Jones G., Magendzo A., Meacham M., Kirby M. A heuristic system to solve mixed-integer Forest planning models. Oper. Res., 42(6):1010-1024, 1994.
[37] Oliveira, E.B. Um sistema computadorizado de prognose do crescimento e produção de Pinus taeda L., com critérios quantitativos para a avaliação técnica e econômica de regimes de manejo. Tese (Doutorado em Ciências Florestais), Universidade Federal do Paraná, Curitiba, 1995.
[38] Ogweno D.C.O. Integrated optimization of operational and tactical planning for log production. Thesis (PhD in Forestry), University of Canterbury, 1995.
[39] Stape J.L. Planejamento global e normatização de procedimentos operacionais da talhadia simples em Eucalyptus. Série Técnica IPEF, 11(30):51-62, 1997.
[40] Laroze A.J., Greber B.J. Using Tabu search to generate stand-level, rule-based bucking patterns. For. Sci., 43(2):157-169, 1997.
[41] Leite H.G. Conversão de árvores em multiprodutos da madeira utilizando programação dinâmica. Tese (Doutorado em Ciência Florestal), Universidade Federal de Viçosa, Viçosa, 1993.
[42] Andrade V.C.L., Leite H.G. Um método para quantificar multiprodutos de árvores individuais na unidade estere. Rev. Árvore, 22(3):299-306, 1998.
[43] Murphy G. Allocation of stands and cutting patterns to logging crews using tabu search heuristics. J. For. Eng., 9(1):31–37, 1998.
[44] Laroze A.J. A linear programming, tabu search method for solving forest-level bucking optimization problems. For. Sci., 45(1):108-116, 1999.
[45] Nobre, S.R. A heurística da Razão-R aplicada a problemas de gestão florestal. Dissertação (Mestrado em Administração Rural), Universidade Federal de Lavras, Lavras, 1999.
[46] Boston K., Bettinger P. An analysis of Monte Carlo integer programming, simulated annealing, and tabu search heuristics for solving spatial harvest scheduling problems. For. Sci., 45(2):292–301, 1999.
[47] Epstein R., Morales R., Serón J., Weintraub A. Use of OR systems in the Chilean forest industries. Interfaces, 29(1):7-29, 1999.
[48] Chichorro J.F. Análise estrutural e econômica de multiprodutos da madeira. Tese (Doutorado em Ciência Florestal), Universidade Federal de Viçosa, Viçosa, 2000.
[49] Rodrigues F.L. Metaheurística e sistema de suporte à decisão no gerenciamento de recursos florestais. Tese (Doutorado em Ciência Florestal), Universidade Federal de Viçosa, Viçosa, 2001.
[50] Arce J.E. Um sistema de análise, simulação e otimização do sortimento florestal em função da demanda por multiprodutos e dos custos de transporte. Tese (Doutorado em Ciências Florestais), Universidade Federal do Paraná, Curitiba, 2000.
[51] Rodrigues F.L., Leite H.G., Santos H.N., Souza A.L. Solução de problemas de planejamento florestal com restrições de inteireza utilizando busca tabu. Rev. Árvore, 27(5):701-713, 2003.
[52] Rodrigues F.L., Leite H.G., Santos H.N., Souza A.L., Silva G.F. Metaheurística algoritmo genético para solução de problemas de planejamento florestal com restrições de integridade. Rev. Árvore, 28(2):233-245, 2004.
[53] Rodrigues F.L., Leite H.G., Santos H.N., Souza A.L., Ribeiro C.A.A.S. Metaheurística simulated annealing para solução de problemas de planejamento florestal com restrições de integridade. Rev. Árvore, 28(2):247-256, 2004.
[54] Rodrigues F.L., Silva G.F., Leite H.G., Xavier A.C., Pezzopane J.E.M. Um modelo de regulação florestal e suas implicações na formulação e solução de problemas com restrições de recobrimento. Rev. Árvore, 30(5):769-778, 2006.
[55] Falcão A.O., Borges J.G. Heurísticas para a integração de níveis estratégico e operacional da gestão florestal em problemas de grande dimensão. Scientia Forestalis, 63:94-102, 2003.
[56] Soares T.S., Vale A.B. do, Leite H.G., Machado C.C. Otimização de multiprodutos em povoamentos florestais. Rev. Árvore, 27(6):811-820, 2003.
[57] Arce J.E., Macdonagh P., Friedl R.A. Geração de padrões ótimos de corte através de algoritmos de traçamento aplicados a fustes individuais. Rev. Árvore, 28(2):207-217, 2004.
[58] Souza, D.O. Algoritmos genéticos aplicados ao planejamento do transporte principal de Madeira. Dissertação (Mestrado em Engenharia Florestal), Universidade Federal do Paraná, Curitiba, 2004.
[59] Mitchel, S.A. Operational forest harvest scheduling optimization: a mathematical model and solution strategy. Tese (Doutorado em Engenharia de Produção), Universidade de Auckland, Auckland, 2004.
[60] Malinovski R.A., Malinovski R.A., Malinovski J.R. Análise das variáveis de influência na produtividade das máquinas de colheita de madeira em função das características físicas do terreno, do povoamento e do planejamento operacional florestal. Rev. Flor., 36(2):169-182, 2006.
[61] Bettinger P., Boston K., Sessions J. Intensifying a heuristic forest harvest scheduling search procedure with 2-opt decision choices. Can. J. For. Res., 29(11):1784-1792, 1999.
[62] Murray A.T., Church R.L. Heuristic solution approaches to operational forest planning problems. OR Spektrum, 17:193-203, 1995.
[63] Yoshimoto A., Brodie J.D., Sessions J. A new heuristic to solve spatially constrained long-term harvest scheduling problems. For. Sci., 40(3):365-396, 1994.
[64] Augustynczik A.L.D., Arce J.E., Silva A.C.L. Spatial forest harvest planning considering maximum operational areas. Cerne, 21(4):649-656, 2015.
[65] Augustynczik, A.L.D., Arce J.E., Yousefpour R., Silva, A.C.L. Promoting harvesting stands connectivity and its economic implications in Brazilian forest plantations applying integer linear programming and simulated annealing. For. Pol. and Econ., 73:120-129, 2016.
[66] Santos P.A.V.H., Silva A.C.L., Arce J.E., Augustynczik A.L.D. A mathematical model for the integrated optimization of harvest and transport scheduling of forest products. Forests, 10(12):1110, 2019.
[67] Gomide L.R., Arce J.E., Silva, A.C.L. Uso do algoritmo genético no planejamento florestal considerando seus operadores de seleção. Cerne, 15(4):460-467, 2009.
[68] Diaz-Balteiro L., González-Pachón J., Romero C. Measuring systems sustainability with multi-criteria methods: A critical review. Eur. J. Oper. Res., 258:607-616, 2017.
[69] Pascual A., Pukkala T., Rodríguez F., De-Miguel S. Using spatial optimization to create dynamic harvest blocks from LiDAR-based small interpretation units. Forests, 7(10):220, 2016.
[70] Álvarez-Miranda E., Garcia-Gonzalo J., Pais C., Weintraub A. A multicriteria stochastic optimization framework for sustainable forest decision making under uncertainty. For. Pol. and Econ., 103:112-122, 2019.
[71] Banhara, J.R., Rodriguez L.C.E., Seixas F., Moreira J.M.M.A.P., Silva L.M.S., Nobre S.R., Cogswell A. Agendamento otimizado da colheita de madeira de eucaliptos sob restrições operacionais, espaciais e climáticas. Scientia Forestalis, 38(85):85-95, 2010.
[72] Santana, C.J.O. Traçamento e alocação ótima de toras de eucalipto por geração de colunas e programação dinâmica. Tese (Doutorado em Engenharia Florestal), Universidade Federal do Paraná, Curitiba, 2013.
Document information
Published on 31/05/21
Accepted on 24/05/21
Submitted on 28/02/20
Volume 37, Issue 2, 2021
DOI: 10.23967/j.rimni.2021.04.007
Licence: CC BY-NC-SA license
Share this document
Keywords
claim authorship
Are you one of the authors of this document?