Partially saturation effect on fine sands and earth pressure in a sheetpile wall

Latest revision as of 16:19, 2 March 2021

Abstract

Generally, the effects of suction in fine sands can be evidenced by a stiffening of the material, as the capillary front advances in the granular skeleton. In geotechnical retention structures this effect can be translated in an increasing of earth pressure, which is not normally considered in geotechnical designs. This study analyzes the capillary effects by implementing a physical modelling in centrifuge and a numerical simulation, using different constitutive models that involve suction within the analysis. The modelling is based on a structure of retention in sheetpiles built on a real scale. Some factors that affect both physical and numerical modelling were taken into account and should be considered in the analysis of the results obtained and, in the comparisons, carried out by both methodologies. As a point of interest, numerical modelling showed less dispersion in the results obtained than physical modelling, these and other aspects are analyzed in the document

Keywords: Unsaturated soils, numerical modelling, full-scale test, sheetpile wall

Resumen

Generalmente los efectos de succión en arenas finas se pueden evidenciar por una rigidización del material, a medida que el frente de capilaridad asciende en el esqueleto granular. En estructuras geotécnicas de contención este efecto puede ser traducido en el aumento de la presión de tierras, que normalmente no es considera-do en los diseños geotécnicos. Este estudio analiza los efectos capilares implementando una modelación física en centrifuga y una simulación numérica usando diferentes modelos constitutivos que involucran la succión dentro del análisis. Las modelaciones están basadas en una estructura de contención en tablestacas construida e instrumentada a escala real. Se tuvieron en cuenta algunos factores que afectan las modelaciones tanto físicas como numéricas y que deben ser considerados en el análisis de resultados obtenidos y en las comparaciones realizadas mediante ambas metodologías. Como punto de interés, la modelación numérica mostró menos dispersión en los resultados obtenidos que la modelación física, estos y otros aspectos son analizados en el documento.

Palabras clave: Suelos no saturados, modelación numérica, ensayo a escala real, tablestacado

1. Introducción

La mejor metodología para obtener los esfuerzos y deformaciones ocurridos en una estructura geotécnica es desarrollar un ensayo a escala real, donde se puedan monitorear, desde el mismo inicio de la instalación de la estructura (condiciones iniciales), hasta su vida útil. No obstante, esta técnica tiene algunos bemoles relacionados con su alto costo, incapacidad de hacer variaciones notorias en el ensayo y restricción para hacer mediciones solo en el contorno de la estructura.

Los modelos físicos reducidos cobran importancia en términos de la posibilidad de realizar más variaciones que en un ensayo a escala real y controlar con relativa facilidad ciertos sensores para la medición de esfuerzos y deformaciones. Sin embargo, extrapolar estas mediciones a estructuras reales no es posible de manera directa, debido a problemas de escalamiento en elementos geotécnicos. Por tal razón en el uso de modelos físicos reducidos se considera que la mejor alternativa es la centrifuga geotécnica. Esta técnica está dentro de la vanguardia de la modelación física al imponer un campo de gravedad específico para el modelo reducido, que permite medir de un modo más adecuado diferentes cantidades en el modelo con la posibilidad de transportarlas mediante leyes de escalamiento apropiadas que están en función del campo de gravedad aplicado.

Por otra parte, existe la posibilidad de plantear un modelo artificial, es decir mediante el uso de una simulación numérica usando un modelo constitutivo adecuado para el problema geotécnico que se piensa abordar. La ventaja de estas modelaciones es que es posible obtener estados de esfuerzos en cualquier parte del dominio del problema, predecir escenarios futuros y realizar innumerables variaciones a un bajo costo.

Ahora bien, combinando técnicas de modelación numérica y física, es posible simular el comportamiento global de una estructura geotécnica eficientemente. En esta investigación se usó un modelo reducidos en centrífuga que guarda las mismas condiciones realísticas del ensayo a escala real. Para la modelación numérica se tuvo en cuenta fielmente el benchmarking realizado con ocasión de la construcción del ensayo a escala natural [1]. Los resultados mostraron una dispersión bastante alta, cuando se intentaron predecir resultados de esfuerzos y deformaciones en la tablestaca principal del problema. La conclusión principal de la alta dispersión de las predicciones con las mediciones fue desconocer el efecto de la succión sobre la arena fina. Por esta razón, las modelaciones numéricas desarrolladas en el estudio actual involucran un modelo hipoplástico para arenas, con una extensión que reproduce el efecto rigidizante mediante un parámetro especial que simula la succión en el suelo [2,3,4].

2. Antecedentes

2.1 ¿Por qué no podemos predecir acertadamente resultados de ensayos a escala real o estructuras geotécnicas reales?

Como bien lo describe Kolymbas, en los últimos años el progreso que se ha tenido en esta materia no ha ido de la mano con el avance de la tecnología en términos de la informática [5]. La falta de estructuras geotécnicas o ensayos a escala real adecuadamente monitoreados e instrumentados que generen benchmarking basados en predicciones llevadas a cabo por diferentes instituciones o firmas, presupone un obstáculo para el intercambio de información expedito y sin restricciones.

Otro de los aspectos que inciden en el rezago de este campo de la ingeniería geotécnica, es la selección y generación apropiada del modelo constitutivo idóneo para el problema geotécnico que ser quiere abordar. En algunos casos estos modelos suelen ser muy complejos y la trasferencia de conocimiento hacia otros investigadores era nula. No obstante, hoy día ese tipo de inconvenientes han sido paulatinamente superados por el trabajo conjunto entre diferentes instituciones, como se puede consultar en el proyecto soilmodels.info [6].

En cuanto a la ingeniería práctica, cambiar la mentalidad de los proyectistas que han diseñado estructuras geotécnicas mediante métodos tradicionales que sobreestiman los esfuerzos y deformaciones ocurridas in-situ sobre el terreno, es sumamente difícil, incluso porque las firmas ganan por la cantidad de materiales utilizados en la construcción. Optimizar los diseños desde el punto de vista investigativo, no está en los planes de los constructores a corto plazo. Esta desarticulación entre la ingeniería práctica y la investigación puede ocasionar un atraso en la generación de nuevo conocimiento y de información. Lo contrario podría traducirse en predicciones más acertadas de escenarios futuros en problemas geotécnicos que pueden ser útiles para toda la comunidad.

2.1.1 Factores intrínsecos que afectan las modelaciones físicas y numéricas

Cuando se aborda la modelación física y numérica de un problema geotécnico, existen diferentes aspectos que controlan los resultados finales de dicha modelación. Dentro de las modelaciones numéricas, uno de los puntos de interés está relacionado con la escogencia adecuada del modelo constitutivo, lo cual va a gobernar en gran parte los resultados éxitos de la modelación. Es importante entender que no existe un modelo constitutivo que simule todos los aspectos que influyen en el comportamiento del suelo, debido a que es un material de una alta heterogeneidad, controlado por procesos naturales producidos de manera errática y no tienen una especificación definida [7].

Estas condiciones naturales e histeréticas del suelo son casi imposibles de simular e implantar como condición inicial en un modelo artificial; entre ellas la génesis, historia geológica, creep, relajación, colapso, saturación parcial, etc.

Kolymbas propone una serie de planteamientos que son útiles para conocer a prior la calidad e idoneidad del modelo constitutivo dentro del contexto de la modelación numérica abordada [8]. Estos están relacionados con la calidad y limitaciones del modelo, definición de una comprobación para saber si el modelo escogido es acorde a lo requerido y la implementación e integración numérica.

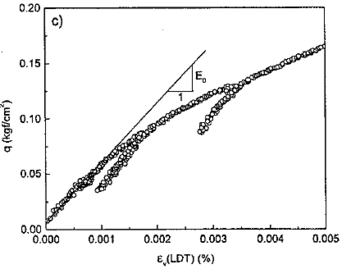
Desde este marco, los modelos constitutivos hoy en día junto con el método numérico adoptado para la simulación pueden tener problemas con grandes deformaciones en el modelo, ya que algunos de ellos basan su formulación matemática en teorías de pequeñas deformaciones. Así mismo, modelos demasiado simplistas descomponen la deformación en una parte elástica y otra plástica, donde la parte elástica se considera reversible. Por supuesto, es conocido ya que el suelo no responde elásticamente sino a muy pequeñas deformaciones como puede notarse en la Figura 1.

Figura 1. Resultados de deformación en una grava densa [9]

En cuanto a las modelaciones físicas en centrífuga, esta técnica es considerada la más idónea, debido a que es impuesto un campo gravitacional a modelo reducido con el objeto de producir esfuerzos geostáticos idénticos en el modelo y el prototipo. No obstante, el análisis depende de unas leyes de escalamiento que permiten la convergencia de modelos de problemas geotécnicos y facilita la obtención de resultados precisos con el fin de plantear soluciones a problemáticas complejas (Tabla 1). La centrifuga en realidad es una metodología bastante didáctica que ayuda entender el comportamiento mecánico del suelo, así como de elementos geotécnicos, que terminan siendo muy útiles para la validación de modelos numéricos, como es el caso que atañe a esta investigación [10].

Tabla 1. Leyes de escalamiento en centrifuga para un campo de n gravedades [11]

Magnitud física	Símbolo	Modelo/Prototipo
Longitud	L	1/n
Desplazamiento	U	1/n
Área	A	1/n²
Volumen	V	1/n³
Deformación	ϵ	1
Fuerza	F	1/n
Esfuerzo	Σ	1/n²
Peso especifico	Γ	1/n³
Masa	M	1/n
Aceleración	A	N
Velocidad	V	1
Frecuencia	F	N
Energía	E	1/n³

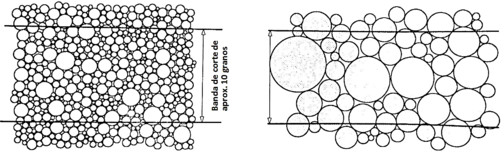
Otros efectos de escala que deben ser analizados de manera exhaustiva y minimizados en lo posible, para evitar su afectación en los resultados son el campo de aceleración no uniforme en el sistema, tamaño de grano en el modelo, aceleración de Coriollis (pluviación de arenas) y efectos de borde (debido a la pequeña escala). Dentro de estos aspectos, se considera que el tamaño de grado es el más notorio y puede llevar a algunos errores en la interpretación de resultados, puesto que las partículas de suelo no pueden ser escaladas de la misma manera, como el resto de elementos de una estructura geotécnica.

Figura 2. (a) Partículas de suelo en el prototipo. (b) Partículas escaladas en un modelo [11]

3. Materiales y métodos

3.1 Ensayo de campo a escala real de referencia

El ensayo a escala real que fue seleccionado para las tareas de validación, tanto del modelo numérico, como físico, es el denominado como: “The Results of the Sheetpile Wall Field Test in Hochstetten” [1]. El cual fue objeto de un benchmarking ente 43 instituciones alrededor del mundo, con el fin de analizar las predicciones numéricas y la posible dispersión al comparar las mediciones con las simulaciones numéricas. Como ya se mencionó anteriormente, el colofón del resultado tuvo como conclusión que la alta dispersión observada en las predicciones fue resultado de no considerar condiciones iniciales en el modelo, como el hincado de la tablestaca, ni tal vez el aspecto más importante, el efecto de la succión sobre las presiones de tierra en la estructura de contención. Esto último es la justificación de la investigación abordada en este documento.

El ensayo tuvo un plan de monitoreo bastante juicioso, donde fueron medidos desplazamientos verticales y horizontales en diferentes puntos de la estructura en general, presiones de tierra en la tablestaca y fuerzas en los puntales. La tablestaca principal que hace parte de la estructura geotécnica, fue hincada en arena de Hochstetten. A partir de la cual fueron desarrolladas diferentes secuencias de excavación, donde se instalaron puntales en las excavaciones más críticas (Figura 3).

Figura 3. Ensayo a escala real en Hochstetten (Alemania) [1]

3.2 Modelo físico reducido

La modelación física se realizó con ensayos en centrifuga, imponiendo un campo de aceleración equivalente a 30-g. Según esto fue construido el modelo reducido a una escala adecuada, conservando una relación altura vs. ancho del modelo dentro de un contenedor de 0.40 x 0.60 x 0.50 m, con el fin de mitigar algunos de los efectos de escala, en especial el tamaño de grano [12]. La instrumentación fue implementada para medir principalmente deformaciones en el trasdós de la excavación y esfuerzos en la tablestaca. Para desplazamientos fueron usados LVDT y celdas de prisión miniatura para medir la presión de tierras en la tablestaca.

Naturalmente, el modelo físico conserva realísticamente los aspectos más importantes del ensayo a escala real, escalando apropiadamente algunos elementos como la tablestaca de acero, de acuerdo con su inercia y el módulo de elasticidad. Fueron instalados unos muros en acrílico lubricados, para minimizar la fricción y el efecto 3D; además para que el modelo tenga condiciones para ser analizado como un problema de deformación plana, incluso en el modelo numérico planteado más adelante (Figura 4).

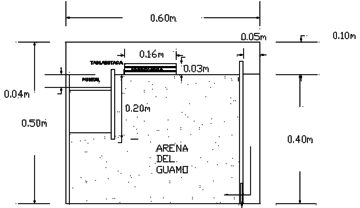
Figura 4. Esquema en Perfil del modelo físico a escala 1:30

Debido a que no era posible importar la arena de Hochstetten, se decidió ajustar la distribución del tamaño de partículas a un material granular local denominado como arena del Guamo (Figura 5). Para garantizar la relación de vacíos inicial del prototipo se usó un dispositivo de pluviación.


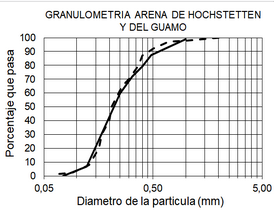
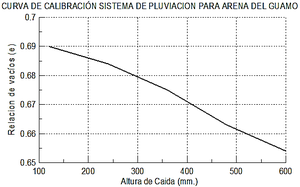
(a)	(b)
Figura 5. Figura 5. (a) Distribución del tamaño de partículas de la arena de Hochstetten y arena del Guamo. (b) Curva de calibración del sistema de pluviación

2.1.3 Modelación numérica en elementos finitos

2.1.3.1 Modelo constitutivo de referencia [2]

Actualmente existen modelos promisorios, algunos de ellos implementados numéricamente para reproducir la respuesta no saturada del suelo [13,14], los cuales han mostrado resultados interesantes, en especial en materiales cohesivos donde la succión alcanza niveles importantes de influencia sobre el comportamiento mecánico del suelo [15–28].

En la Tabla 2 se pueden observar los modelos constitutivos en orden cronológico que se han propuesto hasta la fecha para intentar simular la respuesta no saturada del suelo.

Tabla 2. Modelos constitutivos para el comportamiento mecánico de solos no saturados (modificado de [30])

Modelo constitutivo	Teoría usada	Contribución
Matyas & Radhakrishna (1968) [15]	Elastoplástica	Superficie que representa las variaciones de la relación de vacíos en función del estado de esfuerzos neto y la succión
Fredlund (1979) [16]	Elástica (Lei de Hooke)	Propone un modelo elástico incremental que consiste em la Ley de Hooke generalizada para suelos no sat., donde es considerada la no linealidad de la relación esfuerzo-deformación
Alonso et al. (1990) [13]	Elastoplástica	BBM - extensión del modelo elastoplástico de CCM, para suelos no sat., que integra los cambios de volumen con la resistencia al corte
Balmaceda (1991) [17]	Elastoplástica	Propone una alteración en el cálculo de parámetros hidráulicos de [13] usando una escala bi-log, para el cálculo de las compresibilidades del suelo para diversos parámetros de succión
Gens & Alonso (1992) [18]	Elastoplástica	Extensión del BBM, la modificación está basada en dos niveles en la estructura del suelo: micro y macro. Barcelona Expansive Model (BExM).
Gens & Nova (1993) [19]	Elastoplástica	Concepto de la superficie de plastificación intrínseca
Gudehus (1995) [2]	Hipoplástica	El esqueleto granular es modelado usando 4 constantes del material, La combinación de hipoplasticidad y capilaridad explica la respuesta de elementos de suelo húmedo en el edómetro bajo compresión triaxial y corte simple
Modaressi & Abou-Bekr (1996) [20]	Elastoplástica	El concepto de esfuerzo efectivo es extendido para el caso de materiales parcialmente sat. por la introducción de una presión capilar. Usa un modelo elastoplástico validado en el caso saturado o seco y generalizado para el caso de suelo parcialmente sat.
Loret & Khalili (2002) [21]	Elastoplástica	Principal énfasis en el comportamiento do esqueleto sólido, un modelo elastoplástico simple es descrito requiriendo pocos parámetros para definir el efecto de la desaturación
Wheeler et al. (2003) [22]	Elastoplástica	Incorporación de los efectos de la variación del grado de sat, en el comportamiento esfuerzo-deformación. Representa el cambio de posición de la WRC durante la carga, o sea, el comportamiento hidráulico es acoplado a la relación esfuerzo-deformación
Gallipolli et al. (2003) [23]	Elastoplástica	Considera explícitamente los mecanismos de la succión que afectan el comportamiento mecánico, así como la dependencia sobre el grado de sat.
Sheng et al. (2004) [24]	Elastoplástica	Considera la histéresis hidráulica y las deformaciones irreversibles debidas a los ciclos de humedecimiento y secado capaz de reproducir el comportamiento de solos muy expansivos.
Karstunen et al. (2005) [25]	Elastoplástica	Reproduce el efecto anisotrópico, cementación entre partículas y la desestructuración para suelos saturados
Sheng et al. (2008) [26]	Elastoplástica	Proponen un nuevo modelo elastoplástico para suelos no sat. usando dos variables de estado de esfuerzos independientes
Masín & Khalili (2008) [14]	Hipoplástica	Uno de los primeros intentos basados en hipoplasticidad usando el principio de los esfuerzos efectivos, enfatizando en el efecto de la rigidez sobre la succión, respuesta mecánica y colapso por humedecimiento. Es posible adicionar una extensión para suelos estructurados.
Cordão-Neto et al. (2009) [27]	Elastoplástica	Extienden el modelo elastoplástico S-CLAY1S para capturar el comportamiento del suelo no saturado
Kyokawa (2010) [28]	Elastoplástica	Propone un modelo elastoplástico basado no MCC que reproduce la influencia de unas variables de estado como la relación de vacíos, grado de sat., temperatura y estructura

No obstante, los aportes para reproducir la respuesta no saturada en suelos arenosos finos han sido pocos. Gudehus [2] intenta a partir del concepto de capilaridad simular el posible efecto rigidizante que puede experimentar el suelo, implementando la ecuación de esfuerzos efectivos de Bishop [30], que fue combinada con una teoría hipoplástica ya existente.

Mediante el principio de esfuerzos efectivos de Terzaghi la presión capilar puede ser incluida de la siguiente manera

Gudehus explica que la presión capilar puede ser descrita como una parte del esfuerzo efectivo que depende de la relación de vacíos y la humedad solamente [2]. Con las variables de estado independiente: esfuerzos totales, relación de vacíos y humedad, la ecuación hipoplástica puede ser presentada en la ecuación siguiente con la velocidad de presión capilar incluida

Esta presión capilar será usada en el modelo numérico, como una variable de estado que puede ser modificada para calibrar los resultados obtenidos en las predicciones.

2.1.3 Modelo computacional

Las simulaciones buscaban reproducir el comportamiento del modelo reducido ensayado en la centrifuga geotécnica. Fue usado un programa basado en el método de elementos finitos, en el cual se insertó una subrutina que incluye el modelo constitutivo de referencia usado en los análisis. El análisis de resultados solo se referirá a la última secuencia de excavación que es la que se considera más crítica en el ensayo a escala real. En la Figura 6 se puede observar la malla deformada después de la primera excavación en el modelo.

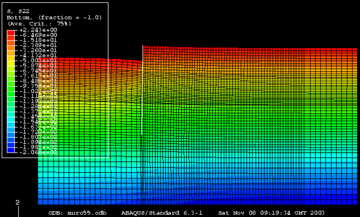
Figura 6. Malla deformada de elementos finitos

Tabla 3 muestra los parámetros hipoplásticos de la arena del Guamo y de la arena de Hochstetten, con el fin de presentar la probable dispersión de resultados al no utilizar exactamente el mismo material del ensayo a escala real, en el modelo reducido. Se observa que los parámetros son muy cercanos en cuanto a los valores obtenidos de los ensayos correspondientes, como lo describe [2].

Tabla 3. Parámetros hipoplásticos del material

Material	$\Phi _{c}$ (º)	$H_{s}$ (MPa)	$n$	$e_{d0}$	$e_{c0}$	$e_{i0}$	$a$	$b$
Arena del Guamo	34,15	153,21	0,33	0,58	0,9	1,035	0,48	1
Arena de Hochstetten	33	1500	0,28	0,55	0,95	1,05	0,25	1,5

4. Resultados y análisis

4.1 Modelación física en centrífuga vs. Prototipo

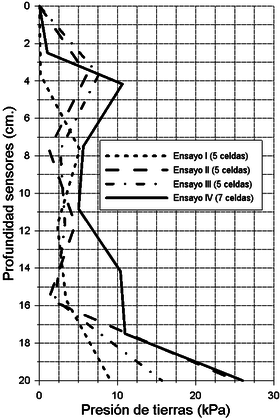
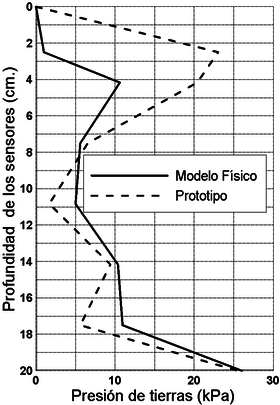
La Figura 7 muestra los resultados del modelo reducido ensayado en centrifuga. Los diferentes ensayos muestran las presiones de tierra obtenidas a diferentes profundidades en la última etapa de excavación. Solo el ensayo con siete celdas midió exactamente el empuje sobre la tablaestaca en los mismos lugares que el ensayo a escala real (prototipo), por lo cual esté será utilizado de ahora en adelante para las comparaciones y el análisis de resultados.

Es importante analizar desde un punto de vista cualitativo los resultados, ya que, aunque el modelo físico acompaña de manera adecuada la tendencia de la curva del prototipo, existe alguna dispersión en los resultados obtenidos. Vale la pena resaltar que el puntal instalado en la última etapa de excavación muestra un salto en las presiones de tierra debido a la reacción o condición pasiva local que puede generar la restricción del puntal a esa profundidad. Esto fue registrado también en el modelo físico por las celdas de carga.


(a)	(b)
Figura 7. (a) Presiones de tierra medidas en el modelo reducido sobre la tablestaca. (b) Comparación entre presiones de tierra obtenidas en el prototipo (ensayo a escala real) y el modelo físico

Como se mencionó anteriormente, la presión capilar que teóricamente simula el efecto de la succión sobre la presión de tierras en la tablestaca fue simulado como una variable de estado en la cual el valor fue variado de cero hasta 1000 kPa con el fin de observar la sensitividad de esta variable al modificar el valor. En la Figura 8 se puede analizar que la simulación numérica sobreestima los valores de presiones de tierra y solo presenta una baja dispersión a la altura del puntal. El cambio del parámetro de presión capilar, denominado en esta investigación “kapill hipoplástico”, realmente ocasionó muy bajas variaciones en las predicciones de presiones de tierra. Esto se podría explicar, debido a que una arena fina, aunque puede presentar valores de succión importantes, es poco probable que estos lleguen hasta 1000 kPa. Sin embargo, la predicción numérica presenta unos resultados aceptables, comparados con el benchmarking realizado en su momento sobre el ensayo a escala real que mostró unas dispersiones muy altas.

Figura 8. Comparación entre la modelación numérica y los resultados de presiones
de tierra en el prototipo y el modelo reducido

5. Conclusiones

Como se mencionó, existen muchos factores que inciden en las predicciones que se hacen sobre un ensayo a gran escala, tanto en la modelación numérica, como física. Por tal razón considerar estos aspectos puede ser de gran utilidad para explicar un comportamiento en la modelación o una alta dispersión de resultados. Referente a la modelación física vs. el prototipo, es claro que medir en los mismos puntos donde fue monitoreada la presión de tierras sobre la tablestaca en el prototipo disminuye considerablemente la incertidumbre de los resultados.

Los análisis de resultados en muchos casos deben hacerse desde una óptica cualitativa, debido a la falta de experiencia en la predicción de este tipo de estructuras, ya que como se describió al comienzo del documento, [5] menciona que el avance de las tecnologías blandas no ha ido de la mano con las predicciones numéricas. La falta de “competencia” entre modelos constitutivos y modelos reducidos puede presuponer obstáculos para la transferencia de conocimiento.

De los resultados de modelación numérica vs. modelación física, se puede analizar que las tendencias en ambos tipos de predicciones se ajustaron apropiadamente a los resultados reales. No obstante, se recomienda explorar otros modelos constitutivos modernos que reproduzcan la respuesta no saturada del suelo, usando parámetro del material dependientes directamente de la succión. En esta investigación se usó la succión como variable de estado impuesta al inicio de cada simulación-.

Referencias

[1] von Wolffersdorff, P.A. The result of the sheetpile wall field test in Hochstetten. Vol. 1, University of Karlsruhe, 1994.

[2] Gudehus, G. A comprehensive concept for non-saturated granular bodies. In: Unsaturated Soils, 1st Int. Conference, 2, 725-737, 1995.

[3] Gudehus G. Grundbautaschenbuch Teil 1. Chapter Stoffgesetze fur Boden aus physikalischer Sicht, 203–254, 2000.

[4] Niemunis, A. Extended hypoplastic models for soils. Dissertation submitted for habilitation, Bochum, 2002.

[5] Kolymbas, D. Constitutive modelling of granular materials. Dimitrios Kolymbas (Ed.), Springer-Verlag, Berlin Heidelberg, 2000.

[6] Gudehus G., Amorosi A., Gens A., Herle I., Kolymbas D., Mašín D., Muir Wood D., Nova R., Niemunis A., Pastor M., Tamagnini C., Viggiani G. The soilmodels.info project. International Journal for Numerical and Analytical Methods in Geomechanics 32(12):1571-1572, 2008.

[7] Negro Jr. A., Karlsrud K., Srithar S., Ervin M., Vorster E. Prediction, monitoring and evaluation of performance of geotechnical structures. Ref.: 17th Intl. Conf. Soil Mechanics and Geot. Eng., Alexandria, SOA3. 2930-3005, 2009.

[8] Kolymbas D. Advanced mathematical and computational geomechnics. University of Innsbruck, Vol. 13, 2007.

[9] Tatsuoka F., Siddiquee M., Yoshida T., Park C., Kamegai Y., Goto S., Kohata Y. Testing methods and results of element testing conditions of plane strain model bearing capacity test using air dried dense Silver Leighton Buzzard sand. Report prepared for class a prediction of the bearing capacity performance of model surface footing on sand under plane strain condition. Institute of Industrial Service, University of Tokyo, 1994.

[10] Garnier J., Gaudin C, Springman S., Culligan P., Goodings D., Konig D., Kutter B., Phillips R, Randolph M., Thorel L. Catalogue of scaling laws and similitude questions in geotechnical centrifuge modelling. IJPMG-International Journal of Physical Modelling in Geotechnics, 3:1-23, 2007.

[11] Stuit H.G. Sand in the geotechnical centrifuge. Ph.D. Thesis, University of Delft (Netherlands), 1995.

[12] Caicedo B. La centrífuga geotécnica de la Universidad de los Andes. En: VIII Congreso Colombiano de Geotecnia, Sociedad Colombiana de Geotecnia, Bogotá, 2002.

[13] Alonso E., Gens A., Josa A. A constitutive model for partially saturated soils. Geótechnique, 40:405–430, 1990.

[14] Masín D., Khalili N. A hypoplastic model for mechanical response of unsaturated soils. International Journal for Numerical and Analytical Methods in Geomechanics, 32:1903–1926, 2008.

[15] Radhakrishna H., Matyas E. Volume change characteristics of partially saturated soils. Geótechnique, 18:432-448, 1968.

[16] Fredlund D.G. Appropriate concepts and technology for unsaturated soils. Second Canadian Geotechnical Colloquium: Can. Geotech. J., 16:121-139, 1979.

[17] Balmaceda A.R. Suelos compactados. Un estudio teórico y experimental. Ph.D. Thesis. Polytechnical University of Catalonia, Spain, 1991.

[18] Gens A., Alonso E.E. A framework for the behaviour of unsaturated expansive clays. Revue Canadienne de Géotechnique, 29:1013-1032, 1992.

[19] Gens A., Nova R. Conceptual bases for a constitutive model for bonded soils and weak rocks. Geomechanical Engineering of Hards Soils-Soft Rocks, Athens, F. Schlosser, N. Kalteziotis & R. Frank, A.A. Balkema, Rotterdam, 1:485-494, 1993.

[20] Modaressi A., Abou-Bekr N. Unified approach to model partially saturated and saturated soil. Proceedings of the 1st International Conference on Unsaturated soils, 3,1495-1502, 1996.

[21] Loret B., Khalili N. An effective stress elastic-plastic model for unsaturated porous media. Mechanics of Materials, 34:97–116, 2002.

[22] Wheeler S., Sharma R., Buisson M. Coupling of hydraulic hysteresis and stress- strain behaviour in unsaturated soils. Géotechnique, 53:41–54, 2003.

[23] Gallipoli D., Gens A., Sharmat R., Vaunat J. An elasto-plastic model for unsaturated soil incorporating the effects of suction and degree of saturation on mechanical behaviour. Géotechnique, 53:123–135, 2003.

[24] Sheng D., Sloan S., Gens A. A constitutive model for unsaturated soils: thermomechanical and computational aspects. Computational Mechanics, 33(6), 453–465. 2004.

[25] Karstunen M., Krenn H., Wheeler S., Koskinen M., Zentar R. Effect of anisotropy and destructuration on the behavior of murro test embankment. International Journal of Geomechanics, 5(2):87-97, 2005.

[26] Sheng D.C., Fredlund D.G., Gens A. A new modelling approach for unsaturated soils using independent stress variables. Canadian Geotechnical Journal, 45:511–34, 2008.

[27] Cordão-Neto M.P., Sanchez M., Karstunen M., Farias M. Extension of the Barcelona basic model considering sub-loading concepts. 4th Asia-Pacific Conference on Unsaturated Soils, Australia, 2, 679-690, 2009

[28] Kyokawa H., Kikumoto M., Nakai T., Shahin H. Simple modeling of stress-strain relation for unnsaturated soil. Geotechnical Special Publication 202, 17-25, 2010.

[29] Ruge J.C. Análise do comportamento de cortina de estacas executada em solo poroso metaestável mediante o uso de um modelo constitutivo hipoplástico considerando a resposta não saturada. PhD. Thesis. Universidade de Brasília, 2014.

[30] Bishop A., Henkel D. The measurement of soil properties in the triaxial test. Edward Arnolds, London, 1962.

@@ Line 180: / Line 180: @@
 <div class="center" style="font-size: 75%;">'''Tabla 2'''. Modelos constitutivos para el comportamiento mecánico de solos no saturados (modificado de [30])
 </div>
-{| style="width: 100%;margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;"
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|'''Modelo constitutivo'''
-|  style="border: 1pt solid black;text-align: center;"|'''Teoría usada'''
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|'''Contribución'''
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Matyas & Radhakrishna (1968) [15]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Superficie que representa las variaciones de la relación de vacíos en función del estado de esfuerzos neto y la succión
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Fredlund (1979) [16]
-|  style="border: 1pt solid black;text-align: center;"|Elástica (Lei de Hooke)
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Propone un modelo elástico incremental que consiste em la Ley de Hooke generalizada para suelos no sat., donde es considerada la no linealidad de la relación esfuerzo-deformación
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Alonso et al. (1990) [13]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|BBM - extensión del modelo elastoplástico de CCM, para suelos no sat., que integra los cambios de volumen con la resistencia al corte
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Balmaceda (1991) [17]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Propone una alteración en el cálculo de parámetros hidráulicos de [13] usando una escala bi-log, para el cálculo de las compresibilidades del suelo para diversos parámetros de succión
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Gens & Alonso (1992) [18]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Extensión del BBM, la modificación está basada en dos niveles en la estructura del suelo: micro y macro. Barcelona Expansive Model (BExM).
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Gens & Nova (1993) [19]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Concepto de la superficie de plastificación intrínseca
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Gudehus (1995) [2]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Hipoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|El esqueleto granular es modelado usando 4 constantes del material, La combinación de hipoplasticidad y capilaridad explica la respuesta de elementos de suelo húmedo en el edómetro bajo compresión triaxial y corte simple
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Modaressi & Abou-Bekr
-(1996) [20]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|El concepto de esfuerzo efectivo es extendido para el caso de materiales parcialmente sat. por la introducción de una presión capilar. Usa un modelo elastoplástico validado en el caso saturado o seco y generalizado para el caso de suelo parcialmente sat.
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Loret & Khalili (2002) [21]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Principal énfasis en el comportamiento do esqueleto sólido, un modelo elastoplástico simple es descrito requiriendo pocos parámetros para definir el efecto de la desaturación
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Wheeler et al. (2003) [22]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Incorporación de los efectos de la variación del grado de sat, en el comportamiento esfuerzo-deformación. Representa el cambio de posición de la WRC durante la carga, o sea, el comportamiento hidráulico es acoplado a la relación esfuerzo-deformación
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Gallipolli et al. (2003) [23]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Considera explícitamente los mecanismos de la succión que afectan el comportamiento mecánico, así como la dependencia sobre el grado de sat.
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Sheng et al. (2004) [24]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Considera la histéresis hidráulica y las deformaciones irreversibles debidas a los ciclos de humedecimiento y secado capaz de reproducir el comportamiento de solos muy expansivos.
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Karstunen et al. (2005) [25]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Reproduce el efecto anisotrópico, cementación entre partículas y la desestructuración para suelos saturados
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Sheng et al. (2008) [26]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Proponen un nuevo modelo elastoplástico para suelos no sat. usando dos variables de estado de esfuerzos independientes
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Masín & Khalili (2008) [14]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Hipoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Uno de los primeros intentos basados en hipoplasticidad usando el principio de los esfuerzos efectivos, enfatizando en el efecto de la rigidez sobre la succión, respuesta mecánica y colapso por humedecimiento. Es posible adicionar una extensión para suelos estructurados.
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Cordão-Neto et al. (2009) [27]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Extienden el modelo elastoplástico S-CLAY1S para capturar el comportamiento del suelo no saturado
-|-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Kyokawa (2010) [28]
-|  style="border: 1pt solid black;text-align: center;vertical-align:center;"|Elastoplástica
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Propone un modelo elastoplástico basado no MCC que reproduce la influencia de unas variables de estado como la relación de vacíos, grado de sat., temperatura y estructura
-|}
 <div id='tab-1'></div>
 {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
-|-style="text-align:center"
+|-style="text-align:left;"
-! Modelo constitutivo !! Teoría usada !! Contribución
+! style="text-align:left" | Modelo constitutivo !! style="text-align:center" | Teoría usada !! style="text-align:left" | Contribución
 |-
 |  style="text-align: left;padding-left:5px;"|Matyas & Radhakrishna (1968) [15]
@@ Line 366: / Line 288: @@
 ===2.1.3 Modelo computacional===
-Las simulaciones buscaban reproducir el comportamiento del modelo reducido ensayado en la centrifuga geotécnica. Fue usado un programa basado en el método de elementos finitos, en el cual se insertó una subrutina que incluye el modelo constitutivo de referencia usado en los análisis. El análisis de resultados solo se referirá a la última secuencia de excavación que es la que se considera más crítica en el ensayo a escala real. En la Figura 6 se puede observar la malla deformada después de la primera excavación en el modelo.
+Las simulaciones buscaban reproducir el comportamiento del modelo reducido ensayado en la centrifuga geotécnica. Fue usado un programa basado en el método de elementos finitos, en el cual se insertó una subrutina que incluye el modelo constitutivo de referencia usado en los análisis. El análisis de resultados solo se referirá a la última secuencia de excavación que es la que se considera más crítica en el ensayo a escala real. En la [[#img-6|Figura 6]] se puede observar la malla deformada después de la primera excavación en el modelo.
+<div id='img-6'></div>
 {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
 |-
@@ Line 376: / Line 299: @@
-La Tabla 3 muestra los parámetros hipoplásticos de la arena del Guamo y de la arena de Hochstetten, con el fin de presentar la probable dispersión de resultados al no utilizar exactamente el mismo material del ensayo a escala real, en el modelo reducido. Se observa que los parámetros son muy cercanos en cuanto a los valores obtenidos de los ensayos correspondientes, como lo describe [2].
+[[#tab-3|Tabla 3]] muestra los parámetros hipoplásticos de la arena del Guamo y de la arena de Hochstetten, con el fin de presentar la probable dispersión de resultados al no utilizar exactamente el mismo material del ensayo a escala real, en el modelo reducido. Se observa que los parámetros son muy cercanos en cuanto a los valores obtenidos de los ensayos correspondientes, como lo describe [2].
 <div class="center" style="font-size: 75%;">'''Tabla 3'''. Parámetros hipoplásticos del material
 </div>
-{| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:60%;"
+<div id='tab-1'></div>
-|-
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;"
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Material
+|-style="text-align:center"
-|  style="border: 1pt solid black;text-align: center;"|'''&#x03a6;<sub>c</sub> (º)'''
+!style="text-align: left;" | Material !! <math>\Phi_c </math> (º) !! <math>H_s</math> (MPa) !! <math>n</math> !! <math>e_{d0}</math> !! <math>e_{c0}</math>!! <math>e_{i0}</math> !! <math>a</math> !! <math>b</math>
-|  style="border: 1pt solid black;text-align: center;"|H<sub>s</sub> (MPa)
-|  style="border: 1pt solid black;text-align: center;"|n
-|  style="border: 1pt solid black;text-align: center;"|e<sub>d0</sub>
-|  style="border: 1pt solid black;text-align: center;"|e<sub>c0</sub>
-|  style="border: 1pt solid black;text-align: center;"|e<sub>i0</sub>
-|  style="border: 1pt solid black;text-align: center;"|a
-|  style="border: 1pt solid black;text-align: center;"|b
 |-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Arena del Guamo
+|  style="text-align: left;padding-left:5px;"|Arena del Guamo
-|  style="border: 1pt solid black;text-align: center;"|34,15
+|  style="text-align: center;"|34,15
-|  style="border: 1pt solid black;text-align: center;"|153,21
+|  style="text-align: center;"|153,21
-|  style="border: 1pt solid black;text-align: center;"|0,33
+|  style="text-align: center;"|0,33
-|  style="border: 1pt solid black;text-align: center;"|0,58
+|  style="text-align: center;"|0,58
-|  style="border: 1pt solid black;text-align: center;"|0,9
+|  style="text-align: center;"|0,9
-|  style="border: 1pt solid black;text-align: center;"|1,035
+|  style="text-align: center;"|1,035
-|  style="border: 1pt solid black;text-align: center;"|0,48
+|  style="text-align: center;"|0,48
-|  style="border: 1pt solid black;text-align: center;"|1
+|  style="text-align: center;"|1
 |-
-|  style="border: 1pt solid black;text-align: left;padding-left:5px;"|Arena de Hochstetten
+|  style="text-align: left;padding-left:5px;"|Arena de Hochstetten
-|  style="border: 1pt solid black;text-align: center;"|33
+|  style="text-align: center;"|33
-|  style="border: 1pt solid black;text-align: center;"|1500
+|  style="text-align: center;"|1500
-|  style="border: 1pt solid black;text-align: center;"|0,28
+|  style="text-align: center;"|0,28
-|  style="border: 1pt solid black;text-align: center;"|0,55
+|  style="text-align: center;"|0,55
-|  style="border: 1pt solid black;text-align: center;"|0,95
+|  style="text-align: center;"|0,95
-|  style="border: 1pt solid black;text-align: center;"|1,05
+|  style="text-align: center;"|1,05
-|  style="border: 1pt solid black;text-align: center;"|0,25
+|  style="text-align: center;"|0,25
-|  style="border: 1pt solid black;text-align: center;"|1,5
+|  style="text-align: center;"|1,5
 |}
@@ Line 418: / Line 334: @@
 ===4.1 Modelación física en centrífuga vs. Prototipo===
-La Figura 7 muestra los resultados del modelo reducido ensayado en centrifuga. Los diferentes ensayos muestran las presiones de tierra obtenidas a diferentes profundidades en la última etapa de excavación. Solo el ensayo con siete celdas midió exactamente el empuje sobre la tablaestaca en los mismos lugares que el ensayo a escala real (prototipo), por lo cual esté será utilizado de ahora en adelante para las comparaciones y el análisis de resultados.
+La [[#img-7|Figura 7]] muestra los resultados del modelo reducido ensayado en centrifuga. Los diferentes ensayos muestran las presiones de tierra obtenidas a diferentes profundidades en la última etapa de excavación. Solo el ensayo con siete celdas midió exactamente el empuje sobre la tablaestaca en los mismos lugares que el ensayo a escala real (prototipo), por lo cual esté será utilizado de ahora en adelante para las comparaciones y el análisis de resultados.
 Es importante analizar desde un punto de vista cualitativo los resultados, ya que, aunque el modelo físico acompaña de manera adecuada la tendencia de la curva del prototipo, existe alguna dispersión en los resultados obtenidos.  Vale la pena resaltar que el puntal instalado en la última etapa de excavación muestra un salto en las presiones de tierra debido a la reacción o condición pasiva local que puede generar la restricción del puntal a esa profundidad. Esto fue registrado también en el modelo físico por las celdas de carga.
+<div id='img-7'></div>
 {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
 |-
@@ Line 430: / Line 347: @@
 |style="text-aling:center;font-size:75%;"|(b)
 |- style="text-align: center; font-size: 75%;"
-| colspan="2" style="padding:10px;"| '''Figura 7'''. (a) Presiones de tierra medidas en el modelo reducido sobre la tablestaca. (b) Comparación entre presiones de tierra obtenidas en el prototipo (ensayo a escala real) y el modelo físico
+| colspan="2" style="padding:10px;"| '''Figura 7'''. (a) Presiones de tierra medidas en el modelo reducido sobre la tablestaca. (b) Comparación entre presiones de tierra<br/> obtenidas en el prototipo (ensayo a escala real) y el modelo físico
 |}
-Como se mencionó anteriormente, la presión capilar que teóricamente simula el efecto de la succión sobre la presión de tierras en la tablestaca fue simulado como una variable de estado en la cual el valor fue variado de cero hasta 1000 kPa con el fin de observar la sensitividad de esta variable al modificar el valor. En la Figura 8 se puede analizar que la simulación numérica sobreestima los valores de presiones de tierra y solo presenta una baja dispersión a la altura del puntal. El cambio del parámetro de presión capilar, denominado en esta investigación “kapill hipoplástico”, realmente ocasionó muy bajas variaciones en las predicciones de presiones de tierra. Esto se podría explicar, debido a que una arena fina, aunque puede presentar valores de succión importantes, es poco probable que estos lleguen hasta 1000 kPa. Sin embargo, la predicción numérica presenta unos resultados aceptables, comparados con el benchmarking realizado en su momento sobre el ensayo a escala real que mostró unas dispersiones muy altas.
+Como se mencionó anteriormente, la presión capilar que teóricamente simula el efecto de la succión sobre la presión de tierras en la tablestaca fue simulado como una variable de estado en la cual el valor fue variado de cero hasta 1000 kPa con el fin de observar la sensitividad de esta variable al modificar el valor. En la [[#img-8|Figura 8]] se puede analizar que la simulación numérica sobreestima los valores de presiones de tierra y solo presenta una baja dispersión a la altura del puntal. El cambio del parámetro de presión capilar, denominado en esta investigación “kapill hipoplástico”, realmente ocasionó muy bajas variaciones en las predicciones de presiones de tierra. Esto se podría explicar, debido a que una arena fina, aunque puede presentar valores de succión importantes, es poco probable que estos lleguen hasta 1000 kPa. Sin embargo, la predicción numérica presenta unos resultados aceptables, comparados con el benchmarking realizado en su momento sobre el ensayo a escala real que mostró unas dispersiones muy altas.
+<div id='img-8'></div>
 {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;"
 |-
 |style="padding:10px;"| [[File:Ruge_et_al_2019a_3627_Figura 8.png|300px]]
 |- style="text-align: center; font-size: 75%;"
-| colspan="1" style="padding:10px;"| '''Figura 8'''. Comparación entre la modelación numérica y los resultados de presiones de tierra en el prototipo y el modelo reducido
+| colspan="1" style="padding:10px;"| '''Figura 8'''. Comparación entre la modelación numérica y los resultados de presiones<br/> de tierra en el prototipo y el modelo reducido
 |}