Evaluation of alternatives for parameterization of momentum and water vapor roughness lengths in lakes

Latest revision as of 14:55, 1 March 2021

Resumo

Uma avaliação do desempenho de diversas alternativas de parametrização dos comprimentos de rugosidade para quantidade de movimento e vapor d'água foi realizada com dados medidos sobre a água no reservatório de Itaipu, Brasil. Foram testadas 4 parametrizações para a estimativa da rugosidade da quantidade de movimento, e 4 para a estimativa da rugosidade do vapor d'água. As parametrizações para quantidade de movimento consistem na equação de Charnock e generalizações, enquanto que as parametrizações para vapor d'água baseiam-se em equações propostas por Brutsaert. As 4 parametrizações para quantidade de movimento produziram resultados muito parecidos em termos de qualidade do ajuste e estatísticas de erros, e se revelaram apenas fracamente dependentes da velocidade de atrito. Já as parametrizações para vapor d'água produziram resultados mais dispersos, sendo que as melhores parametrizações encontradas dependem muito fracamente do número de Reynolds de rugosidade, ou são independentes do mesmo. Tanto no caso de quantidade de movimento quanto de vapor d'água, os valores dos parâmetros ótimos de cada parametrização encontrados para Itaipu são significativamente maiores (uma ordem de grandeza para o parâmetro de Charnock e para a rugosidade de quantidade de movimento; e cerca de sete vezes maior para o inverso do número de Dalton) do que os reportados na literatura.

Palavras chave: Teoria de similaridade de Monin-Obukhov, comprimentos de rugosidade, fluxos superficiais

Abstract

An assessment of the performance of various parameterization alternatives for roughness lengths of momentum and water vapour was performed. The micrometereological data used in this work was measured in the Itaipu reservoir, Brazil. Four models was tested for momentum roughness length, and four for water vapour. The parameterization for horizontal momentum flux are based on the Charnock equation and generalizations while the water vapour model are based on equations proposed by Brutsaert. The four models for momentum flux produced very similar results, in terms of goodness of fit and errors, and turned out only weakly dependent on friction velocity. Already the parameterizations for water vapor produced more dispersed results, and the best parameterizations found very poorly depend on the Reynolds roughness number, or are independent of it. Both in the case of momentum and water vapour, the optimal parameter values of each parameterization found for Itaipu are significantly larger than those reported in the literature (one order of magnitude for the Charnock parameter and for the momentum roughness; and about seven times greater for the inverse of Dalton's number).

Keywords: Monin-Obukhov similarity theory, roughness lengths, superficial fluxes

1. Introdução

A estimativa correta dos fluxos superficiais de quantidade de movimento, calor sensível e massa de vapor d’água é um fator crucial em muitas aplicações de engenharia, incluindo a modelagem de interações superfície-atmosfera em modelos atmosféricos e modelagem e gerenciamento de recursos hídricos [1-5]. A partir de medições feitas na parte superior da camada limite atmosférica, denominada subcamada inercial (onde se aplica a Teoria da Similaridade de Monin-Obukhov (Raupach et. al. [6]), os fluxos de escalares podem ser obtidos a partir da teoria de Brutsaert para a estimativa do comprimento de rugosidade para os escalares [7-9], que estende a Teoria da Renovação Superficial (TRS) de Danckwerts [10] para produzir um conjunto fechado de equações para os comprimentos de rugosidade de um escalar (no nosso caso, a rugosidade $z_{0E}$ para o vapor d’água) e o tempo médio de contato dos vórtices de menores escalas com a superfície. Para ser aplicada, a teoria requer o conhecimento do comprimento de rugosidade para quantidade de movimento $z_{0}$ característico da superfície.

Para superfícies sólidas e com vegetação, $z_{0}$ geralmente pode ser considerado constante, pelo menos sobre uma certa faixa de direções do vento. Sobre a água, $z_{0}$ (m) é mais comumente estimado usando a equação de Charnock [11],

(1)

onde $u_{*}$ (m s $^{-1}$ ) é a velocidade de atrito e $g$ (m s $^{-2}$ ) é a aceleração da gravidade e o número adimensional $\alpha$ é o parâmetro de Charnock. Para oceanos abertos, $\alpha$ é da ordem de $10^{-2}$ como sugerido originalmente (Charnock [11], $\alpha =0,01$ ); (Charnock [12], $\alpha =0,0123$ ) e corroborado por estudos posteriores (Smith [13], $\alpha =0,01$ ); (Smith [14], $\alpha =0,011$ ).

Para o caso de corpos de água rasos, existem evidências de que a parametrização de Charnock não explica totalmente a relação entre a velocidade média do vento e a velocidade de atrito [15]. Por exemplo, nessas condições valores um pouco maiores do coeficiente de Charnock foram encontrados por Garratt [16] ( $\alpha =0{,}0144$ ) e Wu [17] ( $\alpha =0{,}018$ ) e uma ordem de magnitude maiores por Shabani et al. [18] ( $\alpha =0{,}110$ ).

Devido aos diferentes valores encontrados para o parâmetro de Charnock em corpos de água rasos e profundos, e devido à pequena bibliografia sobre o tema, é importante a realização de outros estudos sobre a parametrização de $z_{0}$ em lagos. Uma parte do presente trabalho consiste em parametrizar adequadamente $z_{0}$ , utilizando dados provenientes de uma extensa campanha micrometeorológica no reservatório de Itaipu, Brasil.

Para lagos, a parametrização para o comprimento de rugosidade de escalares da teoria original foi testada por diversos autores (por exemplo, Verburg et. al. [19] e Dias et. al. [20]), com valores de parâmetros sempre muito próximos daqueles propostos originalmente por Charnock [11] e Brutsaert [8,9]. Neste trabalho, nós avaliamos experimentalmente as alternativas existentes, com particular atenção aos erros que elas produzem, e aos valores ótimos de seus parâmetros.

Este trabalho está organizado da seguinte maneira: na Seção 2, a metodologia é apresentada e são revisitadas parametrizações alternativas tanto para $z_{0}$ quanto para $z_{0E}$ ; na Seção 3, o sítio experimental do reservatório de Itaipu, cujos dados são utilizados neste trabalho, é brevemente descrito; na Seção 4, as diversas parametrizações são comparadas, e os resultados obtidos são discutidos. As conclusões são apresentadas na Seção 5.

2. Metodologia

2.1 Fluxos turbulentos e Teoria de Similaridade de Monin-Obukhov

Neste trabalho, nós lidamos com os fluxos turbulentos de quantidade de movimento, calor sensível e calor latente, dados por

(2)

(3)

(4)

Nas equações acima, $u$ (m s $^{-1}$ ) é a velocidade longitudinal do vento; $w$ (m s $^{-1}$ ) é a velocidade vertical; $\rho$ (kg m $^{-3}$ ) é a densidade do ar; $c_{p}$ (J Kg $^{-1}$ K $^{-1}$ ) é o calor específico a pressão constante do ar; $\theta$ (K) é a temperatura do ar; $q$ (Kg $_{H2O}$ Kg $^{-1}$ ) é a umidade específica, e $L$ (J Kg $^{-1}$ ) é o calor latente de evaporação. As equações (2)–(4) definem as escalas turbulentas $u_{*}$ (m s $^{-1}$ ), $\theta _{*}$ (K) e $q_{*}$ (Kg $_{H2O}$ Kg $^{-1}$ ) (velocidade de atrito e escalas turbulentas de temperatura e umidade, respectivamente), a partir das quais obtém-se a variável de similaridade de Obukhov,

(5)

onde $z_{r}$ (m) é uma altura arbitrária acima da superfície, $\kappa =0{,}4$ é a constante de vón Kármán. A temperatura virtual média ( $K$ ) é

(6)

e a escala turbulenta de temperatura virtual (K) é

(7)

Nas equações acima, uma barra indica uma média e uma linha a flutuação turbulenta em torno da média.

Os fluxos turbulentos $\tau$ e $LE$ podem ser estimados a partir da medição de grandezas médias via Teoria de Similaridade de Monin-Obukhov (TSMO), com

(8)

(9)

e substituição em (2) e (4), onde $z$ a (m) é a altura de medição da velocidade média ${\overline {u_{a}}}$ (m s $^{-1}$ ), e $z_{b}$ (m) é a altura de medição da umidade específica média ${\overline {q_{b}}}$ (Kg $_{H2O}$ Kg $^{-1}$ ). Em (8) e (9), $\Psi _{\tau }$ e $\Psi _{E}$ são as funções de similaridade para os fluxos de quantidade de movimento e vapor d’água de Businger-Dyer (Brutsaert [9], seção 4.2). O foco central deste trabalho é a comparação de parametrizações para os comprimentos de rugosidade para a quantidade de movimento $z_{0}$ e para o vapor d'água, $z_{0E}$ (m). Dias et. al. [20] encontraram discrepâncias na parametrização do fluxo de calor sensível que eles atribuíram à advecção de calor sobre o lago. Por esse motivo, neste trabalho nós avaliamos apenas a estimativa do fluxo de calor latente, associado ao fluxo de massa de vapor d'água, via equação (9).

2.2 A parametrização de $z_{0}$ 2.2 A parametrização de z 0 {\displaystyle z {0}}

Em interfaces água-ar $z_{0}$ é usualmente parametrizado através de $u_{*}$ , $g$ e da viscosidade cinemática do ar $\nu _{\tau }$ (m $^{2}$ s $^{-1}$ ). Alguns trabalhos também incluem outras grandezas, relacionadas com o estado das ondas na superfície [21]-[29]. Porém em lagos e outros corpos d’água rasos as ondas não conseguem se desenvolver completamente; além disso, em várias aplicações (mesmo no oceano), as características das ondas na superficie nem sempre estão disponíveis. Por isso neste trabalho nós testamos parametrizações para $z_{0}$ somente com $u_{*}$ , $g$ e $\nu _{\tau }$ . As parametrizações avaliadas são generalizações de parametrizações existentes, com a forma

(10)

Em (10), $\alpha$ e $\beta$ são constantes adimensionais, e $a$ , $b$ e $c$ precisam atender ao sistema subdeterminado

(11)

(12)

para produzir um resultado com dimensões de comprimento. O caso $\alpha =0$ e $c=0$ produz o comprimento de rugosidade para escoamentos turbulentos lisos [14], que é exatamente o segundo argumento de $\max(\cdot ,\cdot )$ na Eq. (10). Note que essa restrição (a escolha do maior valor entre as duas expressões) evita que valores demasiadamente pequenos (ou mesmo negativos) resultem de combinações arbitrárias dos parâmetros $\alpha$ , $\beta$ , $a$ , $b$ e $c$ , principalmente em buscas automáticas do algoritmo de otimização. Para um conjunto de dados medidos, a equação (10) pode ser otimizada em função de $b$ , $\alpha$ , e $\beta$ . Para cada $b$ , $a$ e $c$ ficam determinados via (11)–(12):

(13)

Na seção 4, diversas combinações de $b$ , $\alpha$ e $\beta$ são obtidos por otimização, com o método de Levenberg-Marquardt, para o reservatório de Itaipu.

2.3 A parametrização de $z_{0E}$ 2.3 A parametrização de z 0 E {\displaystyle z {0E}}

Para estimar o fluxo de massa de vapor d'água através da expressão (4) é necessário determinar o comprimento de rugosidade $z0E$ na expressão (9). Um resultado clássico apresentado em Brutsaert [9] é

(14)

onde ${\text{Da}}_{0}$ é o número de Dalton interfacial, e ${\text{Cd}}_{0}$ é o coeficiente de arrasto interfacial. Brutsaert [8] utilizou ${\text{Cd}}_{0}^{-1/2}=5$ . A equação (14) é válida apenas para o regime turbulento rugoso, que é predominante em condições de campo. Para o regime liso, Brutsaert [9] propõe

(15)

Neste trabalho, quando o regime é turbulento liso, a Eq. (15) é sempre adotada, independentemente da parametrização que está sendo utilizada para o regime turbulento rugoso (que constitui a maioria dos casos). Com a Teoria de Renovação Superficial é possível quantificar Da 0 na Eq. (14); Brutsaert [8] obteve

(16)

Em (16), $C_{R}$ é um número adimensional, ${\text{Re}}_{0}$ é o número de Reynolds de rugosidade, definido como

(17)

e ${\text{Sc}}$ é o número de Schmidt,

(18)

onde $\nu _{E}$ (m $^{2}$ s $^{-1}$ ) é a difusividade molecular de vapor de água no ar. Note que o expoente $-1/2$ do número de Schmidt em (16) vem da solução transiente da equação da difusão para uma parcela de fluido na Teoria de Renovação Superficial [7][10]; o valor de $-1/2$ é confirmado por uma série de resultados experimentais (c.f. Figura 2 de Lorke e Peetres [30]). Por este motivo, neste trabalho nós mantivemos o expoente de ${\text{Sc}}$ fixo em $-1/2$ para todas as alternativas de parametrização de ${\text{Da}}_{0}$ .

Uma expressão alternativa para ${\text{Da}}_{0}$ foi apresentada, por exemplo, por Soloviev et. al. [31] (para regimes de ventos moderados), Csanady [32] e Lorke et. al. [30], que encontraram

(19)

onde $C_{R}$ é uma constante da ordem de $10^{-1}$ .

Neste trabalho nós propomos e avaliamos uma generalização das duas expressões para $Da0$ apresentadas anteriormente, da forma

(20)

com $d$ sendo um número a ser determinado experimentalmente. Em particular quando fazemos $d=1/4$ obtemos a expressão (16) de Brutsaert, enquanto que $d=0$ dá origem a (19).

3. Sítio experimental

Os dados utilizados foram medidos em uma estação micrometeorológica instalada em uma pequena ilha do reservatório da usina hidrelétrica de Itaipu, Estado do Paraná, Brasil. As coordenadas da ilha são −25°03'25,72"S e −54°24'33,67"O, e sua altitude é de 220m em relação ao nível do mar. Devido à proximidade do município de Missal - PR, a estação foi denominada Estação Missal.

Na estação micrometeorológica foram instalados sensores de resposta rápida operando a 20Hz, e sensores de resposta lenta medindo a 0,1Hz e calculando médias em intervalos de tempo de 10 minutos. Entre os sensores de resposta rápida instalados na estação, utilizou-se neste trabalho os dados medidos por um Anemômetro Sônico (Campbell Scientific Instruments (CSI) CSAT3), por um analisador de gás infravermelho de CO₂ e H₂O (Licor LI7500) e por um Termopar (CSI FW03) instalado no centro do caminho ótico do analisador de gás infravermelho. Com isso tanto $\theta '$ (medida pelo termopar) quanto $q'$ (obtida a partir da densidade de vapor d'água medida pelo analisador infravermelho) ficam referenciadas ao mesmo ponto, no centro do caminho ótico do analisador. Note que a separação espacial entre o analisador infravermelho e o anemômetro sônico é pequena, tendo pouco impacto sobre o cálculo dos fluxos de escalares.

Tanto o analisador de gás infravermelho quanto o anemômetro sônico estavam na altura de 3,76m em relação à base da estação.

As variáveis medidas na estação pelos sensores de resposta lenta foram temperatura e umidade relativa do ar (CS500, Campbell Scientific Instruments; 2,85m), pressâo atmosférica (CS100, Campbell Scientific Instruments; 1,73m) e radiaçâo solar líquida (Kipp & Zönen; 2,67m).

Para medir a temperatura da água foram instalados dois sensores modelo L108 da Campbell Scientific Instruments em uma bóia nautica situada aproximadamente a 3km a noroeste da estação micrometeorológica. Um dos sensores mediu a temperatura da superfície da água e o outro a temperatura a uma profundidade de 25cm.

As medições apresentadas neste trabalho vão do dia 09 de outubro de 2013 ao dia 01 de novembro de 2013. Durante este período a ilha estava na maior parte do tempo submersa, com a altura da base da estação variando entre 0,95cm de profundidade a 30cm acima do nível da água.

Os fluxos verticais de calor sensível e latente foram obtidos pelo método de covariâncias turbulentas, com as equações (3)-(4). Os fluxos de vapor de água (E) foram corrigidos com a metodologia WPL [33]. Uma rotação de coordenadas [34] foi aplicada em cada bloco de 30 minutos de dados instantâneos (medidos a 20 Hz) para alinhar a direção x do eixo cartesiano com a direção média do vento. As flutuações turbulentas foram obtidas após a remoção da tendência linear de cada amostra [35].

4. Resultados e discussão

4.1 Fluxo de quantidade de movimento

Para a estimativa de $z_{0}$ na Eq. (10), classicamente os modelos apresentados na literatura consideram $b=-1$ . Entre outros trabalhos podemos citar como exemplo dessa abordagem Smith [14] e Fairall et al. [36]. Em oceanos, os valores usuais da Equação (10) com $b=-1$ considerados em interfaces água-ar são $\alpha \approx 0{,}011$ e $\beta \approx 0{,}135$ .

Neste trabalho, nós consideramos 5 alternativas para a parametrização dada pela Eq. (10), com as seguintes siglas:

CHA (Parametrização de Charnock). Fixamos $\beta =0$ , e otimizamos $\alpha$ .

CLA (Parametrização "clássica"). Fixamos $b=-1$ , e otimizamos $\alpha$ e $\beta$ . Neste caso, estamos apenas verificando o quanto os parâmetros $\alpha$ e $\beta$ ótimos no sítio experimental diferem dos valores para mar aberto.

CLM (Parametrização "clássica modificada"). Otimizamos ao mesmo tempo $b$ , $\alpha$ e $\beta$ . Isso corresponde a modificar as parametrizações clássicas e dar bastante liberdade ao parâmetro b. Note que para cada $b$ os valores de $a$ e $c$ ficam restritos pela equação (13).

NCL (Parametrização "não clássica"). Fixamos $\alpha =0$ , e otimizamos $b$ e $\beta$ . Essencialmente, já que $\nu$ é praticamente constante para o ar, e que $g$ é constante, estamos agora investigando qual é o expoente "ótimo" para $u_{*}$ .

CTE (Parametrização com $z_{0}$ constante). Como veremos na sequência, ocorre que a dependência de $z_{0}$ com $u_{*}$ é relativamente fraca. Assim, nós testamos a qualidade de uma parametrização extremamente simples, em que $z_{0}$ é independente de $u_{*}$ .

O valor estimado da velocidade de atrito, ${\widehat {u_{*}}}$ , foi obtido por meio das equações (8) e (10). Neste processo, os valores de $\zeta _{a}$ e, consequentemente, $u_{*}$ e $\theta _{v*}$ , foram considerados conhecidos do lado direito das expressões. Isso significa que, no processo de otimização dos parâmetros $\alpha$ , $\beta$ , $a$ , $b$ e $c$ , o valor de $u_{*}$ utilizado foi o medido; além disso, uma vez obtidos os parâmetros ótimos de cada parametrização descrita acima, os valores de $u_{*}$ e da escala de temperatura virtual $\theta _{v*}$ , necessários para o cálculo de $\zeta _{a}$ a que aparece na equação (8), novamente foram os medidos. Esse procedimento elimina a incerteza adicional gerada por estimativas iterativas de $u_{*}$ e $\theta _{v*}$ que utilizam exclusivamente o método fluxo-gradiente.

Para cada alternativa de parametrização, obtêve-se os parâmetros ótimos correspondentes por meio de otimização não-linear, utilizando a rotina leastsq do pacote scipy.optimize.minpack de scipy (https://www.scipy.org). Em seguida, para cada parametrização, obtêve-se um conjunto ótimo de ${\widehat {u_{*}}}$ parametrizados com a Eq. (8). Esses valores foram então testados estatisticamente contra os valores medidos de $u_{*}$ . Note que esse procedimento utiliza o mesmo conjunto de dados para a obtenção dos parâmetros ótimos e para o teste de desempenho da parametrização: cada parametrização é avaliada para o conjunto “ótimo” de parâmetros. Novamente, este procedimento apenas avalia o melhor desempenho possível com a parametrização proposta.

Para cada parametrização, as estatísticas de desempenho calculadas são as seguintes: REMQ (raiz quadrada do erro médio quadrático), EMA (erro médio absoluto), VIÉS (viés), os valores de $a_{0}$ , $r$ , $s_{y}$ e $s_{a}$ (respectivamente: coeficiente angular, raiz quadrada do coeficiente de determinação, erro padrão das estimativas ${\widehat {u_{*}}}$ e erro padrão da estimativa de $a$ ) para a regressão linear pela origem

(21)

Finalmente, calculou-se os estimadores de Siegel [37] e Stein [38] para $a_{1}$ e $a_{2}$ na equação

(22)

Os estimadores de Siegel são baseados na mediana das inclinações de cada ponto do conjunto de dados, e são menos influenciados por valores extremos (outliers). Para uma parametrização perfeita, esperamos $a_{1}=1$ e $a_{2}=0$ .

As Figuras 1a-1d mostram os resultados obtidos para as 4 primeiras parametrizações, e a Tabela 1 os valores correspondentes dos parâmetros ótimos. A Tabela 2 dá as estatísticas de erros correspondentes.

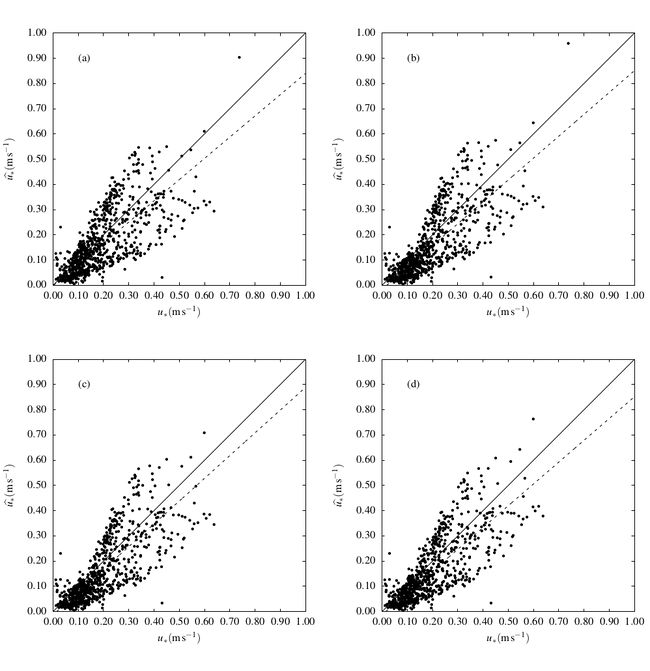
Figura 1. Valores previstos (no eixo vertical) contra observados (no eixo horizontal) de

para 4 parametrizações testadas de

: (a) CHA. (b) CLA. (c) CLM. (d) NCL. A linha contínua é a reta

(indicando concordância perfeita), e a linha tracejada é a linha ajustada pelo método de Siegel (Equação (22); parâmetros

e

na Tabela 2)

Tabela 1. Parâmetros ótimos obtidos para cada parametrização de

Parametrização	$z_{0}$ (m)	$\alpha$	$\beta$	$a$	$b$	$c$
CHA	-	$0{,}3863$	-	-	-	-
CLA	-	$0{,}5308$	$-12{,}92$	$1$	$-1$	$0$
CLM	-	$14{,}386$	$-15{,}050$	$0{,}015$	$1{,}956$	$-0{,}985$
NCL	-	-	$0{,}012$	$0{,}631$	$3{,}892$	$-1{,}631$
CTE	$0{,}0020$	-	-	-	-	-

Tabela 2. Estatísticas de erros de

para cada parametrização de

Parametrização	REMQ	EMA	VIÉS	$a_{0}$	$r$	$s_{a}$	$s_{y}$	$a_{1}$	$a_{2}$
	$\mathrm {m\,s^{-1}}$	$\mathrm {m\,s^{-1}}$	$\mathrm {m\,s^{-1}}$				$\mathrm {m\,s^{-1}}$		$\mathrm {m\,s^{-1}}$
CHA	$0{,}095$	$0{,}071$	$-0{,}022$	$0{,}844$	$0{,}705$	$0{,}019$	$0{,}088$	$0{,}838$	$-0{,}003$
CLA	$0{,}094$	$0{,}072$	$-0{,}033$	$0{,}829$	$0{,}757$	$0{,}021$	$0{,}086$	$0{,}828$	$-0{,}009$
CLM	$0{,}092$	$0{,}071$	$-0{,}034$	$0{,}834$	$0{,}777$	$0{,}021$	$0{,}084$	$0{,}813$	$-0{,}008$
NCL	$0{,}091$	$0{,}068$	$-0{,}031$	$0{,}843$	$0{,}777$	$0{,}021$	$0{,}084$	$0{,}840$	$-0{,}008$
CTE	$0{,}105$	$0{,}079$	$-0{,}022$	$0{,}786$	$0{,}484$	$0{,}017$	$0{,}093$	$0{,}684$	$-0{,}033$

A análise da Figura 1 e das Tabelas 1 e 2 leva a diversas conclusões. Primeiramente, note que as 4 primeiras parametrizações têm desempenhos praticamente iguais. É virtualmente impossível escolher uma parametrização mais adequada. Embora haja duas variáveis físicas além de $u_{*}$ na Eq. (10), $g$ é constante, e $\nu _{\tau }$ é praticamente constante. Isso significa que, na prática, a única variável que efetivamente funciona como preditora de $z_{0}$ é $u_{*}$ . Entretanto, parametrizações tão diversas quanto CHA e NCL (com expoentes de $u_{*}$ iguais a 2 e a 3{,}89; vide Tabela 1) produzem essencialmente as mesmas estatísticas de erros. Somos levados a concluir que $z_{0}$ depende apenas fracamente de $u_{*}$ .

Por sua vez, isso levanta a questão: será melhor utilizar um $z_{0}$ constante, independente de $u_{*}$ ? Será possível que a utilização de parametrizações dependentes de $u_{*}$ esteja piorando as estimativas de $u_{*}$ ? Como se pode ver na 5\ira\ linha da Tabela 2, isso não é verdade: a parametrização para uma rugosidade constante conduz a erros maiores do que os encontrados para as 4 primeiras parametrizações. Mesmo assim, a parametrização CTE leva a uma importante conclusão: o valor de $z_{0}$ encontrado, que pode ser considerado representativo da rugosidade da superfície da água para o sítio experimental, é dez vezes maior do que o reportado por Brutsaert [39] para superfícies líquidas, que é de $0{,}0002\,\mathrm {m}$ .

Outra observação importante é a comparação dos parâmetros ótimos obtidos para CHA e para CLM na Tabela 1: uma rápida inspeção mostra que, na verdade, o algoritmo de otimização encontrou, essencialmente, a mesma forma da equação de Charnock. De fato, além de $\nu _{\tau }$ já ser praticamente constante, o seu expoente $a$ é muito pequeno ( $0{,}015$ ); o expoente de $u_{*}$ , $1{,}908$ , é praticamente igual ao 2 da equação de Charnock, e o expoente de $g$ , $-0,969$ , também é muito próximo ao $-1$ da equação de Charnock. Portanto, na prática CLM é quase igual à equação de Charnock com um valor de $\alpha =14{,}386-15{,}050\times (\nu _{\tau })^{0{,}015}=1{,}631$ (para um $\nu _{\tau }=1{,}62\times 10^{-5}\,\mathrm {m\,s^{-2}}$ médio dos dados), que não difere tanto do parâmetro ótimo para a equação de Charnock "pura", que é $0{,}3863$ . Note que CLM é a parametrização que utiliza o maior número de parâmetros, e que isso se reflete em um desempenho marginalmente melhor para algumas estatísticas da Tabela 2. Dadas as diferenças muito pequenas encontradas, entretanto, é altamente questionável a utilização de CLM. Entre outras coisas, isso mostra que o ganho obtido com o termo em que aparece $\beta$ na Eq. (10) é muito pequeno.

É importante observar que o sinal da estabilidade atmosférica possui um efeito razoável tanto sobre os valores dos parâmetros encontrados quanto sobre as estatísticas de erro. A Tabela 3 mostra os valores ótimos de $\alpha$ e $\beta$ de CLA para 3 situações: todos os dados, dados estáveis ( $\zeta _{r}\geq 0$ ) e dados instáveis ( $\zeta _{r}<0$ ). A inclusão de ( $\zeta _{r}=0$ ) na classe dos dados estáveis é meramente convencional, já que esse valor exato nunca ocorre na prática. Já a Tabela 4 mostra os erros para esses 3 casos (note que a primeira linha de cada uma dessas tabelas é uma repetição das linhas correspondentes nas Tabelas 1 e 2). Apresenta-se apenas os resultados para CLA porque eles são bastante representativos do que ocorre (em termos de dependência da estabilidade atmosférica) com todas as demais parameterizações, e porque ela é a parametrização utilizada na próxima seção, que trata da parametrização da rugosidade para vapor d’água. Note que os parâmetros em condições estáveis são bastante diferentes, mas o resultado em termos de erros varia muito menos. De modo geral, os erros em condições estáveis são um pouco maiores e os erros em condições instáveis são um pouco menores do que os erros para o conjunto de todos os dados.

Tabela 3. Parâmetros ótimos obtidos para cada parametrização da CLA de

, em função da estabilidade atmosférica

Estabilidade	$\alpha$	$\beta$
Todas	$0{,}5308$	$-12{,}92$
$\zeta \geq 0$	$1{,}7731$	$-188{,}23$
$\zeta <0$	$0{,}3980$	$-11{,}937$

Tabela 4. Estatísticas de erros de

para a parametrização CLA de

, em função da estabilidade atmosférica

Estabilidade	REMQ	EMA	VIÉS	$a_{0}$	$r$	$s_{a}$	$s_{y}$	$a_{1}$	$a_{2}$
	$\mathrm {m\,s^{-1}}$	$\mathrm {m\,s^{-1}}$	$\mathrm {m\,s^{-1}}$				$\mathrm {m\,s^{-1}}$		$\mathrm {m\,s^{-1}}$
Todas	$0{,}094$	$0{,}072$	$-0{,}033$	$0{,}829$	$0{,}757$	$0{,}021$	$0{,}086$	$0{,}828$	$-0{,}009$
$\zeta _{r}\geq 0$	$0{,}109$	$0{,}084$	$-0{,}049$	$0{,}799$	$0{,}751$	$0{,}029$	$0{,}096$	$0{,}745$	$-0{,}002$
$\zeta _{r}<0$	$0{,}066$	$0{,}048$	$-0{,}019$	$0{,}892$	$0{,}840$	$0{,}029$	$0{,}062$	$0{,}898$	$-0{,}002$

Finalmente, uma última observação muito importante: em consonância com o alto valor médio de $z_{0}$ encontrado para a parametrização CTE, os valores de $\alpha$ e $\beta$ de CLA são muito maiores em módulo do que os valores típicos para o oceano. Compare $\alpha =0{,}5308$ com o valor de $\alpha =0{,}011$ da literatura, e $\beta =-12{,}92$ com $0{,}135$ . O valor ótimo de $\alpha$ encontrado no presente trabalho é cerca de uma ordem de grandeza maior que o usual para corpos de água profundos. Esse valor no entanto é coerente com alguns trabalhos realizados em águas rasas presentes na literatura. Por exemplo os trabalhos de Hsu [40], Geernaert et al. [41] e Smith [14] que observaram um aumento de $u_{*}$ relacionada à profundidade do corpo de água e Shabani et al. [19] que mediram $u_{*}$ em uma zona de arrebentação de ondas e obtiveram um valor médio de $\alpha$ da ordem de $10^{-1}$ .

4.2 Parametrização do fluxo de calor latente

Para testar os modelos para o fluxo de vapor de água foram utilizadas medições de ${\overline {\theta _{0}}}$ , ${\overline {q_{b}}}$ , $\zeta _{b}$ e $u_{*}$ . Com tais dados é possível estimar o fluxo de vapor de água através das expressões (9), (14), (15) e (20).

As parametrizações testadas foram as seguintes, todas baseadas na Eq. (20):

BRT. Este é o modelo originalmente proposto por Brutsaert [9] (expressão (20) com $C_{R}^{1/2}=7$ , $d=1/4$ e ${\text{Cd}}_{0}=5$ ).

BRM ("Brutsaert modificado"). Otimizamos $C_{R}$ , mantendo $d=1/4$ .

SOL ("Soloviev"). Forçamos $d=0$ e otimizamos $C_{R}$ .

GEN ("Modelo generalizado"). Otimizamos $C_{R}$ e $d$ .

O valor estimado do fluxo de calor latente, ${\widehat {LE}}$ , foi obtido por meio das equações (4), (8) e (9), com $z_{0}$ sempre estimado com a parametrização CLA (note que as 4 parametrizações CHA, CLA, CLM e NCL produzem resultados muito parecidos). Em todos os casos, o calor latente de evaporação, $L$ foi calculado à temperatura da superfície da água. O valor de rugosidade para vapor d'água, $z_{0E}$ , foi estimado com as Eqs. (14)-(15), mantendo ${\text{Cd}}_{0}^{-1/2}=5$ (tentativas de otimizar também este parâmetro produziram estimativas de parâmetros com valores muito grandes; note que ${\text{Da}}_{0}$ e ${\text{Cd}}_{0}$ se somam dentro do argumento da expoencial, e que não faz sentido tentar otimizar ambos; portanto, preferimos manter ${\text{Cd}}_{0}$ constante).

Da mesma maneira que no caso da otimização dos parâmetros envolvidos na estimativa de $z_{0}$ , os valores de $\zeta _{b}$ , $u_{*}$ e $\theta _{v*}$ foram considerados conhecidos do lado direito das expressões. Também da mesma maneira, para cada alternativa de parametrização, obtêve-se os parâmetros ótimos correspondentes por meio de otimização não-linear, novamente com a rotina leastsq mencionada acima.

Da mesma maneira que antes, os testes de desempenho envolvem o REMQ, o EMA, o VIÉS, e os valores de $a_{0}$ , $r$ , $s_{y}$ , $s_{a}$ , $a_{1}$ e $a_{2}$ , exceto que as regressões são, agora,

(23)

(24)

onde ${\widehat {LE}}$ é a estimativa do fluxo de calor latente obtida em cada parametrização e $LE$ é o fluxo de calor latente medido. As Figuras 2a-2d mostram os resultados obtidos para cada uma das 4 parametrizações. A Tabela 5 lista os valores de $C_{R}^{-1}$ e $d$ encontrados em cada caso, e a Tabela 6 lista as estatísticas de erros correspondentes.

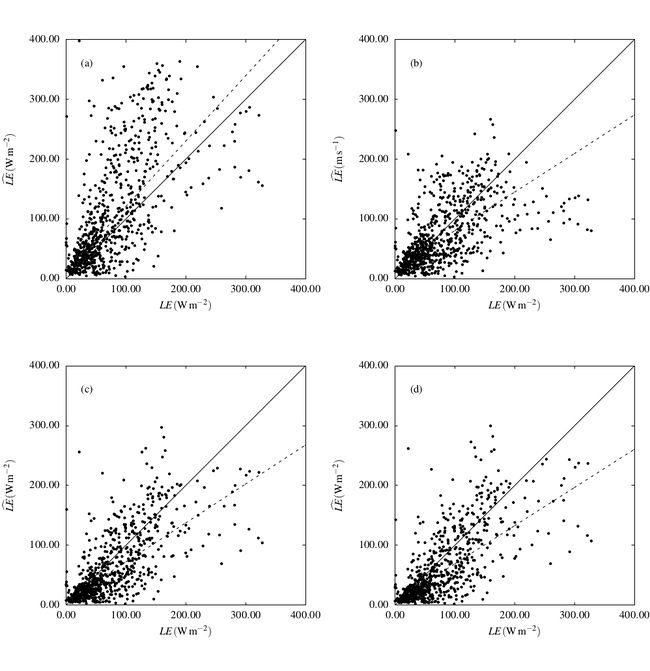
Figura 2. Valores previstos (no eixo vertical) contra observados (no eixo horizontal) de

para 4 parametrizações testadas de

: (a) BRT. (b) BRM. (c) SOL. (d) GEN. A linha contínua é a reta

(indicando concordância perfeita) e a linha tracejada é a linha ajustada pelo método de Siegel (Equação (22); parâmetros

e

na Tabela 6

Tabela 5. Parâmetros ótimos obtidos para cada parametrização de

(para a parametrização BRT, os valores são de literatura)

Parametrização	$C_{R}^{-1}$	$d$
BRT	$7{,}3$	$0{,}25$
BRM	$17{,}43$	$0{,}25$
SOL	$49{,}45$	$0{,}00$
GEN	$58{,}31$	$-0{,}037$

Tabela 6. Estatísticas de erros de LE para cada parametrização de

Parametrização	REMQ	EMA	VIÉS	$a_{0}$	$r$	$s_{a}$	$s_{y}$	$a_{1}$	$a_{2}$
	$\mathrm {W\,m^{-2}}$	$\mathrm {W\,m^{-2}}$	$\mathrm {W\,m^{-2}}$				$\mathrm {W\,m^{-2}}$		$\mathrm {W\,m^{-2}}$
BRT	$81{,}04$	$53{,}25$	$-32{,}86$	$1{,}207$	$0{,}562$	$0{,}034$	$78{,}39$	$1{,}092$	$11{,}87$
BRM	$57{,}00$	$35{,}71$	$-05{,}30$	$0{,}714$	$0{,}301$	$0{,}019$	$49{,}43$	$0{,}645$	$16{,}09$
SOL	$50{,}76$	$32{,}56$	$-11{,}81$	$0{,}737$	$0{,}655$	$0{,}021$	$43{,}52$	$0{,}651$	$07{,}15$
GEN	$50{,}63$	$32{,}80$	$-13{,}33$	$0{,}736$	$0{,}679$	$0{,}021$	$43{,}33$	$0{,}638$	$05{,}21$

A análise desses resultados leva a algumas conclusões importantes. A primeira delas é que o uso da parametrização BRT sem otimização local dos parâmetros produz erros muito maiores do que todas as outras. As causas desse comportamento não estão claras, mas talvez seja possível reunir argumentos físicos, e em particular argumentos relacionados com a transferência de vapor d'água sobre uma superfície líquida natural, para explicá-lo. Mesmo com otmização de $C_{R}$ , o expoente $d=1/4$ que também aparece na parametrização BRM não leva aos melhores resultados.

As parametrizações SOL e GEN, que possuem $d=0$ ou próximo disso, foram as que obtiveram os menores erros, e o melhor desempenho, de maneira geral. A conclusão é que as melhores parametrizações de $z_{0E}$ em Itaipu são aquelas em que não entra o número de Reynolds de rugosidade ${\text{Re}}_{0}$ . É importante enfatizar que o escopo de nossa investigação aqui é puramente empírico: uma investigação mais profunda das possíveis causas físicas do comportamento encontrado será necessária em estudos adicionais.

Para a rugosidade do vapor d'água $z_{0E}$ , a superioridade das duas últimas parametrizações é evidente. Além disso, o ganho adicional de se otimizar $d$ é muito pequeno: é evidente que é suficiente fazer $d=0$ , e utilizar a parametrização SOL.

5. Conclusões

No presente trabalho foram testadas algumas parametrizações para os comprimentos de rugosidade de momentum e vapor de água em lagos. Com relação a $z_{0}$ a comparação dos diferentes modelos leva a conclusão que $u_{*}$ tem pouca capacidade preditiva do mesmo. Isso ocorre porque modelos com expoentes muito diferentes de $u_{*}$ fornecem estatísticas de erro muito similares. O modelo que resulta em um maior erro é considerar $z_{0}$ constante; neste caso o valor ótimo encontrado para $z_{0}$ foi uma ordem de grandeza maior que o usualmente considerado em superfícies líquidas. Os valores encontrados para as constantes de calibração dos melhores modelos (com $z_{0}$ variando em função de $u_{*}$ ) foram consideravelmente diferentes dos valores usuais para corpos de água profundos; o valor ótimo do parâmetro de Charnock $\alpha =0{,}3863$ encontrado é também uma ordem de grandeza maior que em oceanos. Esse resultado está de acordo com o valor sugerido em Shabani et al. [18] para medições realizadas em uma zona de arrebentação de ondas, e também com o comentário de Smith [14] de que o parâmetro de Charnock é maior em regiões costeiras onde as ondas mais íngremes parecem produzir rugosidades maiores.

Com relação a $z_{0E}$ foi observado que o modelo clássico BRT com a constante de calibração original ( $C_{R}^{-1}=7{,}3$ ) produziu o maior erro. Com a parametrização clássica o valor ótimo de $C_{R}^{-1}=17{,}42$ obtido com os dados de Itaipu resultou em uma diminuição do erro de $29{,}66\%$ com relação à parametrização BRT. Com isso podemos concluir os coeficientes de calibração de diferentes experimentos têm que ser usados com cuidado em situações diversas do experimento original. Os modelos que apresentaram os melhores desempenhos foram os independentes do número de Reynolds de rugosidade. Do ponto de vista prático podemos concluir que a parametrização SOL com o coeficiente de calibração $C_{R}^{-1}=49{,}45$ gerou os melhores resultados. Note que esse coeficiente de calibração é maior que o sugerido por Soloviev et. al. [31] que é $C_{R}^{-1}=13{,}3$ .

Os resultados obtidos neste estudo indicam que a parametrização de Charnock para $z_{0}$ pode ser utilizada de maneira direta sem perda considerável de performace com a inclusão de outros termos. Já para $z_{0E}$ também a parametrização mais simples (independente do número de Reynolds de rugosidade) se mostrou mais eficiente. Porém as contantes de calibração encontradas foram considerávelmente diferentes, e isso levanta a dúvida sobre a universalidade dessas parametrizações. Outros estudos da mesma natureza devem ser realizados em outras localidades para essa questão ser sanada.

É importante notar também que durante o período analisado a ilha da estação de medição estava praticamente coberta por água. Com isso, a própria ilha não representava um obstáculo aerodinâmico, o que foi um importante critério de qualidade dos dados analisados. No entanto, isso também limitou a análise a um período específico do ano. Embora a época do ano e as condições sinóticas não influenciem diretamente as parametrizações de rugosidade, efeitos indiretos podem ser importantes, porque tanto a direção quanto a velocidade do vento podem ter impacto sobre a formação de ondas e consequentemente sobre (pelo menos) a rugosidade para a quantidade de movimento. Estudos adicionais serão necessários para levar em conta esses efeitos indiretos.

Referências

[1] Mahrer Y., Assouline S. Evaporation from lake kinneret: 2. estimation of the horizontal variability using a two-dimensional numerical mesoscale model. Water. Resour. Res., 29:911–916, 1993.

[2] Heikinheimo M., Kangas M., Tourola T., Venalainen A., Tattari S. Momentum and heat fluxes over lakes tamnaren and raksjo determined by the bulk-aerodynamic and eddy-correlation methods. Agric. For. Meteorol., 98:521–534, 1999.

[3] Kelman J., Kelman R., Pereira M.V.F. Energia firme de sistemas hidrelétricos e usos múltiplos dos recursos hídricos. Rev. Bras. Rec. Hídr., 9:189–198, 2004.

[4] Thomas C., Martin J., Goeckede M., Siqueira M., Foken T., Law B., Loescher H., Katul G. Estimating daytime subcanopy respiration from conditional sampling methods applied to multi-scalar high frequency turbulence time series. Agric. For Meteorol., 148:1210–1229, 2008.

[5] Siqueira M., Katul G. A sensitivity analysis of the nocturnal boundary-layer properties to atmospheric emissivity formulations. Boundary-Layer Meteorol., 2:223–242, 2010.

[6] Raupach M.R., Thom A.S. Turbulence in and above plant canopies. Annu. Rev. Fluid Mech., 13:97–129, 1981.

[7] Brutsaert W. A model for evaporation as a molecular diffusion process into a turbulent atmosphere. J. Geophys. Res., 70:5017–5024, 1965.

[8] Brutsaert W. A theory for local evaporation (or heat transfer) from rough and smooth surfaces at ground level. Water. Resour. Res., 11:543–550, 1975.

[9] Brutsaert W. The roughness length for water vapor, sensible heat and other scalars. J. Atmos. Sci., 32:2028–2031, 1975.

[10] Danckwerts P.V. Signficance of liquid-film coefficients in gas absorption. Ind. Eng. Chem., 43:1460–1467, 1951.

[11] Charnock H. Wind stress on a water surface. Q. J. R. Meteorol. Soc., 81:639–640, 1955.

[12] Charnock H. A note on empirical wind-wave formulae. Quarterly Journal of the Royal Meteorological Society, 84:443–447, 1958.

[13] Smith S. Wind stress and heat flux over the ocean in gale force winds. J. Phys. Ocean., 10:709–726, 1980.

[14] Smith S. Coefficients for sea surface wind stress, heat flux, and wind profiles as a function of wind speed and temperature. J. Geophys. Res-Oceans, 93:467–472, 1988.

[15] Anctil F., Donelan M. Air-water momentum flux observations over shoaling waves. J. Phys. Oceanogr., 26:1344–1354, 1996.

[16] Garratt J. Review of drag coefficients over oceans and continents. Mon. Wea. Rev., 105:915–929, 1977.

[17] Wu J. Wind-stress coefficients over sea surface near neutral conditions—a revisit. J. Phys. Oceanogr., 10:727–740, 1980.

[18] Shabani B., Nielsen P., Baldock T. Direct measurements of wind stress over the surf zone. J. Geophys. Res., 119:2949–2973, 2014.

[19] Verburg P., Antenucci J.P. Persistent unstable atmospheric boundary layer enhances sensible and latent heat loss in a tropical great lake: Lake tanganyika. J. Geophys. Res. Atmos., 115:D11109, 2010.

[20] Dias N.L., Vissotto D. The effect of temperature-humidity similarity on bowen ratios, dimensionless standard deviations, and mass transfer coefficients over a lake. Hydrol. Process., 31:256–269, 2017.

[21] Drennan W.M., Graber H.C., Hauser D., Quentin C. On the wave age dependence of wind stress over pure wind seas. J. Geophys. Res., 108:C3, 2003.

[22] Johnson H.K., Hojstrup J., Vested H.J., Larsen S.E. On the dependence of sea surface roughness on wind waves. J. Phys. Oceanogr., 28:1702–1716, 1998.

[23] Kitaigorodskii S.A., Volkov Y.A. On the roughness parameter of the sea surface and the calculation of momentum flux in the near-water layer of the atmosphere. Izv. Atm. Oceanic Phys., 1:973–988, 1965.

[24] Maat N., Kraan C., Oost W. The roughness of wind waves. Boundary-Layer Meteorol., 54:89–103, 1991.

[25] Mascart P., Noilhan J., Giordani H. A modified parameterization of flux-profile relationships in the surface layer using different roughness length values for heat and momentum. Boundary-Layer Meteorol., 72:331–344, 1995.

[26] Monbaliu J. On the use of the donelan wave spectral parameter as a measure for the roughness of wind waves. Boundary-Layer Meteorol., 67:277–291, 1994.

[27] Oost W., Komen G., Jacobs C., Van Oort C. New evidence for a relation between wind stress and wave age from measurements during asgamage. Boundary-Layer Meteorol., 103:409–438, 2002.

[28] Taylor P.K., Yelland M.J. The dependence of sea surface roughness on the height and steepness of the waves. J. Phys. Oceanogr., 31:572–590, 2001.

[29] Vickers D., Mahrt L. Fetch limited drag coefficients. Boundary-Layer Meteorol., 85:53–79, 1997.

[30] Lorke A., Peetres F. Toward a unified scaling relation for interfacial fluxes. J. Phys. Oceanogr., 36:955–961, 2006.

[31] Soloviev A.V., Schlüssel P. Parameterization of the cool skin of the ocean and air-ocean gas transfer on the basis of modelling surface renewal. J. Phys. Oceanogr., 24:1339–1347, 1994.

[32] Csanady G.T. The role of breaking wavelets in air-sea gas transfer. J. Geophys. Res., 95:749–759, 1990.

[33] Webb E.K., Pearman G.I., Leuning R. Correction of flux measurements for density effects due to heat and water vapor transfer. Q. J. Roy. Meteorol. Soc., 106:85–100, 1980.

[34] Finnigan J.J., Clement R., Malhi Y., Leuning R., Cleugh H.A. A re-evaluation of long-term flux measurement techniques part I: averaging and coordinate rotation. Boundary-Layer Meteorol., 107:1–48, 2003.

[35] Falge E., Baldocchi D., Olson R., Anthoni P., Aubinet M., Bernhofer C., Burba G., Ceulemans R., Clement R., Dolman H., Granier A., Gross P., Grenwald T., Hollinger D., Jensen N.O., Katul G., Keronen P., Kowalski A., Lai C.T., Law B.E., Meyers T., Moncrieff J., Moors E., Munger J.W., Pilegaard K., Rannik R., Rebmann C., Suyker A., Tenhunen J., Tu K., Verma S., Vesala T., Wilson K., Wofsy S. Gap filling strategies for long term energy flux data sets. Agric. For Meteorol., 107:71–77, 2001

[36] Fairall C.W., Bradley E.F., Grachev A.A. Bulk parameterization of air sea fluxes: Updates and verification. J. Climate, 16:571–591, 2003.

[37] Siegel A.F. Robust regression using repeated medians. Biometrika, 69:242–244, 1982.

[38] Stein A., Werman M. Finding the repeated median regression line. Proceedings of the Third Symposium on Discrete Algorithms (SODA). Society for Industrial and Applied Mathematics (SIAM), 409–413, 1992.

[39] Brutsaert W. Evaporation into the atmosphere. Dordrecht, D. Reidel, September 1982.

[40] Hsu S. A dynamic roughness equation and its application to wind stress determination at the air-sea interface. J. Phys. Oceanogr., 4:116–120, 1974.

[41] Geernaert G.L., Larsen S.E., Hansen F. Measurements of the wind stress, heat flux and turbulence intensity during storm conditions over the north sea. J. Geophys. Res., 92:127–139, 1987.

Latest revision as of 14:55, 1 March 2021

Resumo

Abstract

1. Introdução

2. Metodologia

2.1 Fluxos turbulentos e Teoria de Similaridade de Monin-Obukhov

2.2 A parametrização de $z_{0}$ 2.2 A parametrização de z 0 {\displaystyle z {0}}

2.3 A parametrização de $z_{0E}$ 2.3 A parametrização de z 0 E {\displaystyle z {0E}}

3. Sítio experimental

4. Resultados e discussão

4.1 Fluxo de quantidade de movimento

4.2 Parametrização do fluxo de calor latente

5. Conclusões

Referências

Document information

Document Score

Share this document

Keywords

@@ Line 1: / Line 1: @@
-== Avaliação de alternativas para a parametrização dos comprimentos de rugosidade de quantidade de movimento e vapor d'água em lagos==<!-- Your document should start with a concise and informative title. Titles are often used in information-retrieval systems. Avoid abbreviations and formulae where possible. Capitalize the first word of the title.
+==Resumo==
-Provide a maximum of 6 keywords, and avoiding general and plural terms and multiple concepts (avoid, for example, 'and', 'of'). Be sparing with abbreviations: only abbreviations firmly established in the field should be used. These keywords will be used for indexing purposes.
+Uma avaliação do desempenho de diversas alternativas de parametrização dos comprimentos de rugosidade para quantidade de movimento e vapor d'água foi realizada com dados medidos sobre a água no reservatório de Itaipu, Brasil. Foram testadas 4 parametrizações para a estimativa da rugosidade da quantidade de movimento, e 4 para a estimativa da rugosidade do vapor d'água. As parametrizações para quantidade de movimento consistem na equação de Charnock e generalizações, enquanto que as parametrizações para vapor d'água baseiam-se em equações propostas por Brutsaert. As 4 parametrizações para quantidade de movimento produziram resultados muito parecidos em termos de qualidade do ajuste e estatísticas de erros, e se revelaram apenas fracamente dependentes da velocidade de atrito. Já as parametrizações para vapor d'água produziram resultados mais dispersos, sendo que as melhores parametrizações encontradas dependem muito fracamente do número de Reynolds de rugosidade, ou são independentes do mesmo. Tanto no caso de quantidade de movimento quanto de vapor d'água, os valores dos parâmetros ótimos de cada parametrização encontrados para Itaipu são significativamente maiores (uma ordem de grandeza para o parâmetro de Charnock e para a rugosidade de quantidade de movimento; e cerca de sete vezes maior para o inverso do número de Dalton) do que os reportados na literatura.
-An abstract is required for every document; it should succinctly summarize the reason for the work, the main findings, and the conclusions of the study. Abstract is often presented separately from the article, so it must be able to stand alone. For this reason, references and hyperlinks should be avoided. If references are essential, then cite the author(s) and year(s). Also, non-standard or uncommon abbreviations should be avoided, but if essential they must be defined at their first mention in the abstract itself. -->
+'''Palavras chave''': Teoria de similaridade de Monin-Obukhov, comprimentos de rugosidade, fluxos superficiais
-Resumo: Uma avaliação do desempenho de diversas alternativas de parametrização dos comprimentos de rugosidade para quantidade de movimento e vapor d'água foi realizada com dados medidos sobre a água no reservatório de Itaipu, Brasil. Foram testadas 4 parametrizações para a rugosidade para a quantidade de movimento, e 4 para a rugosidade para o vapor d'água. As parametrizações para quantidade de movimento consistem na equação de Charnock e generalizações, enquanto que as parametrizações para vapor d'água baseiam-se em equações propostas por Brutsaert. As 4 parametrizações para quantidade de movimento produziram resultados muito parecidos em termos de bondade de ajuste e erros, e se revelaram apenas fracamente dependentes da velocidade de atrito. Já as parametrizações para vapor d'água produziram resultados mais dispersos, sendo que as melhores parametrizações encontradas dependem muito fracamente do número de Reynolds de rugosidade, ou são independentes do mesmo. Tanto no caso de quantidade de movimento quanto de vapor d'água, os valores dos parâmetros ótimos de cada parametrização encontrados para Itaipu são significativamente maiores do que os reportados na literatura.
+==Abstract==
-Palavras chave: teoria de similaridade de Monin-Obukhov, Comprimentos de rugosidade, Fluxos superficiais.
+An assessment of the performance of various parameterization alternatives for
-Abstract:  An assessment of the performance of various parameterization alternatives for
 roughness lengths of ''momentum'' and water vapour was performed. The micrometereological data used in this work
 was measured in the Itaipu reservoir, Brazil. Four models was tested for ''momentum'' roughness
@@ Line 22: / Line 19: @@
 very poorly depend on the Reynolds roughness number, or
 are independent of it. Both in the case of ''momentum'' and
-water vapour, the optimal parameter values? of each parameterization found
+water vapour, the optimal parameter values of each parameterization found
-for Itaipu are significantly larger than those reported in the literature.
+for Itaipu are significantly larger than those reported in the literature (one order of magnitude for the Charnock parameter and for the ''momentum'' roughness; and about seven times greater for the inverse of Dalton's number).
-keywords: Monin-Obukhov Similarity Theory, Roughness lengths, Superficial fluxes
+'''Keywords''': Monin-Obukhov similarity theory, roughness lengths, superficial fluxes
-==1 Introdução ==
+==1. Introdução ==
-A estimativa correta dos fluxos superficiais de quantidade de movimento, calor sensível e massa de vapor d’água é um fator crucial em muitas aplicações de engenharia, incluindo a modelagem de interações superfície-atmosfera em modelos atmosféricos e modelagem e gerenciamento de recursos hídricos [1]-[5]. A partir de medições feitas na parte superior da camada limite atmosférica, denominada subcamada inercial (onde se aplica a Teoria da Similaridade de Monin-Obukhov; ver (6)), os fluxos de escalares podem ser obtidos a partir da teoria de Brutsaert para a estimativa do comprimento de rugosidade para os escalares [7]-[9], que estende a Teoria da Renovação Superficial (TRS) de Danckwerts [10] para produzir um conjunto fechado de equações para os comprimentos de rugosidade de um escalar (no nosso caso, a rugosidade <math>z_{0E}</math> para o vapor d’água) e o tempo médio de contato dos vórtices de menor escala com a superfície. Para ser aplicada, a teoria requer o conhecimento do comprimento de rugosidade para quantidade de movimento <math>z_0</math> característico da superfície.
+A estimativa correta dos fluxos superficiais de quantidade de movimento, calor sensível e massa de vapor d’água é um fator crucial em muitas aplicações de engenharia, incluindo a modelagem de interações superfície-atmosfera em modelos atmosféricos e modelagem e gerenciamento de recursos hídricos [1-5]. A partir de medições feitas na parte superior da camada limite atmosférica, denominada subcamada inercial (onde se aplica a Teoria da Similaridade de Monin-Obukhov (Raupach et. al. [6]), os fluxos de escalares podem ser obtidos a partir da teoria de Brutsaert para a estimativa do comprimento de rugosidade para os escalares [7-9], que estende a Teoria da Renovação Superficial (TRS) de Danckwerts [10] para produzir um conjunto fechado de equações para os comprimentos de rugosidade de um escalar (no nosso caso, a rugosidade <math>z_{0E}</math> para o vapor d’água) e o tempo médio de contato dos vórtices de menores escalas com a superfície. Para ser aplicada, a teoria requer o conhecimento do comprimento de rugosidade para quantidade de movimento <math>z_0</math> característico da superfície.
-Para superfícies sólidas e com vegetação, <math>z_0</math> geralmente pode ser considerado constante, pelo menos sobre uma certa faixa de direções do vento. Sobre a água, <math>z_0</math> é mais comumente estimado usando a equação de Charnock [11],
+Para superfícies sólidas e com vegetação, <math>z_0</math> geralmente pode ser considerado constante, pelo menos sobre uma certa faixa de direções do vento. Sobre a água, <math>z_0</math> (m) é mais comumente estimado usando a equação de Charnock [11],
 {| class="formulaSCP" style="width: 100%; text-align: left;"
@@ Line 42: / Line 39: @@
 | style="width: 5px;text-align: right;white-space: nowrap;" | (1)
 |}
-onde <math>u_*</math> é a velocidade de atrito e <math>g</math> é a aceleração da gravidade e o número adimensional <math>\alpha</math> é o parâmetro de Charnock. Para oceanos abertos, <math>\alpha</math> é da ordem de <math>10^{-2}</math> como sugerido originalmente e corroborado por diversos estudos posteriores [12]-[15].
-Para o caso de corpos de água rasos, existem evidências de que a parametrização de Charnock não explica totalmente a relação entre a velocidade média do vento e a velocidade de atrito [16]. Por exemplo, valores maiores do coeficiente de Charnock foram encontrados por Garratt [17] (<math>\alpha = 0{,}0145</math>) , Wu [18] (<math>\alpha = 0{,}018</math>) e Shabani et al. [19] (<math>\alpha = 0{,}110</math>).
+onde <math>u_*</math> (m s<math>^{-1}</math>) é a velocidade de atrito e <math>g</math> (m s<math>^{-2}</math>) é a aceleração da gravidade e o número adimensional <math>\alpha</math> é o parâmetro de Charnock. Para oceanos abertos, <math>\alpha</math> é da ordem de <math>10^{-2}</math> como sugerido originalmente (Charnock [11], <math>\alpha = 0,01</math>); (Charnock [12], <math>\alpha = 0,0123</math>) e corroborado por estudos posteriores (Smith [13], <math>\alpha = 0,01</math>); (Smith [14], <math>\alpha = 0,011</math>).
+Para o caso de corpos de água rasos, existem evidências de que a parametrização de Charnock não explica totalmente a relação entre a velocidade média do vento e a velocidade de atrito [15]. Por exemplo, nessas condições valores um pouco maiores do coeficiente de Charnock foram encontrados por Garratt [16] (<math>\alpha = 0{,}0144</math>) e Wu [17] (<math>\alpha = 0{,}018</math>) e uma ordem de magnitude maiores por Shabani et al. [18] (<math>\alpha = 0{,}110</math>).
-Devido aos diferentes valores encontrados para o parâmetro de Charnock em corpos de água rasos e profundos, e devido à pequena bibliografia sobre o tema, é importante a realização de outros estudos sobre a parametrização de <math>z_0</math> em lagos. Uma parte do presente trabalho consiste em parametrizar adequadamente <math>z_0</math> , utilizando dados provenientes de uma extensa campanha micrometeorológica no lago de Itaipu, Brasil.
+Devido aos diferentes valores encontrados para o parâmetro de Charnock em corpos de água rasos e profundos, e devido à pequena bibliografia sobre o tema, é importante a realização de outros estudos sobre a parametrização de <math>z_0</math> em lagos. Uma parte do presente trabalho consiste em parametrizar adequadamente <math>z_0</math> , utilizando dados provenientes de uma extensa campanha micrometeorológica no reservatório de Itaipu, Brasil.
-Para lagos, a parametrização para o comprimento de rugosidade de escalares da teoria original foi testada por diversos autores (ver, por exemplo, [20] e [21]), com valores de parâmetros sempre muito próximos daqueles propostos originalmente por Charnock [11] e Brutsaert [8][9]. Neste trabalho, nós avaliamos experimentalmente as alternativas existentes, com particular atenção aos erros que elas produzem, e aos valores ótimos de seus parâmetros.
+Para lagos, a parametrização para o comprimento de rugosidade de escalares da teoria original foi testada por diversos autores (por exemplo, Verburg et. al. [19] e Dias et. al. [20]), com valores de parâmetros sempre muito próximos daqueles propostos originalmente por Charnock [11] e Brutsaert [8,9]. Neste trabalho, nós avaliamos experimentalmente as alternativas existentes, com particular atenção aos erros que elas produzem, e aos valores ótimos de seus parâmetros.
-Este trabalho está organizado da seguinte maneira: na seção 2, nós apresentamos a metodologia e revisitamos parametrizações alternativas tanto para <math>z_0</math> quanto para <math>z_{0E}</math>; na seção 3, nós descrevemos brevemente o sítio experimental do lago de Itaipu, cujos dados são utilizados neste trabalho; na seção 4, nós comparamos as diversas parametrizações, e discutimos os resultados obtidos. As conclusões são apresentados na seção 5.
+Este trabalho está organizado da seguinte maneira: na Seção 2, a metodologia é apresentada e são revisitadas parametrizações alternativas tanto para <math>z_0</math> quanto para <math>z_{0E}</math>; na Seção 3, o sítio experimental do reservatório de Itaipu, cujos dados são utilizados neste trabalho, é brevemente descrito; na Seção 4, as diversas parametrizações são comparadas, e os resultados obtidos são discutidos. As conclusões são apresentadas na Seção 5.
-==2 Metodologia ==
+==2. Metodologia ==
 ===2.1 Fluxos turbulentos e Teoria de Similaridade de Monin-Obukhov ===
@@ Line 84: / Line 82: @@
 | style="width: 5px;text-align: right;white-space: nowrap;" | (4)
 |}
-Nas equações acima, <math>u</math> é a velocidade longitudinal do vento; <math>w</math> é a velocidade vertical; <math>\rho</math> é a densidade do ar; <math>c_p</math> é o calor específico a pressão constante do ar; <math>\theta</math> é a temperatura do ar; <math>q</math> é a umidade específica, e <math>L</math> é o calor latente de evaporação. As equações (2)–(4) definem as escalas turbulentas <math>u_*</math>, <math>\theta_*</math> e <math>q_*</math> (velocidade de atrito e escalas turbulentas de temperatura e umidade, respectivamente), a partir das quais obtém-se a variável de similaridade de Obukhov,
+Nas equações acima, <math>u</math> (m s<math>^{-1}</math>) é a velocidade longitudinal do vento; <math>w</math> (m s<math>^{-1}</math>) é a velocidade vertical; <math>\rho</math> (kg m<math>^{-3}</math>) é a densidade do ar; <math>c_p</math> (J Kg<math>^{-1}</math>K<math>^{-1}</math>) é o calor específico a pressão constante do ar; <math>\theta</math> (K) é a temperatura do ar; <math>q</math> (Kg<math>_{H2O}</math>Kg<math>^{-1}</math>) é a umidade específica, e <math>L</math> (J Kg<math>^{-1}</math>) é o calor latente de evaporação. As equações (2)–(4) definem as escalas turbulentas <math>u_*</math> (m s<math>^{-1}</math>), <math>\theta_*</math> (K) e <math>q_*</math> (Kg<math>_{H2O}</math>Kg<math>^{-1}</math>) (velocidade de atrito e escalas turbulentas de temperatura e umidade, respectivamente), a partir das quais obtém-se a variável de similaridade de Obukhov,
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 94: / Line 92: @@
 | style="width: 5px;text-align: right;white-space: nowrap;" | (5)
 |}
-onde <math>z_r</math> é uma altura arbitrária acima da superfície, <math>\kappa=0{,}4</math> é a constante de vón Kármán, e
+onde <math>z_r</math> (m) é uma altura arbitrária acima da superfície, <math>\kappa=0{,}4</math> é a constante de vón Kármán.
+A temperatura virtual média (<math>K</math>) é
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 100: / Line 99: @@
 {| style="text-align: left; margin:auto;width: 100%"
 |-
-| style="text-align: center;" | <math> \overline{\theta_v} = (1 + 0{,}61\overline{q})\overline{\theta},</math>
+| style="text-align: center;" | <math>\overline{\theta}= (1+0{,}61\overline{q})\overline{\theta},</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (6)
 |}
+e a escala turbulenta de temperatura virtual (K) é
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 109: / Line 109: @@
 {| style="text-align: left; margin:auto;width: 100%"
 |-
-| style="text-align: center;" | <math> \theta_{v*} = (1 + 0.61\overline{q})\theta_* + 0{,}61\overline{\theta}q_*,</math>
+| style="text-align: center;" | <math>\theta_{v*} = (1+0{,}61\overline{q})\theta_* + 0,61\overline{\theta}q_*.</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (7)
 |}
-são a temperatura virtual média e a escala turbulenta de temperatura virtual, respectivamente. Nas equações acima, uma barra indica uma média e uma linha a flutuação turbulenta em torno da média.
+Nas equações acima, uma barra indica uma média e uma linha a flutuação turbulenta em torno da média.
 Os fluxos turbulentos <math>\tau</math> e <math>LE</math> podem ser estimados a partir da medição de grandezas médias via Teoria de Similaridade de Monin-Obukhov (TSMO), com
@@ Line 134: / Line 134: @@
 | style="width: 5px;text-align: right;white-space: nowrap;" | (9)
 |}
-e substituição em (2) e (4), onde <math>z</math> a é a altura de medição da velocidade média <math>\overline{u_a}</math>, e <math>z_b</math> é a altura de medição da umidade específica média <math>\overline{q_b}</math>. Em (8) e (9), <math>\Psi_\tau</math> e <math>\Psi_E</math> são as funções de similaridade para os fluxos de quantidade de movimento e vapor d’água de Businger-Dyer (Brutsaert, 1982, seção 4.2). O foco central deste trabalho é a comparação de parametrizações para os comprimentos de rugosidade para a quantidade de movimento <math>z_0</math> e para o vapor d'água, <math>z_{0E}</math>. Dias e Vissotto [21] encontraram discrepâncias na parametrização do fluxo de calor sensível que eles atribuíram à advecção de calor sobre o lago. Por esse motivo, neste trabalho nós avaliamos apenas a estimativa do fluxo de calor latente, associado ao fluxo de massa de vapor d'água, via equação (9).
+e substituição em (2) e (4), onde <math>z</math> a (m) é a altura de medição da velocidade média <math>\overline{u_a}</math> (m s<math>^{-1}</math>), e <math>z_b</math> (m) é a altura de medição da umidade específica média <math>\overline{q_b}</math> (Kg<math>_{H2O}</math>Kg<math>^{-1}</math>). Em (8) e (9), <math>\Psi_\tau</math> e <math>\Psi_E</math> são as funções de similaridade para os fluxos de quantidade de movimento e vapor d’água de Businger-Dyer (Brutsaert [9], seção 4.2). O foco central deste trabalho é a comparação de parametrizações para os comprimentos de rugosidade para a quantidade de movimento <math>z_0</math> e para o vapor d'água, <math>z_{0E}</math> (m). Dias et. al. [20] encontraram discrepâncias na parametrização do fluxo de calor sensível que eles atribuíram à advecção de calor sobre o lago. Por esse motivo, neste trabalho nós avaliamos apenas a estimativa do fluxo de calor latente, associado ao fluxo de massa de vapor d'água, via equação (9).
 === 2.2 A parametrização de <math>z_0</math> ===
-Em interfaces água-ar <math>z_0</math> é usualmente parametrizado através de <math>u_*</math> , <math>g</math> e da viscosidade cinemática do ar <math>\nu_{\tau}</math> . Alguns trabalhos também incluem outras grandezas, relacionadas com o estado das ondas na superfície [23]-[31]. Porém em lagos e outros corpos d’água rasos as ondas não conseguem se desenvolver completamente; além disso, em várias aplicações (mesmo no oceano), as características das ondas na superficie nem sempre estão disponíveis. Por isso neste trabalho nós testamos parametrizações para <math>z_0</math> somente com <math>u_*</math>, <math>g</math> e <math>\nu_{\tau}</math>. As parametrizações avaliadas são generalizações de parametrizações existentes, com a forma
+Em interfaces água-ar <math>z_0</math> é usualmente parametrizado através de <math>u_*</math>, <math>g</math> e da viscosidade cinemática do ar <math>\nu_{\tau}</math> (m<math>^2</math>s<math>^{-1}</math>). Alguns trabalhos também incluem outras grandezas, relacionadas com o estado das ondas na superfície [21]-[29]. Porém em lagos e outros corpos d’água rasos as ondas não conseguem se desenvolver completamente; além disso, em várias aplicações (mesmo no oceano), as características das ondas na superficie nem sempre estão disponíveis. Por isso neste trabalho nós testamos parametrizações para <math>z_0</math> somente com <math>u_*</math>, <math>g</math> e <math>\nu_{\tau}</math>. As parametrizações avaliadas são generalizações de parametrizações existentes, com a forma
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 144: / Line 144: @@
 {| style="text-align: left; margin:auto;width: 100%"
 |-
-| style="text-align: center;" | <math>z_0 = \max\left(\alpha\frac{u_*^2}{g} + \beta \nu_{\tau}^a u_*^b g^c,\frac{0.135\nu_\tau}{u_*}\right).</math>
+| style="text-align: center;" | <math>z_0 = \max\left(\alpha\frac{u_*^2}{g} + \beta \nu_{\tau}^a u_*^b g^c,\frac{0{,}135\nu_\tau}{u_*}\right).</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (10)
@@ Line 168: / Line 168: @@
 | style="width: 5px;text-align: right;white-space: nowrap;" | (12)
 |}
-para produzir um resultado com dimensões de comprimento.  O caso <math>\alpha=0</math> e <math>c=0</math> produz o comprimento de rugosidade para escoamentos turbulentos lisos [43], que é exatamente o segundo argumento de <math>\max(\cdot,\cdot)</math> na Eq. (10). Note que essa restrição (a escolha do maior valor entre as duas expressões) evita que valores demasiadamente pequenos (ou mesmo negativos) resultem de combinações arbitrárias dos parâmetros <math>\alpha</math>, <math>\beta</math>, <math>a</math>, <math>b</math> e <math>c</math>, principalmente em buscas automáticas do algoritmo de otimização. Para um conjunto de dados medidos, a equação (10) pode ser otimizada em função de <math>b</math>, <math>\alpha</math>, e <math>\beta</math>. Para cada <math>b</math>, <math>a</math> e <math>c</math> ficam determinados via (11)–(12):
+para produzir um resultado com dimensões de comprimento.  O caso <math>\alpha=0</math> e <math>c=0</math> produz o comprimento de rugosidade para escoamentos turbulentos lisos [14], que é exatamente o segundo argumento de <math>\max(\cdot,\cdot)</math> na Eq. (10). Note que essa restrição (a escolha do maior valor entre as duas expressões) evita que valores demasiadamente pequenos (ou mesmo negativos) resultem de combinações arbitrárias dos parâmetros <math>\alpha</math>, <math>\beta</math>, <math>a</math>, <math>b</math> e <math>c</math>, principalmente em buscas automáticas do algoritmo de otimização. Para um conjunto de dados medidos, a equação (10) pode ser otimizada em função de <math>b</math>, <math>\alpha</math>, e <math>\beta</math>. Para cada <math>b</math>, <math>a</math> e <math>c</math> ficam determinados via (11)–(12):
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 178: / Line 178: @@
 | style="width: 5px;text-align: right;white-space: nowrap;" | (13)
 |}
-Na seção 4, diversas combinações de <math>b</math>, <math>\alpha</math> e <math>\beta</math> são obtidos por otimização, com o método de Levenberg-Marquardt, para o lago de Itaiu.
+Na seção 4, diversas combinações de <math>b</math>, <math>\alpha</math> e <math>\beta</math> são obtidos por otimização, com o método de Levenberg-Marquardt, para o reservatório de Itaipu.
 === 2.3 A parametrização de <math>z_{0E}</math> ===
@@ Line 192: / Line 193: @@
 | style="width: 5px;text-align: right;white-space: nowrap;" | (14)
 |}
-onde <math>\text{Da}_0</math> é o número de Dalton interfacial, e <math>\text{Cd}_0</math> é o coeficiente de arrasto interfacial. Brutsaert [8] obteve <math>\text{Cd}_{0}^{-1/2} = 5</math>.
+onde <math>\text{Da}_0</math> é o número de Dalton interfacial, e <math>\text{Cd}_0</math> é o coeficiente de arrasto interfacial. Brutsaert [8] utilizou <math>\text{Cd}_{0}^{-1/2} = 5</math>.
 A equação (14) é válida apenas para o regime turbulento rugoso, que é predominante em condições de campo. Para o regime liso, Brutsaert [9] propõe
 {| class="formulaSCP" style="width: 100%; text-align: left;"
@@ Line 199: / Line 200: @@
 {| style="text-align: left; margin:auto;width: 100%"
 |-
-| style="text-align: center;" | <math>z_{0E} = \frac{0.135\nu_\tau}{u_*}\exp\left[-\kappa(13.6\text{Sc}^{2/3} - 13.5)\right].</math>
+| style="text-align: center;" | <math>z_{0E} = \frac{0{,}135\nu_\tau}{u_*}\exp\left[-\kappa(13{,}6\text{Sc}^{2/3} - 13{,}5)\right].</math>
 |}
 | style="width: 5px;text-align: right;white-space: nowrap;" | (15)
@@ Line 233: / Line 234: @@
 | style="width: 5px;text-align: right;white-space: nowrap;" | (18)
 |}
-onde <math>\nu_{E}</math> é a difusividade molecular de vapor de água no ar. Note que o expoente <math>-1/2</math> do número de Schmidt em (16) vem da solução transiente da equação da difusão para uma parcela de fluido na Teoria de Renovação Superficial [7][10]; o valor de <math>-1/2</math> é confirmado por uma série de resultados experimentais (''c.f.'' Figura 2 de Lorke e Peetres [32]). Por este motivo, neste trabalho nós mantivemos o expoente de <math>\text{Sc}</math> fixo em <math>-1/2</math> para todas as alternativas de parametrização de <math>\text{Da}_0</math>.
+onde <math>\nu_{E}</math> (m<math>^2</math>s<math>^{-1}</math>) é a difusividade molecular de vapor de água no ar. Note que o expoente <math>-1/2</math> do número de Schmidt em (16) vem da solução transiente da equação da difusão para uma parcela de fluido na Teoria de Renovação Superficial [7][10]; o valor de <math>-1/2</math> é confirmado por uma série de resultados experimentais (''c.f.'' [[#img-2|Figura 2]] de Lorke e Peetres [30]). Por este motivo, neste trabalho nós mantivemos o expoente de <math>\text{Sc}</math> fixo em <math>-1/2</math> para todas as alternativas de parametrização de <math>\text{Da}_0</math>.
+Uma expressão alternativa para <math>\text{Da}_0</math> foi apresentada, por exemplo, por Soloviev et. al. [31] (para regimes de ventos moderados), Csanady [32] e Lorke et. al. [30], que encontraram
-Uma expressão alternativa para <math>\text{Da}_0</math> foi apresentada, por exemplo, por Soloviev e Schlüssel [33] (para regimes de ventos moderados), Csanady [34] e Lorke e Peetres [32], que encontraram
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 248: / Line 248: @@
 onde <math>C_R</math> é uma constante da ordem de <math>10^{-1}</math>.
-Neste trabalho nós propomos e avaliamos uma generalização das duas expressões para Da 0 apresentadas anteriormente, da forma
+Neste trabalho nós propomos e avaliamos uma generalização das duas expressões para <math>Da 0</math> apresentadas anteriormente, da forma
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 260: / Line 260: @@
 com <math>d</math> sendo um número a ser determinado experimentalmente. Em particular quando fazemos <math>d = 1/4</math> obtemos a expressão (16) de Brutsaert, enquanto que <math>d = 0</math> dá origem a (19).
-==3 Sítio experimental ==
+==3. Sítio experimental ==
+Os dados utilizados foram medidos em uma estação micrometeorológica instalada em uma pequena ilha do reservatório da usina hidrelétrica de Itaipu, Estado do Paraná, Brasil. As coordenadas da ilha são −25°03'25,72"S e −54°24'33,67"O, e sua altitude é de 220m em relação ao nível do mar. Devido à proximidade do município de Missal - PR, a estação foi denominada Estação Missal.
-Os dados do lago de Itaipu utilizados neste trabalho foram medidos em uma estação micrometeorológica instalada em uma pequena ilha do Reservatório da Usina Hidrelétrica de Itaipu, Estado do Paraná, Brasil. As coordenadas da ilha são -25°03'25,72"S e -54°24'33,67"O, e sua altitude é de 220m em relação ao nível do mar. Devido à proximidade do município de Missal - PR, a estação foi denominada Estação Missal.
+Na estação micrometeorológica foram instalados sensores de resposta rápida operando a 20Hz, e sensores de resposta lenta medindo a 0,1Hz e calculando médias em intervalos de tempo de 10 minutos. Entre os sensores de resposta rápida instalados na estação, utilizou-se neste trabalho os dados medidos por um Anemômetro Sônico (Campbell Scientific Instruments (CSI) CSAT3), por um analisador de gás infravermelho de CO<sub>2</sub> e H<sub>2</sub>O (Licor LI7500) e por um Termopar (CSI FW03) instalado no centro do caminho ótico do analisador de gás infravermelho. Com isso tanto <math>\theta'</math> (medida pelo termopar) quanto <math>q'</math> (obtida a partir da densidade de vapor d'água medida pelo analisador infravermelho) ficam referenciadas ao mesmo ponto, no centro do caminho ótico do analisador. Note que a separação espacial entre o analisador infravermelho e o anemômetro sônico é pequena, tendo pouco impacto sobre o cálculo dos fluxos de escalares.
-Na estação micrometeorológica foram instalados sensores de resposta rápida operando a 20 Hz, e sensores de resposta lenta medindo a 0,1 Hz e calculando médias em intervalos de tempo de 10 minutos. Entre os sensores de resposta rápida instalados na estação, utilizou-se neste trabalho os dados medidos por um Anemômetro Sônico (Campbell Scientific Instruments (CSI) CSAT3), por um analisador de gás infravermelho de CO<sub>2</sub> e H<sub>2</sub>O (Licor LI7500) e por um Termopar (CSI FW03) instalado no centro do caminho ótico do analisador de gás infravermelho. Tanto o analisador de gás infravermelho quanto o anemômetro sônico estavam na altura de 3,76 m em relaçâo à base da estaçâo.
+Tanto o analisador de gás infravermelho quanto o anemômetro sônico estavam na altura de 3,76m em relação à base da estação.
-As variáveis medidas na estação pelos sensores de resposta lenta foram temperatura e umidade relativa do ar (CS500, Campbell Scientific Instruments; 2{,}85 m), pressâo atmosférica (CS100, Campbell Scientific Instruments; 1{,}73 m) e radiaçâo solar líquida (Kipp & Zönen; 2{,}67 m).
+As variáveis medidas na estação pelos sensores de resposta lenta foram temperatura e umidade relativa do ar (CS500, Campbell Scientific Instruments; 2,85m), pressâo atmosférica (CS100, Campbell Scientific Instruments; 1,73m) e radiaçâo solar líquida (Kipp & Zönen; 2,67m).
-Para medir a temperatura da água foram instalados dois sensores modelo L108 da Campbell Scientific Instruments em uma bóia nautica situada aproximadamente a 3 km a noroeste da estaçâo micrometeorológica. Um dos sensores mediu a temperatura da superfície da água e o outro a temperatura a uma profundidade de 25 cm.
+Para medir a temperatura da água foram instalados dois sensores modelo L108 da Campbell Scientific Instruments em uma bóia nautica situada aproximadamente a 3km a noroeste da estação micrometeorológica. Um dos sensores mediu a temperatura da superfície da água e o outro a temperatura a uma profundidade de 25cm.
-As medições apresentadas neste trabalho vão do dia 09 de outubro de 2013 ao dia 01 de novembro de 2013. Durante este período a ilha estava na maior parte do tempo submersa, com a altura da base da estação variando entre 0,95 cm de profundidade a 30 cm acima do nível da água.
+As medições apresentadas neste trabalho vão do dia 09 de outubro de 2013 ao dia 01 de novembro de 2013. Durante este período a ilha estava na maior parte do tempo submersa, com a altura da base da estação variando entre 0,95cm de profundidade a 30cm acima do nível da água.
-Os fluxos verticais de calor sensível e latente foram obtidos pelo método de covariâncias turbulentas, com as equações (3)-(4). Os fluxos de vapor de água (E) foram corrigidos com a correção WPL [35]. Uma rotação de coordenadas [36] foi aplicada em cada bloco de 30 minutos de dados instantâneos (medidos a 20 Hz) para alinhar a direção x do eixo cartesiano com a direção média do vento. As flutuações turbulentas foram obtidas após a remoção da tendência linear de cada amostra [37].
+Os fluxos verticais de calor sensível e latente foram obtidos pelo método de covariâncias turbulentas, com as equações (3)-(4). Os fluxos de vapor de água (E) foram corrigidos com a metodologia WPL [33]. Uma rotação de coordenadas [34] foi aplicada em cada bloco de 30 minutos de dados instantâneos (medidos a 20 Hz) para alinhar a direção x do eixo cartesiano com a direção média do vento. As flutuações turbulentas foram obtidas após a remoção da tendência linear de cada amostra [35].
-==4 Resultados e discussão ==
+==4. Resultados e discussão ==
 ===4.1 Fluxo de quantidade de movimento ===
-Para a estimativa de <math>z_0</math> na Eq. (10), classicamente os modelos apresentados na literatura consideram <math>b = -1</math>. Entre outros trabalhos podemos citar como exemplo dessa abordagem Smith [43] e Fairall et al. [38]. Em oceanos, os valores usuais da Equação (10) com <math>b = -1</math> considerados em interfaces água-ar são <math>\alpha \approx 0,011</math> e <math>\beta \approx 0,135</math>.
+Para a estimativa de <math>z_0</math> na Eq. (10), classicamente os modelos apresentados na literatura consideram <math>b = -1</math>. Entre outros trabalhos podemos citar como exemplo dessa abordagem Smith [14] e Fairall et al. [36]. Em oceanos, os valores usuais da Equação (10) com <math>b = -1</math> considerados em interfaces água-ar são <math>\alpha \approx 0{,}011</math> e <math>\beta \approx 0{,}135</math>.
 Neste trabalho, nós consideramos 5 alternativas para a parametrização dada pela Eq. (10), com as seguintes siglas:
@@ Line 289: / Line 291: @@
 Isso corresponde a modificar as parametrizações clássicas e dar bastante liberdade ao parâmetro b. Note que para cada <math>b</math> os valores de <math>a</math> e <math>c</math> ficam restritos pela equação (13).
-'''NCL''' (Parametrização “não clássica"). Fixamos <math>\alpha = 0</math>, e otimizamos <math>b</math> e <math>\beta</math> . Essencialmente, já que <math>\nu</math> é praticamente constante para o ar, e que <math>g</math> é constante, estamos agora investigando qual é o expoente "ótimo" para <math>u_*</math>.
+'''NCL''' (Parametrização "não clássica"). Fixamos <math>\alpha = 0</math>, e otimizamos <math>b</math> e <math>\beta</math> . Essencialmente, já que <math>\nu</math> é praticamente constante para o ar, e que <math>g</math> é constante, estamos agora investigando qual é o expoente "ótimo" para <math>u_*</math>.
 '''CTE''' (Parametrização com <math>z_0</math> constante). Como veremos na sequência, ocorre que a dependência de <math>z_0</math> com <math>u_*</math> é relativamente fraca. Assim, nós testamos a qualidade de uma parametrização extremamente simples, em que <math>z_0</math> é independente de <math>u_*</math> .
@@ Line 298: / Line 300: @@
 Para cada parametrização, as estatísticas de desempenho calculadas são as seguintes: REMQ (raiz quadrada do erro médio quadrático), EMA (erro médio absoluto), VIÉS (viés), os valores de <math>a_0</math>, <math>r</math>, <math>s_y</math> e <math>s_a</math> (respectivamente: coeficiente angular, raiz quadrada do coeficiente de determinação, erro padrão das estimativas <math>\widehat{u_*}</math> e erro padrão da estimativa de <math>a</math>) para a regressão linear pela origem
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 308: / Line 311: @@
 |}
-Finalmente, calculou-se os estimadores de Siegel [39][40] para <math>a_1</math> e <math>a_2</math> na equação
+Finalmente, calculou-se os estimadores de Siegel [37] e Stein [38] para <math>a_1</math> e <math>a_2</math> na equação
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 320: / Line 323: @@
 Os estimadores de Siegel são baseados na mediana das inclinações de cada ponto do conjunto de dados, e são menos influenciados por valores extremos (''outliers''). Para uma parametrização perfeita, esperamos <math>a_1 = 1</math> e <math>a_2 = 0</math>.
-As figuras 1-a - 1-d mostram os resultados obtidos para as 4 primeiras parametrizações, e a Tabela 1 os valores correspondentes dos parâmetros ótimos, e das estatísticas de erro. A Tabela 2 dá as estatísticas de desempenho correspondentes.
+As [[#img-1|Figuras 1a]]-[[#img-1|1d]] mostram os resultados obtidos para as 4 primeiras parametrizações, e a [[#tab-1|Tabela 1]] os valores correspondentes dos parâmetros ótimos. A [[#tab-2|Tabela 2]] dá as estatísticas de erros correspondentes.
+<div id='img-1'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;"
+|-
+|  style="text-align: center;padding-top:10px;"| [[File:Review_220770795596_4913_fig01.jpg|650px]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding-bottom:10px;"| '''Figura 1'''. Valores previstos (no eixo vertical) contra observados (no eixo horizontal) de <math>u_*</math> para 4 parametrizações testadas de <math>z_{0}</math>: (a) CHA. (b) CLA. (c) CLM. (d) NCL. A linha contínua é a reta <math>\hat{u_*} = u_*</math> (indicando concordância perfeita), e a linha tracejada é a linha ajustada pelo método de Siegel (Equação (22); parâmetros <math>a_{1}</math> e <math>a_{2}</math> na [[#tab-2|Tabela 2]])
+|}
+<div id='tab-1'></div>
+<div class="center" style="font-size: 75%;">'''Tabela 1'''. Parâmetros ótimos obtidos para cada parametrização de <math>z_0</math></div>
-[[File:Draft_Armani_989287210_8214_fig01.jpg]]
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:40%;"
+|-style="text-align:center;"
-Figura 1: Valores previstos (no eixo vertical) contra observados (no eixo horizontal) de <math>u_*</math> para 4 parametrizações testadas de <math>z_{0}</math>: (a) CHA; (b) CLA; (c) CLM; e (d) NCL. A linha contínua é a reta 1:1, e a linha tracejada é a linha ajustada pelo método de Siegel.
-Tabela 1: Parâmetros ótimos obtidos para cada parametrização de <math>z_0</math>.
-{| class="wikitable"
-|-
 ! Parametrização !! <math>z_0</math> (m) !! <math>\alpha</math> !! <math>\beta</math> !! <math>a</math> !! <math>b</math> !! <math>c</math>
-|-
+|-style="text-align:center;"
 | CHA || -      || <math>0{,}3863</math> || -      || -       || -     || -
-|-
+|-style="text-align:center;"
 | CLA || -      || <math>0{,}5308</math> || <math>-12{,}92</math> || <math>1</math>       || <math>-1</math>    || <math>0</math>
-|-
+|-style="text-align:center;"
-| CLM || -      || <math>3{,}830</math>  || <math>-3{,}995</math> || <math>0{,}030</math>   || <math>1{,}908</math> || <math>-0{,}969</math>
+| CLM || -      || <math>14{,}386</math>  || <math>-15{,}050</math> || <math>0{,}015</math>   || <math>1{,}956</math> || <math>-0{,}985</math>
-|-
+|-style="text-align:center;"
 | NCL || -      || -      || <math>0{,}012</math>  || <math>0{,}631</math>  || <math>3{,}892</math> || <math>-1{,}631</math>
-|-
+|-style="text-align:center;"
 | CTE || <math>0{,}0020</math> || -      || -      || -       || -     || -
 |}
-Tabela 2: Estatísticas de erros para cada parametrização de <math>z_0</math>.
+<div id='tab-2'></div>
+<div class="center" style="font-size: 75%;">'''Tabela 2'''. Estatísticas de erros de <math>u_*</math> para cada parametrização de <math>z_0</math></div>
-{| class="wikitable"
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:40%;"
-|-
+|-style="text-align:center;"
 !    Parametrização !! REMQ   !! EMA    !! VIÉS  !! <math>a_0</math> !! <math>r</math> !! <math>s_a</math> !! <math>s_y</math> !! <math>a_1</math> !! <math>a_2</math>
-|-
+|-style="text-align:center;"
 !                   !! <math>\mathrm{m\,s^{-1}}</math> !! <math>\mathrm{m\,s^{-1}}</math> !! <math>\mathrm{m\,s^{-1}}</math> !!   !!    !!   !! <math>\mathrm{m\,s^{-1}}</math> !!      !! <math>\mathrm{m\,s^{-1}}</math>
-|-
+|-style="text-align:center;"
 |    CHA              || <math>0{,}095</math>              || <math>0{,}071</math>              || <math>-0{,}022</math>             || <math>0{,}844</math> || <math>0{,}705</math> || <math>0{,}019</math> || <math>0{,}088</math>  || <math>0{,}838</math>    || <math>-0{,}003</math>
-|-
+|-style="text-align:center;"
 |    CLA              || <math>0{,}094</math>              || <math>0{,}072</math>              || <math>-0{,}033</math>             || <math>0{,}829</math> || <math>0{,}757</math> || <math>0{,}021</math> || <math>0{,}086</math>  || <math>0{,}828</math> || <math>-0{,}009</math>
-|-
+|-style="text-align:center;"
 |    CLM              || <math>0{,}092</math>              || <math>0{,}071</math>              || <math>-0{,}034</math>             || <math>0{,}834</math> || <math>0{,}777</math> || <math>0{,}021</math> || <math>0{,}084</math>  || <math>0{,}813</math> || <math>-0{,}008</math>
-|-
+|-style="text-align:center;"
 |    NCL              || <math>0{,}091</math>              || <math>0{,}068</math>              || <math>-0{,}031</math>             || <math>0{,}843</math> || <math>0{,}777</math> || <math>0{,}021</math> || <math>0{,}084</math>  || <math>0{,}840</math> || <math>-0{,}008</math>
-|-
+|-style="text-align:center;"
 |    CTE              || <math>0{,}105</math>              || <math>0{,}079</math>              || <math>-0{,}022</math>             || <math>0{,}786</math> || <math>0{,}484</math> || <math>0{,}017</math> || <math>0{,}093</math>  || <math>0{,}684</math> || <math>-0{,}033</math>
 |}
-A análise da Figura 1 e das Tabelas 1 e 2 leva a diversas conclusões. Primeiramente, note que as 4 primeiras parametrizações têm desempenhos praticamente iguais. É virtualmente impossível escolher uma parametrização "vencedora".
+A análise da [[#img-1|Figura 1]] e das [[#tab-1|Tabelas 1]] e [[#tab-2|2]] leva a diversas conclusões. Primeiramente, note que as 4 primeiras parametrizações têm desempenhos praticamente iguais. É virtualmente impossível escolher uma parametrização mais adequada.
 Embora haja duas variáveis físicas além de <math>u_*</math> na Eq. (10), <math>g</math> é constante, e <math>\nu_{\tau}</math> é
 praticamente constante. Isso significa que, na prática, a única variável que efetivamente funciona como preditora de <math>z_0</math> é
-<math>u_*</math>. Entretanto, parametrizações tão diversas quanto CHA e NCL (com expoentes de <math>u_*</math> iguais a 2 e a 3{,}89; vide Tabela
+<math>u_*</math>. Entretanto, parametrizações tão diversas quanto CHA e NCL (com expoentes de <math>u_*</math> iguais a 2 e a 3{,}89; vide [[#tab-1|Tabela 1]]) produzem essencialmente as mesmas estatísticas de erros. Somos levados a concluir que <math>z_0</math> depende apenas fracamente de <math>u_*</math>.
-) produzem essencialmente as mesmas estatísticas de erro. Somos levados a concluir que <math>z_0</math> depende apenas fracamente de <math>u_*</math>.
 Por sua vez, isso levanta a questão: será melhor utilizar um <math>z_0</math>
 constante, independente de <math>u_*</math>? Será possível que a utilização de
 parametrizações dependentes de <math>u_*</math> esteja ''piorando'' as
-estimativas de <math>u_*</math>?  Como se pode ver na 5\ira\ linha da Tabela 2, isso não é verdade: a parametrização para uma
+estimativas de <math>u_*</math>?  Como se pode ver na 5\ira\ linha da [[#tab-2|Tabela 2]], isso não é verdade: a parametrização para uma
 rugosidade constante conduz a erros maiores do que os encontrados para
 as 4 primeiras parametrizações. Mesmo assim, a parametrização CTE leva
@@ Line 379: / Line 385: @@
 considerado representativo da rugosidade da superfície da água para o
 sítio experimental, é dez vezes maior do que o reportado por
-Brutsaert [22] para superfícies líquidas, que é de
+Brutsaert [39] para superfícies líquidas, que é de
 <math>0{,}0002\,\mathrm{m}</math>.
 Outra observação importante é a comparação dos parâmetros ótimos
-obtidos para CHA e para CLM na Tabela 1: uma rápida
+obtidos para CHA e para CLM na [[#tab-1|Tabela 1]]: uma rápida
 inspeção mostra que, na verdade, o algoritmo de otimização encontrou,
 essencialmente, a mesma forma da equação de Charnock. De fato, além de
-<math>\nu_\tau</math> já ser praticamente constante, o seu expoente <math>a</math> é muito
+<math>\nu_\tau</math> já ser praticamente constante, o seu expoente <math>a</math> é muito pequeno (<math>0{,}015</math>); o expoente de <math>u_*</math>, <math>1{,}908</math>, é praticamente igual ao 2 da equação de Charnock, e o expoente de <math>g</math>, <math>-0,969</math>, também é muito próximo ao <math>-1</math> da equação de Charnock. Portanto, na prática CLM é quase igual à equação de Charnock com um valor de <math>\alpha = 14{,}386 - 15{,}050\times(\nu_\tau)^{0{,}015}=1{,}631</math> (para um <math>\nu_\tau=1{,}62 \times 10^{-5}\,\mathrm{m\,s^{-2}}</math> médio dos dados), que não difere tanto do parâmetro ótimo para a equação de Charnock "pura", que é <math>0{,}3863</math>. Note que CLM é a parametrização que utiliza o maior número de
-pequeno (0,030); o expoente de <math>u_*</math>, 1,908, é praticamente igual ao 2
-da equação de Charnock, e o expoente de <math>g</math>, <math>-0,969</math>, também é muito
-próximo ao <math>-1</math> da equação de Charnock. Portanto, na prática CLM é
-quase igual à equação de Charnock com um valor de <math>\alpha = 3{,}830 -
-{,}995\times(\nu_\tau)^{0{,}030}=0{,}980</math> (para um <math>\nu_\tau=1{,}62 \times
-^{-5}\,\mathrm{m\,s^{-2}}</math> médio dos dados), que não difere tanto do
-parâmetro ótimo para a equação de Charnock "pura", que é
-,3824. Note que CLM é a parametrização que utiliza o maior número de
 parâmetros, e que isso se reflete em um desempenho marginalmente
-melhor para algumas estatísticas da Tabela 2. Dadas
+melhor para algumas estatísticas da [[#tab-2|Tabela 2]]. Dadas
 as diferenças muito pequenas encontradas, entretanto, é altamente
 questionável a utilização de CLM. Entre outras coisas, isso mostra que
 o ganho obtido com o termo em que aparece <math>\beta</math> na Eq. (10) é muito
 pequeno.
+É importante observar que o sinal da estabilidade atmosférica possui um efeito razoável
+tanto sobre os valores dos parâmetros encontrados quanto sobre as estatísticas de erro. A
+[[#tab-3|Tabela 3]] mostra os valores ótimos de <math>\alpha</math> e <math>\beta</math> de CLA para 3 situações: todos os dados, dados estáveis
+(<math>\zeta_r \geq 0 </math>) e dados instáveis (<math>\zeta_r < 0 </math>). A inclusão de (<math>\zeta_r = 0 </math>) na classe dos dados estáveis é meramente convencional, já que esse valor exato nunca ocorre na prática. Já a [[#tab-4|Tabela 4]] mostra os erros para esses 3 casos (note que a primeira linha de cada uma dessas tabelas é uma repetição das linhas correspondentes nas [[#tab-1|Tabelas 1]] e [[#tab-2|2]]).
+Apresenta-se apenas os resultados para CLA porque eles são bastante representativos do
+que ocorre (em termos de dependência da estabilidade atmosférica) com todas as demais
+parameterizações, e porque ela é a parametrização utilizada na próxima seção, que trata da parametrização da rugosidade para vapor d’água. Note que os parâmetros em condições
+estáveis são bastante diferentes, mas o resultado em termos de erros varia muito menos.
+De modo geral, os erros em condições estáveis são um pouco maiores e os erros em
+condições instáveis são um pouco menores do que os erros para o conjunto de todos os
+dados.
+<div id='tab-3'></div>
+<div class="center" style="font-size: 75%;">'''Tabela 3'''. Parâmetros ótimos obtidos para cada parametrização da CLA de <math>z_0</math>, em função da estabilidade atmosférica <math>\zeta_r</math></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:30%;"
+|-style="text-align:center;"
+! Estabilidade !! <math>\alpha</math> !! <math>\beta</math>
+|-style="text-align:center;"
+| Todas                      ||       <math>0{,}5308</math> ||   <math>-12{,}92</math>
+|-style="text-align:center;"
+| <math>\zeta \geq 0 </math> ||       <math>1{,}7731</math> ||   <math>-188{,}23</math>
+|-style="text-align:center;"
+| <math>\zeta < 0 </math>    ||       <math>0{,}3980</math> ||   <math>-11{,}937</math>
+|}
+<div id='tab-4'></div>
+<div class="center" style="font-size: 75%;">'''Tabela 4'''. Estatísticas de erros de <math>u_*</math> para a parametrização CLA de <math>z_0</math>, em função da estabilidade atmosférica <math>\zeta_r</math></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:30%;"
+|-style="text-align:center;"
+!    Estabilidade !! REMQ   !! EMA    !! VIÉS  !! <math>a_0</math> !! <math>r</math> !! <math>s_a</math> !! <math>s_y</math> !! <math>a_1</math> !! <math>a_2</math>
+|-style="text-align:center;"
+!                   !! <math>\mathrm{m\,s^{-1}}</math> !! <math>\mathrm{m\,s^{-1}}</math> !! <math>\mathrm{m\,s^{-1}}</math> !!   !!    !!   !! <math>\mathrm{m\,s^{-1}}</math> !!      !! <math>\mathrm{m\,s^{-1}}</math>
+|-style="text-align:center;"
+|    Todas               || <math>0{,}094</math>              || <math>0{,}072</math>              || <math>-0{,}033</math> || <math>0{,}829</math> || <math>0{,}757</math> ||      <math>0{,}021</math> || <math>0{,}086</math>  || <math>0{,}828</math>    || <math>-0{,}009</math>
+|-style="text-align:center;"
+| <math>\zeta_{r} \geq 0 </math>  || <math>0{,}109</math>  || <math>0{,}084</math>              || <math>-0{,}049</math> || <math>0{,}799</math> || <math>0{,}751</math> ||      <math>0{,}029</math> || <math>0{,}096</math>  || <math>0{,}745</math>    || <math>-0{,}002</math>
+|-style="text-align:center;"
+| <math>\zeta_{r} < 0 </math>  || <math>0{,}066</math>  || <math>0{,}048</math>              || <math>-0{,}019</math> || <math>0{,}892</math> || <math>0{,}840</math> ||      <math>0{,}029</math> || <math>0{,}062</math>  || <math>0{,}898</math>    || <math>-0{,}002</math>
+|}
 Finalmente, uma última observação muito importante: em consonância com
 o alto valor médio de <math>z_0</math> encontrado para a parametrização CTE, os
-valores de <math>\alpha</math> e <math>\beta</math> de CLA são ''muito maiores'' do que
+valores de <math>\alpha</math> e <math>\beta</math> de CLA são ''muito maiores'' em módulo do que os valores típicos para o oceano. Compare <math>\alpha = 0{,}5308</math> com o valor de <math>\alpha = 0{,}011</math> da literatura, e <math>\beta = -12{,}92</math> com <math>0{,}135</math>.
-os valores típicos para o oceano. Compare <math>\alpha = 0{,}5059</math> com o
-valor de 0.011 da literatura, e <math>\beta = -10{,}33</math> com <math>0.135</math>.
 O valor ótimo de <math>\alpha </math> encontrado no presente
 trabalho é cerca de uma ordem de grandeza maior que o usual para corpos de água
 profundos. Esse valor no entanto é coerente com alguns trabalhos realizados em
 águas rasas presentes na literatura.  Por exemplo os trabalhos de
-Hsu [41], Geernaert et al. [42] e Smith [43] que observaram um
+Hsu [40], Geernaert et al. [41] e Smith [14] que observaram um
 aumento de <math>u_*</math> relacionada à profundidade do corpo de água e
 Shabani et al. [19] que mediram <math>u_*</math> em uma zona de arrebentação de ondas
 e obtiveram um valor médio de <math>\alpha</math> da ordem de <math>10^{-1}</math>.
 ===4.2 Parametrização do fluxo de calor latente ===
 Para testar os modelos para o fluxo de vapor de água foram utilizadas medições
@@ Line 427: / Line 463: @@
 As parametrizações testadas foram as seguintes, todas baseadas na Eq. (20):
-'''BRT''' Este é o modelo originalmente proposto por Brutsaert [9] (expressão (20) com <math>C_R^{1/2} = 7</math>, <math>d = 1/4</math> e <math>\text{Cd}_0=5</math>).
+'''BRT'''. Este é o modelo originalmente proposto por Brutsaert [9] (expressão (20) com <math>C_R^{1/2} = 7</math>, <math>d = 1/4</math> e <math>\text{Cd}_0=5</math>).
-'''BRM''' (``Brutsaert modificado''). Otimizamos <math>C_R</math>, mantendo <math>d=1/4</math>.
+'''BRM''' ("Brutsaert modificado"). Otimizamos <math>C_R</math>, mantendo <math>d=1/4</math>.
-'''SOL''' (``Soloviev''). Forçamos <math>d=0</math> e otimizamos <math>C_R</math>.
+'''SOL''' ("Soloviev"). Forçamos <math>d=0</math> e otimizamos <math>C_R</math>.
-'''GEN''' (``Modelo generalizado''). Otimizamos <math>C_R</math> e <math>d</math>.
+'''GEN''' ("Modelo generalizado"). Otimizamos <math>C_R</math> e <math>d</math>.
 O valor estimado do fluxo de calor latente, <math>\widehat{LE}</math>, foi obtido por meio
@@ Line 440: / Line 476: @@
 todos os casos, o calor latente de evaporação, <math>L</math> foi calculado à temperatura
 da superfície da água. O valor de rugosidade para vapor d'água, <math>z_{0E}</math>, foi
-estimado com as Eqs. (14) - (15), mantendo <math>\text{Cd}_0^{-1/2} = 5</math> (tentativas de otimizar também este parâmetro
+estimado com as Eqs. (14)-(15), mantendo <math>\text{Cd}_0^{-1/2} = 5</math> (tentativas de otimizar também este parâmetro
 produziram estimativas de parâmetros com valores muito grandes; note que
 <math>\text{Da}_0</math> e <math>\text{Cd}_0</math> se somam dentro do argumento da expoencial, e que
@@ Line 455: / Line 491: @@
 EMA, o VIÉS, e os valores de <math>a_0</math>, <math>r</math>, <math>s_y</math>, <math>s_a</math>, <math>a_1</math>
 e <math>a_2</math>, exceto que as regressões são, agora,
 {| class="formulaSCP" style="width: 100%; text-align: left;"
 |-
@@ Line 475: / Line 512: @@
 onde <math>\widehat{LE}</math> é a estimativa do fluxo de calor latente obtida em
 cada parametrização e <math>LE</math> é o fluxo de calor latente medido. As
-figuras 2-a - 2-d mostram os resultados obtidos
+[[#img-2|Figuras 2]]a-2d mostram os resultados obtidos
-para cada uma das 4 parametrizações. A Tabela 3 lista os
+para cada uma das 4 parametrizações. A [[#tab-5|Tabela 5]] lista os
-valores de <math>C_R^{-1}</math> e <math>d</math> encontrados em cada caso, e a Tabela 4 exibe as estatísticas de erros para cada
+valores de <math>C_R^{-1}</math> e <math>d</math> encontrados em cada caso, e a [[#tab-6|Tabela 6]] lista as estatísticas de erros correspondentes.
-parametrização de <math>z_{0E}</math>.
+<div id='img-2'></div>
+{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: 80%;"
+|-
+| [[File:Review_220770795596_9269_fig02.jpg|650px]]
+|- style="text-align: center; font-size: 75%;"
+| colspan="1" style="padding-bottom:10px;"| '''Figura 2'''. Valores previstos (no eixo vertical) contra observados (no eixo horizontal) de <math>LE</math> para 4 parametrizações testadas de <math>z_{0E}</math>: (a) BRT. (b) BRM. (c) SOL. (d) GEN. A linha contínua é a reta <math>\hat{LE} = LE</math> (indicando concordância perfeita) e a linha tracejada é a linha ajustada pelo método de Siegel (Equação (22); parâmetros <math>a_{1}</math> e <math>a_{2}</math> na [[#tab-6|Tabela 6]]
+|}
-[[File:Draft_Armani_989287210_1920_fig02.jpg]]
+<div id='tab-5'></div>
+<div class="center" style="font-size: 75%;">'''Tabela 5'''. Parâmetros ótimos obtidos para cada parametrização de <math>z_{0E}</math> (para a parametrização BRT, os valores são de literatura)</div>
-Figura 2: Valores previstos (no eixo vertical) contra observados (no eixo horizontal) de <math>LE</math> para 4 parametrizações testadas de <math>z_{0E}</math>: (a) BRT; (b) BRM; (c) SOL; e (d) GEN. A linha contínua é a reta 1:1, e a linha tracejada é a linha ajustada pelo método de Siegel.
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:30%;"
+|-style="text-align:center;"
-Tabela 3: Parâmetros ótimos obtidos para cada parametrização de <math>z_{0}</math> (para a parametrização BRT, os valores são de literatura).
-{| class="wikitable"
-|-
 ! Parametrização !! <math>C_R^{-1}</math> !! <math>d</math>
-|-
+|-style="text-align:center;"
 |    BRT || <math>7{,}3</math>   || <math>0{,}25</math>
-|-
+|-style="text-align:center;"
 |    BRM || <math>17{,}43</math> || <math>0{,}25</math>
-|-
+|-style="text-align:center;"
 |    SOL || <math>49{,}45</math> || <math>0{,}00</math>
-|-
+|-style="text-align:center;"
 |    GEN || <math>58{,}31</math> || <math>-0{,}037</math>
 |}
-Tabela 4: Estatísticas de erros para cada parametrização de <math>z_{0E}</math>.
-{| class="wikitable"
+<div id='tab-6'></div>
-|-
+<div class="center" style="font-size: 75%;">'''Tabela 6'''. Estatísticas de erros de LE para cada parametrização de <math>z_{0E}</math></div>
+{| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:30%;"
+|-style="text-align:center;"
 !    Parametrização !! REMQ   !! EMA    !! VIÉS  !! <math>a_0</math> !! <math>r</math> !! <math>s_a</math> !! <math>s_y</math> !! <math>a_1</math> !! <math>a_2</math>
-|-
+|-style="text-align:center;"
-!                   !! <math>\mathrm{m\,s^{-1}}</math> !! <math>\mathrm{m\,s^{-1}}</math> !! <math>\mathrm{m\,s^{-1}}</math> !!   !!    !!   !! <math>\mathrm{m\,s^{-1}}</math> !!      !! <math>\mathrm{m\,s^{-1}}</math>
+!                   !! <math>\mathrm{W\,m^{-2}}</math> !! <math>\mathrm{W\,m^{-2}}</math> !! <math>\mathrm{W\,m^{-2}}</math> !!   !!    !!   !! <math>\mathrm{W\,m^{-2}}</math> !!      !! <math>\mathrm{W\,m^{-2}}</math>
-|-
+|-style="text-align:center;"
 |    BRT              || <math>81{,}04</math>   || <math>53{,}25</math>     || <math>-32{,}86</math>   || <math>1{,}207</math> || <math>0{,}562</math> || <math>0{,}034</math> || <math>78{,}39</math>  || <math>1{,}092</math> || <math>11{,}87</math>
-|-
+|-style="text-align:center;"
 |    BRM              || <math>57{,}00</math>   || <math>35{,}71</math>     || <math>-05{,}30</math>   || <math>0{,}714</math> || <math>0{,}301</math> || <math>0{,}019</math> || <math>49{,}43</math>  || <math>0{,}645</math> || <math>16{,}09</math>
-|-
+|-style="text-align:center;"
 |    SOL              || <math>50{,}76</math>   || <math>32{,}56</math>     || <math>-11{,}81</math>   || <math>0{,}737</math> || <math>0{,}655</math> || <math>0{,}021</math> || <math>43{,}52</math>  || <math>0{,}651</math> || <math>07{,}15</math>
-|-
+|-style="text-align:center;"
 |    GEN              || <math>50{,}63</math>   || <math>32{,}80</math>     || <math>-13{,}33</math>   || <math>0{,}736</math> || <math>0{,}679</math> || <math>0{,}021</math> || <math>43{,}33</math>  || <math>0{,}638</math> || <math>05{,}21</math>
 |}
@@ Line 522: / Line 565: @@
 reunir argumentos físicos, e em particular argumentos relacionados com
 a transferência de vapor d'água sobre uma superfície líquida natural,
-para explicá-lo. Mesmo com otmização de <math>C_R</math>, o expoente <math>d=1/4</math> que
+para explicá-lo. Mesmo com otmização de <math>C_R</math>, o expoente <math>d=1/4</math> que também aparece na parametrização BRM não leva aos melhores resultados.
-também aparece na parametrização BRM não leva aos melhores resultados.
 As parametrizações SOL e GEN, que possuem <math>d=0</math> ou próximo disso, foram as que
@@ Line 538: / Line 580: @@
 <math>d=0</math>, e utilizar a parametrização SOL.
+==5. Conclusões==
-==5 Conclusões==
 No presente trabalho foram testadas algumas parametrizações para os comprimentos
-de rugosidade de ''momentum'' e vapor de água em lagos.  Os dados
+de rugosidade de ''momentum'' e vapor de água em lagos.
-apresentados neste trabalho foram obtidos em uma campanha realizada no
-resevatório de Itaipu, no município de Missal.  As expressões para o comprimento
-de rugosidade de ''momentum'' (<math>z_0</math>) testadas e calibradas neste trabalho
-são generalizações da expressão clássica de Charnock [11]. Já a
-expressão do comprimento de rugosidade de vapor de água (<math>z_{0E}</math>) pode ser
-vista como uma generalização da expressão clássica apresentada em
-Brutsaert [8].
 Com relação a <math>z_0</math> a comparação dos diferentes modelos leva a conclusão que
-<math>u_*</math> tem pouca capacidade preditiva do mesmo. Isso se dá porque modelos com
+<math>u_*</math> tem pouca capacidade preditiva do mesmo. Isso ocorre porque modelos com
 expoentes muito diferentes de <math>u_*</math> fornecem estatísticas de erro muito
 similares. O modelo que resulta em um maior erro é considerar <math>z_0</math> constante;
@@ Line 561: / Line 593: @@
 função de <math>u_*</math>) foram consideravelmente diferentes dos valores usuais para
 corpos de água profundos; o valor ótimo do parâmetro de Charnock <math>\alpha =
-{,}3862</math> encontrado é também uma ordem de grandeza maior que em oceanos. Esse
+{,}3863</math> encontrado é também uma ordem de grandeza maior que em oceanos. Esse
-resultado está de acordo com o valor sugerido em Shabani et al. [19] para
+resultado está de acordo com o valor sugerido em Shabani et al. [18] para
-medições realizadas em uma zona de arrebentação de ondas.
+medições realizadas em uma zona de arrebentação de ondas, e também com o comentário de Smith [14] de que o parâmetro de Charnock é maior em regiões costeiras onde as ondas mais íngremes parecem produzir rugosidades maiores.
 Com relação a <math>z_{0E}</math> foi observado que o modelo clássico BRT com a constante
@@ Line 574: / Line 606: @@
 foram os independentes do número de Reynolds de rugosidade.  Do ponto de vista
 prático podemos concluir que a parametrização SOL com o coeficiente de
-calibração <math>C_R^{-1} = 49{,}45 </math> gerou os melhores resultados. Note que esse coeficiente de
+calibração <math>C_R^{-1} = 49{,}45 </math> gerou os melhores resultados. Note que esse coeficiente de calibração é maior que o sugerido por Soloviev et. al. [31] que é <math>C_R^{-1} = 13{,}3</math>.
-calibração é maior que o sugerido por
-Soloviev e Schlüssel [33] que é <math>C_R^{-1} = 13{,}3
-</math>.
 Os resultados obtidos neste estudo indicam que a parametrização de Charnock para
@@ Line 588: / Line 617: @@
 localidades para essa questão ser sanada.
+É importante notar também que durante o período analisado a ilha da estação de medição estava praticamente coberta por água. Com isso, a própria ilha não representava um obstáculo aerodinâmico, o que foi um importante critério de qualidade dos dados analisados. No entanto, isso também limitou a análise a um período específico do ano. Embora a época do ano e as condições sinóticas não influenciem diretamente as parametrizações de rugosidade, efeitos indiretos podem ser importantes, porque tanto a direção quanto a velocidade do vento podem ter impacto sobre a formação de ondas e consequentemente sobre (pelo menos) a rugosidade para a quantidade de movimento. Estudos adicionais serão necessários para levar em conta esses efeitos indiretos.
+==Referências==
+<div class="auto" style="text-align: left;width: auto; margin-left: auto; margin-right: auto;font-size: 85%;">
+[1] Mahrer Y., Assouline S. Evaporation from lake kinneret: 2. estimation of
+the horizontal variability using a two-dimensional numerical mesoscale model.
+Water. Resour. Res., 29:911–916, 1993.
-==6 References<!--[1] Author, A. and Author, B. (Year) Title of the article. Title of the Publication. Article code. Available: http://www.scipedia.com/ucode.
+[2] Heikinheimo M., Kangas M., Tourola T., Venalainen A., Tattari S. Momentum
-[2] Author, A. and Author, B. (Year) Title of the article. Title of the Publication. Volume number, first page-last page.
-[3] Author, C. (Year). Title of work: Subtitle (edition.). Volume(s). Place of publication: Publisher.
-[4] Author of Part, D. (Year). Title of chapter or part. In A. Editor & B. Editor (Eds.), Title: Subtitle of book (edition, inclusive page numbers). Place of publication: Publisher.
-[5] Author, E. (Year, Month date). Title of the article. In A. Editor, B. Editor, and C. Editor. Title of published proceedings. Paper presented at title of conference, Volume number, first page-last page. Place of publication.
-[6] Institution or author. Title of the document. Year. [Online] (Date consulted: day, month and year). Available: http://www.scipedia.com/document.pdf.
--->==
-[1] Y. Mahrer and S. Assouline, Evaporation from lake kinneret: 2. estimation of
-the horizontal variability using a two-dimensional numerical mesoscale model,
-Water Resour Res, vol. 29, no. 4, pp. 911–916, 1993. Available:
-http://dx.doi.org/10.1029/92WR02433
-[2] M. Heikinheimo, M. Kangas, T. Tourola, A. Venalainen, and S. Tattari, Momentum
 and heat fluxes over lakes tamnaren and raksjo determined by the bulk-aerodynamic
-and eddy-correlation methods, Agric For Meteorol, vol. 98–99, pp. 521–534, 1999.
+and eddy-correlation methods. Agric. For. Meteorol., 98:521–534, 1999.
-[3] J. Kelman, R. Kelman, and M. V. F. Pereira, Energia firme de sistemas hidrelétricos
+[3] Kelman J., Kelman R., Pereira M.V.F. Energia firme de sistemas hidrelétricos
-e usos múltiplos dos recursos hídricos, Rev Bras Rec Hídr, vol. 9, no. 1, pp. 189–
+e usos múltiplos dos recursos hídricos. Rev. Bras. Rec. Hídr., 9:189–198, 2004.
-, 2004.
-[4] C. Thomas, J. Martin, M. Goeckede, M. Siqueira, T. Foken, B. Law, H. Loescher,
+[4] Thomas C., Martin J., Goeckede M., Siqueira M., Foken T., Law B., Loescher H.,
-and G. Katul, Estimating daytime subcanopy respiration from conditional sampling
+Katul G. Estimating daytime subcanopy respiration from conditional sampling
-methods applied to multi-scalar high frequency turbulence time series, Agric For
+methods applied to multi-scalar high frequency turbulence time series. Agric. For
-Meteorol, vol. 148, pp. 1210–1229, 2008.
+Meteorol., 148:1210–1229, 2008.
-[5] M. Siqueira and G. Katul, A sensitivity analysis of the nocturnal boundary-layer
+[5] Siqueira M., Katul G. A sensitivity analysis of the nocturnal boundary-layer
-properties to atmospheric emissivity formulations, Boundary-Layer Meteorol, vol.
+properties to atmospheric emissivity formulations. Boundary-Layer Meteorol., 2:223–242, 2010.
-, no. 2, pp. 223–242, 2010. Available: http://dx.doi.org/10.1007/
-s10546-009-9440-0
-[6] M. R. Raupach and A. S. Thom, Turbulence in and above plant canopies, Annu Rev
+[6] Raupach M.R., Thom A.S. Turbulence in and above plant canopies. Annu. Rev.
-Fluid Mech, vol. 13, no. 1, pp. 97–129, 1981.
+Fluid Mech., 13:97–129, 1981.
-[7] W. Brutsaert, A model for evaporation as a molecular diffusion process into a tur-
+[7] Brutsaert W. A model for evaporation as a molecular diffusion process into a turbulent atmosphere. J. Geophys. Res., 70:5017–5024, 1965.
-bulent atmosphere, J Geophys Res, vol. 70, pp. 5017–5024, 10 1965.
-[8] W. Brutsaert, A theory for local evaporation (or heat transfer) from rough and smooth sur-
+[8] Brutsaert W. A theory for local evaporation (or heat transfer) from rough and smooth surfaces at ground level. Water. Resour. Res., 11:543–550, 1975.
-faces at ground level, Water Resour Res, vol. 11, pp. 543–550, 1975.
-[9] W. Brutsaert, The roughness length for water vapor, sensible heat and other scalars, J Atmos
+[9] Brutsaert W. The roughness length for water vapor, sensible heat and other scalars. J. Atmos.
-Sci, vol. 32, pp. 2028–2031, 1975.
+Sci., 32:2028–2031, 1975.
-[10] P. V. Danckwerts, Signficance of liquid-film coefficients in gas absorption, Ind Eng
+[10] Danckwerts P.V. Signficance of liquid-film coefficients in gas absorption. Ind. Eng.
-Chem, vol. 43, pp. 1460–1467, 1951.
+Chem., 43:1460–1467, 1951.
-[11] H. Charnock, Wind stress on a water surface, Q J R Meteorol Soc, vol. 81, pp.
+[11] Charnock H. Wind stress on a water surface. Q. J. R. Meteorol. Soc., 81:639–640, 1955.
-–640, 1955.
-[12] S. Smith, Wind stress and heat flux over the ocean in gale force winds, J. Phys.
+[12] Charnock H. A note on empirical wind-wave formulae. Quarterly Journal of the Royal Meteorological Society, 84:443–447, 1958.
-Ocean., vol. 10, pp. 709–726, 1980.
-[13] M. W. Stacey, Simulation of the wind-forced near-surface circulation in knight inlet:
+[13] Smith S. Wind stress and heat flux over the ocean in gale force winds. J. Phys.
-A parameterization of the roughness length, J Phys Oceanogr, vol. 29, pp. 1363–
+Ocean., 10:709–726, 1980.
-, 1999.
-[14] W. G. Large and S. Pond, Open ocean momentum flux measurements in moderate
+[14] Smith S. Coefficients for sea surface wind stress, heat flux, and wind profiles as a function of wind speed and temperature. J. Geophys. Res-Oceans, 93:467–472, 1988.
-to strong winds, J Phys Oceanogr, vol. 11, pp. 324–336, 1981.
-[15] S. D. Smith, Coefficients for sea surface wind stress, heat flux, and wind profiles
+[15] Anctil F., Donelan M. Air-water momentum flux observations over shoaling waves. J. Phys. Oceanogr., 26:1344–1354, 1996.
-as a function of wind speed and temperatureicients for sea surface wind stress, heat
-flux, and wind profiles as a function of wind speed and temperature, J Geophys
-Res-Oceans, vol. 93, no. C12, pp. 15 467–15 472, 1988.
-[16] F. Anctil and M. Donelan, Air-water momentum flux observations over shoaling
+[16] Garratt J. Review of drag coefficients over oceans and continents. Mon. Wea. Rev., 105:915–929, 1977.
-waves, J Phys Oceanogr, vol. 26, pp. 1344–1354, 1996.
-[17] J. Garratt, Review of drag coefficients over oceans and continents, Mon Wea Rev,
+[17] Wu J. Wind-stress coefficients over sea surface near neutral conditions—a revisit.
-vol. 105, no. 7, pp. 915–929, 1977.
+J. Phys. Oceanogr., 10:727–740, 1980.
-[18] J. Wu, Wind-stress coefficients over sea surface near neutral conditions—a revisit,
+[18] Shabani B., Nielsen P., Baldock T. Direct measurements of wind stress over
-J Phys Oceanogr, vol. 10, no. 5, pp. 727–740, 1980.
+the surf zone. J. Geophys. Res., 119:2949–2973, 2014.
-[19] B. Shabani, P. Nielsen, and T. Baldock, Direct measurements of wind stress over
+[19] Verburg P., Antenucci J.P. Persistent unstable atmospheric boundary layer
-the surf zone, J Geophys Res-Oceans, vol. 119, pp. 2949–2973, 2014.
+enhances sensible and latent heat loss in a tropical great lake: Lake tanganyika. J.
+Geophys. Res. Atmos., 115:D11109, 2010.
-[20] P. Verburg and J. P. Antenucci, Persistent unstable atmospheric boundary layer
+[20] Dias N.L., Vissotto D. The effect of temperature-humidity similarity on
-enhances sensible and latent heat loss in a tropical great lake: Lake tanganyika, J
-Geophys Res-Atmos, vol. 115, no. D11, p. D11109, Jun 2010. Available:
-http://dx.doi.org/10.1029/2009JD012839
-[21] N. L. Dias and D. Vissotto, The effect of temperature-humidity similarity on
 bowen ratios, dimensionless standard deviations, and mass transfer coefficients over
-a lake, Hydrol Process, vol. 31, no. 2, pp. 256–269, 2017. Available:
+a lake. Hydrol. Process., 31:256–269, 2017.
-http://dx.doi.org/10.1002/hyp.10925
-[22] W. Brutsaert, Evaporation into the atmosphere.
+[21] Drennan W.M., Graber H.C., Hauser D., Quentin C. On the wave age dependence of wind stress over pure wind seas. J. Geophys. Res., 108:C3, 2003.
-Dordrecht: D. Reidel, 1982, 309 pp.
-[23] S. A. Kitaigorodskii and Y. A. Volkov, On the roughness parameter of the sea
+[22] Johnson H.K., Hojstrup J., Vested H.J., Larsen S.E. On the dependence of sea
-surface and the calculation of momentum flux in the near-water layer of the atmosphere,
+surface roughness on wind waves. J. Phys. Oceanogr., 28:1702–1716, 1998.
-Izv An Fiz Ok+, vol. 1, pp. 973–988, 1965.
-[24] N. Maat, C. Kraan, and W. Oost, The roughness of wind waves, Boundary-Layer
+[23] Kitaigorodskii S.A., Volkov Y.A. On the roughness parameter of the sea
-Meteorol, vol. 54, no. 1-2, pp. 89–103, 1991.
+surface and the calculation of momentum flux in the near-water layer of the atmosphere.
+Izv. Atm. Oceanic Phys., 1:973–988, 1965.
-[25] J. Monbaliu, On the use of the donelan wave spectral parameter as a measure for the
+[24] Maat N., Kraan C., Oost W. The roughness of wind waves. Boundary-Layer
-roughness of wind waves, Boundary-Layer Meteorol, vol. 67, no. 3, pp. 277–291,
+Meteorol., 54:89–103, 1991.
-.
-[26] D. Vickers and L. Mahrt, Fetch limited drag coefficients, Boundary-Layer Meteo-
+[25] Mascart P., Noilhan J., Giordani H. A modified parameterization of flux-profile
-rol, vol. 85, no. 1, pp. 53–79, 1997.
+relationships in the surface layer using different roughness length values for heat and
+momentum. Boundary-Layer Meteorol., 72:331–344, 1995.
-[27] H. K. Johnson, J. Hojstrup, H. J. Vested, and S. E. Larsen, On the dependence of sea
+[26] Monbaliu J. On the use of the donelan wave spectral parameter as a measure for the
-surface roughness on wind waves, J Phys Oceanogr, vol. 28, no. 9, pp. 1702–1716,
+roughness of wind waves. Boundary-Layer Meteorol., 67:277–291, 1994.
-.
-[28] P. Mascart, J. Noilhan, and H. Giordani, A modified parameterization of flux-profile
-relationships in the surface layer using different roughness length values for heat and
-momentum, Boundary-Layer Meteorol, vol. 72, pp. 331–344, 1995.
-[29] P. K. Taylor and M. J. Yelland, The dependence of sea surface roughness on the
+[27] Oost W., Komen G., Jacobs C., Van Oort C. New evidence for a relation
-height and steepness of the waves, J Phys Oceanogr, vol. 31, no. 2, pp. 572–590,
+between wind stress and wave age from measurements during asgamage. Boundary-Layer Meteorol., 103:409–438, 2002.
-.
-[30] W. Oost, G. Komen, C. Jacobs, and C. Van Oort, New evidence for a relation
+[28] Taylor P.K., Yelland M.J. The dependence of sea surface roughness on the
-between wind stress and wave age from measurements during asgamage, Boundary-
+height and steepness of the waves. J. Phys. Oceanogr., 31:572–590, 2001.
-Layer Meteorol, vol. 103, no. 3, pp. 409–438, 2002.
-[31] W. M. Drennan, H. C. Graber, D. Hauser, and C. Quentin, On the wave age depen-
+[29] Vickers D., Mahrt L. Fetch limited drag coefficients. Boundary-Layer Meteorol., 85:53–79, 1997.
-dence of wind stress over pure wind seas, J Geophys Res, vol. 108, no. C3, 2003.
-[32] A. Lorke and F. Peetres, Toward a unified scaling relation for interfacial fluxes, J
+[30] Lorke A., Peetres F. Toward a unified scaling relation for interfacial fluxes. J.
-Phys Oceanogr, vol. 36, no. 5, pp. 955–961, 2006.
+Phys. Oceanogr., 36:955–961, 2006.
-[33] A. V. Soloviev and P. Schlüssel, Parameterization of the cool skin of the ocean and
+[31] Soloviev A.V., Schlüssel P. Parameterization of the cool skin of the ocean and
-air-ocean gas transfer on the basis of modelling surface renewal, J Phys Oceanogr,
+air-ocean gas transfer on the basis of modelling surface renewal. J. Phys. Oceanogr.,
-vol. 24, pp. 1339–1347, 1994.
+:1339–1347, 1994.
-[34] G. T. Csanady, The role of breaking wavelets in air-sea gas transfer, J Geophys
+[32] Csanady G.T. The role of breaking wavelets in air-sea gas transfer. J. Geophys.
-Res, vol. 95, pp. 749–759, 1990.
+Res., 95:749–759, 1990.
-[35] E. K. Webb, G. I. Pearman, and R. Leuning, Correction of flux measurements for
+[33] Webb E.K., Pearman G.I., Leuning R. Correction of flux measurements for
-density effects due to heat and water vapor transfer, Q J Roy Meteorol Soc, vol. 106,
+density effects due to heat and water vapor transfer. Q. J. Roy. Meteorol. Soc., 106:85–100, 1980.
-pp. 85–100, 1980.
-[36] J. J. Finnigan, R. Clement, Y. Malhi, R. Leuning, and H. A. Cleugh, A re-evaluation
+[34] Finnigan J.J., Clement R., Malhi Y., Leuning R., Cleugh H.A. A re-evaluation
-of long-term flux measurement techniques part i: averaging and coordinate rotation,
+of long-term flux measurement techniques part I: averaging and coordinate rotation.
-Boundary-Layer Meteorol, vol. 107, pp. 1–48, 2003.
+Boundary-Layer Meteorol., 107:1–48, 2003.
-[37] E. Falge, D. Baldocchi, R. Olson, P. Anthoni, M. Aubinet, C. Bernhofer, G. Burba,
+[35] Falge E., Baldocchi D., Olson R., Anthoni P., Aubinet M., Bernhofer C., Burba G.,
-R. Ceulemans, R. Clement, H. Dolman, A. Granier, P. Gross, T. Gr?nwald, D. Hollinger, N.-O. Jensen,
+Ceulemans R., Clement R., Dolman H., Granier A., Gross P., Grenwald T., Hollinger D., Jensen N.O.,
-G. Katul, P. Keronen, A. Kowalski, C. T. Lai, B. E. Law, T. Meyers,
+Katul G., Keronen P., Kowalski A., Lai C.T., Law B.E., Meyers T.,
-J. Moncrieff, E. Moors, J. W. Munger, K. Pilegaard, . Rannik, C. Rebmann, A. Suyker,
+Moncrieff J., Moors E., Munger J.W., Pilegaard K., Rannik R., Rebmann C., Suyker A.,
-J. Tenhunen, K. Tu, S. Verma, T. Vesala, K. Wilson, and S. Wofsy, Gap filling
+Tenhunen J., Tu K., Verma S., Vesala T., Wilson K., Wofsy S. Gap filling
-strategies for long term energy flux data sets, Agric For Meteorol, vol. 107, pp.
+strategies for long term energy flux data sets. Agric. For Meteorol., 107:71–77, 2001
-–77, 2001.
-[38] C. W. Fairall, E. F. Bradley, and A. A. Grachev, Bulk parameterization of air sea
+[36] Fairall C.W., Bradley E.F., Grachev A.A. Bulk parameterization of air sea
-fluxes: Updates and verification, J Climate, vol. 16, no. 4, pp. 571–591, 2003.
+fluxes: Updates and verification. J. Climate, 16:571–591, 2003.
-[39] A. F. Siegel, Robust regression using repeated medians, Biometrika, vol. 69, no. 1,
+[37] Siegel A.F. Robust regression using repeated medians. Biometrika, 69:242–244, 1982.
-pp. 242–244, 1982.
-[40] A. Stein and M. Werman, Finding the repeated median regression line. in Procee-
+[38] Stein A., Werman M. Finding the repeated median regression line. Proceedings of the Third Symposium on Discrete Algorithms (SODA). Society for Industrial and Applied Mathematics (SIAM), 409–413, 1992.
-dings of the Third Symposium on Discrete Algorithms (SODA). Society for Industrial
-and Applied Mathematics (SIAM), 1992, pp. 409–413.
-[41] S. Hsu, A dynamic roughness equation and its application to wind stress determina-
+[39] Brutsaert W. Evaporation into the atmosphere. Dordrecht, D. Reidel, September 1982.
-tion at the air-sea interface. J Phys Oceanogr, vol. 4, pp. 116–120, 1974.
-[42] G. L. Geernaert, S. E. Larsen, and F. Hansen, Measurements of the wind stress, heat
+[40] Hsu S. A dynamic roughness equation and its application to wind stress determination at the air-sea interface. J. Phys. Oceanogr., 4:116–120, 1974.
-flux and turbulence intensity during storm conditions over the north sea, J Geophys
-Res, vol. 92, pp. 127–139, 1987.
-[43] S. Smith, Coefficients for sea surface wind stress, heat flux, and wind profiles as a
+[41] Geernaert G.L., Larsen S.E., Hansen F. Measurements of the wind stress, heat
-function of wind speed and temperature. J Geophys Res-Oceans, vol. 93, pp. 467–
+flux and turbulence intensity during storm conditions over the north sea. J. Geophys. Res., 92:127–139, 1987.
-, 1988.
+</div>

Latest revision as of 14:55, 1 March 2021

Resumo

Abstract

1. Introdução

2. Metodologia

2.1 Fluxos turbulentos e Teoria de Similaridade de Monin-Obukhov

2.2 A parametrização de z 0 {\displaystyle z_{0}} 2.2 A parametrização de z 0 {\displaystyle z {0}}

2.3 A parametrização de z 0 E {\displaystyle z_{0E}} 2.3 A parametrização de z 0 E {\displaystyle z {0E}}

3. Sítio experimental

4. Resultados e discussão

4.1 Fluxo de quantidade de movimento

4.2 Parametrização do fluxo de calor latente

5. Conclusões

Referências

Document information

Document Score

Share this document

Keywords

2.2 A parametrização de $z_{0}$ 2.2 A parametrização de z 0 {\displaystyle z {0}}

2.3 A parametrização de $z_{0E}$ 2.3 A parametrização de z 0 E {\displaystyle z {0E}}