| (6 intermediate revisions by the same user not shown) | |||
| Line 89: | Line 89: | ||
donde <math>{\delta }_i</math> es la profundidad de penetración de la señal electromagnética (electrodinámica clásica), <math>\omega </math> la frecuencia de la señal en radianes/segundo, <math>\mu </math> la permeabilidad magnética del espacio vacío y <math>{\mu }_r</math> la permeabilidad relativa del medio conductor. | donde <math>{\delta }_i</math> es la profundidad de penetración de la señal electromagnética (electrodinámica clásica), <math>\omega </math> la frecuencia de la señal en radianes/segundo, <math>\mu </math> la permeabilidad magnética del espacio vacío y <math>{\mu }_r</math> la permeabilidad relativa del medio conductor. | ||
| − | Para un volumen <math>\forall </math> cualquiera de material de conductor eléctrico, es notable que puede establecerse lo que llamamos generación de calor por unidad de volumen <math>g</math>; lo cual en forma diferencial queda estipulado según puede verse en la Figura 1 por: | + | Para un volumen <math>\forall </math> cualquiera de material de conductor eléctrico, es notable que puede establecerse lo que llamamos generación de calor por unidad de volumen <math>g</math>; lo cual en forma diferencial queda estipulado según puede verse en la [[#img-1|Figura 1]] por: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 101: | Line 101: | ||
|} | |} | ||
| − | donde <math>A</math> se diferencia de <math>A_{ei}</math>, al ser la primera un área geométrica (en caso de un cable como el de la Figura 1, es un área circular perfecta) y la segunda un área efectiva para el flujo de corriente eléctrica, determinada de acuerdo a la Ec.(2). | + | donde <math>A</math> se diferencia de <math>A_{ei}</math>, al ser la primera un área geométrica (en caso de un cable como el de la [[#img-1|Figura 1]], es un área circular perfecta) y la segunda un área efectiva para el flujo de corriente eléctrica, determinada de acuerdo a la Ec.(2). |
| + | <div id='img-1'></div> | ||
{| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | {| style="text-align: center; border: 1px solid #BBB; margin: 1em auto; width: auto;max-width: auto;" | ||
|- | |- | ||
| Line 111: | Line 112: | ||
| − | El calor es conducido de los puntos con mayor temperatura (medida potencial de calor) a aquellos con menor temperatura. Considerando que un caso de conductor eléctrico como cobre o aluminio, es también un excelente conductor de calor; no recapitularemos en tensores de transferencia de calor adentro del propio conductor, pues su temperatura en estado estable será aproximadamente la misma a lo largo del material conductor [19]. Las diferencias térmicas se verán del conductor al aislante y del aislante hacia el medio ambiente, por tanto, el flujo de calor será principalmente radial, como se muestra en la Figura 1. | + | El calor es conducido de los puntos con mayor temperatura (medida potencial de calor) a aquellos con menor temperatura. Considerando que un caso de conductor eléctrico como cobre o aluminio, es también un excelente conductor de calor; no recapitularemos en tensores de transferencia de calor adentro del propio conductor, pues su temperatura en estado estable será aproximadamente la misma a lo largo del material conductor [19]. Las diferencias térmicas se verán del conductor al aislante y del aislante hacia el medio ambiente, por tanto, el flujo de calor será principalmente radial, como se muestra en la [[#img-1|Figura 1]]. |
Para la parte conductiva del calor a través del aislante, podemos utilizar la ecuación unidimensional de conducción de calor de Fourier, con flujo de calor en dirección radial <math>r</math> [20]: | Para la parte conductiva del calor a través del aislante, podemos utilizar la ecuación unidimensional de conducción de calor de Fourier, con flujo de calor en dirección radial <math>r</math> [20]: | ||
| Line 127: | Line 128: | ||
donde <math>{\dot{q}}_r</math> es el calor total que fluye por unidad de tiempo a través del área transversal <math>A_{trans}</math>, <math>A_{trans}=2\pi r\cdot dz</math> el área transversal de flujo de calor (donde está el aislante), para una longitud de cable <math>dz</math>, <math>k_T</math> la conductividad térmica usualmente en <math>\left(\frac{Watt}{m\cdot {^\circ}K}\right)</math>. Se usará <math display="inline">k_{T-ins}</math> para referirse específicamente a la conductividad térmica del aislamiento. <math>r</math> es la variable radial lineal, que direcciona el flujo de calor. | donde <math>{\dot{q}}_r</math> es el calor total que fluye por unidad de tiempo a través del área transversal <math>A_{trans}</math>, <math>A_{trans}=2\pi r\cdot dz</math> el área transversal de flujo de calor (donde está el aislante), para una longitud de cable <math>dz</math>, <math>k_T</math> la conductividad térmica usualmente en <math>\left(\frac{Watt}{m\cdot {^\circ}K}\right)</math>. Se usará <math display="inline">k_{T-ins}</math> para referirse específicamente a la conductividad térmica del aislamiento. <math>r</math> es la variable radial lineal, que direcciona el flujo de calor. | ||
| − | Se puede resolver por separación de variables y agregando los límites que condicionan las fronteras que se muestran para el aislante en la Figura 1: | + | Se puede resolver por separación de variables y agregando los límites que condicionan las fronteras que se muestran para el aislante en la [[#img-1|Figura 1]]: |
{| class="formulaSCP" style="width: 100%; text-align: center;" | {| class="formulaSCP" style="width: 100%; text-align: center;" | ||
| Line 215: | Line 216: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math display="inline">\left(T_{co}-T_{\infty }\right)=\left[\displaystyle\frac{r_{co}^2ln\left(\displaystyle\frac{r_{ins}}{r_{co}}\right)}{2k_{T-ins}}+ | + | | <math display="inline">\left(T_{co}-T_{\infty }\right)=\left[\displaystyle\frac{r_{co}^2ln\left(\displaystyle\frac{r_{ins}}{r_{co}}\right)}{2k_{T-ins}}+ \displaystyle\frac{r_{co}{}^2}{2r_{ins}h_f}\right]g=\left[R_{term\_insulation}+ R_{term\_convection}\right]g</math> |
|} | |} | ||
| style="width: 5px;text-align: right;white-space: nowrap;" | (11) | | style="width: 5px;text-align: right;white-space: nowrap;" | (11) | ||
| Line 258: | Line 259: | ||
| <math>g=\displaystyle\frac{I^2\left({\rho }_0+{\rho }_0\cdot {\alpha }_{co}\left[T_{co}-T_0\right]\right)}{A\cdot A_{ei}}</math> | | <math>g=\displaystyle\frac{I^2\left({\rho }_0+{\rho }_0\cdot {\alpha }_{co}\left[T_{co}-T_0\right]\right)}{A\cdot A_{ei}}</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (14) |
|} | |} | ||
| Line 279: | Line 280: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{\rho }_o=1.7\times {10}^{-8}\left[\Omega \cdot m\right]</math> a la temperatura <math>T_0=23{^\circ}C</math> | + | | <math>{\rho }_o=1.7\times {10}^{-8}\left[\Omega \cdot m\right]</math> a la temperatura <math>T_0=23{^\circ}C\quad </math> [12] |
|} | |} | ||
| − | |||
|} | |} | ||
| Line 289: | Line 289: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{\alpha }_{co}=0.00323</math> a la temperatura <math>T=75{^\circ}C</math> | + | | <math>{\alpha }_{co}=0.00323</math> a la temperatura <math>T=75{^\circ}C\quad </math> [10] |
|} | |} | ||
| − | |||
|} | |} | ||
| Line 301: | Line 300: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | |<math>{\rho }_o=2.8\times {10}^{-8}\left[\Omega \cdot m\right]</math> a la temperatura <math>T_0=23{^\circ}C</math> | + | |<math>{\rho }_o=2.8\times {10}^{-8}\left[\Omega \cdot m\right]</math> a la temperatura <math>T_0=23{^\circ}C\quad </math> [12] |
|} | |} | ||
| − | |||
|} | |} | ||
| Line 311: | Line 309: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | <math>{\alpha }_{co}=0.00330</math> a la temperatura <math>T=75{^\circ}C</math> | + | | <math>{\alpha }_{co}=0.00330</math> a la temperatura <math>T=75{^\circ}C\quad </math> [10] |
|} | |} | ||
| − | |||
|} | |} | ||
| Line 319: | Line 316: | ||
En ambos casos los coeficientes de incremento térmico se utilizan a 75ºC para que los cálculos sean más aproximados en los rangos de temperatura de carga nominal de los conductores. De lo contrario se tendrían que utilizar <math>{\alpha }_{co}</math> como funciones de temperatura que no se tienen estipuladas actualmente, y existen muy pocos datos a temperaturas muy diferentes, como para estipular modelos continuos de confianza. | En ambos casos los coeficientes de incremento térmico se utilizan a 75ºC para que los cálculos sean más aproximados en los rangos de temperatura de carga nominal de los conductores. De lo contrario se tendrían que utilizar <math>{\alpha }_{co}</math> como funciones de temperatura que no se tienen estipuladas actualmente, y existen muy pocos datos a temperaturas muy diferentes, como para estipular modelos continuos de confianza. | ||
| − | Mientras más cercana esté la <math>T_{co}</math> que escogemos en la primera iteración a la <math>T_{co}</math> real final, es lógico que tendremos menos iteraciones. Pero para probar la viabilidad y rápida convergencia de este modelo, escogeremos nuestro primer <math>T_{co}</math> igual en valor a la temperatura ambiente. De forma analítica es necesario usar la Ec.(4) para calcular una aproximación a <math>g</math>, pero en forma práctica, al ser resuelto numéricamente, es suficiente con usar la reducción a la forma de la Ec.( | + | Mientras más cercana esté la <math>T_{co}</math> que escogemos en la primera iteración a la <math>T_{co}</math> real final, es lógico que tendremos menos iteraciones. Pero para probar la viabilidad y rápida convergencia de este modelo, escogeremos nuestro primer <math>T_{co}</math> igual en valor a la temperatura ambiente. De forma analítica es necesario usar la Ec.(4) para calcular una aproximación a <math>g</math>, pero en forma práctica, al ser resuelto numéricamente, es suficiente con usar la reducción a la forma de la Ec.(14). |
| − | Para el uso de la Ec.(4) o ( | + | Para el uso de la Ec.(4) o (14), se requiere calcular el valor para <math>h_f</math>, dependiente de varios parámetros físicos termodinámicos (en bases de datos), que son a su vez dependientes de la temperatura del aire que esta rodeando al cable, la cual se puede estimar como un promedio entre la temperatura del cable y la del ambiente. En nuestro caso, al ver la cantidad de recurso y memoria que consumen esas operaciones, hemos modelado los resultados de las bases de datos, por medio de ecuaciones continuas de regresiones polinomiales ajustadas a partir de [21], en la siguiente forma: |
Calculamos una temperatura promedio de la capa de aire que rodea al cable: | Calculamos una temperatura promedio de la capa de aire que rodea al cable: | ||
| Line 332: | Line 329: | ||
| <math>T_{film}=\left(\frac{T_{co}+T_{\infty }}{2}\right){^\circ}C</math> o <math>T_{film-{^\circ}K}=\left(\frac{T_{co}+T_{\infty }}{2}+ 273.15\right){^\circ}K</math> | | <math>T_{film}=\left(\frac{T_{co}+T_{\infty }}{2}\right){^\circ}C</math> o <math>T_{film-{^\circ}K}=\left(\frac{T_{co}+T_{\infty }}{2}+ 273.15\right){^\circ}K</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (15) |
|} | |} | ||
| Line 344: | Line 341: | ||
| <math>\beta =\frac{1}{T_{film-{^\circ}K}}</math> | | <math>\beta =\frac{1}{T_{film-{^\circ}K}}</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (16) |
|} | |} | ||
| Line 359: | Line 356: | ||
| <math>{\nu }_{air}=\mbox{(9}\mbox{.41}\times {\mbox{10}}^{-5}\mbox{T}_{film}^2\mbox{+8}\mbox{.731}\times {\mbox{10}}^{-2}\mbox{T}_{film}^{}\mbox{+13}{\mbox{.377)10}}^{-6}</math> | | <math>{\nu }_{air}=\mbox{(9}\mbox{.41}\times {\mbox{10}}^{-5}\mbox{T}_{film}^2\mbox{+8}\mbox{.731}\times {\mbox{10}}^{-2}\mbox{T}_{film}^{}\mbox{+13}{\mbox{.377)10}}^{-6}</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (17) |
|} | |} | ||
| Line 372: | Line 369: | ||
| <math>{\alpha }_{air}\mbox{=(1}\mbox{.5667}\times {\mbox{10}}^{-4}\mbox{T}_{film}^2\mbox{+0}{\mbox{.1269T}}_{film}^{}\mbox{+18}{\mbox{.1461)10}}^{-6}</math> | | <math>{\alpha }_{air}\mbox{=(1}\mbox{.5667}\times {\mbox{10}}^{-4}\mbox{T}_{film}^2\mbox{+0}{\mbox{.1269T}}_{film}^{}\mbox{+18}{\mbox{.1461)10}}^{-6}</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (18) |
|} | |} | ||
| Line 385: | Line 382: | ||
| <math>k_{T-air}\mbox{=(0}{\mbox{.07192T}}_{film}^{}\mbox{+23}{\mbox{.72169)10}}^{-3}</math> | | <math>k_{T-air}\mbox{=(0}{\mbox{.07192T}}_{film}^{}\mbox{+23}{\mbox{.72169)10}}^{-3}</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (19) |
|} | |} | ||
| Line 398: | Line 395: | ||
| <math>\mbox{Pr=5}\mbox{.19258}\times {\mbox{10}}^{-7}\mbox{T}_{film}^2\mbox{-3}\mbox{.05418}\times {\mbox{10}}^{-4}\mbox{T}_{film}^{}\mbox{+0}\mbox{.73662}</math> | | <math>\mbox{Pr=5}\mbox{.19258}\times {\mbox{10}}^{-7}\mbox{T}_{film}^2\mbox{-3}\mbox{.05418}\times {\mbox{10}}^{-4}\mbox{T}_{film}^{}\mbox{+0}\mbox{.73662}</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (20) |
|} | |} | ||
| Line 413: | Line 410: | ||
| Número de Rayleigh: <math>\quad Ra=\frac{g_T\beta \left(T_{ins}-T_{\infty }\right)D^3}{{\alpha }_{air}{\nu }_{air}}</math> | | Número de Rayleigh: <math>\quad Ra=\frac{g_T\beta \left(T_{ins}-T_{\infty }\right)D^3}{{\alpha }_{air}{\nu }_{air}}</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (21) |
|} | |} | ||
| Line 424: | Line 421: | ||
{| style="text-align: center; margin:auto;" | {| style="text-align: center; margin:auto;" | ||
|- | |- | ||
| − | | Número de Nusselt: <math>\quad Nu=\ | + | | Número de Nusselt: <math>\quad Nu=\left\{ 0.6+\frac{0.387Ra^{\frac{1}{6}}}{{\left[1+{\left(\frac{0.559}{Pr}\right)}^{\frac{9}{16}}\right]}^{\frac{8}{27}}}\right\}^2</math> |
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (22) |
|} | |} | ||
| Line 438: | Line 435: | ||
| <math>h_f=\frac{Nu\cdot k_{T-air}}{D}</math> | | <math>h_f=\frac{Nu\cdot k_{T-air}}{D}</math> | ||
|} | |} | ||
| − | | style="width: 5px;text-align: right;white-space: nowrap;" | ( | + | | style="width: 5px;text-align: right;white-space: nowrap;" | (23) |
|} | |} | ||
| Line 450: | Line 447: | ||
Presentamos primeramente un cable 500 MCM AWG de cobre, con aislante THHW operando con 620 amperios al aire libre, con una temperatura ambiental de 30ºC (condición para la cual está normado). Este cable es muy común en instalaciones americanas industriales y comerciales con alta intensidad de corriente. Su parte conductora es de cobre trenzado con 37 hebras de 2.95 mm de diámetro cada una y 253 mm<sup>2</sup> de sección transversal total efectiva de conducción, con aislante termoplástico resistente a calor, a humedad y retardante a la llama [10]. La frecuencia del sistema de alimentación es de 60 hercios, lo cual es usual en los sistemas industriales americanos (480 Volt – 3 fases – 60 Hz). | Presentamos primeramente un cable 500 MCM AWG de cobre, con aislante THHW operando con 620 amperios al aire libre, con una temperatura ambiental de 30ºC (condición para la cual está normado). Este cable es muy común en instalaciones americanas industriales y comerciales con alta intensidad de corriente. Su parte conductora es de cobre trenzado con 37 hebras de 2.95 mm de diámetro cada una y 253 mm<sup>2</sup> de sección transversal total efectiva de conducción, con aislante termoplástico resistente a calor, a humedad y retardante a la llama [10]. La frecuencia del sistema de alimentación es de 60 hercios, lo cual es usual en los sistemas industriales americanos (480 Volt – 3 fases – 60 Hz). | ||
| − | Los resultados del ejemplo indicado, luego de correr el algoritmo descrito con las ecuaciones de cálculo en Matlab [13], se presentan en la Tabla 1, considerando un valor inicial <math>T_{co}=30{^\circ}C</math>. | + | Los resultados del ejemplo indicado, luego de correr el algoritmo descrito con las ecuaciones de cálculo en Matlab [13], se presentan en la [[#tab-1|Tabla 1]], considerando un valor inicial <math>T_{co}=30{^\circ}C</math>. |
<div class="center" style="font-size: 75%;">'''Tabla 1'''. Resultados por pasos para el caso presentado de cable 500 MCM AWG THHW de cobre | <div class="center" style="font-size: 75%;">'''Tabla 1'''. Resultados por pasos para el caso presentado de cable 500 MCM AWG THHW de cobre | ||
</div> | </div> | ||
| − | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width: | + | <div id='tab-1'></div> |
| + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" | ||
| + | |-style="text-align:center" | ||
| + | ! Iter. !! <math>g</math> !! <math>\beta </math> !! <math>{\nu }_{air} \times 10^{-5}</math> !! <math>{\alpha }_{air} \times 10^{-5}</math> !! <math>k_{T-air}\times 10^{-2}</math> !! <math>\mbox{Pr}</math> !! |<math>Ra \times 10^{4}</math> !! <math>Nu</math> !! <math>h_f</math> !! <math>T_{co}</math> ºC !! <math>T_{ins}</math> ºC !! Err . <math>T_{co}</math> | ||
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 1 |
| − | | | + | | 61356.4 |
| − | | | + | | 0.0033 |
| − | | | + | | 1.608 |
| − | | | + | | 2.209 |
| − | | | + | | 2.588 |
| − | | | + | | 0.7279 |
| − | | | + | | 0 |
| − | | | + | | 0.3600 |
| − | | | + | | 0.3656 |
| − | | | + | | 736.1 |
| − | | | + | | 732.1 |
| − | | | + | | 706.1 |
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 2 |
| − | | | + | | 192456 |
| − | | | + | | 0.0015 |
| − | | | + | | 6.031 |
| − | | | + | | 8.925 |
| − | | | + | | 5.113 |
| − | | | + | | 0.6956 |
| − | | | + | | 3.232 |
| − | | | + | | 5.8101 |
| − | | | + | | 11.658 |
| − | | | + | | 111.8 |
| − | | | + | | 99.1 |
| − | | | + | | 624.3 |
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 3 |
| − | | | + | | 75323.4 |
| − | | | + | | 0.0030 |
| − | | | + | | 1.940 |
| − | | | + | | 2.699 |
| − | | | + | | 2.836 |
| − | | | + | | 0.7191 |
| − | | | + | | 6.332 |
| − | | | + | | 6.9186 |
| − | | | + | | 7.7015 |
| − | | | + | | 75.88 |
| − | | | + | | 70.92 |
| − | | | + | | 35.9 |
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 4 |
| − | | | + | | 69081.3 |
| − | | | + | | 0.0031 |
| − | | | + | | 1.802 |
| − | | | + | | 2.495 |
| − | | | + | | 2.735 |
| − | | | + | | 0.7225 |
| − | | | + | | 4.559 |
| − | | | + | | 6.3649 |
| − | | | + | | 6.8322 |
| − | | | + | | 76.86 |
| − | | | + | | 72.30 |
| − | | | + | | 0.98 |
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 5 |
| − | + | | 69248.0 | |
| − | + | | 0.0031 | |
| − | + | | 1.809 | |
| − | + | | 2.505 | |
| − | + | | 2.740 | |
| − | + | | 0.7224 | |
| − | + | | 4.667 | |
| − | + | | 6.4028 | |
| − | + | | 6.8854 | |
| − | + | | 76.64 | |
| − | + | | 72.08 | |
| − | + | | 0.22 | |
| − | + | ||
| − | + | ||
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
| − | | | + | |
|} | |} | ||
| − | De la Tabla 1 puede verse que a pesar de que se escogió un valor inicial que en nada ayuda a la convergencia del algoritmo, luego de la tercera iteración ya el resultado ha convergido en más de un 98%, diferenciándose por menos de 1ºC del resultado final. Si se deja correr el programa hasta la sexta y séptima iteración, sus valores para <math>T_{co}</math> son en ambos casos 76.66ºC, diferenciándose solo por milésimas de grado, lo cual es imperceptible. | + | De la [[#tab-1|Tabla 1]] puede verse que a pesar de que se escogió un valor inicial que en nada ayuda a la convergencia del algoritmo, luego de la tercera iteración ya el resultado ha convergido en más de un 98%, diferenciándose por menos de 1ºC del resultado final. Si se deja correr el programa hasta la sexta y séptima iteración, sus valores para <math>T_{co}</math> son en ambos casos 76.66ºC, diferenciándose solo por milésimas de grado, lo cual es imperceptible. |
Experimentación real ha sido realizada por Cardenas y Ezekoye bajo condiciones similares a la expuesta en este caso [15], encontrándose lectura térmica experimental del conductor en el orden de los 77ºC, lo que deja ver la alta precisión del algoritmo con respecto de las pruebas reales. El código NFPA 70 indica que este cable puede ser utilizado al aire libre con 620 amperios de corriente nominal alterna a 60 hercios, en un ambiente de 30ºC, y no debería superar los 75ºC de temperatura extrema [10]. El tipo de aislante es termoplástico a base de PVC y plastificadores, por lo cual, por encima de los 60ºC el mismo ya esta sufriendo los daños debido a la deshidrocloración y pérdida de los plastificadores en el PVC [22,23,24]. | Experimentación real ha sido realizada por Cardenas y Ezekoye bajo condiciones similares a la expuesta en este caso [15], encontrándose lectura térmica experimental del conductor en el orden de los 77ºC, lo que deja ver la alta precisión del algoritmo con respecto de las pruebas reales. El código NFPA 70 indica que este cable puede ser utilizado al aire libre con 620 amperios de corriente nominal alterna a 60 hercios, en un ambiente de 30ºC, y no debería superar los 75ºC de temperatura extrema [10]. El tipo de aislante es termoplástico a base de PVC y plastificadores, por lo cual, por encima de los 60ºC el mismo ya esta sufriendo los daños debido a la deshidrocloración y pérdida de los plastificadores en el PVC [22,23,24]. | ||
| Line 549: | Line 535: | ||
El siguiente ejemplo consta de un cable europeo H07V – R 1x240 mm<sup>2</sup> de acuerdo a IEC 60364-5-52 y UNE-H-60364-5-52 [25], que sería del tipo termoplástico a base de PVC, normado para su uso hasta 70ºC en el conductor con frecuencia de 50 hercios. A diferencia de la normativa americana, la norma europea no tabula este caso específico en bases de datos con una “corriente admisible oficial”, pues sería una configuración de cableado unipolar al aire libre, que no consta entre las configuraciones normalizadas, a pesar de tener un uso industrial común. Lo más parecido (y a nuestra opinión adecuado), sería la configuración tipo G de la normativa eléctrica citada, donde se tienen cables unipolares totalmente al aire libre separados a un mínimo de un diámetro de distancia entre ellos. Esta configuración, se encuentra según la propia norma, fuera del alcance prescriptivo de las tablas de UNE-H-60364-5-52; con lo que se vuelve un excelente recurso la opción de tener un sistema de modelaje iterativo simple y de alta precisión como el presentado aquí, para la caracterización térmica de estos cables. Para efectos de comparación con algunos datos normalizados, en este caso tomaremos el cable unipolar instalado sin canalización sobre pared de madera, según la configuración tipo C de la tabla B-52-1 de UNE-H-60364-5-52, el cual de no ser por la pared de madera que tiene de uno de sus lados, estaría como si estuviese al aire libre, por tanto nos da un buen indicio comparativo. Según esta tabla, este cable en dimensión de 240 mm<sup>2</sup> con aislante termoplástico, debería portar 401 amperios calentándose aproximadamente a 70ºC cuando la temperatura ambiental es de 40ºC. | El siguiente ejemplo consta de un cable europeo H07V – R 1x240 mm<sup>2</sup> de acuerdo a IEC 60364-5-52 y UNE-H-60364-5-52 [25], que sería del tipo termoplástico a base de PVC, normado para su uso hasta 70ºC en el conductor con frecuencia de 50 hercios. A diferencia de la normativa americana, la norma europea no tabula este caso específico en bases de datos con una “corriente admisible oficial”, pues sería una configuración de cableado unipolar al aire libre, que no consta entre las configuraciones normalizadas, a pesar de tener un uso industrial común. Lo más parecido (y a nuestra opinión adecuado), sería la configuración tipo G de la normativa eléctrica citada, donde se tienen cables unipolares totalmente al aire libre separados a un mínimo de un diámetro de distancia entre ellos. Esta configuración, se encuentra según la propia norma, fuera del alcance prescriptivo de las tablas de UNE-H-60364-5-52; con lo que se vuelve un excelente recurso la opción de tener un sistema de modelaje iterativo simple y de alta precisión como el presentado aquí, para la caracterización térmica de estos cables. Para efectos de comparación con algunos datos normalizados, en este caso tomaremos el cable unipolar instalado sin canalización sobre pared de madera, según la configuración tipo C de la tabla B-52-1 de UNE-H-60364-5-52, el cual de no ser por la pared de madera que tiene de uno de sus lados, estaría como si estuviese al aire libre, por tanto nos da un buen indicio comparativo. Según esta tabla, este cable en dimensión de 240 mm<sup>2</sup> con aislante termoplástico, debería portar 401 amperios calentándose aproximadamente a 70ºC cuando la temperatura ambiental es de 40ºC. | ||
| − | Los resultados de cálculo para este cable con el algoritmo termoconductivo se muestran por pasos en la Tabla 2, considerando una temperatura de inicio iterativo <math>T_{co}=40{^\circ}C</math>. | + | Los resultados de cálculo para este cable con el algoritmo termoconductivo se muestran por pasos en la [[#tab-2|Tabla 2]], considerando una temperatura de inicio iterativo <math>T_{co}=40{^\circ}C</math>. |
<div class="center" style="font-size: 75%;">'''Tabla 2'''. Resultados por pasos para el caso presentado de cable H07V – R 1x240 mm<sup>2</sup> | <div class="center" style="font-size: 75%;">'''Tabla 2'''. Resultados por pasos para el caso presentado de cable H07V – R 1x240 mm<sup>2</sup> | ||
</div> | </div> | ||
| − | {| style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width: | + | <div id='tab-2'></div> |
| − | |-style="text-align:center | + | {| class="wikitable" style="margin: 1em auto 0.1em auto;border-collapse: collapse;font-size:85%;width:auto;" |
| − | + | |-style="text-align:center" | |
| − | + | ! Iter. !! <math>g</math> !! <math>\beta </math> !! <math>{\nu }_{air} \times 10^{-5}</math> !! <math>{\alpha }_{air} \times 10^{-5}</math> !! <math>k_{T-air}\times 10^{-2}</math> !! <math>\mbox{Pr}</math> !! |<math>Ra \times 10^{4}</math> !! <math>Nu</math> !! <math>h_f</math> !! <math>T_{co}</math> ºC !! <math>T_{ins}</math> ºC !! Err . <math>T_{co}</math> | |
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
| − | + | ||
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 1 |
| − | | | + | | 44533.1 |
| − | | | + | | 0.0032 |
| − | | | + | | 1.702 |
| − | | | + | | 2.347 |
| − | | | + | | 2.660 |
| − | | | + | | 0.7252 |
| − | | | + | | 0 |
| − | | | + | | 0.3600 |
| − | | | + | | 0.4145 |
| − | | | + | | 419.4 |
| − | | | + | | 416.7 |
| − | | | + | | 379.4 |
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 2 |
| − | | | + | | 96260.4 |
| − | | | + | | 0.0020 |
| − | | | + | | 3.822 |
| − | | | + | | 5.529 |
| − | | | + | | 4.015 |
| − | | | + | | 0.6940 |
| − | | | + | | 4.293 |
| − | | | + | | 6.2388 |
| − | | | + | | 10.842 |
| − | | | + | | 76.85 |
| − | | | + | | 71.13 |
| − | | | + | | 3.42 |
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 3 |
| − | | | + | | 49558.1 |
| − | | | + | | 0.0030 |
| − | | | + | | 1.852 |
| − | | | + | | 2.568 |
| − | | | + | | 2.772 |
| − | | | + | | 0.7213 |
| − | | | + | | 2.406 |
| − | | | + | | 5.4208 |
| − | | | + | | 6.5045 |
| − | | | + | | 69.66 |
| − | | | + | | 66.72 |
| − | | | + | | 7.19 |
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 4 |
| − | | | + | | 48577.6 |
| − | | | + | | 0.0031 |
| − | | | + | | 1.830 |
| − | | | + | | 2.536 |
| − | | | + | | 2.756 |
| − | | | + | | 0.7218 |
| − | | | + | | 2.129 |
| − | | | + | | 5.2604 |
| − | | | + | | 6.2759 |
| − | | | + | | 70.03 |
| − | | | + | | 67.14 |
| − | | | + | | 0.37 |
|-style="text-align:center;" | |-style="text-align:center;" | ||
| − | | | + | | 5 |
| − | | | + | | 48627.6 |
| − | | | + | | 0.0031 |
| − | | | + | | 1.832 |
| − | | | + | | 2.539 |
| − | | | + | | 2.757 |
| − | | | + | | 0.7217 |
| − | | | + | | 2.157 |
| − | | | + | | 5.2770 |
| − | | | + | | 6.2992 |
| − | | | + | | 69.96 |
| − | | | + | | 67.07 |
| − | | | + | | 0.07 |
|} | |} | ||
| − | Los resultados de las iteraciones sucesivas a la quinta, continúan dando <math>T_{co}=69.96{^\circ}C</math> y <math>T_{ins}=67.07{^\circ}C</math>, teniendo variaciones de milésimas de ºC. Se puede ver nuevamente la rápida convergencia del modelo, desde la tercera iteración. Se puede evidenciar que ciertamente, la norma tiene razón en no permitir para este conductor más de 401 Amperios. Si bien en este caso nos ha servido para corroborar la veracidad del modelo también con cableado europeo, la verdadera aplicación de este modelo surge cuando no tengo una referencia de cálculo para una operación de un conductor. Por ejemplo, el conductor H07V – R 1x240 mm< | + | Los resultados de las iteraciones sucesivas a la quinta, continúan dando <math>T_{co}=69.96{^\circ}C</math> y <math>T_{ins}=67.07{^\circ}C</math>, teniendo variaciones de milésimas de ºC. Se puede ver nuevamente la rápida convergencia del modelo, desde la tercera iteración. Se puede evidenciar que ciertamente, la norma tiene razón en no permitir para este conductor más de 401 Amperios. Si bien en este caso nos ha servido para corroborar la veracidad del modelo también con cableado europeo, la verdadera aplicación de este modelo surge cuando no tengo una referencia de cálculo para una operación de un conductor. Por ejemplo, el conductor H07V – R 1x240 mm<math>^2</math> en las condiciones de carga dadas pero en un ambiente de 50ºC se calentaría hasta los <math>T_{co}=80.92{^\circ}C</math> con <math>T_{ins}=77.94{^\circ}C</math>; y si fuese utilizado en un ambiente de 30ºC, el mismo se calentaría hasta los <math>T_{co}=59.0{^\circ}C</math> con <math>T_{ins}=56.2{^\circ}C</math>. |
==6. Conclusiones== | ==6. Conclusiones== | ||
Latest revision as of 15:06, 9 December 2020
Resumen
Los modelos termoconductivos para el cálculo de conductores eléctricos y sus disipaciones energéticas han sido capaces de resolver dudas acerca de los conductores de potencia, que de otra forma hubiesen permanecido en la sombra del desconocimiento pues eran incluso insospechadas. Antes se pensaba que para caracterizar térmicamente un conductor eléctrico, era suficiente con la aplicación de ecuaciones simples tipo Joule, considerando propiedades intrínsecas resistivas como constantes en el conductor, y despreciando la variabilidad de las condiciones que rodean al conductor. De hecho, así esta estipulado en la mayor parte de las más conocidas normas eléctricas, entre ellas las editadas por la National Fire Protection Association (NFPA), así como las editadas por la International Electrotechnical Commission (IEC). Se ha demostrado que a medida que los cables eléctricos conducen mayores intensidades eléctricas, se alejan mucho del comportamiento predicho por los modelos tipo Joule, en ocasiones, con disipaciones energéticas 50% superiores a las predichas por Joule. Esto se debe a las no-linealidades de las propiedades intrínsecas de los mismos, y a la inconstancia de las condiciones ambientales que rodean al cable en el momento en que se va calentando. Los novedosos modelos termoconductivos, con apenas diez años de desarrollo, son hoy una solución técnica muy completa y con precisión inigualable (errores inferiores al 0.01% en energía y temperatura) en las predicciones térmicas de los conductores; pero que por su alto grado de complejidad matemática requiere en la mayor parte de las ocasiones la necesidad de utilizar métodos numéricos para obtener soluciones prácticas. En este artículo se presenta un nuevo algoritmo general, que destaca por su simplicidad frente a los primeros modelos termoconductivos desarrollados, y funciona para resolver modelos termoconductivos en predicciones térmicas de cables eléctricos de potencia, sin la necesidad de enormes bases de datos, con simplicidad, maniobrabilidad y excelentes resultados prácticos.
Palabras clave: Modelado, algoritmo termoconductivo, cableado sobrecalentado, propiedades termodinámicas, código eléctrico
Abstract
The thermal-conductive models for the calculation of the electrical conductors and their energy dissipations have been able to solve doubts about the power conductors, which has been permanently unsuspected. Before thinking about thermally characterizing an electrical conductor, it was enough with the application of simple Joule-type equations, with constant resistive intrinsic properties in the conductor, as well as invariable considerations in the conditions that surround the conductor. In fact, just as is exposed, this has been published on the top of the best known electrical standards, such as those issued by the National Fire Protection Association (NFPA), as well as those edited by the International Electrotechnical Commission (IEC). It has been demonstrated that electric cables with higher electrical intensities, move away from the behavior predicted by the Joule type models, sometimes with energy dissipations 50% higher than those predicted by Joule. This is due to the non-linearities of the intrinsic properties of the cable, and the inconsistency of the environmental conditions surrounding the cable at the time it is going to heat. The novel thermal-conductive models with just ten years of development, are today a very complete solution with unparalleled accuracy (errors less than 0.01% in energy and temperature) in the thermal predictions of conductors; but due to its high degree of mathematical complexity requires in the most of cases to use numerical methods to obtain practical solutions. In this paper a new general algorithm is shown, which stands out for its simplicity compared to the first thermoconductive models, solving the models in thermal predictions of power electrical cables, without the need of huge databases, with simplicity, maneuverability and excellent practical results.
Keywords: Modeling, thermal-conductive algorithm, wire overheating, thermodynamic properties, electrical code
1. Introducción
El calentamiento de los cables eléctricos de potencia, es en la mayoría de los casos indeseable, pues representa un riesgo de incendio y un desempeño inapropiado en cuanto eficiencia energética. Salvo dados casos industriales muy específicos, donde lo que se desea es generar calor por medio de la electricidad, en las instalaciones eléctricas se intenta mantener cada uno de los elementos conductores a la temperatura más baja posible. Varias publicaciones con estadísticas de incendios muestran que las causas eléctricas se encuentran liderando las posiciones de generación de siniestros en diferentes partes del mundo [1,2,3,4].
Desde 1841, se intenta modelar la disipación energética en conductores eléctricos; en ese año James Prescott Joule publica su famosa ecuación que luego se convertirá en la famosa Ley de Joule. Los modelos que se ajustan a esta ley son conocidos como modelos de resistividad, modelos óhmicos o modelos tipo Joule. Si bien este modelo parece que continúa siendo la base del modelado disipativo en conductores eléctricos, muchas cosas han mejorado desde entonces. Estudios posteriores al de Joule, pero ya ingresados al siglo XX, dieron resultados que demostraron la dependencia de las capacidades conductivas con la temperatura [5]. Luego de esto los métodos han sido ampliamente mejorados en torno a la forma de medir o caracterizar la resistividad [6], e incluso hay estudios recientes que aún tratan de obtener lo mejor de estos modelos resistivos [7].
No se puede negar que los modelos tipo Joule han contribuido al modelado de disipación energética en conductores, pues de hecho son la base; pero el problema sobreviene cuando el conductor eléctrico deja de comportarse linealmente como un conductor óhmico, lo cual es fundamental para la aplicación de los modelos tipo Joule; y esto básicamente sucede cuando el conductor va portando mayores intensidades de corriente. Varias publicaciones han llamado la atención acerca de correcciones que se hacen necesarias para el cálculo de cables eléctricos de potencia portadores de altas intensidades [8], con respecto a lo que se indica en las normativas actuales de mayor uso [9,10], sin embargo, las normas continúan sin cambios sustanciales. La poca atención que han prestado las instituciones dedicadas a la protección contra incendios con respecto a esto, parece ser una razón importante en cuanto a la poca o nula mejora en las estadísticas de incendio presentadas al inicio de esta sección, pues tal parece, en muchos casos no se cuenta con personal altamente especializado en temas eléctricos que pueda hacer frente a las necesidades de comprensión y actualización de modelos, diseños, proyectos y normas.
Los modelos termoconductivos por su parte, consideran las no linealidades que se presentan en la resistividad de los conductores eléctricos, a medida que los mismos conducen mayores intensidades [11]; y al mismo tiempo las diferentes implicaciones que se dan como fenómenos de campo eléctrico por causa de la saturación de cargas, que llevan a una mayor generación de calor por unidad de volumen en el material conductor. También consideran los efectos que son externos al propio material conductor, como lo son el medio ambiente que lo rodea y las formas geométricas que pueda tener, lo que le facilitará o dificultará en alguna medida la disipación de calor hacia fuera del mismo. Finalmente, cuentan con la posibilidad de considerar las implicaciones debidas a los fenómenos magnéticos internos del conductor por efectos de la forma de la onda eléctrica que pasa a través de él (corriente directa, corriente alterna, corriente variable continua o discontinua) [12].
En lo siguiente detallaremos el modelo y la forma de un algoritmo simple que es capaz de resolver los complicados modelos termoconductivos, presentando la información de forma que pueda ser usada en forma práctica, para ayudar en las aplicaciones de modelado en investigaciones, diseños, proyectos y normativa eléctrica en el área de sistemas de potencia.
2. Materiales y métodos
El algoritmo de cálculo ha sido desarrollado sobre la base analítico-diferencial de un modelo termoconductivo simplificado que explicamos en la siguiente sección de teoría, y el programa de pruebas de éste algoritmo, ha sido hecho sobre la plataforma de programación de Matlab [13], sin utilizar librerías, bloques, ni scripts prediseñados, para favorecer la completa repetitividad de resultados sin la intervención de productos de solución numérica propietarios, en cualquier otro lenguaje de programación diferente a Matlab.
Experimentalmente se han realizado pruebas exitosas utilizando para ello cable conductor THHW (Thermoplastic High Heat Water) que es un cableado comercial ampliamente utilizado bajo la normativa NFPA, con aislamiento termoplástico muy resistente al calor y al agua. Como los conductores que mayor calentamiento presentan, son aquellos que manejan mayores intensidades, se ha tomado como ejemplo específico un cable conductor 500 MCM AWG de cobre, con aislante THHW, en un ambiente con temperatura de 30ºC al aire libre. Este cable de fabricación estandarizada americana, tiene un conductor metálico de cobre según IACS (International Annealed Copper Standard) [14], que sería equiparable físicamente a un conductor que según IEC tendría 253 mm2 de sección transversal efectiva de cobre. El aislante THHW por su parte tiene una mezcla termoplástica a base de PVC (cloruro de polivinilo) con plastificadores y retardantes a llama, que le brinda propiedades de alta resistencia al calor y la humedad. Se considera para comparación experimental, el comportamiento térmico del cable descrito, sometido a una intensidad de corriente eléctrica alterna a 60 hertz, de 620 amperios efectivos (RMS: raíz media cuadrada). Las mediciones han sido obtenidas utilizando termografía digital, con un equipo Flir E40 capaz de medir desde -20ºC hasta 650ºC con calibración de verificación realizada en función de su sensibilidad, con errores máximos de 0.07ºC.
3. Teoría
En esta sección desarrollaremos analíticamente la forma como llegamos a la solución de un sistema termoconductivo eléctrico, y las mejoras que planteamos para efectos de lograr que pueda ser aplicado por medio de un algoritmo simple. Primeramente, es importante plantear que el modelo termoconductivo es actualmente el único método de solución para caracterizar térmicamente conductores eléctricos de alta potencia, que considera factores internos del conductor como las no linealidades en la resistividad del conductor, los cambios en los tensores del campo electrodinámico (forma y frecuencia de las señales), la saturación electrónica por aumento de la corriente, y los efectos físicos intrínsecos propios de la autogeneración de calor. Al mismo tiempo, considera también factores externos al conductor, como los efectos geométricos de la forma y las propiedades físicas de los medios circundantes, incluyendo los posibles cambios en las características de sus parámetros [12]. Aunque el modelo termoconductivo ya ha sido presentado e incluso utilizado en varias aplicaciones industriales [15], ha quedado claro también que su utilización es engorrosa por efectos de que las soluciones al sistema son muy complejas. Esto lo hace un producto de aplicación práctica limitada solo a las necesidades de modelado más complejas [16]. Buscando un mayor aprovechamiento de estos modelos, presentamos varias mejoras teóricas notables, que simplifican grandemente el proceso numérico de solución.
La potencia real disipada en forma de calor radiado por un conductor eléctrico cualquiera, puede ser expresada según [11]:
|
|
(1) |
donde es la intensidad de corriente que fluye a través de la sección transversal (o área efectiva de conducción) , de un conductor de longitud . De esta forma:
: intensidad de corriente (amperios).
: área efectiva de conducción para la corriente .
: función o valor de resistividad referencial a la temperatura .
: elemento diferencial lineal de conductor en el que fluye .
: longitud total del conductor de elemento diferencial .
: función de incremento térmico del conductor.
: diferencial de incremento térmico.
: temperatura de referencia a la cual fue medida la resistividad que de referencia .
: temperatura real (o actual) del conductor, bajo las condiciones de carga eléctrica.
El área efectiva de conducción es calculada considerando las variaciones térmicas y la frecuencia de la señal que pasa por un conductor de acuerdo a [17,18]:
|
|
(2) |
|
|
(3) |
donde es la profundidad de penetración de la señal electromagnética (electrodinámica clásica), la frecuencia de la señal en radianes/segundo, la permeabilidad magnética del espacio vacío y la permeabilidad relativa del medio conductor.
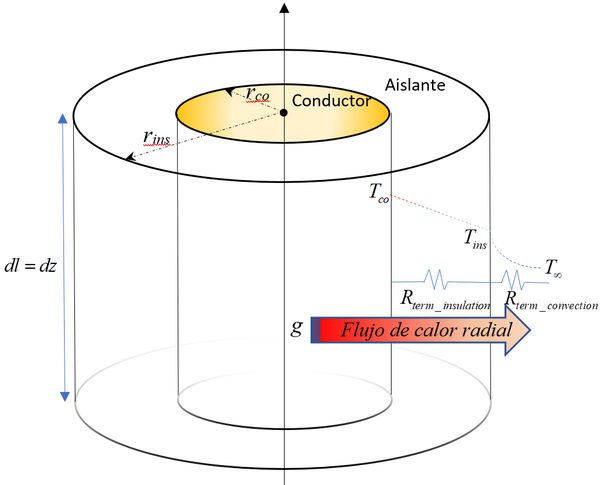
Para un volumen cualquiera de material de conductor eléctrico, es notable que puede establecerse lo que llamamos generación de calor por unidad de volumen ; lo cual en forma diferencial queda estipulado según puede verse en la Figura 1 por:
|
|
(4) |
donde se diferencia de , al ser la primera un área geométrica (en caso de un cable como el de la Figura 1, es un área circular perfecta) y la segunda un área efectiva para el flujo de corriente eléctrica, determinada de acuerdo a la Ec.(2).
|
| Figura 1. Representación de un elemento volumétrico diferencial de cable conductor, para análisis de termoconducción |
El calor es conducido de los puntos con mayor temperatura (medida potencial de calor) a aquellos con menor temperatura. Considerando que un caso de conductor eléctrico como cobre o aluminio, es también un excelente conductor de calor; no recapitularemos en tensores de transferencia de calor adentro del propio conductor, pues su temperatura en estado estable será aproximadamente la misma a lo largo del material conductor [19]. Las diferencias térmicas se verán del conductor al aislante y del aislante hacia el medio ambiente, por tanto, el flujo de calor será principalmente radial, como se muestra en la Figura 1.
Para la parte conductiva del calor a través del aislante, podemos utilizar la ecuación unidimensional de conducción de calor de Fourier, con flujo de calor en dirección radial [20]:
|
|
(5) |
donde es el calor total que fluye por unidad de tiempo a través del área transversal , el área transversal de flujo de calor (donde está el aislante), para una longitud de cable , la conductividad térmica usualmente en . Se usará para referirse específicamente a la conductividad térmica del aislamiento. es la variable radial lineal, que direcciona el flujo de calor.
Se puede resolver por separación de variables y agregando los límites que condicionan las fronteras que se muestran para el aislante en la Figura 1:
|
|
(6) |
El calor total conducido viene a ser, bajo las consideraciones dadas, muy similar a , pues como indicamos antes, las conducciones en otras direcciones diferentes de , pueden ser despreciadas. De acuerdo a la Ec.(4), podemos por comparación indicar que:
|
|
(7) |
Sustituyendo la aproximación de la Ec.(7) en la Ec.(6), resolviendo las integrales y reduciendo términos, llegamos a:
|
|
(8) |
donde:
: radio máximo de material conductor.
: radio máximo del aislamiento.
: temperatura del conductor en .
: temperatura del aislante en .
El calor que ha sido conducido a través del aislante hasta el radio externo , es finalmente llevado al ambiente por medios principalmente convectivos, de acuerdo al modelo de convección unidimensional [20]:
|
|
(9) |
donde:
: área externa del aislante, por donde sale finalmente todo el .
: coeficiente convectivo del medio que rodea al cable.
: Temperatura del medio que rodea al cable (ambiente).
Con lo que podemos indicar luego de reducir que:
|
|
(10) |
Las Ecs.(8) y (10) se refieren a la conducción hasta el ambiente de la misma generación de calor por unidad de volumen dada por Ec.(4). De aquí que pueda trabajarlas como ecuaciones óhmicas térmicas, identificando sus parámetros de interrelación proporcional como respectivas conductancias térmicas, por tanto sus inversos serían resistencias térmicas:
|
|
(11) |
donde se reconoce como resistencia térmica del aislamiento a:
|
|
(12) |
Y como resistencia térmica por causas convectivas a:
|
|
(13) |
La base teórica fundamental del modelo termoconductivo finaliza al realizar la comparación de cálculo de una temperatura de conductor , que satisfaga la Ec.(11), para una que ha sido pre-calculada partir de la Ec.(4), en la cual un gran problema de solución ha sido la inmensa cantidad de matrices de datos que se deben manejar para seleccionar valores aproximados de las propiedades ambientales que permiten calcular , y que son dependientes de la temperatura que rodea el cable en esa zona de convección, la cual depende directamente de la temperatura del conductor , que esperamos tener también como solución. Esto nos lleva a un sistema iterativo cíclico, donde se desarrollan los siguientes pasos:
- 1. Establecer las variables que sean de interés. En nuestro caso simplificado, utilizaremos a las ya descritas , , (internas al conductor), , , (externas al conductor). Aparte de estas variables, podrían ser consideradas de interés todas las demás que han sido definidas teóricamente, pero a medida que se consideran, ingresan también sus ecuaciones al modelo iterativo, haciéndolo más complejo. Por ejemplo, si se estuviese interesado en conocer la temperatura externa del aislamiento del cable, se ingresa la variable , que en muchos casos no representa un dato de real interés.
- 2. Se escoge una temperatura inicial para , superior a la temperatura (para ayudar a una convergencia más rápida, ya que el calor va del conductor al ambiente), y se calcula por medio de las Ecs.(2), (3) y (4) (haciendo a ), una primera aproximación para . Nótese que en los casos que sea constante, la Ec.(4) pasa a ser una ecuación algebraica muy manejable:
|
|
(14) |
- 3. Se obtienen los parámetros y . El primero de ellos es bastante estable en amplios rangos de temperatura, pero en el aire es muy variable, y depende de parámetros adimensionales como el número de Rayleigh y el número de Nusselt. La obtención de estos parámetros es sumamente engorrosa, pues depende de variables termodinámicas experimentales usualmente registradas en bases de datos muy diversas, como lo son la difusividad térmica, la viscosidad cinemática, conductividad térmica del aire y el número de Prandtl. Estos parámetros tienen amplia variación con la temperatura de los gases. Cuando se utilizan modelos de solución con métodos numéricos, se suelen utilizar bases de datos discretos, en los que en muchas ocasiones el manejo de las mismas hace complejo al algoritmo de programación, pues se trata de modelar un modelo continuo, pero dependiente de datos discretos en una base de datos. En nuestro caso, hemos eliminado en su totalidad la necesidad de estas extensas bases de datos, modelando los mismos en ecuaciones que hemos introducido en nuestro algoritmo, las cuales serán presentadas en la sección de cálculos. Con esto el algoritmo de cálculo es mucho más ágil, requiere una cantidad mucho menor de líneas de comando, y una memoria de menos del 10% de la memoria requerida por un algoritmo similar que use bases de datos.
- 4. Se reemplazan los valores obtenidos de y en Ec.(11), con lo que se obtiene una nueva (para una siguiente iteración o terminar el proceso).
- 5. Se compara la nueva (del acápite anterior), con la que se tenía considerada antes del uso de la Ec.(11) ( de la iteración anterior). Se escoge un nivel de precisión en grados térmicos para esta comparación (el deseado). Usualmente si se escoge 0.5ºC la convergencia se logra en 3 a 5 iteraciones. A medida que se escoja una precisión mayor (menor cantidad de grados en la comparación), se requerirán más iteraciones para llegar al final del proceso, pero en la mayor parte de los casos después de la quinta iteración ya la precisión global de se encuentra en las milésimas de grado (0.00xºC) o a lo sumo centésimas. Si la convergencia no ha sido satisfecha, por causa de que la diferencia en la comparación ( nueva - anterior) es aún superior al “error máximo permisible”, se repiten todos los pasos desde el acápite “b”, donde la nueva para calcular será siempre la de la última iteración.
4. Cálculos
Presentamos en esta sección los ajustes y la forma práctica, en la cual conducimos los cálculos del modelo.
Para los efectos de las propiedades de los conductores, se pueden utilizar los siguientes valores para el cobre:
|
|
Mientras que para el aluminio tenemos:
|
|
En ambos casos los coeficientes de incremento térmico se utilizan a 75ºC para que los cálculos sean más aproximados en los rangos de temperatura de carga nominal de los conductores. De lo contrario se tendrían que utilizar como funciones de temperatura que no se tienen estipuladas actualmente, y existen muy pocos datos a temperaturas muy diferentes, como para estipular modelos continuos de confianza.
Mientras más cercana esté la que escogemos en la primera iteración a la real final, es lógico que tendremos menos iteraciones. Pero para probar la viabilidad y rápida convergencia de este modelo, escogeremos nuestro primer igual en valor a la temperatura ambiente. De forma analítica es necesario usar la Ec.(4) para calcular una aproximación a , pero en forma práctica, al ser resuelto numéricamente, es suficiente con usar la reducción a la forma de la Ec.(14).
Para el uso de la Ec.(4) o (14), se requiere calcular el valor para , dependiente de varios parámetros físicos termodinámicos (en bases de datos), que son a su vez dependientes de la temperatura del aire que esta rodeando al cable, la cual se puede estimar como un promedio entre la temperatura del cable y la del ambiente. En nuestro caso, al ver la cantidad de recurso y memoria que consumen esas operaciones, hemos modelado los resultados de las bases de datos, por medio de ecuaciones continuas de regresiones polinomiales ajustadas a partir de [21], en la siguiente forma:
Calculamos una temperatura promedio de la capa de aire que rodea al cable:
|
(15) |
Un factor térmico de capa, que no será mas que el inverso de la temperatura absoluta:
|
|
(16) |
Las cuatro ecuaciones siguientes sustituyen cada una de las bases de datos para propiedades termodinámicas del aire otorgadas por [21], las cuales se encuentran en función de la considerada y se han obtenido usando regresión polinomial de segundo grado para todas ellas, menos para la conductividad térmica, que se aproximó mucho mejor con una regresión lineal simple.
Viscosidad cinemática del aire:
|
|
(17) |
Difusividad térmica del aire:
|
|
(18) |
Conductividad térmica del aire:
|
|
(19) |
El número de Prandtl:
|
|
(20) |
Estos resultados funcionales han sido cuidadosamente comparados contra los resultados experimentales que se tienen, y han sido ajustados para que en ningún caso se tengan errores que no puedan ser despreciados con respecto a la medición experimental dada en la base de datos. Se ha logrado un coeficiente de determinación de grado de ajuste R2 superior a 0.9999 en todas las regresiones de las propiedades del aire y 0.9997 para el número de Prandtl. Estas cuatro ecuaciones eliminan totalmente la necesidad de tener bases de datos para correr el algoritmo de programación, y las reemplazan por cuatro líneas simples de comando.
Procedemos a calcular el número de Rayleigh y seguido el número de Nusselt, donde en este caso utilizaremos la ecuación para el caso de cilindros horizontales [20], dado que nuestro conductor eléctrico en los casos más usuales tendrá esta configuración. Estos números son parámetros adimensionales con modelización empírica, que se requieren para los efectos de lograr un calculo preciso del factor
|
(21) |
donde es la intensidad de campo gravitacional terrestre o aceleración terrestre y es el diámetro del cilindro, en nuestro caso el diámetro externo del aislamiento en metros
|
(22) |
Con lo cual se calcula el factor
|
|
(23) |
El valor de se encuentra entre 0.15 y 0.19 W/(mºK) para aislantes termoplásticos a base de PVC, poliolefinas, plastificadores hidrocloradores y aditivos, y su variabilidad es función casi exclusiva de la mezcla química y densidad del material resultante en cada caso. Podemos utilizar con confianza el promedio del valor, a 0.17 W/(mºK).
Con ello, de acuerdo a la Ec.(11), podemos obtener el resultado de la primera iteración para . Este resultado, lo comparamos con el asumido inicialmente, y luego, con el de cada iteración anterior, repitiendo todo el ciclo de cálculo hasta que consideremos un error diferencial de valores de aceptable entre dos iteraciones sucesivas. Si es de interés, con las Ecs.(8) o (10) se puede obtener la temperatura externa del aislamiento . Téngase en cuenta que la temperatura crítica sigue siendo , pues es la temperatura de contacto entre el conductor y el aislamiento por su lado interno, donde se comienza a degradar.
5. Resultados y discusión
Presentamos primeramente un cable 500 MCM AWG de cobre, con aislante THHW operando con 620 amperios al aire libre, con una temperatura ambiental de 30ºC (condición para la cual está normado). Este cable es muy común en instalaciones americanas industriales y comerciales con alta intensidad de corriente. Su parte conductora es de cobre trenzado con 37 hebras de 2.95 mm de diámetro cada una y 253 mm2 de sección transversal total efectiva de conducción, con aislante termoplástico resistente a calor, a humedad y retardante a la llama [10]. La frecuencia del sistema de alimentación es de 60 hercios, lo cual es usual en los sistemas industriales americanos (480 Volt – 3 fases – 60 Hz).
Los resultados del ejemplo indicado, luego de correr el algoritmo descrito con las ecuaciones de cálculo en Matlab [13], se presentan en la Tabla 1, considerando un valor inicial .
| Iter. | ºC | ºC | Err . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 61356.4 | 0.0033 | 1.608 | 2.209 | 2.588 | 0.7279 | 0 | 0.3600 | 0.3656 | 736.1 | 732.1 | 706.1 |
| 2 | 192456 | 0.0015 | 6.031 | 8.925 | 5.113 | 0.6956 | 3.232 | 5.8101 | 11.658 | 111.8 | 99.1 | 624.3 |
| 3 | 75323.4 | 0.0030 | 1.940 | 2.699 | 2.836 | 0.7191 | 6.332 | 6.9186 | 7.7015 | 75.88 | 70.92 | 35.9 |
| 4 | 69081.3 | 0.0031 | 1.802 | 2.495 | 2.735 | 0.7225 | 4.559 | 6.3649 | 6.8322 | 76.86 | 72.30 | 0.98 |
| 5 | 69248.0 | 0.0031 | 1.809 | 2.505 | 2.740 | 0.7224 | 4.667 | 6.4028 | 6.8854 | 76.64 | 72.08 | 0.22 |
De la Tabla 1 puede verse que a pesar de que se escogió un valor inicial que en nada ayuda a la convergencia del algoritmo, luego de la tercera iteración ya el resultado ha convergido en más de un 98%, diferenciándose por menos de 1ºC del resultado final. Si se deja correr el programa hasta la sexta y séptima iteración, sus valores para son en ambos casos 76.66ºC, diferenciándose solo por milésimas de grado, lo cual es imperceptible.
Experimentación real ha sido realizada por Cardenas y Ezekoye bajo condiciones similares a la expuesta en este caso [15], encontrándose lectura térmica experimental del conductor en el orden de los 77ºC, lo que deja ver la alta precisión del algoritmo con respecto de las pruebas reales. El código NFPA 70 indica que este cable puede ser utilizado al aire libre con 620 amperios de corriente nominal alterna a 60 hercios, en un ambiente de 30ºC, y no debería superar los 75ºC de temperatura extrema [10]. El tipo de aislante es termoplástico a base de PVC y plastificadores, por lo cual, por encima de los 60ºC el mismo ya esta sufriendo los daños debido a la deshidrocloración y pérdida de los plastificadores en el PVC [22,23,24].
El siguiente ejemplo consta de un cable europeo H07V – R 1x240 mm2 de acuerdo a IEC 60364-5-52 y UNE-H-60364-5-52 [25], que sería del tipo termoplástico a base de PVC, normado para su uso hasta 70ºC en el conductor con frecuencia de 50 hercios. A diferencia de la normativa americana, la norma europea no tabula este caso específico en bases de datos con una “corriente admisible oficial”, pues sería una configuración de cableado unipolar al aire libre, que no consta entre las configuraciones normalizadas, a pesar de tener un uso industrial común. Lo más parecido (y a nuestra opinión adecuado), sería la configuración tipo G de la normativa eléctrica citada, donde se tienen cables unipolares totalmente al aire libre separados a un mínimo de un diámetro de distancia entre ellos. Esta configuración, se encuentra según la propia norma, fuera del alcance prescriptivo de las tablas de UNE-H-60364-5-52; con lo que se vuelve un excelente recurso la opción de tener un sistema de modelaje iterativo simple y de alta precisión como el presentado aquí, para la caracterización térmica de estos cables. Para efectos de comparación con algunos datos normalizados, en este caso tomaremos el cable unipolar instalado sin canalización sobre pared de madera, según la configuración tipo C de la tabla B-52-1 de UNE-H-60364-5-52, el cual de no ser por la pared de madera que tiene de uno de sus lados, estaría como si estuviese al aire libre, por tanto nos da un buen indicio comparativo. Según esta tabla, este cable en dimensión de 240 mm2 con aislante termoplástico, debería portar 401 amperios calentándose aproximadamente a 70ºC cuando la temperatura ambiental es de 40ºC.
Los resultados de cálculo para este cable con el algoritmo termoconductivo se muestran por pasos en la Tabla 2, considerando una temperatura de inicio iterativo .
| Iter. | ºC | ºC | Err . | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 44533.1 | 0.0032 | 1.702 | 2.347 | 2.660 | 0.7252 | 0 | 0.3600 | 0.4145 | 419.4 | 416.7 | 379.4 |
| 2 | 96260.4 | 0.0020 | 3.822 | 5.529 | 4.015 | 0.6940 | 4.293 | 6.2388 | 10.842 | 76.85 | 71.13 | 3.42 |
| 3 | 49558.1 | 0.0030 | 1.852 | 2.568 | 2.772 | 0.7213 | 2.406 | 5.4208 | 6.5045 | 69.66 | 66.72 | 7.19 |
| 4 | 48577.6 | 0.0031 | 1.830 | 2.536 | 2.756 | 0.7218 | 2.129 | 5.2604 | 6.2759 | 70.03 | 67.14 | 0.37 |
| 5 | 48627.6 | 0.0031 | 1.832 | 2.539 | 2.757 | 0.7217 | 2.157 | 5.2770 | 6.2992 | 69.96 | 67.07 | 0.07 |
Los resultados de las iteraciones sucesivas a la quinta, continúan dando y , teniendo variaciones de milésimas de ºC. Se puede ver nuevamente la rápida convergencia del modelo, desde la tercera iteración. Se puede evidenciar que ciertamente, la norma tiene razón en no permitir para este conductor más de 401 Amperios. Si bien en este caso nos ha servido para corroborar la veracidad del modelo también con cableado europeo, la verdadera aplicación de este modelo surge cuando no tengo una referencia de cálculo para una operación de un conductor. Por ejemplo, el conductor H07V – R 1x240 mm en las condiciones de carga dadas pero en un ambiente de 50ºC se calentaría hasta los con ; y si fuese utilizado en un ambiente de 30ºC, el mismo se calentaría hasta los con .
6. Conclusiones
Como puede apreciarse, los diferenciales térmicos no son tan lineales como se esperaría y esto se debe a las variabilidades termoconductivas expuestas. Mientras mayor sea la sección del cable conductor, mayor será el impacto de la mayoría de los parámetros analizados en este artículo, por efectos de la frecuencia alterna. También esta claro que mientras mayor sea la frecuencia, aumentará el impacto de las concentraciones de generación de calor en los bordes de contacto del conductor con el aislante. Puede verse que existe cableado que esta normado en América para su uso hasta 75ºC a un amperaje especificado; sin embargo, el mismo no tiene la capacidad real de disipación de calor para lograr asegurar que no se supere la temperatura indicada en el conductor.
El algoritmo del modelo termoconductivo presentado, se vuelve un método simple, rápidamente convergente y de muy fácil programación, por medio del cual se puede asegurar la caracterización térmica real de los conductores, sobre todo aquellos de uso industrial, que pueden tener configuraciones de instalación que no se encuentran necesariamente estipuladas en la normativa eléctrica de cada país. Para la aplicación de esto, es necesario conocer siempre los valores de las propiedades termodinámicas del medio que rodea al conductor (usualmente aire, pero puede ser cualquier otro gas, fluido o sólido). La ventaja de modelar por medio de regresiones polinomiales los datos experimentales de estas propiedades, se aprecian comparativamente al permitirnos hacer un algoritmo libre de bases de datos pesadas, que ocupan cantidades de memoria y procesos, que no son requeridos cuando estas bases son remplazadas por una ecuación simple en una línea de comando.
La convergencia del modelo siempre se asegura al reestablecer el comportamiento o valor de todas las propiedades termodinámicas de acuerdo a la temperatura más actualizada que se obtiene para el conductor iteración tras iteración. Con ello, si se usaran bases de datos se consumiría una extensa memoria de proceso, pero en nuestro caso, simplemente se actualiza cada valor por medio de una ecuación simple, y se asegura al mismo tiempo una muy alta precisión al utilizar siempre las condiciones más aproximadas con cada iteración sucesiva.
Agradecimientos
Se reconoce para este trabajo el apoyo económico de la Secretaría Nacional de Ciencia, Tecnología e Innovación (SENACYT), por medio del programa del Sistema Nacional de Investigación (SNI), así como las contribuciones del Centro de Estudios Multidisciplinarios en Ciencias Ingeniería y Tecnología (CEMCIT-AIP), y del Grupo de Investigación y Laboratorio de Energía Radiante y Disipaciones Irreversibles (ERDI) de la Universidad Tecnológica de Panamá.
Referencias
| [1] | Hall J. Jr., Cote A. An Overview of the fire problem and fire protection. Fire Protection Handbook 20th Edition, 3-14 - 3-15, 2008. |
| [2] | Babrauskas V. Ignition Handbook. Issaquah WA: Fire Science Publishers/Society of Fire Protection Engineers, U.S.A., 2003. |
| [3] | Keski-Rahkonen O., Mangs J., Turtola A. Ignition of and fire spread on cables and electronic components. Valtion Teknillinen Tutkimuskeskus (VTT Publications 387), Finland, 1999. |
| [4] | Rosenberg T. Statistics for fire prevention in Sweden. Fire Safety Journal, 33-4: 283-294, 1999. |
| [5] | Dellinger J. The temperature coefficient of resistance of cooper. Journal of the Franklin Institute, 110:213-216, 1910. |
| [6] | Montgomery H. Method for measuring electrical resistivity of anisotropic materials. Journal of Applied Physics, 42:2971-2975, 1971. |
| [7] | Borup K., Toberer E., Zoltan L., Nakatsukasa G., Errico M., Fleurial J., Iversen B., Snyder G. Measurement of the electrical resistivity and Hall coefficient at high temperatures. Journal of Applied Physics, 83:123902, 2013. |
| [8] | Cárdenas D. True calculus of the warming in electrical wires in low voltage: A design correction. IEEE Latin America Transactions, 13:172-180, 2015. |
| [9] | IEC, IEC 60364 - Electrical Installations for Buildings, 2009. |
| [10] | NFPA, National Electrical Code - NFPA 70, Masashusets, 2017. |
| [11] | Cárdenas D. Propuesta de un modelo matemático para calcular el calentamiento de conductores eléctricos. Tecnociencia, 12-2:71-88, 2010. |
| [12] | Cárdenas D. Modelado de fuentes generadoras de incendios eléctricos por termoconducción. Universidat Politécnica de Catalunya, Barcelona, 2011. |
| [13] | MATLAB, The MathWorks. Inc, [En línea]. Available: https://www.mathworks.com/products/matlab.html. [Último acceso: 16 mayo 2019]. |
| [14] | Circular of the bureau of standards. Copper Wire Tables, Department of Commerce, United States, October 1, 1914. |
| [15] | Cardenas D., Ezekoye O. Thermal characterization of electrical wires and insulation operated in variable frequency mode. Fire Technology, 51:1071-1092, 2015. |
| [16] | Cárdenas D. “Phantom Impedances” as an option to solve 3D symmetrical circuit arrangements. IEEE Latin America Transactions, 16-1:155-162, 2018. |
| [17] | Kim S., Neikirk D. Compact equivalent circuit model for the skin effect. Microwave Symposium Digest, 3:1815-1818, 1996. |
| [18] | Wheeler H. Formulas for the skin effect. Proc. IRE, 30:412-424, 1942. |
| [19] | Cárdenas D., Gracia S., Fernández F., Dzul L. El recalentamiento eléctrico por termoconducción. Una perspectiva fisicoquímica del calentamiento eléctrico. Revista Facultad de Ingeniería Universidad de Antioquía, 64:57-67, 2012. |
| [20] | Incropera F., Dewitt D., Bergman T., Lavine A. Fundamentals of heat and mass transfer. John Wiley & Sons, U.S.A., 2007. |
| [21] | Coronel J. Colección de tablas, gráficas y ecuaciones de transmisión de calor. v3.5, Universidad de Sevilla, Sevilla, 2014. |
| [22] | Alvares N., Lipska-Quinn A., Hasegawa H. Thermal degradation of cable and wire insulations. Behavior of Polymeric Materials in Fire, Philadelphia, 1:42-66, 1983. |
| [23] | Benes M., Placek V., Matuschek G., Kettrup A., Gyoryova K., Emmerich W., Balek V. Lifetime simulation and thermal characterization of PVC cable insulation materials. Journal of Thermal Analysis and Calorimetry, 82-3:761-768, 2005. |
| [24] | Gumargalieva K., Ivanov V., Zaikov G., Moiseev J., Pokholok T. Problems of ageing and stabilization of poly(vinyl chloride). Polymer Degradation and Stability, 52-1:73-79, 1996. |
| [25] | UNE, UNE-H-60364-5-52, Madrid: Normalización Española, España, 2014. |
Document information
Published on 22/01/20
Accepted on 24/12/19
Submitted on 20/06/19
Volume 36, Issue 1, 2020
DOI: 10.23967/j.rimni.2020.01.002
Licence: CC BY-NC-SA license