A new method of satellite radar altimeter waveform retracking based on waveform derivative

Latest revision as of 09:01, 19 November 2020

Abstract

Waveform retracking for precise sea surface height (SSH) is an important method to improve the quality of satellite altimeter data. Combining the physical explanation of the function fitting and the high adaptability of empirical statistical methods, we effort to provide a comprehensive method for processing the waveforms over the open ocean and coastal area. The new retracking method that uses the maximum slope of leading edge to determine midpoint is proposed, the midpoint is determined by zero of second derivative of theoretical model. The unknown parameters are estimated based on the function fitting. Then combined with the advantage of empirical method, the leading edge midpoint is redetermined by interpolating the estimated midpoint on the measured waveform. The new method is validated by comparison with crossover discrepancies, geoid heights and tide gauges. The RMS of crossover discrepancy obtained by new method is 0.107 m, which is smaller than 0.192 m, 0.124 m, 0.121 m, 0.114 m, 0.112 m obtained by Ice-1,Threshold 50%, 5- $\beta$ , MLE3 and MLE4 retrackers. The STD and improvement percentage of the differences between SSHs obtained by new method and geoid heights are also better than the results of single kind of retracker. Comparison with tide gauge records, the STDs difference of height anomaly obtained by new method are 0.183 m and 0.269 m at different regions, which are smaller than 0.239 m, 0.220 m, 0.195 m and 0.303 m, 0.278 m, 0.272 m obtained by Ice-1, MLE4 and Threshold 50% retrackers, respectively. Therefore, the new method can recover more reliable SSH in the open ocean and coastal area.

Keywords: Satellite altimeter, waveform retracking, derivative, leading edge slope, crossover discrepancy, tide gauge

1. Introduction

Satellite altimetry, one of the most powerful technique of remote sensing in measuring ocean surfaces, obtains the sea surface height (SSH), the significant wave height and the backscatter coefficient. A large amount of ocean data has been collected, which provides basic information for oceanography, marine geodesy, geophysics etc. [1-6]. However, in order to get more reliable SSH, it is necessary to make corrections to altimeter data. Unfortunately, although great progress has been made in geophysical and media corrections in the last decade, it is still a challenge for obtaining accurate SSH, especially for processing the radar echo waveform. The echo signal is mainly affected by sea surface condition, bright target and contaminated by land or island. The echo waveform does not conform to the theoretical model, resulting in reduction of range accuracy [7-11].

In order to improve the accuracy of SSH and the quality of altimeter data, it is necessary to retrack the interfered echo waveform in the open ocean and coastal area. Several retrackers have been developed and are divided into two kinds [12-13]: the empirical statistical method and the function-fitting method, which are based on either full-waveform or sub-waveform. The retracking method based on empirical statistics is an algorithm that relies on empirical formulas, such as Threshold [14] algorithm. This method is of high adaptability and stability, the result of retracking is determined based on the emprical formula. Function fitting algorithm, such as $5-\beta$ algorithm [15], selects function form to fit the measured waveform. The algorithm has reliable accuracy, and has clear physical meaning and interpretation. The sub-waveform is defined as the partial waveform by processing multiple leading edges. The most important of the algorithm is the judgment and selection of sub-waveform [16-18], such as ALES [19] algorithm, the sub-waveform is adapting the width of the estimation window according to the significant wave height. For a single kind of retracker, it has certain limitations, for example, the emprical method is lack of physical interpretation and the function fitting method is susceptible to the influence of waveform [20-23]. Due to the complexity of the echo waveform, the accuracy of retracking method is different in the open ocean and coastal area [13]. Therefore, the waveform retracking method need to be further studied.

According to theoretical analysis and practical application of echo waveform, the method based on function fitting is still the most rigorous retracking method [19,22]. Combining the physical explanation of the function fitting and the high adaptability of empirical statistical retrackers, we effort to provide a comprehensive waveform retracking method. We expect it can be used to process simultaneously waveforms over the open ocean and coastal area with higher accuracy. The theoretical echo model [24] provides a theoretical basis for waveform research. Based on the analysis of echo power principle and theoretical echo waveform, this paper proposes new methods to determine the leading edge midpoint by using the maximum slope of waveform leading edge. The theoretical echo model is used to derive the first and second derivative function of waveform. The leading edge midpoint is determined by the second derivative zero point. In order to be combined with the measured waveform, the leading edge midpoint is redetermined by interpolating the theoretical power value of the estimated midpoint to the leading edge of measured waveform. In the open ocean, through comparison with the crossover discrepancy of SSH and the differece between the retracked SSHs and geoid heights, the accuracy of the new methods is verified. Also, through comparison with the tide gauge records, the adaptable of the new methods is verified by analysis of several retracking methods in the coastal area.

2. Data

2.1 Satellite radar altimetry

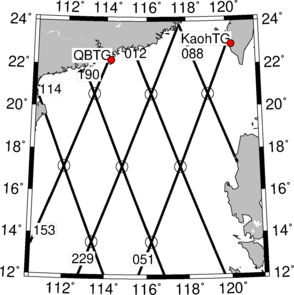
In this study, we used the Jason-2 Sensor Geophysical Data Records (SGDRs) within the area of the South China Sea (0 °- 30 ° N, 105 °-125 ° E), which are released by AVISO (Archiving Validation and Interpretation of Satellite Oceanographic data, http://www.aviso.altimetry.fr/). The SGDRs include waveforms and the state of the art geophysical and environment corrections for altimeter measurements [25]. These altimeter data of passes 012, 051, 088, 114, 153, 190 and 229 were processed from cycles 001 to 200 over the South China Sea (SCS). The passes 051, 229 and 153 are the ascending passes among those passes, and the others are the descending passes. These pass ground tracks are shown in Figure 1. Based on the range correction of waveform retracking and the geophysical corrections extracted from SGDRs, the altimetry-derived SSHs are computed.

Figure 1. Ground tracks of Jason-2 satellite over the SCS and the two tide gauges (red point represent the tide gauge)

2.2 In situ tide gauge records

To assess the performance of the new waveform retracking corrected SSH in the coastal area, we compared two tide gauge records in this region. The Quarry Bay tide gauge (QBTG) is located at ～114.22°E, ～22.28°N, near the northern coast of the Hong Kong Island. The tide gauge is located near pass 153 ground track of Jason-2. The Kaohsiung tide gauge (KaohTG) is located at ～120.29°E, ～22.62°N in Taiwan Island. The tide gauge is located near pass 051 ground track of Jason-2. The two tide gauges are shown in Figure 1. The hourly tide gauge records, referred to the WGS84 reference ellipsoid, were available from the Sea Level Center of the University of Hawaii (https://uhslc.soest.hawaii.edu). We obtained the hourly data from July 2008 to December 2013 for QBTG records, corresponds to satellite altimeter ground tracks from cycles 001 to 200, and the hourly data from July 2008 to July 2013 for KaohTG records, corresponds to satellite altimeter ground tracks from cycles 001 to 186. The altimetry-derived SSHs were determined close to the tide gauge stations. Altimetry-derived SSHs using several waveform retracking methods were compared to the stable tide gauge records.

3. Methodology

3.1 Retracking principle of waveform derivative

The SSH within the altimeter footprint is approximately symmetric with respect to a certain mean sea level in most cases. The leading edge of echo waveform is an odd function relative to leading edge midpoint [26-27]. The slope of waveform leading edge reaches the maximum value at the midpoint, and the maximum value of the leading edge slope can be derived when the second derivative is equal to zero. The model of echo waveform [19,28] can be expressed as,

(1)

where

${\it {v}}={\it {a}}{[(t}-{t}_{0}{)}-{\frac {a}{2}}{\sigma }_{c}^{2}{]}$

${\it {u}}={\frac {{(t}-{t}_{0}{)}-{a}\times {\sigma }_{c}^{2}}{{\sqrt {2}}{\sigma }_{c}}}$

${\it {a}}={\it {\alpha }}-{\frac {\beta ^{2}}{4}}$

${\alpha }={\frac {ln4}{sin^{2}(\theta /2)}}\times {\frac {c}{h}}\times {\frac {1}{1+h/R}}\times cos(2\xi )$

${\it {\beta }}={\frac {ln4}{sin^{2}(\theta /2)}}\times {\sqrt {{\frac {c}{h}}\times {\frac {1}{1+h/R}}}}\times {sin(2\xi )}$

$A_{\it {p}}={\frac {{\it {A}}_{\it {0}}}{2}}{exp(-}{\frac {4}{\gamma }}{sin}^{2}{\xi )}$

in which $h$ is the height of satellite, $R$ is the radius of the Earth, $c$ is the speed of light in vacuum, $A_{0}$ is the amplitude of waveform, $\theta$ is the antenna beam width of satellite altimeter, $\xi$ is the off-nadir mispointing angle, $t_{0}$ is the time migration with respect to the nominal tracking gate, ${\sigma }_{c}$ is the rise time of the leading edge linked to the significant wave height, $\gamma$ represents the parameter related to the beam width, and $erf(x)$ is the error function.

From Equation (1), the functions of first and second waveform derivative are given as

(2)

(3)

when ${\it {W}}''{(t)}=0$ , the leading edge midpoint $(t_{m})$ where the leading edge slope is maximum can be computed, that is

(4)

For Equation (4), the unknown parameters $t_{0}\,,\sigma _{c}$ need to be solved.

3.2 Midpoint Determination based on the measured waveform

Generally there are three parameters ( ${\it {A}}_{\it {0}},\,{\it {t}}_{\it {0}},\,{\it {\sigma }}_{\it {c}}$ ) that need to be estimated in that there is a strong correlation between the waveform amplitude parameter and the off-nadir mispointing angle parameter [29], and the the off-nadir mispointing angle is usually less than 0.3° [18,19]. These parameters are obtained with the least squares estimator by using the Equation (1) to fit the measured waveform. The error equation is:

(5)

where ${\textstyle {\bf {L}}}$ is a vector that indicates the difference between the measured waveform and the estimated waveform by Equation (1), ${\textstyle {\bf {X}}(dA_{0},dt_{0},d\sigma _{c})}$ is the correction vector of unknown parameters, and ${\textstyle {\bf {A}}}$ is the partial derivative matrix as

{\bf {A}}=\left[{\begin{array}{ccc}{\left.\displaystyle {\frac {\partial {\it {W}}}{\partial {\it {t}}_{\it {0}}}}\right|_{{\it {t}}={1}}}&{\left.\displaystyle {\frac {\partial {W}}{\partial {\sigma }_{c}}}\right|_{{t}={1}}}&{\left.\displaystyle {\frac {\partial {W}}{\partial {A}_{0}}}\right|_{{t}={1}}}\\{\left.\displaystyle {\frac {\partial {W}}{\partial {t}_{0}}}\right|_{{t}={2}}}&{\left.\displaystyle {\frac {\partial {W}}{\partial {\sigma }_{c}}}\right|_{{t}={2}}}&{\left.\displaystyle {\frac {\partial {W}}{\partial {A}_{0}}}\right|_{{t}={2}}}\\{\vdots }&{\vdots }&{\vdots }\\{\left.\displaystyle {\frac {\partial {W}}{\partial {t}_{0}}}\right|_{{t}={n}}}&{\left.\displaystyle {\frac {\partial {W}}{\partial {\sigma }_{c}}}\right|_{{t}={n}}}&{\left.\displaystyle {\frac {\partial {W}}{\partial {A}_{0}}}\right|_{{t}={n}}}\end{array}}\right]

(6)

in which the three partial derivatives of the unknown parameter are as following:

{\frac {\partial {\it {W}}}{\partial {\it {t}}_{\it {0}}}}={\frac {{\it {A}}_{\it {0}}}{2}}{exp(-}{\frac {4}{\gamma }}{sin}^{2}{\xi )exp(}-{v)}\left\{-\left[{1}+{erf(u)}\right]{\frac {\partial {v}}{\partial {t}_{0}}}+{\frac {2}{\sqrt {\pi }}}{exp(}-{u}^{2}{)}{\frac {\partial {u}}{\partial {t}_{0}}}\right\}

(7)

{\frac {\partial {W}}{\partial {\sigma }_{c}}}={\frac {{A}_{0}}{2}}{exp(-}{\frac {4}{\gamma }}{sin}^{2}{\xi )exp(}-{v)}\left\{-\left[{1}+{erf(u)}\right]{\frac {\partial {v}}{\partial {\sigma }_{c}}}+{\frac {2}{\sqrt {\pi }}}{exp(}-{u}^{2}{)}{\frac {\partial {u}}{\partial {\sigma }_{c}}}\right\}

(8)

(9)

Due to the waveform samples are decorrelation between the range gates [27,30], these unknown parameters are estimated with the least squares estimator as:

(10)

The initial value will affect parameters estimation. The initial value of unknown parameters are determined by using Off-Center of Gravity (OCOG) algorithm [31]. The unknown parameters are estimated until iterative convergence. The convergence criterion is based on the merit function ${\textstyle {\boldsymbol {\chi }}^{\boldsymbol {2}}}$ defined by:

(11)

where ${\textstyle {\boldsymbol {L}}_{\boldsymbol {i}}}$ is the difference between the estimated waveform and the measured waveform.

The leading edge midpoint is computed via Equation (4). This leading edge midpoint obtained by this way is called the first wave derivative retracker (FWDR) in this paper. However, the midpoint is only determined by the parameter ${\textstyle {t}_{0}}$ [27], is called as MLE3 and MLE4 retracker. Our main improvement is that the leading edge midpoint is determined by two parameters ( ${\textstyle {t}_{0}}$ , ${\textstyle {\sigma }_{c}^{}}$ ) instead of one ( ${\textstyle {t}_{0}}$ ).

The leading edge midpoint determined based on the function-fitting method is possbile not on the measured waveform. In order to more accurately determine the leading edge midpoint on the measured waveform, combining the advantages of the empirical statistical retracker (similar to Threshold 50% method), the leading edge midpoint is redetermined. The leading edge midpoint power value is obtained by Equation (1), which is linearly interpolated to the adjacent power value of the leading edge of measured waveform to redetermine the midpoint. This leading edge midpoint obtained by this way is called the first leading edge interpolation retracker (FLEIR), that is:

(12)

where ${\textstyle {t}_{m}}$ is the re-determined leading edge midpoint, ${\textstyle {T}}$ is the midpoint power from the estimated waveform by Equation (1), ${\textstyle {\hat {n}}}$ the first gate (sampling) position beyond the theoretical midpoint power, and ${\textstyle {W}_{\hat {n}}}$ and ${\textstyle {W}_{{\hat {n}}{-}{1}}}$ are the measured waveform power values respectively.

3.3 Midpoint determination the based on the first-order difference quotient of waveform

The leading edge midpoint is determined based on the first-order difference quotient of waveform. The waveform is actually a discrete set of echo power on the sampling interval of the altimeter. The power of each gate is composed of the echo signal of reflective surface and noise. The noise of adjacent sampling gate is similar, and can be reduced by the first-order difference quotient. Thus, the unknown parameters can be estimated by using the Equation (2) to fit the first-order difference quotient. Then, the leading edge midpoint can be computed with Equation (4).

The first-order difference quotient of waveform, ${\textstyle {W}^{'}(t_{k+1/2})}$ , can be computed as,

(13)

where ${\textstyle {W}{(t}_{{k}+{1}}{)}}$ and ${\textstyle {W}{(t}_{k}{)}}$ are the echo powers corresponding to gate ${\textstyle {k}+{1}}$ and ${\textstyle {k}}$ respectively, while ${\textstyle {\Delta }{t}}$ is the sampling interval. Equation (13) indicates that the ${\textstyle {W}^{'}(t_{k+1/2})}$ is correlated between different gates based on the covariance propagation law.

Similarly, these unknown parameters are estimated with the least squares method. The error equation is:

(14)

where ${\textstyle {L}_{1}}$ is a vector that indicates the difference between the estimated by Equation (2) and the first order difference quotient of waveform, ${\textstyle {\boldsymbol {X}}}$ ( ${\textstyle {d}{A}_{0}}$ , ${\textstyle {d}{t}_{0}}$ , ${\textstyle {d}{\sigma }_{c}}$ ) is the correction vector of unknown parameters, and ${\textstyle {\boldsymbol {A}}_{1}}$ is the partial derivative matrix as

{\boldsymbol {A}}_{1}=\left[{\begin{array}{ccc}{\left.{\frac {\partial {W}^{'}}{\partial {t}_{0}}}\right|_{{t}={1}}}&{\left.{\frac {\partial {W}^{'}}{\partial {\sigma }_{c}}}\right|_{{t}={1}}}&{\left.{\frac {\partial {W}^{'}}{\partial {A}_{0}}}\right|_{{t}={1}}}\\{\left.{\frac {\partial {W}^{'}}{\partial {t}_{0}}}\right|_{{t}={2}}}&{\left.{\frac {\partial {W}^{'}}{\partial {\sigma }_{c}}}\right|_{{t}={2}}}&{\left.{\frac {\partial {W}^{'}}{\partial {A}_{0}}}\right|_{{t}={2}}}\\{\vdots }&{\vdots }&{\vdots }\\{\left.{\frac {\partial {W}^{'}}{\partial {t}_{0}}}\right|_{{t}={n}}}&{\left.{\frac {\partial {W}^{'}}{\partial {\sigma }_{c}}}\right|_{{t}={n}}}&{\left.{\frac {\partial {W}^{'}}{\partial {A}_{0}}}\right|_{{t}={n}}}\end{array}}\right]

(15)

The three partial derivatives of the unknown parameters based on the function of first derivatives are formulated as,

{\frac {\partial {W}^{'}}{\partial {t}_{0}}}={\frac {{A}_{0}}{2}}{exp(-}{\frac {4}{\gamma }}{sin}^{2}{\xi )exp(}-{v)}\left\{\left[-{a}\left[{1}+{erf(u)}\right]+{\frac {\sqrt {2}}{{\sqrt {\pi }}{\sigma }_{c}}}{exp(}-{u}^{2}{)}\right]{\frac {-\partial {v}}{\partial {t}_{0}}}\right.+

(16)

{\frac {\partial {W}^{'}}{\partial {\sigma }_{c}}}={\frac {{A}_{0}}{2}}{exp(-}{\frac {4}{\gamma }}{sin}^{2}{\xi )exp(}-{v)}\left\{\left[-{a}\left[{1}+{erf(u)}\right]+{\frac {\sqrt {2}}{{\sqrt {\pi }}{\sigma }_{c}}}{exp(}-{u}^{2}{)}\right]{\frac {-\partial {v}}{\partial {\sigma }_{c}}}+\right.

(17)

(18)

Due to the difference quotient ${\textstyle {W}^{'}(t_{k+1/2})}$ is computed by Equation (13), it is correlated between different gates based on the covariance propagation law. The unknown parameters are estimated with the least squares estimator as:

(19)

where ${\textstyle {P}}$ is the weight matrix as

{\boldsymbol {P}}=\left[{\begin{array}{ccccc}{2}&{-{1}}&{0}&{\cdots }&{0}\\{-{1}}&{2}&{-{1}}&{\ddots }&{0}\\{0}&{-{1}}&{2}&{\ddots }&{0}\\{\vdots }&{\ddots }&{\ddots }&{\ddots }&{-{1}}\\{0}&{\cdots }&{0}&{-{1}}&{2}\end{array}}\right]_{{(}{n}-{1)}\times {(n}-{1)}}^{-1}

(20)

The initial values of the unknown parameters are also determined by the OCOG algorithm. The unknown parameters are estimated until iterative convergence (the convergence criterion is similar to Equation (11)). The waveform leading edge midpoint is computed via Equation (4). The midpoint obtained by this way is called the second wave derivative retracker (SWDR) in this paper.

Similar to Equation (12), the leading edge midpoint is redetermined. The leading edge midpoint power value is obtained by Equation (1), which is linearly interpolated to the adjacent power value of the leading edge of measured waveform to redetermine the midpoint. The midpoint obtained by this way is called the second leading edge interpolation retracker (SLEIR).

A flow chart of the new waveform retracking is shown in Figure 2.

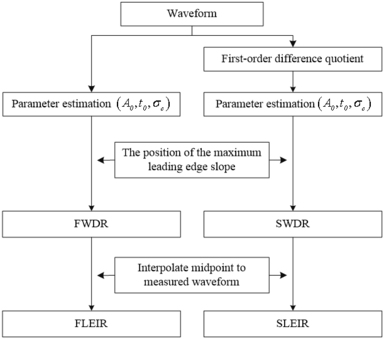
Figure 2. Flow chart of waveform retracking based on waveform derivative

4. Experiment Results and Analysis

4.1 Comparison with crossover discrepancies of SSHs

The crossover is the intersection of two tracks between ascending pass and descending pass. The crossover discrepancy of SSHs is an evaluation criterion of waveform retracking method in the open ocean. To obtain the statistical results, we define SSH as given by

{\begin{array}{l}{{SSH}={H}_{alt}-\left({Tracker}+{Corr}_{doppler}+{Corr}_{model}+{Corr}_{system\_bias}+{Corr}_{Dry}+\right.{Corr}_{Wet}}\\{+{Corr}{}_{Iono}+{Corr}_{SSB}+{Corr}_{Ib}+{Corr}_{hf}+{H}_{ocean}+{H}_{solid}+{H}_{pole}+\left.{R}_{retracking}\right)}\end{array}}

(21)

where ${\textstyle {H}_{alt}}$ is the altitude of Jason-2 satellite, ${\textstyle {Tracker}}$ is the range between satellite and reflective surface (partial instrumental corrections included, i.e. distance antenna-COG, USO drift correction, internal path correction), ${\textstyle {Corr}_{doppler}}$ is the Doppler correction, ${\textstyle {Corr}_{model}}$ is the modeled instrumental correction, ${\textstyle {Corr}_{system\_bias}}$ is the system bias of instrument, ${\textstyle {Corr}_{Dry}}$ is the dry tropospheric correction which is calculated from the atmospheric pressure and tide published by the European Centre for Medium-range Weather Forecasts (ECMWF), ${\textstyle {Corr}_{Wet}}$ is the wet tropospheric correction, which is calculated from the data measured by the microwave radiometer carried by the satellite, ${\textstyle {Corr}{}_{Iono}}$ is the ionospheric delay corrected using Dual-frequency, ${\textstyle {Corr}{}_{SSB}}$ is the sea state bias correction, which is calculated by empirical fitting of significant wave height and wind speed, ${\textstyle {Corr}{}_{Ib}}$ (inverted barometer correction) and ${\textstyle {Corr}_{hf}}$ (high frequency atmospheric pressure loading correction) are the dynamic atmospheric corrections, ${\textstyle {H}_{ocean}}$ is the geocentric ocean tide height correction, obtained by GOT4.10 model, ${\textstyle {H}_{solid}}$ is the solid earth tide height correction, and ${\textstyle {H}_{pole}}$ is the pole tide height correction. These above corrections are available in the SGDRs.

The range correction ${\textstyle {R}_{retracking}}$ of waveform retracking is given by

(22)

where ${\textstyle {t}_{m}}$ is the leading edge midpoint, ${\textstyle {\tau }}$ the nominal tracking gate ( ${\textstyle {\tau }}$ =32 gate of Jason-2 altimeter wavefrom), ${\textstyle {\Delta }{G}_{a}}$ the sampling interval of a gate (1 gate=3.125 ns of Jason-2 altimeter).

The waveform data of cycles 001 to 200 are processed. For assessing the performance of the new retracker, we compared the retracked SSH from Threshold 50%, OCOG and $5-\beta$ retrackers, as well as the Ice-1 and MLE4 (or Ocean) retrackers from SGDRs. Also, we obtained the ALES [19] retracked SSH data (http://openadb.dgfi.tum.de/), which is widely recognized as a high-precision SSH products [22,32]. The retracked SSHs and the crossover discrepancies of SSHs in each cycle were computed. Some data of cycles are missing (Such as cycles 174, 175, 190, 191), and the gross error ( ${\textstyle >1}$ m) of the crossover discrepancies of SSHs are removed. There are 1502 crossover discrepancies in total. The statistics of crossover discrepancies of SSHs obtained by several retrackers are listed in Table 1. The Unretracked represents the raw SSHs without waveform retracking.

By analyzing the RMS of the crossover discrepancies of SSHs, it is found that the results of several retracking methods are smaller than unretracked results, indicating that the waveform retracking can reduce the RMS of crossover discrepancies of SSH and improve the quality of satellite altimeter data. The RMSs obtained by FWDR, FLEIR, SWDR and SLEIR are 0.108 m, 0.107 m, 0.114 m and 0.119 m, which are smaller than 0.124 m, 0.177 m and 0.121 m obtained by Threshold 50%, OCOG and ${\textstyle 5-\beta }$ methods, respectively, indicating that the new methods can get more accurate results than the common methods in this region. The RMSs obtained by new mthods, which are less than 0.192 m, and 0.112 m obtained by Ice-1 and MLE4 methods from SGDR data, indicating that it can provide more accurate results than SGDRs (retracked SSH by MLE4, Ice-1 retracker) in the open ocean. In addition, the RMSs obtained by FWDR and FLEIR are 0.108 m and 0.107 m, which are smaller than 0.114 m obtained by MLE3 retracker, indicating that the midpoint determined by two parameters ( ${\textstyle {t}_{0}}$ , ${\textstyle {\sigma }_{c}^{}}$ ) is more accurate than one parameter ( ${\textstyle {t}_{0}}$ ).

Table 1. Statistics of crossover discrepancies of SSHs obtained by several retracking methods (Unit: m)

Retracker	MAX	MIN	MEAN	STD	RMS
Unretracked	0.996	-0.805	0.001	0.225	0.225
Threshold(50%)	0.936	-0.714	-0.004	0.124	0.124
OCOG	0.940	-0.981	-0.005	0.177	0.177
${\textstyle 5-\beta }$	0.692	-0.692	-0.007	0.120	0.121
Ice-1	0.783	-0.774	-0.031	0.190	0.192
MLE3	0.716	-0.506	-0.005	0.114	0.114
MLE4	0.773	-0.652	-0.004	0.112	0.112
ALES	0.741	-0.724	-0.002	0.105	0.105
FWDR	0.693	-0.524	-0.003	0.108	0.108
FLEIR	0.696	-0.623	-0.003	0.107	0.107
SWDR	0.740	-0.714	0.000	0.114	0.114
SLEIR	0.772	-0.749	-0.005	0.119	0.119

Furthermore, we comparison with the retracked SSH by ALES retraker. The RMS obtained by FLEIR is 0.107 m, which is slightly smaller than 0.105 m obtained by ALES products. The difference may be caused by different correction models, such as sea state bias correction and ocean tide correction. This also shown that the retracked SSH by new methods is reliable compared with the SSH obtained by ALES products.

4.2 Comparison with geoid heights

In order to contrast and analyze the retracked SSHs, the regional geoid heights are derived from the Earth Gravity Field Model EGM2008 [33] up to degree 2160 (Http://icgem.gfz-postdam.de/ICGEM). The performance of retracked SSHs can be assessed in comparison with geoid heights [7,34].

If the retracked SSHs did not resemble the geoid heights, then the retracked SSHs was considered to be not valid, even if it had been able to correct the errors of SSH [6,9,35]. The correlation coefficient and improvement of percentage (IMP) of the difference between retracked SSHs and geoid heights are used to analyze the quality of retracked SSHs. It is widely accepted that the higher the IMP value is, the better the retracked result is. The IMP can be computed as

(23)

where ${\textstyle {IMP}}$ is the improvement percentage, ${\textstyle {\delta }_{raw}}$ is the STD of the difference between geoid heights and SSHs without waveform retracking correction. ${\textstyle {\delta }_{retracked}}$ is the STD of the difference between geoid heights and altimetry-derived SSHs with waveform retracking correction.

Figure 3 shows retracked SSHs and geoid heights of by several methods. For the image to be clearly distinguishable, we only show results from the Ice-1, MLE4, Threshold 50% and FLEIR methods.

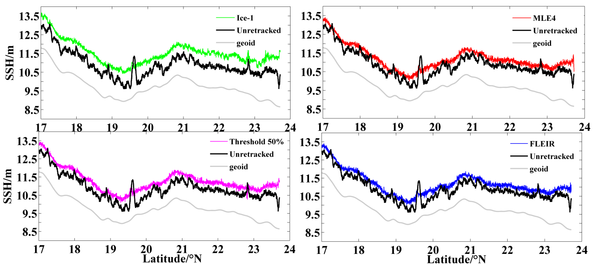
Figure 3. Comparison of the Ice-1, MLE4, Threshold 50%, FLEIR retracked SSHs and geoid heights

Table 2 gives the statistical results of the IMP and correlation coefficient of the differences between retracked SSHs (cycle010pass229) and geoid heights. The cycle is selected randomly, and using other cycles will not alter our findings.

Table 2. Statistics of the differences between retracked SSHs and geoid heights (Unit: m)

Retracker	MAX	MIN	MEAN	STD	IMP/（%）	Correlation coefficient
Unretracked	2.118	0.388	1.149	0.265	—	0.921
Threshold（50%）	2.799	0.913	1.551	0.222	16.2%	0.940
OCOG	3.096	0.517	2.075	0.273	-3.0%	0.920
Βeta-5	3.104	0.906	1.461	0.226	14.7%	0.939
Ice-1	3.144	1.328	1.777	0.239	9.8%	0.930
MLE4	2.775	0.959	1.463	0.225	15.1%	0.939
FWDR	2.700	0.928	1.456	0.217	18.1%	0.944
FLEIR	2.601	0.946	1.456	0.216	18.5%	0.944
SWDR	2.533	0.921	1.480	0.219	17.4%	0.943
SLEIR	2.739	0.909	1.458	0.226	14.7%	0.939

Table 2 provides a summary of results, where the STD (0.265 m) of the difference is large, which indicates that the unretracked SSH has poor smoothness and fluctuation. After waveform retracking, the STD is reduced, and the smoothness of SSH is improved, which eliminated large abrupt changes and maintained good smoothness of SSH. The IMP and correlation coefficient obtained by new methods are better than the results of the common methods. The IMPs obtained by FWDR, FLEIR, SWDR, and SLEIR are 18.1%, 18.5%, 17.4% and 14.7%, respectively, while the IMPs obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1, and MLE4 methods are 16.2%, -3.0%, 14.7%, 9.8% and 15.1%. The correlation coefficients obtained by FWDR, FLEIR, SWDR and SLEIR are 0.944, 0.944, 0.943 and 0.939 respectively, while the value obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 are 0.940, 0.920, 0.939, 0.930 and 0.939.

Therefore, it is concluded that the new proposed retracking methods in this paper are reliable, and exhibit better performance than the common retrackers.

4.3 Comparsion with tide gauge records

In addition, we compared the retracked SSH using several retracking methods with the tide gauge records in the coastal area. As the tide gauge records are not corrected for tidal and dynamic atmospheric effects, we also do not apply these corrections to the altimeter data by employing [23,36]

{\begin{array}{l}{{SSH}={H}_{alt}-\left({Tracker}+{Corr}_{doppler}+{Corr}_{model}+{Corr}_{system\_bias}+{Corr}_{Dry}+\right.}\\{+{Corr}_{Wet}+{Corr}{}_{Iono}+{Corr}_{SSB}++{H}_{load}+{H}_{solid}+{H}_{pole}+\left.{R}_{retracking}\right)}\end{array}}

(24)

where ${\textstyle {H}_{load}}$ is the solid earth tide correction; the other corrections is the same as Equation (21), and all corrections are available in the SGDRs.

The hourly tide gauge records were interpolated to the time of the altimeter measurement. To avoid possible discrepancy datum of both altimetry-derived SSHs and tide gauge records, the temporal mean is removed from each time series, referring to as height anomaly [15]. For assessed the performance of the retracked SSH in the coastal area, we have categorized the altimetry-derived SSH to two spatial intervasl: namely 10-20 km and 0-10 km away from coastline, correspond to cases 1 and 2, respectively. Finally, the correlation coefficient and STD of the difference between height anomaly from several retrackers and tide gauge records were computed.

In the near QBTG, the height anomaly from several retrackers and tide gauge records in cases 1 and 2 are shown in Figures 4 and 5, respectively. For the image to be clearly distinguishable, we only shown results obtained by the Ice-1, MLE4, Threshold 50% and FLEIR methods.

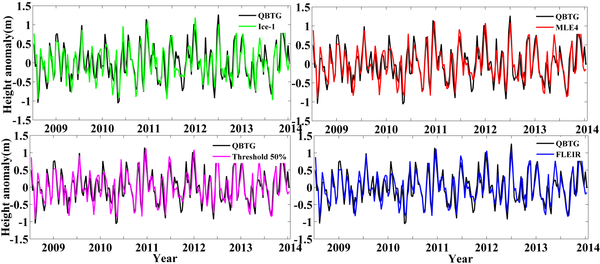
Figure 4. Height anomaly variation obtained by the Ice-1, MLE4, Threshold 50% and FLEIR retrackers and QBTG records in case 1

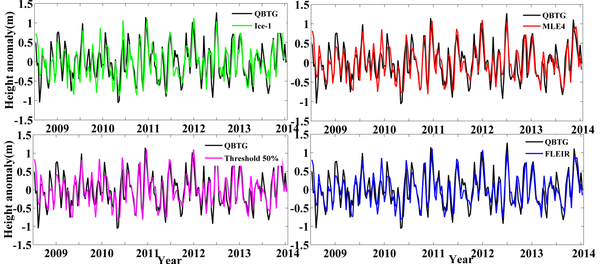
Figure 5. Height anomaly variation obtained by the Ice-1, MLE4, Threshold 50%, FLEIR retrackers and QBTG records in case 2

Table 3 gives the STD and correlation coefficient of the height anomaly between the retracked SSH and QBTG records in cases 1 and 2.

Table 3. Statistical results of height anomaly between the retracked SSH and QBTG records

Retracker	Case 1		Case 2
Retracker	STD (m)	Correlation coefficient	STD (m)	Correlation coefficient
Unretracked	0.302	0.789	0.370	0.666
Threshold (50%)	0.248	0.854	0.272	0.820
OCOG	0.271	0.813	0.334	0.729
${\textstyle 5-\beta }$	0.237	0.858	0.293	0.786
Ice-1	0.262	0.837	0.303	0.778
MLE4	0.242	0.860	0.278	0.809
FWDR	0.232	0.870	0.271	0.817
FLEIR	0.236	0.867	0.269	0.821
SWDR	0.232	0.871	0.269	0.820
SLEIR	0.237	0.867	0.277	0.811

Table 3 in which the STD of the difference of height anomaly with waveform retracking is smaller than the unretracked and the correlation coefficient is higher than the result of unretracked, shows that each retracker method improves the accuracy of SSH in cases 1 and 2. There is a high correlation coefficient (～0.8) of the height anomaly between retracked SSH and QBTG records in case 1. The STD obtained by MLE4 is 0.242 m, which is smaller than 0.248 m, 0.271 m, 0.245 m, and 0.262 m obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ and Ice-1 methods in case 1. The STDs obtained by FDWR, FLEIR, SDWR and SLEIR are 0.232 m, 0.236 m, 0.232 m and 0.237 m respectively, which are also smaller than MLE4 method. The correlation coefficient obtained by MLE4 is 0.860, which is higher than 0.854, 0.813, 0.858 and 0.837 obtained by Threshold (50%), OCOG, ${\textstyle 5-\beta }$ and Ice-1 methods in case 1. The correlation coefficients obtained by FDWR, FLEIR, SDWR and SLEIR are 0.870, 0.867, 0.871 and 0.867, which are also higher than MLE4 method.

The STDs and correlation coefficients obtained by FDWR, FLEIR, SDWR and SLEIR are the same as that of Threshold 50%, which are better than the result of OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods in case 2. The STDs obtained by FDWR, FLEIR, SDWRand SLEIR are 0.271 m, 0.269 m, 0.269 m, and 0.277 m, while the STDs obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods are 0.272 m, 0.334 m, 0.293 m, 0.303 m and 0.278 m. The correlation coefficients obtained by FDWR, FLEIR, SDWR and SLEIR are 0.817, 0.821, 0.820 and 0.811, while the correlation coefficients obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods are 0.820, 0.729, 0.786, 0.778, and 0.809. In addition, the STD and correlation coefficient obtained by FLEIR are better than the result of FDWR in cases 1 and 2.

In the near KaohTG, the height anomaly from several retrackers and KaohTG records are shown in Figures 6 and 7, respectively. Similarly, we only shown the results obtained by the Ice-1, MLE4, Threshold 50% and FLEIR methods.

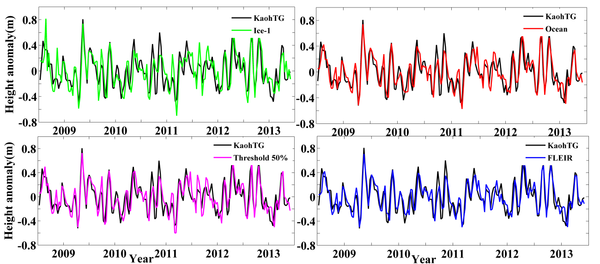
Figure 6. Height anomaly variation obtained by the Ice-1, MLE4, Threshold 50%, FLEIR retrackers and KaohTG records in case 1

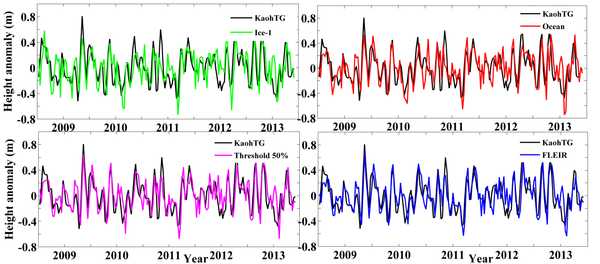
Figure 7. Height anomaly variation obtained by Ice-1, MLE4, Threshold 50%, FLEIR retrackers and KaohTG records in case 2

Table 4 gives the STD and correlation coefficient of the height anomaly between the retracked SSH and KaohTG records in cases 1 and 2.

Table 4. Statistical results of height anomaly between the retracked SSH and KaohTG records

Retracker	Case 1		Case 2
Retracker	STD (m)	Correlation coefficient	STD (m)	Correlation coefficient
Unretracked	0.227	0.626	0.248	0.514
Threshold (50%)	0.153	0.819	0.195	0.696
OCOG	0.234	0.623	0.268	0.407
${\textstyle 5-\beta }$	0.149	0.823	0.208	0.638
Ice-1	0.188	0.740	0.239	0.560
MLE4	0.141	0.841	0.220	0.632
FWDR	0.145	0.828	0.198	0.679
FLEIR	0.135	0.851	0.191	0.711
SWDR	0.140	0.838	0.183	0.716
SLEIR	0.143	0.833	0.201	0.685

Table 4 shows that each retracker methods improves the accuracy of SSH in cases 1 and 2. There is a small STD and high correlation coefficient (～0.8) of the height anomaly between retracked SSH and tide gauge (KaohTG) distance from coastline 10-20 km. The STD obtained by MLE4 is 0.141 m, which is smaller than 0.153 m, 0.234 m, 0.149 m, 0.188 m obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ and Ice-1 methods in case 1. The STDs obtained by FDWR, FLEIR, SDWR and SLEIR are 0.145 m, 0.135 m, 0.140 m and 0.143 m, which are smaller than MLE4 method. The correlation coefficient obtained by MLE4 is 0.841, which is higher than 0.819, 0.623, 0.823 and 0.740 obtained by Threshold (50%), OCOG, ${\textstyle 5-\beta }$ and Ice-1 methods in case 1. The correlation coefficients obtained by FDWR, FLEIR, SDWR and SLEIR are 0.828, 0.851, 0.838 and 0.833, which are higher than MLE4 method.

The STDs and correlation coefficients obtained by FDWR, FLEIR, SDWR and SLEIR are better than the result of Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods in case 2. The STDs obtained by FDWR, FLEIR, SDWR and SLEIR are 0.198 m, 0.191 m, 0.183 m and 0.201 m, while the STDs obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods are 0.195 m, 0.268 m, 0.208 m, 0.239 m and 0.220 m. The correlation coefficients obtained by FDWR, FLEIR, SDWR and SLEIR are 0.679, 0.711, 0.716, and 0.685, while the correlation coefficients obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods are 0.696, 0.407, 0.630, 0.560 and 0.632. Also, the STD and correlation coefficient obtained by FLEIR are better than the result of FDWR in case 1 and 2.

Through comparison with two tide gauges, we reached the following conclusions. The performance of MLE4 method is better than Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 methods in case 1, and the performance of Threshold 50% method is better than OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods in case 2. But, the new methods have a better performance than Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods in cases 1 and 2. The STD and correlation coefficient obtained by FLEIR are better than the result of FDWR, indicating that the re-determined midpoint is more accurate through interpolating the estimated lead edge midpoint on the measured waveform.

Therefore, the accuracy of the new method is better than that of the common retrackers. The new method has been validated in the coastal area.

5. Conclusion

In order to deal with the disturbed satellite radar altimeter echo waveform in the open ocean and coastal area, a retracking method based on waveform derivative is proposed in this paper. The leading edge midpoint is determined by the second derivative zero point, and combining the advantages of function-fitting and empirical statistical method, the leading edge midpoint is redetermined by interpolating the theoretical power value of the estimated midpoint to the leading edge of measured waveform. Four new waveform retracking results are given.

By processing the waveforms from the Jason-2 SGDRs, we computed the retracked SSHs. In the open ocean, through comparison with the RMS of crossover discrepancies of SSH, the RMSs obtained by FWDR, FLEIR, SWDR, SLEIR are 0.108 m, 0.107 m, 0.114 m, and 0.119 m respectively, which are smaller than 0.124 m, 0.177 m, 0.121 m, 0.192 m, and 0.112 obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods. Further, through comparison with the geoid heights, the IMP and correlation coefficient of the differences between retracked SSHs with respect to geoid heights were computed. The IMP and correlation coefficient obtained by new retracking methods are better than the result of common retracker methods. The IMPs obtained by FWDR, FLEIR, SWDR, and SLEIR are 18.1%, 18.5%, 17.4%, and 14.7%, while the IMPs obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods are 16.2%, 14.7%, -3.0%, 9.8% and 15.1%. The correlation coefficients obtained by FWDR, FLEIR, SWDR, and SLEIR are 0.944, 0.944, 0.943, and 0.939, while the correlation coefficients obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods are 0.940, 0.920, 0.939, 0.930 and 0.939.

In addtion, through comparison with tide gauge records, the STD and correlation coefficient of the height anomaly between the retracked SSH and tide gauge records were computed. The STDs obtained by the new method are 0.135-0.269 m, which are better than 0.153-0.272 m, 0.234-0.334 m, 0.149-0.293 m, 0.188-0.303 m, and 0.141-0.278 m obtained by Threshold 50%, OCOG, ${\textstyle 5-\beta }$ , Ice-1 and MLE4 methods in cases 1 and 2. Both in the open ocean and coastal area, the performance of the new method is better than the Threshold 50%, OCOG, ${\textstyle 5-\beta }$ methods as well as the Ice-1 and MLE4 retracker from SGDRs.

Therefore, the new method has been validated from Jason-2 SGDRs, it can recover more reliable SSH and improve the SGDRs quality both in the open ocean and coastal area. For the improvement of the quanlity of satellite altimeter data, especially the processing of waveform data, it also provides a new way for studying waveform retracking.

Acknowledgments

We are very grateful to AVISO for providing the SGDRs, and the University of Hawaii for providing the tide gauge records. This research was funded by National Natural Science Foundation of China (Grant Nos. 41774001, 41374009, 41874091) and SDUST Research Fund (Grant No. 2014TDJH101).

References

[1] Fu L.L., Cazenave A. Satellite altimetry and earth sciences: A handbook of techniques and applications. California, San Diego Academic Press, 373-375, 2001.

[2] Guo J.Y., Wang J.B., Hu Z.B., Hwang C.W., Chen C.F., Gao Y.G.. Temporal-spatial variations of sea level over Chinese seas derived from altimeter data of TOPEX/Poseidon, Jason-1 and Jason-2 from 1993 to 2012. Chinese Journal of Geophysics, 58(9):3103-3120, 2015.

[3] Hsiao Y.S., Hwang C., Cheng Y.S., Chen L.C., Hsu H.J., Tsai J.H., Liu C.L., Wang C.C., Kao Y.C. High-resolution depth and coastline over major atolls of South China Sea from satellite altimetry and imagery. Remote Sensing of Environment, 176:69-83, 2016.

[4] Stammer D., Cazenave A. Satellite altimetry over oceans and land surfaces. Florida: Taylor & Francis Boca Raton, CRC Press, 670 pp., 2017.

[5] Zhu C., Guo J., Hwang C., Gao J., Yuan J., Liu X. How HY-2A/GM altimeter performs in marine gravity derivation: assessment in the South China Sea. Geophysical Journal International, 219:1056-1064, 2019.

[6] Gómez-Enri J., González C. J., Passaro M., Vignudelli S., Álvarez O., Cipollini P., Mañanes R., Bruno M., Lopez-Carmona P., Izquierdo A. Wind-induced cross-strait sea level variability in the Strait of Gibraltar from coastal altimetry and in-situ measurements. Remote Sensing of Environment, 221:596-608, 2019.

[7] Hwang C., Guo J., Deng X., Hsu H.Y., Liu Y. Coastal gravity anomalies from retracked Geosat/GM altimetry: Improvement, limitation and the role of airborne gravity data. Journal of Geodesy, 80(4):204-216, 2006.

[8] Guo J.Y., Gao Y.G., Hwang C.W., Sun J.L. A multi-subwaveform parametric retracker of the radar satellite altimetric waveform and recovery of gravity anomalies over coastal oceans. Science China Earth Sciences, 53(4):610-616, 2010.

[9] Huang Z., Wang H., Luo Z., Shum C., Tseng K.H., Zhong B. Improving Jason-2 sea surface heights within 10 km offshore by retracking decontaminated waveforms. Remote Sensing, 9(10):1077, 2017.

[10] Cipollini P., Calafat F.M., Jevrejeva S., Melet A., Prandi P. Monitoring sea level in the coastal zone with satellite altimetry and tide gauges. Surveys in Geophysics, 38(1):33-57, 2017.

[11] Lyszkowicz A.B., Bernatowicz A. Current state of art of satellite altimetry. Geodesy and Cartography, 66(2):259-270, 2017.

[12] Anzenhofer M., Shum C.K., Renstch M. Coastal altimetry and applications. Dept Geod Sci and Surveying, Ohio State University, Columbus, 1999.

[13] Vignudelli S., Kostianoy A.G., Cipollini P., Benveniste J. Coastal altimetry. Berlin Heidelberg: Springer-Verlag, 2011.

[14] Davis C.H. A robust threshold retracking algorithm for measuring ice-sheet surface elevation change from satellite radar altimeters. IEEE Transactions on Geoscience & Remote Sensing, 35(4):974-979, 1997.

[15] Martin T.V., Zwally H.J., Brenner A.C., Bindschadler R.A. Analysis and retracking of continental ice sheet radar altimeter waveforms. Journal of Geophysical Research, 88(C3):1608-1616, 1983.

[16] Guo J., Hwang C., Chang X., Liu Y. Improved threshold retracker for satellite altimeter waveform retracking over coastal sea. Progress in Natural Science, 16(7):732-738, 2006.

[17] Guo J.Y., Gao Y.G., Chang X.T., Hwang C.W. Optimal threshold algorithm of EnviSat waveform retracking over coastal sea. Chinese Journal of Geophysics, 53(4):807-814, 2010b.

[18] Idris N.H., Deng X. The retracking technique on multi-peak and quasi-specular waveforms for Jason-1 and Jason-2 missions near the coast. Marine Geodesy, 35(sup1):217-237, 2012.

[19] Passaro M., Cipollini P., Vignudelli S., Quartly G.D., Snaith H.M. ALES: A multi-mission adaptive subwaveform retracker for coastal and open ocean altimetry. Remote Sensing of Environment, 145:173-189, 2014.

[20] Tseng K.H., Shum C.K., Yi Y., Emery W.J., Kuo C.Y., Lee H., Wang H.H. The improved retrieval of coastal sea surface heights by retracking modified radar altimetry waveforms. IEEE Transactions on Geoscience & Remote Sensing, 52(2):991-1001, 2013.

[21] Guo J., Chang X., Gao Y., Sun J., Hwang C. Lake level variations monitored with satellite altimetry waveform retracking. IEEE Journal of Selected Topics in Applied Earth Observations & Remote Sensing, 2(2):80-86, 2009.

[22] Peng F., Deng X. A new retracking technique for Brown peaky altimetric waveforms. Marine Geodesy, 41(2):99-125, 2017.

[23] Arabsahebi R., Voosoghi B., Tourian M.J. The inflection-point retracking algorithm: improved Jason-2 sea surface heights in the Strait of Hormuz. Marine Geodesy, 41(4):331-352, 2018.

[24] Brown G. The average impulse responce of a rough surface and its applications. IEEE Journal of Oceanic Engineering, 2(1):67-74, 1977.

[25] Dumont J.P., Rosmorduc V., Picot N., Bronner E., Desai S., Bonekamp H. OSTM/Jason-2 products Hand-book. available online http://www.aviso.altimetry.fr/fileadmin/documents/data/tools/hdbk_j2.pdf, 2011.

[26] Deng X., Featherstone W.E., Hwang C., Berry P.A.M. Estimation of contamination of ERS-2 and POSEIDON satellite radar altimetry close to the coasts of Australia. Marine Geodesy, 25(4):249-271, 2002.

[27] Benveniste J., Cipollini P., Vignudelli S. Challenges and opportunities for coastal altimetry. Eos Trans. AGU, 98, 2017.

[28] Amarouche L., Thibaut P., Zanife O.Z., Dumont J.P., Vincent P., Steunou N. Improving the Jason-1 ground retracking to better account for attitude effects. Marine Geodesy, 27(1-2):171-197, 2004.

[29] Quartly G.D. Optimizing σ0 information from the Jason-2 altimeter. IEEE Geoscience & Remote Sensing Letters, 6(3):398-402, 2009.

[30] Gommenginger C., Thibaut P., Fenoglio-Marc L., Quartly G., Deng X., Gomez-Enri J., Challenor P., Gao Y. Retracking altimeter waveforms near coasts. In: Vignudelli S, Kostianoy A, Cipollini P, Benveniste J. Coastal altimetry. Berlin Heidelberg: Springer-Verlag, 61-102, 2011.

[31] Wingham D.J., Rapley C.G., Griffiths H. New techniques in satellite altimeter tracking systems. In Proceedings of the IGARSS’86 Symposium, Zurich, Switzerland, 8-11 September, 1986.

[32] Xu X.Y., Birol F., Cazenave A. Evaluation of coastal sea level offshore Hong Kong from Jason-2 altimetry. Remote Sensing, 10(2):282, 2018.

[33] Pavlis N.K., Holmes S.A., Kenyon S.C., Factor J.K. The development and evaluation of the Earth Gravitational Model 2008(EGM2008). Journal of Geophysical Research, 117:B04406, 2012.

[34] Khaki M., Forootan E., Sharifi M.A. Satellite radar altimetry waveform retracking over the Caspian Sea. International Journal of Remote Sensing, 35(17):6329-6356, 2014.

[35] Lee H., Shum C.K., Emery W., Calmant S., Deng X., Kuo C.Y., Roesler C., Yi Y. Validation of Jason-2 altimeter data by waveform retracking over California coastal ocean. Marine Geodesy, 33(sup1):304-316, 2010.

[36] Fenoglio-Marc L., Dinardo S., Scharroo R., Roland A., Dutour Sikiric M., Lucas B., Becker M., Benveniste J., Weiss R. The German Bight: a validation of CryoSat-2 altimeter data in SAR mode. Advances in Spach Research, 55(11):2641-2656, 2015.